数据计算 | jjyaoao's Home

以下具体框架来自华中科技大学谭志虎老师，本人根据框架补充自己的一些体会和见解。仅当作学习笔记使用

Target：

定点数的运算
- 定点数的移位运算
  - 算术右移：符号位保持不变，移动数值位
    - 符号位不变，且向右移动
    - x/2 运算需要考虑向 0 舍入的问题
    - 有符号时通常会将符号位累加在最低位后再进行算术右移
  - 逻辑移位：将操作数视为无符号数，全移
    - 不管左移还是右移，都补0
    - 2x 运算在无符号运算时可能会发生溢出
  - 循环移位
    - 带进位标志位CF（大循环）
      - CF参与循环
    - 不带CF（小循环）
      - CF存储最新移出的数字的副本
  - 移位运算实例
  - 考研真题
    - 真题1
- 原码定点数的加减运算（没考过）
  - 符号位不能直接参与运算
  - 加法运算需要“同号求和，异号求差”
  - 减法运算需要“异号求和，同号求差”
  - 求差时还需要先比较大小，然后用大数减去小数
  - 结果的符号选择也相对复杂，运算复杂
- 补码定点数的加减运算
  - 运算公式
    - 补码加法
    - 补码减法
  - 运算规则
    - 操作数采用补码表示，符号位参加运算
    - 运算的结果为补码，符号位的进位位（模）直接丢弃
    - 运算结果就是补码，符号位也是直接运算得到
  - 逻辑实现
    - 对于定点数加减法可以首先利用如下公式实现一位全加器FA，再利用n个全加器串联构成n位串行进位加法器
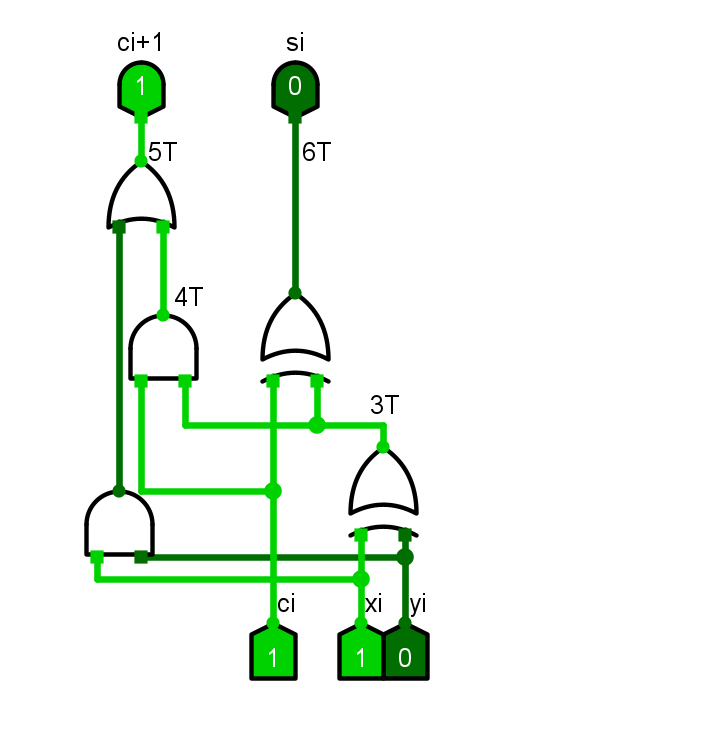
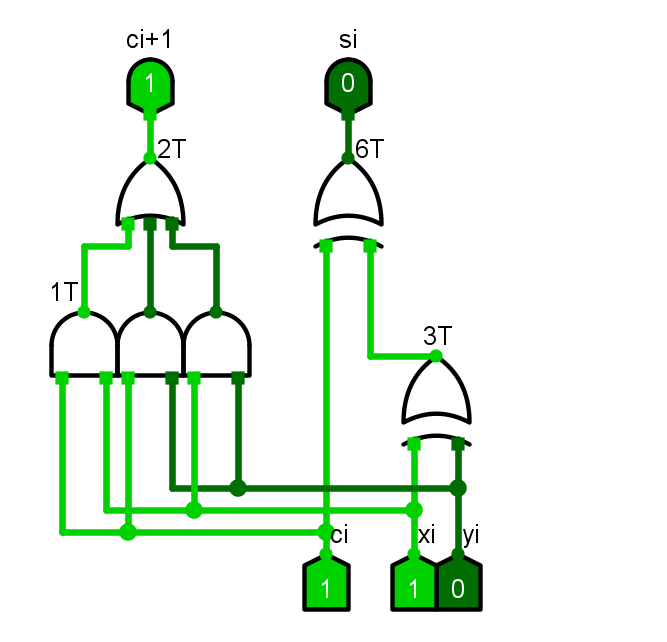
    - 全加器FA电路（对称电路，输入可随意连接）
    - 半加器HA，没有进位输入，电路更简单
- *定点数的乘除运算（几乎没考*）
  - 原码一位乘法
    - 符号位单独运算
      - 乘积符号位等于乘数和被乘数符号的异或
    - 数值位采用绝对值进行运算
      - 求积过程就是n个n位位积的累加问题
      - 采用一个n位加法器进行循环累加进行求解
      - 具体运算规则
        
        部分积P的初值为零
        
        每次将部分积P累加上y_n|x|y**n∣x∣后连同数据yy一起同步右移得到新的部分积
        
        注意进位位参与移位，也就是上溢也可以继续运算
      - n次运算和移位操作
      - 最终的2n位乘积存放在P和y两个寄存器中。
      - 图解
  - 补码一位乘法（乘法用加法实现）
    - 符号位参加运算
    - 乘数取单符号位，末位增加一位附加位y_{n+1}y**n+1=0
    - 部分积P初值为0
    - 运算规则
    - 当y_{n}y_{n+1}＝00或11yny**n+1＝00或11时，部分积加0，当 y_{n}y_{n+1}＝01yny**n+1＝01时，部分积加[x]补；当 y_{n}y_{n+1}＝10yny**n+1＝10时，部分积加[-x]补，部分积计算完毕后连同乘数y一起同步算术右移一位
    - 移位n次，累加n+1次
    - 图解
  - 阵列乘法器
    - 采用全加器阵列由组合逻辑电路直接完成
    - 现代CPU中的乘法器
      - 采用Booth两位乘法+华莱士树+流水线
  - 定点除法运算（除法用减法实现）
  - 原码定点小数的一位除法
    - 恢复余数法 (运算时间不固定)
      - 减的动就减+商上1，减不动就减了再加减数（变回原来的数），再商上0
    - 不恢复余数法 (运算时间固定)
      - 通过观察总结一下思路：
      - 通过第一轮减法（x，y）以后
        
        1.判断该余数<>0，并定商
        
        2.商和此时的余数同时左移
        
        3.若此时余数>0，则+（-y补），否则+y补[计算机运算补码完成]
  - 要求|x|<|y|，否则运算可能会发生溢出。
  - 商的符号单独处理，即由两数的符号异或得到。
  - 数值部分的运算规则
- 溢出概念和判断方法
  - 溢出概念
    - 上溢（大于最大可以表示的正数）
    - 下溢（小于最小可以表示的负数）
    - 精度溢出（超出可表示的精度）
  - 有符号溢出判断
    - 1、单符号判断法，利用操作数和运算结果的符号位进行判断。
      - 加法溢出规则：“正正得负，负负得正”
      - 减法溢出规则：“正负得负，负正得负”
    - 2、进位位判断法
      - 符号位进位和最高数据位进位进行异或操作
      - V=C_f \oplus C_dV=C**f⊕C**d
      - 加减法均适用，实际计算机中采用
    - 3、双符号判断法
      - 将运算结果的两个符号位进行异或操作
      - V=C_{f1} \oplus C_{f2}V=C**f1⊕C**f2
      - 符号位相同无溢出，01表示上溢，10表示下溢
      - 最高位用于表示正确的符号位
      - 用于手工计算，方便肉眼识别，计算机因为成本问题不采用
  - 无符号溢出判断
    - V=C \oplus SubV=C⊕Sub
    - C为进位输出，Sub=1表示减法，0表示加法
浮点数的表示
- 浮点数
  - 表示方法：两个定点数分别表示阶码和尾数
    - 图解
    - 阶码（决定表示范围）
      - 阶符：阶码正负性
      - 阶值：指数部分
    - 尾码（和阶码一起决定表示精度）
      - 数符：浮点数的符号
      - 尾数：尾数数字部分
    - 表示范围大和精度高，运算复杂
  - 溢出问题
    - 存在上溢和下溢问题（阶码溢出）
    - 也存在精度溢出问题（无法精确表示，只能舍入处理）
  - 尾数规格化
    - 保证表示唯一
      - 调整尾数和阶码，保证尾数最高位是有效值1
      - 提高运算精度，充分利用尾数有效位
        
        左归：
        
        尾数左边无效位太多，往左移
        
        左归可多位
        
        阶码减少，尾数增大
        
        右归
        
        尾数运算溢出是要进行右归
        
        右归最多一位
        
        阶码增加，尾数减小
      - 原码规格化数（绝对值大于等于0.5）
        
        正数：0.1xxx
        
        负数：1.1xxx
        
        尾数最高位为1
      - 补码规格化数
        
        正数：0.1xxx
        
        负数：1.0xxx 注意﹣0.5补码不是规格化数
        
        符号位和尾数最高位相反
  - 浮点数在数轴上的分布
    - 刻度并不均匀，越往右，浮点数越稀疏
    - 浮点运算不满足结合律
      - 小数a+大数b=大数b（有可能）精度损失
      - 编程时浮点数比较要小心
- IEEE754标准
  - 二进制浮点数
    - 数符S、阶码E和尾数M
    - 阶码采用移码表示
    - 尾数采用原码数据表示，
      - 隐藏高位1，运算时还原成1.M形式
    - 二进制浮点数无法精确表示一些十进制小数
      - 0.1 0.2 0.4等转换成二进制都是循环小数
  - 对32位单精度格式而言：S为1位， E为8位，采用偏移值为127的移码，M为23位
    - 为什么是127而不是128？
      - 主要原因是使得任何一个规格化数的倒数能用另外一个浮点数表示，而采用128的偏移量表示的最小规格化数的倒数会发生溢出。
  - 10进制浮点数
    - 可精确表示十进制浮点数，保证运算精度
    - 解决二进制浮点运算引起的误差问题
    - IEEE-754 2008标准中有定义
  - IEEE754表示范围
    - e为阶码，M为尾数
    - 阶码为全1时，表示无穷大或非数，浮点数除零不会异常
    - 阶码和尾码全零时表示机器零
    - 阶码为零，尾数不为零时表示非规格化数
    - 其他表示区间为规格化数
    - 最大值，最小值问题
    - 十进制数与浮点数的转换（常考）
    - 考研真题：多次考察，小题大题都有
      - 真题
浮点数加减运算
- 对阶
  - 小阶向大阶看齐
  - 阶码增加，尾数右移
- 尾数运算
- 规格化
  - 尾数运算上溢：右归最多一位
  - 尾数规格化下溢：左归处理，可以多位
- 舍入处理
  - 0舍1入：舍去位最高位为1，尾数最低位加1，否则舍去
    - 舍入后尾数可能上溢，还需要进行二次规格化
  - 恒置1法：舍去中有一位是 1，尾数最低位置 1
  - 截断法：移出位全舍去（不常用）
- 溢出判断
  - 阶码溢出时浮点数才会发生溢出
  - 上溢：进入异常处理
  - 下溢：按机器零处理
- 注意IEEE754浮点数与采用补码表示阶码和尾数的浮点运算法则的相同和不同之处
- 考研真题
  - 真题
程序中的数据表示与运算（常考）
- 汇编语言中的数据类型
  - 寄存器、存储器操作数本没有数据类型
  - 对该数进行何种数据类型的操作完全取决于指令功能
  - 有符号运算、无符号运算、定点运算、浮点运算指令
- C语言中数据类型
  - 整型
    - 有符号整型包括char、short、int、long
    - 分别采用8、16、32、64位补码进行表示
    - 通过unsigned声明为无符号类型
  - 整型运算溢出问题
    - 有符号整数和无符号整数、浮点数都存在运算溢出的问题
    - C语言不做溢出判断，需要程序员特别注意
    - 考研真题
      - 真题1
      - 真题2
  - 浮点型
    - C语言中常见的浮点数为float、double
    - 分别对应IEEE 754中的单精度和双精度浮点数
    - 不同数据类型的运算会在编译器的翻译下变成不同类型的汇编指令
  - 强制类型转换
    - 相同位宽的整型数据进行强制转换时机器码保持不变
    - 小字长转大字长时
      - 无符号整型进行零扩展
      - 有符号整型进行符号扩展
    - 大字长转小字长时直接将机器码截短
    - float→double：由于double型数据的尾数、阶码宽度都比float型大，因此其表示范围更大、精度更高，转换后的 double 型数据与原 float 型数据完全相等。
    - double→float：大数转换时可能发生溢出，高精度数转换时会发生舍入。
    - float/double→int：小数部分会截断，大数转换时可能会溢出。
    - int→float：两种类型都是 32 位，所表示的状态数是一样的，在数轴上表示的数据并不完全重叠，float 型用其中一部分状态表示了更大的整数和小数；int 型中一些比较大的整数无法用float型精确表示。浮点数尾数连隐藏位在内一共24位，当int型数据的24～31位数据非0时，无法精确转换成 24 位浮点数的尾数，此时会发生精度溢出，需要进行舍入处理。
    - int→double：浮点数尾数字段为 53 位，可以精确表示所有 32 位整数。
    - 实例
    - 考研真题
      - 真题1
      - 真题2
算术逻辑单元ALU
- 串行加减法电路
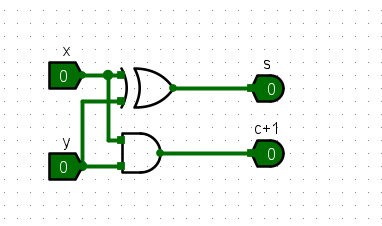
  - 半加器（x，y为数据位，s为运算和，c+1为进位信号（输出））不带进位输入
    - 实现如下
  - 全加器
    - 实现如下
    - (1)
    - (2)
    - PS：
      - 1.所需硬件开销是不同的
      - 2.异或门信号由A非B + AB非组成需要判断三次，则为3T
  - 串行加法器
    - 将n个全加器进位信号串联即可得到n位的加法电路
      - 注意时间延迟分析，电路内部有并行性，详见教材
      - 进位链依赖，运算速度和位数是线性关系，速度较慢
  - 可控加减法电路
    - 减法变加法，输入增加异或门，控制位送进位输入，逐位取反，末位加1
      - 有符号无符号运算均适用，区别是溢出检测逻辑
      - 具体实现效果：
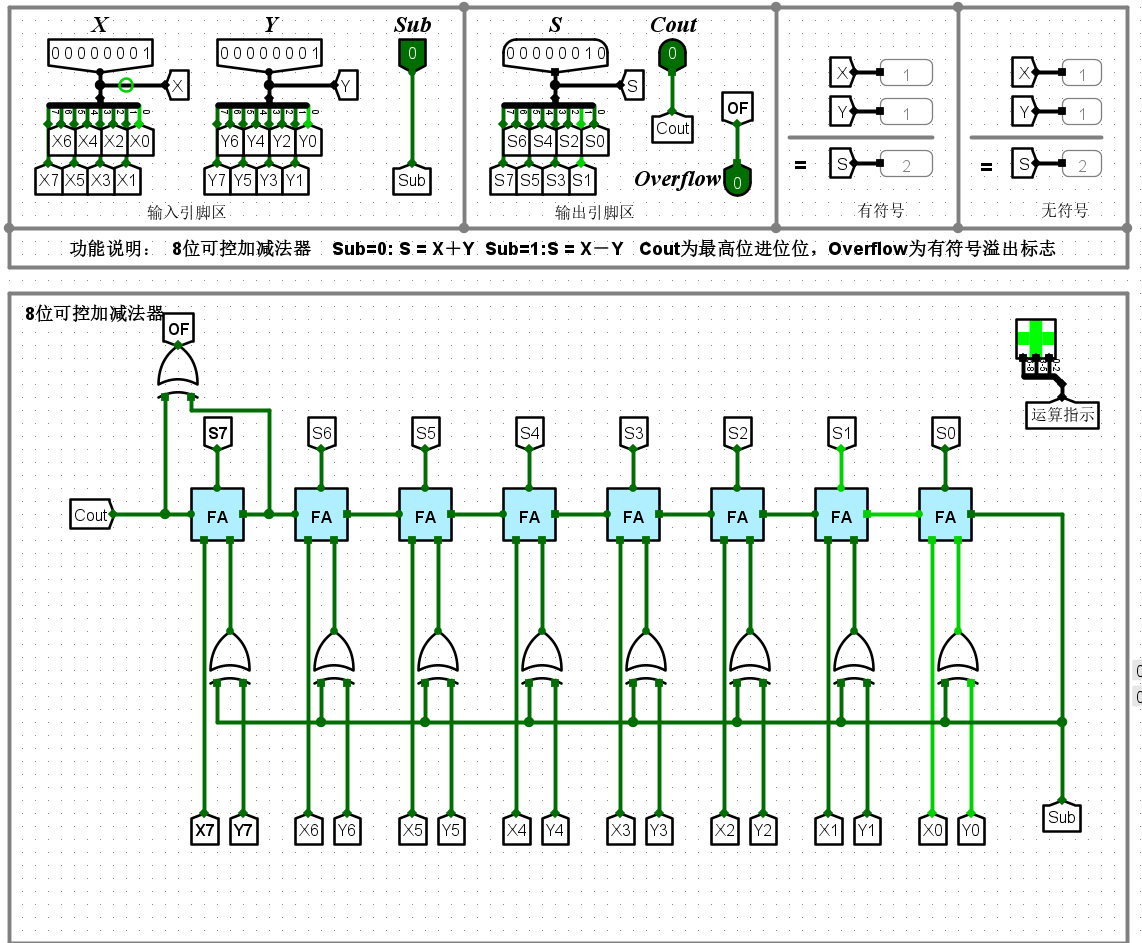
- 并行加法器
  - 主要原理
    - 采用先行进位电路提前得到所有进位位
    - 各位的求和运算可以并发运算
    - 注意先行进位电路也有开销和时间延迟
  - 进位生成函数
  - 进位传递函数
  - 进位信号仅仅与G，P，C0有关
  - 先行进位电路
    - C为进位信号，进位方式有两种
      - G为1
      - P为1（X,Y分别一个1一个0）且上一个C为1
  - 四位快速加法器
  - 先行进位电路级联
    - 多级先行进位方式：组内并行，组间并行(高效)
    - 可以尝试进行延迟分析，详见教材、
    - 目前计算机任采用这种方式进行计算
- ALU功能和结构
  - 定点运算器
    - 算术逻辑运算单元ALU
      - 算术逻辑运算单元是运算器的核心，由它实现算术逻辑运算
    - 通用寄存器组
      - 通用寄存器组的作用是暂存参加运算的数据、运算的中间结果或最后结果
    - 输人选择电路
      - 输入选择电路的作用是对若干个数据的输入进行选择或控制
    - 输出控制电路
      - 输出控制电路对加法器的输出进行控制
  - 运算器结构
    - 单总线结构: 2个缓冲器，3个时钟完成运算
    - 双总线结构：1个缓冲器，2个时钟完成运算
    - 三总线结构：0个缓冲器，1个时钟完成运算
  - 运算流水线
    - 浮点流水线，将浮点运算的步骤进行细分
    - 不提升单个运算的性能，优化密集型浮点运算性能