数学建模算法
本笔记用作个人学习和查漏补缺使用,欢迎借鉴学习,提出建议,转载需标注出处www.jjyaoao.space
线性规划(LP)
线性函数通常就是一次函数的别称

线性规划求最大值
求最大值只需要改变这个形式就行了,让上面三个式子倾向于能取最大值(x)


f数据全部转为负数,则求出来的是负数的最小值(换成正数也就是最大值了)
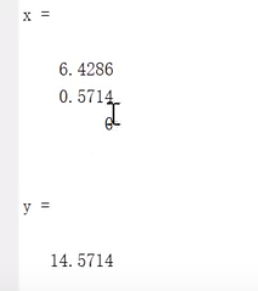
x1 = 6.4286 x2 = 0.5714 x3 = 0 时y取得最大值14.5714
可以转化为线性规划的问题

线性规划模型实例
问题提出

相关数据
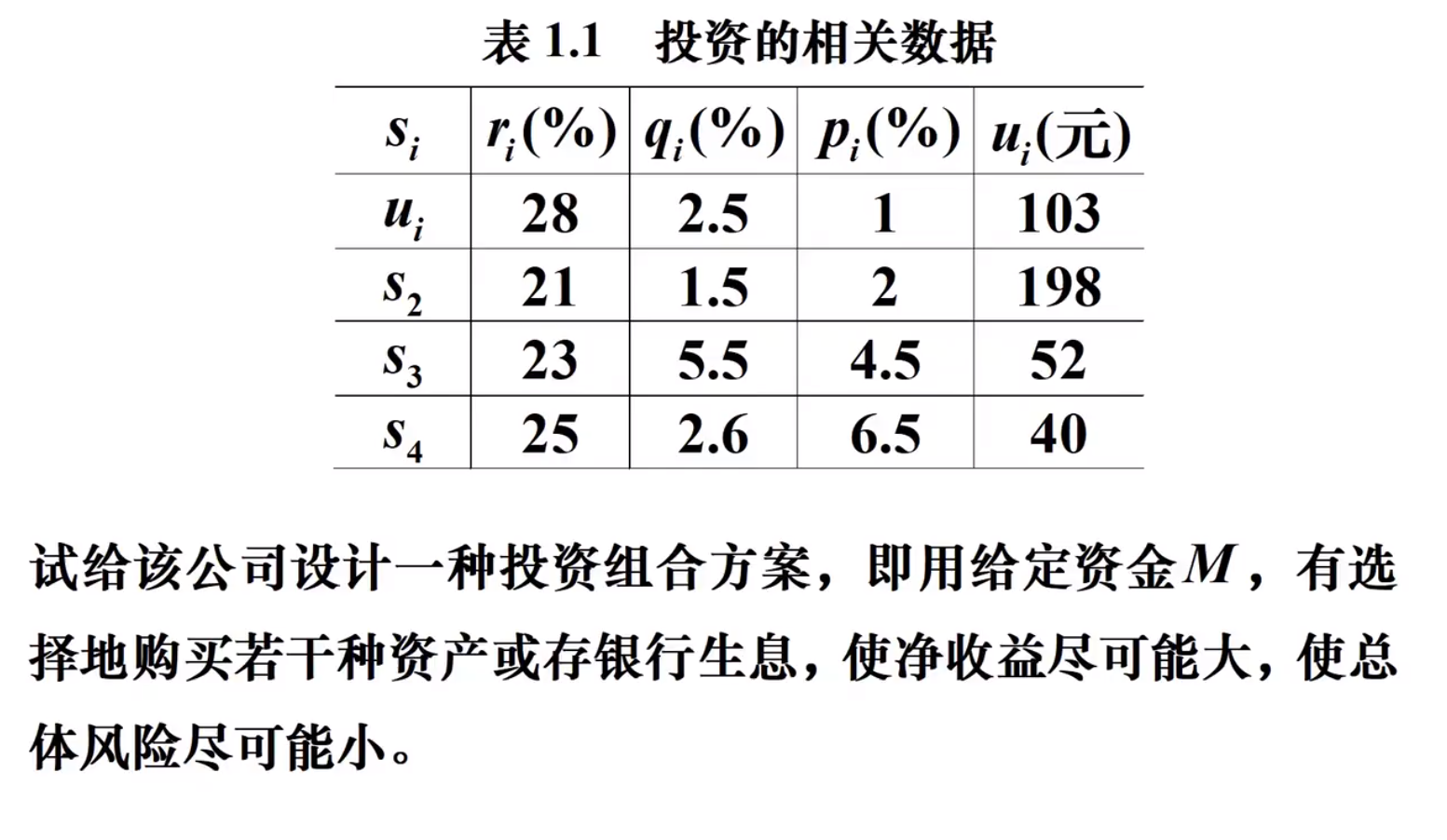
符号规定与基本假设


模型分析与建立

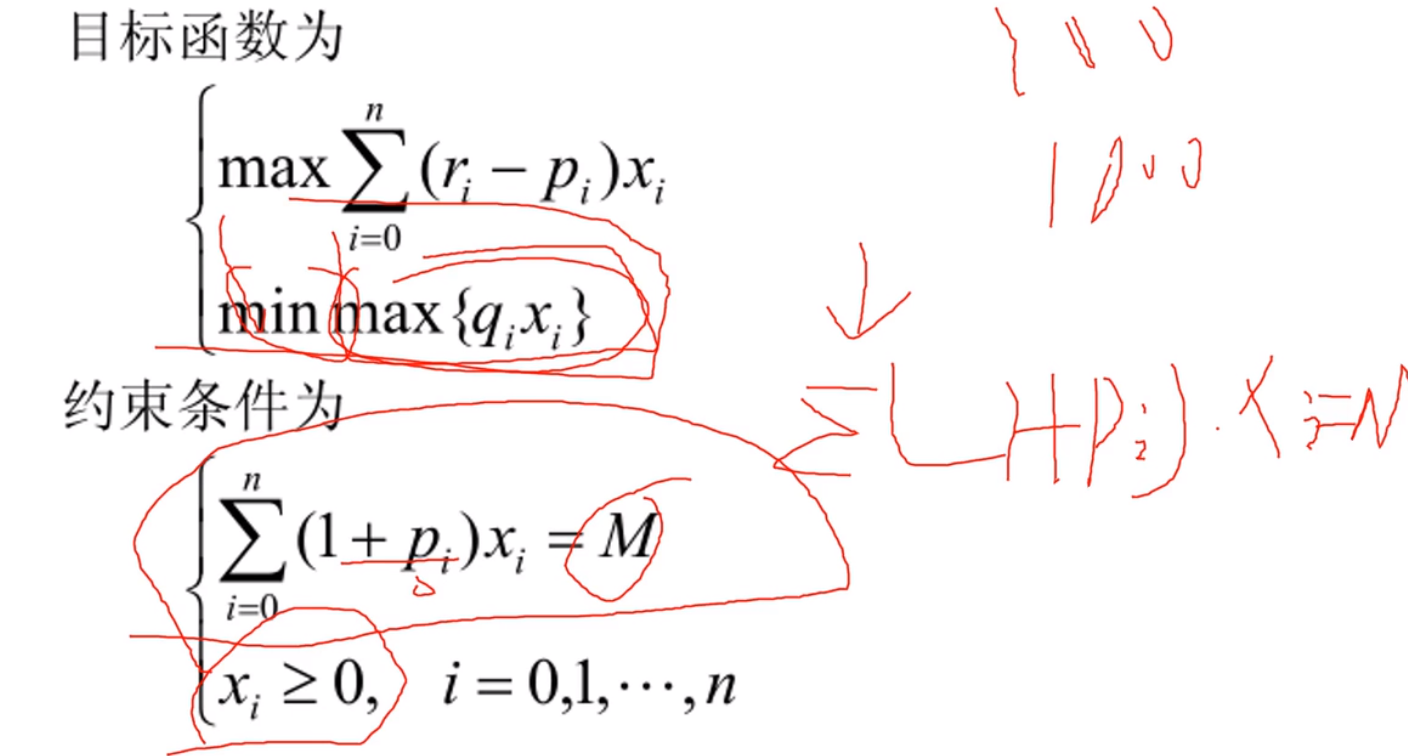



上面f数据全部加负号,因为matlab只能求最小值,全部负号的最小值就是最大值了

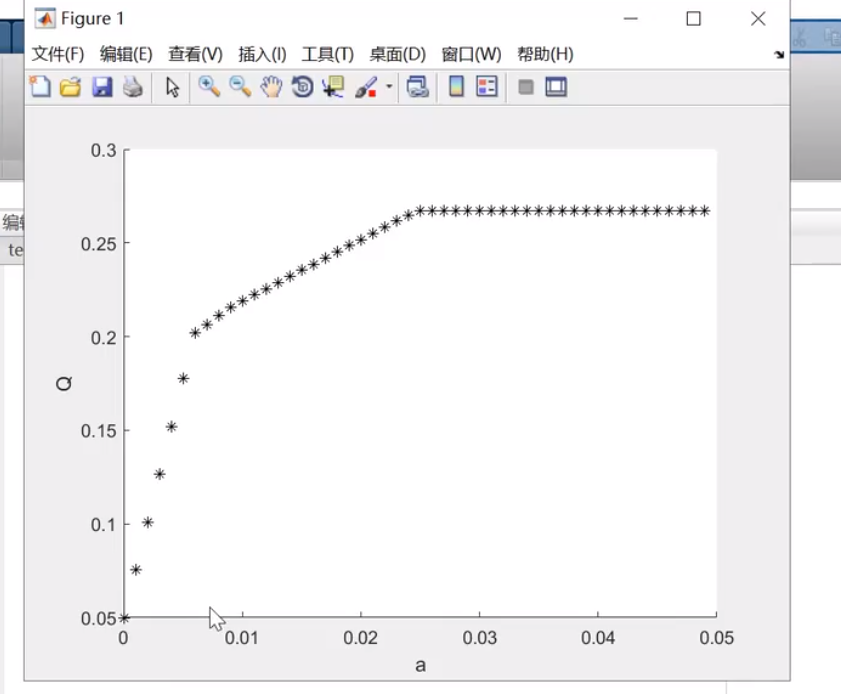

整数规划
规划分类



整数规划特点

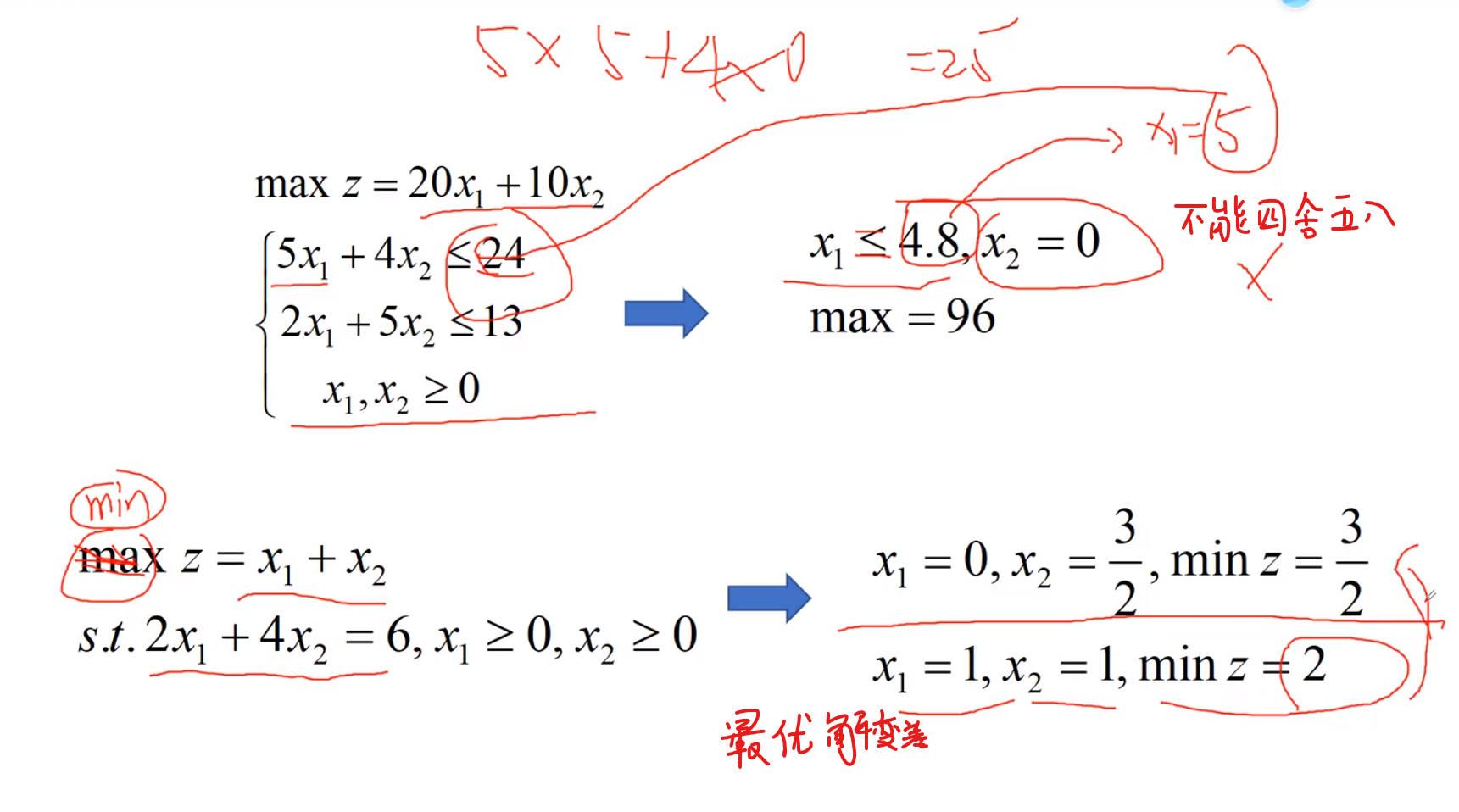
线性规划和整数规划关系

合理下料问题
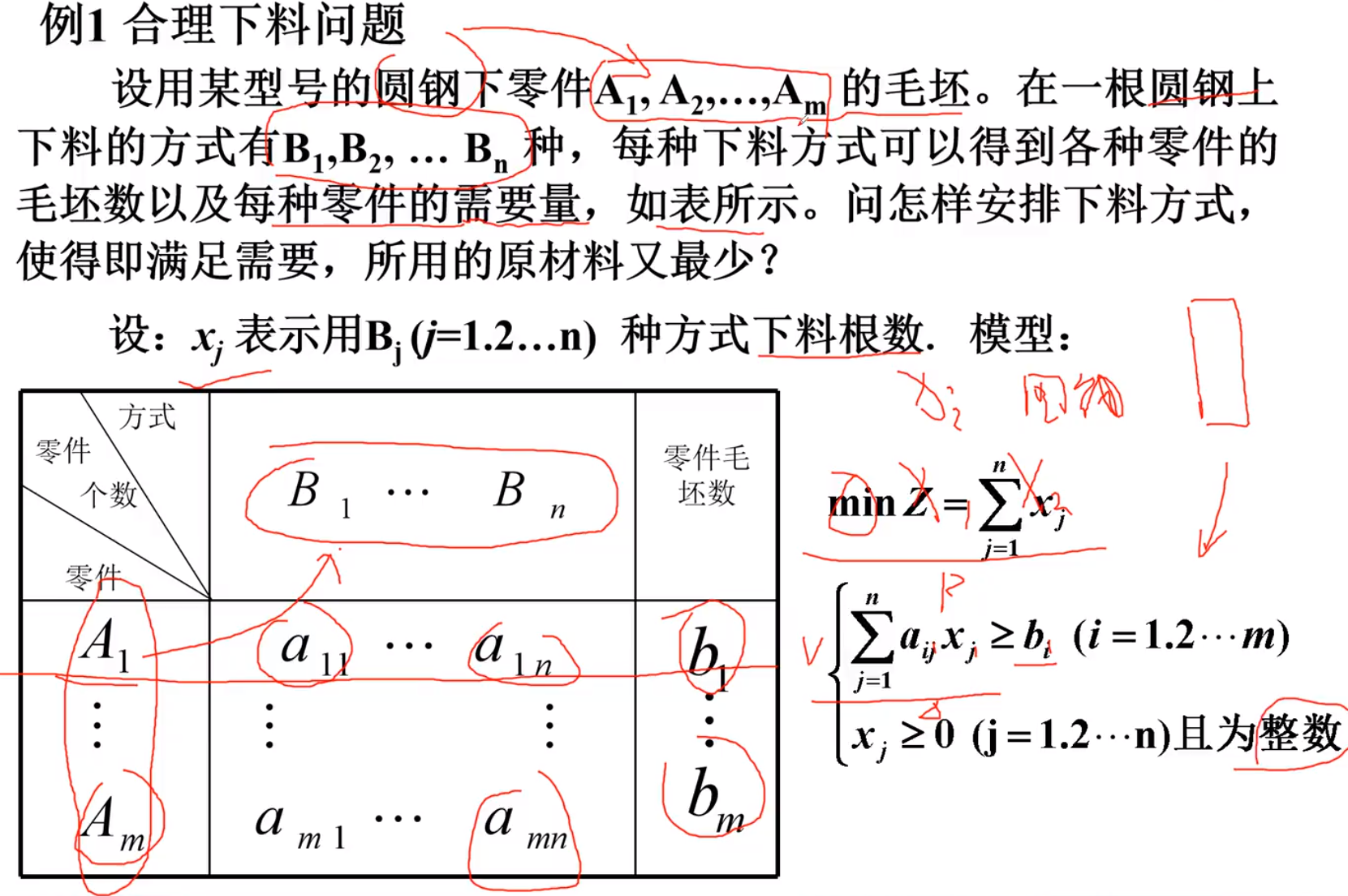
建厂问题
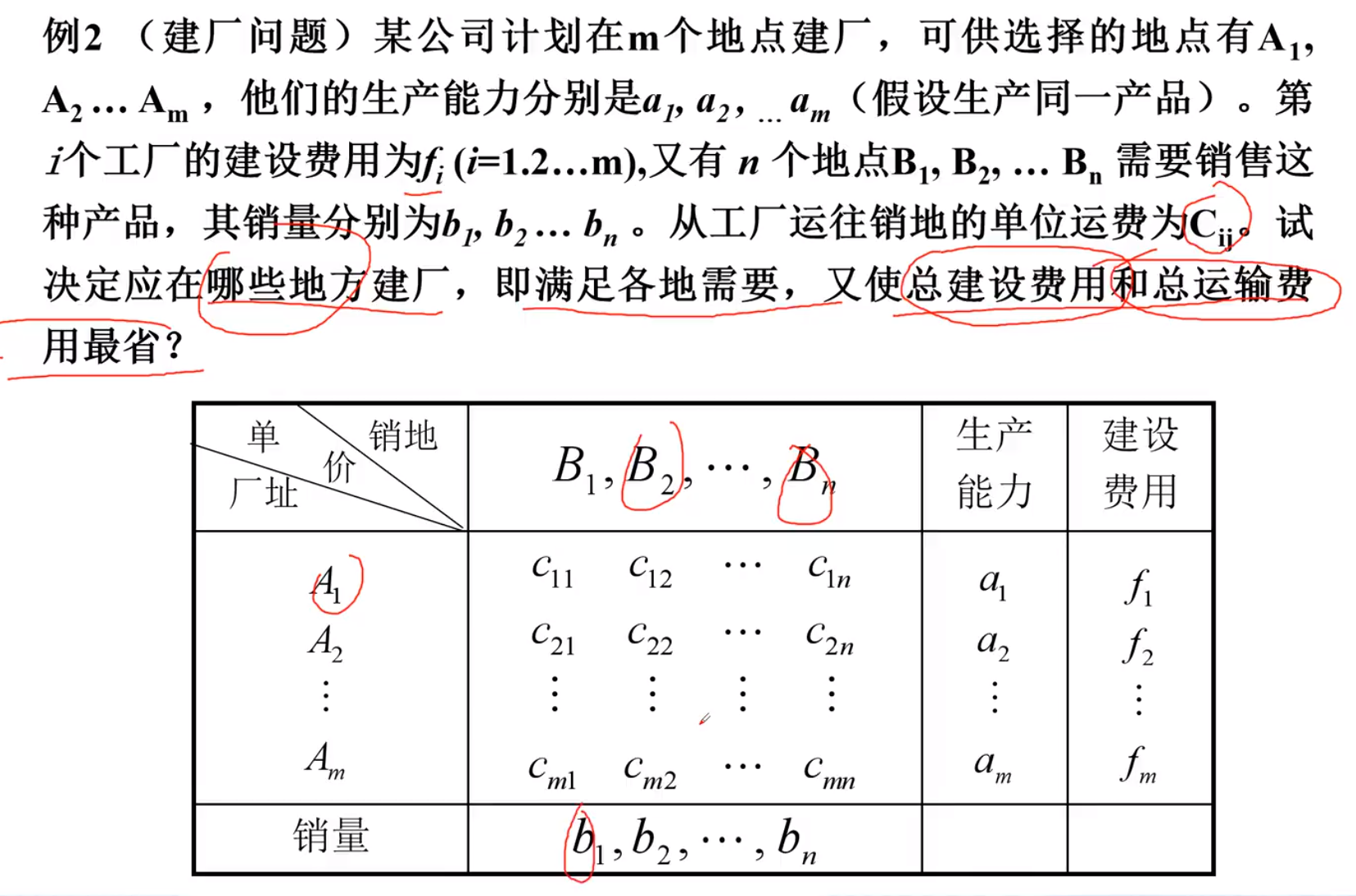
模型

求解方法

分支定界算法




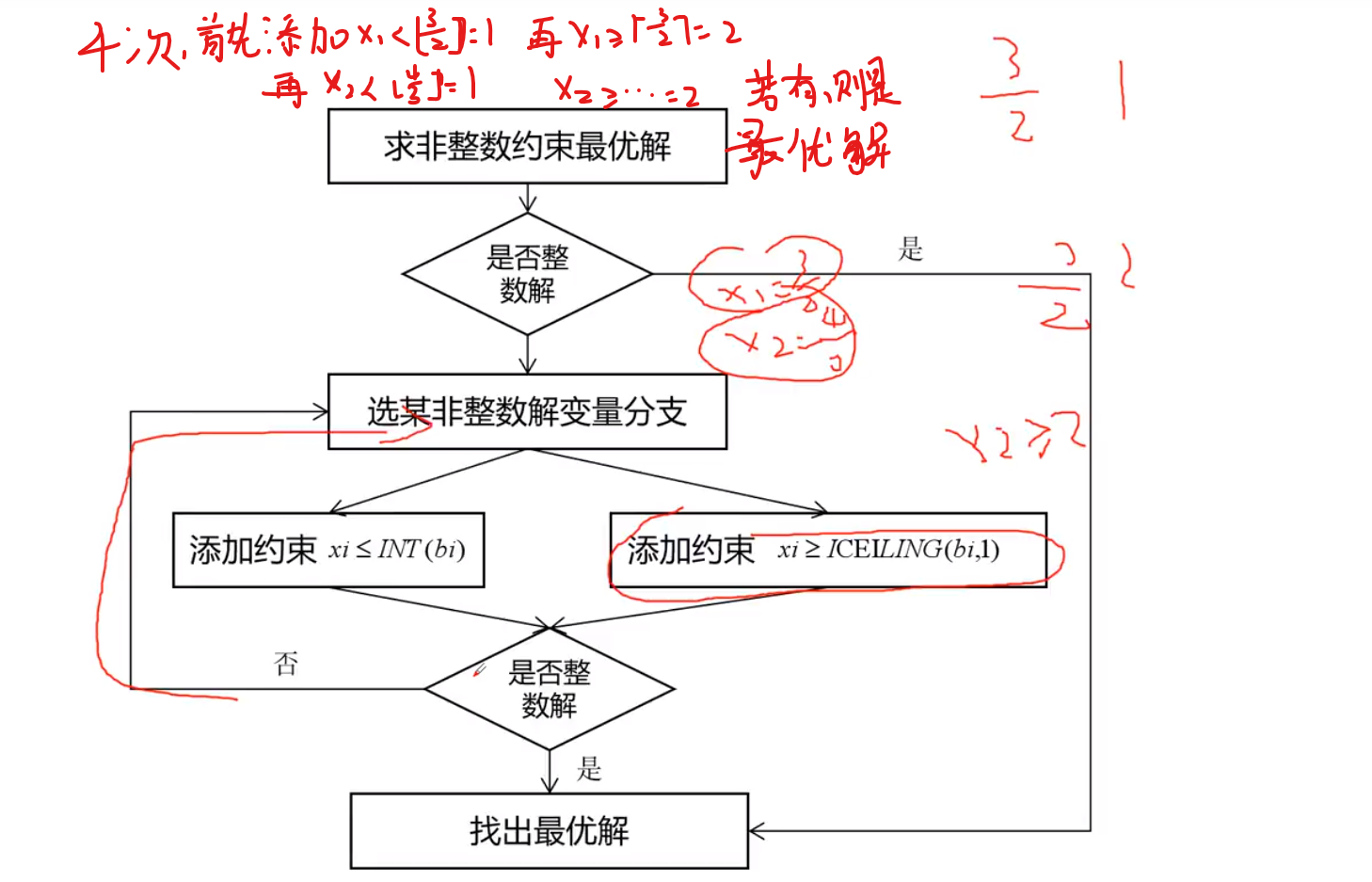
若找到了,则是最优解,若这样也没能找到,则需采用其他方式
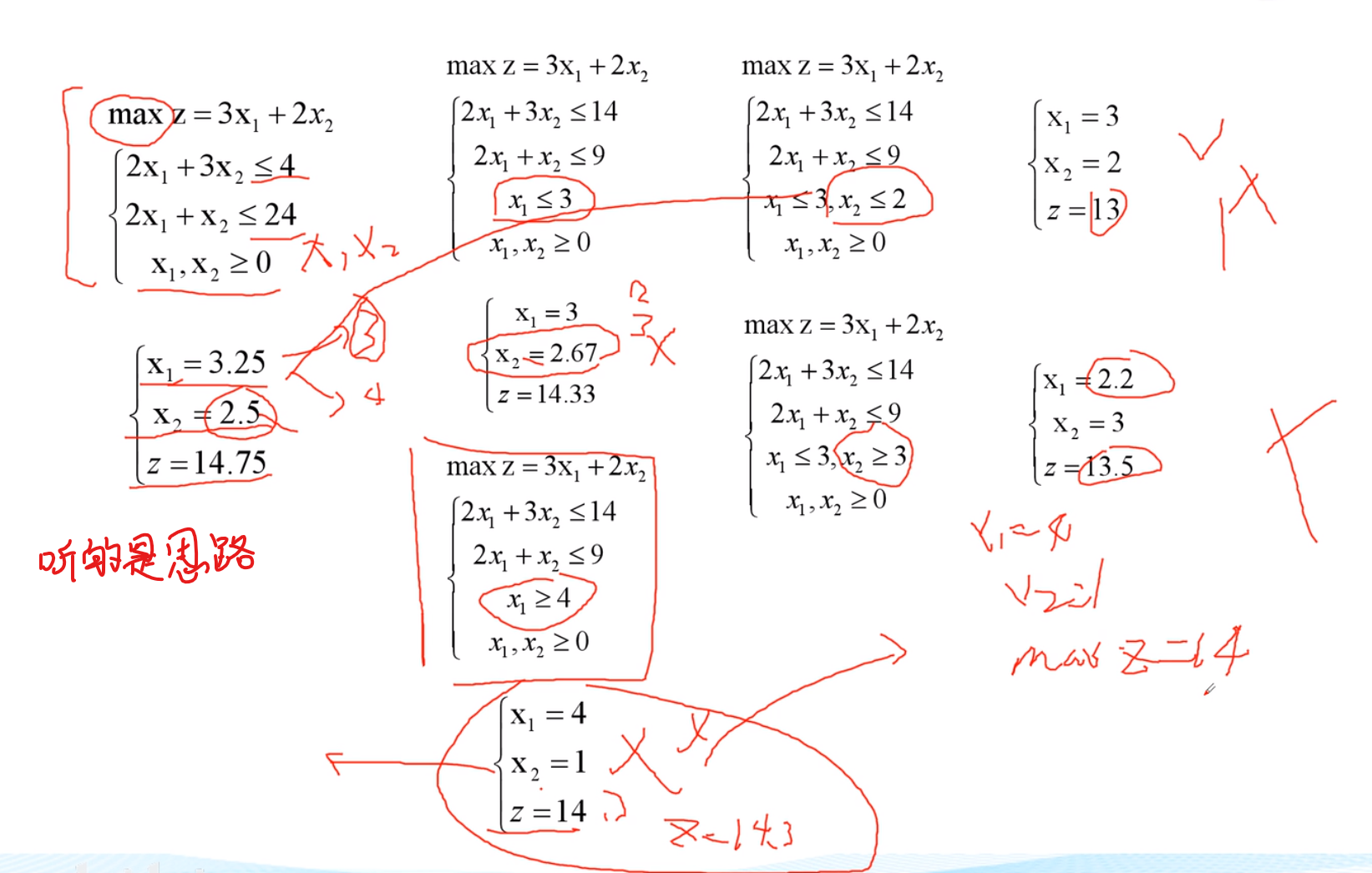
例题
intprog.m
I:1/2这样的数,只是起到一个变量赋值的作用
e:误差,整个函数相当于在intprog上进行改进


控制默认值



branchbound.m
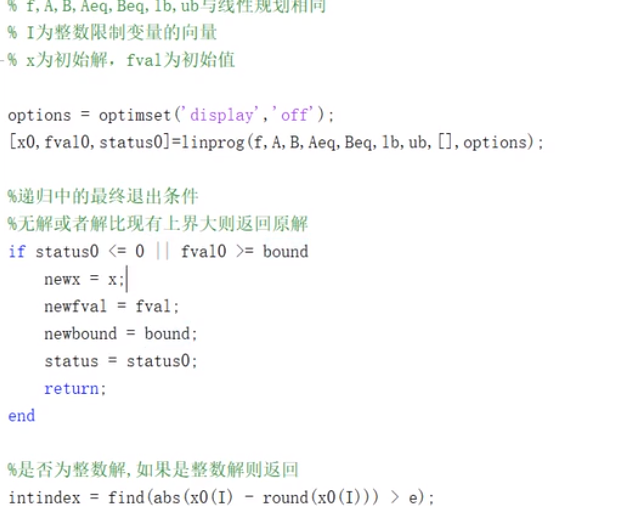
具体细节参照p3.2
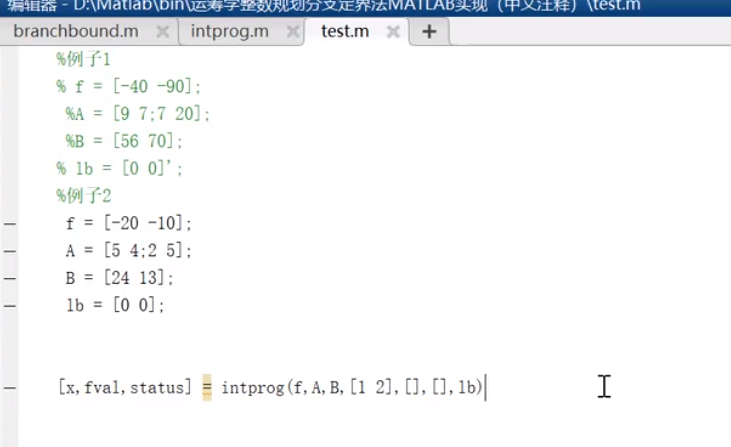
test.m

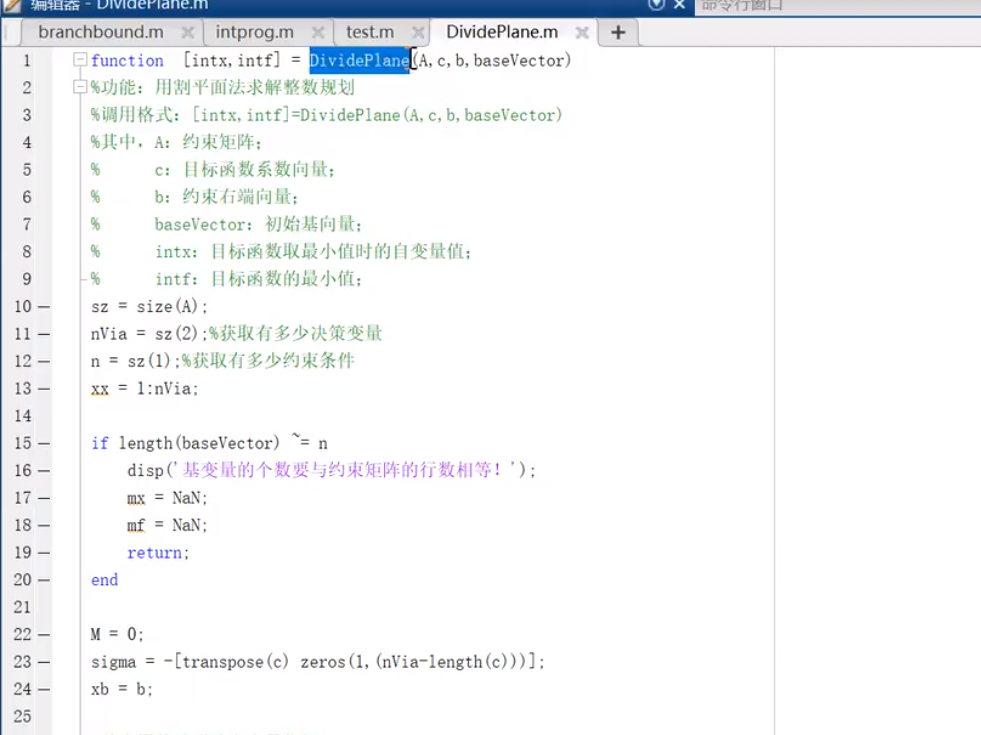
割平面法

大概流程演示

例:

首先由不等式得到等式(左上角得左下角)
再整合出右上角的方程(线性代数),注意4式没有x2,5式没有x1
然后将4式每一项构造成整数+小数的形式将整数移到左边,小数移到右边
得出了x3,x4的关系式,用这个关系式再带入5式,得到了x2<=1;

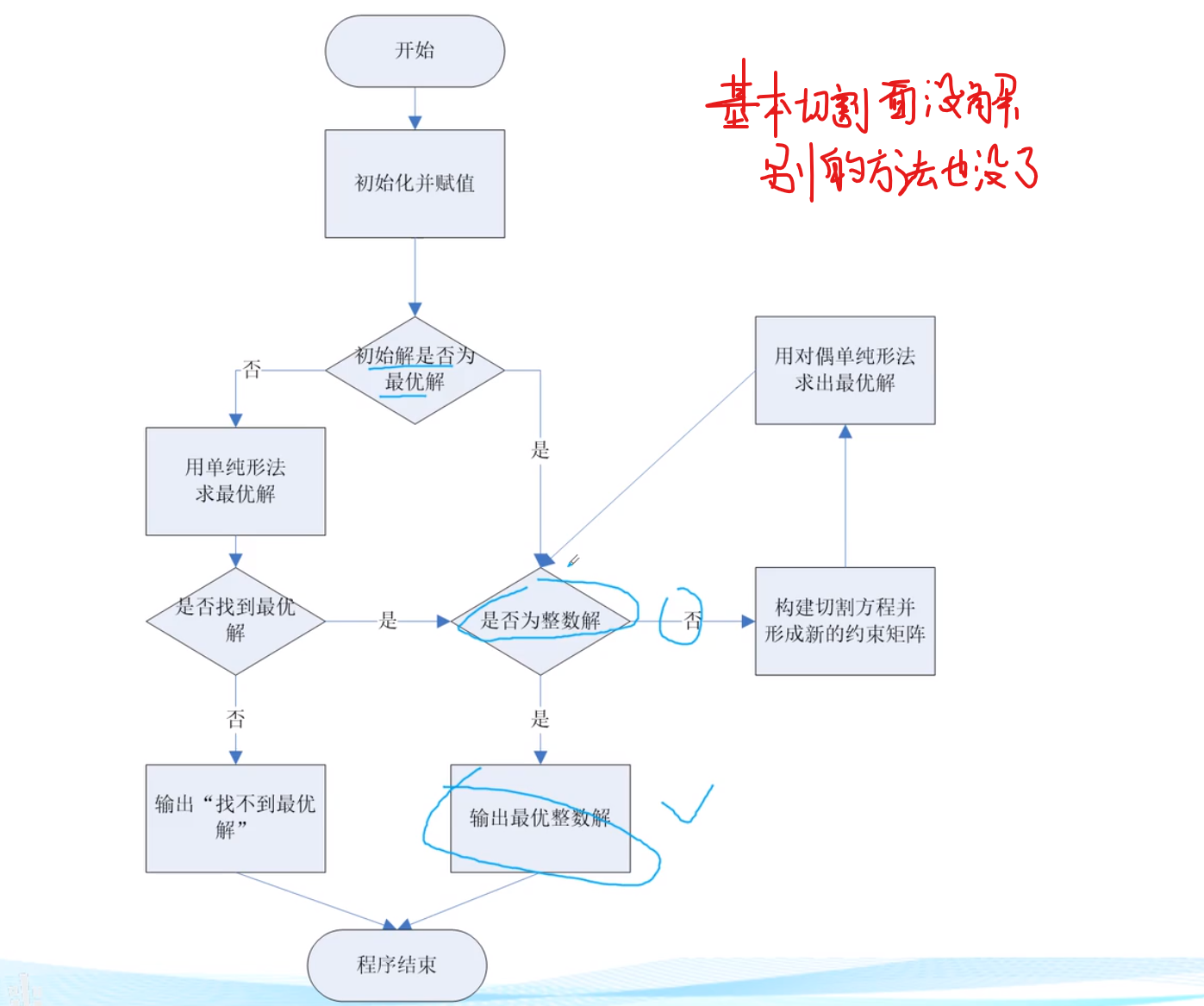
流程图
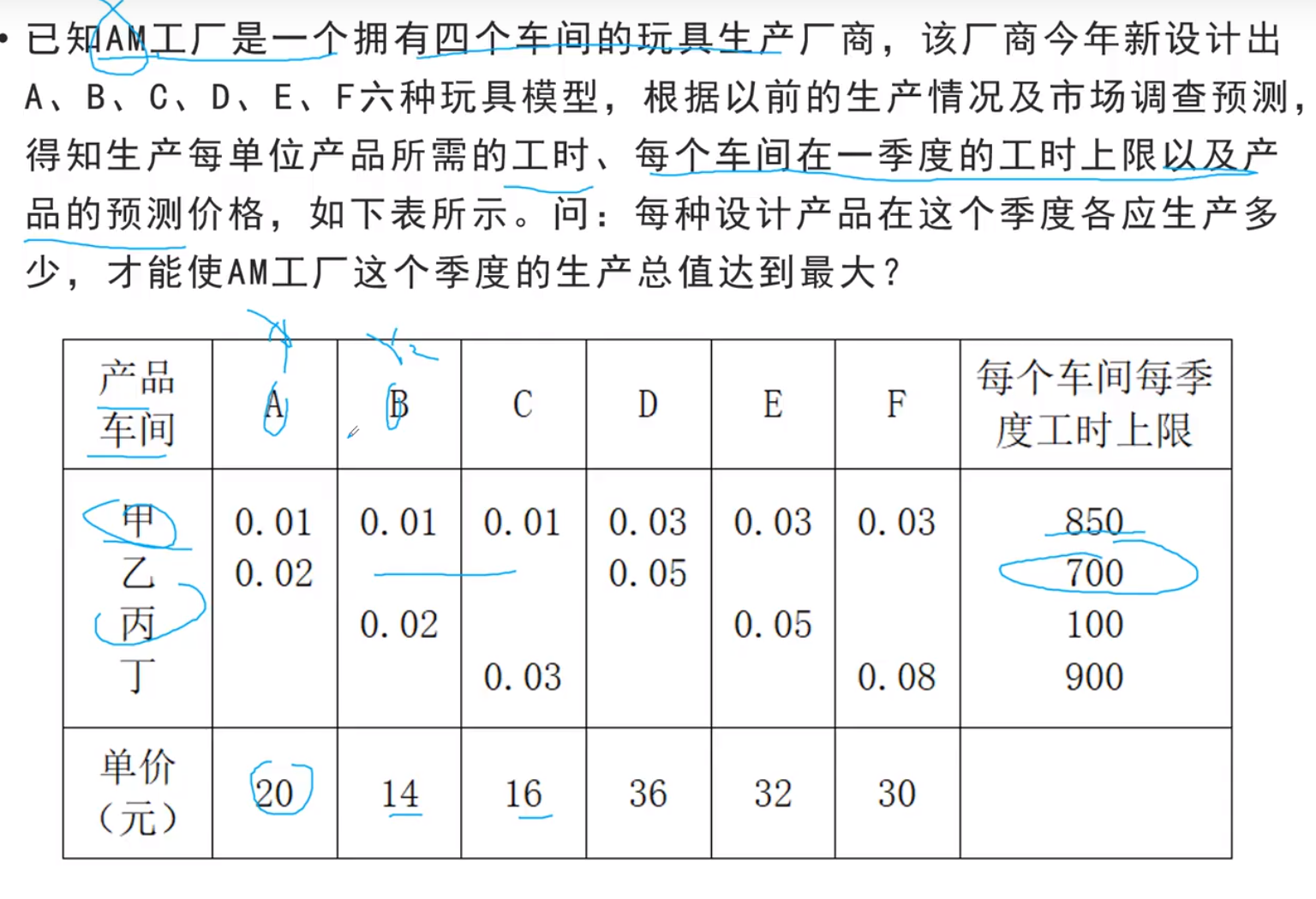
例题


01规划
-投资问题

-互斥约束问题
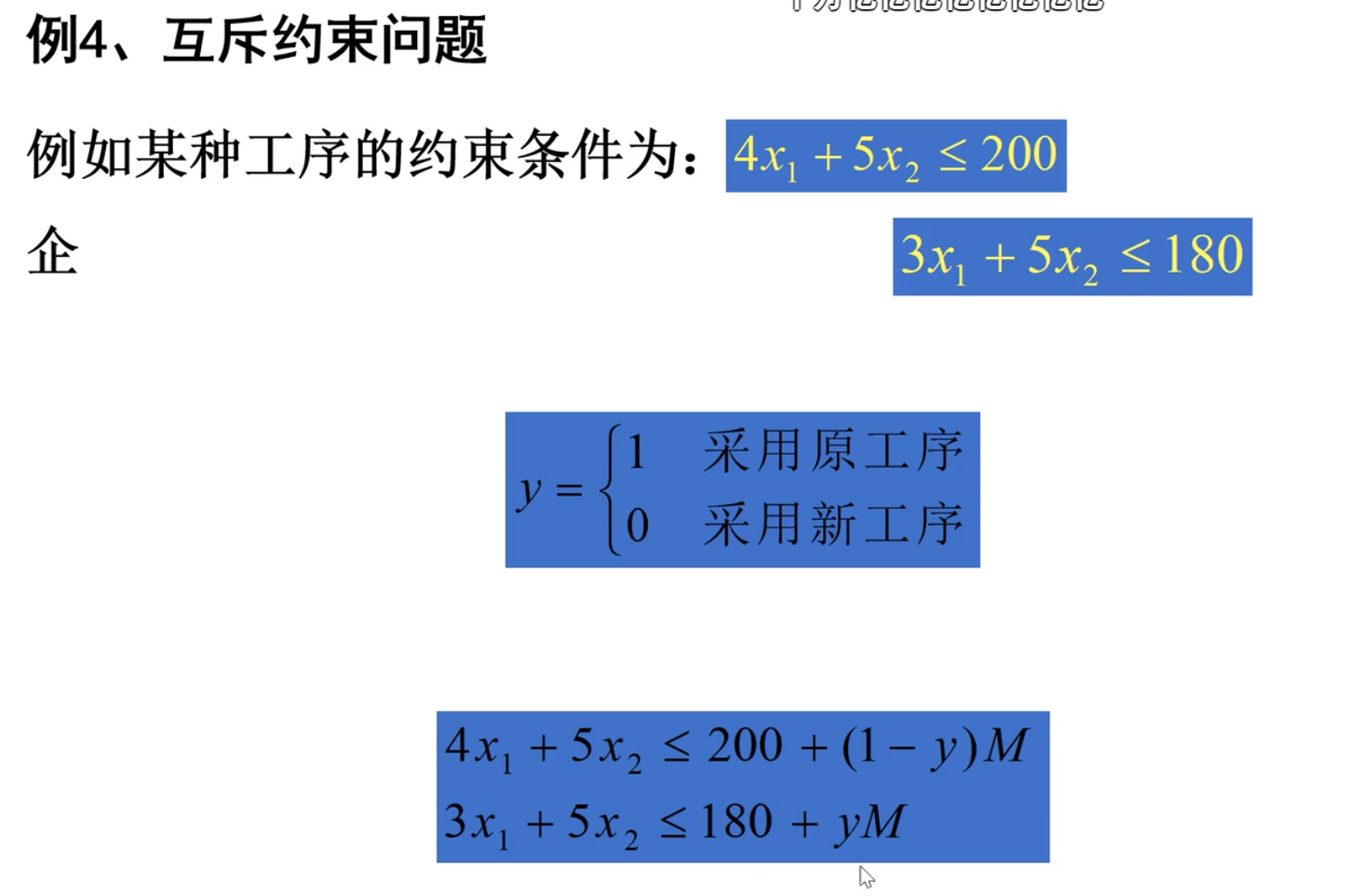
y为决策,M为自定义变量,目的就是要y为1/0时,其中一项失去它的作用
例如y为1,则上面一个式子成立,下面一个式子,要想失效,则只需M取无穷大即可摆脱束缚,y=0也差不多的意思
推广

-固定费用问题
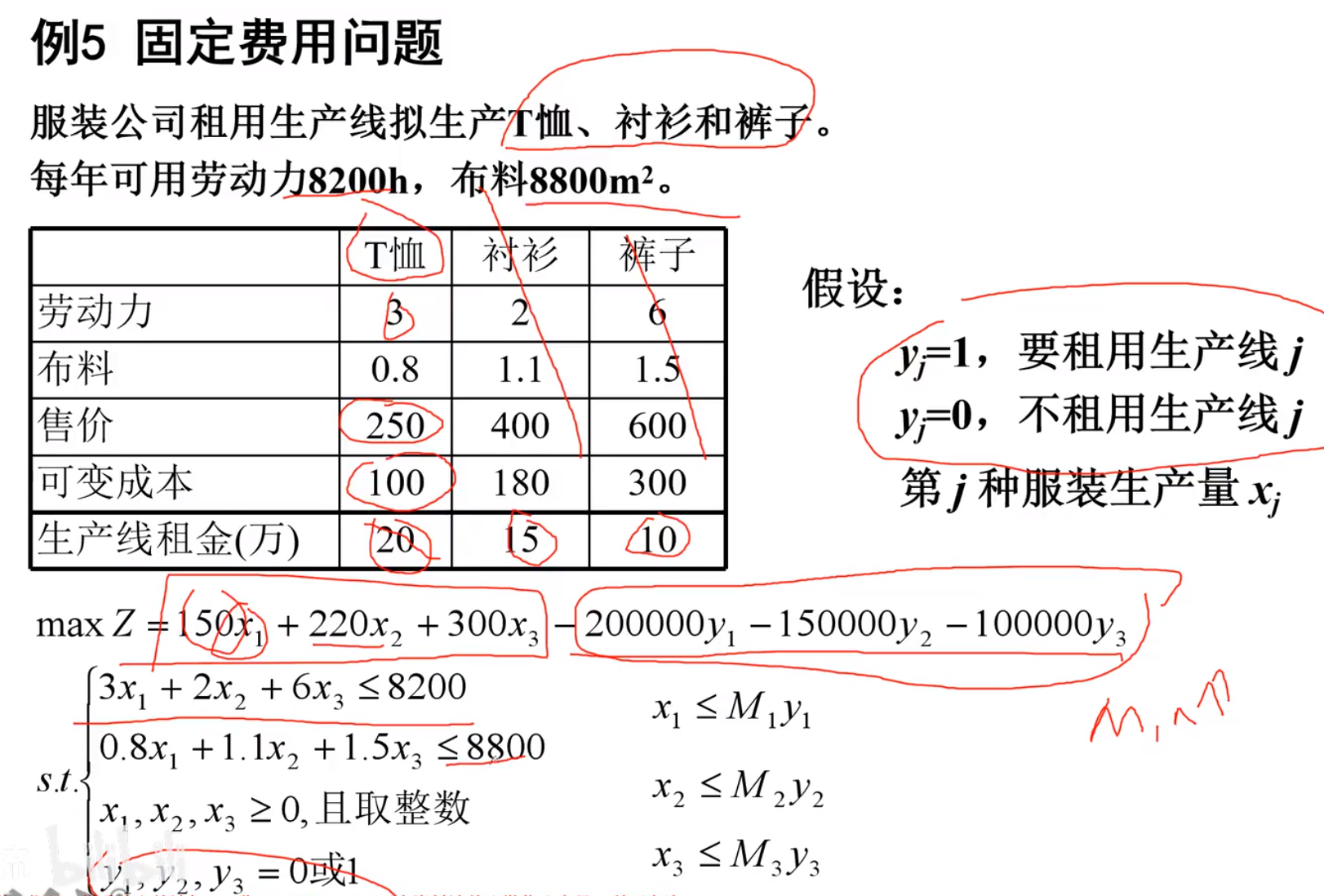
-指派问题
通常用于求最小值
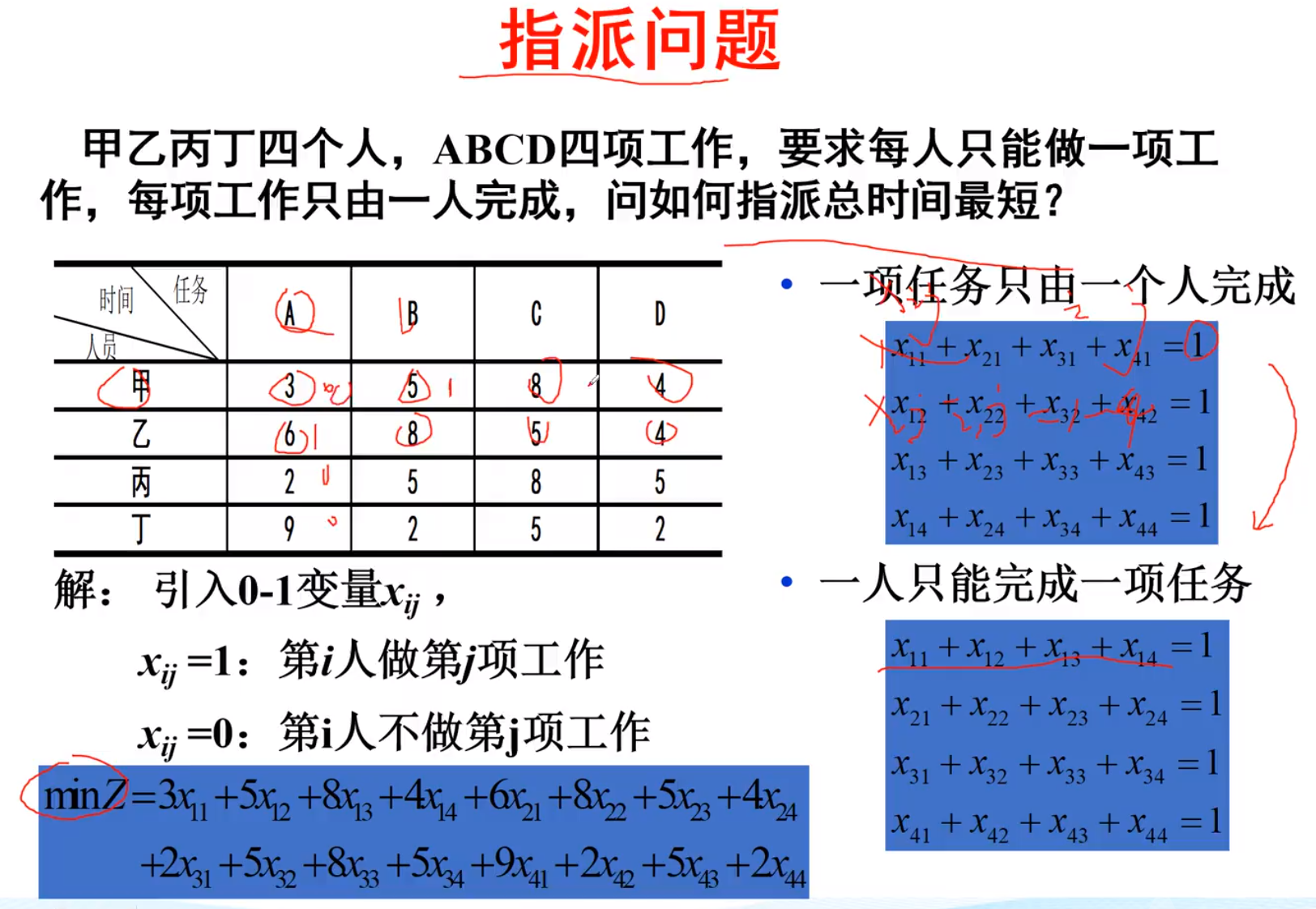
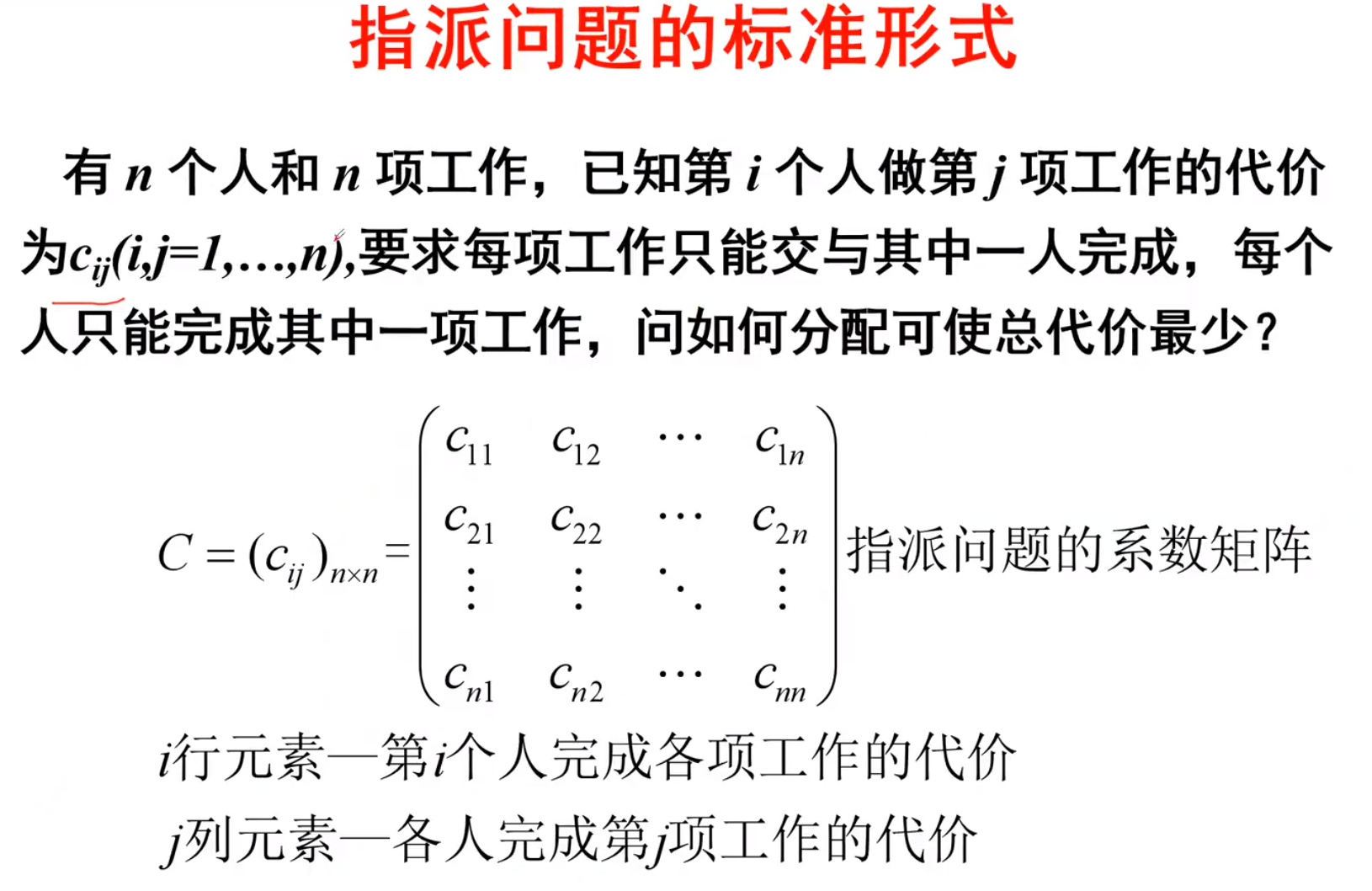
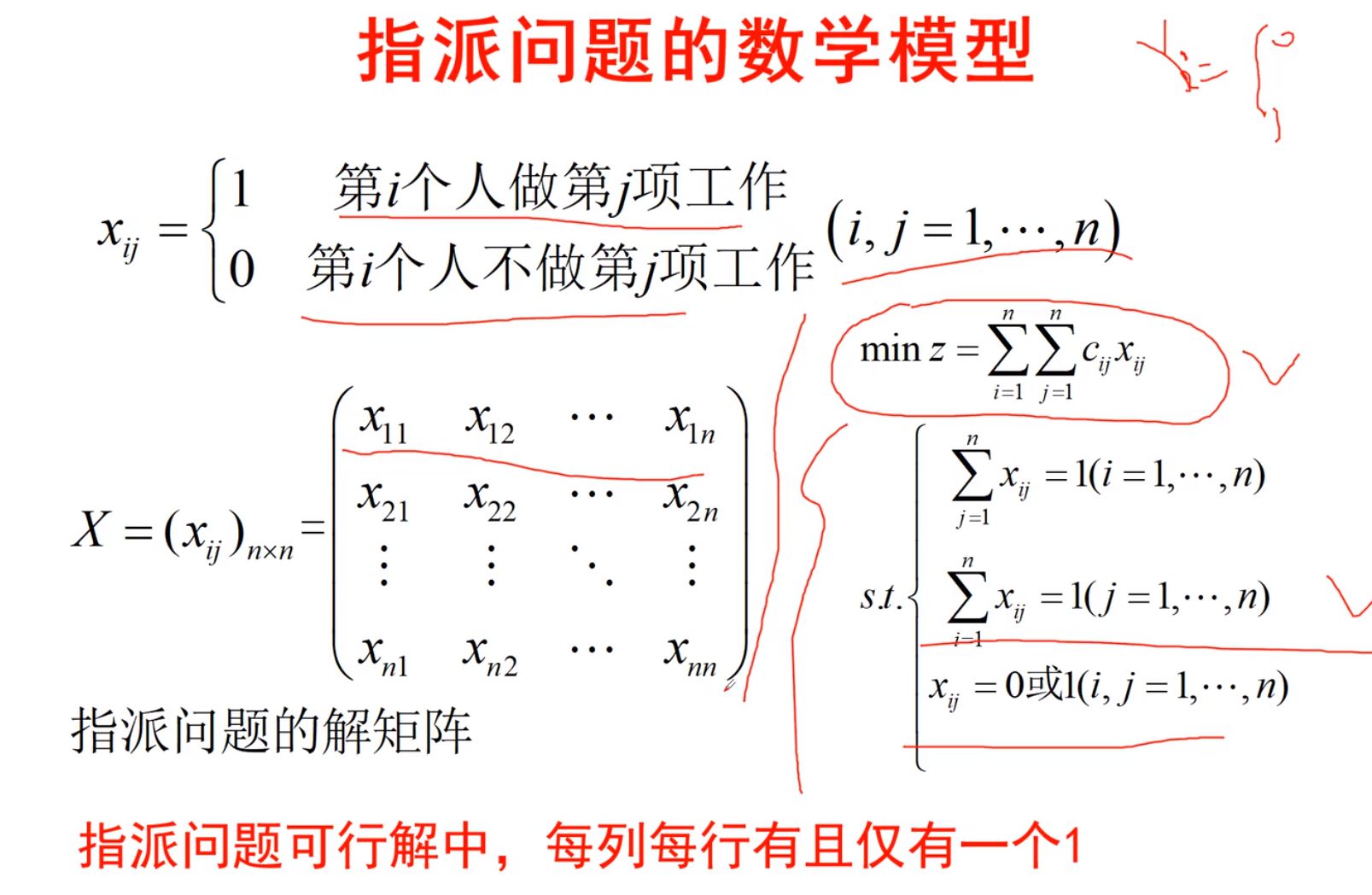
-非标准形式指派问题

1.求利润之内的最大值
2,3添加虚拟变量,使之变成标准指派
4.将某人设置成0或者小于0即可
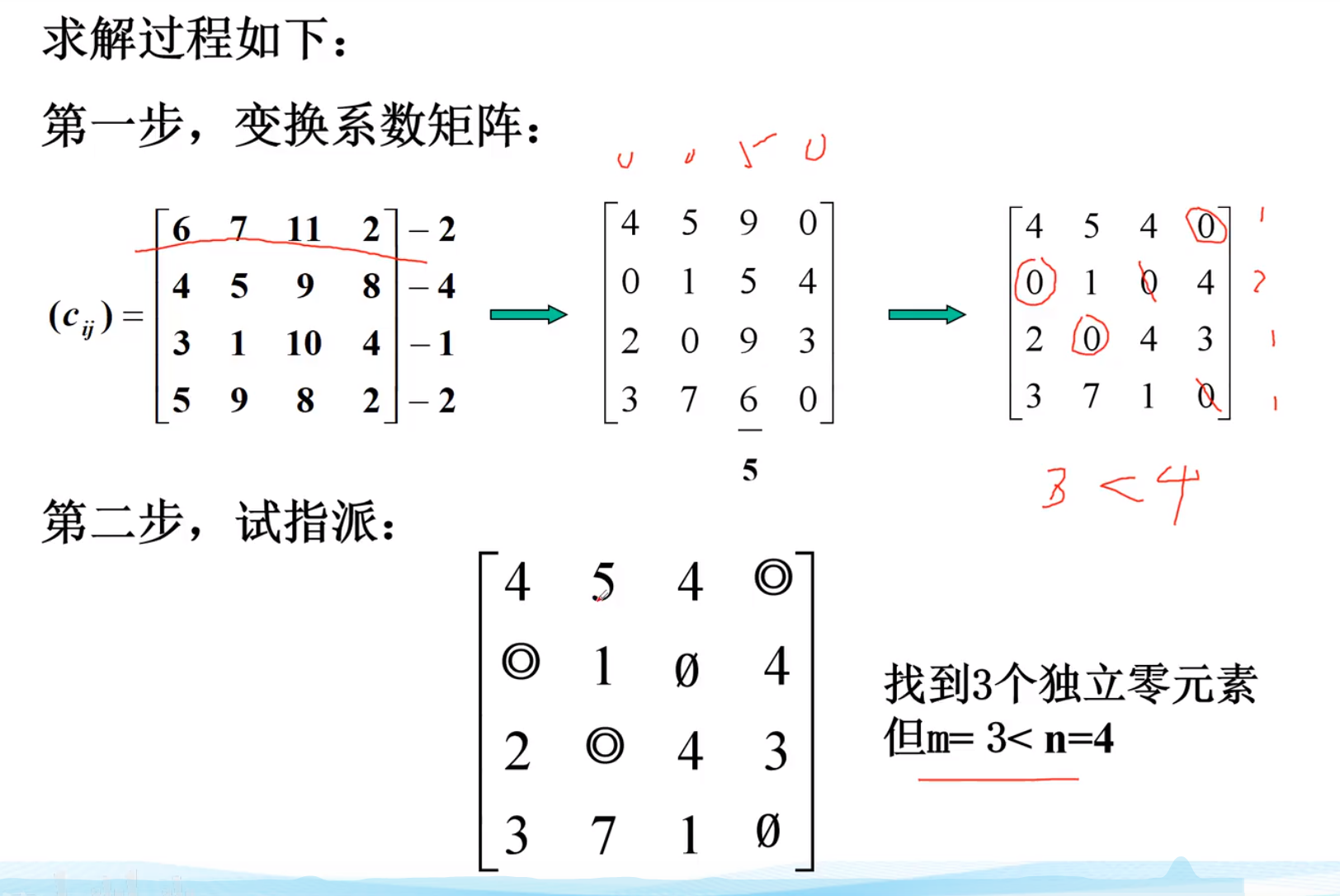
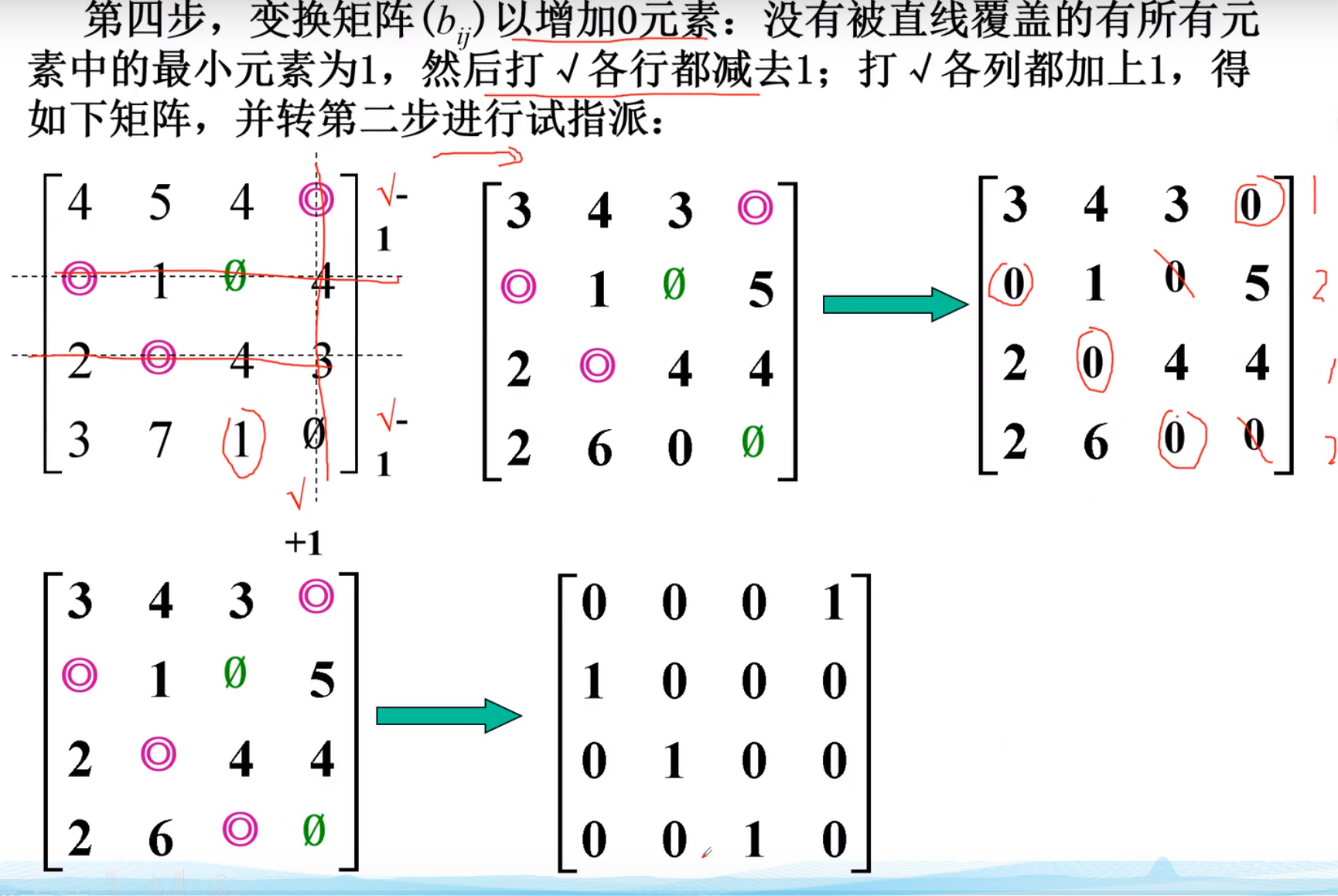
-匈牙利算法


先将矩阵进行初等变换,然后再行列(列行)依次划啊划,直到没有可划的了
行列行列交替进行


实例-1
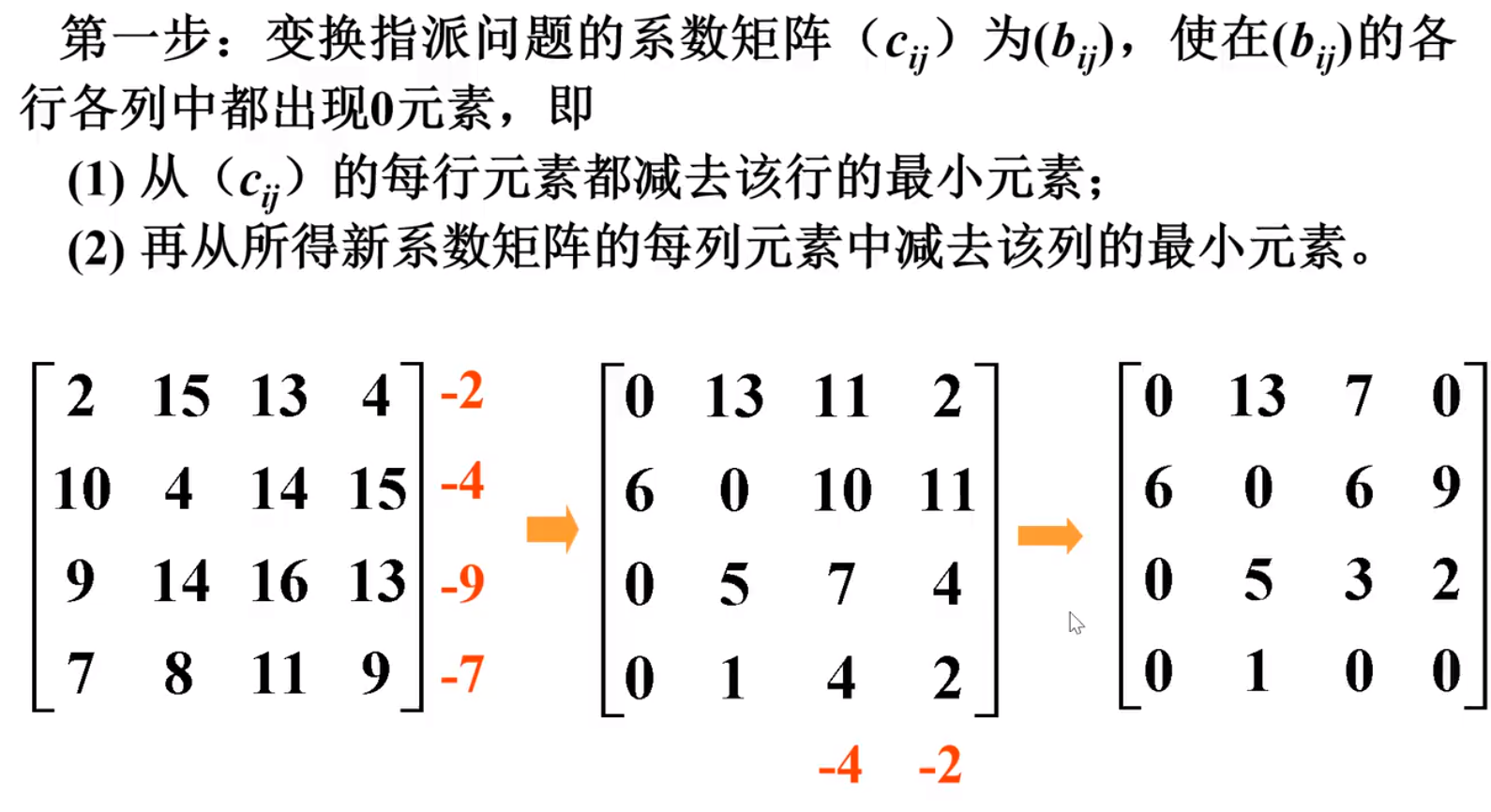

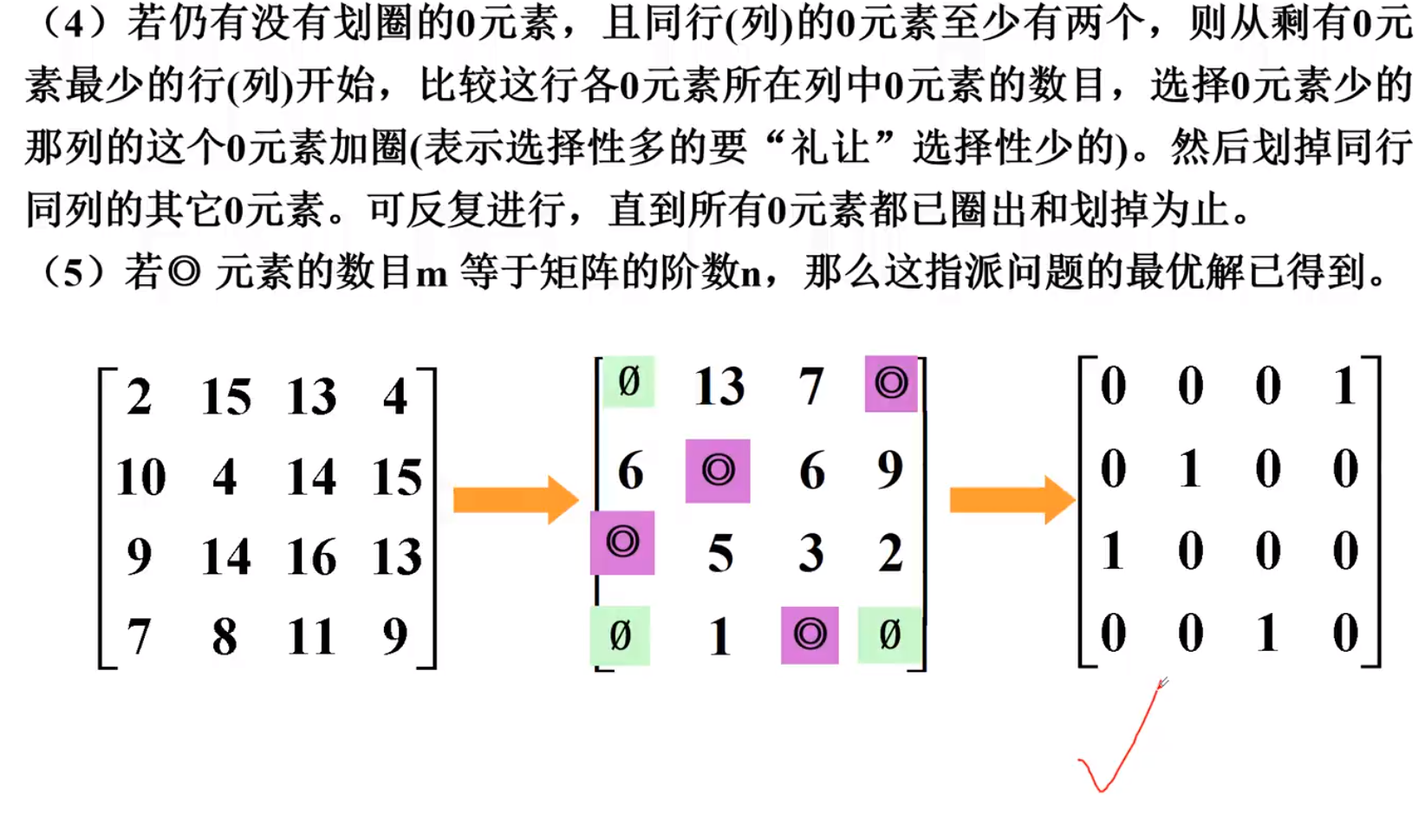
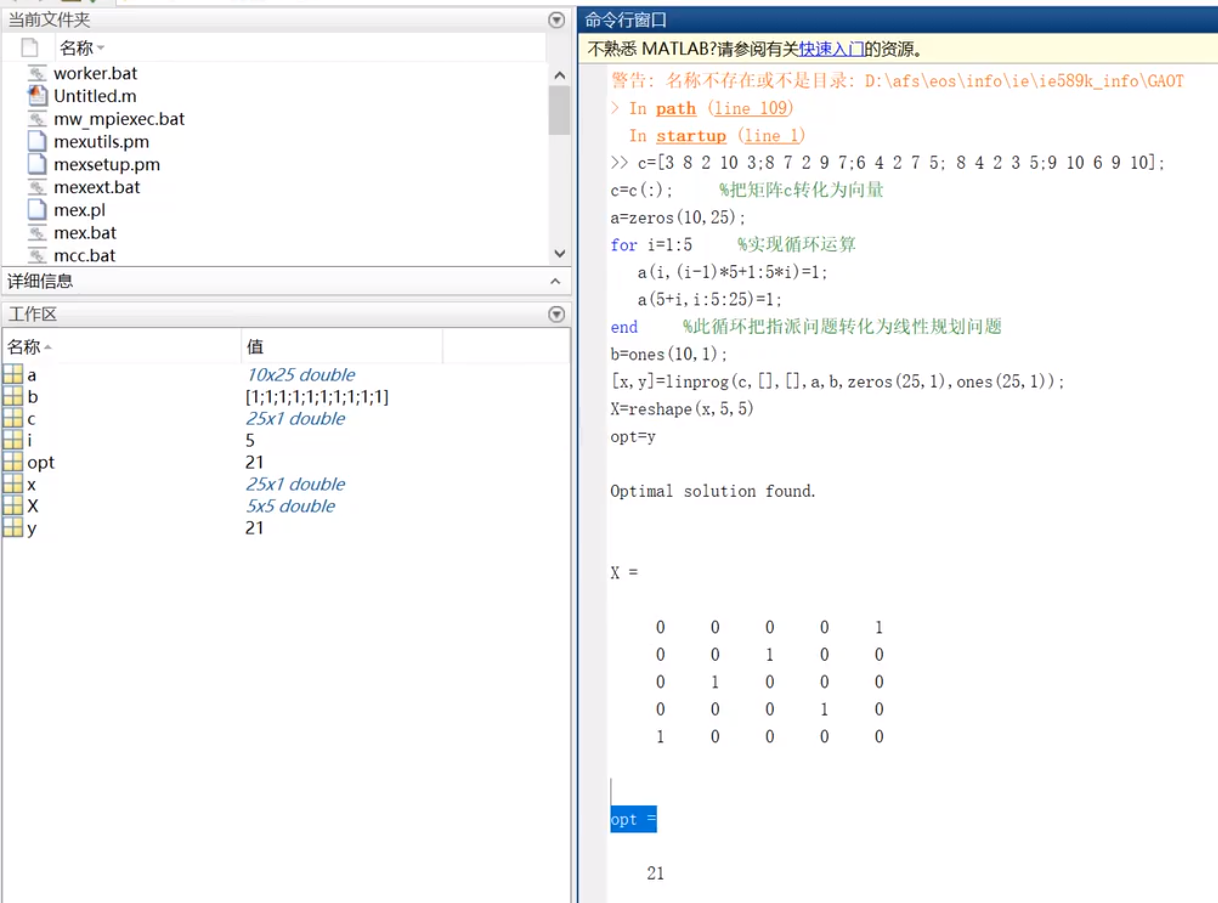
实例-2
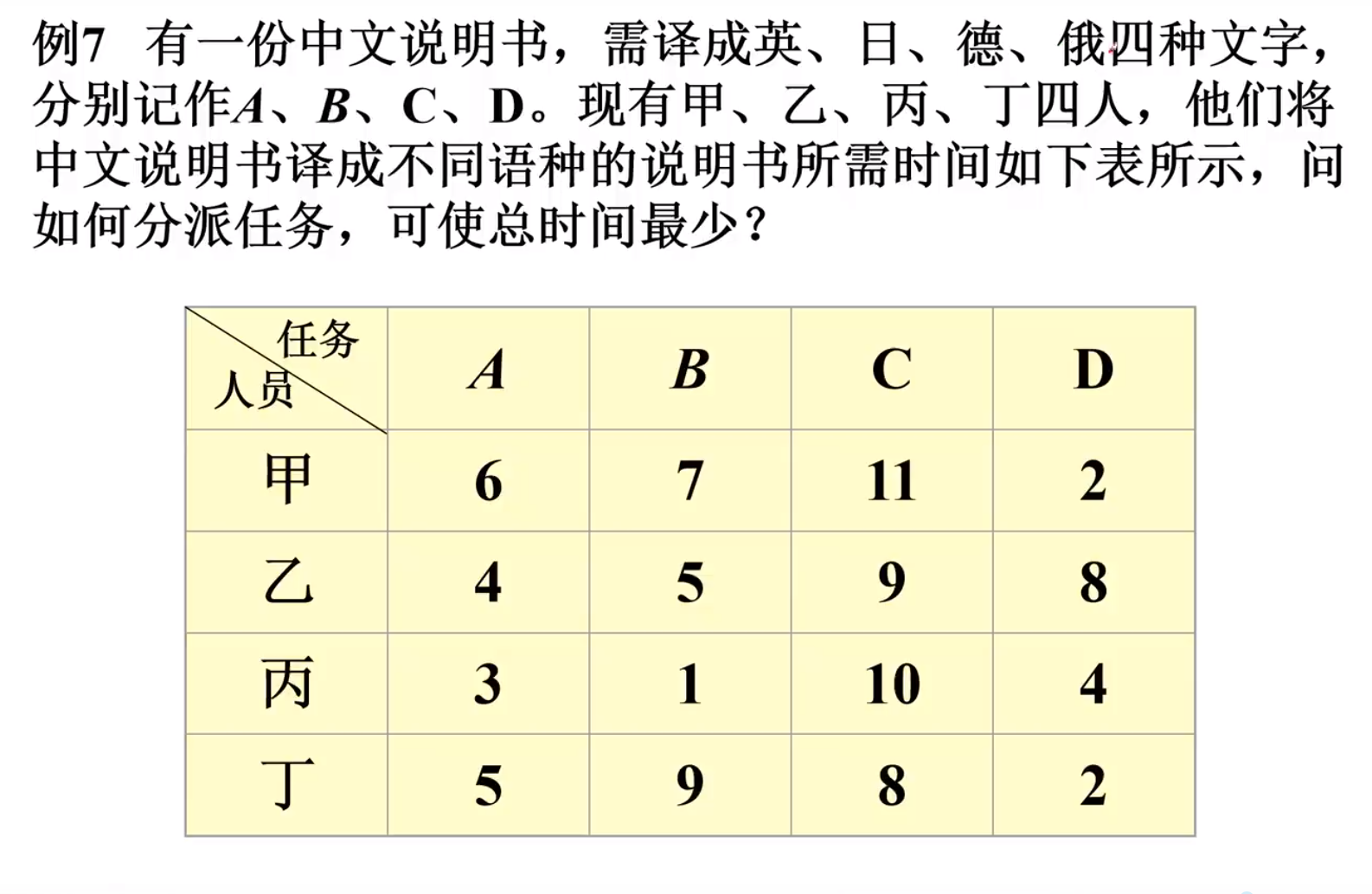


非线性规划(NP)
只要不是y = a1x1 + a2x2……这种类型,其他的一般都属于非线性函数
线性函数通常就是一次函数的别称

数学模型


注意:x0为初始值,例如有三个,可以直接rand(3,1),来代表这个位置,生成三个初始值,3为列,1为行,而matlab默认变量储存方式都是列储存的,故就这样ok
其中,初值最开始随机设置的,如果之后得到了另外一组和初值规格一样的数据(返回值x)
可以用x回代成初值进一步尝试,如果接下来得到的结果比之前那个好,那么用这个,反之,用那个就可以了

投资决策问题


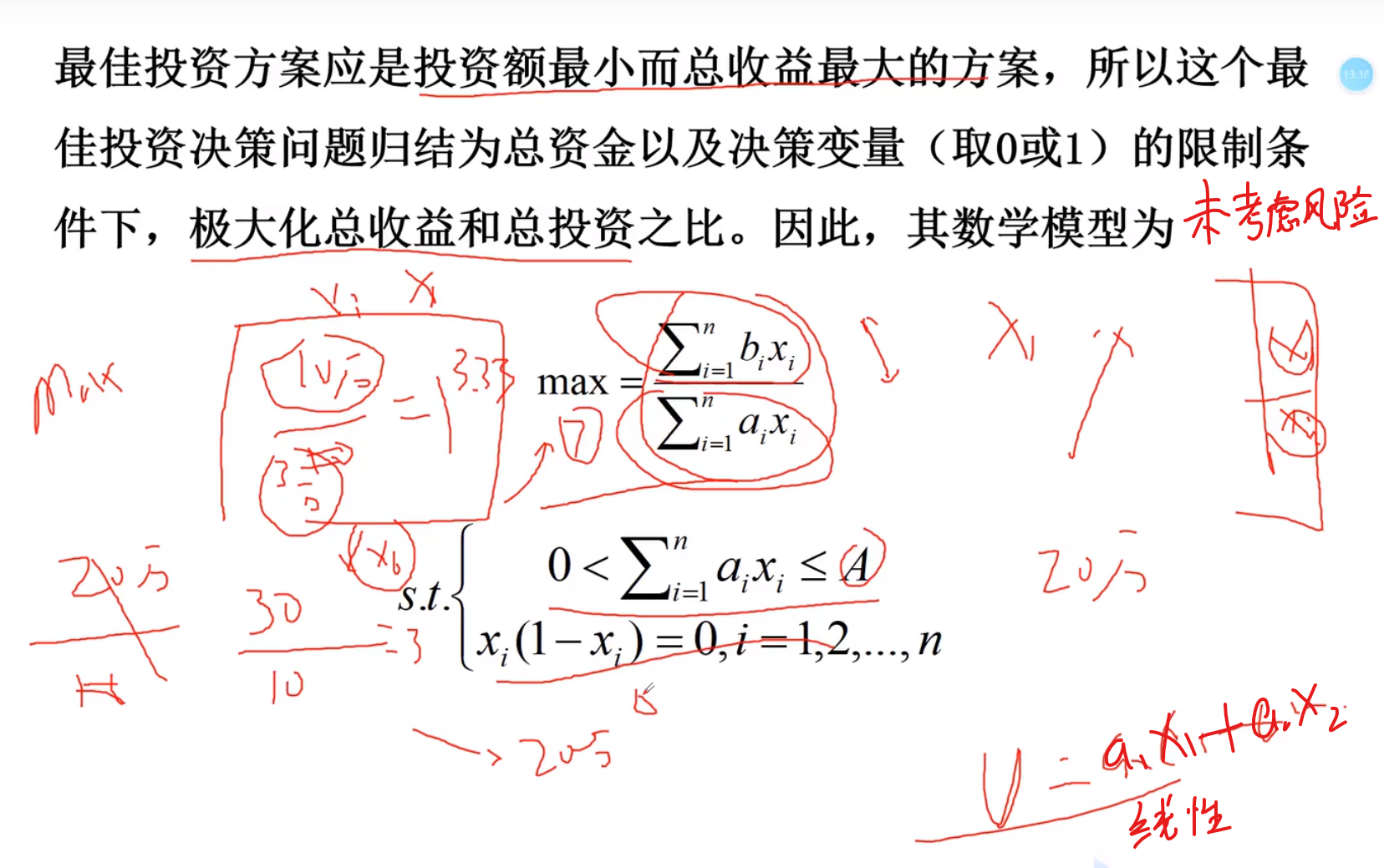
使用模型的例题

对应上面数学模型的规范,依次改变形式放就是(注意c(x) = 0 < 0 这种,他们右边都是0,做的时候如果右边有,要移动到左边去)都要变换式子,将全部移到<号左边,或者>号右边

(1)中的是点乘,也就是每一个里面的元素都^2
这里是伪式子
二次规划
数学模型


实例
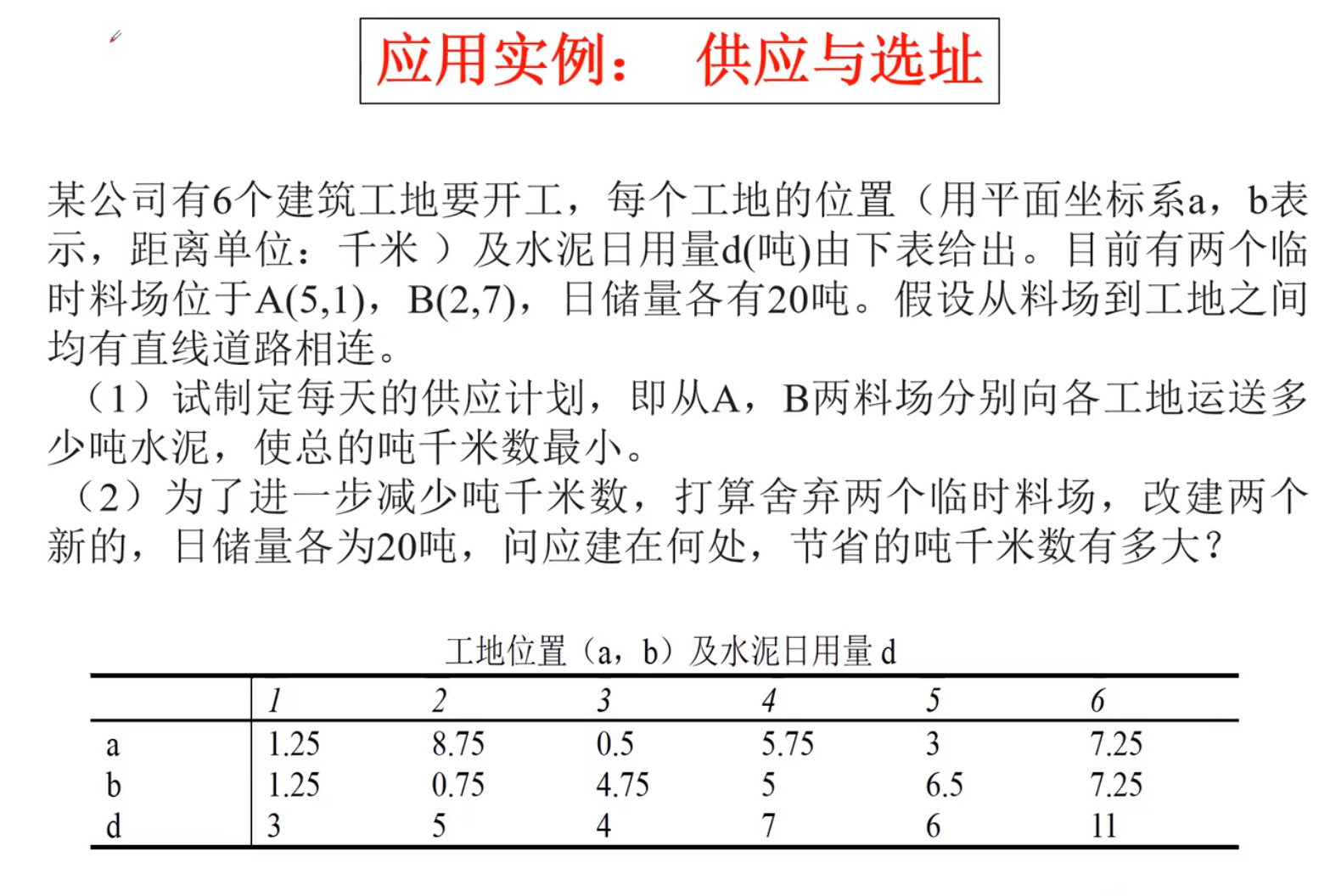
建立模型


代码


第二个程序
liaoch.m

guing2.m


后四位为坐标地址
层次分析法(AHP)评价
评价类题型

基本概述


基本原理

方法和步骤

步骤归纳


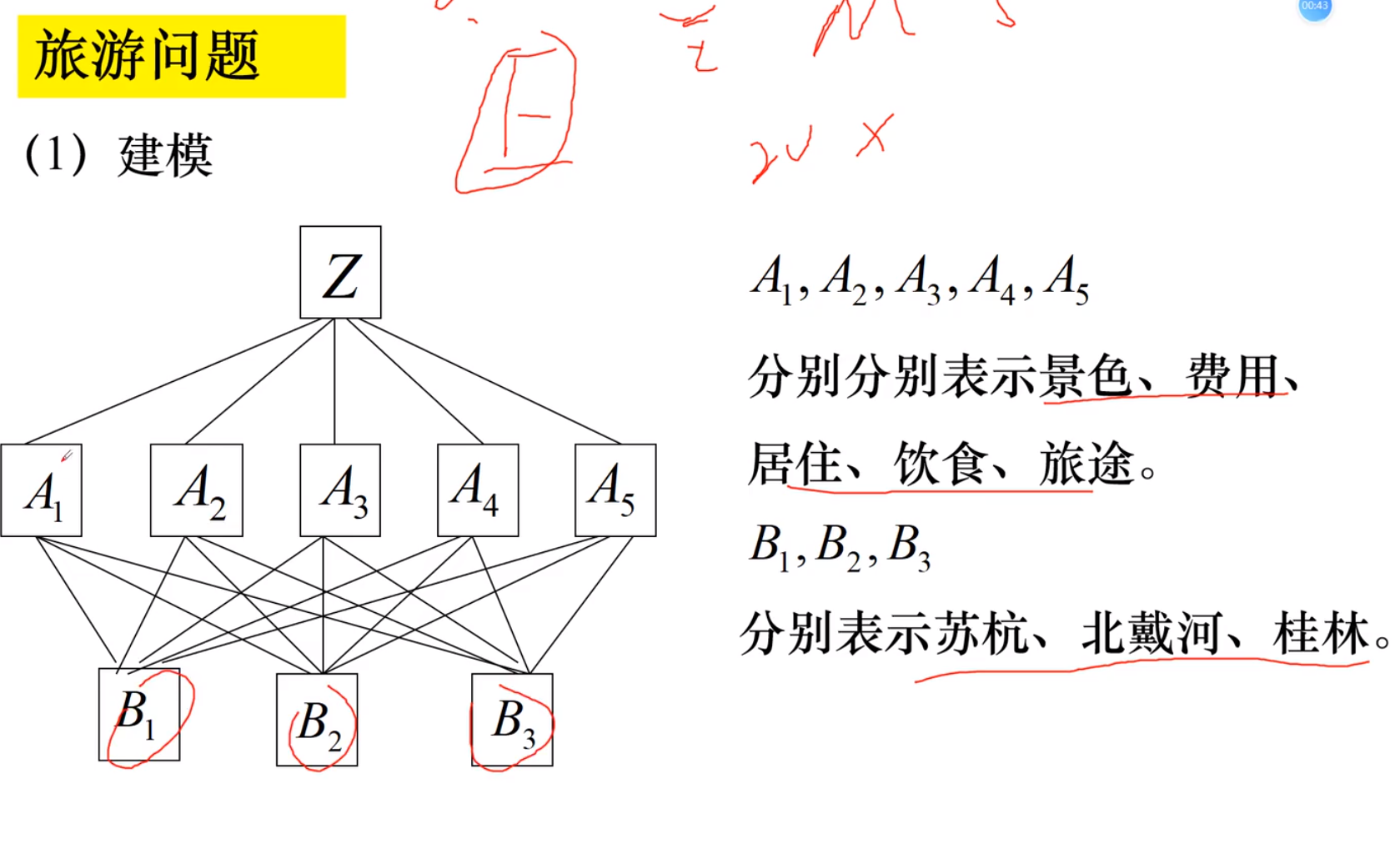
1.建立层次结构模型

例子:

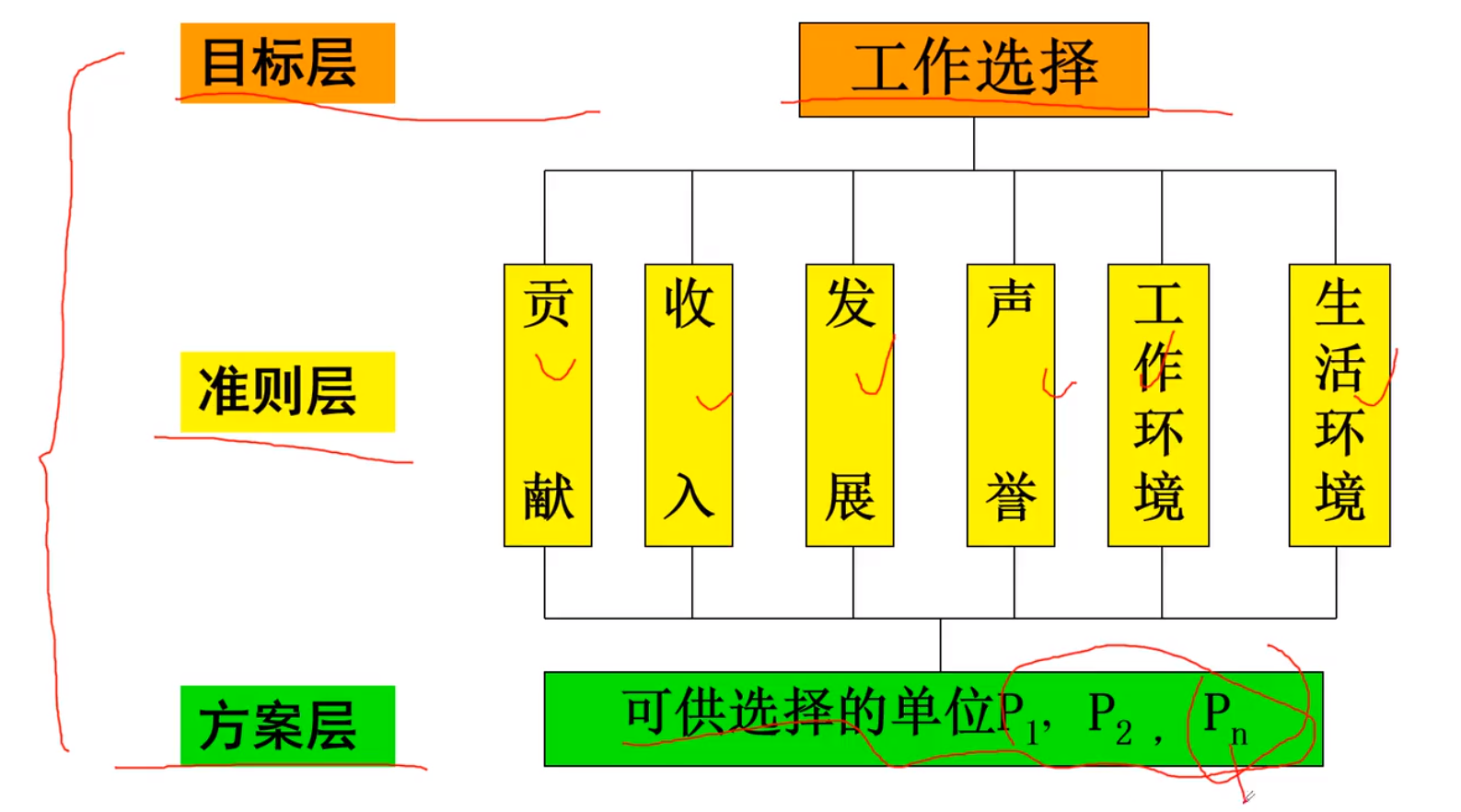
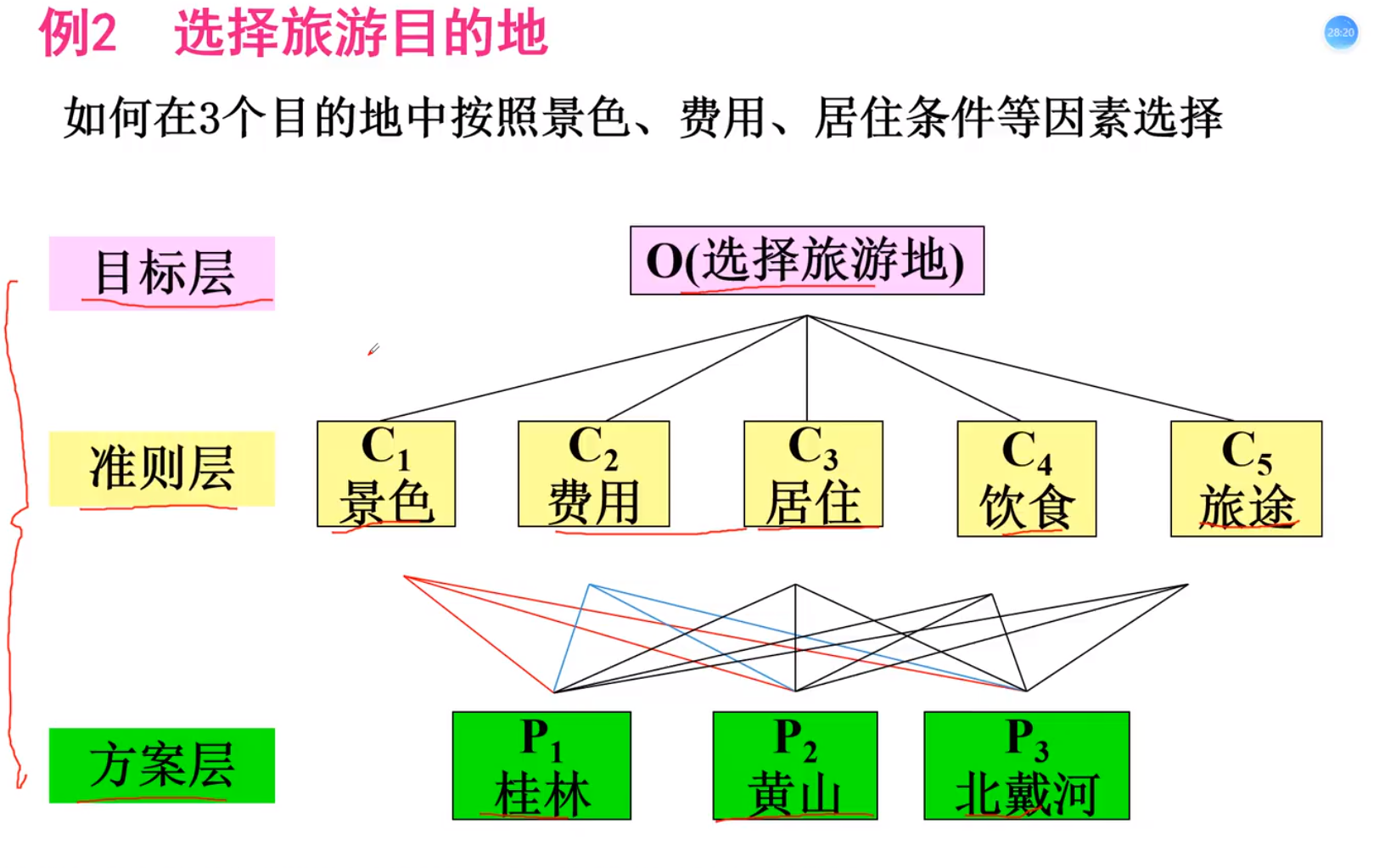
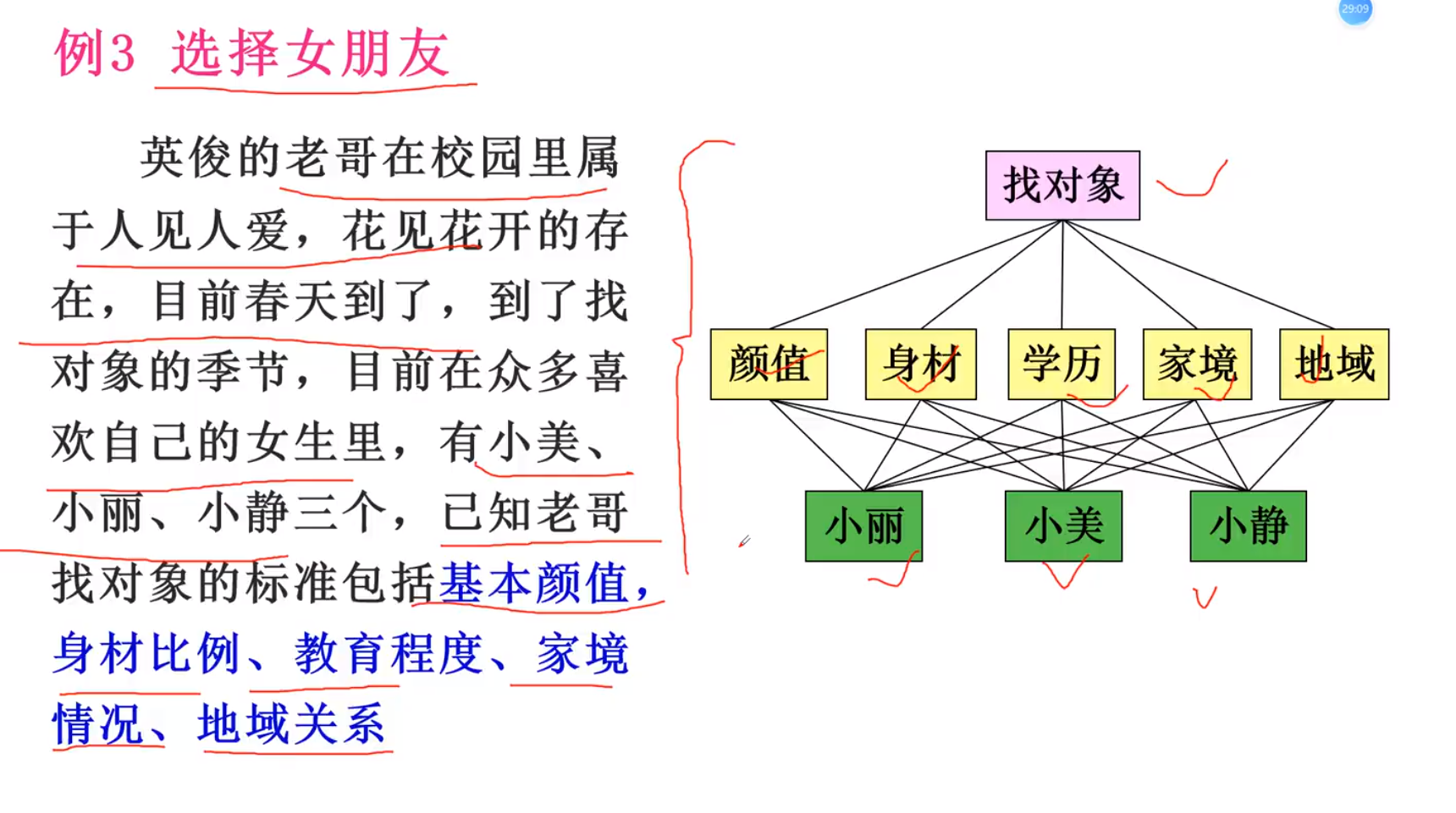


如果a:b是5那么b:a是1/5; 两个因素判断互为倒数
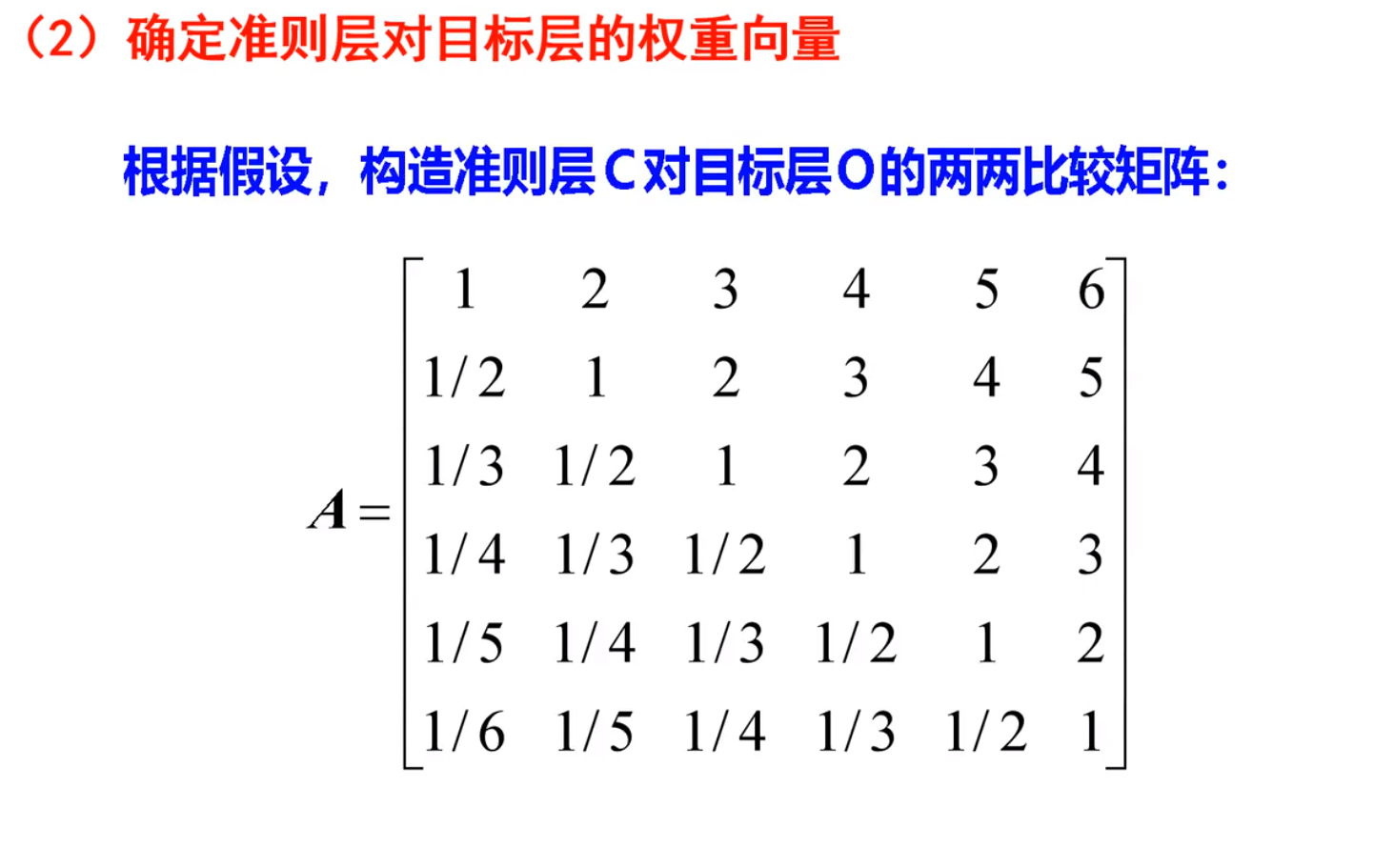
2.构造目标矩阵
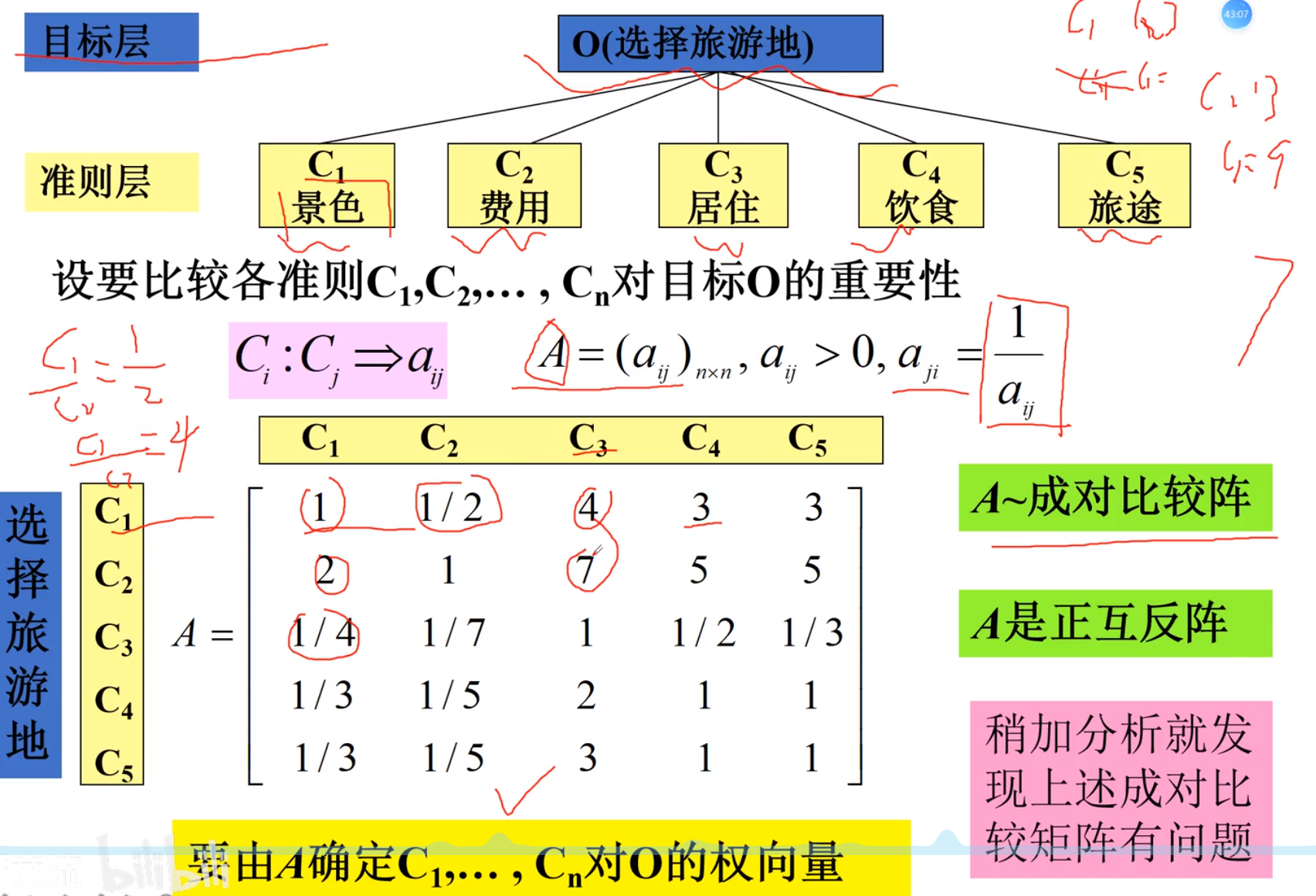
3.计算向量,一致性检验
出现问题,边际效应类似

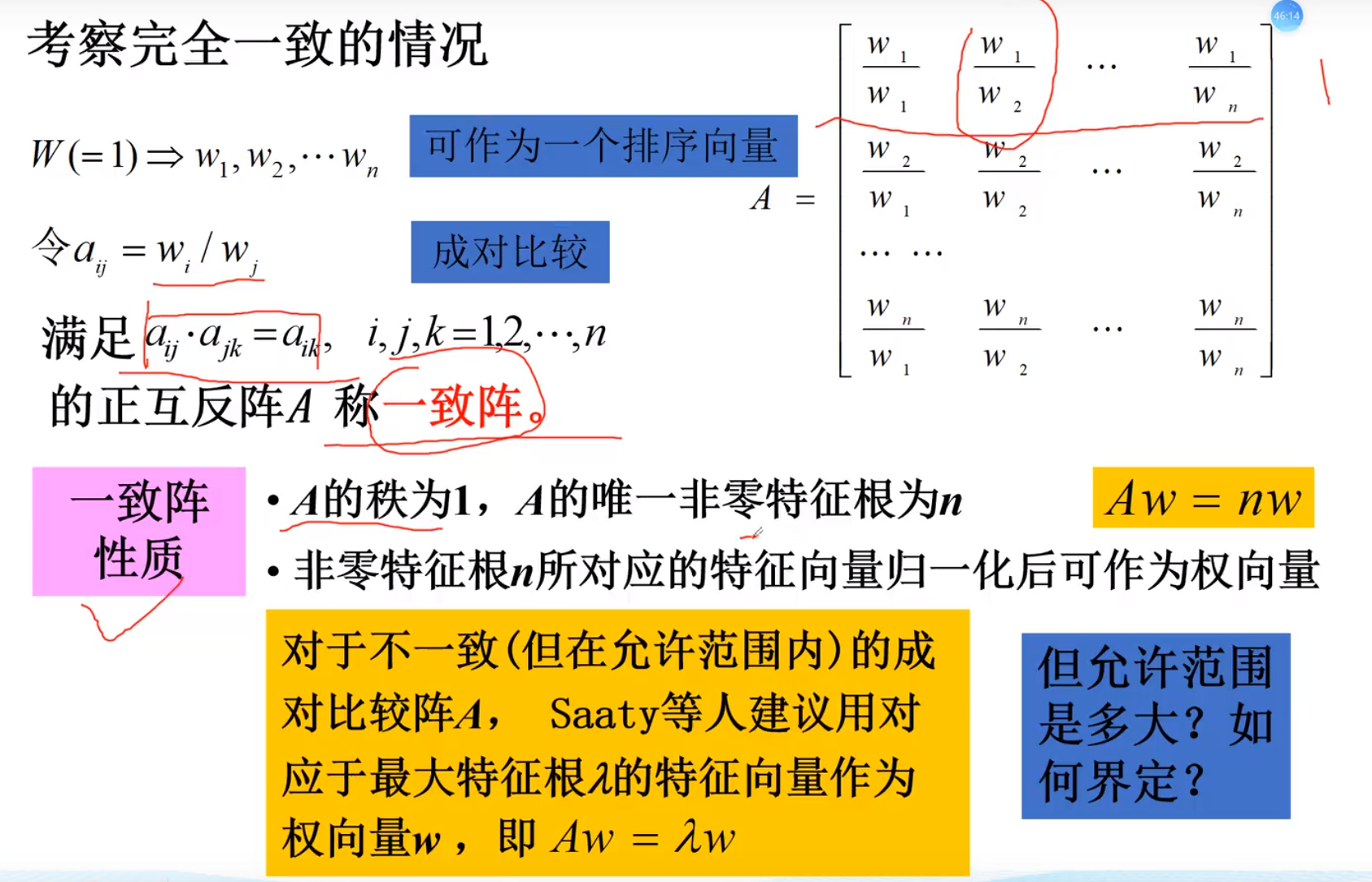
层次单排序


但是无法衡量满意的标准,因此
一致性检验
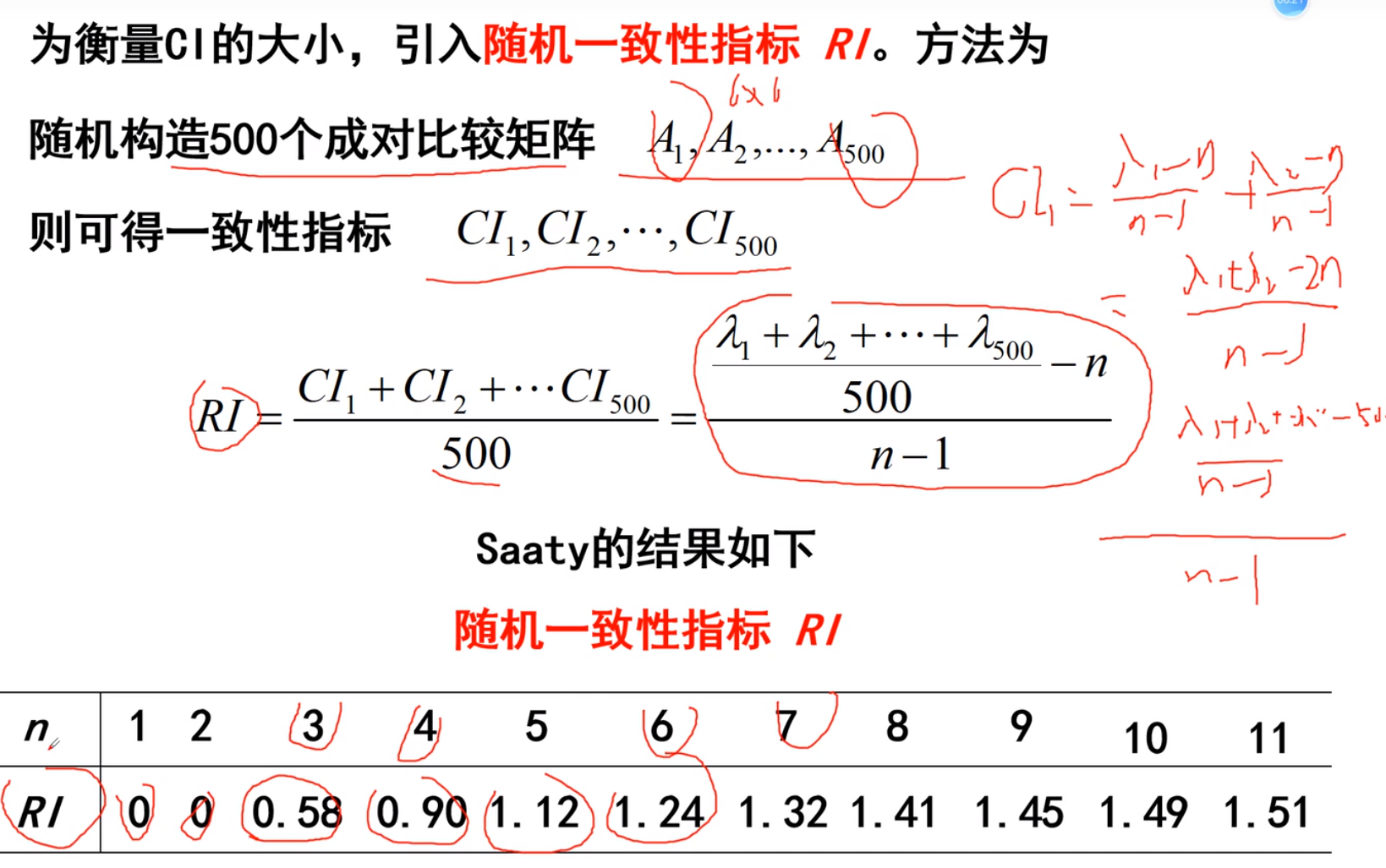

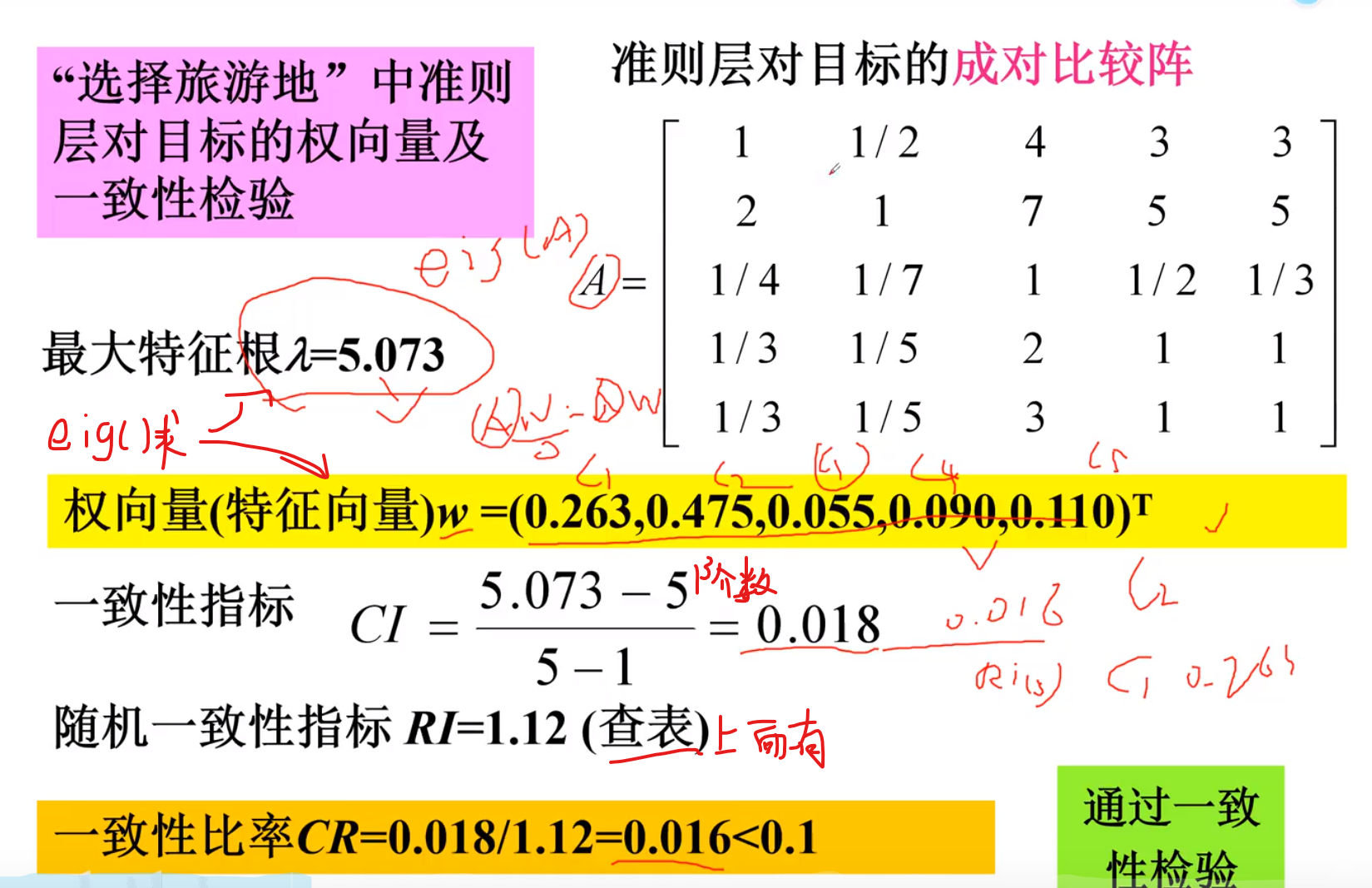

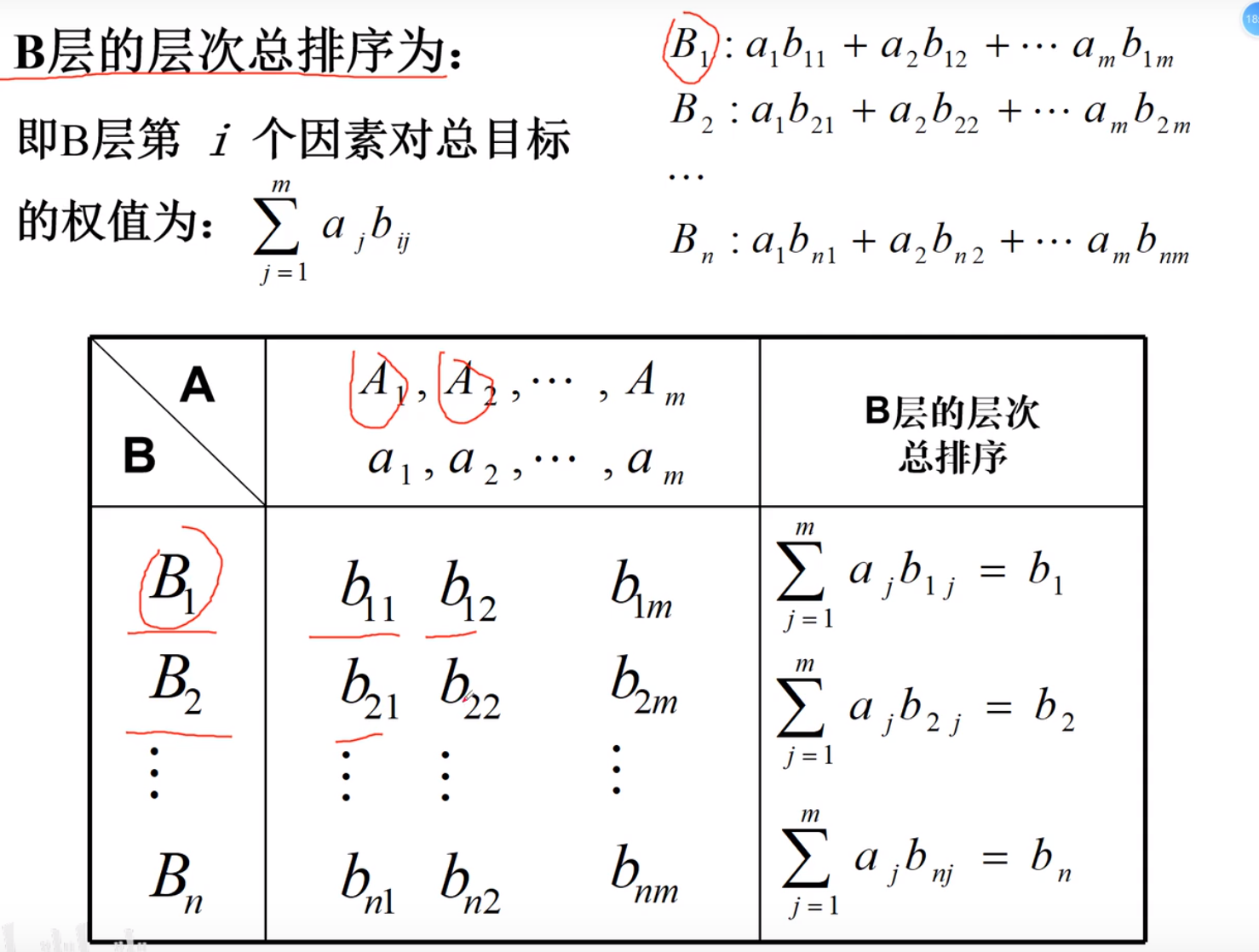
层次总排序
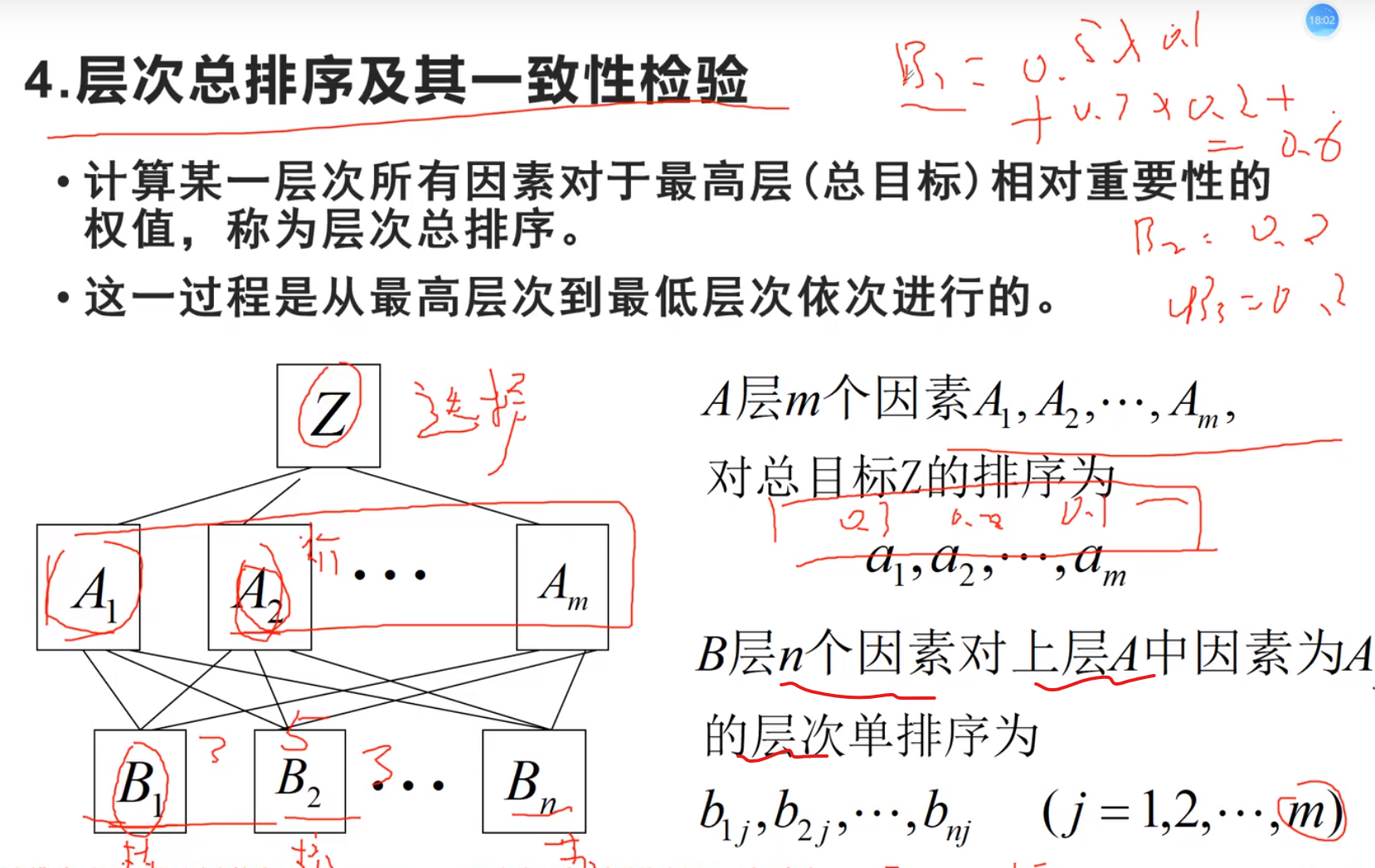
对于Ai 每一个b都判断一次,拍出对于Ai这一个指标来讲,b1,b2….的权重结果
再将Ai占A1,A2….的综合的权重相乘,就成了b1的一个小权重
一致性检验

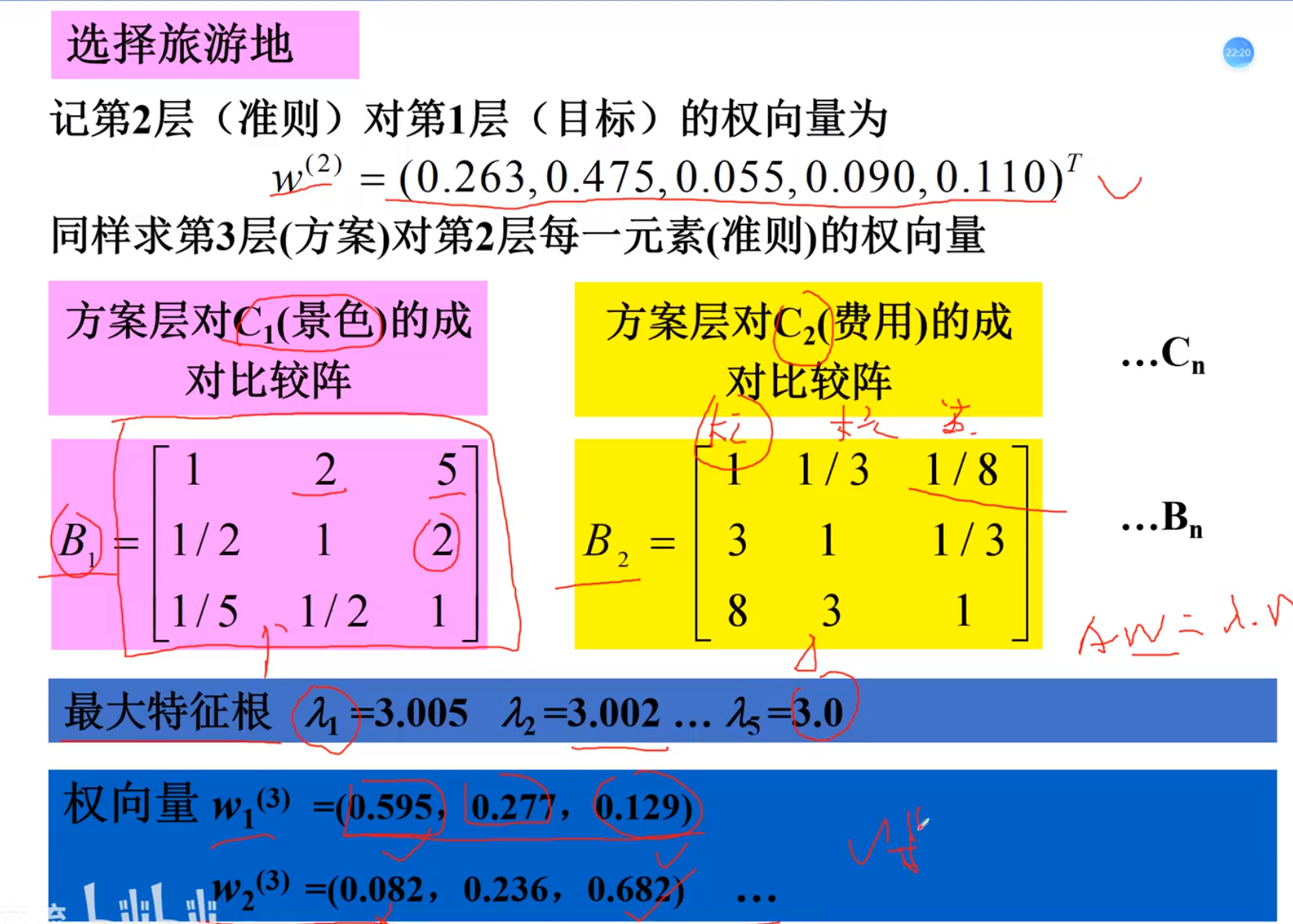
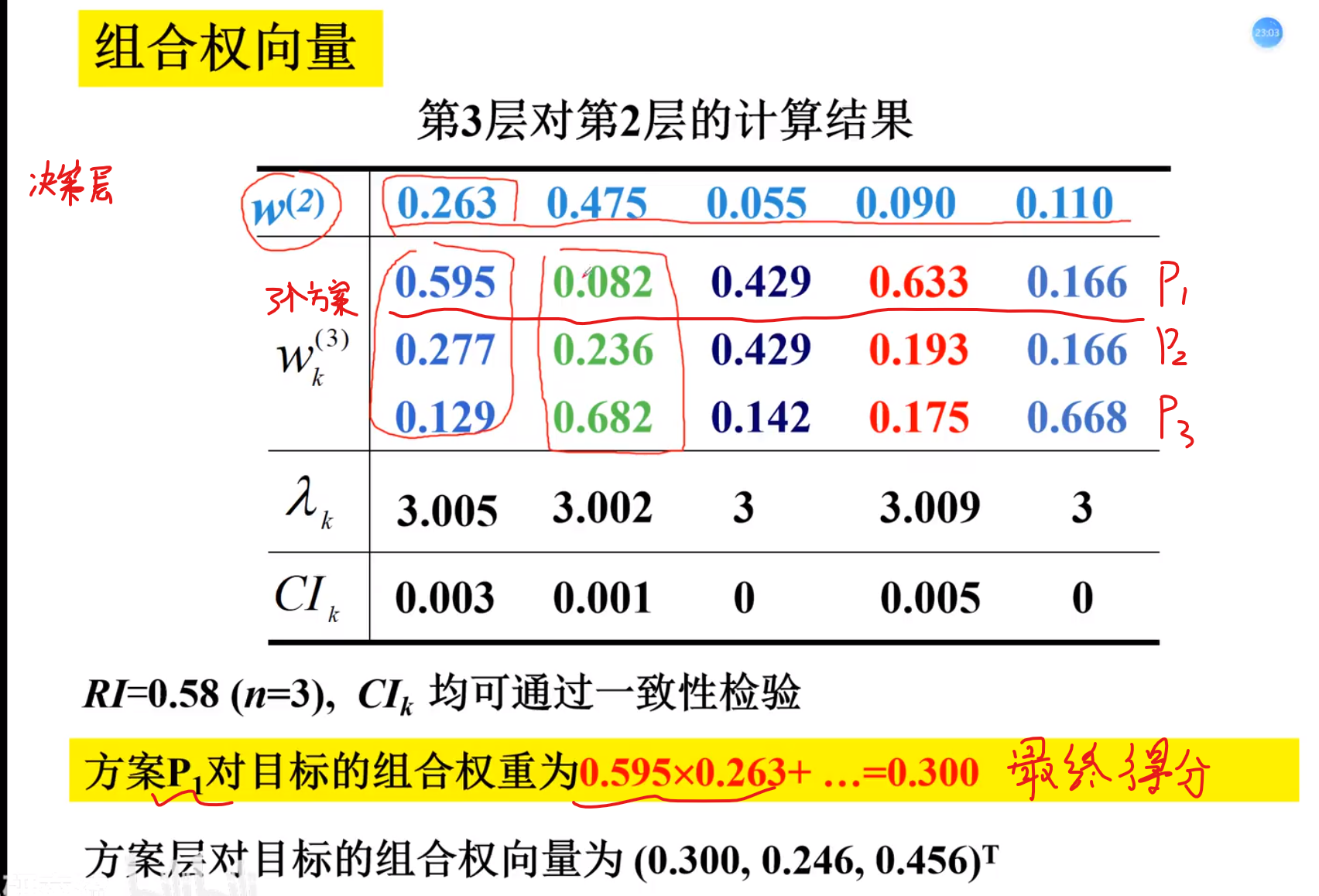
建模实例


一定要进行归一化检验!!!!!可能最后结果不为1(特征向量)规划方程 过程就是把全部加起来,然后用需要归一化的数据x除以全部,得到在全部的比值
案例
问题提出

数据
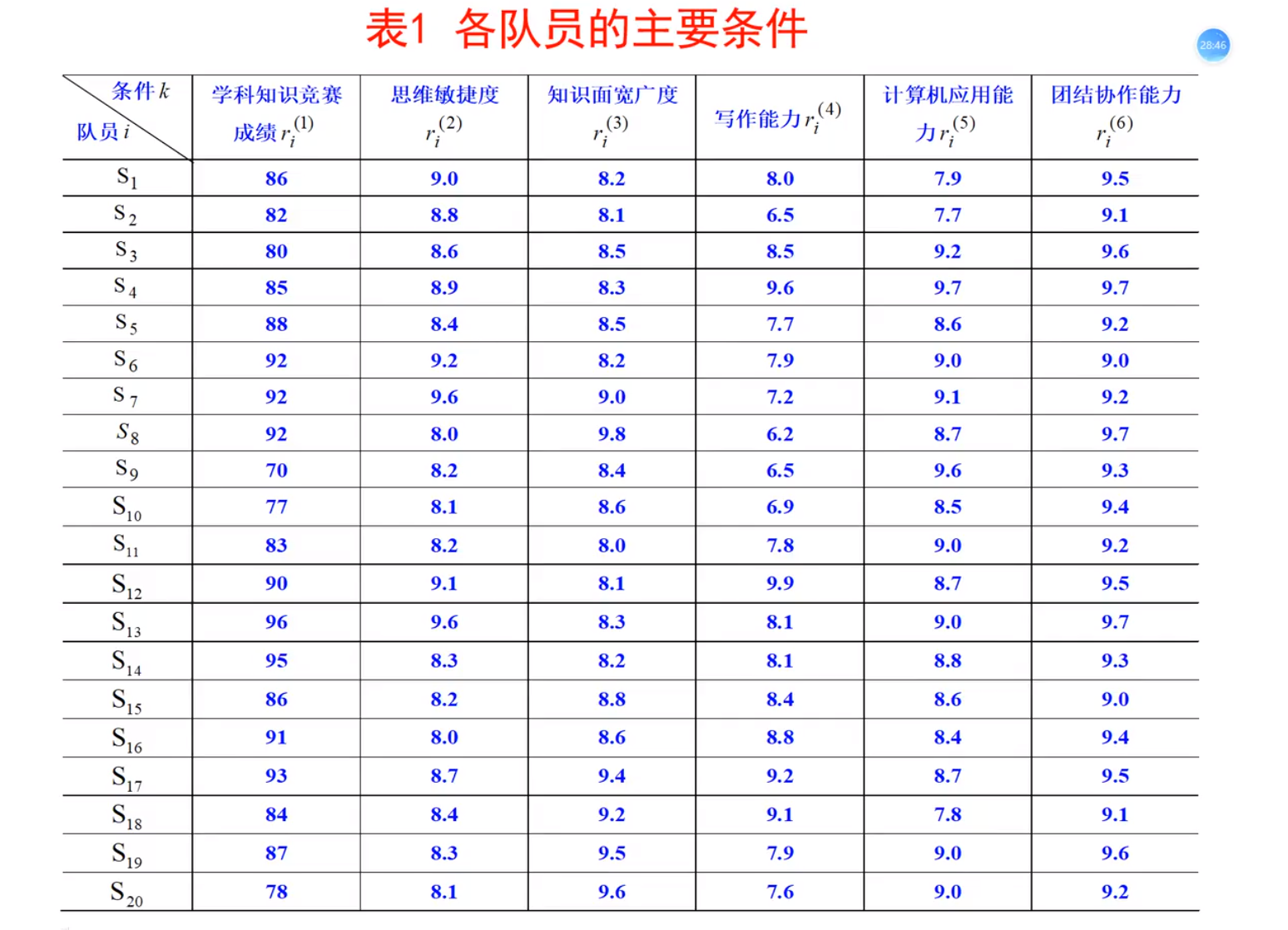
问题假设


模型的建立与求解









灰色系统分析
适用场景




第五题提意见,一定要结合前面的内容
主要内容提纲
灰色预测概念
(1)灰色系统、白色系统和黑色系统
白色系统是指一个系统的内部特征是完全 已知的,即系统的信息是完全充分的
黑色系统是指一个系统的内部信息对外界 来说是一无所知的,只能通过它与外界的 联系来加以观测研究。 (多次尝试)
灰色系统内的一部分信息是已知的,另一 部分信息是未知的,系统内各因素间有不 确定的关系。(少量尝试)
(2)灰色预测法
灰色预测法是一种对含有不确定因素的系 统进行预测的方法。
灰色预测是对既含有已知信息又含有不确定 信息的系统进行预则,就是对在一定范围内 变化的、与时间有关的灰色过程进行预测
灰色预测通过鉴别系统因素之间发展趋势的相异程 度,即进行关联分析,并可对原始数据进行生成处 理来寻找系统变动的规律,生成有较强规律性的数 据序列,然后建立相应的微分方程模型,从而预测 事物未来发展趋势的状况
灰色预测法用等时距观测到的反映预测对象特征 的一系列数量值构造灰色预测模型,预测未来某 一时刻的特征量,或达到某一 特征量的时间
(3)灰色预测的四种常见类型
- 灰色时间序列预测 即用观察到的反映预测对象特征的时间序 列来构造灰色预测模型,预测未来某一时刻 的特征量,或达到某一特征量的时间。
- 畸变预测 即通过灰色模型预测异常值出现的时刻, 预测异常值什么时候出现在特定时区内。
- 系统预测 通过对系统行为特征指标建立一组相互 关联的灰色预测模型,预测系统中众多 变量间的相互协调关系的变化。(用的很少)
- 拓扑预测 将原始数据做曲线,在曲线上按定值寻 找该定值发生的所有时点,并以该定值 为框架构成时点数列,然后建立模型预 测该定值所发生的时点。
灰色关联度与优势分析(评价)





案例分析
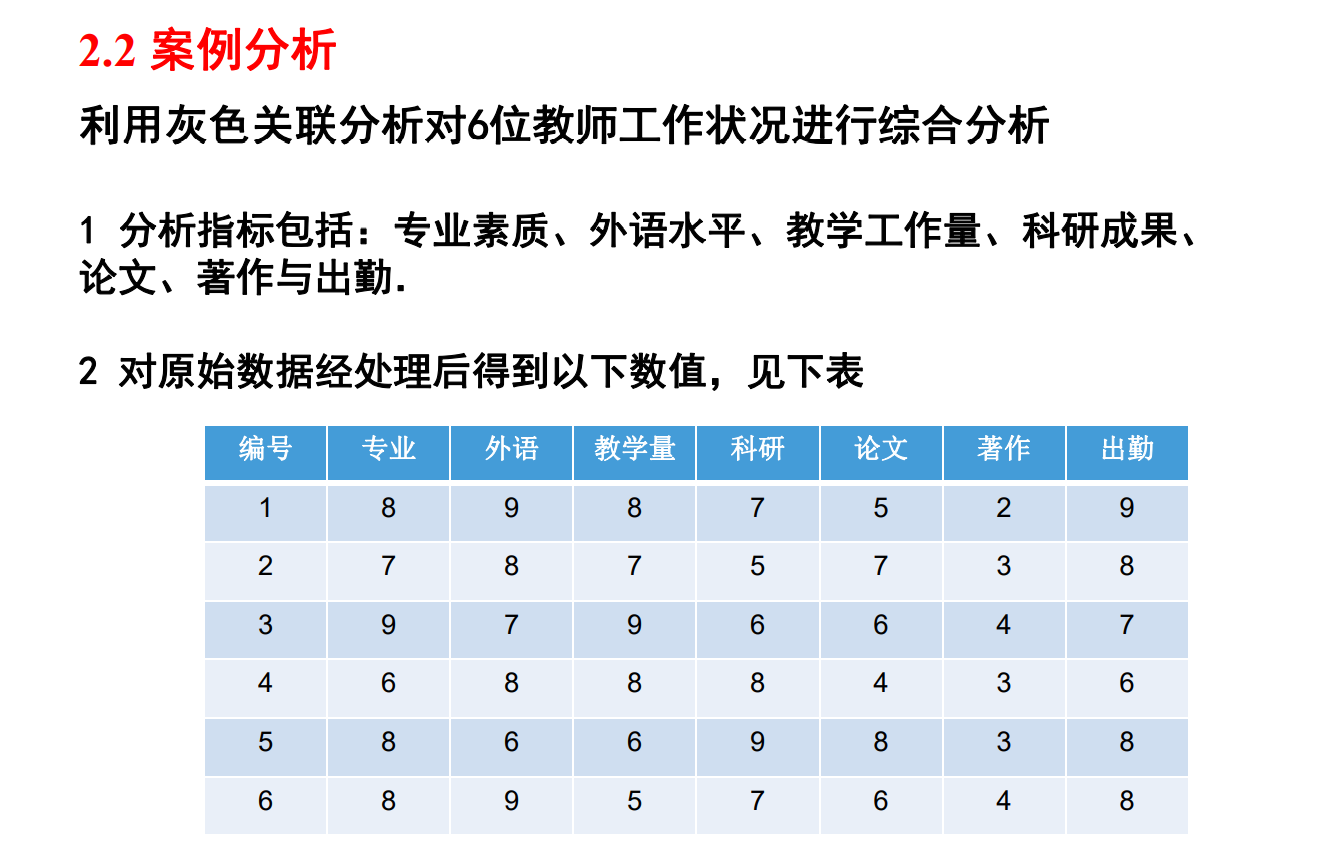
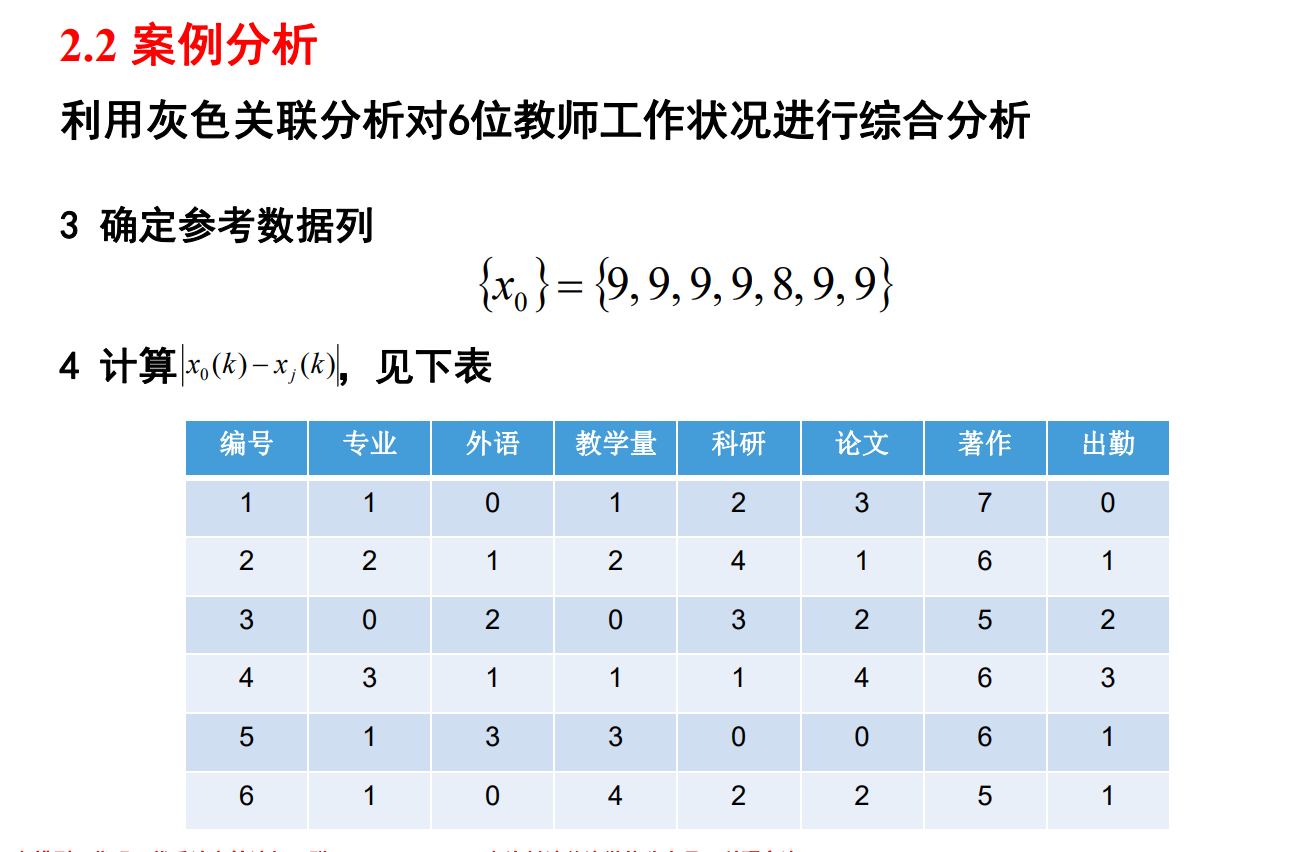

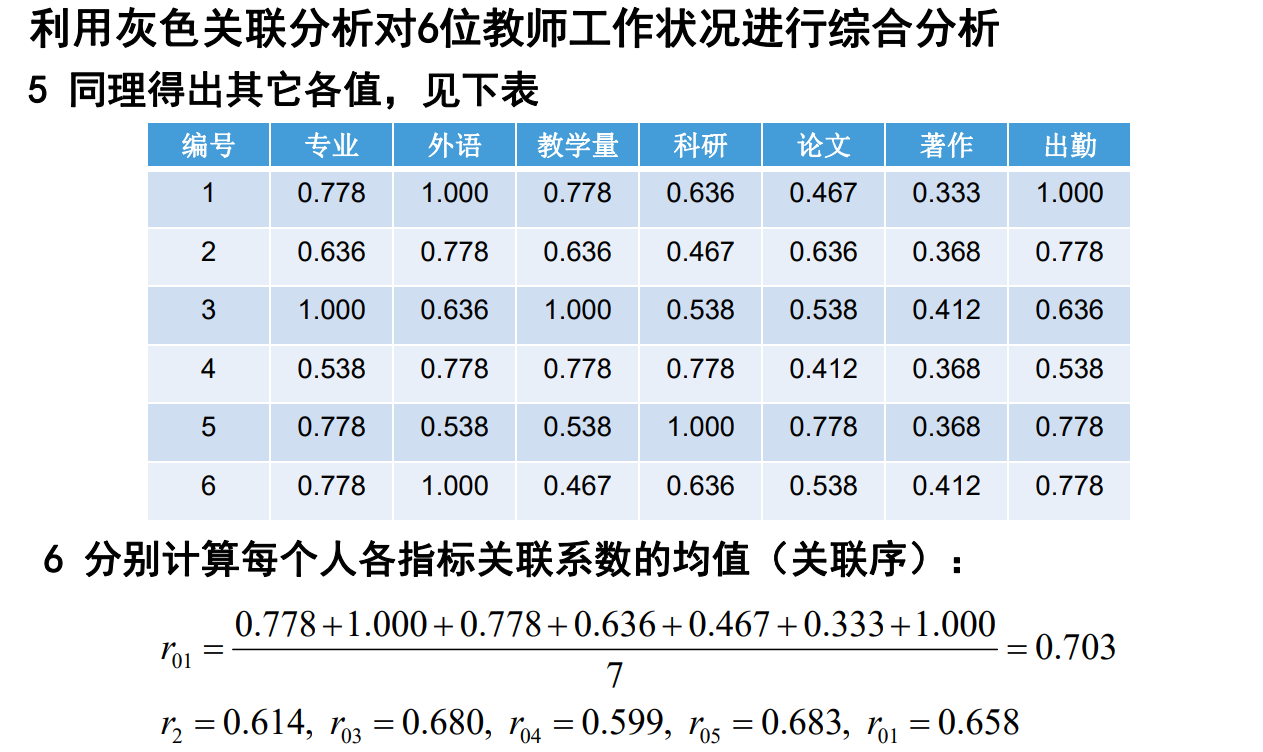
灰色生成数列

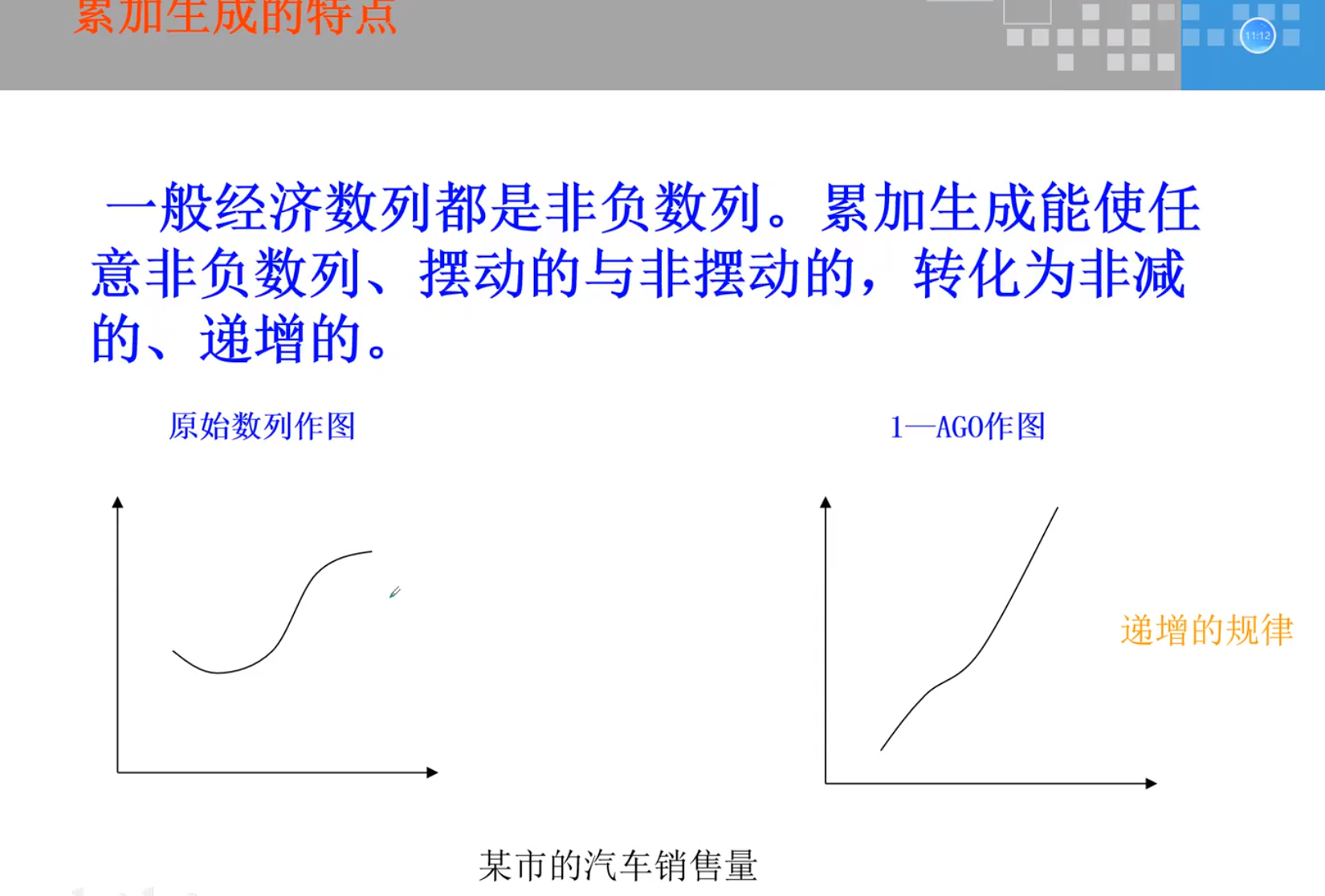
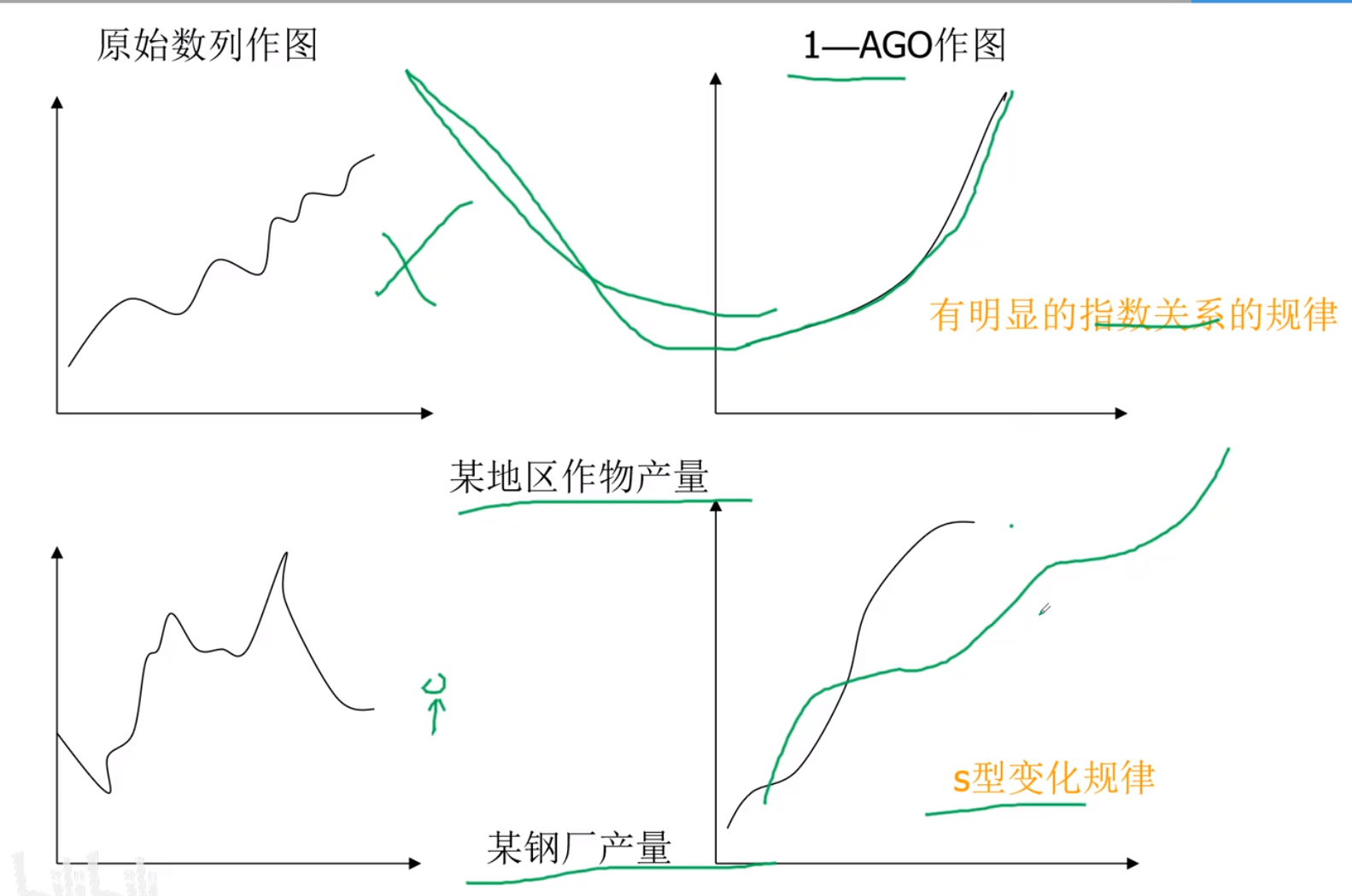
累加生成

该项与前一项相加,为高阶的该项

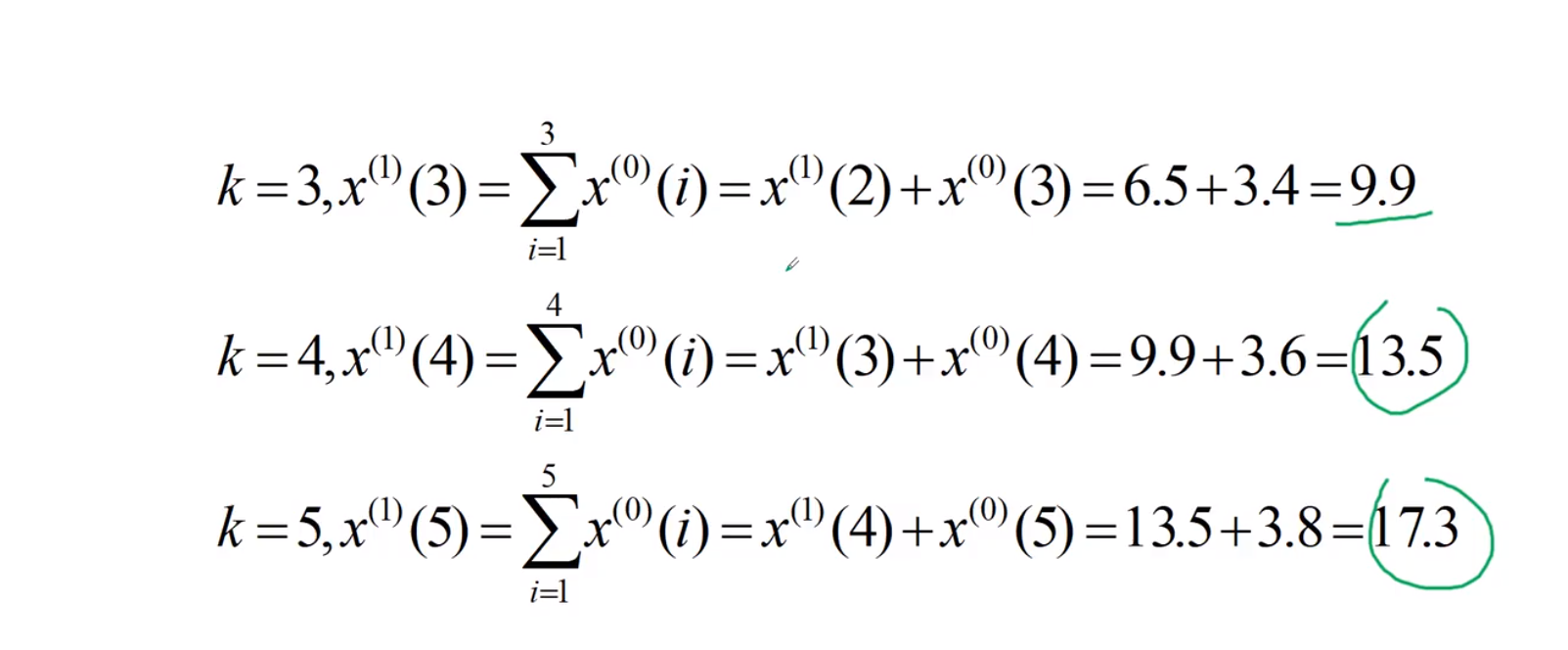
累减生成(累加的逆过程)


该项与前一项相减等于低阶的该项

灰倒数,相似倒数,不是倒数
灰色模型

故不是真正的微分方程

灰色预测(预测)
1.检验级比
2.建微分方程
3.残差检验
使用灰色预测,一定要加上,经过数列的级比检验,本文采用灰色预测模型

使得数据成功。符合模型使用条件,再建立GM模型



实例



B的解法,上面灰色模型部分有

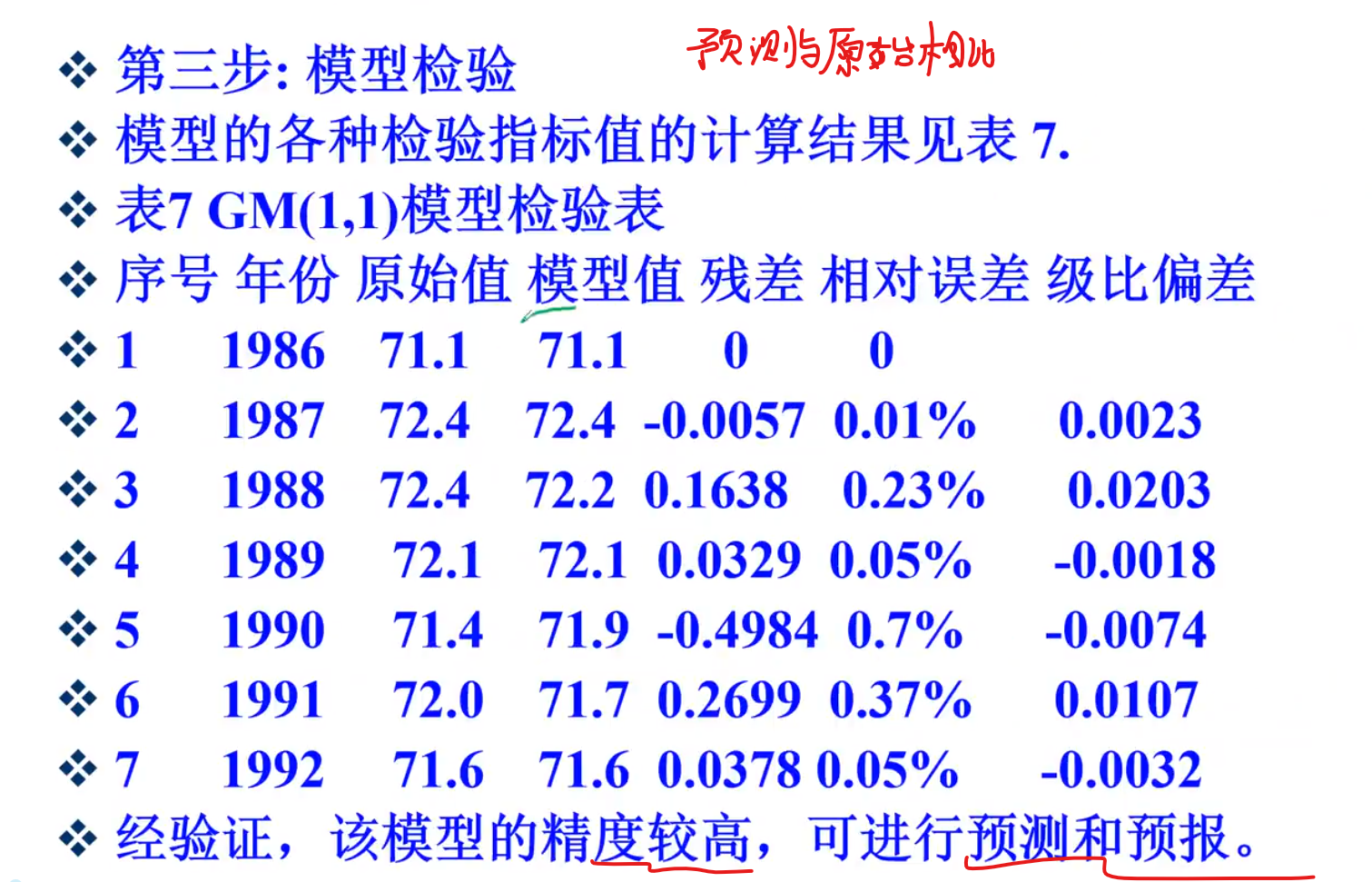
残差公式上面也有,级比偏差也是
残差和级比残差有一个比较小,就说明模型可以了,只要满足一个就可以了,可以用于预测!
以此得出结果!
SARS模型实例
问题提出


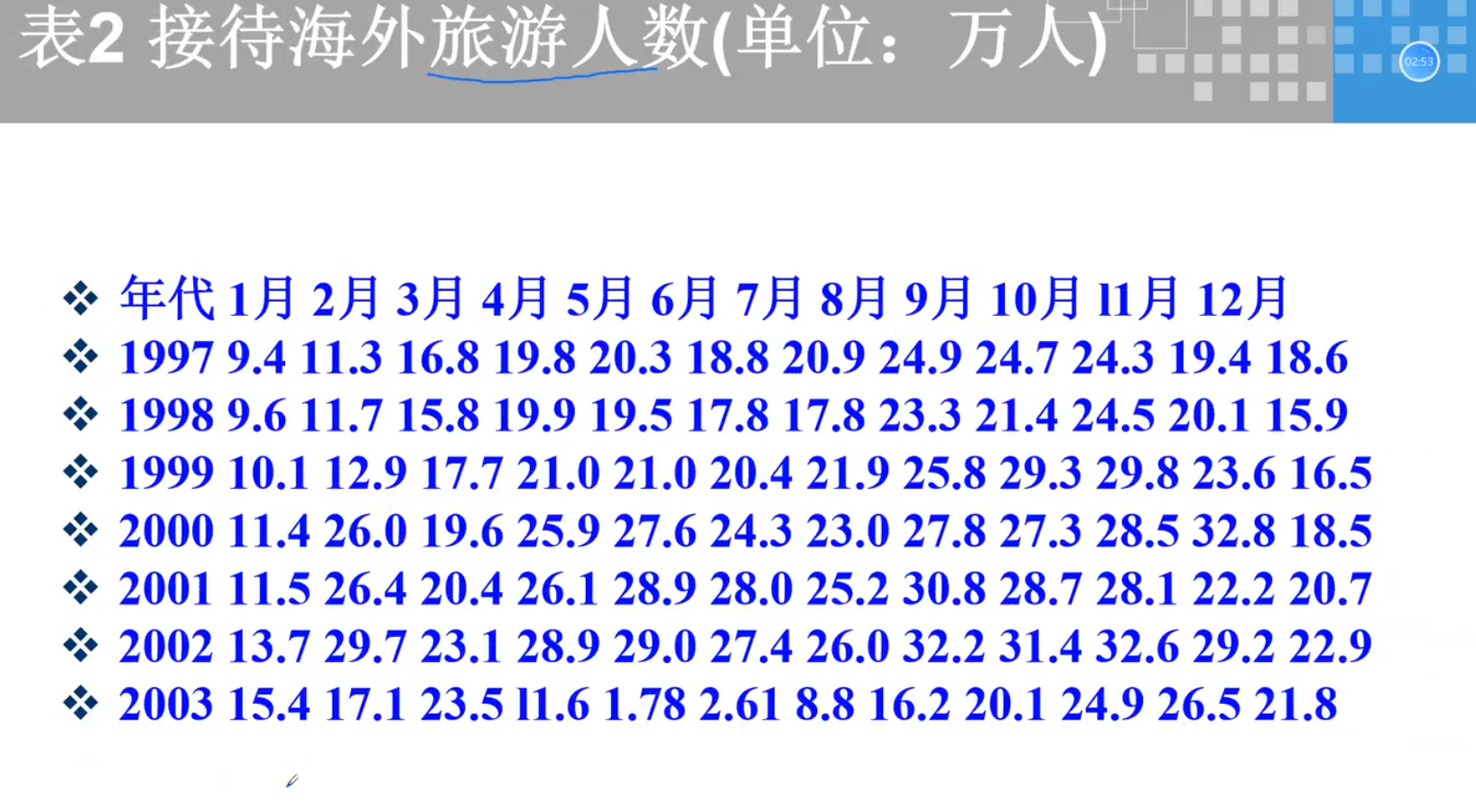

预测出03年和实际的作比较,两者的差距就是影响
模型的分析和假设


建立灰色预测模型


模型的求解




模型结果分析


插值和拟合
拟合是插值的外延,插值是拟合的特殊形式

插值
推导在范围内的数据 已知离散求连续
灰色预测不一定满足拟合检验,这是求一组离散数之间的数据
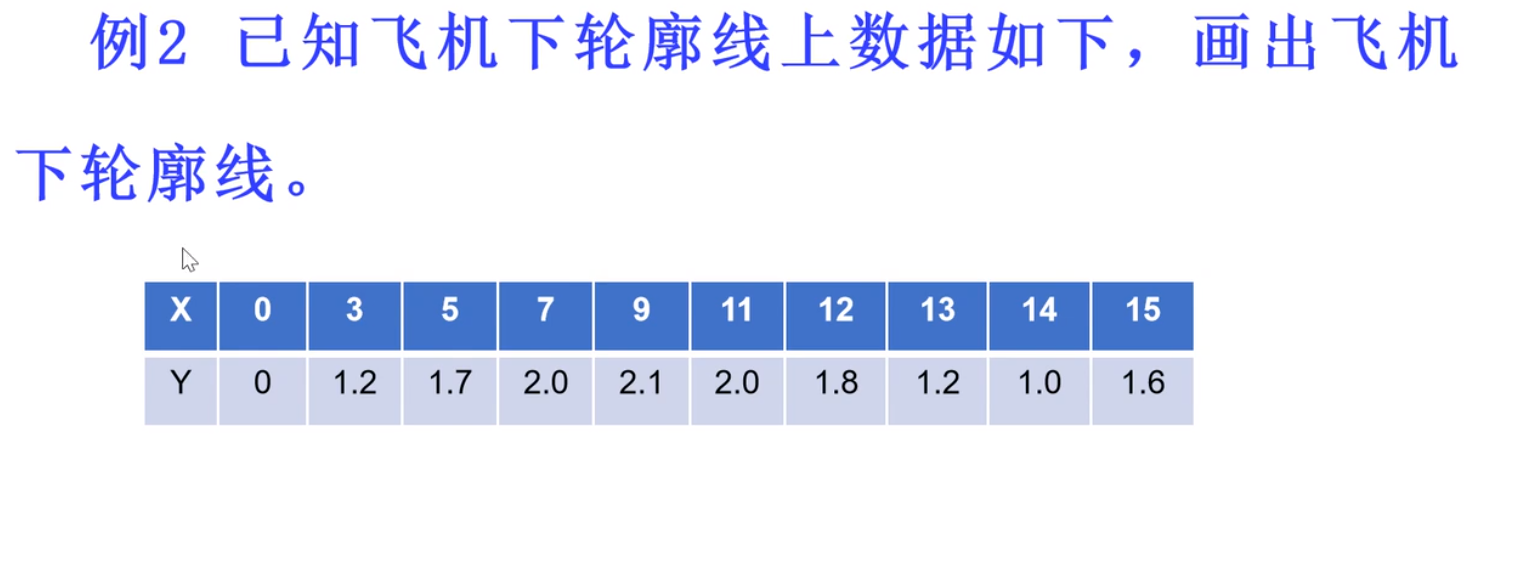
并且灰色预测要求间隔相同
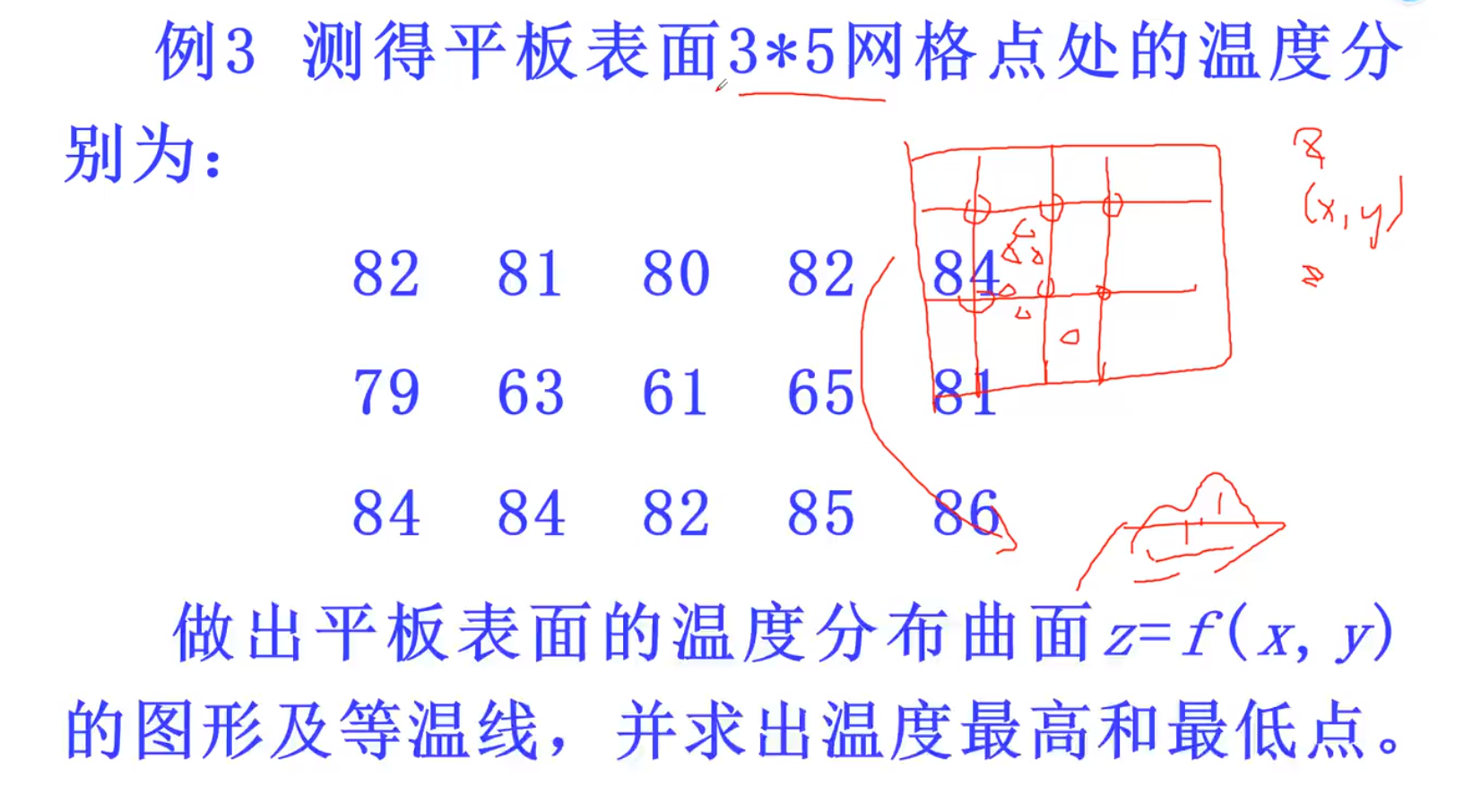


拉格朗日插值(不适用)
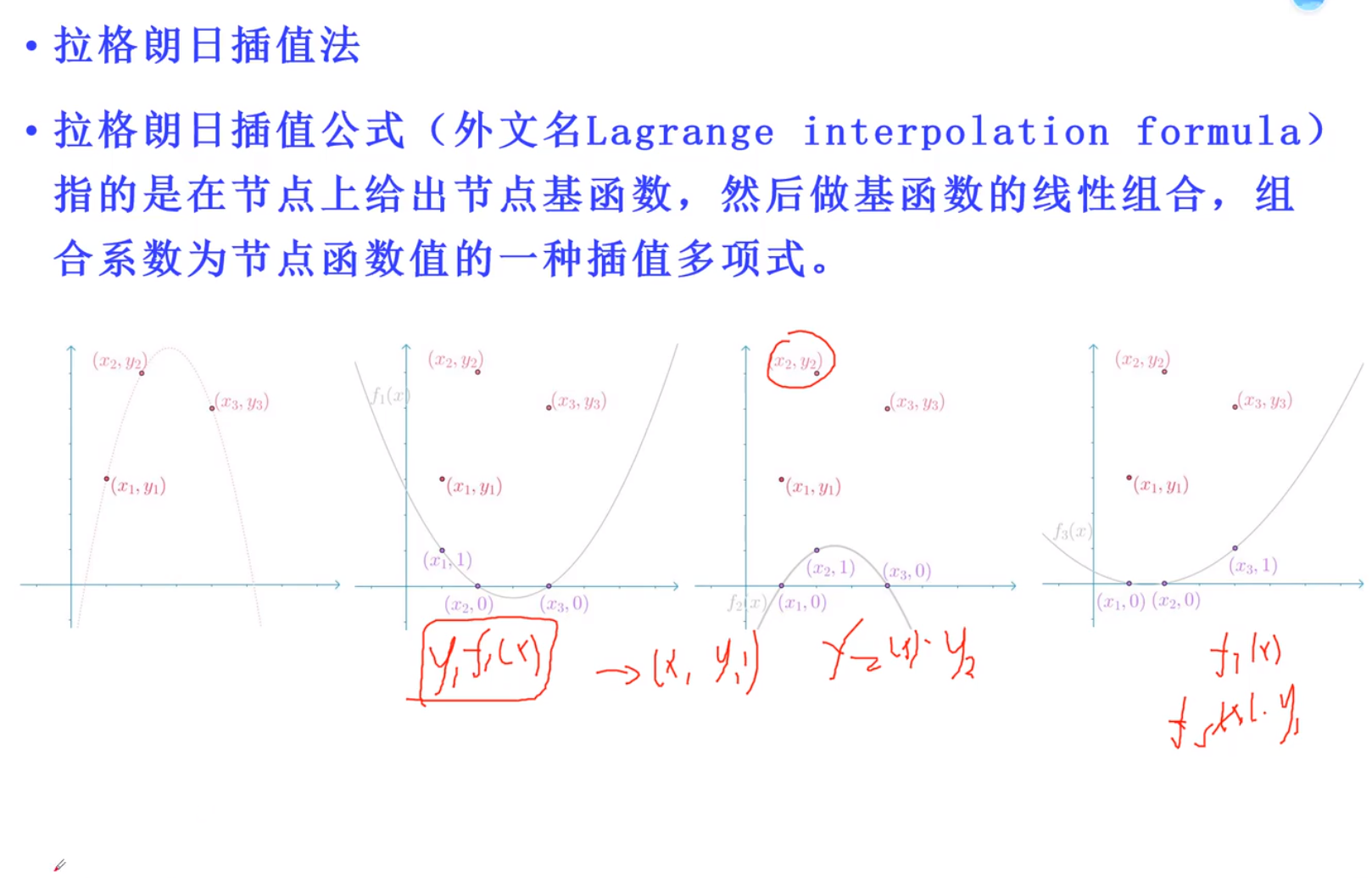
想得到左边那个图,则分为三条简单的曲线,每一条曲线保证能通过一个点,并且x为另外两个时,该曲线为0,则将三者相加,能得到左边的曲线!
f(x) = y1 × f(x1)+y2 × f(x)2 + …..
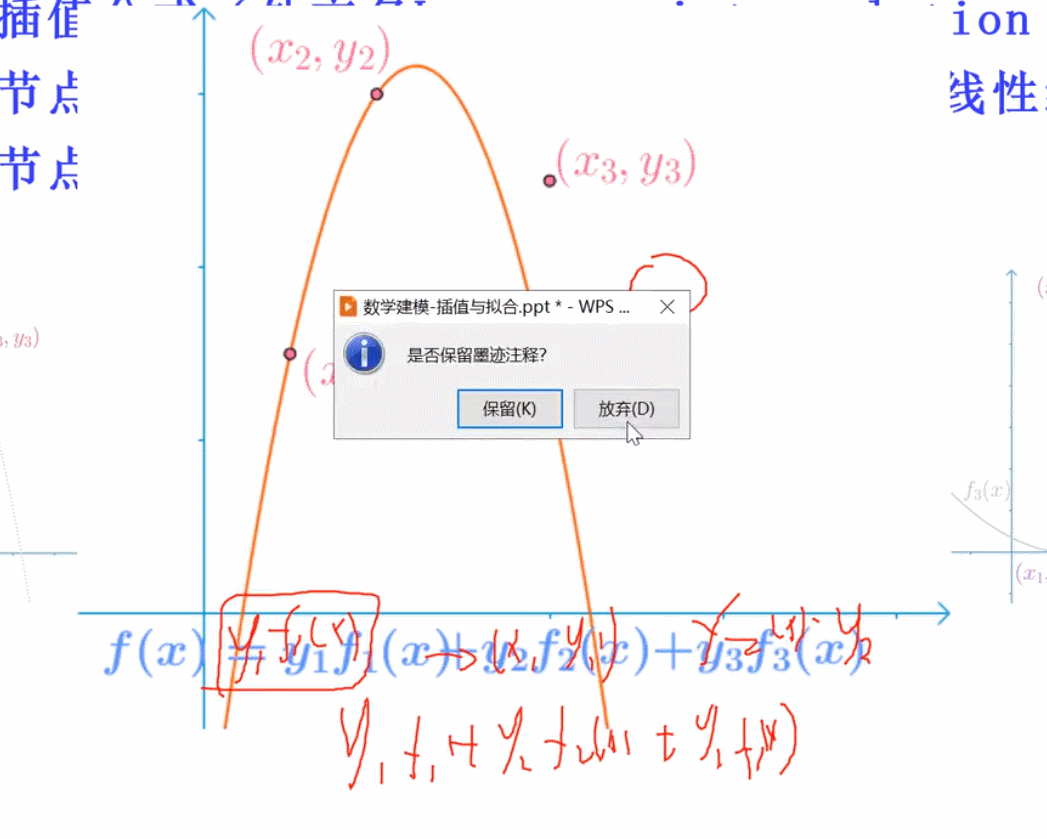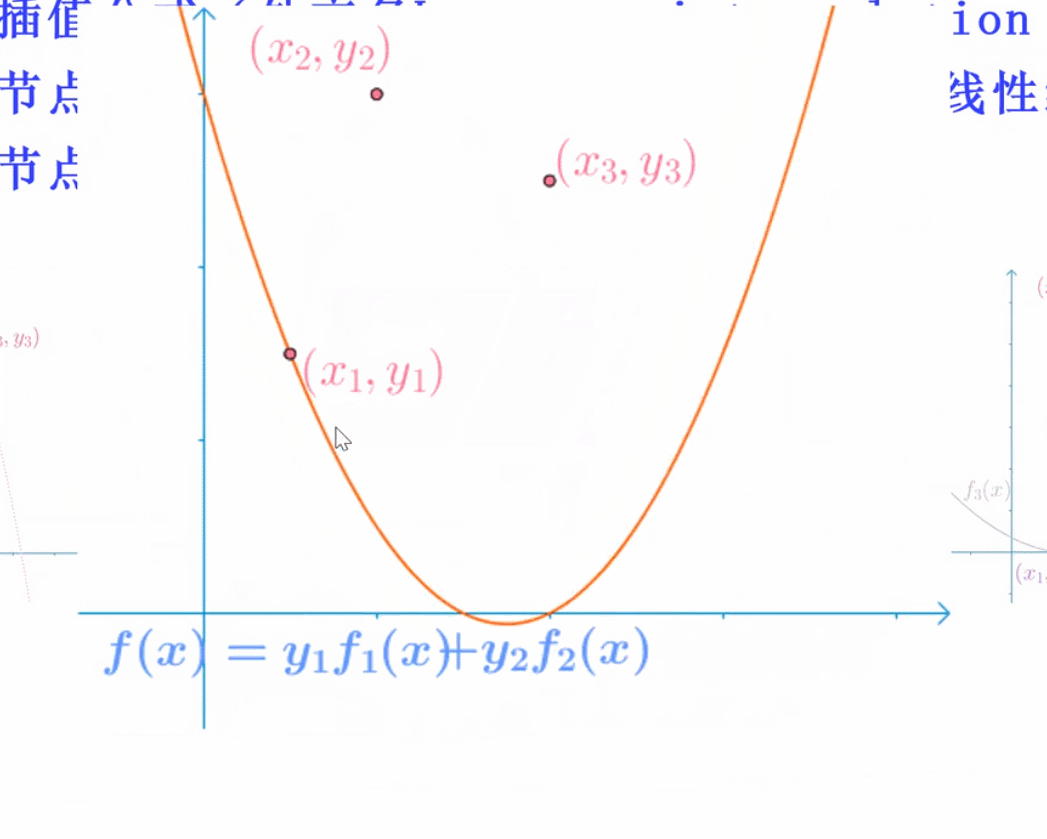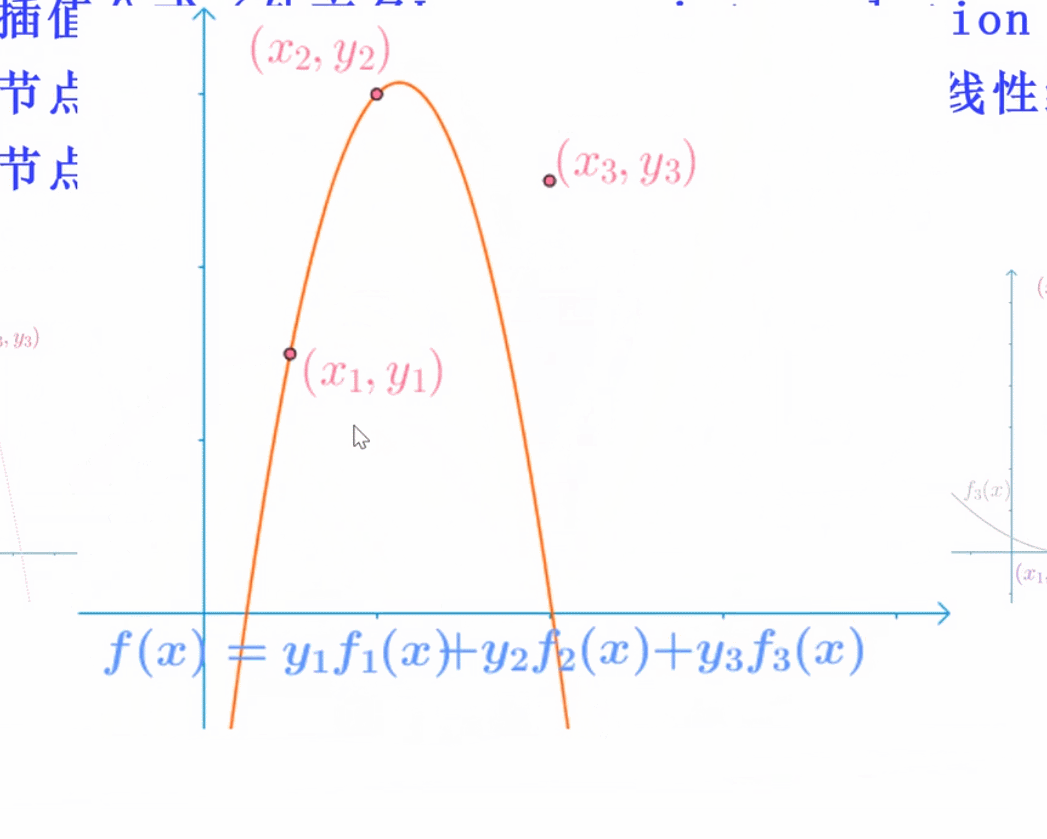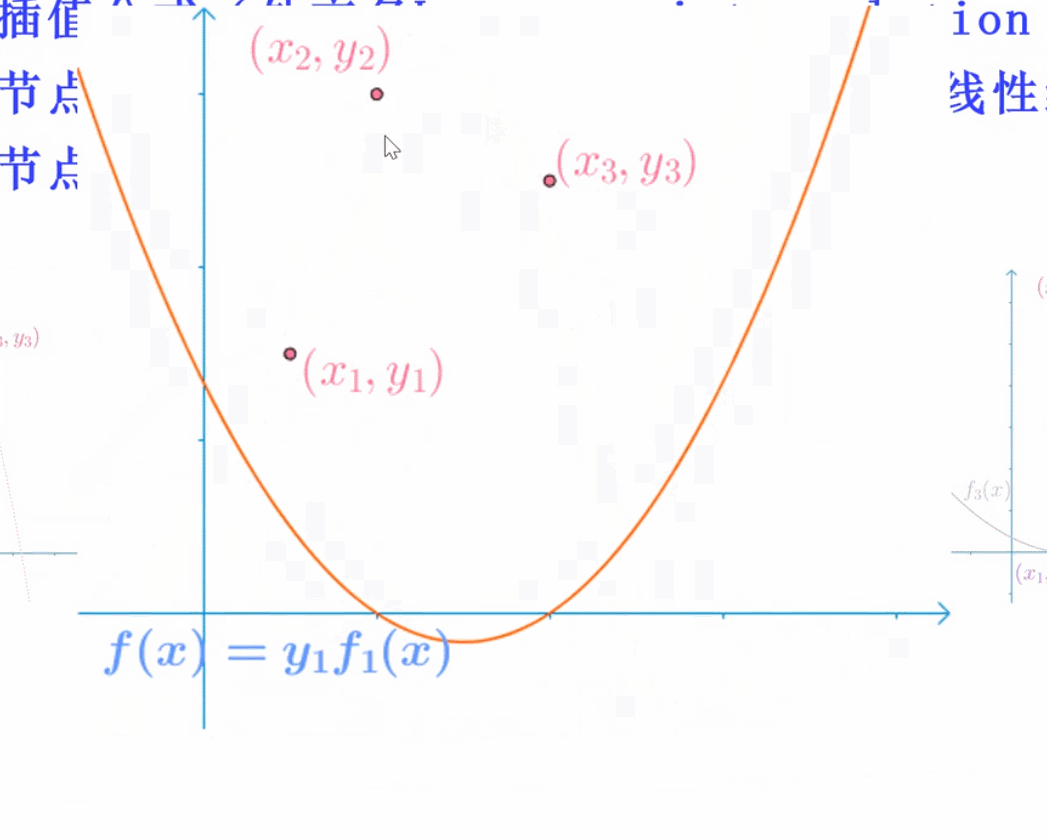
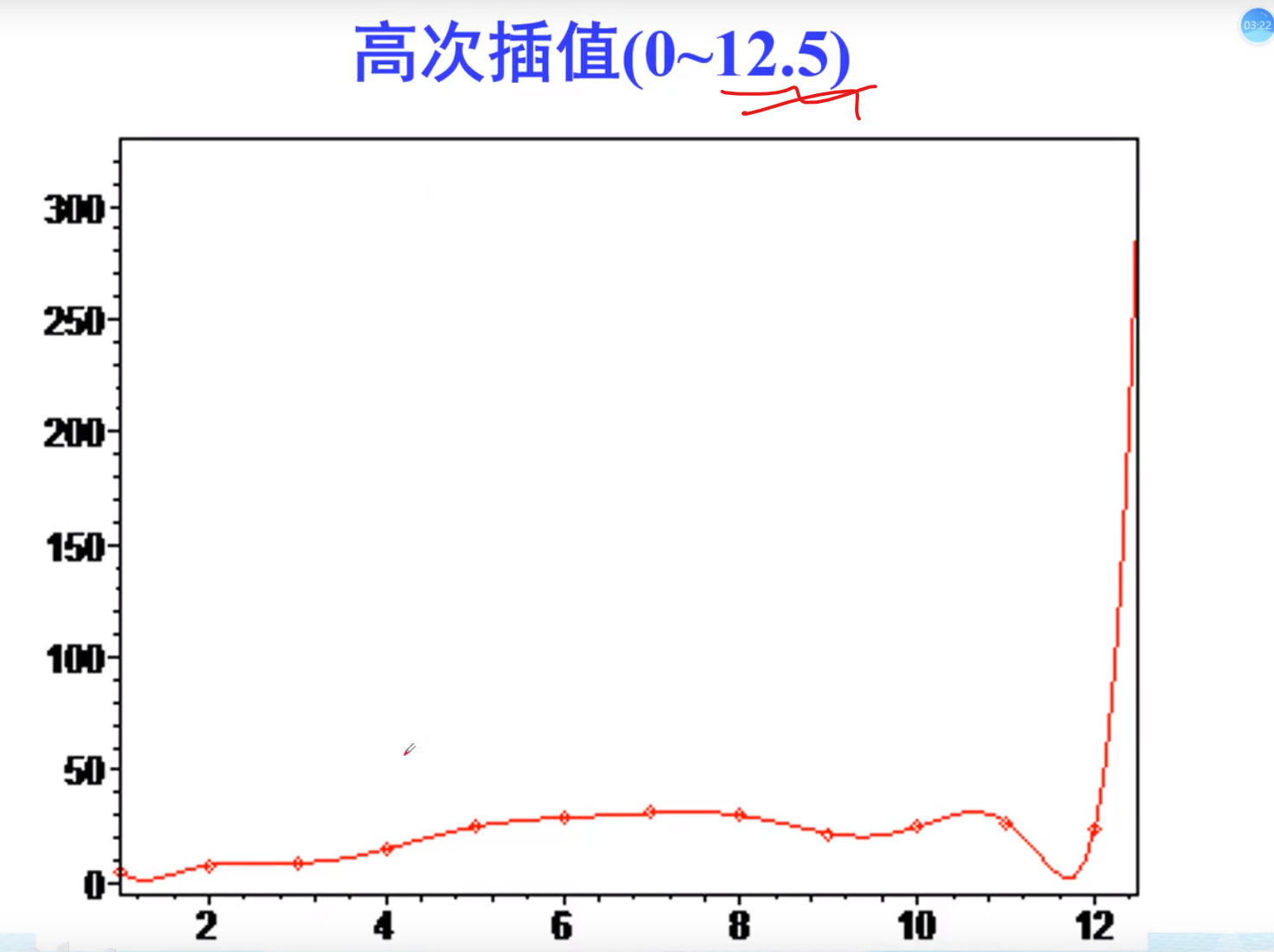
Runge插值

龙格现象
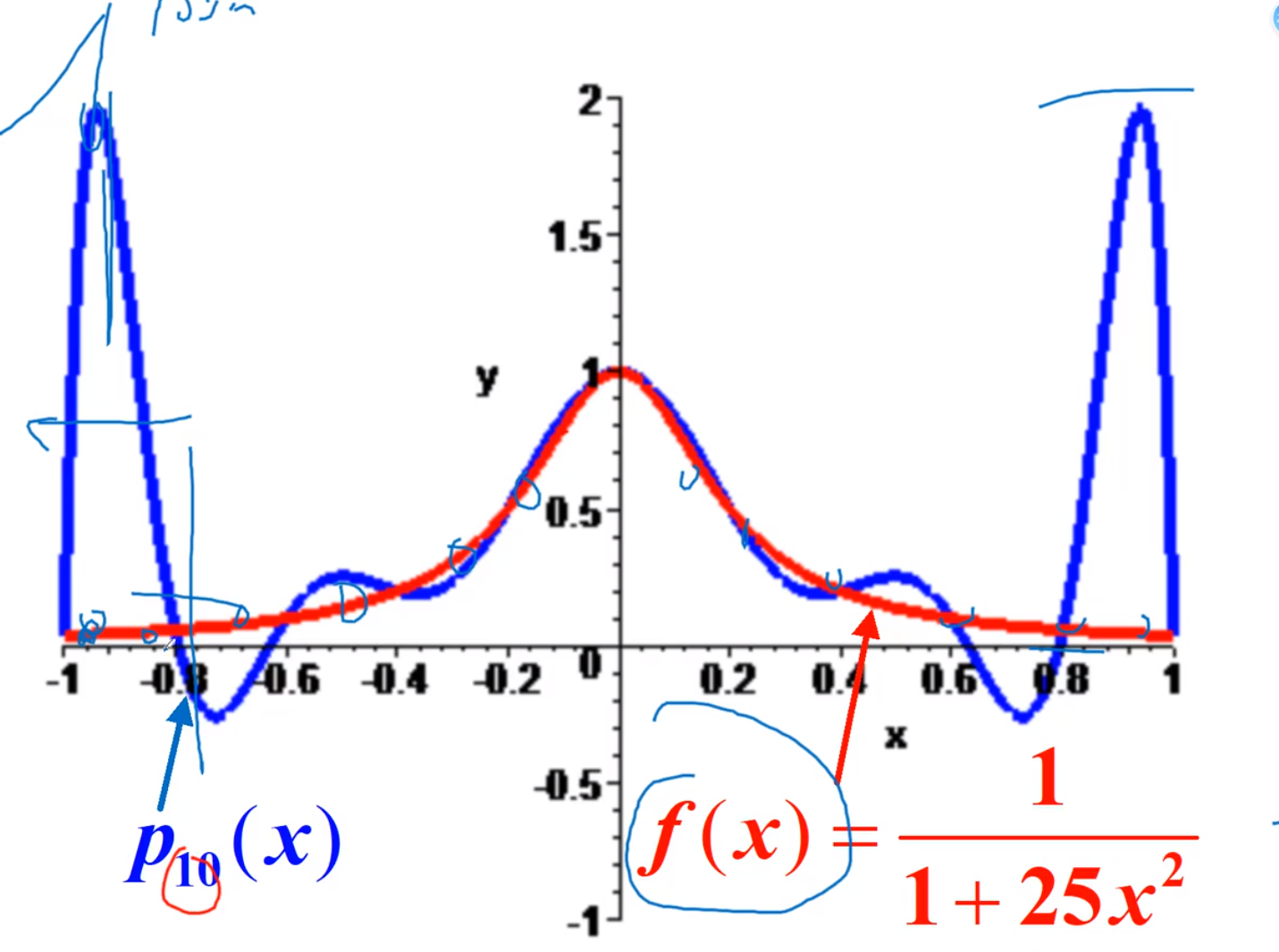

蚌埠住了,痛苦
最好的办法,将凹凸不平的段,分段进行插值,从而消除误差
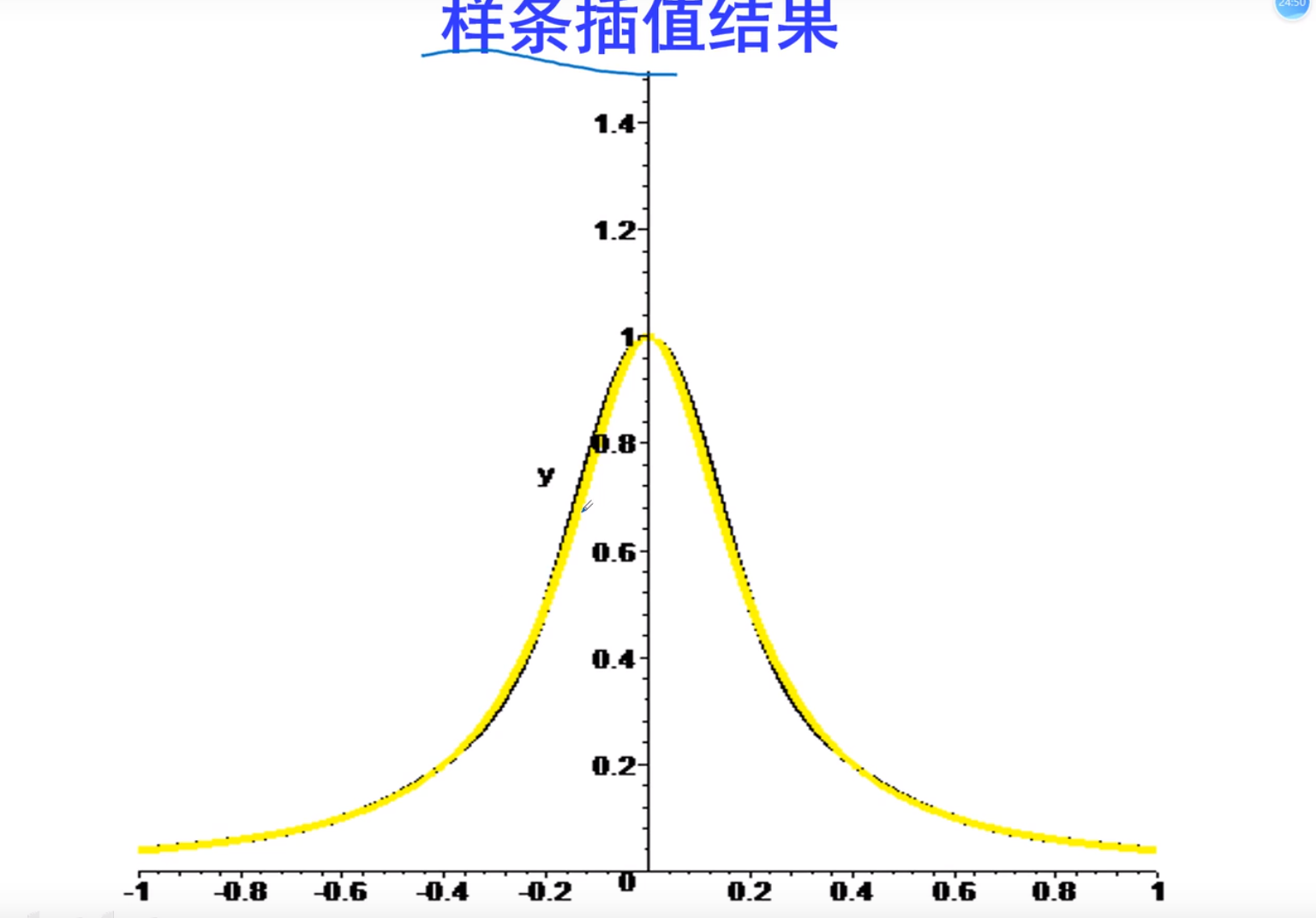
Matlab插值
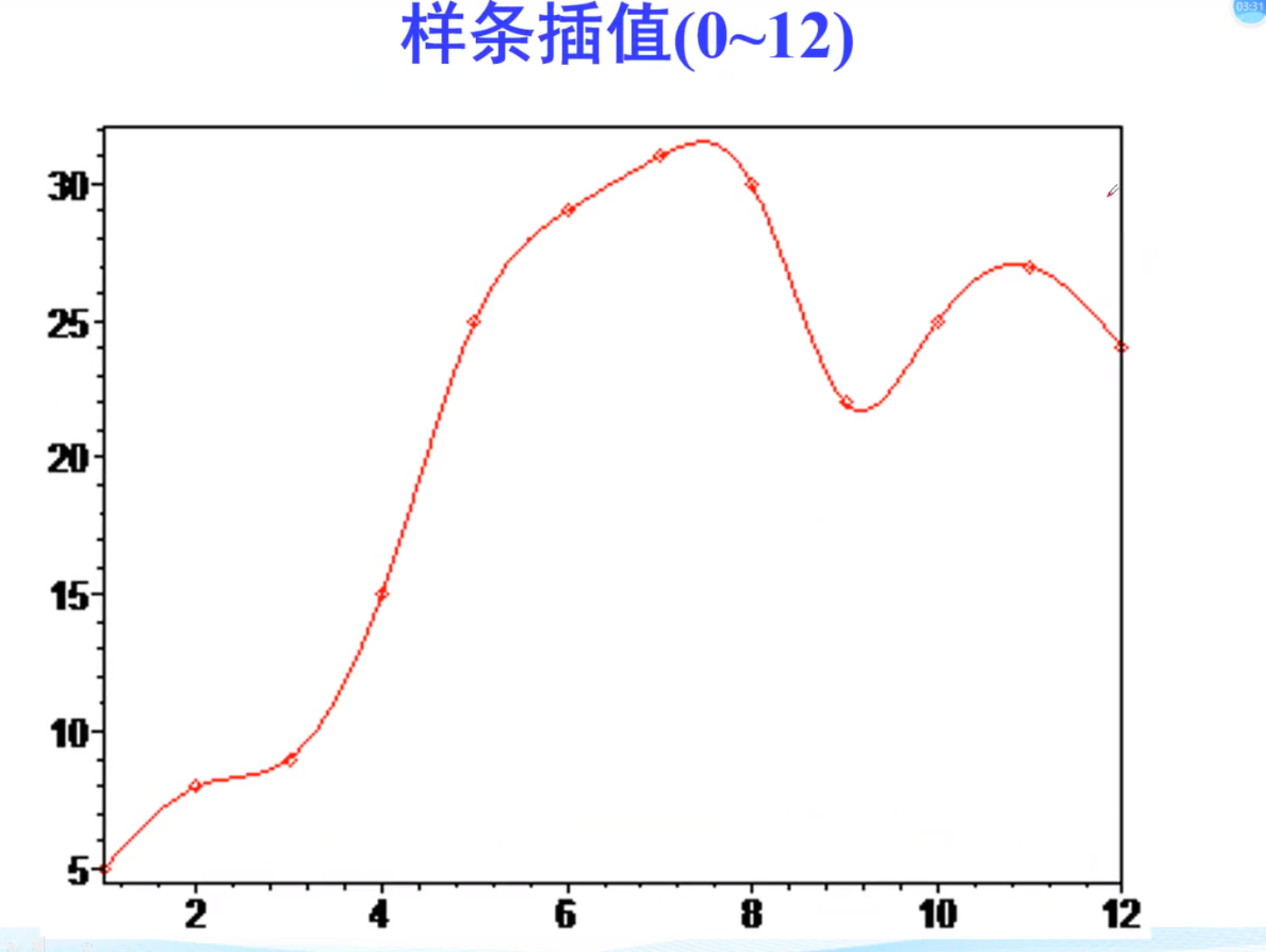
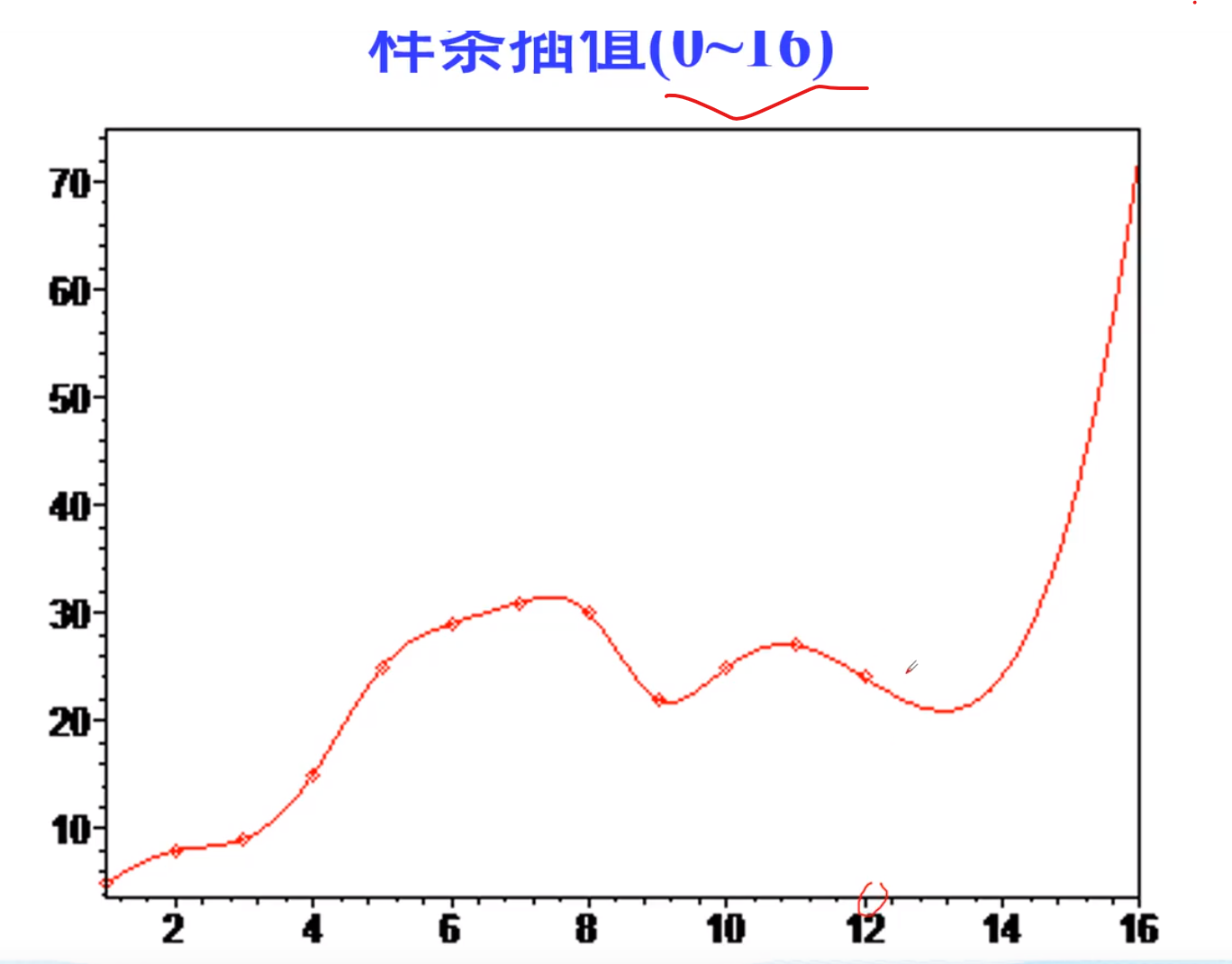
一维优先样条插值,二维优先立方插值

拉格朗日实现过程



人家给你12个点,你给插出3600个

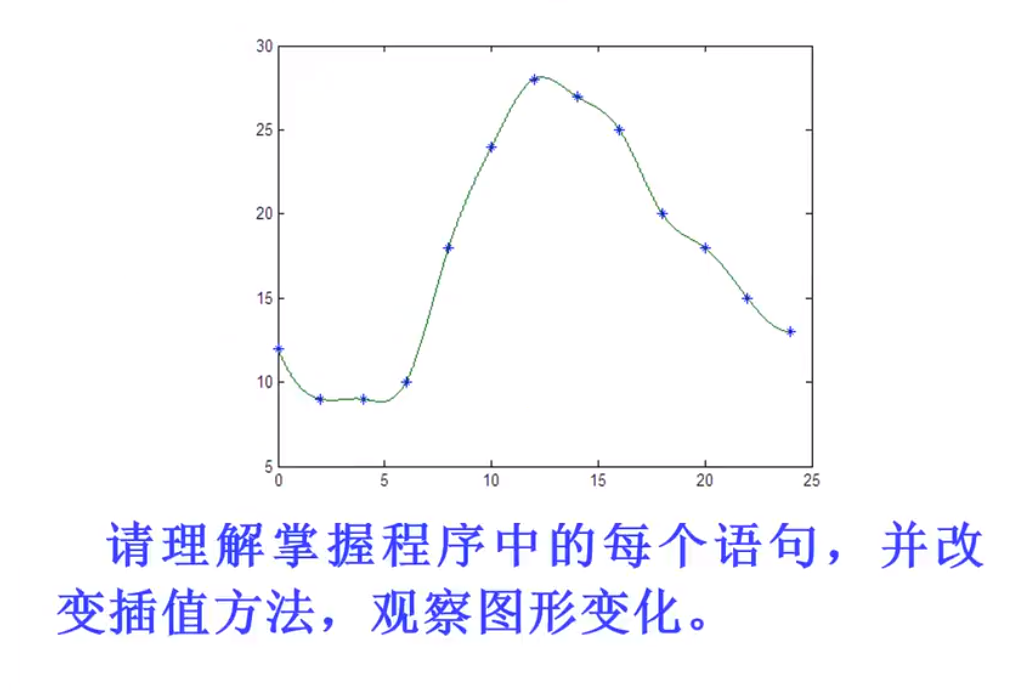


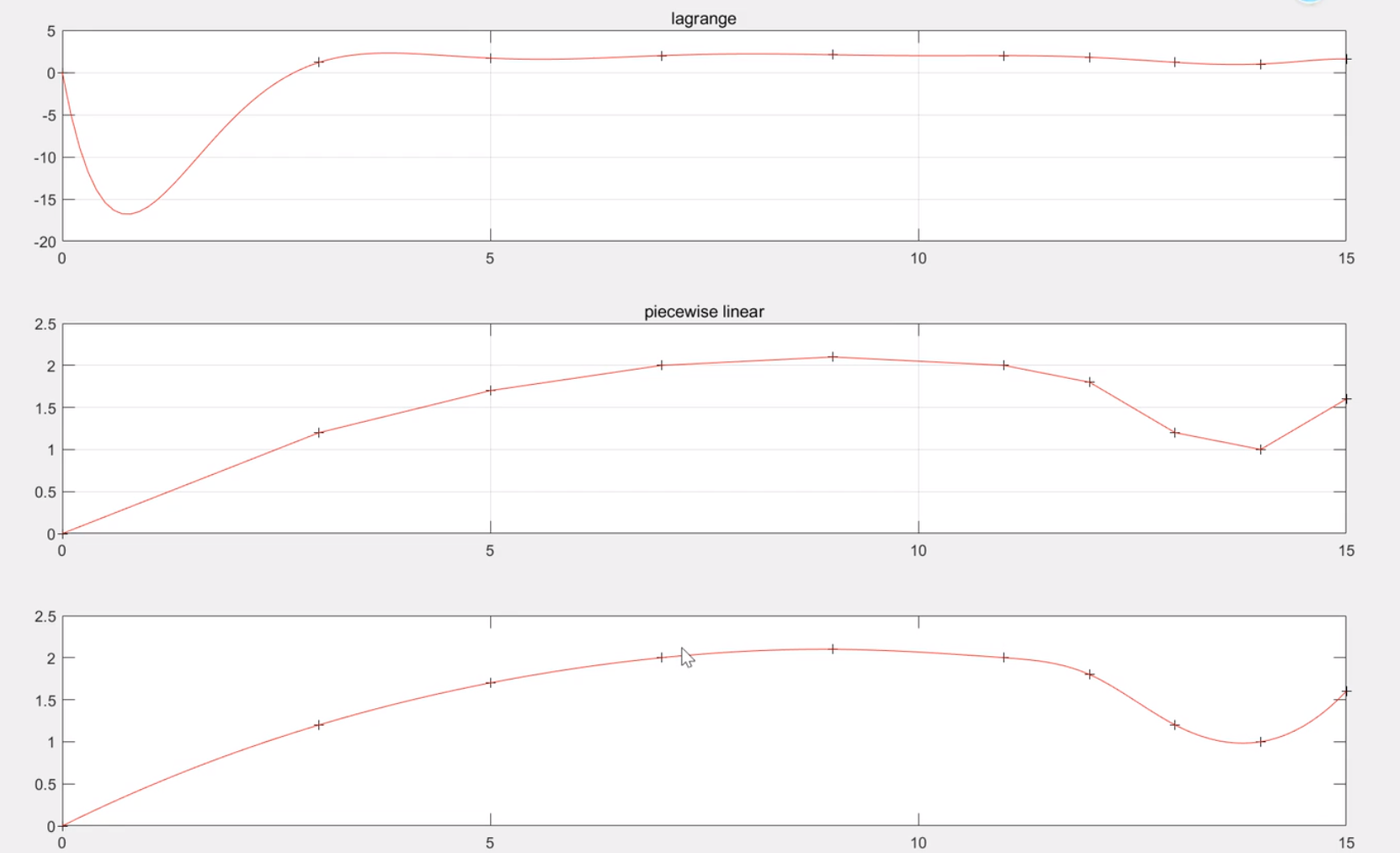
三种插值对比,三次插值明显光滑,并且龙格现象小,拉格朗日不常用,因为有龙格现象
例题



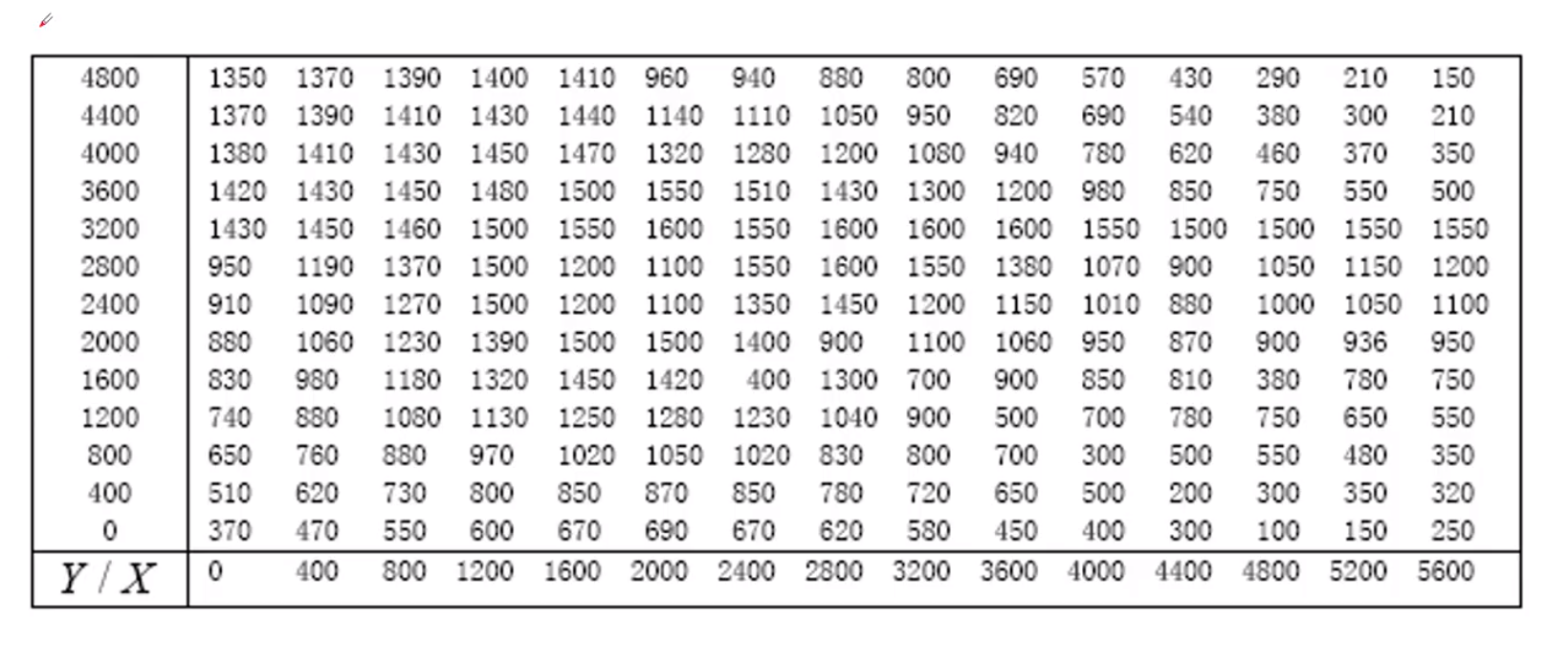

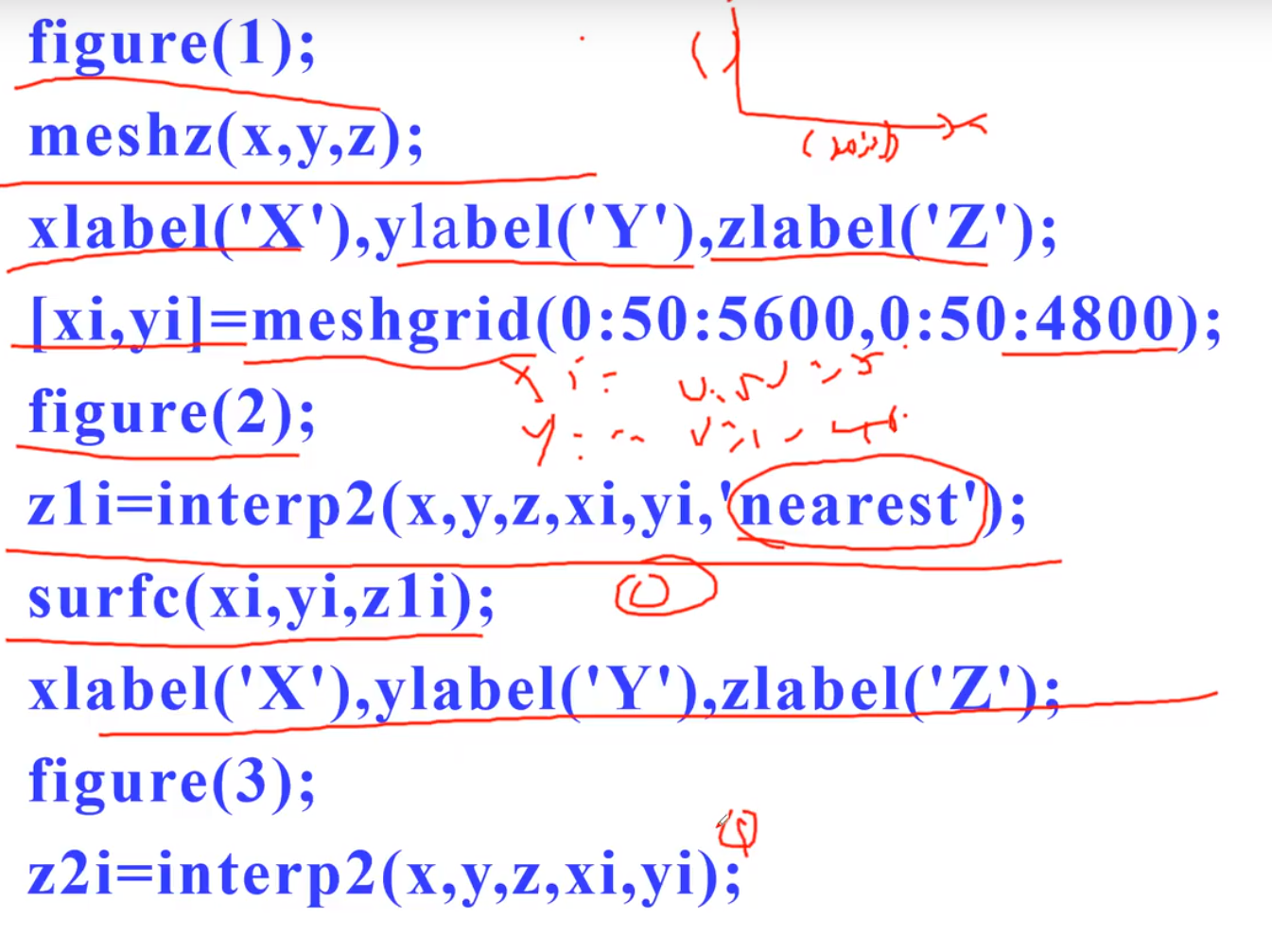




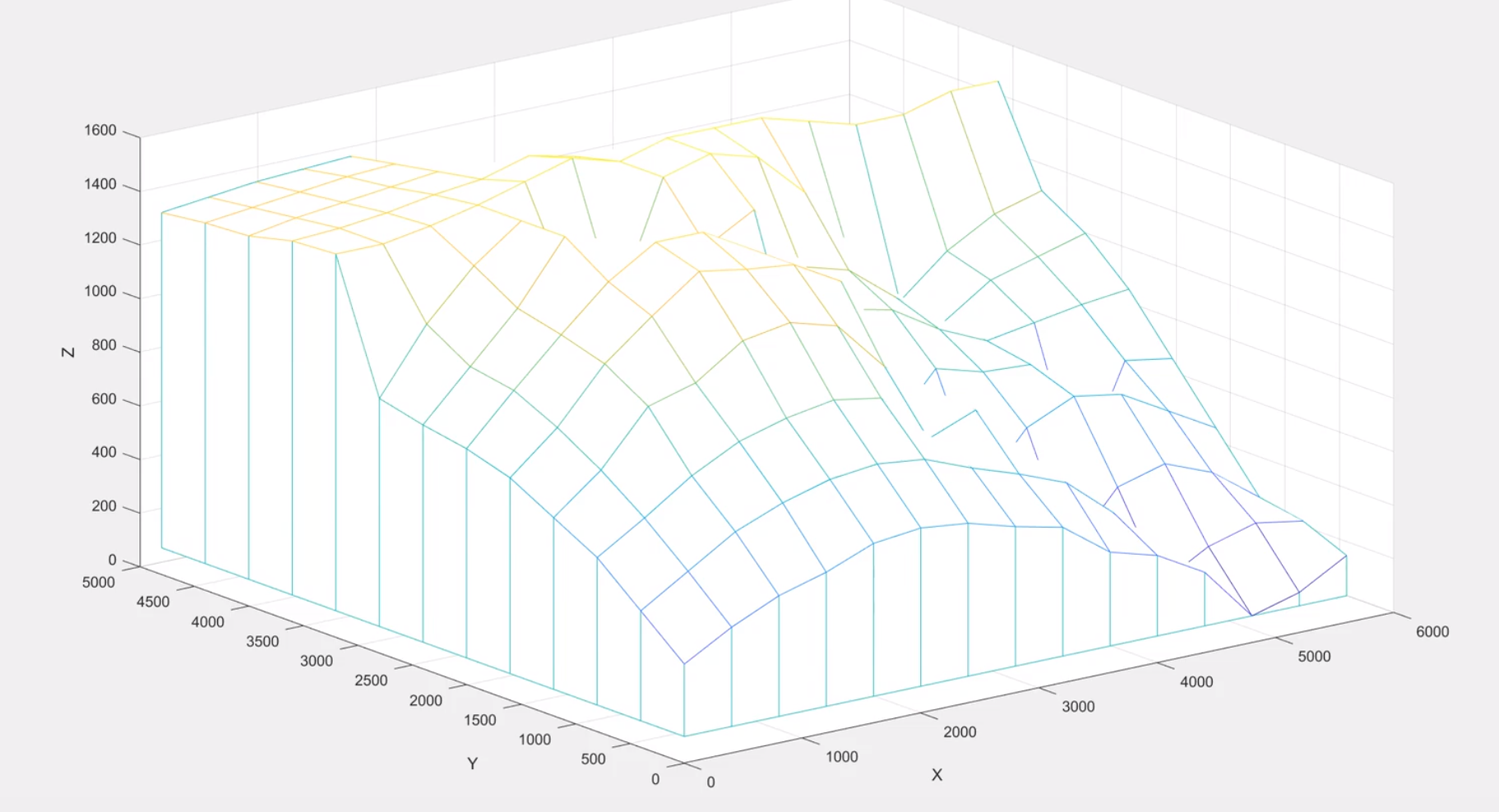
最近邻插值
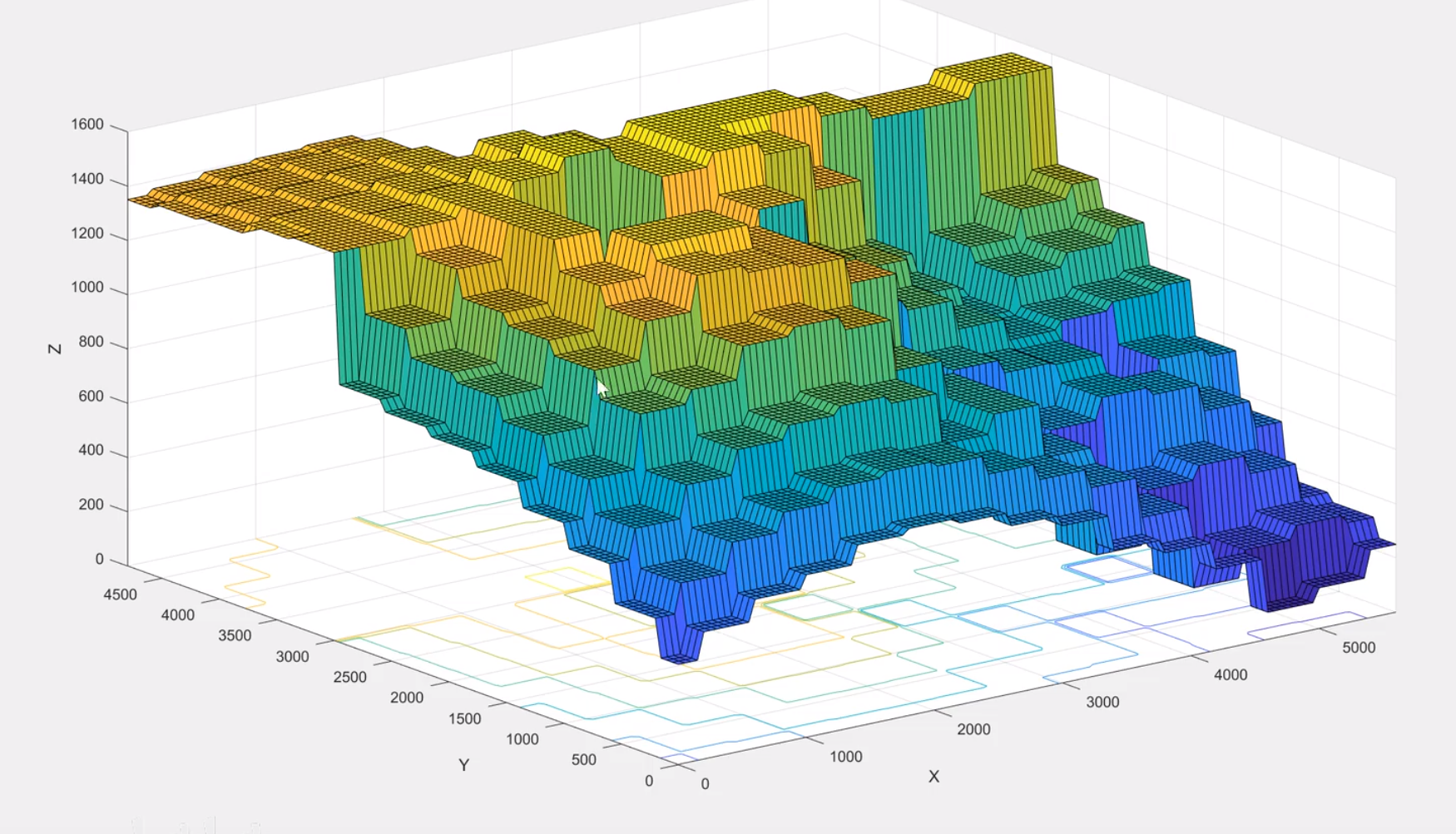
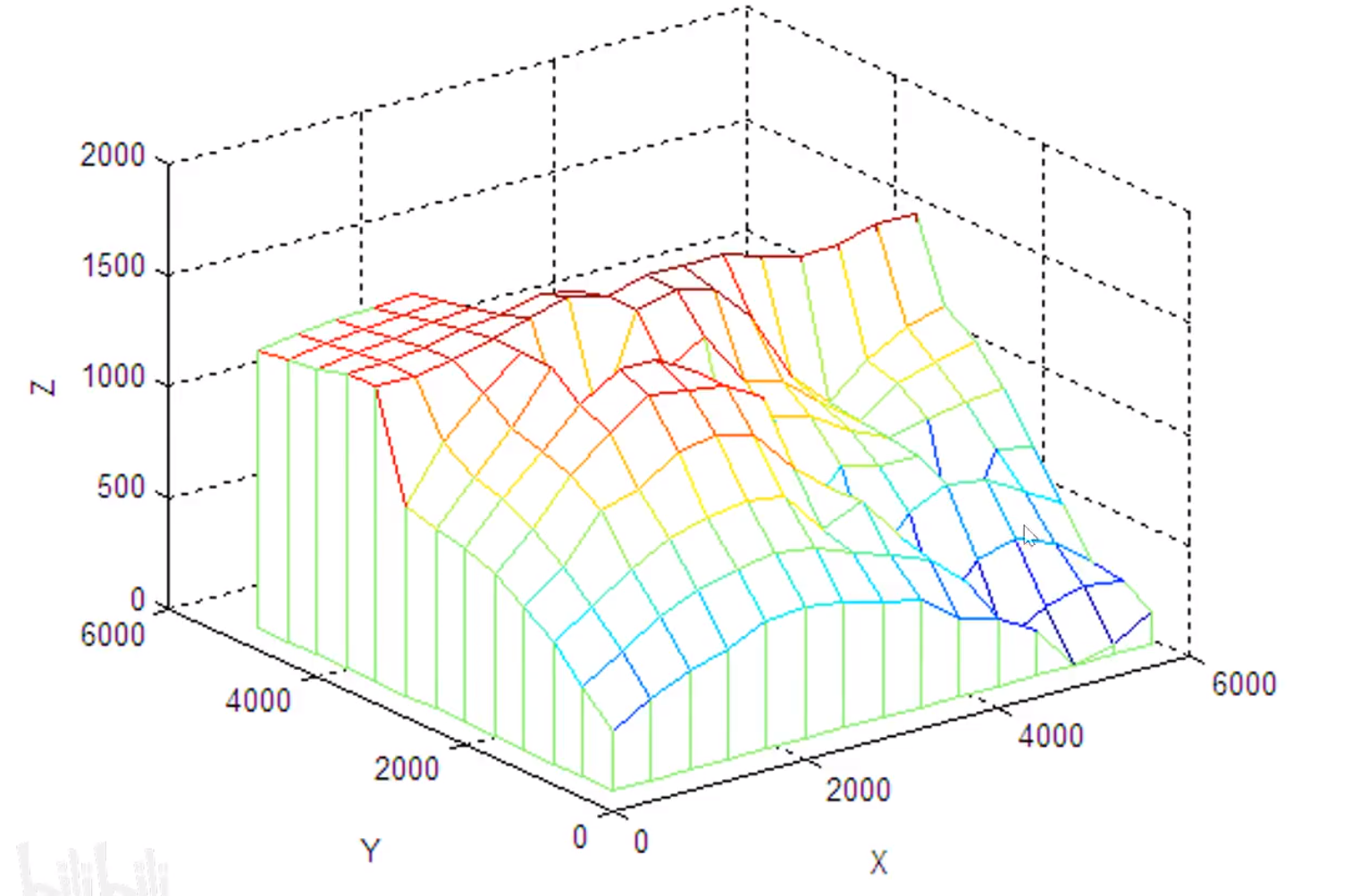
线性插值
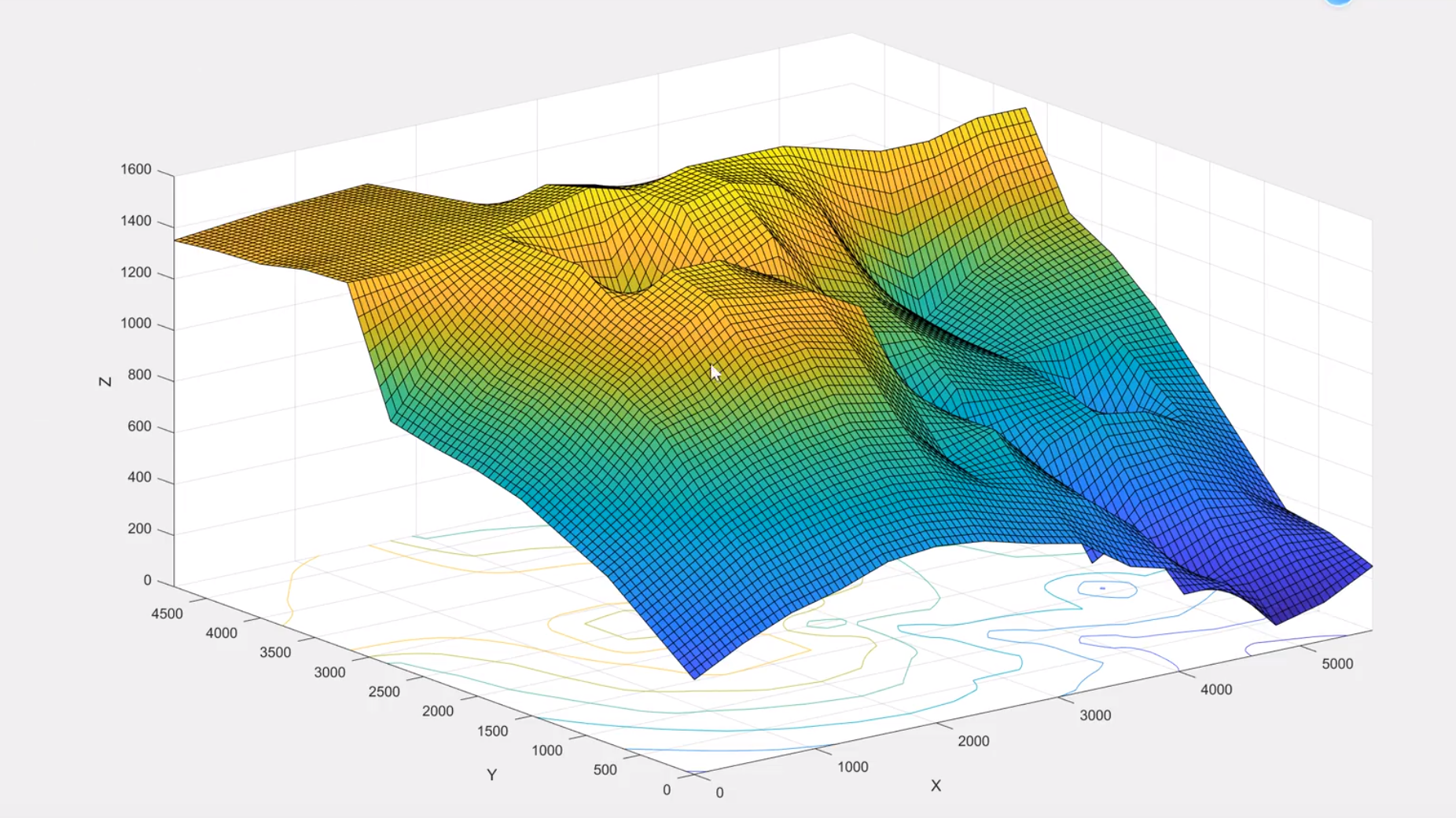
立方插值
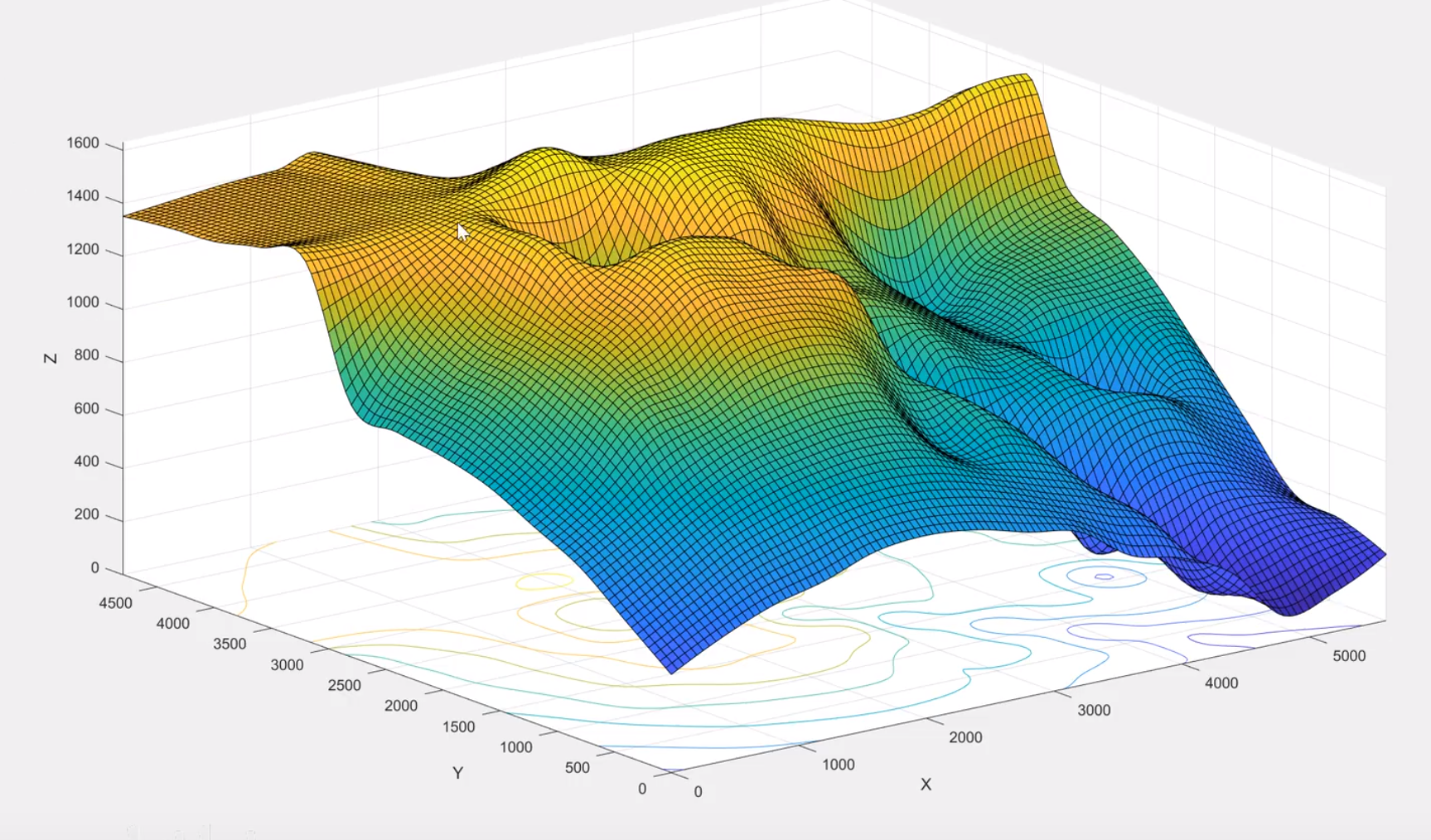
最近邻,线性,立方对比
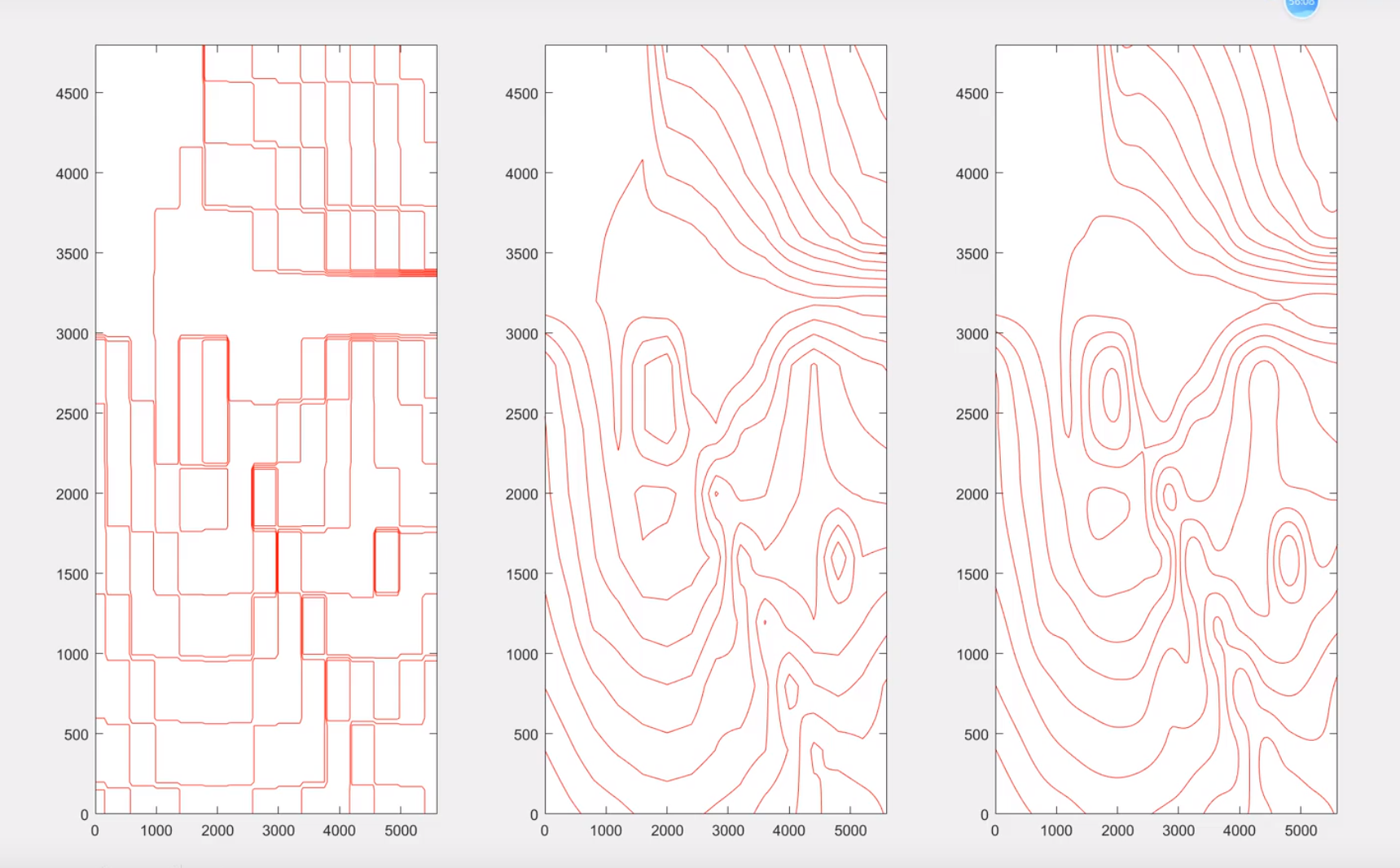
散乱点插值

山高用正数,水深用负数


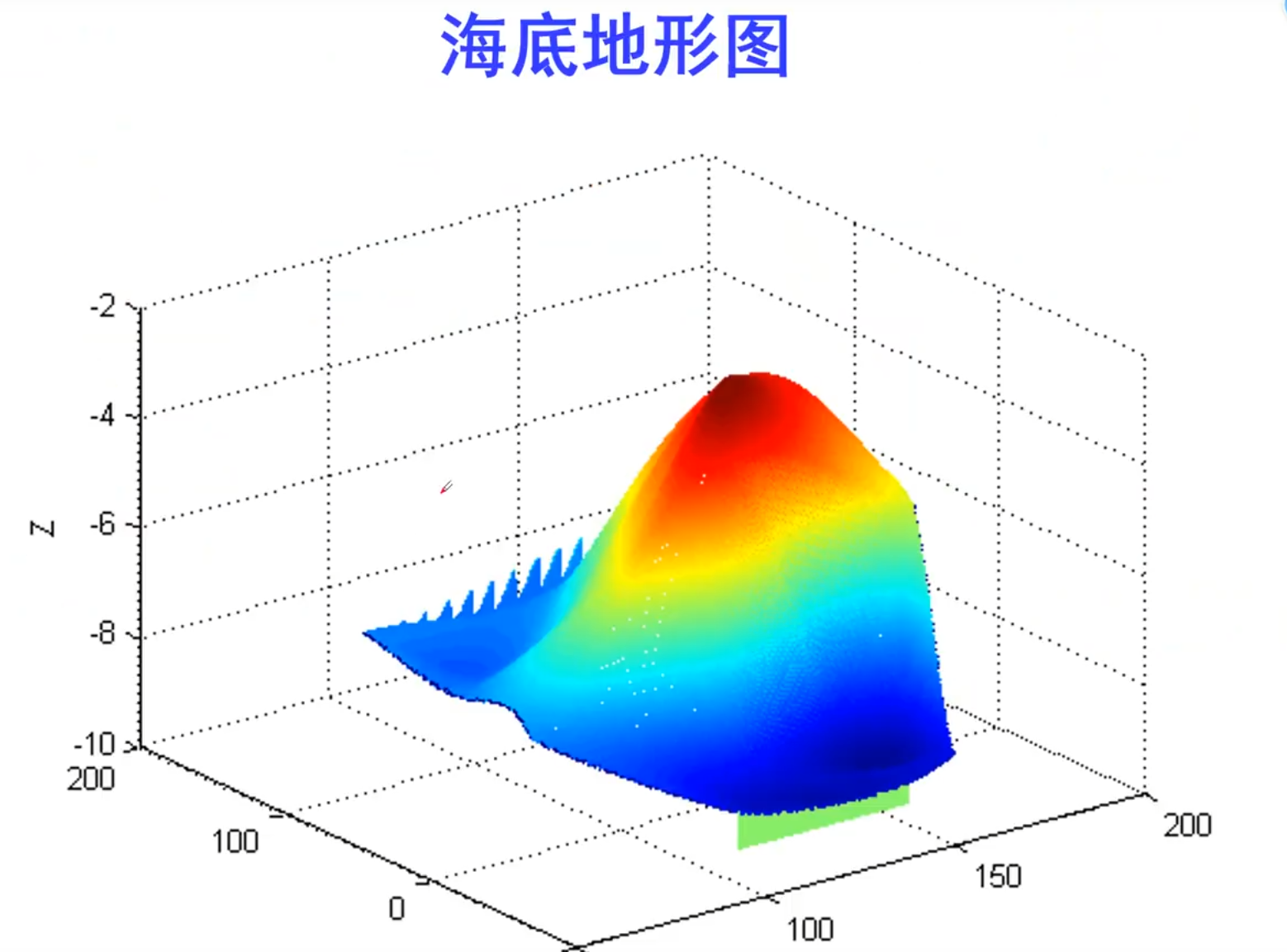
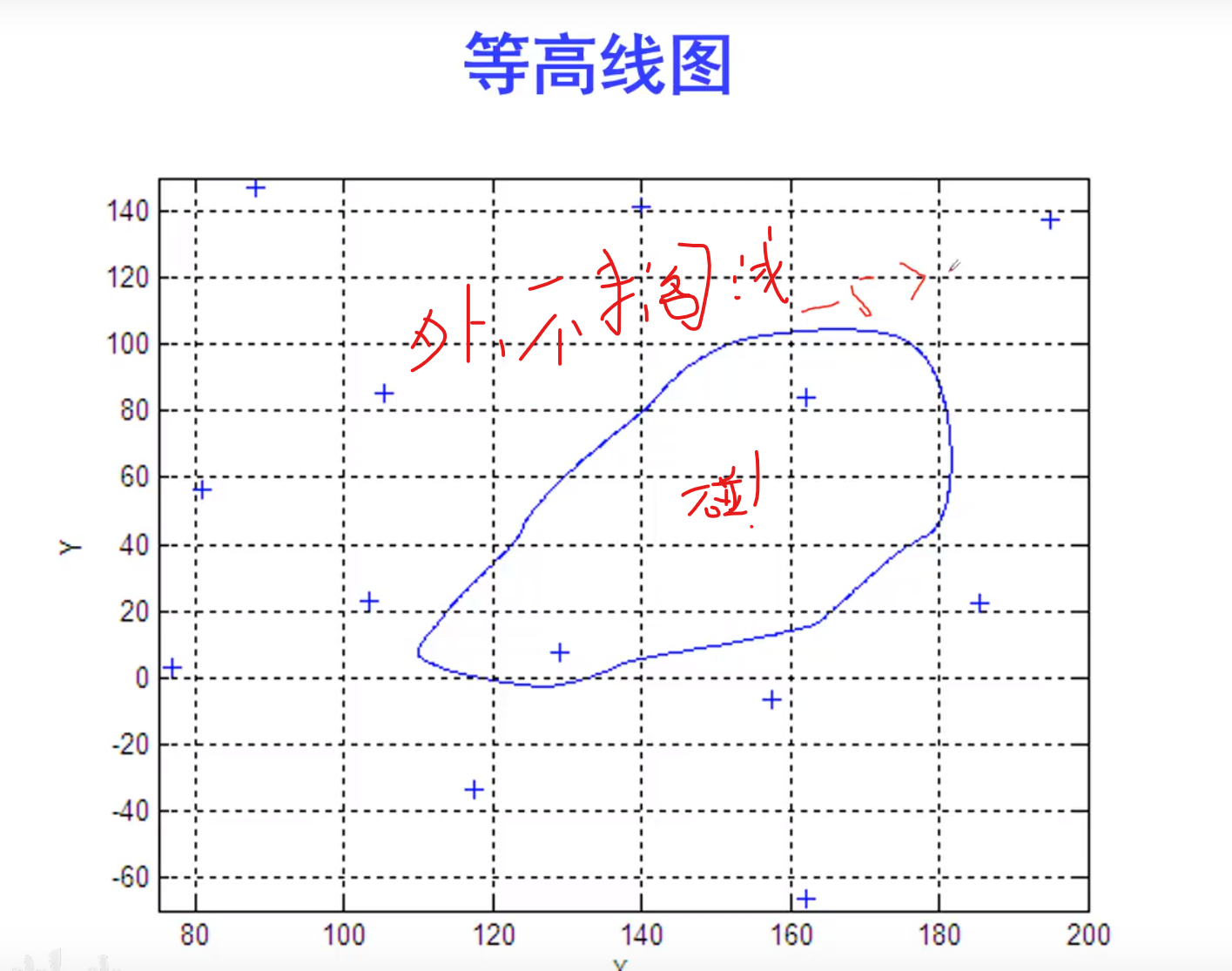
拟合
推导在数据范围外的数据(外延)用于小样本预测 对未来很小的一个范围做预测
需要根据数据得到函数,然后再求导之类找到目标时使用
拟合问题

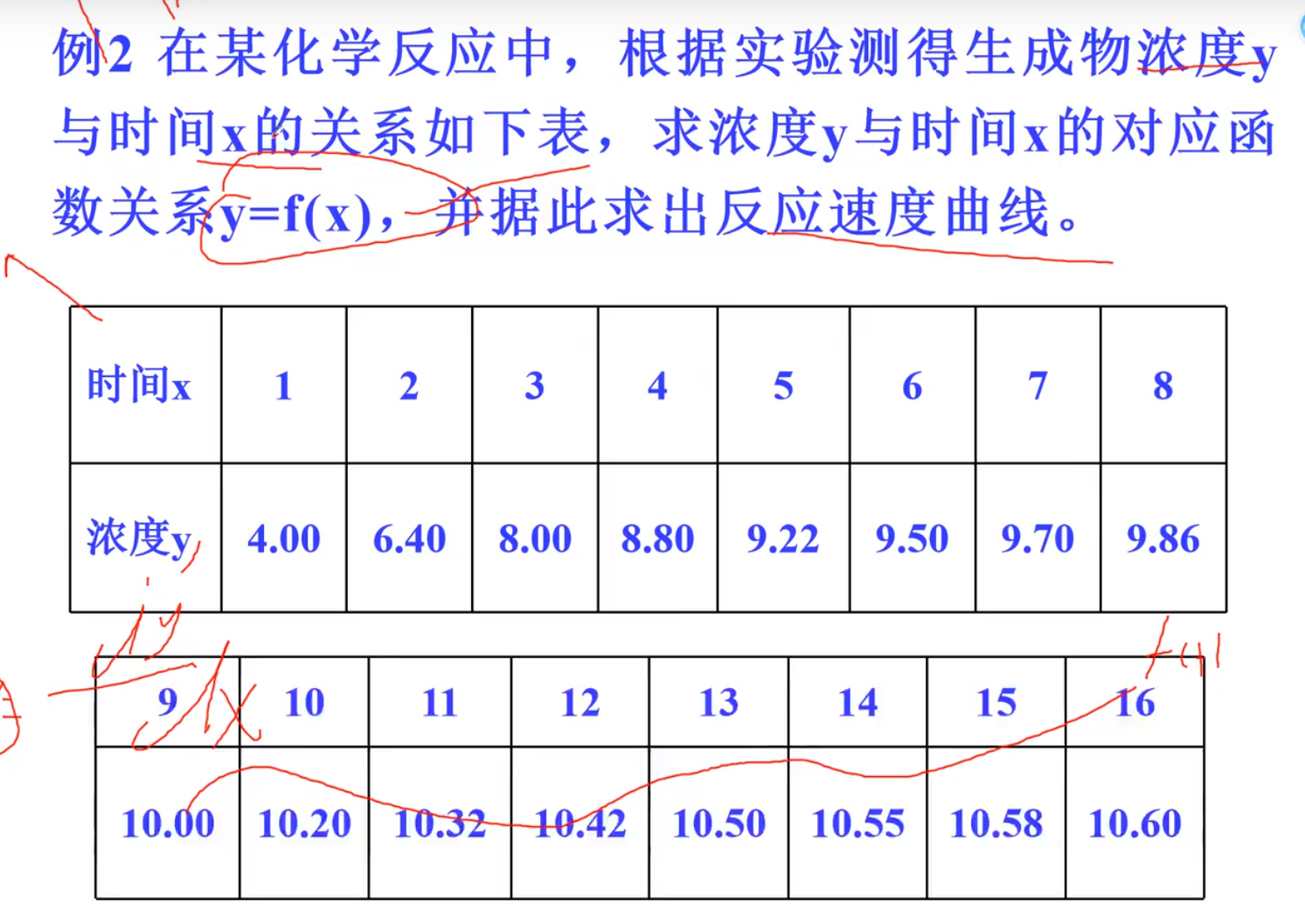

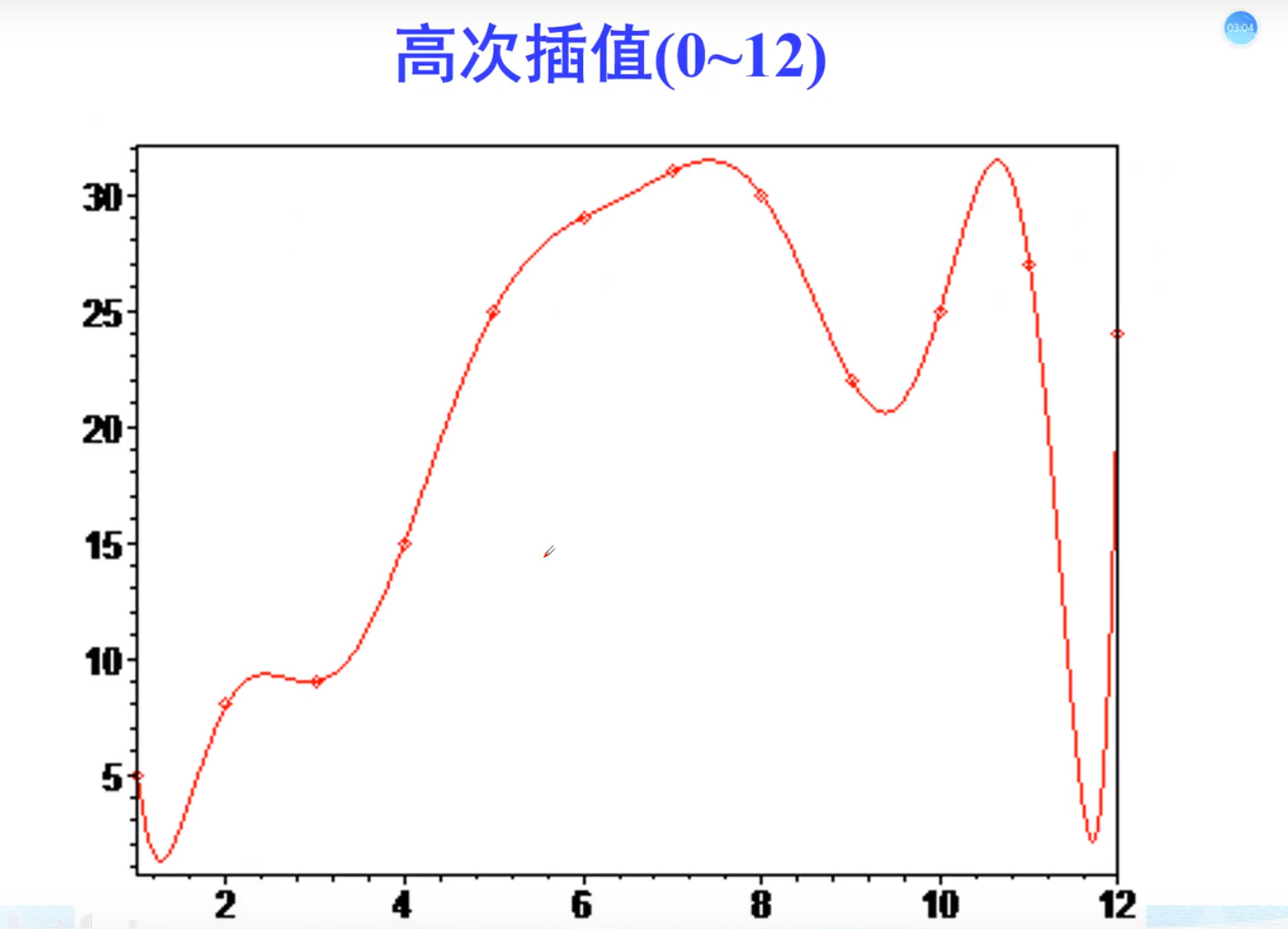


拟合的计算

matlab拟合
多项式拟合

polyval:找出在你求解的那个拟合函数的基础上,待求点的值是多少
黑色的.来表示,红色的线来表示,9是自定义的拟合次数(次方)

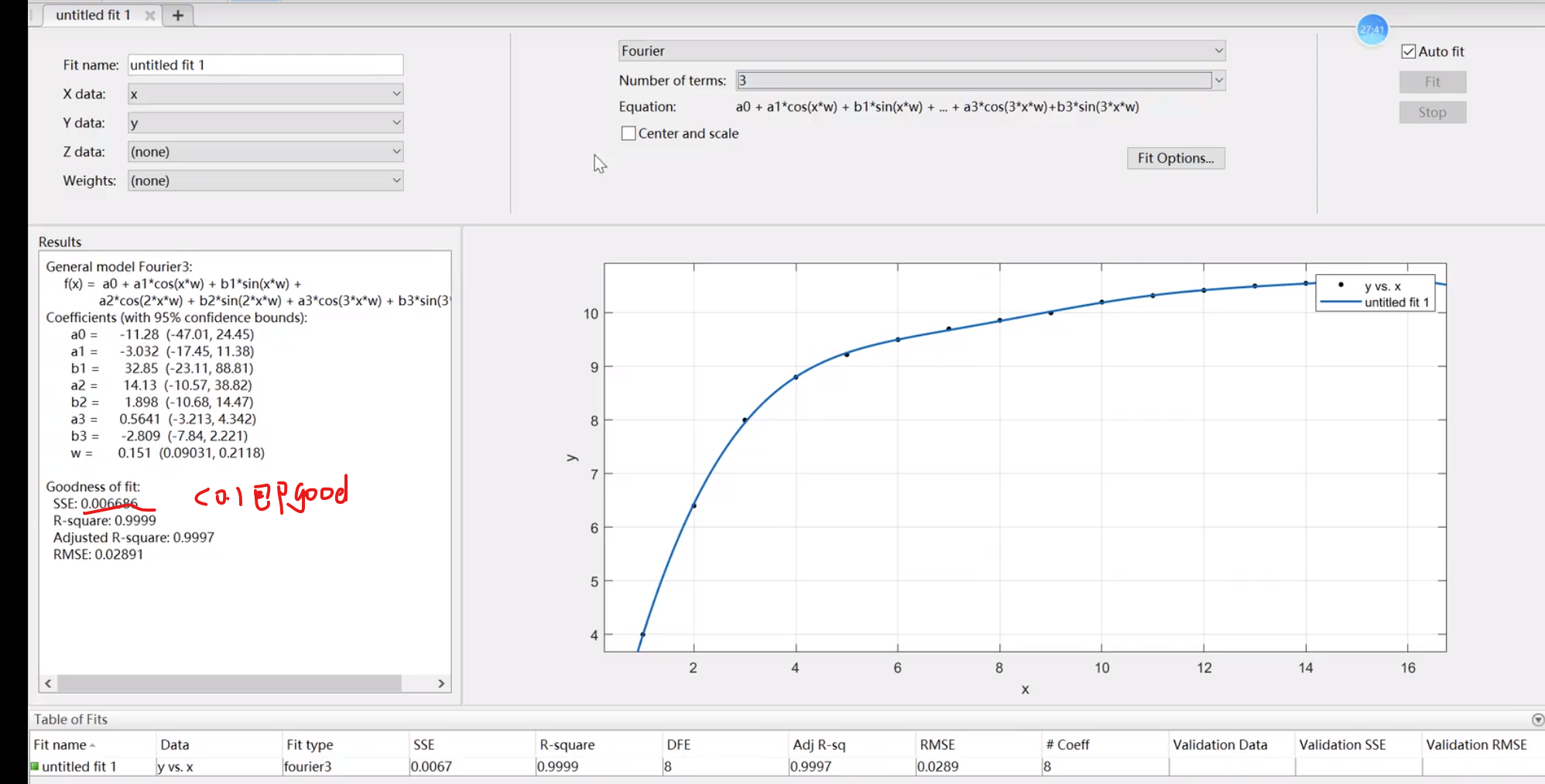
非线性拟合
(18条消息) MATLAB曲线拟合工具箱(cftool)介绍(完结)_Wendy的博客-CSDN博客_matlab曲线拟合工具箱

模糊数学(评价)

模糊集


不知道评判标准,但可以大概估计他是标准的概率是多少
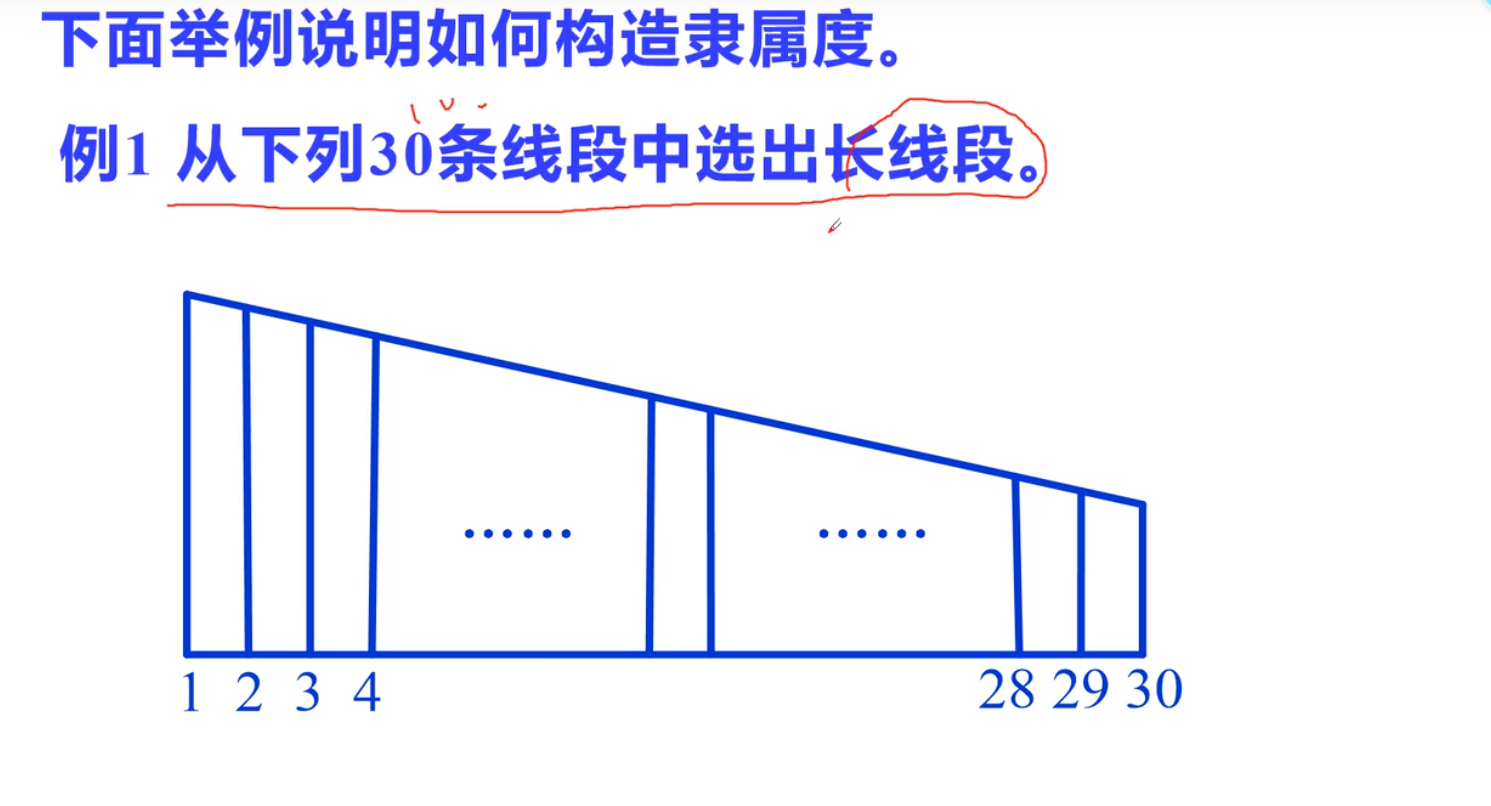
1一定是长线段,在我们的眼中

线段越长,成为长线段的概率就越大

隶属度函数

模糊综合评价



确定指标和等级

例题


构造矩阵


一定为1


评价指标权重确定


变异系数法
不考虑每一个指标的重要性

设计原理


变异系数法流程
mean(x)求均值, std(x)求方差

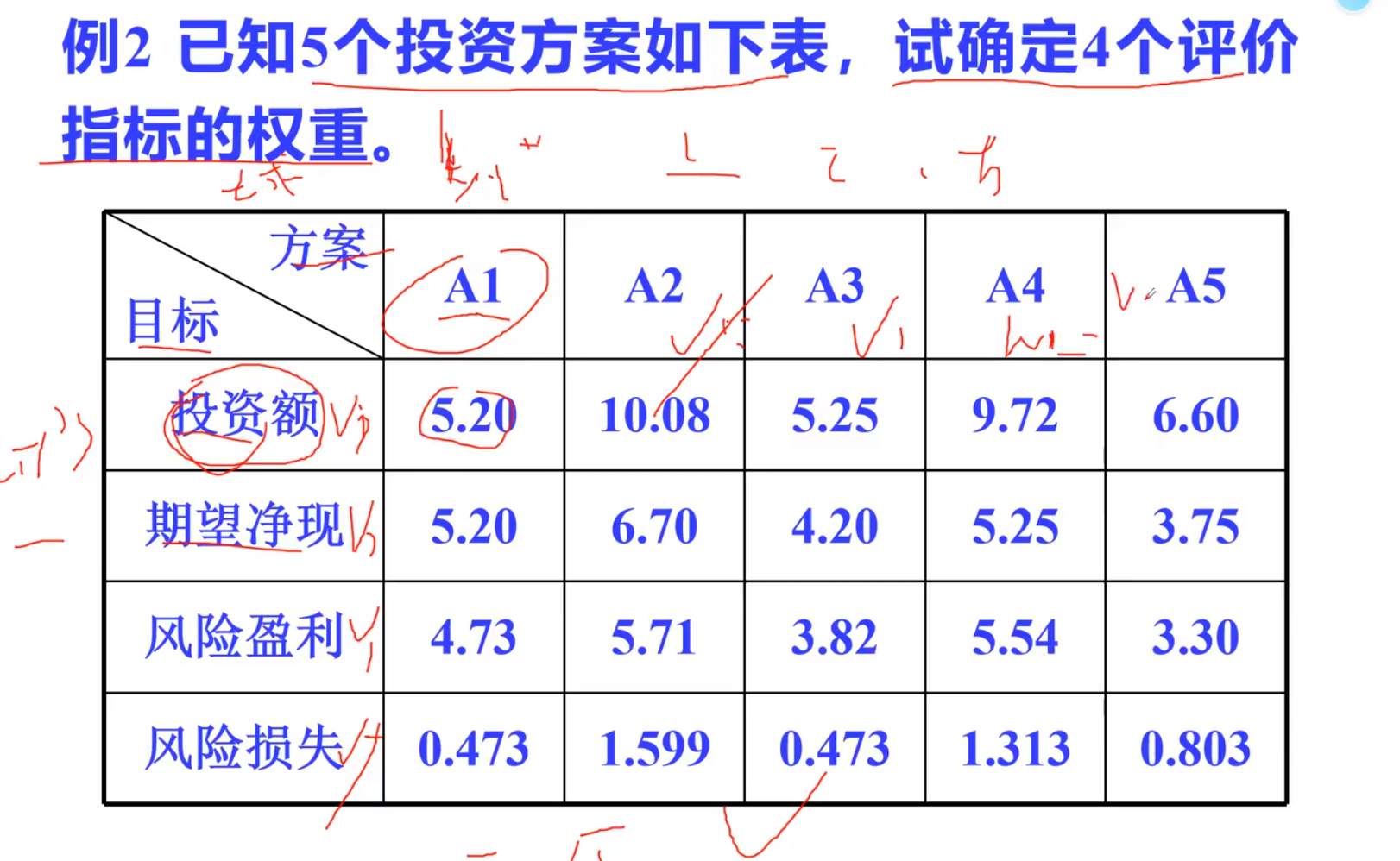



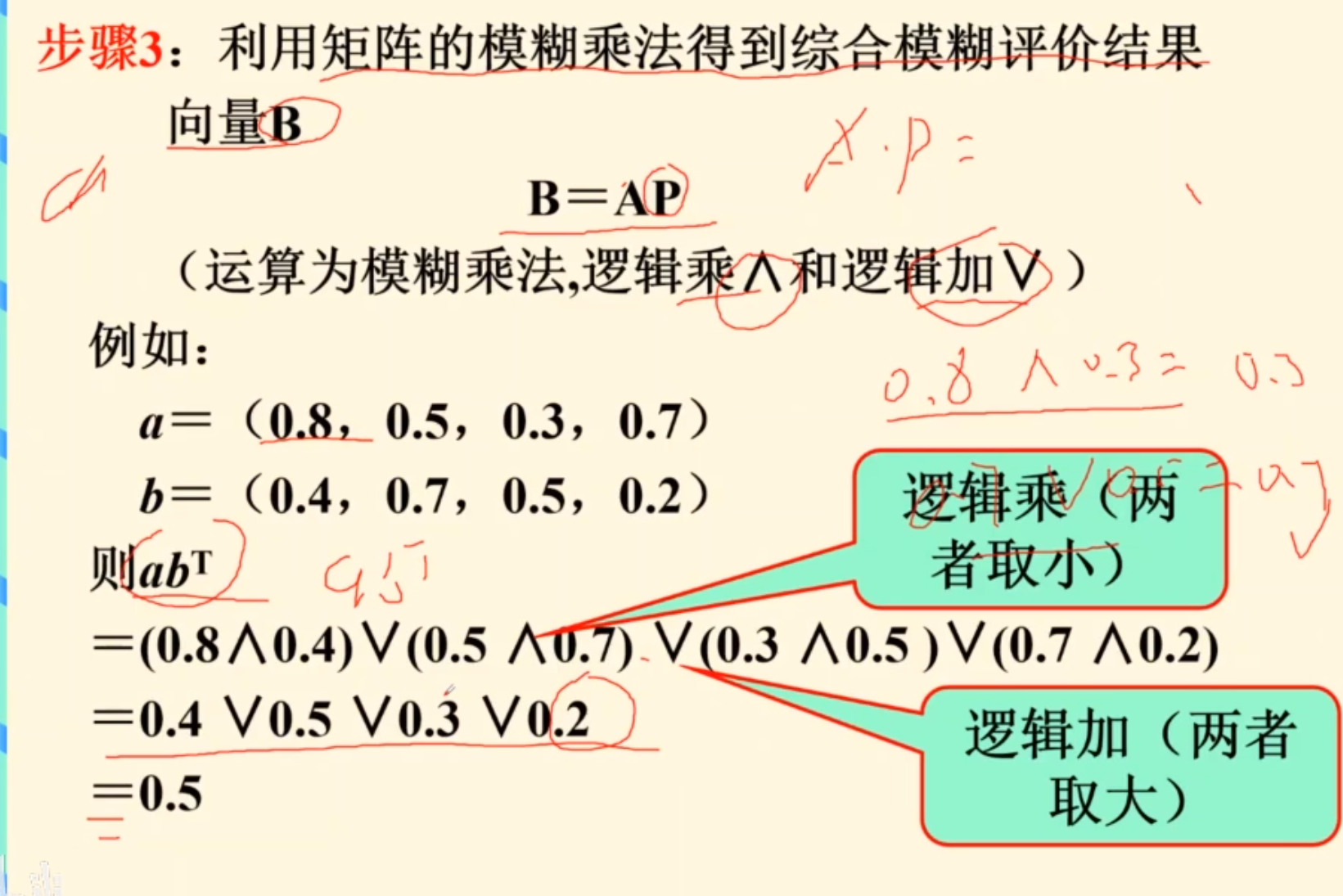
模糊合成与综合评价

模糊合成算子

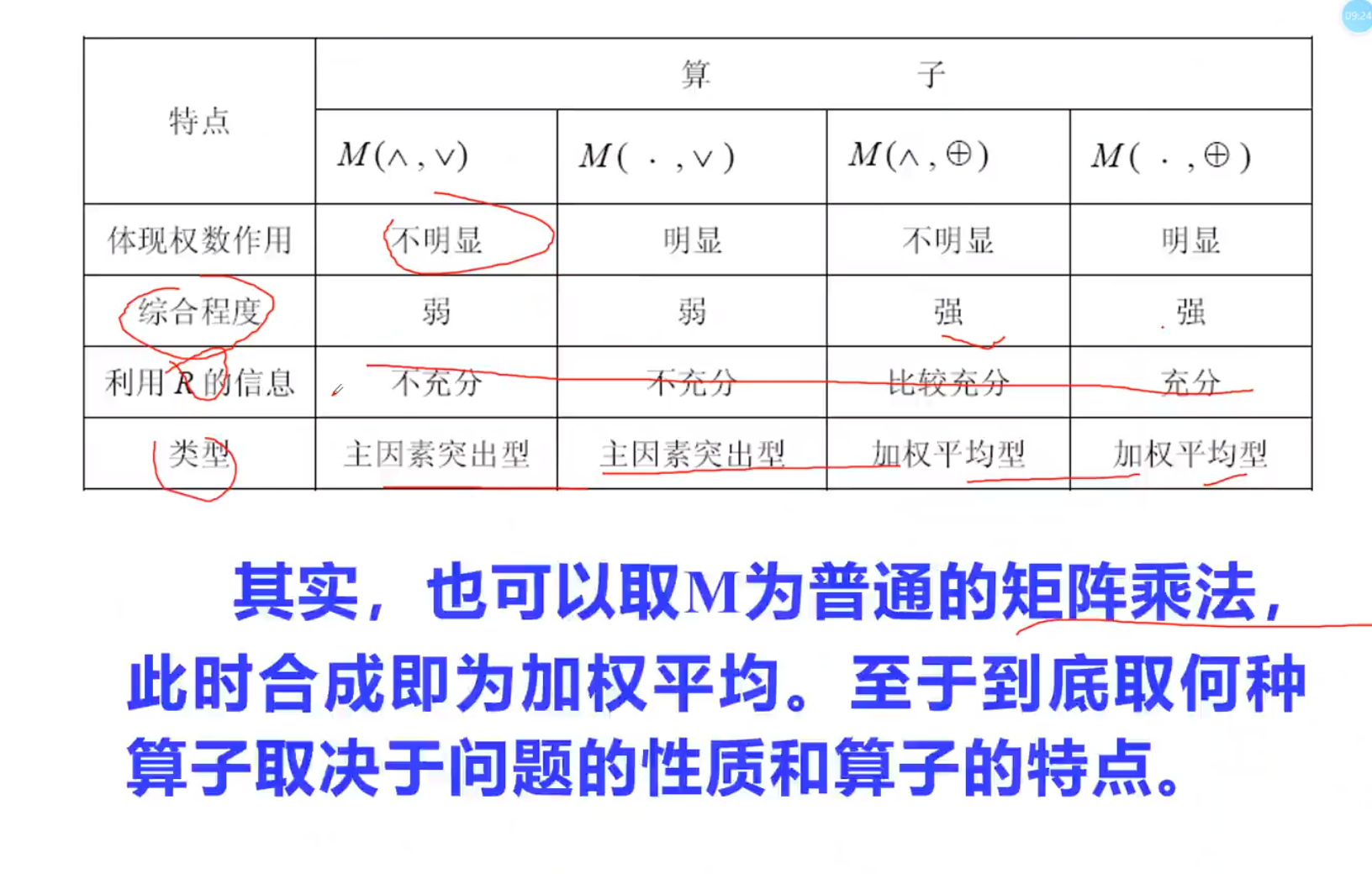




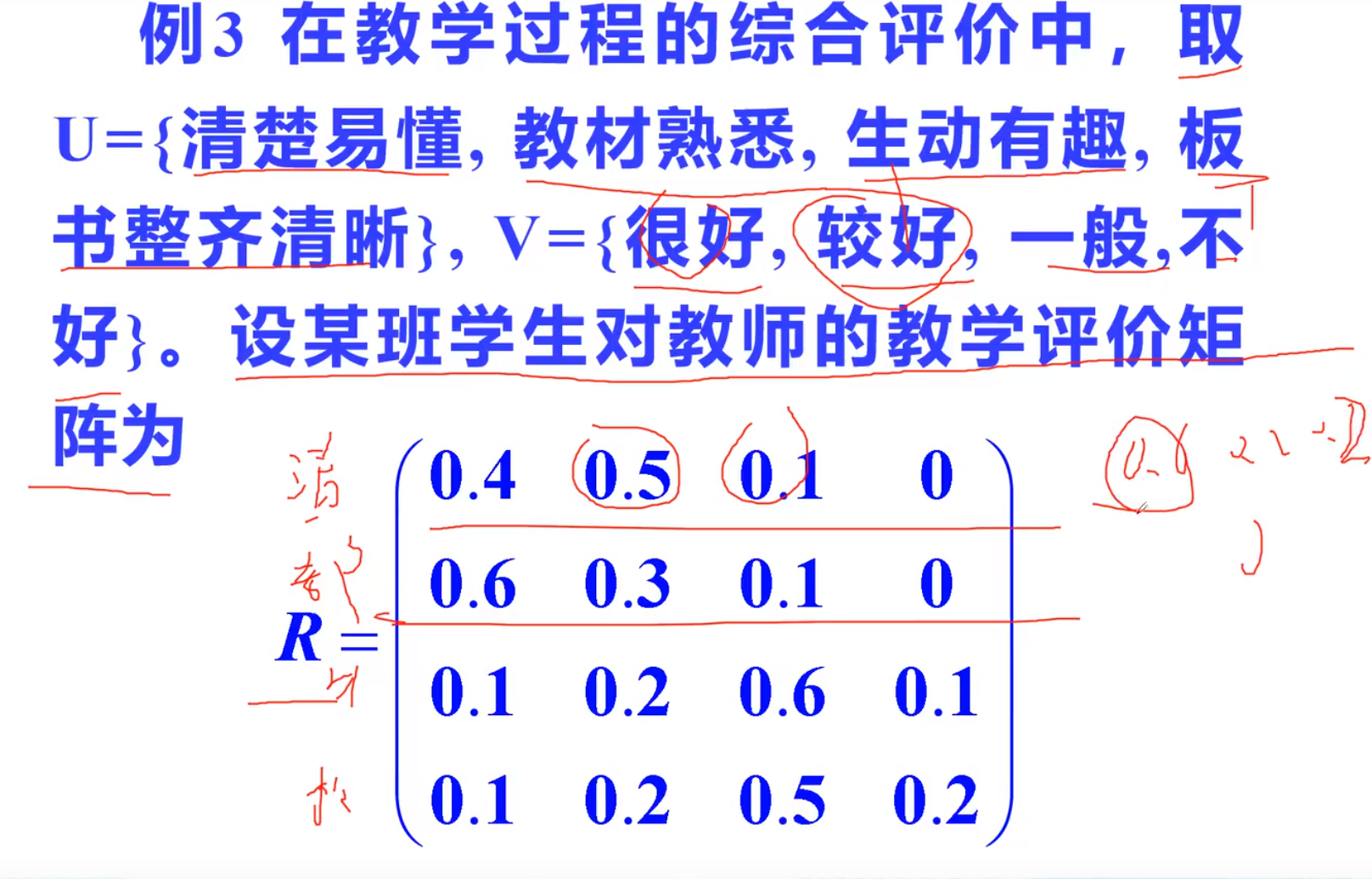
例:A为该权的权重

总结

相对偏差模糊矩阵评价法

步骤

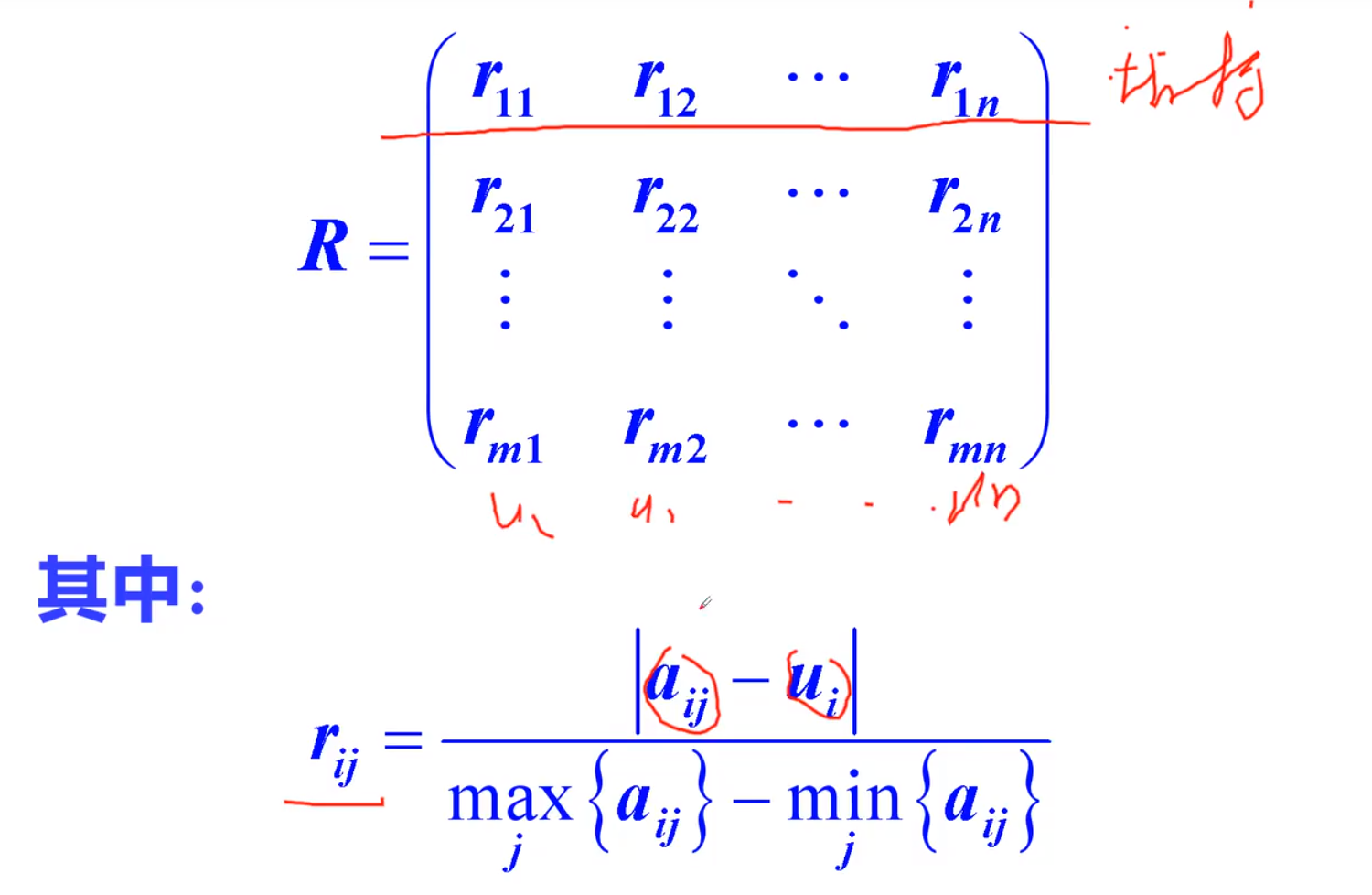
aij:具体数据,uj:理想型数据(该列) 注意:ppt写错了,应该是uj
再除以一个这一列的最大值减去这一列的最小值

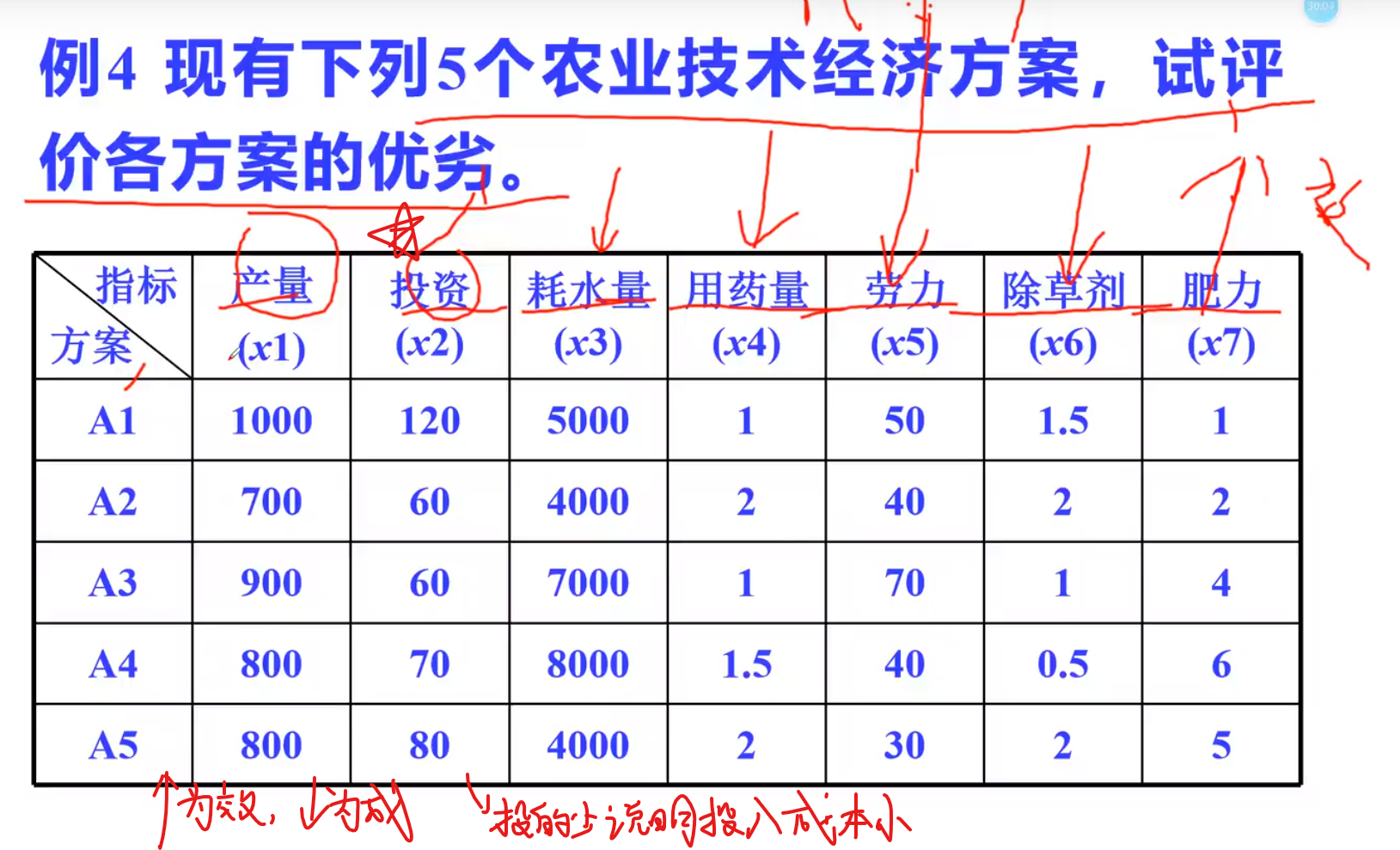

选出来的理想指标,肥力是土壤肥力
实际数据就是上表的(aij)理想数据就是上面列的最好数据(uj),由此可以得到r的矩阵
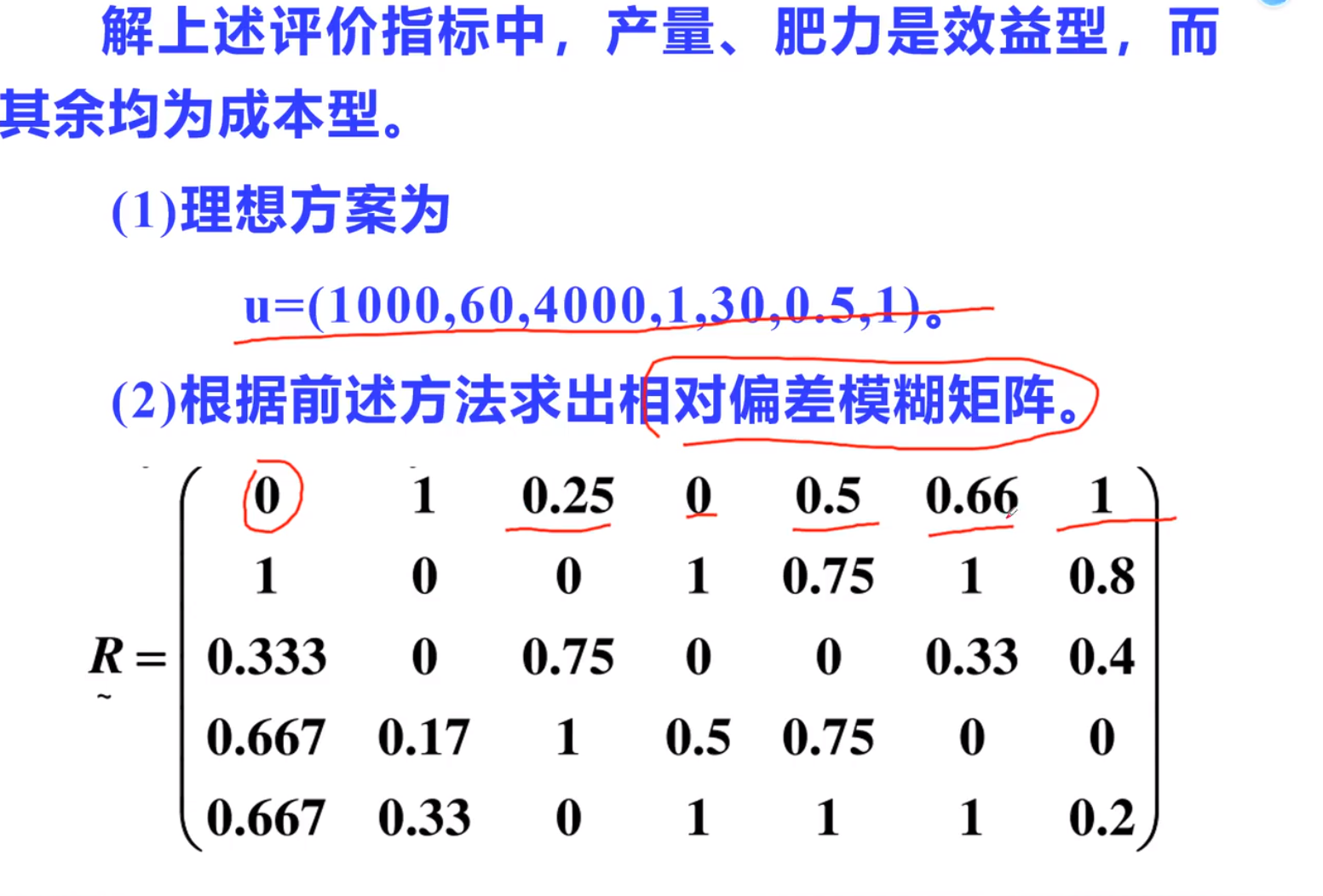

注意,平均数x,一定是同一个指标的平均数这样才能通过变异系数得到每一个指标的真正权重,(w需要归一化,由v得到),再乘以相对偏差模糊矩阵 –5×7 * 7×1 等于五个加权平均偏差(列)也就是每一项方案的优劣,(由于是偏差,是距离最优的理想数据的偏差,所以越小,越优秀)
相对优属度模糊矩阵评价法



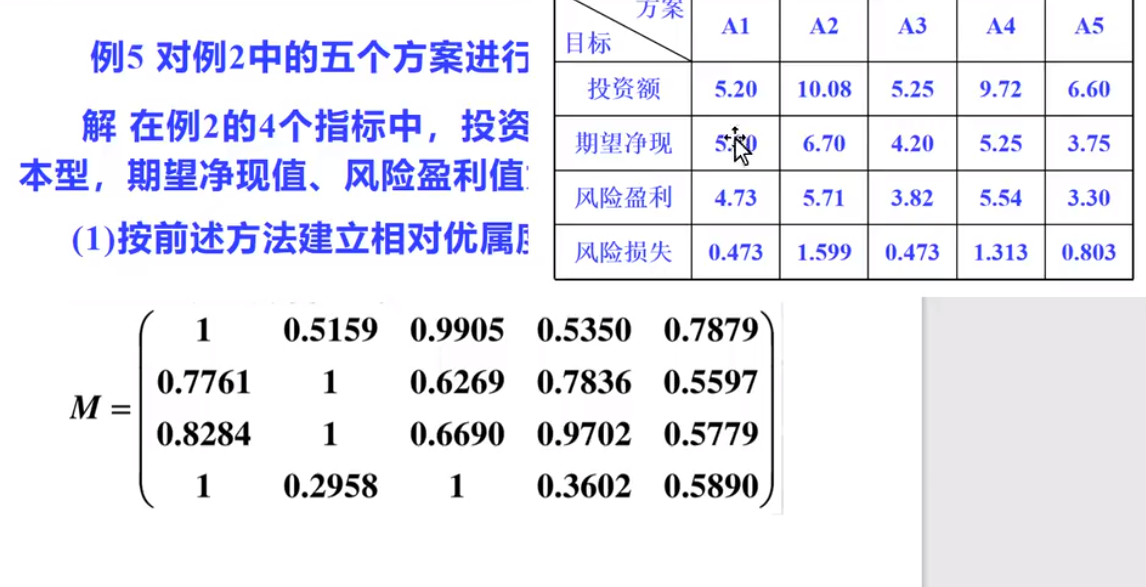

讨论







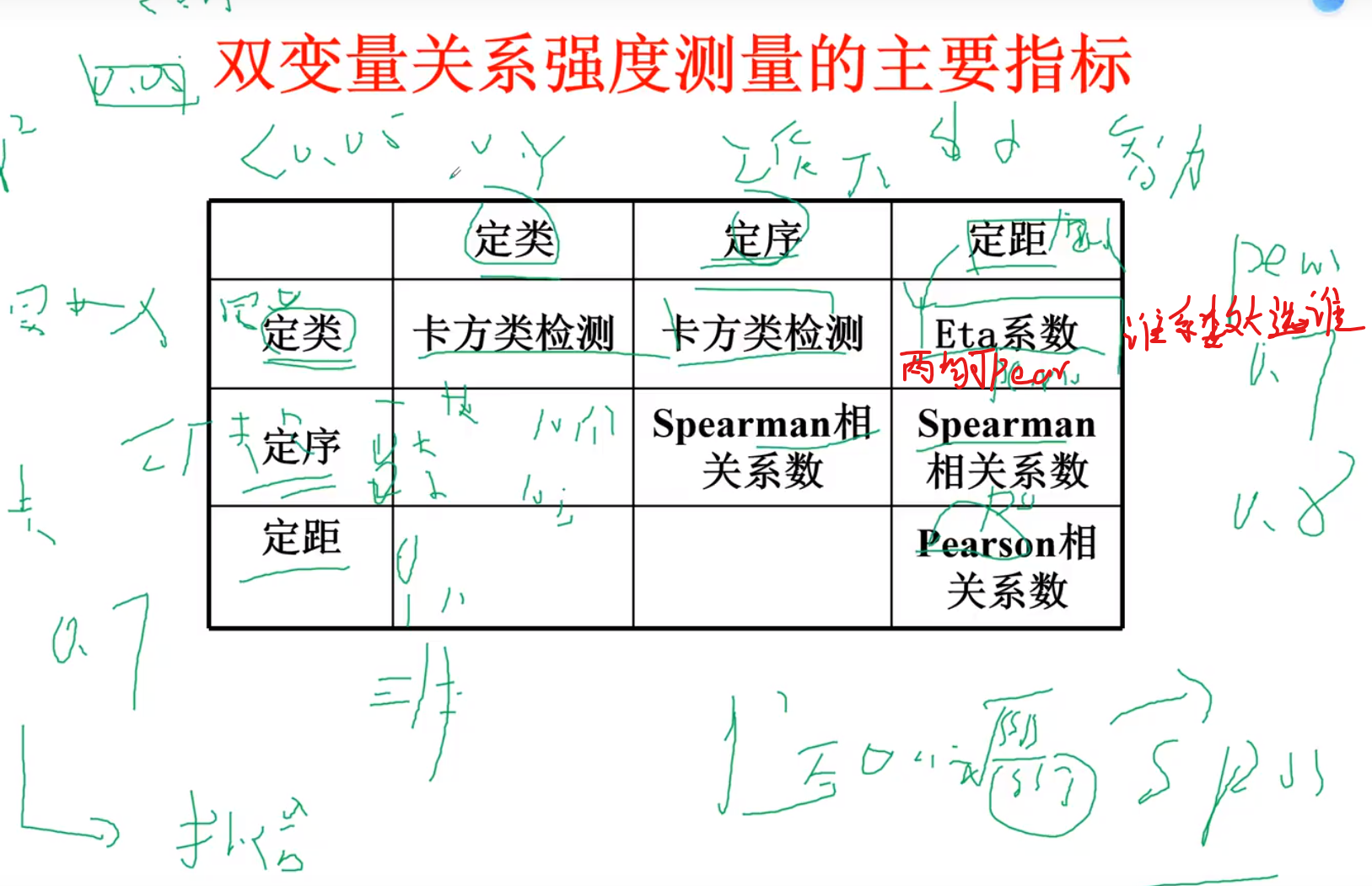
相关性分析

四种基本变量

两变量的相关性分析
Pearson

a/2单侧检验 T在概率论中有一个表,n为样本数据
(P value)就是当原假设为真时,比所得到的样本观察结果更极端的结果出现的概率。如果P值很小,说明原假设情况的发生的概率很小,而如果出现了,根据小概率原理,我们就有理由拒绝原假设,P值越小,我们拒绝原假设的理由越充分。总之,P值越小,表明结果越显著。但是检验的结果究竟是“显著的”、“中度显著的”还是“高度显著的”需要我们自己根据P值的大小和实际问题来解决。
双尾显著性只要小于0.1就可以,为成功数据(10%的概率判定他是不满足的)(也就是相关性高)(如果大于0.1了,就说他们之间关系并不大,或者不存在关系
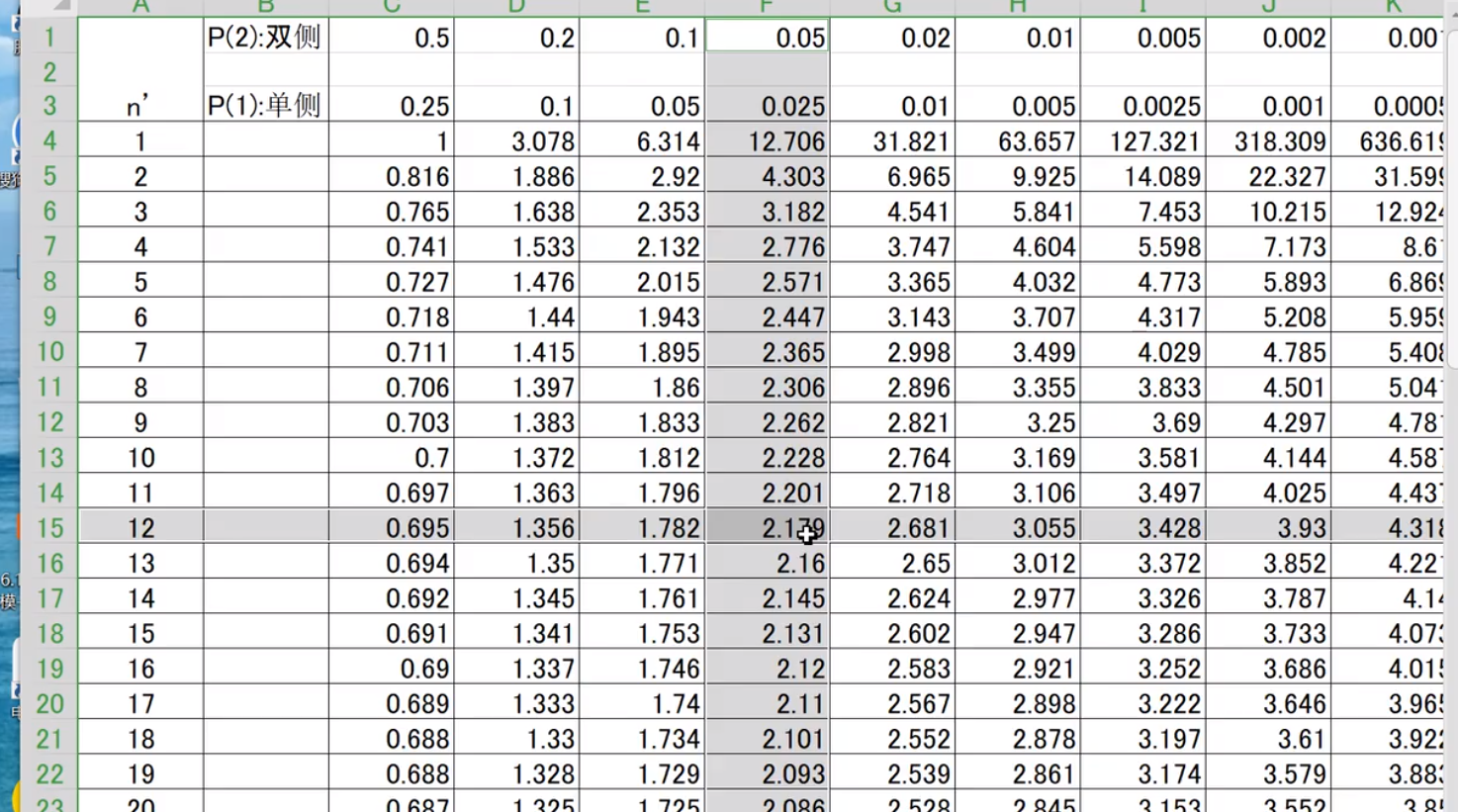
t大于这个数(对应的数)则通过检验
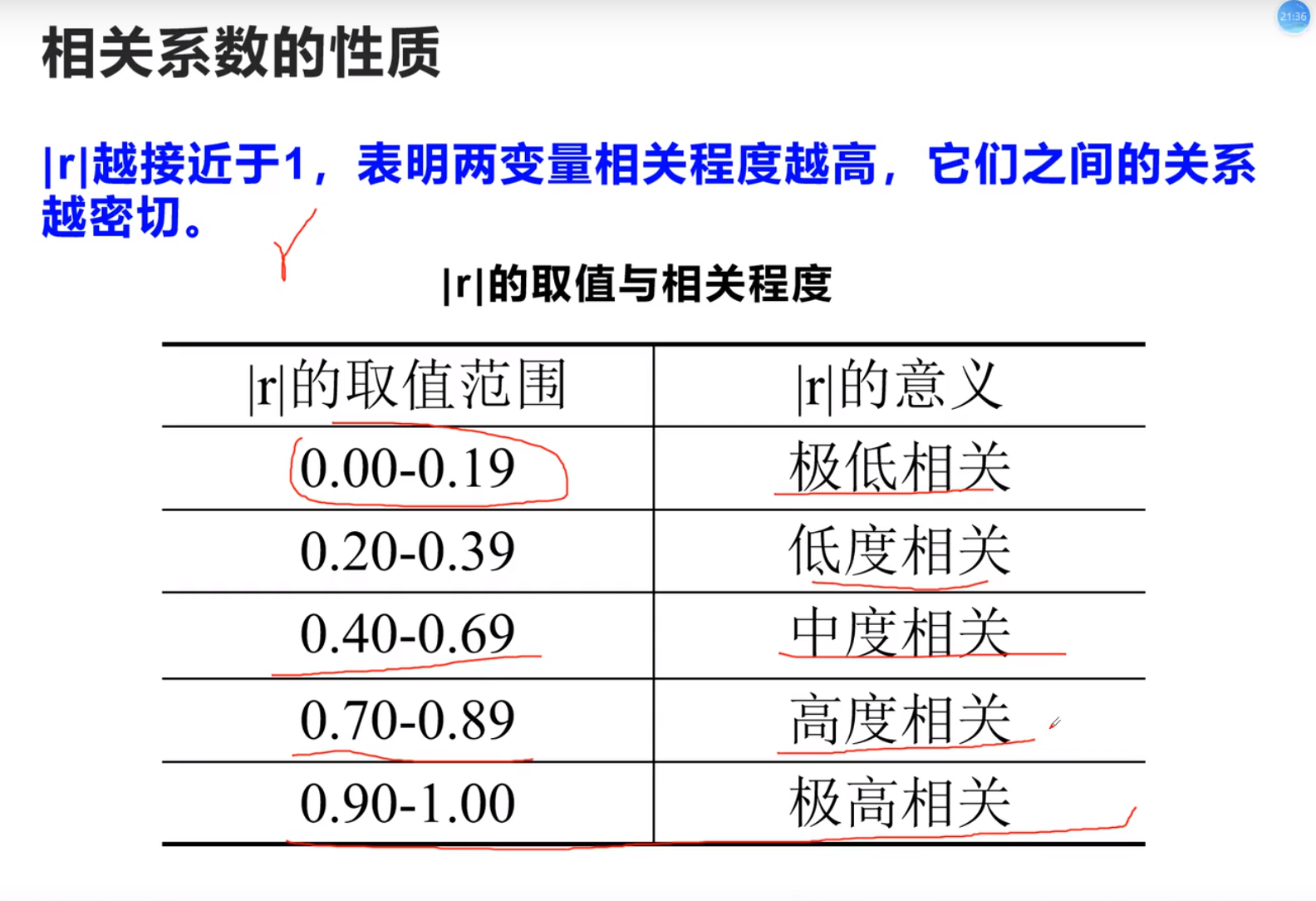

必须线性关系!
Spearman

主要指标
因为存在相关性,才能做拟合 ETA系数大,呈现非线性相关,pearson大,呈现线性相关
卡方就是高中学过的,比如小于0.05则有关那种题型
明显能看出相关性,则不用做拟合
SPSS输出变为英文
https://jingyan.baidu.com/article/e6c8503c3deff3a44e1a182f.html
SPSS较大数据的归一化
(18条消息) SPSS实现数据归一化_Prophet.Z的博客-CSDN博客_spss归一化
SPSS-Z字标准化
SPSS Pearson Spearman
一般双尾检测
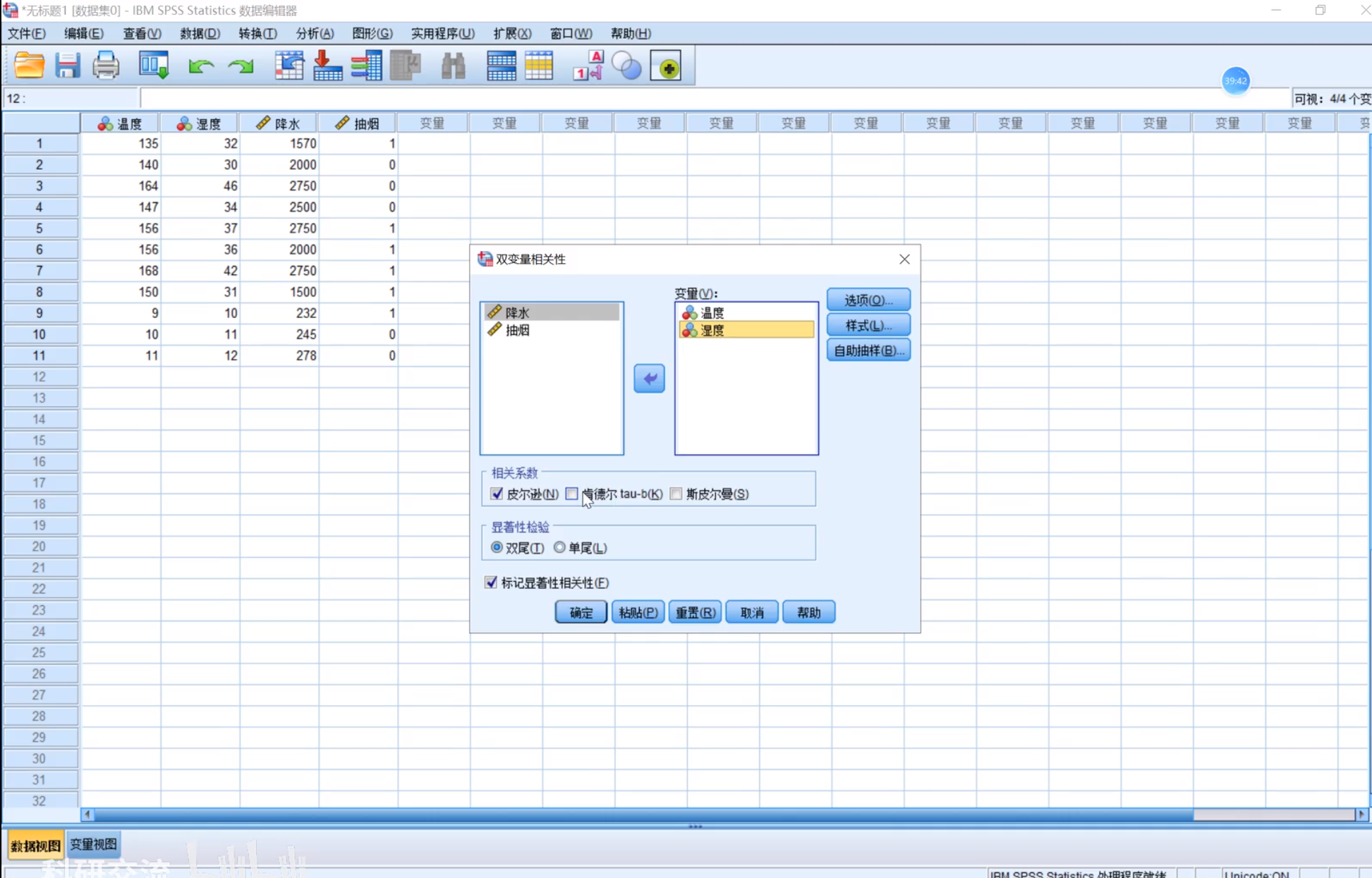
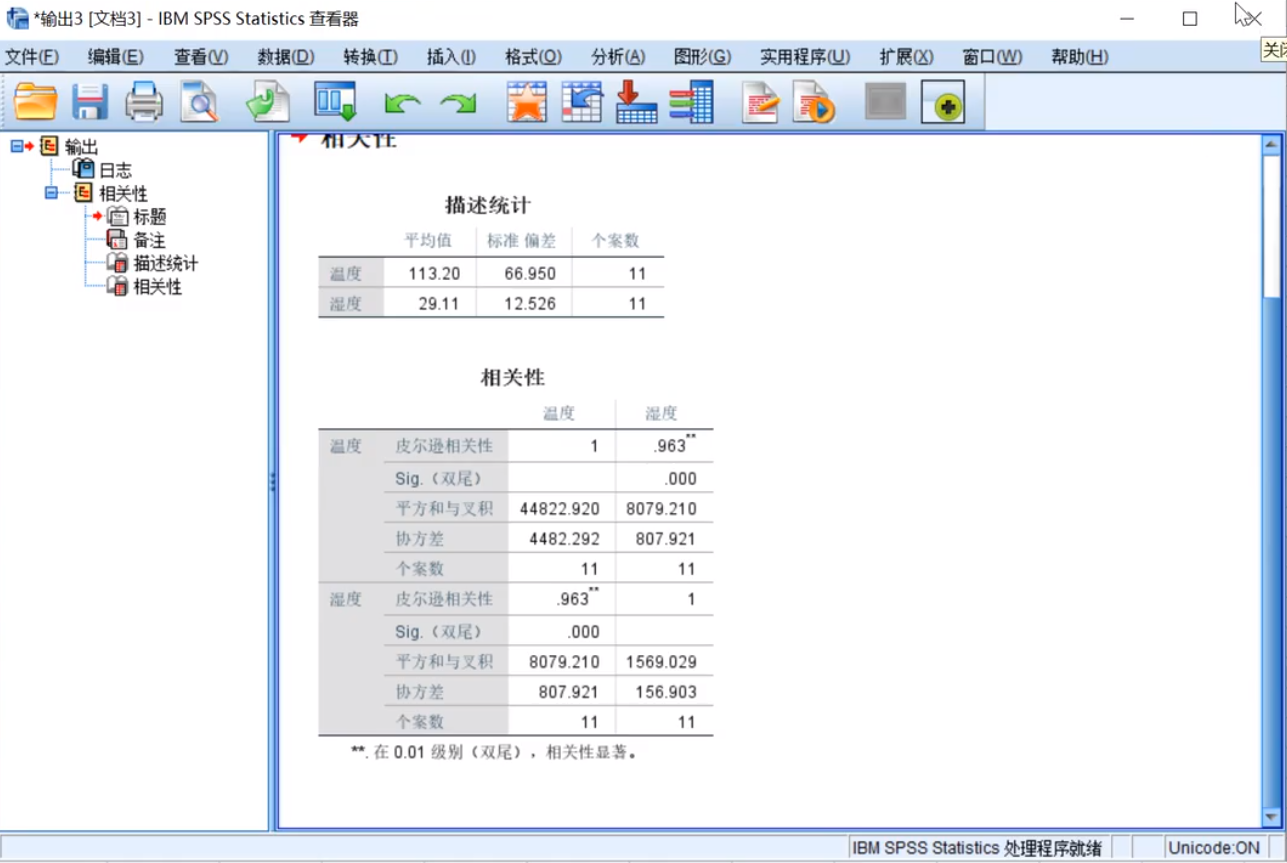
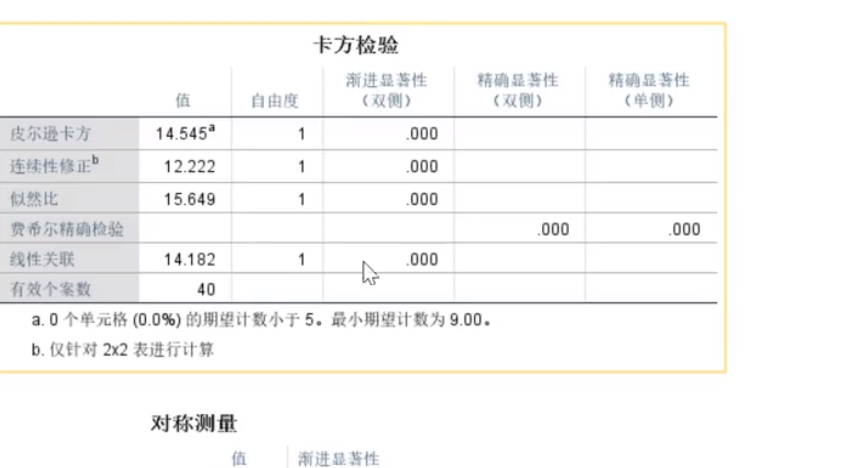
SPSS卡方检验
行:应变量 列:自变量
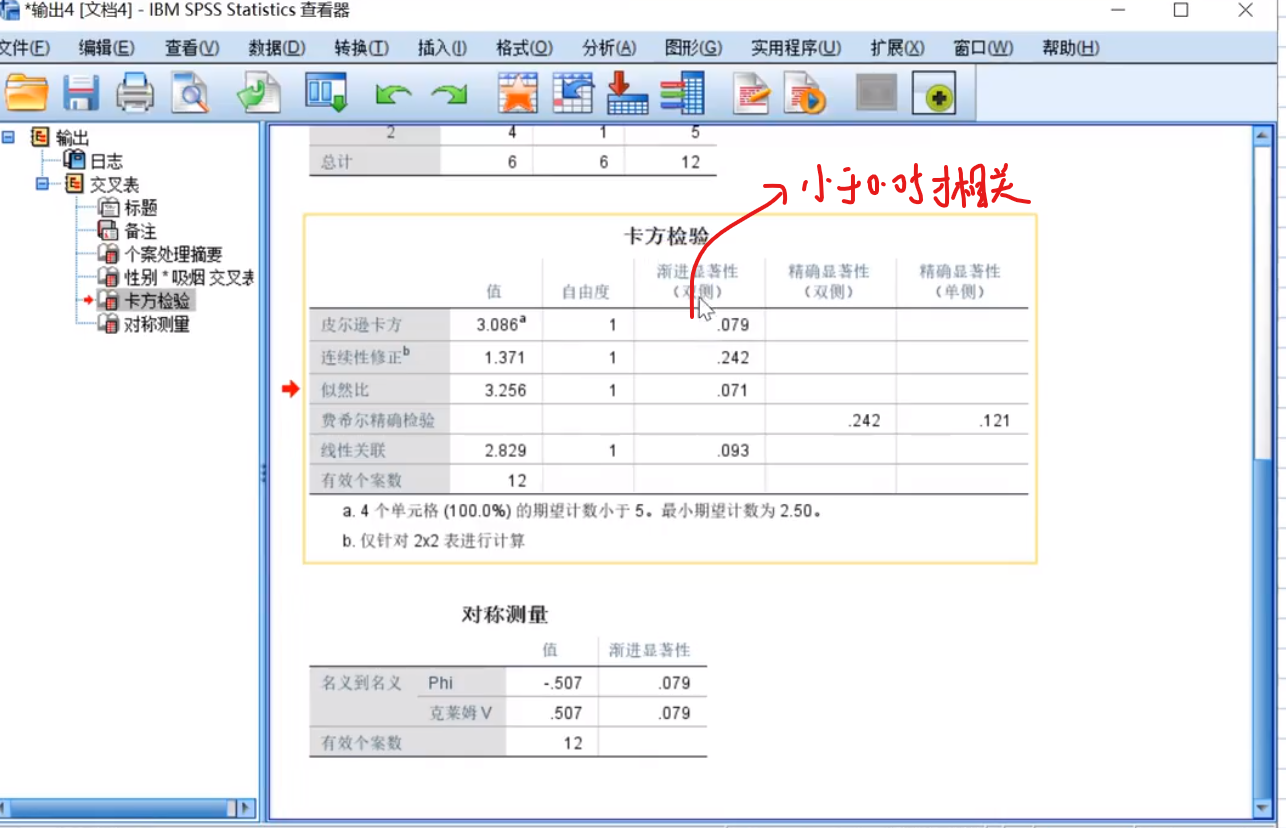
现在是0.79,说明显著性并不强,说明性别和吸烟不存在很强的关系
SPSS ETA
行:应变量(y) 列:自变量(x)
如何使用SPSS进行相关性分析(三):实战案例操作(内附案例数据) - 知乎 (zhihu.com)

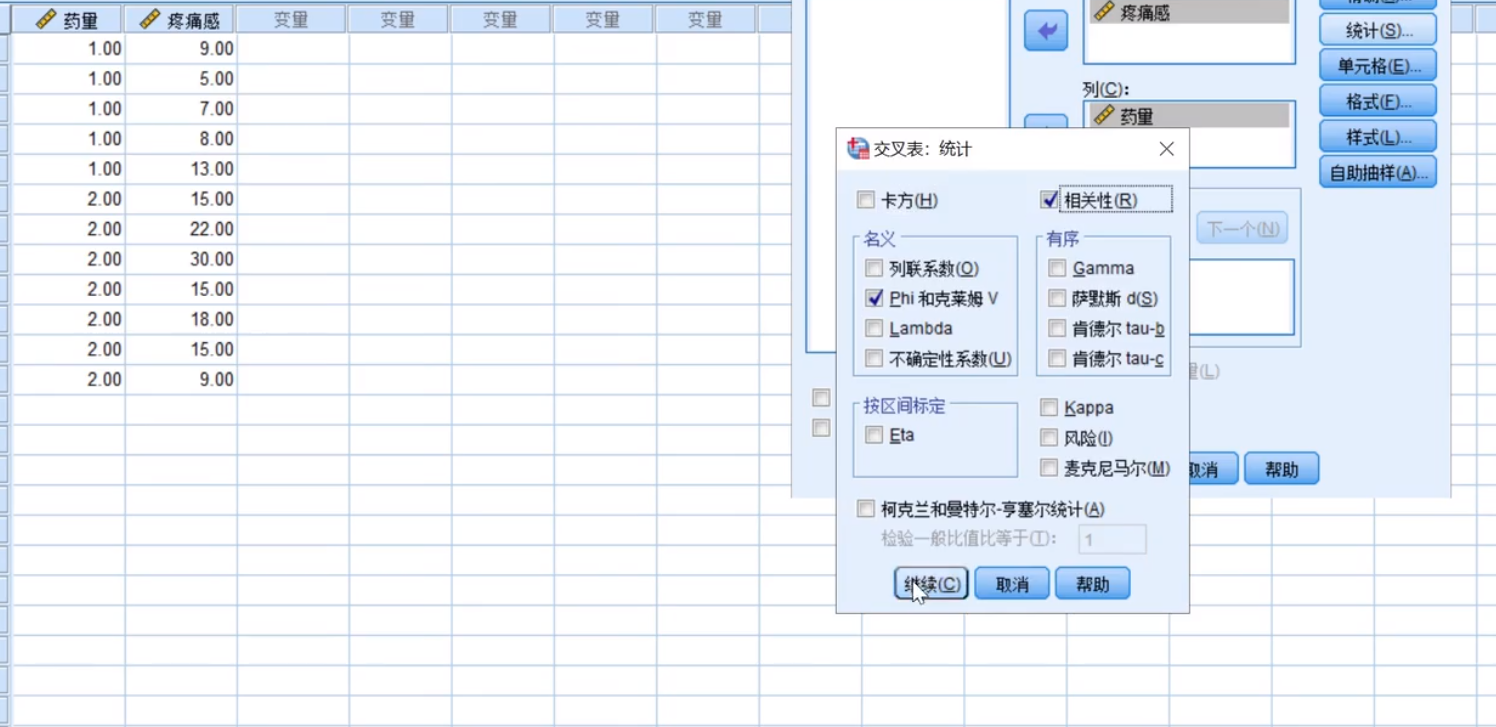
ETA>0.5就是呈现相关,0.91为高度相关,并且大于皮尔逊,所以是非线性函数
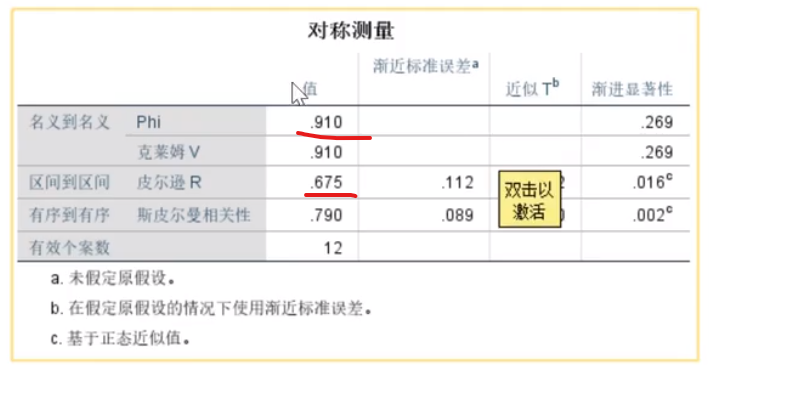
SPSS处理频数数据
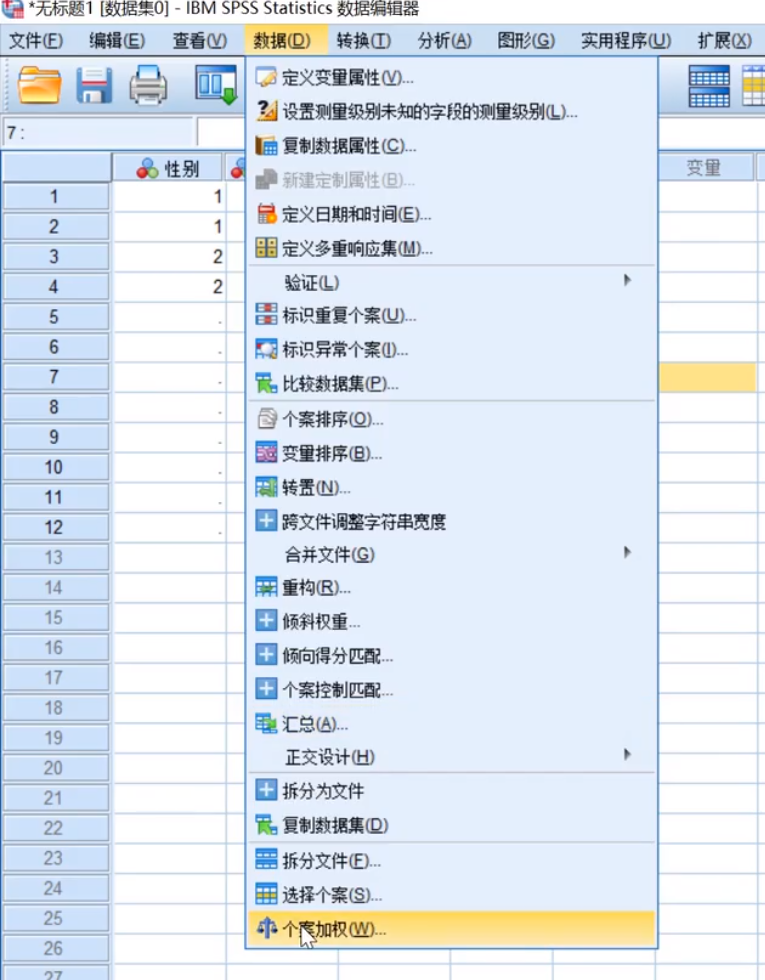
接下来继续进行步骤就可以得到想要检验类型的结果(上面几个检验的步骤)
SPSS 和 matlab应该都是可以使用的,spss最简单,就用这个吧!
偏相关分析

控制变量法
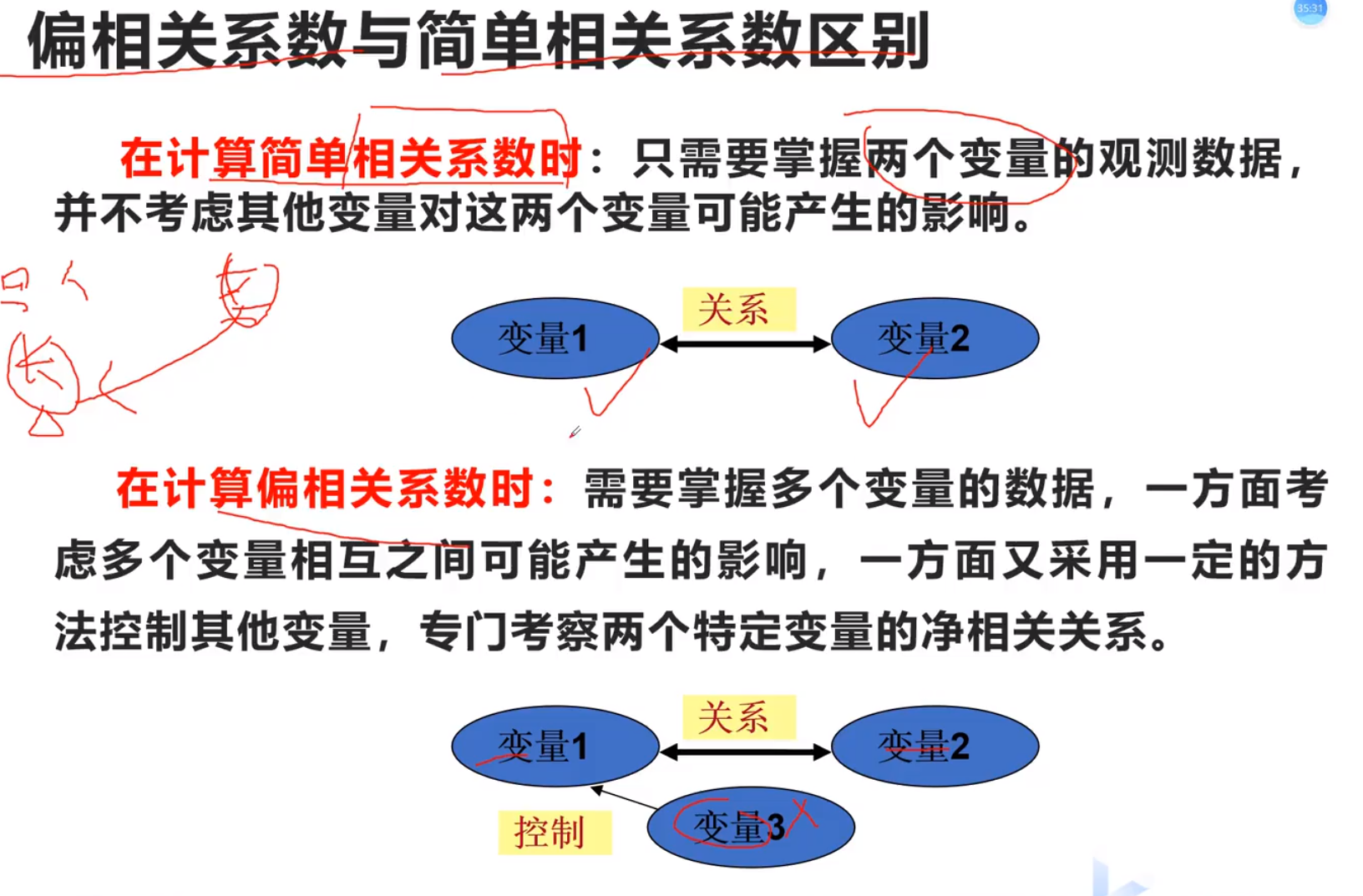
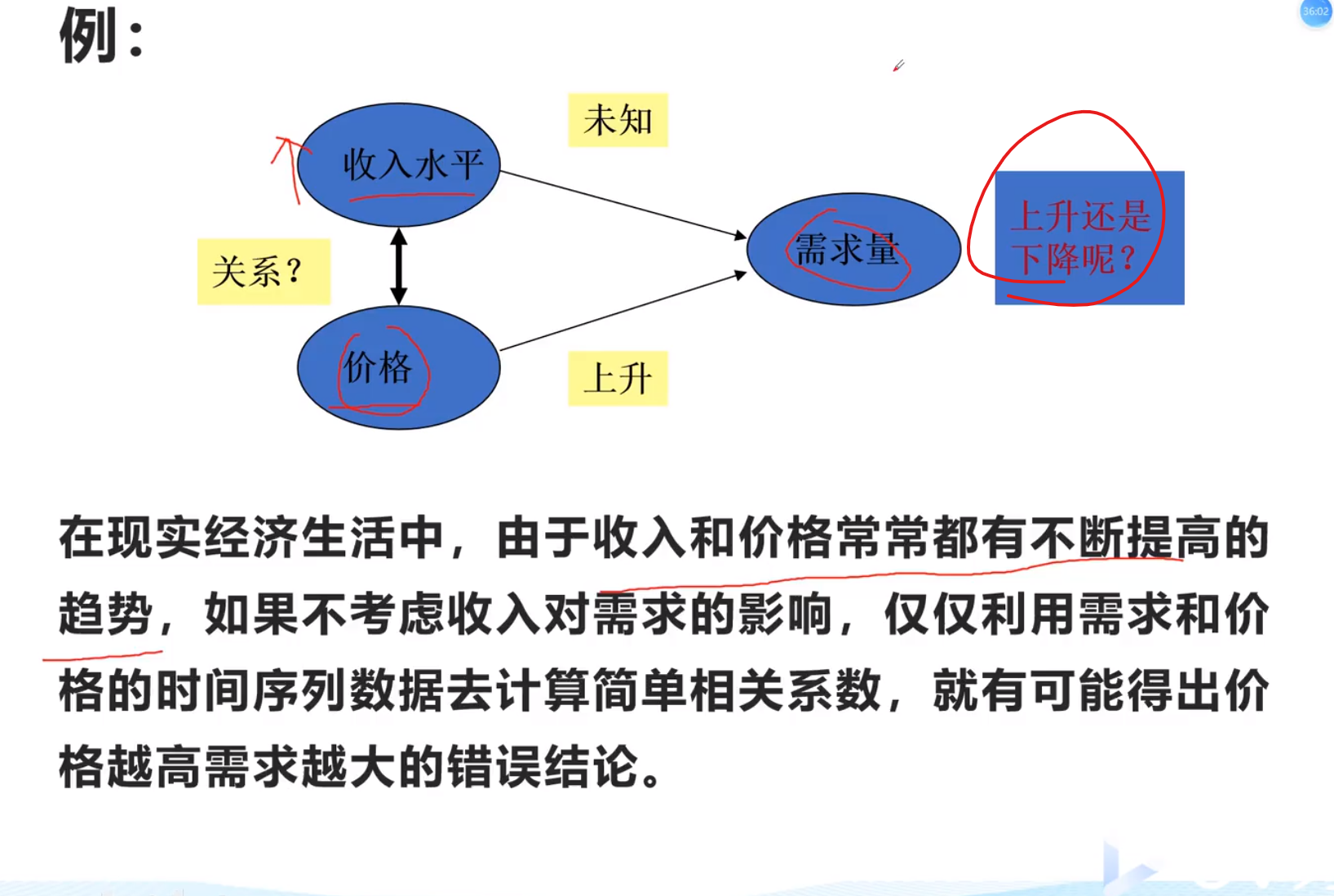
SPSS实现
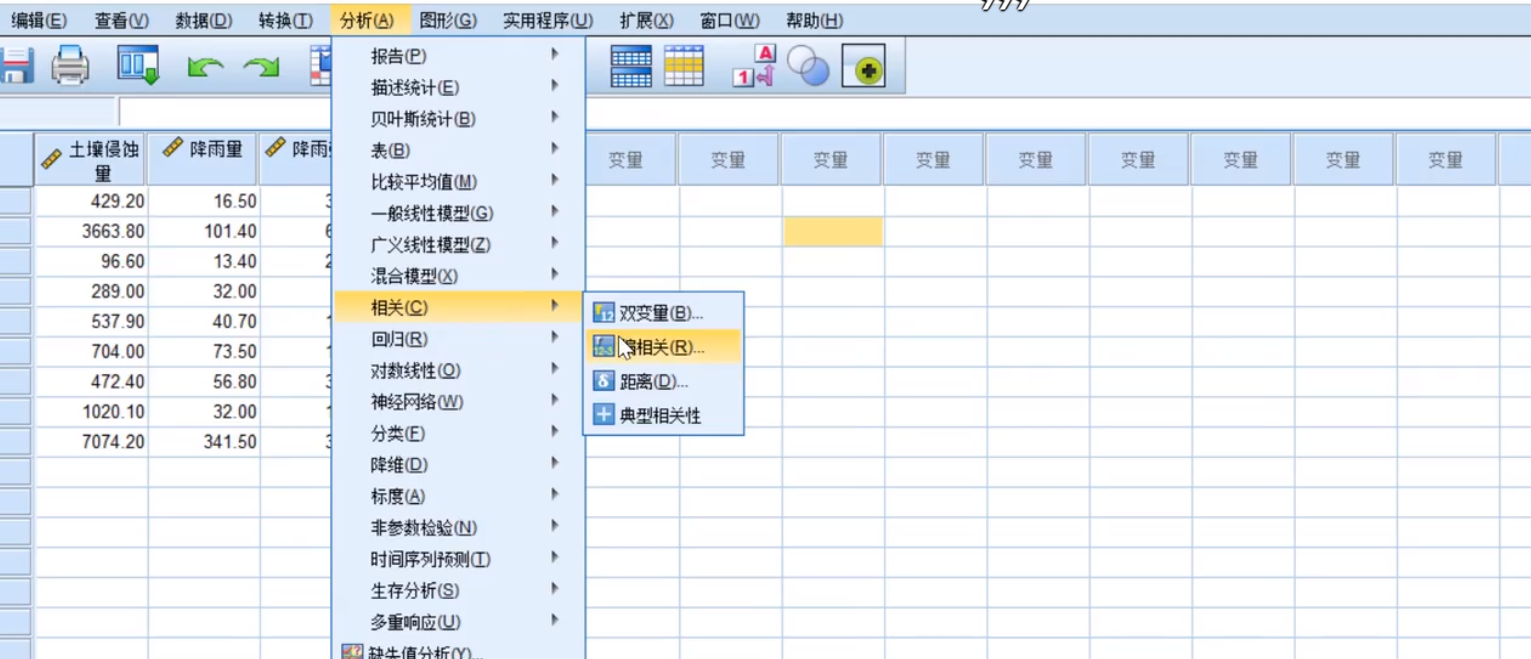
偏相关系数和检验

下面的图可以说明,抛弃降雨强度以后,土壤侵蚀量和降雨量达到高度相关,比之前更加相关
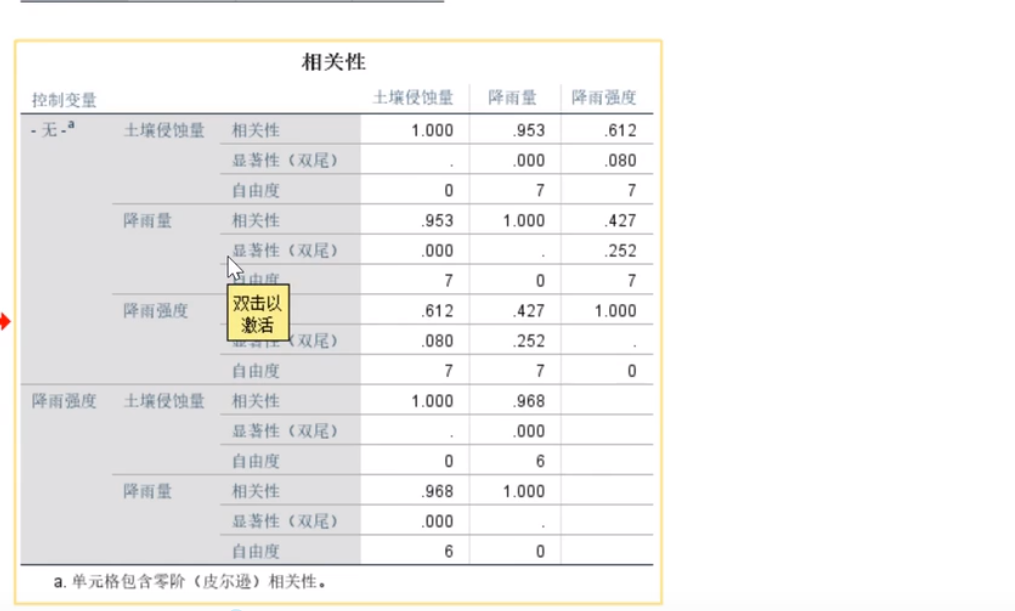
例题
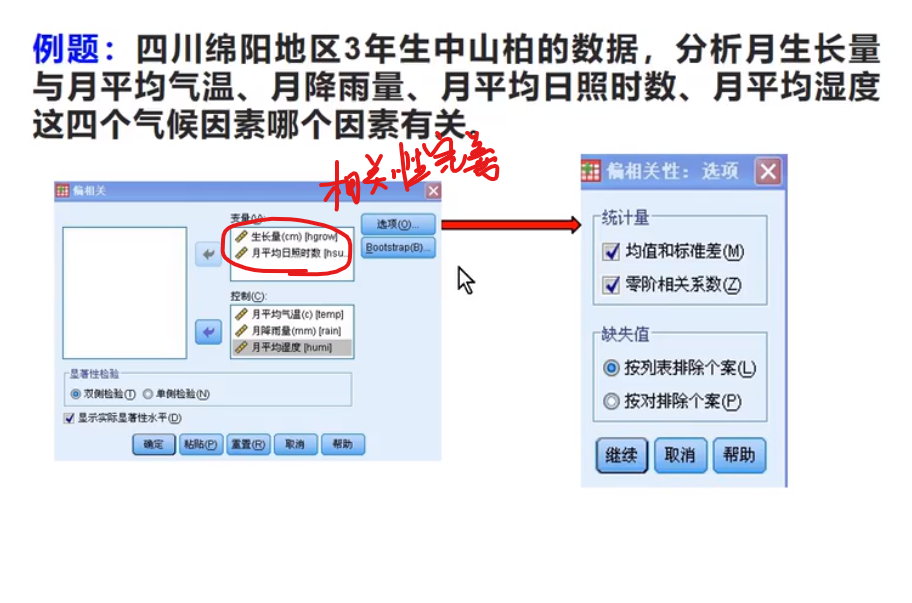
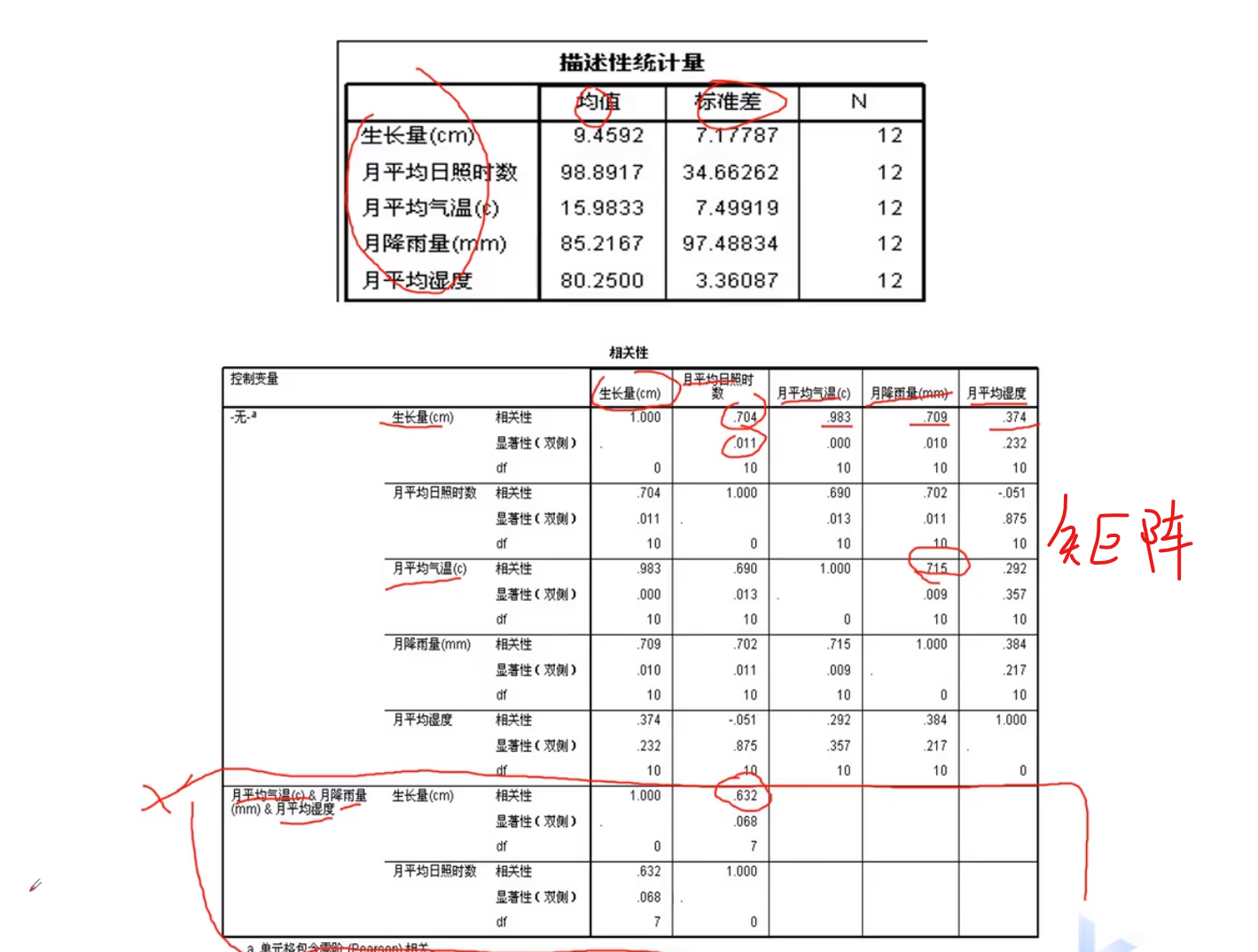
说明抛去的三者,是对两个变量起促进作用的,会变相的提高生产量
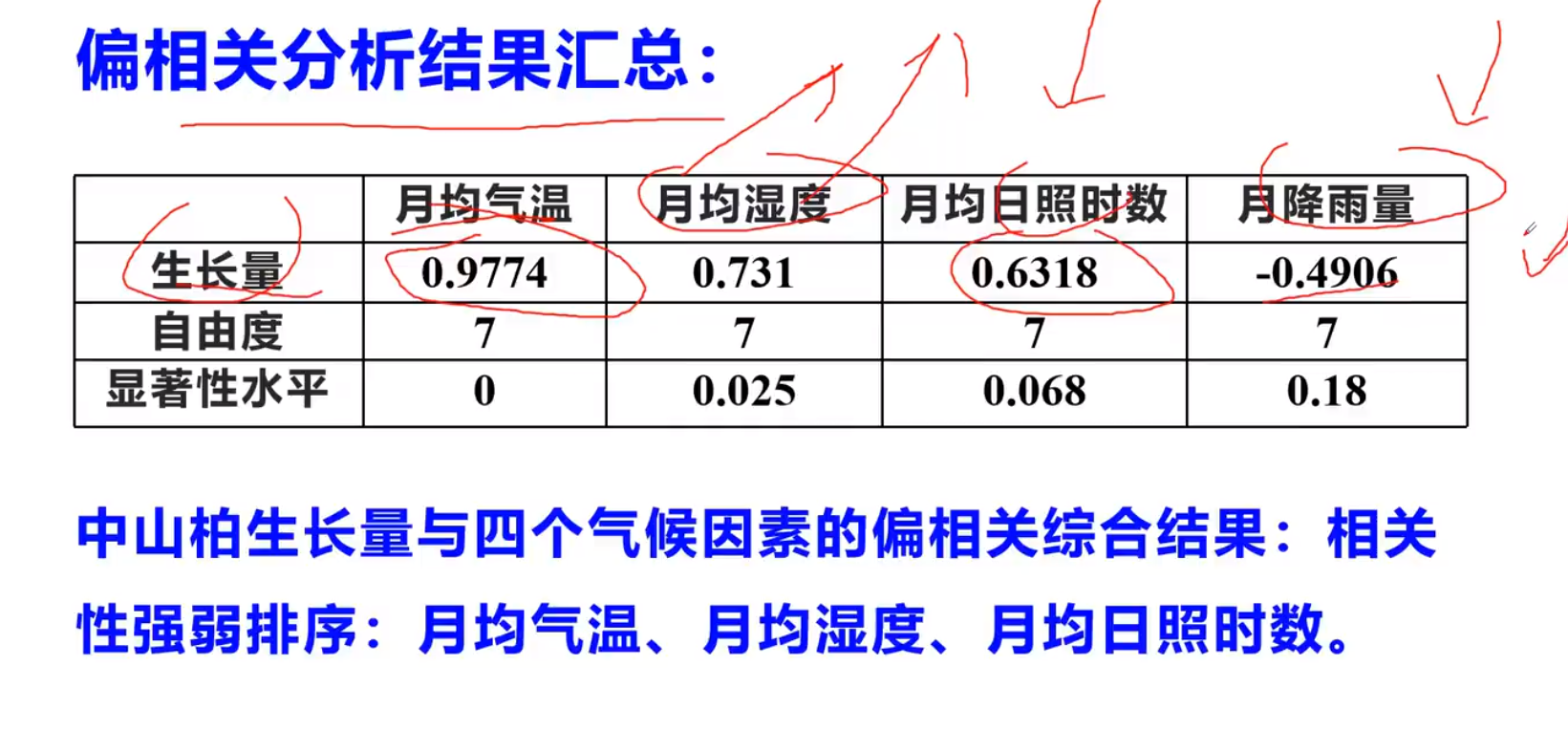
为了分析单独两个,一定要用偏相关,控制变量!
数据降维
使用降维之后的变量进行拟合,评价之内的操作会简化很多
主成分分析
有很多个指标的时候,发现前三个的信息量超过后面n个,达到全部的85%以上,那我们可以说用前三个替代了所有的指标进行分析v
基本原理

数据的压缩:第一指标能代替2,3,5,7,那么我们就只对第一指标进行分析,数据的解释:另外,如果2,3,5,7是关于经济的指标,那么我们说第一指标能解释原先指标中关于经济的那一部分
基本思想:例如大家的数学成绩都是75左右,语文成绩分布在25-100,那么我们完全可以用语文成绩来代替这个人成绩是否好

最主要的目的是找到a1和a2,这样我们就可以把两个坐标合并成一个坐标
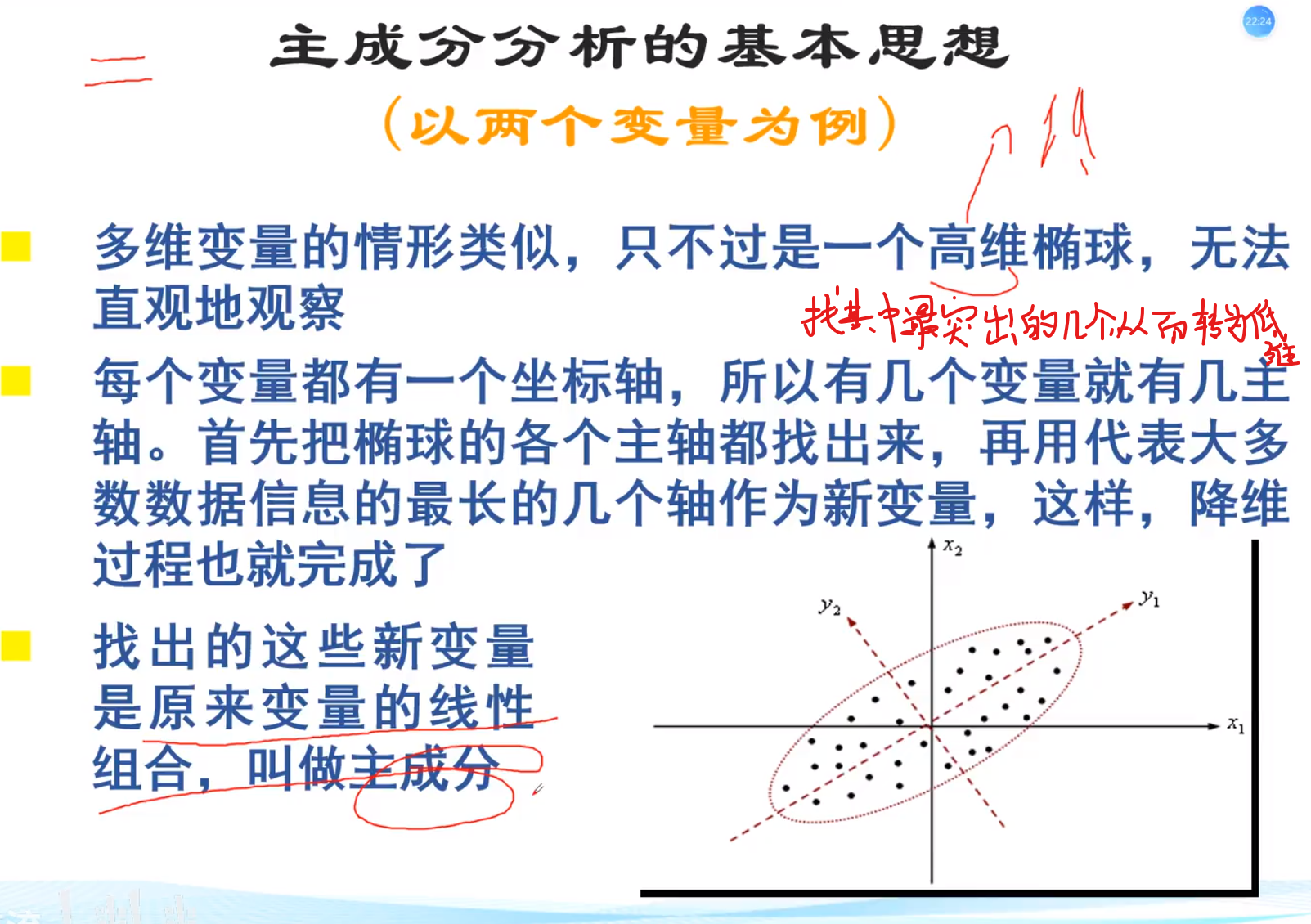


数学模型
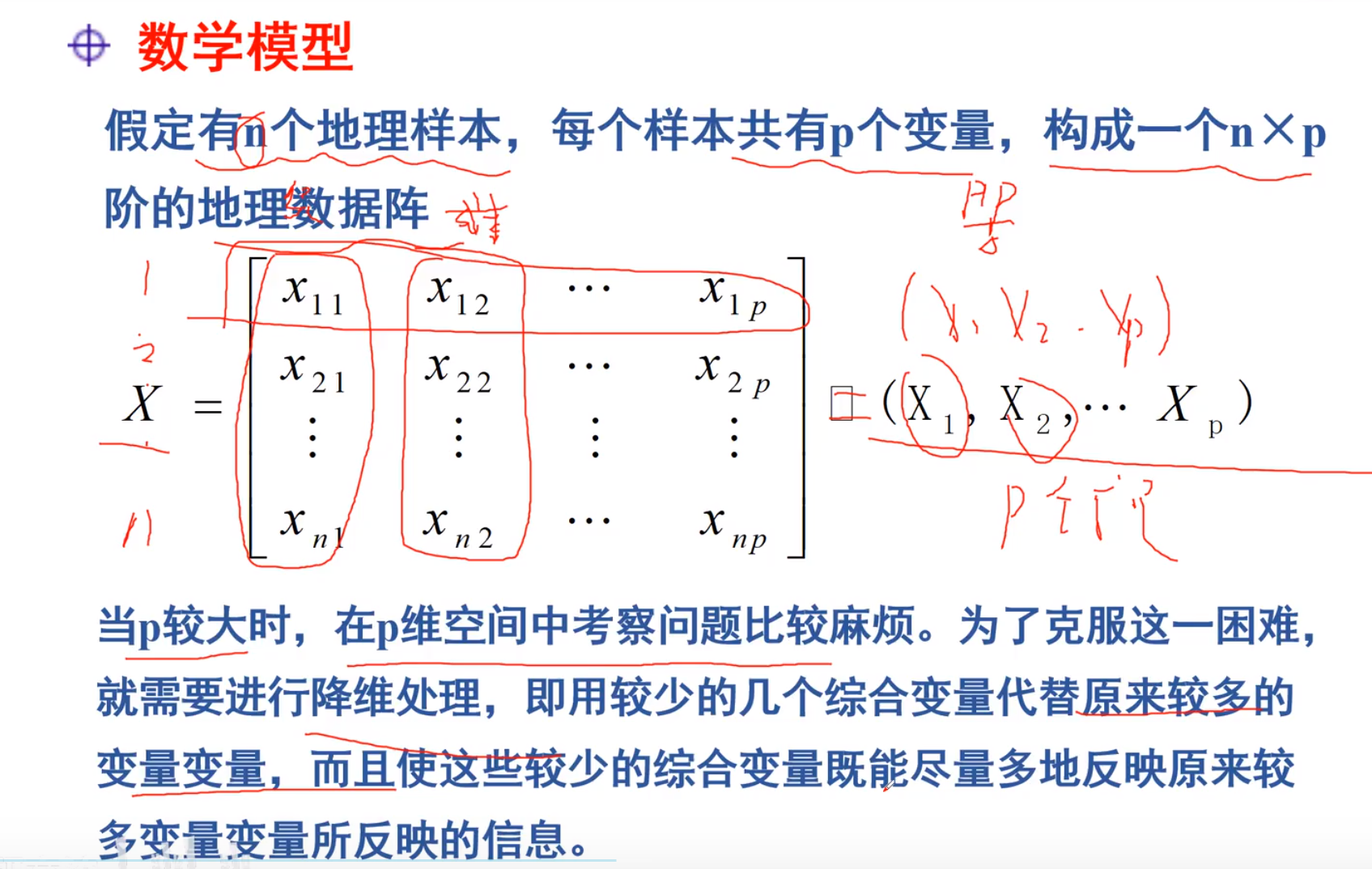

条件

标准化处理一定要到(-1,1)范围内(归一化)

KMO大于0.5意味着很适合,0.3,0.5代表着适合,但可以做(不一定准确),小于0.3意味着不太适合做主成分
bartlett数(sig)如果小于0.05,意味着可以做,大于0.05代表不推荐
两个数只要满足一个就可以做!
推导
不懂QWQ,溜了溜了


主成分提取


最开始数据一定要做标准化处理!!
步骤

例子
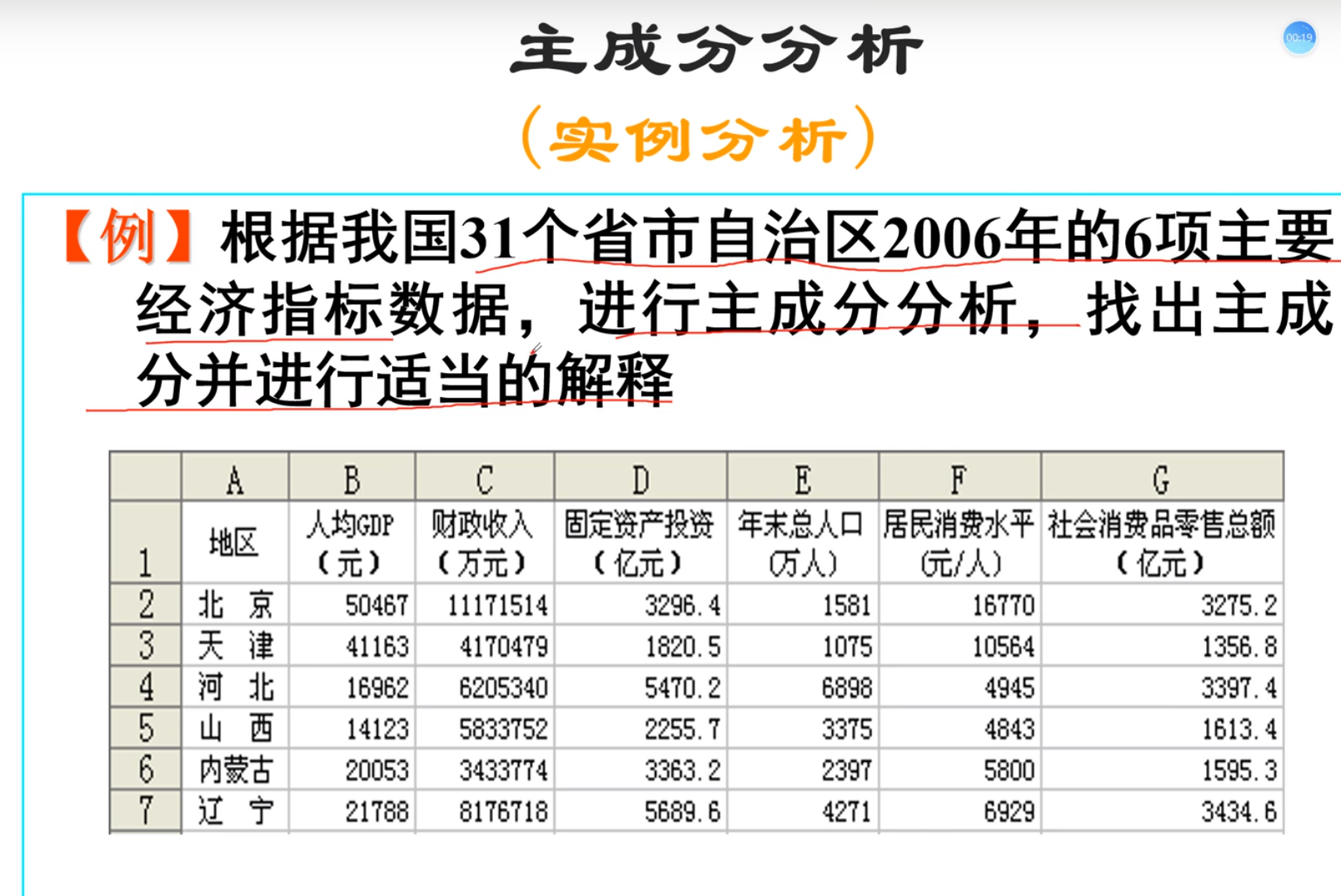
SPSS主成分分析

分析–描述统计–描述,把所有数据导入,并且左下角将标准化值另存为变量点击选上
计算结果
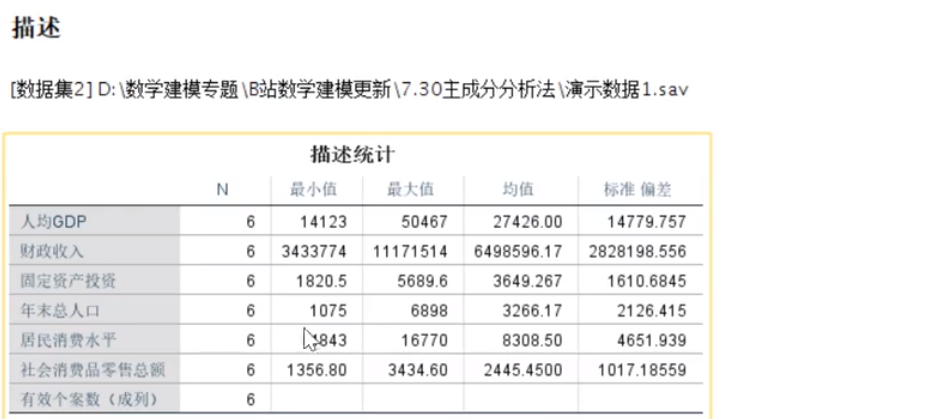
整个数据在-10- 10 范围内
补充:SPSS因子降维
点描述
点提取,碎石图也可以点,效果很明显,代表每个因子的方差,斜率变化比较大的地方是拐点,我们可以选前两个
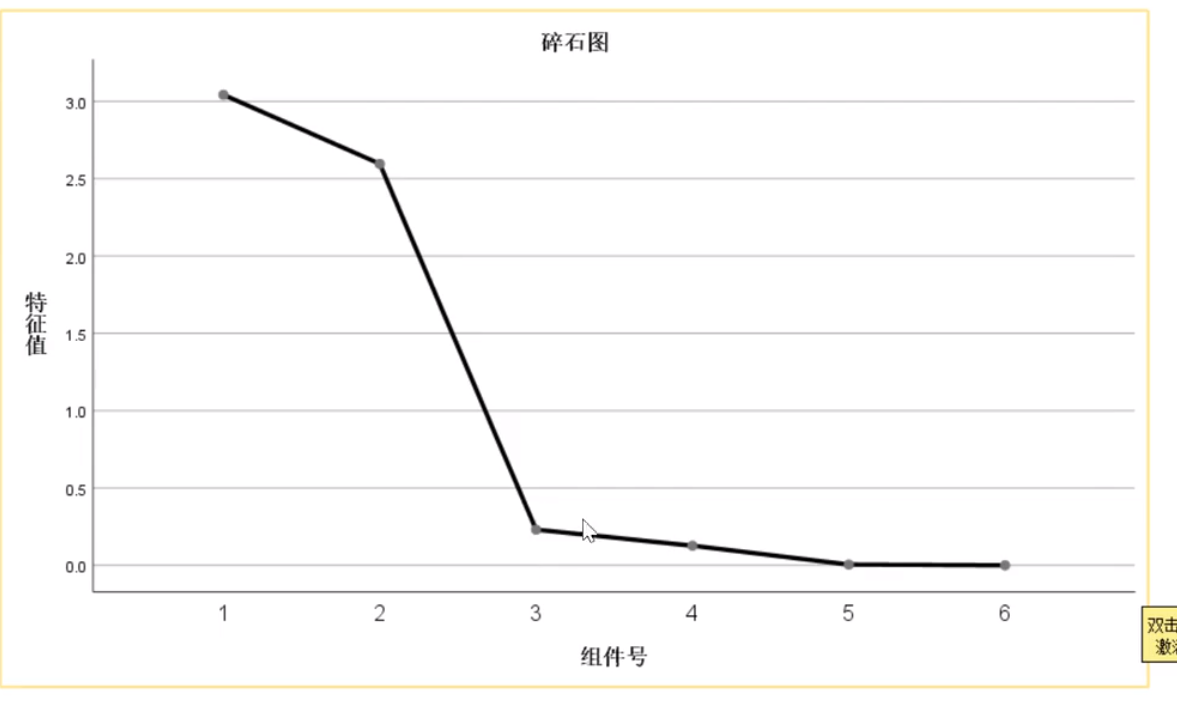
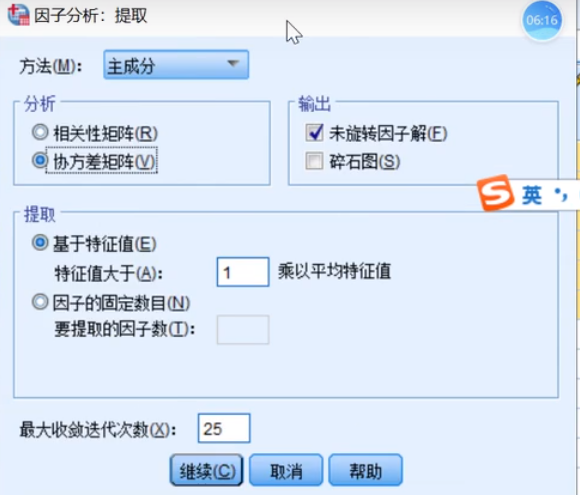
点旋转,旋转里面那个载荷图,我们也可以勾选上
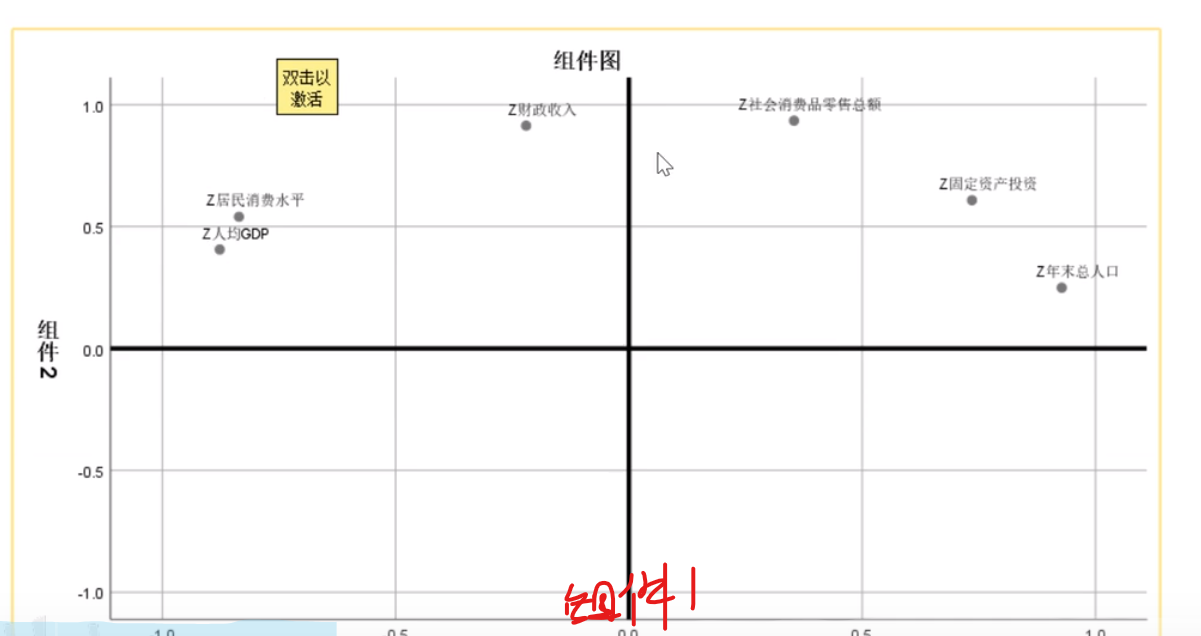
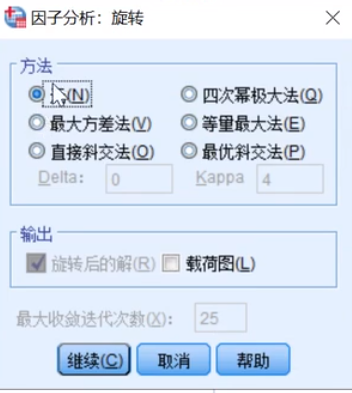
点得分
然后确定!!!
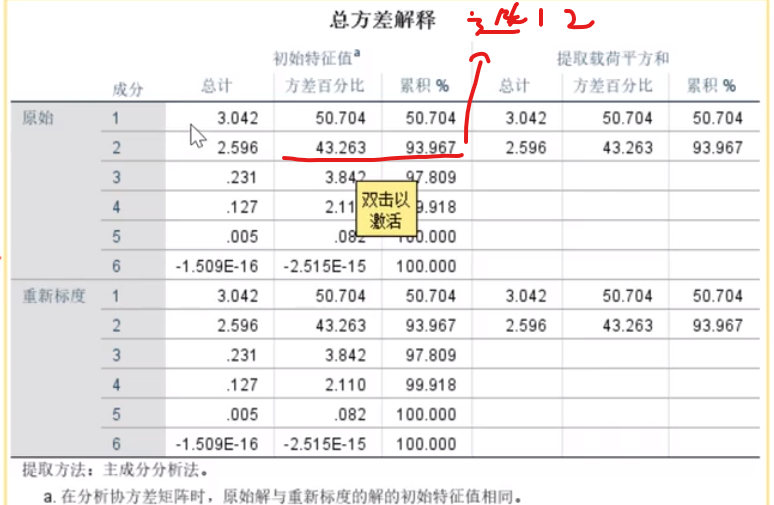
第一主成分和gdp,固定资产,人口,消费水平高度相关
第二主成分和财政收入和零售总额高度相关
右键下图可以编辑内容
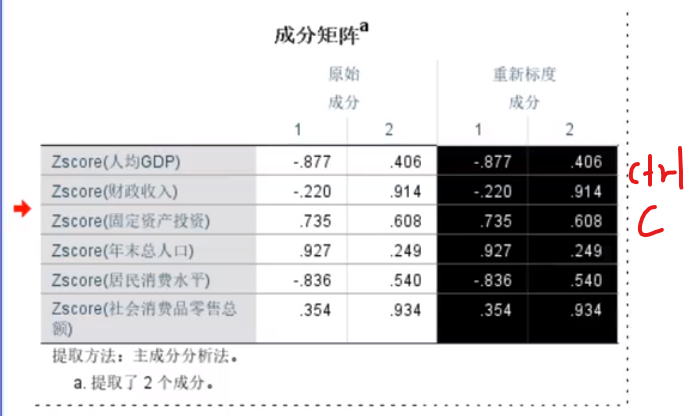
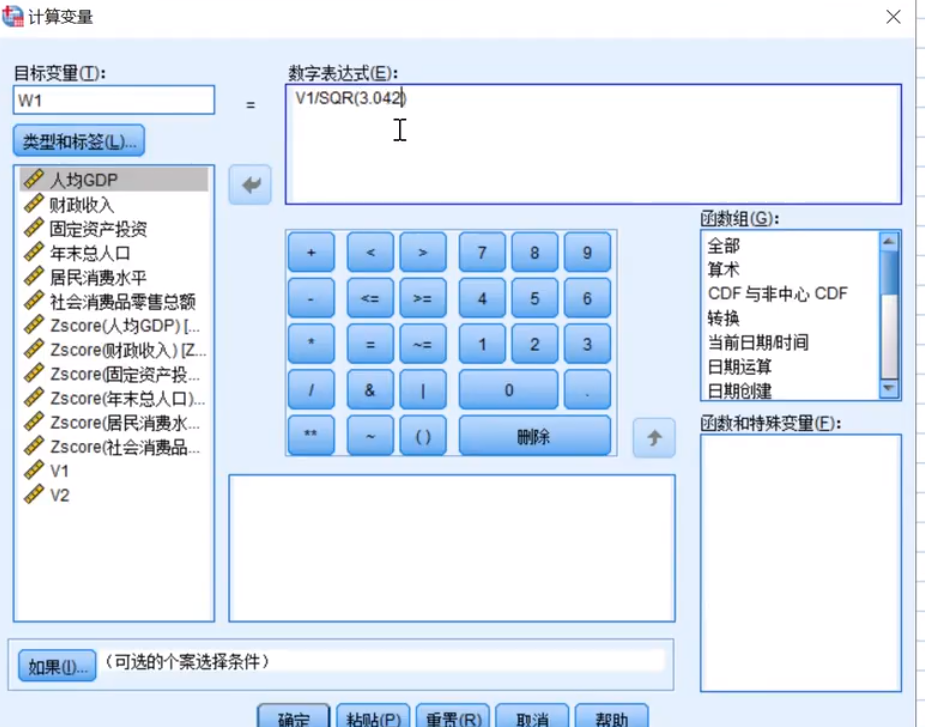
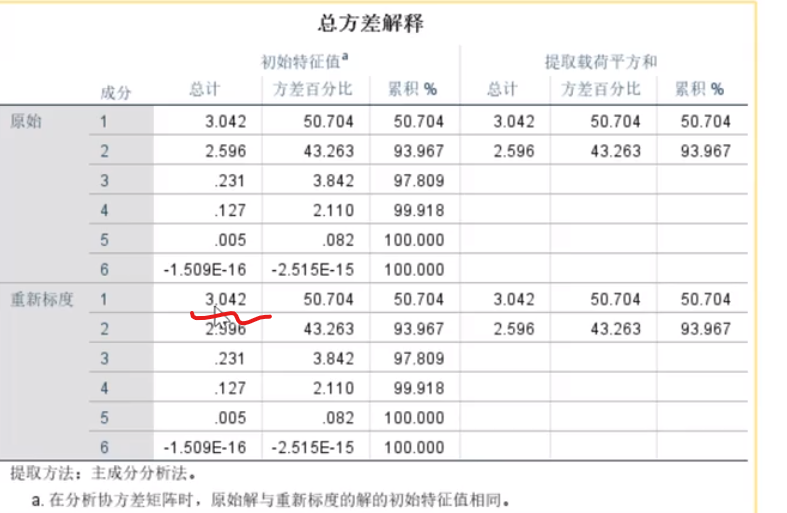
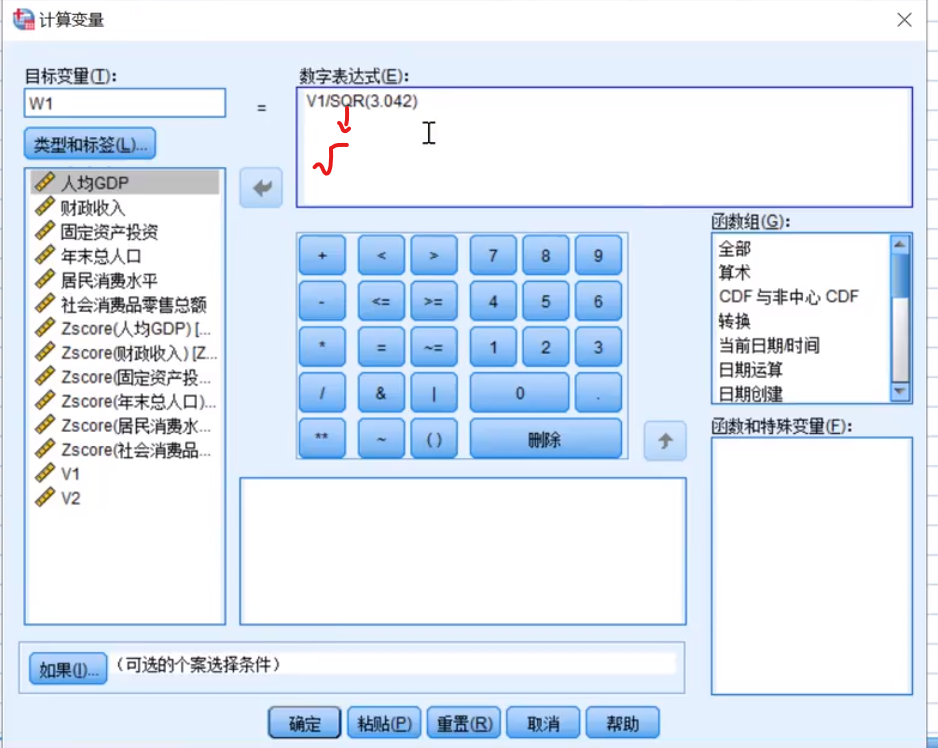
这个w1,也就是a11,a21,a….(在上面数学模型哪里)
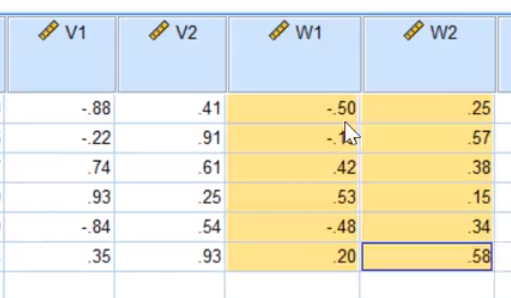
注意使用标准化之后的(Zscore)
一个指标代替了六个指标

六个变量变成了两个变量
回归分析算法
作用:1.预测 2.控制
所有这些回归方程都是建立在你认为他存在的基础上才求的,所以一切应检验
一元线性回归
数学模型
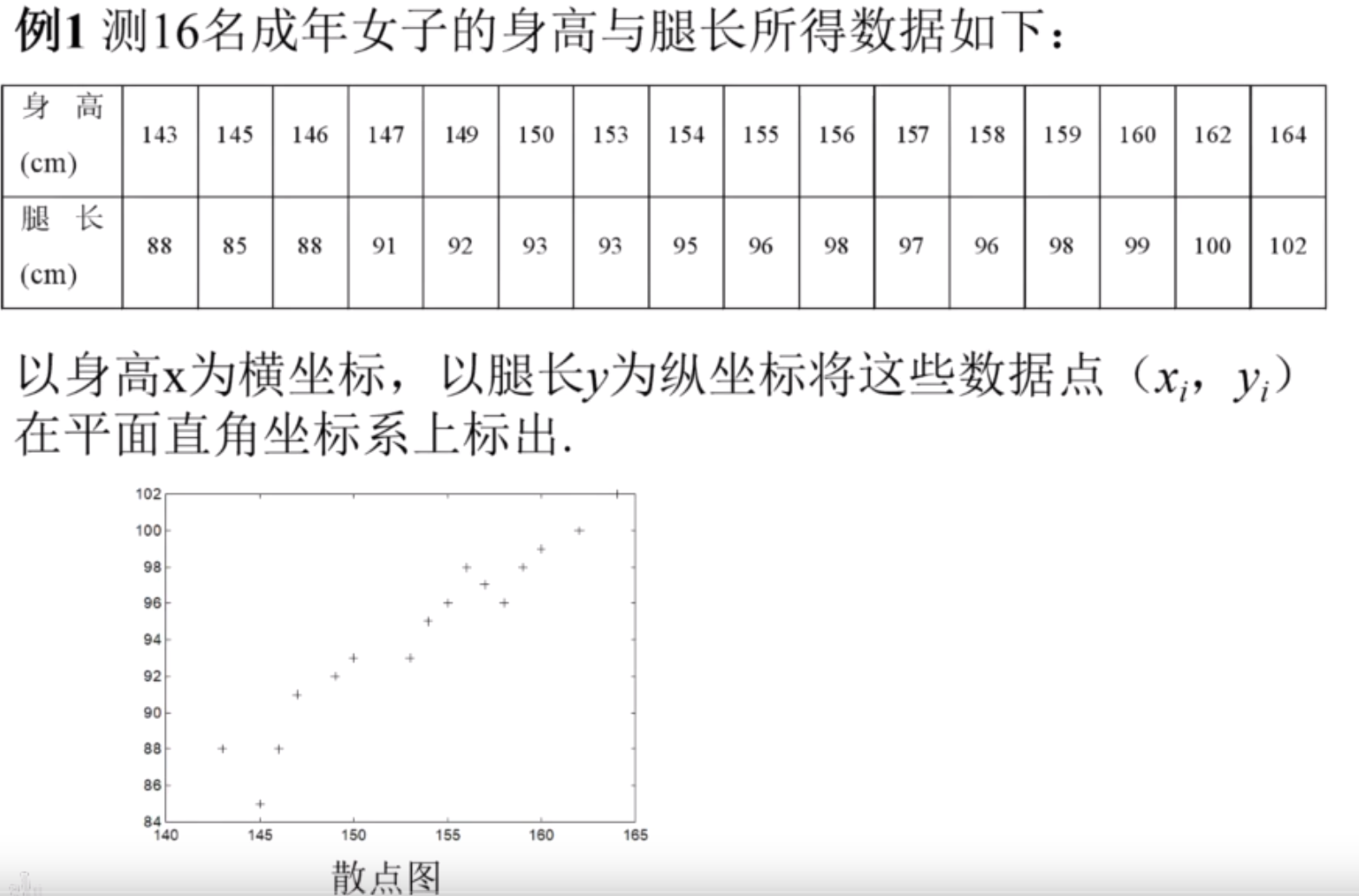
数据多,肯定存在多余解,不止一个一元一次方程
最小二乘:在多余解中求出使得误差达到最少的那组解叫做最优解.

模型参数评估

求导,使得Q最小,即为我们想求的数



误差的方差 方差:标准差的平方
检验,预测,控制
显著性水平:估测总体参数落在某一个区间的概率

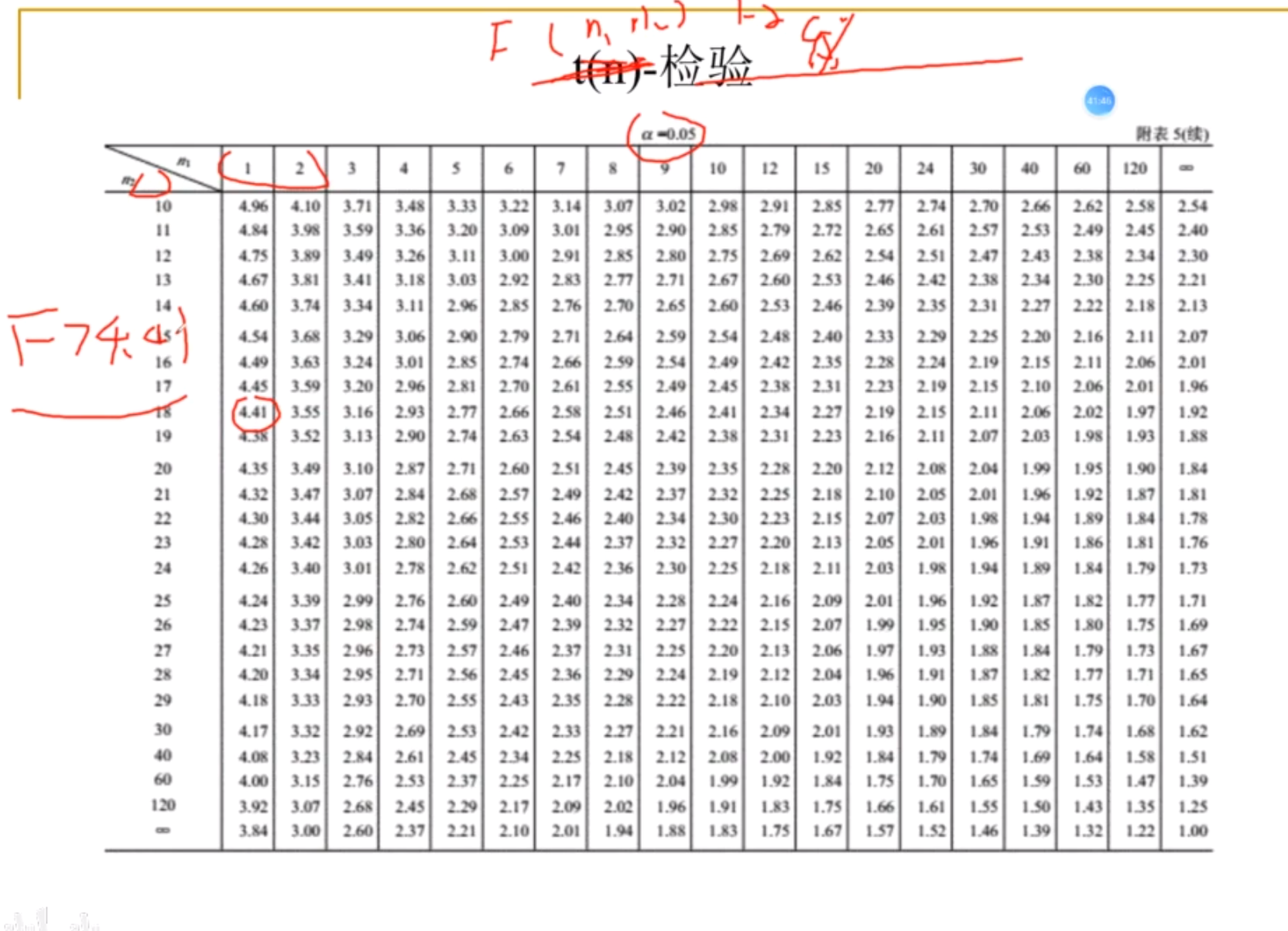
-F检验

H存在,则你说的小概率事件在我这里不成立,拒绝
数据n1 = 1 n2 = 18时,如果F>4.41,那么我们说小概率事件发生了,不成立,拒绝
拒绝了说明回归方程很好,可以用,接受了,那么说明回归方程不好,不能用
若显著性sig值很少,比如<0.05(少於5%机率),亦即是说,「如果」总体「真的」没有差别,那麼就只有在机会很少(5%)、很罕有的情况下,才会出现目前这样本的情况。虽然还是有5%机会出错(1-0.05=5%),但我们还是可以「比较有信心」的说:目前样本中这情况(男女生出现差异的情况)不是巧合,是具统计学意义的,「总体中男女生不存差异」的虚无假设应予拒绝,简言之,总体应该存在著差异。
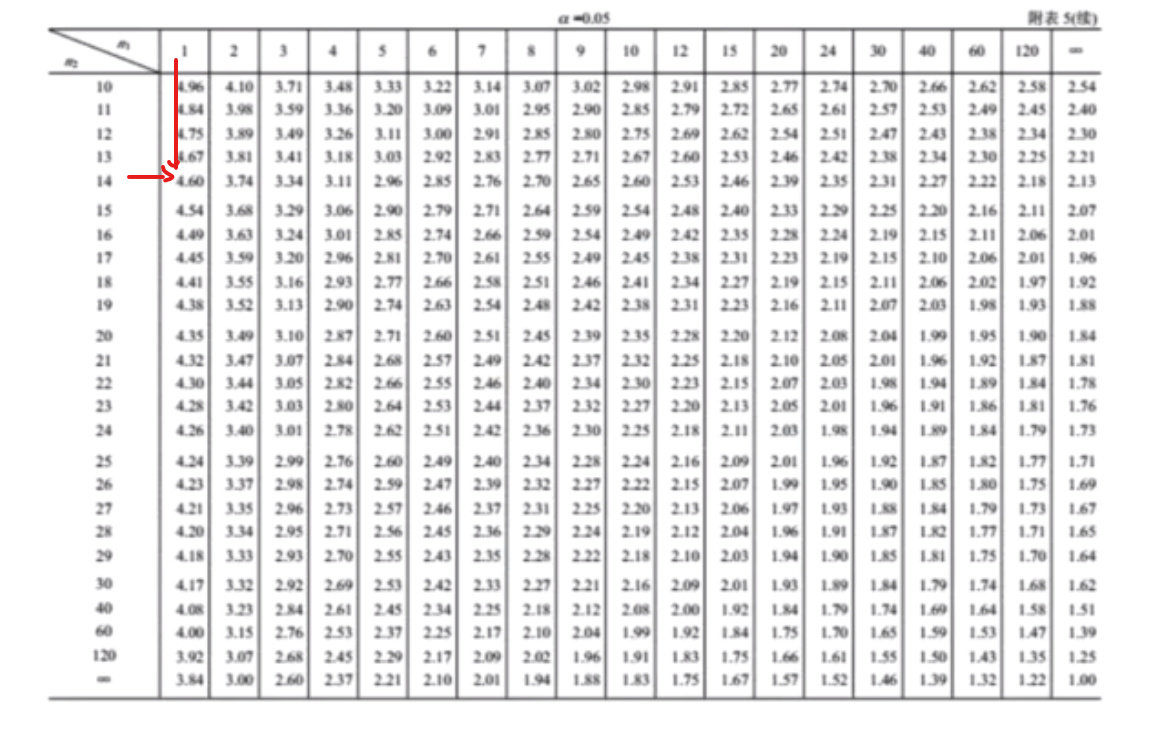
F检验表
-T检验
适合于小样本数据 (n<30)

T检验表
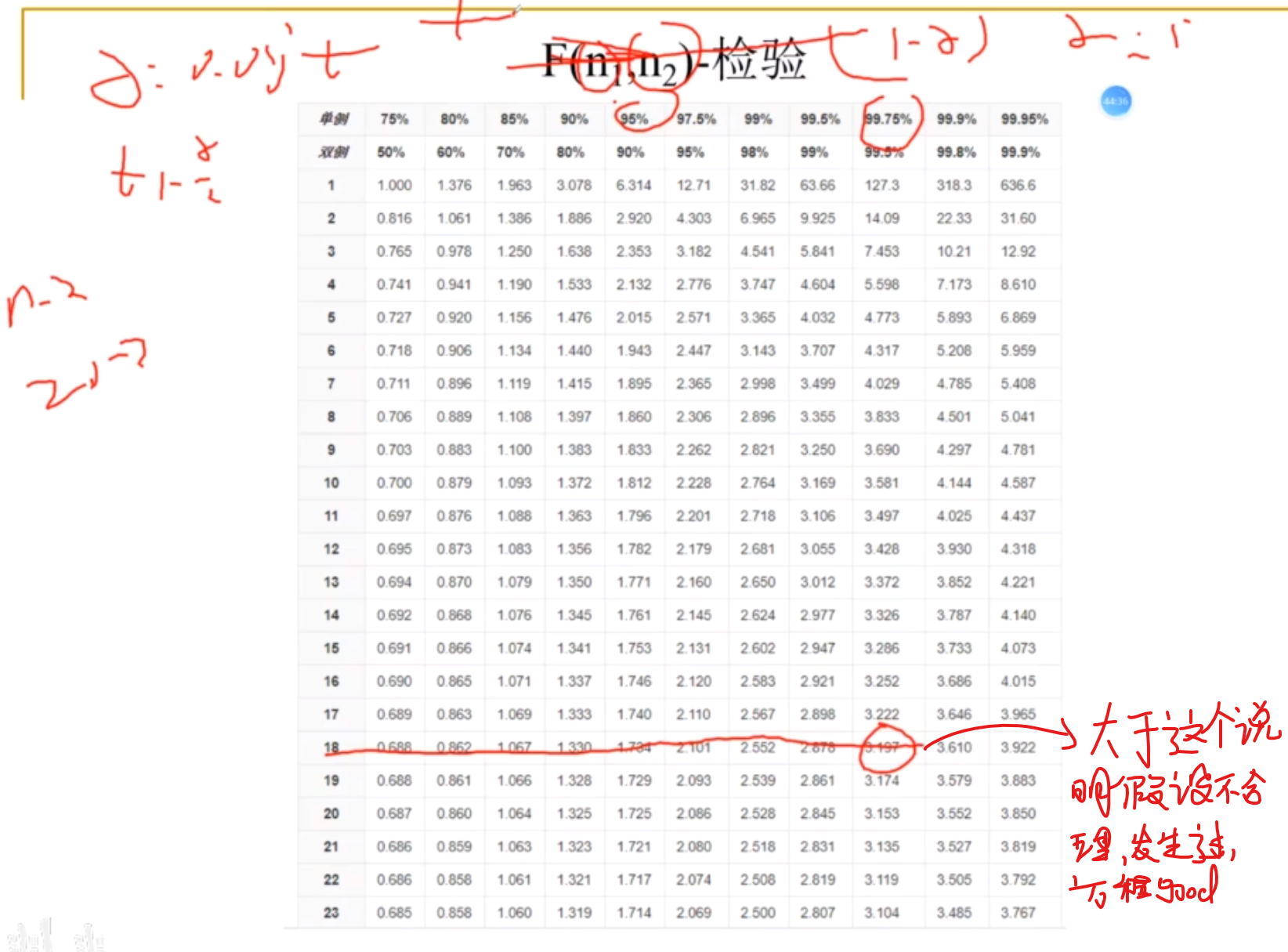
-R检验
通过建立与F检验的关系来得出结果
假设回归不合理,不存在,如果通过检验,发现,所谓的小概率事件很难发生,但通过实验,发现他发生了,说明你的假设是存在问题的,拒绝假设H0,拒绝了假设,也就是反证了回归方程存在

置信区间

预测区间

其实二者很容易区分,置信区间是针对因变量均值的区间,而预测区间是针对因变量个体值的区间。不难理解,针对均值的置信区间肯定要窄一些,而具体想预测某一个体值,那区间肯定要宽,因为误差会很大。
控制

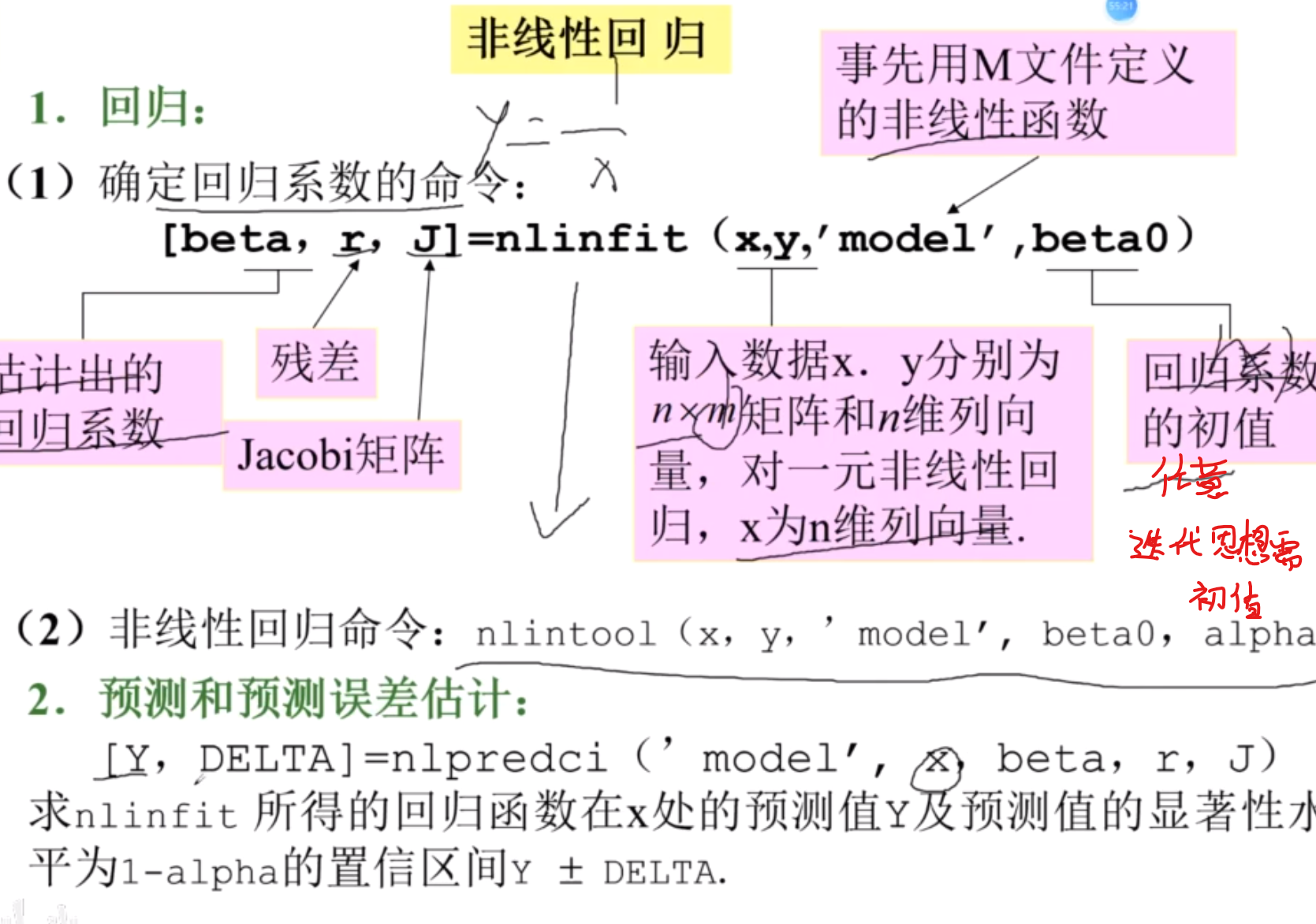
一元非线性
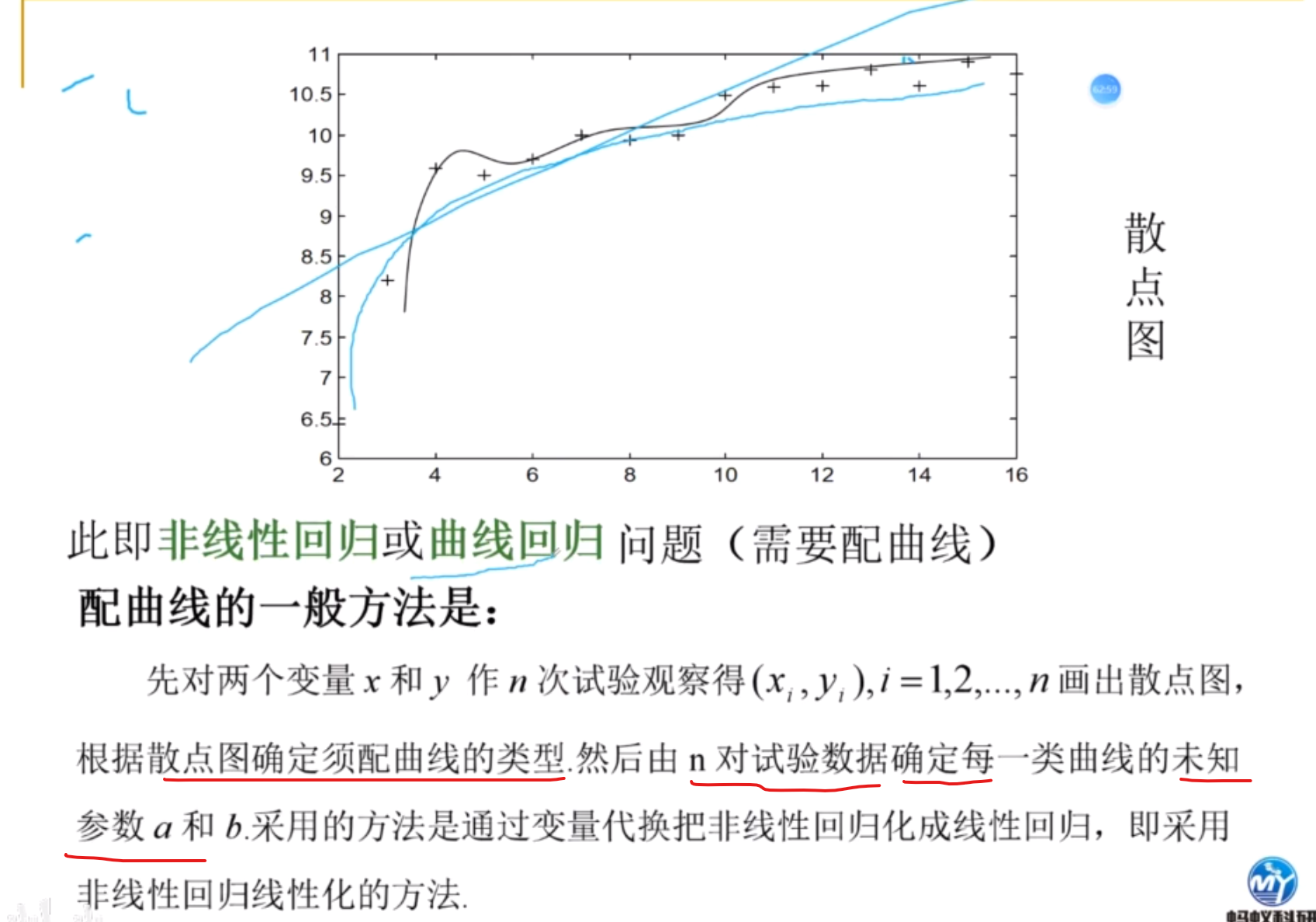


常用非线性函数的线性化
倒幂函数
(1) y = a + b / x —->> y = v 1/x = u v = a + bu
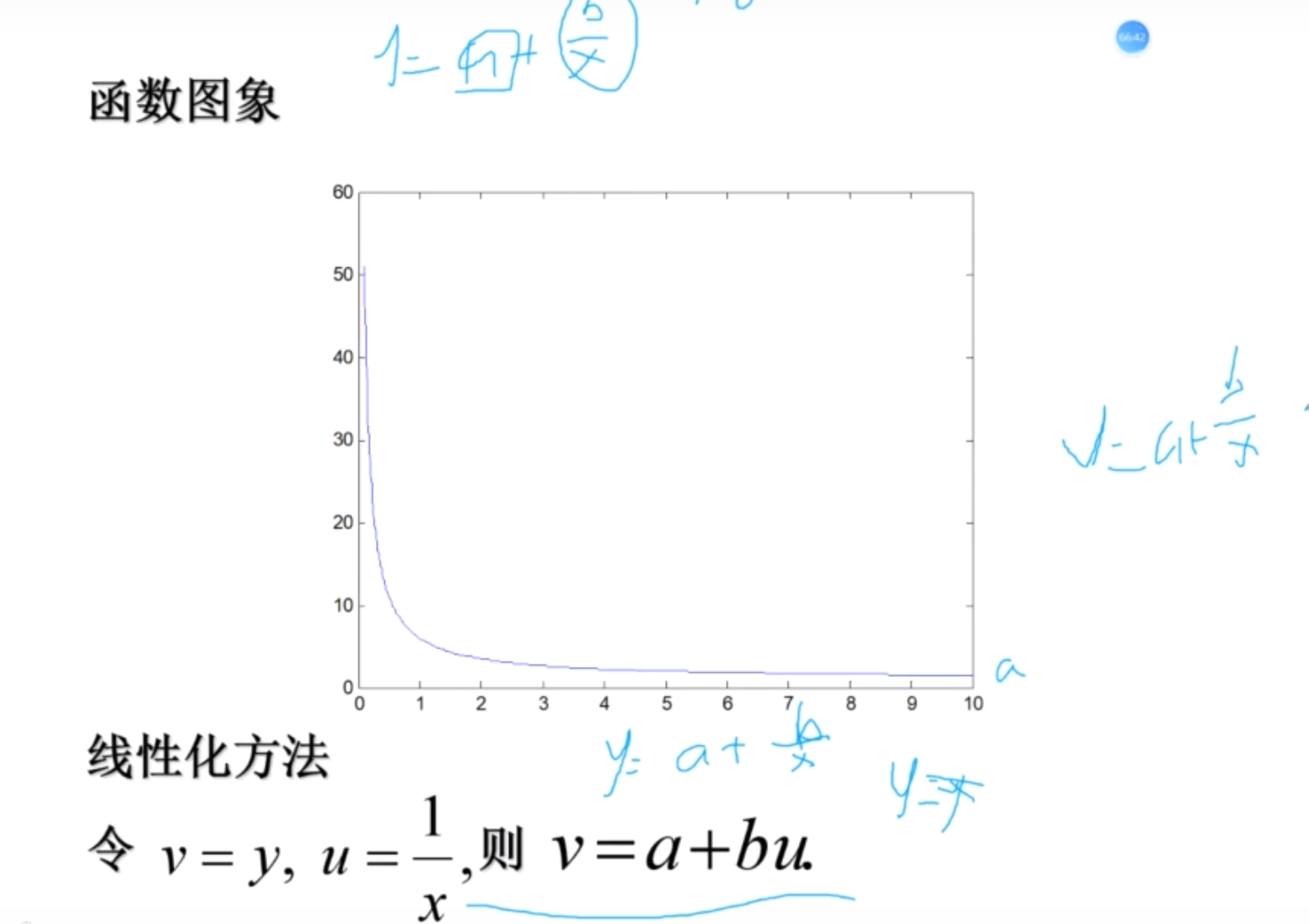
双曲线函数
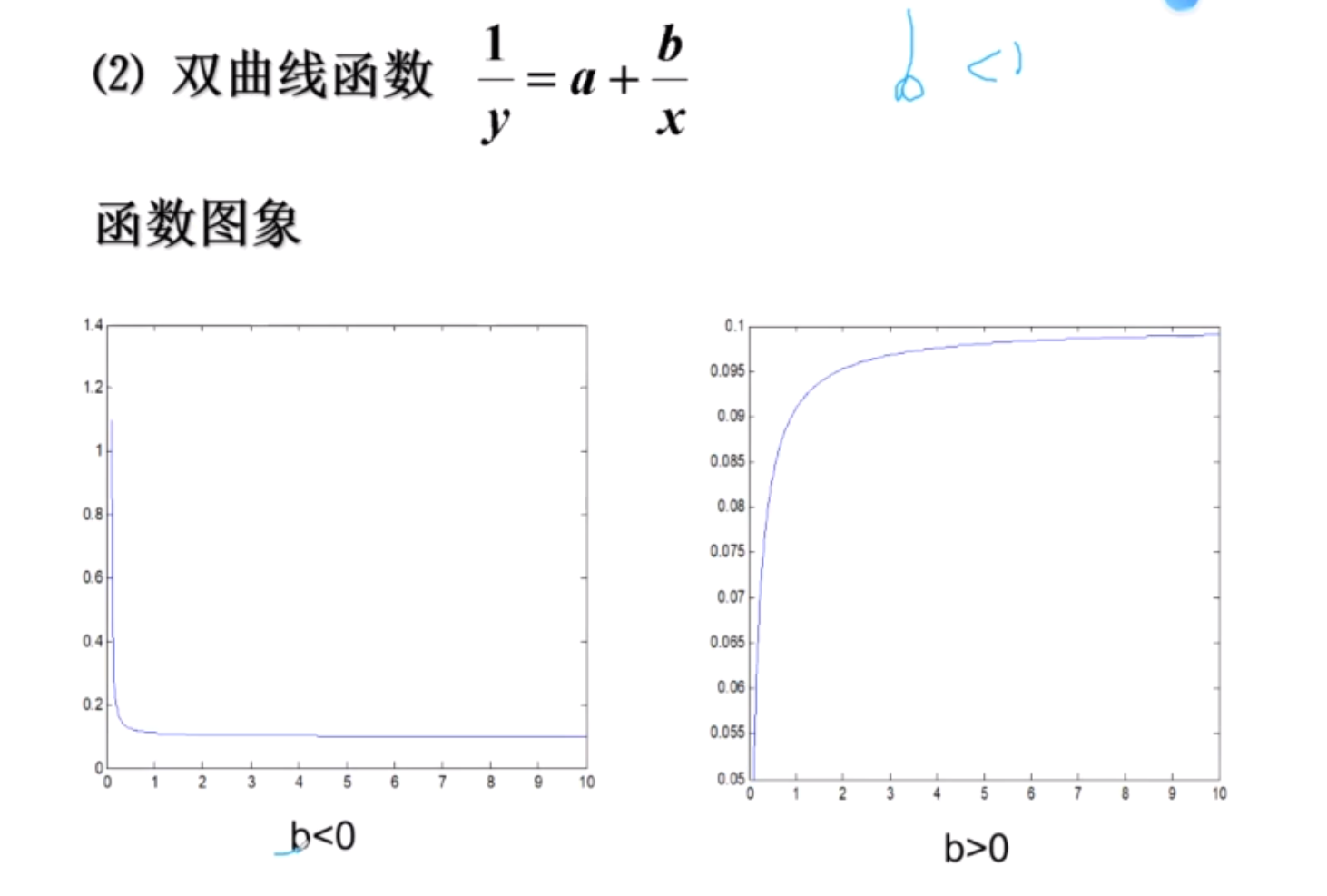

幂函数
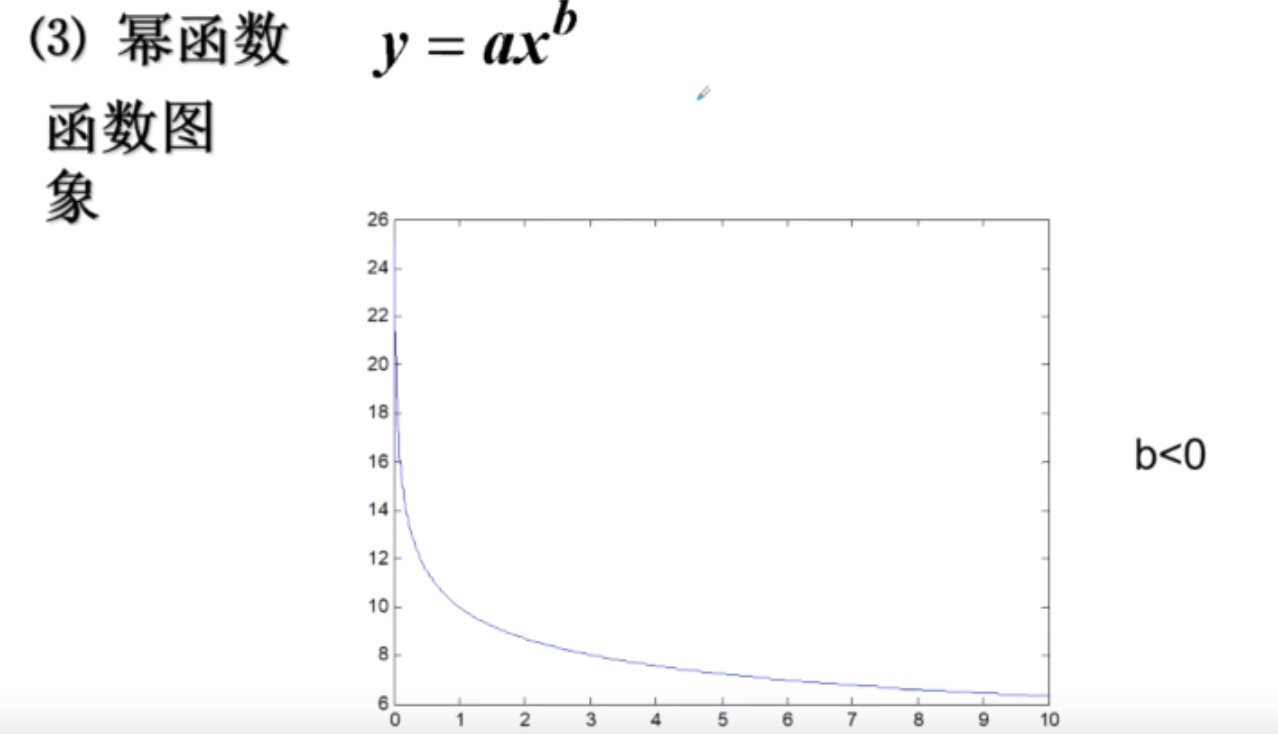
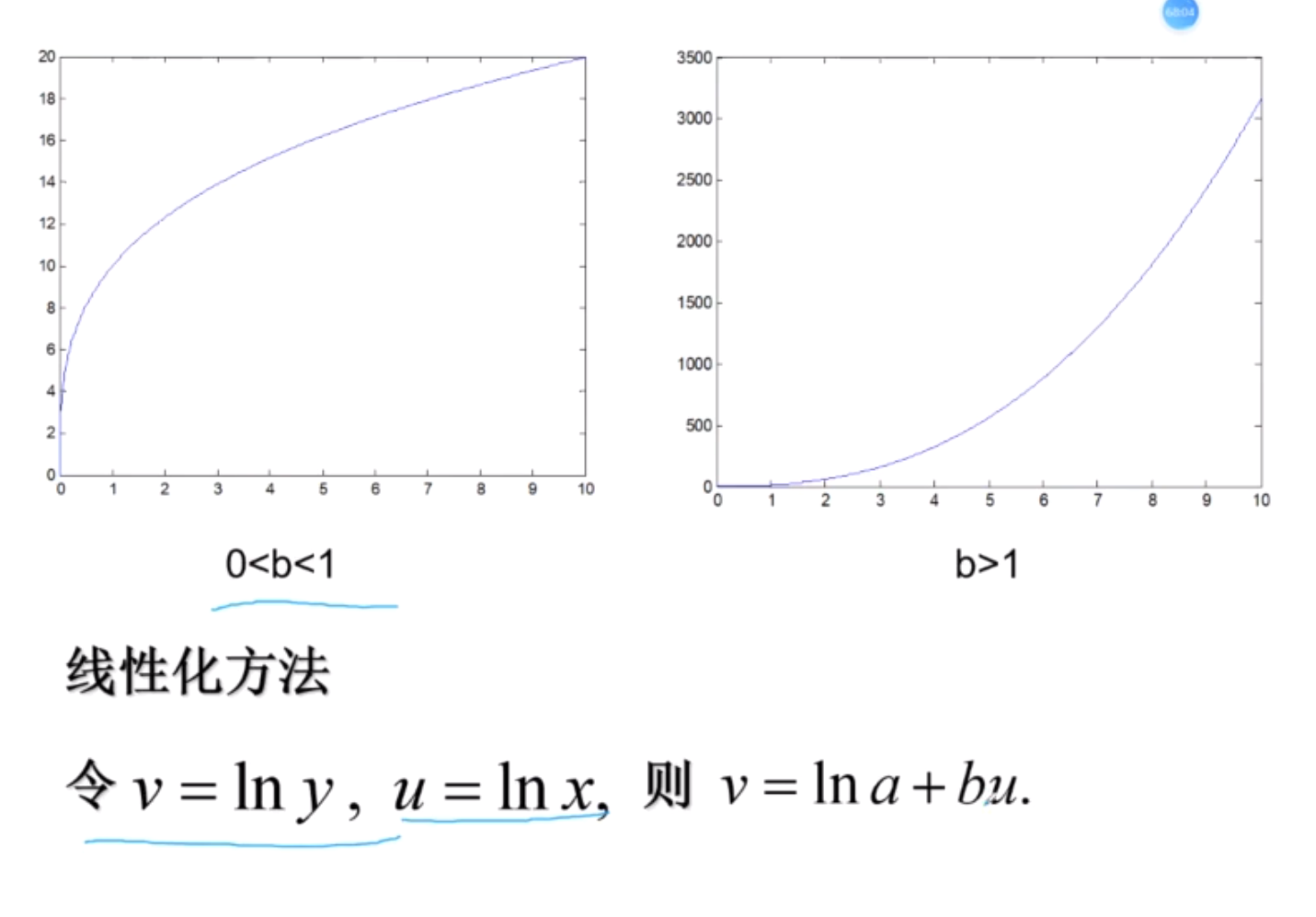
指数函数
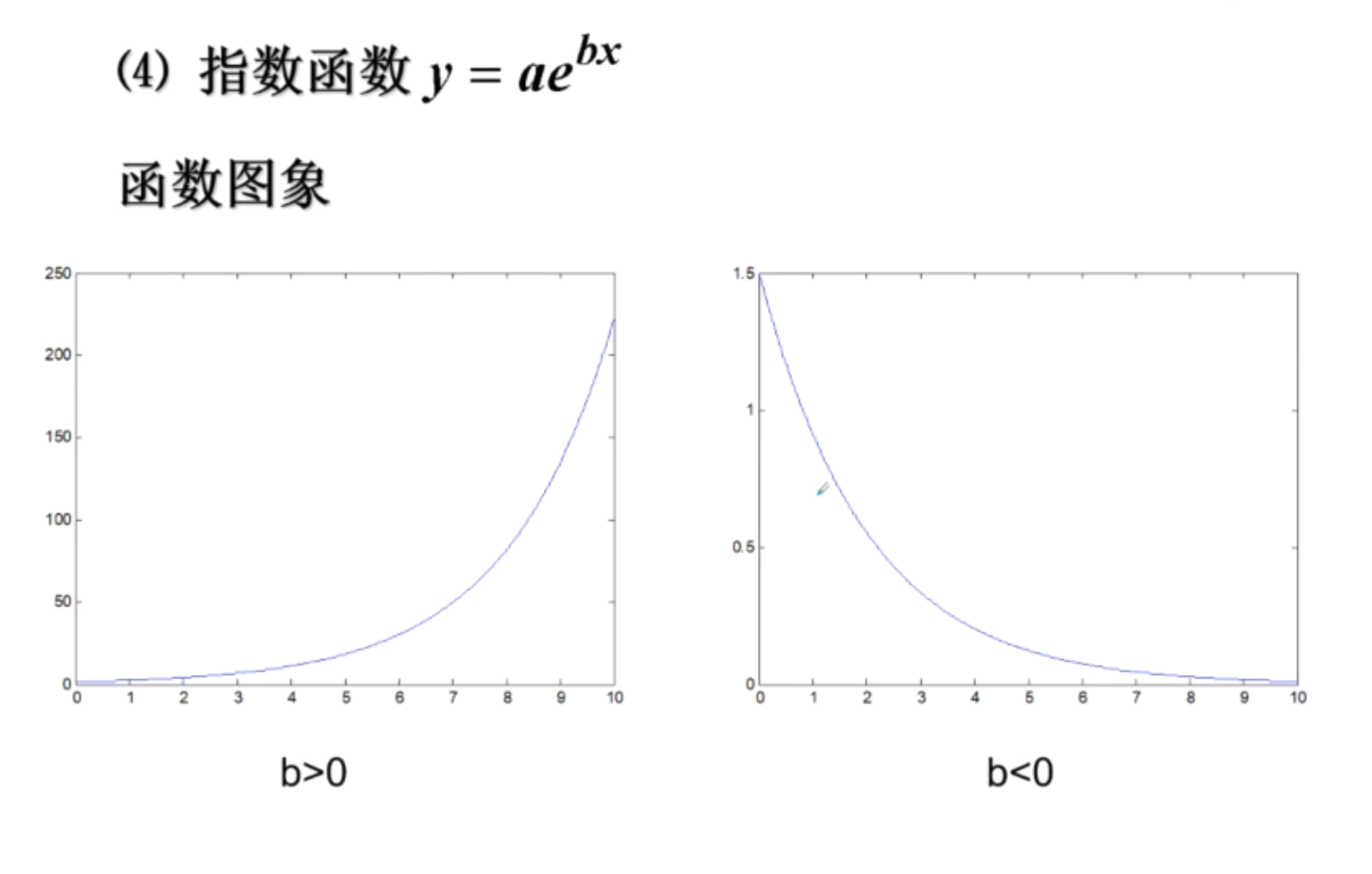
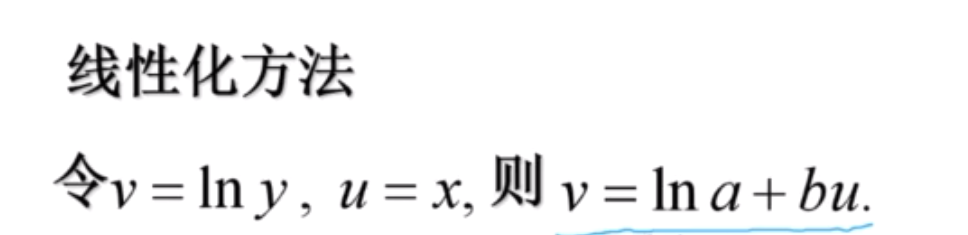
倒指数函数
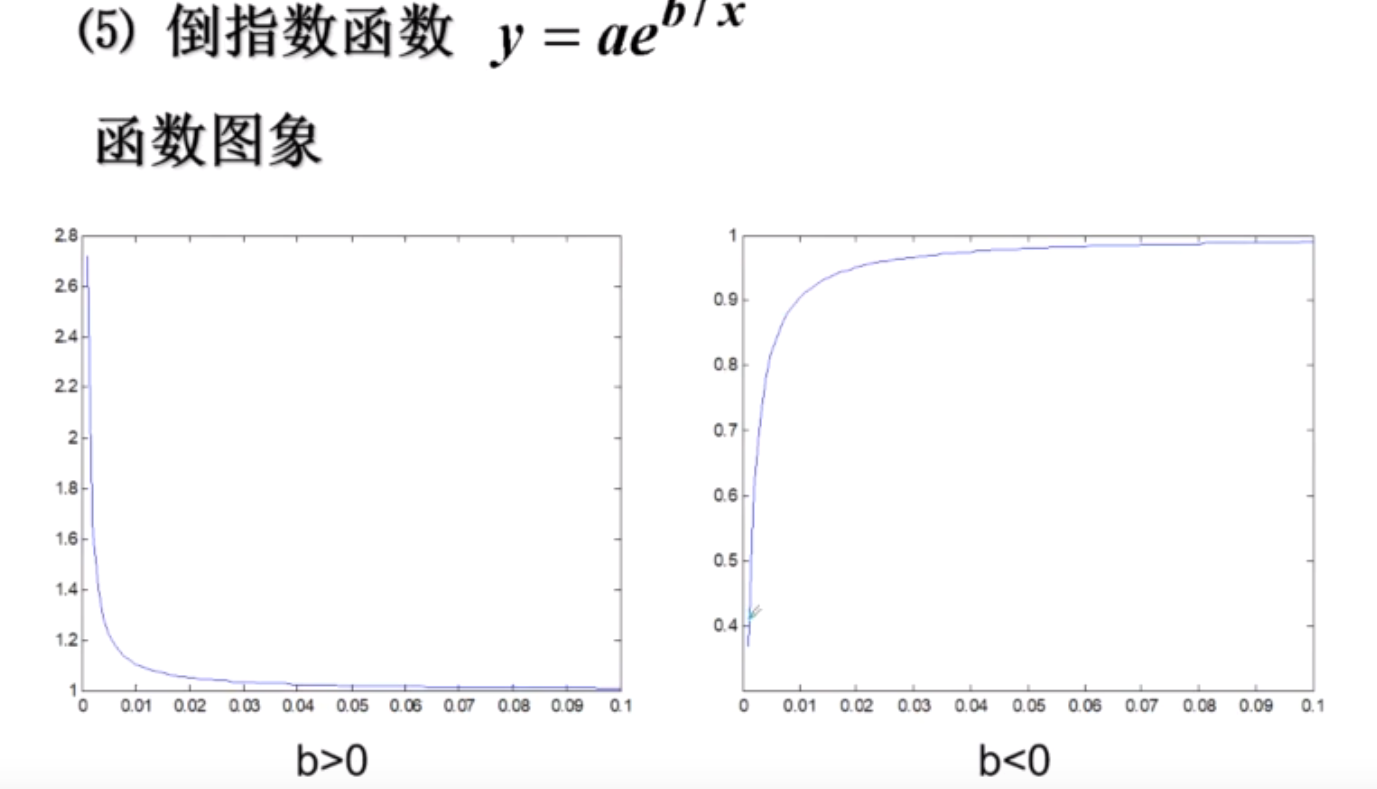
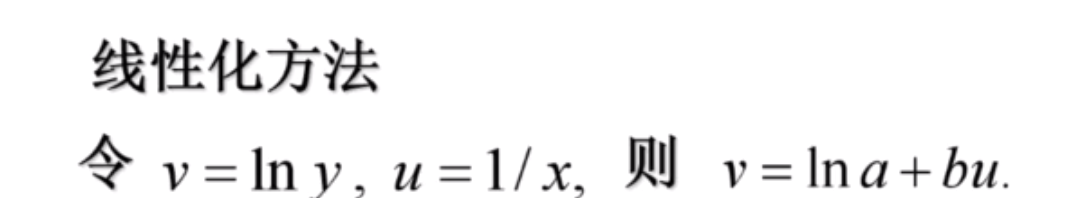
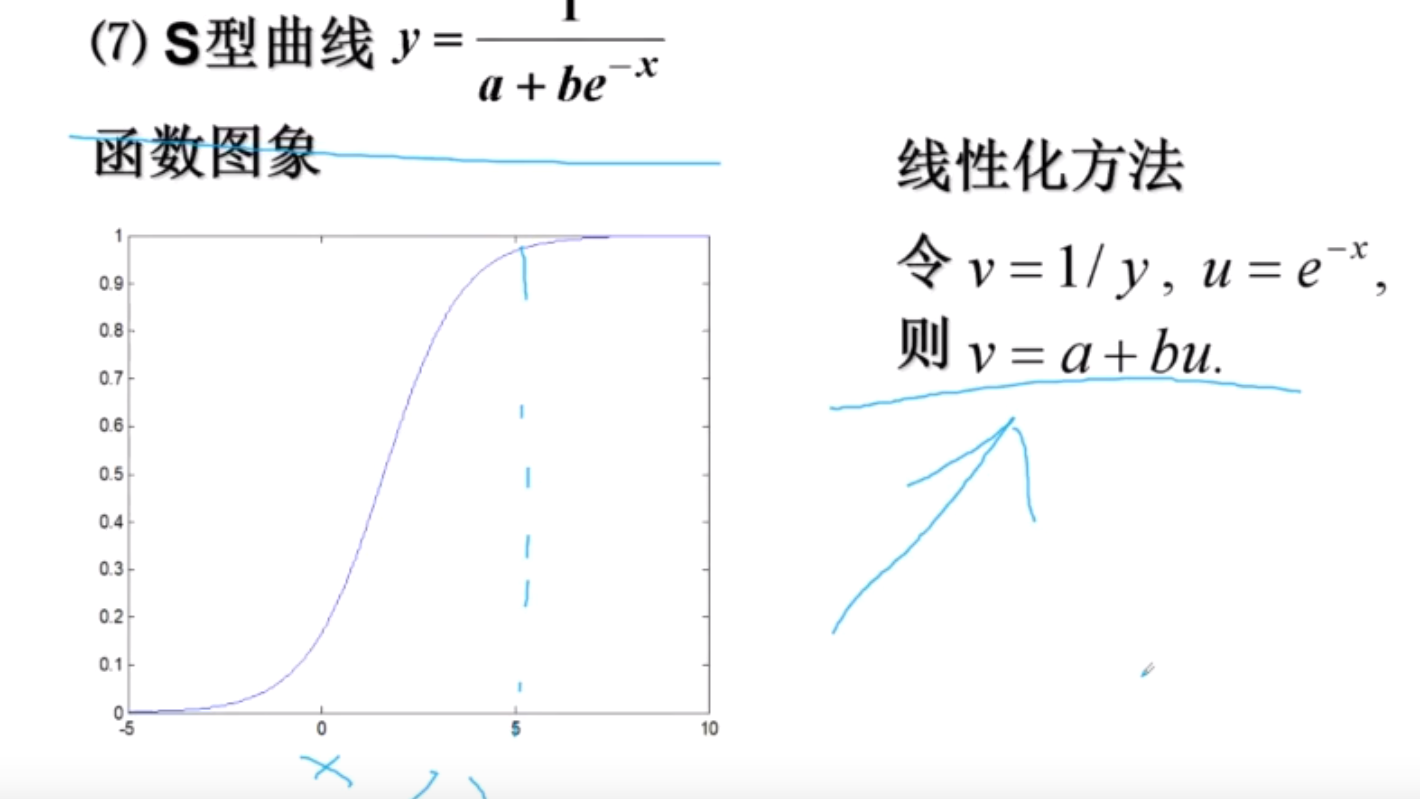
对数函数
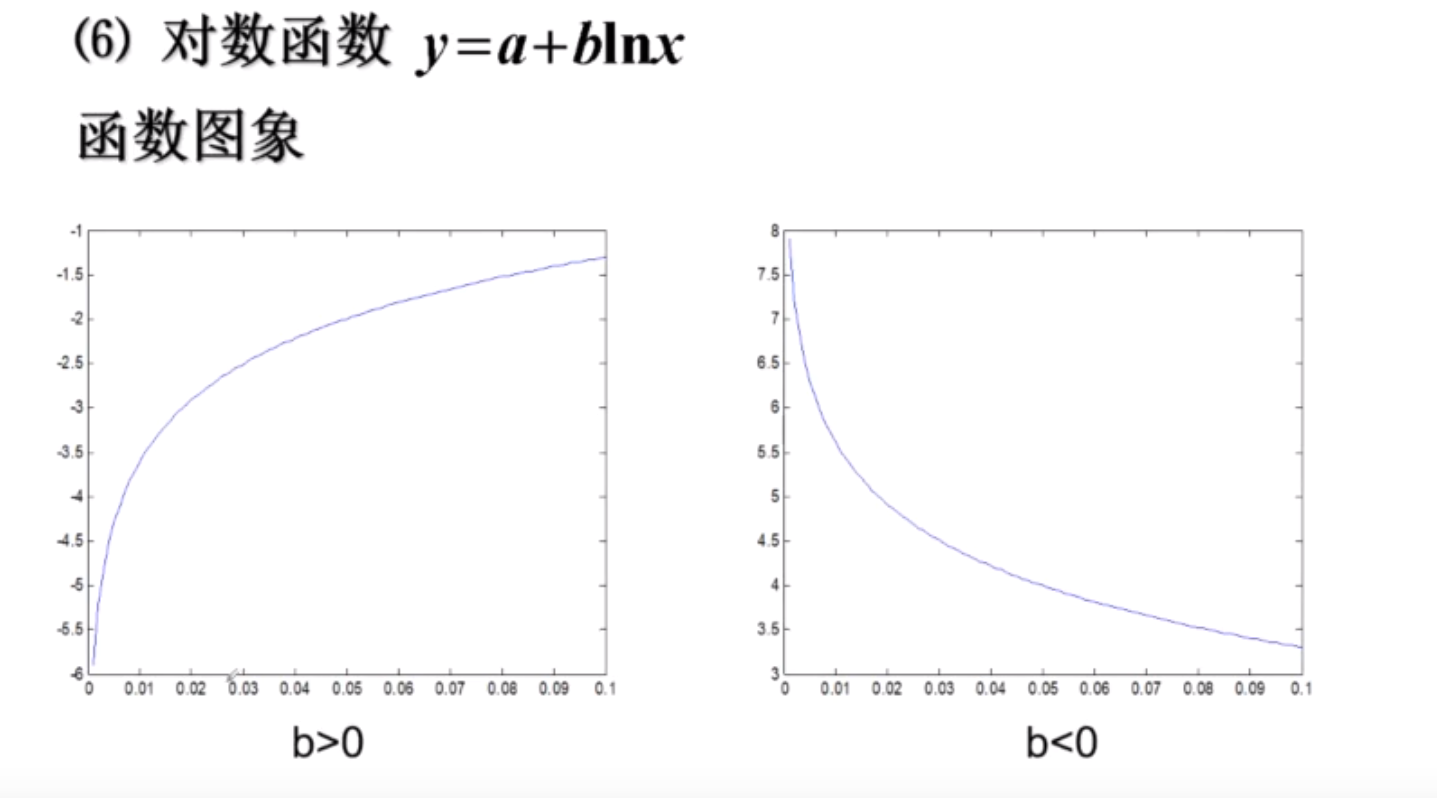
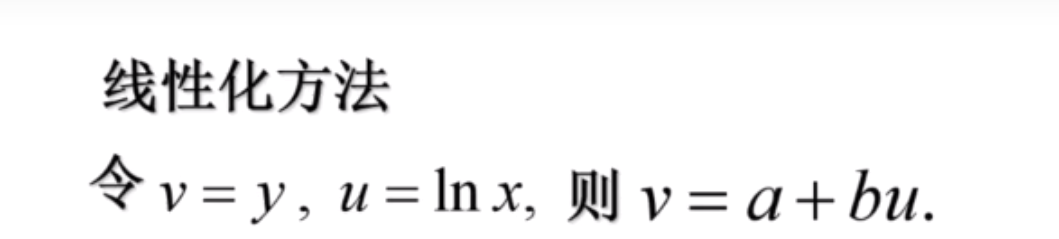
S型曲线
神经网络常用
多元线性回归
数学模型

模型参数评估

多项式回归
系数不在为1
注意看清每个模型到底长什么样子,多项式回归啊,线性回归这些,别搞错了

检验
F和R直接能建立联系—-等效,只需要一个就可以了

预测

逐步回归分析
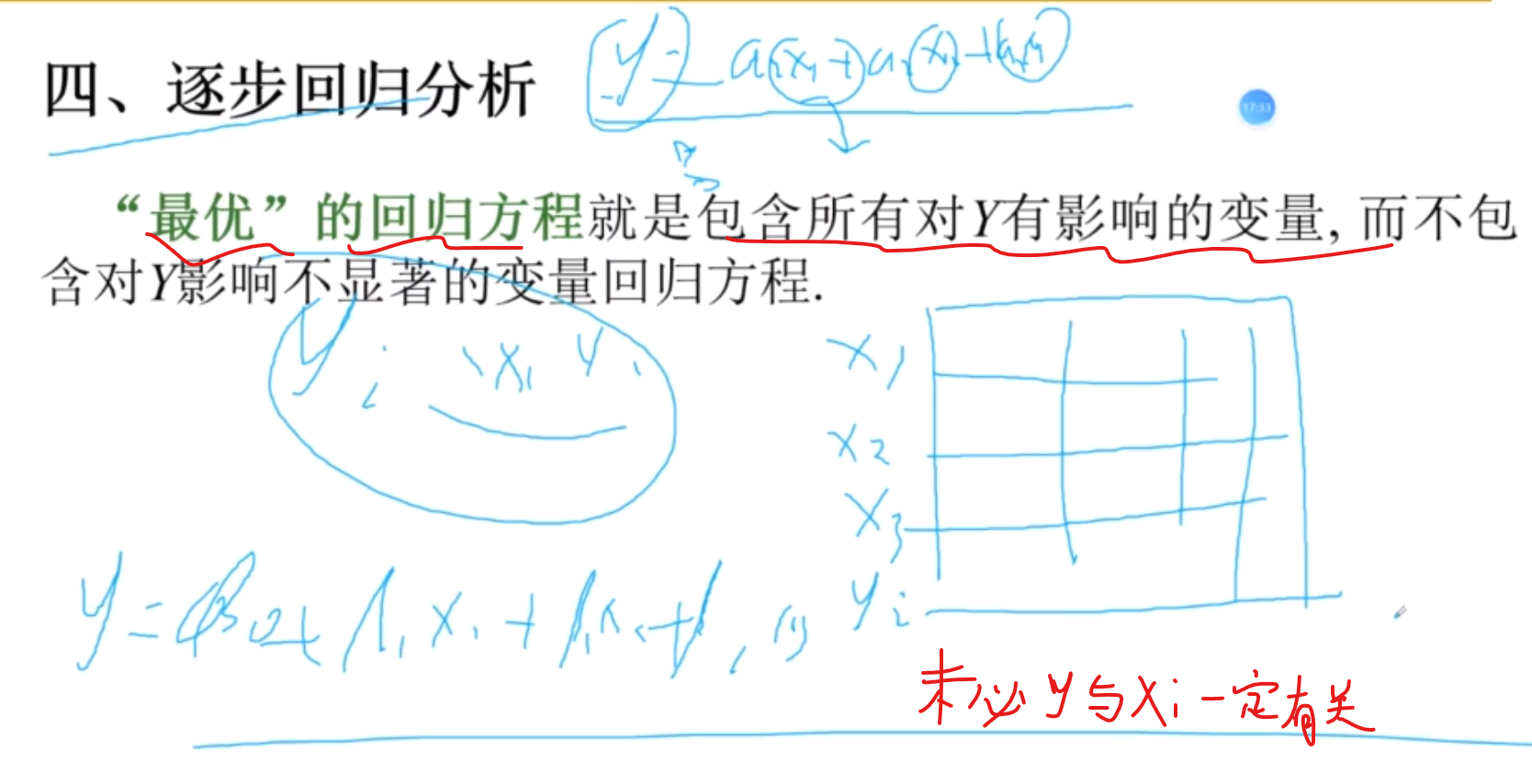
思想

筛选
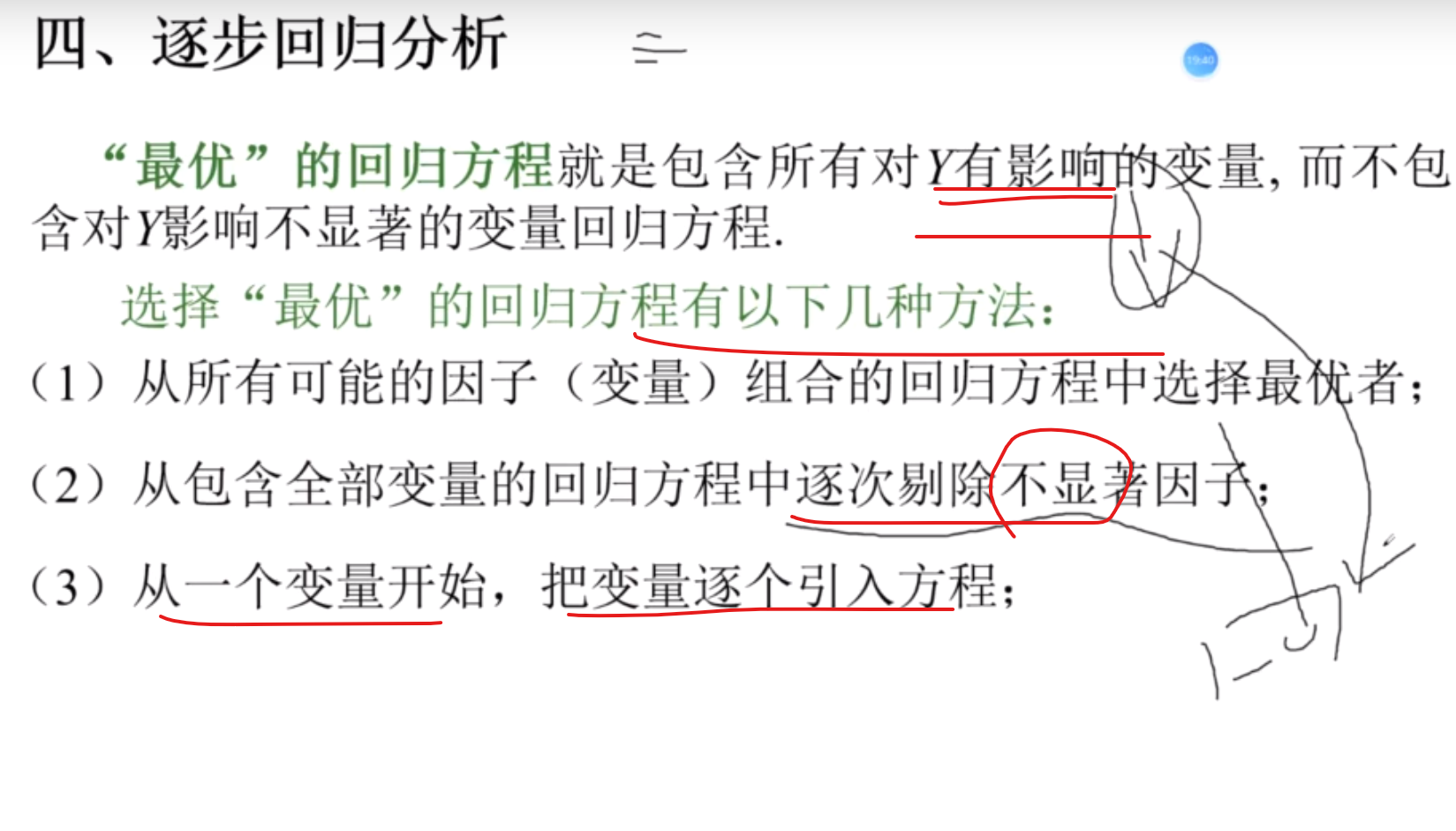
Matlab实现多元线性回归
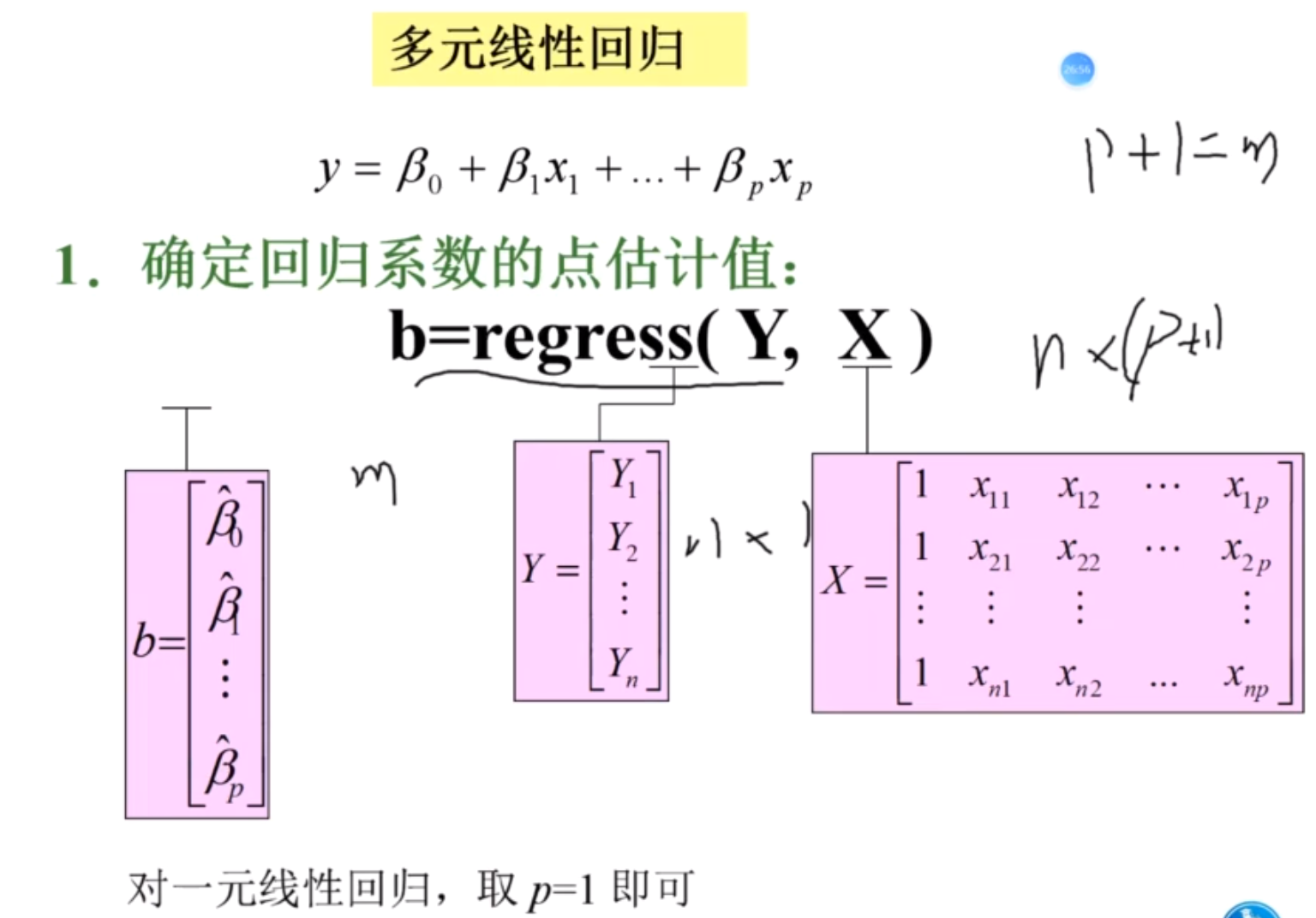
一元也可以使用 记住x的第一列一定是1
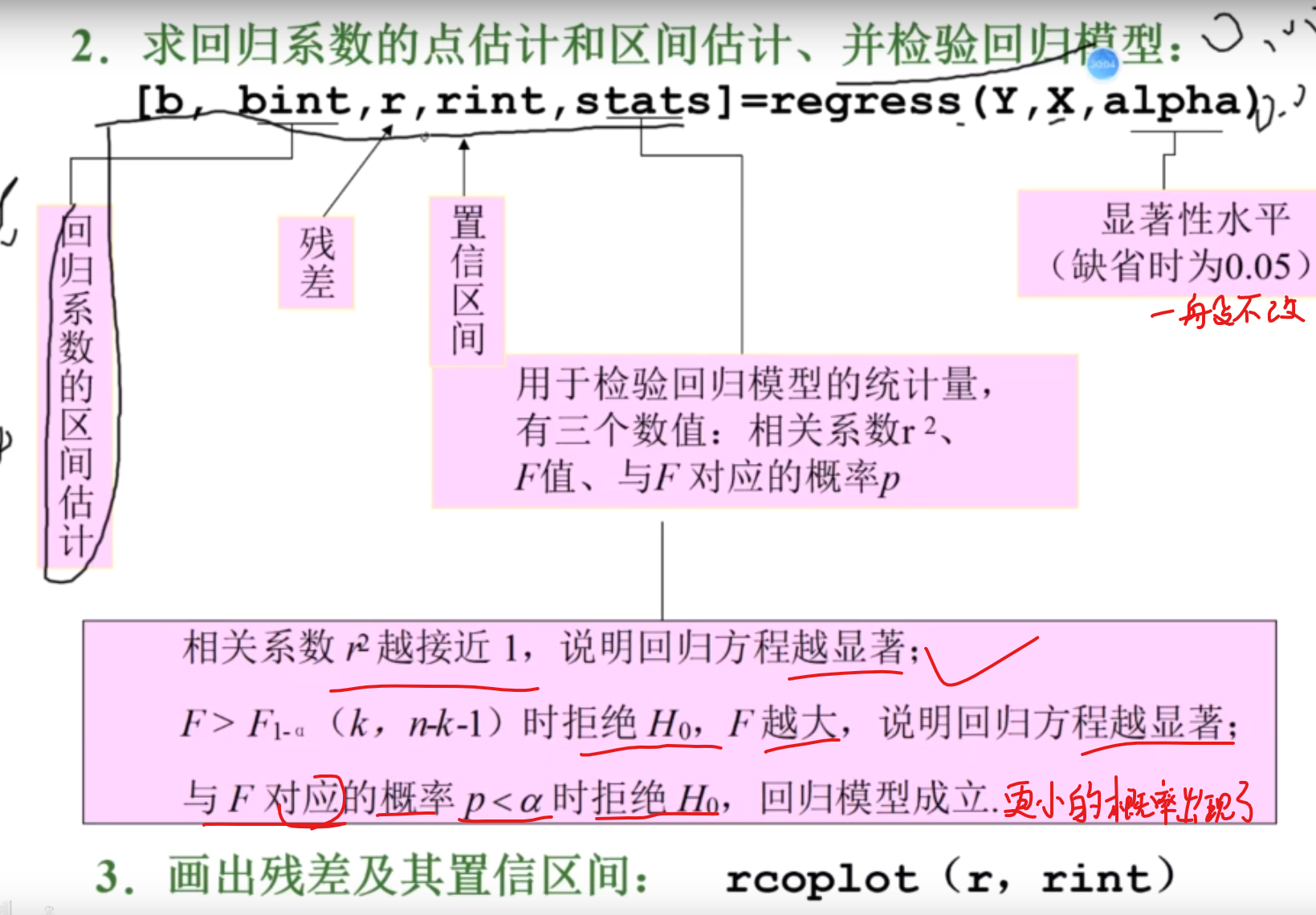
alpha一般是0.05
求系数和检验


所以 y = -16.0730 + 0.7194*x

β0的取值范围(预测区间)(也就是上面的-16.0730的)为-33.7071 – 1.5612

r^2 为0.9282
x共16个数据,那么查表就应该查F表的1,14(只有一个未知数) 所以180肯定超过4.6
与F对应的P的概率是0.000xxxx说明概率小于0.05 所以就没放上去
1.7437没有啥卵用
残差图
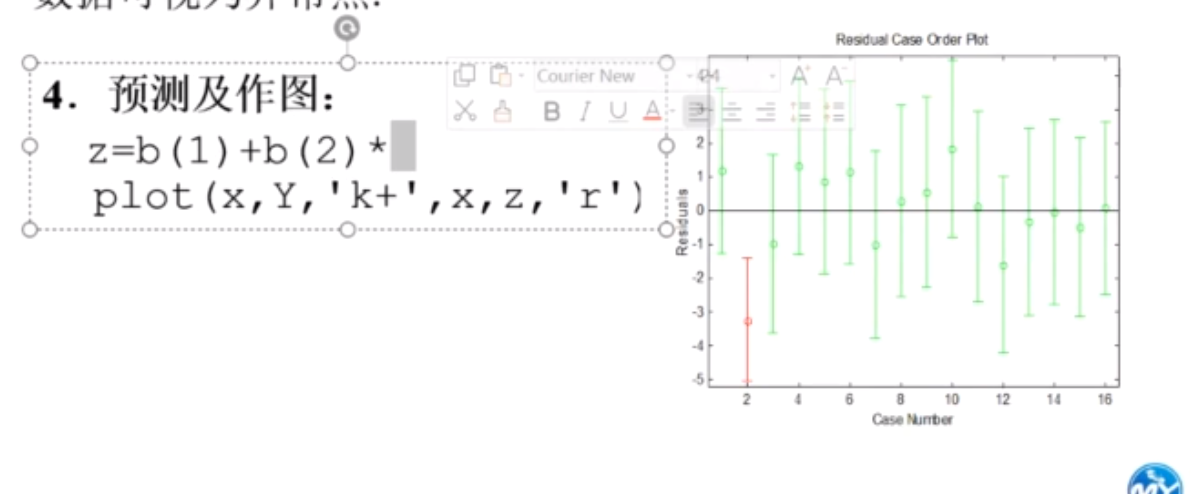
所以第二个的结果可能不是很好
多项式回归matlab
我认为可以用拟合,应该更方便


多元二次回归
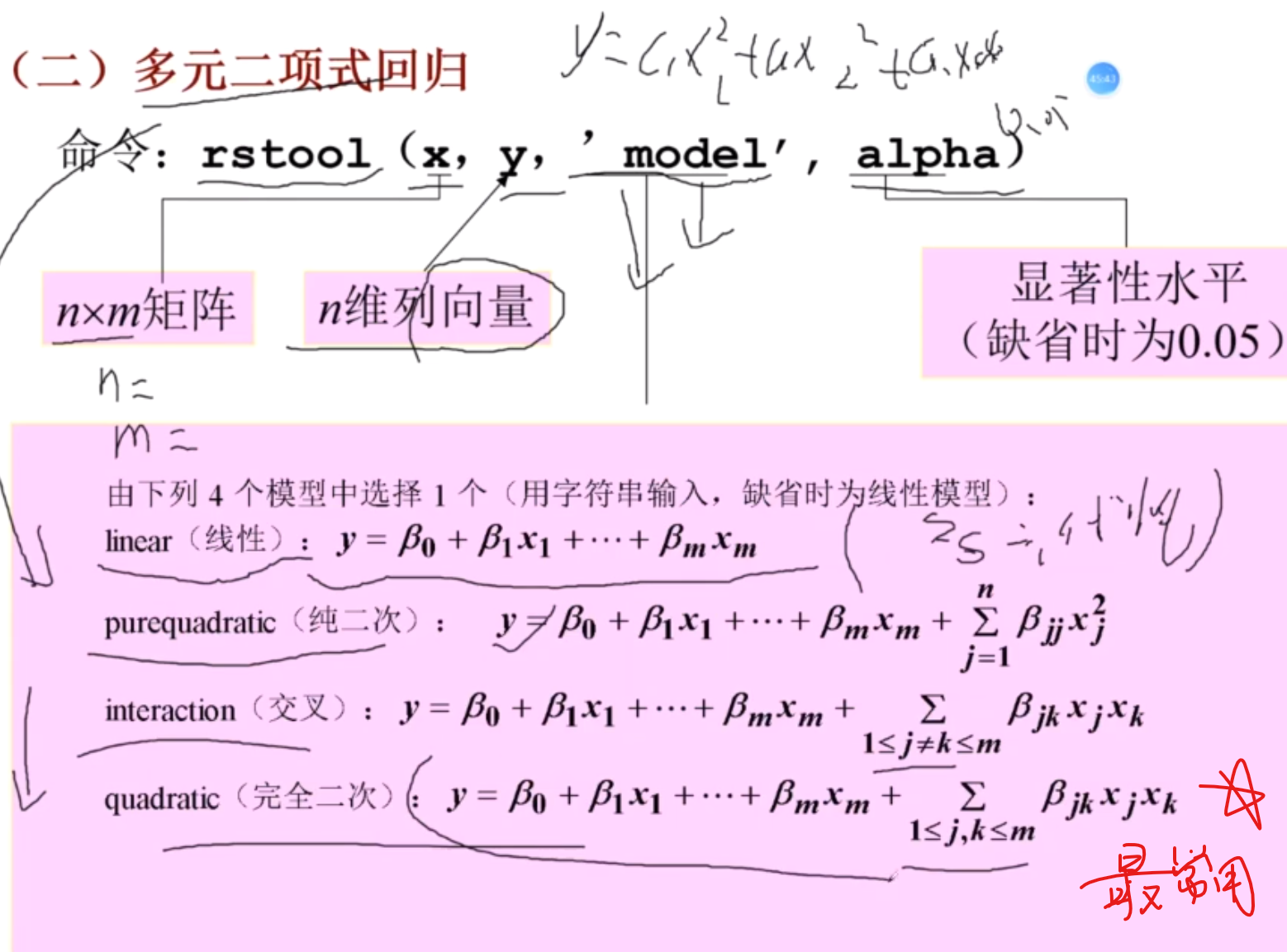
beta为系数



主要观察beta
逐步回归
stepwise()

例题
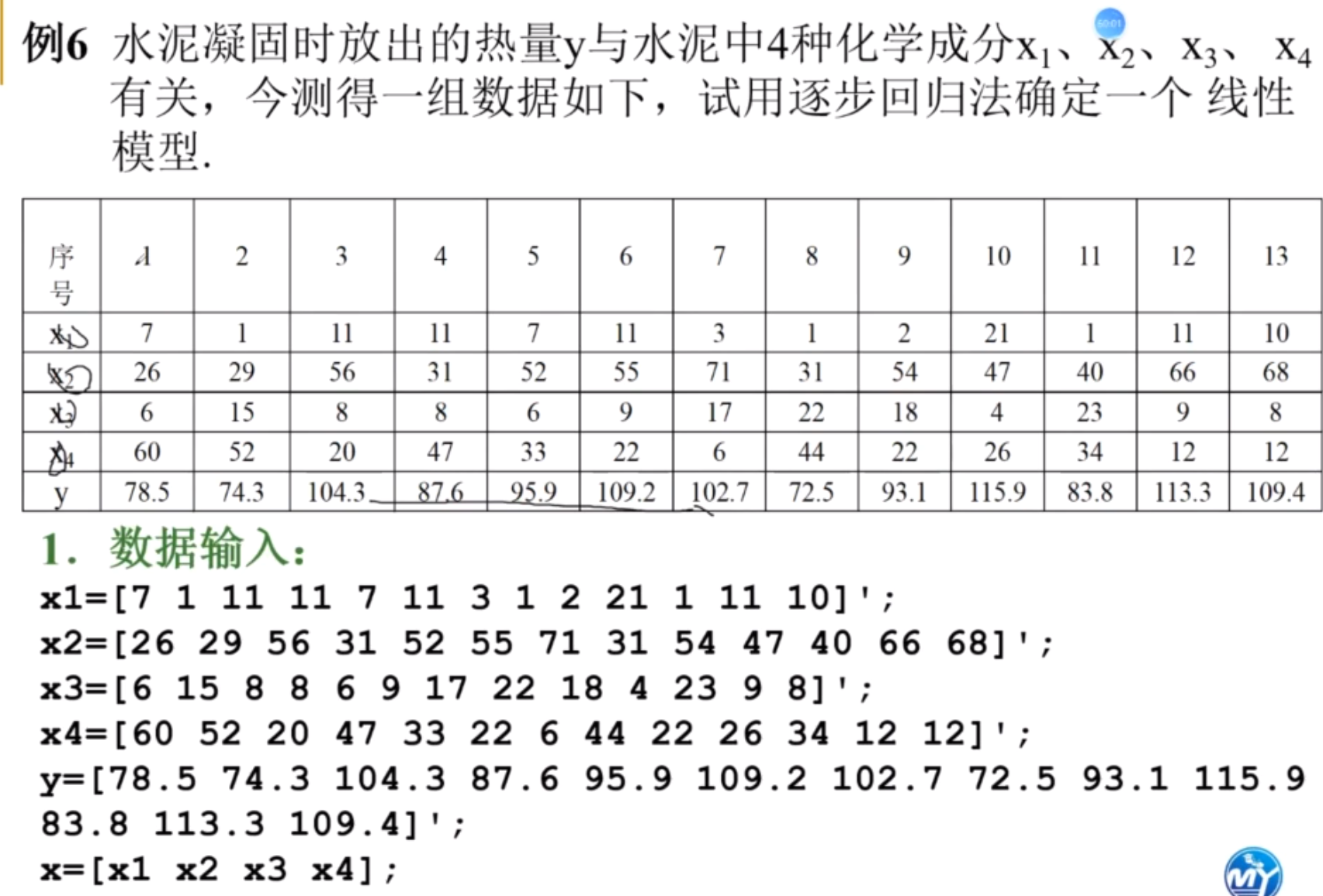
首先,这么多成分,我们应该做数据分析
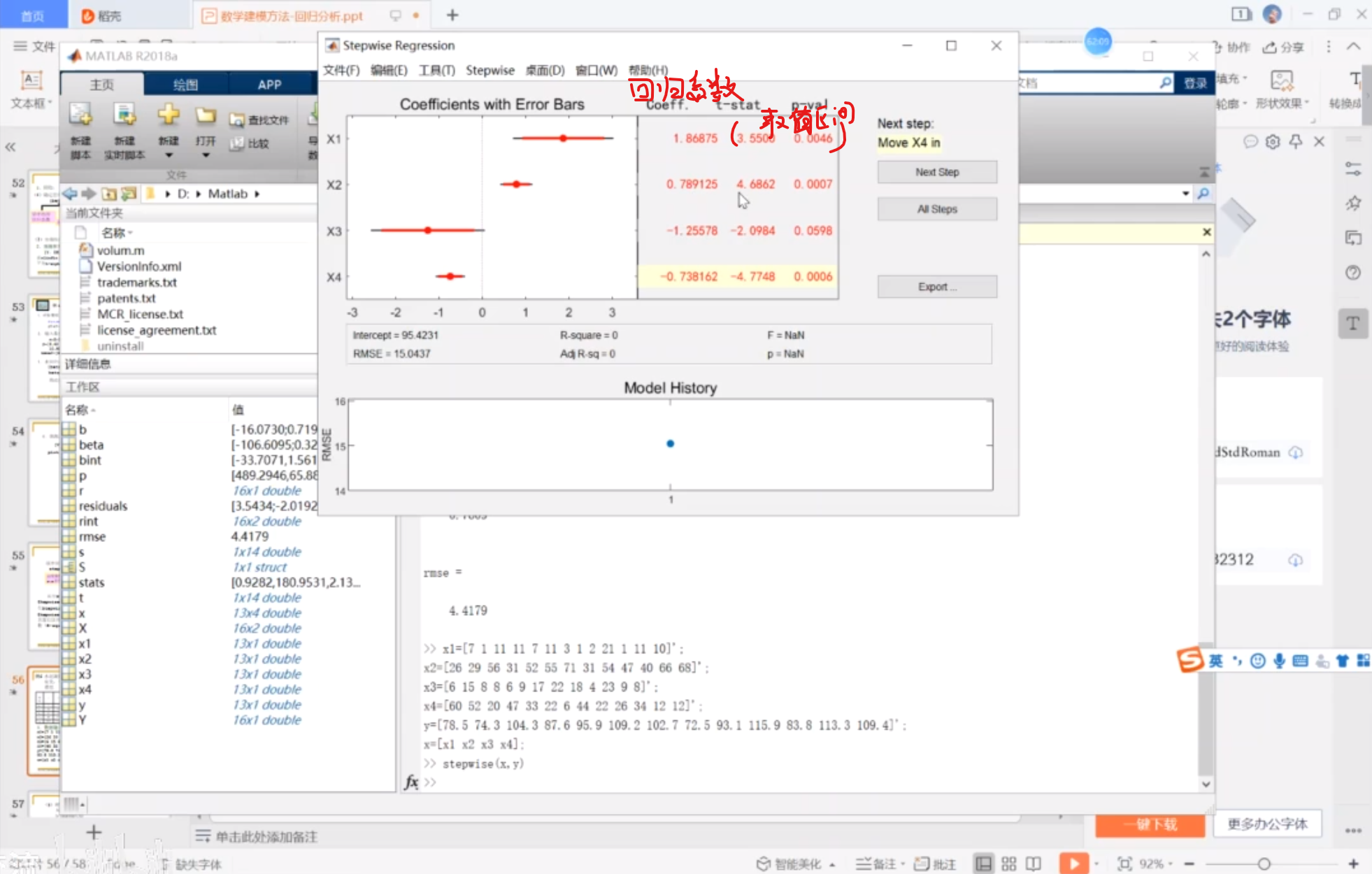
从上到下分别是四个系数
然后选择next step
相关系数R变成0.67,F变大
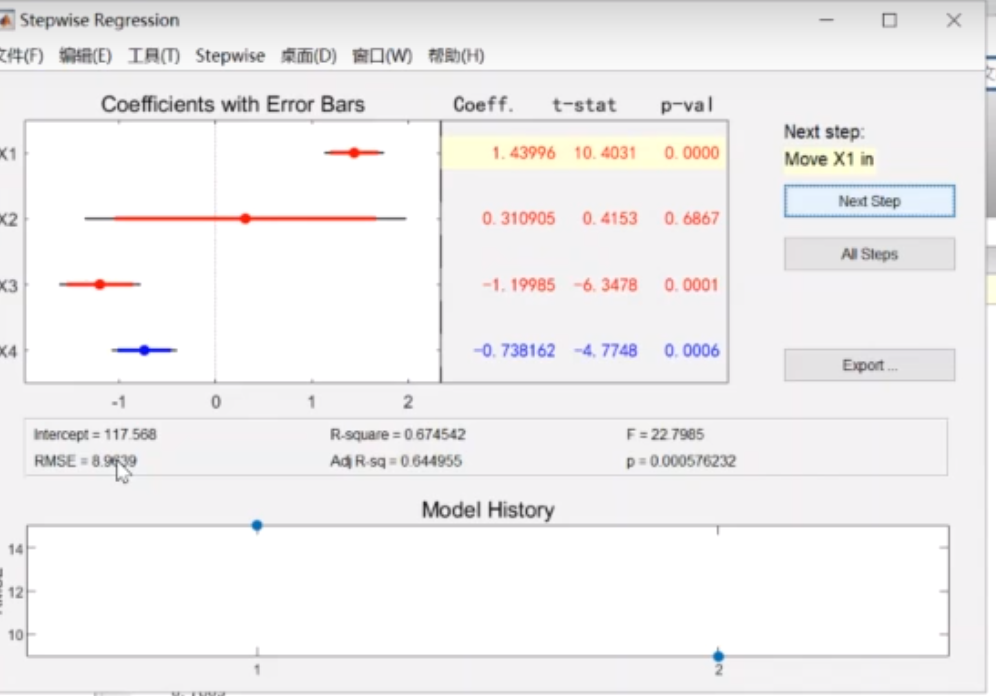
R变成0.97 F变成176
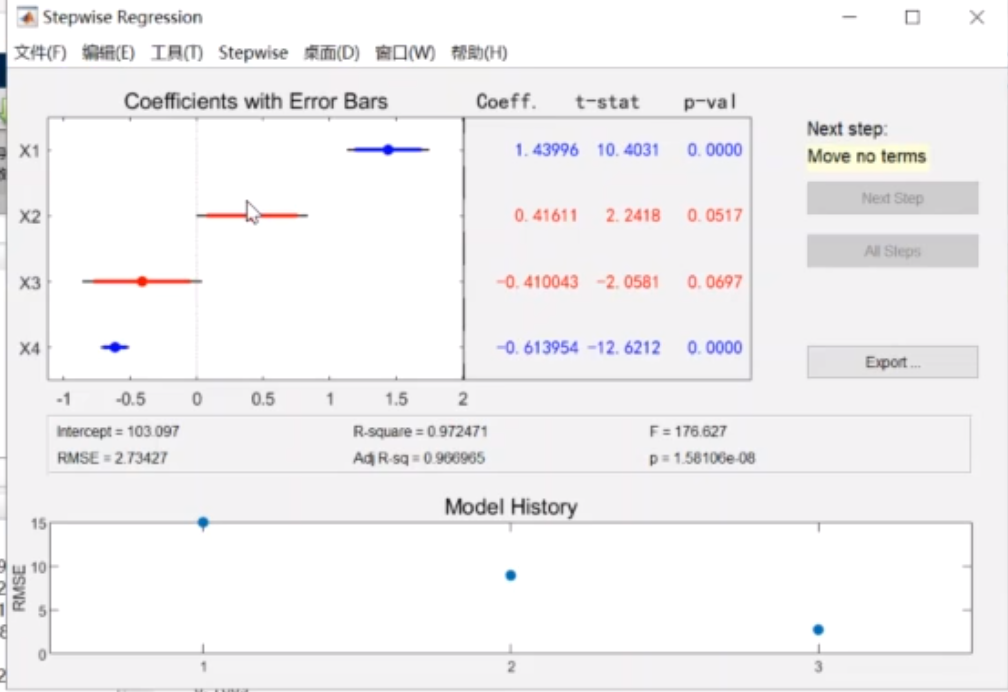
当然,也可以手动移除,点击红/蓝的线就可以蓝为移除,红为目前存在
(不过没有啥必要噢)
确定了两个变量之后在使用多元线性回归

就得到了系数了
综合评价类算法汇总(前面都有)

解决的问题模式
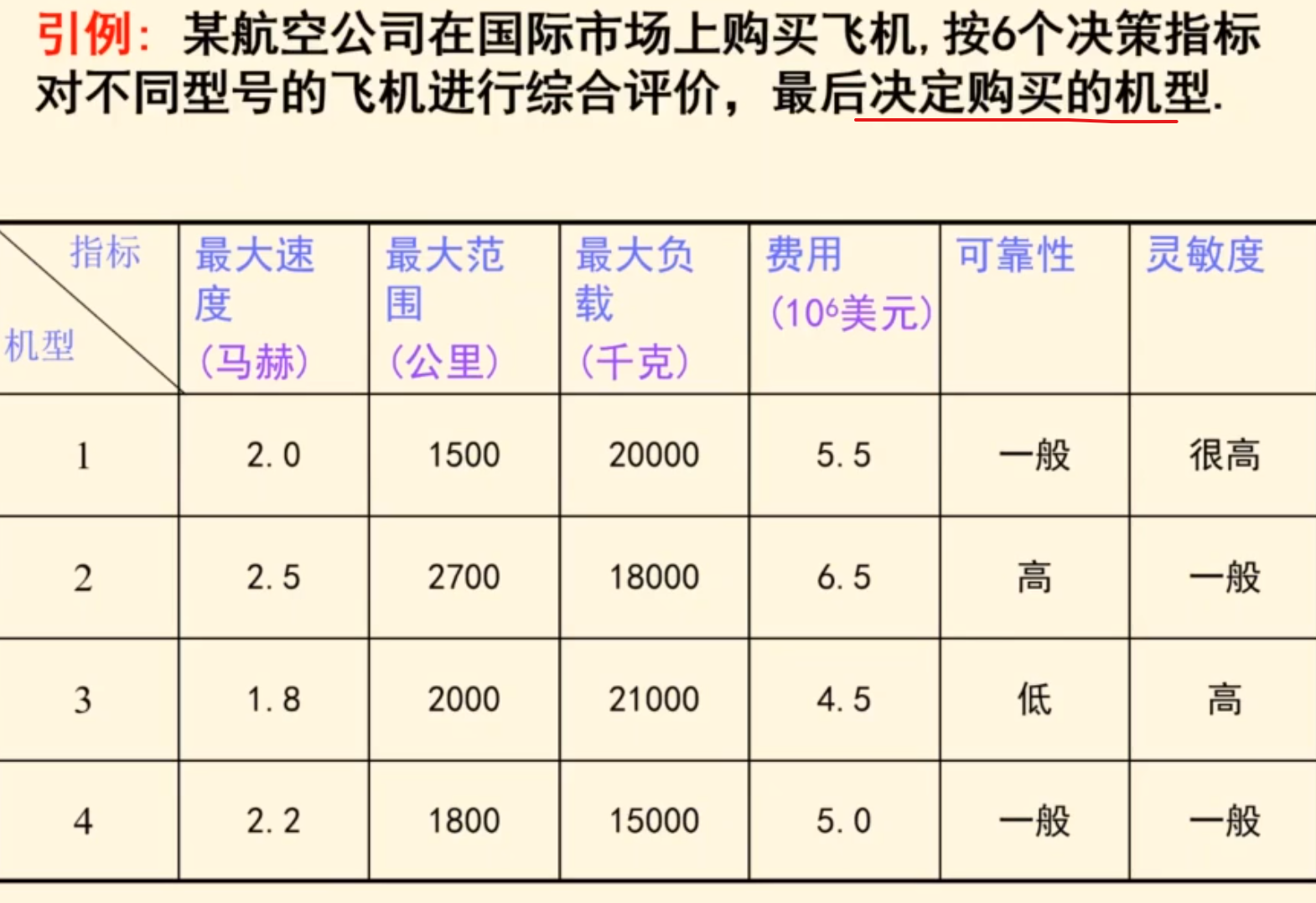
综合评价的目的

五要素





一般步骤

无量纲:转化为可以比较的

确定权重
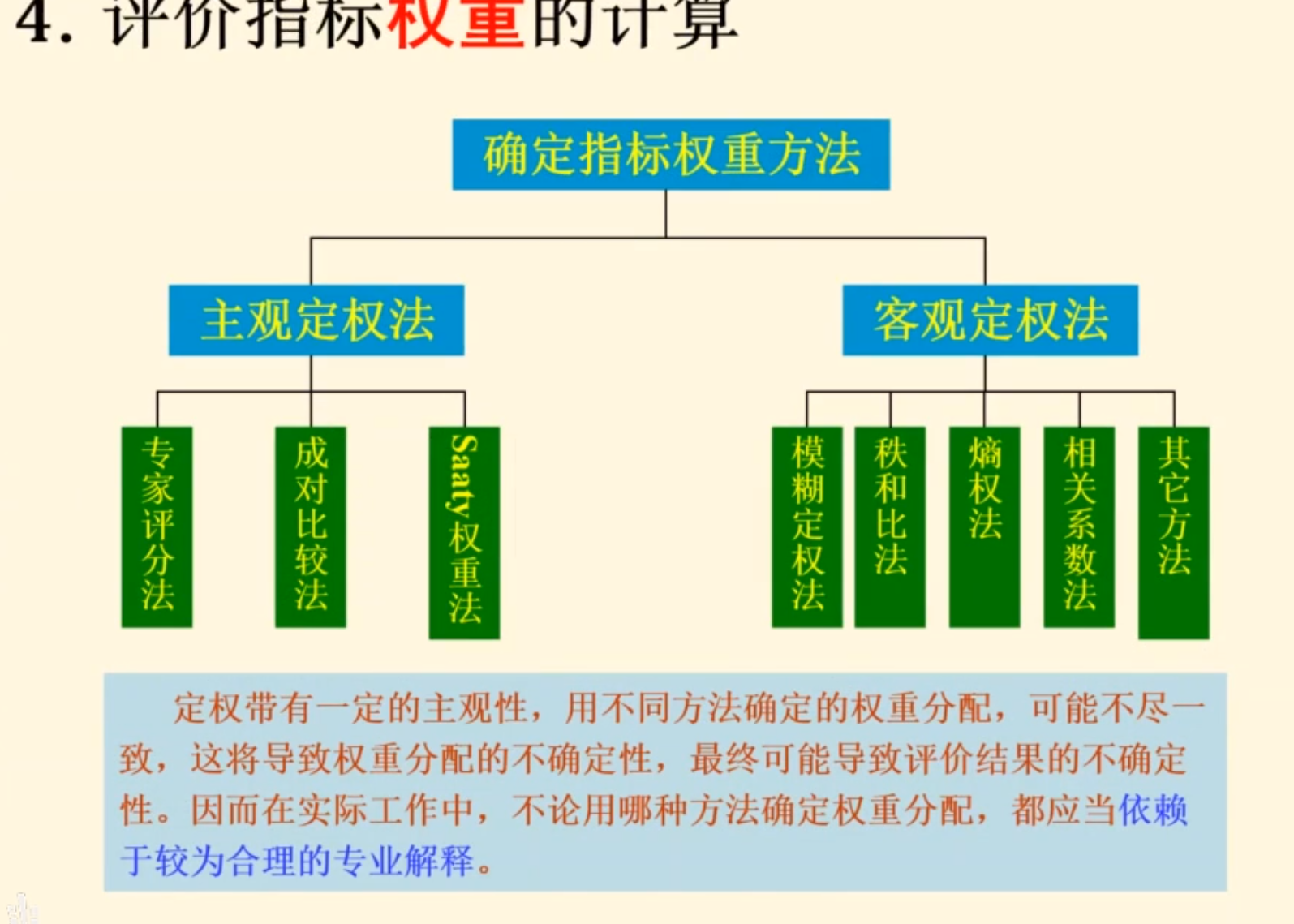
层次分析法就是典型的成对比较法
定权一定要解释一下为啥这样
指标的规范化处理

一致化


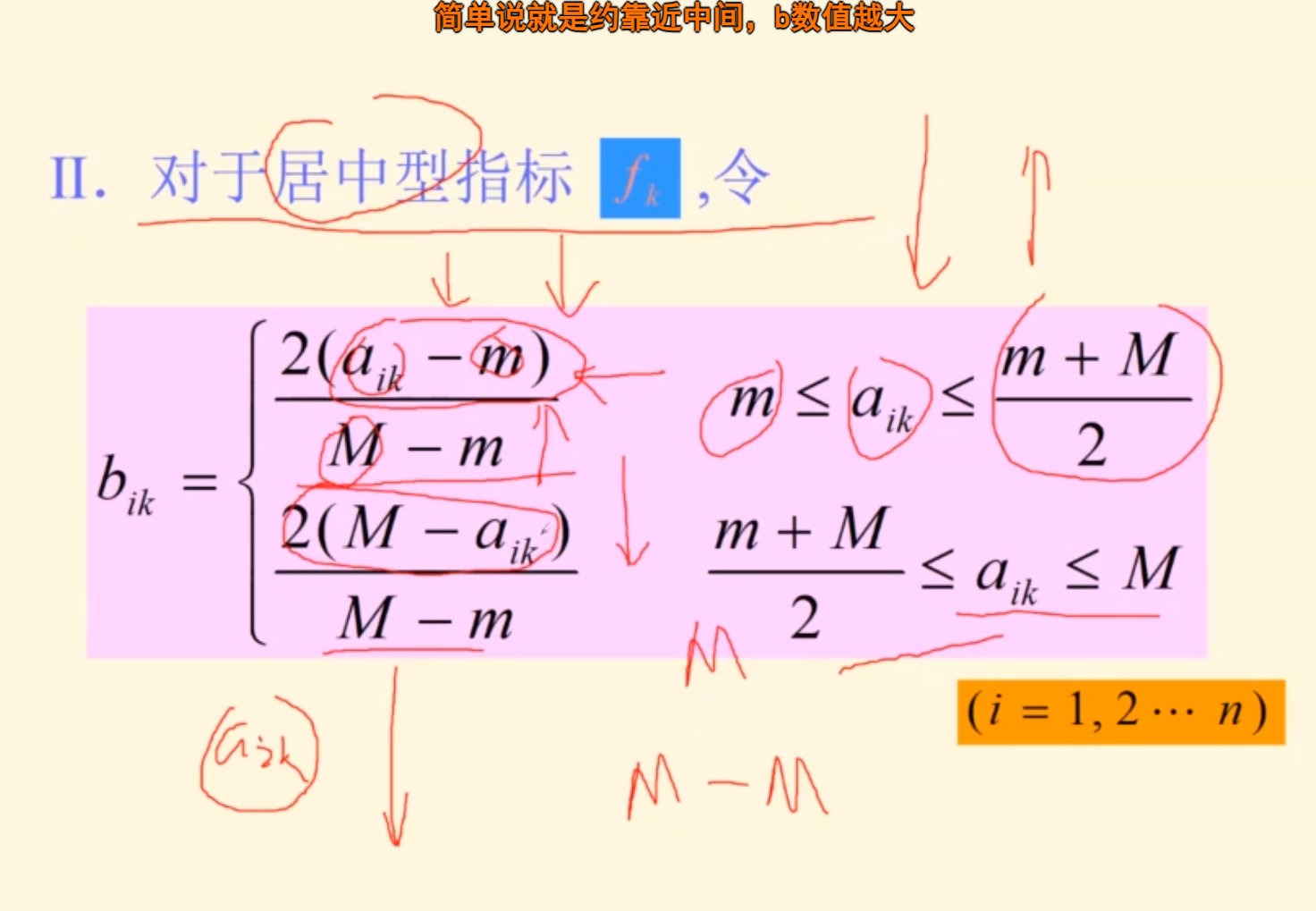
m与M为指标fk允许的下界和上界
其实不用分成两部分,直接取绝对值,那都是正的
指标数据无量纲化

用向量归一,那么所有数据都需要向量归一
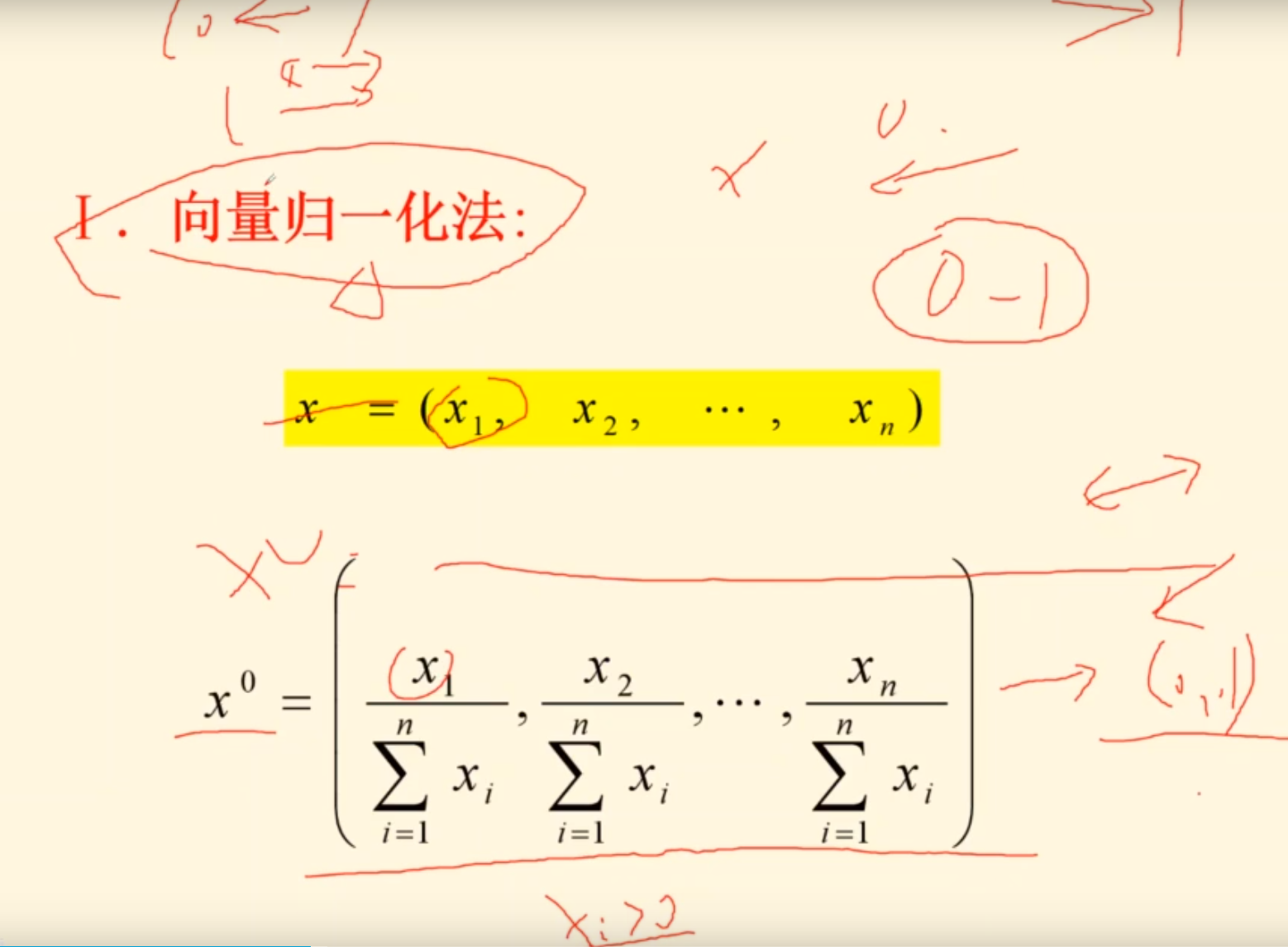
方法2趋向于0到1之间,=-=意思就是没有趋向
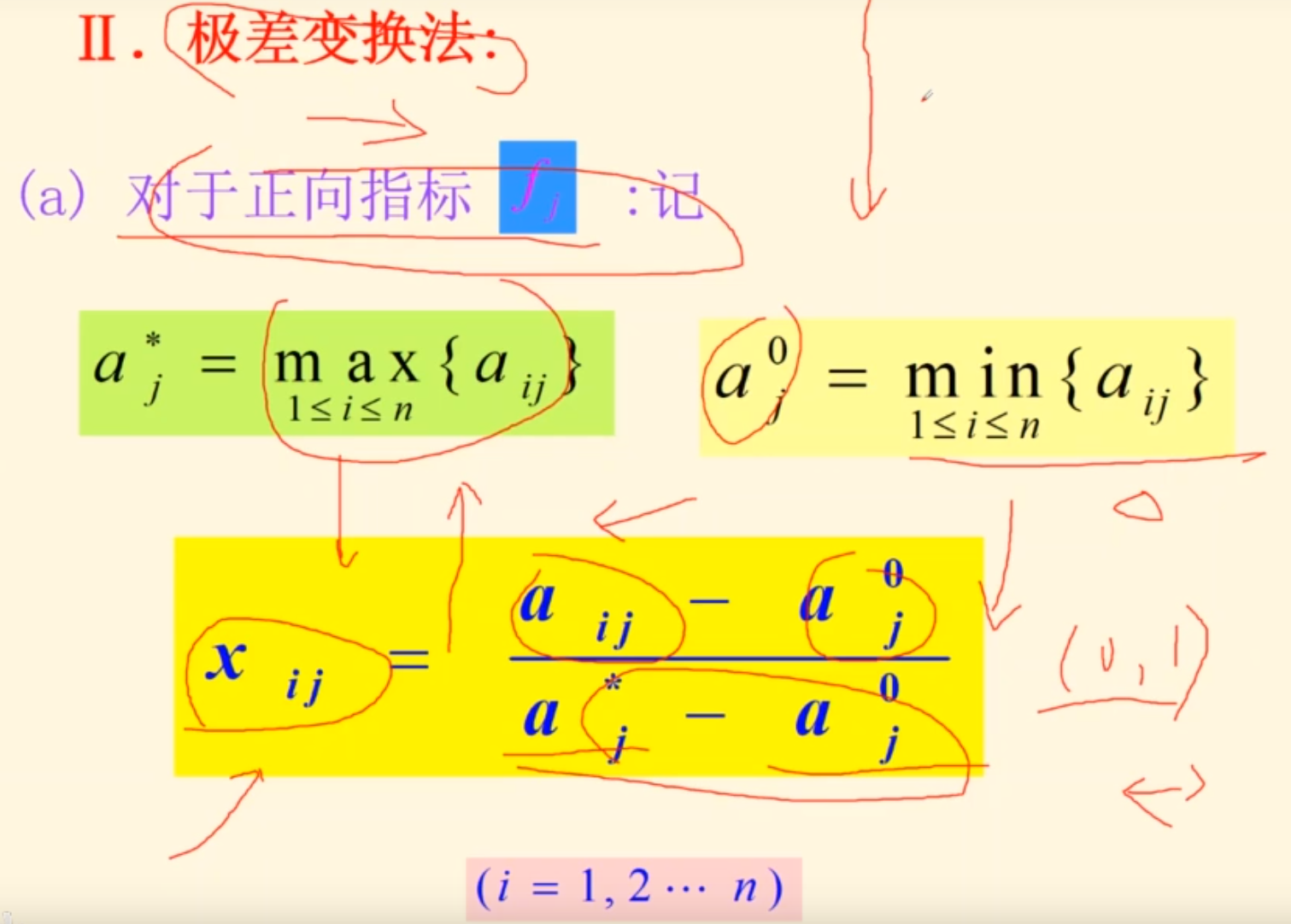
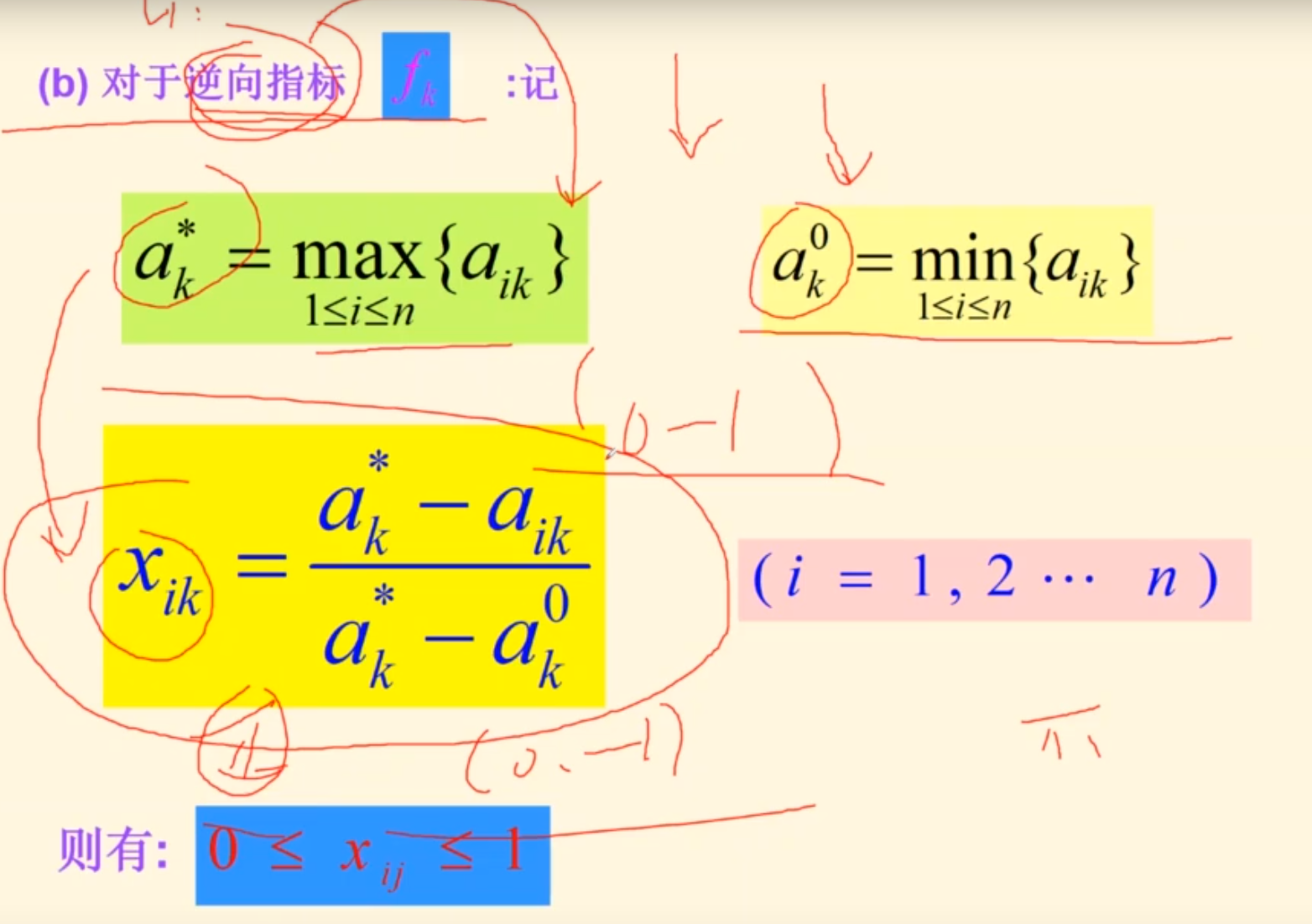
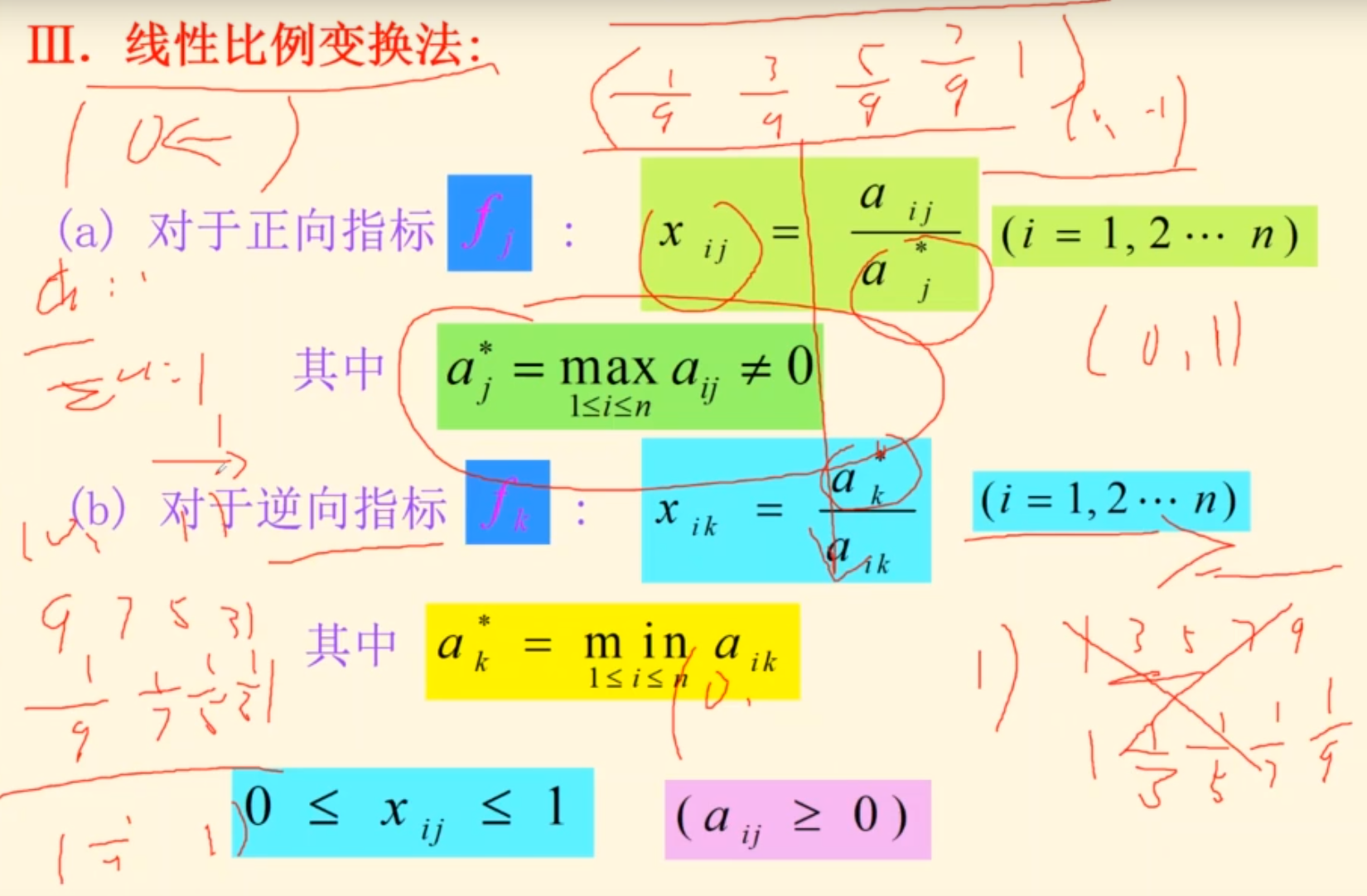
只要只用一个方法,就可以消除这中影响
常用综合评价方法
线性加权综合

非线性加权综合

TOPSIS
和灰色评价哪里差不多


模糊综合评价

模糊概念

模糊子集和隶属函数

一级模糊评价步骤

例题


美赛一定不要说有专家帮忙得出数据,要说用层次分析法

例题2
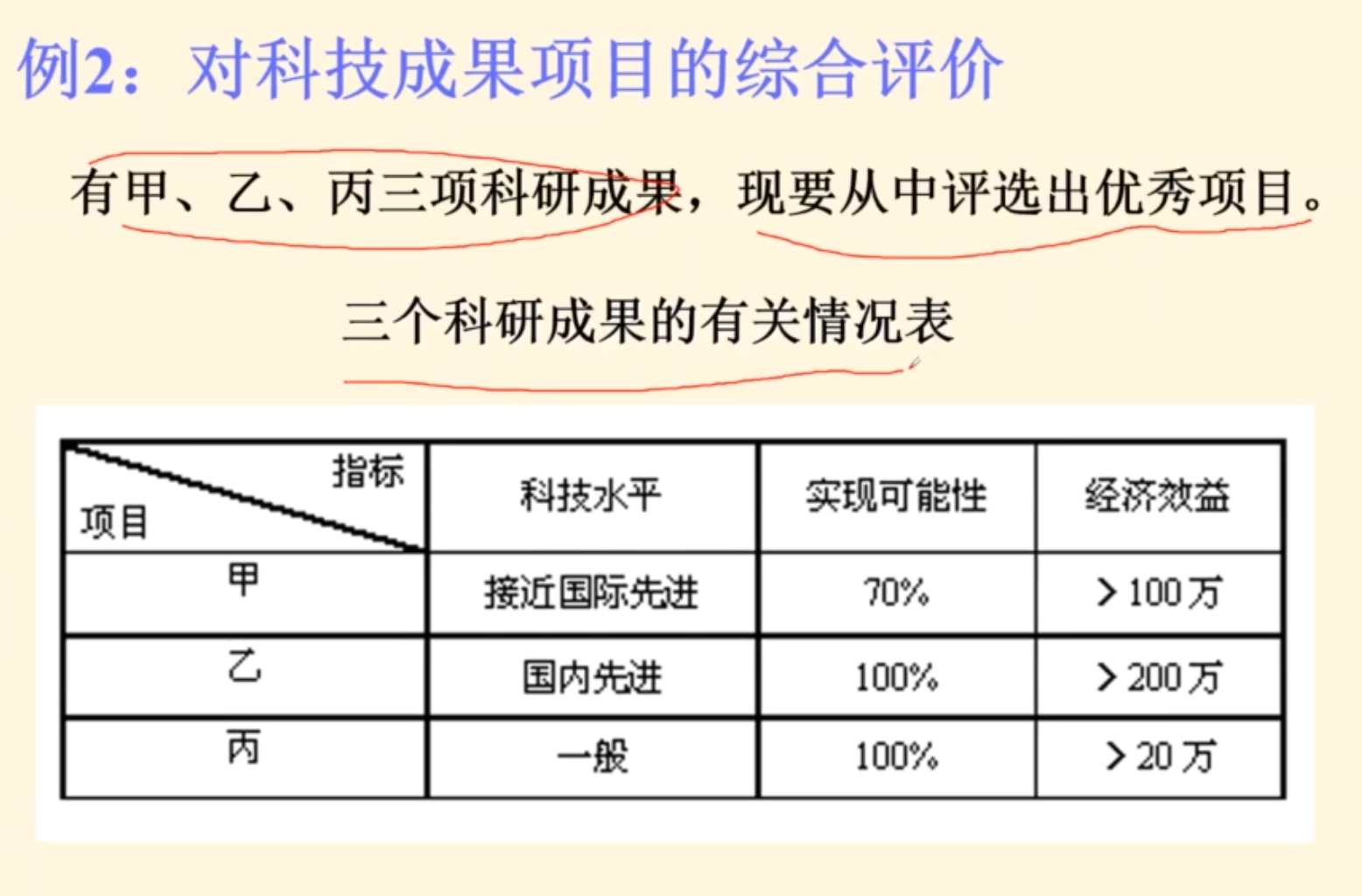
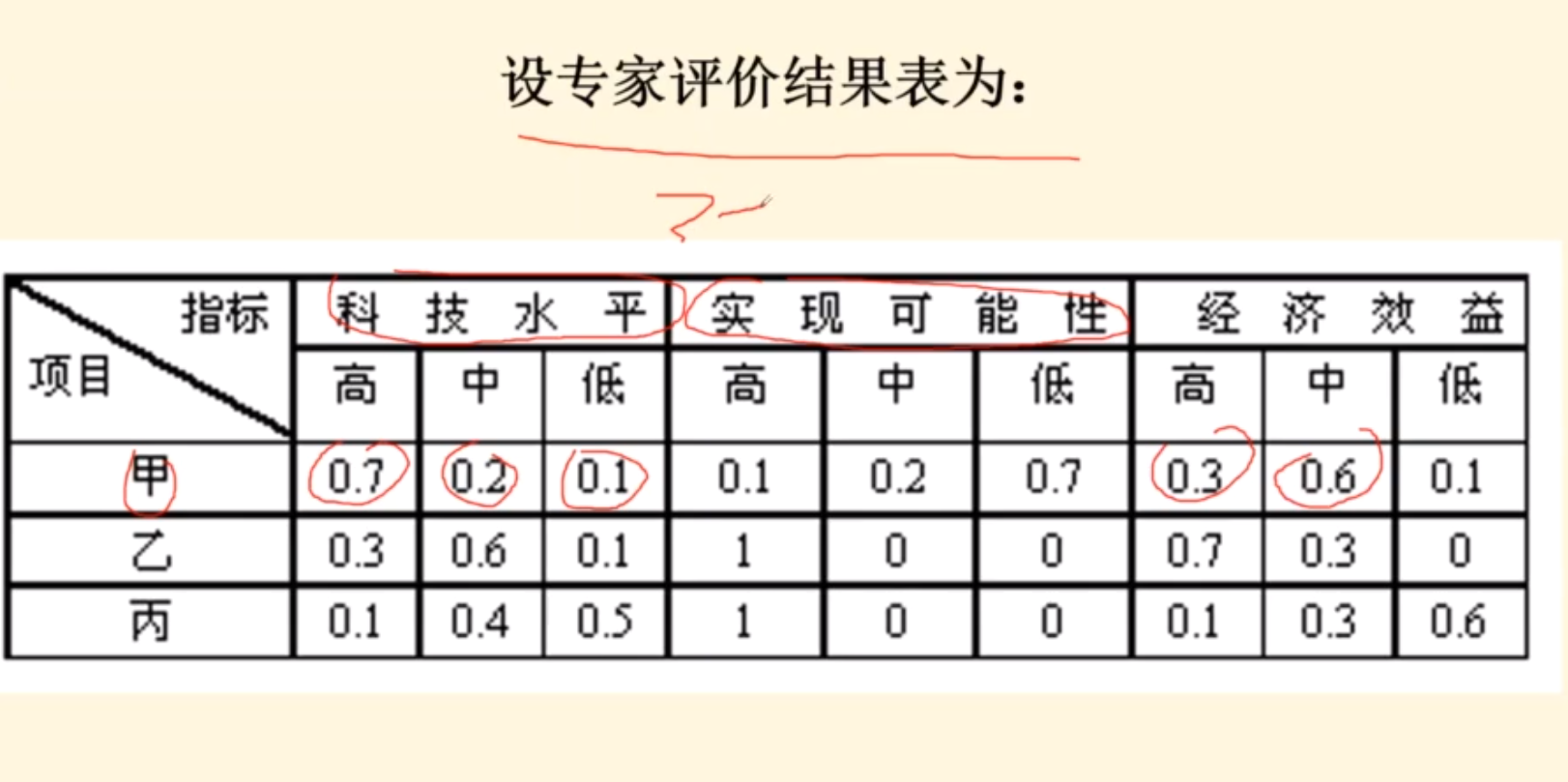



B2他高的部分占比多,高也就是科技高呗啥的
所以推荐乙
多级模糊评价

例题






灰色关联分析
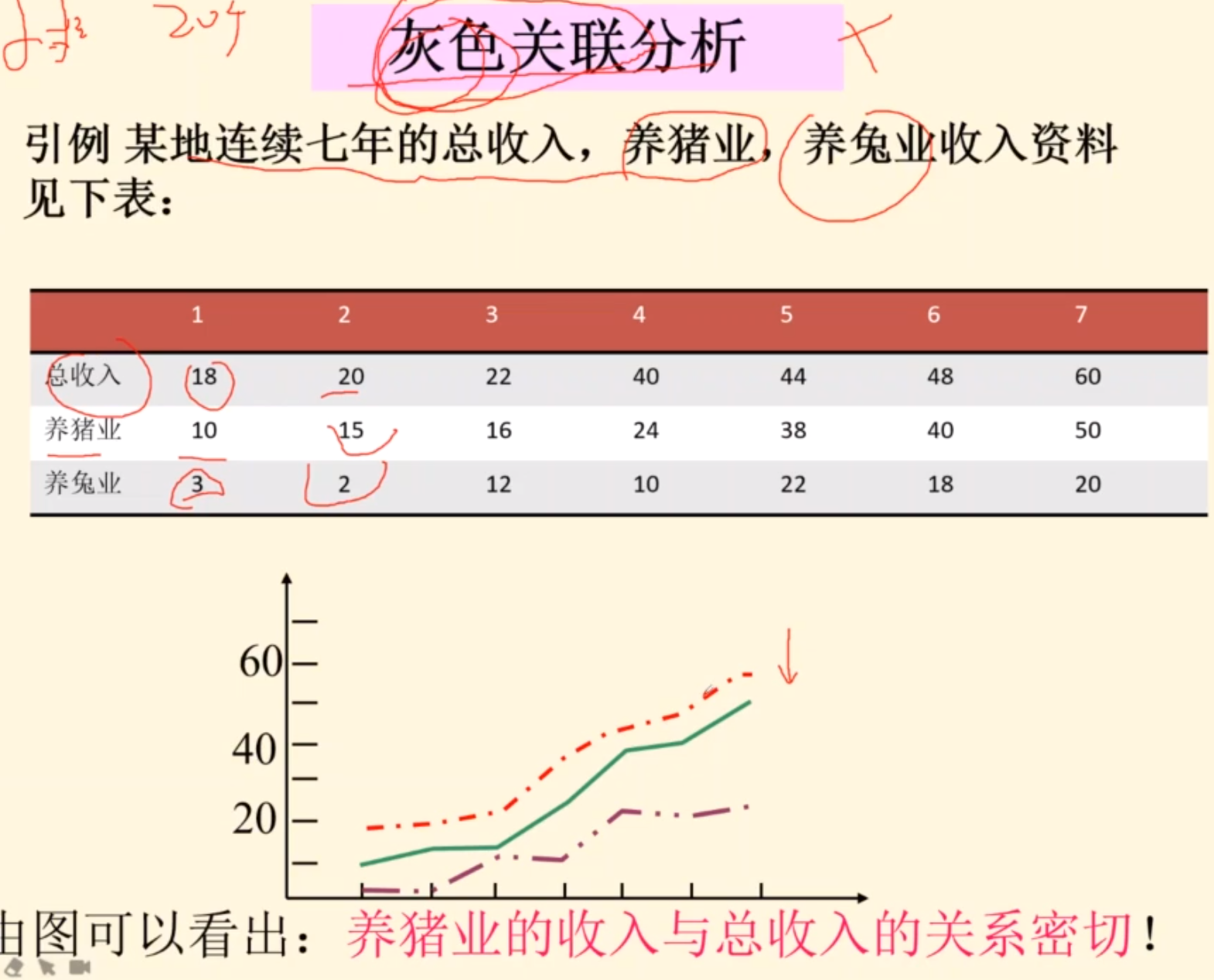



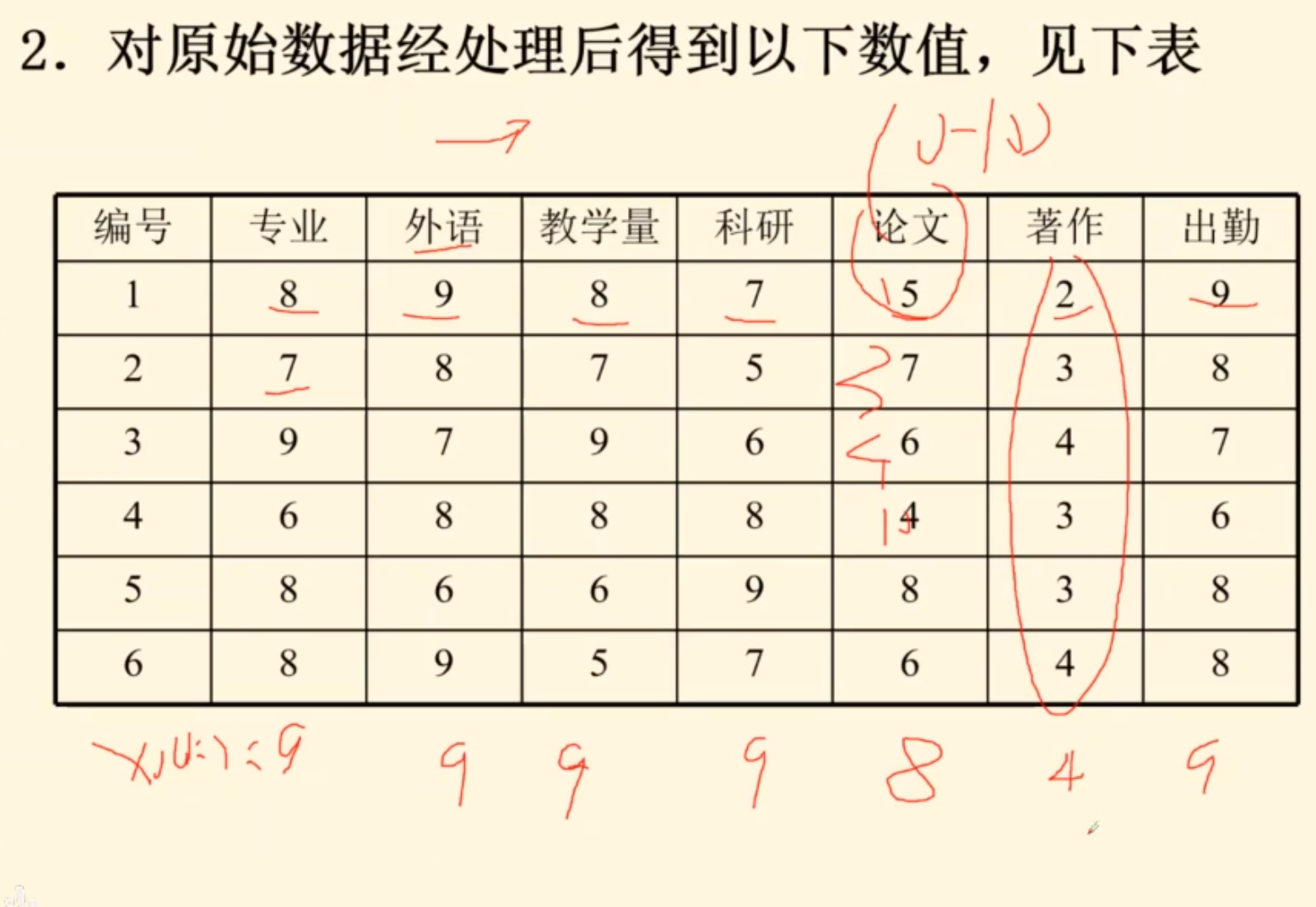
步骤




例子也是之前有的
元胞自动机
拥堵,洪水,山火,都有可能会用到元胞自动机基本思想
理论


构成


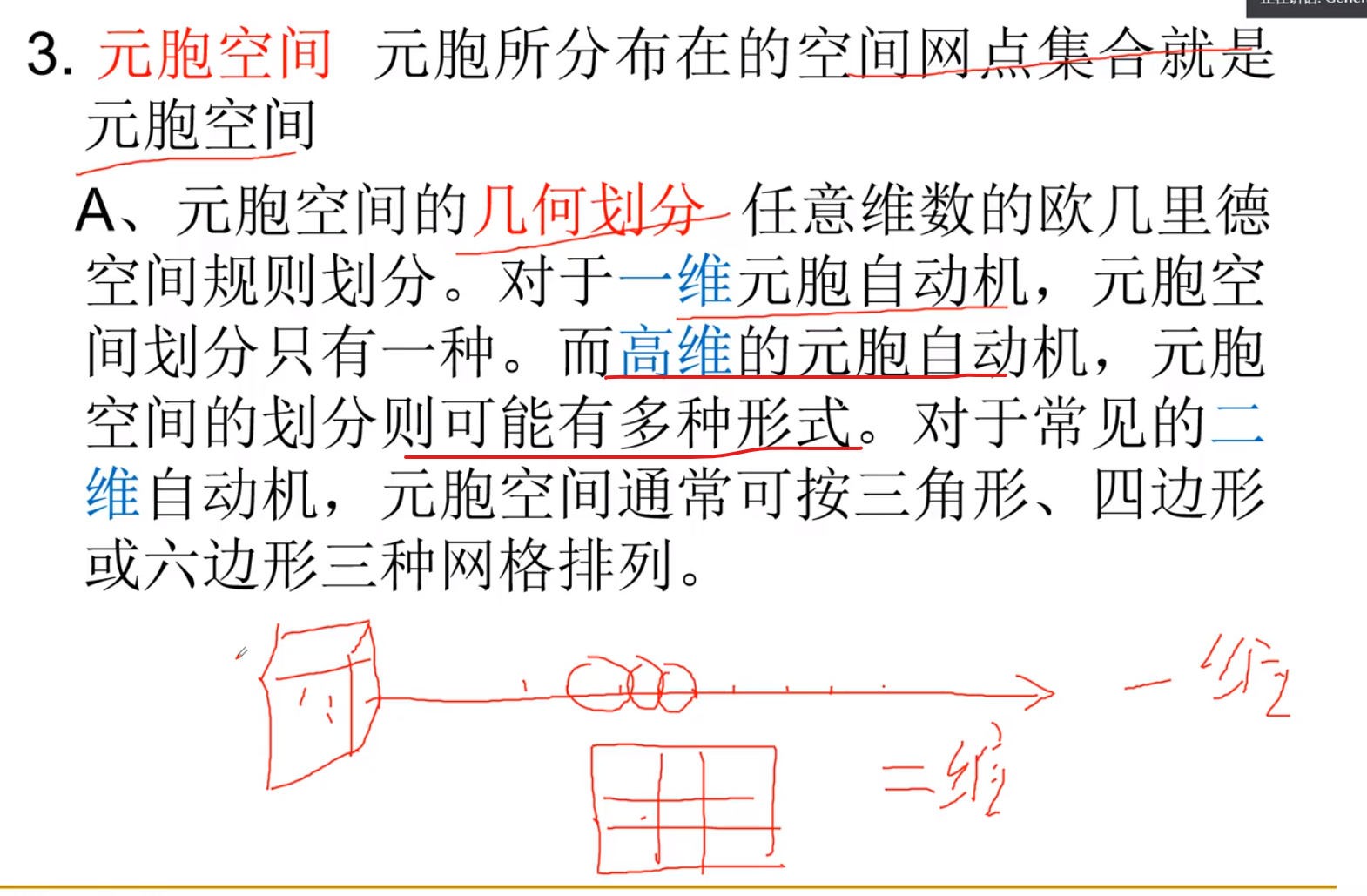
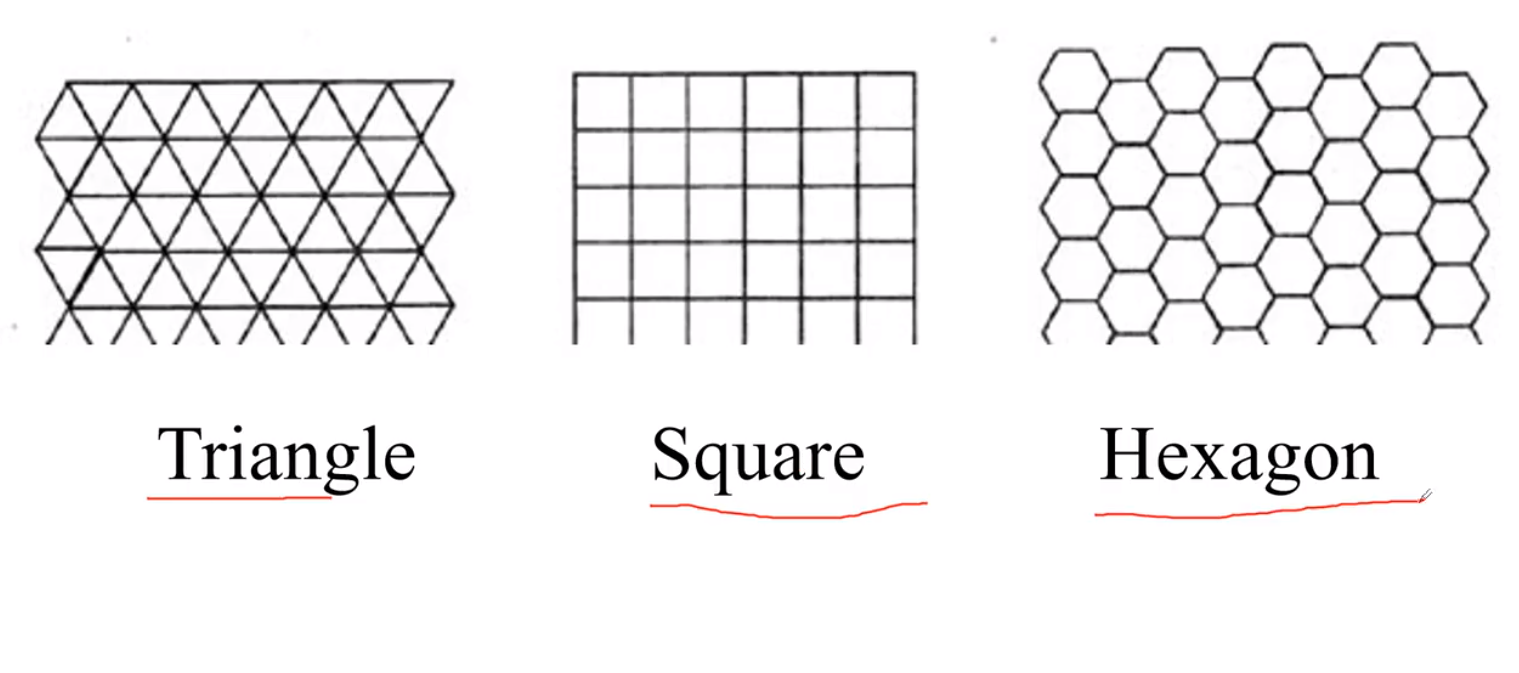
元胞空间的划分



邻居模型
不同的状态确定不同的邻居模型
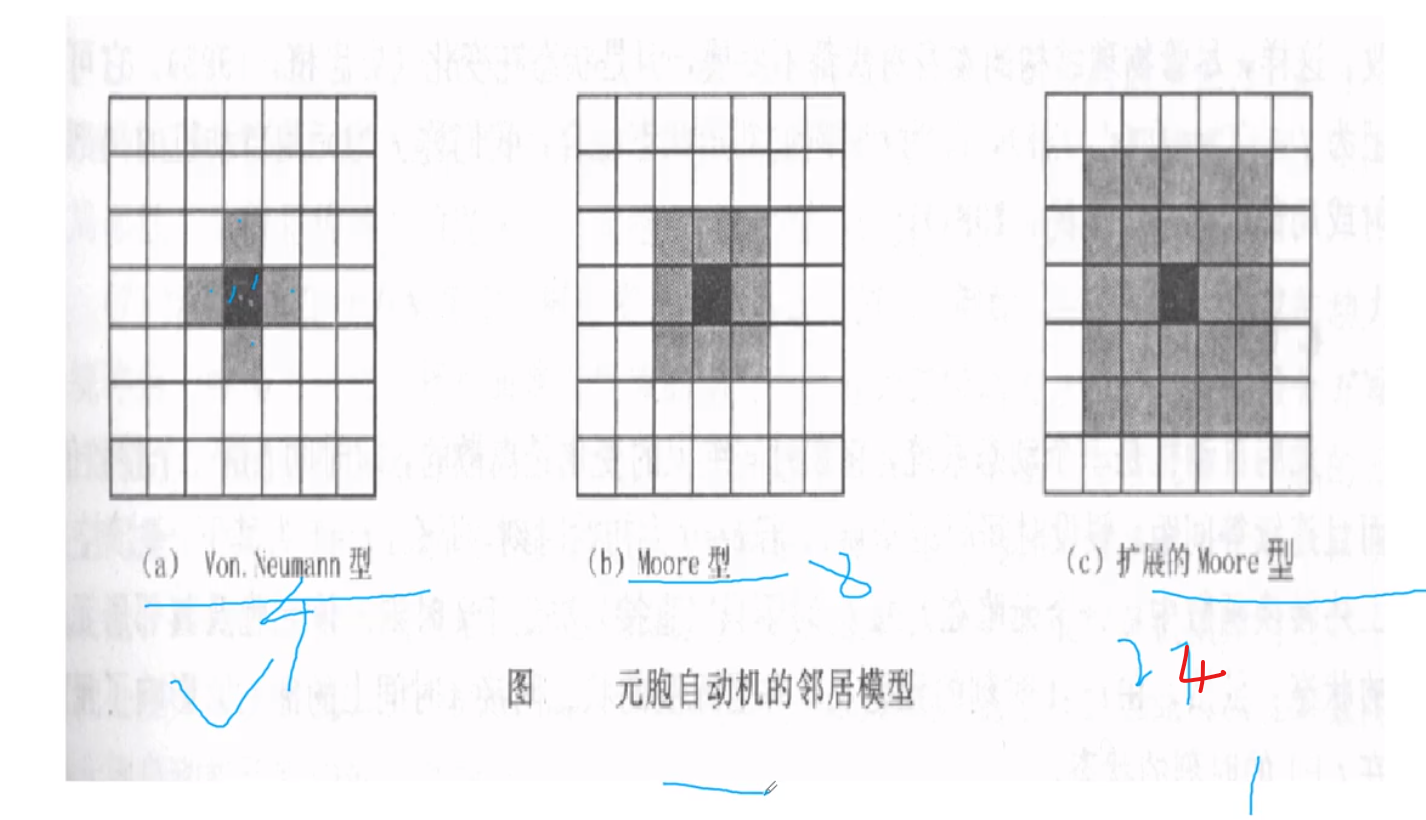

特性

应用思想


初等元胞自动机
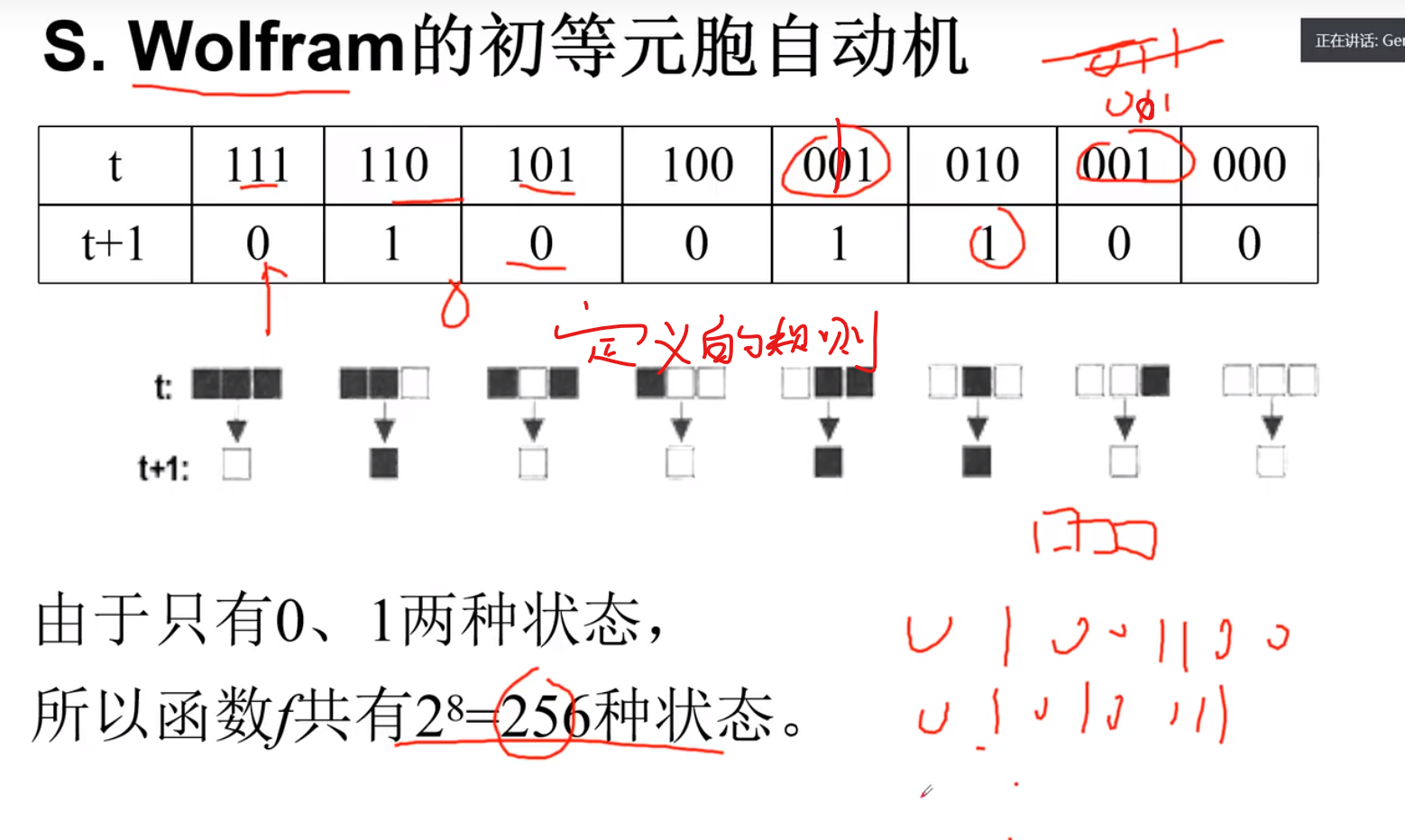
二维自动机


行为统计特征

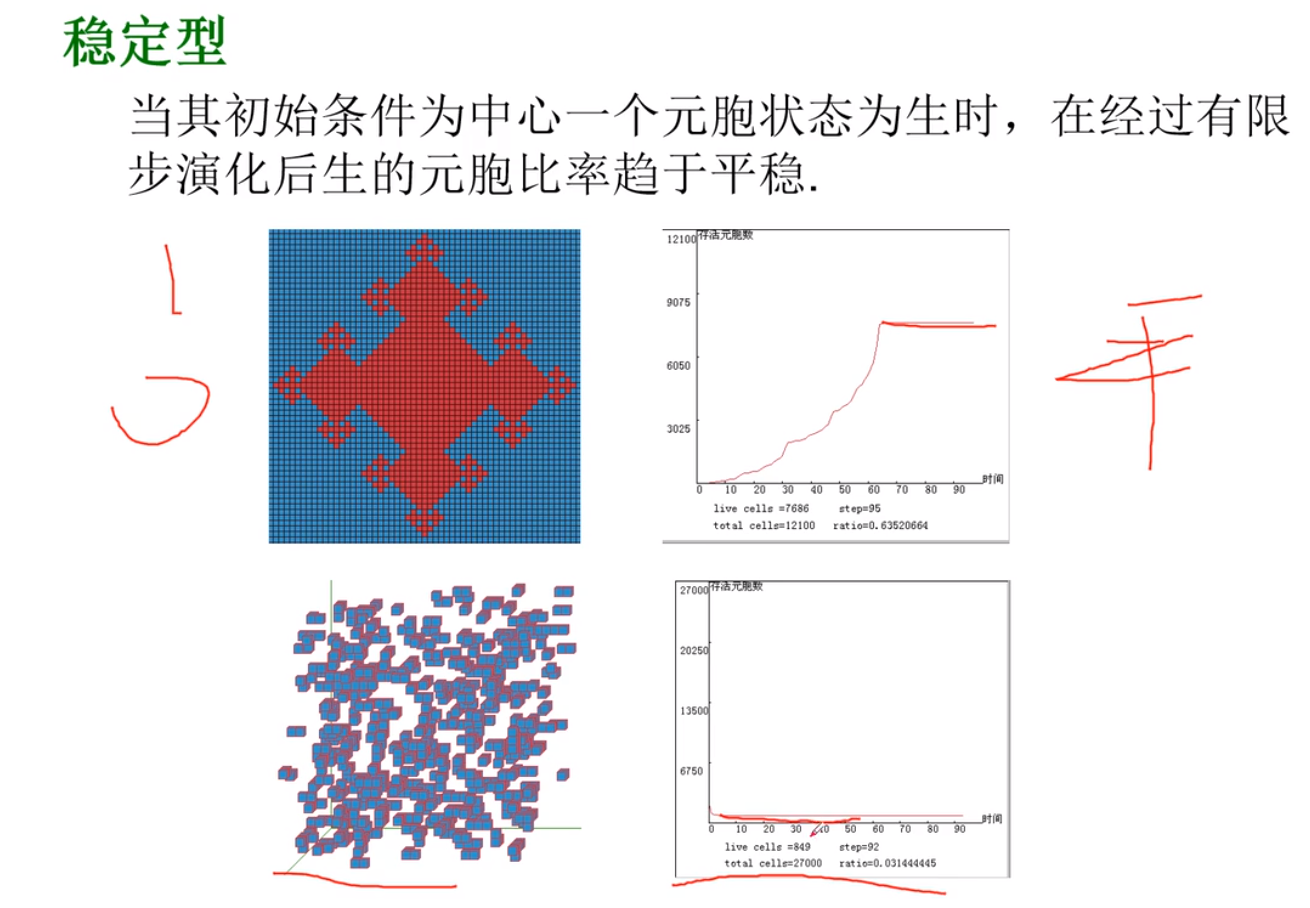
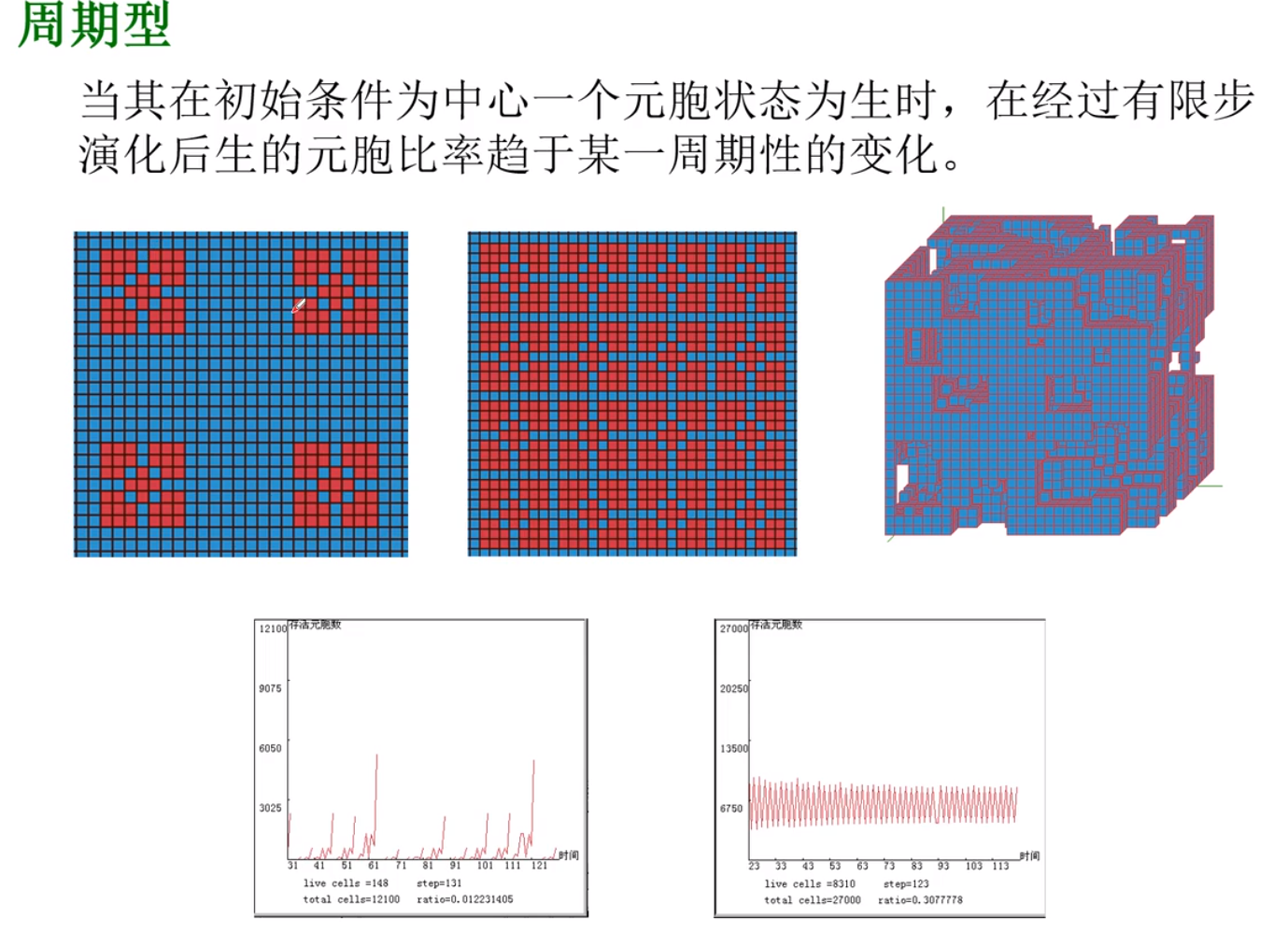
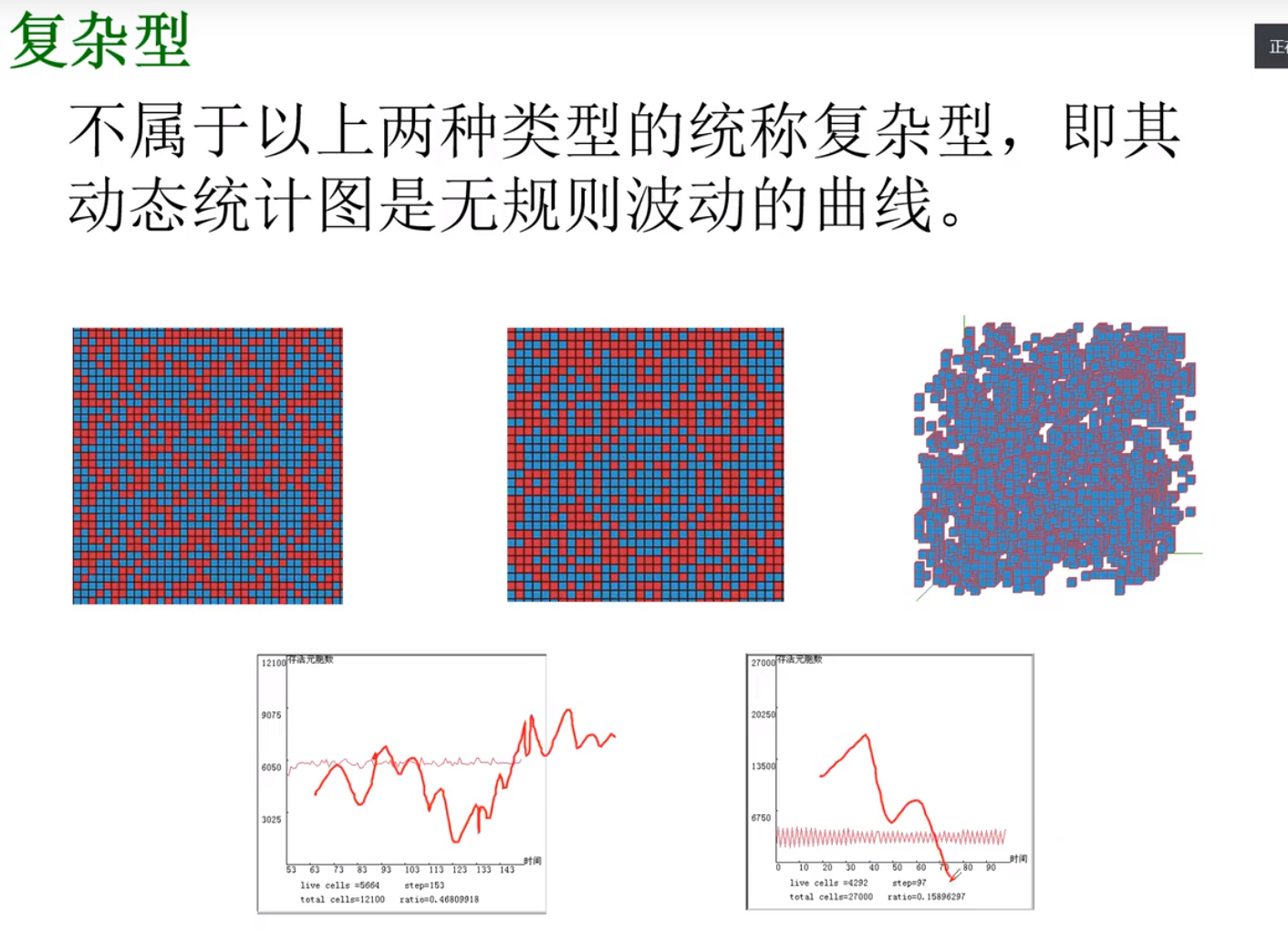
例题

交通模型
CA模型
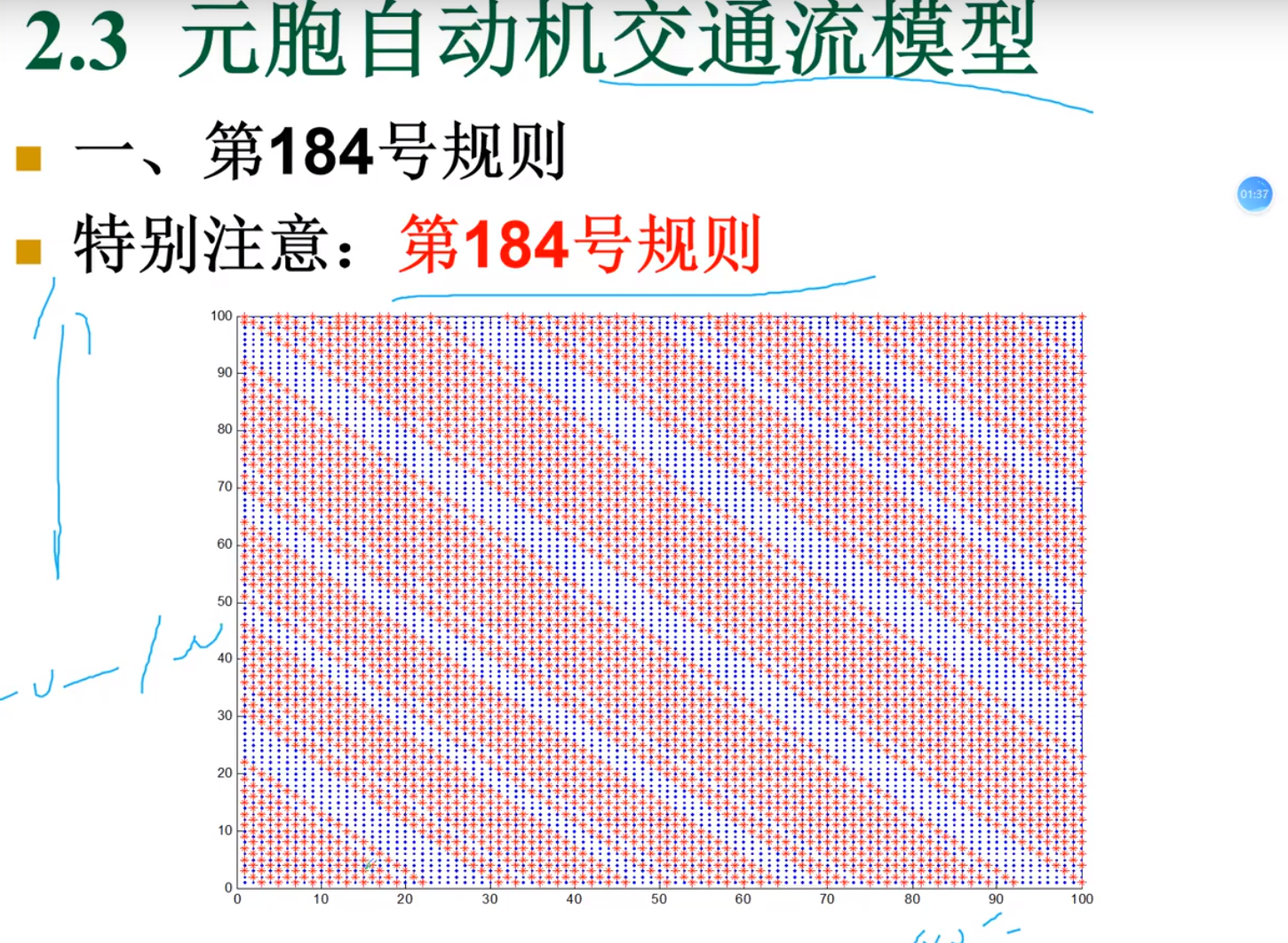

NS模型


演化过程


图论
问题引入与分析


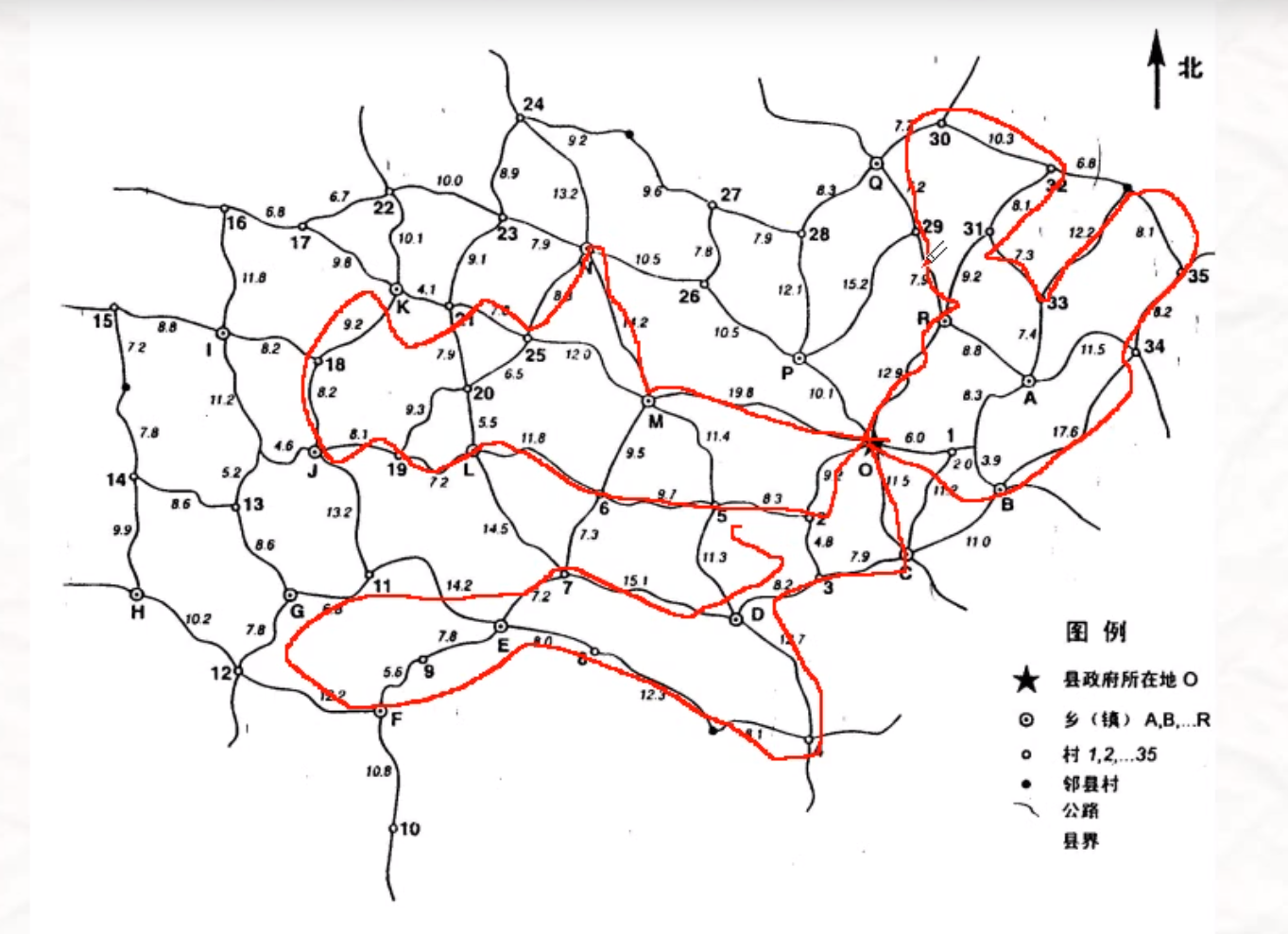

图的概念



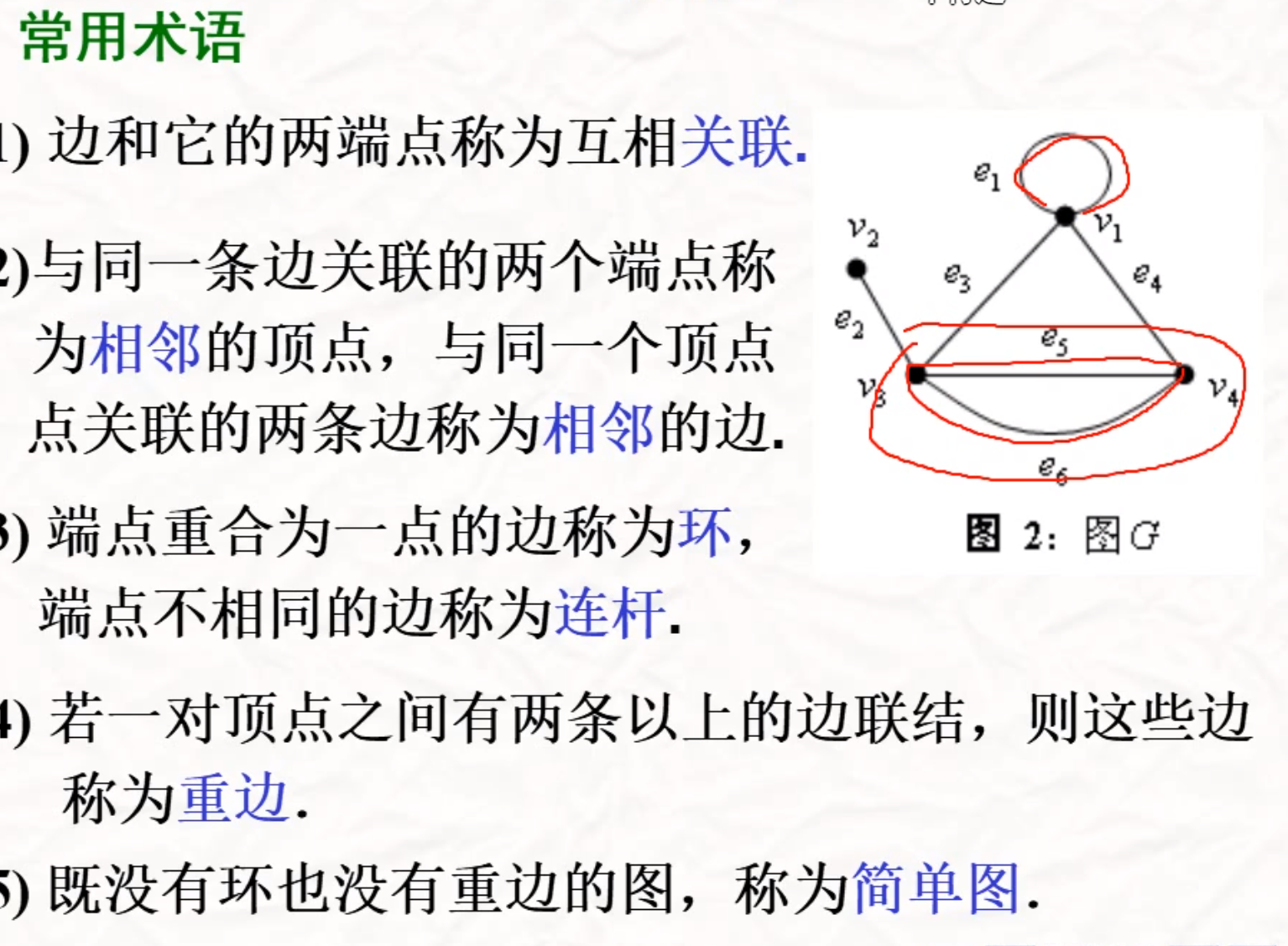
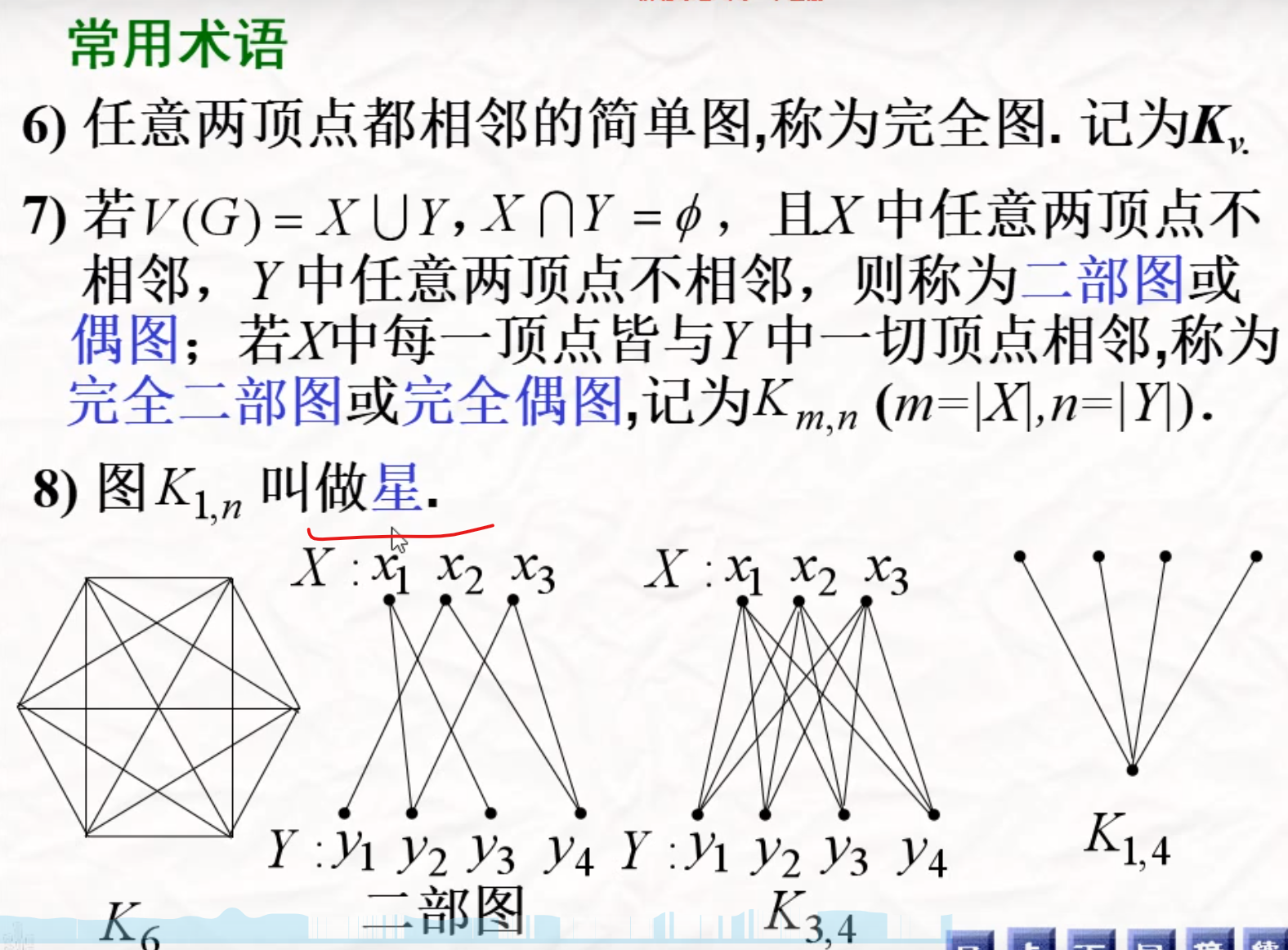
赋权图与子图

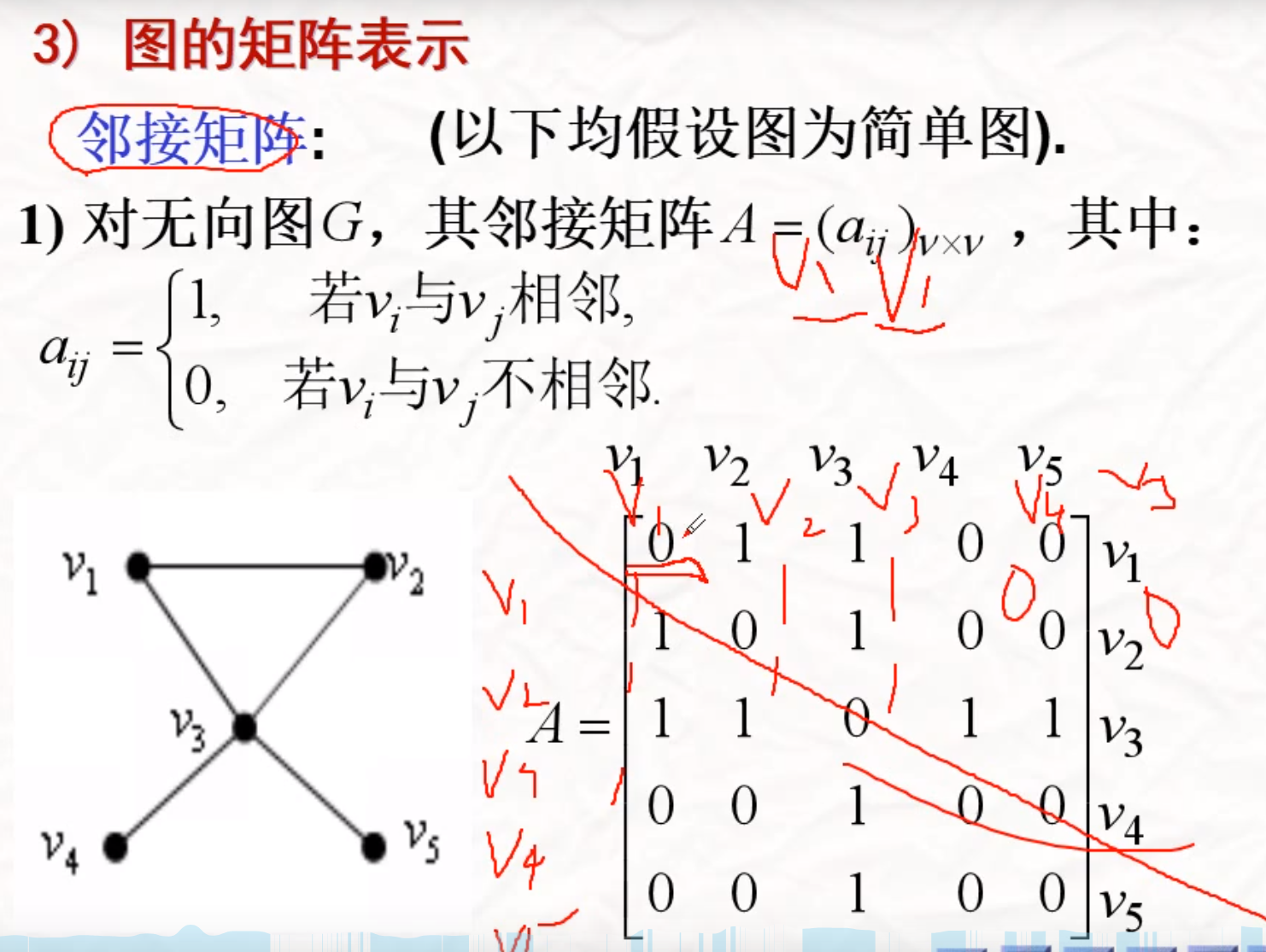
图的矩阵表示
邻接矩阵
点与点之间的关系
邻接矩阵需要是简单图
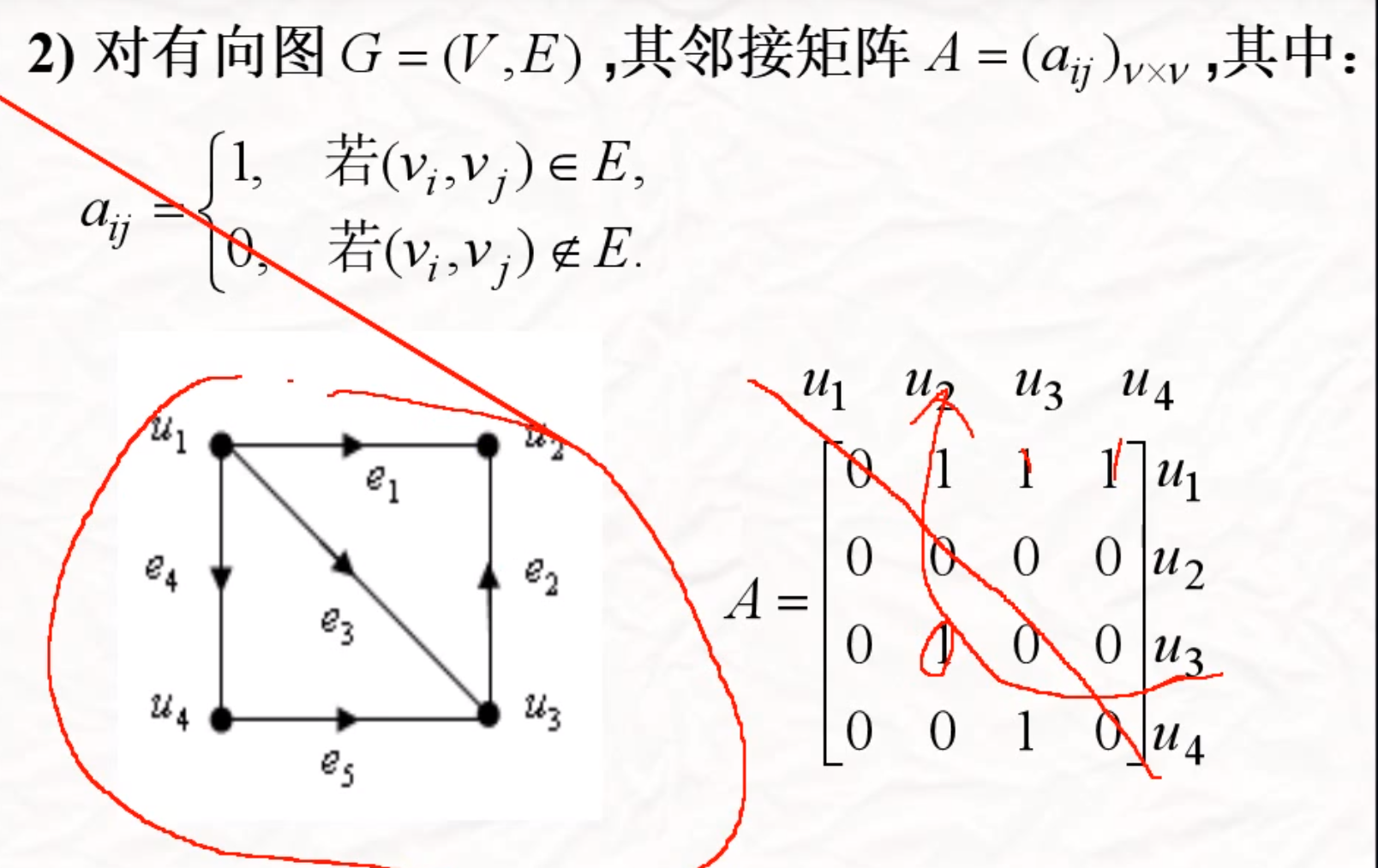
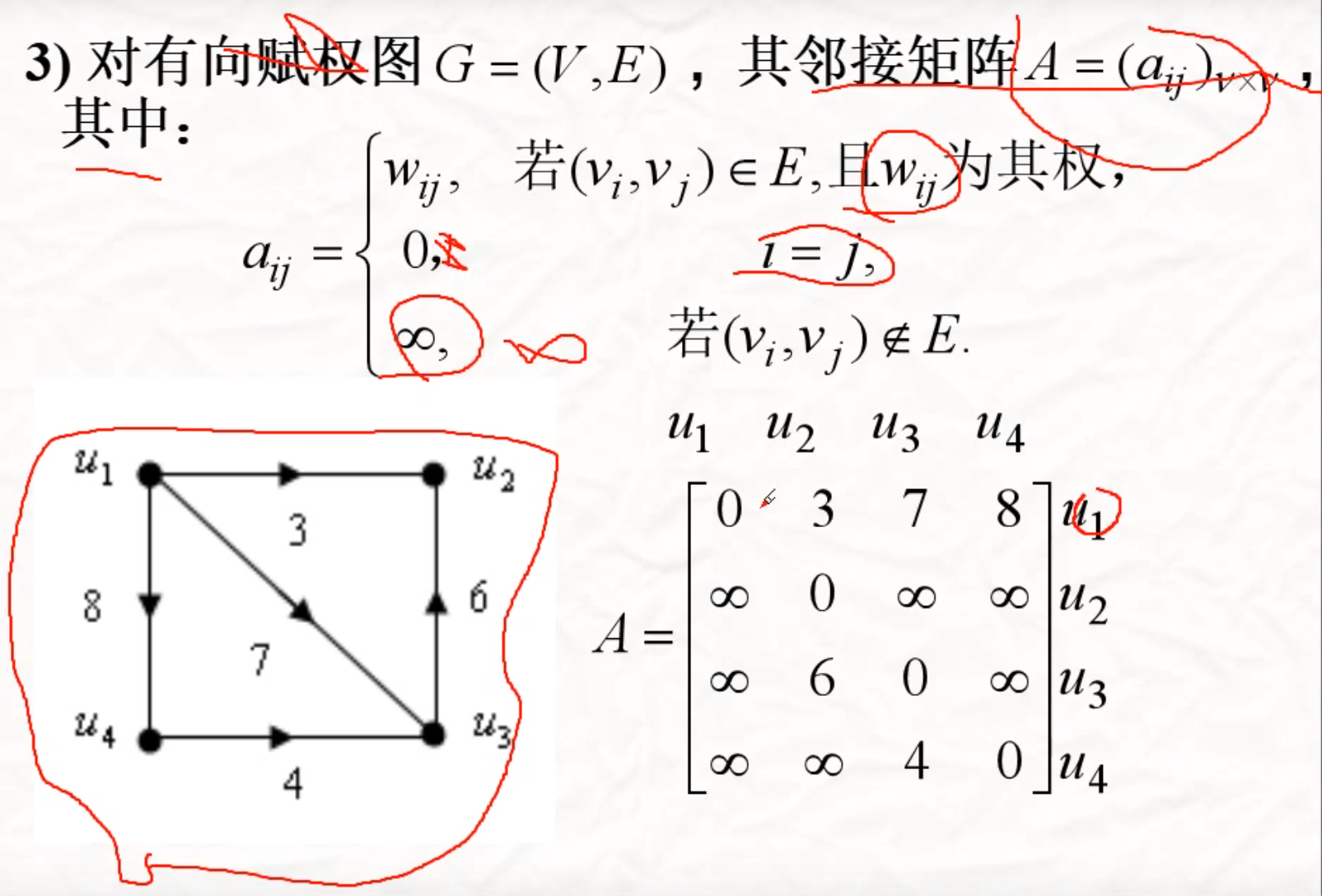
关联矩阵
顶点和边之间的关系
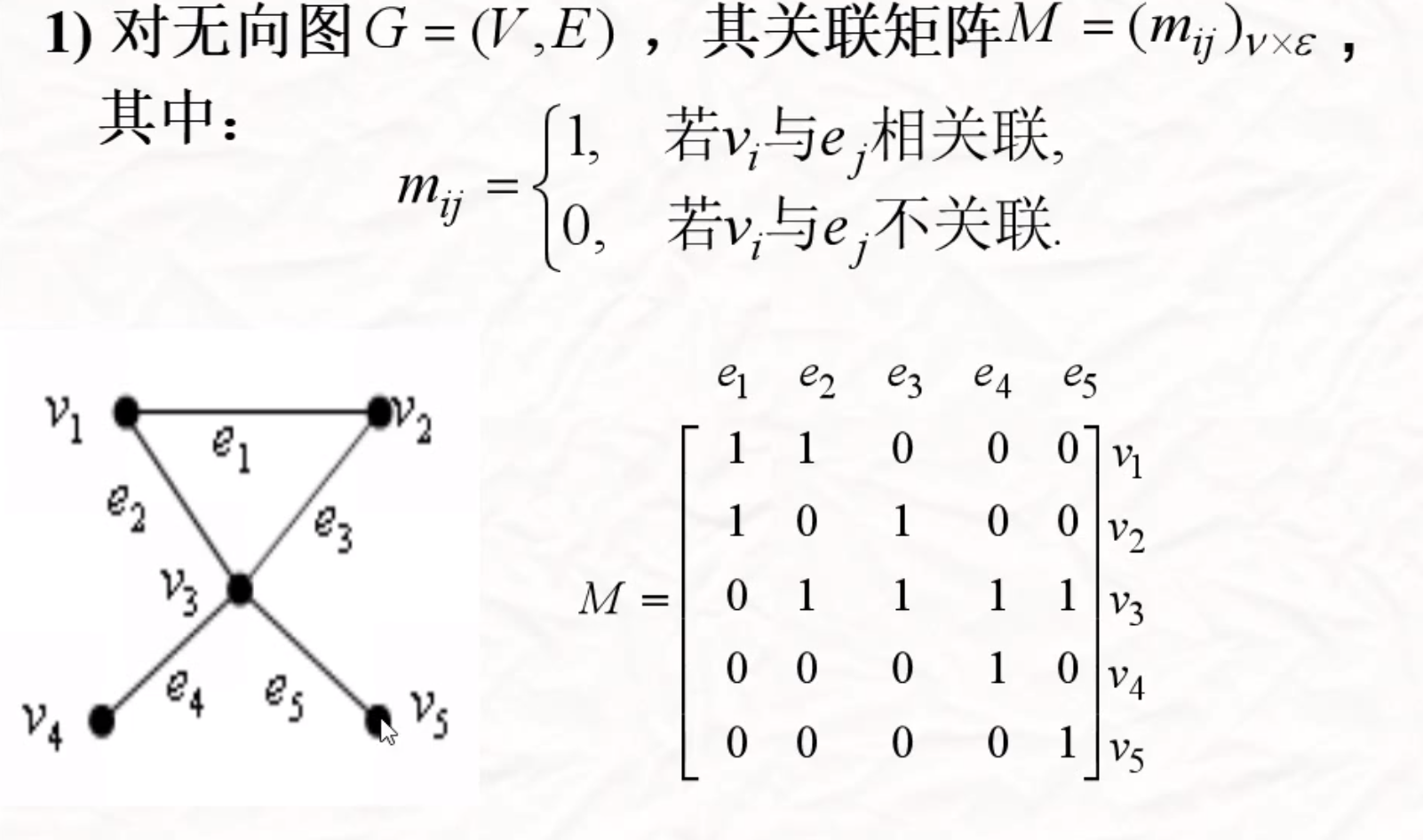
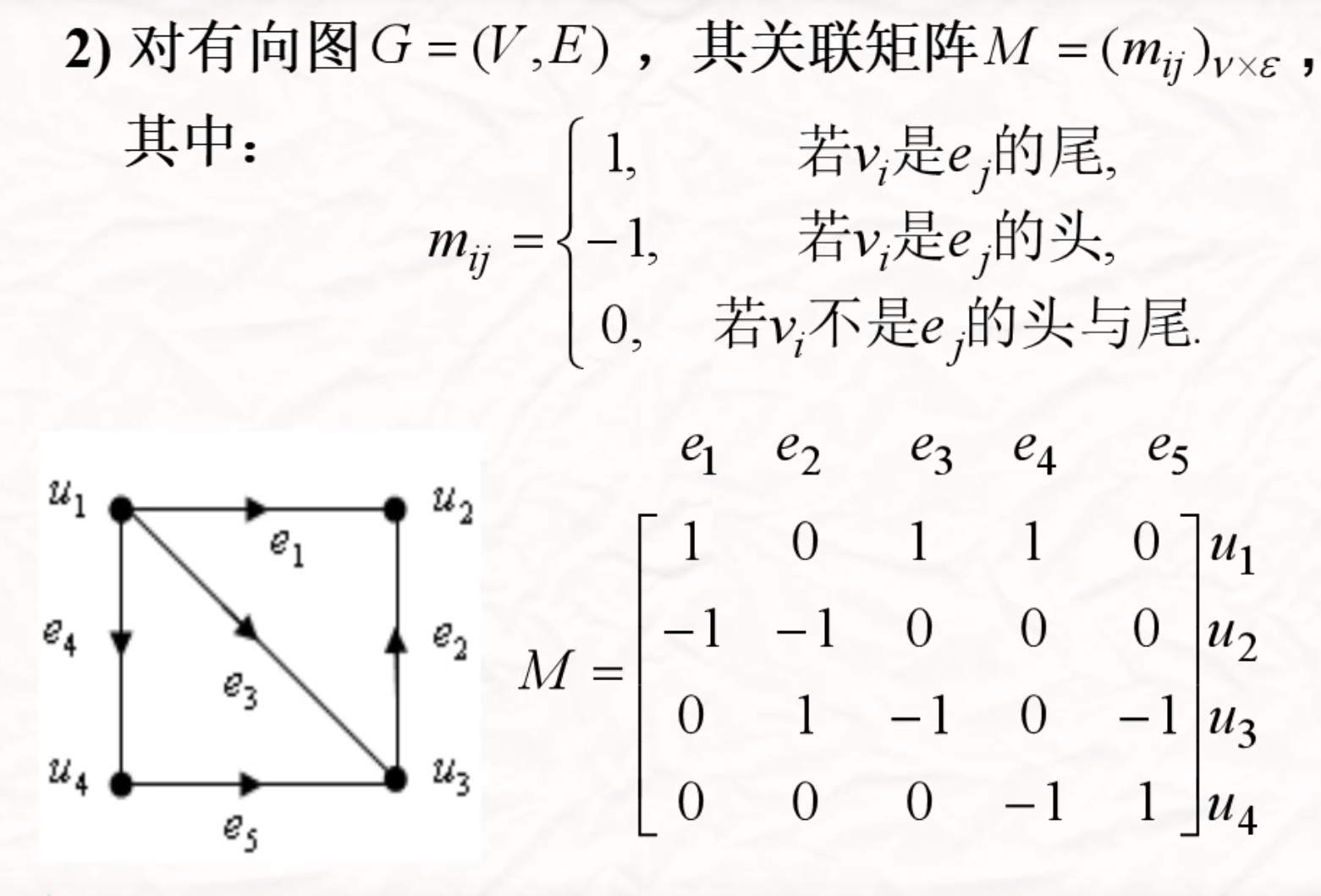
度

途径路径理论基础不一样,真正计算一样的,没必要分的这么细致



最短路问题和算法


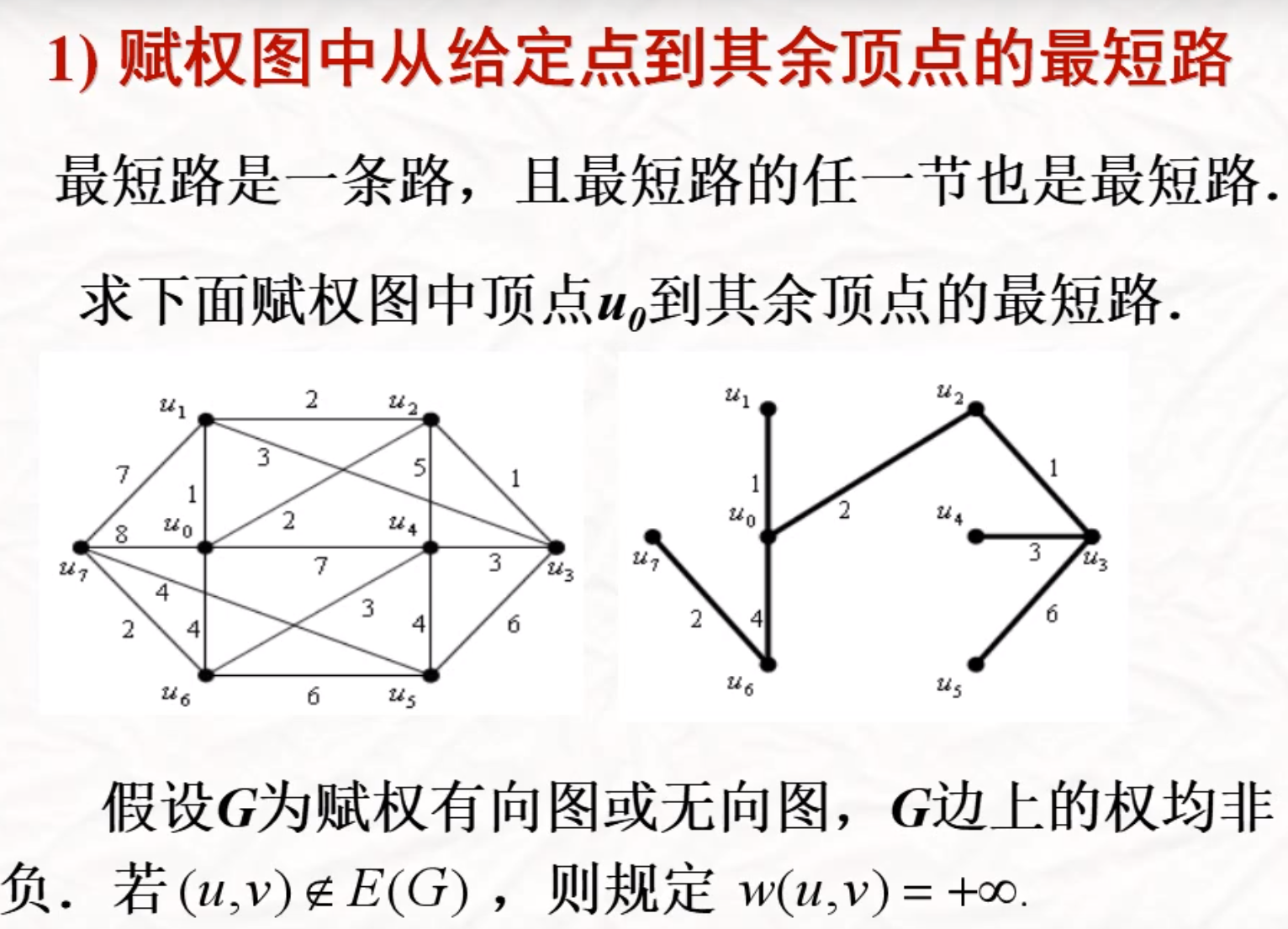
Dijkstra
一个点到其余顶点的最短路



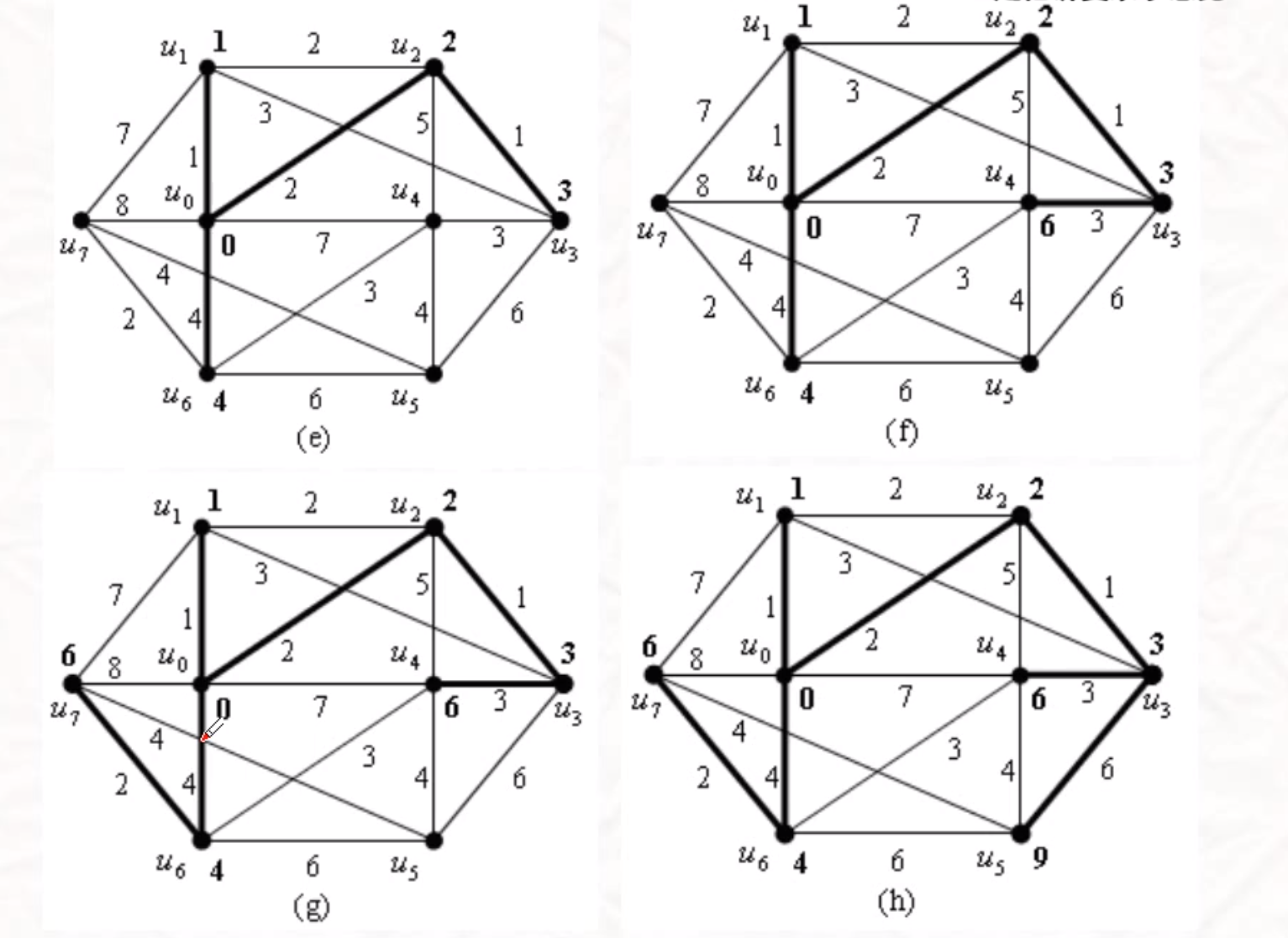
图论软件——>程序包
Floyd
求任意两顶点之间的最短路


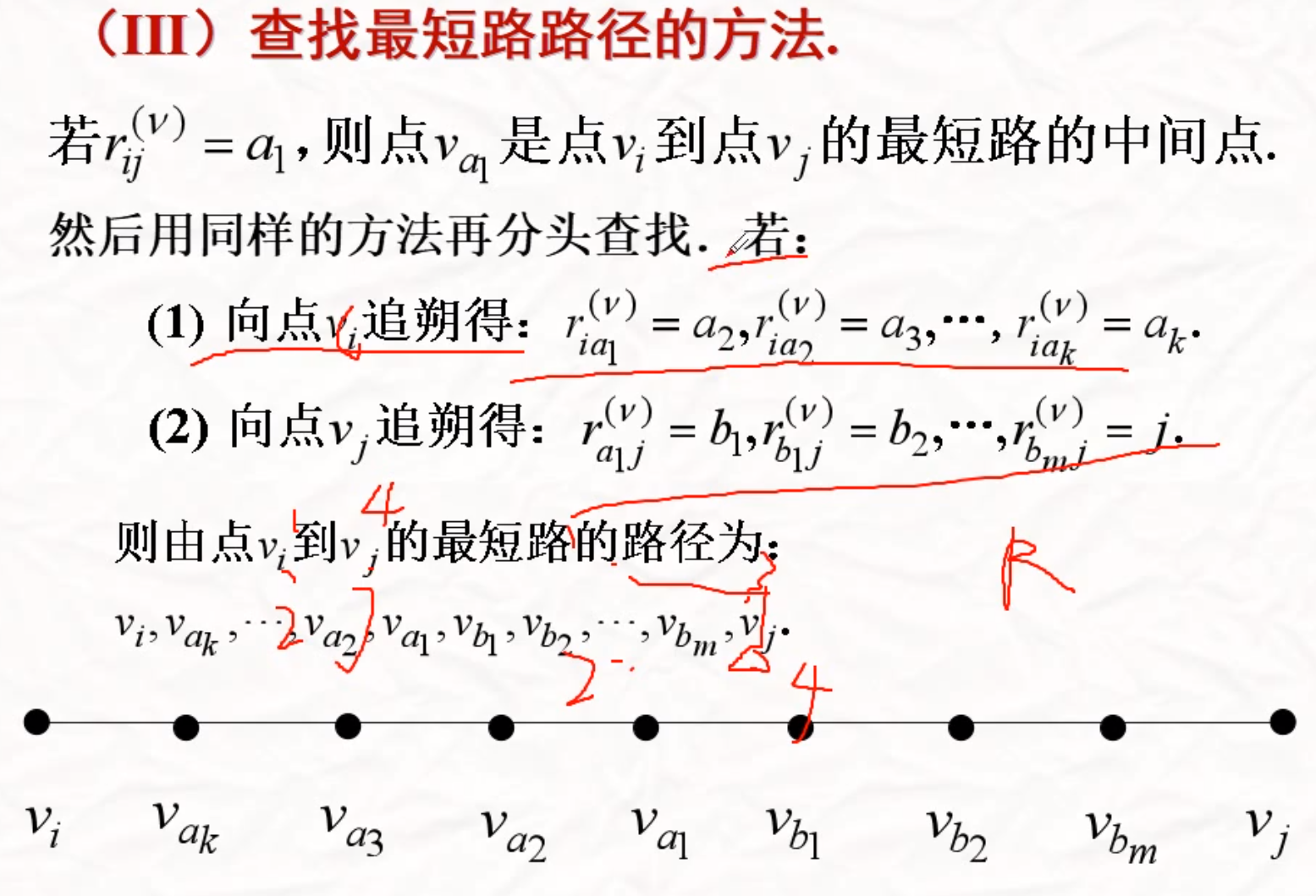

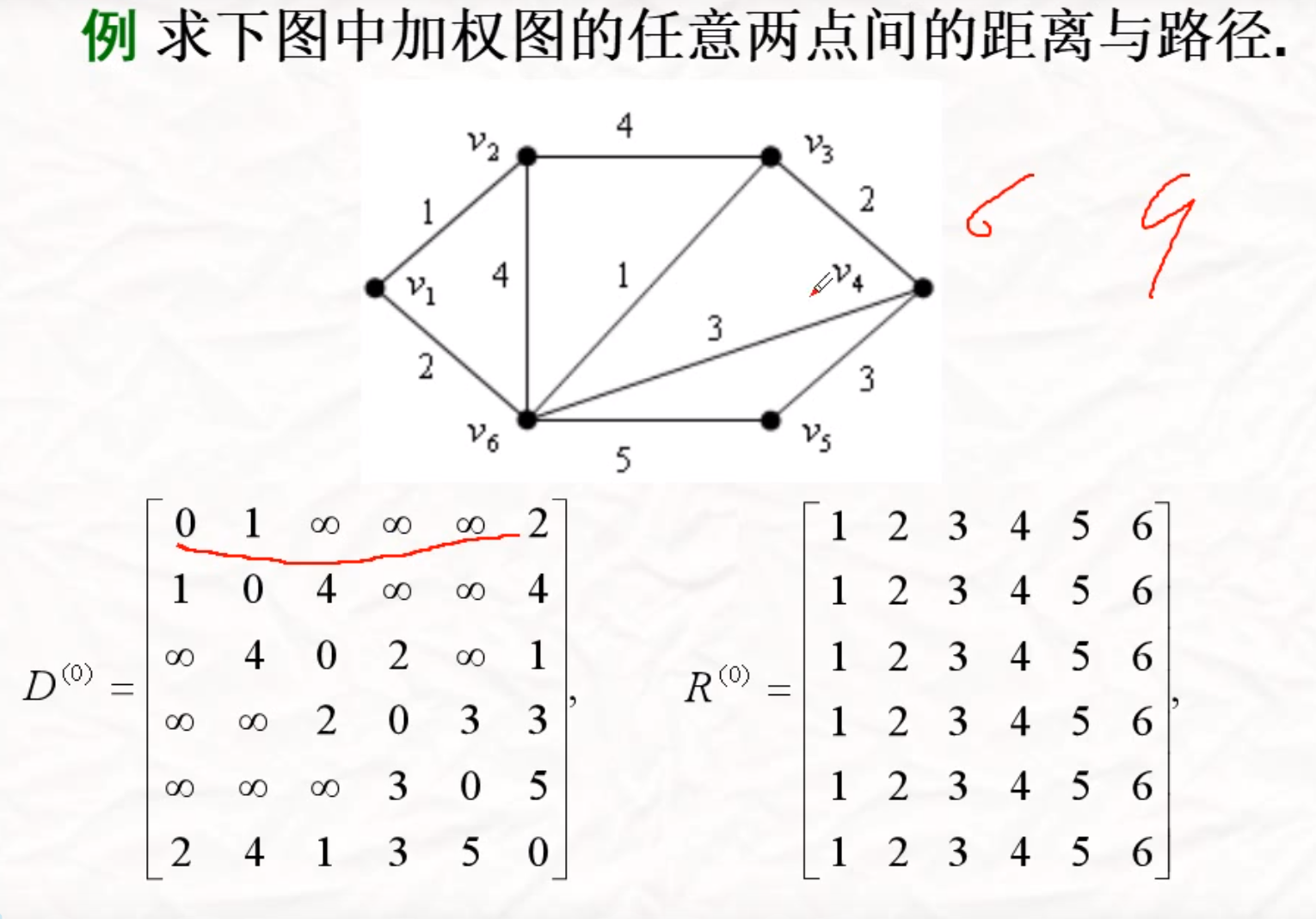
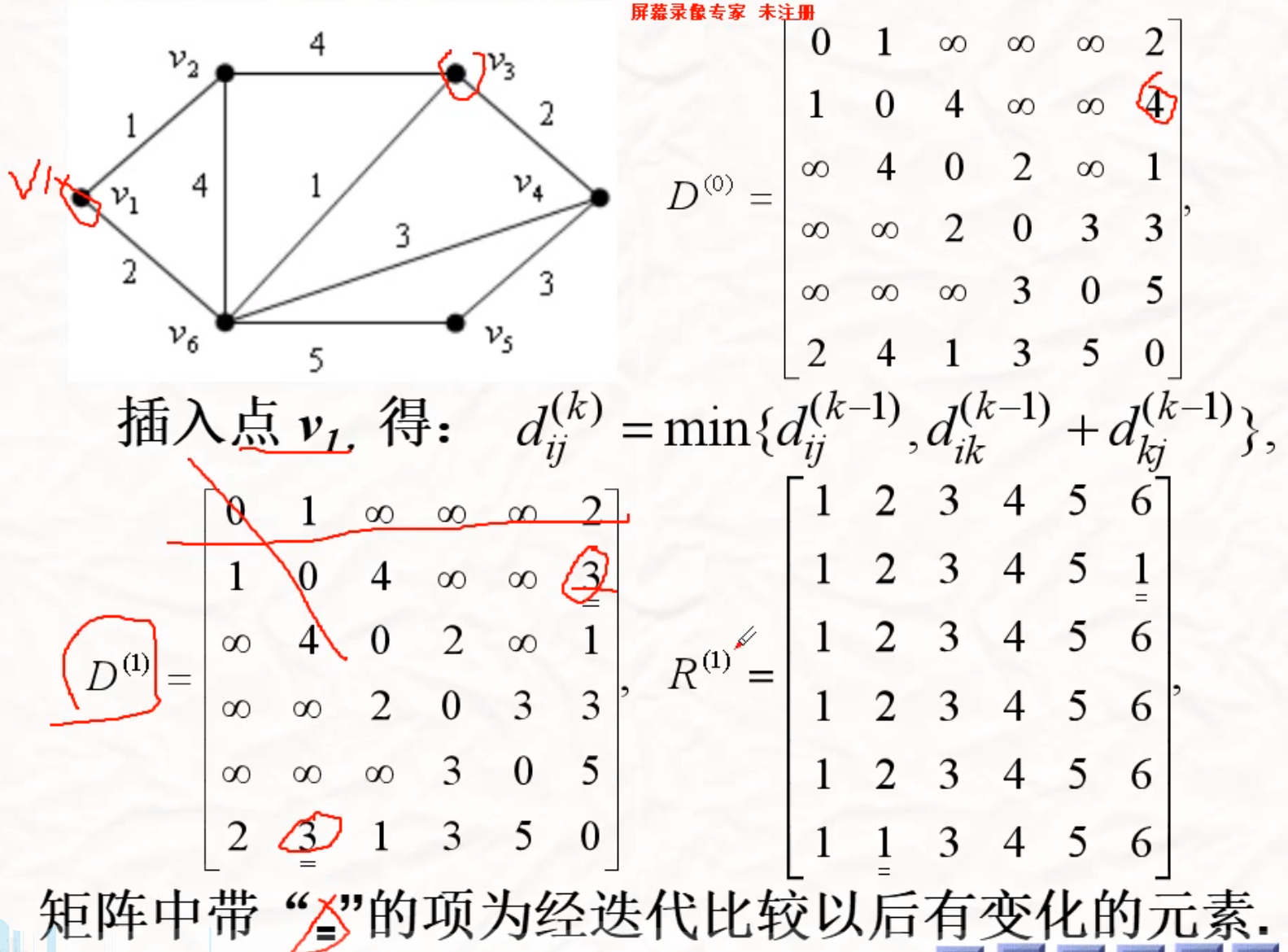
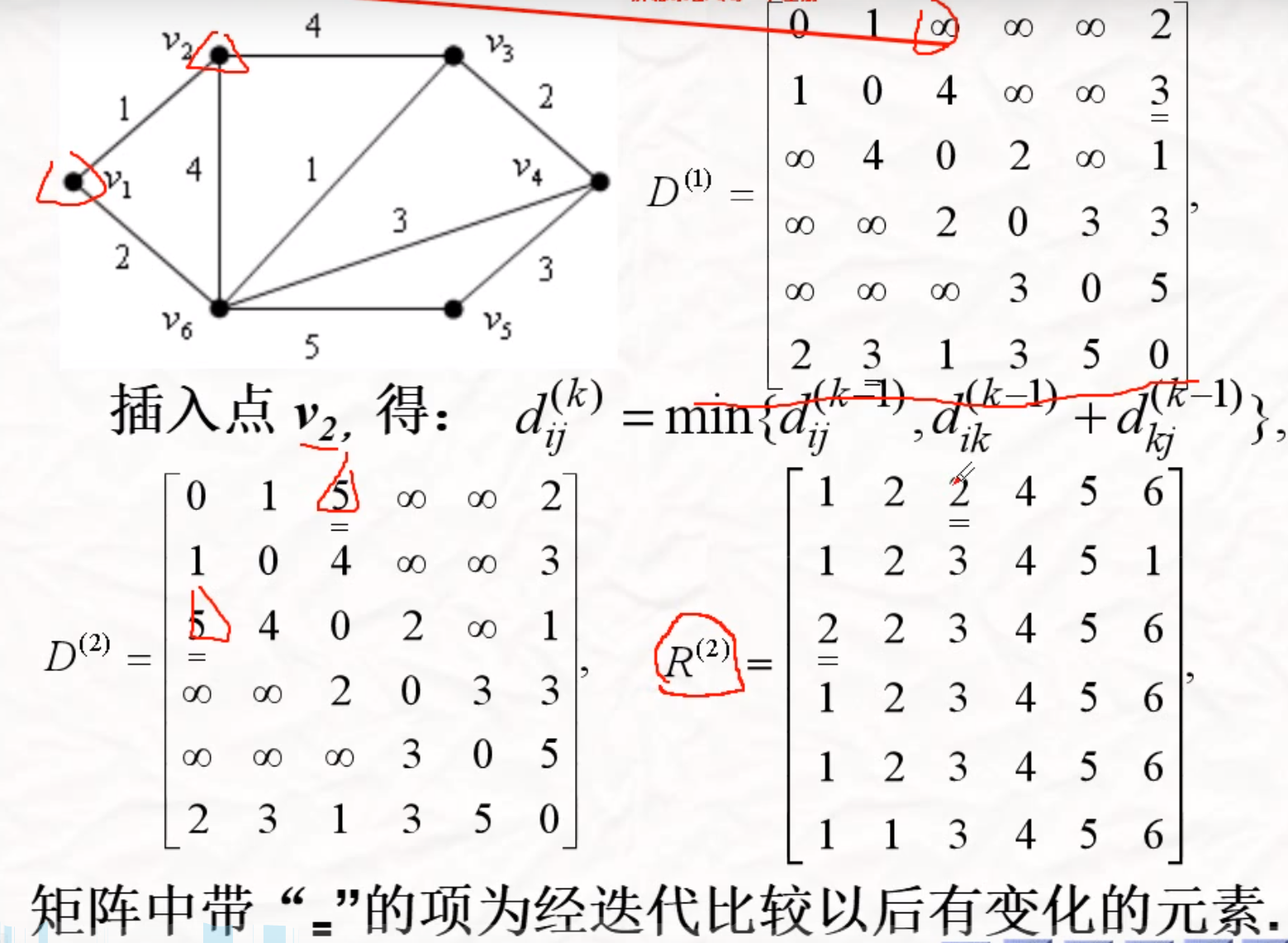

…………..

最小生成树
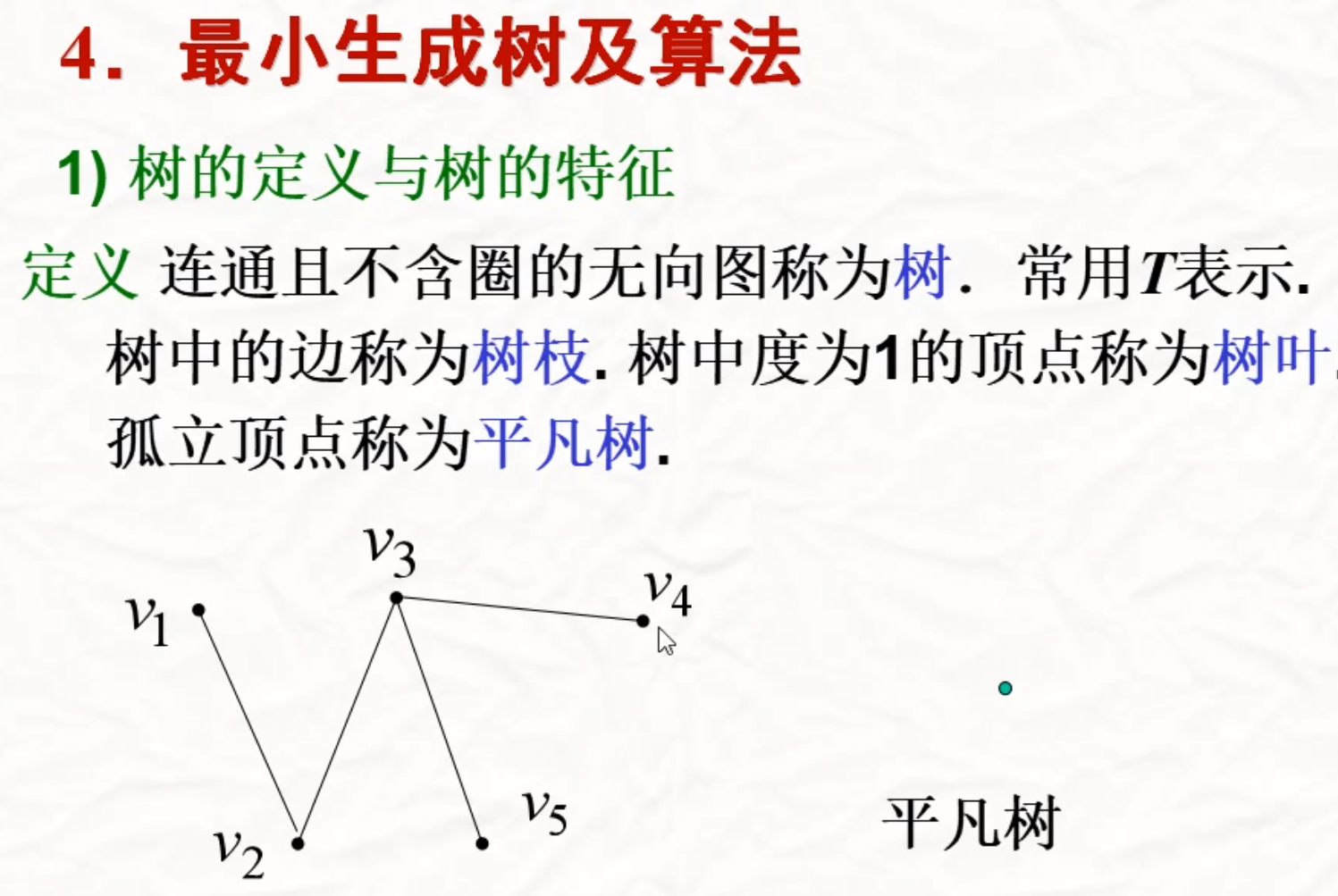



剩下的就=-=数据结构在说la
例题

=-=这些就就就
神经网络
预测–评价–分类
适用于大样本数据不然还不如线性拟合 一般成千上万OK几百的那种就不用了
小样本灰色预测
基本原理简介
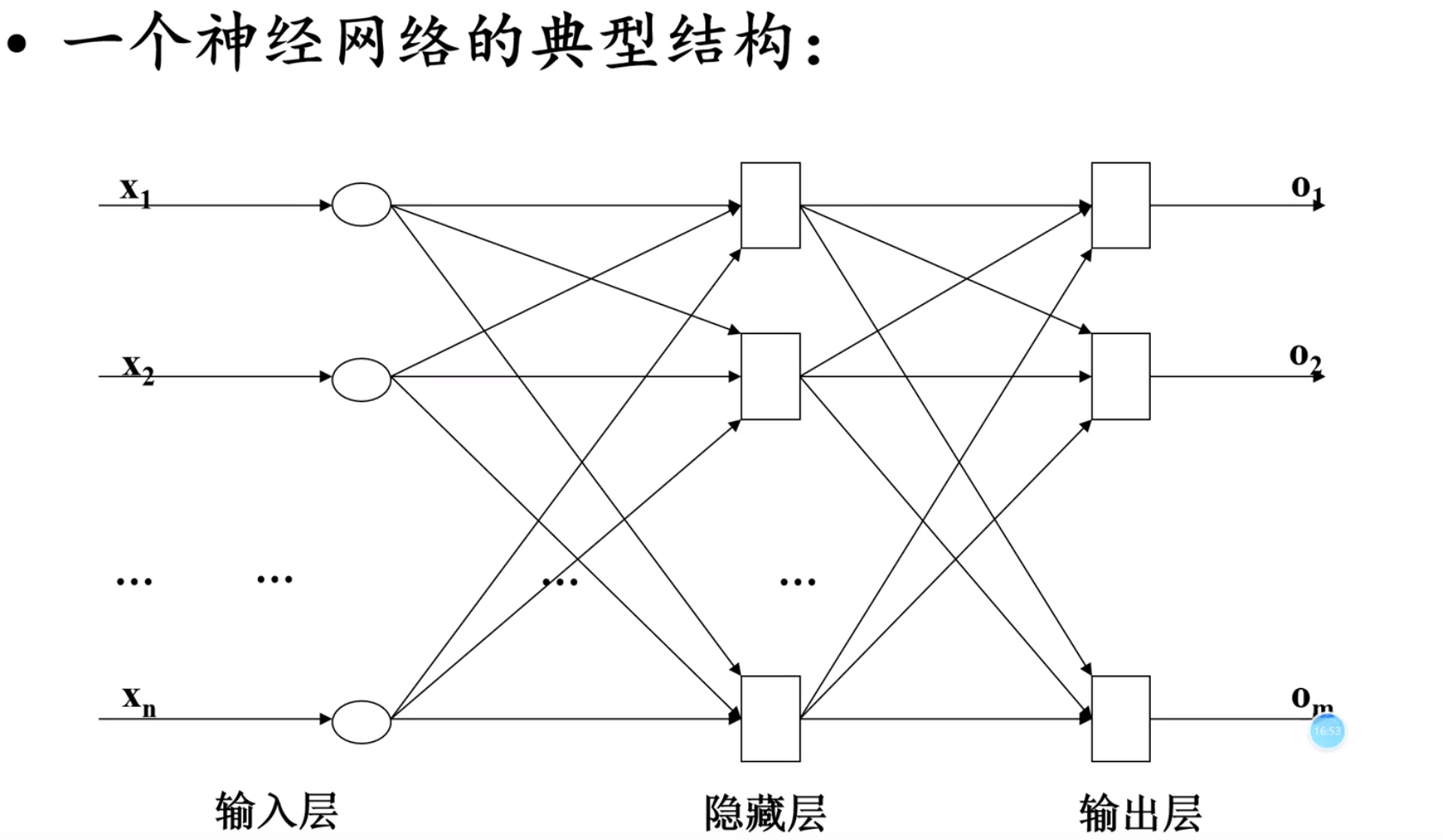

所以现实中发现线性结构是很罕见的

建立的步骤

神经元
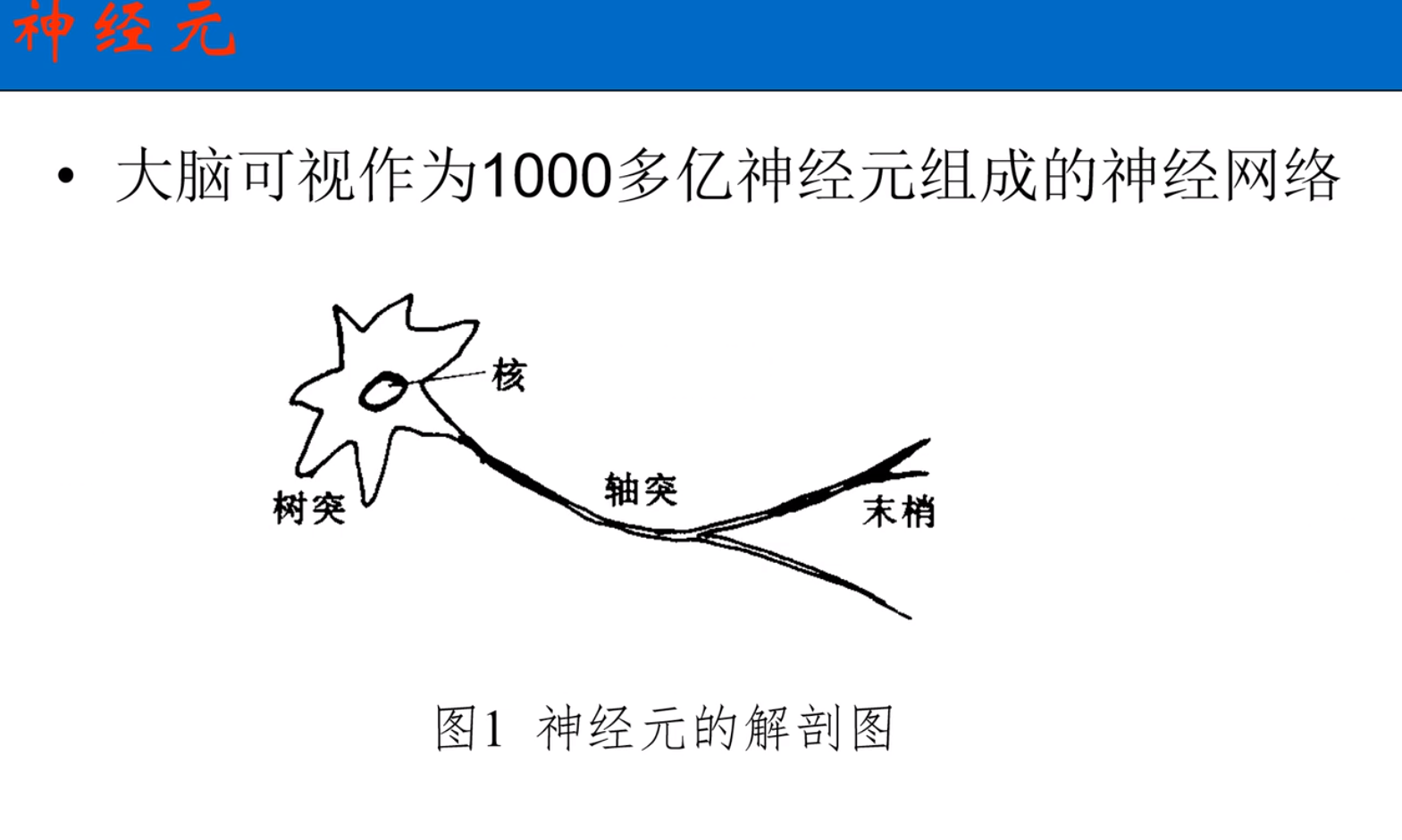
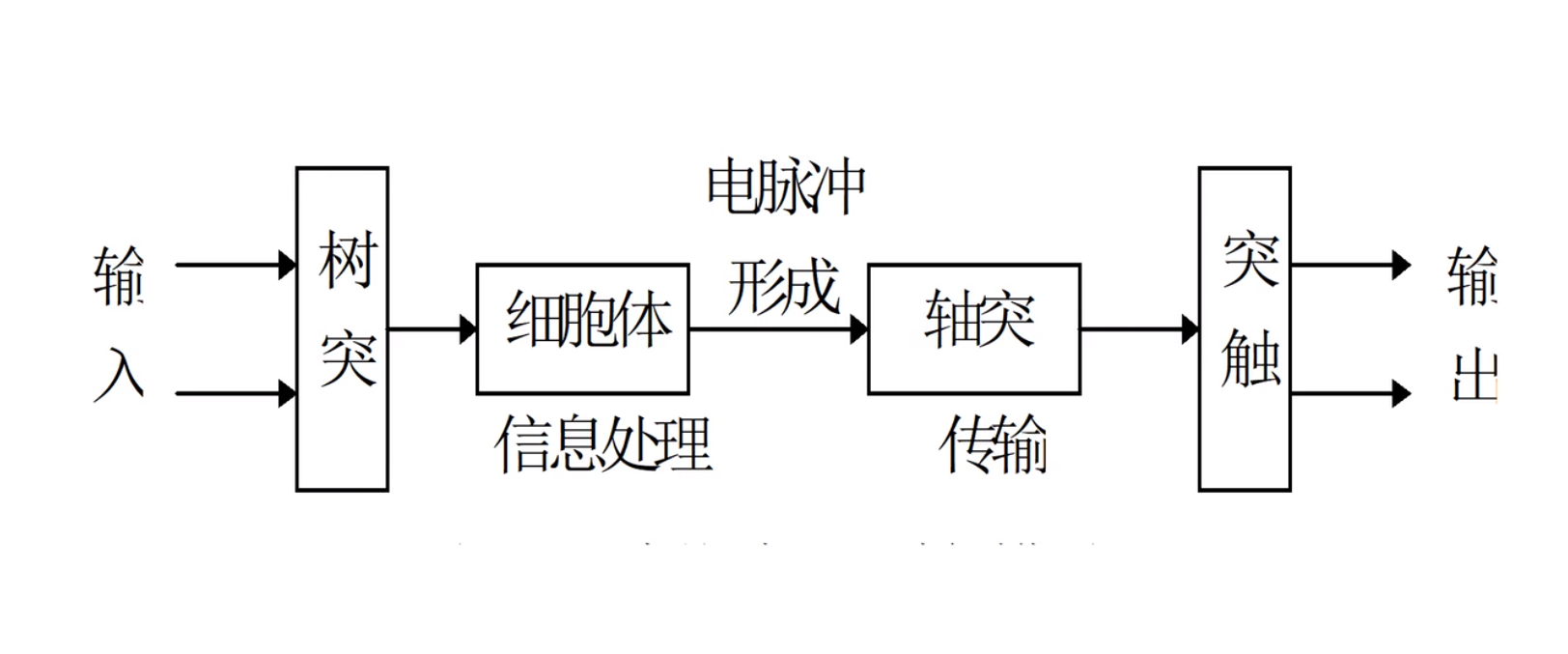

多种输入单输出
神经元模型
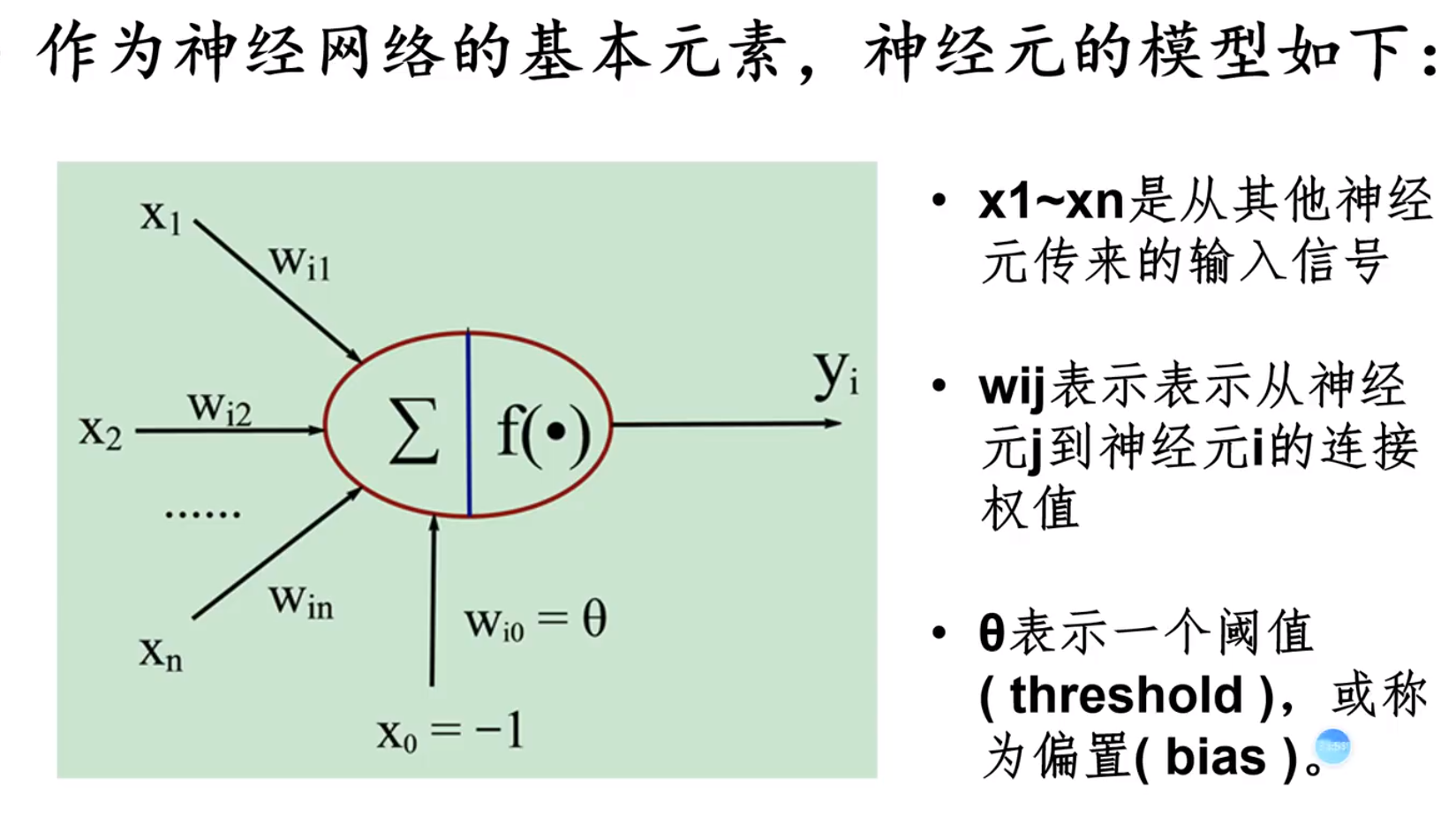
阈值:给出的,能够让我们的大脑产生最低的刺激的一个值

离散数据net不可导,用激活函数变连续,就可以求导了(前提f为连续函数)
激活函数

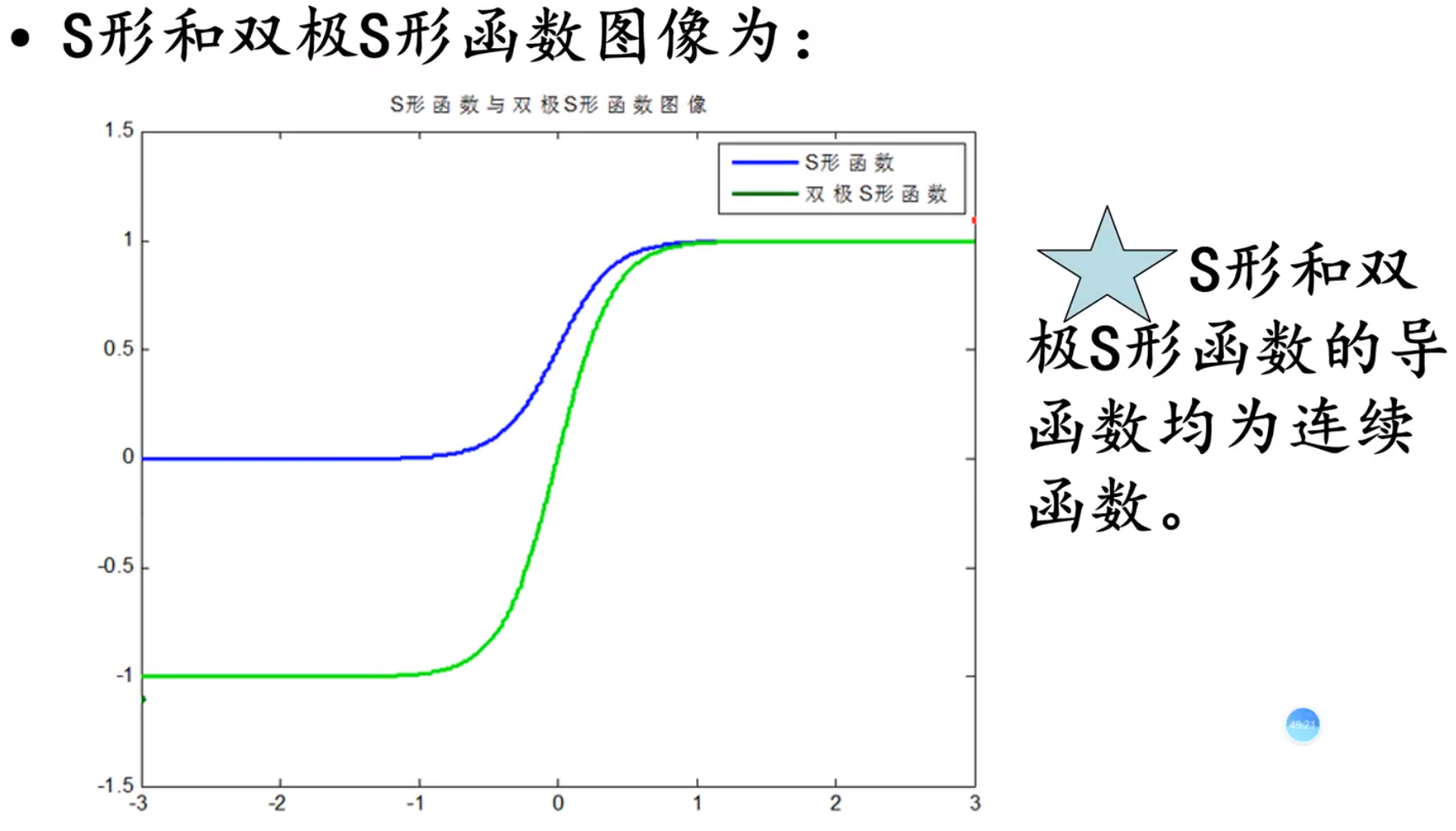
网络模型

自组织:产生混乱 前馈:只顾着冲,不知道回头
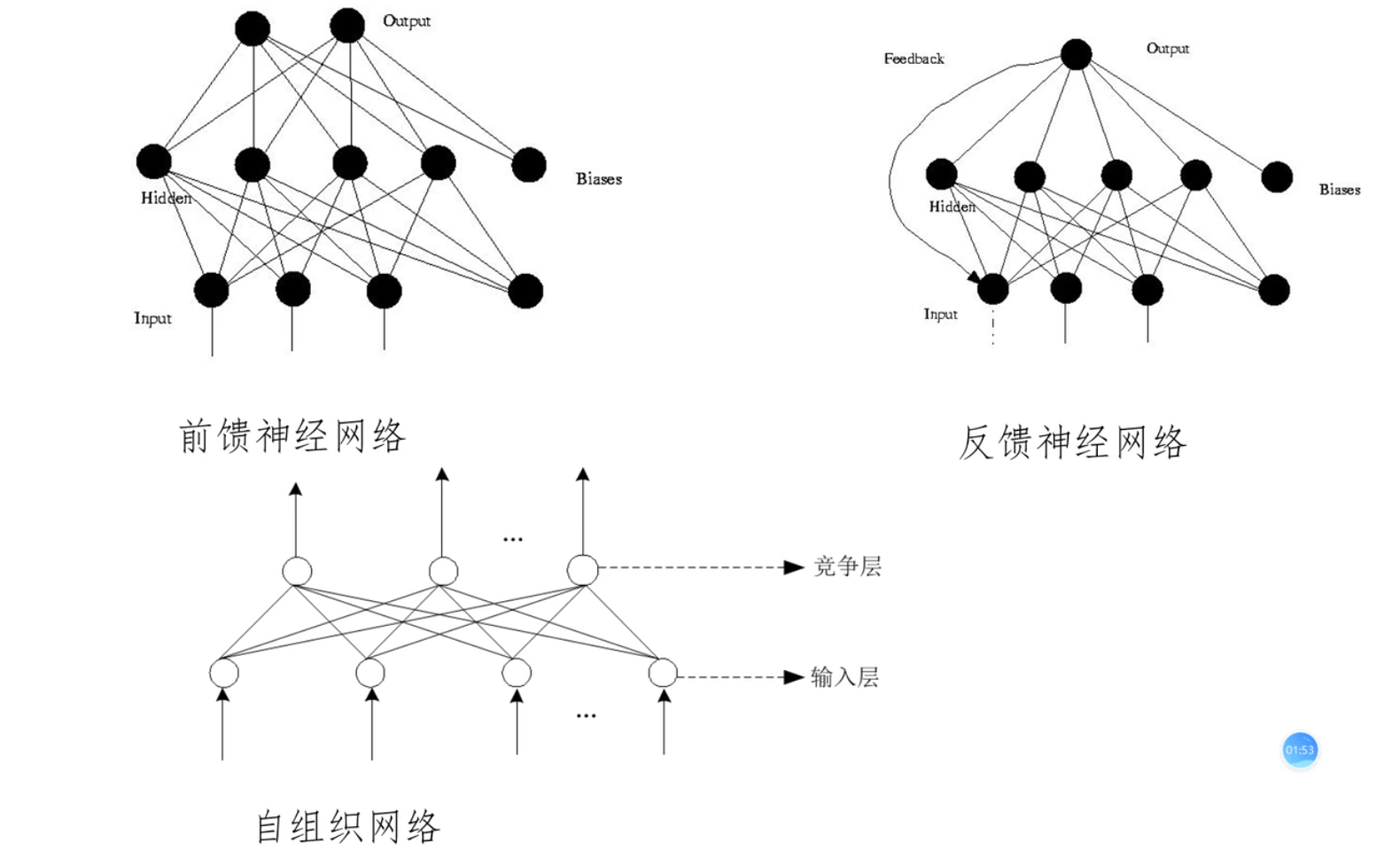
工作状态

学习方式

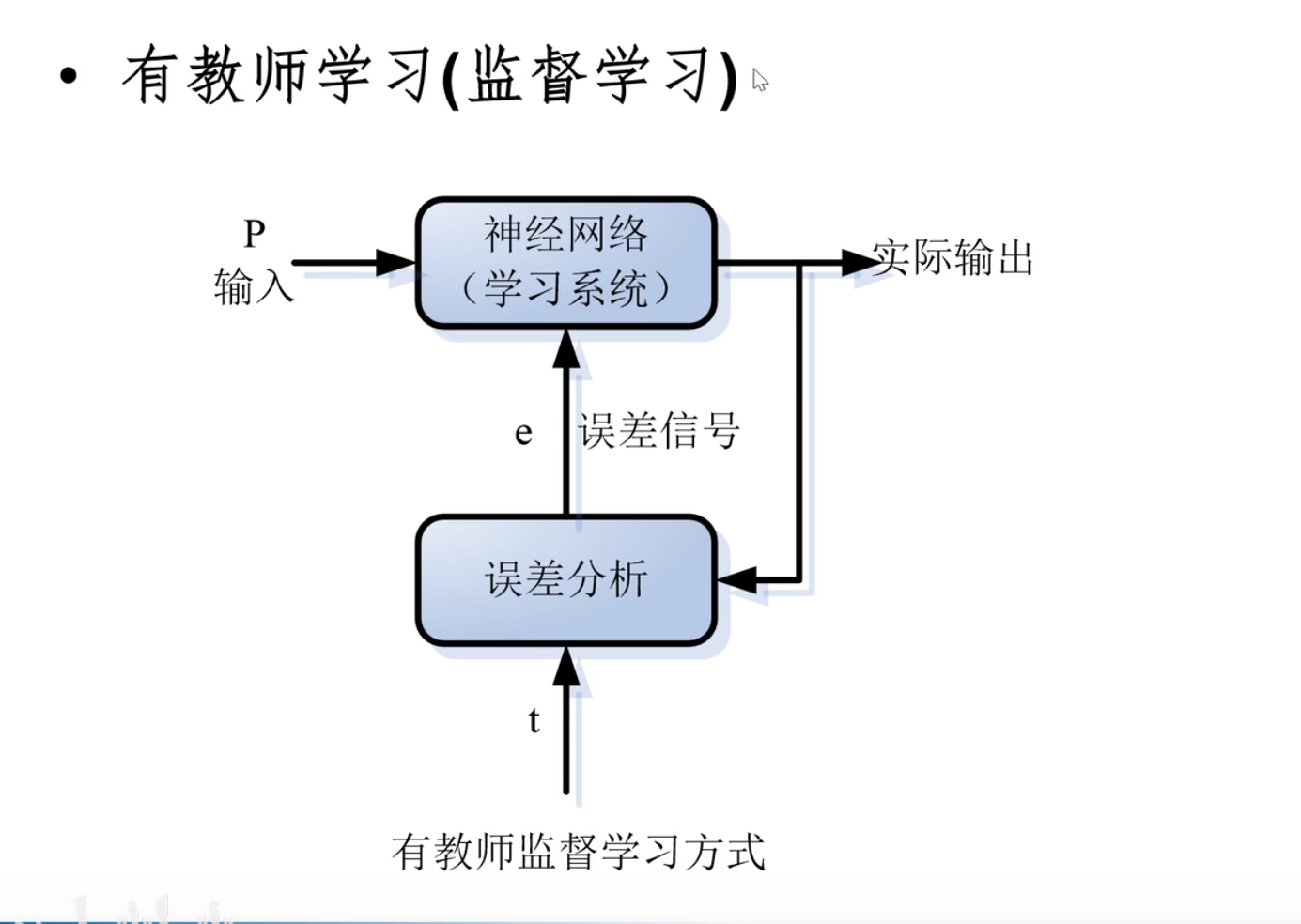
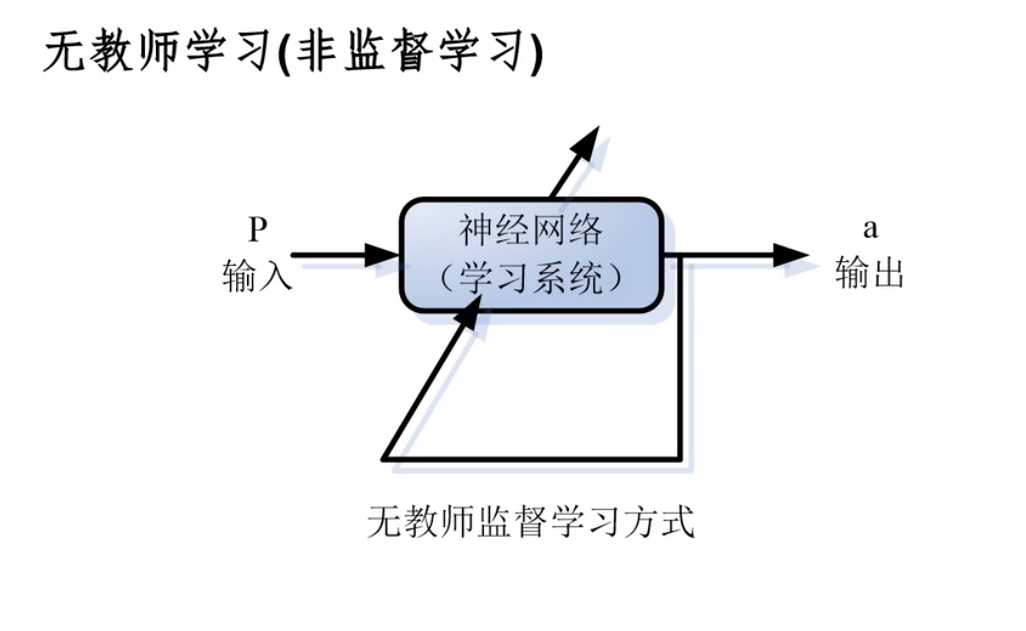
BP
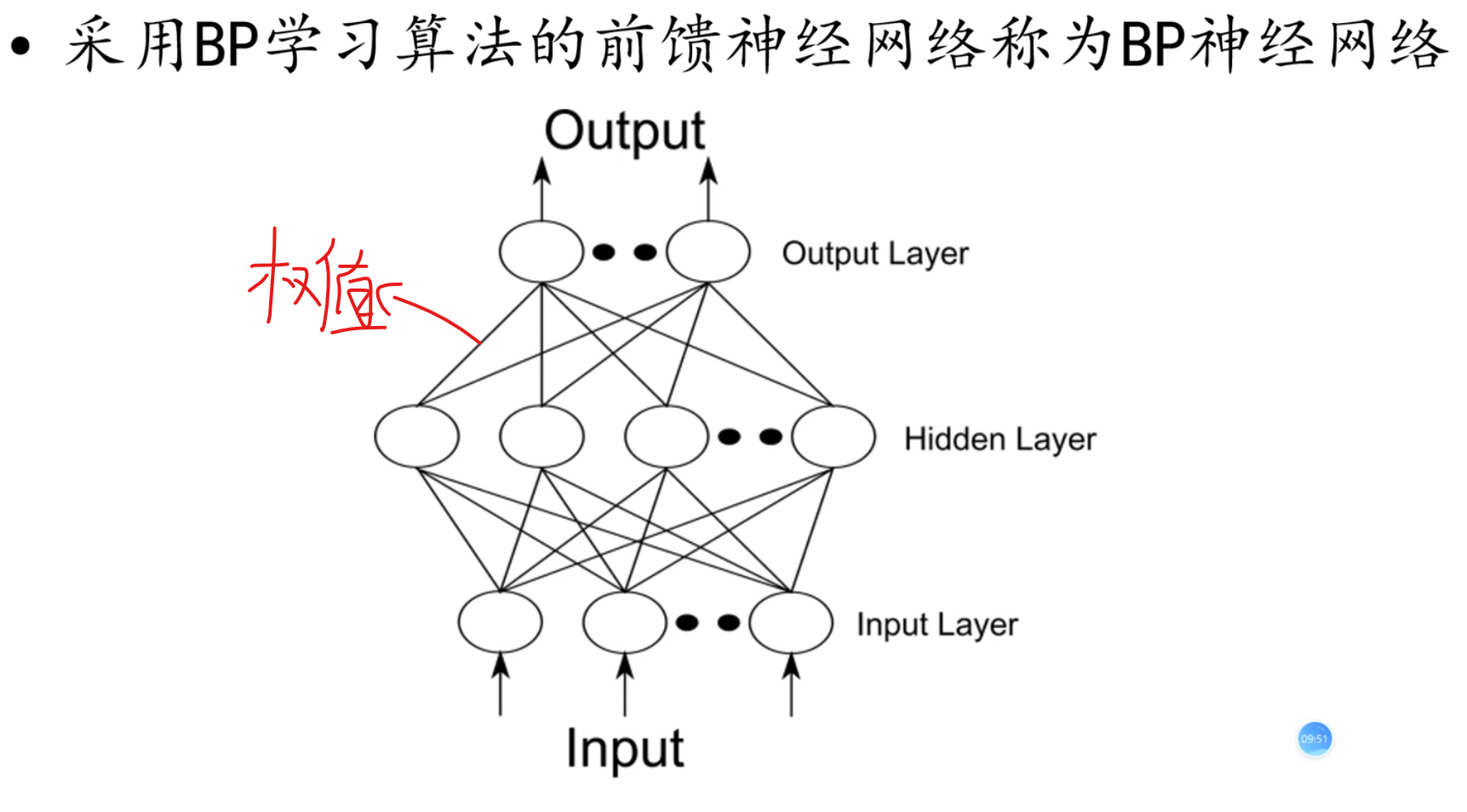

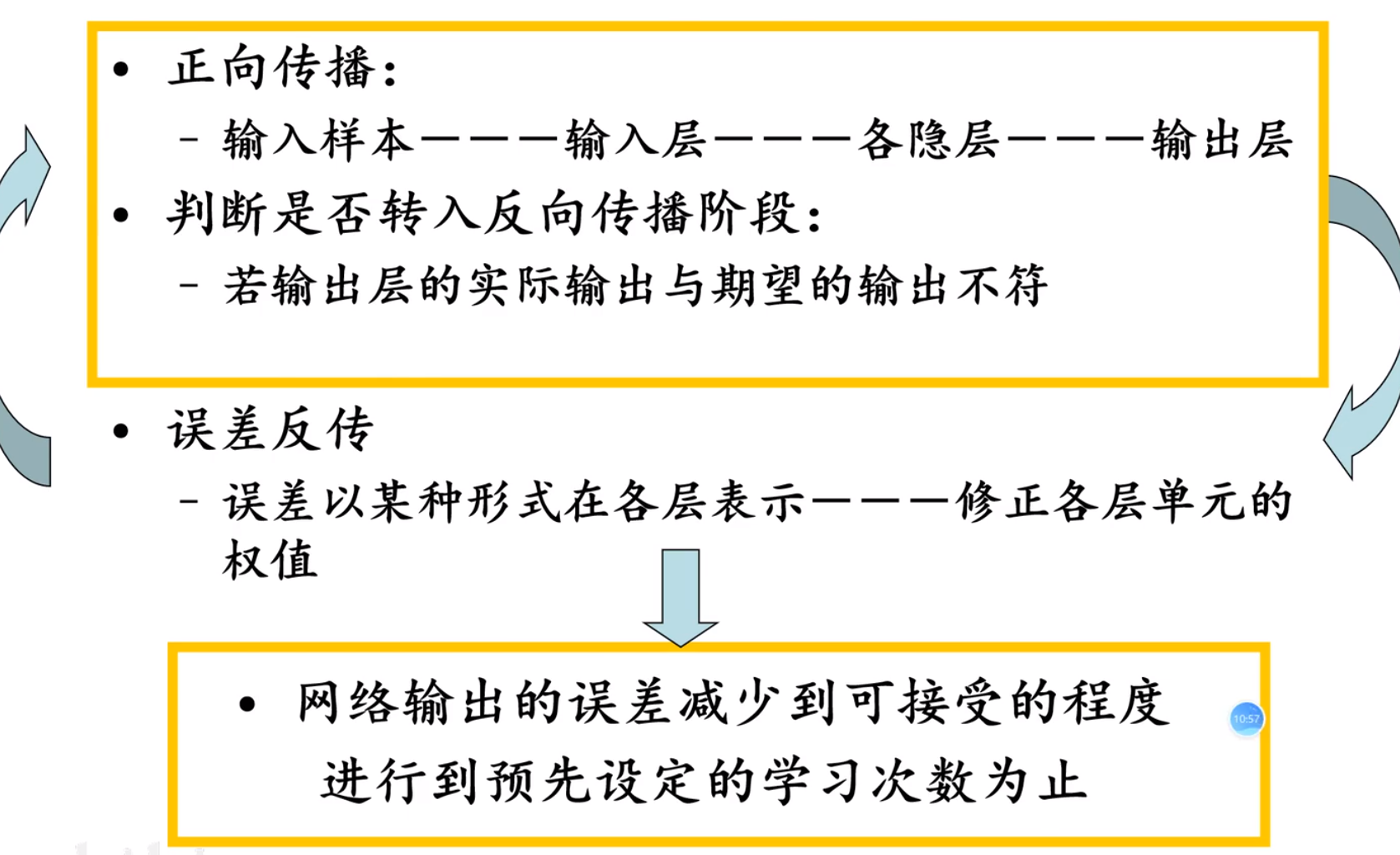


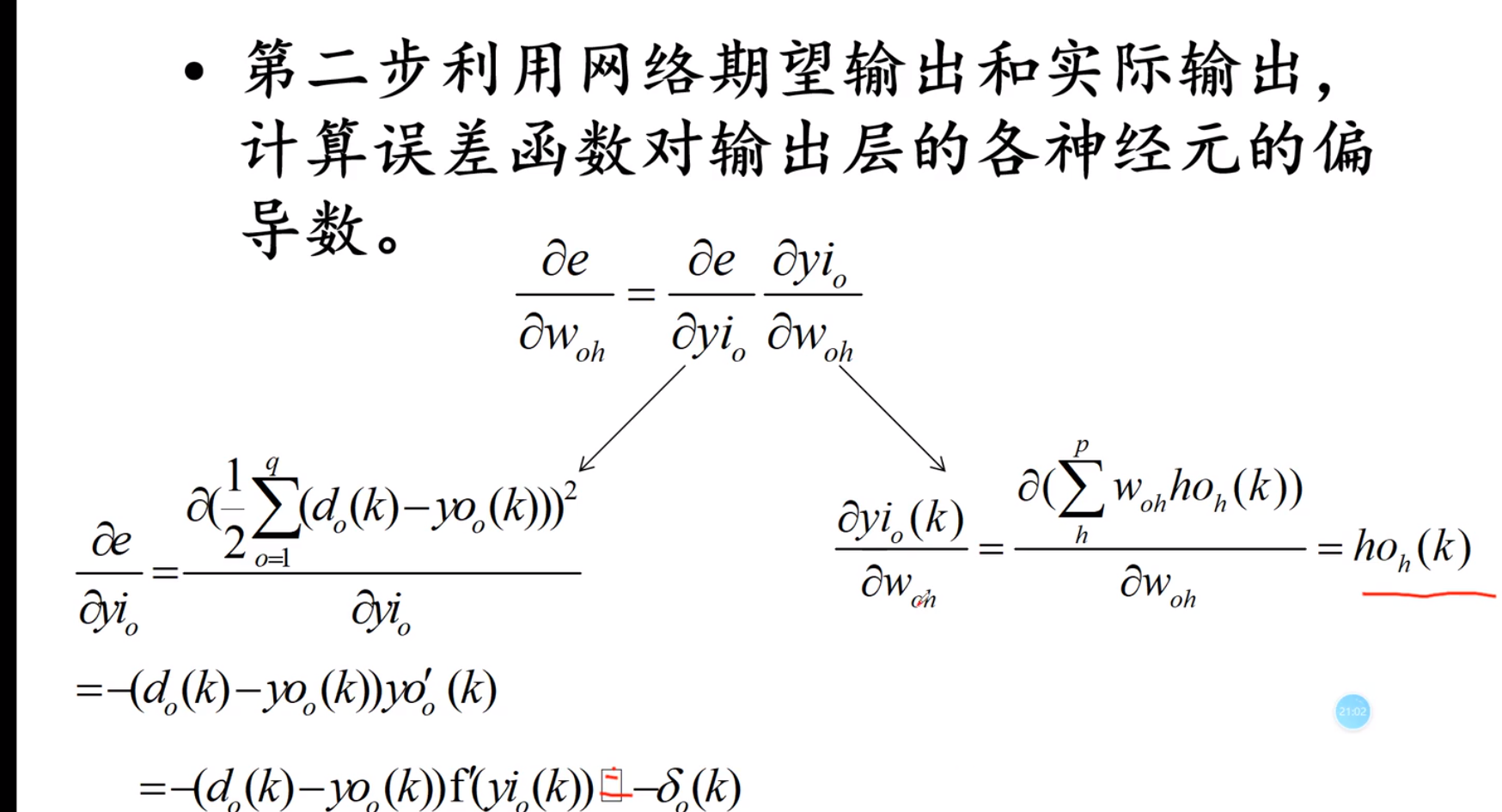

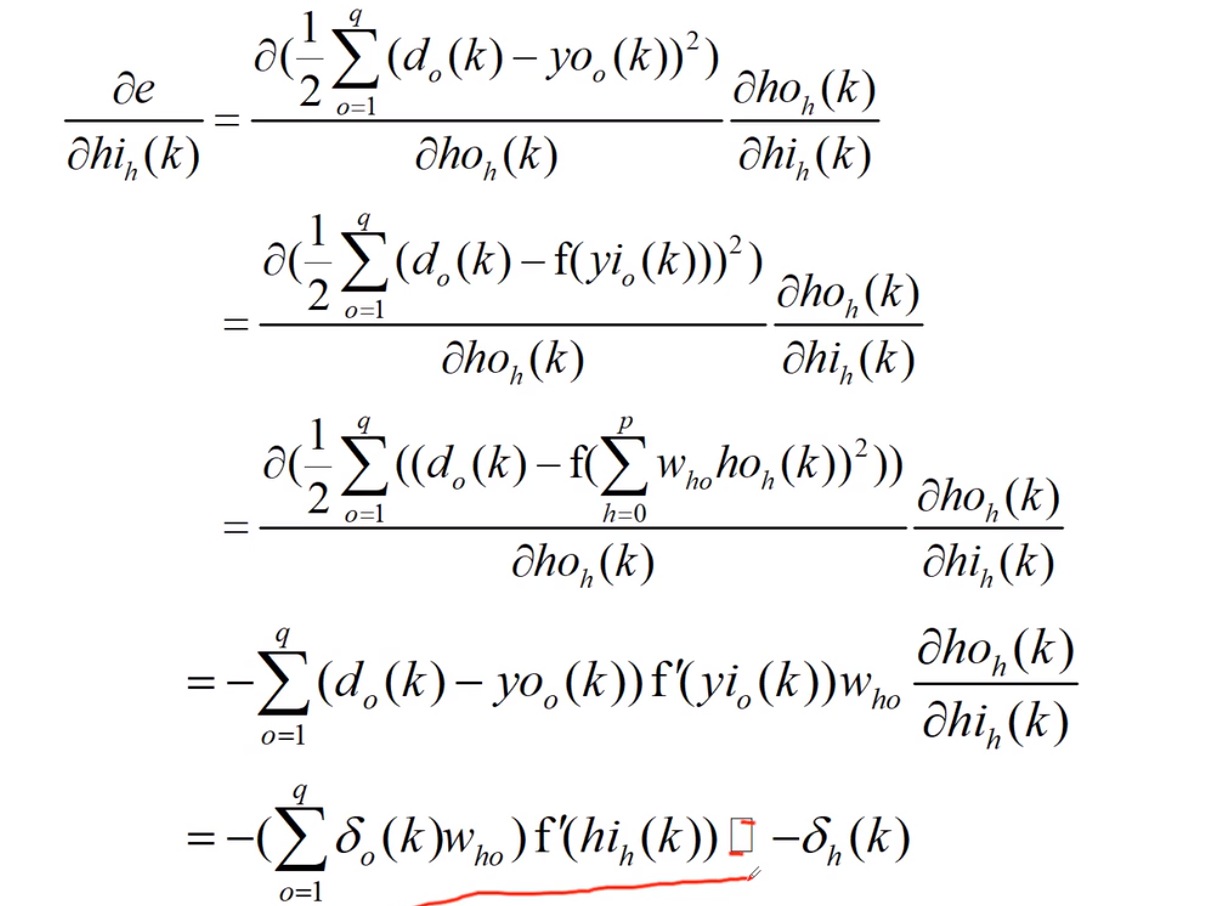


神经网络的应用

引例
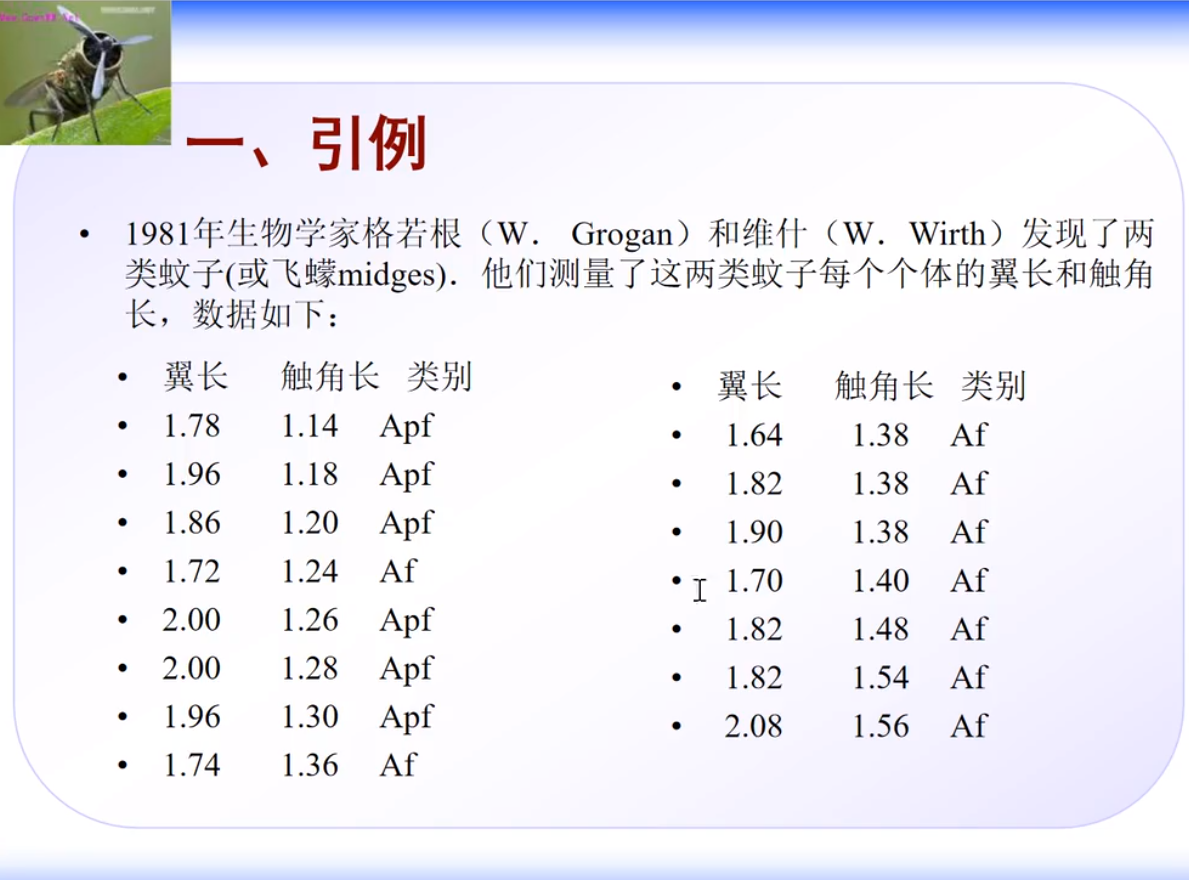
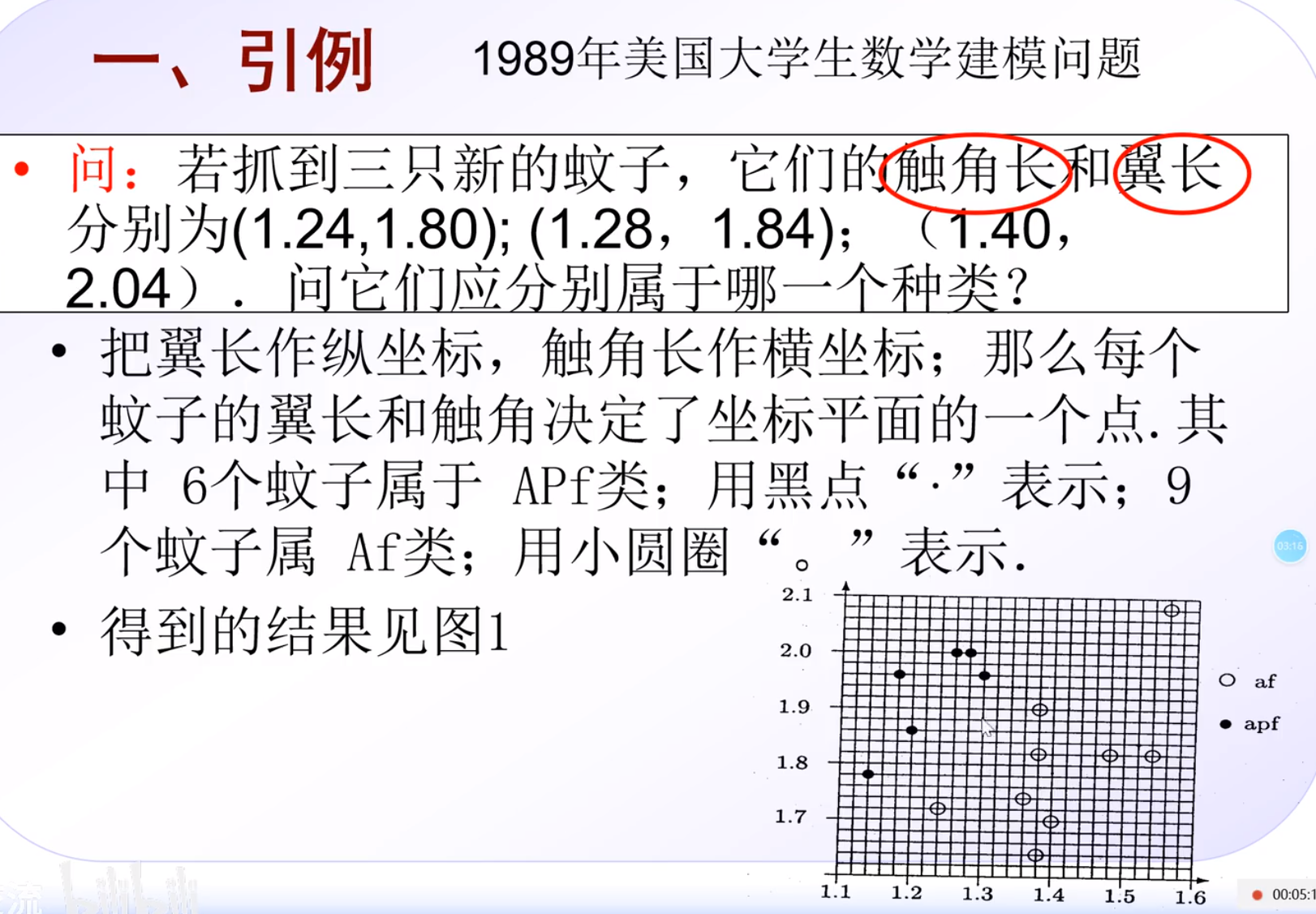
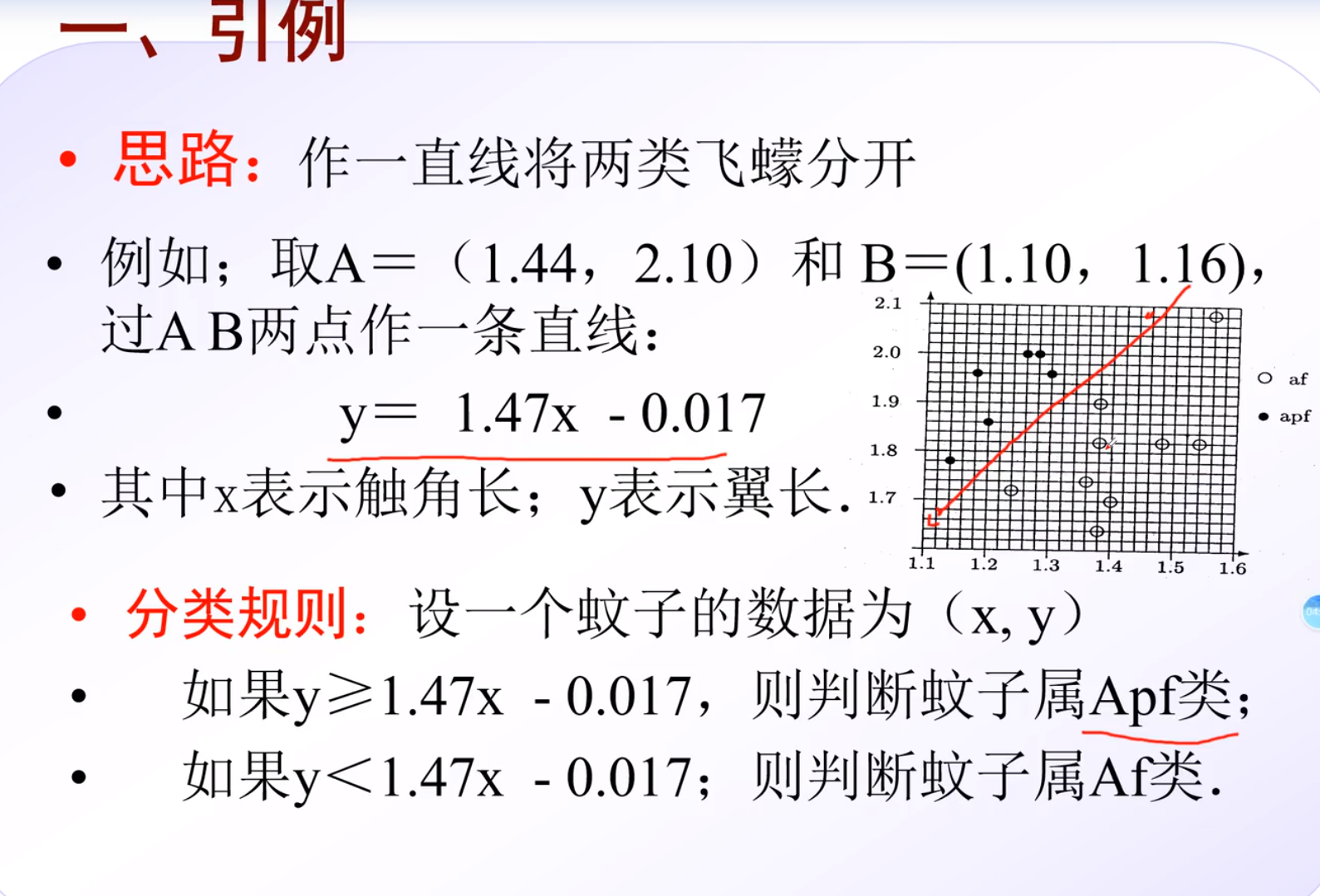
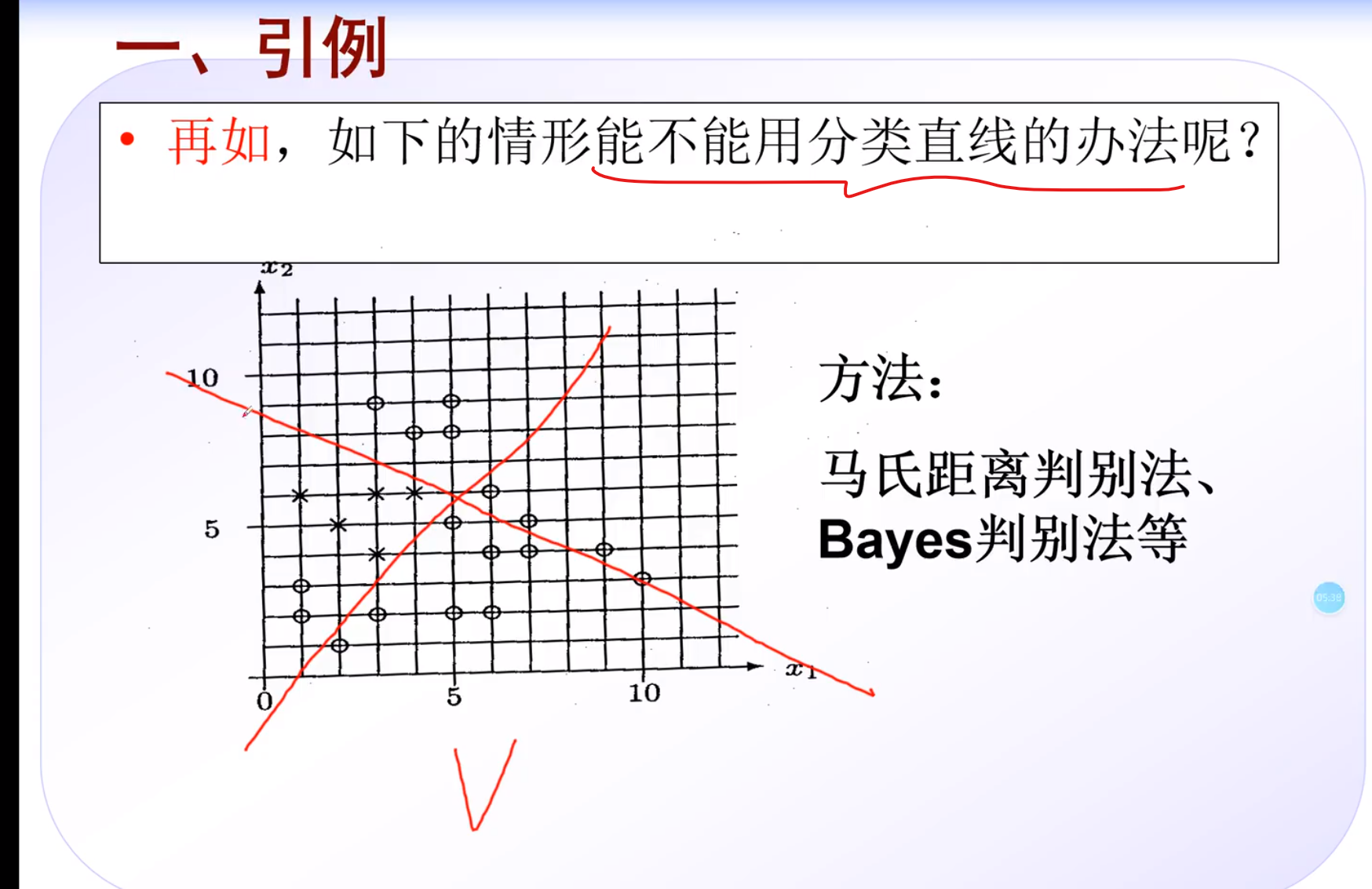

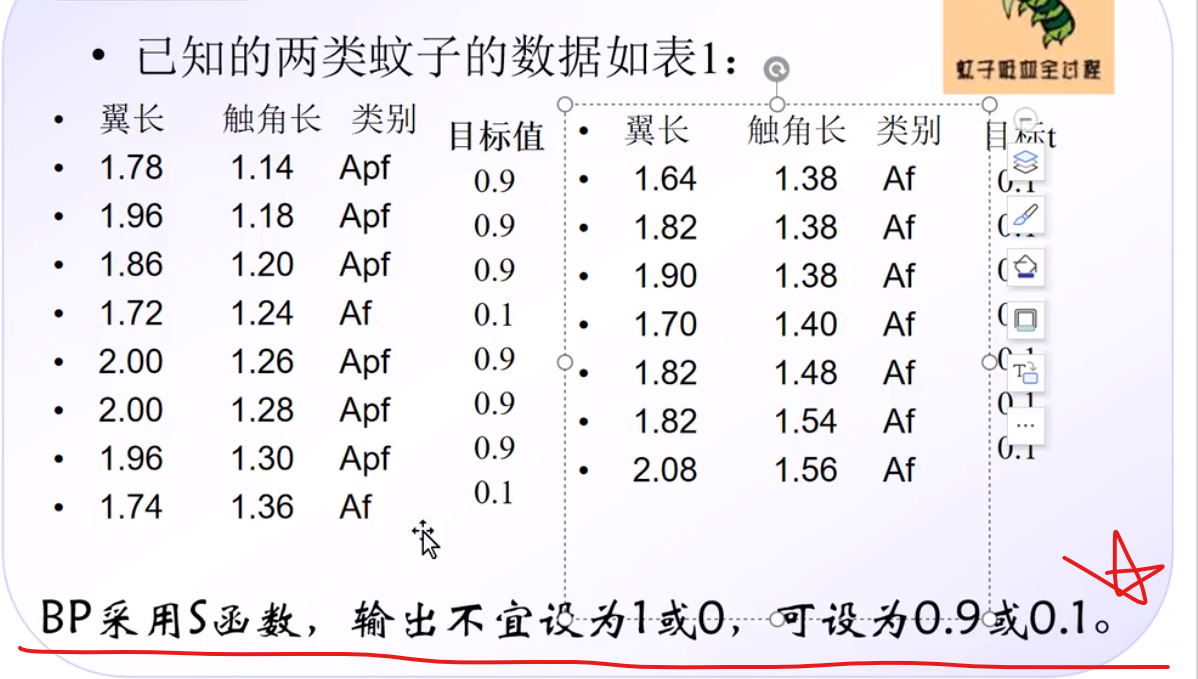
编程实战
分类

PR是这一层数据的范围-1到2 和0-5
输出层小的时候隐层可以稍微大一点,这样精确,隐层越大,算的越复杂
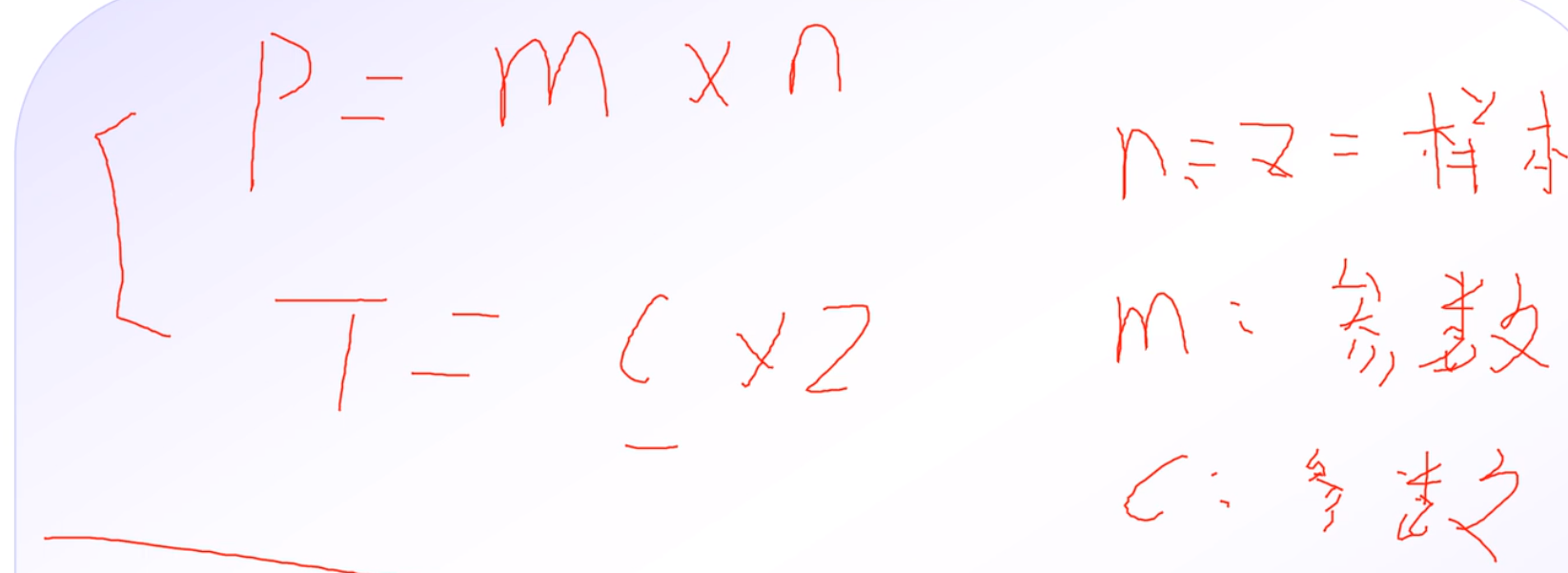

50哪里代表每次循环五十步,以五十步作为输出
500代表来回调整,一共调整500次
0.01为误差接受范围
train为反复训练
Y = sim(net,p)代表你是为了验证某一个结果,才训练
统计了60名同学的语数外成绩,用来评价这个同学成绩是好是坏
那么n为60 m为语数外 成绩是c
所以P = 3 * 60
T = 1 * 60
预测
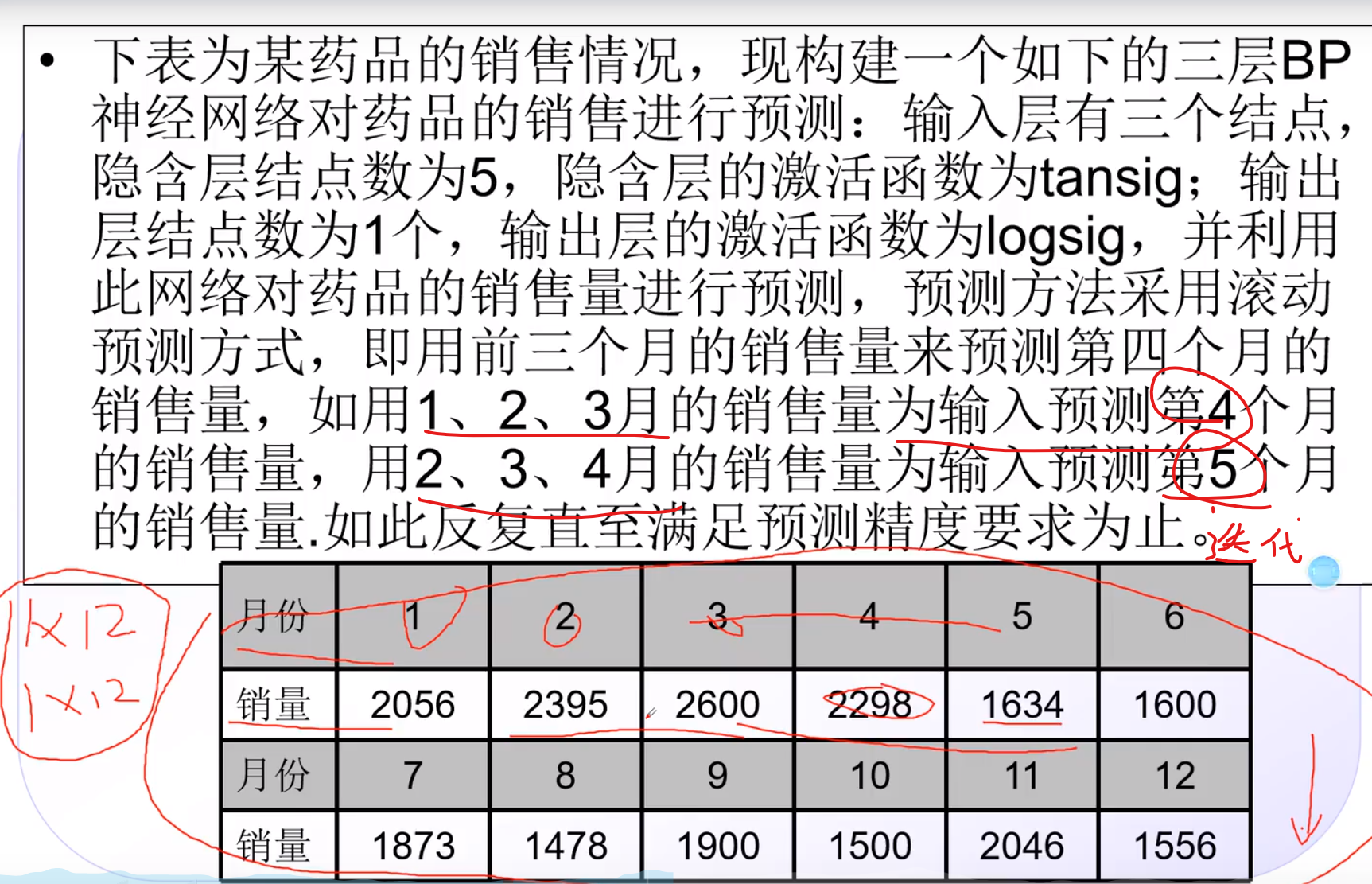
一般大数据进行归一化,变成小数据来处理

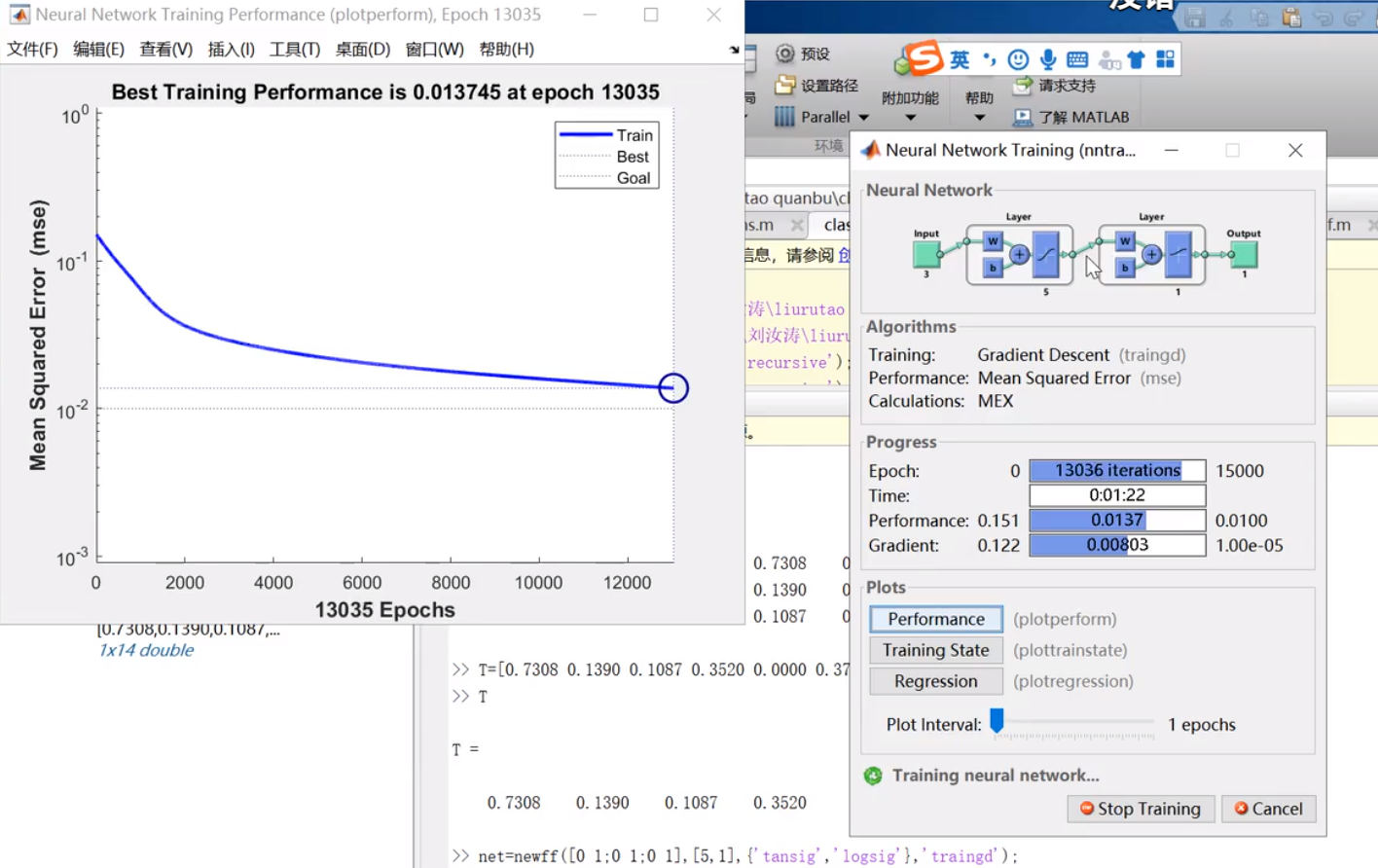
训练过程 右界面输入层框框里蓝色的w代表权值,b阈值相加,经过一个激活函数以后在经过隐含层传入到输出层框框,经过输出层的激活函数处理最后输出出去,中间那个绿色的箭头就是隐含层
Epoch代表训练步数 Gradient代表当前训练的误差是多少
左图代表训练误差随着训练步数的一个变化
训练结束需要任意满足达到设定步数,或小于预估误差,即可退出
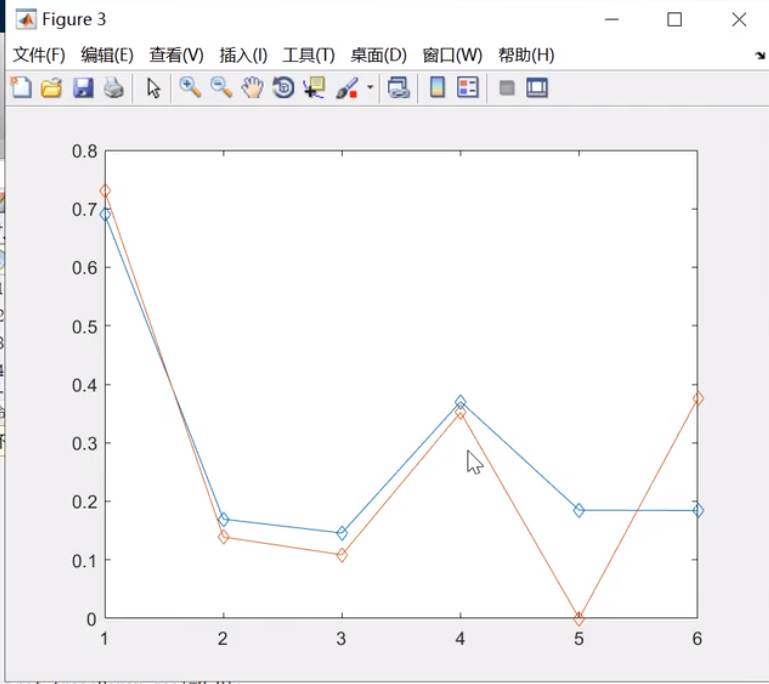
预测的时候带入下一个,然后算就完事了,算出来归一化结果 ,再用公式
(xi - xmin)/(xmax-xmin)= 归一化结果 从而得到XI
这个15000步的预测结果
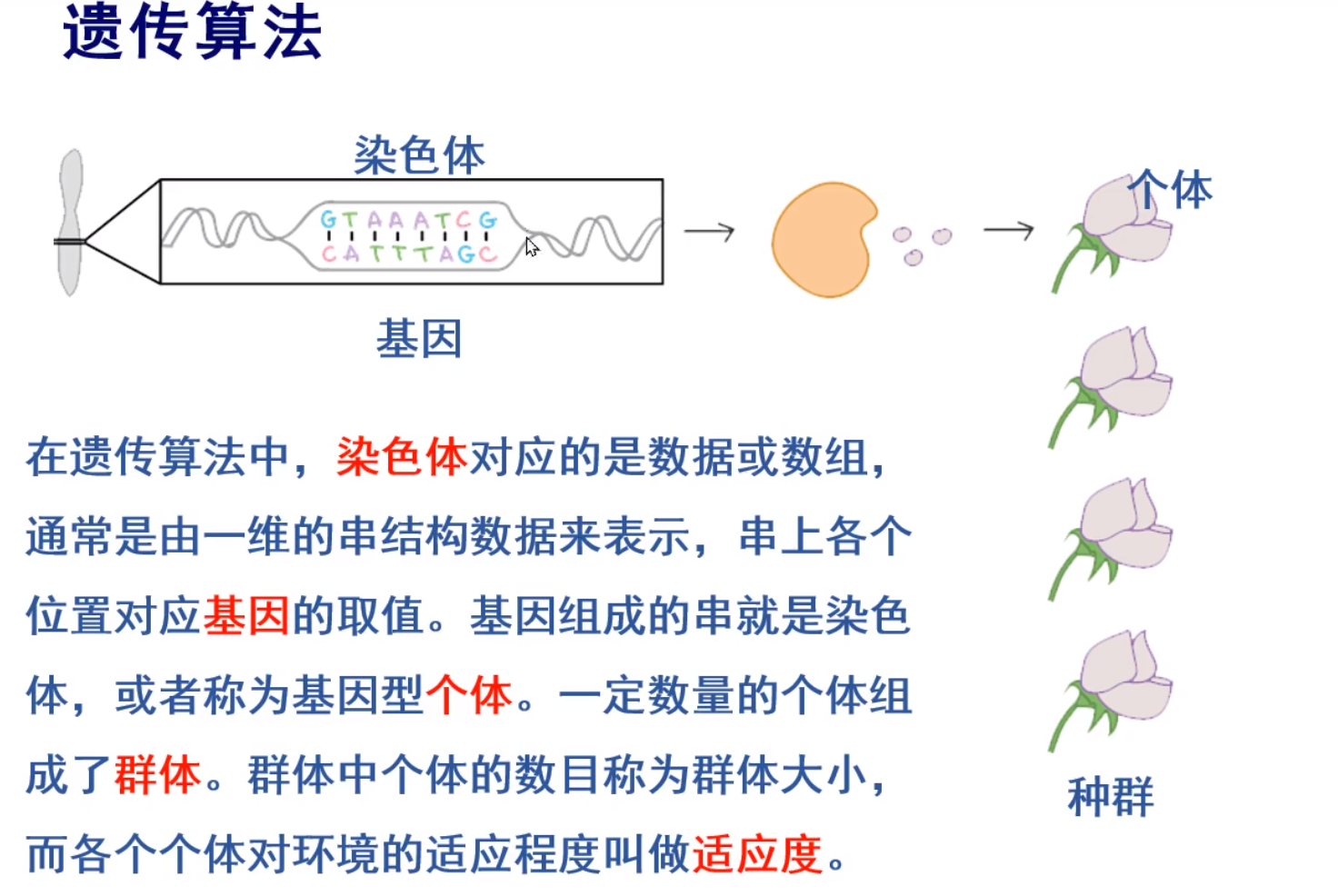
优化-遗传
什么是优化


遗传概念
**不过算出来的也是局部最优解,肯定不一定能找到全局最优解 ** 谁也不知道最好的是多少
算法框架
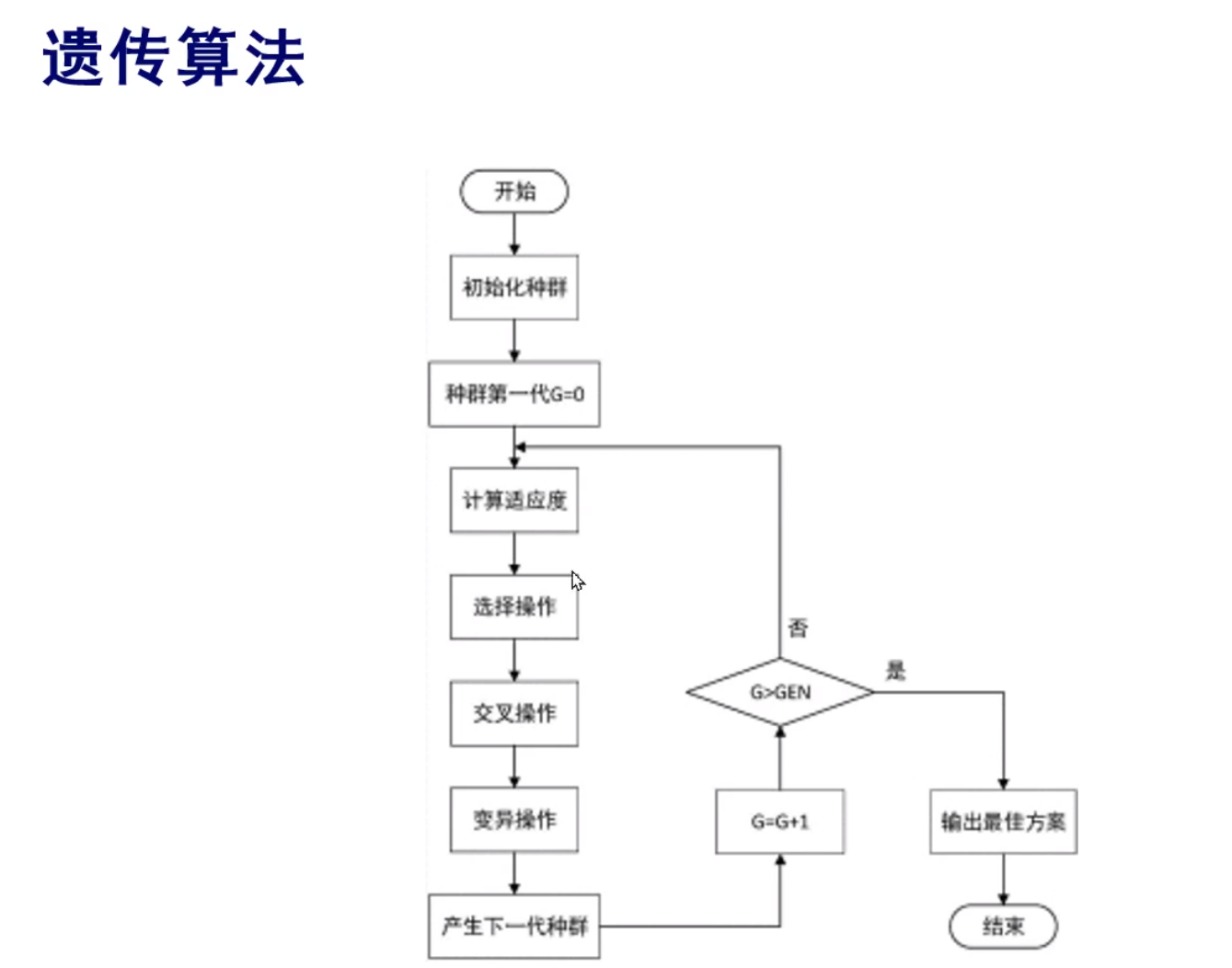
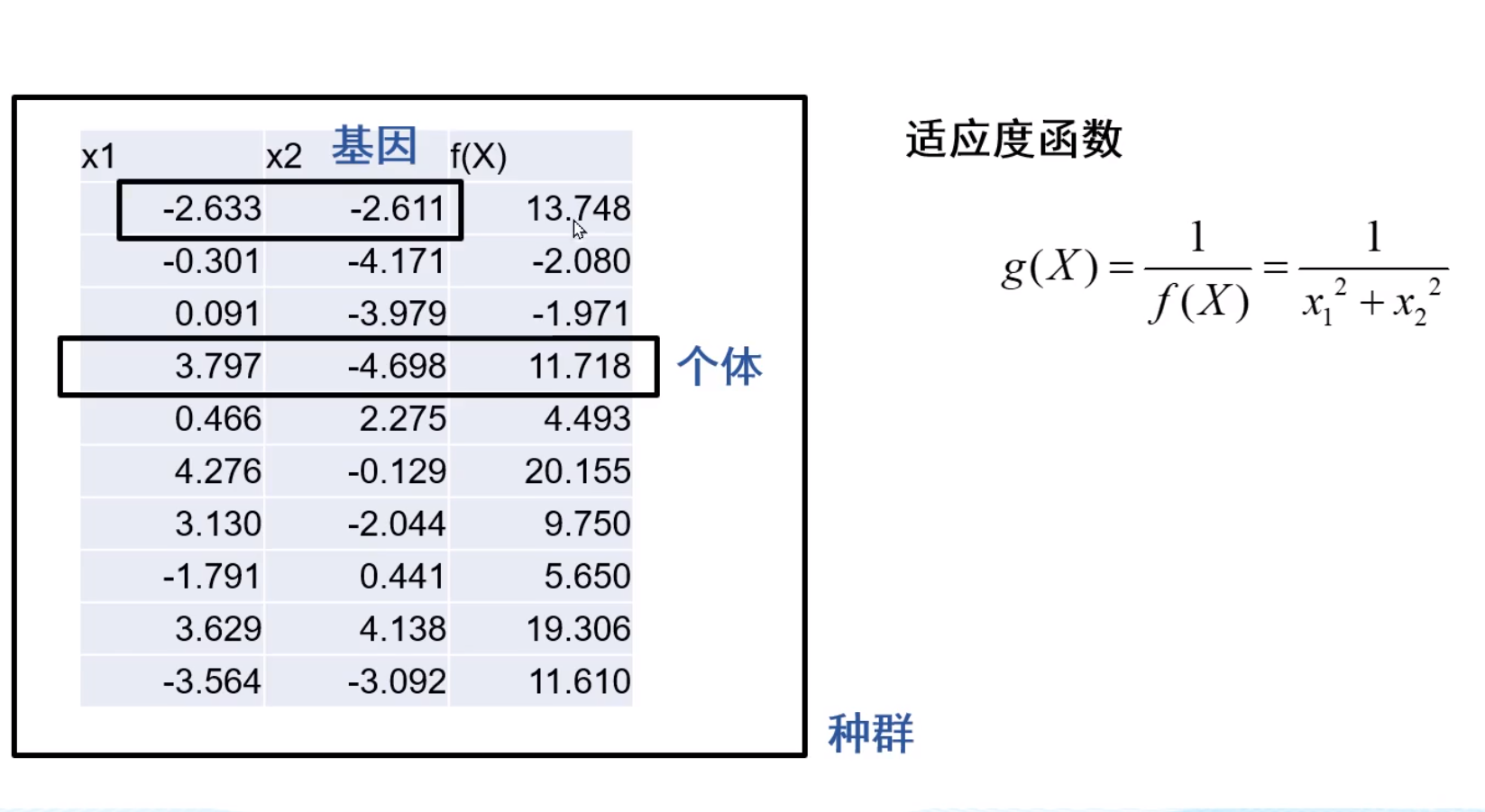
适应度:用于判断他是否活下来 有一个适应度函数计算出,
选择操作: 与活下来的指标相比较,比如适应度前10%的可以活下来
交叉,变异操作:和基因DNA片段的交叉错位和突变对应 相似,但不一致
选,交叉,变异为算法核心
G:迭代次数 generation GEN就是为了限制,不能让他一直执行下去,不一定有结果

选择操作

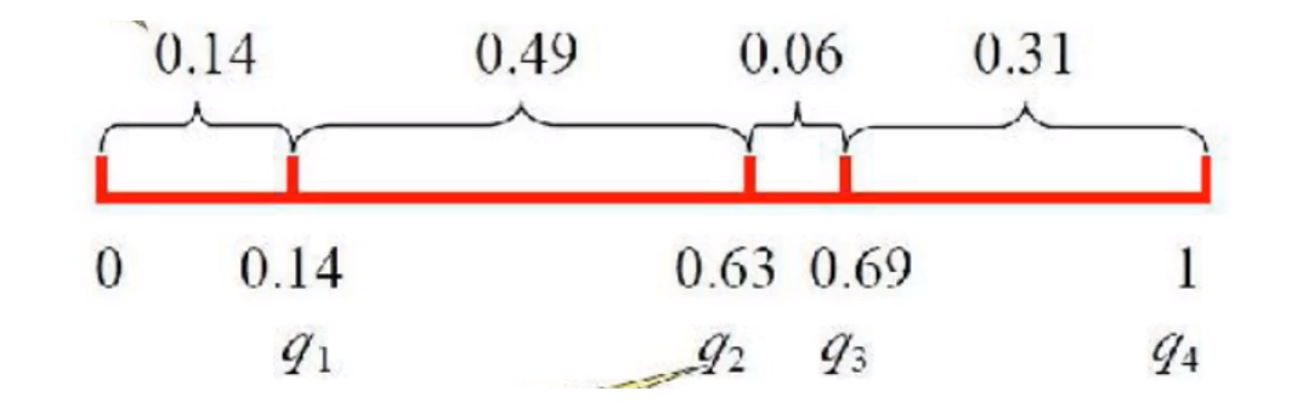
交换操作

若b等于1,意思也就是将两个染色体交换,0则是不交换
变异操作
变异方式有很多,不用纠结与下面这一种

aij:第i个个体的第j个位点
直接取得随机数也是可以的
取最大值
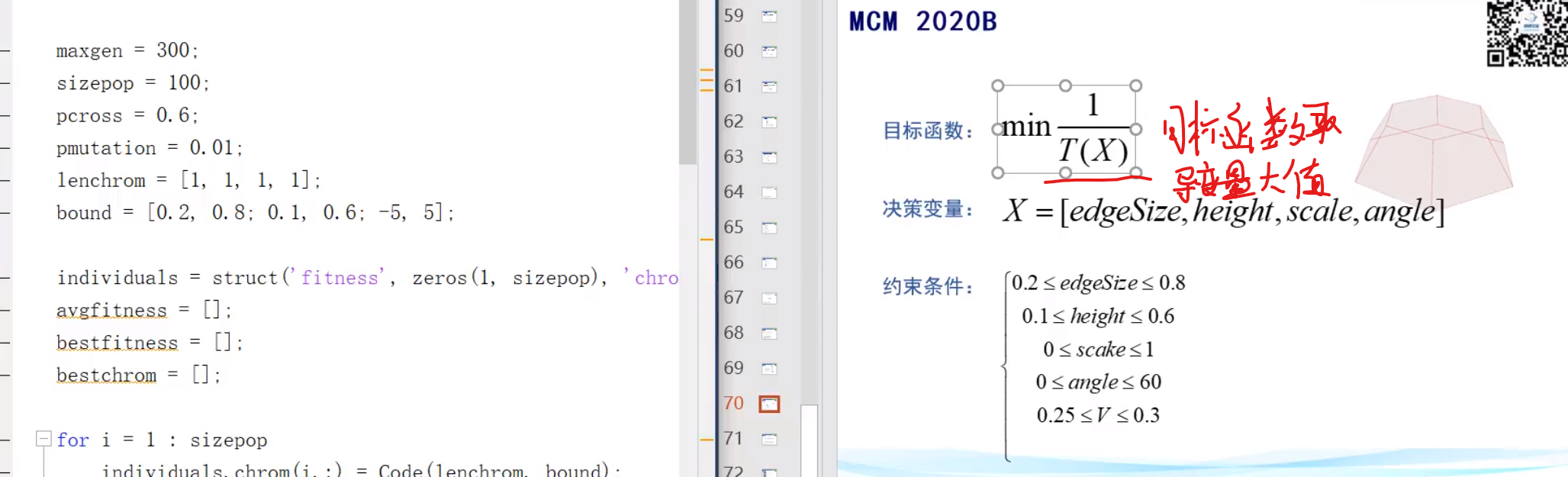
粒子群算法
与遗传算法相似,在写论文之前可以两个都做,然后比较那个的效果更好

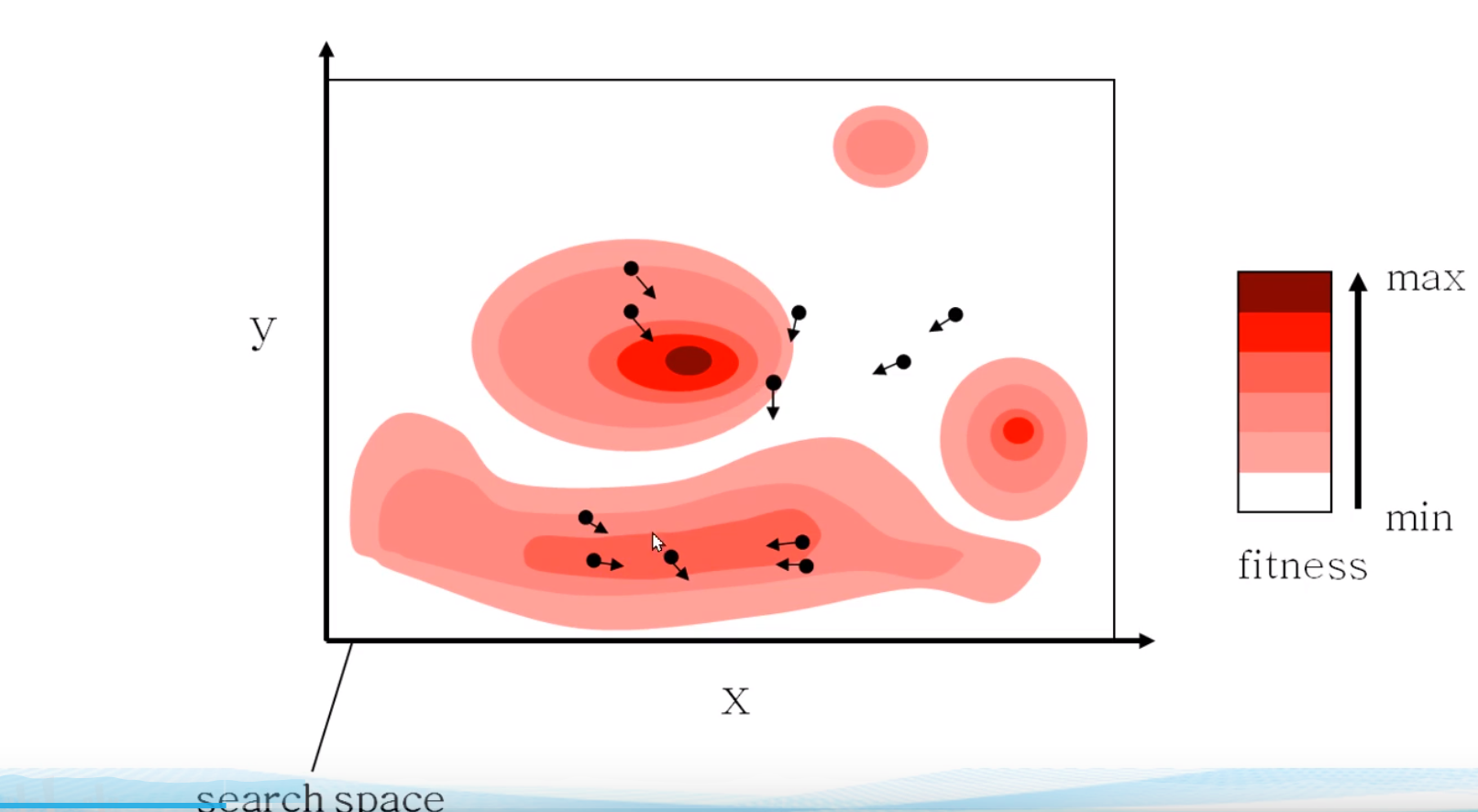
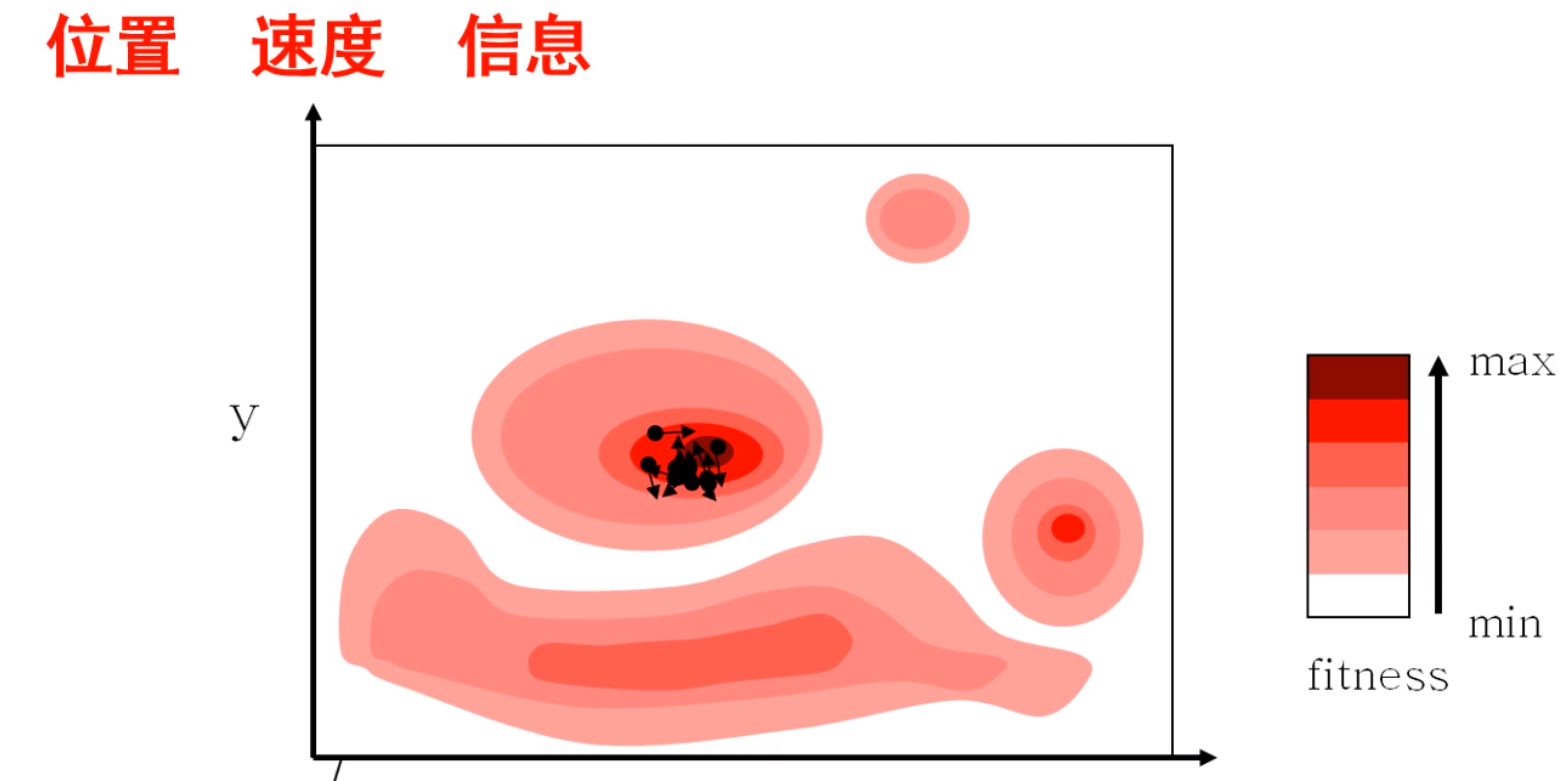
算法框架
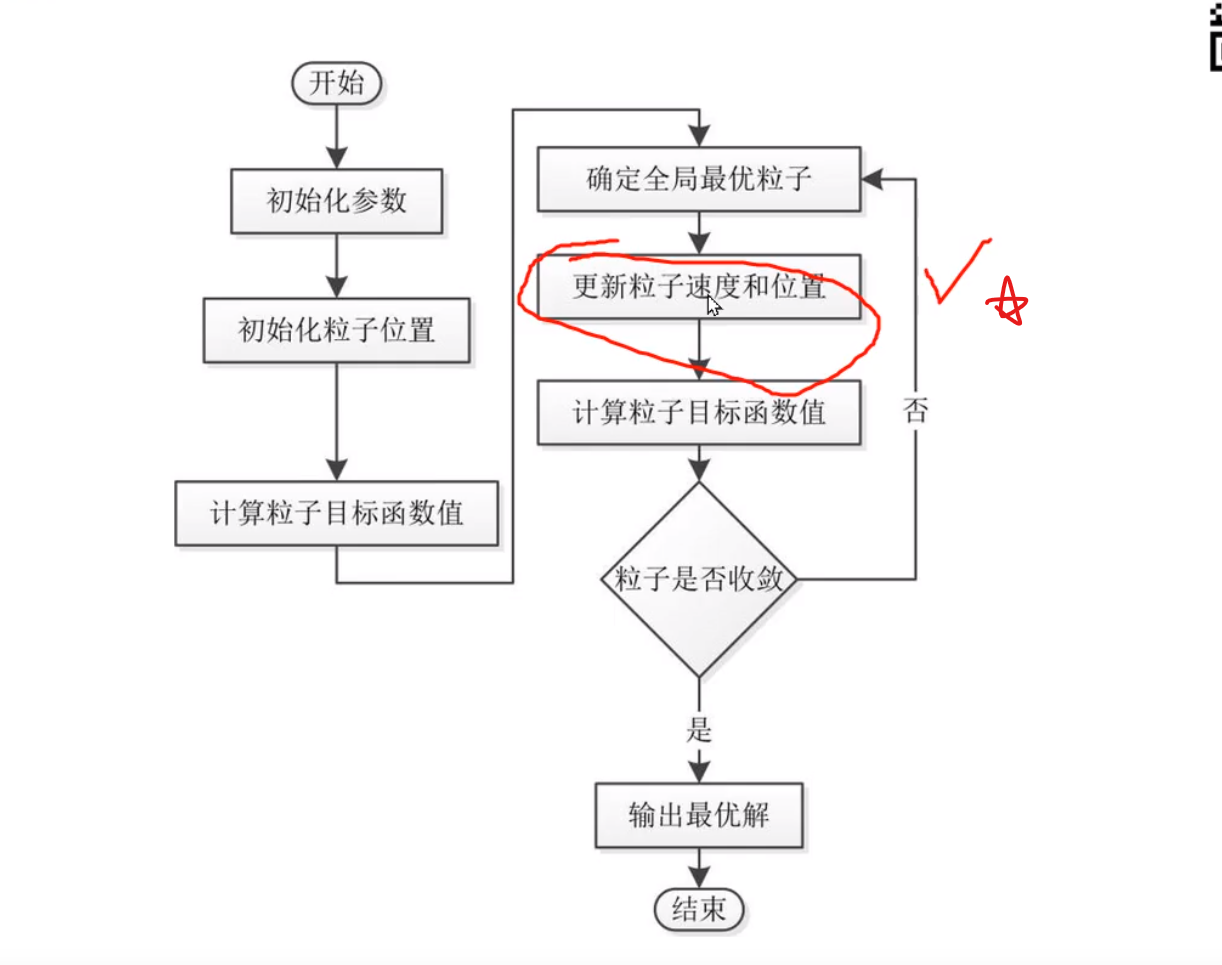
全局最优:整个种群的最优,位置确定 个体最优:他飞过很多带,对于他自己来说,所找到的最优值
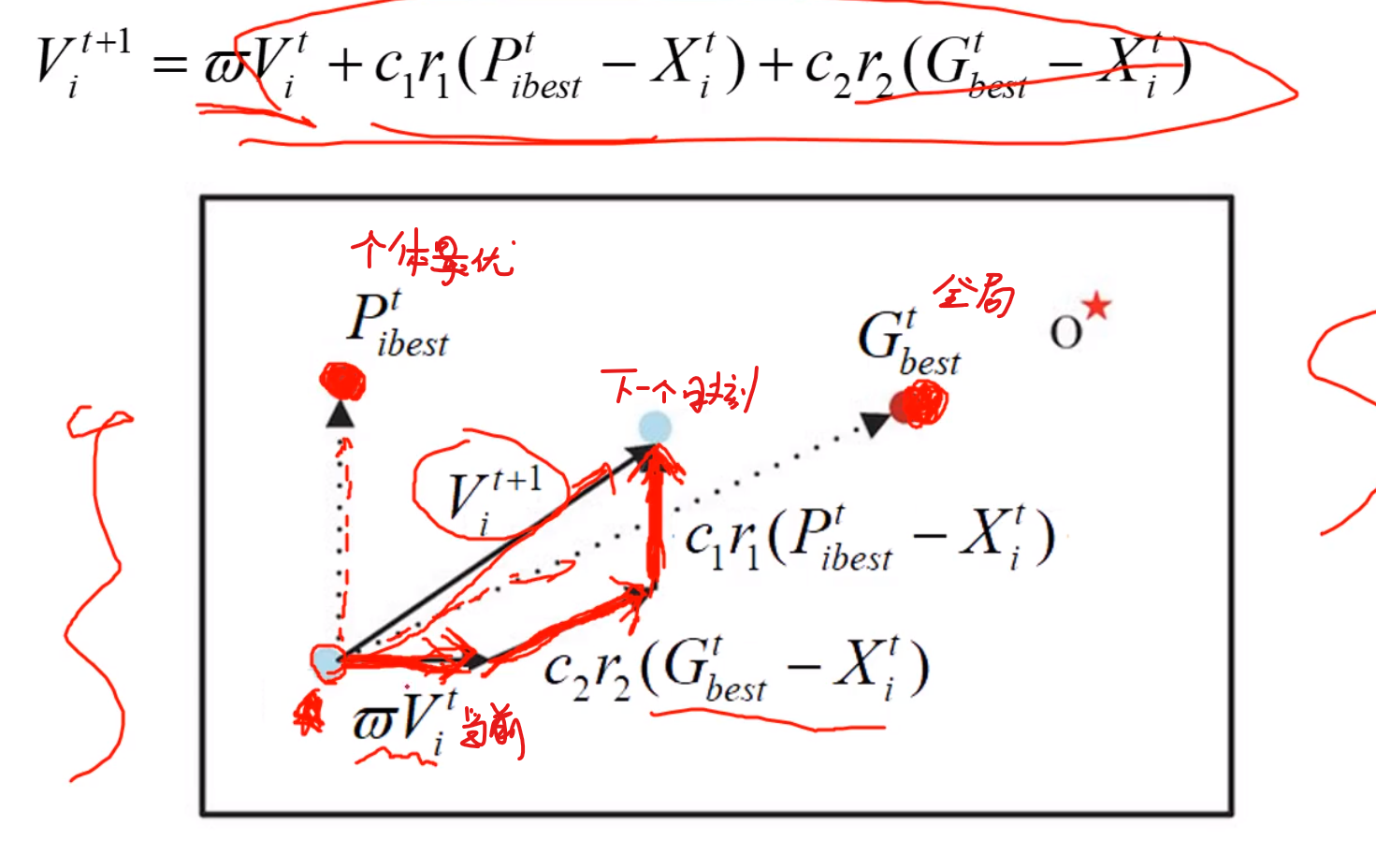

w可以设置为定值0.98之内的 c1 = c2 = 2 或者 = 1.5都是可接受的参数 r1,r2这些就是看你自己偏好来设置
多目标优化求解
多目标问题可以转化为单目标问题
引例

例如你的舒适度和空调的价格,一个达到最优解另外一个必然不可能达到最优解。并且两个函数具有相似的参数,不一定要完全相同。
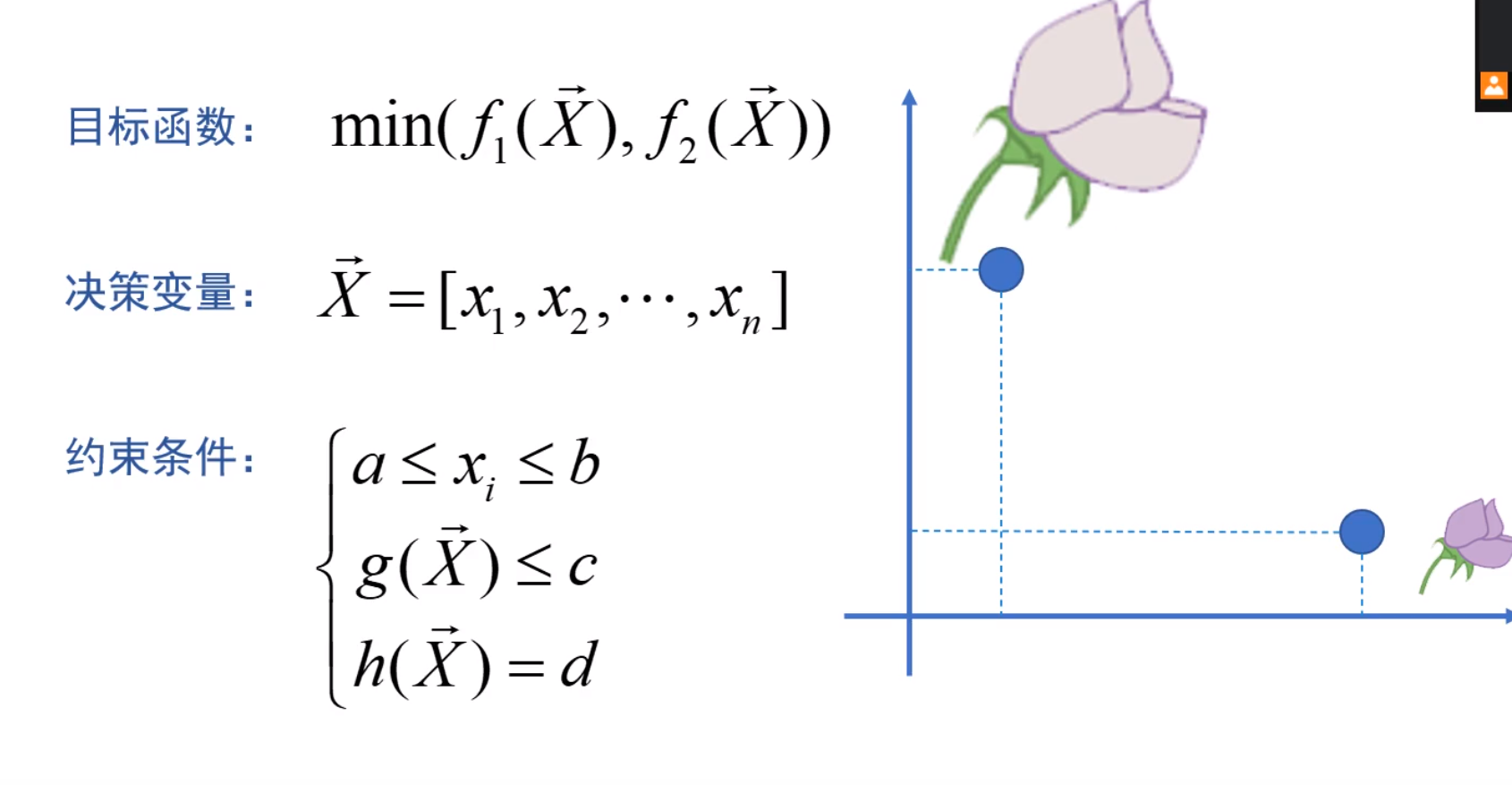
例如颜色越深,越容易被猫发现并且吃掉,如果越大,也是越容易被猫发现并且吃掉,恰巧颜色越浅,花越大,颜色越深,花越小,这就是多目标优化问题了
支配
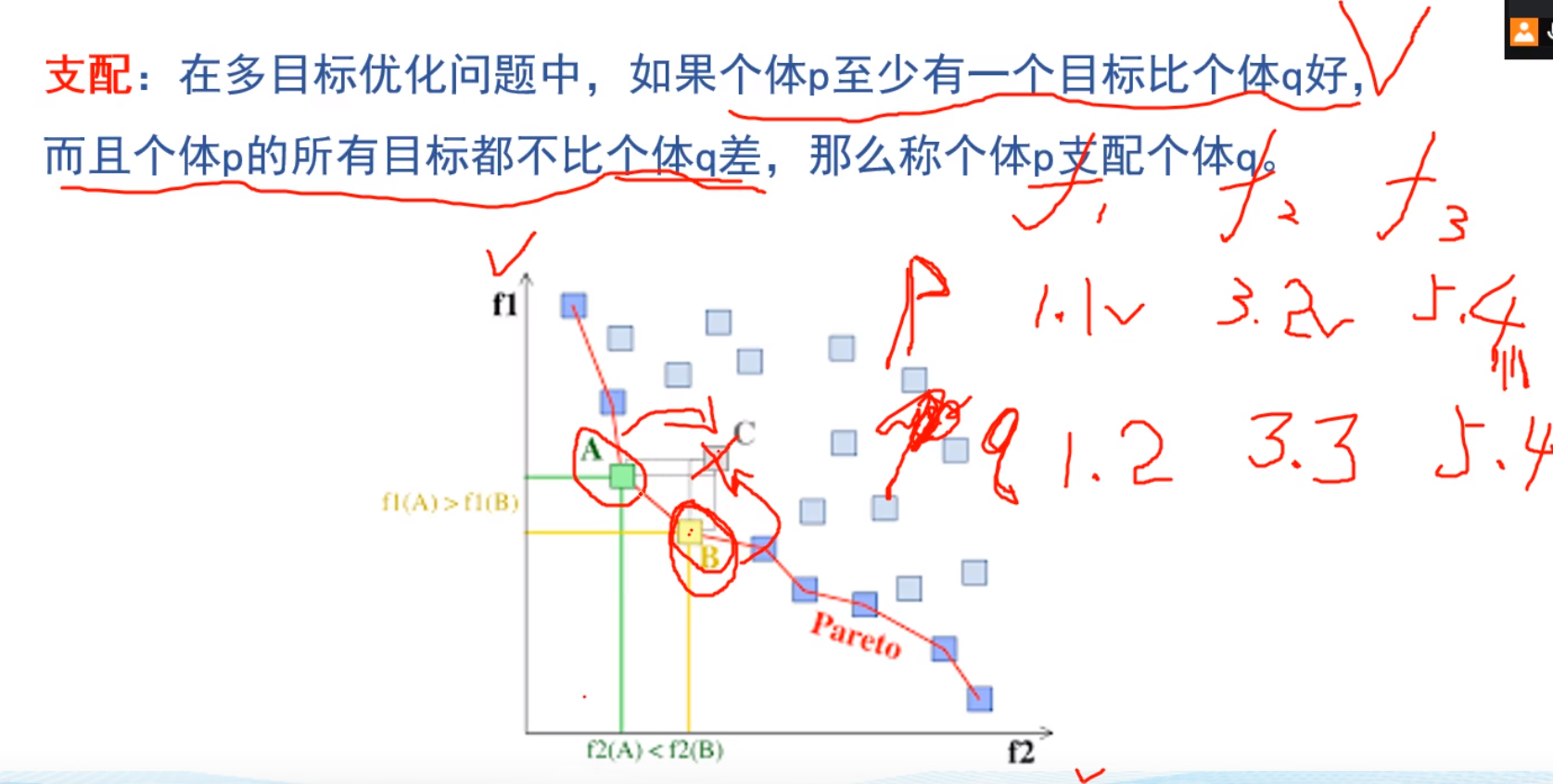
A,B都能支配C f1,f2都比c要小,越小越好(求最小值)
下一轮C会淘汰,AB会制约,不会被淘汰
支配需要至少一个函数比被支配个体好,然后全部都不差于(<=)被支配个体
序值
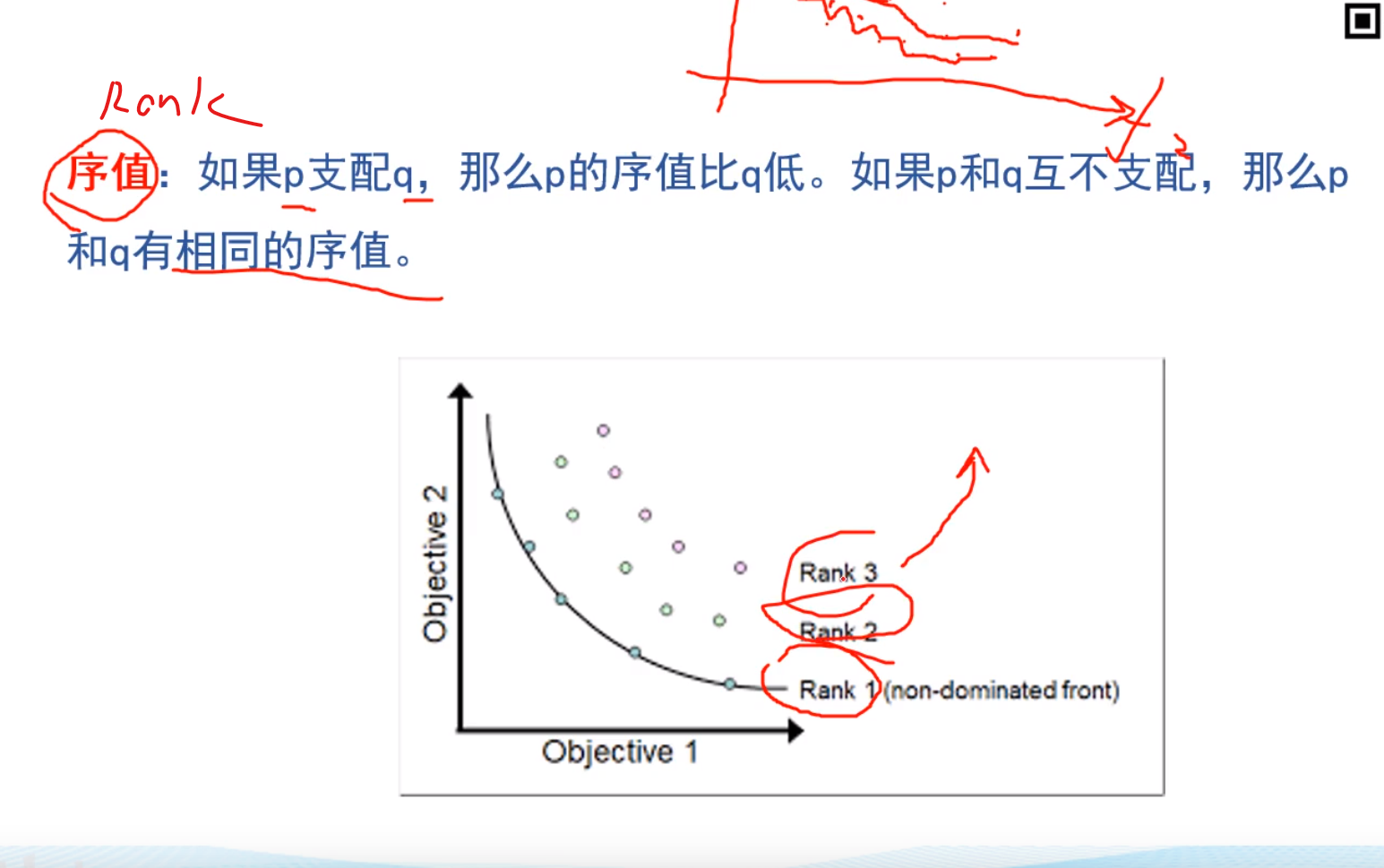
最终结果就是Rank1这张图
但是无法体现决策变量的值,可能需要赋一个表来体现一下
拥挤距离
可以用来删掉多余的点,选择全局最优
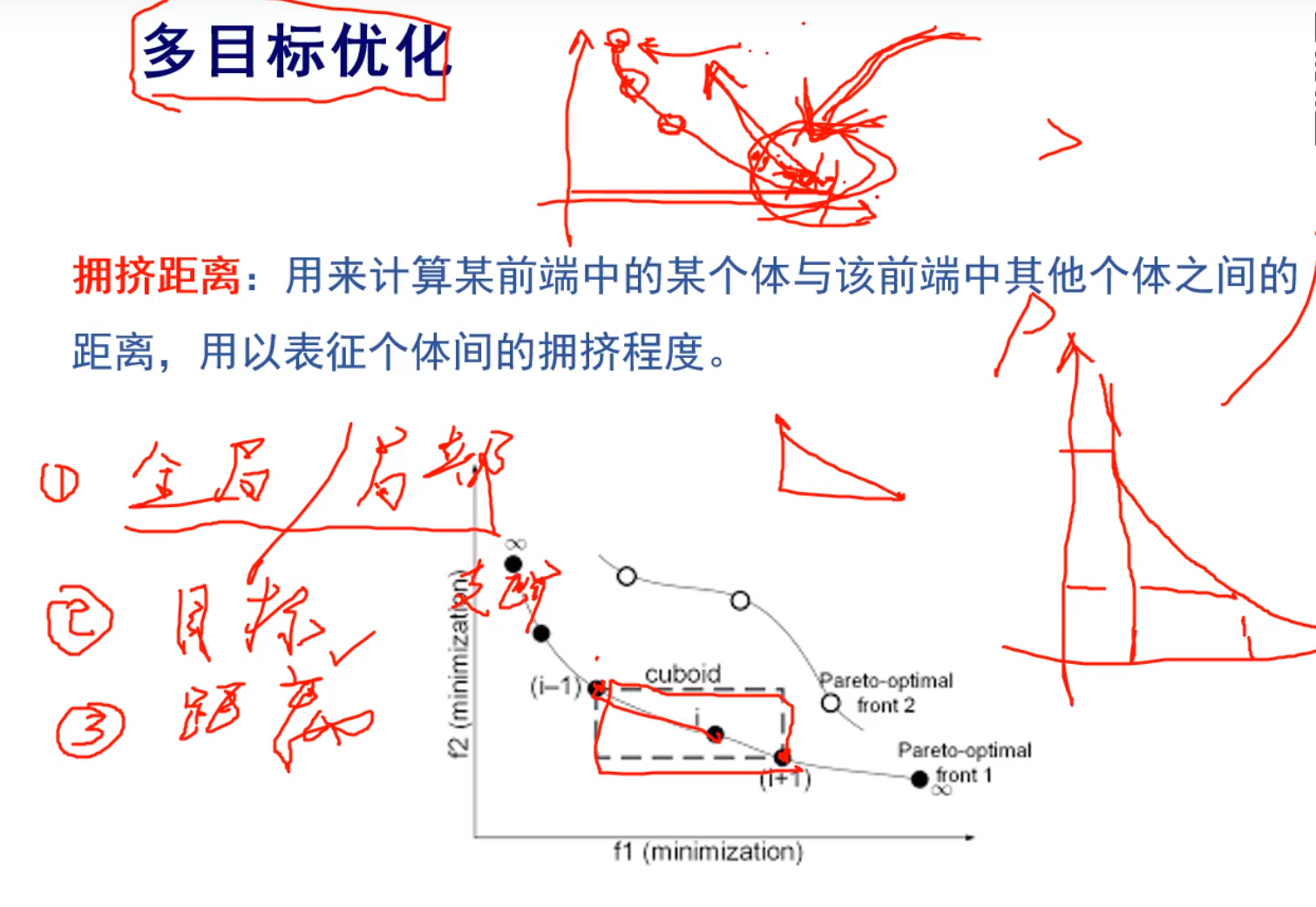
Pareto最优前沿
美赛中可以直接呈现这个图给评委(下图)
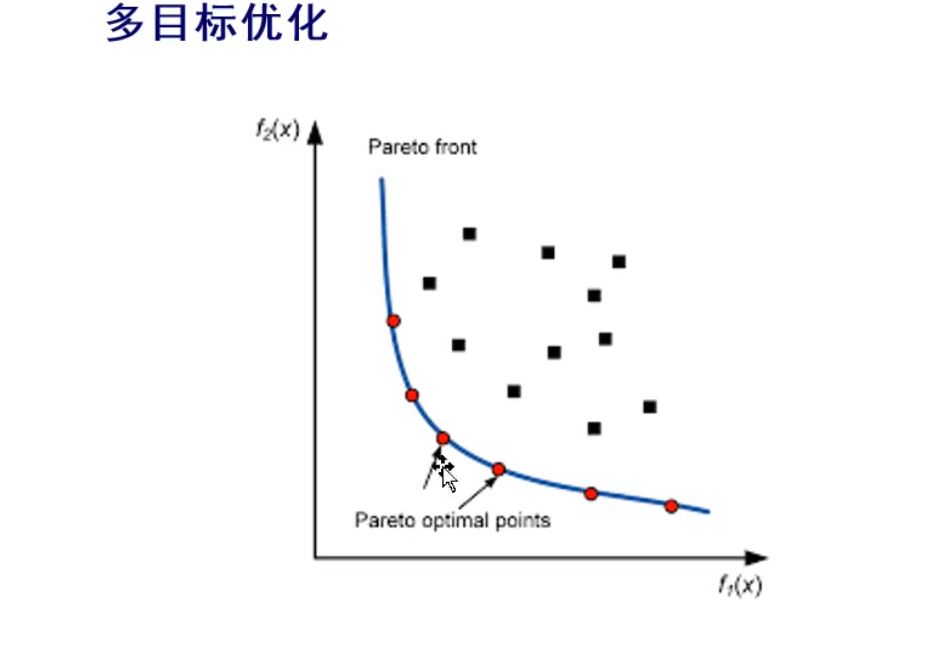
我们也可以分析,对红点分析,由什么特征,导致了,然后对几个对比,得到一个最优解也可以(最优红点)
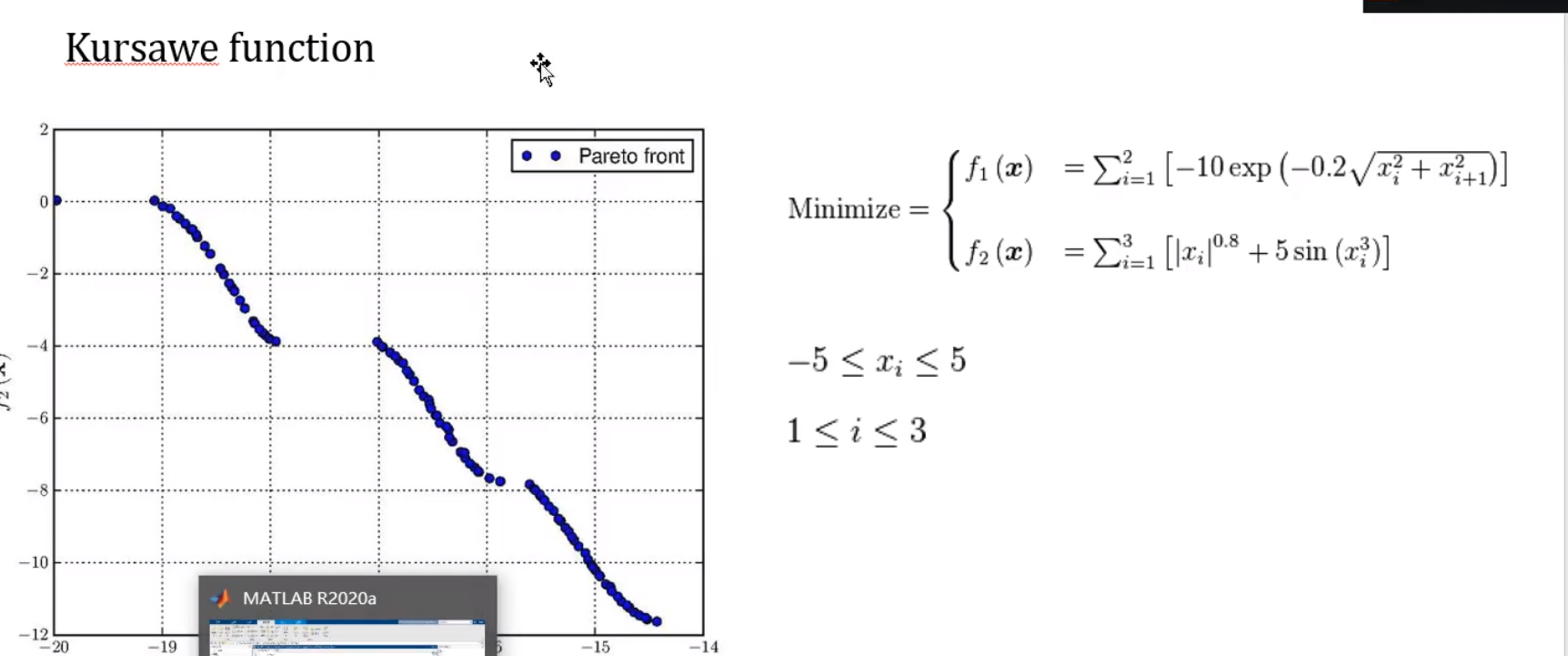
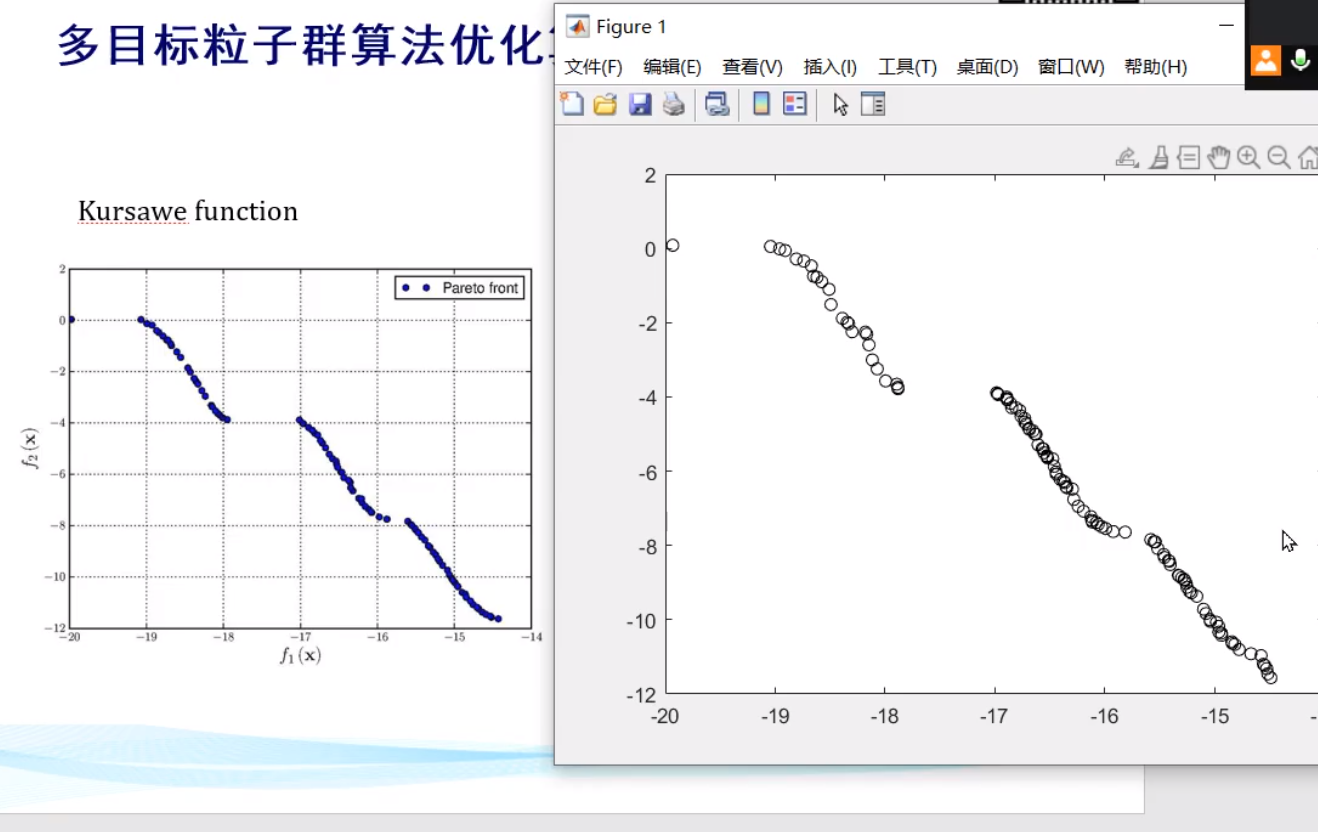
那么,我们怎么样从这条曲线中选择继续往下推进的解呢?
看你追求什么,你追求f1好,还是追求f2好,还是追求一个折中解,取中间点,用加权,返回选择我们下一步推进的点(对f1,f2加权)确定我们想要的最好的
模拟退火

少用。
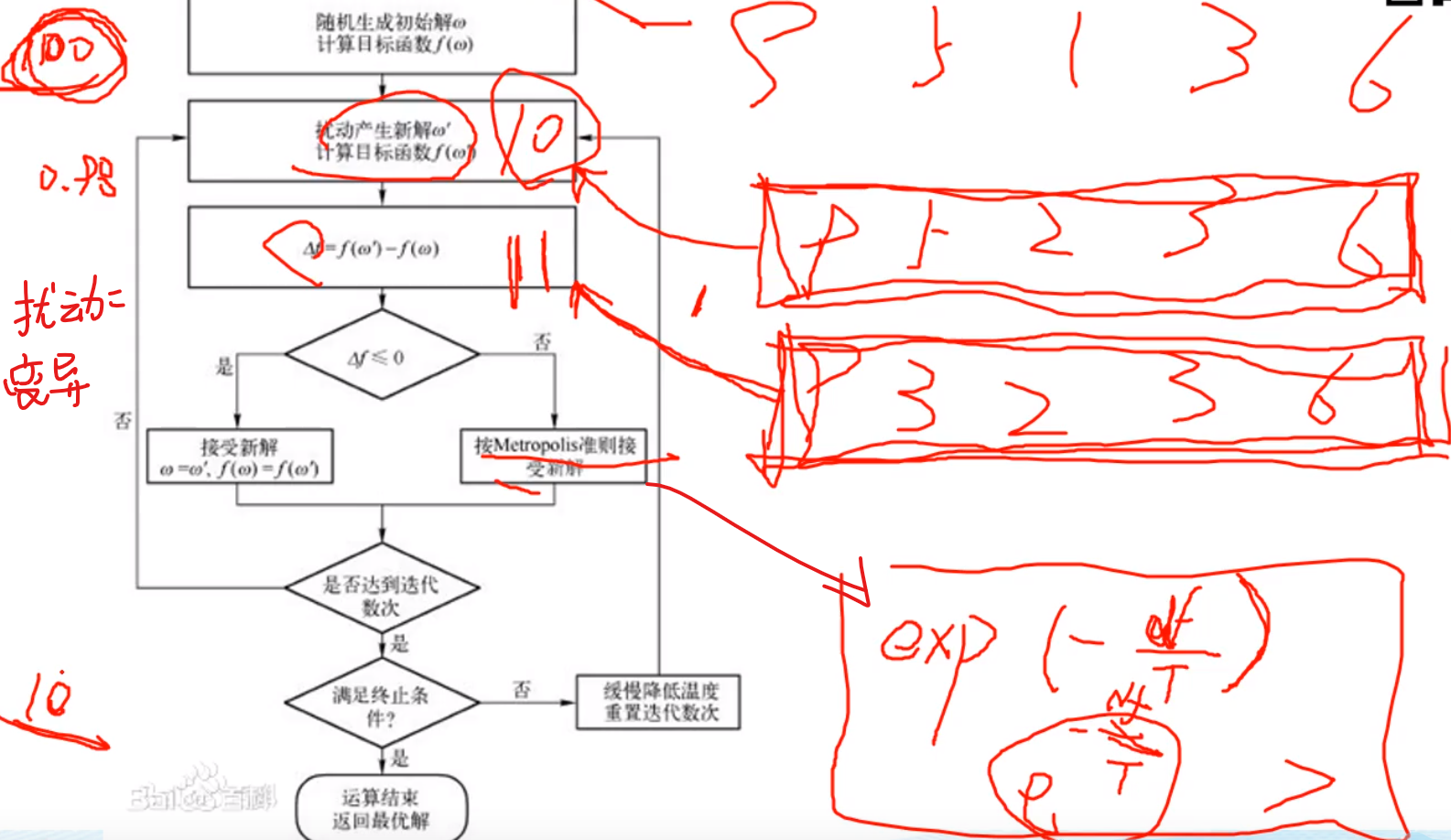

当温度低于多少多少时,算法终止
扰动
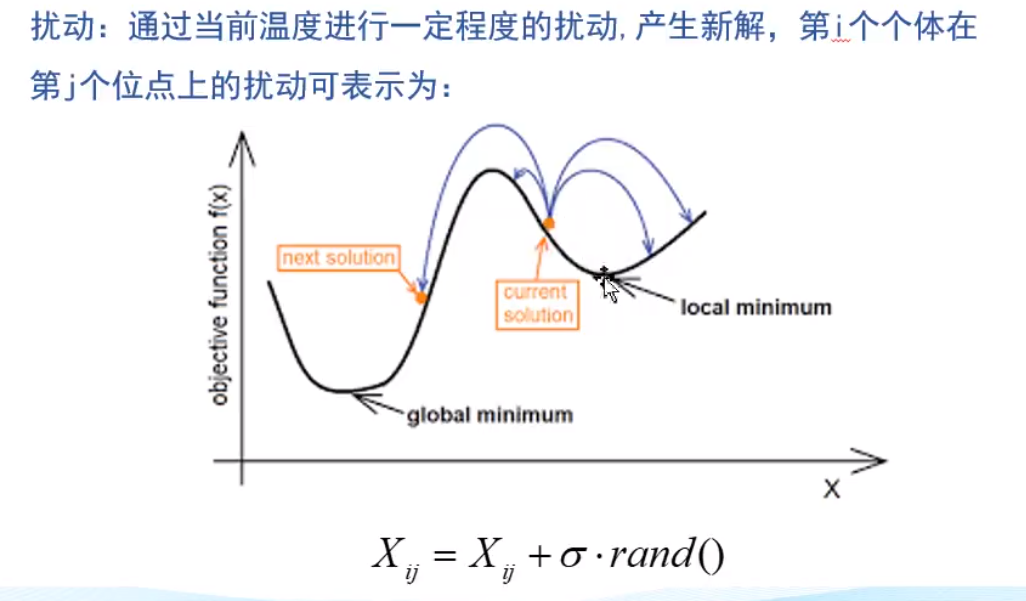
差分进化
简称DE

DE != GA
变异交叉选择的内容是不一样的,并且顺序也不一样
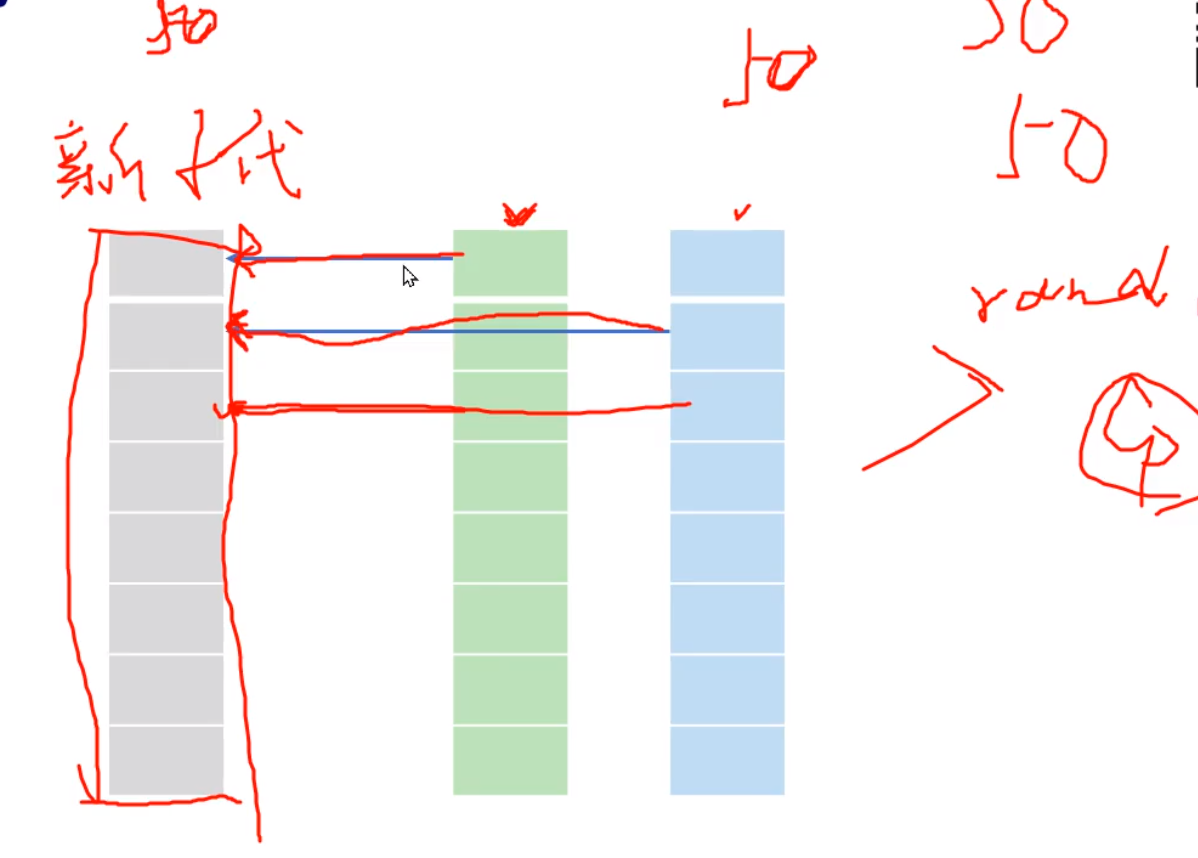
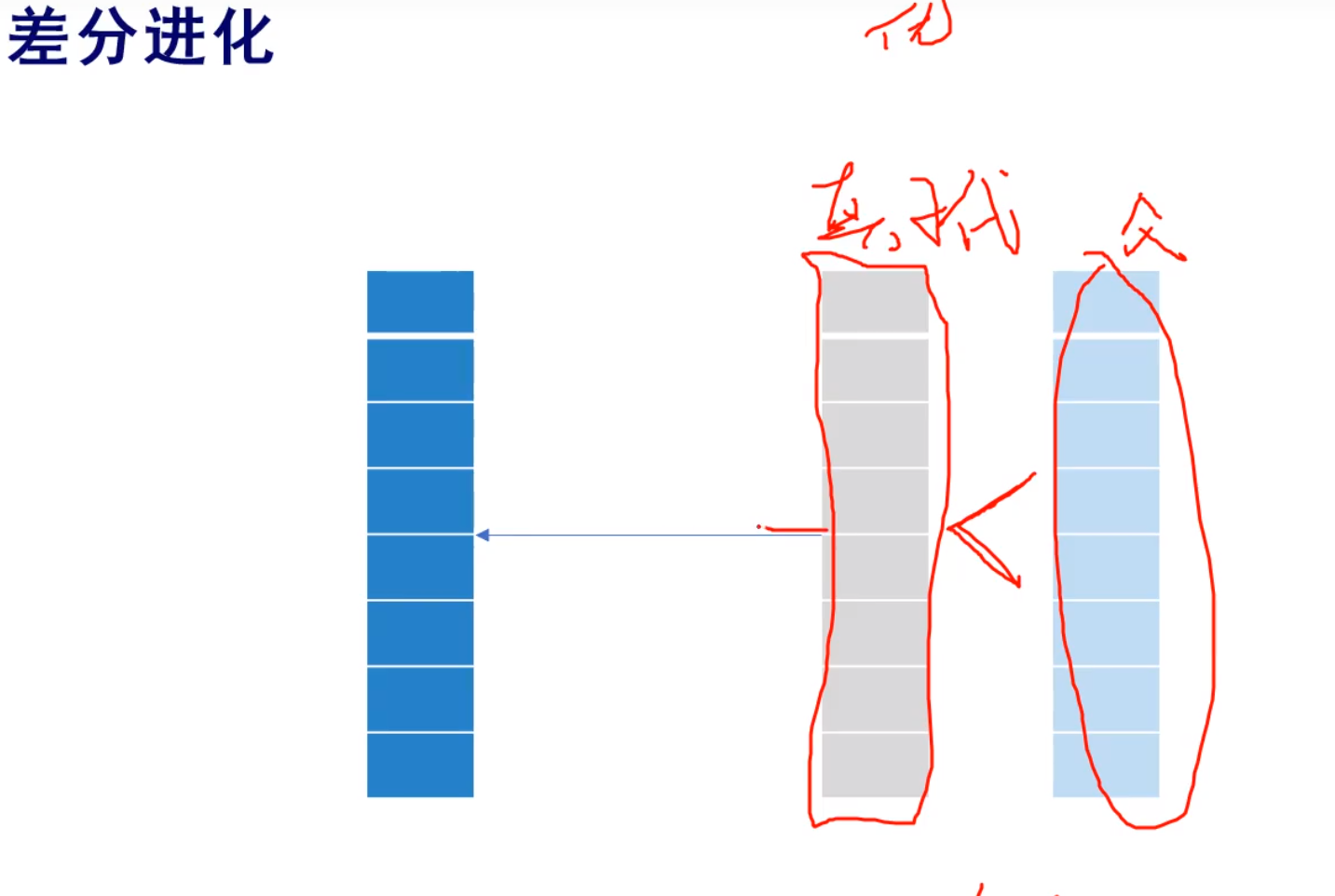
子代和父代比较,谁小谁进入下一代
马尔可夫预测

引例
随着时间在变化


定义

无后效性


转移概率矩阵

马氏链模型


例子

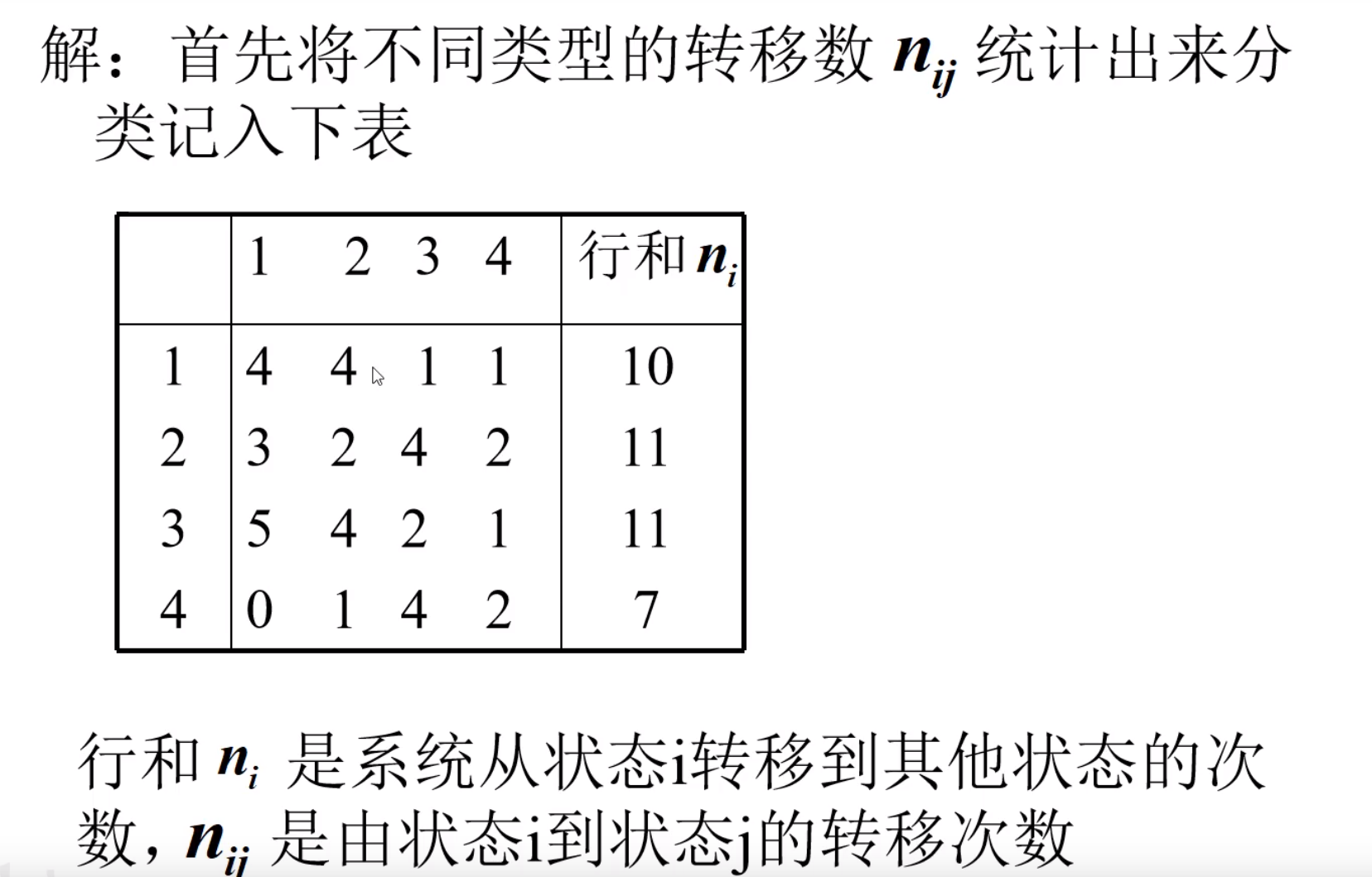
行为本身,然后列为下一个转移到的数据

转移概率的极限分布

正则即是自己可以乘自己,并且一直有意义

两个类型
正则链
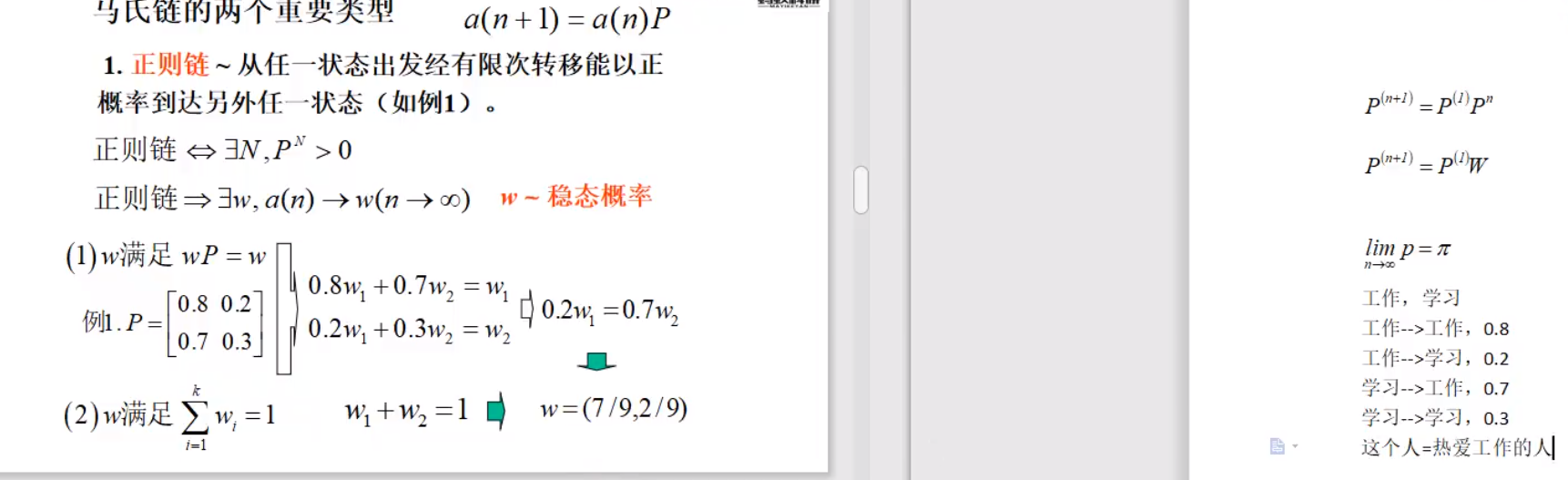
得到概率向量来量化这个事情
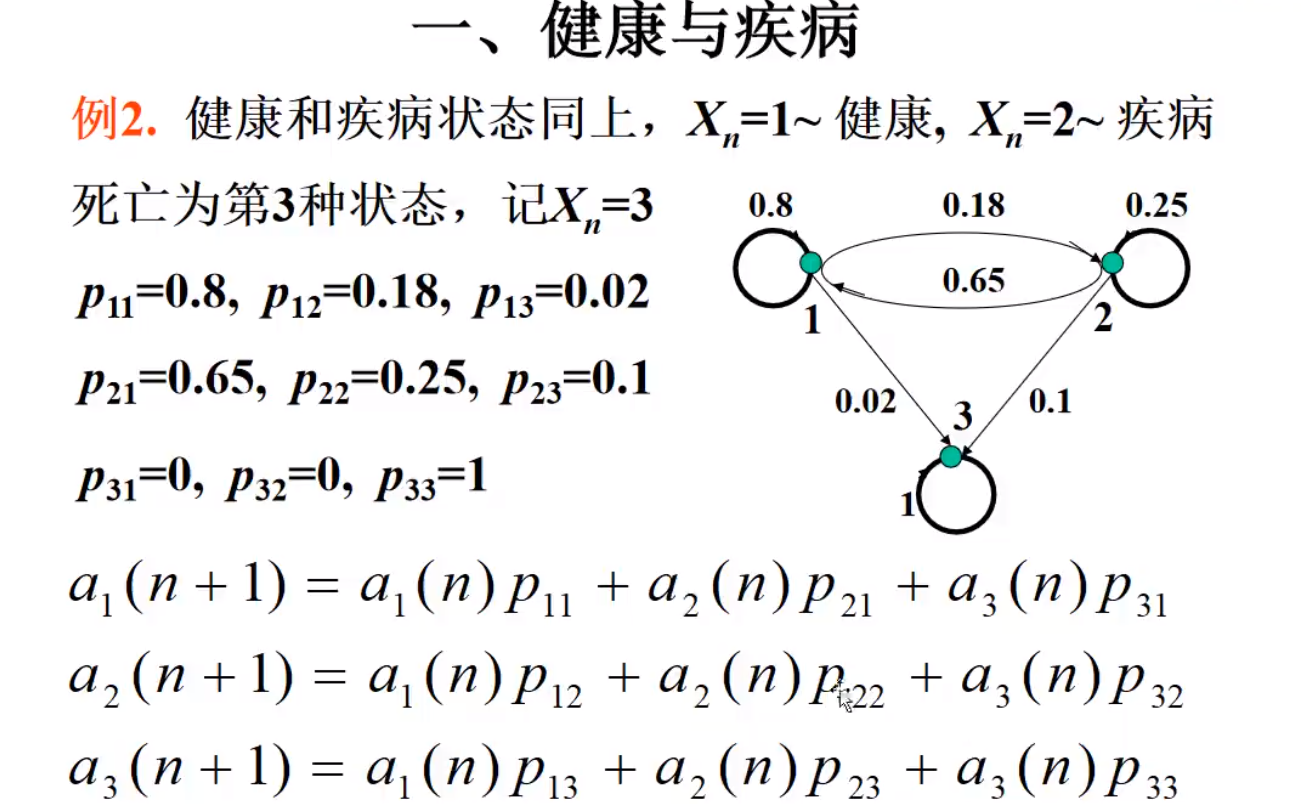
吸收链


死亡就是吸收状态,健康-生病-死亡就是吸收链
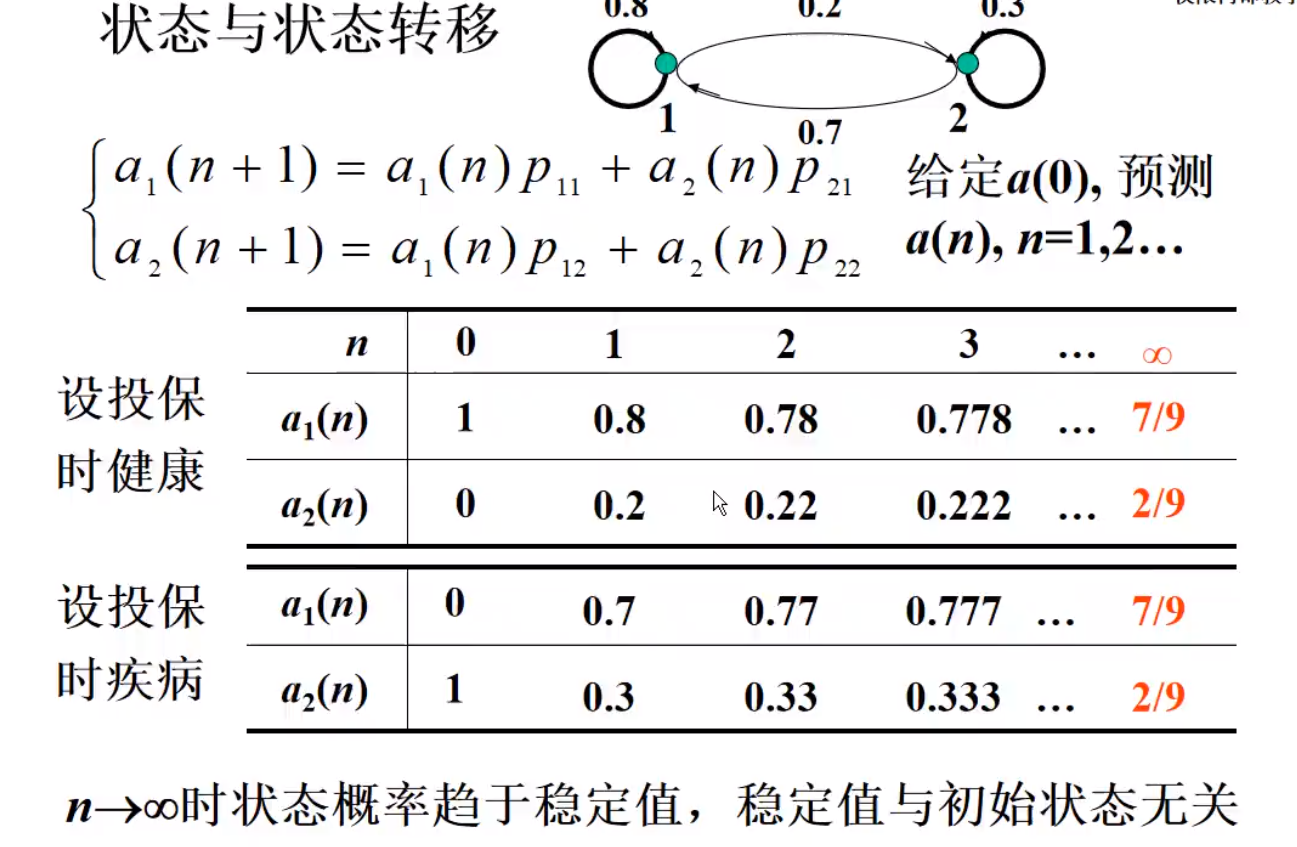
健康与疾病
正则案例


吸收案例
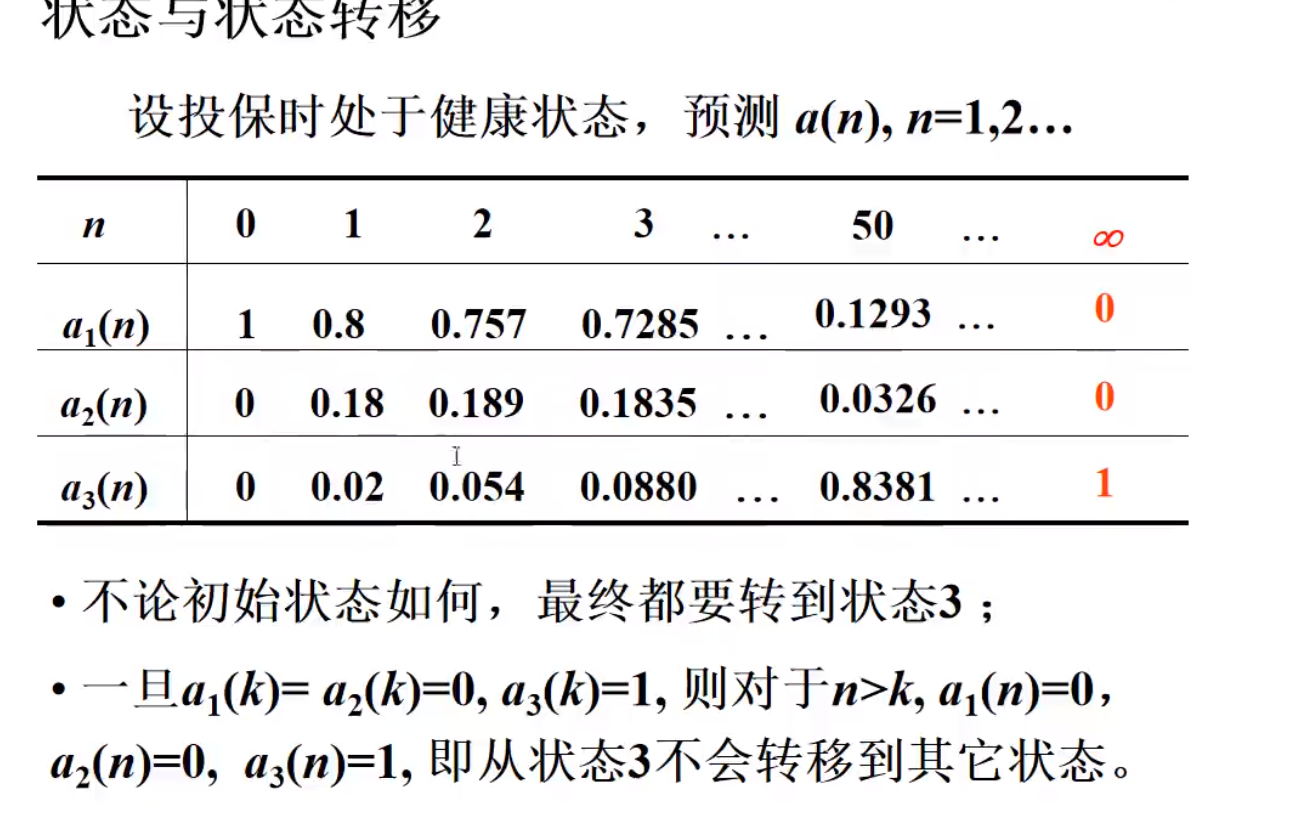
钢琴销售存储
经典例题

问题分析

动态用来描述概率,稳态用来计算最后的问题

模型建立

模型求解


让我们再回到假设

泊松分布为长期统计的规律,万一你买了三架,但是一周要了四架,那么有些资金流就会被锁在里面,说不定下一周就会没有钱买之类的=-=
智力竞赛


B是错地,(1,1)和(3,3)应该是(1-pq)q
更多算法补充
熵权法