序章

以下系列内容，是基于清华大学邓俊辉教授所授课程数据结构的笔记，本人结合PPT与自身感悟制成，算是学习后的填坑，仅当作学习笔记使用，欢迎借鉴学习和提出相关建议，转载需标明出处www.jjyaoao.space

1.序章

时间复杂度

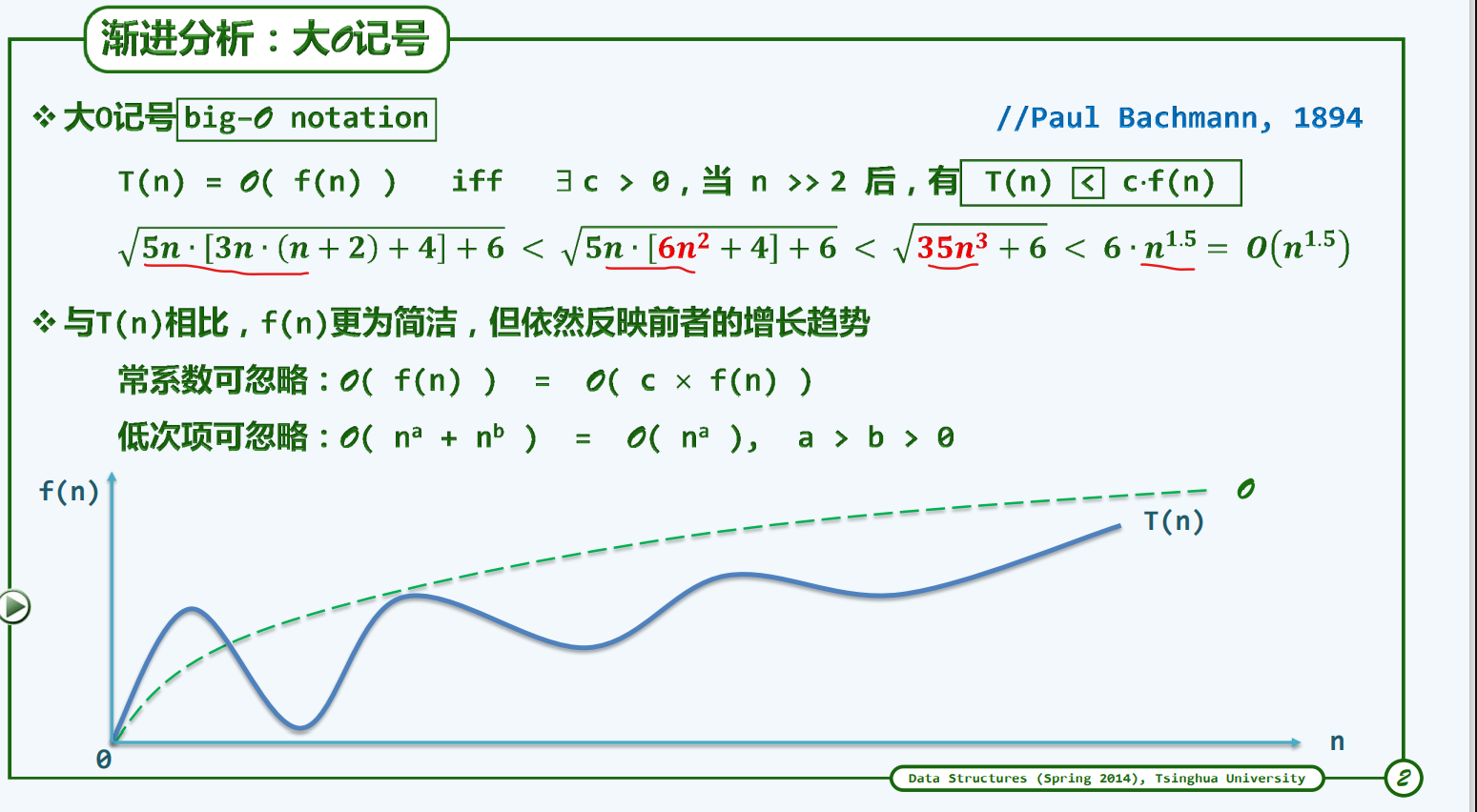
• 最坏情况：以大O记号形式表示的时间复杂度，给出了一个算法的最坏情况，即–对于规模为n的任意输入，算法的运行时间都不会超过O(f(n))
• 最好情况 ：大 Ω记号–>如果存在正的常数c和函数g(n)，对任意n>>2，有T(n) > c * g(n)，即认为：在n足够 大后，g(n)给出了T(n)的一个下界，记为：

​ T(n) =Ω (g(n))

• 大 Θ记号–>存在正的常数c1和c2，以及函数h(n)，对任意n>>2，有 c1*h(n) < T(n) < c2 * h(n)，即认为：在n足够大后，h(n)给出了T(n)的一个确界，记为：

​ T(n) =Θ (g(n))

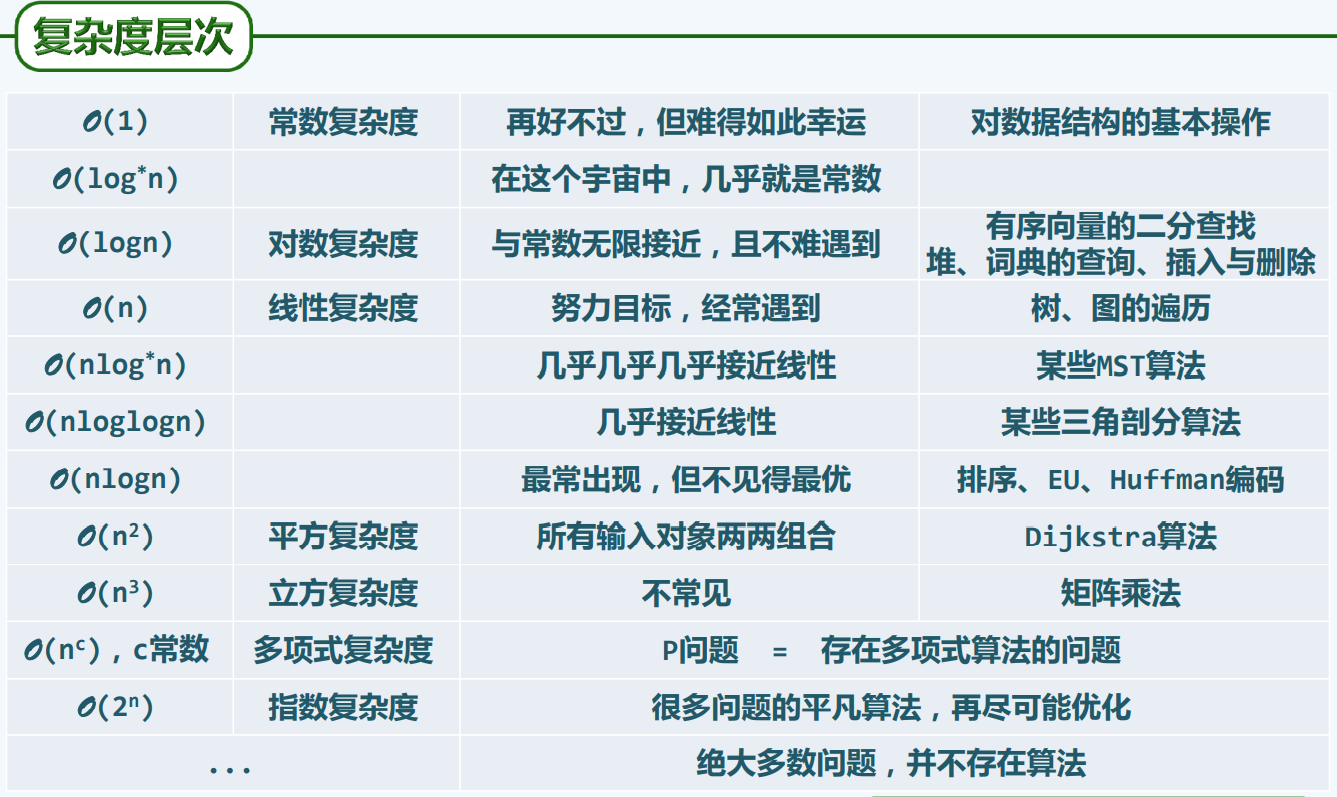
级数

循环VS级数

越外层循环，复杂度越高！

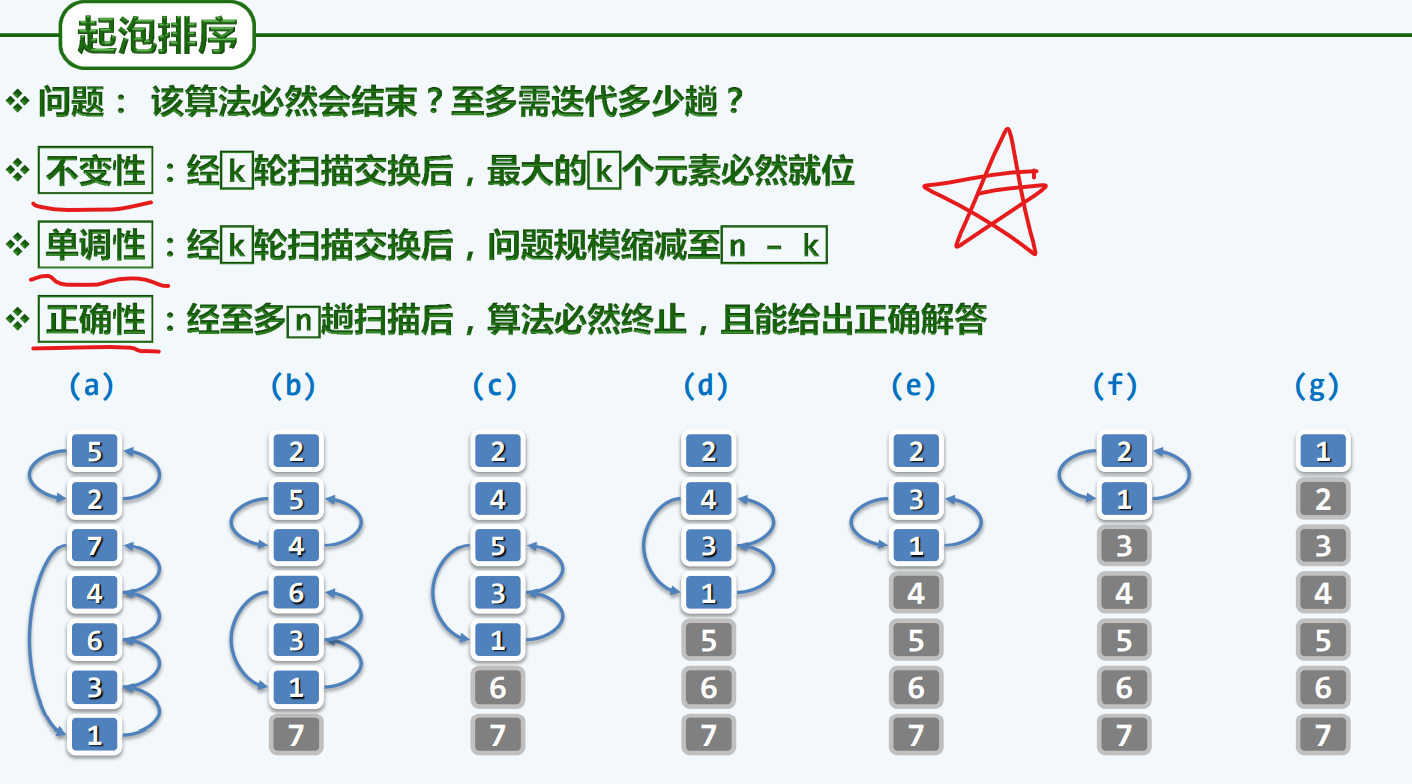
冒泡排序

void bubblesort(int A[], int n) {
		for (bool sorted = false; sorted = !sorted; n--) {
			for (int i = 1; i < n; i++) {
				if (A[i - 1] > A[i]) {
					swap(A[i - 1], A[i]);
					sorted = false;
				}
			}
		}
	}

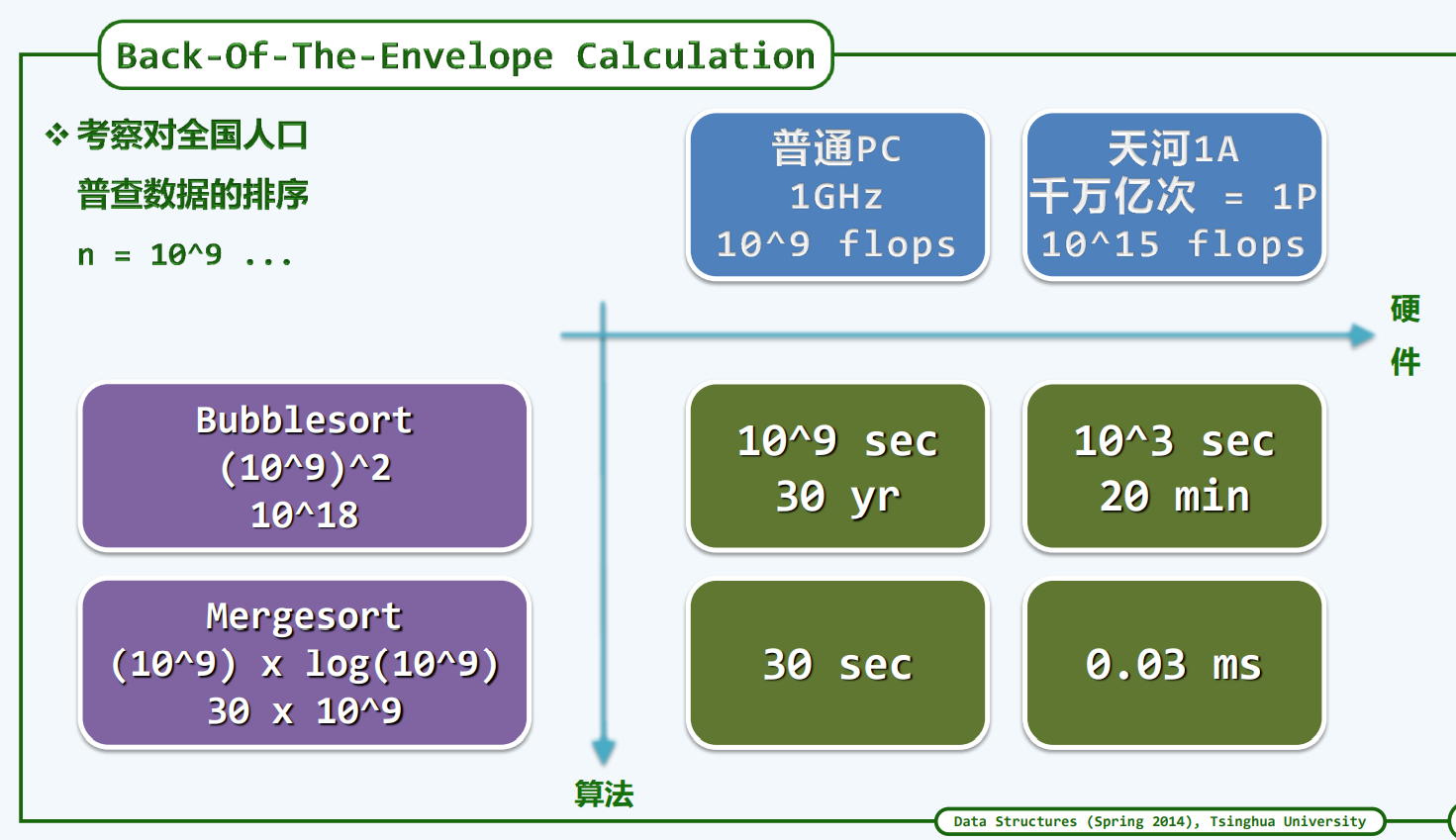
封底估算

迭代与递归

引入迭代

计算任意n个整数之和不同思路

普通方式

递归跟踪

递推方程

数组倒置

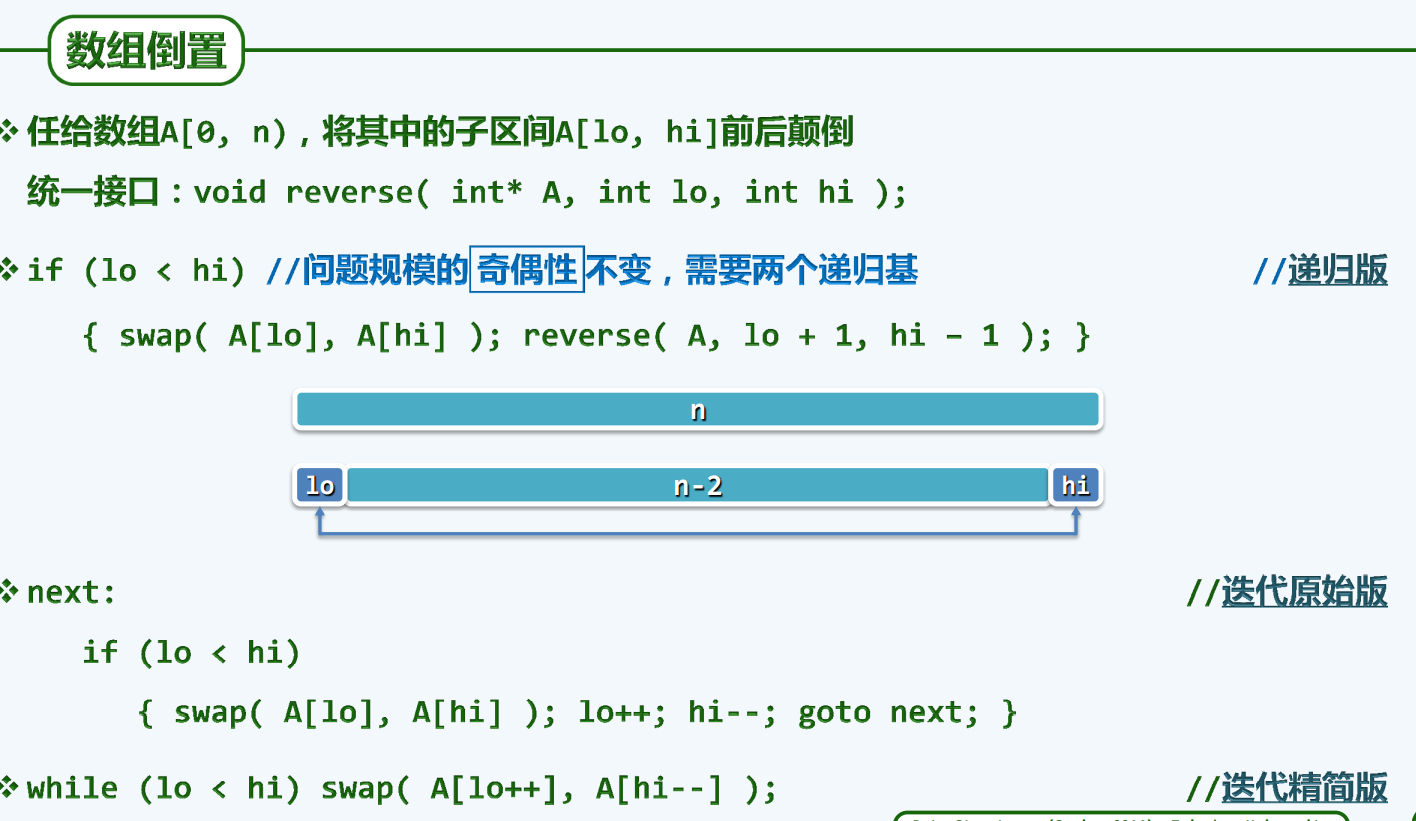
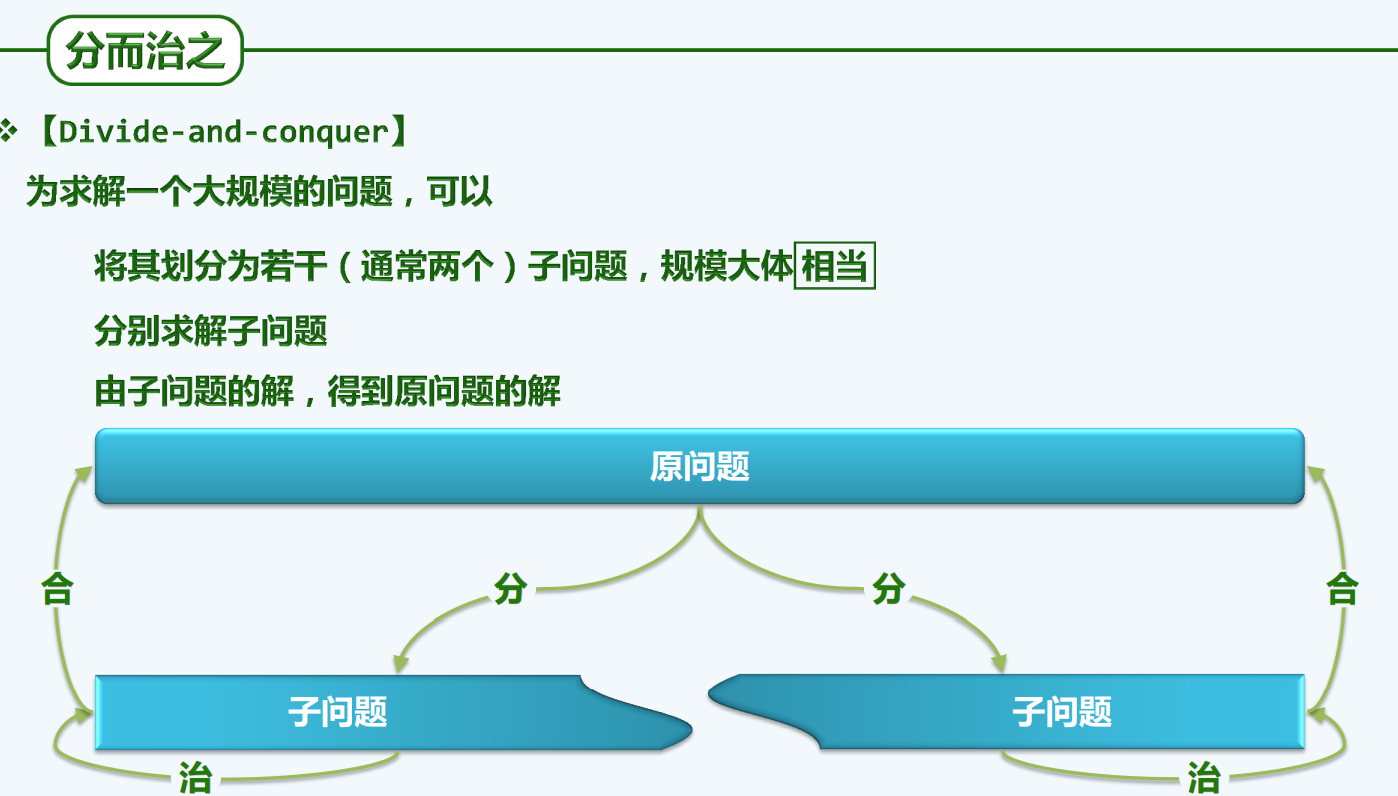
分而治之

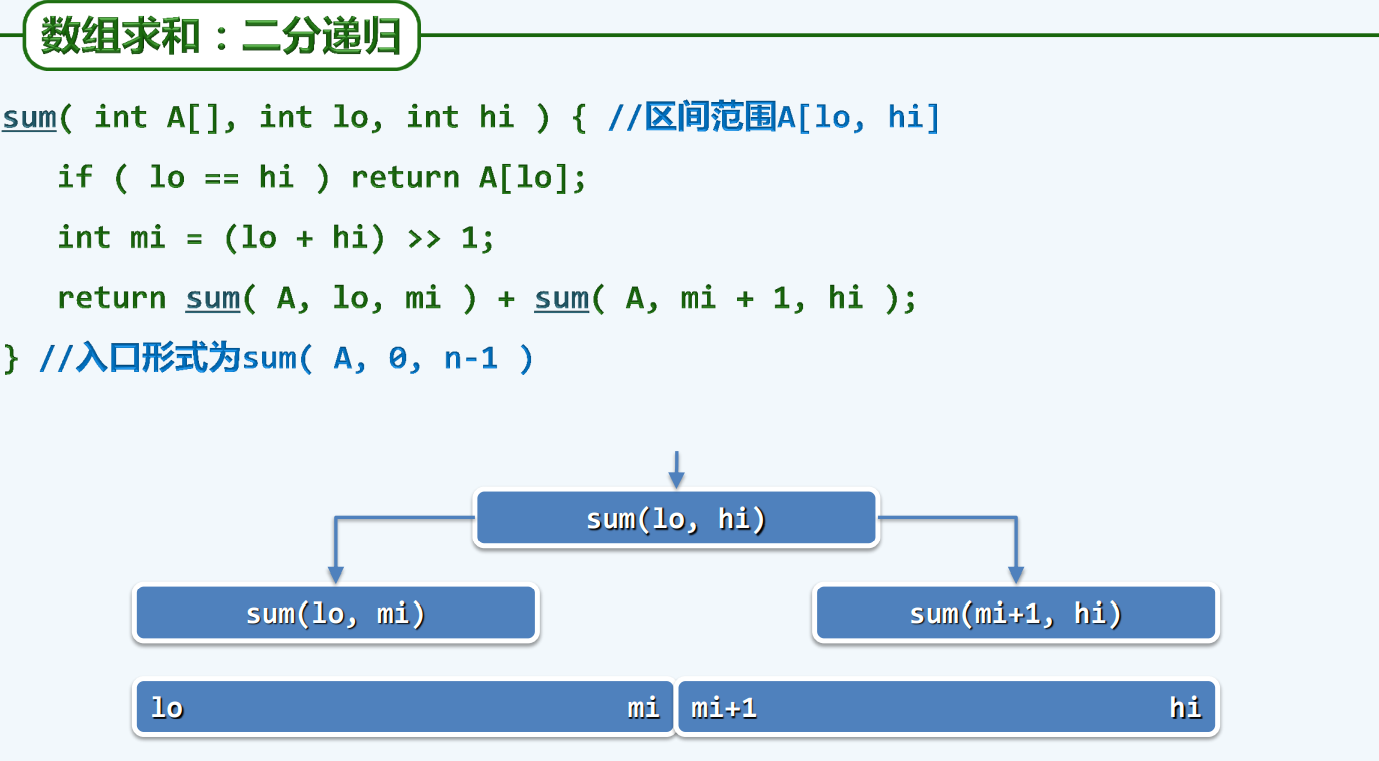
二分递归

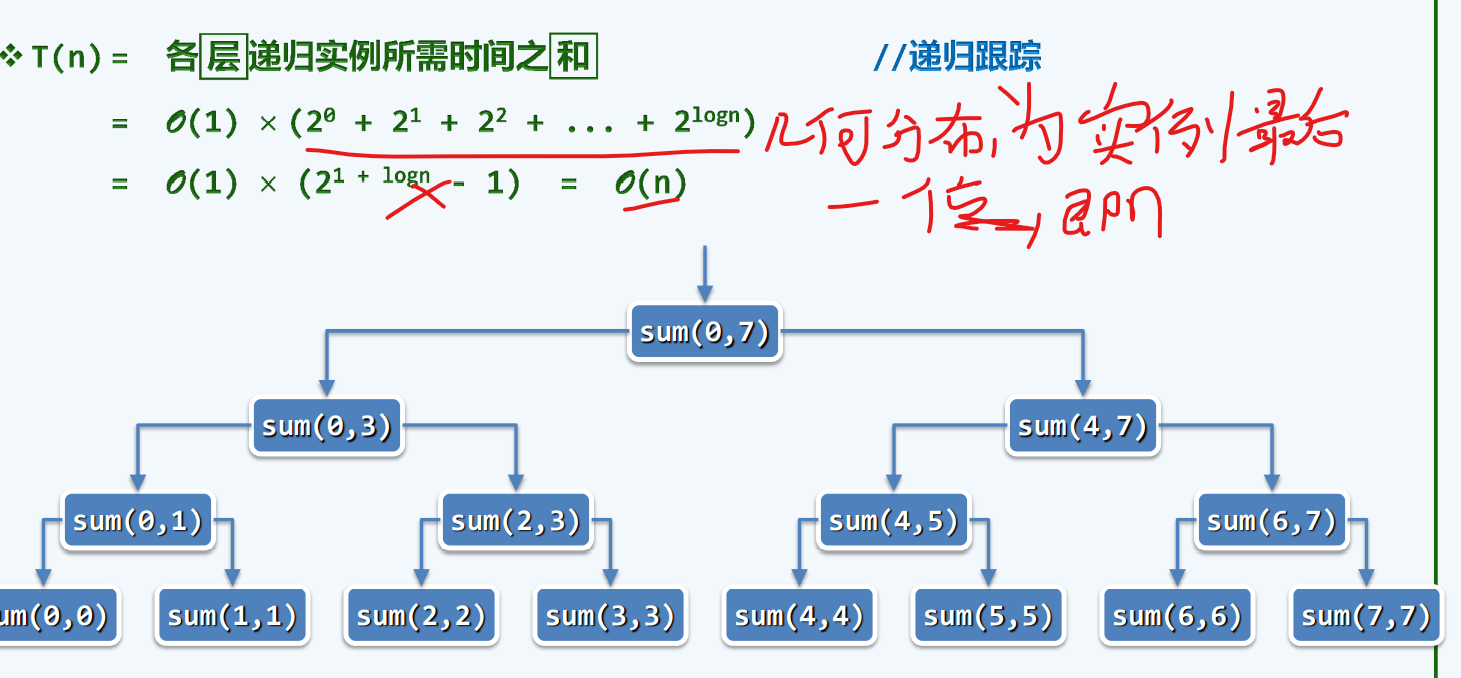
处理递推式(大师定理)

一些递推式

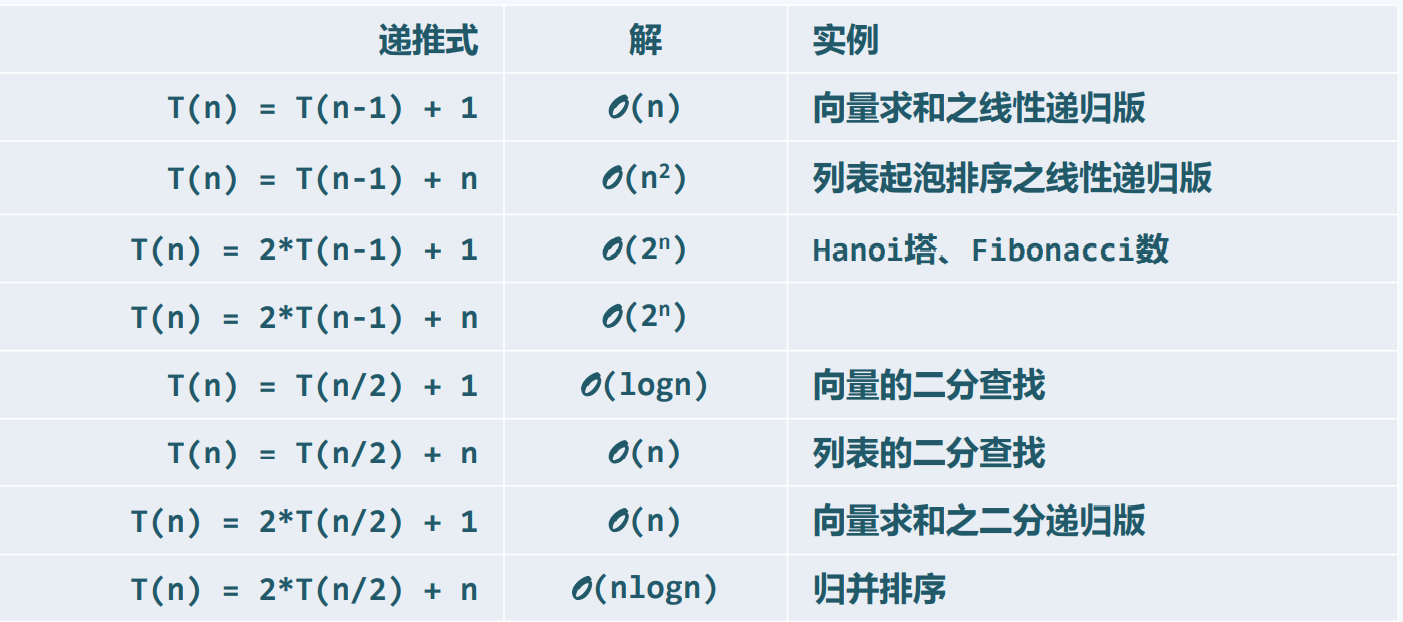
动态规划

兔子数列解决方案

低效递归

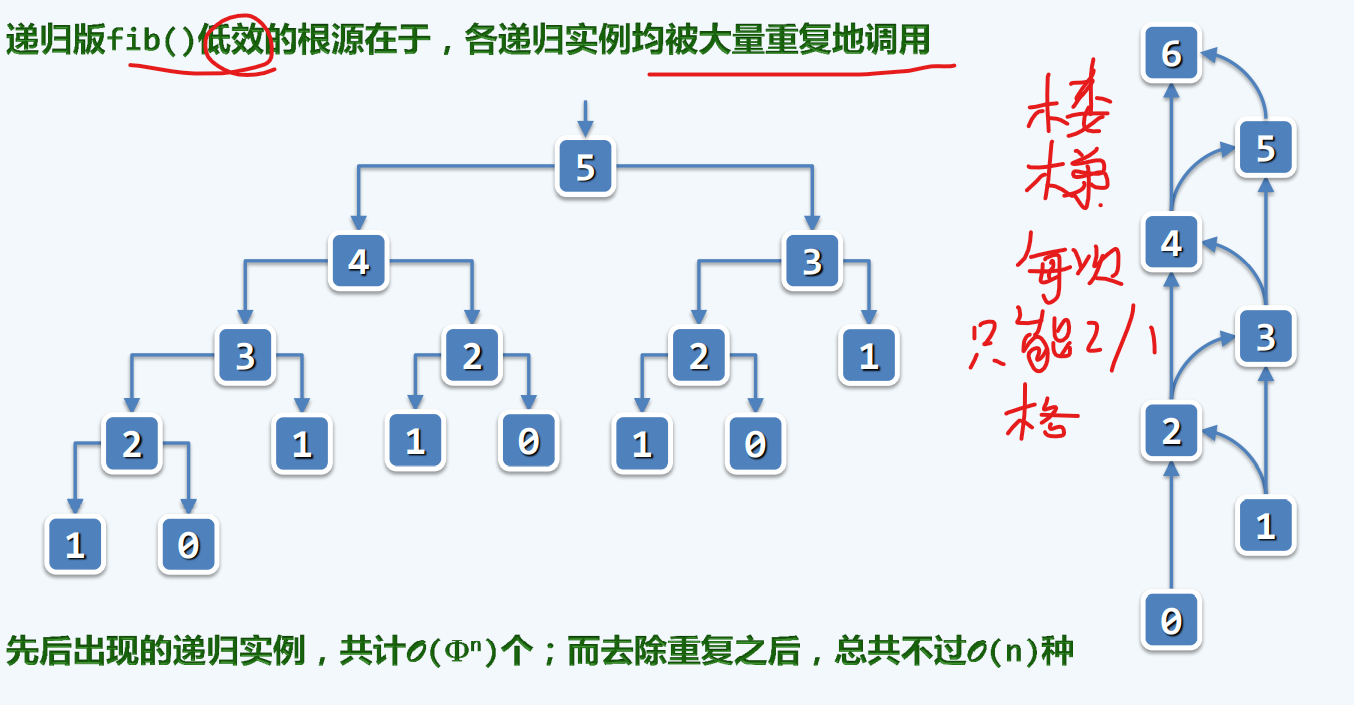
高效迭代

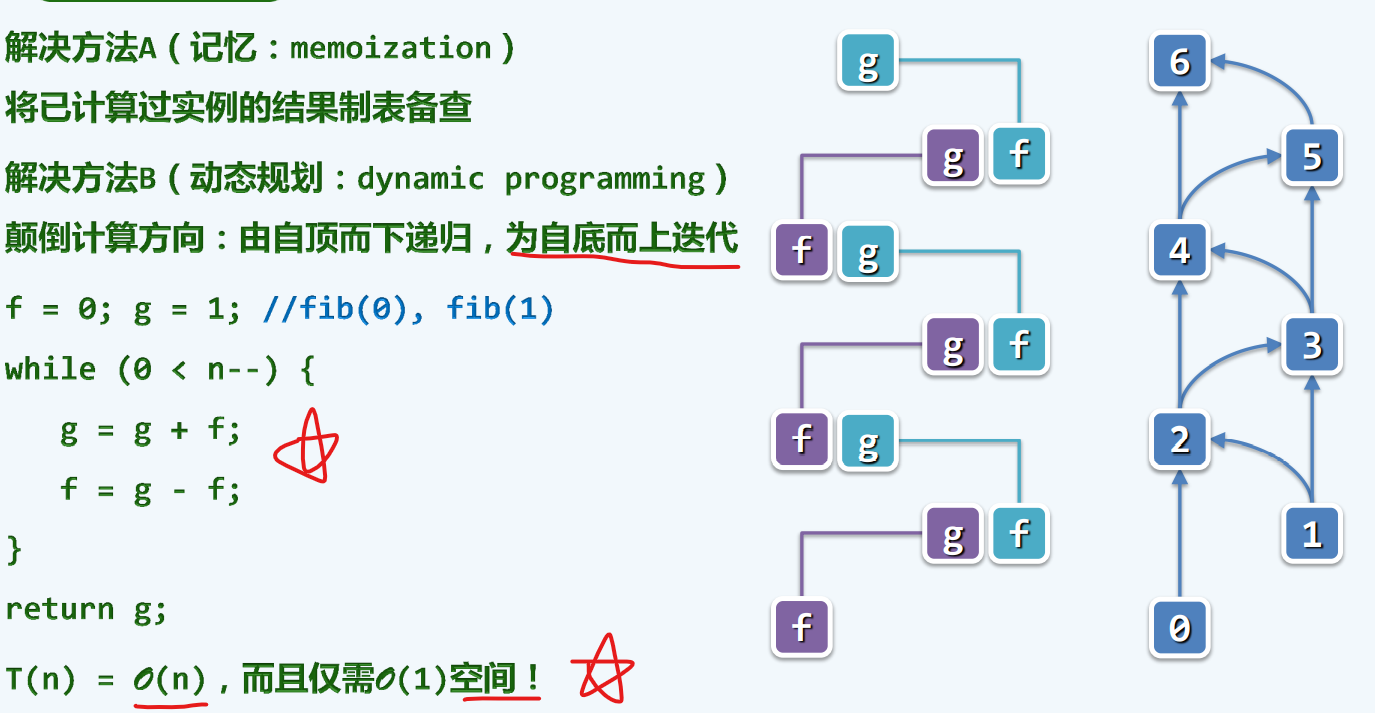
最长公共子序列

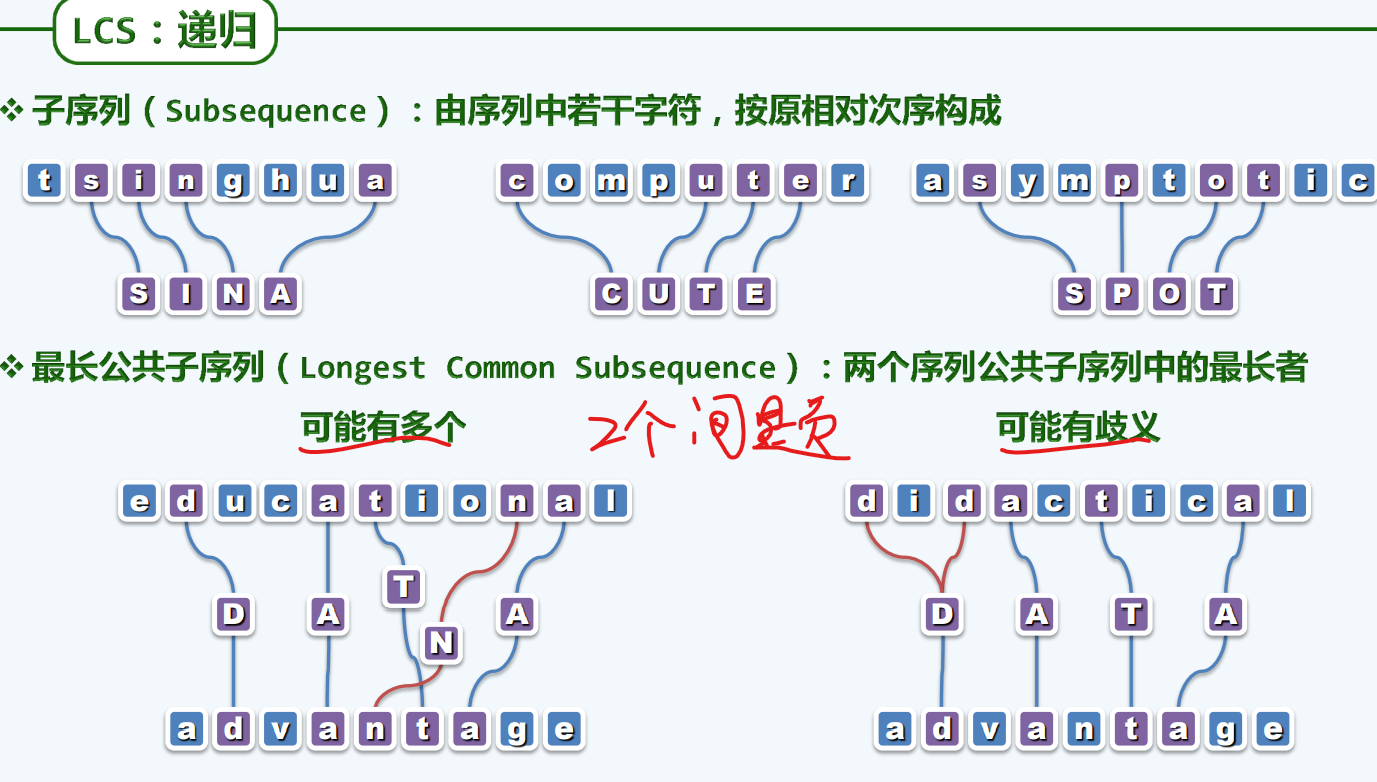
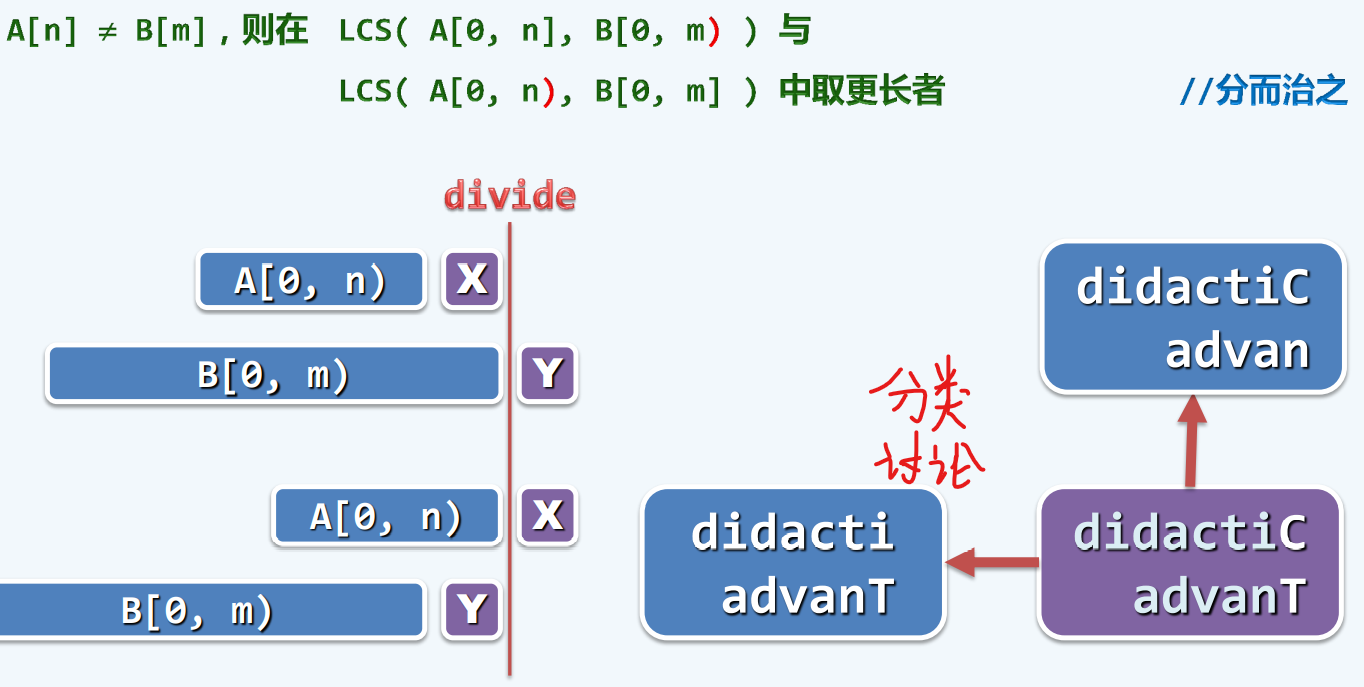
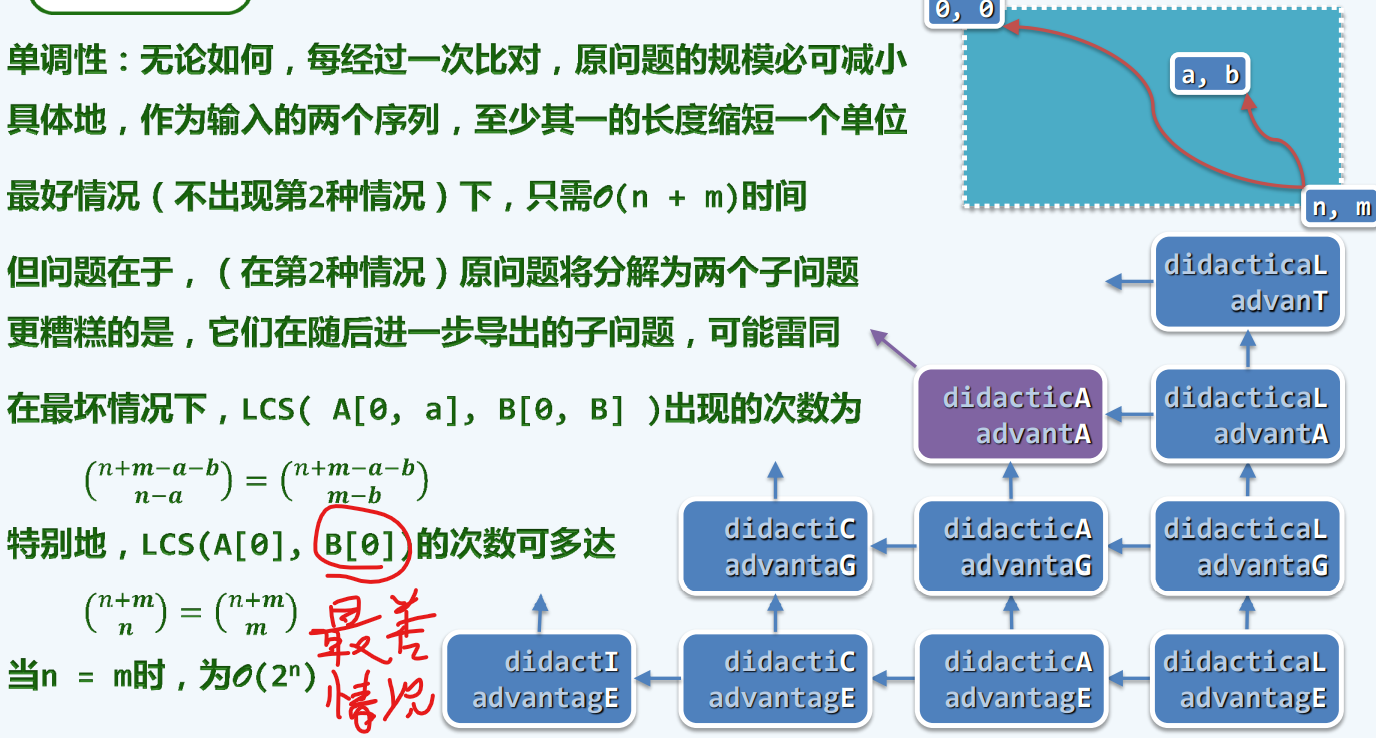
局限

循环移位

底层数学方法

看起来速度快其实不然，计算机缓存自动保存一个数据及其附近一段

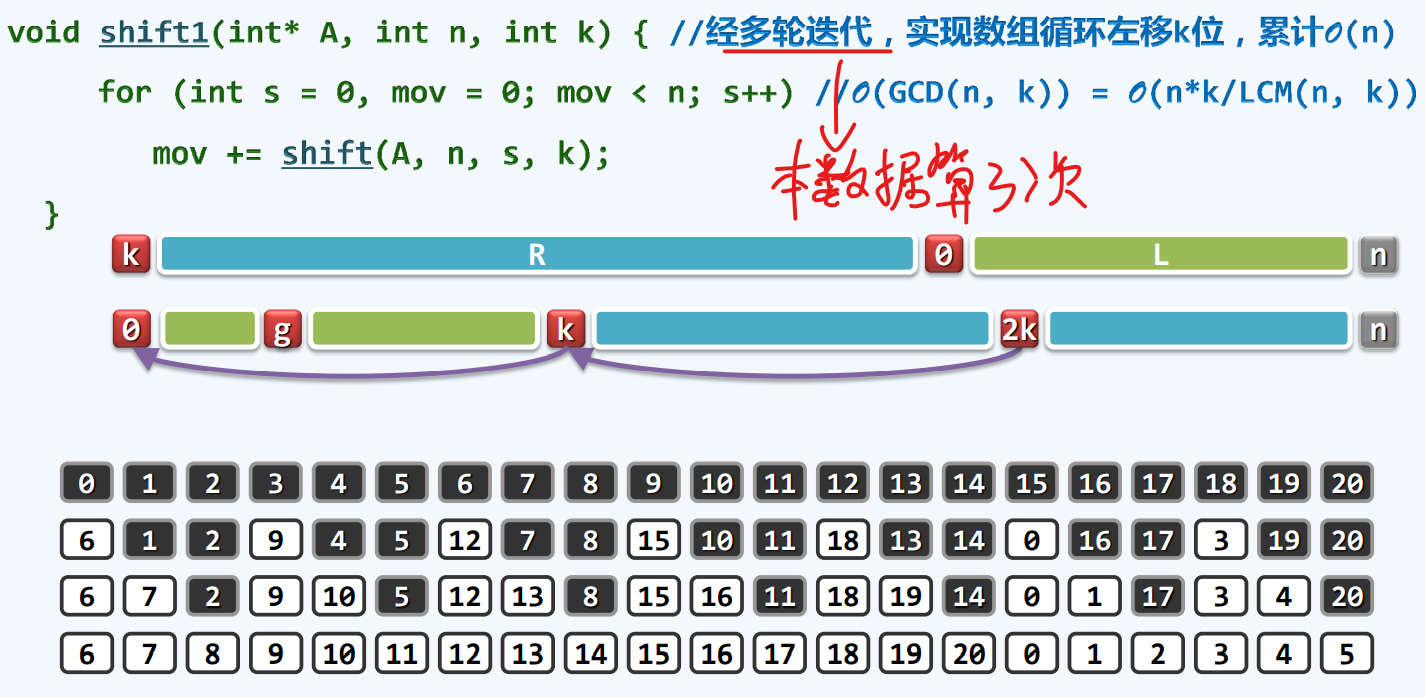
倒置版顶级方法

前交换，后交换，最后总体交换，实现总体倒置效果

reverse.h

#include"REVERSE.H"

void reverse ( int*, int, int ); //重载的倒置算法原型
void reverse ( int* A, int n ) //数组倒置（算法的初始入口，调用的可能是reverse()的递归版或迭代版）
{ reverse ( A, 0, n - 1 ); } //由重载的入口启动递归或迭代算法

reverse-iterative-1.cpp

#include <iostream>
#include"REVERSE.H"

void reverse ( int* A, int lo, int hi ) { //数组倒置（规范整理之后的迭代版）
   while ( lo < hi ) //用while替换跳转标志和if，完全等效
      swap ( A[lo++], A[hi--] ); //交换A[lo]和A[hi]，收缩待倒置区间
} //O(hi - lo + 1)

reverse.cpp 具体实现过程

void shift2(int* A, int n, int k) {//O(3n)
	reverse(A, k);
	reverse(A + k, n - k);
	reverse(A, n);

}

平均-平摊分析