以下笔记为jjyaoao本人制作,欢迎借鉴学习和提出相关建议,转载需要标明出处www.jjyaoao.space
2.向量
接口与实现

抽象数据类型:即自定义的class
数据结构:解决某类问题的可靠模板
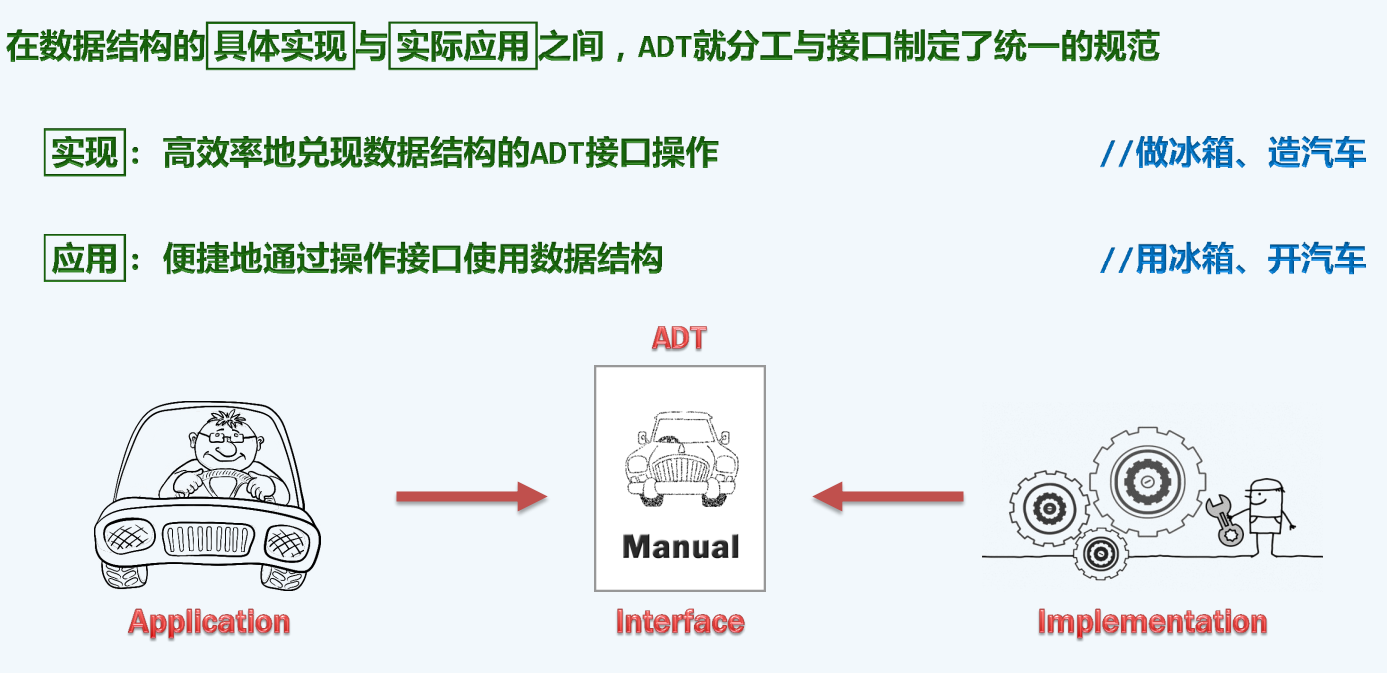
ADT即为说明书,也就是接口
Vector

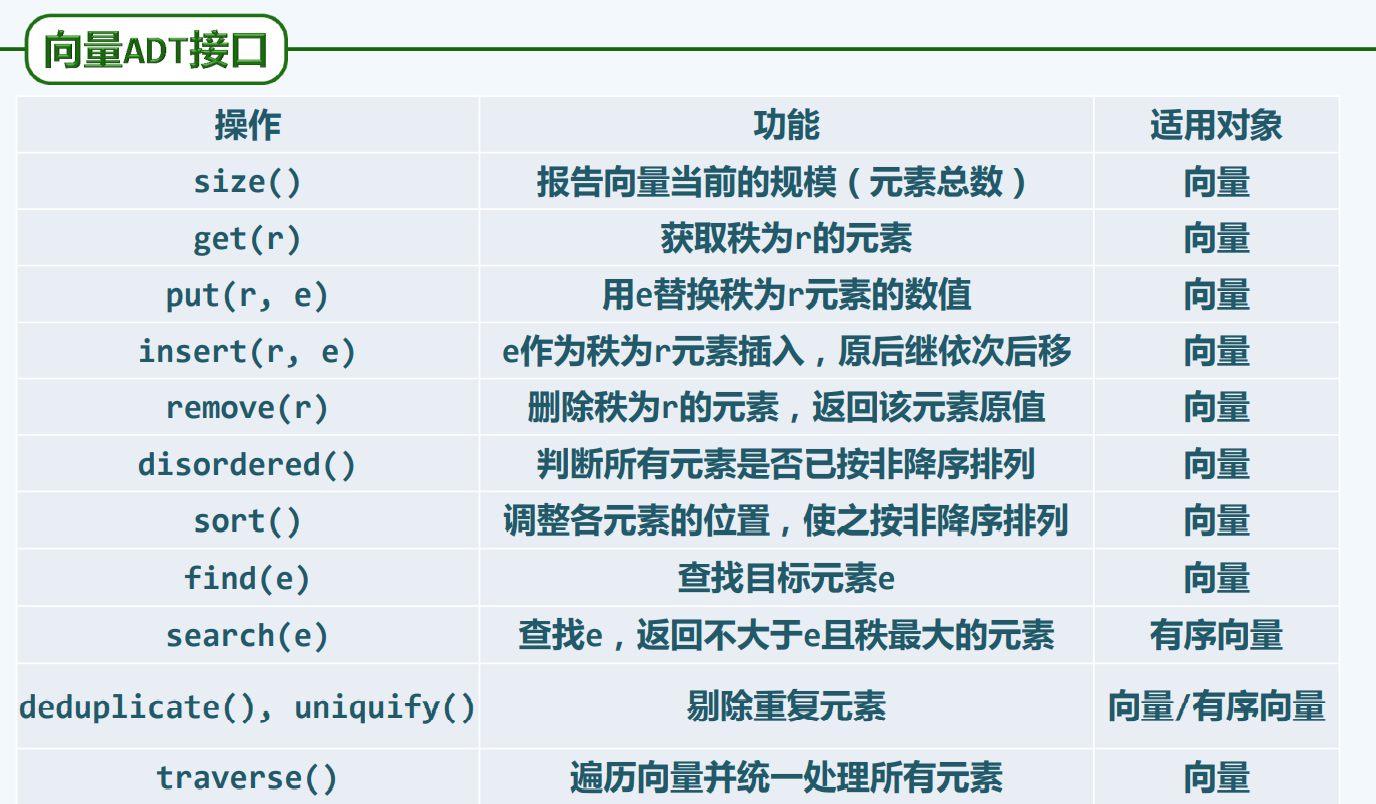
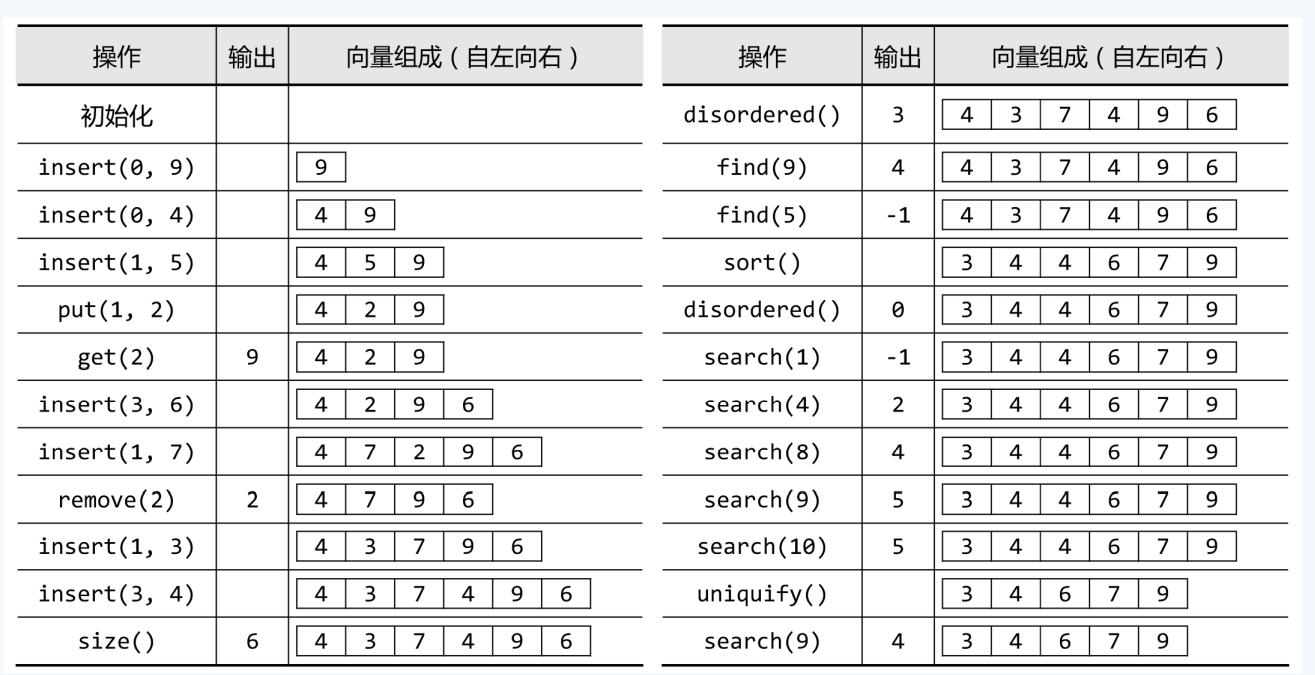
Vector的底层实现
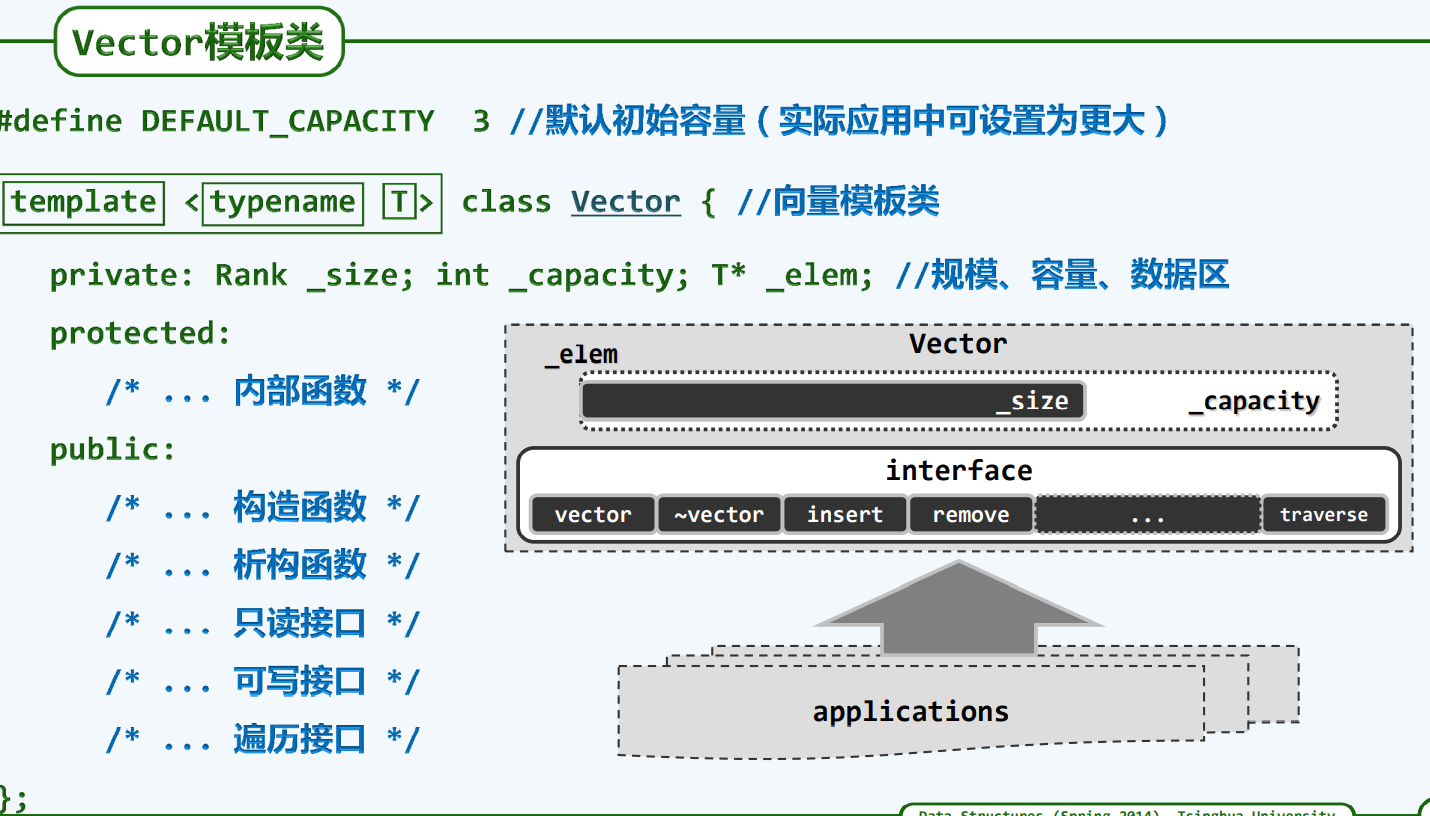
构造器与析构器

使用一次构造器,销毁一次 [] _elem,以便重新调用新的内存空间,_size还需要初始化哈,虽然好像int本身初始化就是0安。
copyFrom函数实现

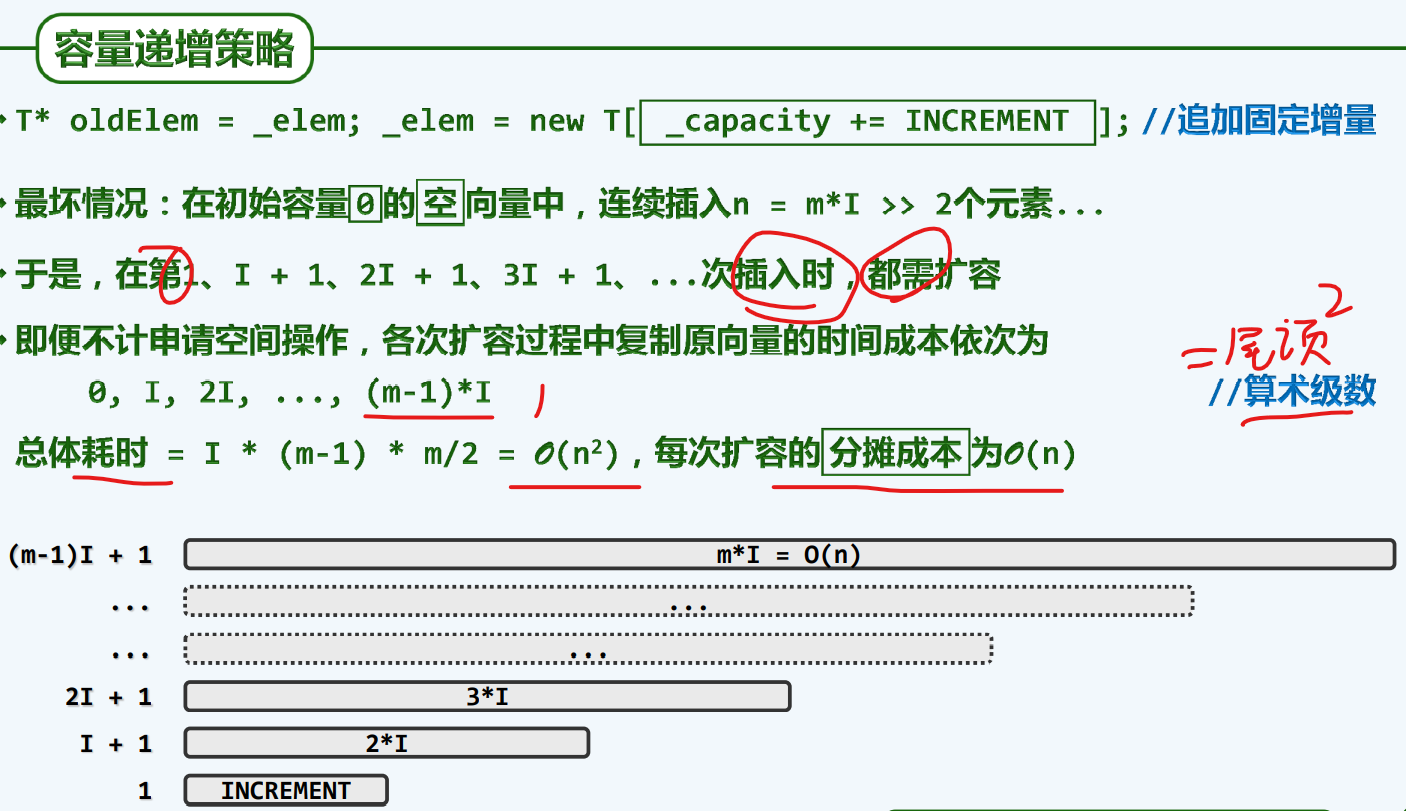
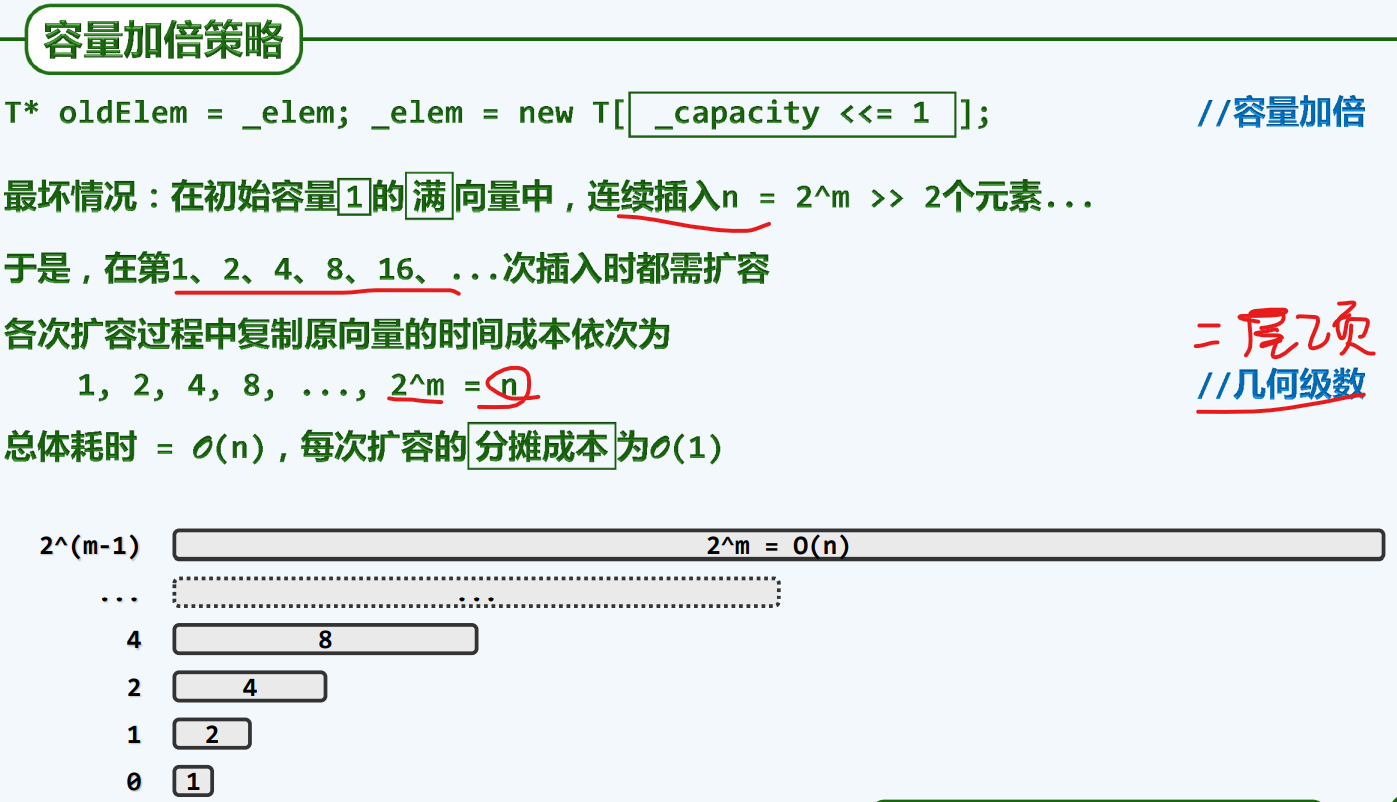
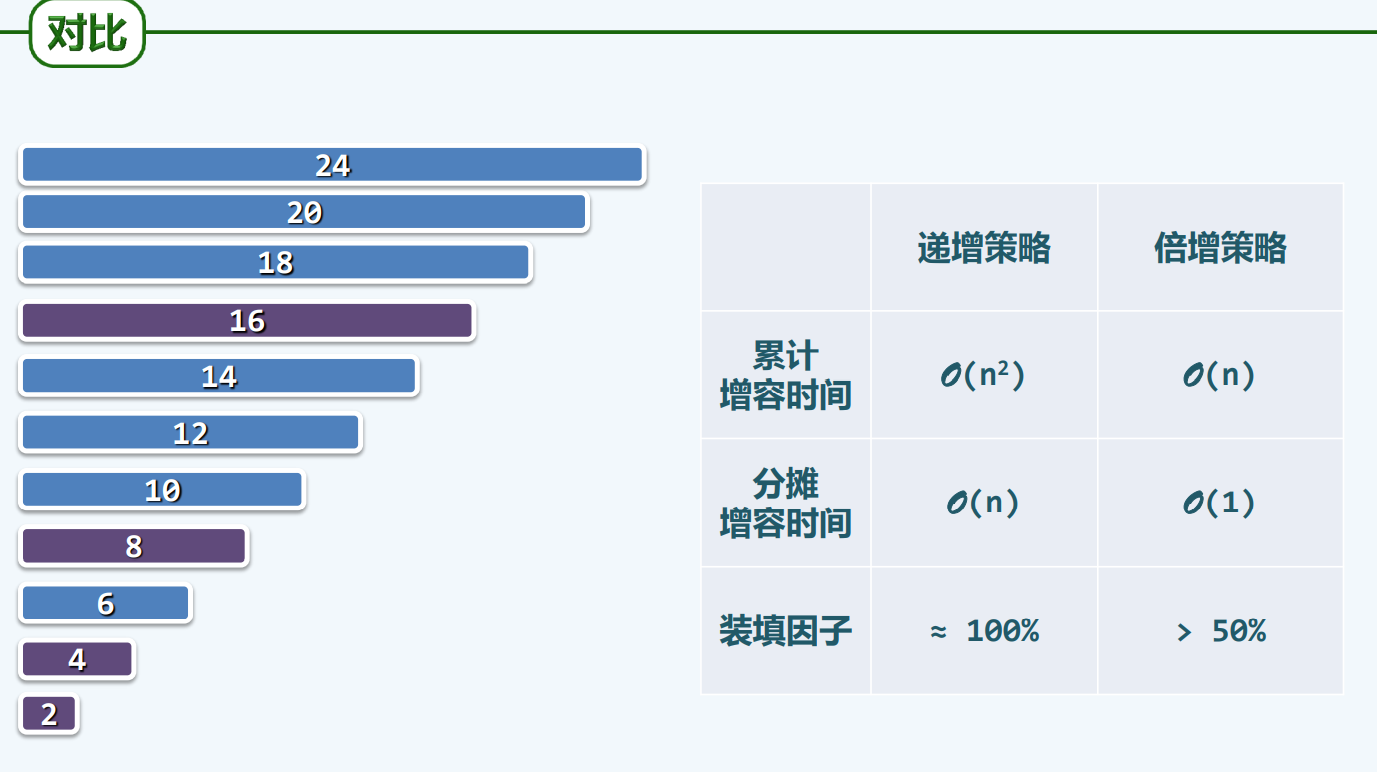
可扩充容量
静态

动态

算法与策略

无序向量
插入
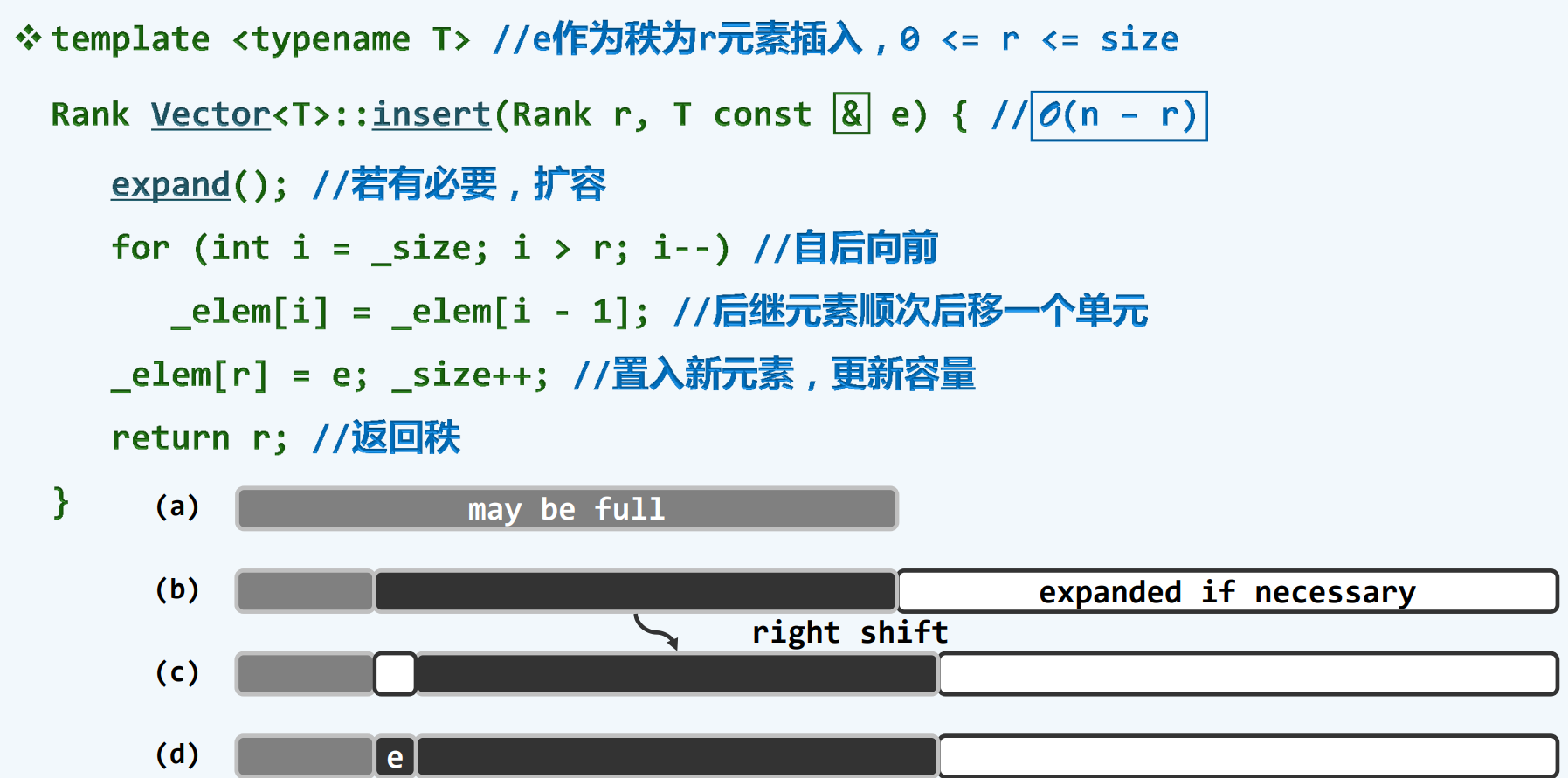
1
2
3
4
5
6
7
8
9
10
11
12
13
| #include <iostream>
#include "vector.h"
template <typename T>
Rank Vector<T>::insert(Rank r, T const& e) {
expand();
for (int i = _size; i > r; i--) {
_elem[i] = _elem[i - 1];
}
_elem[r] = e;
_size++;
}
|
删除
区间删除

单删除

代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| #include "vector.h"
template <typename T>
int Vector<T>::remove(Rank lo, Rank hi) {
if (lo == hi) return 0;
while (hi < _size) {
_elem[lo++] = _elem[hi++];
_size = lo; shrink();
return hi - lo;
}
}
template <typename T>
T Vector<T>::remove(Rank r) {
T e = _elem[r];
remove(r, r + 1);
return e;
}
|
查找

1
2
3
4
5
6
| #include "vector.h"
template <typename T>
Rank Vector<T>::find(T const& e, Rank lo, Rank hi)const {
while ((lo < hi--) && (e != _elem[hi]));
return hi;
}
|
归一化-去重
繁琐+错误版

复杂度
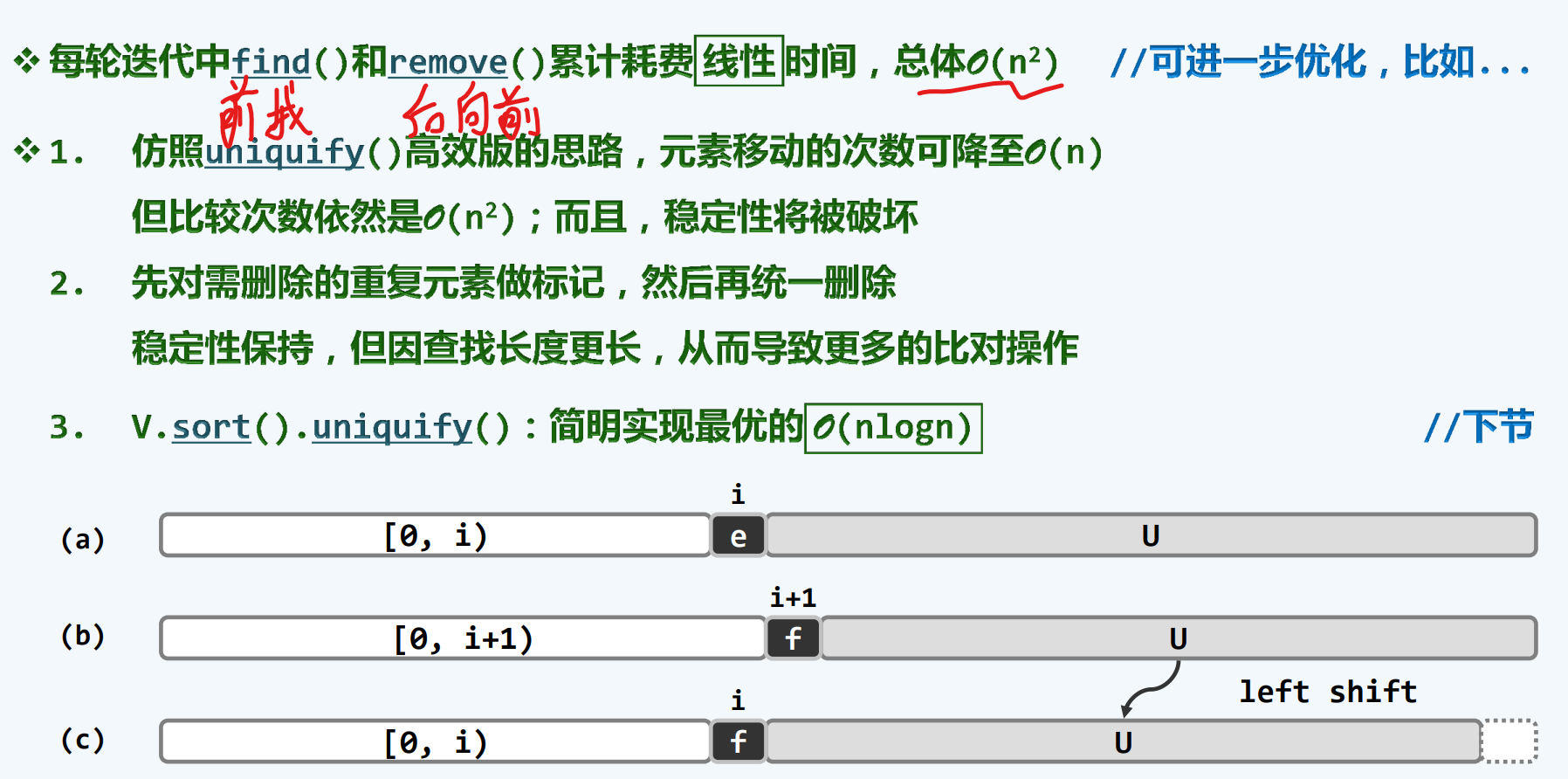
优化
1
2
3
4
5
6
7
8
| template <typename T> Rank Vector<T>::uniquify() {
0002 Rank i = 0, j = 0;
0003 while ( ++j < _size )
0004 if ( _elem[i] != _elem[j] )
0005 _elem[++i] = _elem[j];
0006 _size = ++i; shrink();
0007 return j - i;
0008 }
|
有序向量
有序性

唯一化
低效
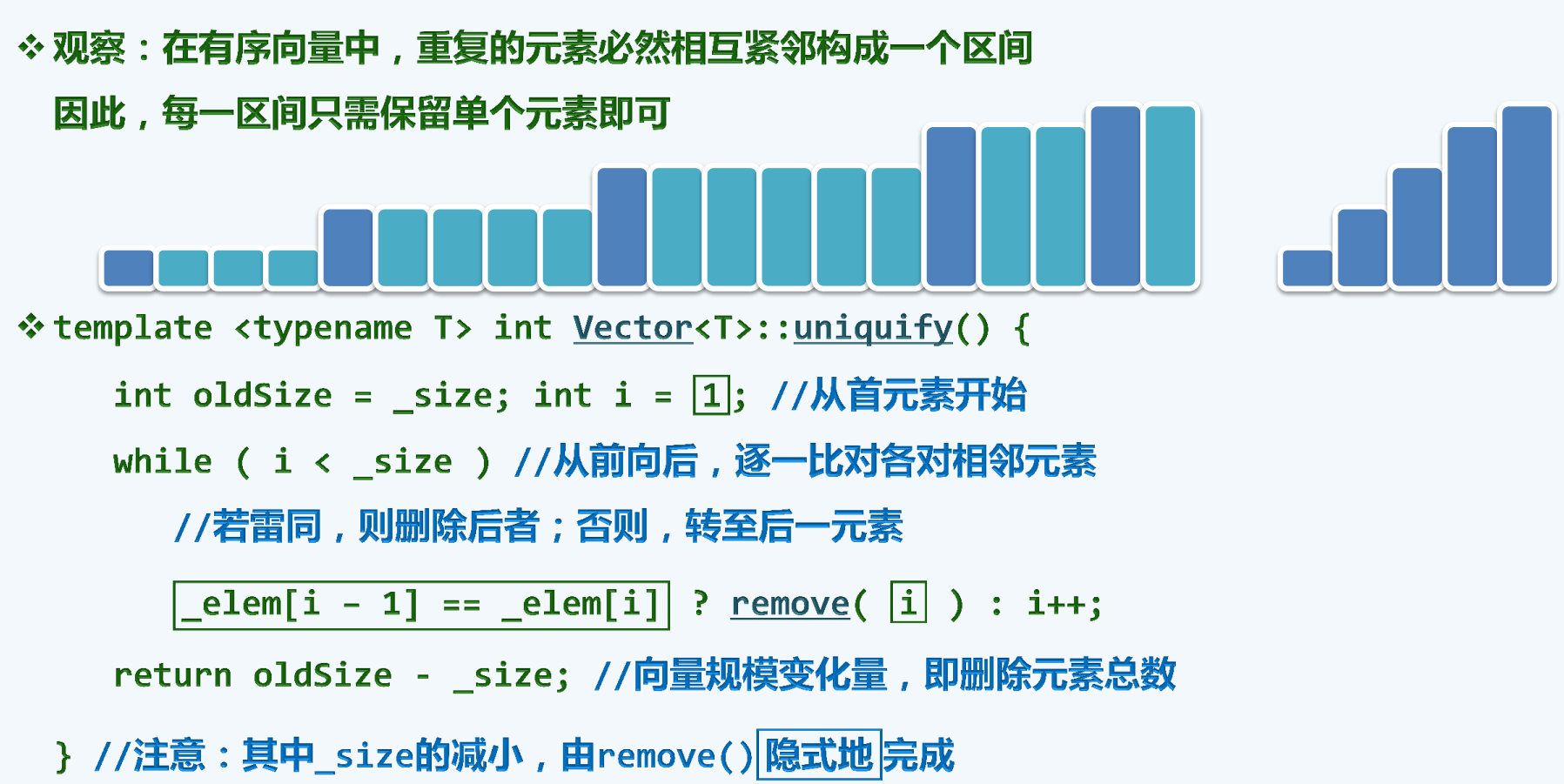
复杂度
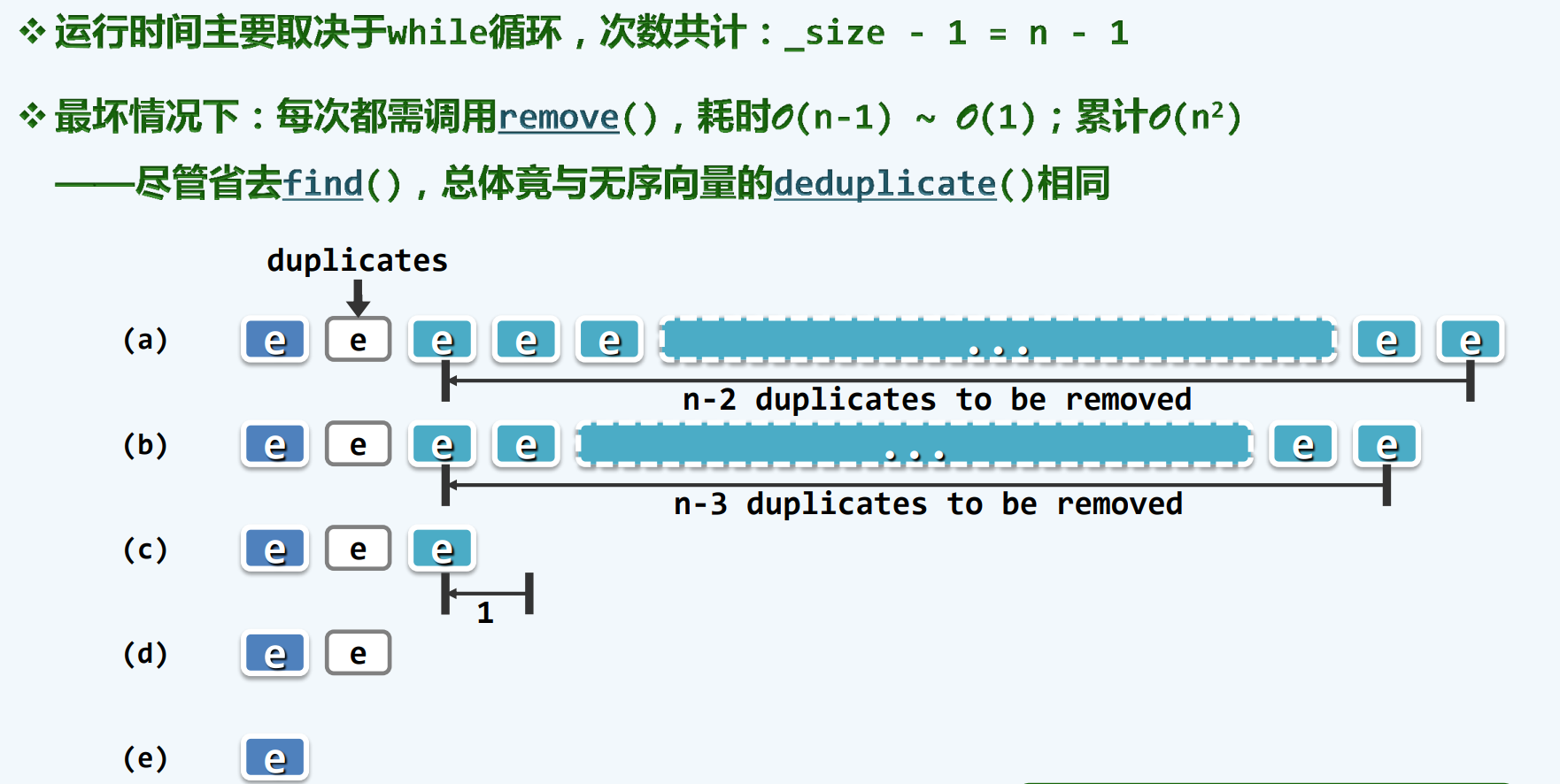
高效

复杂度
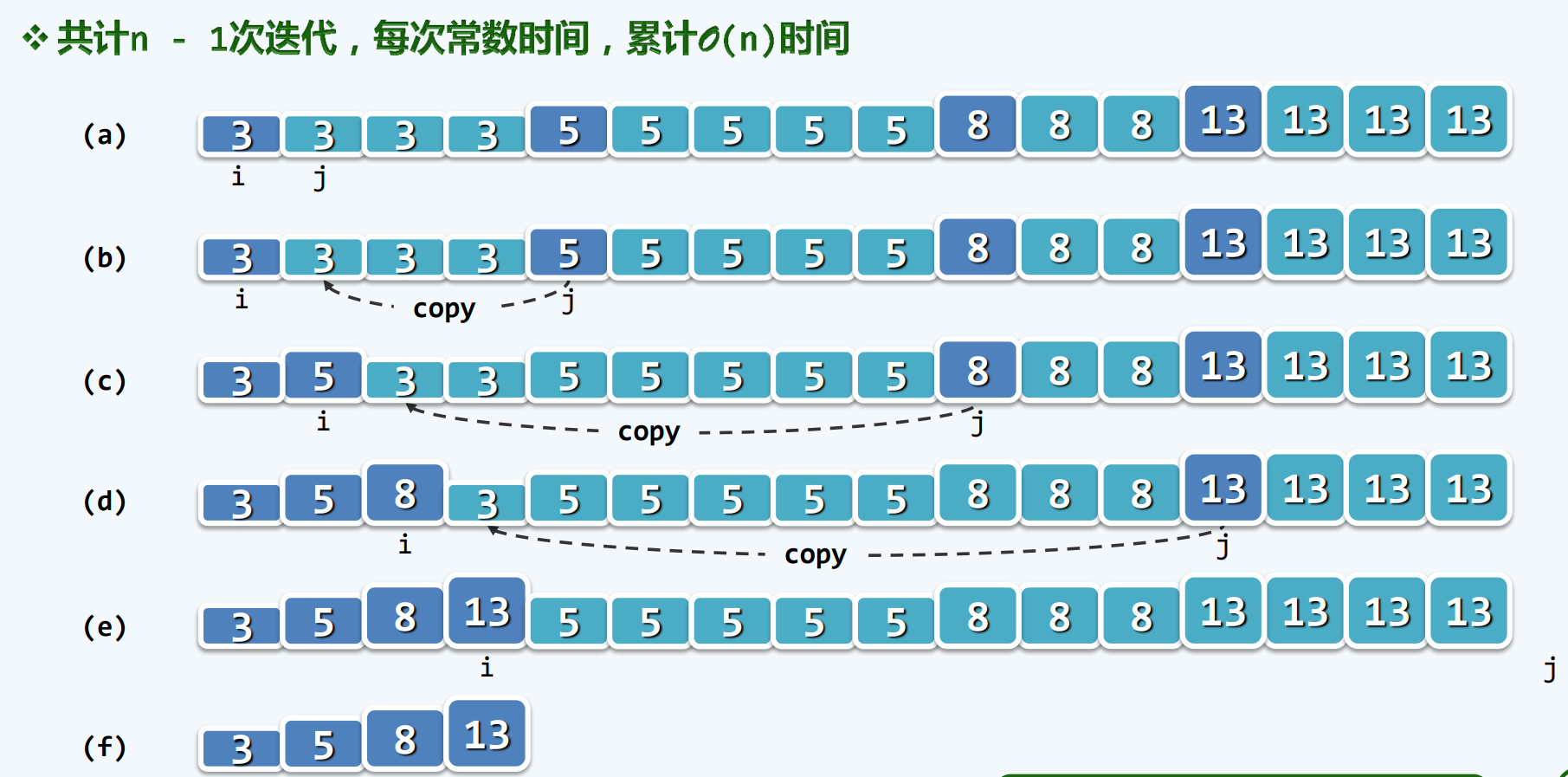
二分查找
接口

语义约定
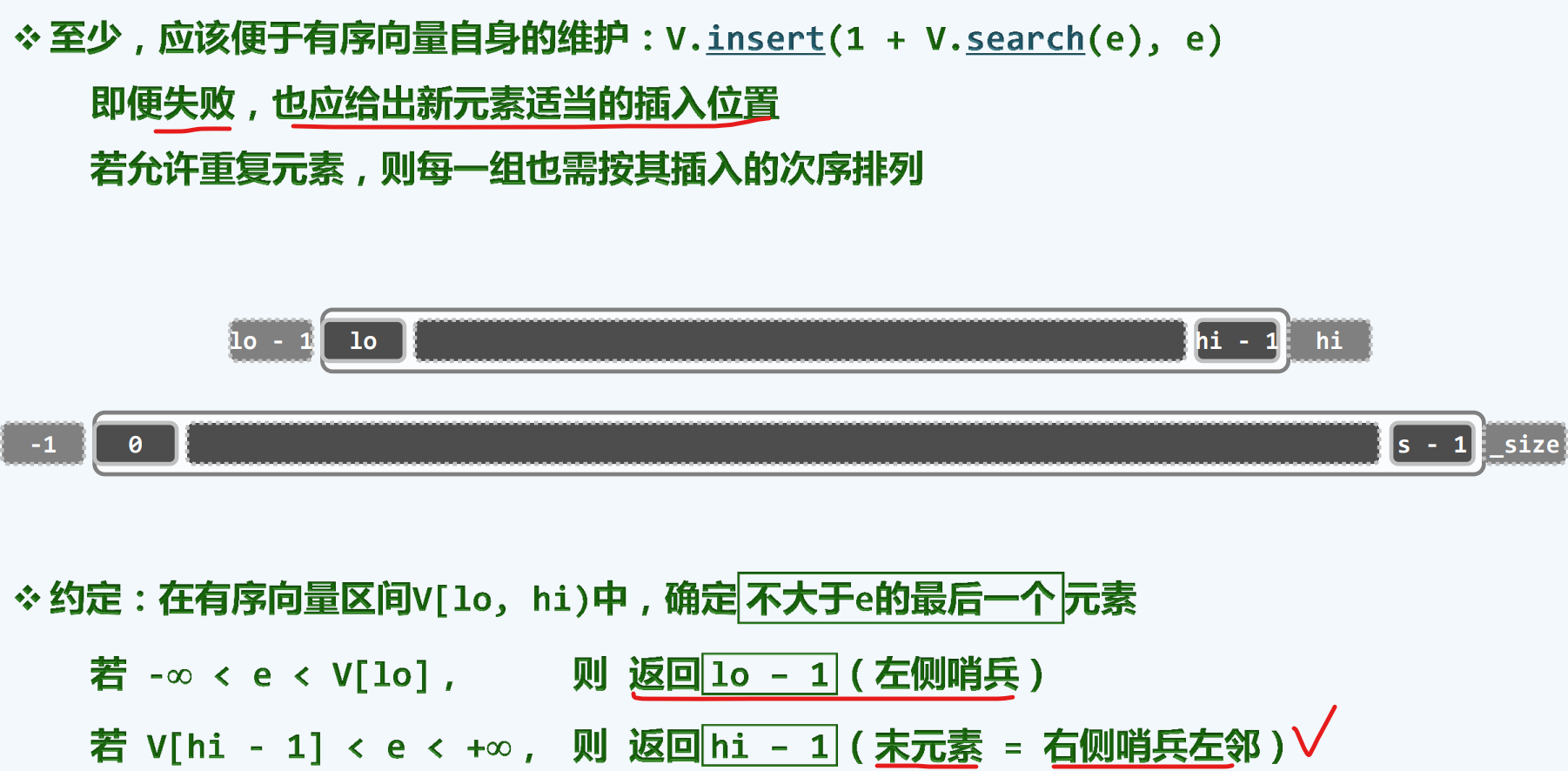
A版本实现
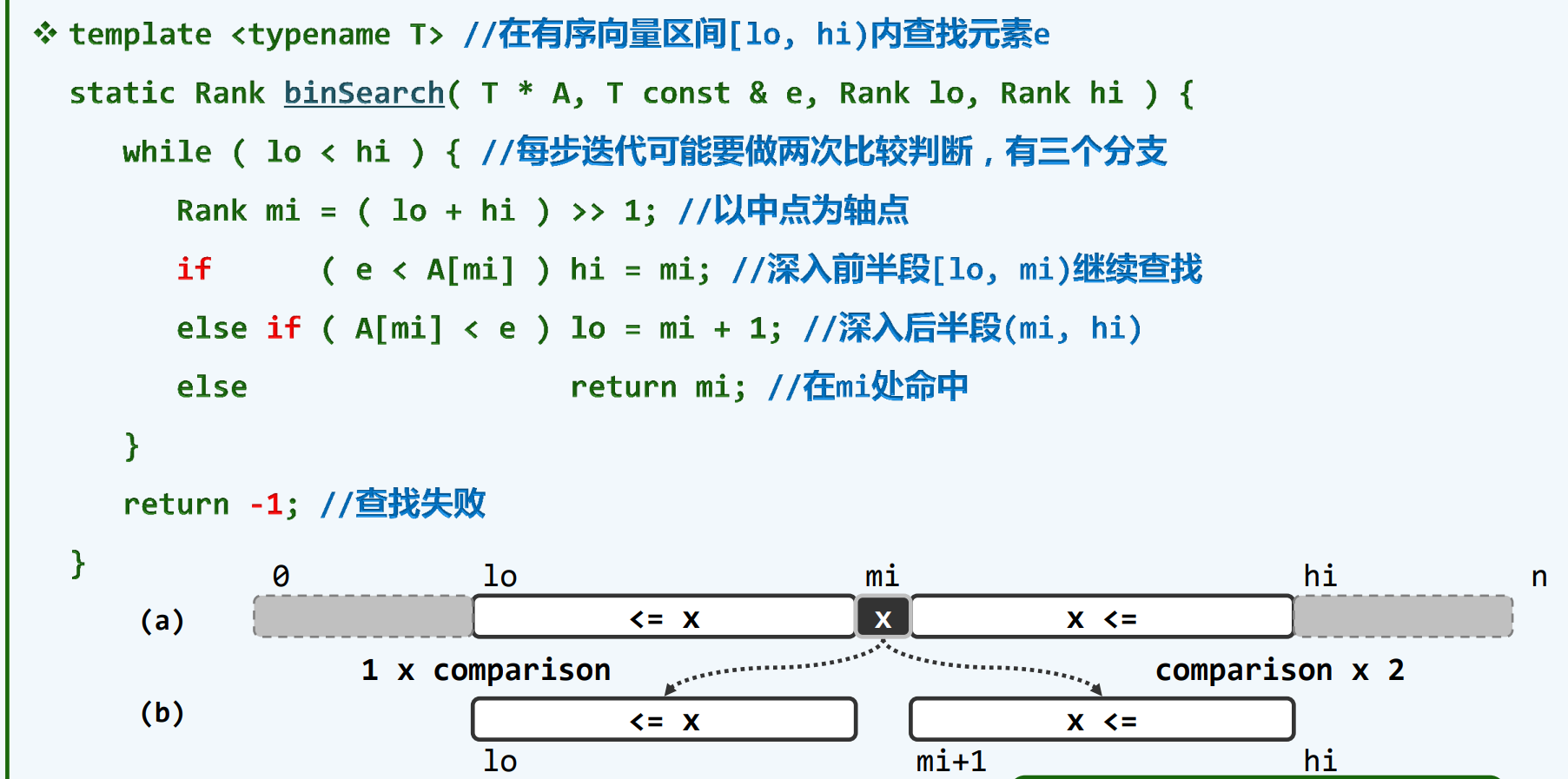
1
2
3
4
5
6
7
8
9
10
|
0002 template <typename T> static Rank binSearch ( T* S, T const& e, Rank lo, Rank hi ) {
0003 while ( lo < hi ) {
0004 Rank mi = ( lo + hi ) >> 1;
0005 if ( e < S[mi] ) hi = mi;
0006 else if ( S[mi] < e ) lo = mi + 1;
0007 else return mi;
0008 }
0009 return -1;
0010 }
|
复杂度

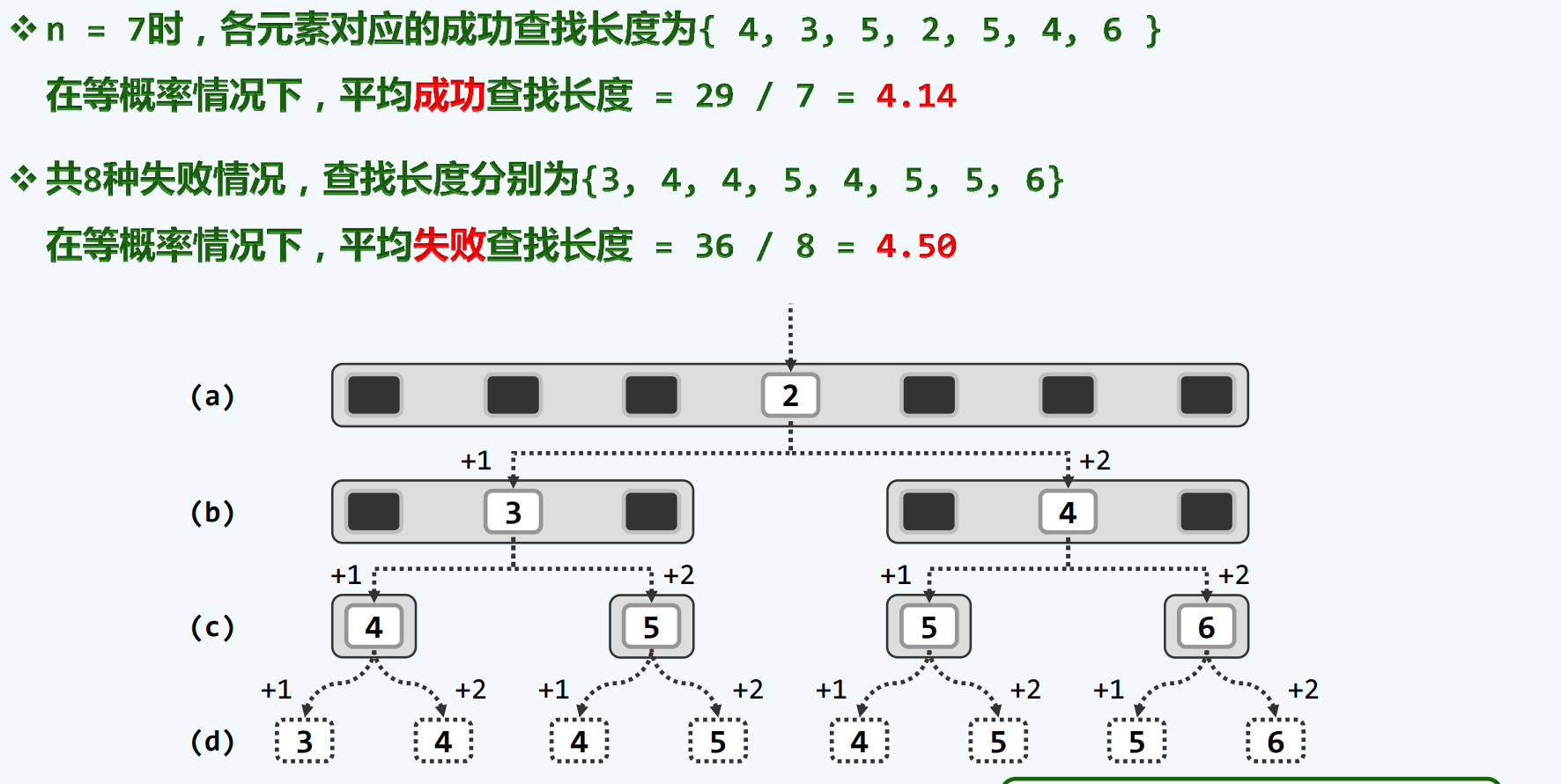
改进:B版本

C版本[我的最爱]

FibSearch实现
思想

1
2
3
4
5
6
7
8
9
10
11
12
13
| #include "fibonacci/Fib.h"
0002
0003 template <typename T> static Rank fibSearch ( T* S, T const& e, Rank lo, Rank hi ) {
0004
0005 for ( Fib fib ( hi - lo ); lo < hi; ) {
0006 while ( hi - lo < fib.get() ) fib.prev();
0007 Rank mi = lo + fib.get() - 1;
0008 if ( e < S[mi] ) hi = mi;
0009 else if ( S[mi] < e ) lo = mi + 1;
0010 else return mi;
0011 }
0012 return -1;
0013 }
|
讨论结果
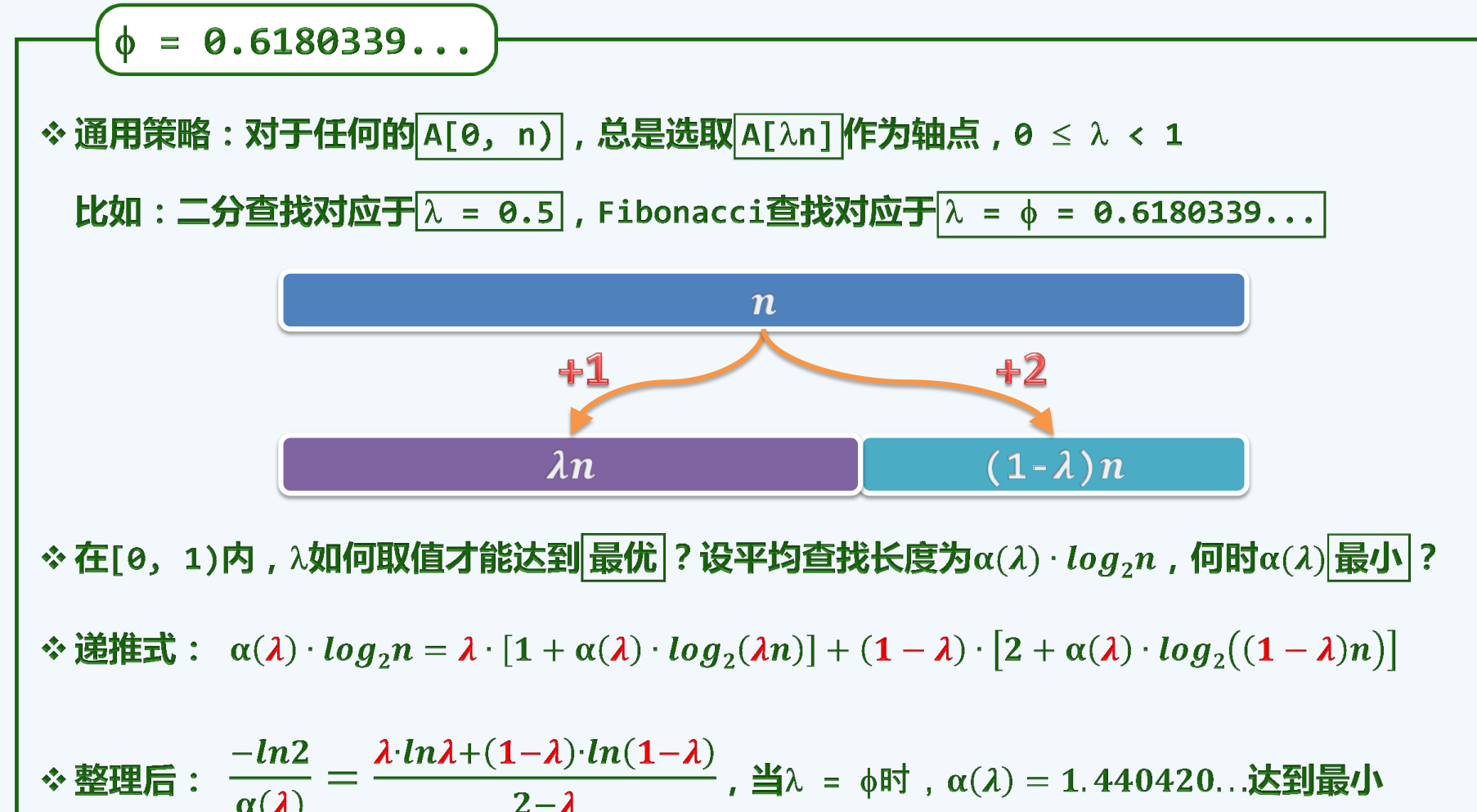
插值查找
思路

是否值得?

向量-冒泡排序
最初版本

改进

向量-归并排序
原理
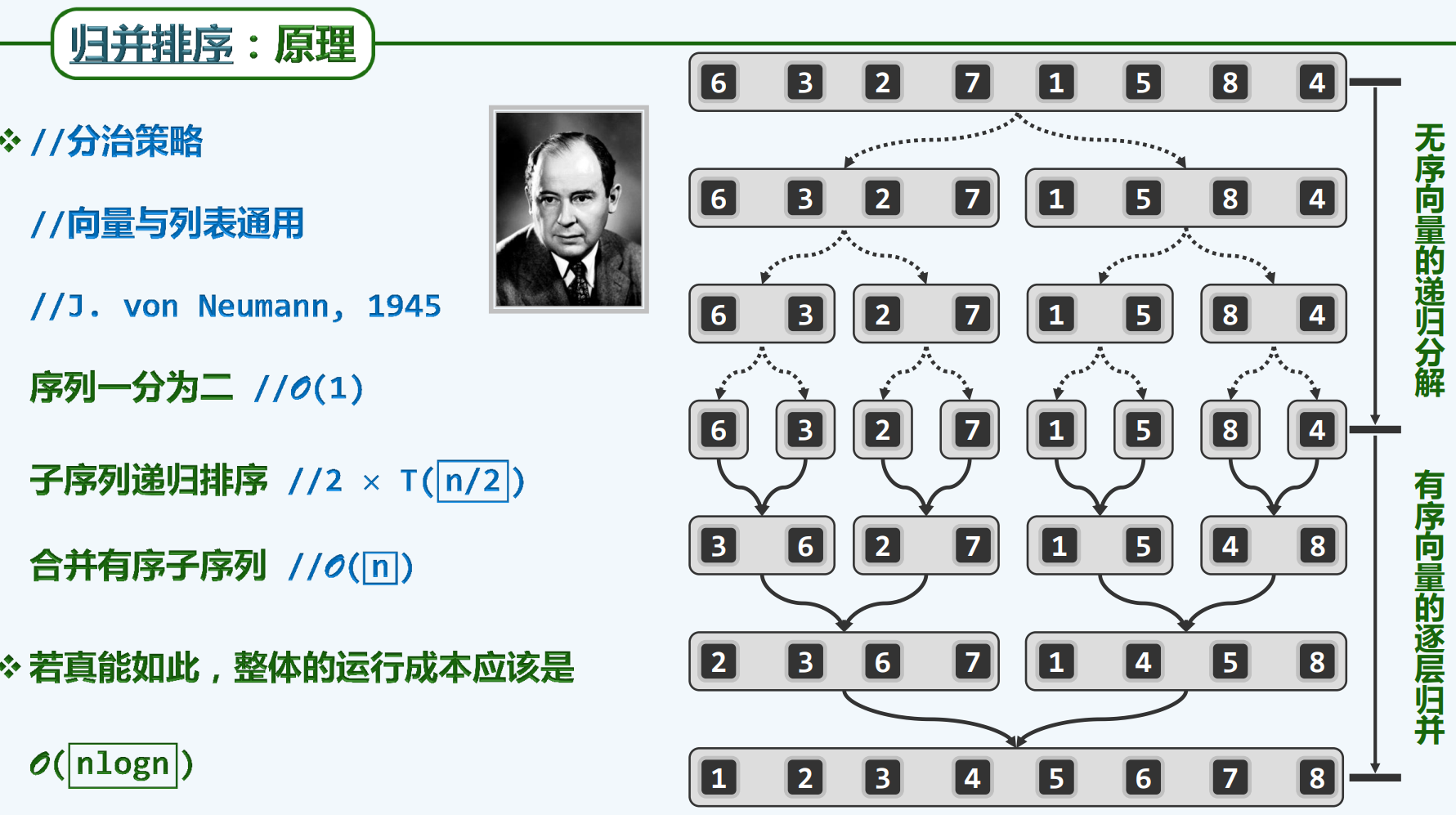
实现

二路归并
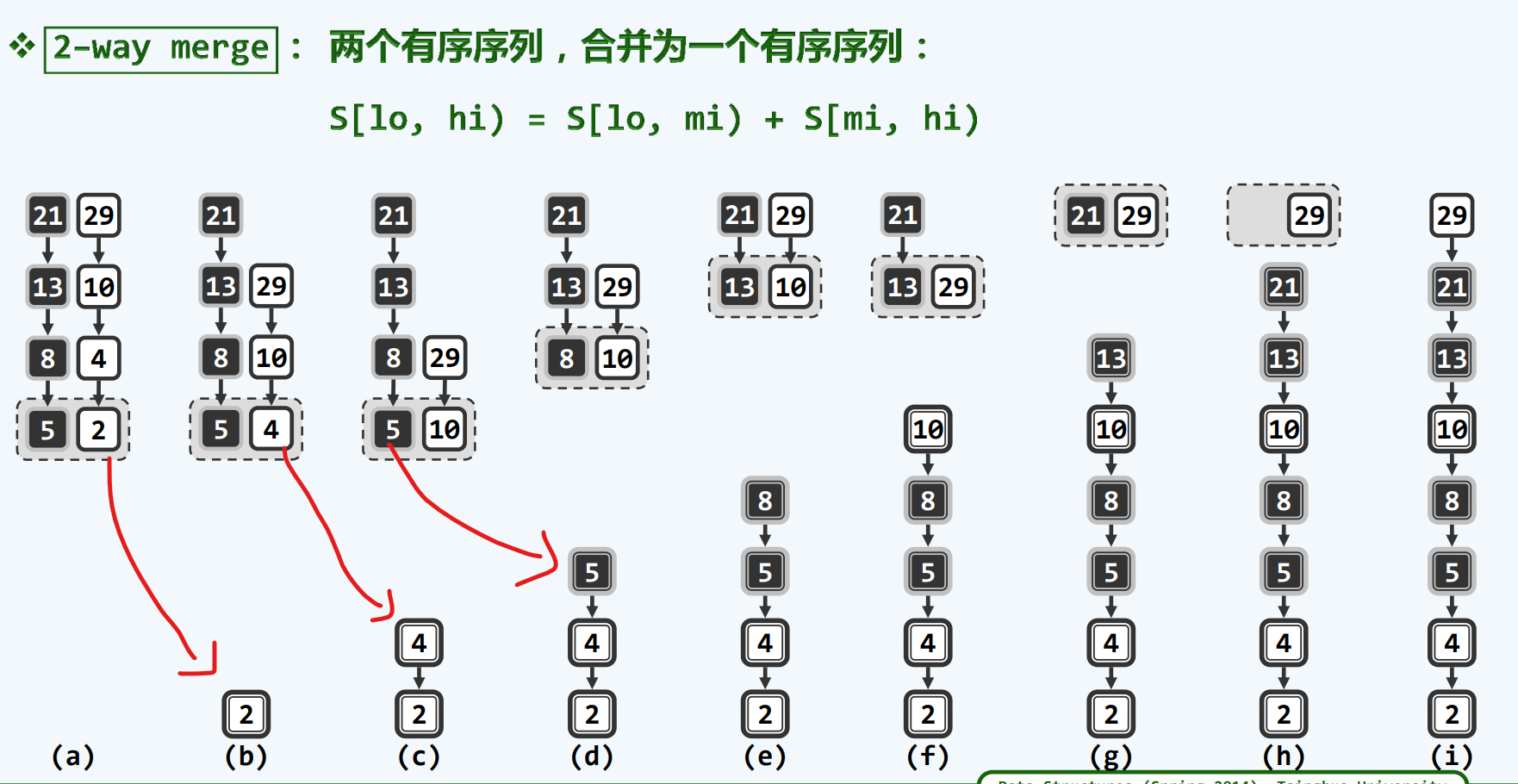
基本实现

精简实现

复杂度分析

优缺点评价






















































