以下笔记为jjyaoao本人制作，欢迎借鉴学习和提出相关建议，转载需要标明出处www.jjyaoao.space

3.列表

从向量到列表

没有前驱/后继的唯一节点称为首/末

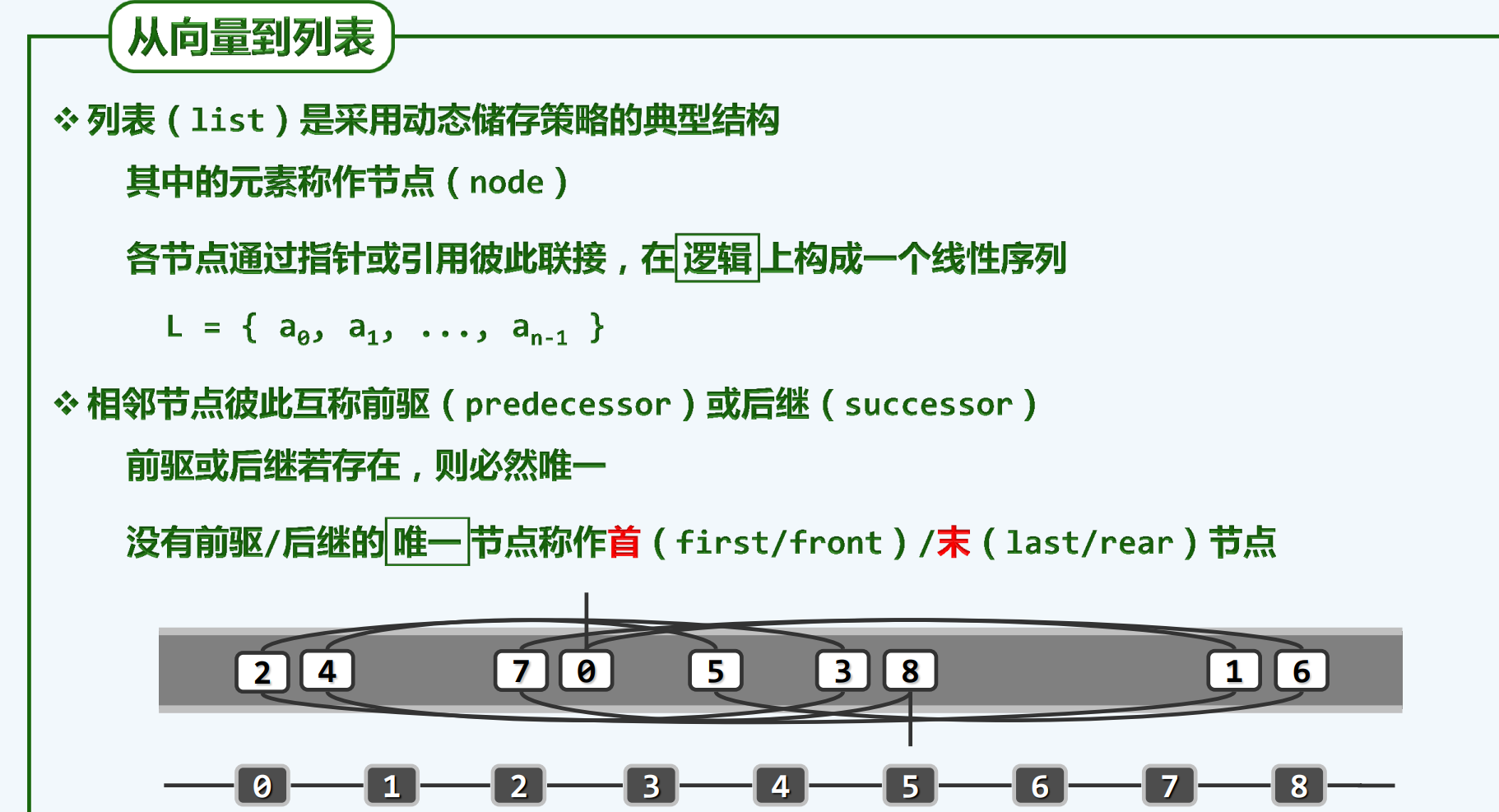
image-20220226204245562

从静态到动态

image-20220226204337372

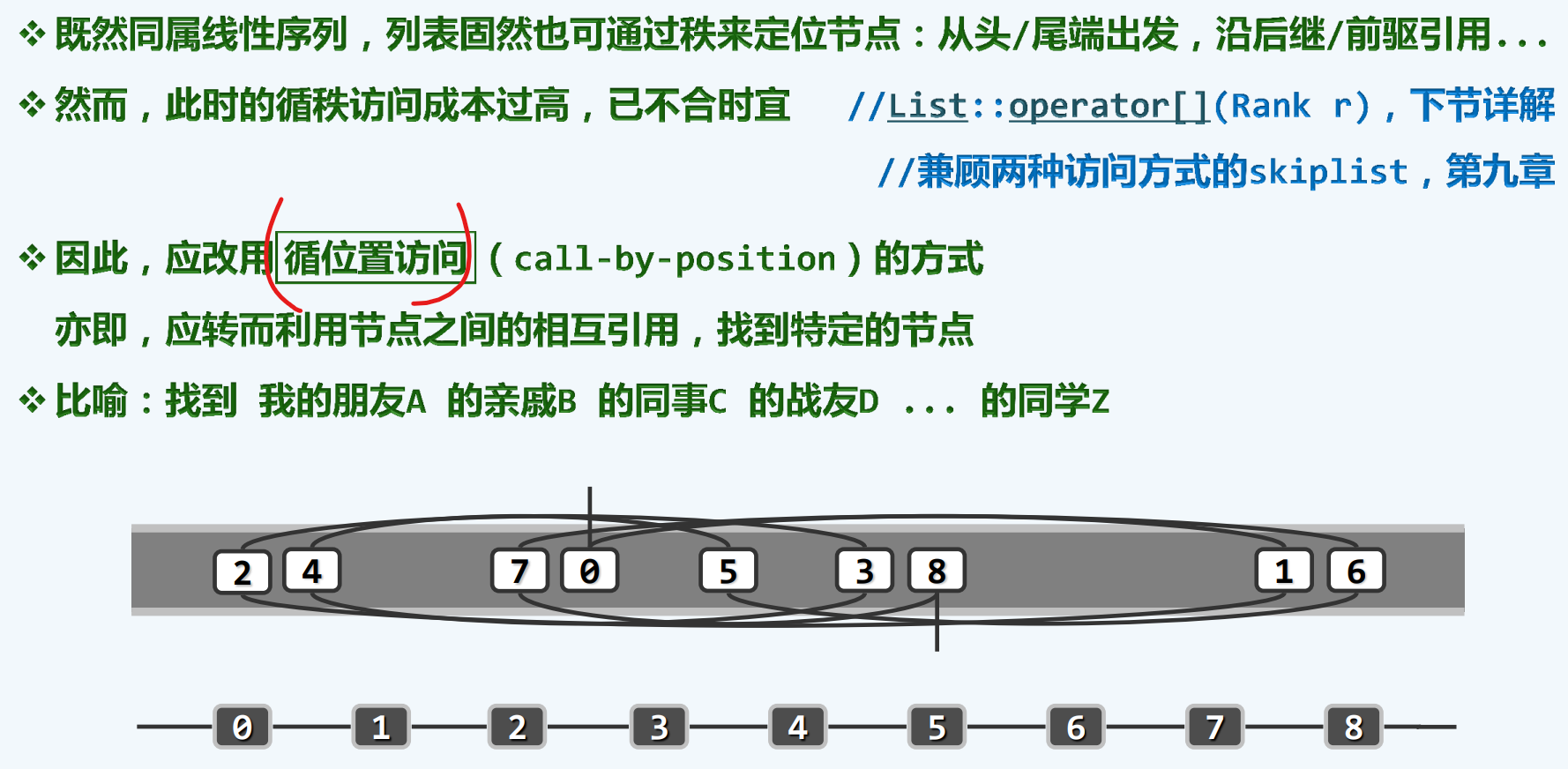
从秩到位置

寻秩访问到循位置访问

image-20220226204710183

列表所需模板类

ListNode

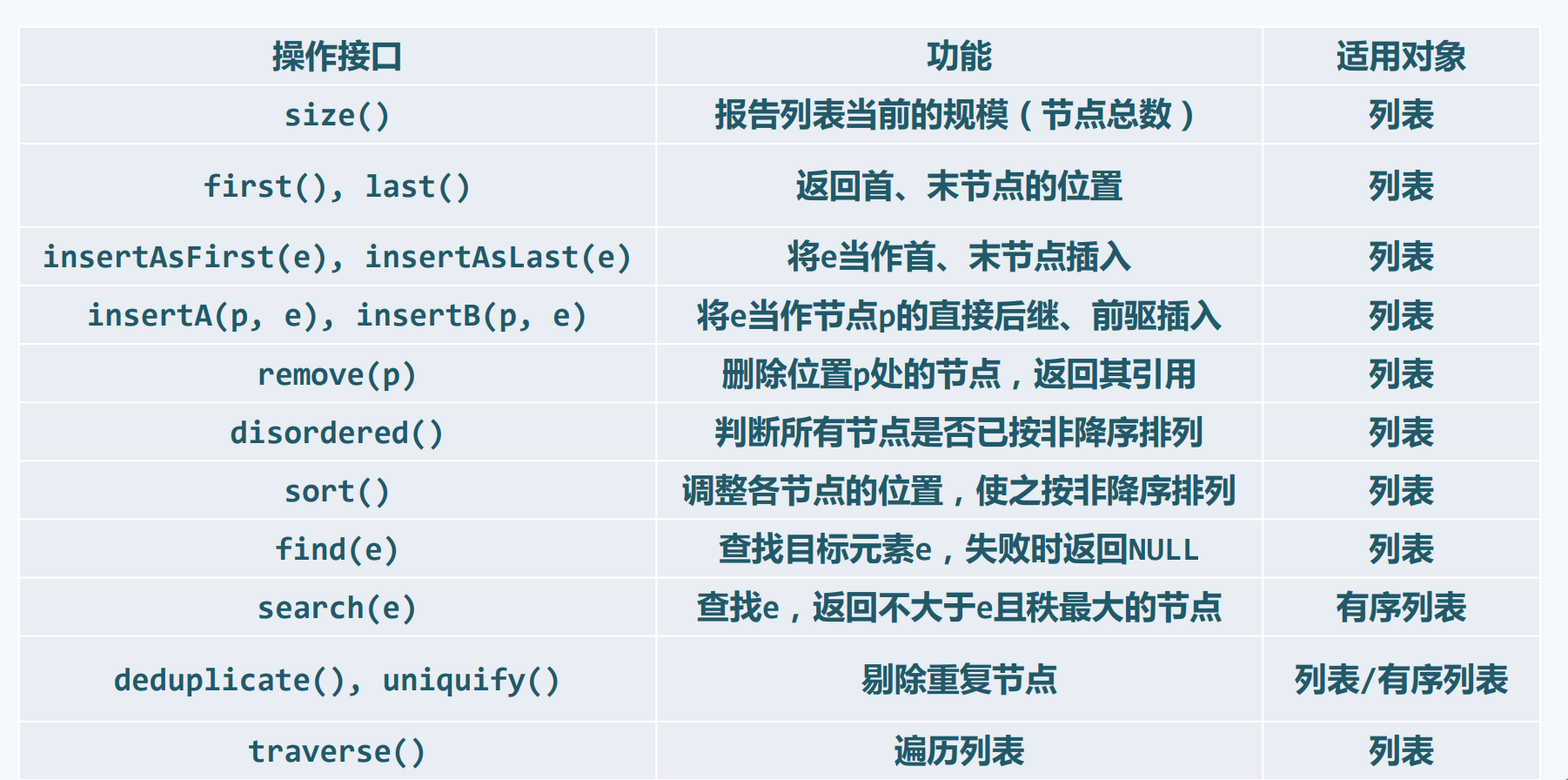
接口

image-20220226204759399

1
2
3
4
5
6
7
8
9
10
11
12
13
14
using Rank = int; //秩
0002 template <typename T> struct ListNode;
0003 template <typename T> using ListNodePosi = ListNode<T>*; //列表节点位置
0004 template <typename T> struct ListNode { //列表节点模板类（以双向链表形式实现）
0005 // 成员
0006    T data; ListNodePosi<T> pred; ListNodePosi<T> succ; //数值、前驱、后继
0007 // 构造函数
0008    ListNode() {} //针对header和trailer的构造
0009    ListNode ( T e, ListNodePosi<T> p = NULL, ListNodePosi<T> s = NULL )
0010       : data ( e ), pred ( p ), succ ( s ) {} //默认构造器
0011 // 操作接口
0012    ListNodePosi<T> insertAsPred ( T const& e ); //紧靠当前节点之前插入新节点
0013    ListNodePosi<T> insertAsSucc ( T const& e ); //紧随当前节点之后插入新节点
0014 };

List

接口

image-20220226205137775

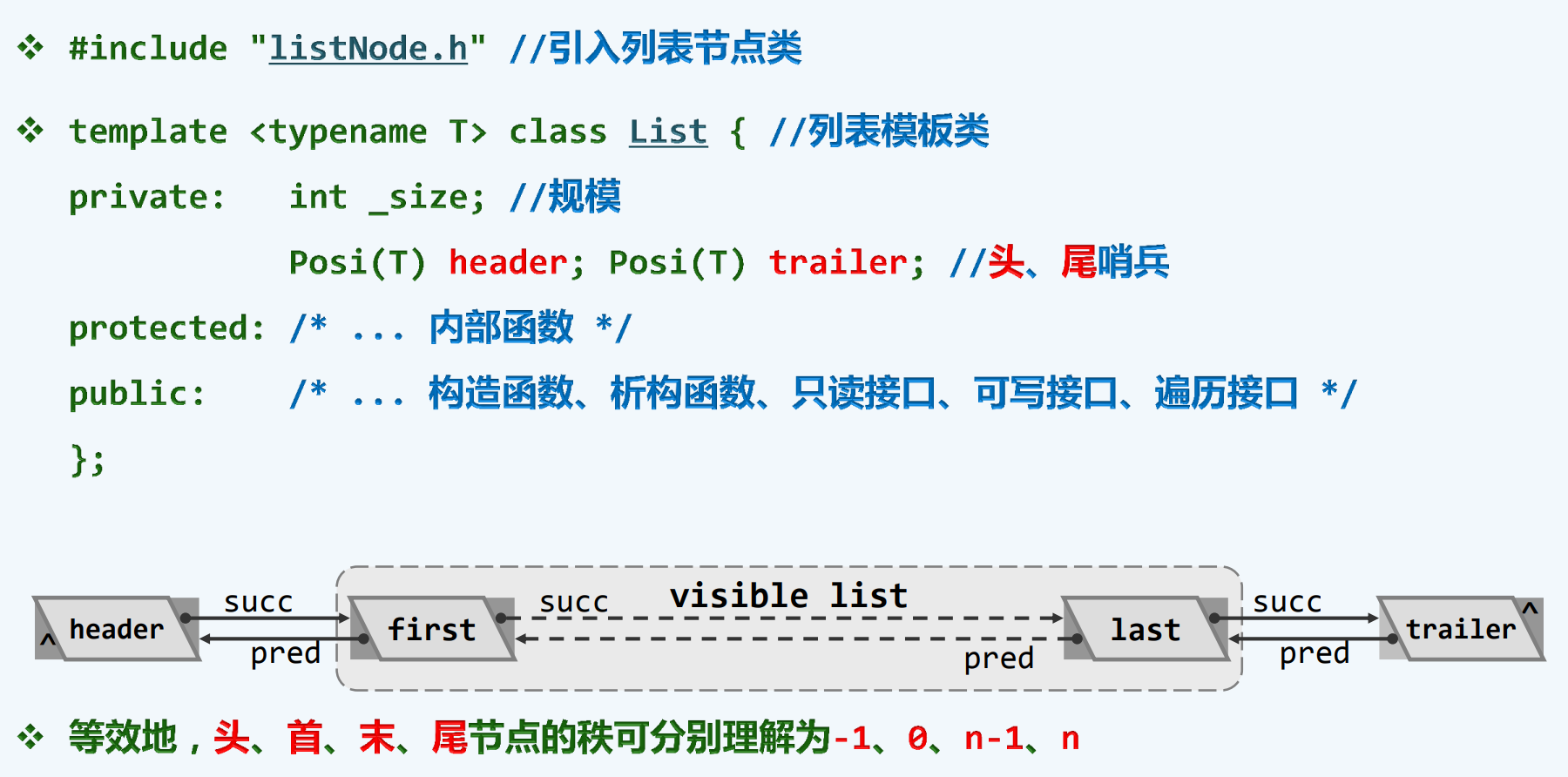
宏观结构

header 和 trailer 是不可见的，可他们的作用非常巨大！

头与尾是与生俱来的，而且并不保证可以相同

而first和last并不见得不相同，甚至不能保证他们存在，但对外而言，first和last是可见的

image-20220226205414158

初始化

1
2
3
4
5
6
7
template <typename T> void List<T>::init() { //列表初始化，在创建列表对象时统一调用
0002    header = new ListNode<T>; //创建头哨兵节点
0003    trailer = new ListNode<T>; //创建尾哨兵节点
0004    header->succ = trailer; header->pred = NULL;
0005    trailer->pred = header; trailer->succ = NULL;
0006    _size = 0; //记录规模
0007 }

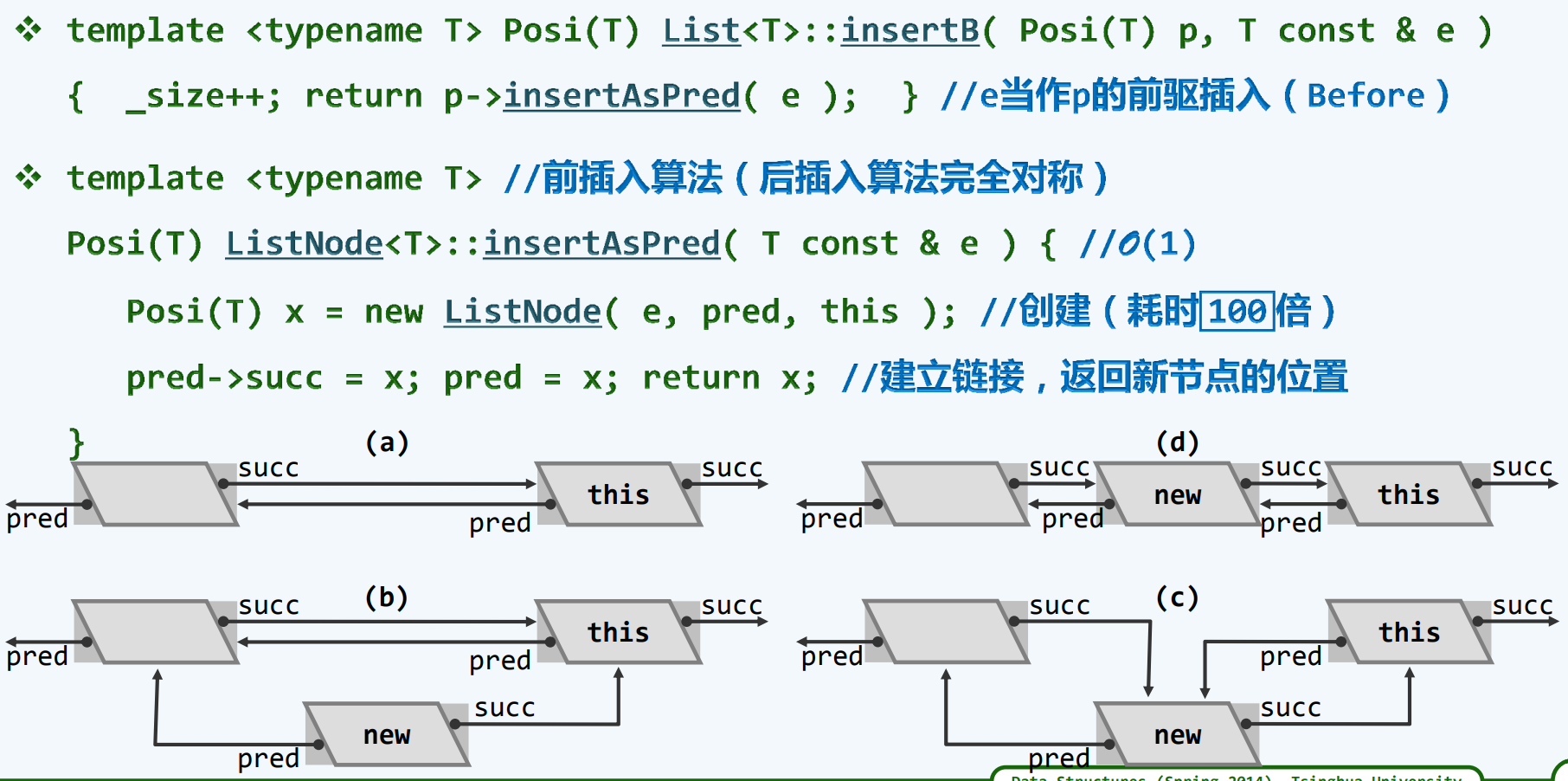
插入与构造

前驱插入

即便是第一个节点和最后一个节点，我们说他仍然是正确的，因为有哨兵头尾的存在！

image-20220226210042192

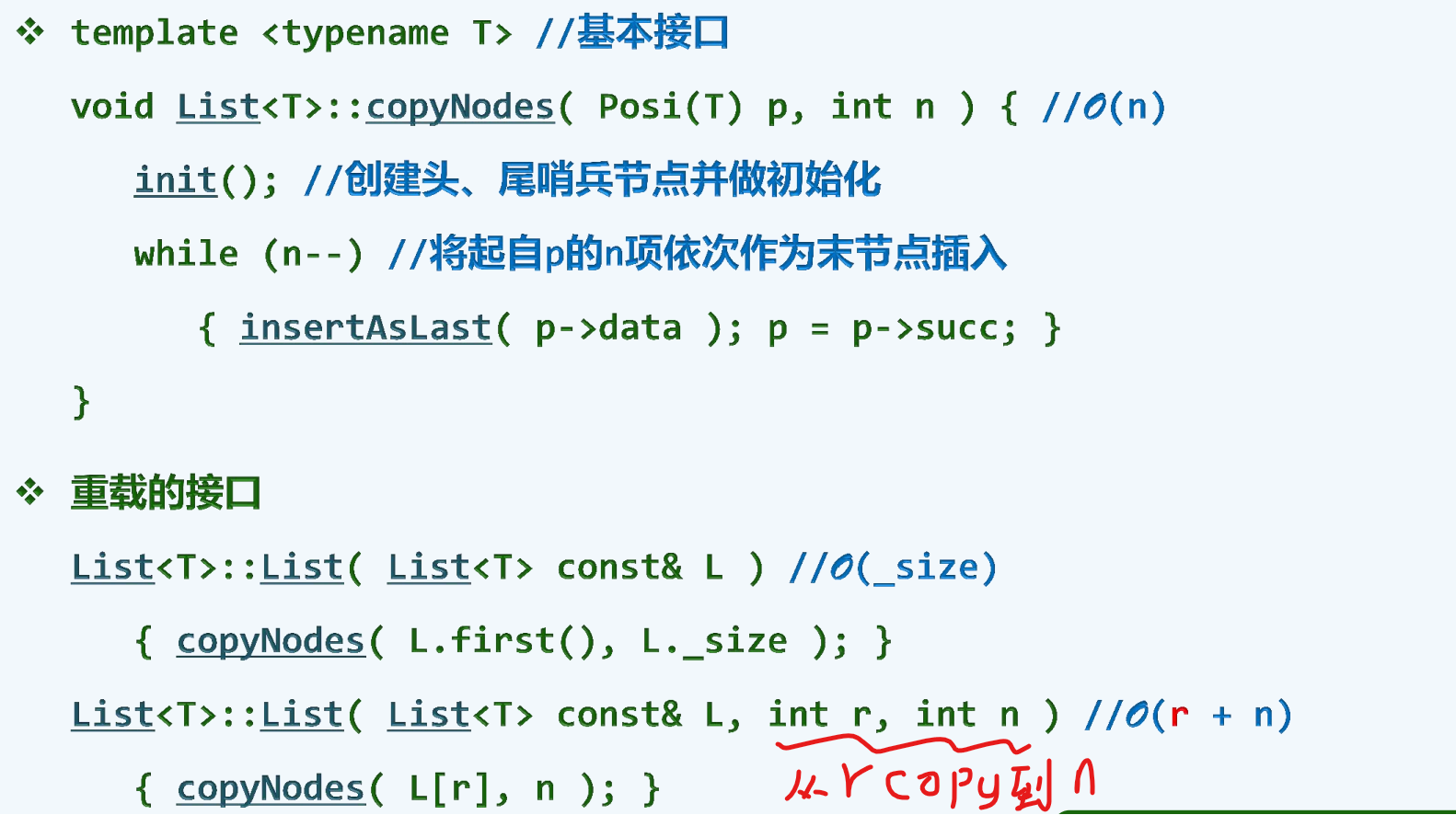
复制（构造）

image-20220226210326483

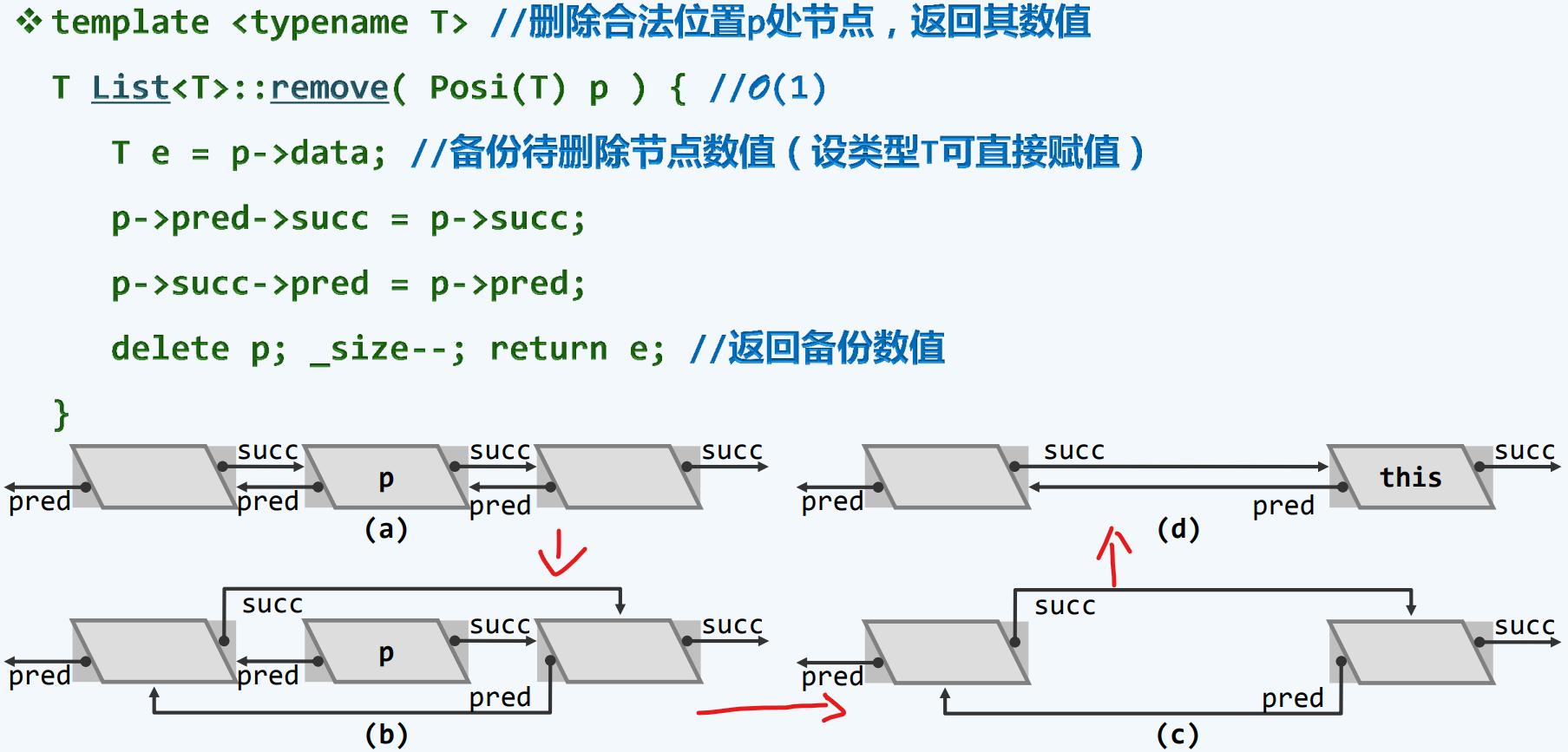
删除与析构

删除

可以说P与原来的系统，在拓扑关系上脱离开了

微创手术型 O(1)

image-20220226210621457

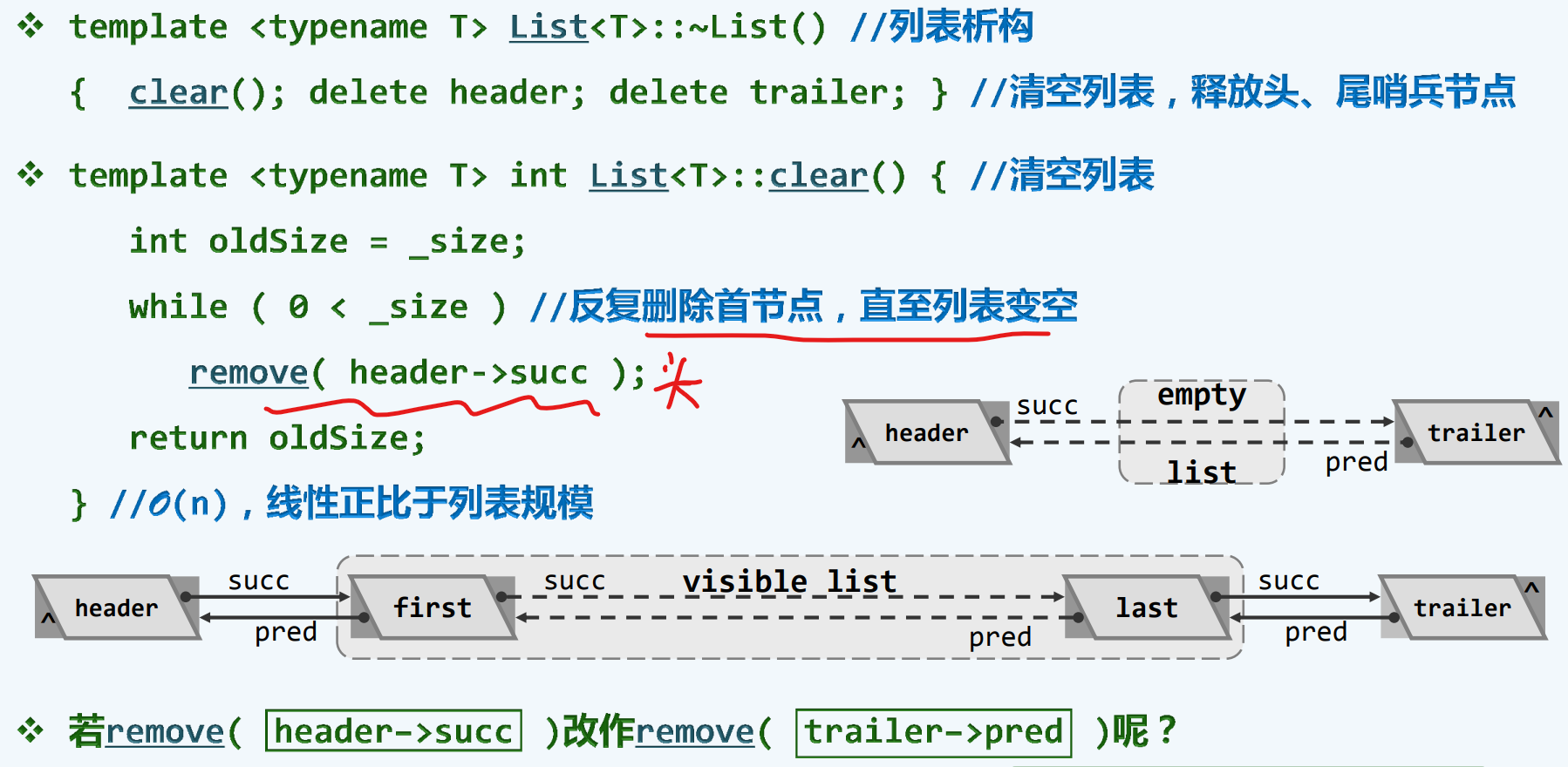
析构

image-20220226210809580

查找

如果一串列表里有多个同样的，并且是查找的对象，则将会首先停止与最靠后的那个

为什么我们把n放在p的前端呢？（find传入参数）

因为这样我们很好理解，是在p的n个前驱中寻找

换而言之我们完全可以重载另一个接口find(e,p,n)

image-20220226210910729

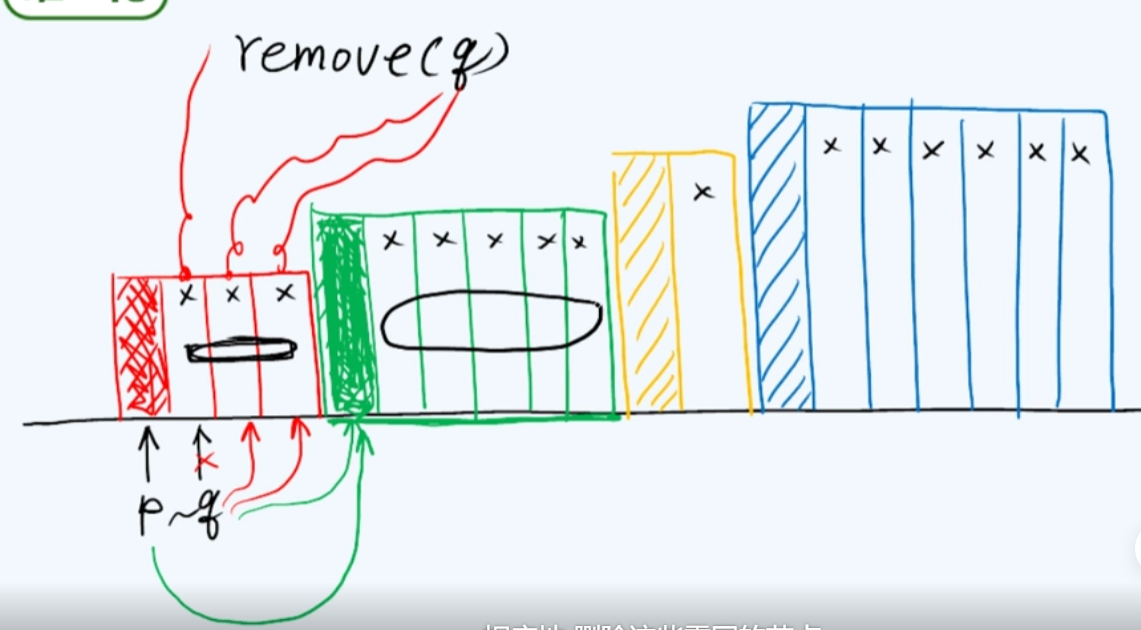
去重

r在任何时候其实就等于整个前缀(p)的长度

为什么删除q而不删除p呢

对于p而言，先删除q是一个更安全的方法（不改变目前遍历所达到的位置

image-20220226211826088

1
2
3
4
5
6
7
8
template <typename T> int List<T>::deduplicate() {
0002    int oldSize = _size; ListNodePosi<T> p = first();
0003    for ( Rank r = 0; p != trailer; p = p->succ ) //O(n)
0004       if ( ListNodePosi<T> q = find(p->data, r, p) )
0005          remove(q); //此时q与p雷同，但删除前者更为简明
0006       else r++; //r为无重前缀的长度
0007    return oldSize - _size; //删除元素总数
0008 }

实现(可忽略)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include "listNode.h" //引入列表节点类
0002 
0003 template <typename T> class List { //列表模板类
0004 
0005 private:
0006    int _size; ListNodePosi<T> header; ListNodePosi<T> trailer; //规模、头哨兵、尾哨兵
0007 
0008 protected:
0009    void init(); //列表创建时的初始化
0010    int clear(); //清除所有节点
0011    void copyNodes ( ListNodePosi<T>, int ); //复制列表中自位置p起的n项
0012    ListNodePosi<T> merge ( ListNodePosi<T>, int, List<T> &, ListNodePosi<T>, int ); //归并
0013    void mergeSort ( ListNodePosi<T> &, int ); //对从p开始连续的n个节点归并排序
0014    void selectionSort ( ListNodePosi<T>, int ); //对从p开始连续的n个节点选择排序
0015    void insertionSort ( ListNodePosi<T>, int ); //对从p开始连续的n个节点插入排序
0016    void radixSort(ListNodePosi<T>, int); //对从p开始连续的n个节点基数排序
0017 
0018 public:
0019 // 构造函数
0020    List() { init(); } //默认
0021    List ( List<T> const& L ); //整体复制列表L
0022    List ( List<T> const& L, Rank r, int n ); //复制列表L中自第r项起的n项
0023    List ( ListNodePosi<T> p, int n ); //复制列表中自位置p起的n项
0024 // 析构函数
0025    ~List(); //释放（包含头、尾哨兵在内的）所有节点
0026 // 只读访问接口
0027    Rank size() const { return _size; } //规模
0028    bool empty() const { return _size <= 0; } //判空
0029    T& operator[] ( Rank r ) const; //重载，支持循秩访问（效率低）
0030    ListNodePosi<T> first() const { return header->succ; } //首节点位置
0031    ListNodePosi<T> last() const { return trailer->pred; } //末节点位置
0032    bool valid ( ListNodePosi<T> p ) //判断位置p是否对外合法
0033    { return p && ( trailer != p ) && ( header != p ); } //将头、尾节点等同于NULL
0034    ListNodePosi<T> find ( T const& e ) const //无序列表查找
0035    { return find ( e, _size, trailer ); }
0036    ListNodePosi<T> find ( T const& e, int n, ListNodePosi<T> p ) const; //无序区间查找
0037    ListNodePosi<T> search ( T const& e ) const //有序列表查找
0038    { return search ( e, _size, trailer ); }
0039    ListNodePosi<T> search ( T const& e, int n, ListNodePosi<T> p ) const; //有序区间查找
0040    ListNodePosi<T> selectMax ( ListNodePosi<T> p, int n ); //在p及其n-1个后继中选出最大者
0041    ListNodePosi<T> selectMax() { return selectMax ( header->succ, _size ); } //整体最大者
0042 // 可写访问接口
0043    ListNodePosi<T> insertAsFirst ( T const& e ); //将e当作首节点插入
0044    ListNodePosi<T> insertAsLast ( T const& e ); //将e当作末节点插入
0045    ListNodePosi<T> insert ( ListNodePosi<T> p, T const& e ); //将e当作p的后继插入
0046    ListNodePosi<T> insert ( T const& e, ListNodePosi<T> p ); //将e当作p的前驱插入
0047    T remove ( ListNodePosi<T> p ); //删除合法位置p处的节点,返回被删除节点
0048    void merge ( List<T> & L ) { merge ( header->succ, _size, L, L.header->succ, L._size ); } //全列表归并
0049    void sort ( ListNodePosi<T> p, int n ); //列表区间排序
0050    void sort() { sort ( first(), _size ); } //列表整体排序
0051    int deduplicate(); //无序去重
0052    int uniquify(); //有序去重
0053    void reverse(); //前后倒置（习题）
0054 // 遍历
0055    void traverse ( void (* ) ( T& ) ); //遍历，依次实施visit操作（函数指针，只读或局部性修改）
0056    template <typename VST> //操作器
0057    void traverse ( VST& ); //遍历，依次实施visit操作（函数对象，可全局性修改）
0058 }; //List

有序列表

唯一化

构思

image-20220226212058366

处理

image-20220226212222134

1
2
3
4
5
6
7
8
9
template <typename T> int List<T>::uniquify() { //成批剔除重复元素，效率更高
0002    if ( _size < 2 ) return 0; //平凡列表自然无重复
0003    int oldSize = _size; //记录原规模
0004    ListNodePosi<T> p = first(); ListNodePosi<T> q; //p为各区段起点，q为其后继
0005    while ( trailer != ( q = p->succ ) ) //反复考查紧邻的节点对(p, q)
0006       if ( p->data != q->data ) p = q; //若互异，则转向下一区段
0007       else remove ( q ); //否则（雷同），删除后者
0008    return oldSize - _size; //列表规模变化量，即被删除元素总数
0009 }

查找

image-20220226212429736

1
2
3
4
5
6
7
8
template <typename T> //在有序列表内节点p（可能是trailer）的n个（真）前驱中，找到不大于e的最后者
0002 ListNodePosi<T> List<T>::search ( T const& e, int n, ListNodePosi<T> p ) const {
0003 // assert: 0 <= n <= rank(p) < _size
0004    do {
0005       p = p->pred; n--;  //从右向左
0006    } while ( ( -1 < n ) && ( e < p->data ) ); //逐个比较，直至命中或越界
0007    return p; //返回查找终止的位置
0008 } //失败时，返回区间左边界的前驱（可能是header）——调用者可通过valid()判断成功与否

列表-选择排序

构思

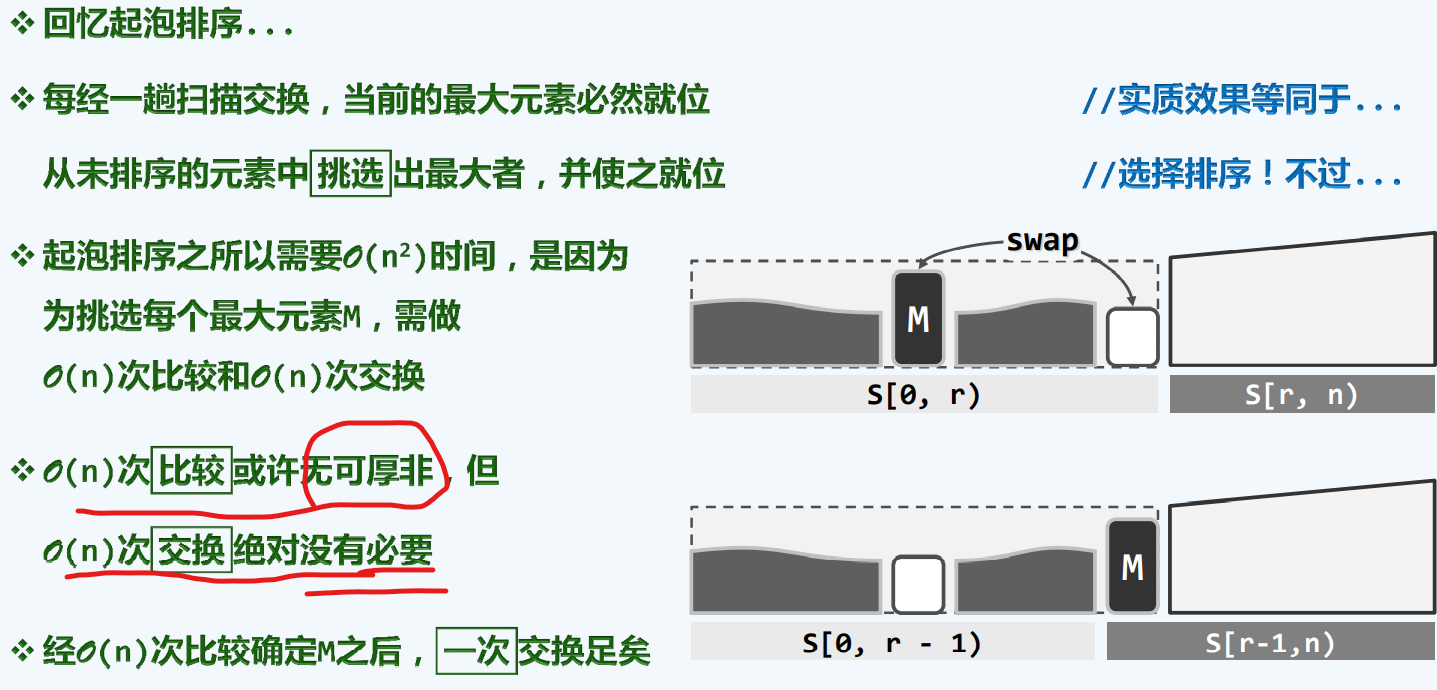
image-20220227153540139

实例

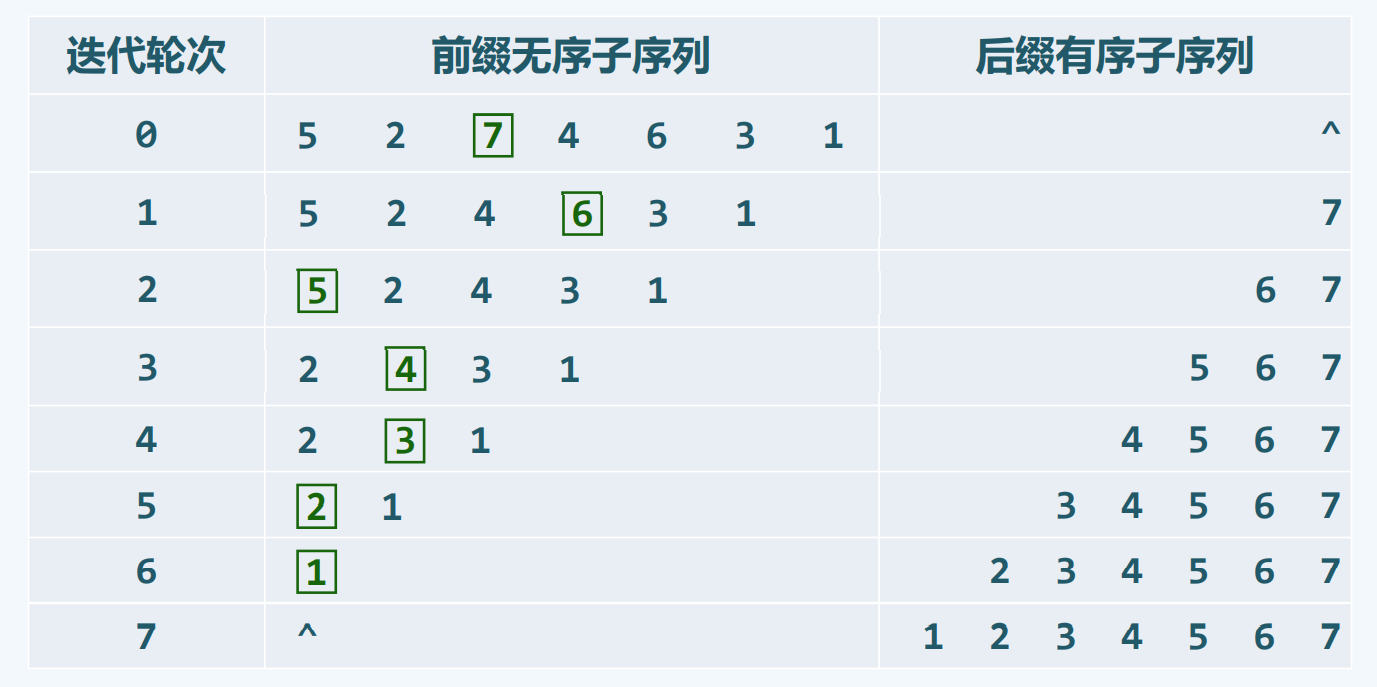
image-20220227153826907

selectionSort

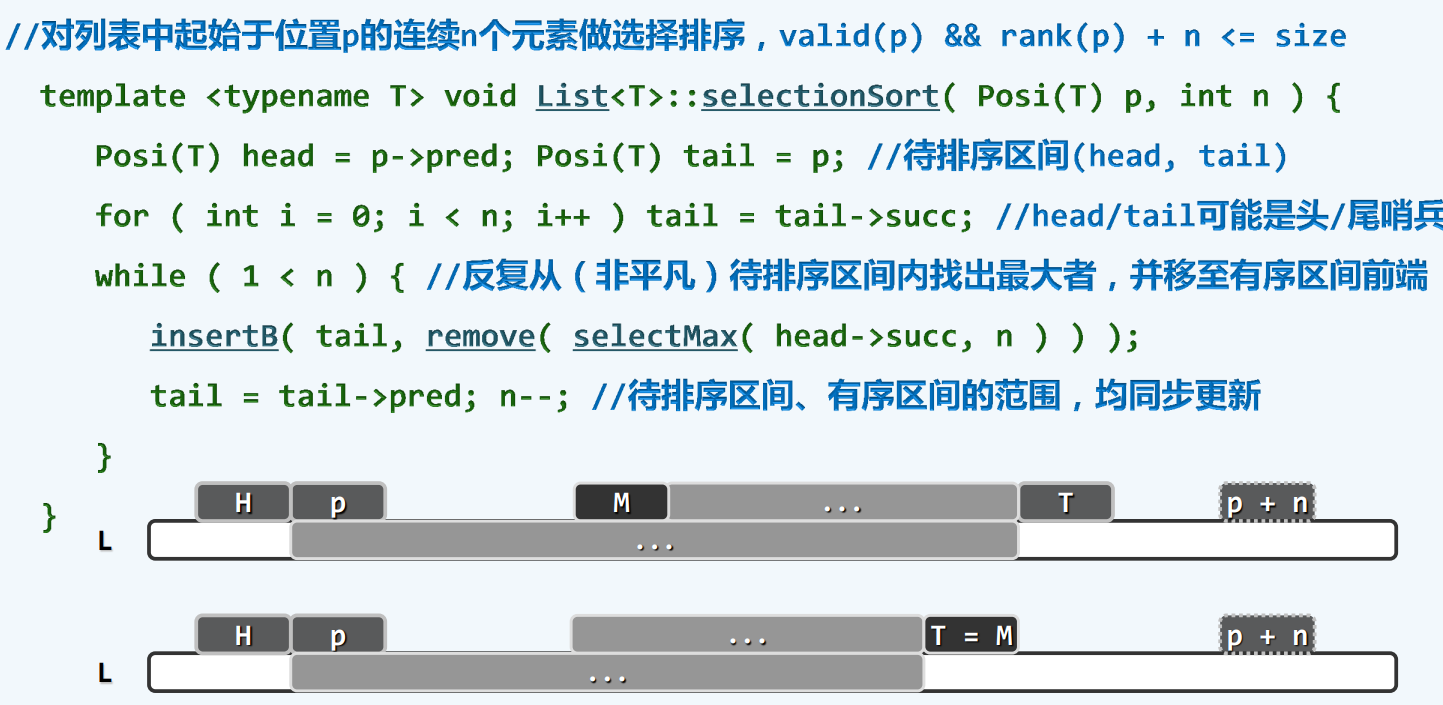
image-20220227154035448

1
2
3
4
5
6
7
8
9
10
template <typename T> //对列表中起始于位置p、宽度为n的区间做选择排序
0002 void List<T>::selectionSort ( ListNodePosi<T> p, int n ) { //valid(p) && rank(p) + n <= size
0003    ListNodePosi<T> head = p->pred, tail = p;
0004    for ( int i = 0; i < n; i++ ) tail = tail->succ; //待排序区间为(head, tail)
0005    while ( 1 < n ) { //在至少还剩两个节点之前，在待排序区间内
0006       ListNodePosi<T> max = selectMax ( head->succ, n ); //找出最大者（歧义时后者优先）
0007       insert ( remove ( max ), tail ); //将其移至无序区间末尾（作为有序区间新的首元素）
0008       tail = tail->pred; n--;
0009    }
0010 }

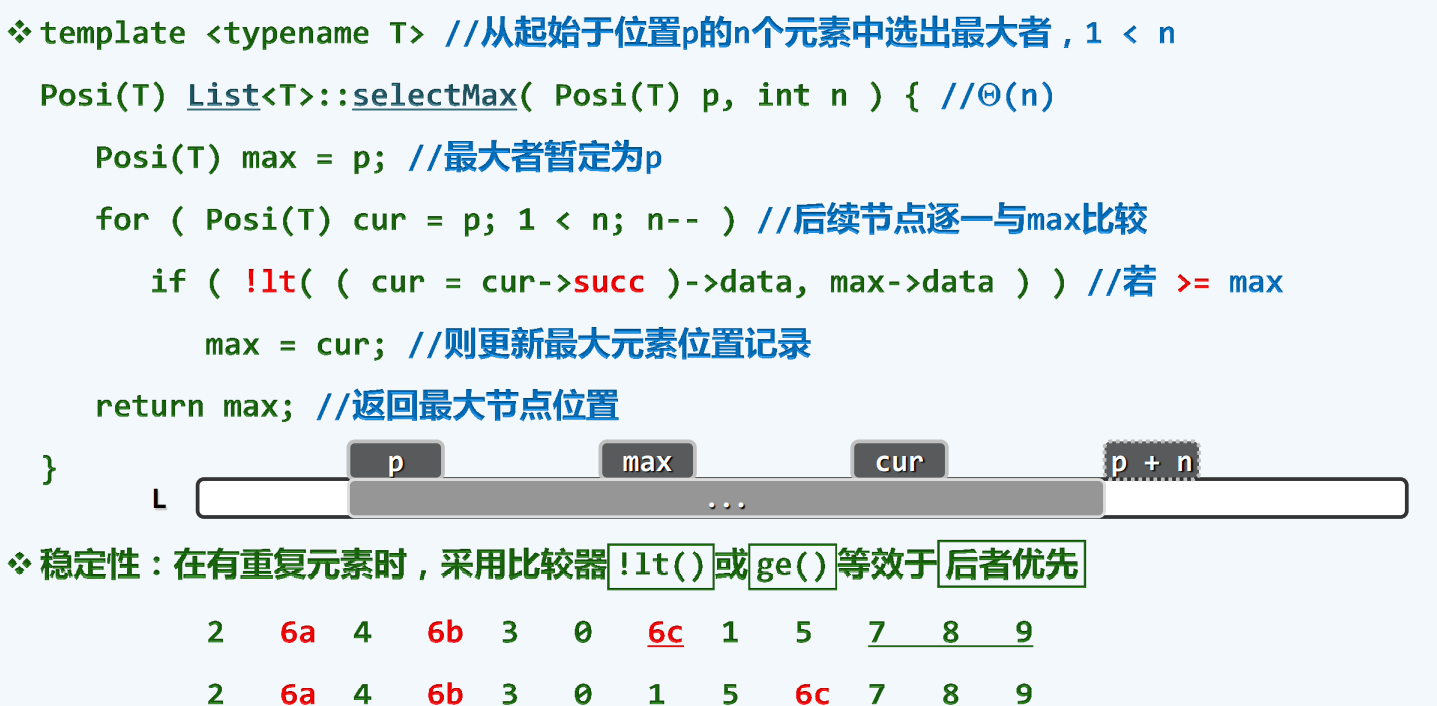
selectMax

image-20220227154133871

1
2
3
4
5
6
7
8
template <typename T> //从起始于位置p的n个元素中选出最大者
0002 ListNodePosi<T> List<T>::selectMax ( ListNodePosi<T> p, int n ) {
0003    ListNodePosi<T> max = p; //最大者暂定为首节点p
0004    for ( ListNodePosi<T> cur = p; 1 < n; n-- ) //从首节点p出发，将后续节点逐一与max比较
0005       if ( !lt ( ( cur = cur->succ )->data, max->data ) ) //若当前元素不小于max，则
0006          max = cur; //更新最大元素位置记录
0007    return max; //返回最大节点位置
0008 }

insertB

详情参考前驱插入部分

1
2
3
4
5
6
7
8
9
10
11
template <typename T> ListNodePosi<T> List<T>::insertAsFirst ( T const& e )
0002 {  _size++; return header->insertAsSucc ( e );  } //e当作首节点插入
0003 
0004 template <typename T> ListNodePosi<T> List<T>::insertAsLast ( T const& e )
0005 {  _size++; return trailer->insertAsPred ( e );  } //e当作末节点插入
0006 
0007 template <typename T> ListNodePosi<T> List<T>::insert ( ListNodePosi<T> p, T const& e )
0008 {  _size++; return p->insertAsSucc ( e );  } //e当作p的后继插入
0009 
0010 template <typename T> ListNodePosi<T> List<T>::insert ( T const& e, ListNodePosi<T> p )
0011 {  _size++; return p->insertAsPred ( e );  } //e当作p的前驱插入

性能分析

image-20220227154336540

列表-插入排序

image-20220227153230057

构思

image-20220227155040696

与选择排序区别

  1. 插入排序有序部分是前部分，选择排序有序部分是后部分
  2. 选择排序无序部分必然小于有序部分，插入排序并没有类似的规定，后面所选取的数字和此前所选取的没有任何关系

实例

减而治之，此消彼减

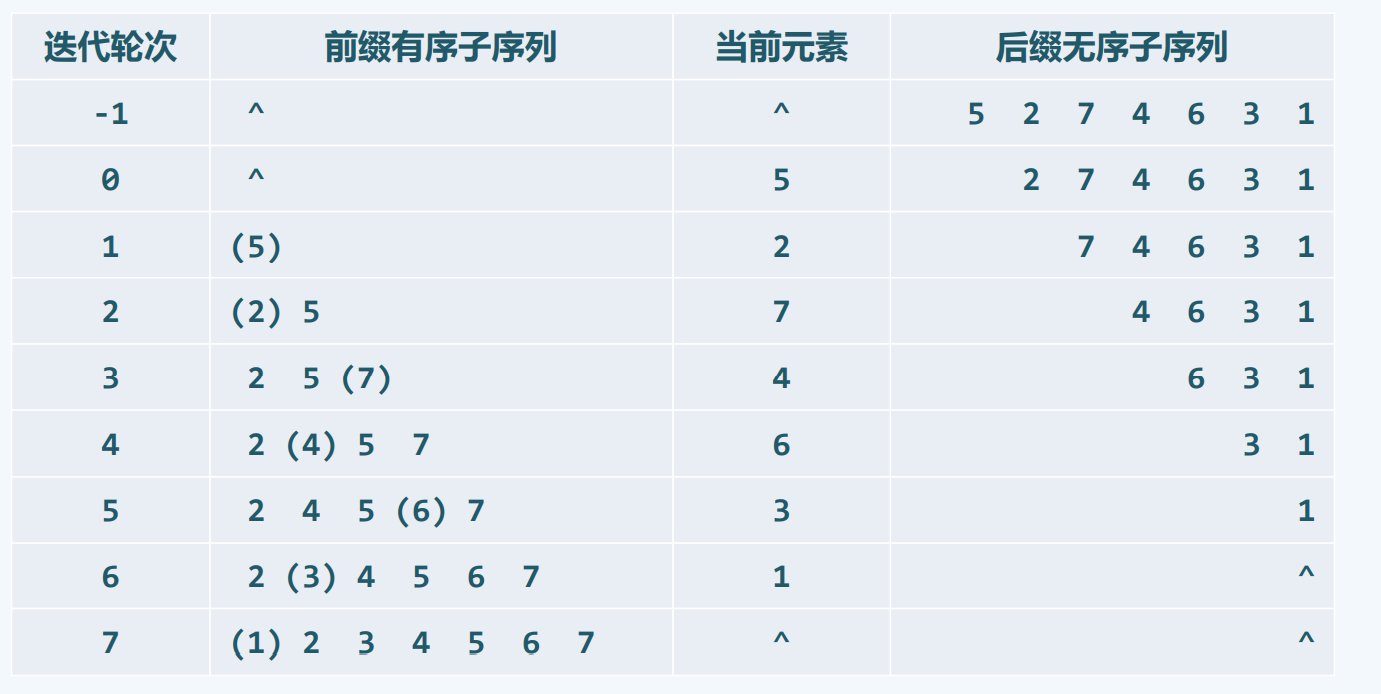
image-20220227155702678

实现

insertA到选择排序的insertB里找（B：before A：after）

image-20220227155938102

1
2
3
4
5
6
7
8
template <typename T> //在有序列表内节点p（可能是trailer）的n个（真）前驱中，找到不大于e的最后者
0002 ListNodePosi<T> List<T>::search ( T const& e, int n, ListNodePosi<T> p ) const {
0003 // assert: 0 <= n <= rank(p) < _size
0004    do {
0005       p = p->pred; n--;  //从右向左
0006    } while ( ( -1 < n ) && ( e < p->data ) ); //逐个比较，直至命中或越界
0007    return p; //返回查找终止的位置
0008 } //失败时，返回区间左边界的前驱（可能是header）——调用者可通过valid()判断成功与否

remove

1
2
3
4
5
6
template <typename T> T List<T>::remove ( ListNodePosi<T> p ) { //删除合法节点p，返回其数值
0002    T e = p->data; //备份待删除节点的数值（假定T类型可直接赋值）
0003    p->pred->succ = p->succ; p->succ->pred = p->pred; //后继、前驱
0004    delete p; _size--; //释放节点，更新规模
0005    return e; //返回备份的数值
0006 }

性能分析

image-20220227161039930

平均性能

运用数学期望的线性率，一组随机变量总和的期望（平均值）等于他们各自期望的总和

无论他们是互不相关的还是相关的，这都是正确的

image-20220227161222904