栈与队列
以下笔记为jjyaoao本人制作,欢迎借鉴学习和提出相关建议,转载需要标明出处www.jjyaoao.space
4.栈
ADT接口
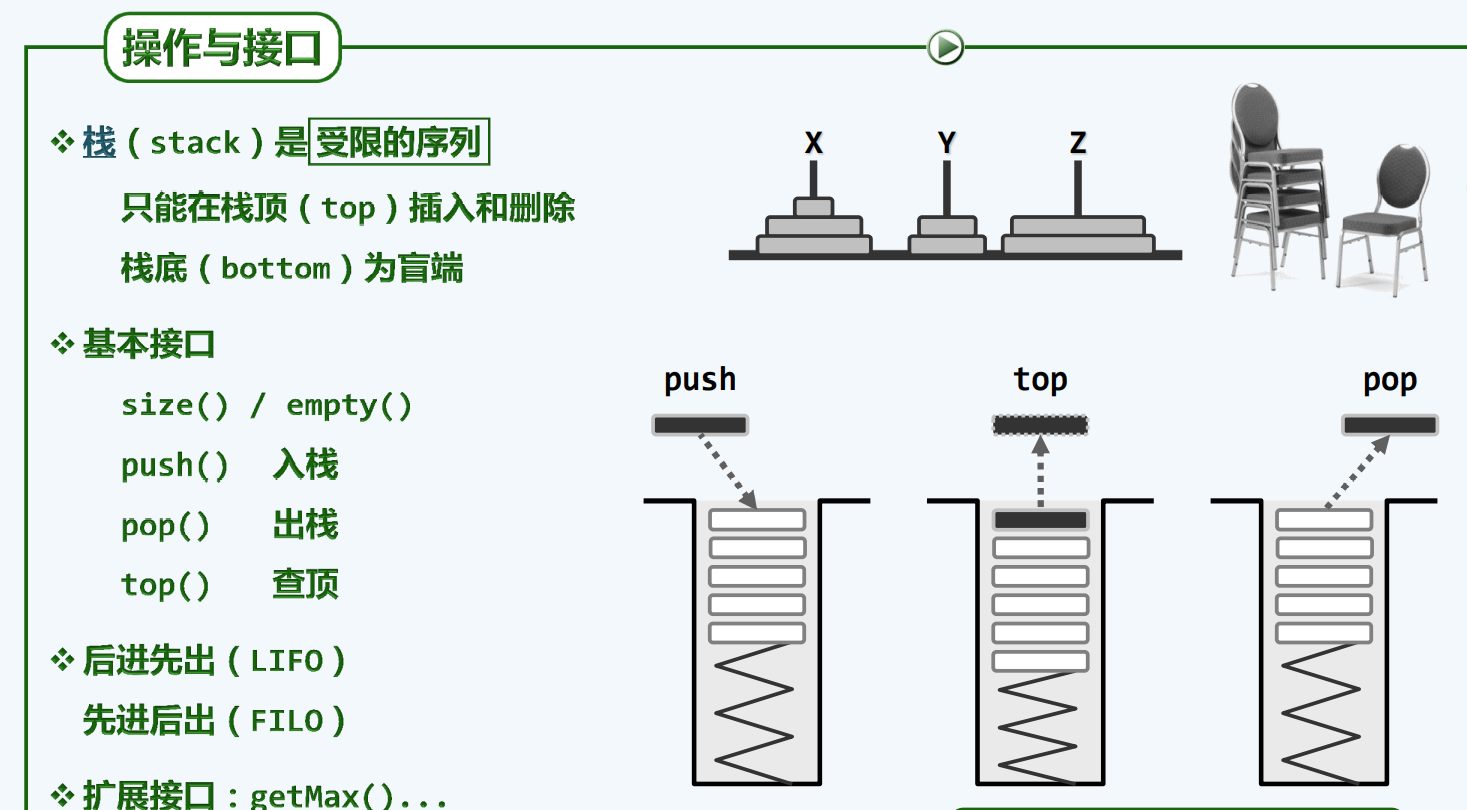
操作实例
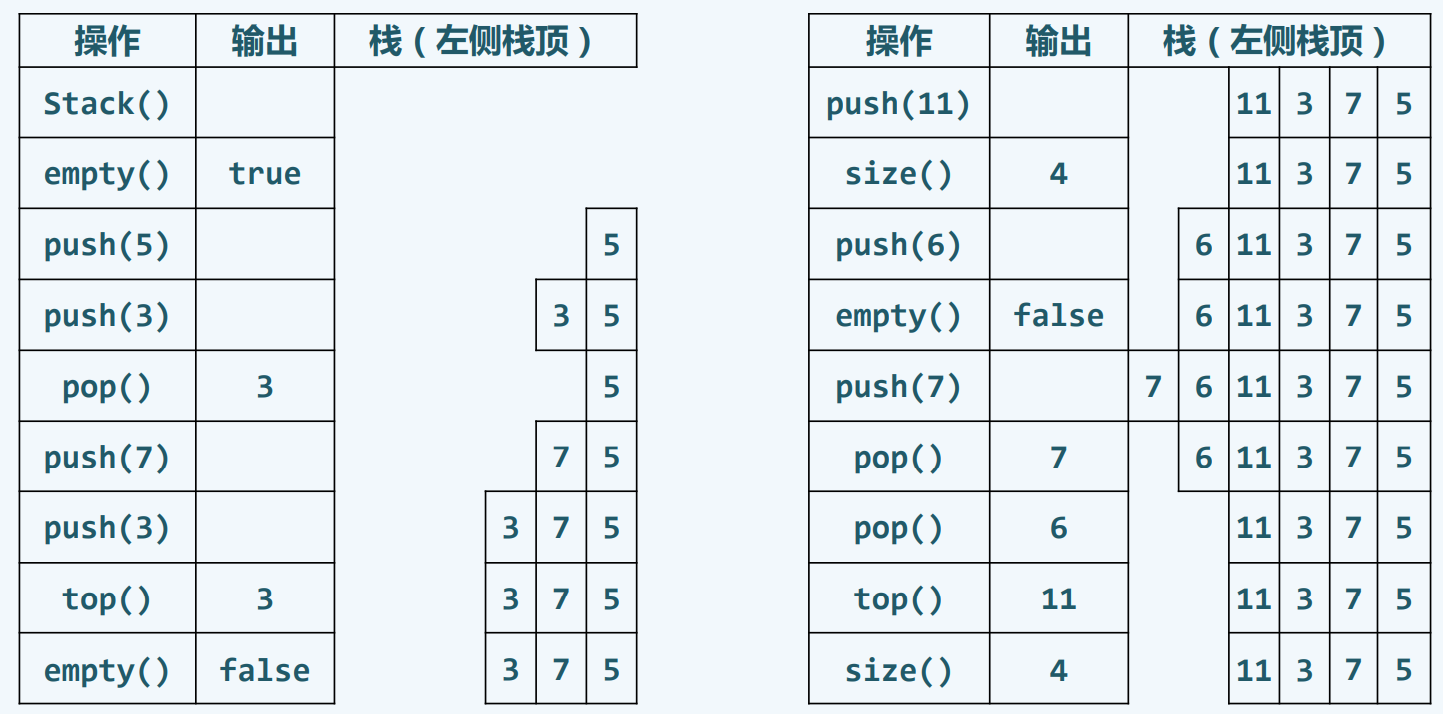
实现

实际应用

进制转换
手动实现

难点
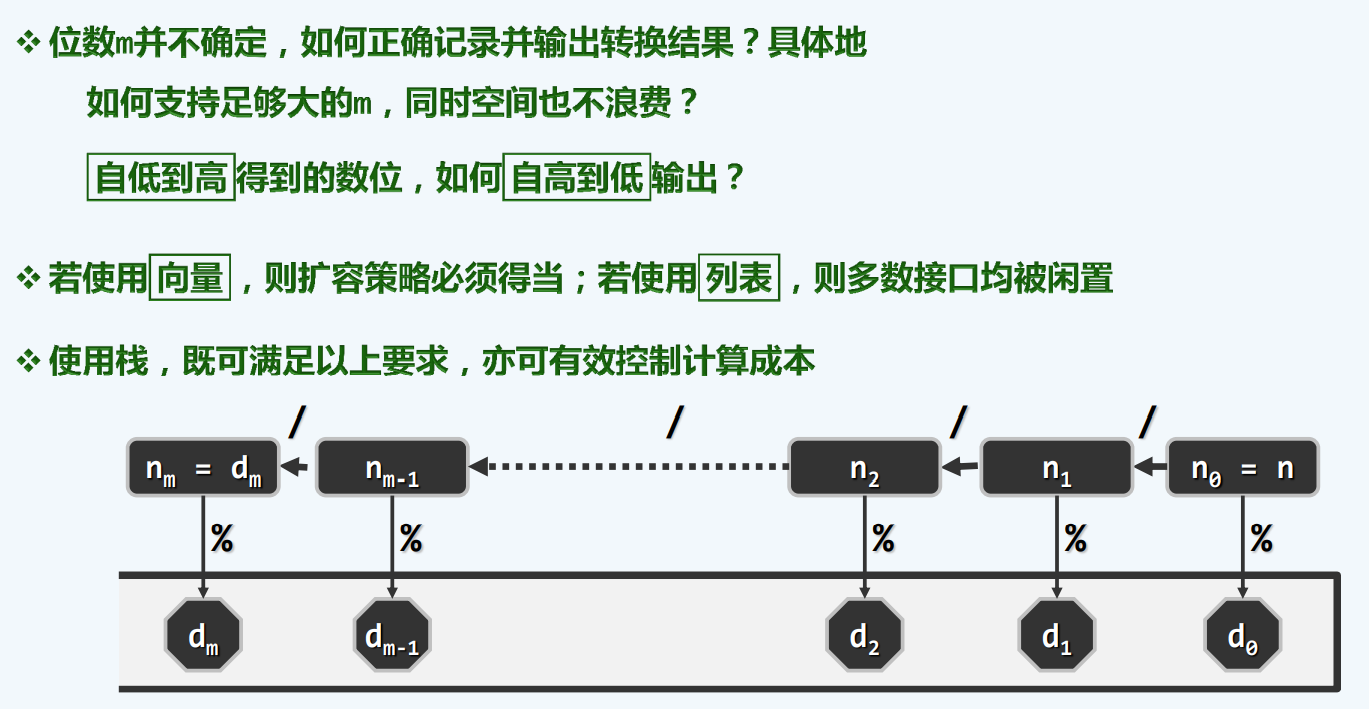
思路
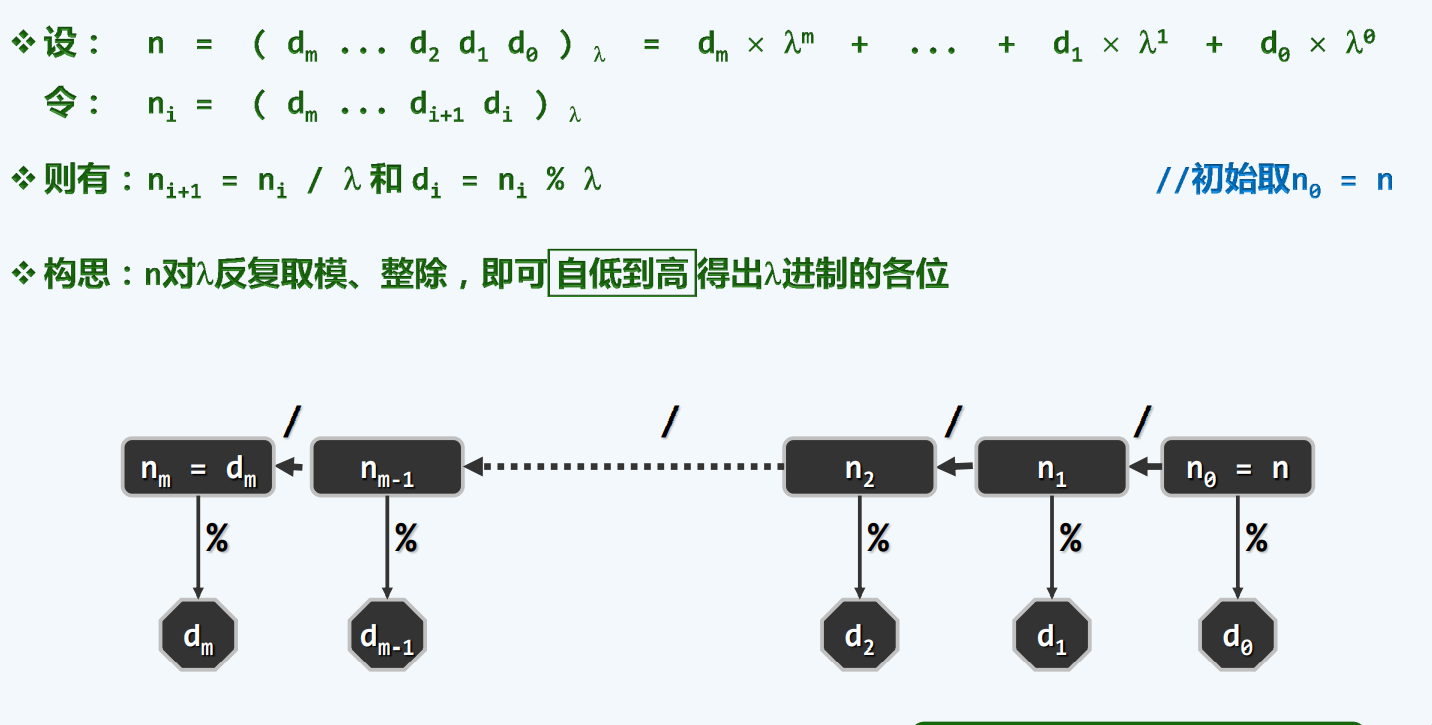
算法实现

convert
1 | void convert ( Stack<char>& S, __int64 n, int base ) { //整数n的1<base<=16进制打印(迭代版) |
括号匹配
问题描述
判断括号是匹配还是失配

尝试
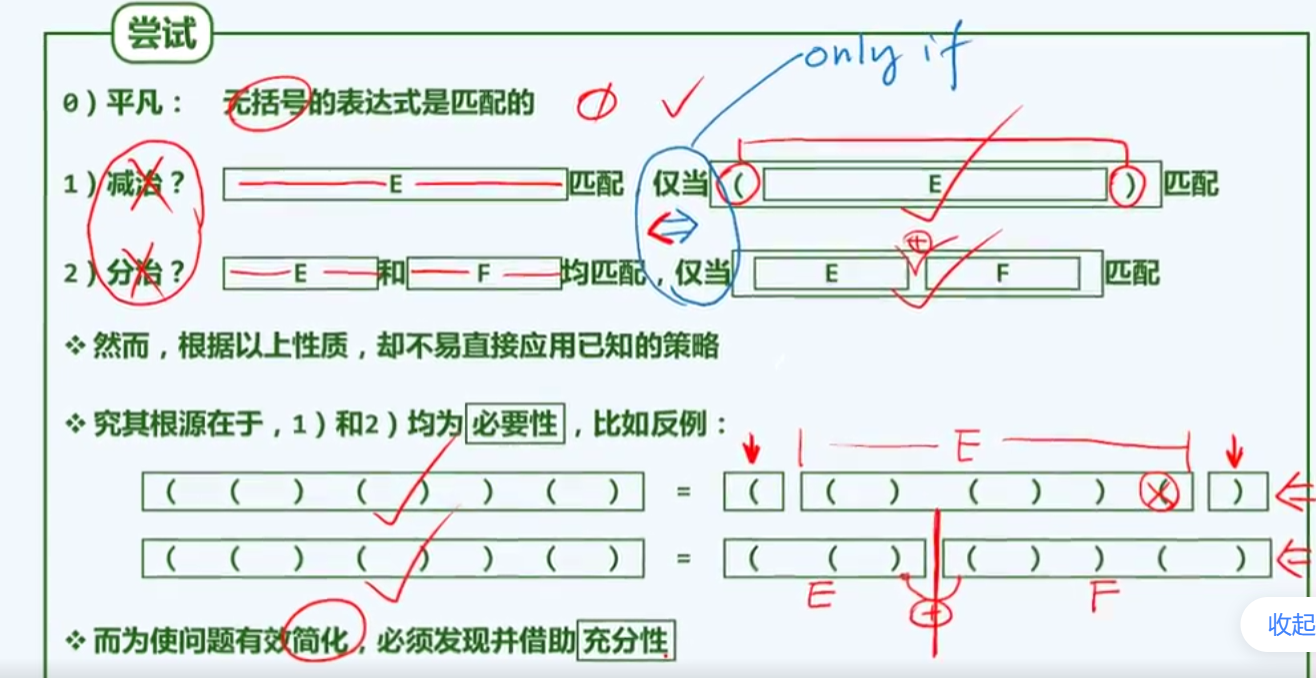
构思
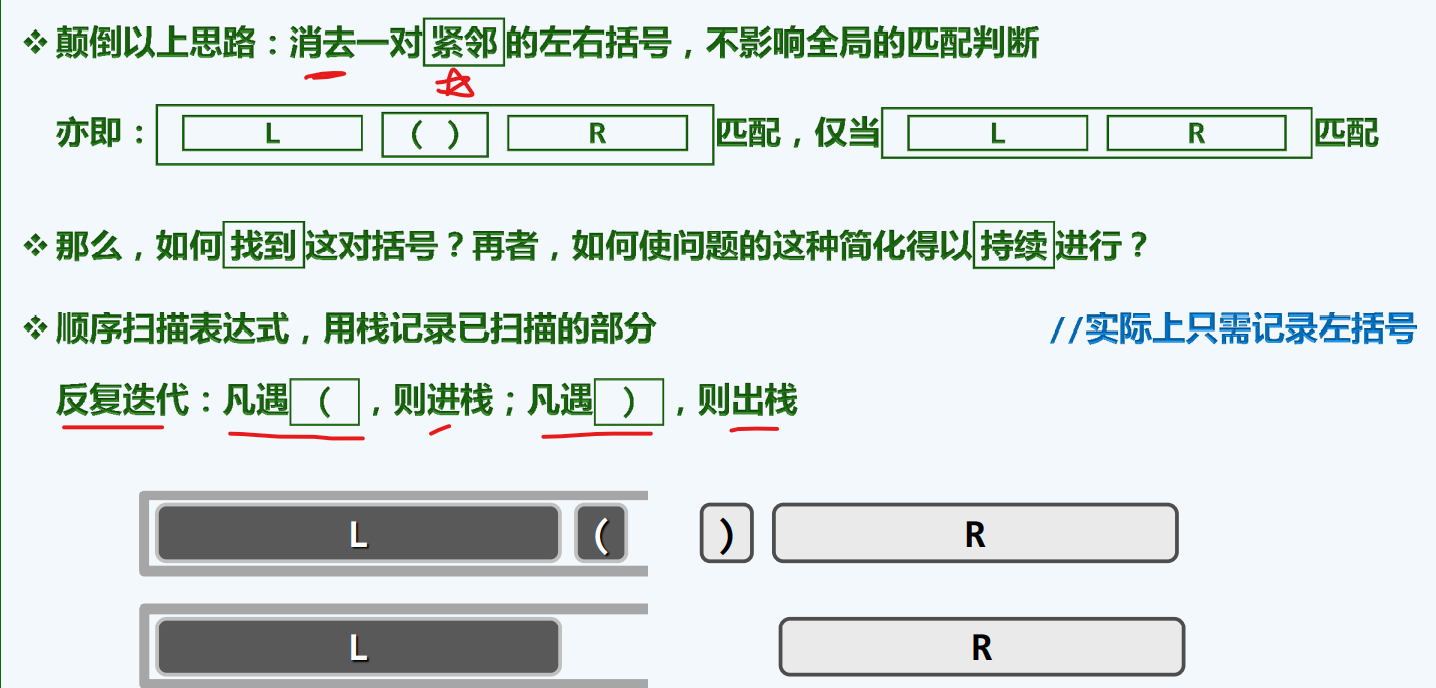
实现

1 | bool paren ( const char exp[], int lo, int hi ) { //表达式括号匹配检查,可兼顾三种括号 |
反思
如果我们只考虑一个括号,又为什么不只用一个计数器来记录括号,而使用更加复杂的栈结构呢?
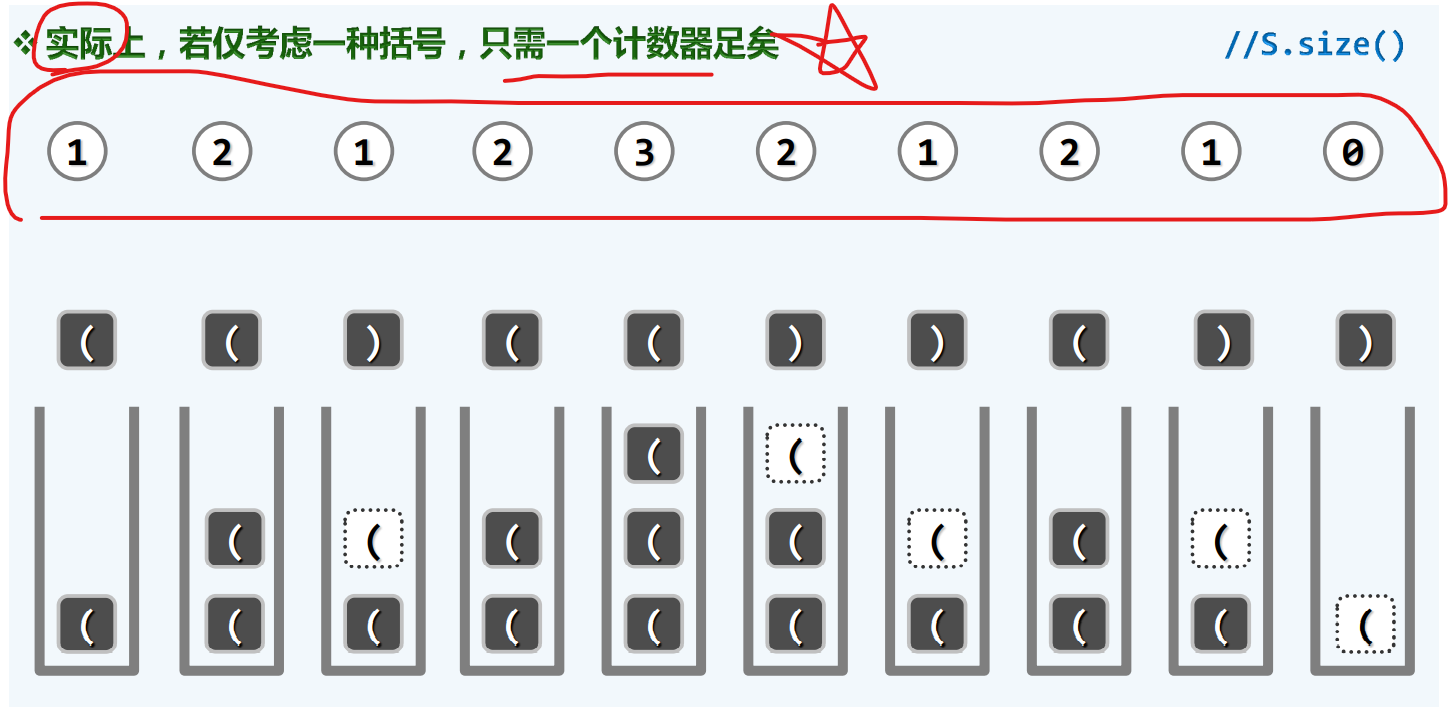
原因在于……
采用栈,可以更便捷的推广到多种括号并存的情况

教材与习题解析有这个的具体实现….
栈混洗
分别用尖括号和方括号来对应栈的顶部和底部
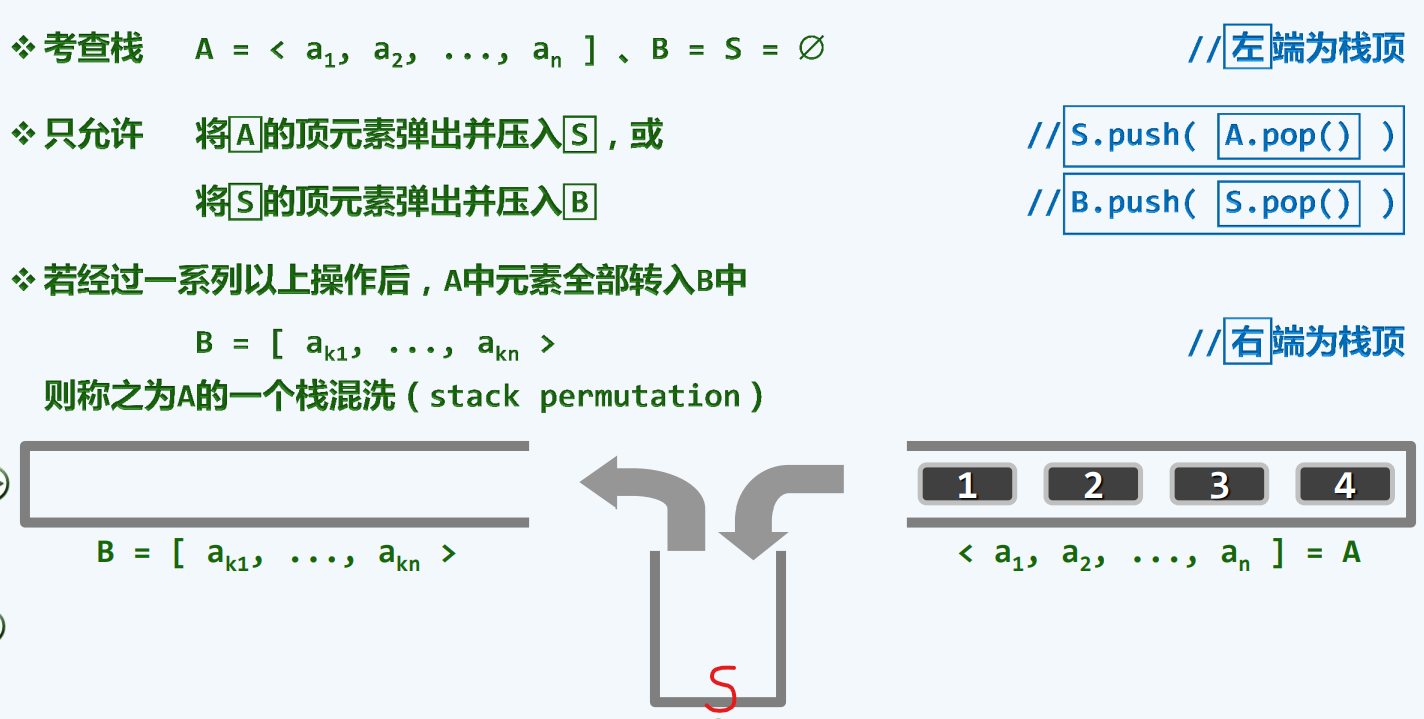
计数
对于长度为n的序列,栈混洗总数可能是多少呢?
A -> S S -> B他们所需的栈混洗次数其实是相互独立的
SP(1) = 1 (平凡情况)

甄别

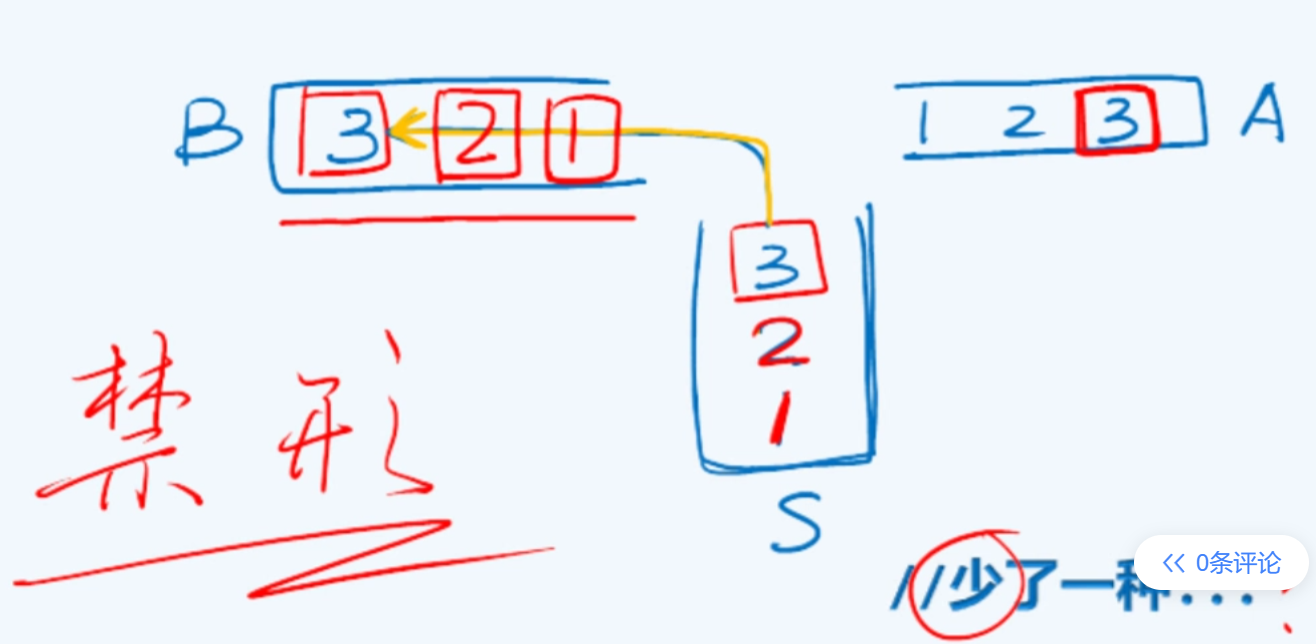

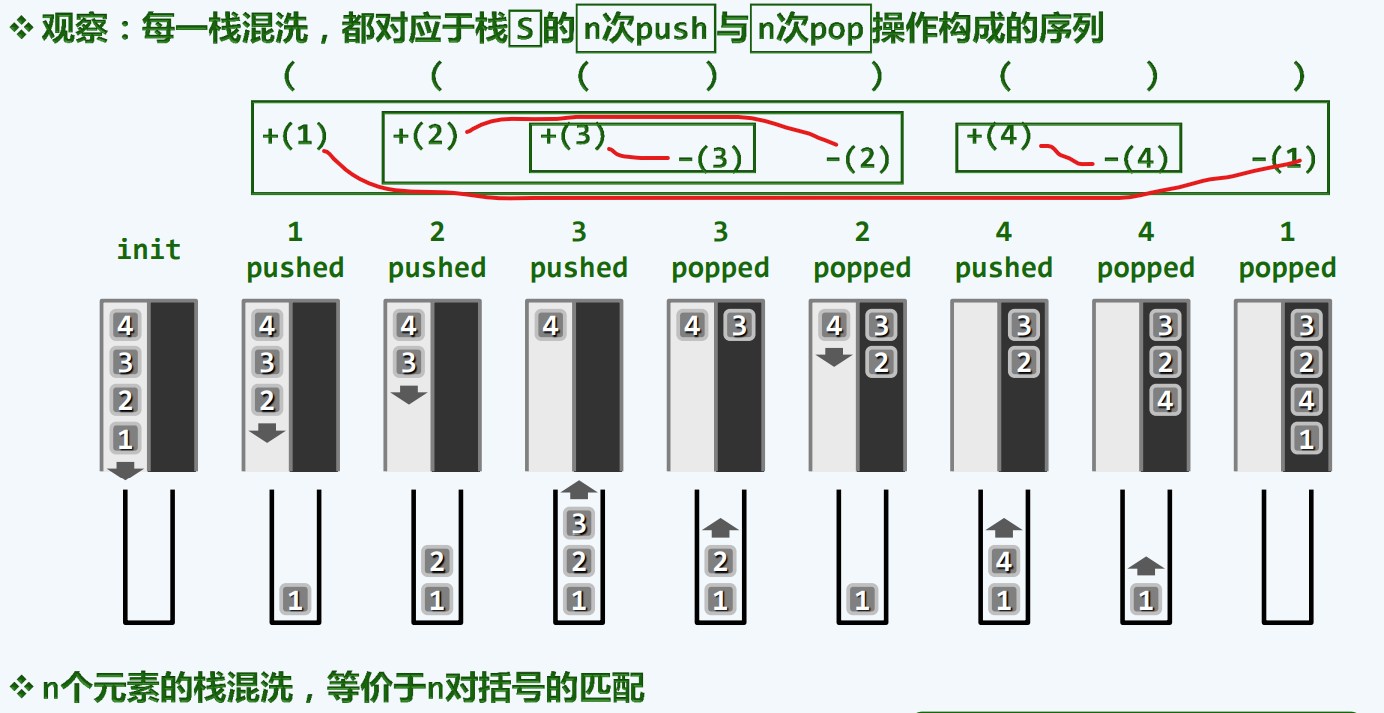
+括号匹配
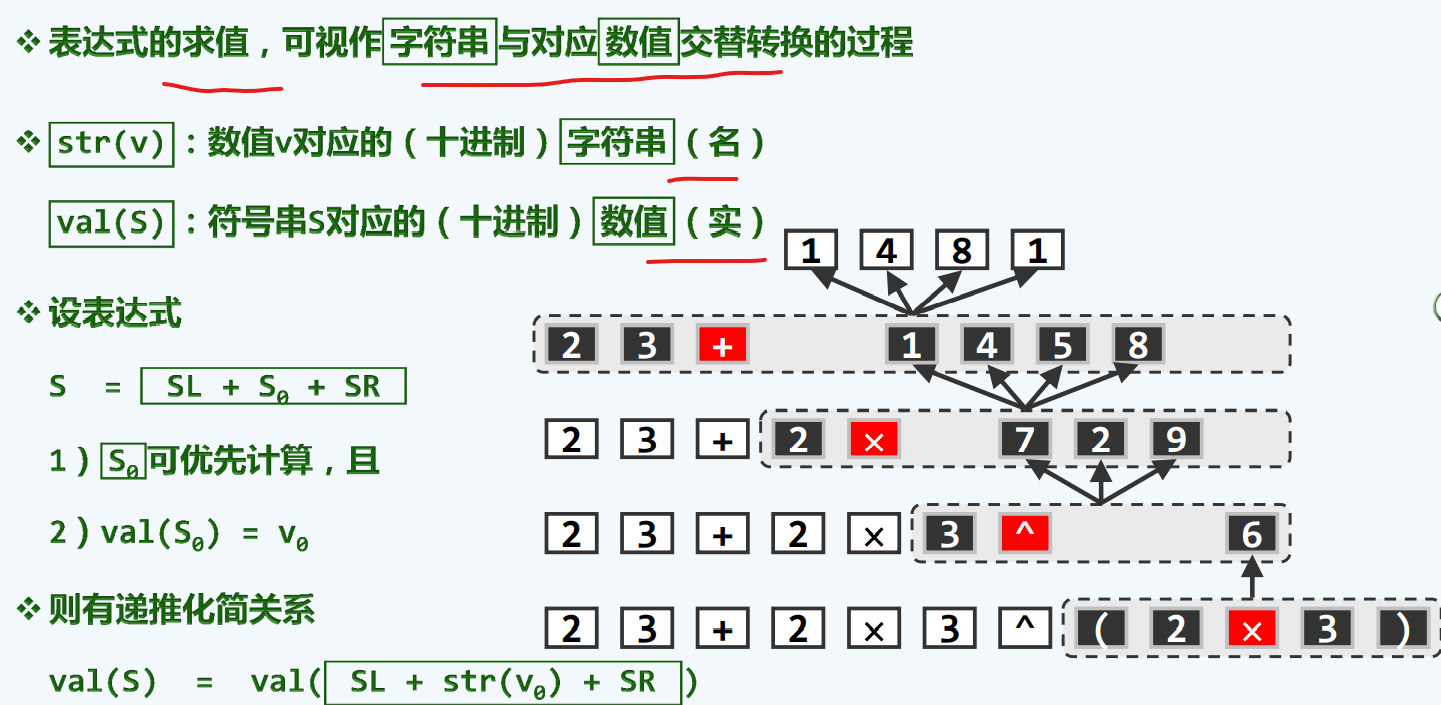
中缀表达式求值
构思
难点
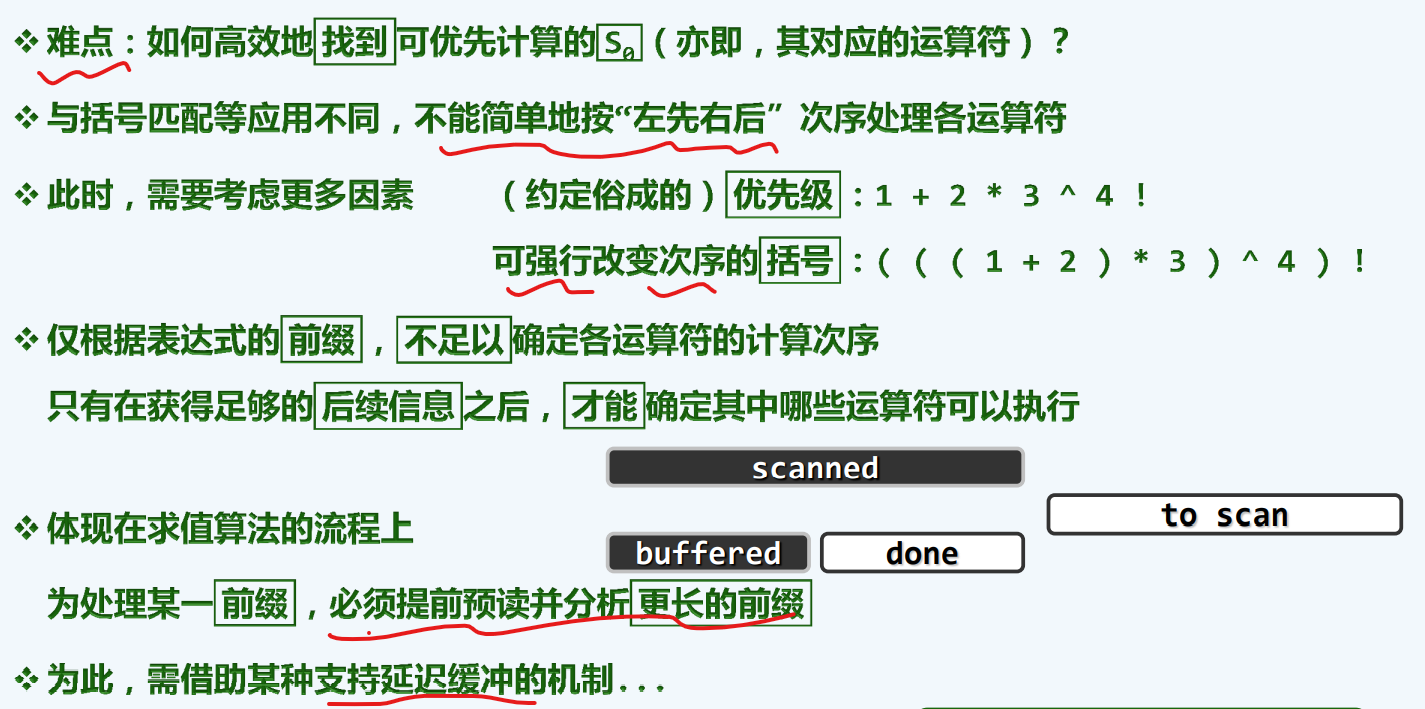
栈+线性扫描

实现

readNumber
1 | void readNumber ( char*& p, Stack<double>& stk ) { //将起始于p的子串解析为数值,并存入操作数栈 |
orderBetween
1 | Operator optr2rank ( char op ) { //由运算符转译出编号 |
优先级表

理解
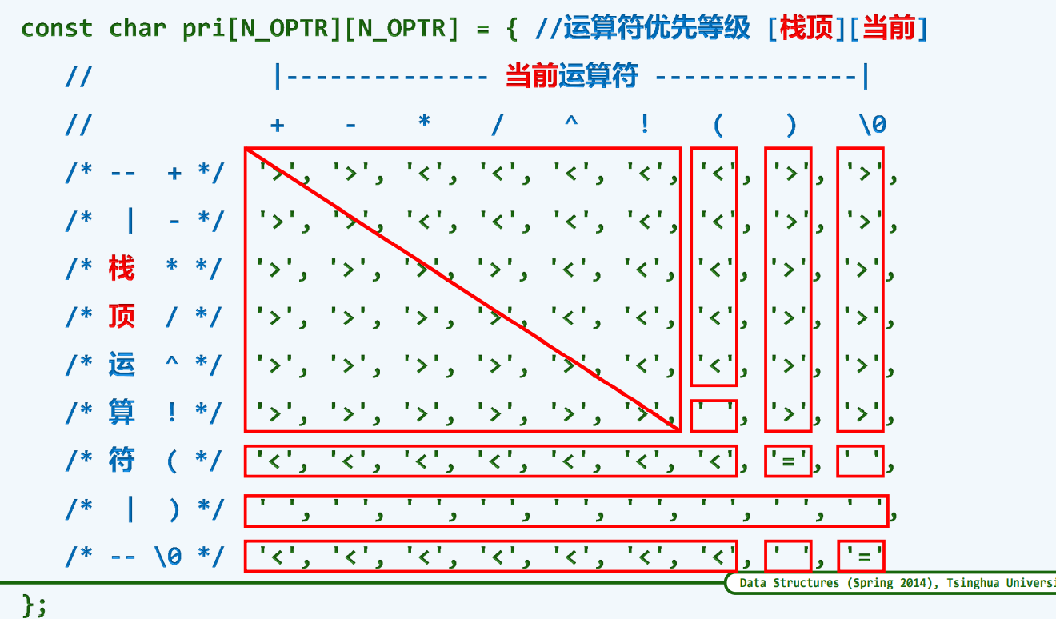
switch内具体细节

理解:
相等情况时,观察优先级表,不难得出,相等的情况只有两个括号相遇,或者\0遇上\0也就是,需要’’(‘’ And ‘’)’’共同退出历史舞台,将注意力转移到下一个元素的时候,或者结束while循环的时候
而优先级表出现 > 的时候,即可以执行运算的时候,也就是即便栈顶元素和当前运算符相同,或者栈顶运算符大于当前运算符的时候,可以开始栈顶运算符的出栈,并且执行相应的运算
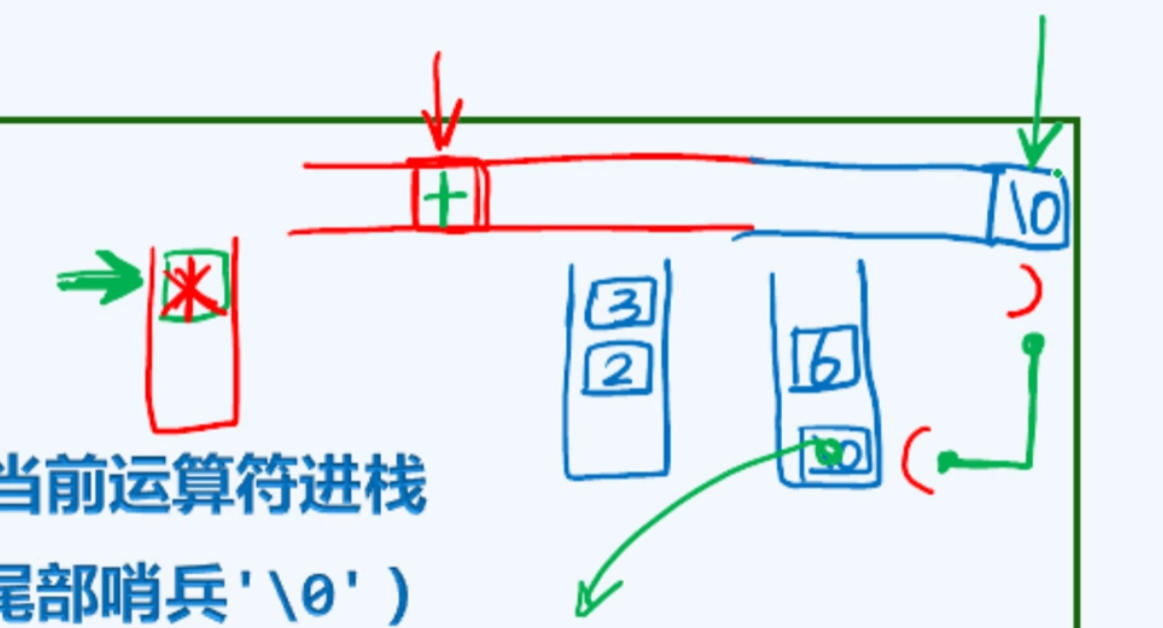
思考
为什么不直接opnd.push(calcu( opnd.pop(), op , opnd.pop() ) )?
理解:
紧凑的写法对于讲究先后顺序的运算符会出错,比如对于除法运算,由于栈先进后出的性质,就成了除数/被除数,颠倒了
实例
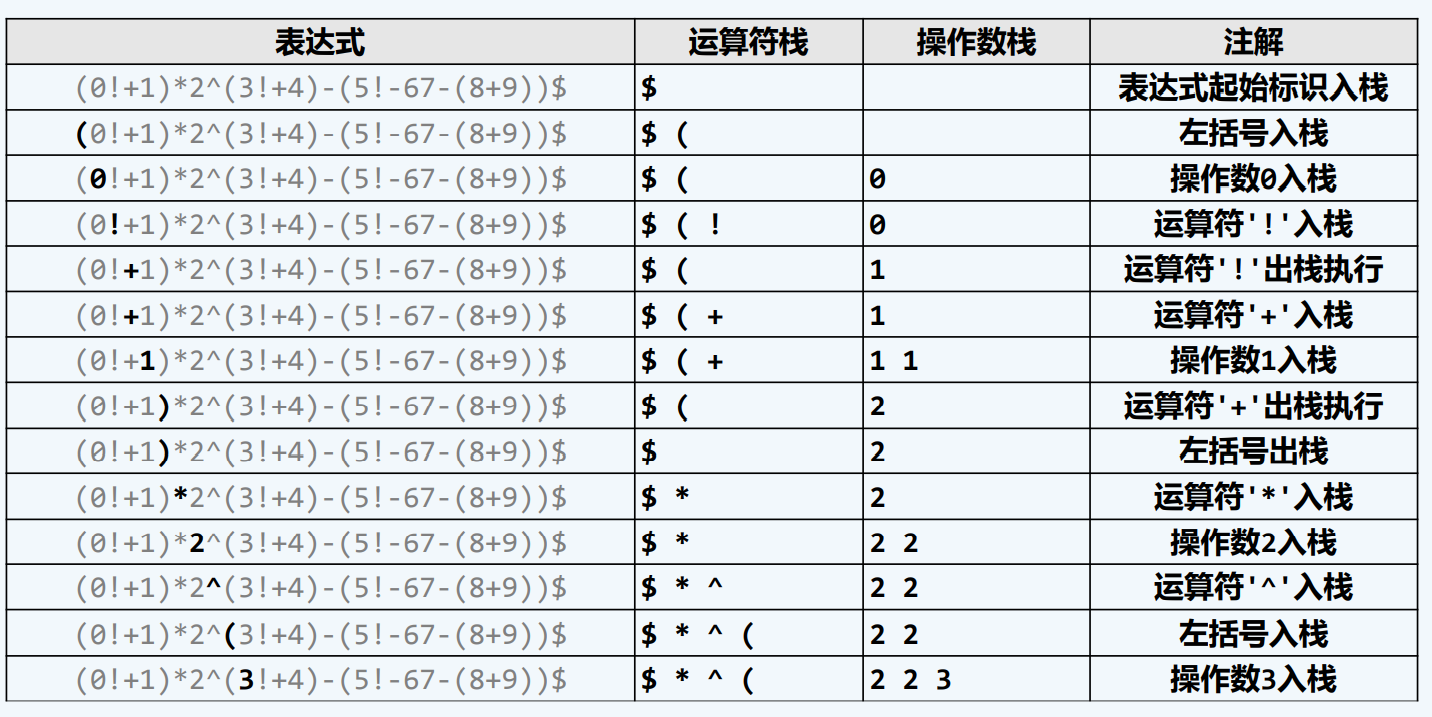
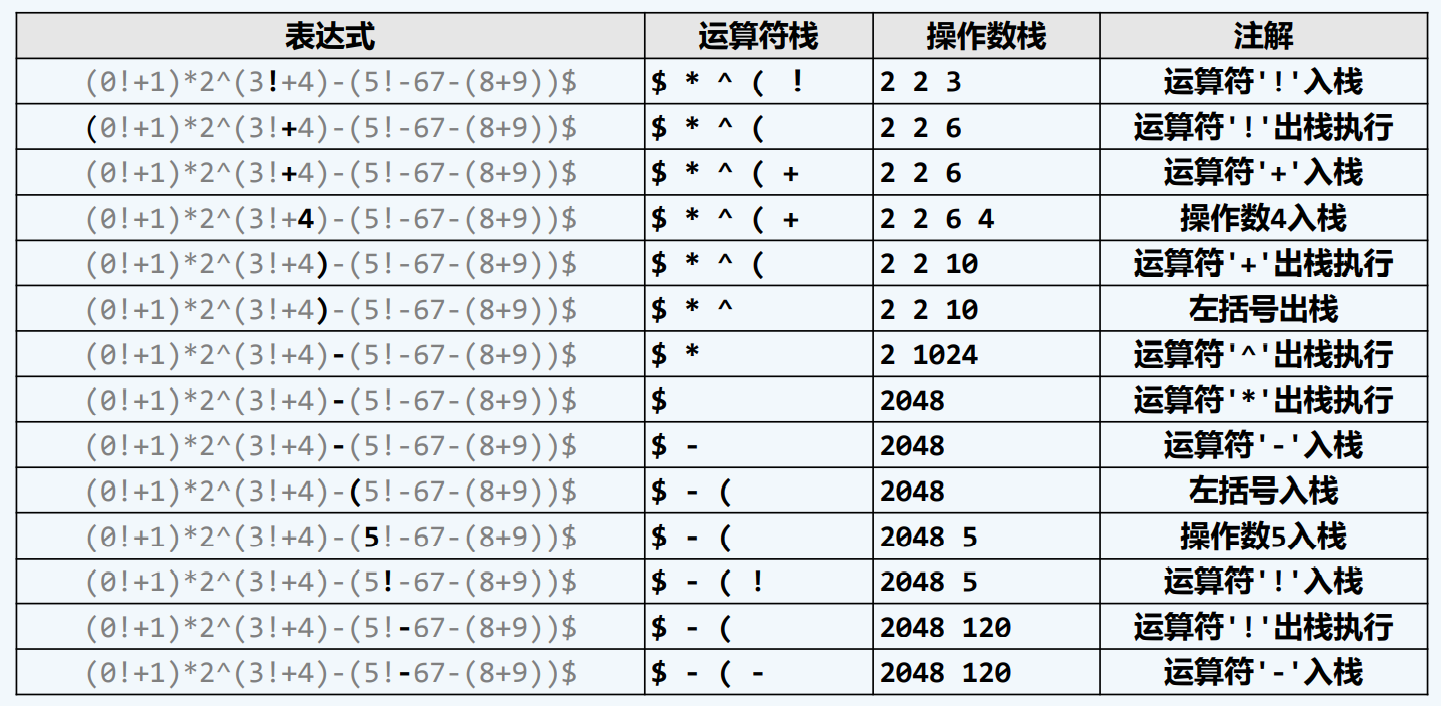
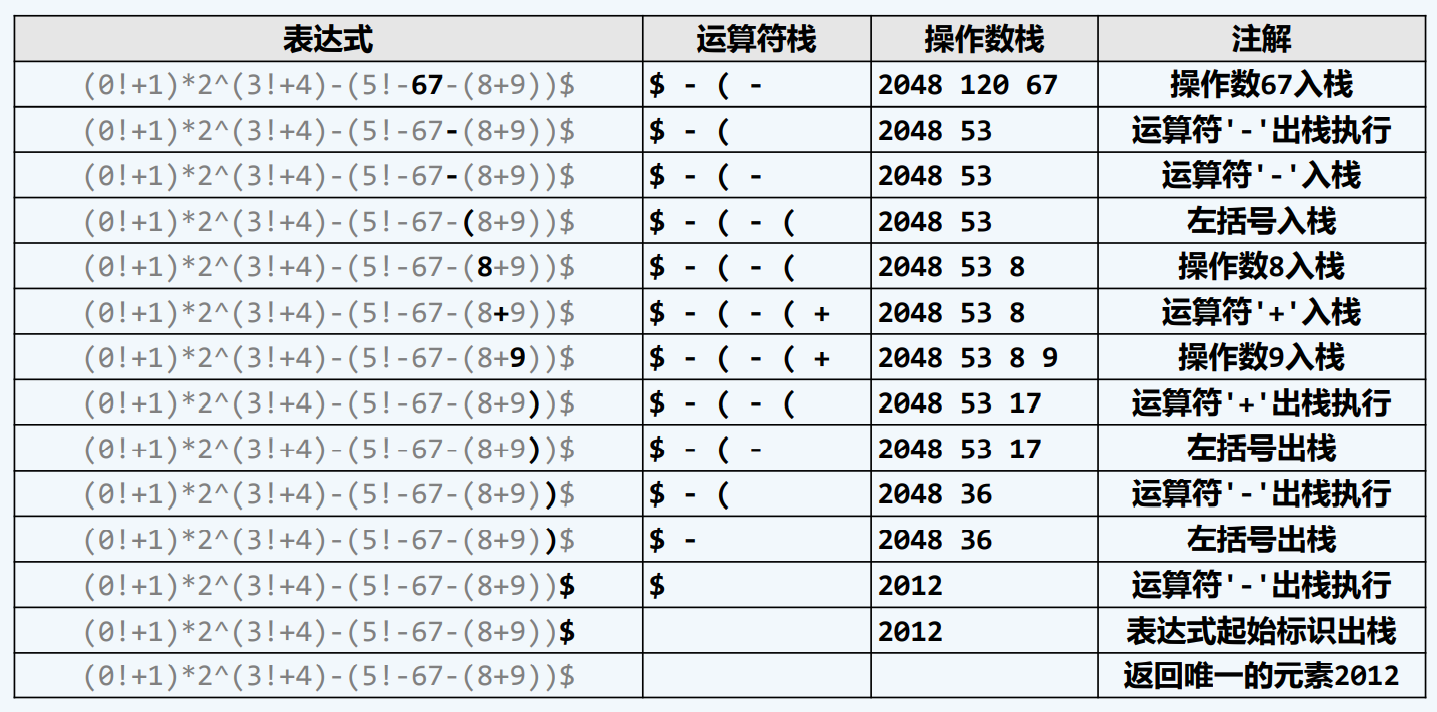
逆波兰表达式 (后缀式)RPN
- 摒弃掉约定俗成的优先级
- 摒弃掉强制优先级的括号
算法框架

实例
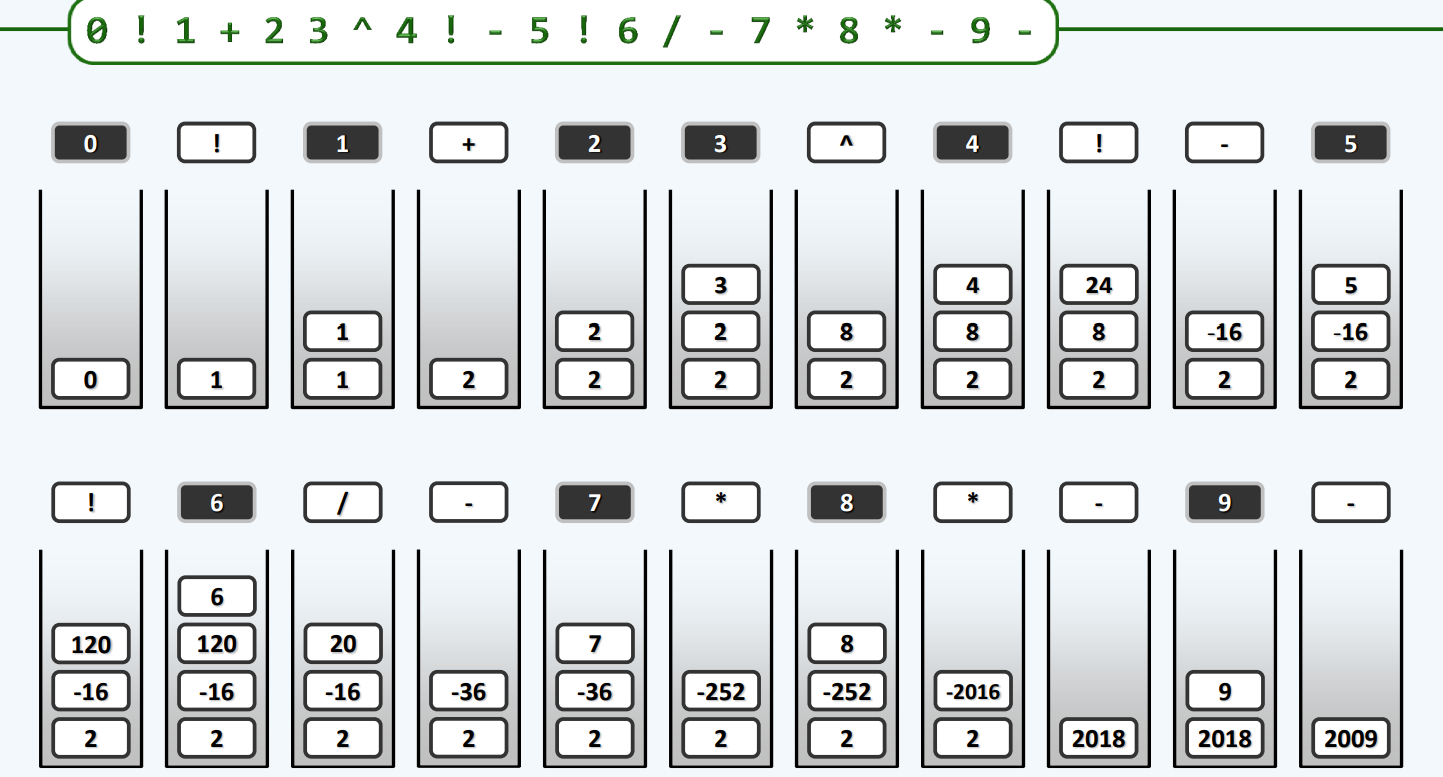
中缀转后缀

转换算法

队列
ADT接口
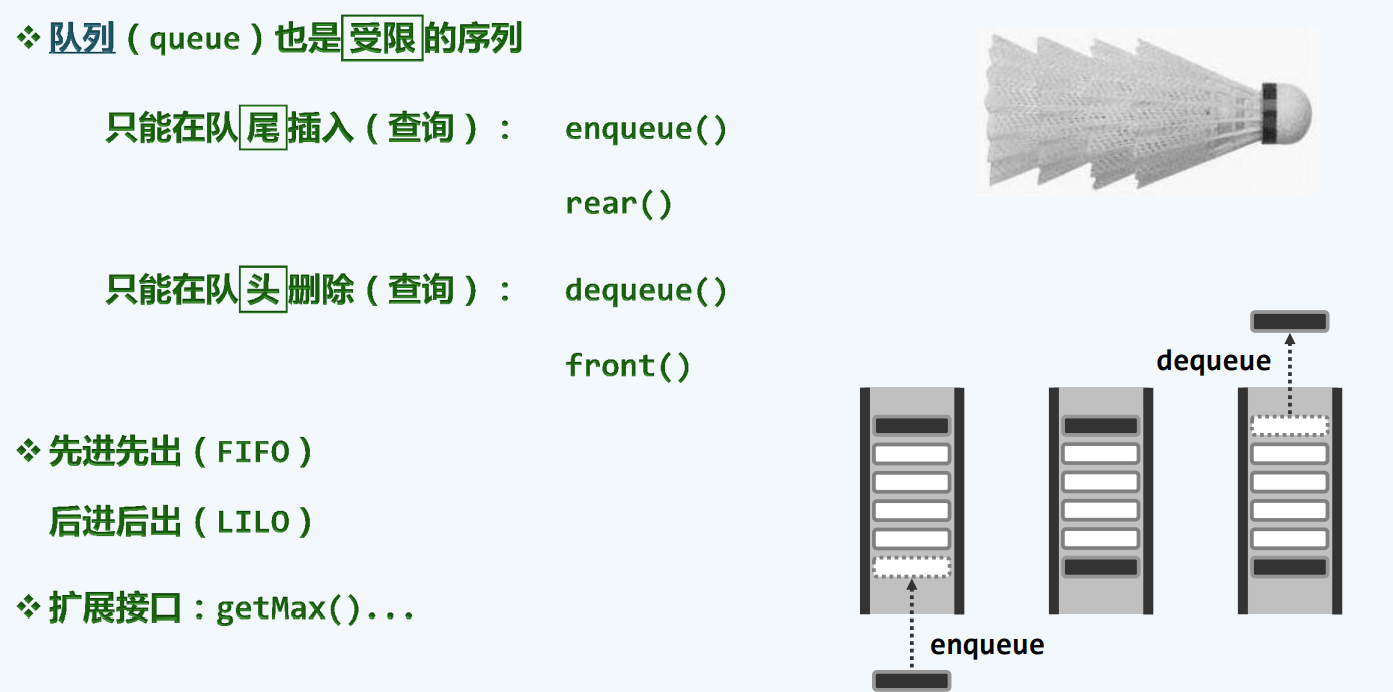
操作实例
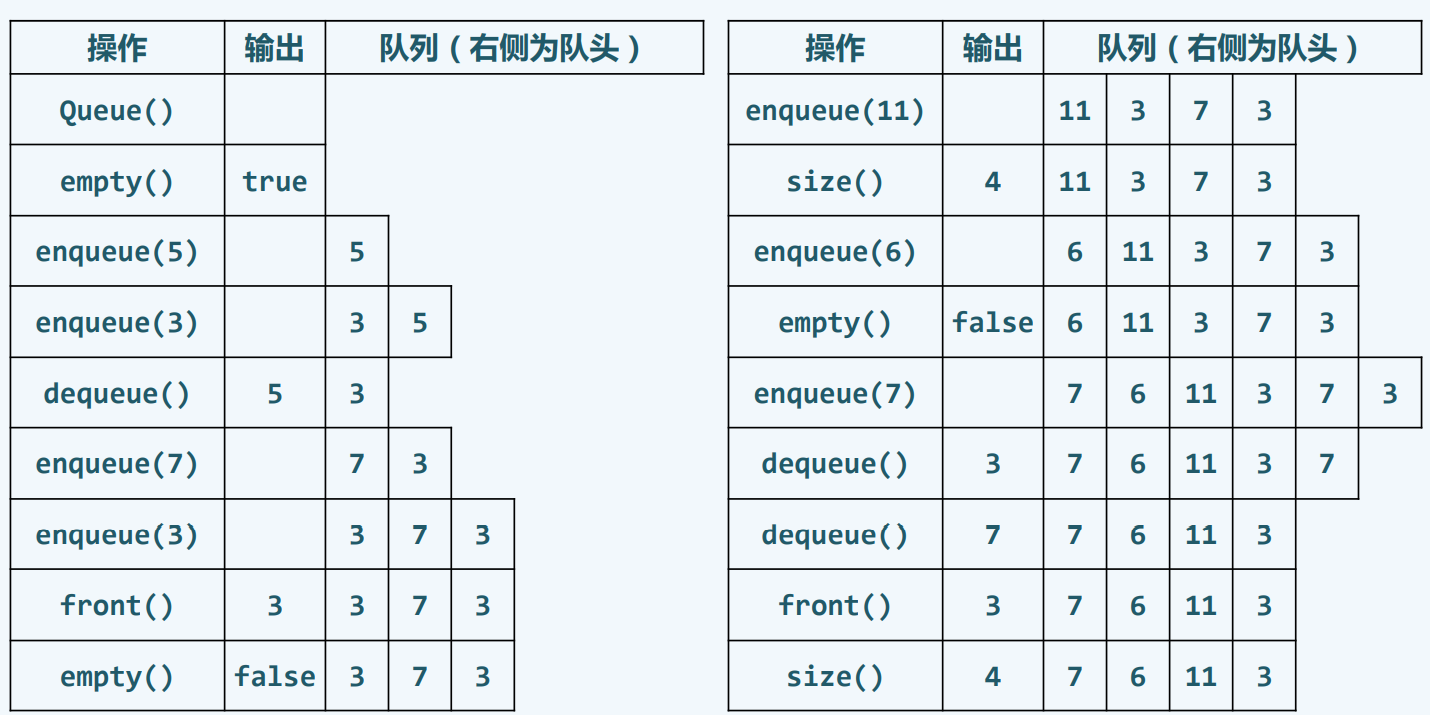
基于列表模板类

本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 jjyaoao's Home!
评论
LivereValine








