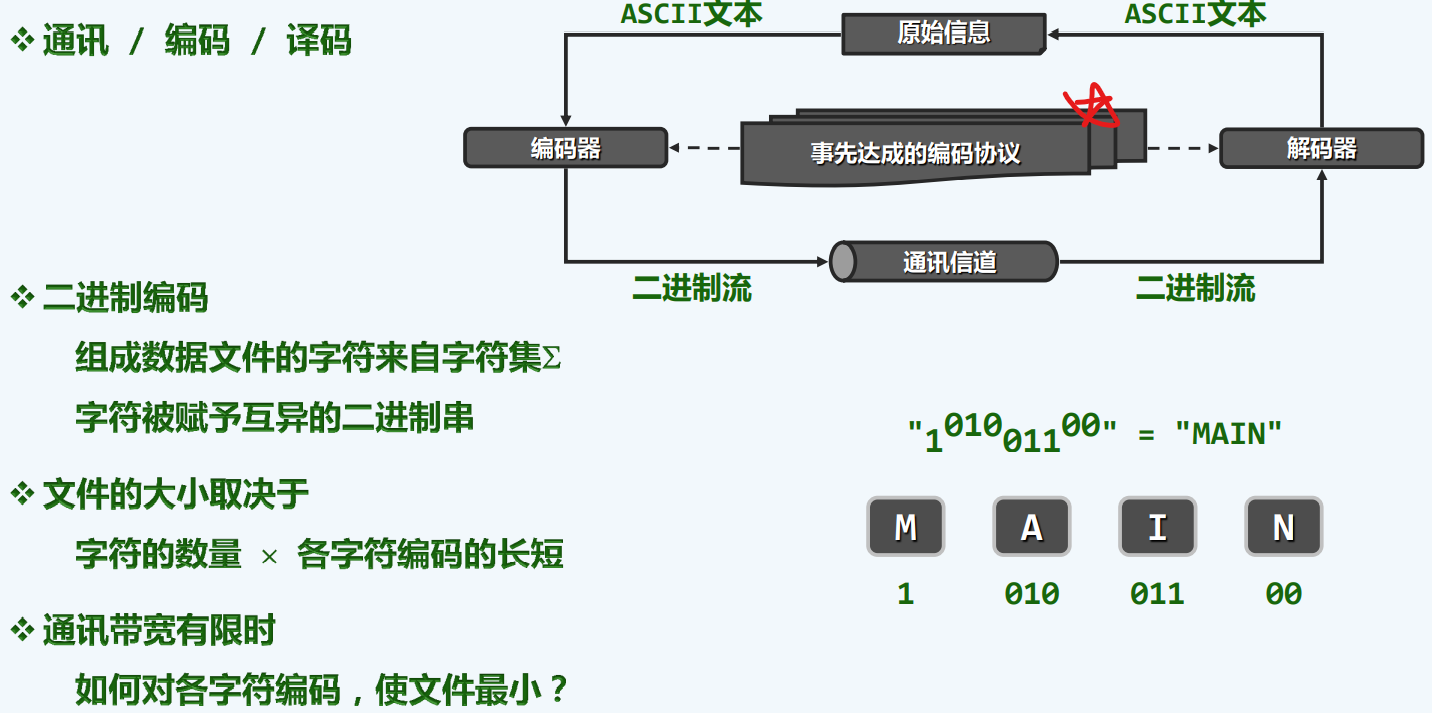
二叉树
以下笔记为jjyaoao本人制作,欢迎借鉴学习和提出相关建议,转载需要标明出处www.jjyaoao.space
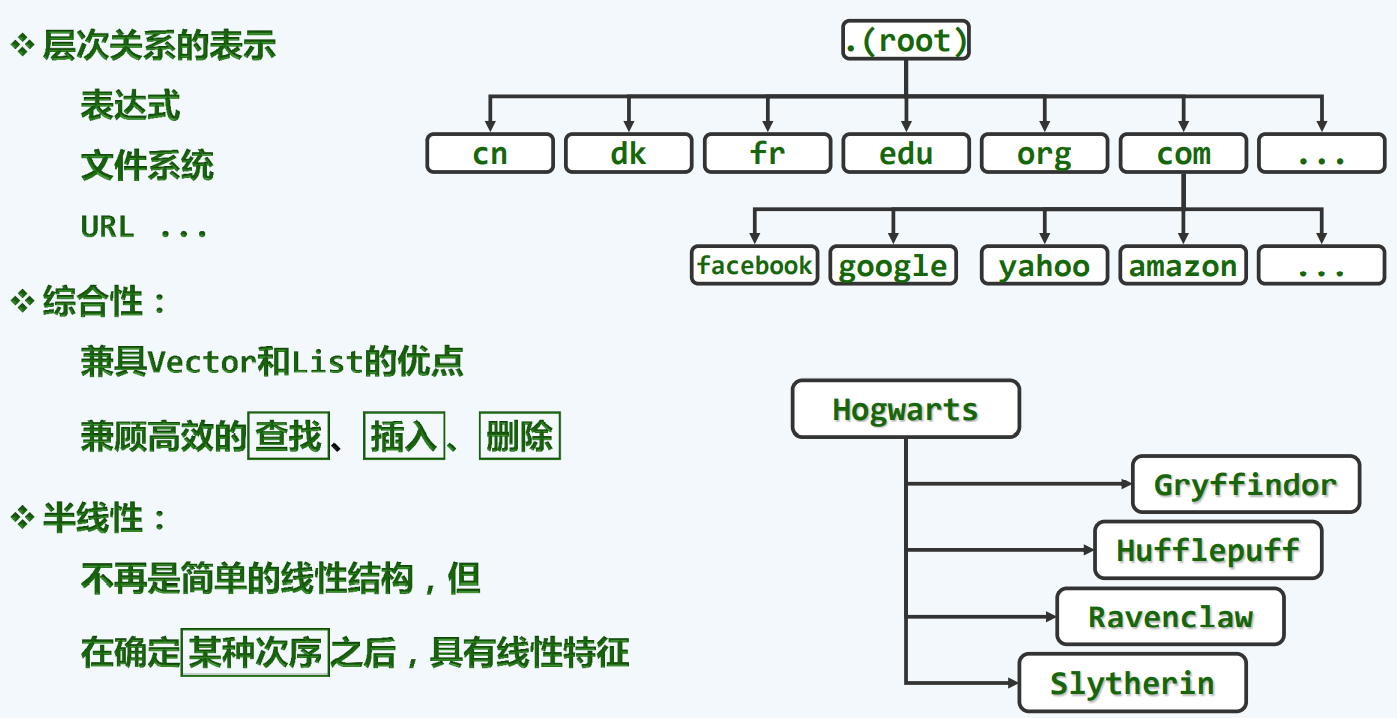
树
应用
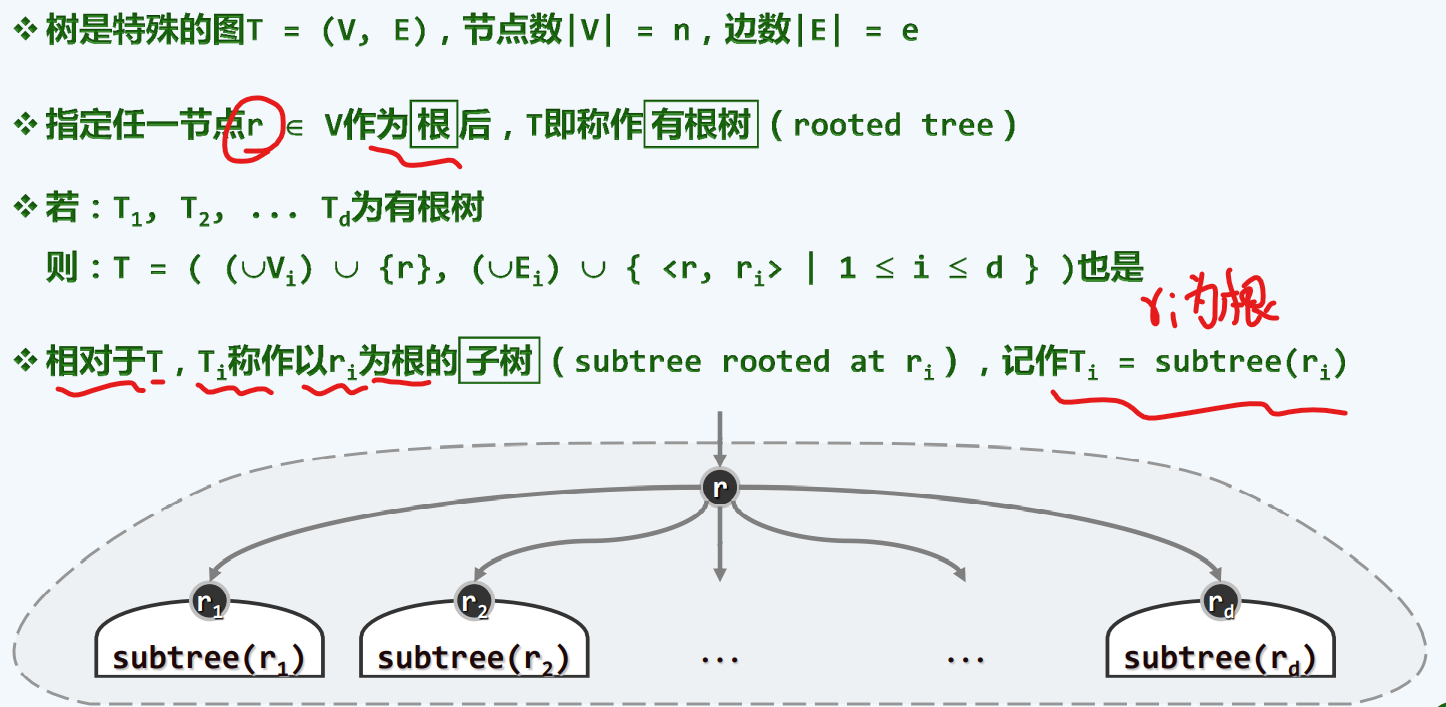
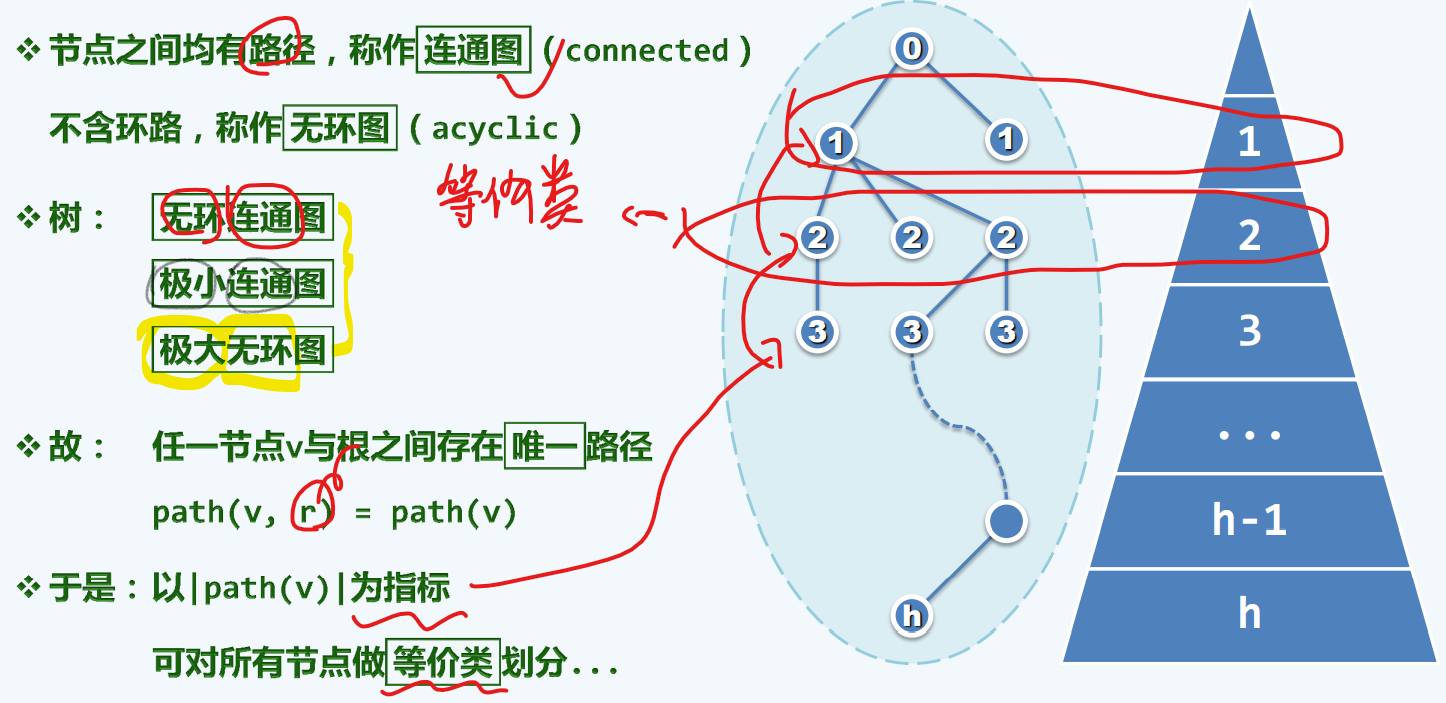
有根树
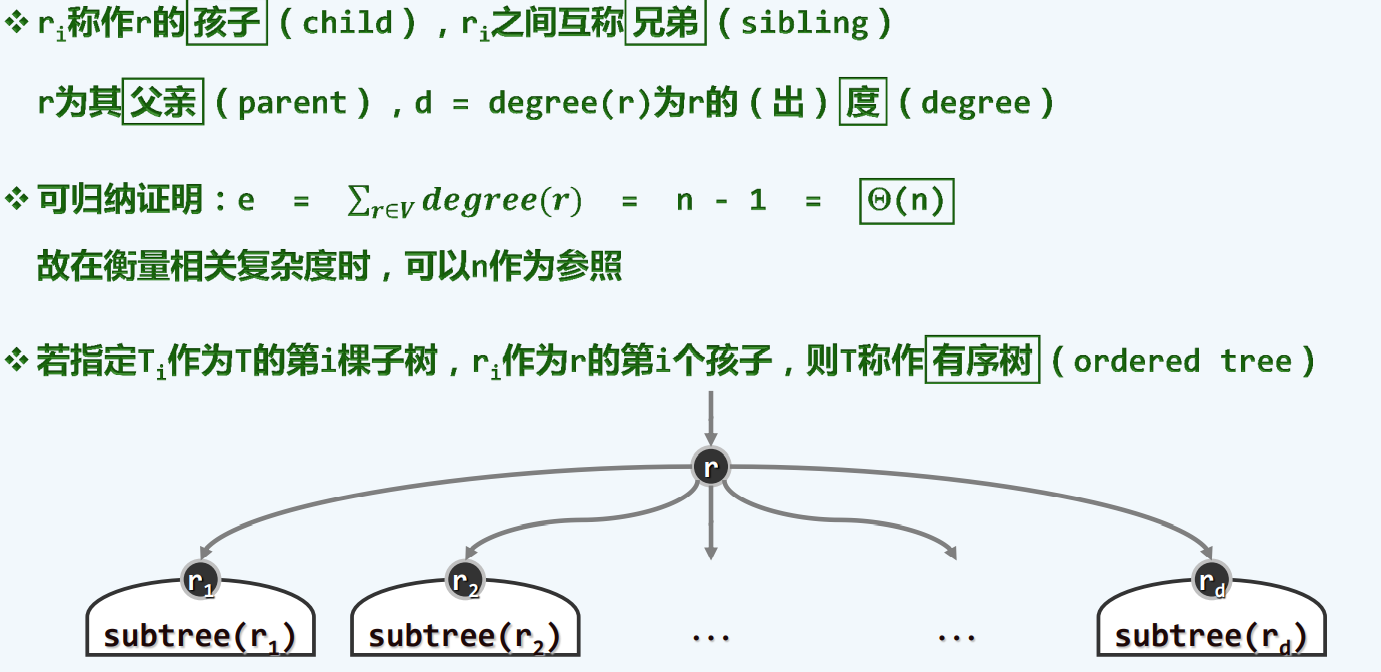
有序树
凡是兄弟之间有明确次序的树,我们把它叫做有序树
任何一颗树中所含的边数 = 顶点数目-1 = 其中所有定点度数之和
这个结论之所以重要,是因为我们可以得到边数和顶点个数是同阶的
也就是说,如果一棵树的总体规模,如果可以度量为顶点数+边数,那么它从渐进的意义来讲,是与顶点个数同阶的,也就是我们后面评判一棵树的规模,可以以顶点的数目n作为参照
路径+环路
这里我们用边的数目来代表它的路径长度
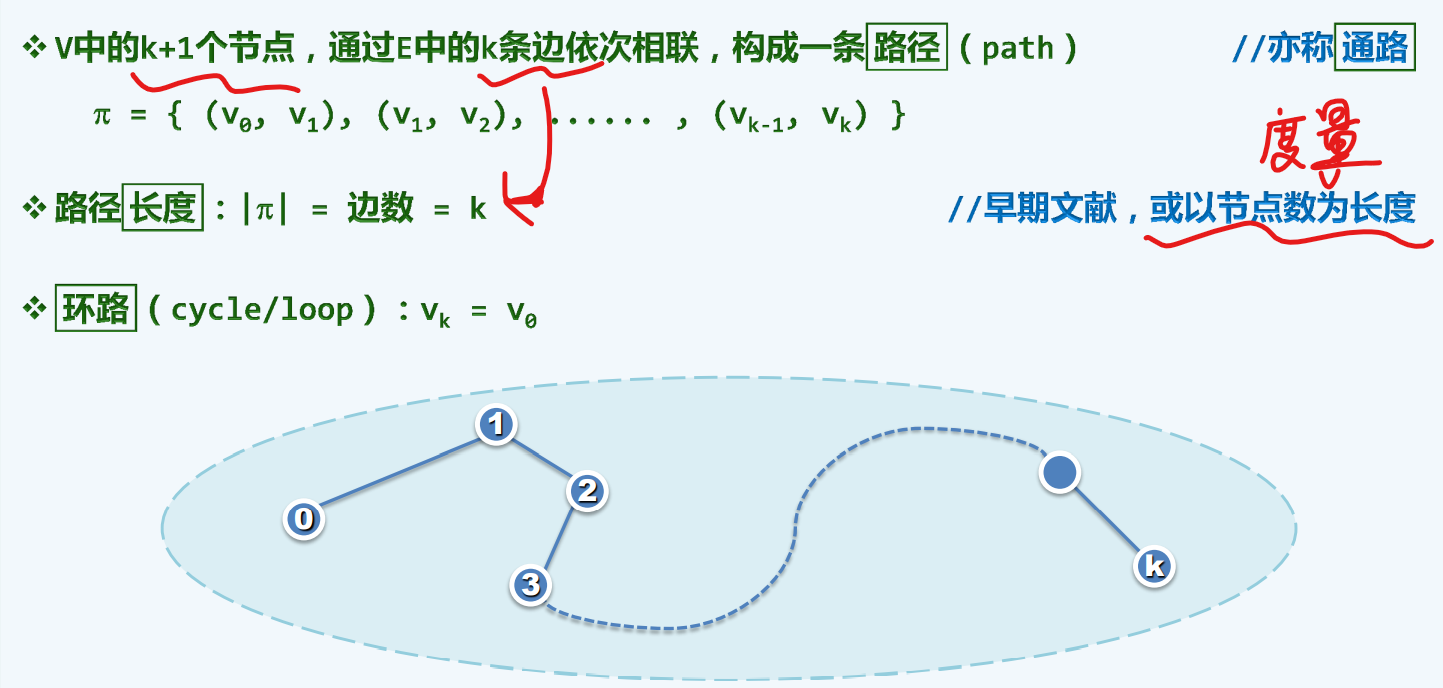
连通+无环
深度+层次
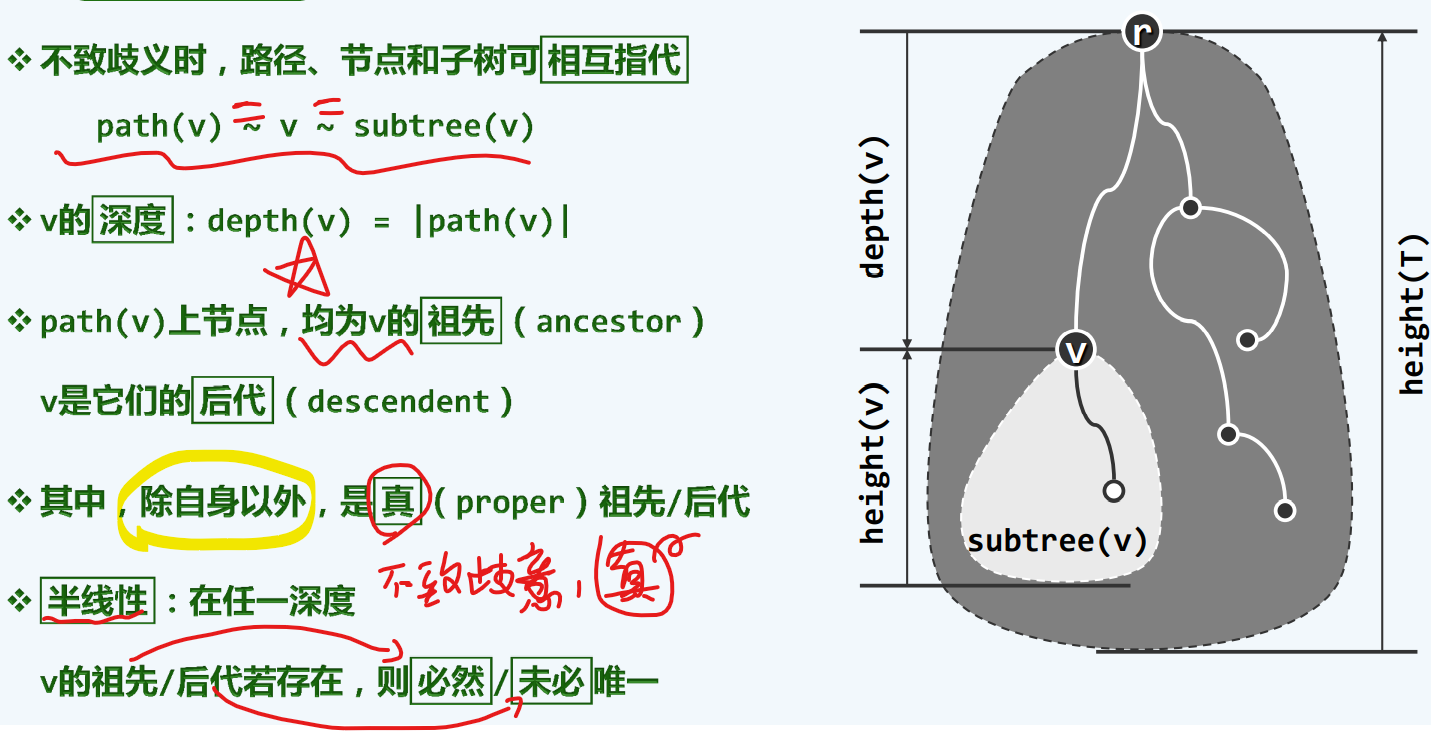
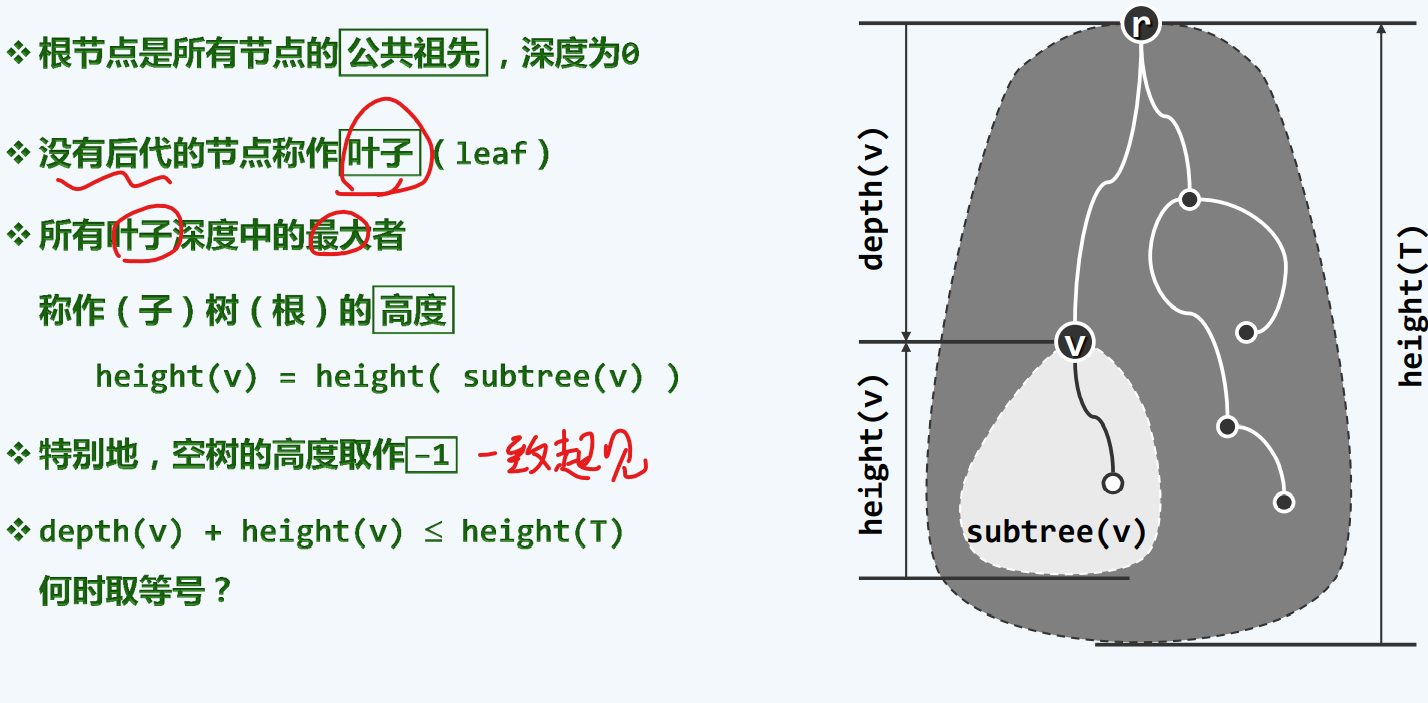
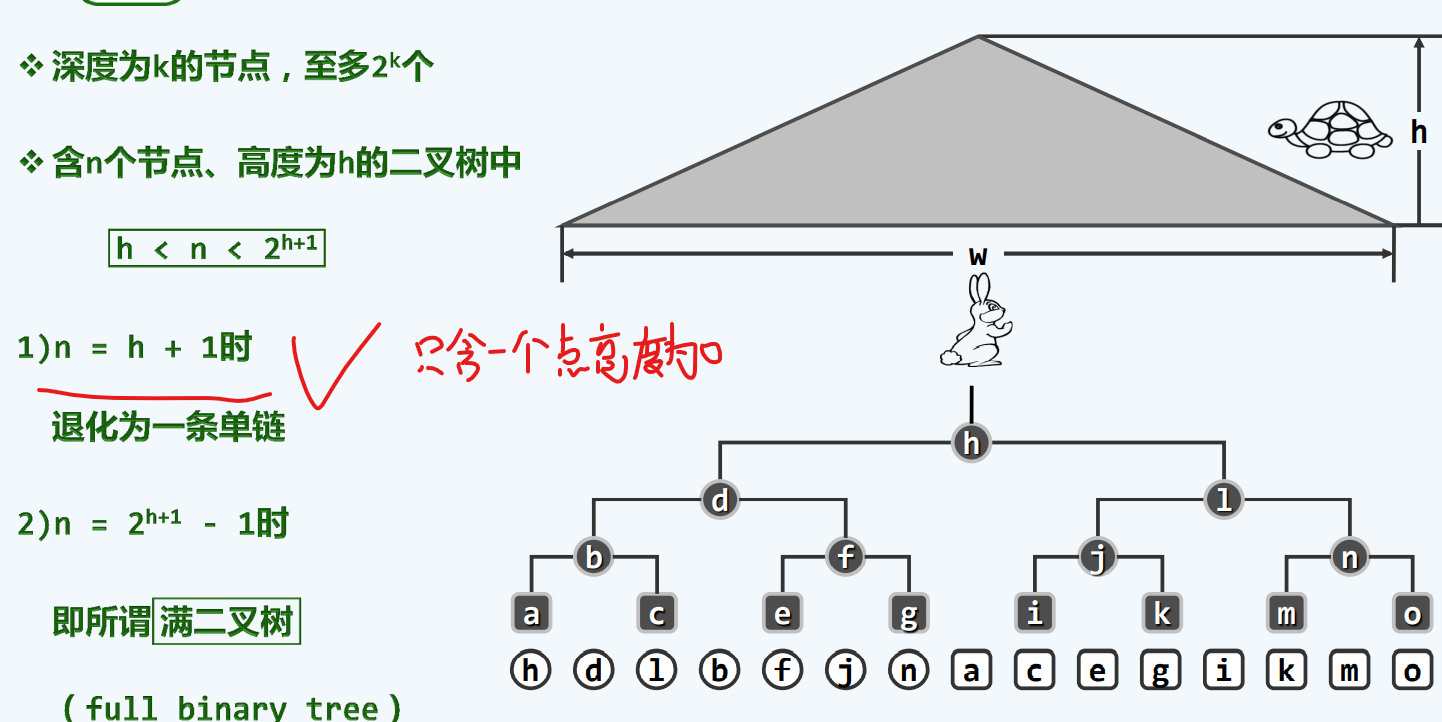
何时取等号?
当节点v是深度最大的叶节点或祖先节点时,取等号
树的表示
ADT接口

父节点
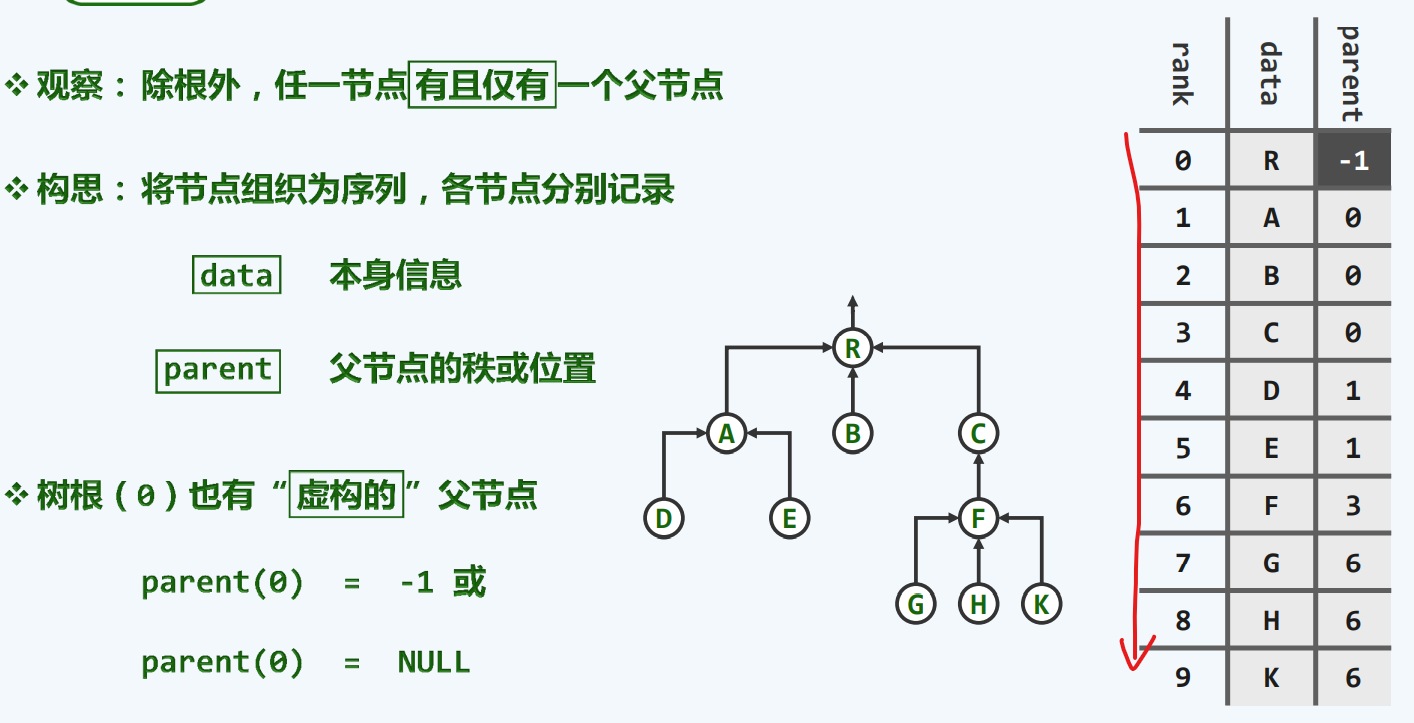
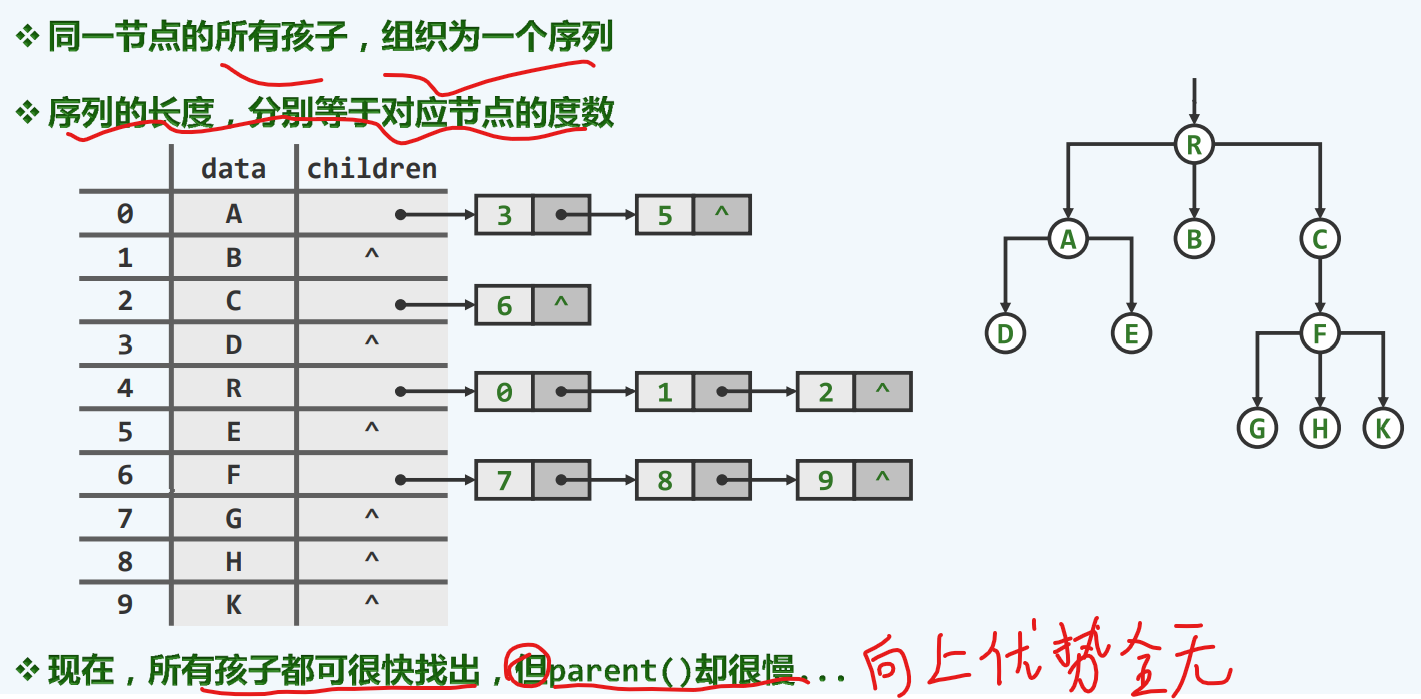
孩子节点
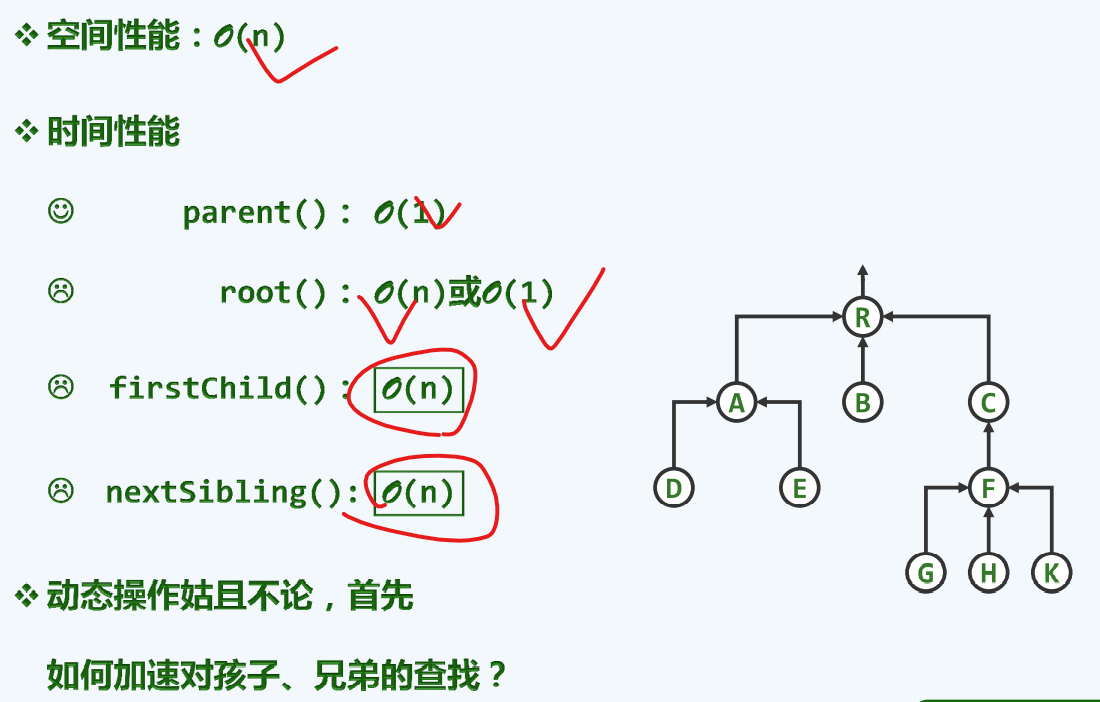
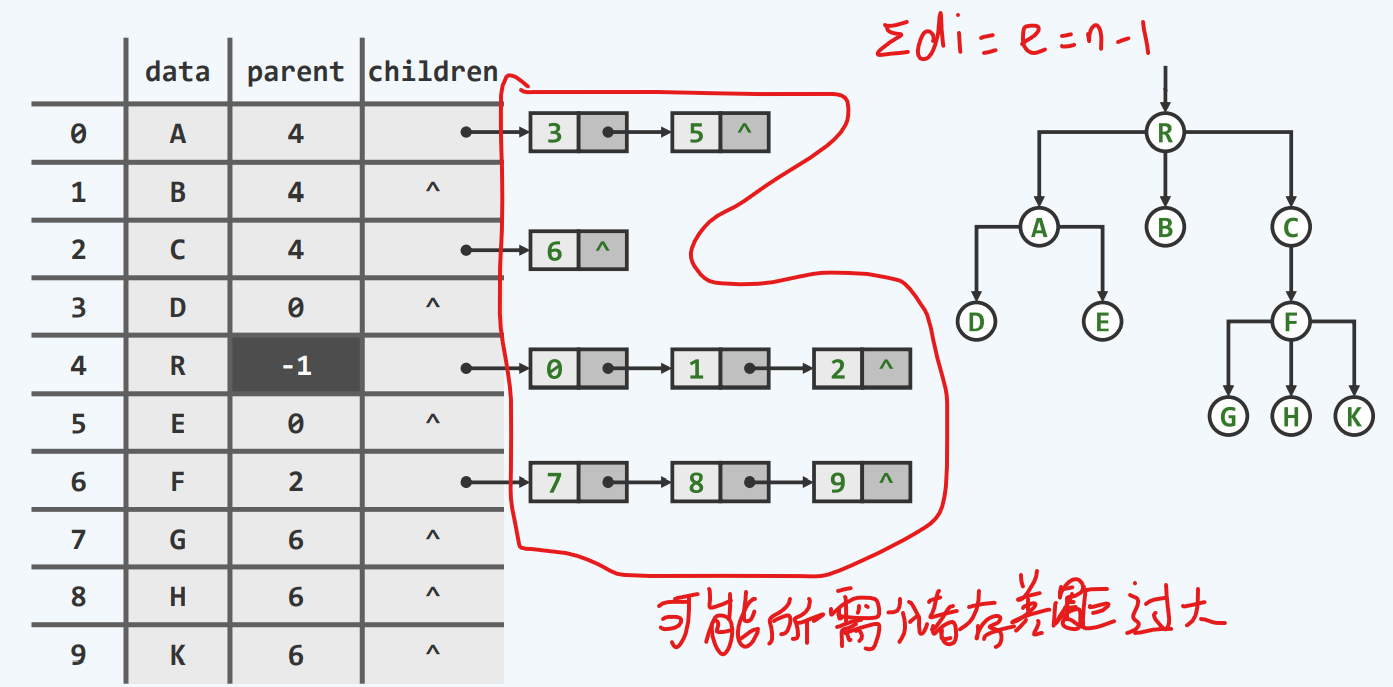
父亲+孩子
整合了父亲 和 孩子的优点
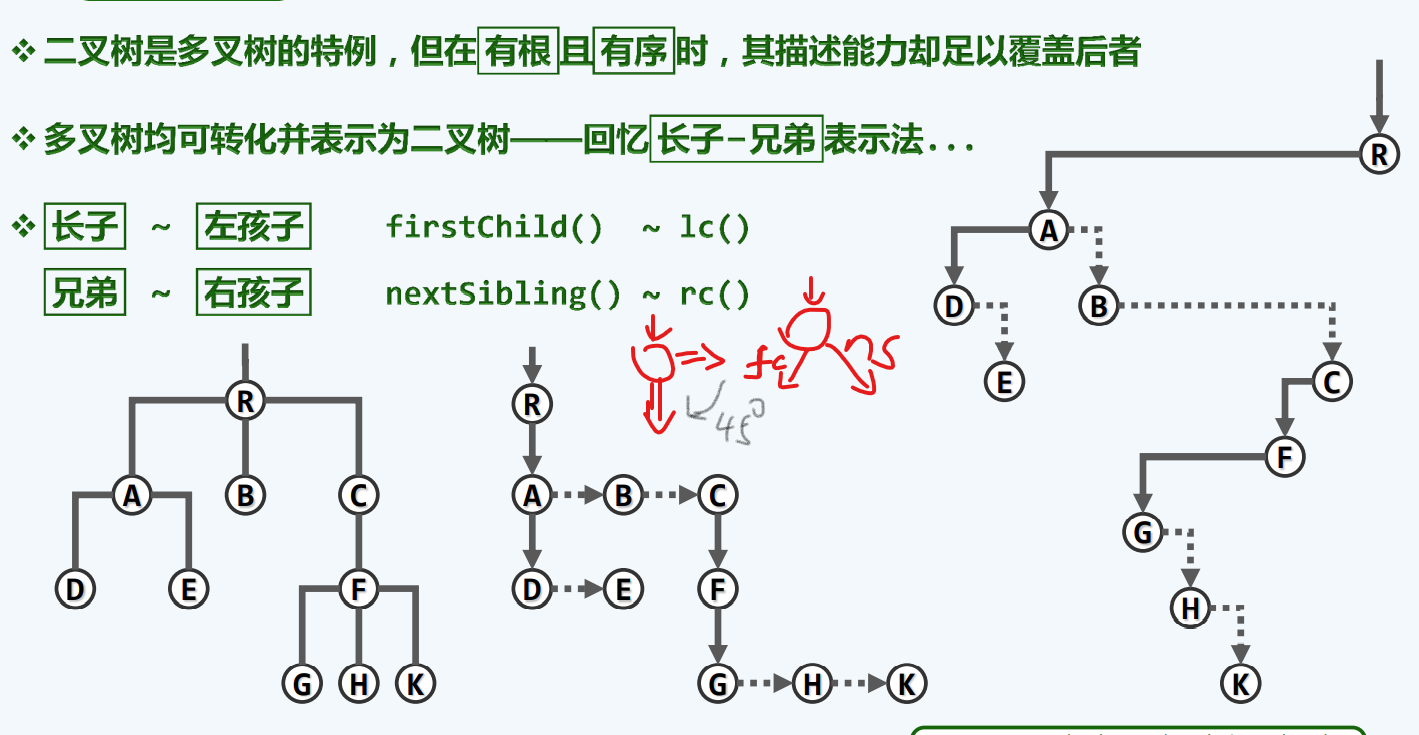
长子+兄弟
反观父亲+孩子出现的问题
根源在于每一个节点的出度是不尽相同的
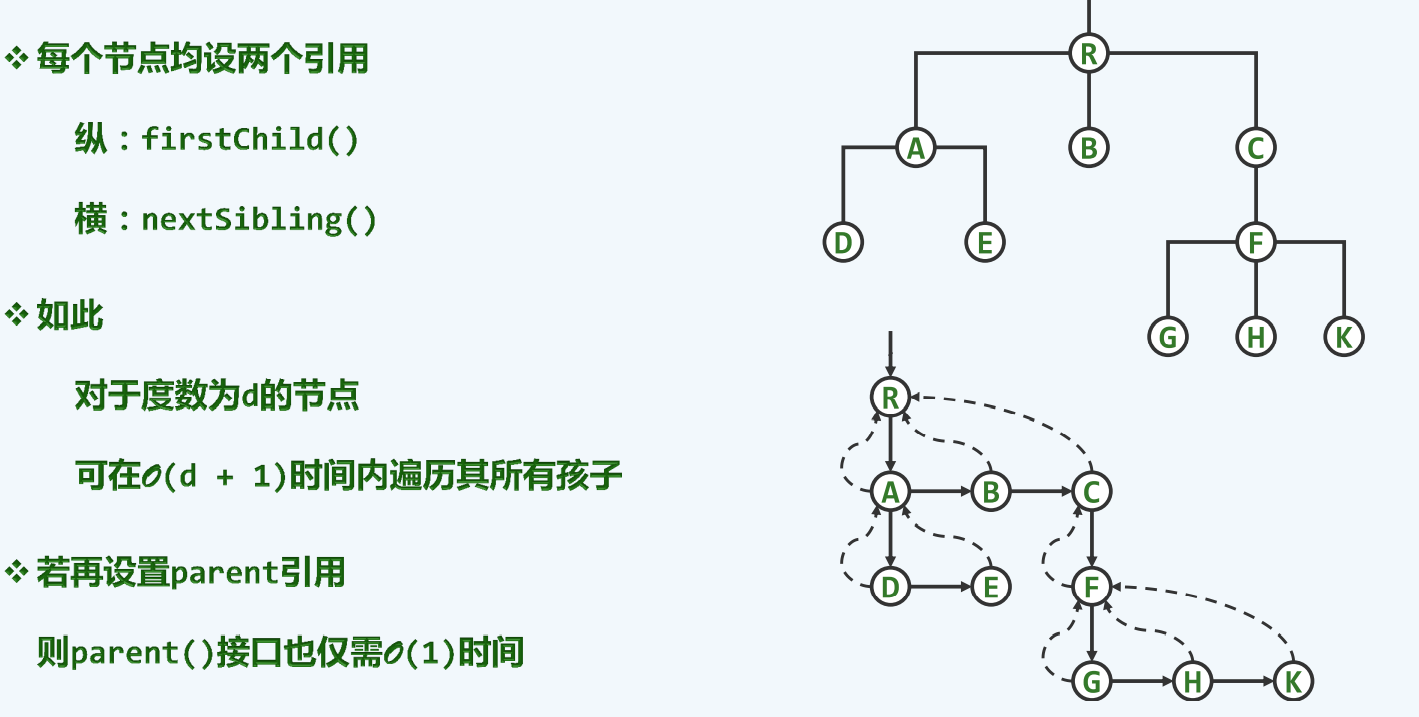
解决方案:每一个节点均设两个引用
这种方式是 对树本质的深刻理解
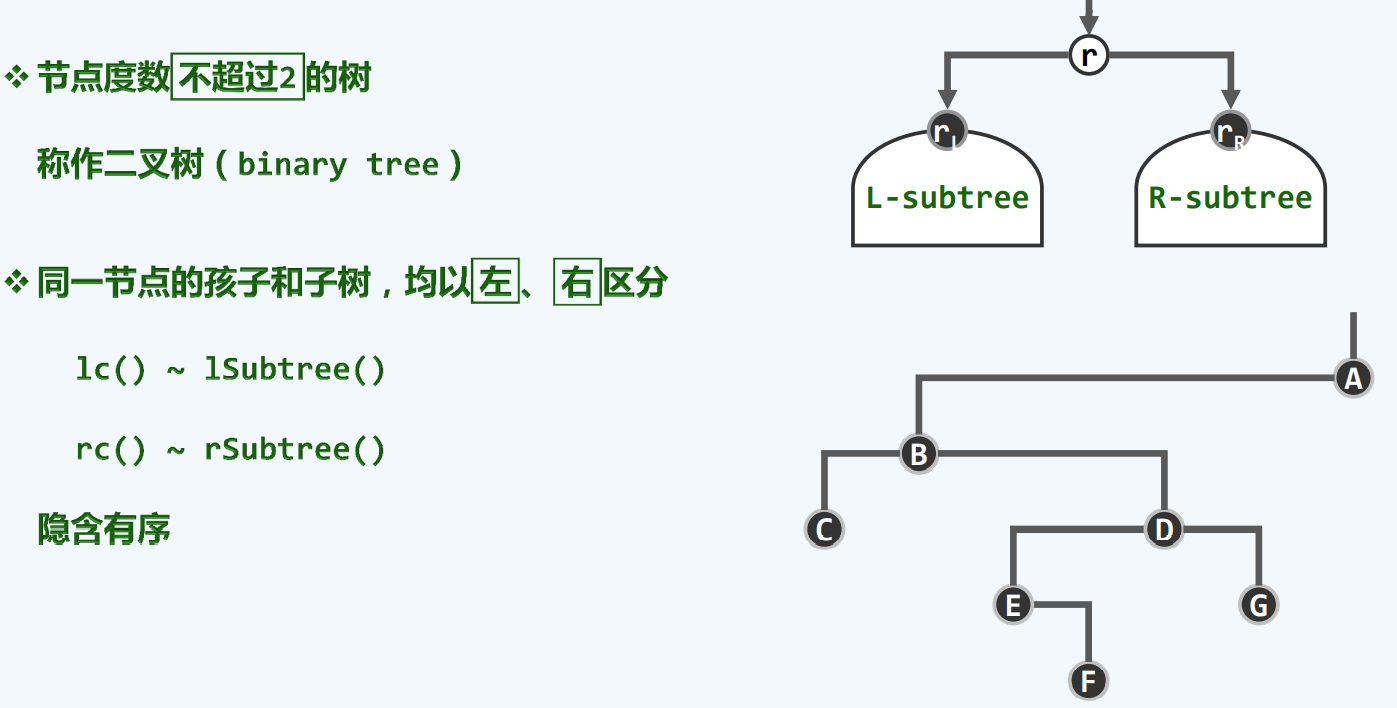
二叉树
有根有序树
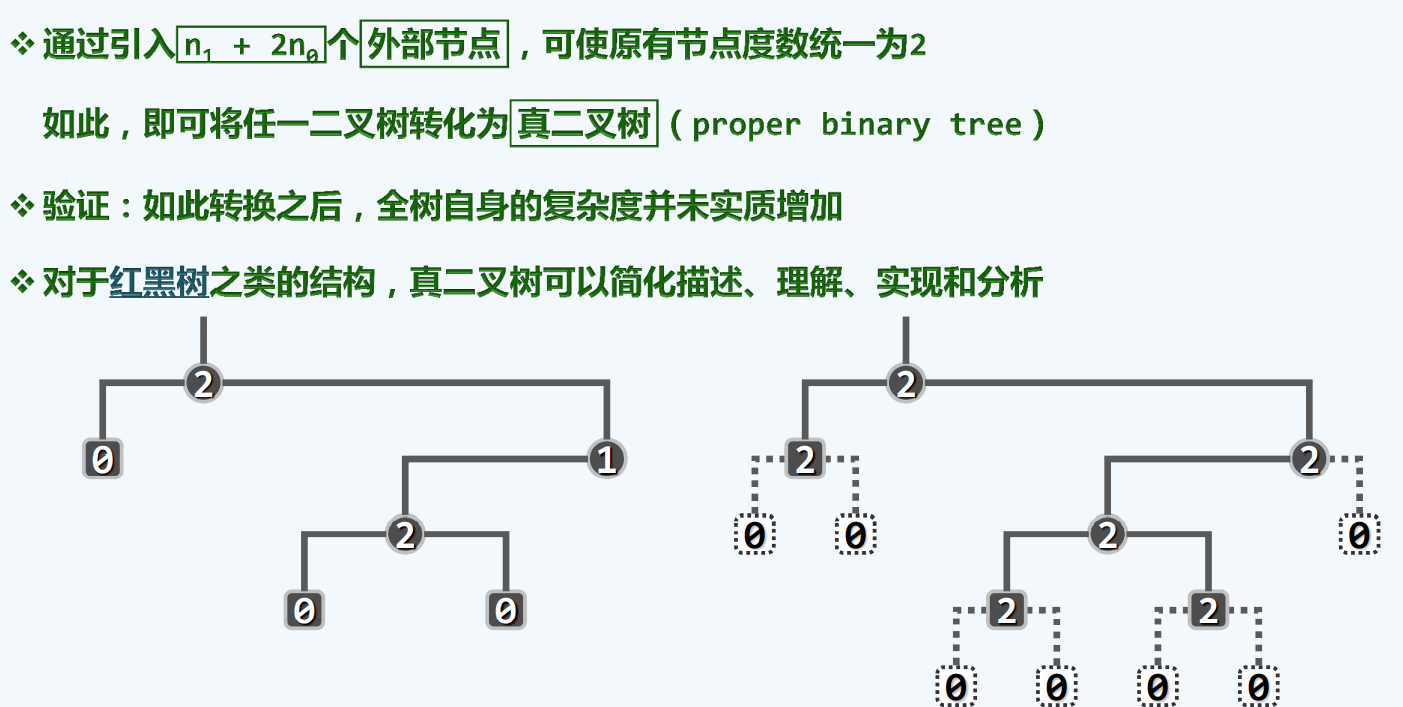
真二叉树
如果某一棵树原先度数是0,那么我们为他引入两个节点,如果原先度数是1,那么我们为他引入一个节点。
- 一方面从渐进的意义上讲,阶数相当
- 另一方面,当我们后续实现就能看出,这种添加完全是假象的,不需要实际的添加节点进入,只是方便理解,实现。
- 犹如虚拟实现,想象它背后的逻辑是对的,不需要实际的实现它
描述多叉树
表面上是不可能的,竟然用一个特例,来描述整个现象
这也解释了为何树会变成一个小的标题;:因为二叉树就可以代表树
二叉树实现
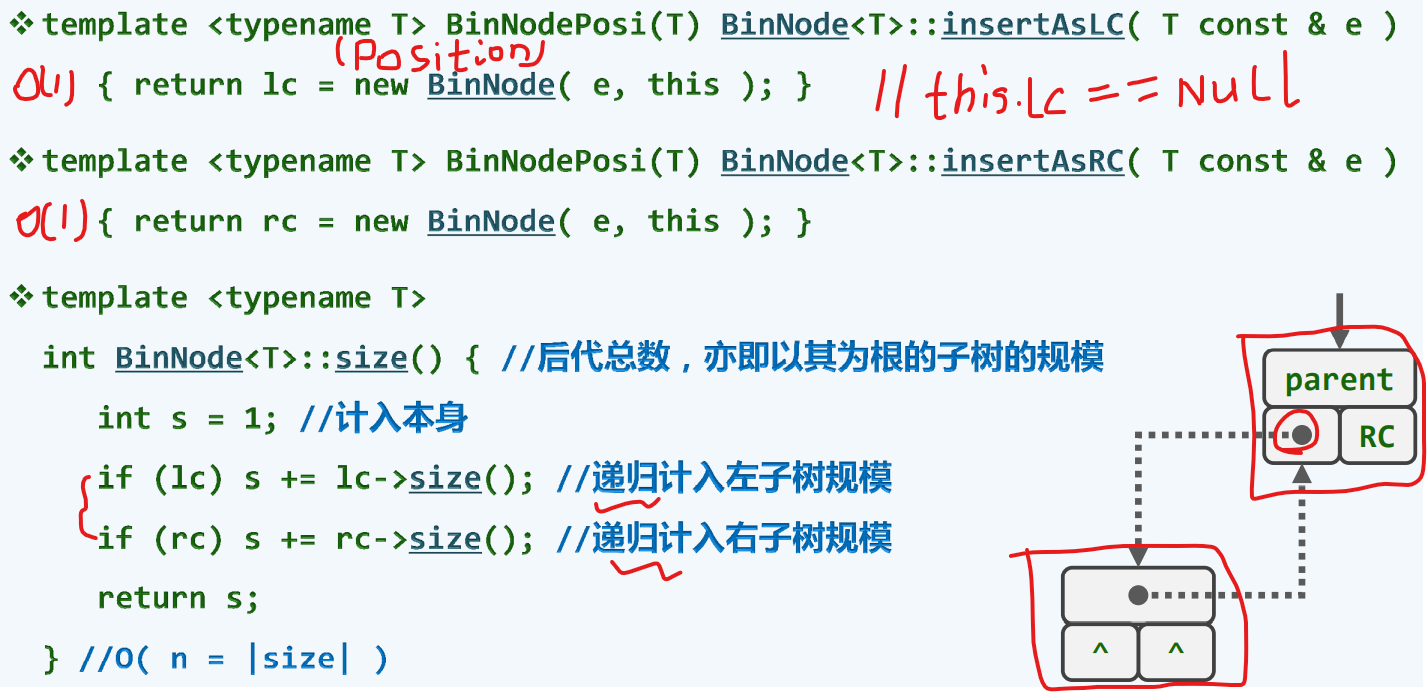
BinNode类

接口实现
BinTree类
虚方法updateHeight是为了,后面庞大的衍生类能对这个方法进行适当的重写

高度更新
未涉及到变种,仍采用常规定义

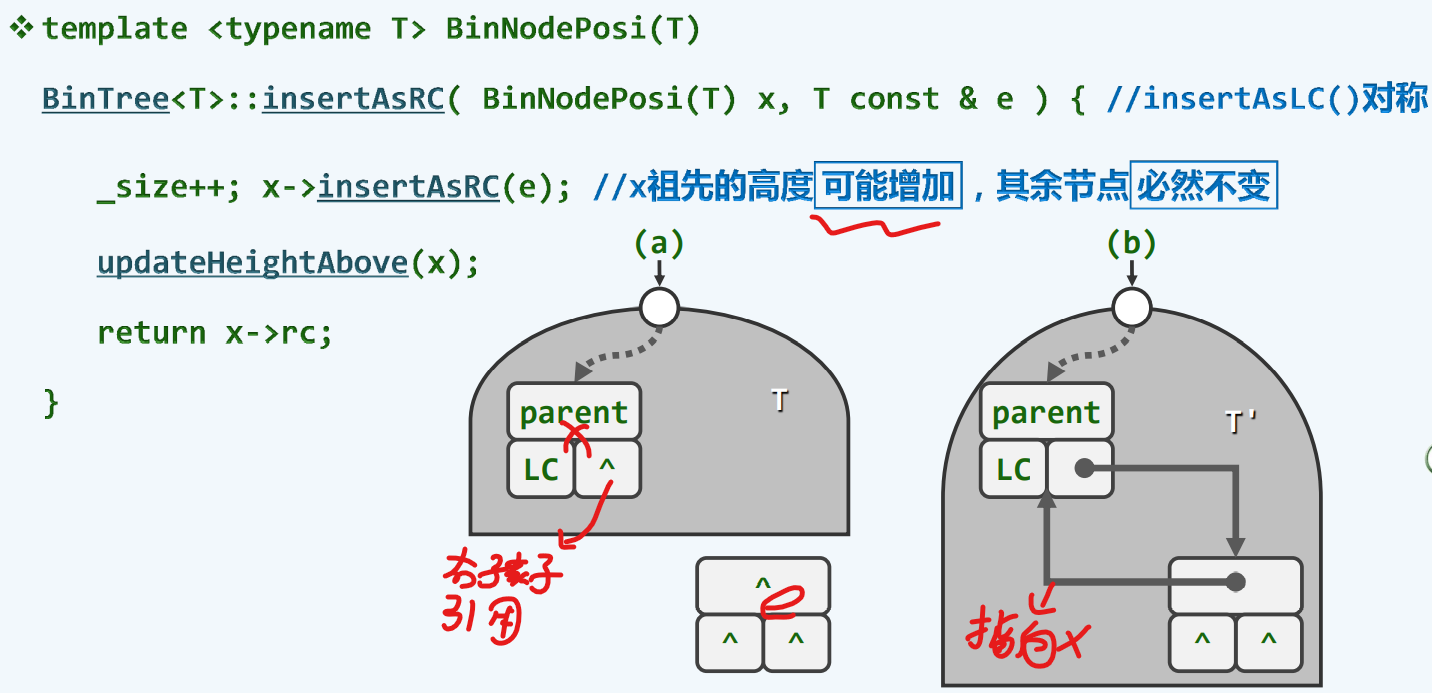
节点插入
通过调用binNode类的同名接口insertAsrc() 传入参数e,意味着创建一个e的节点,并且让x指向这个接口所返回的那个地址交给x此前为空的右孩子引用,从而使得引用能指向新晋生成的节点
子树接入
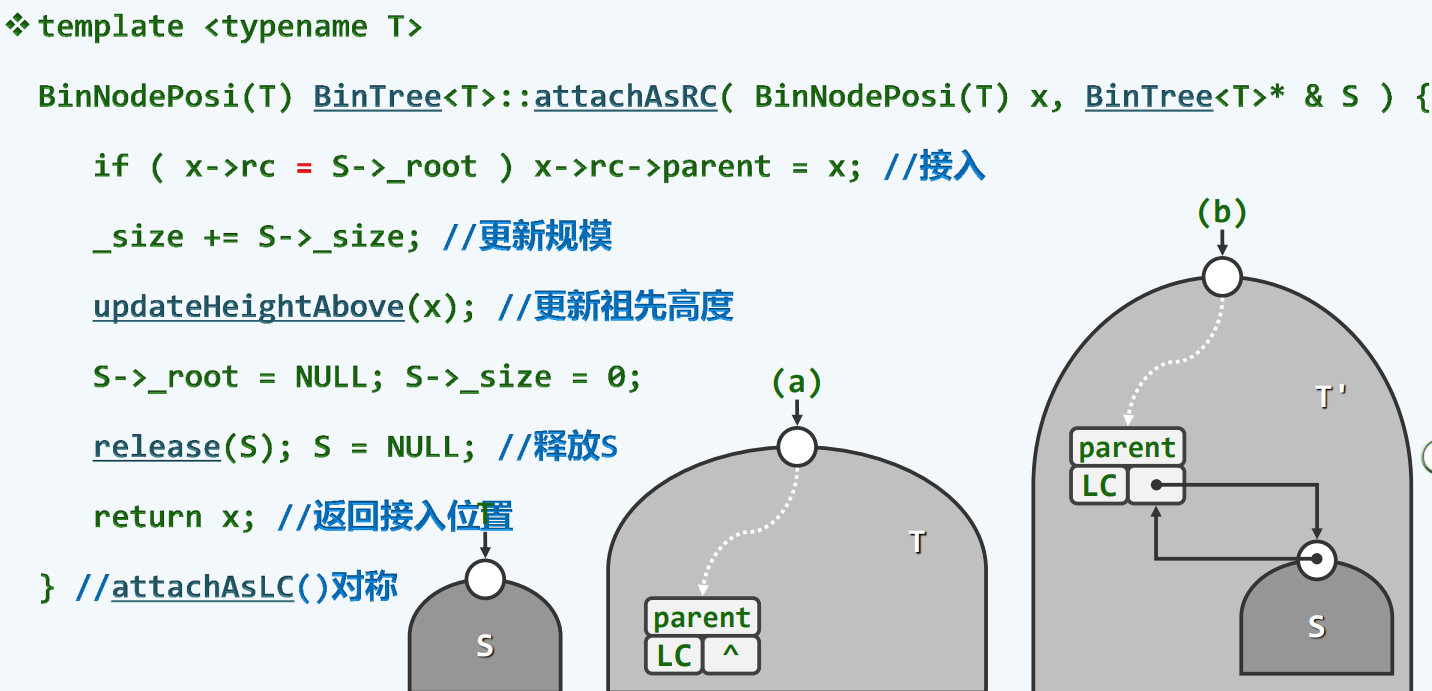
1 | template <typename T> //将S当作节点x的左子树接入二叉树,S本身置空 |
子树删除
1 | template <typename T> //删除二叉树中位置x处的节点及其后代,返回被删除节点的数值 |
子树分离
1 | template <typename T> //二叉树子树分离算法:将子树x从当前树中摘除,将其封装为一棵独立子树返回 |
遍历
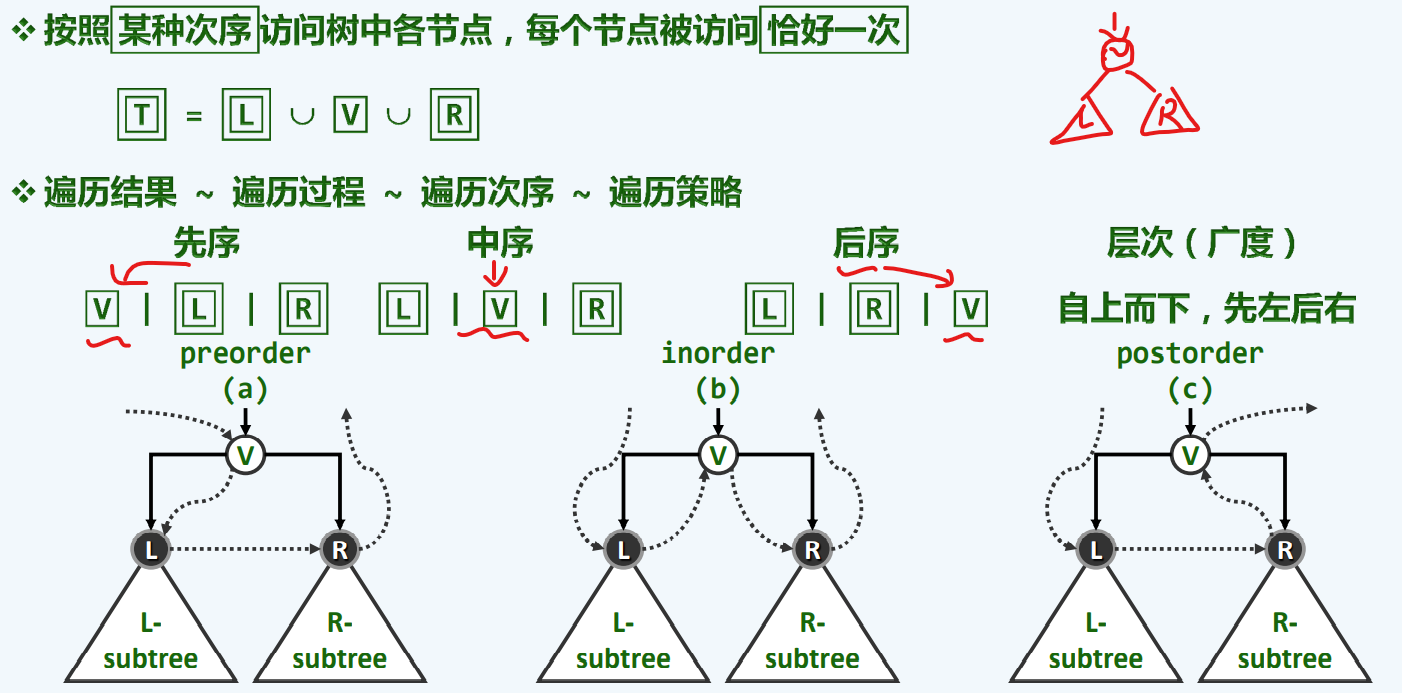
递归—-》迭代是很有必要的,递归的过程只具有渐进意义的O(n),因为它每一步所装的箱子都是一样的大小,我们完全可以根据实际情况,来把他箱子改小,这在实际应用具有巨大的意义,虽然只是常数的提升!
先中后都属于深度搜索
VST貌似是指针函数的引用
先序遍历
visit里面则放你需要做的事情(取来干嘛)
递归

迭代
为此,我们只需引入栈
版本1
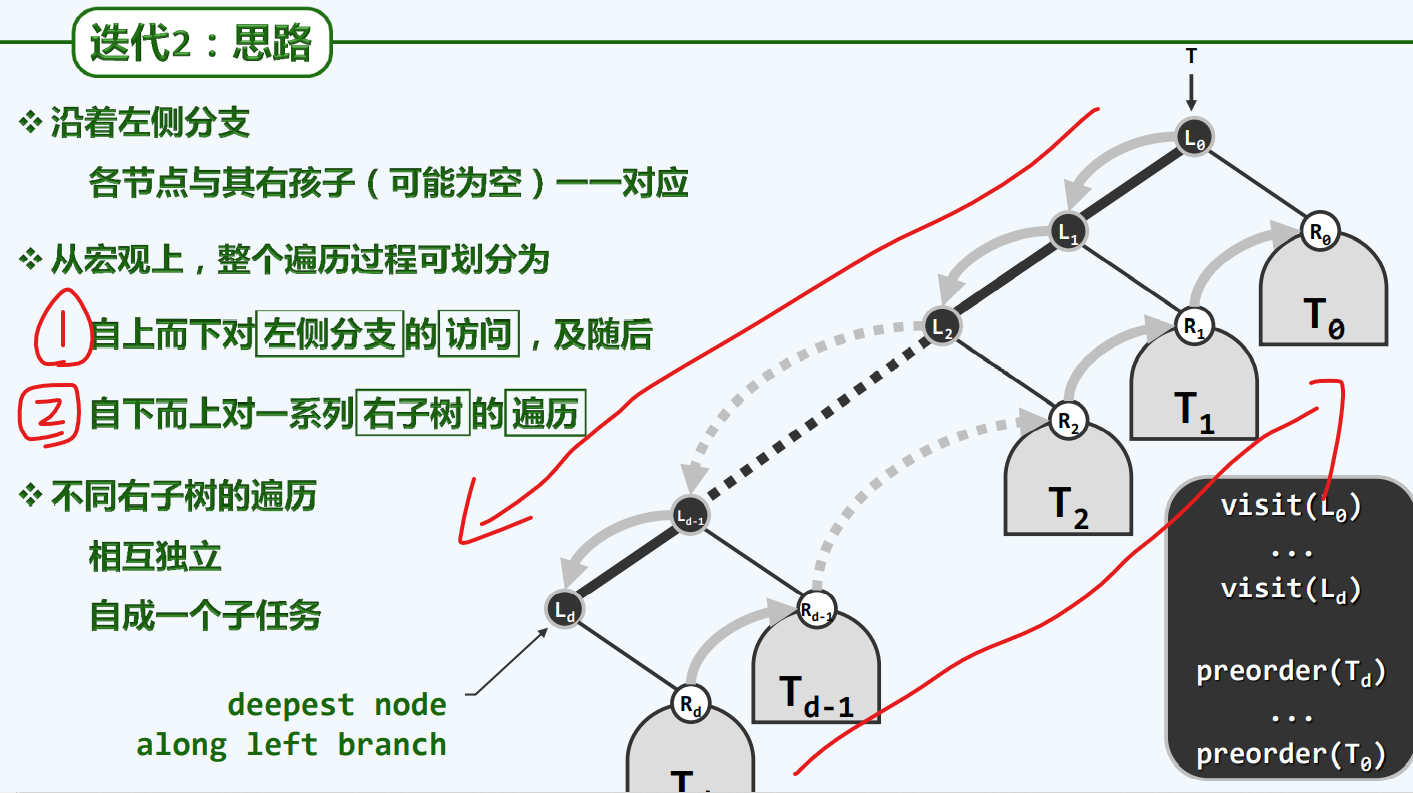
思路
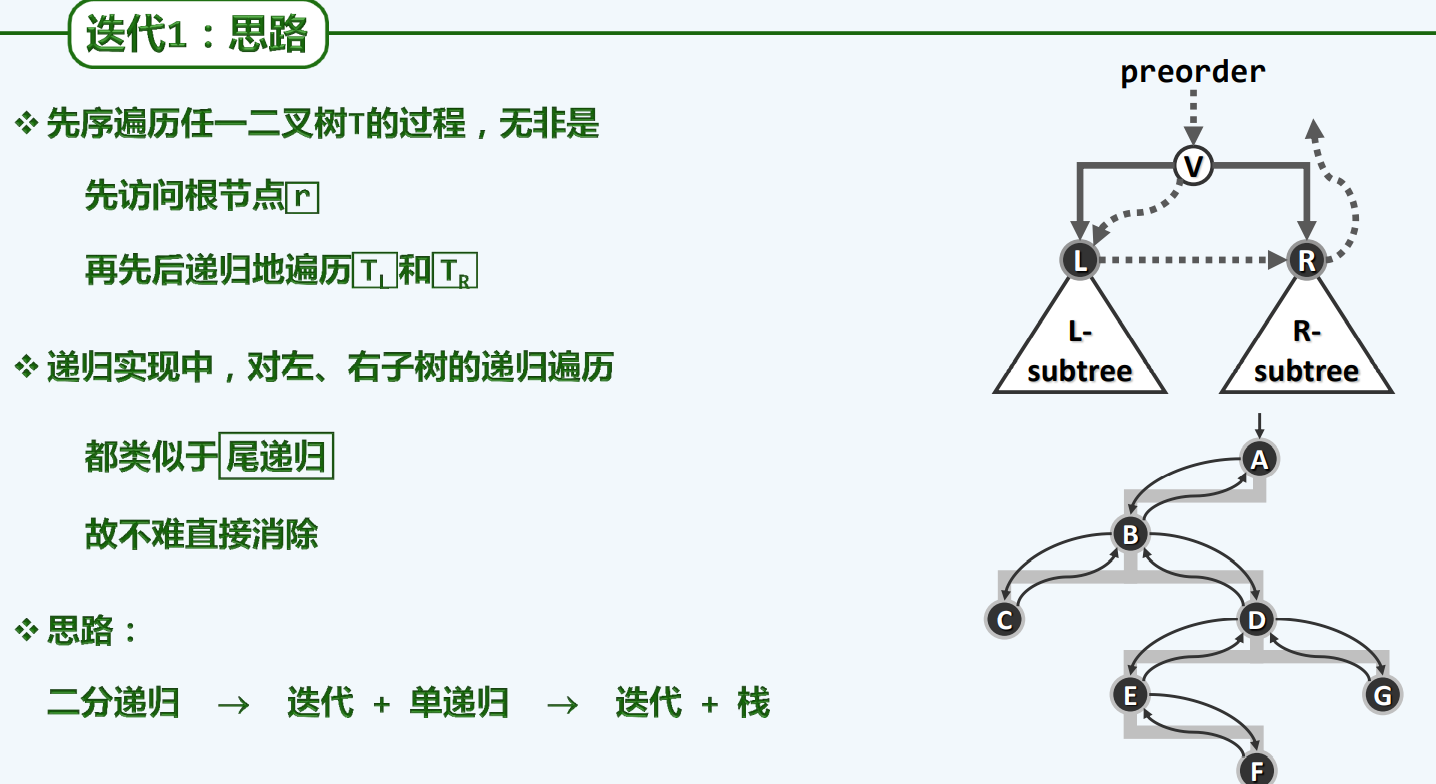
实现

实例
染黑来代表这个节点接受访问
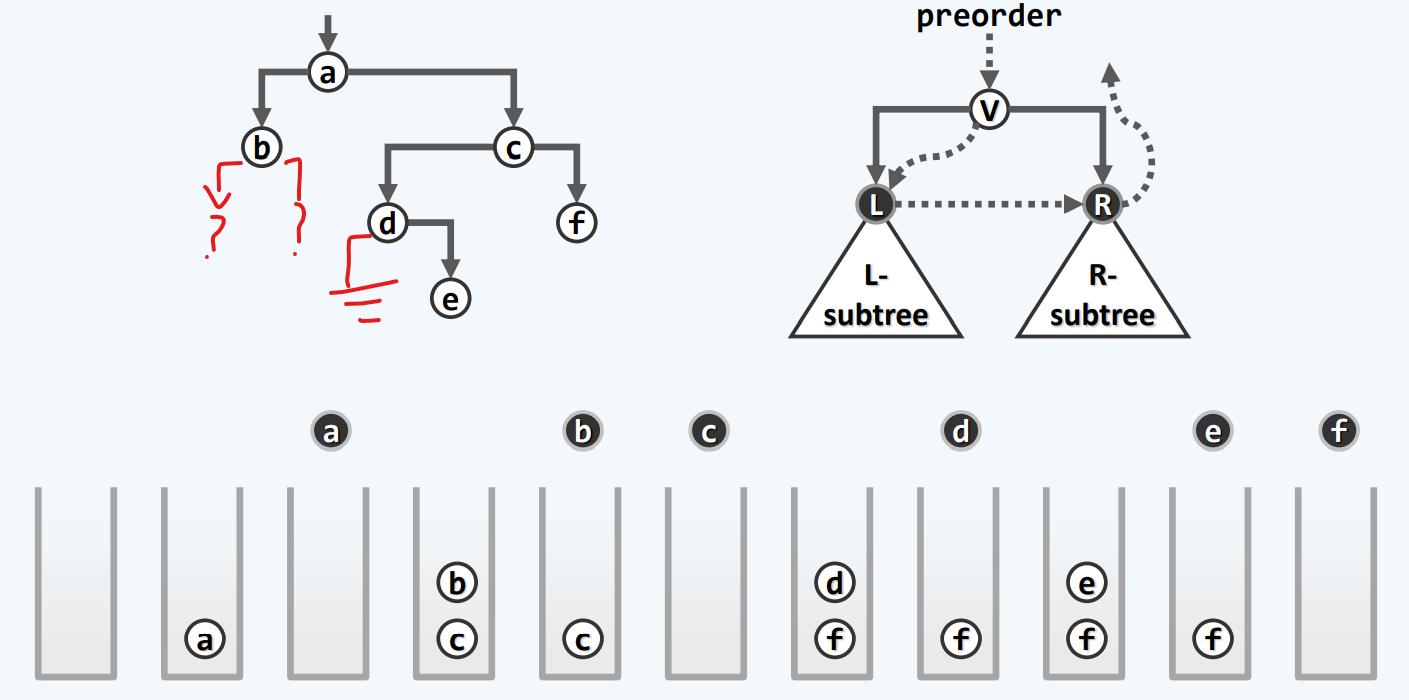

迭代版2
为了推广到后面的中序,后序算法
新思路
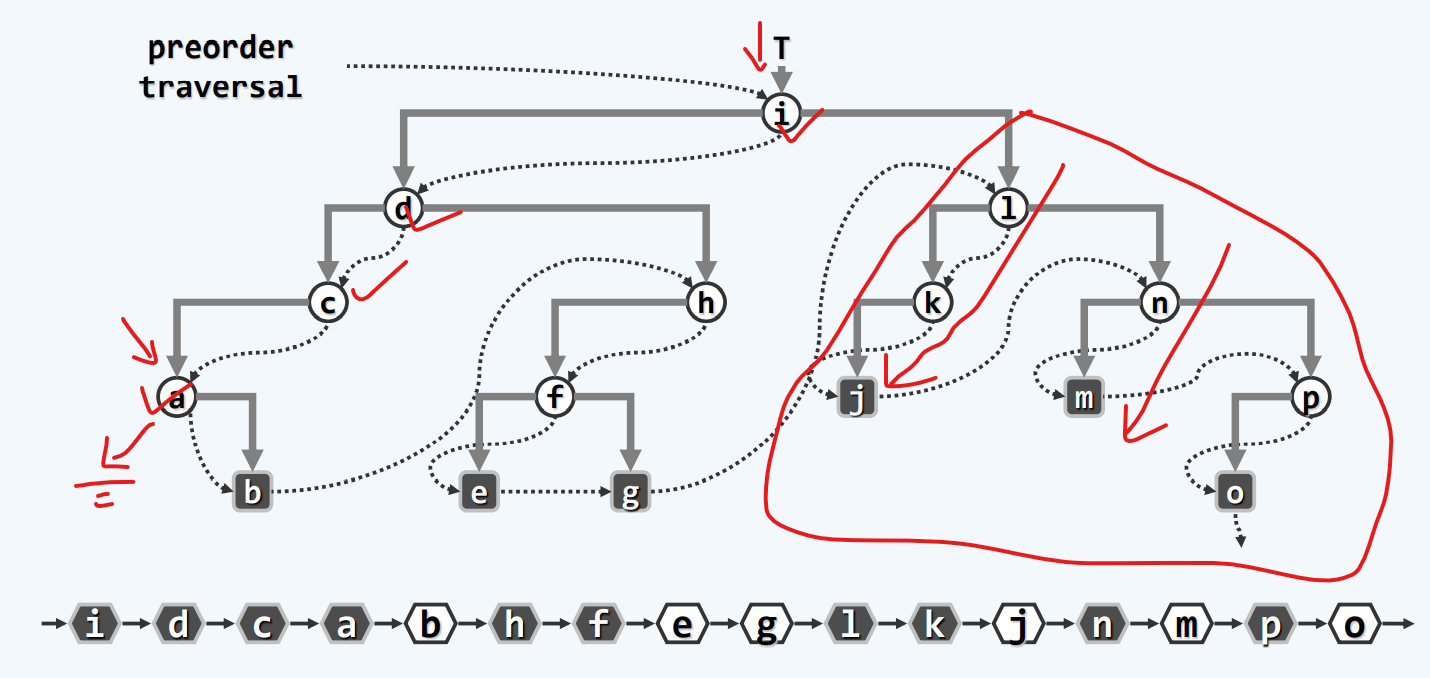
实现
最好熟读,并且背下来!
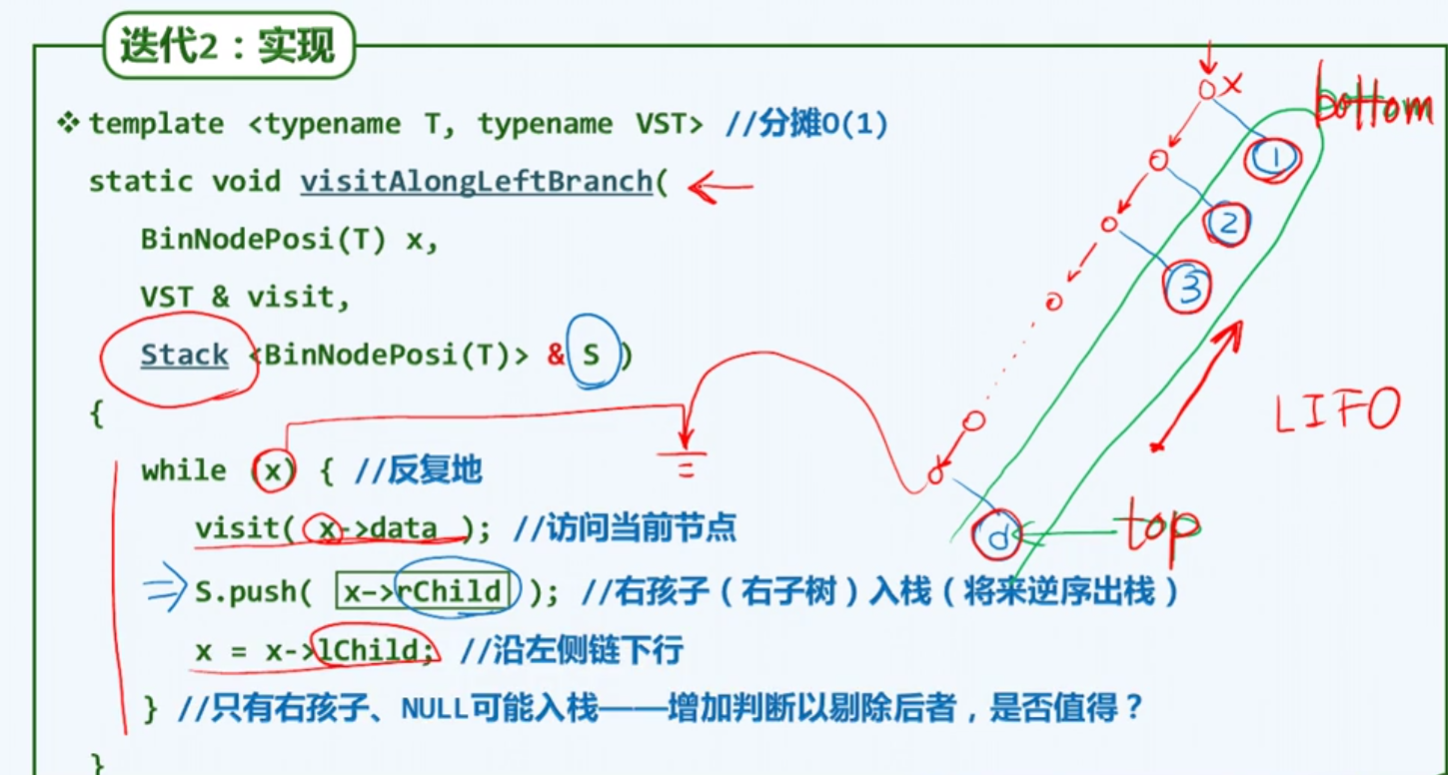

1 | //从当前节点出发,沿左分支不断深入,直至没有左分支的节点;沿途节点遇到后立即访问 |
实例
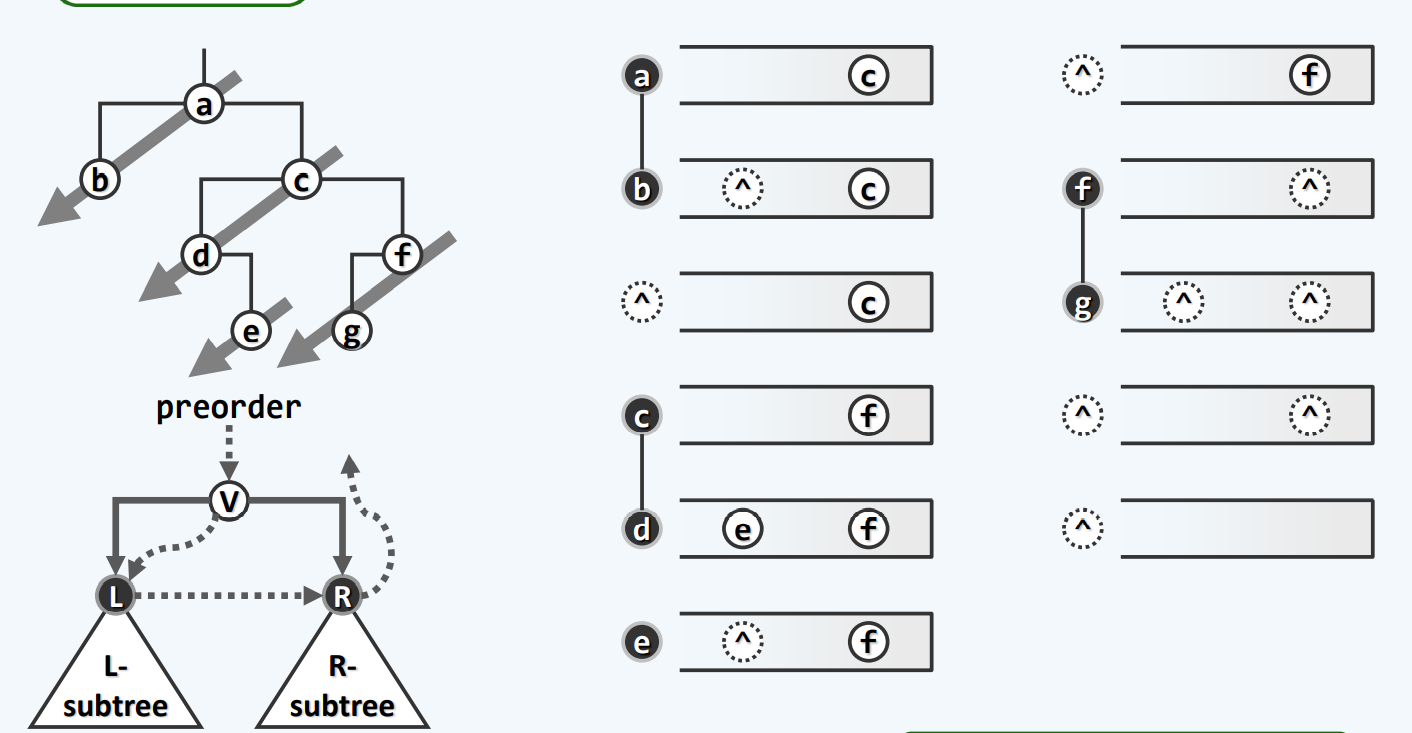
中序遍历
递归

改写迭代难度比先序要大,因为它并不是全是尾递归!!!
难点

观察
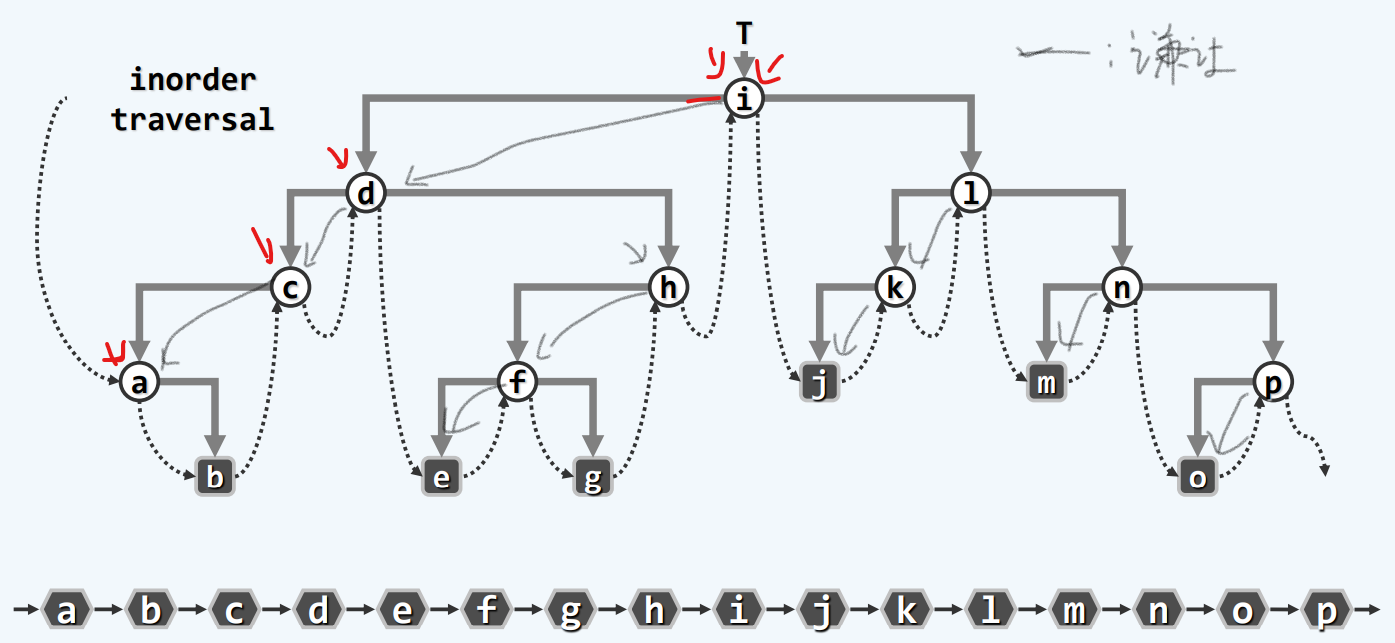
思路
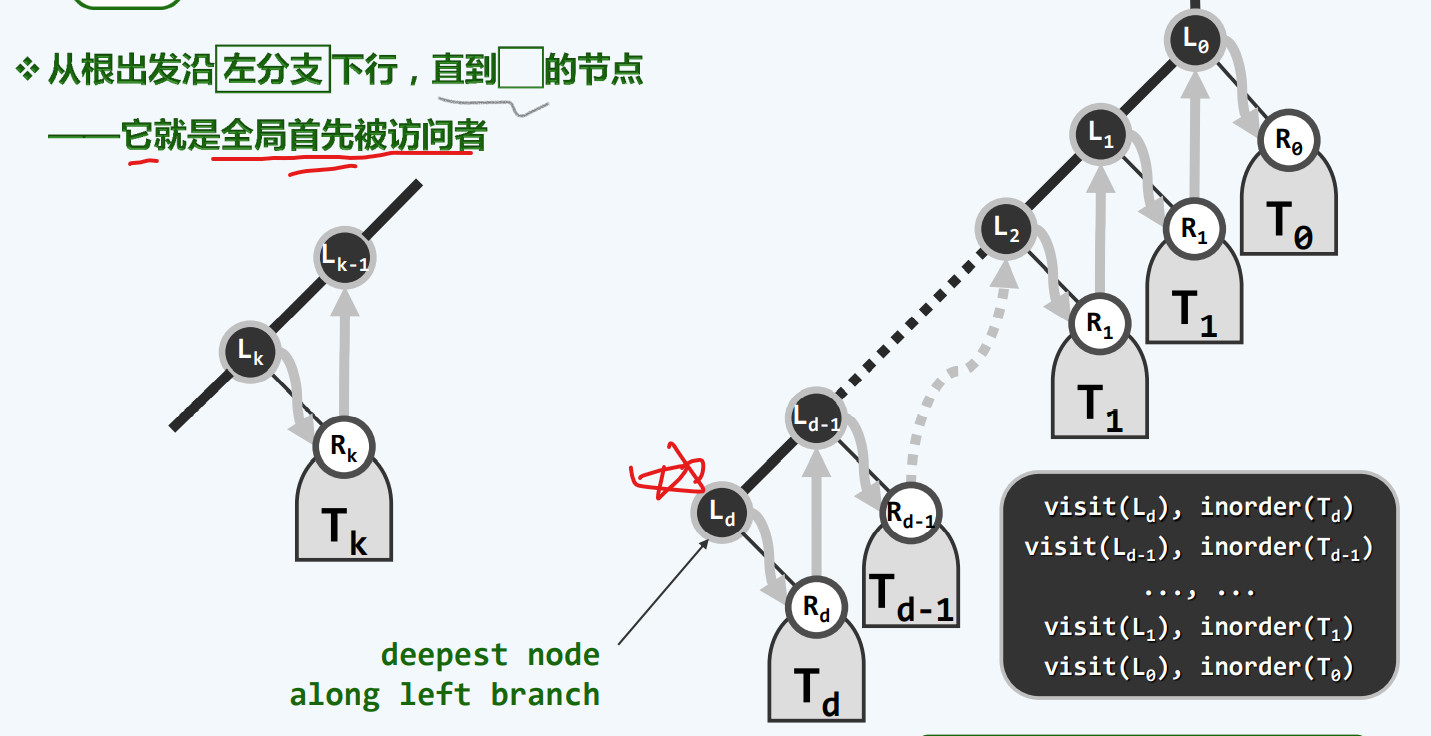
实现
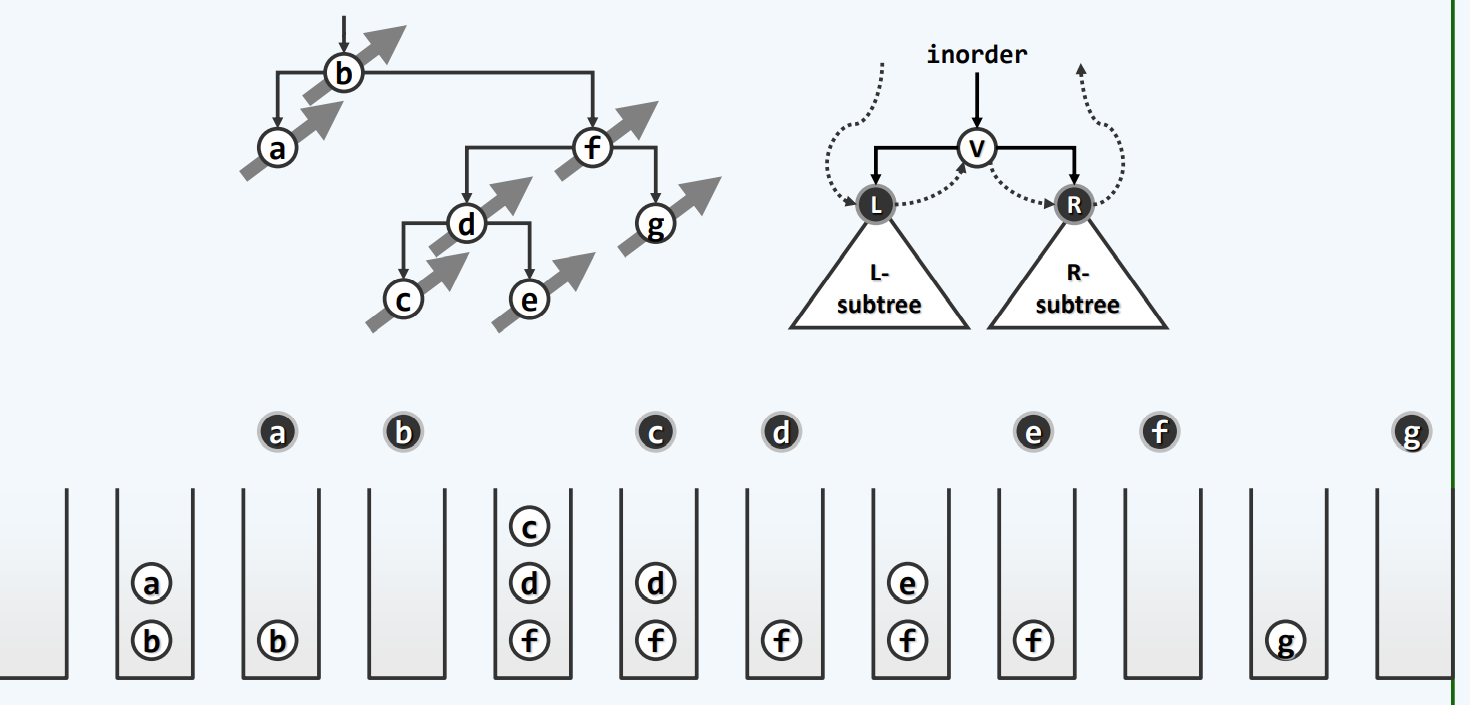
与先序遍历的区别——-visit –> go(vine)

1 | template <typename T> //从当前节点出发,沿左分支不断深入,直至没有左分支的节点 |
实例
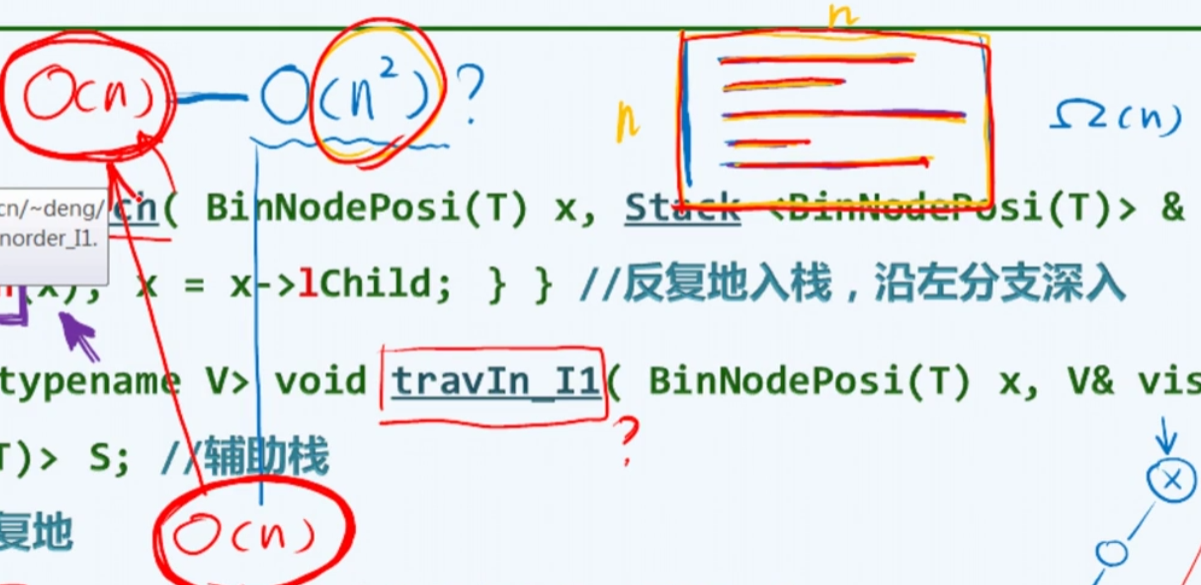
分摊分析

难道我们的结论是总体需要n²的时间吗???
整个算法的确呈现迭代,而且每一步的goalongleftbranch或长或短,甚至有可能有达到Ω(n)的量级
不过我们不难发现,所有左侧链的长度加起来,也只是n 因此,我们刚才所得到的n²的结果只是一个假象
而我们得到n²的结论只是将估计量括起来当成一个方框,而累计的复杂度则是方框的面积
后序遍历
递归

思路
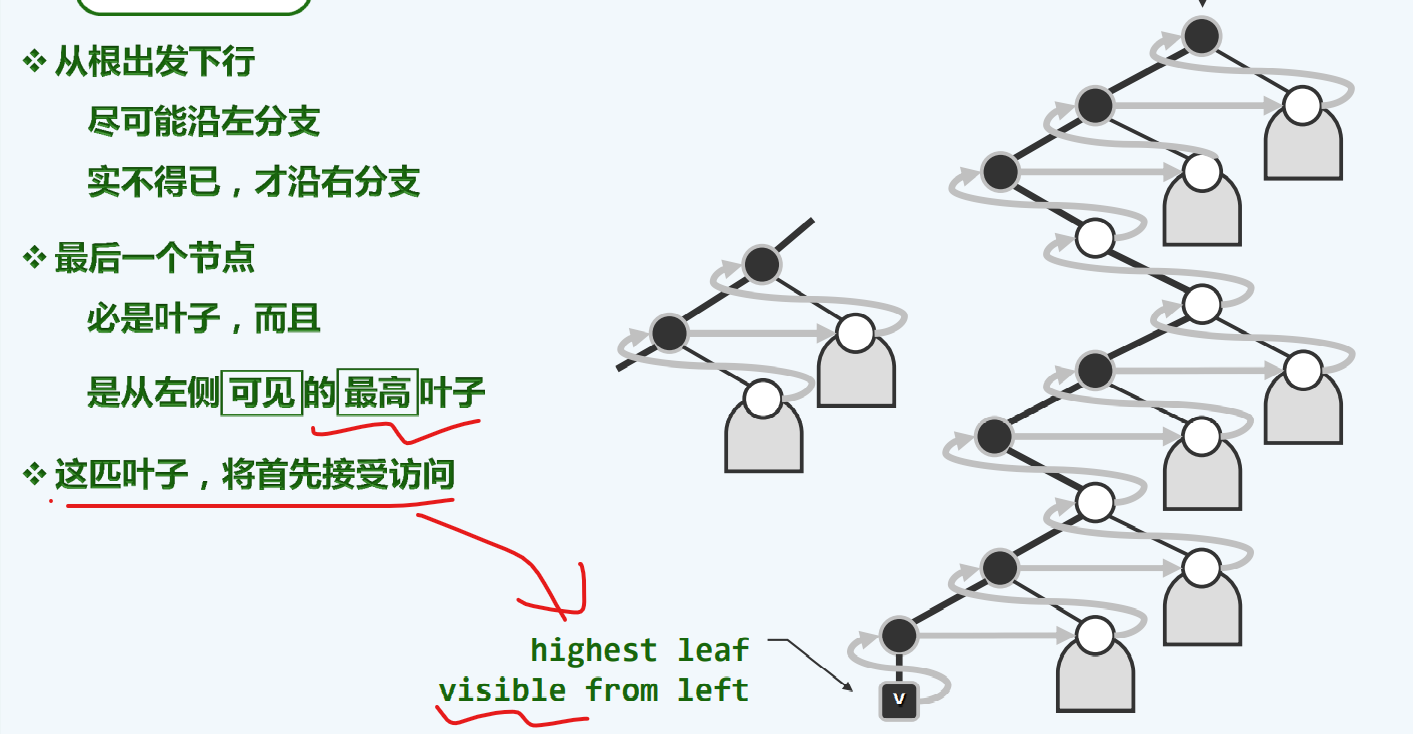
实现


1 | template <typename T> //在以S栈顶节点为根的子树中,找到最高左侧可见叶节点 |
表达式树(RPN)
盯住红色部分
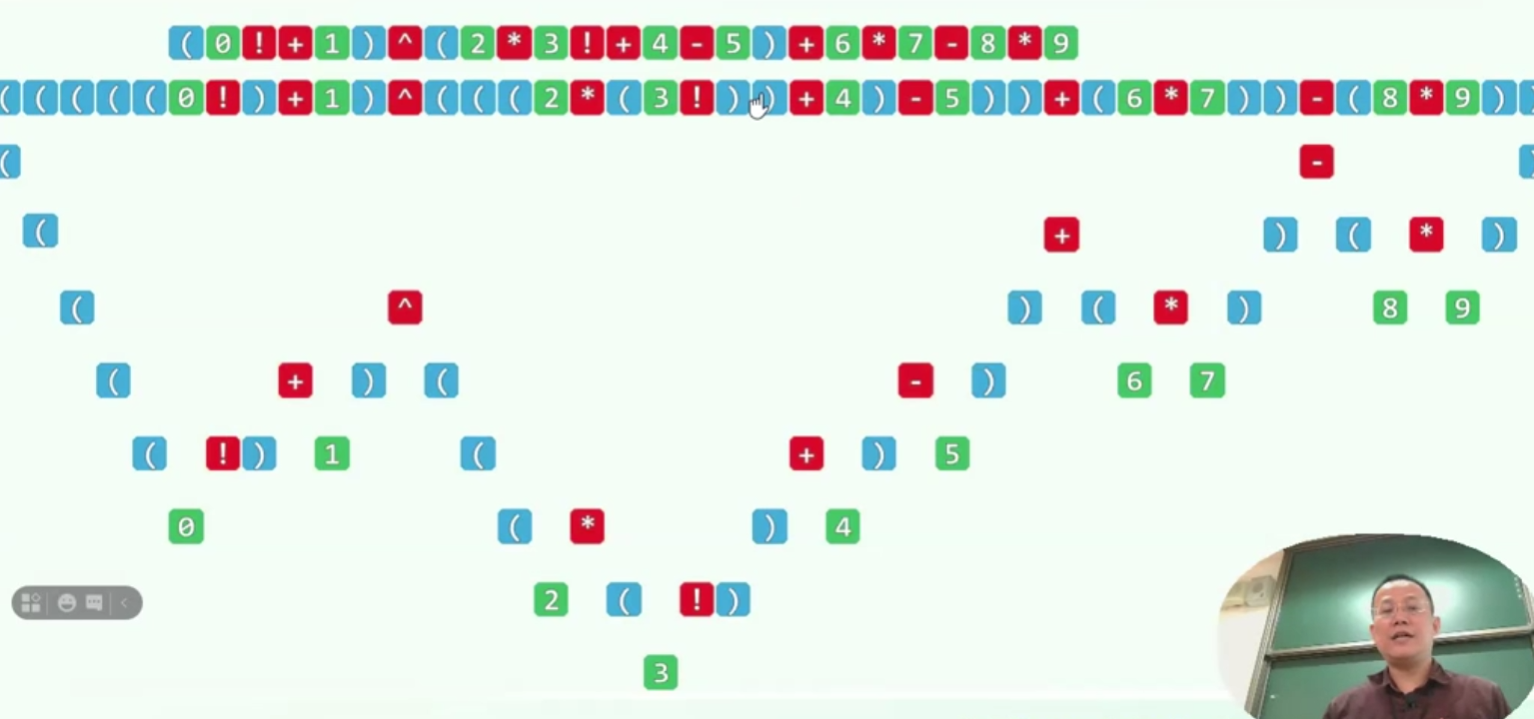
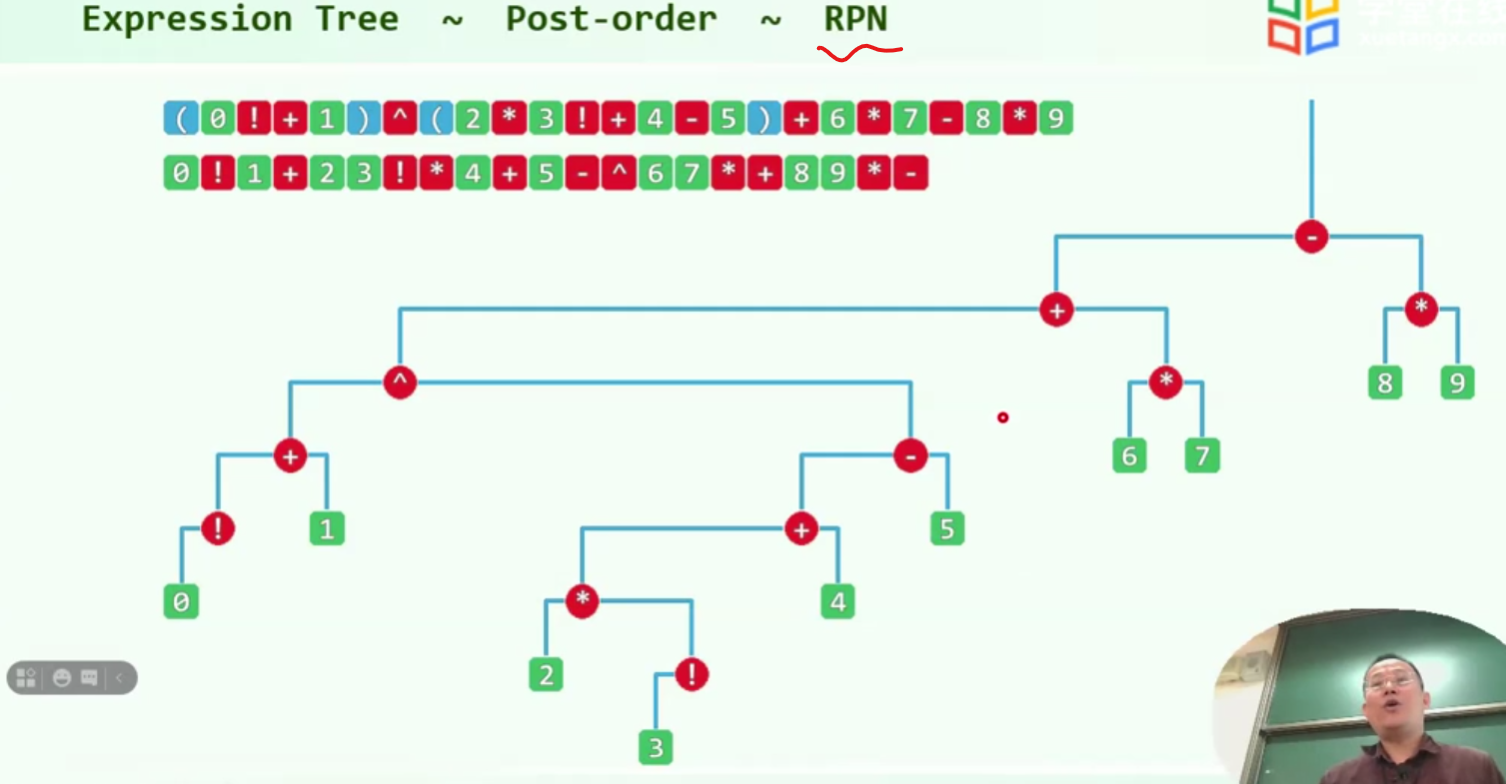
仔细观察,这就是一个后序遍历
也可以理解为不断求值的过程
所以说RPN是不需要括号的,与其说是不需要,不如说是背后隐藏了一棵树在里面
层次遍历
实现
可以看到层次遍历的接口形式和其他遍历完全一致

1 | template <typename T> template <typename VST> //元素类型、操作器 |
实例
节点进入后,左顾右盼,先左顾后右判 这里使用的是队列 和之前先序遍历使用的栈不同,先序遍历就是先右后左
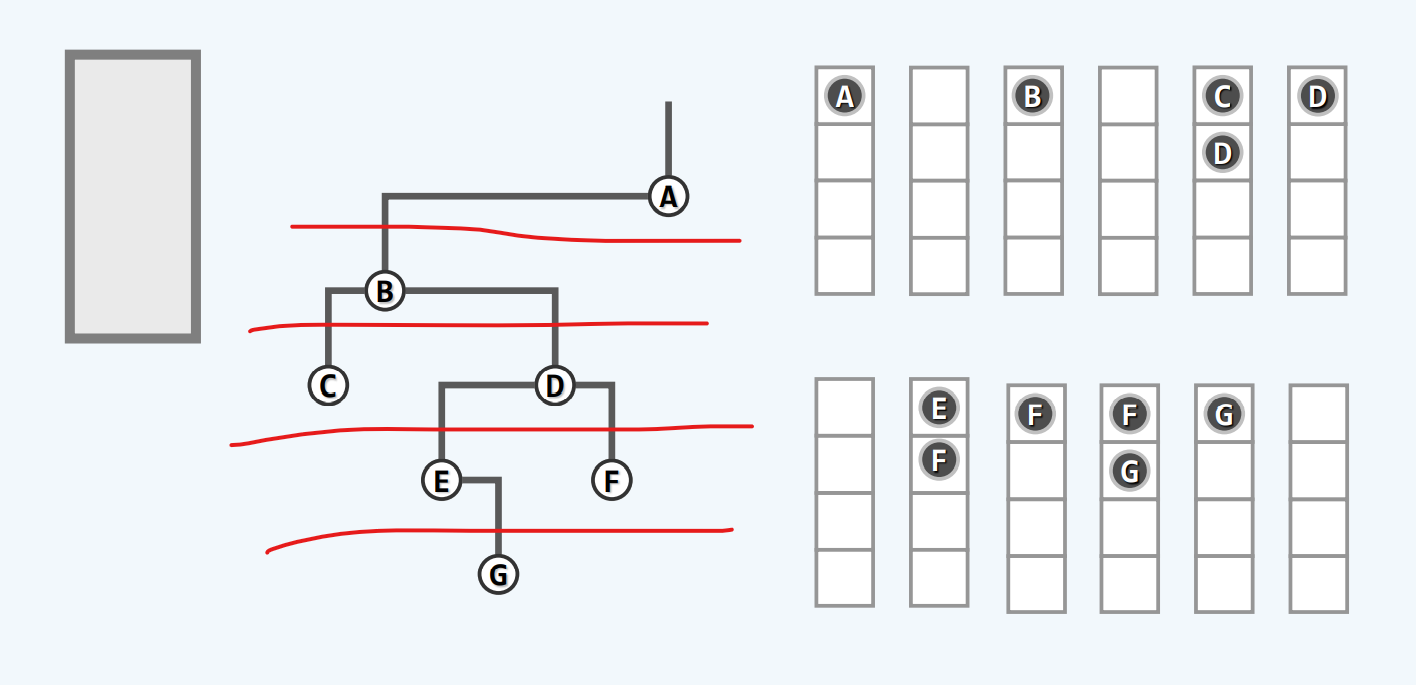
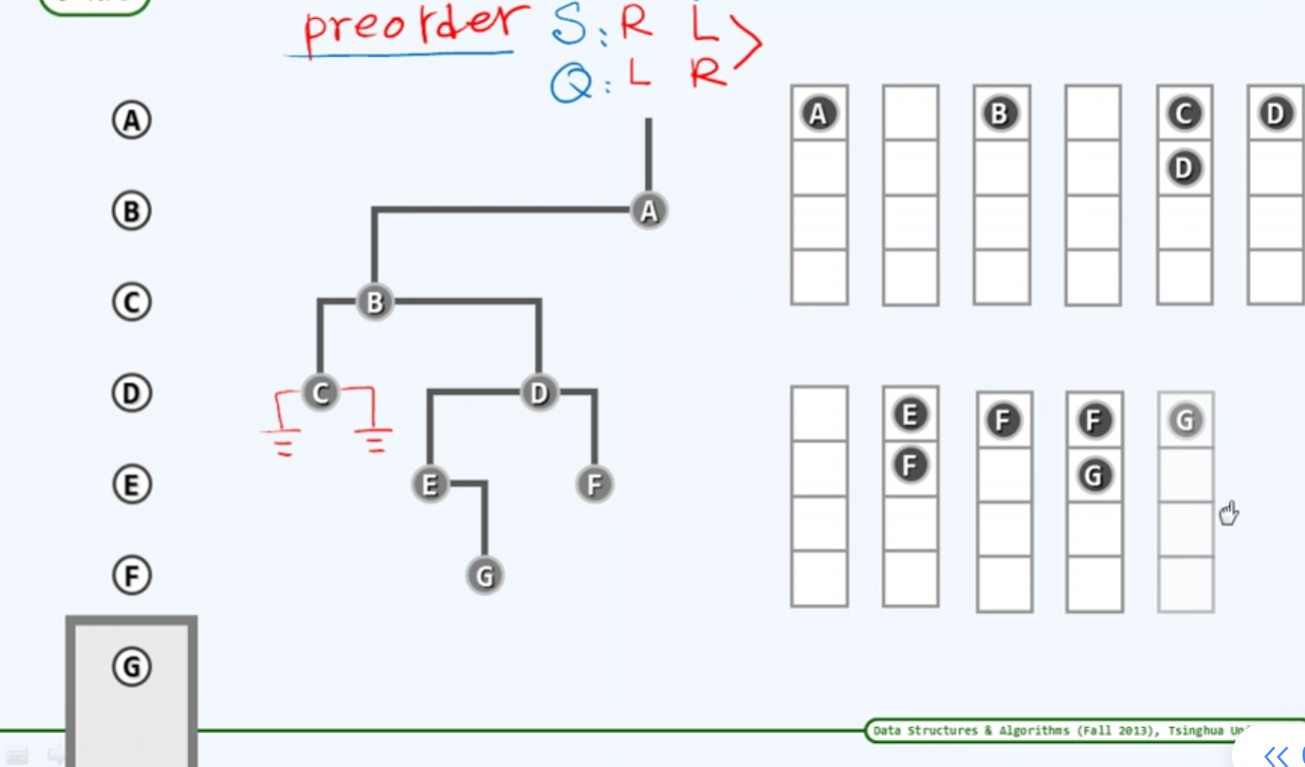
遍历序列
我们可以知道,任何一棵树都能有三种遍历序列,
那现在我们试想一下,如果我们知道某棵树的遍历序列是否我们能够还原成那一棵树的初始状态,如果可以,那我们使用什么方法?
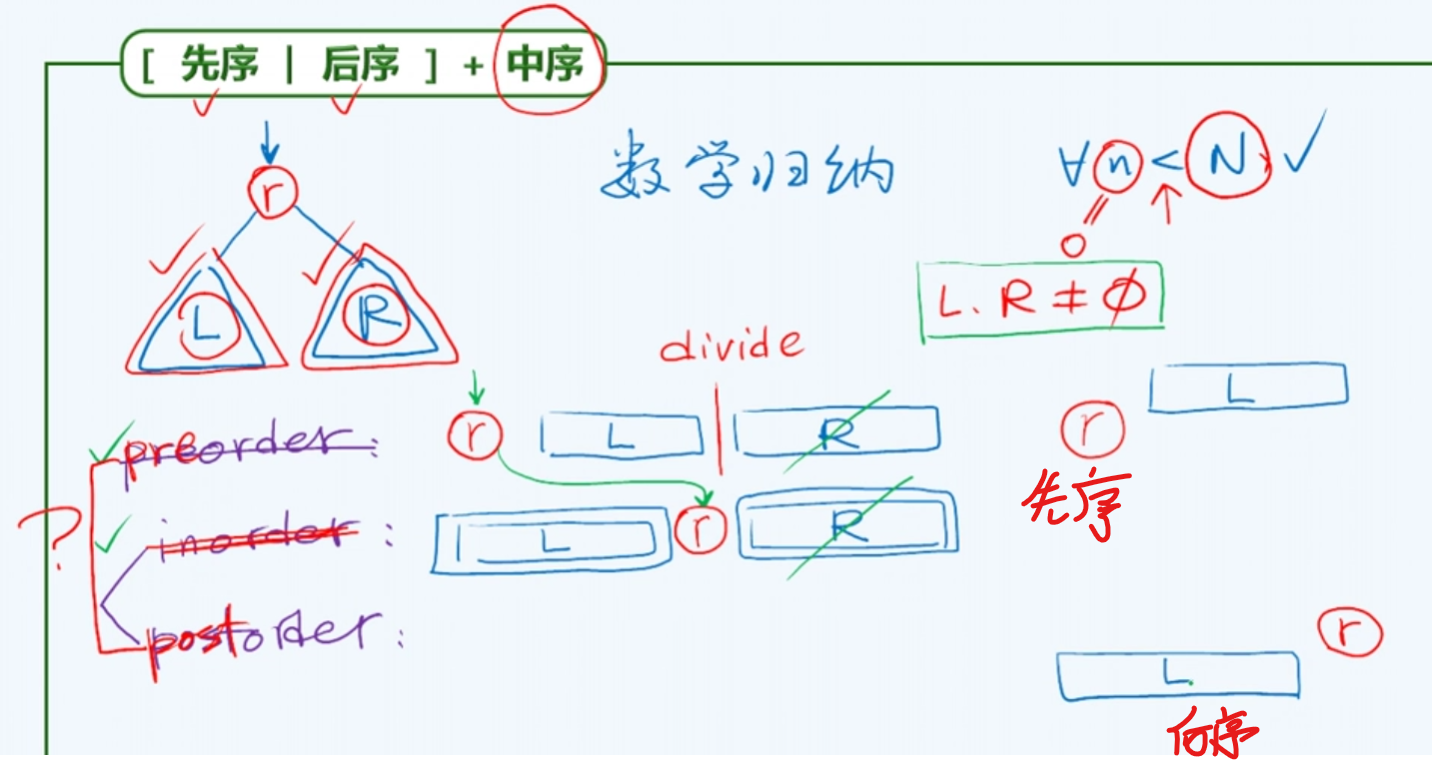
先序|后序+中序
首先通过 先/后 序遍历序列知道了根
再通过中序遍历,我们就可以很容易的将左右子树拆分开
为何我们不能通过先/后序列来确定整棵树的位置?
当右子树是空的的时候。我们得到的数据是这样的。
当左子树是空的,我们得到的图是这样的
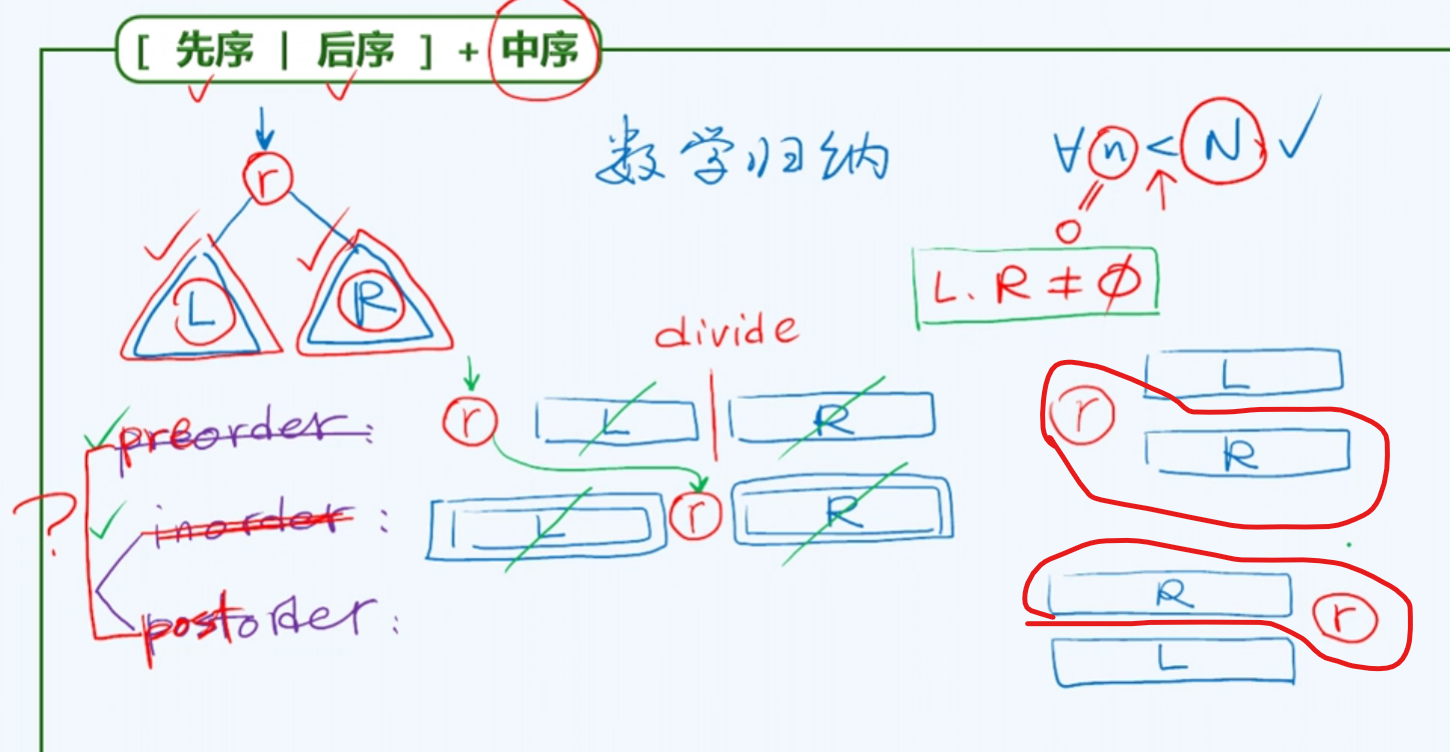
可以看到,这里出现了歧义——>
也就是,我们无法确定,到底真正的图是缺少了左子树还是右子树
(先序+后续)*真
既然是真二叉树,那么它一定会有左子树和右子树,也就是说,我们先序遍历的第二个位置一定是左子树节点,后序遍历倒数第二个位置一定是右子树节点,我们从而可以快速,相互的定位他们在不同遍历中的位置。
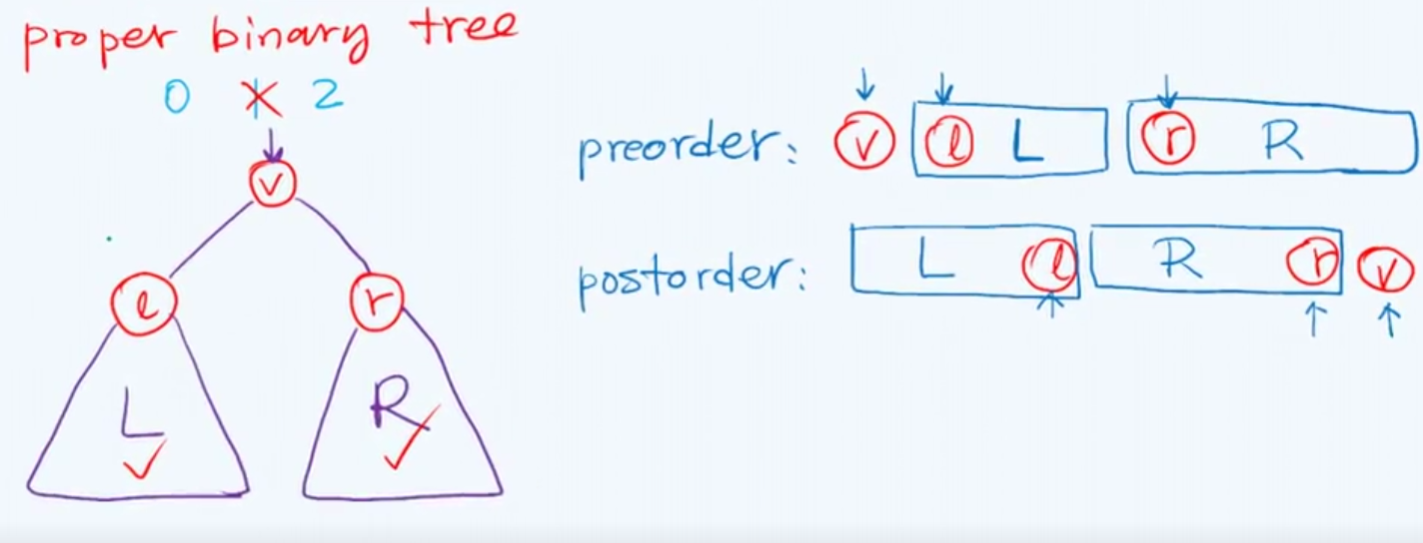
在这里,确实可以进行分而治之,从而通过递归的形式,完全可以重现出二叉树完整的结构
知道序列画树
我们通过观察,可知:

先序遍历的顺序,即为子树向左下方画出一条一条的线,同理可得,后序遍历的访问次序,是向着左上的箭头,而中序遍历是从左往右的结点顺序,因此,可得如下思路: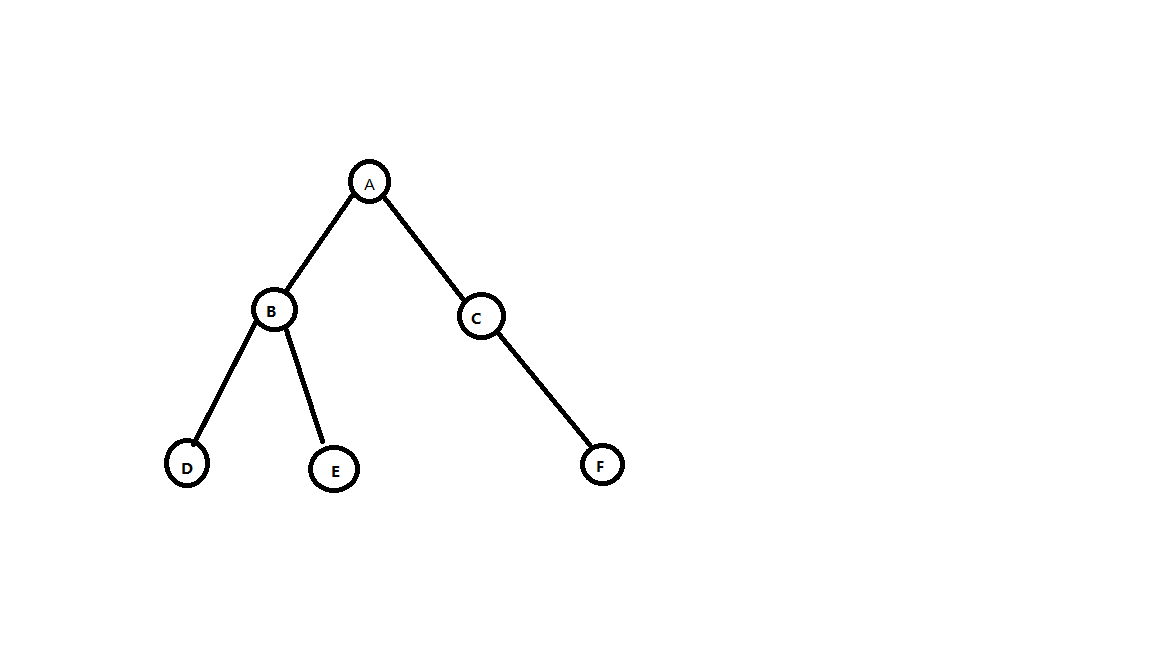
我们可以得到,他的顺序
- 先序A B D E C F
- 中序D B E A C F
- 后序D E B F C A
观察,因为能构建出树,必有中序,所以通过中序和先(后)序得到的根节点,画出基础树,这里,我们用后序+中序来举例
A 不知道已经发现了吗,中序中,我们先不考虑根结点,可以发现,我们这里采用的遍历是按照左上
D B E C F 一列一列划线,意味着我们只需要默想后序的顺序,然后看着左边的基础树,脑海中一直想象着划线,如果与脑海中的相违背,就断一下,逐渐就会画好了hhhh,只是突然想到了,记忆下来图一乐,不知道会不会用到哟,估计到时候都忘了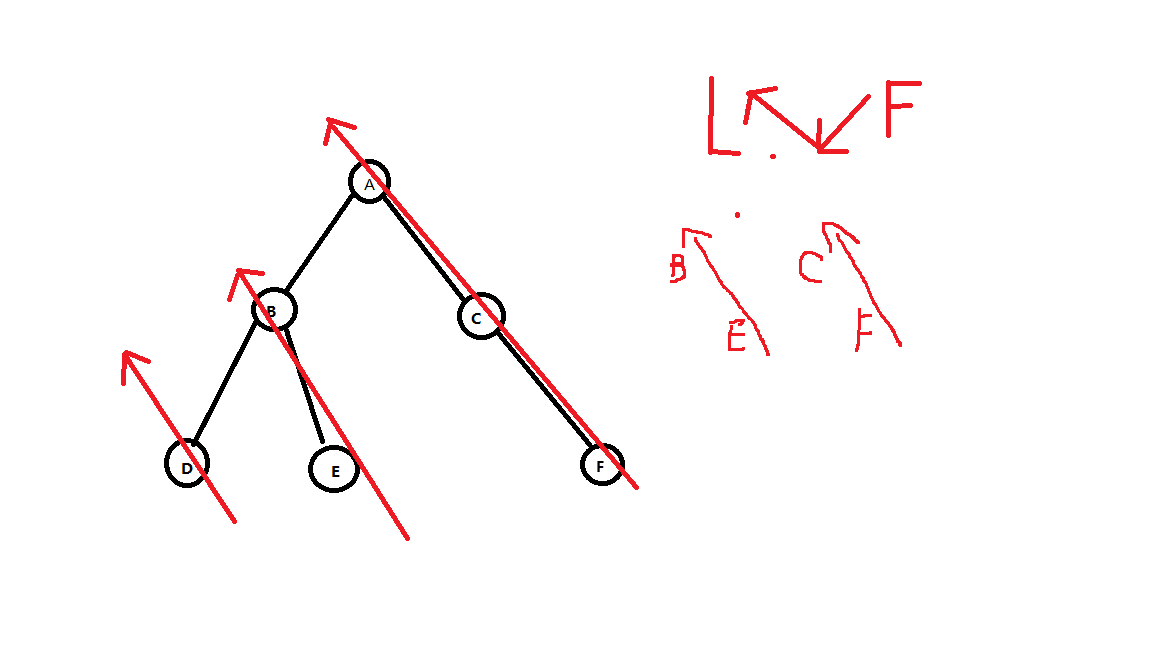
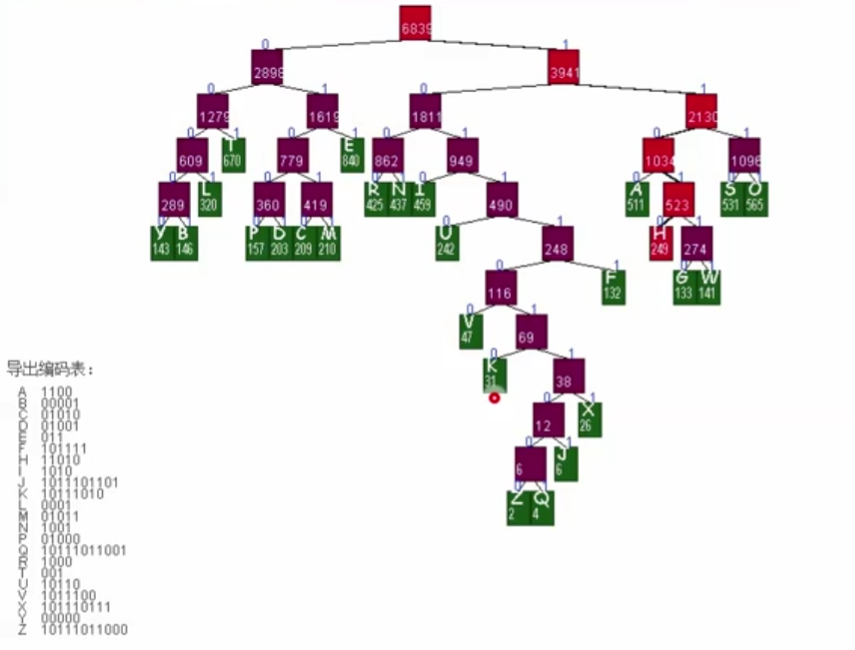
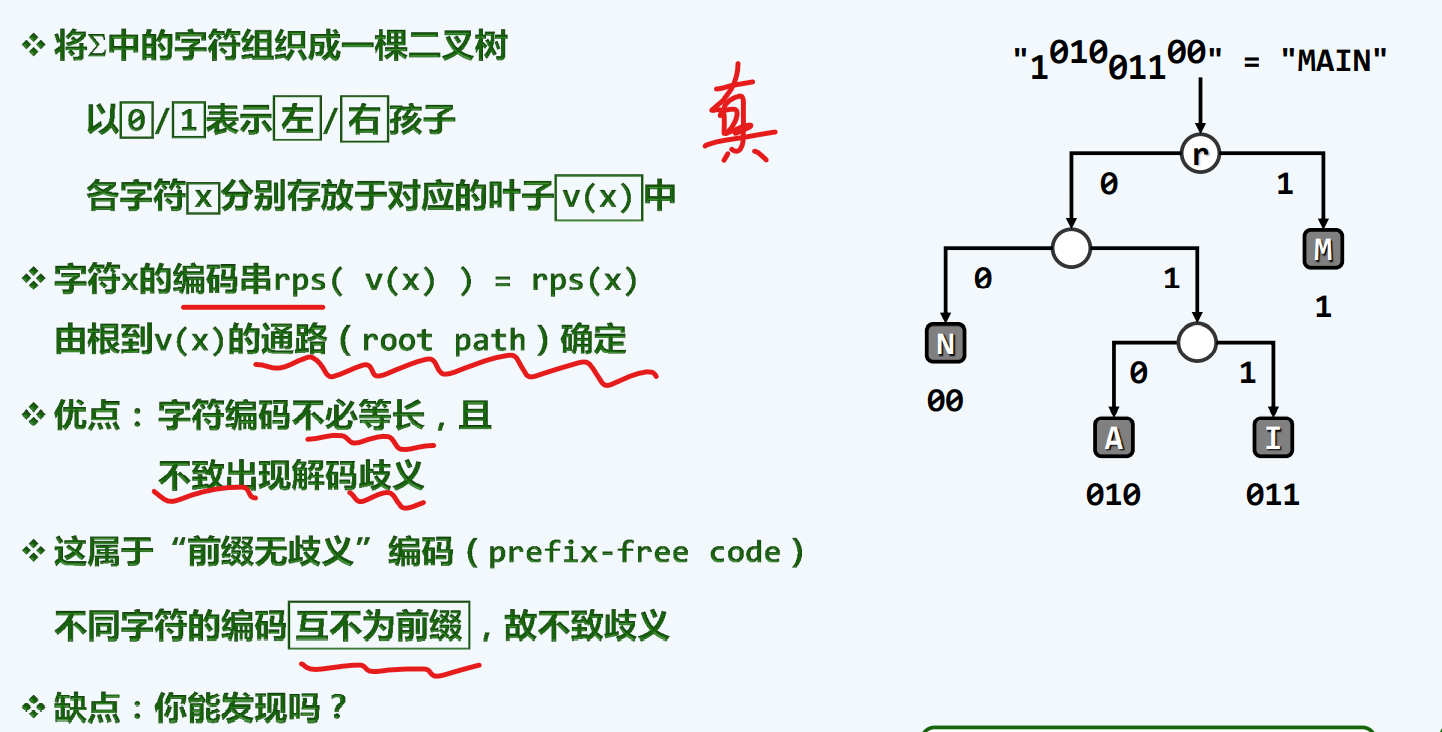
Huffman树
PFC编码
编码成本
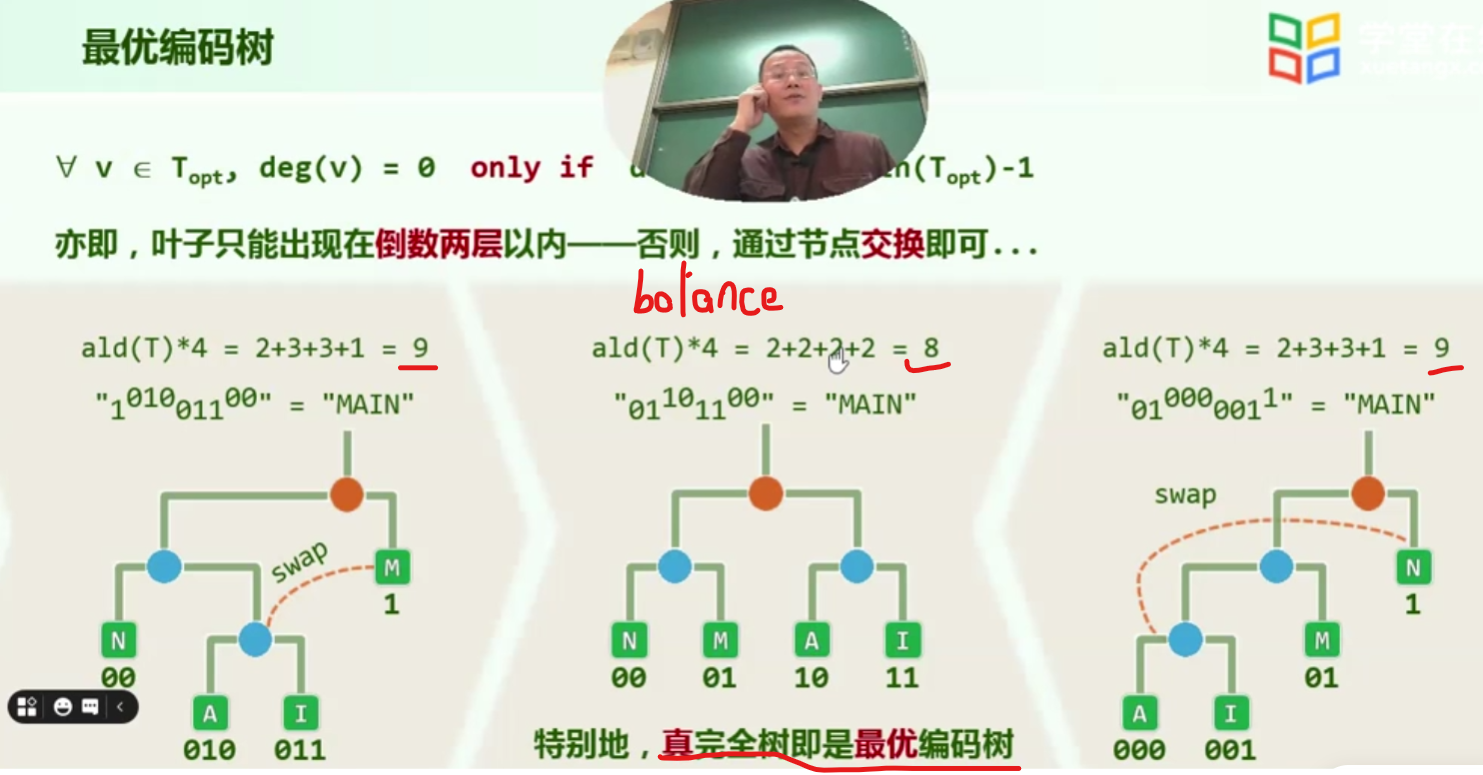
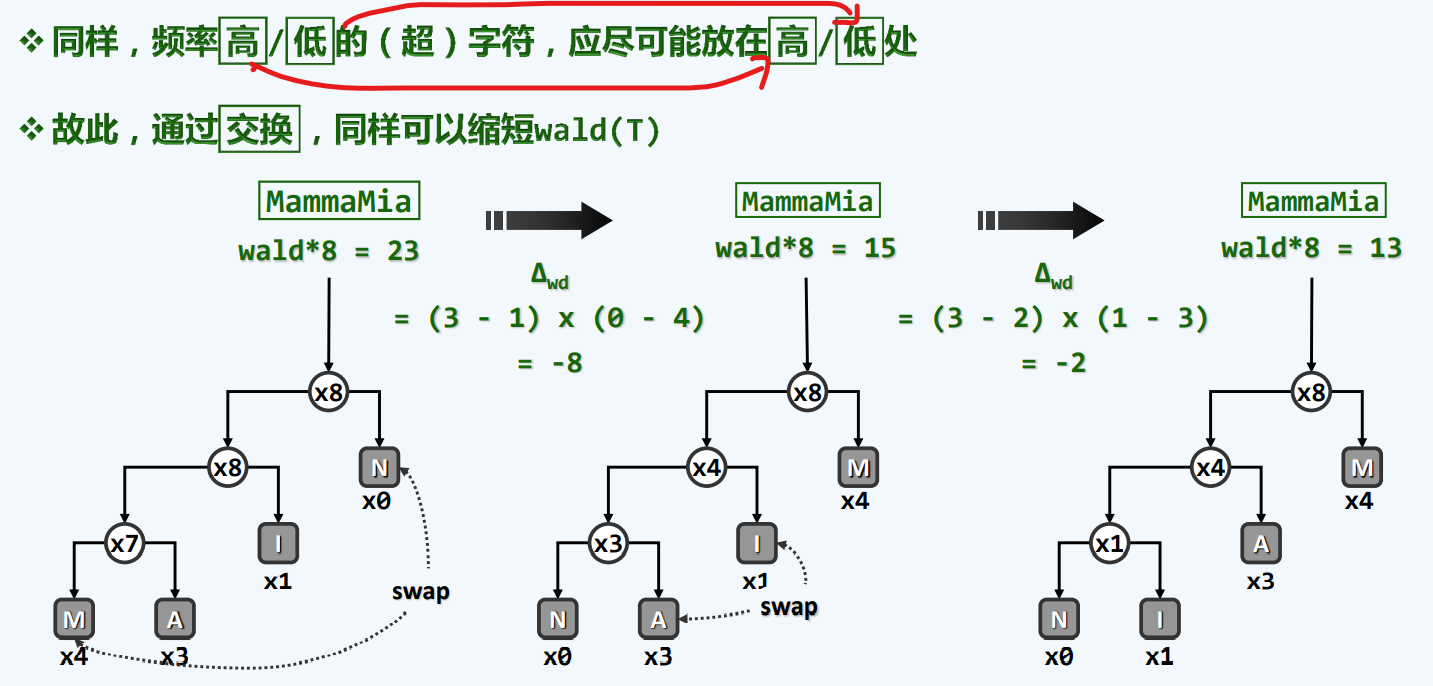
其实优化的过程就是把M节点和那个蓝色节点交换,则得到了较优的结果
那么,为什么我们能赚到呢?
是因为我们出现了高度差为2的’’叶子’’节点,3,4更不用说,但这也必然会赚到,因为更多的点深度低了,(相比于深度高了的少量节点)以多博少
频度

带权编码成本
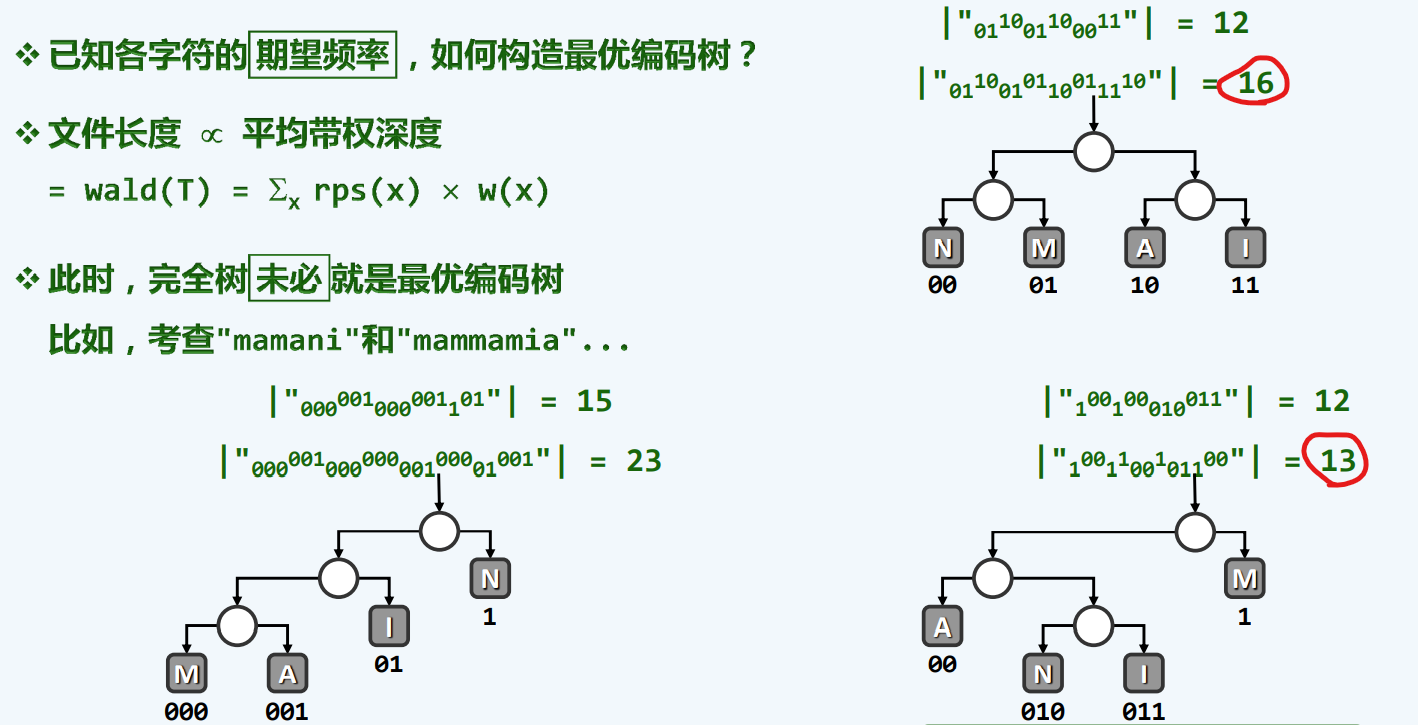
四平八稳的方式不一定是最好的了……
高高 低低,一定是赚的
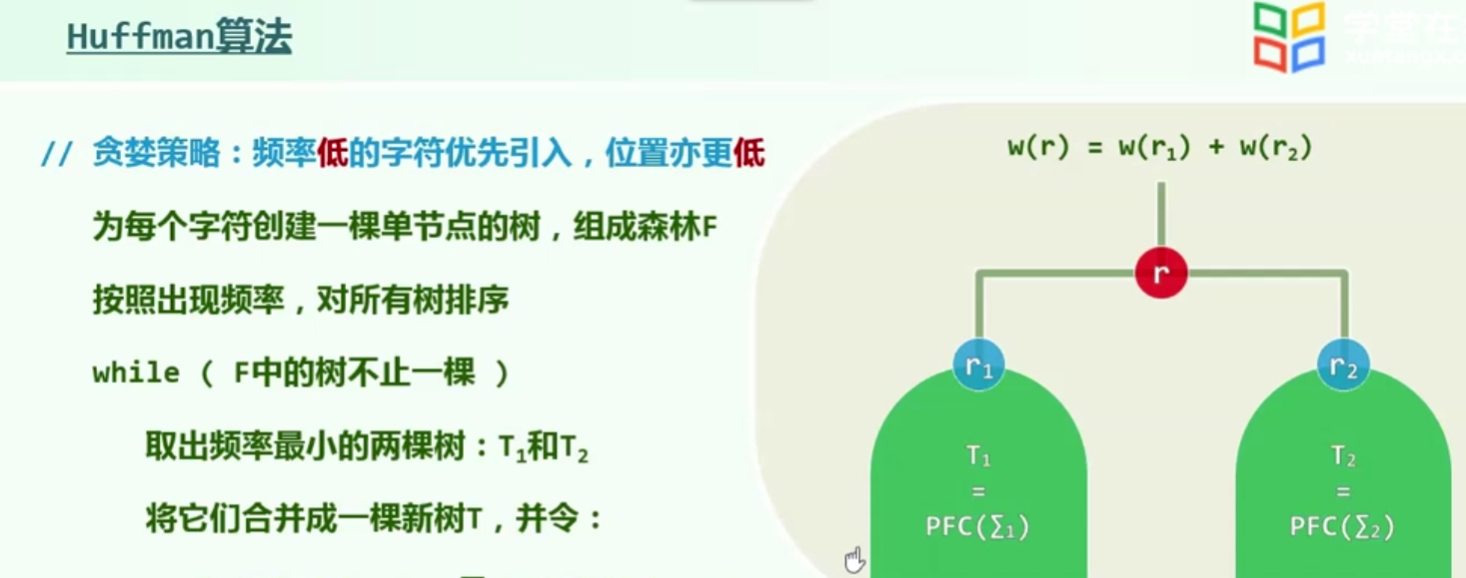
编码算法
我要构建出理想的树,有两个考虑方式,历史只记住的成功的一个,但我们作为学习,也需要考虑失败的那个,从高处开始挂下去,从低处往高树挂

构造编码树
使用先中后随便一种遍历方式,都可以得到他们的次序(DFS)
访问到以后,会记录绳子,我们把他从底端打印到顶端(栈未完全封装)
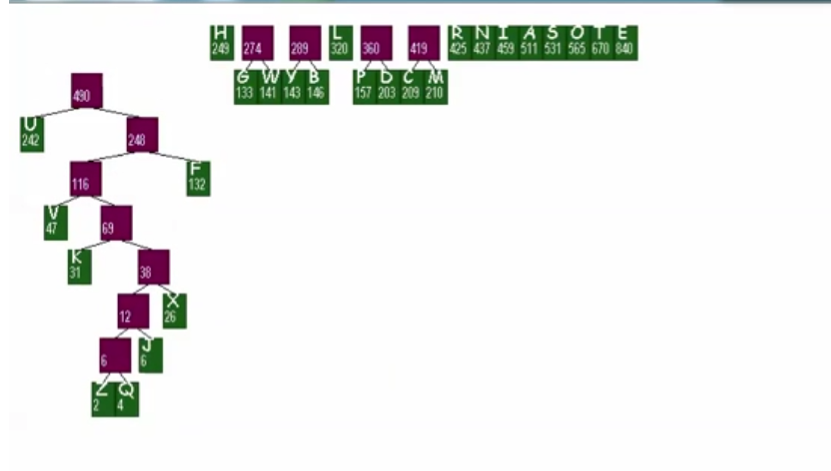
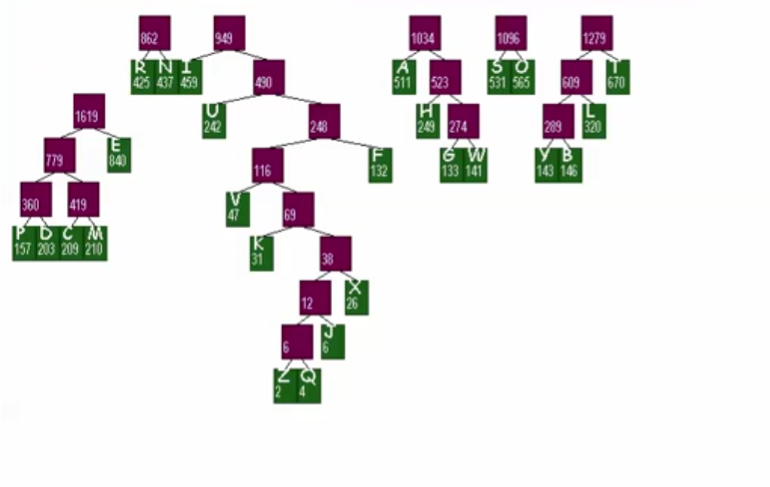
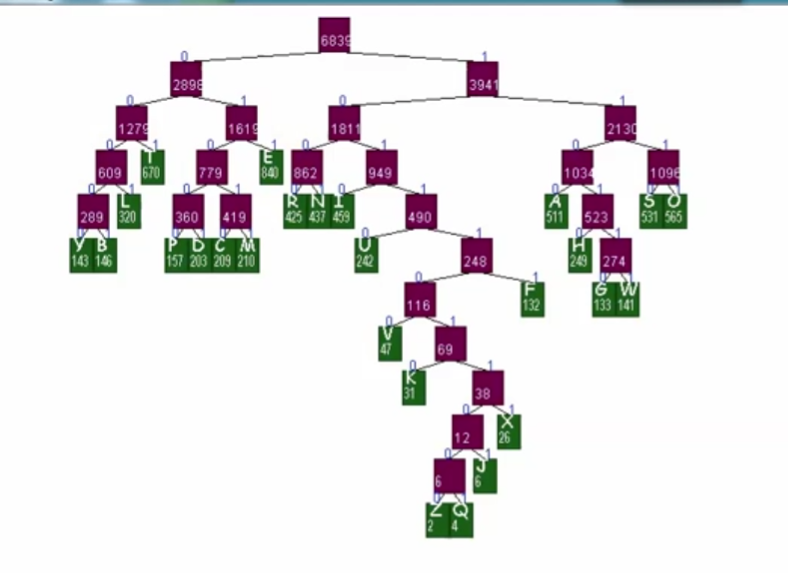
解码
从第一个bit开始,最开始位置到根,如果是0就往左,1就往右,找到了叶子,就把叶子的那个字符pop()打印出来,然后自己reset()回到根,随着不断迭代,终止到最后一个叶子,从而完成了解码的工作