以下笔记为jjyaoao本人制作，欢迎借鉴学习和提出相关建议，转载需要标明出处www.jjyaoao.space

图

概述

邻接+关联

此课程不讨论自环

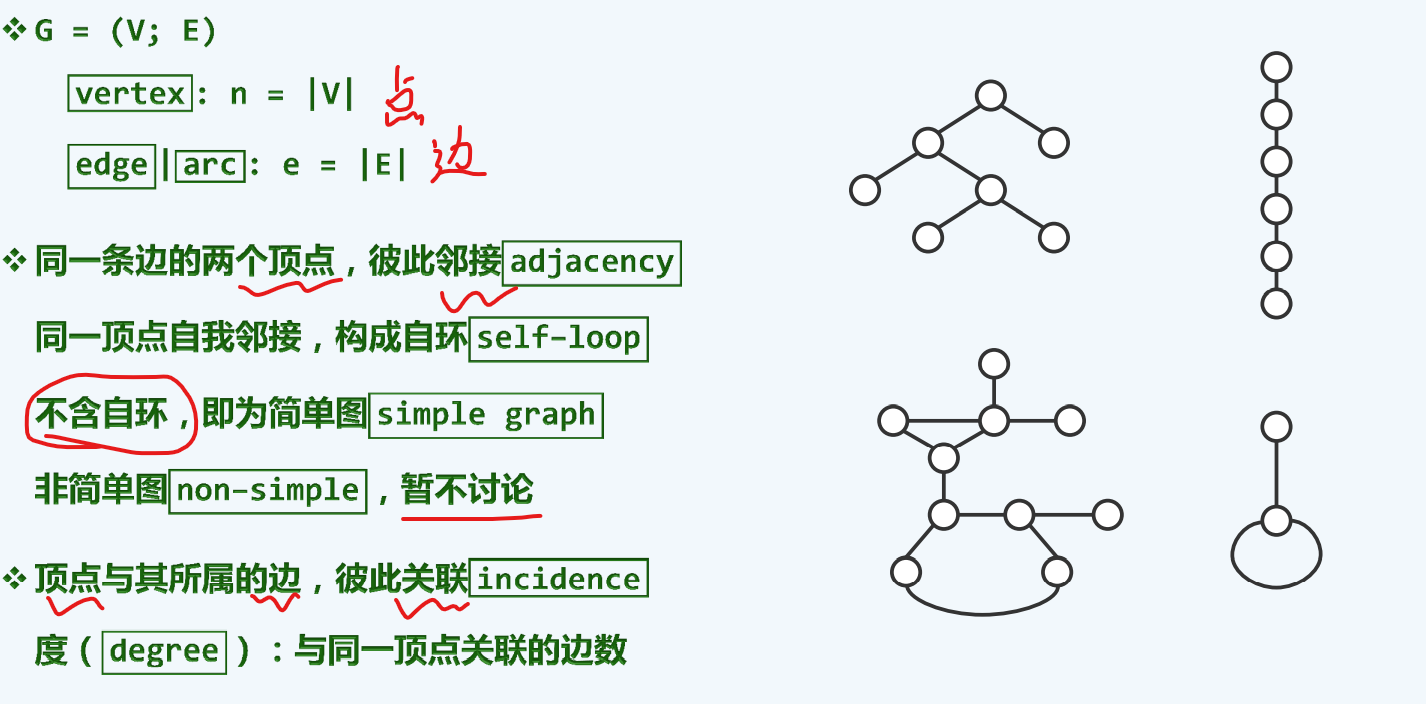
image-20220228185336006

无向+有向

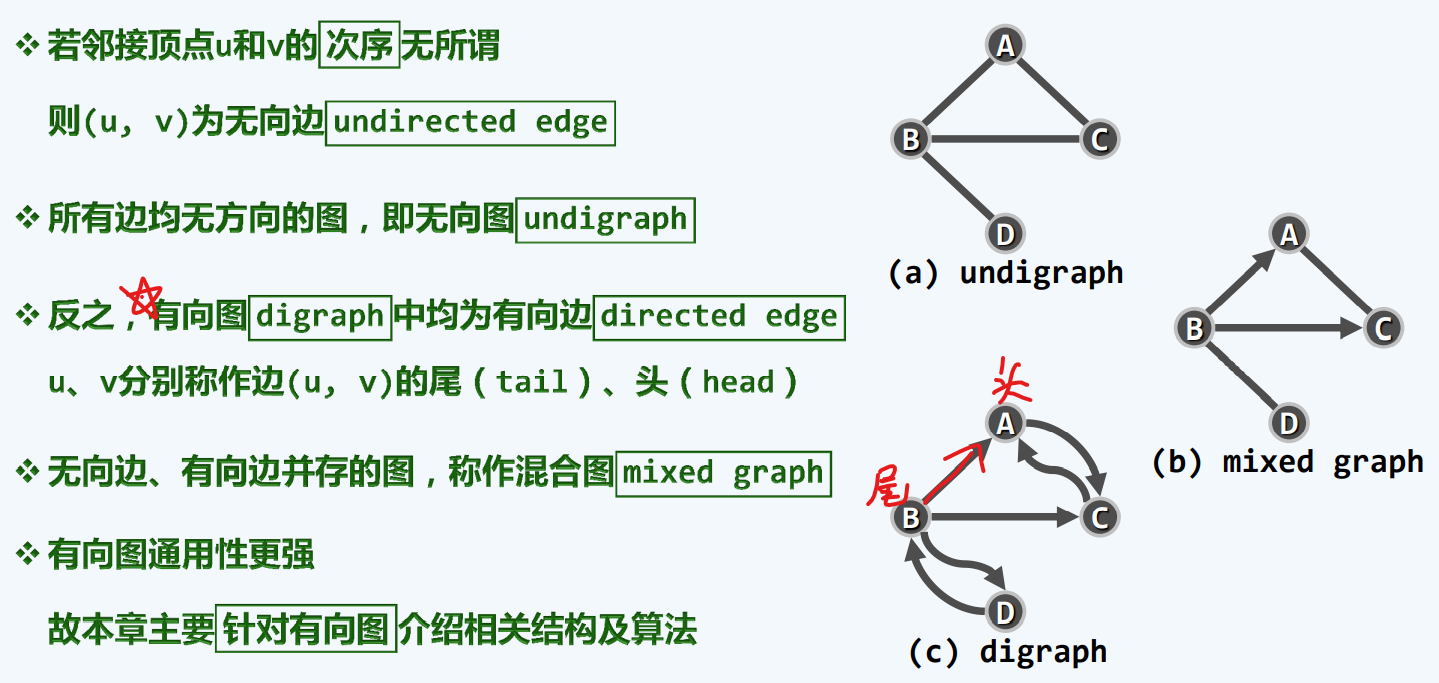
image-20220228185558219

路径+环路

欧拉环路，所有的边可以拉通走一遍（恰好一次）

哈密尔顿环路，每一个顶点可以拉通走一次（恰好一次）

环：一条只有第一个和最后一个顶点重复的非空路径

image-20220228190112865

邻接矩阵

接口

image-20220228190529556

邻接矩阵和关联矩阵

在这堂课中，使用邻接矩阵来描述（尽管有些时候关联矩阵同样可以大显身手）

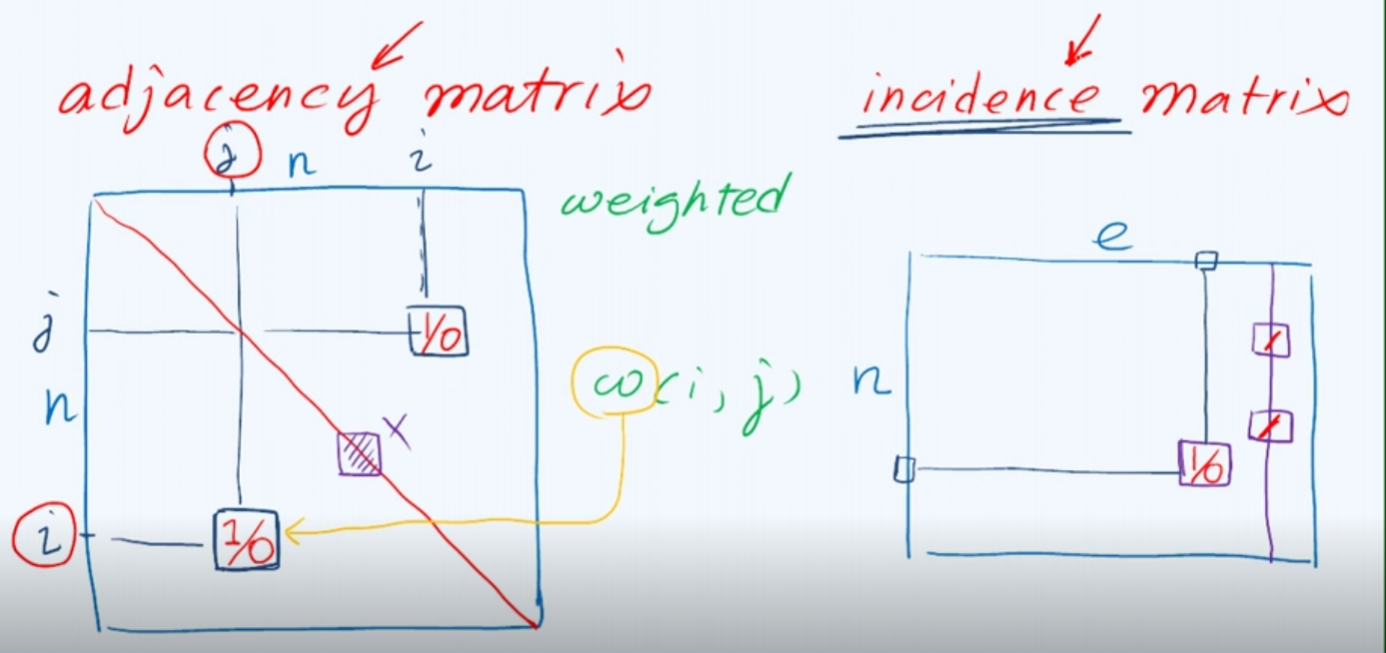
image-20220228190756672

image-20220228190849374

实例

邻接矩阵在无向图，有向图，带权图中的表现形式

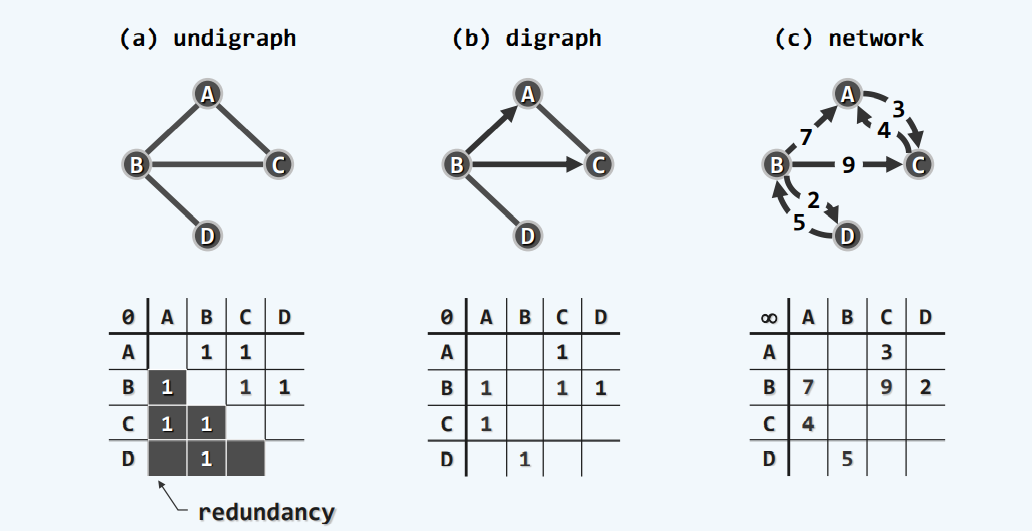
image-20220228191046766

顶点和边

顶点

五角星部分后续遍历时详细介绍

入度，出度，也就是当前顶点和多少个别的顶点相互关联

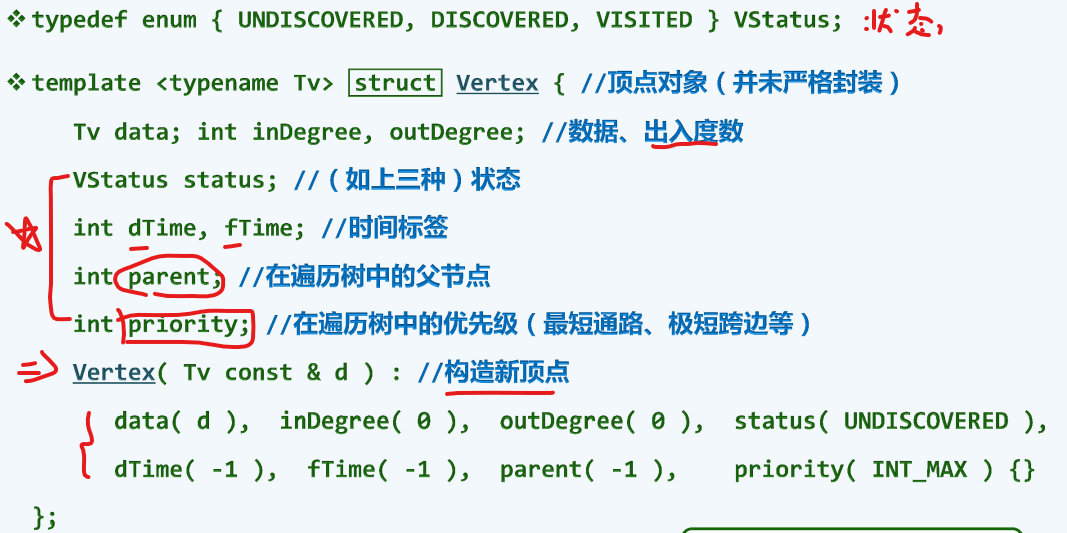
image-20220228191340917

边

边需要有data记录自己携带的信息，对于带权网络，还需要记录权重，并且边也有含义，为了创建一条边，我们也需对相应的各项进行初始化设置即可

image-20220228191536584

实现图(邻接矩阵)

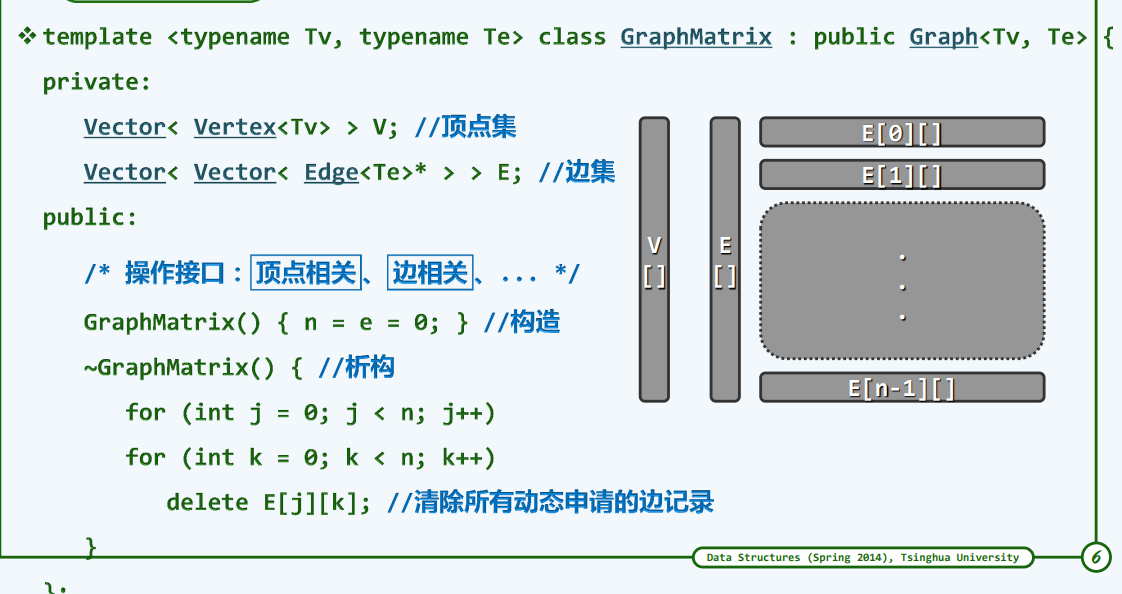
顶点集：由一组顶点所构成的向量

边集：由一组边所构成的向量，进而由这一组向量所构成的向量

每个顶点，最多可能与n条边相关，所以每个向量的长度也是n

总共可能就n个向量（每一个向量是E[0] [ ]) —-这n个向量构成一个边集

0是第0个顶点，后面是与他关联的边的个数，每个顶点可能与n个向量相关联，所以这个n个向量的每一个向量的长度也是n

image-20220301163846123

邻接表实现

(20条消息) 数据结构之图（邻接表实现）（C++）_碣石观海的博客-CSDN博客_c++邻接表

顶点

顶点静态操作

一系列基本操作：

image-20220301164232436

定义一个n，尽管它并不存在：n是一个假象的哨兵，并且和i里的任何顶点都相邻

我们可以看到整个算法的复杂度最多是O（n），我们也可以使用邻接表进行改进，将会看到时间是线性正比于当前顶点的出度

image-20220301164949419

顶点动态操作

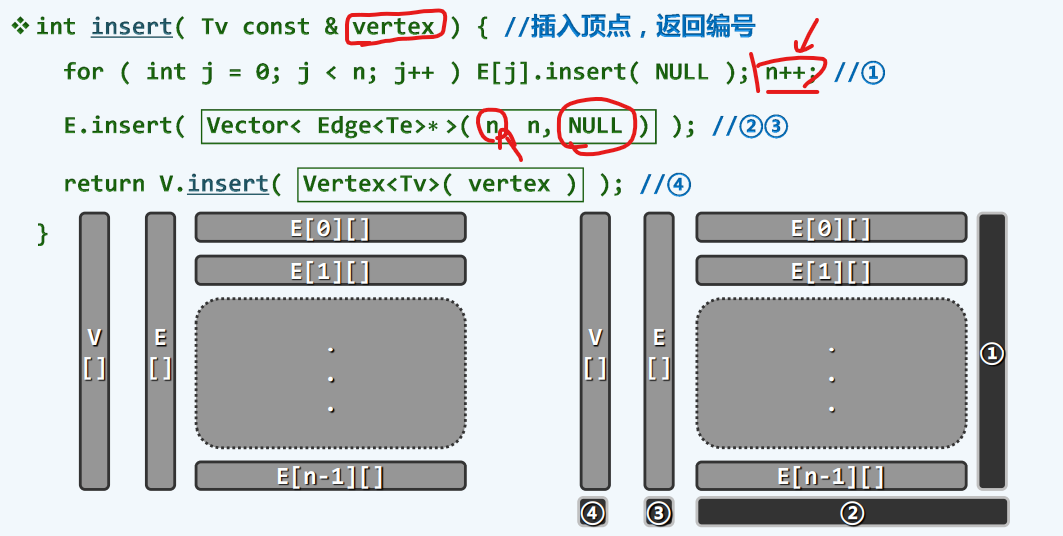
顶点插入

①每个行向量的尾部各自延长一个单位

②③我们需要生成一个行向量，行向量的元素都是一系列的边记录，它的总数是n，其中所有边引用都初始化为空

注意：在第一步延长了每一个行向量之后，曾经随手将n++了，因此，我们生成了新的行向量会在原来的基础上增加一个单位，总而言之，我们能生成一个长度为新的n的行向量

接下来呢，我们还要取出行向量的地址并将他存到E[] (第一级) 的链表中，而这一步是由在第一级的链表中调用insert来实现的

④最终，我们创造一个对应的顶点记录，并且存入于整个的顶点向量（V[]）之中，才整体完成了新顶点的引入，尽管于其他的顶点还没有任何的连边

image-20220301171412083

顶点删除

也就是插入的逆过程

image-20220301171244748

边操作

边存在

image-20220301165356478

边插入

image-20220301165652838

边删除

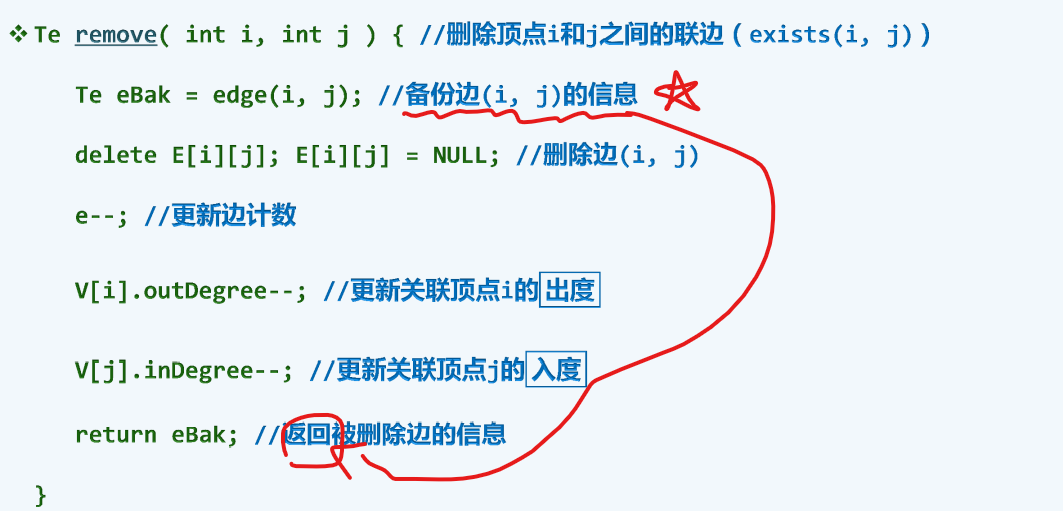
image-20220301170335972

概括和总结

优点

image-20220301172055216

缺点

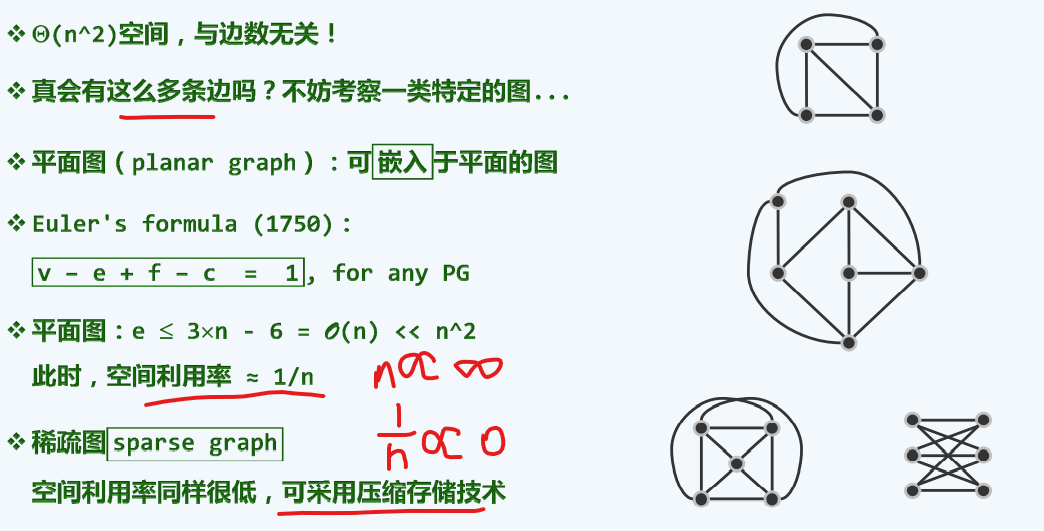
image-20220301172142493

广度优先搜索(BFS)

策略

图的广度优先可以视为树的层次遍历的推广

image-20220301193000567

实现

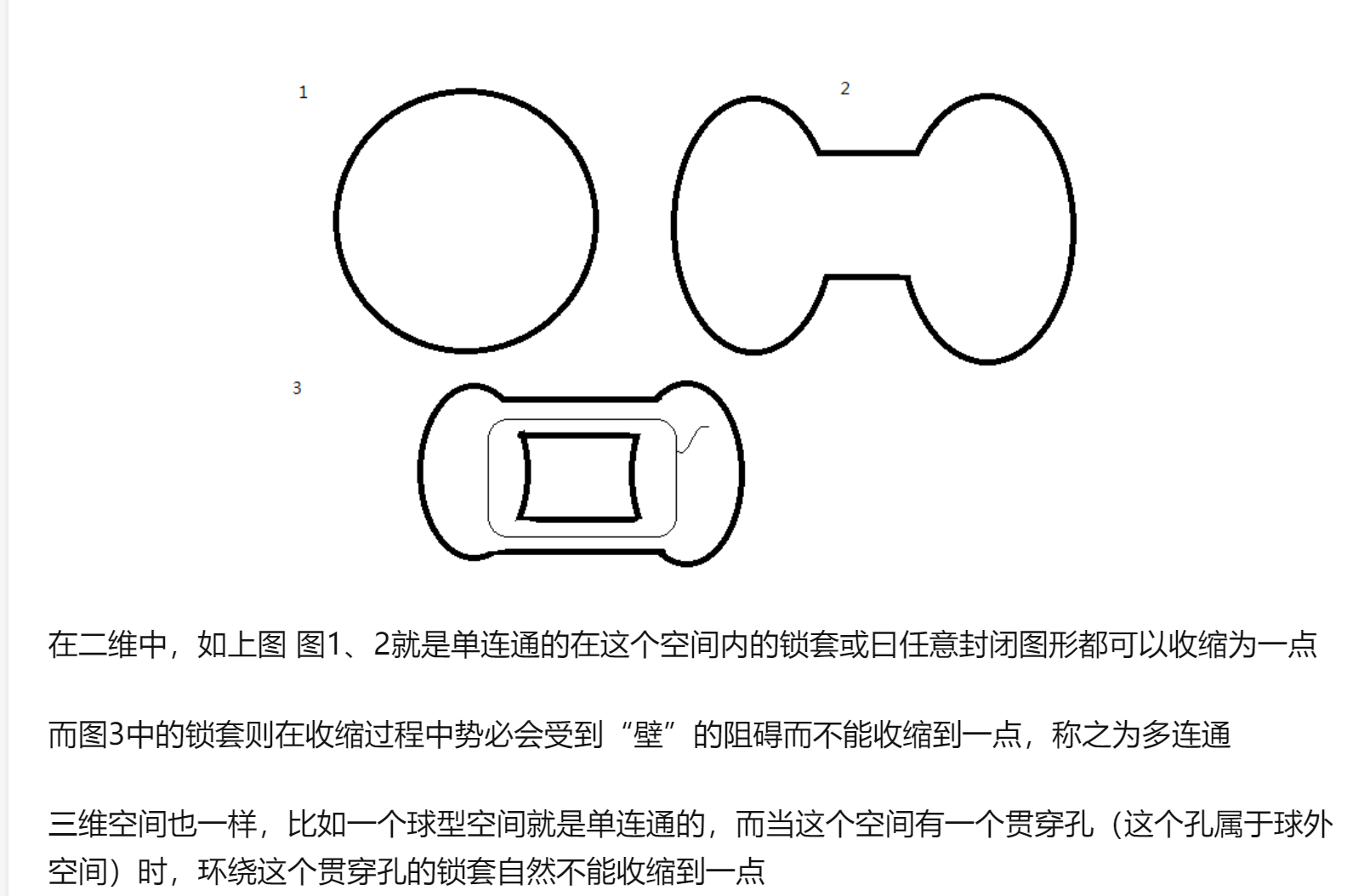
单连通

单连通：设D是一区域，若属于D内任一简单闭曲线的内部都属于D，则称D为单连通区域，单连通区域也可以这样描述：D内任一封闭曲线所围成的区域内只含有D中的点。更通俗地说，单连通区域是没有“洞”的区域。

树边：上图策略中的黑色实心边

跨边：虚线部分边，用不上，不是真正组成树的边

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
template <typename Tv, typename Te> //广度优先搜索BFS算法（单个连通域）
0011 void Graph<Tv, Te>::BFS ( Rank v, int& clock ) { //v < n
0012    Queue<Rank> Q; //引入辅助队列
0013    status ( v ) = DISCOVERED; Q.enqueue ( v ); //初始化起点
0014    while ( !Q.empty() ) { //在Q变空之前，不断弹出队列的首位置
0015       Rank v = Q.dequeue(); dTime ( v ) = ++clock; //取出队首顶点v
0016       for ( Rank u = firstNbr ( v ); -1 < u; u = nextNbr ( v, u ) ) //枚举v的所有邻居u    
0017          if ( UNDISCOVERED == status ( u ) ) { //若u尚未被发现，则
0018             status ( u ) = DISCOVERED; Q.enqueue ( u ); //发现该顶点
0019             type ( v, u ) = TREE; parent ( u ) = v; //引入树边拓展支撑树
0020          } else { //若u已被发现，或者甚至已访问完毕，则
    			if(parent(u) != v	)//不然nextNbr还是会访问到父节点
0021             type ( v, u ) = CROSS; //将(v, u)归类于跨边
0022          }
0023       status ( v ) = VISITED; //至此，当前顶点访问完毕
0024    }
0025 }

多连通

image-20220301200003158

image-20220301200107816

1
2
3
4
5
6
7
8
template <typename Tv, typename Te> //广度优先搜索BFS算法（全图）
0002 void Graph<Tv, Te>::bfs ( Rank s ) { //s < n
0003    reset(); int clock = 0; Rank v = s; //初始化
0004    do //逐一检查所有顶点
0005       if ( UNDISCOVERED == status ( v ) ) //一旦遇到尚未发现的顶点
0006          BFS ( v, clock ); //即从该顶点出发启动一次BFS
0007    while ( s != ( v = ( ( v+1 ) % n ) ) ); //按序号检查，故不漏不重
0008 }

​ 这样，就可以把每一个顶点开始的来访问一次，看看是否有undiscovered，这样，可能会引起我们的担心，毕竟循环好像是线性次，然而，我们说不必要担心，因为必须经过当前if判断后，才可能启动一次bfs搜索，这种处理方式可以保证，每一个连通域启动，而且只启动一次，所以花费在搜索上的时间只是对全图的一次遍历，而不是多次

​ 小bfs套上面单连通的大bfs

实例

空心圆为未发现，实心圆为已发现，双重实心为已经访问

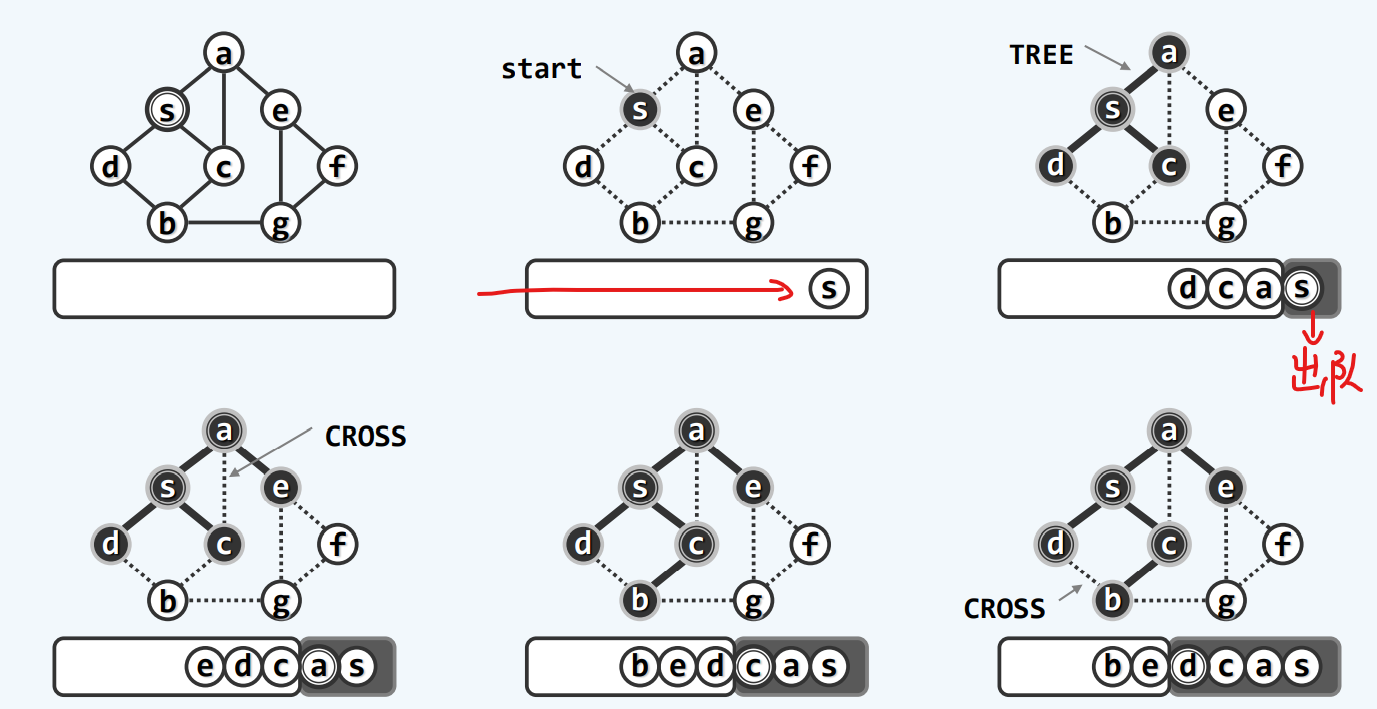
image-20220301194925906

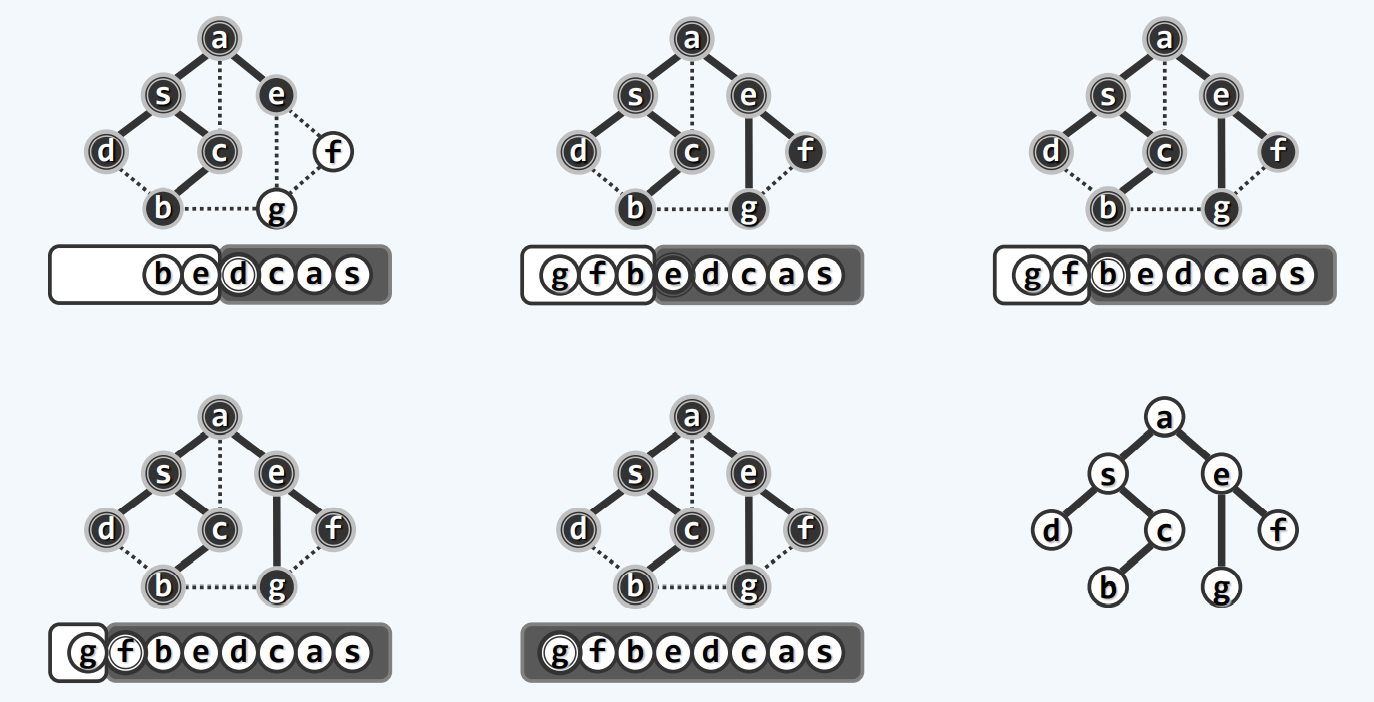
image-20220301194951160

最终得到遍历支撑树。

复杂度

对于while循环而言，外框架需要O（n）次

对于for循环而言，需要回顾他的实现机制，其实就是对顶点v的行向量进行一次线性的扫描（自后向前），所以于while叠加，我们需要n*n 但是，我们真正取出，只有e次（边的个数），按理应该是O(n²)

​ 但，这只具有理论上的意义，实际情况，因为我们的操作简单，再加上cache高速缓冲，因此，我们完全可以得出真正

image-20220301201218250

image-20220301201241622

我们说，这已经不能是更好的了（bfs，dfs只是基本的别的算法的实现框架

最短路径

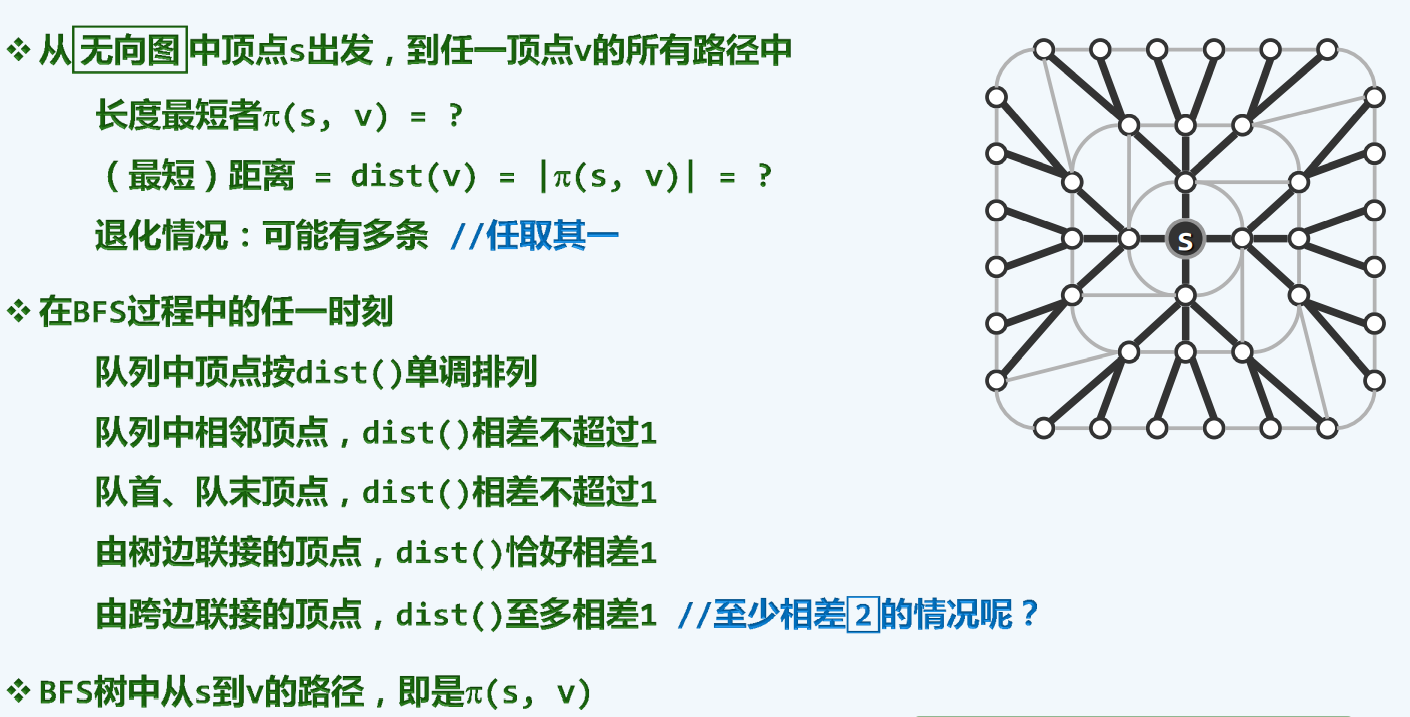
image-20220301201703266

深度优先搜索(DFS)

算法

image-20220301201855812

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
template <typename Tv, typename Te> //深度优先搜索DFS算法（单个连通域）
0011 void Graph<Tv, Te>::DFS ( Rank v, int& clock ) { //v < n
0012    dTime ( v ) = ++clock; status ( v ) = DISCOVERED; //发现当前顶点v
0013    for ( Rank u = firstNbr ( v ); -1 < u; u = nextNbr ( v, u ) ) //枚举v的所有邻居u
0014       switch ( status ( u ) ) { //并视其状态分别处理
0015          case UNDISCOVERED: //u尚未发现，意味着支撑树可在此拓展
0016             type ( v, u ) = TREE; parent ( u ) = v; DFS ( u, clock ); break;
0017          case DISCOVERED: //u已被发现但尚未访问完毕，应属被后代指向的祖先
0018             type ( v, u ) = BACKWARD; break;
0019          default: //u已访问完毕（VISITED，有向图），则视承袭关系分为前向边或跨边
0020             type ( v, u ) = ( dTime ( v ) < dTime ( u ) ) ? FORWARD : CROSS; break;
0021       }
0022    status ( v ) = VISITED; fTime ( v ) = ++clock; //至此，当前顶点v方告访问完毕
0023 }

多连通

1
2
3
4
5
6
7
8
template <typename Tv, typename Te> //深度优先搜索DFS算法（全图）
0002 void Graph<Tv, Te>::dfs ( Rank s ) { //s < n
0003    reset(); int clock = 0; Rank v = s; //初始化
0004    do //逐一检查所有顶点
0005       if ( UNDISCOVERED == status ( v ) ) //一旦遇到尚未发现的顶点
0006          DFS ( v, clock ); //即从该顶点出发启动一次DFS
0007    while ( s != ( v = ( ( v+1 ) % n ) ) ); //按序号检查，故不漏不重
0008 }

实例

无向图

​ 没有前向边

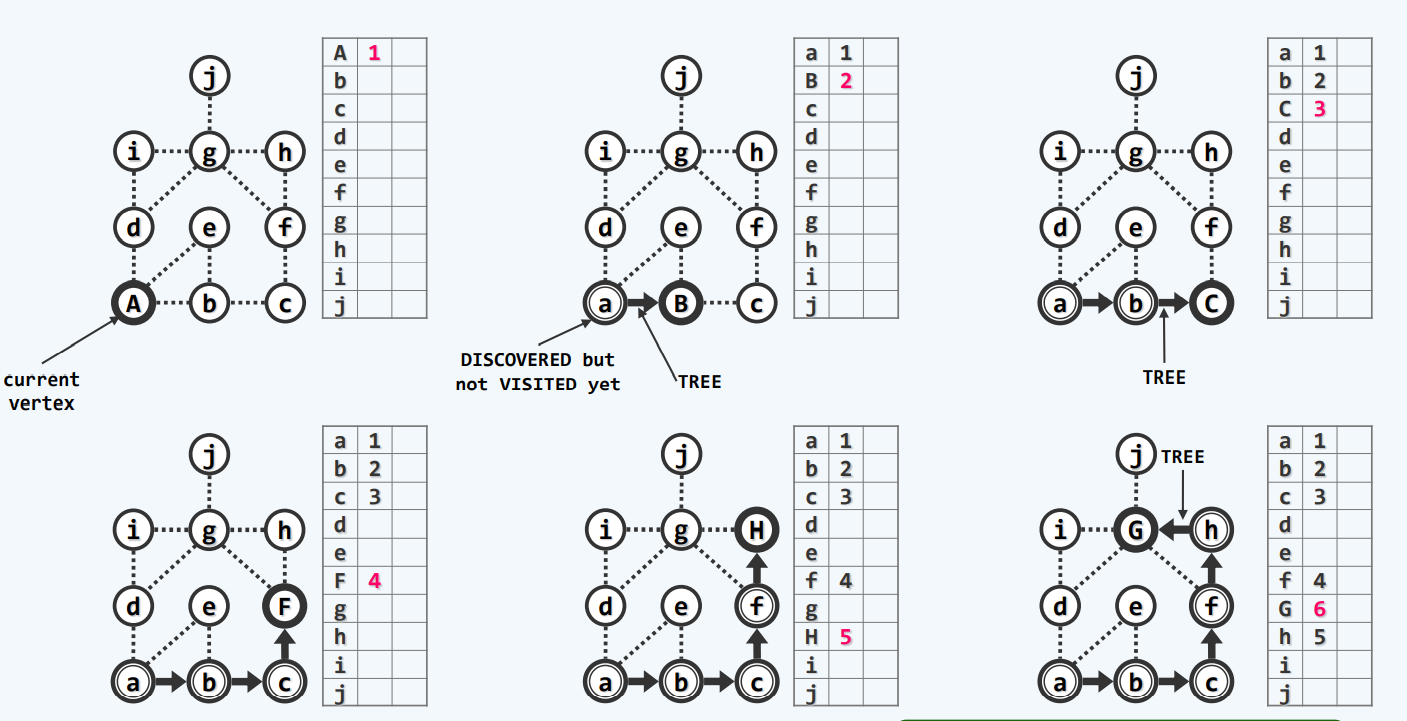
image-20220301202558960

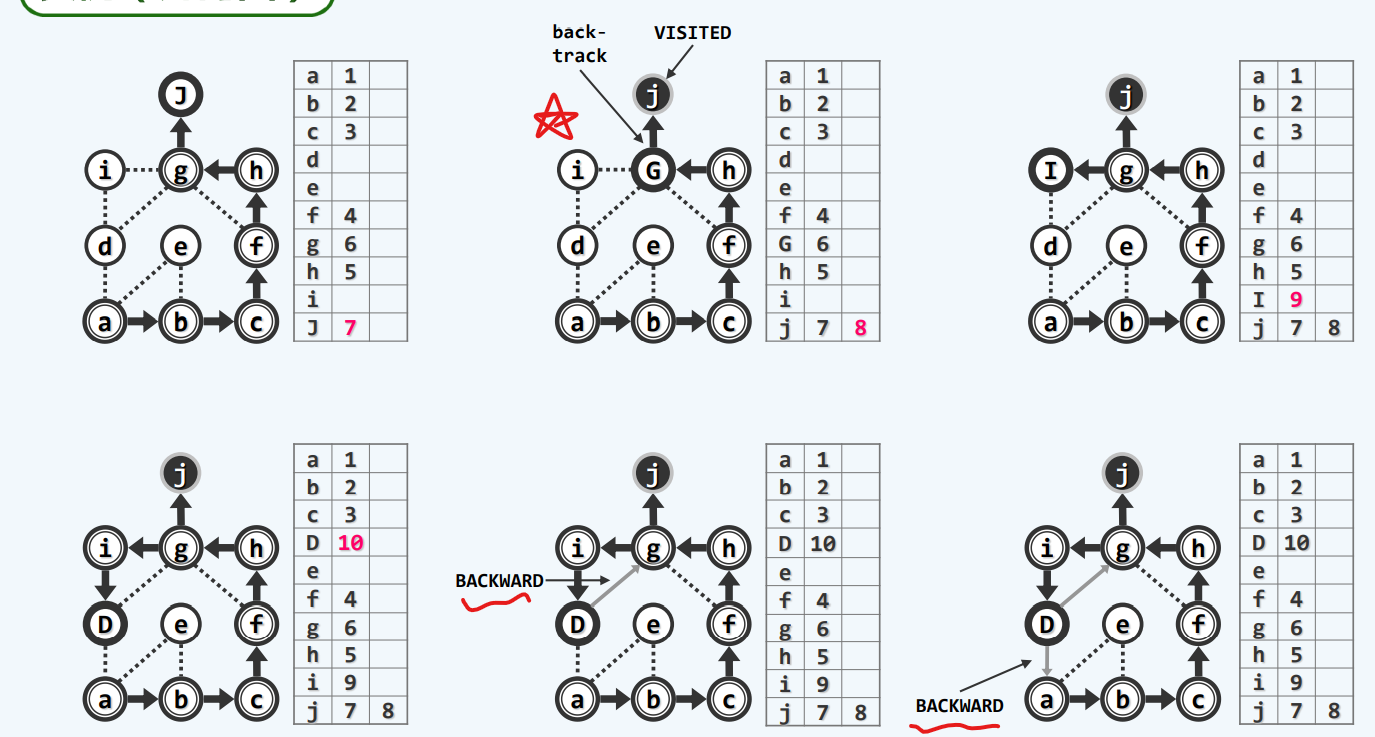
image-20220301202741286

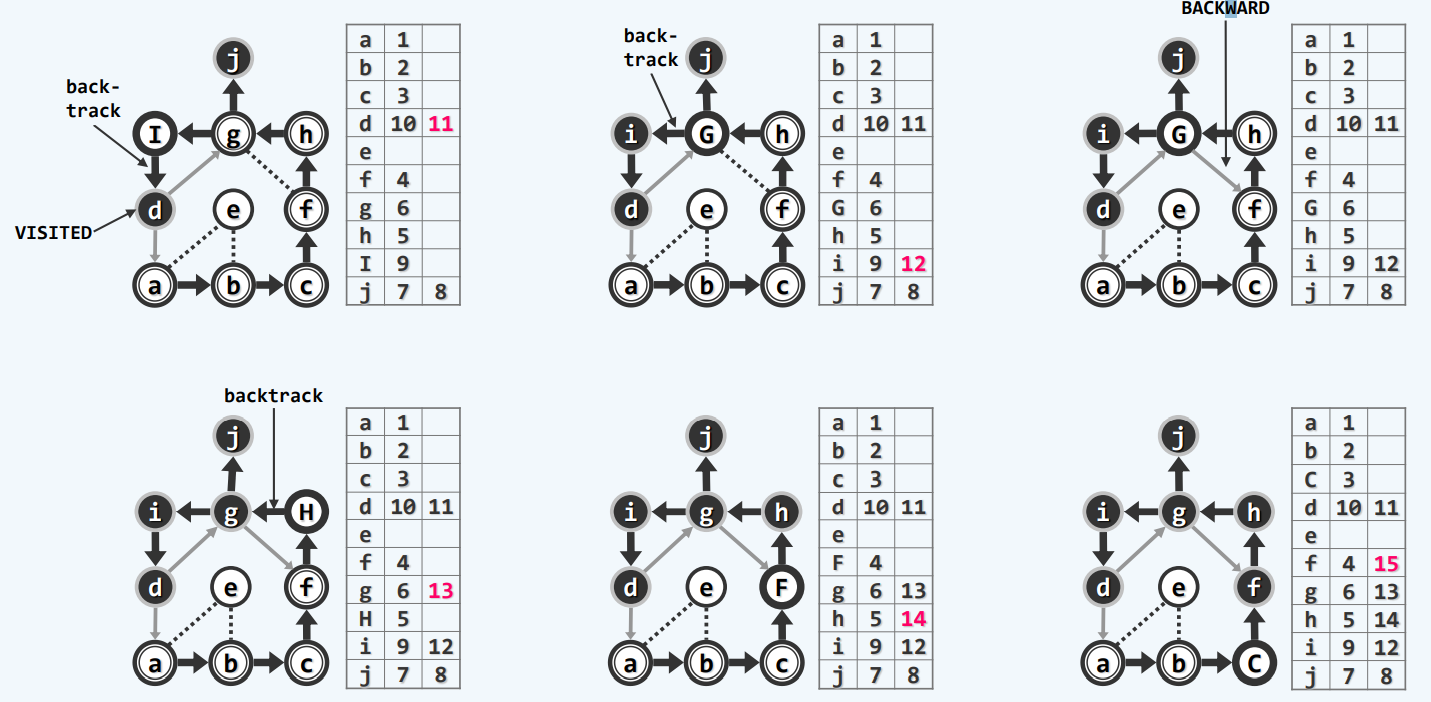
image-20220301202757098

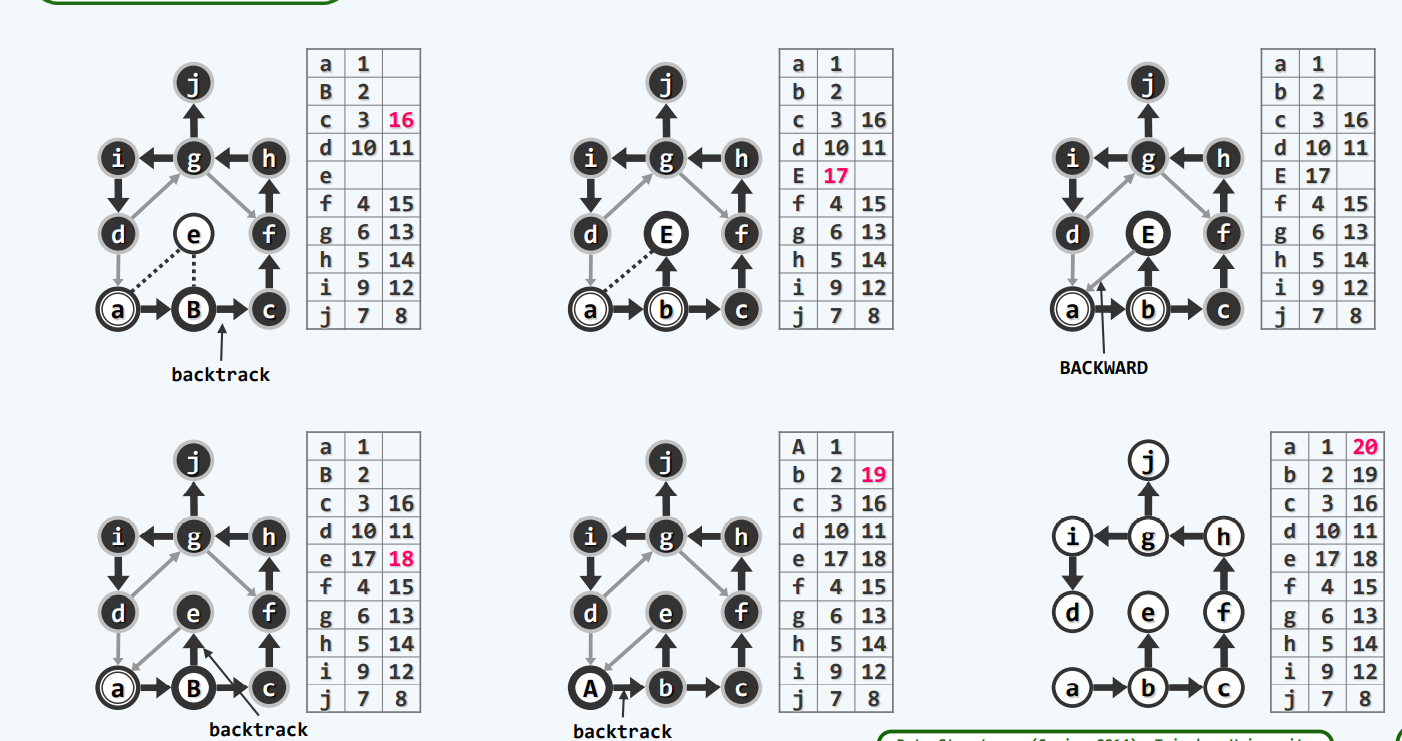
image-20220301202812236

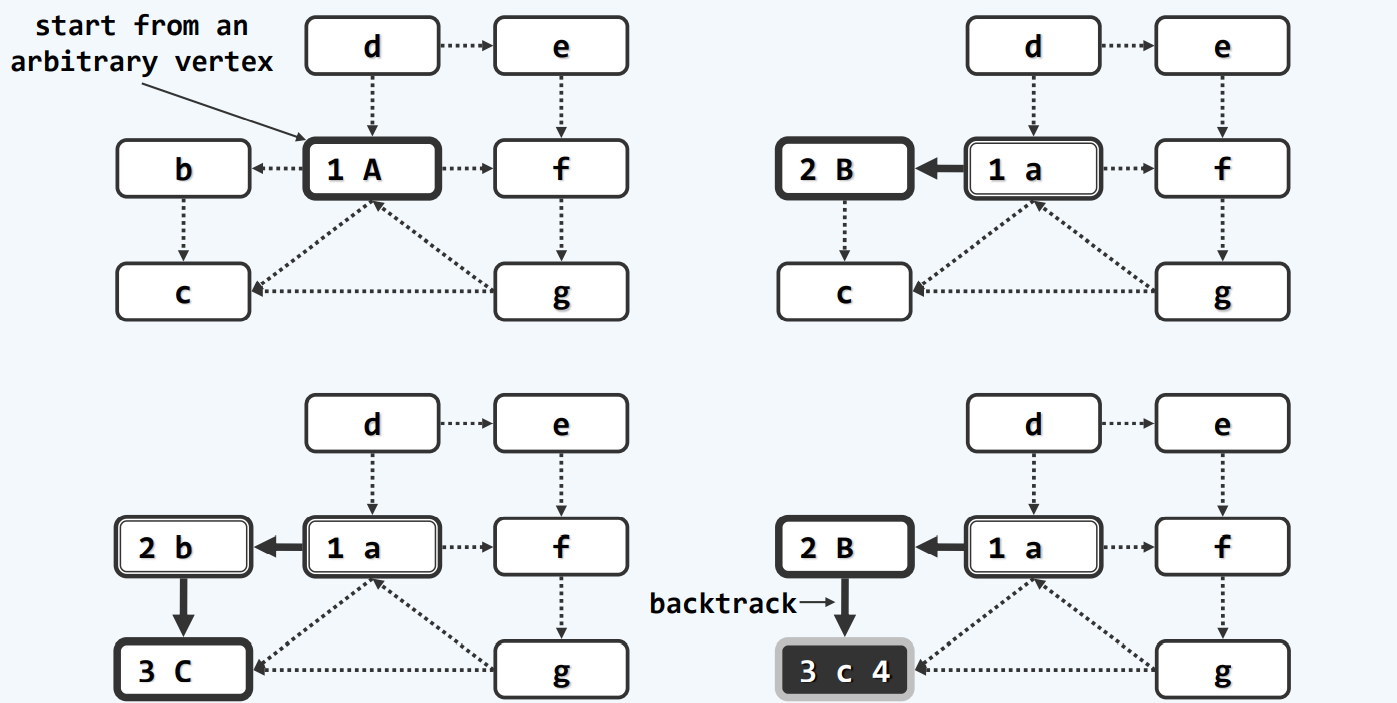
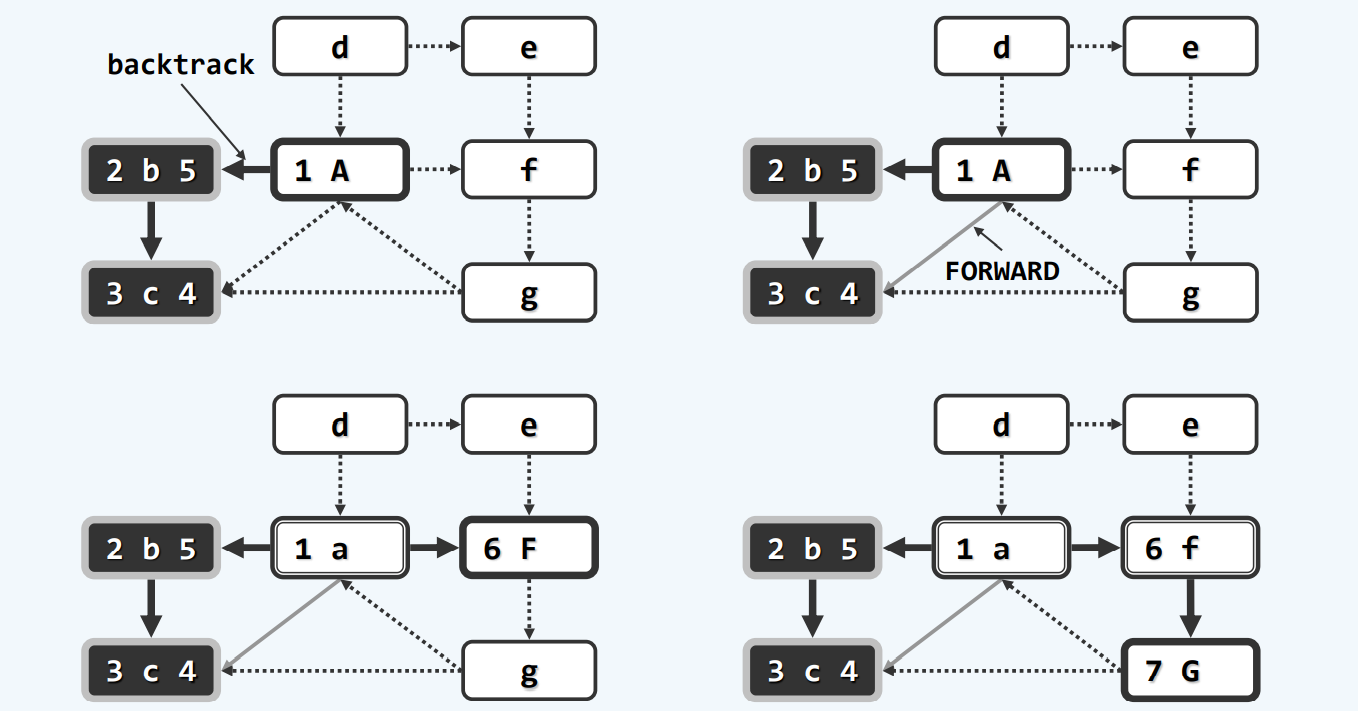
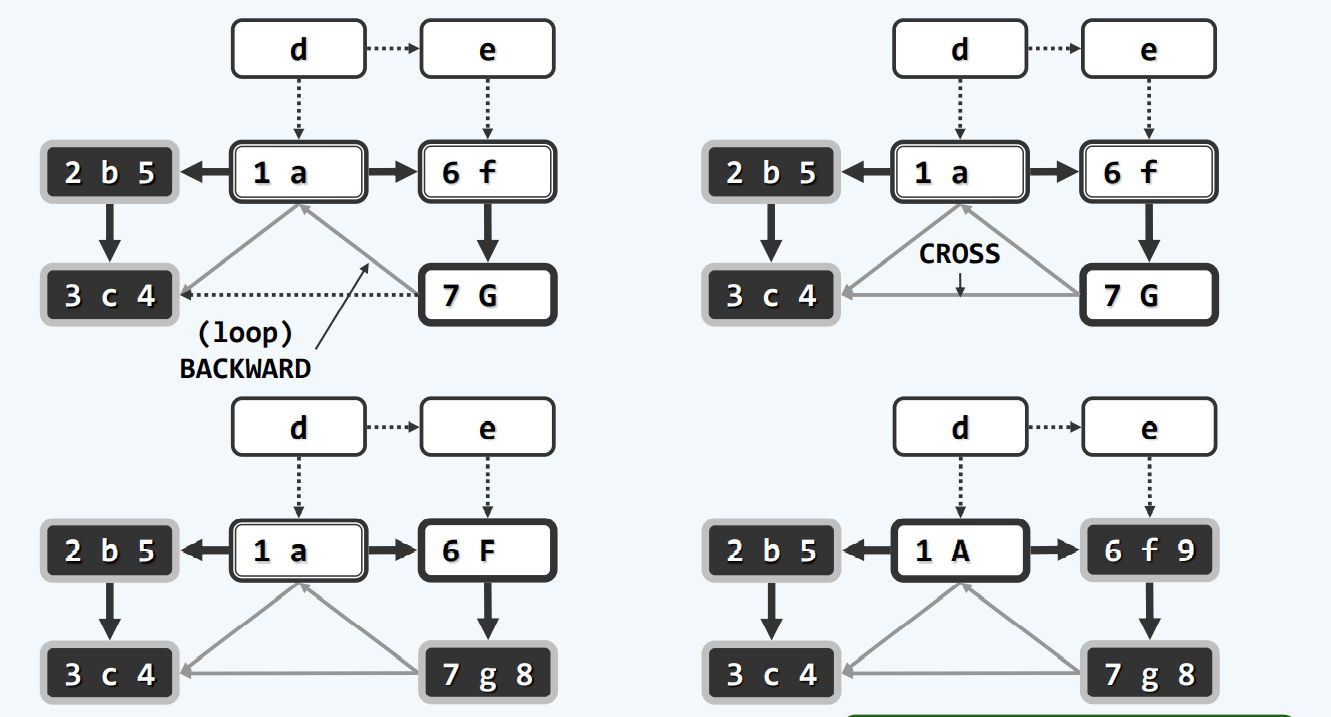
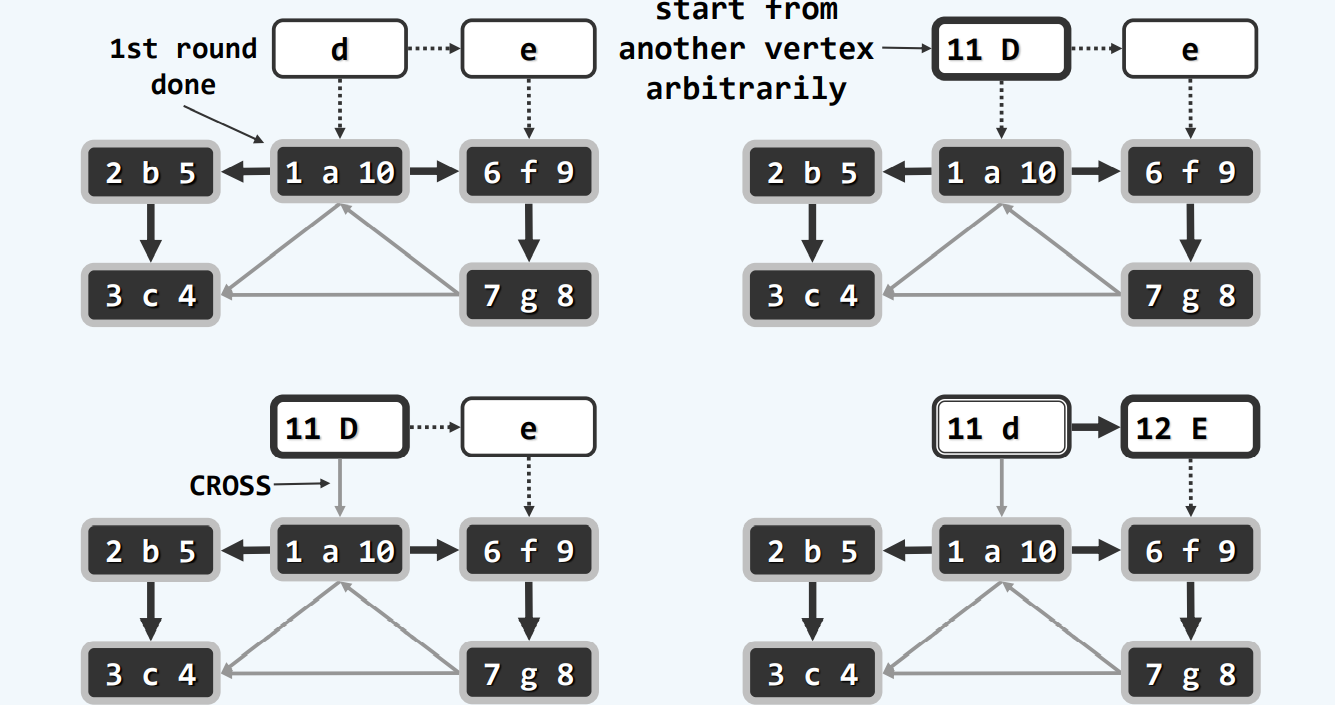
有向图

前向边（forward）：这条边是由遍历树的祖先节点向前指向它的后代

回边（backward）：这条边由后代指向它的祖先

一旦遇到backward那我们至少发现了一个回路

image-20220301202950275

image-20220301203004281

image-20220301203015839

image-20220301203050978

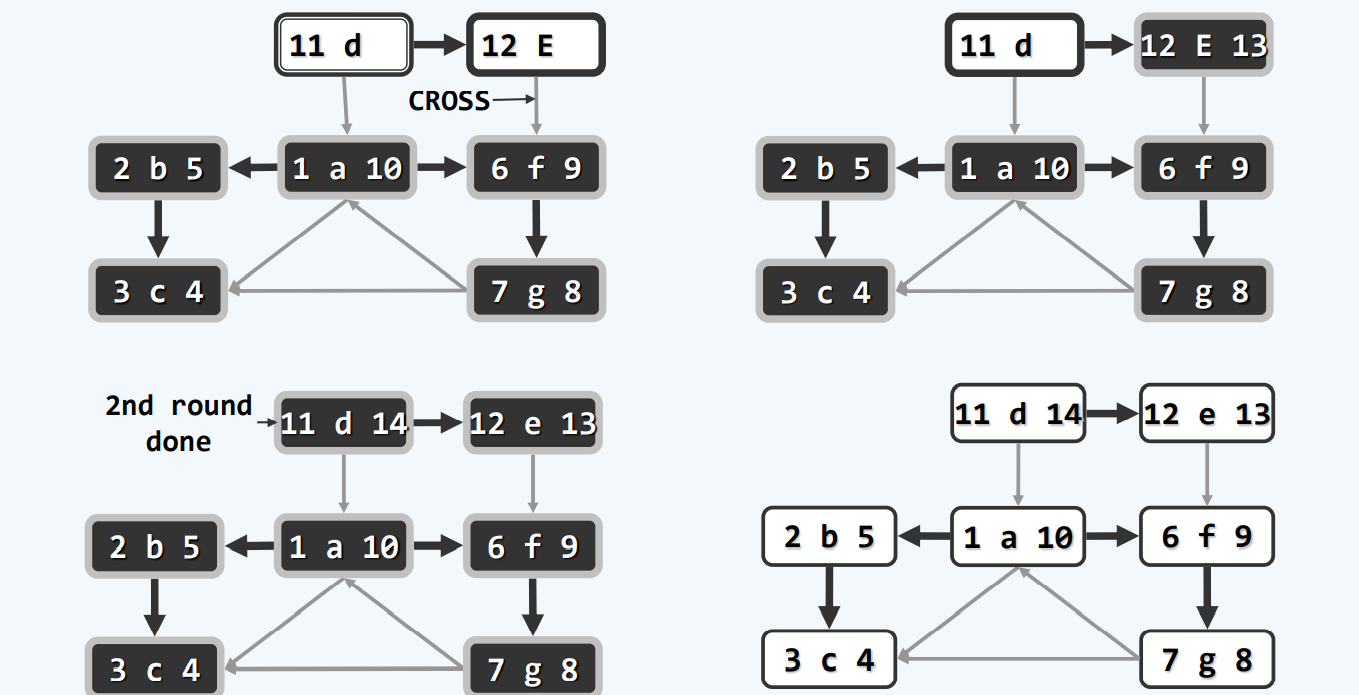
image-20220301203103489

嵌套(括号)引理

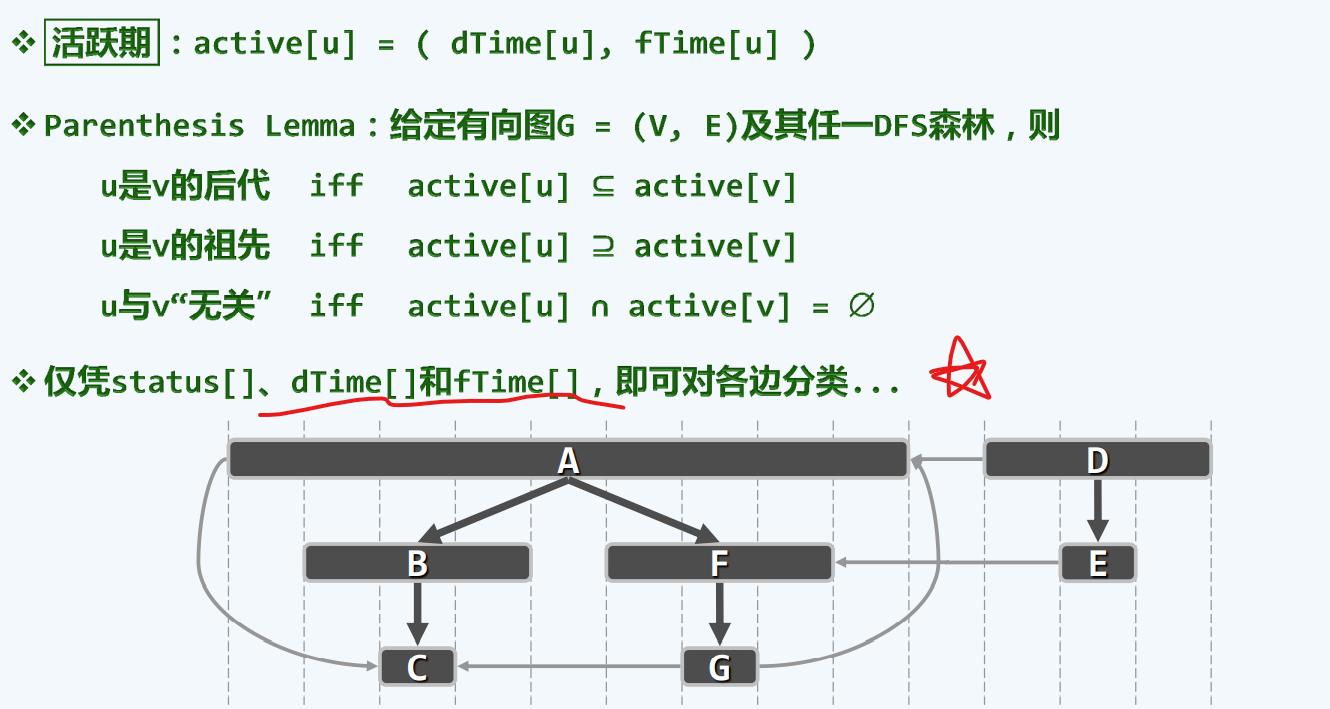
image-20220301203439567

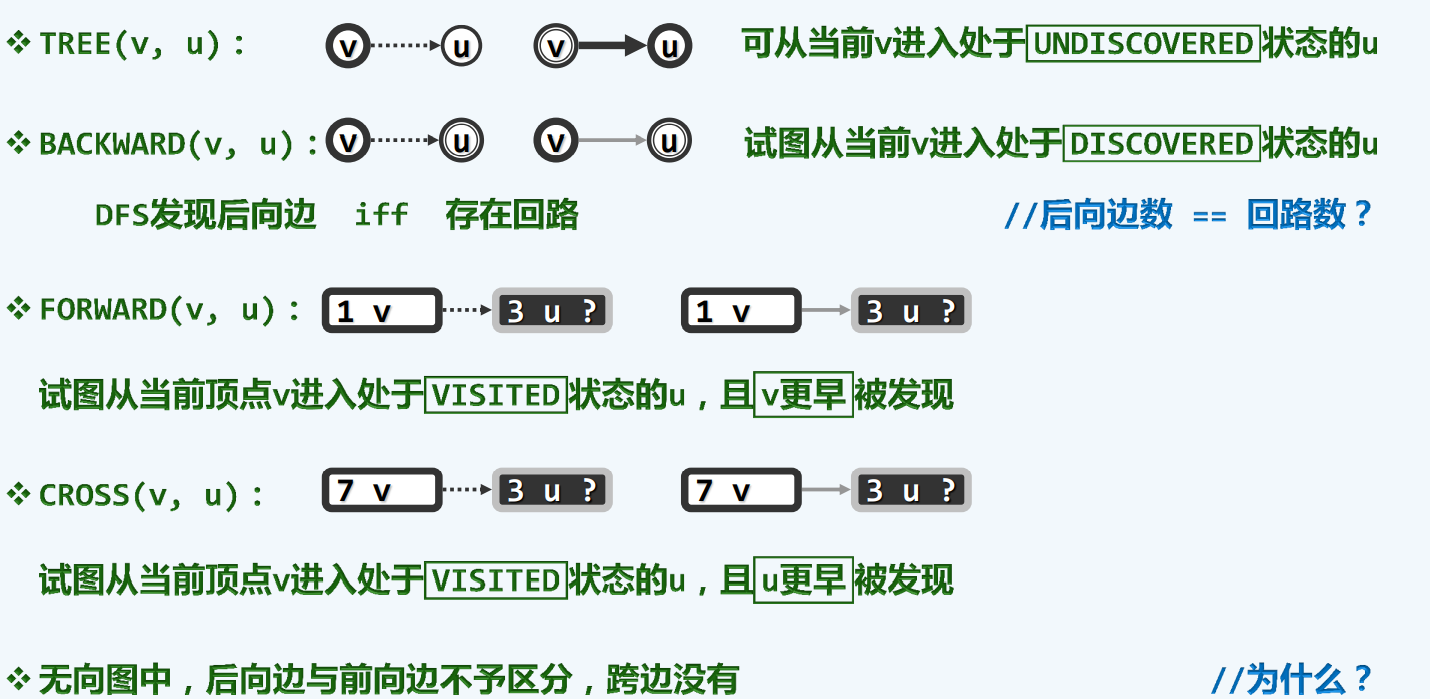
image-20220301203502098

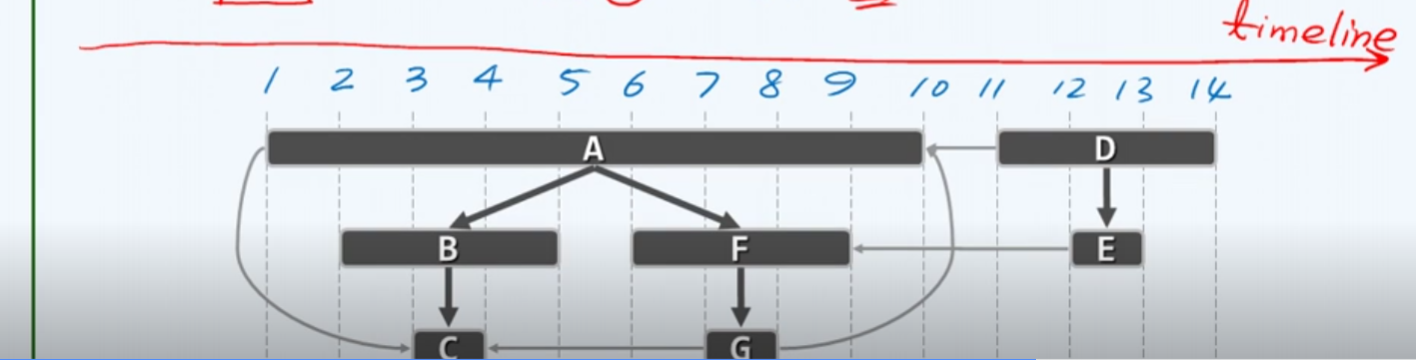
image-20220301203556330

强大的工具，无序再不断溯流而上，判断各节点有无血缘关系….

更多便利之处，还需要后续不断深入体会。

DFS的一些总结

注意此处的单连通(singleconnected)指任意两个结点u,v，从u到v至多只有一条简单路径。这个问题作为上星题有难度，对于一次DFS来讲，如果存在forward edge则表明必定不是单连通图，但还要考虑cross edge，如果在一个DFS树来讲只要存在cross edge，就表明不是单连通

引理1：图G的DFS树中不含有forwardedge或cross edge，u是v的祖先结点，则从u到v的任何路径均会经过u到v的DFS树上的所有点

这个引理相当直观，可以对DFS树上u到v的tree edge数目使用数学归纳法严格证明

引理2：图G的DFS树中不含有forwardedge或cross edge，如果点u到v有两条完全不同的简单路径(路径上的点各不相同)，则v必定为u的祖先结点

拓扑排序

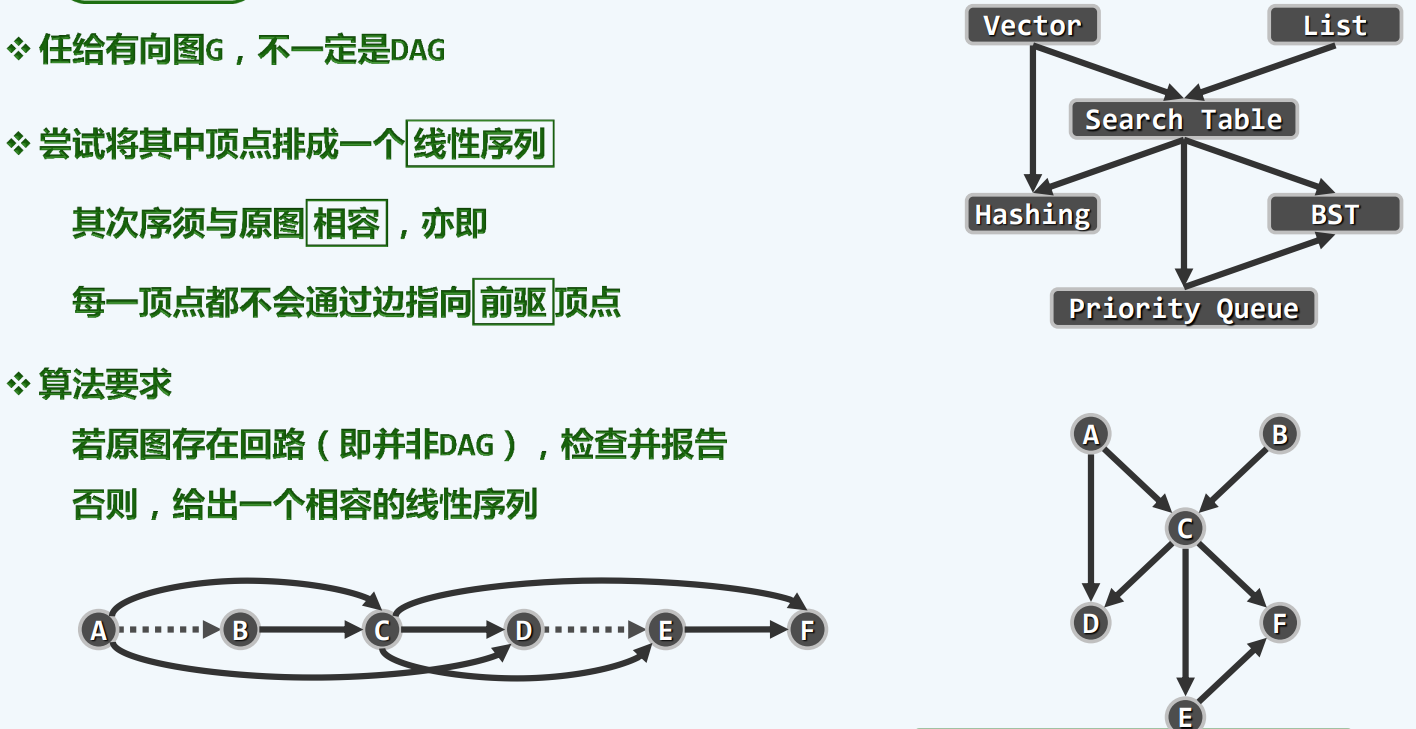
image-20220302101814244

举个例子，也就是编排书本，一个好的拓扑排序就是，每当我讲到这一个知识点的时候，它所依赖的知识点，都应该在此前的某个时刻已经学过了，数学上，我们认为，也许，可能，存在这样一个线性序列

​ 所以他是一个不折不扣的有向图(directed acyclic graph)[DAG]，但是不能有环(学a先学b，学b先学c，学c先学a)

零入度

不推荐使用

算法

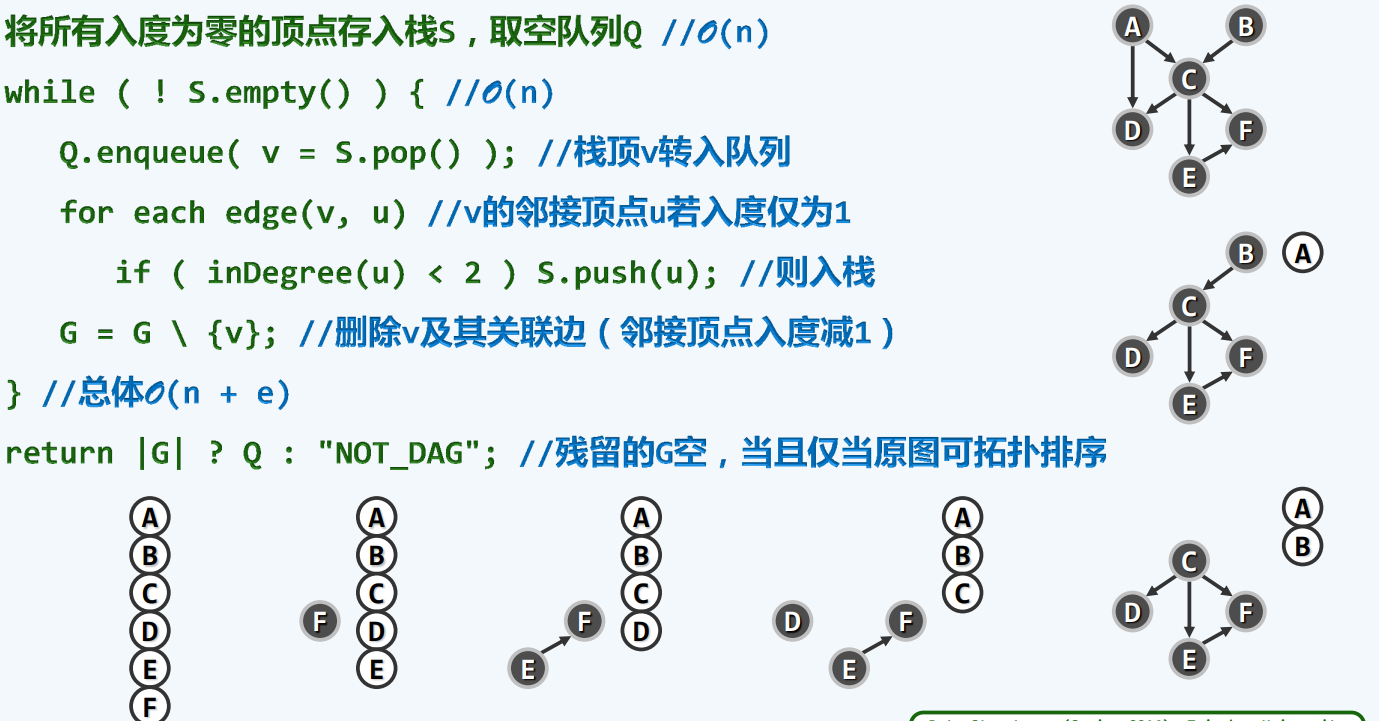
image-20220302103204085

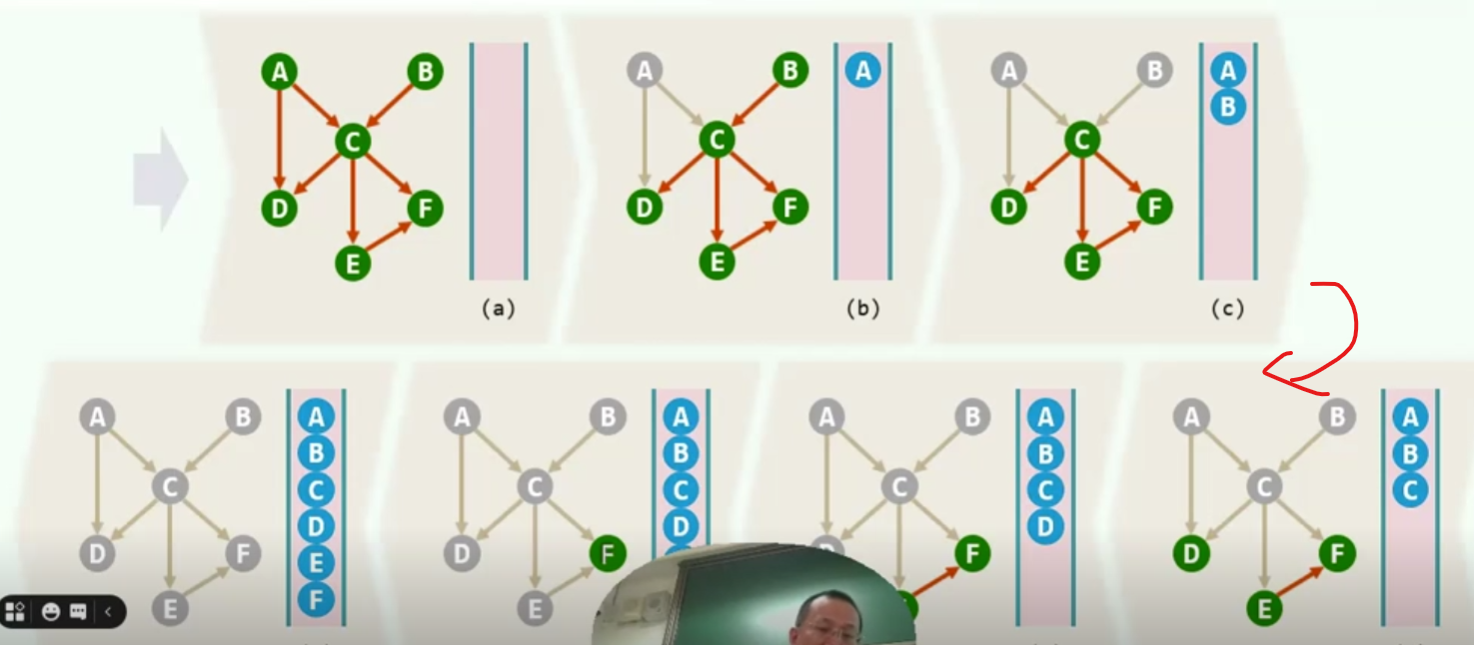
实例

一个一个找零入度的点，并且删除还要更新，可能对图本身也会造成伤害

image-20220302103323968

零出度

算法

随机一个点开始，先找到第一个backtrack的点，那个就是你最终需要到达的地方，然后不断backtrack，通过DFS的ftime排序，我们至少可以得到一个合理，甚至推荐使用的顺序。

​ 当然，可能会有点没有遍历到，但是，我们实际使用，外面是要包一层dfs的！

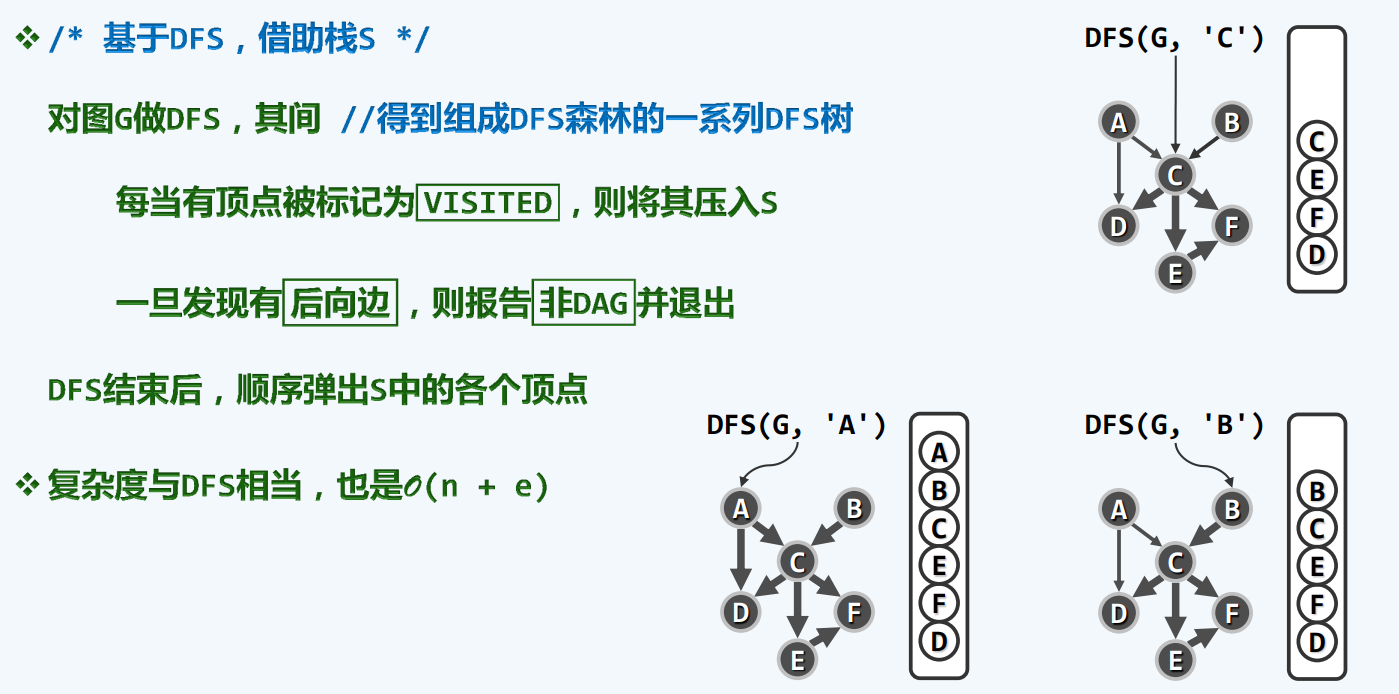
image-20220302103556556

image-20220302103759994

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
template <typename Tv, typename Te> //基于DFS的拓扑排序算法
0002 Stack<Tv>* Graph<Tv, Te>::tSort ( Rank s ) { //assert: 0 <= s < n
0003    reset(); int clock = 0; Rank v = s;
0004    Stack<Tv>* S = new Stack<Tv>; //用栈记录排序顶点
0005    do {
0006       if ( UNDISCOVERED == status ( v ) )
0007          if ( !TSort ( v, clock, S ) ) { //clock并非必需
0008             while ( !S->empty() ) //任一连通域（亦即整图）非DAG
0009                S->pop(); break; //则不必继续计算，故直接返回
0010          }
0011    } while ( s != ( v = ( ++v % n ) ) );
0012    return S; //若输入为DAG，则S内各顶点自顶向底排序；否则（不存在拓扑排序），S空
0013 }
0014 
0015 template <typename Tv, typename Te> //基于DFS的拓扑排序算法（单趟）
0016 bool Graph<Tv, Te>::TSort ( Rank v, int& clock, Stack<Tv>* S ) { //v < n
0017    dTime ( v ) = ++clock; status ( v ) = DISCOVERED; //发现顶点v
0018    for ( Rank u = firstNbr ( v ); -1 < u; u = nextNbr ( v, u ) ) //枚举v的所有邻居u
0019       switch ( status ( u ) ) { //并视u的状态分别处理
0020          case UNDISCOVERED:
0021             parent ( u ) = v; type ( v, u ) = TREE;
0022             if ( !TSort ( u, clock, S ) ) //从顶点u处出发深入搜索
0023                return false; //若u及其后代不能拓扑排序（则全图亦必如此），故返回并报告
0024             break;
0025          case DISCOVERED:
0026             type ( v, u ) = BACKWARD; //一旦发现后向边（非DAG），则
0027             return false; //不必深入，故返回并报告
0028          default: //VISITED (digraphs only)
0029             type ( v, u ) = ( dTime ( v ) < dTime ( u ) ) ? FORWARD : CROSS;
0030             break;
0031       }
0032    status ( v ) = VISITED; S->push ( vertex ( v ) ); //顶点被标记为VISITED时，随即入栈
0033    return true; //v及其后代可以拓扑排序
0034 }

双连通分量(BCC)

引入连通

设D是一个有向图，如果D中任意两个结点都彼此可达，则称D为**强连通图。如果D中任意两点img之间，有img 到img可达或img到img可达（称为单向可达），则称D为单向连通图。如果有向图的底图是无向连通图，则称D为弱连通图**。

注意：强连通图必是单向连通图，单向连通图必是弱连通图。但反之未必。

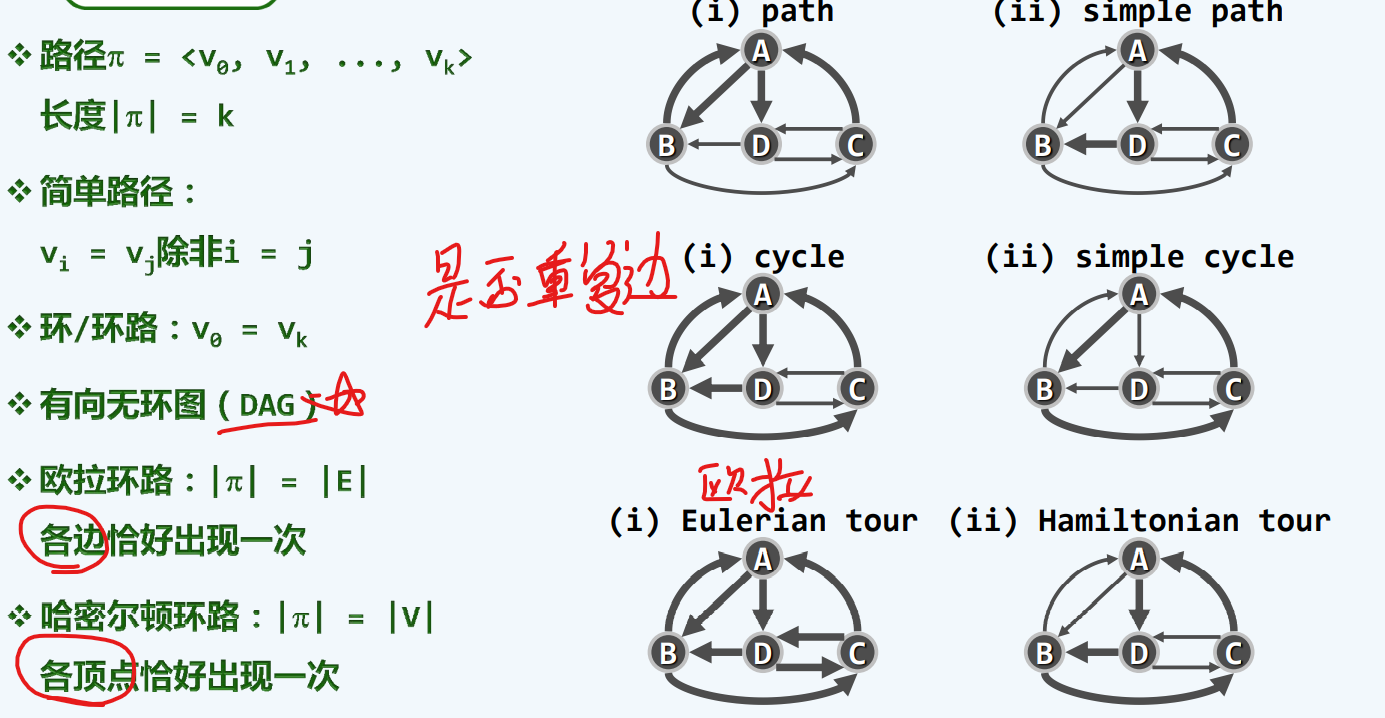
例1 图1(a)是强连通图，图1(b)是单向连通图，图1(c)是弱连通图，图1(d)不是弱连通图。 [2]

图1（a）、（b）图1（a）、（b）

图1（c）、（d）图1（c）、（d）

双连通介绍

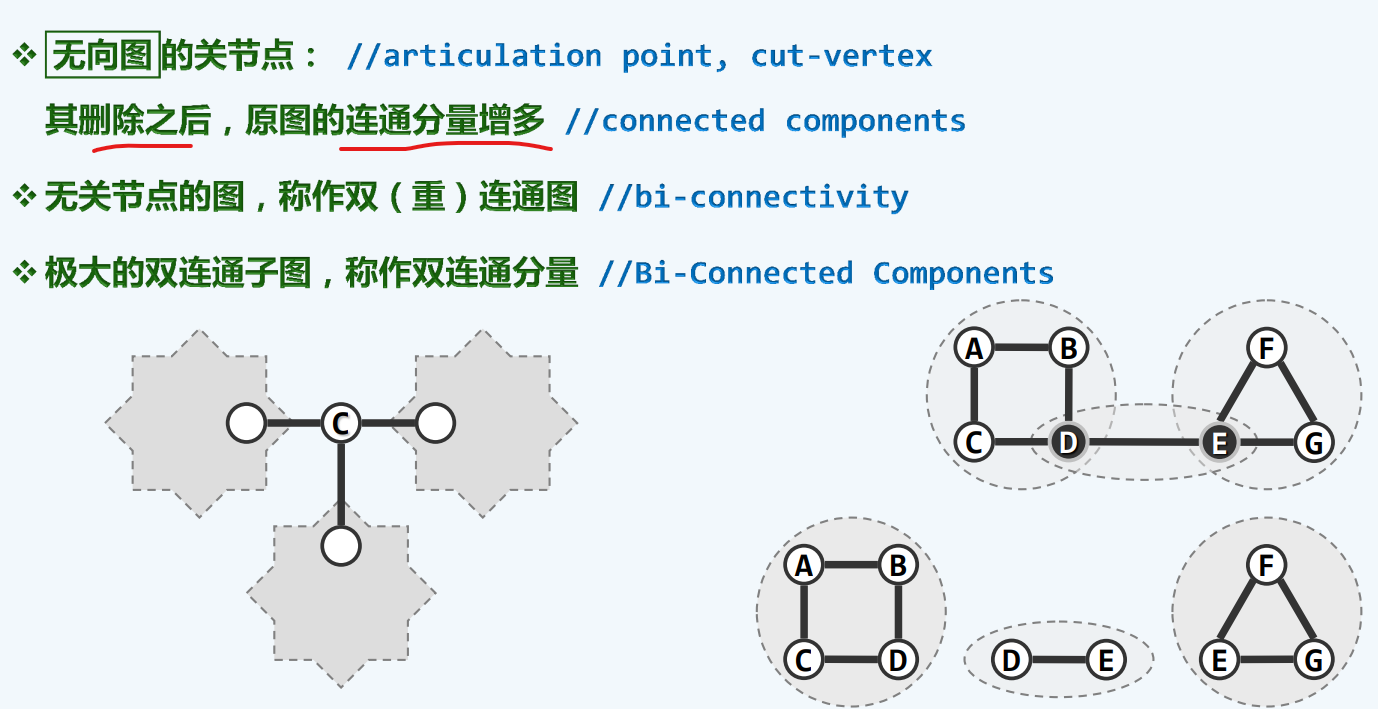
image-20220302104746807

image-20220302104833355

判定准则

因为叶节点就算摘出，即便对那个树来说也不会影响连通性，更何况是连通图呢。

对于根节点而言，因为你是率性的取得，有可能是，有可能也不是

当根节点只有一度，那它和叶子无异，则不可能是，反过来，它是两度或者三度，那么它必然就是关节点，无形中成为了关节点，不然他的两个孩子不可能连接起来

对于内部节点而言

image-20220302110515951

v的右儿子的小家族，有人可以够着比v还高的祖先，所以即便他消失了，这个小家族也能和整个家族连接起来，所以这个角度来说v不是关键节点。

v的左儿子的小家族则不行，所以从这个意义上来说v是关键节点。

如何判断是否是祖先？虽然这个时候我们没有ftime，但是我们有dtime，dtime越小，辈分越高。使用括号引理

算法实现

image-20220302110932504

image-20220302111703354

image-20220302111807631

如果以V作为pop的最终的话，可能会出现把一些不该pop的提前pop了，尽管他们是父子，但物理上进站未必是连续的

实例

紫色代表当前节点，红色代表已经发现，还未利用，蓝色代表燃烧殆尽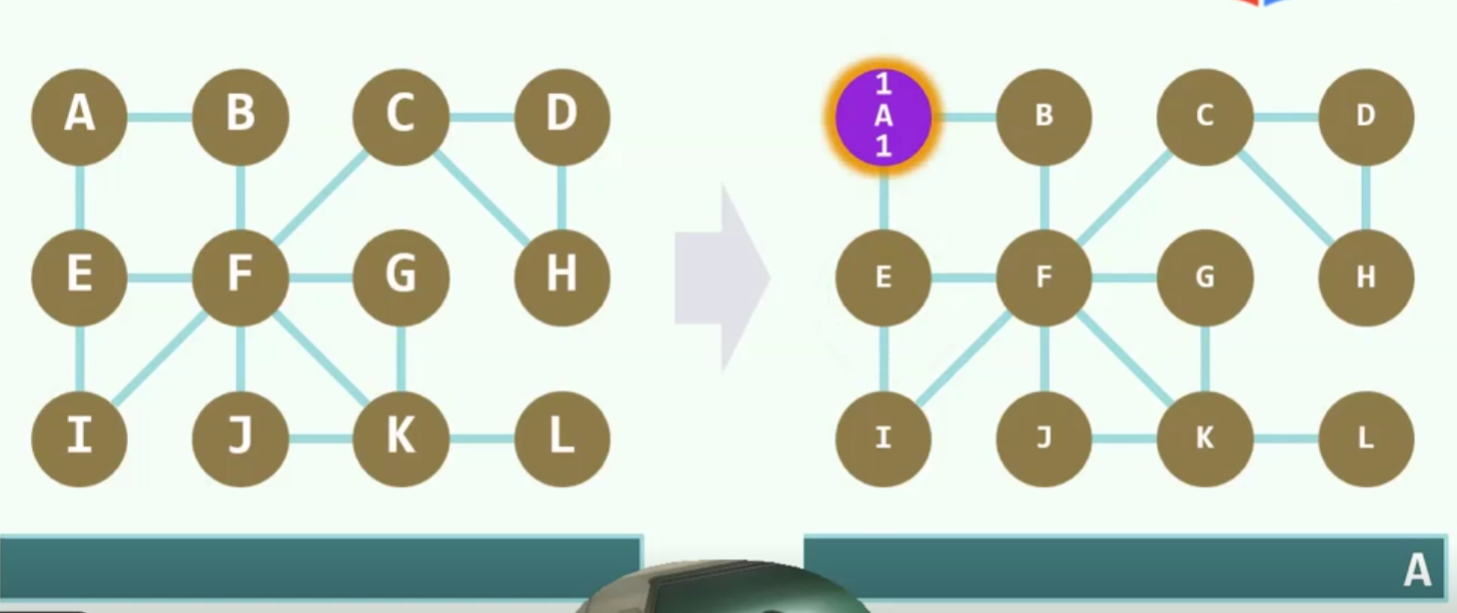image-20220302112208487

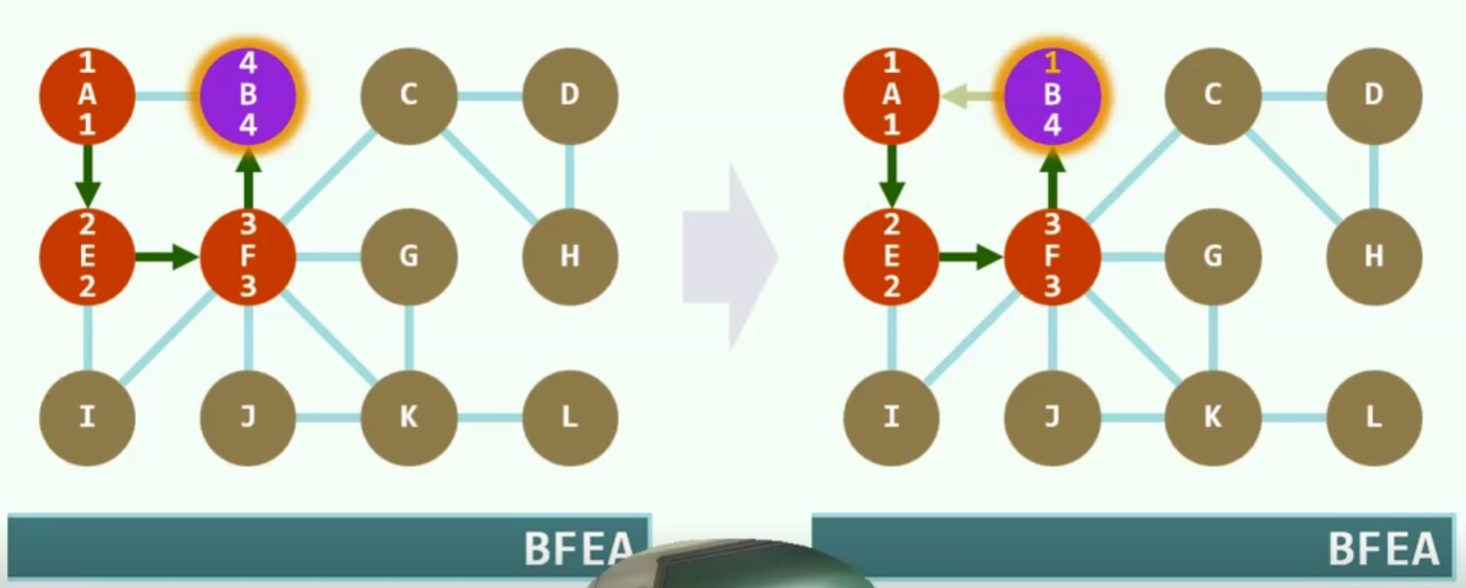
image-20220302112312263

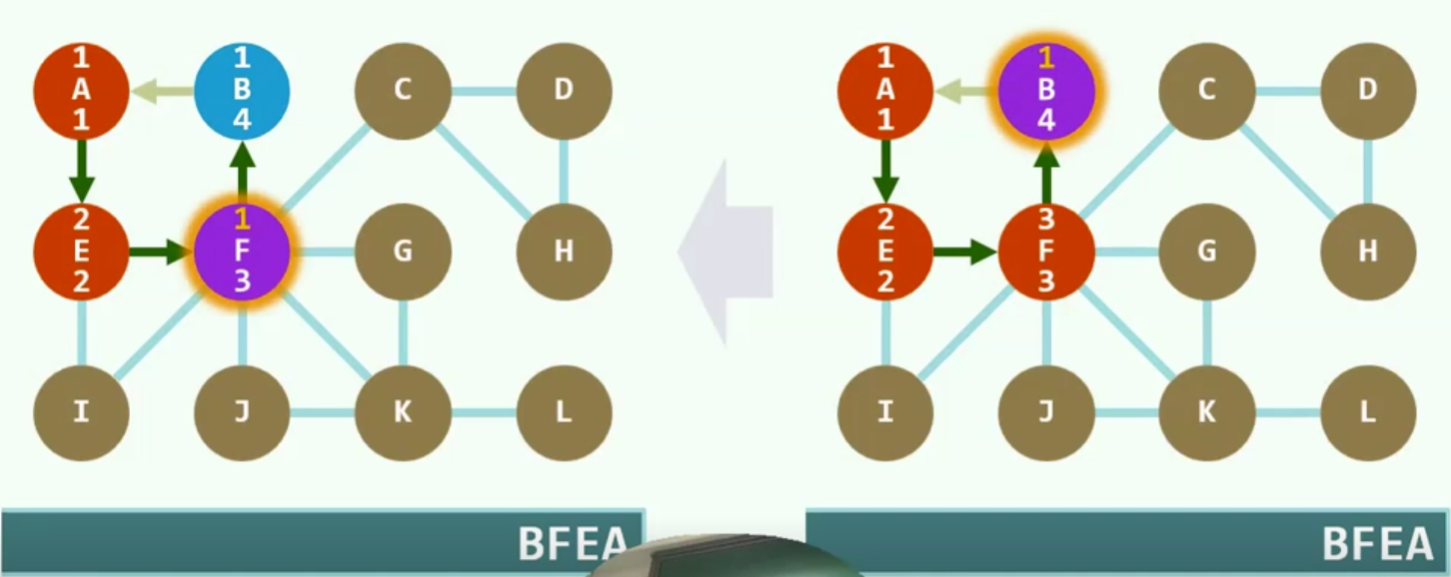
image-20220302112324914

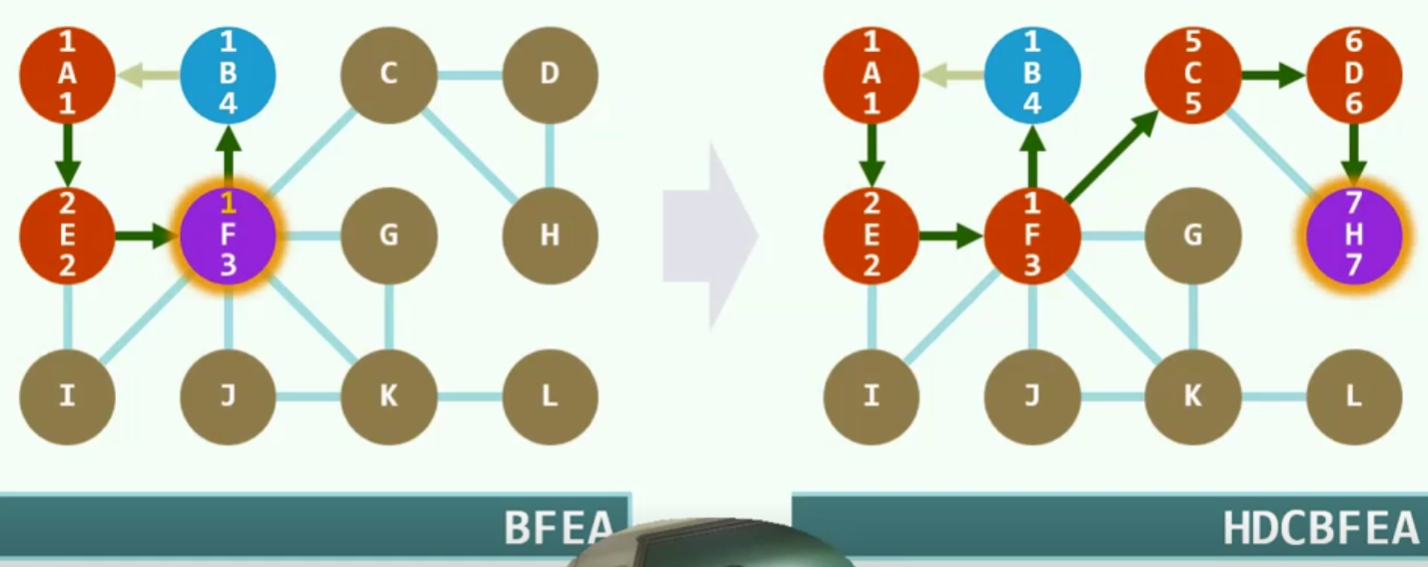
image-20220302112343121

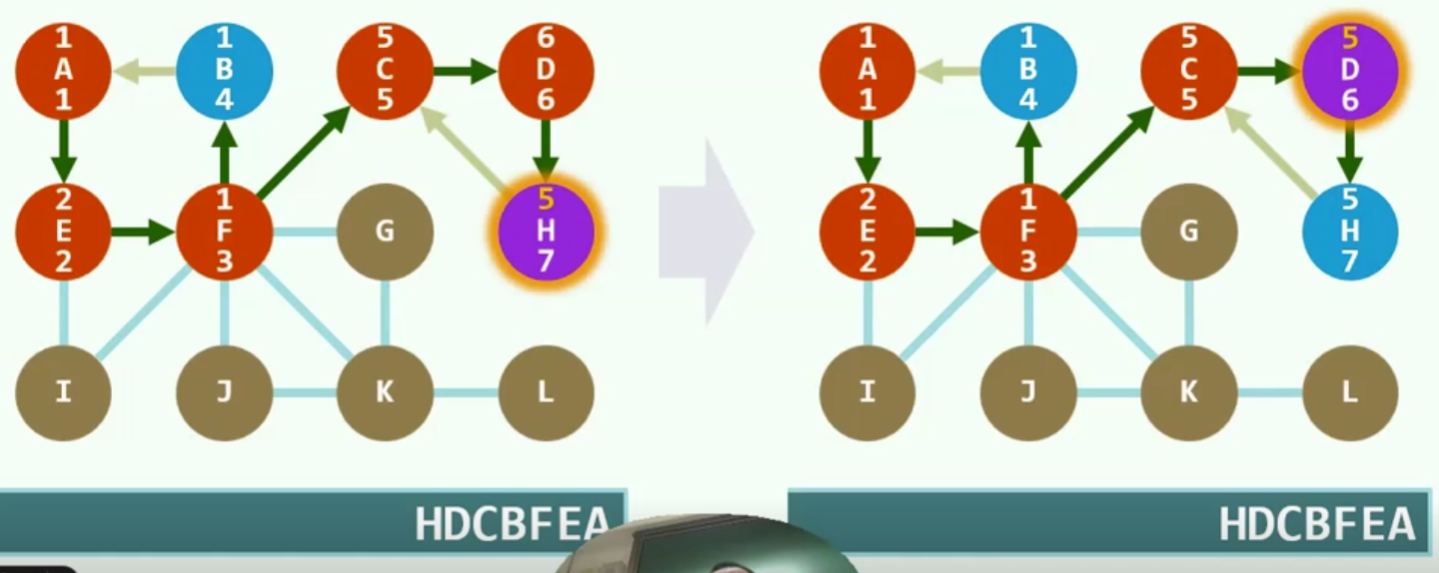
image-20220302112355762

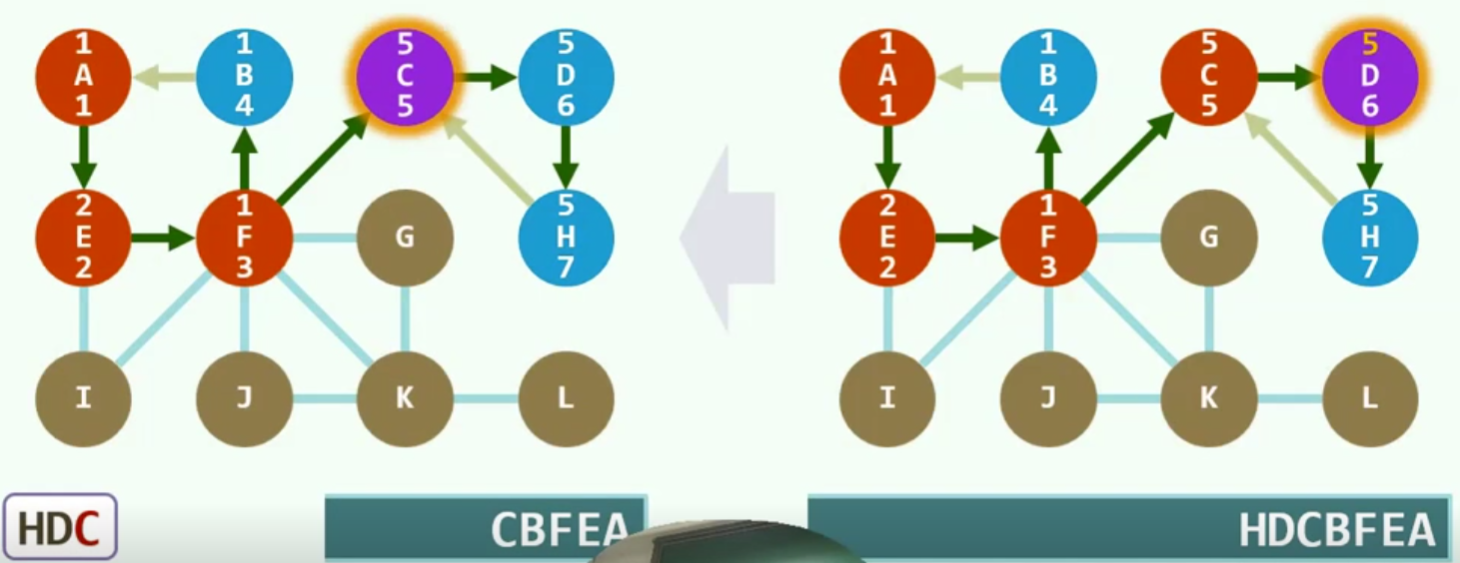
image-20220302112436549

注意：此时c在栈顶，可是它的父亲F并不在栈顶，所以不要直接popF

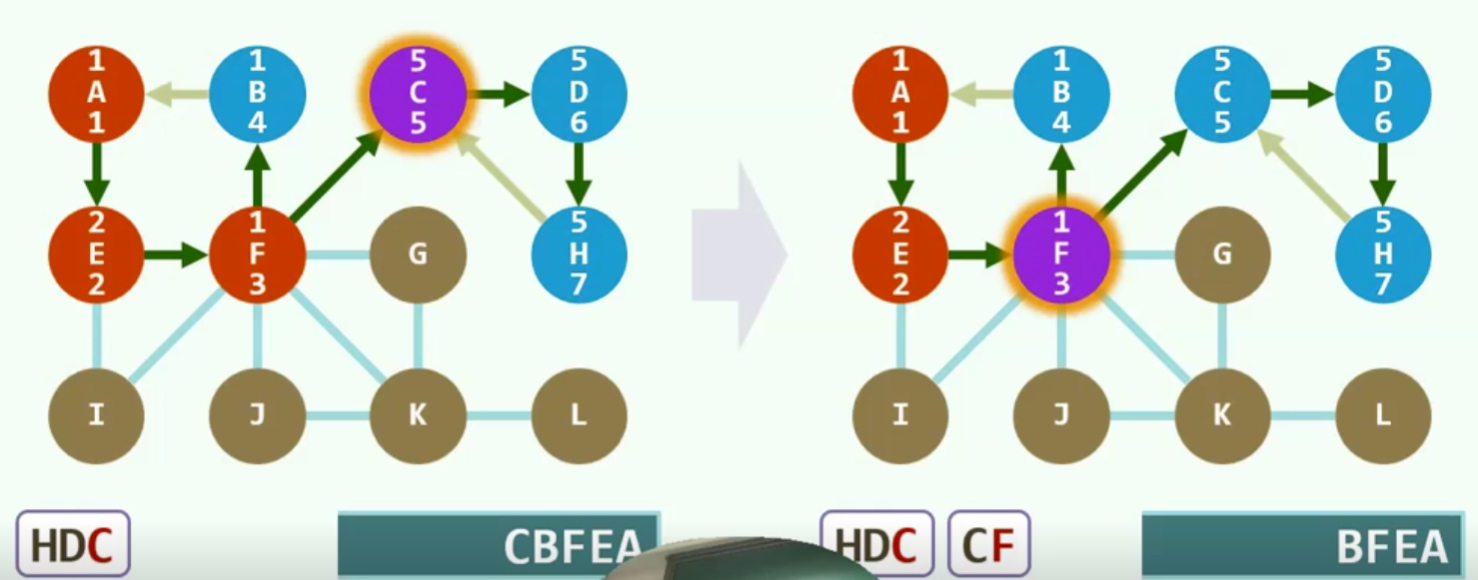
image-20220302112442366

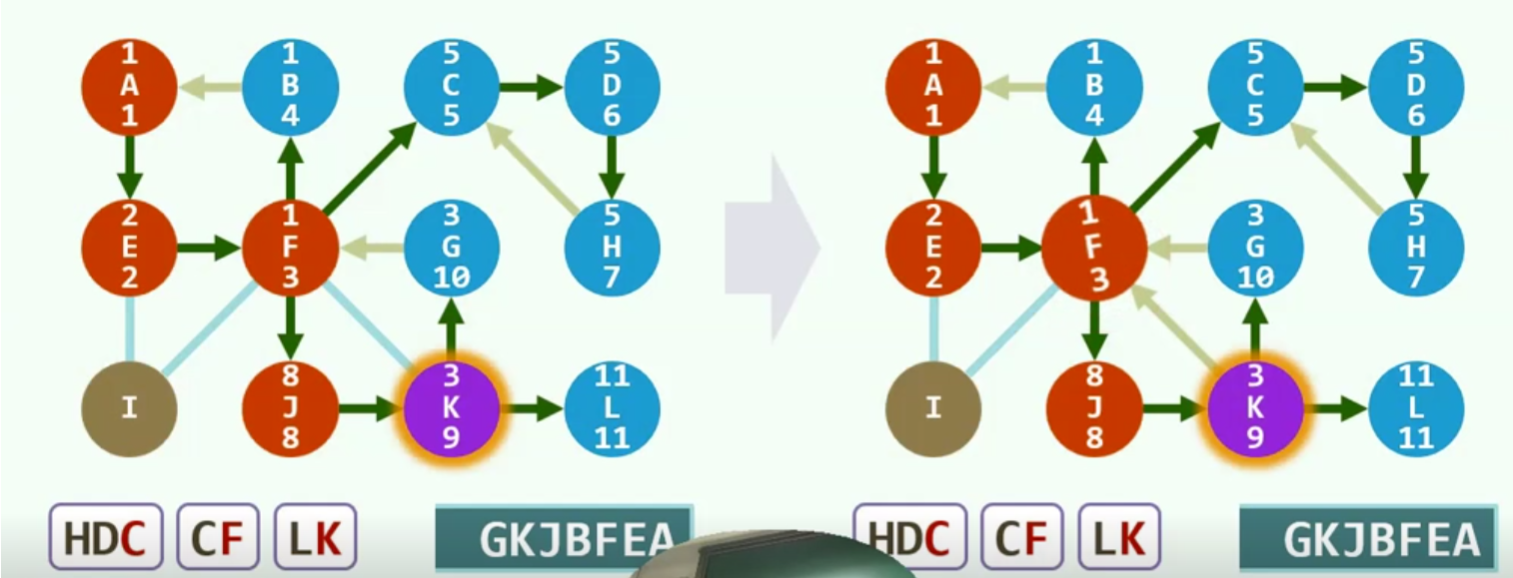
image-20220302112534907

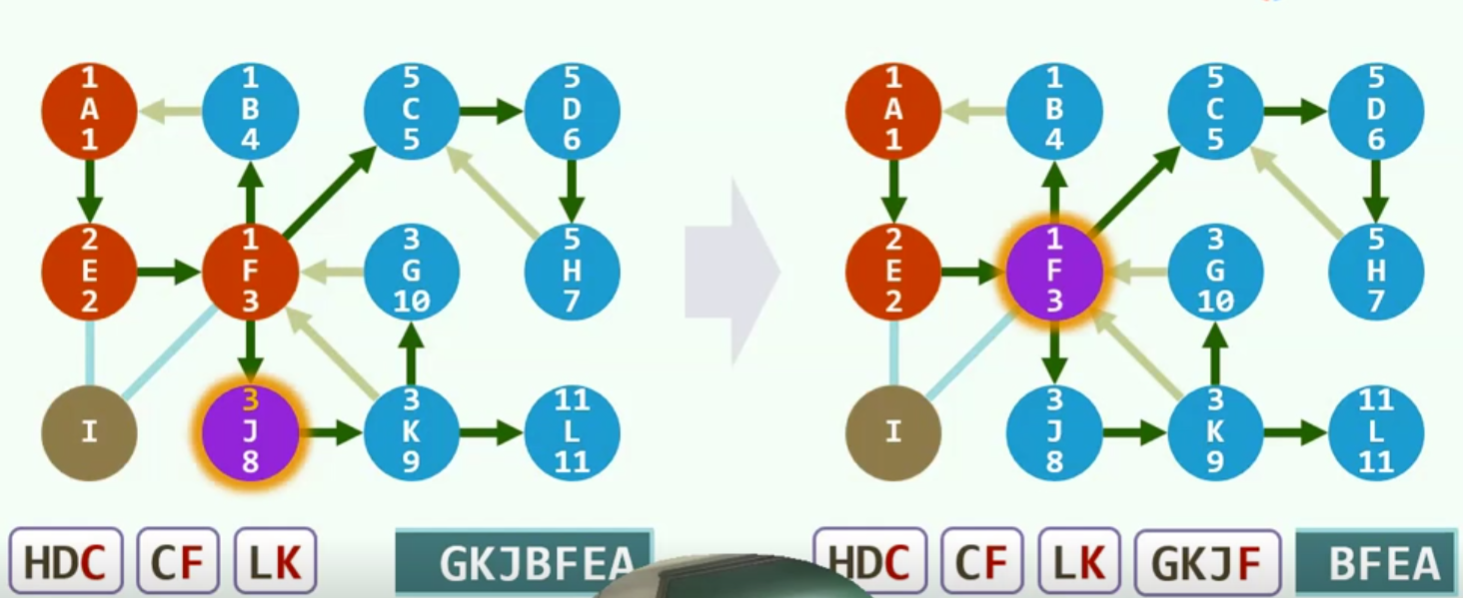
image-20220302112545951

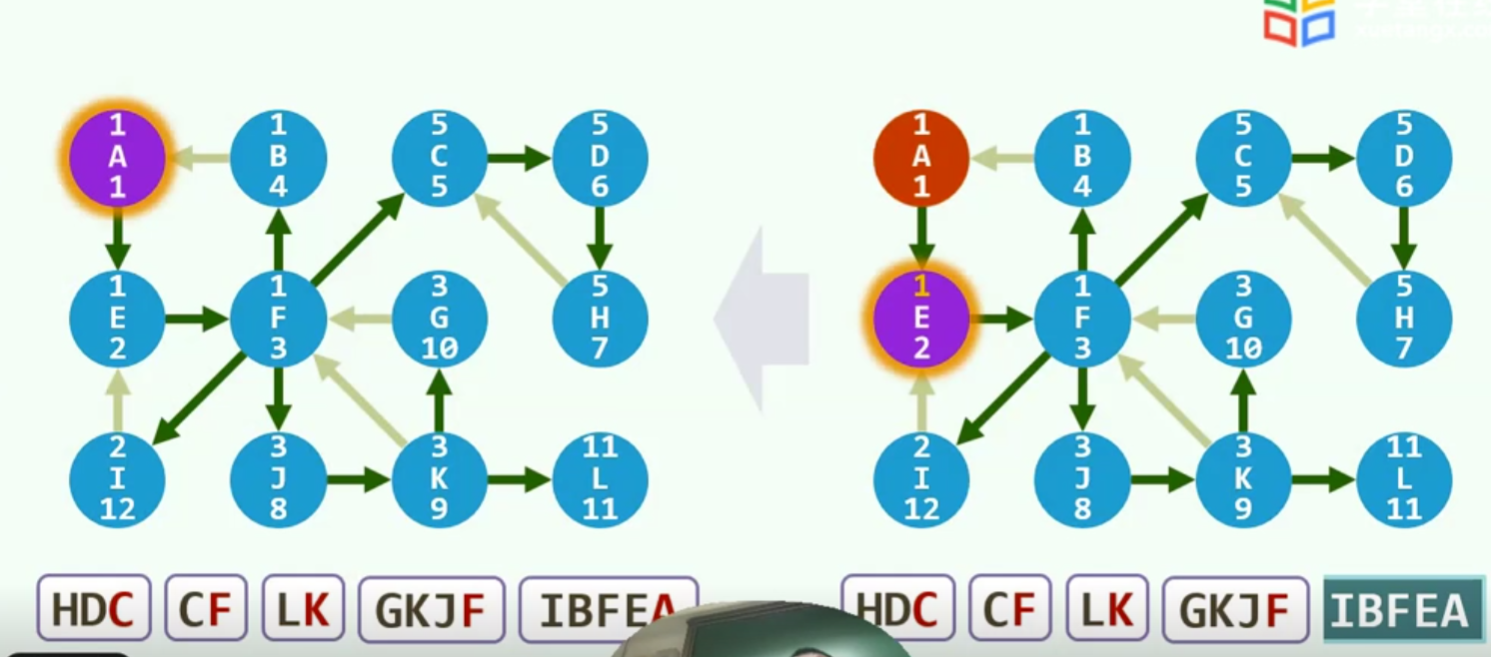
image-20220302112600567

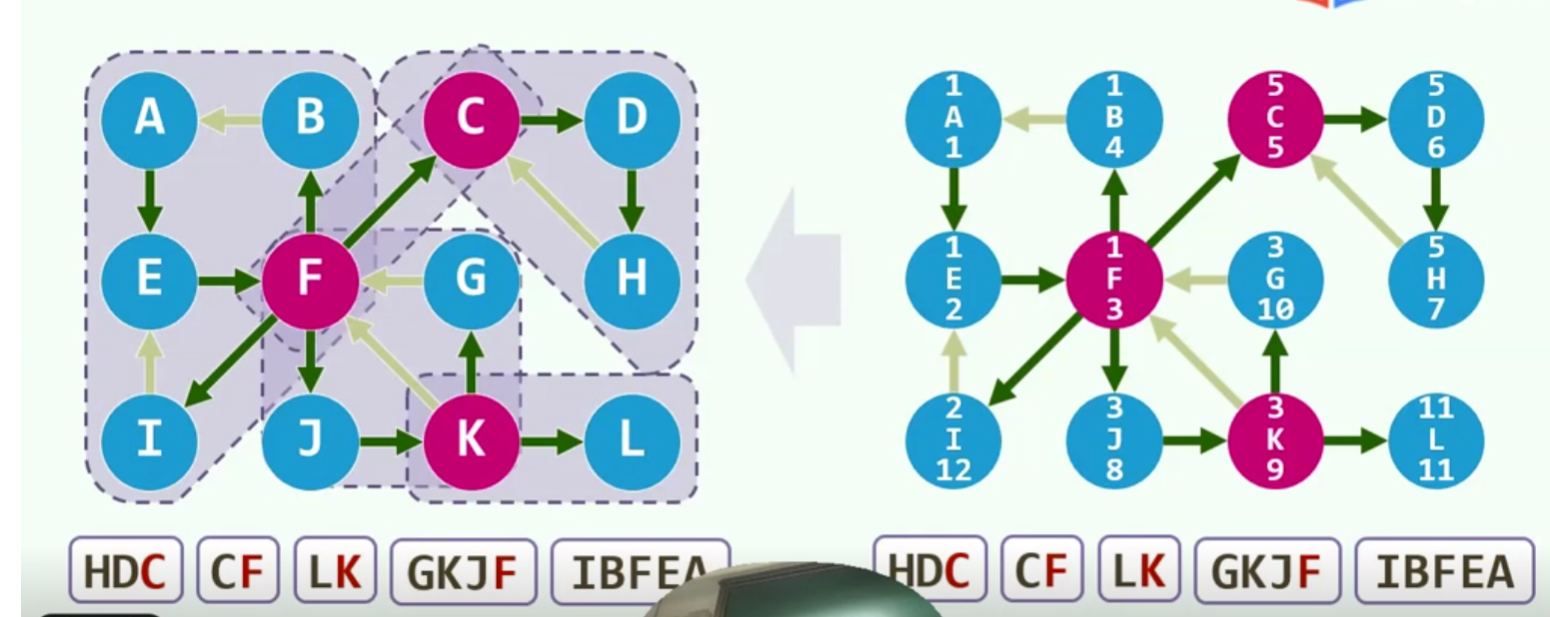
image-20220302112615512

所有完成后，得到四个社交的子网络，各自是双连通的

优先级搜索

BAG

蓝色代表已经选出来的点，红色代表待选，通过每个点的参数max/min，依次排序选出

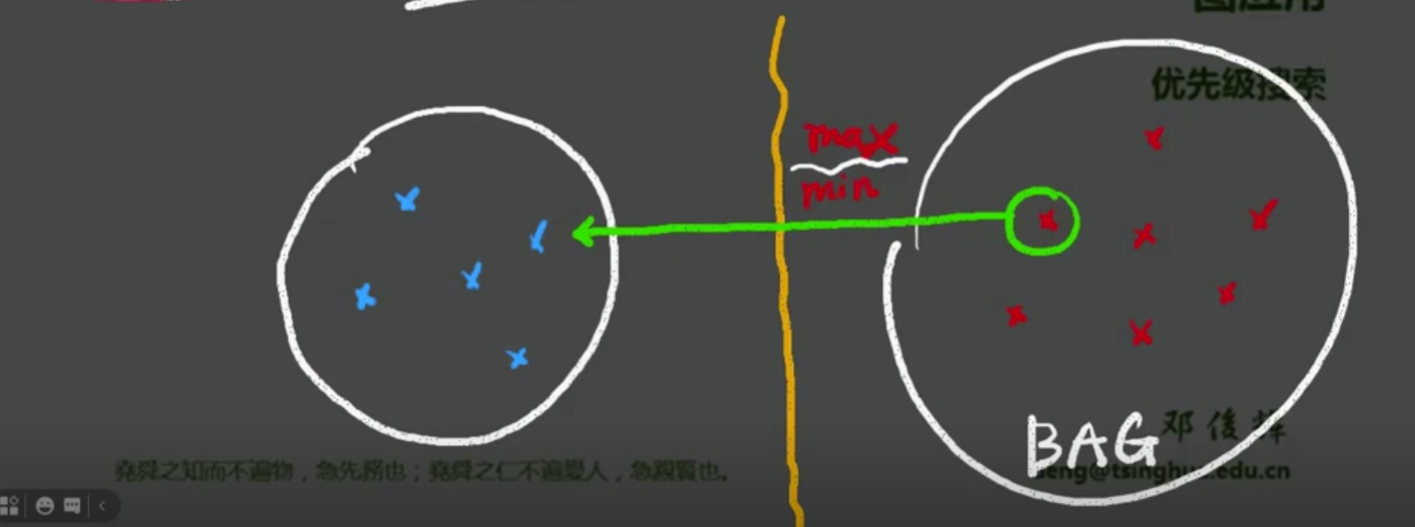
image-20220303211757880

BAG如果是queue，我们用bfs也许更好，如果是stack，一猛子扎进去，最近的优先，那么dfs也不错

算法其实是依赖于数据结构的

ADT

image-20220303212103273

image-20220303212208043

while+for，时间复杂度n²

更新器更新策略，虽然不具体知道，但是知道他是依据于什么的。

this就是这幅图，在这幅图中，如果s刚刚被访问过，那么他的邻居（w）就有机会上位

for+if+if嵌套，其实就是做一个select 这个叫shortest 那个叫highest

那么，这么效率这么低，那么我们如何改进呢？有了这个想法，有了这个动力，那我们就能继续往下深入，（代码的结构差异非常的小）差别不会到两行，一行半

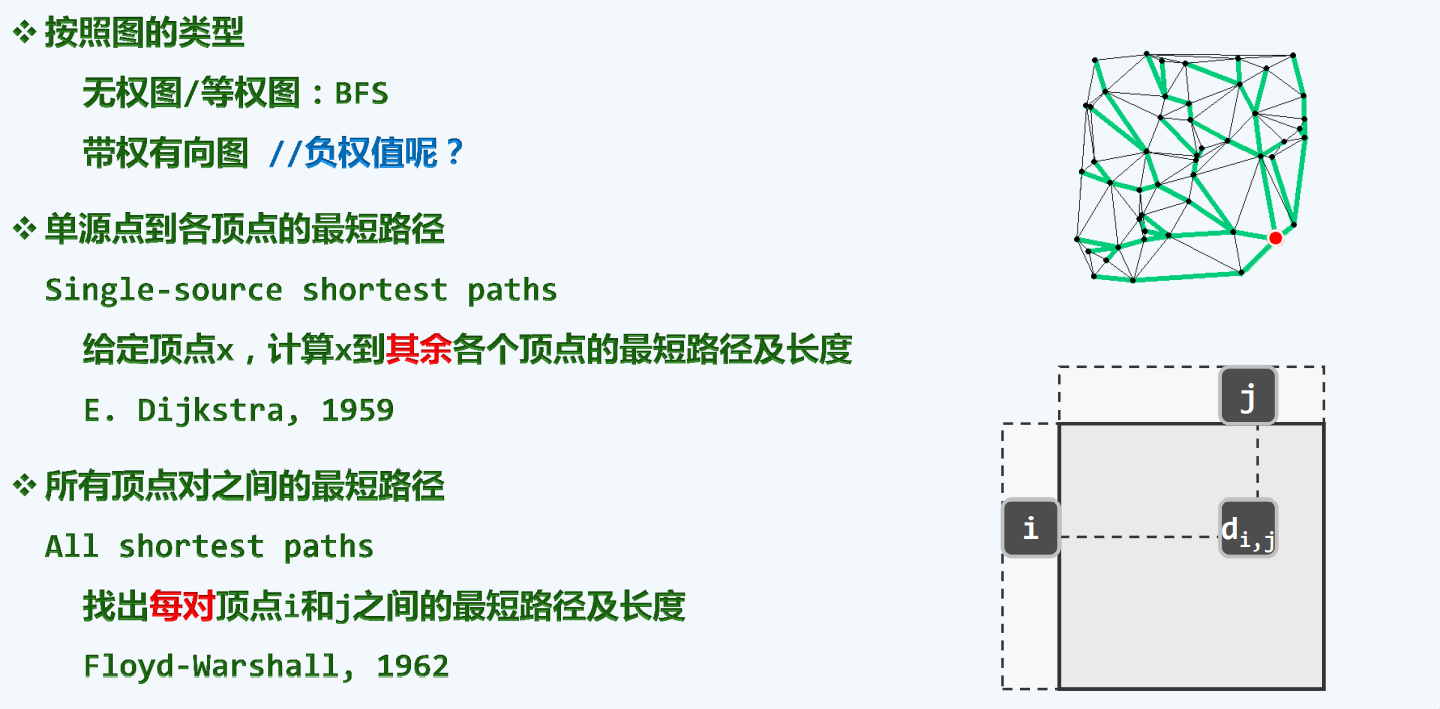
Dijkstra

Shortest Path

image-20220303213031657

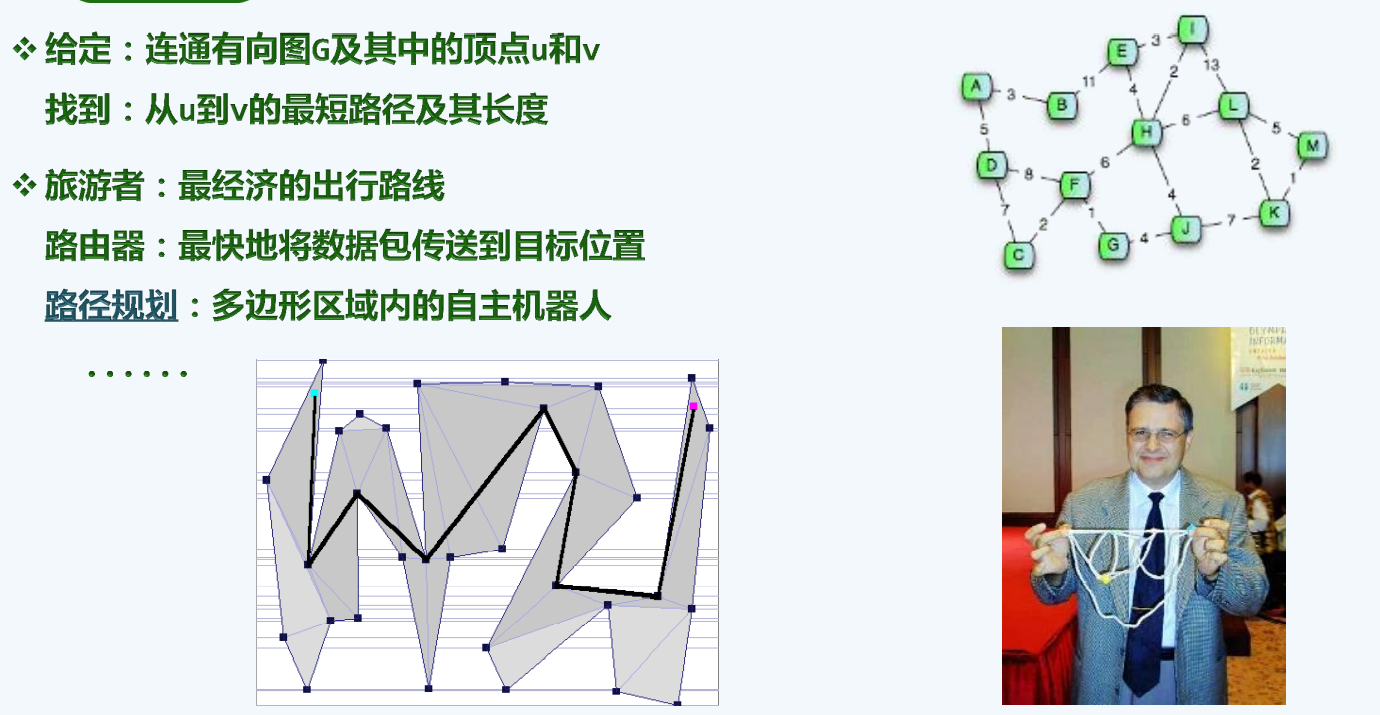
Humble Programmer

image-20220303212818320

String Computer

其实，最短路问题，如果我们能造一个绳子计算机的话,,,,,,,

image-20220303212941225

Insight

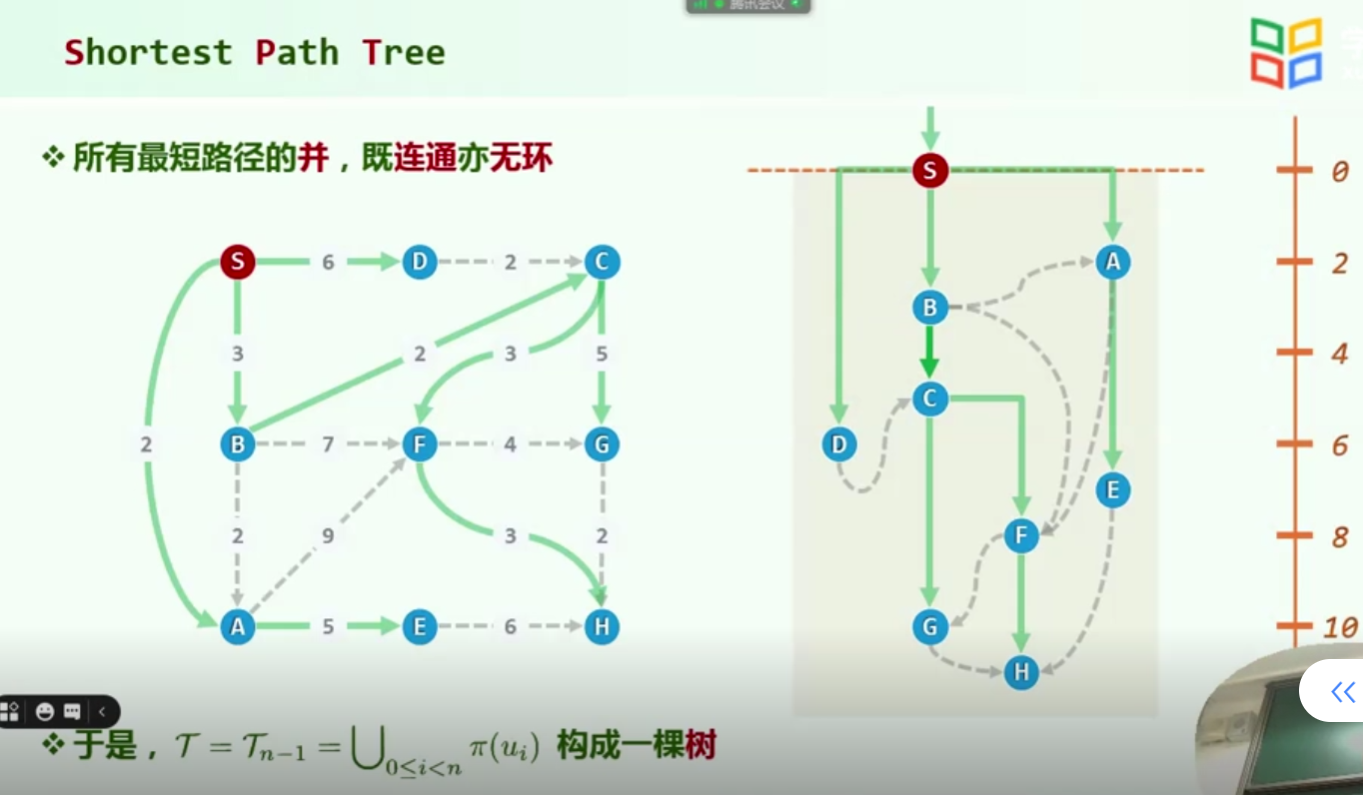
image-20220303213542691

n - 1条边没有回路，最短路支撑树，理解的过程，软的，刚性的网，拉住S，匀速的，让这个网，离开桌面，而离开桌面的时间就是最短路距离的一个精确度量，而我们要做的事情，就是去模拟这个过程

过程推导–> 如果有k个点已经离开了桌面，那么第K+1个，又应该如何呢？(简而治之)

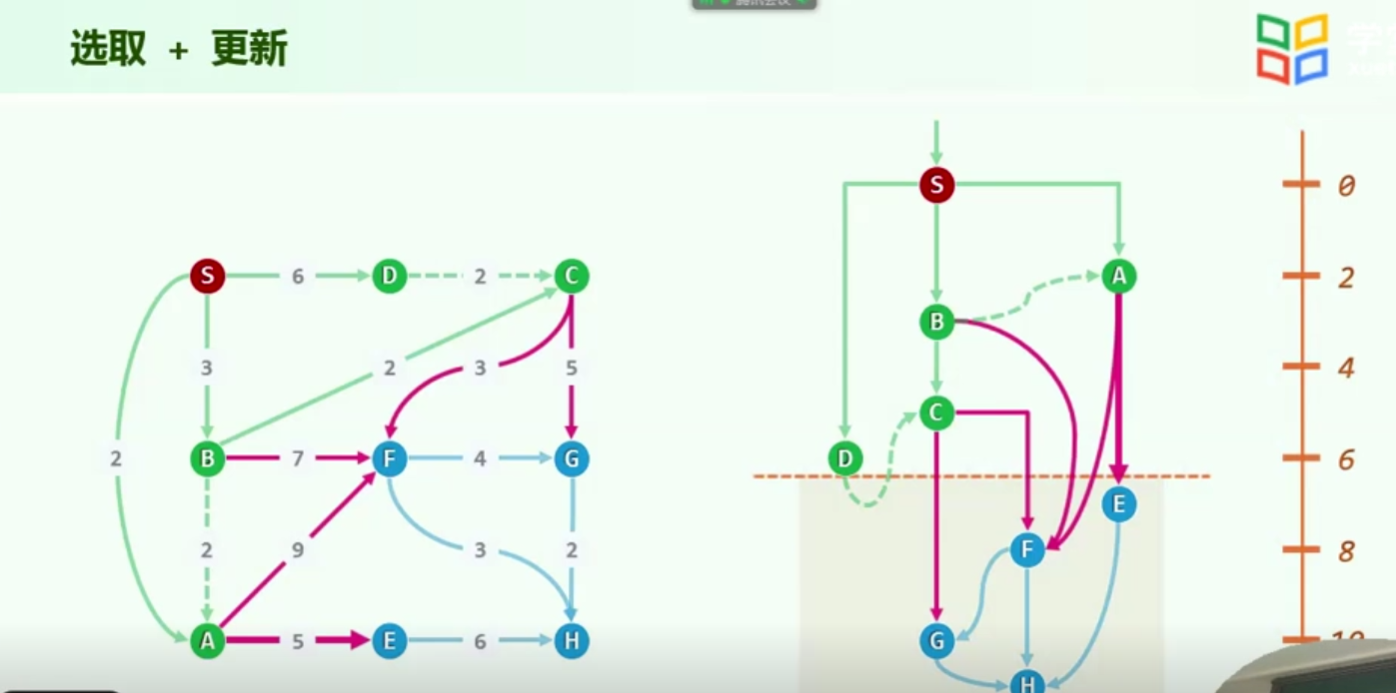
image-20220303214524431

每一个人再拉起来之前，都可能收到它朋友的offer，它可以选择采纳，也可以选择不采纳（不止一个朋友）拉起来之后，都会再继续向它的还没有起来的朋友，提供offer，延续前人们的传统，而判断是否接受谁的offer，就是看它朋友给他提供的优先级，加上他们之间的边的优先级，谁的更好，就选谁的

更新器-kstra

image-20220303215130894

Parent

科学，人文，人生，一定要区分开，计算机是追求功利，追求极致的效率，而人生未必如此

Prim

引入(MST)

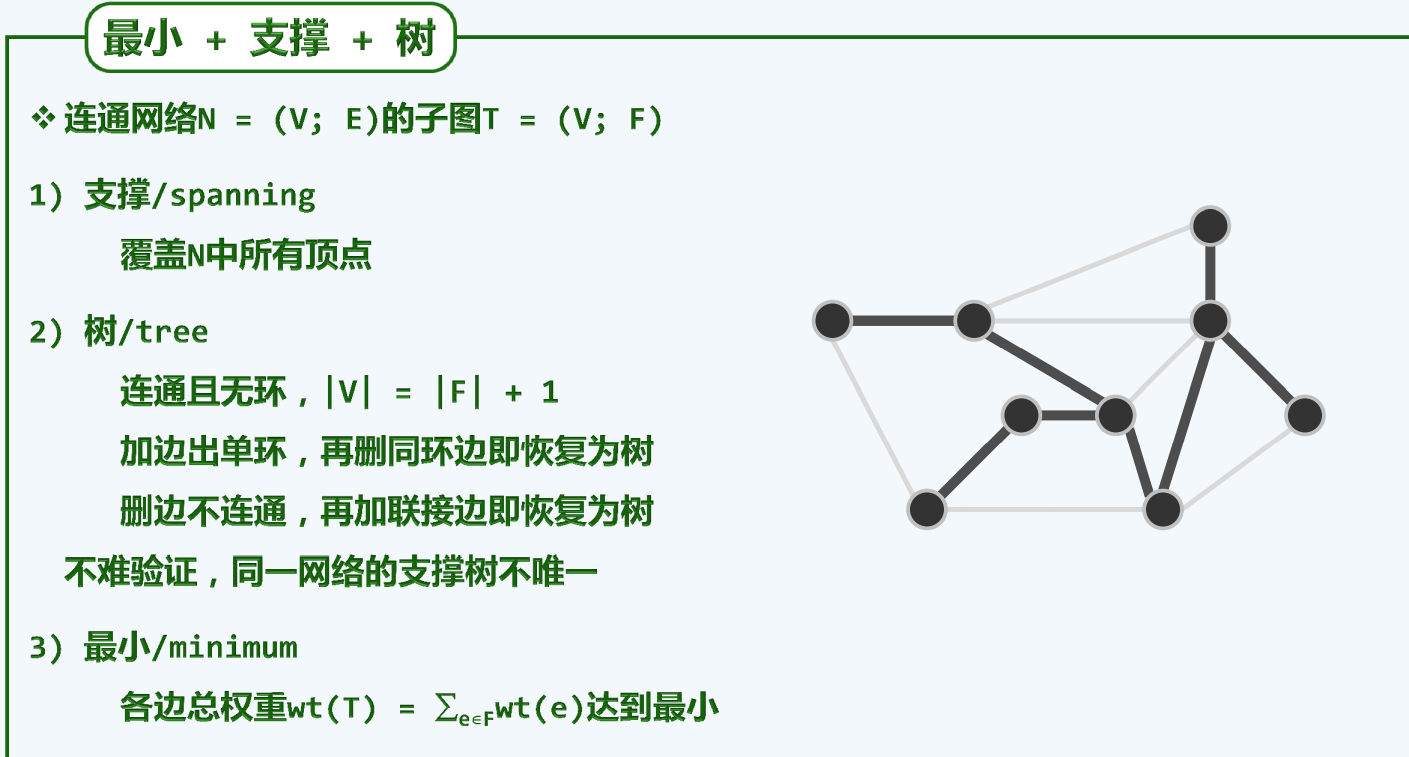
image-20220303215421435

从一个点，连到很多个点，最小生成树

任何一种网络何尝不是这样

应用

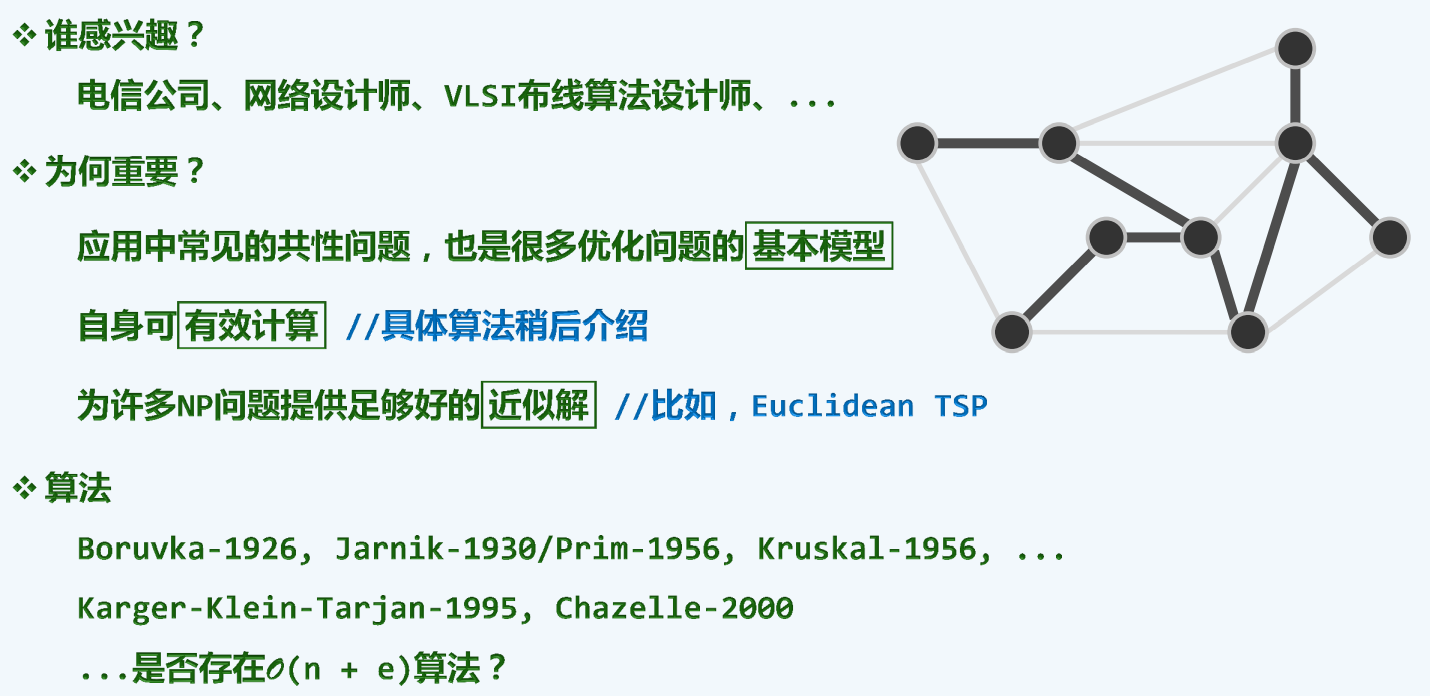
image-20220303215546300

算法实用性

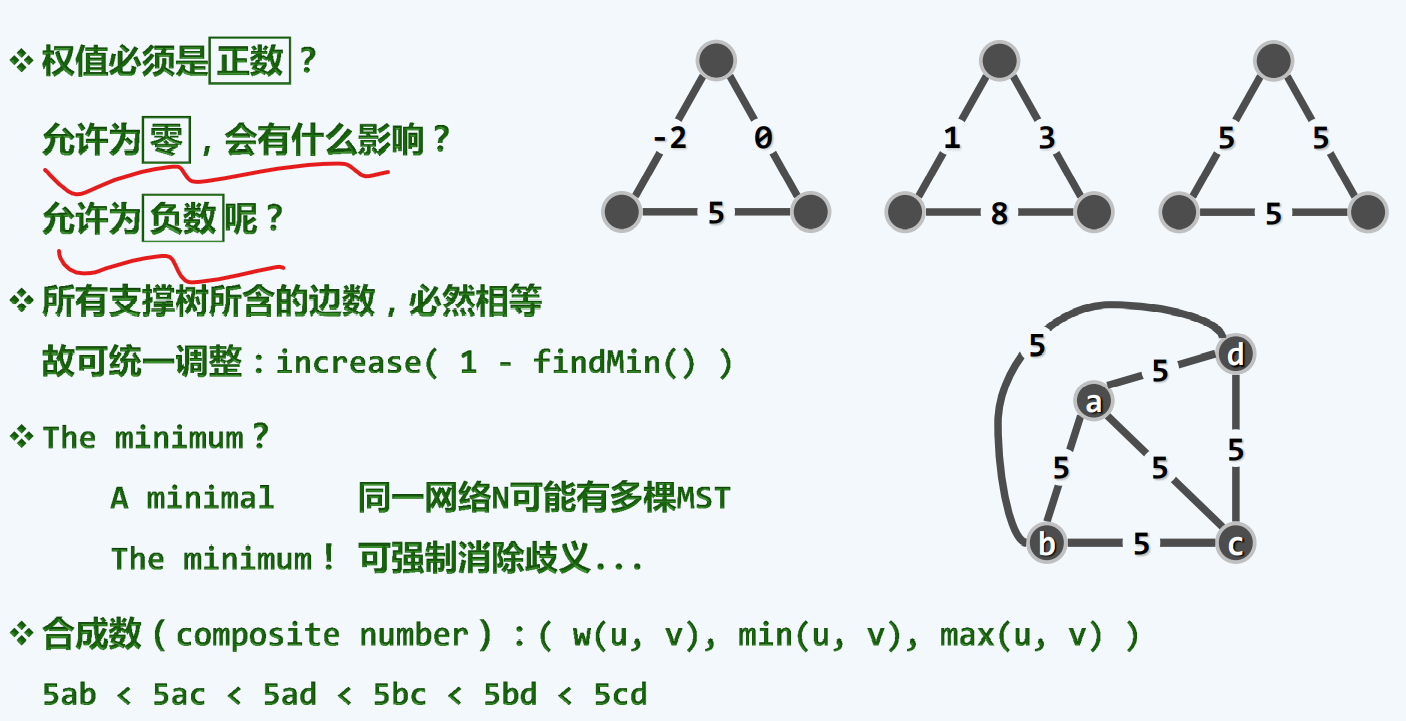
image-20220303215642346

不怕负数，是总体来算的，即便有负边，也一定有最小的负数，那我们可以给他们全部加上这个数，然后全部变成正的，当你运算结束后，再减回去就是

​ 不过，如果有重边，可能会出现多种最小生成方案 所以，实际意义上可以说是minimal而不是minimum

证明

cut只是对顶点集随便的分一下，此/彼 子集/补集

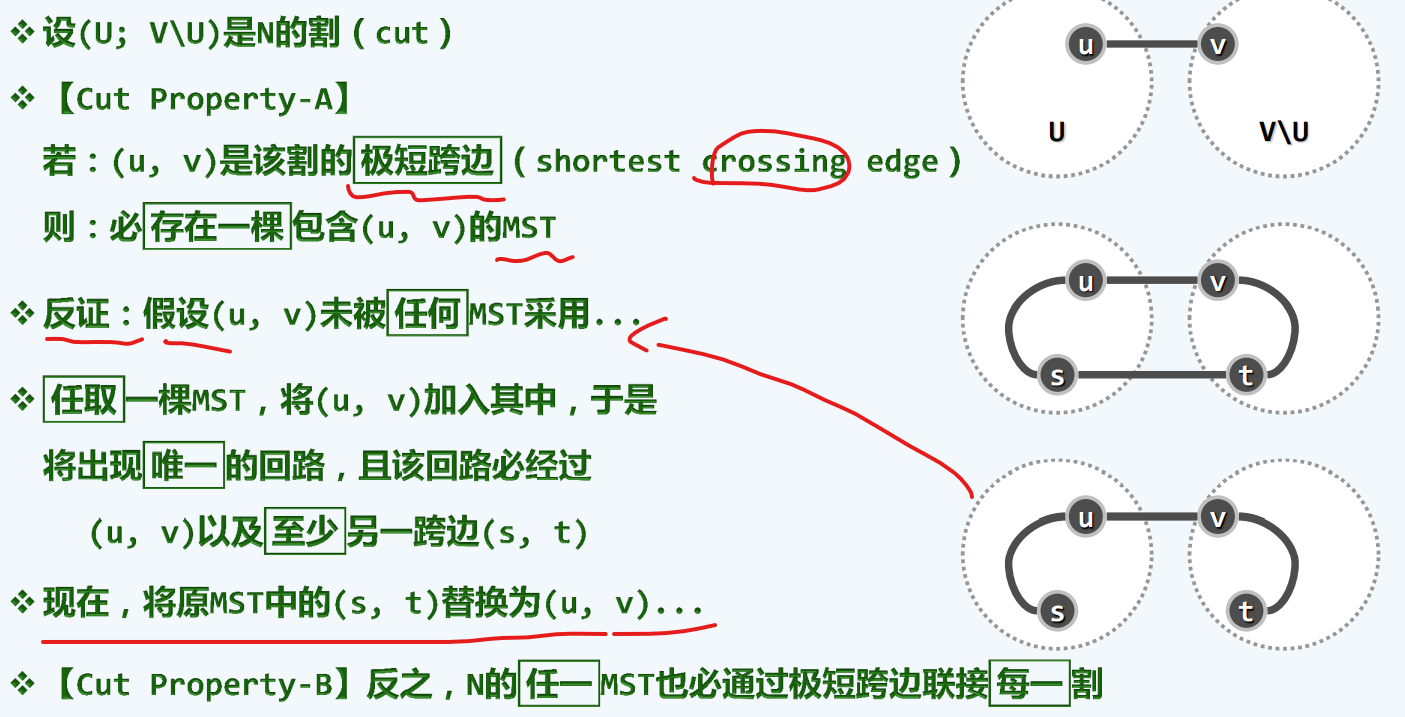
image-20220303220158605

增加矛盾

image-20220303220317556

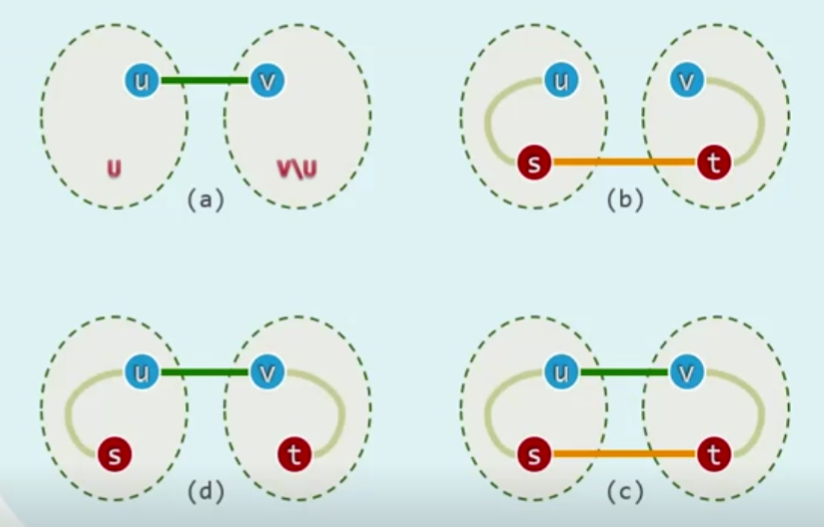
image-20220303220406274

证明不够严谨

s，u v，t可能是同一个点？

而且，MST隔断之后，未必只有一个跨边，可能会采用bridges

只用最短的就够了，可能同时我们会有更多的

算法

贪心的思想，每次吞进一个，找他们的跨边，找最短的跨边

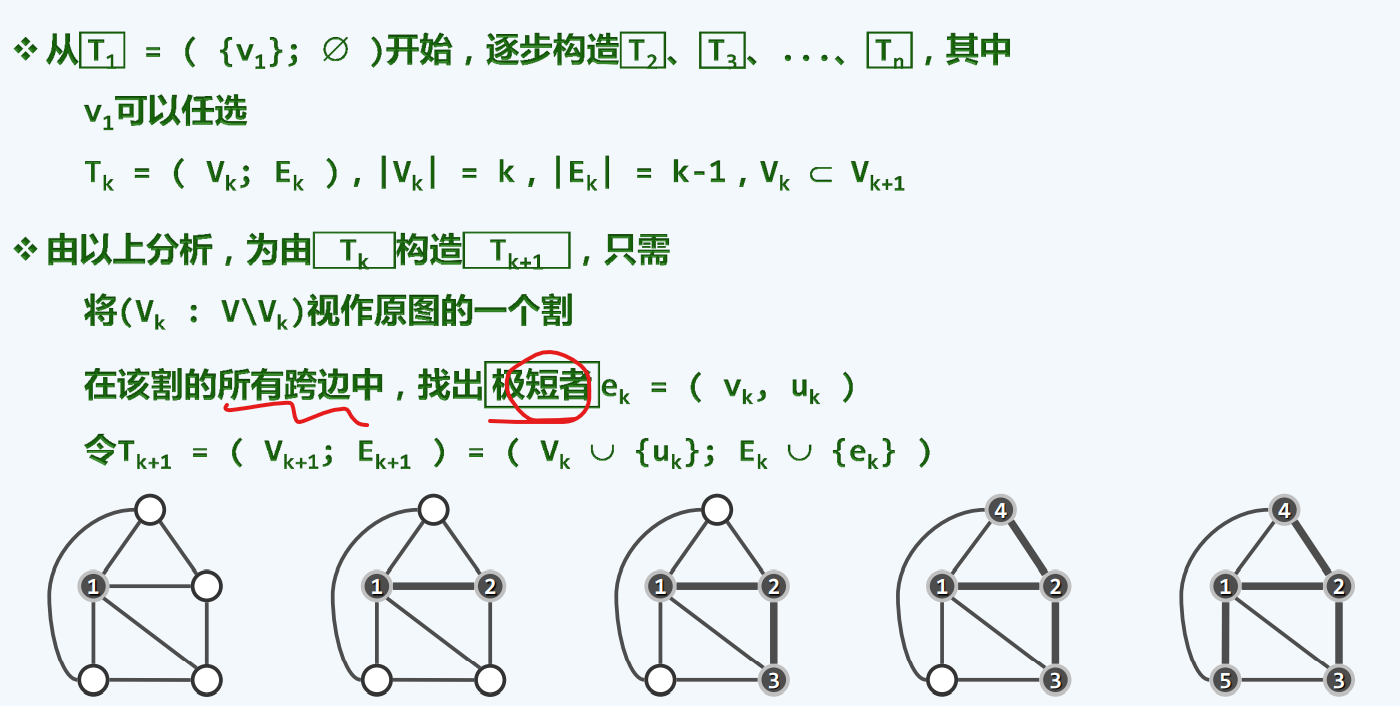
image-20220304130736269

image-20220304130902634

image-20220304131001350

Correctness

虽然说很幸运，这个算法算出来的是对的，没有漏洞，但是这种思想是有漏洞的，因为比如每一割，可能会产生几条最小权边，也就是最小生成树可能不止一颗，我们试想，比如四大美人，如果我们取每一个的五官中的一部分，组合在一起，那么最后真的一定是美人吗？这里也是一样，不同的最小权边，拼凑起来，还真不一定是最后的最小的，不过很幸运（再次）这里确实是对的！

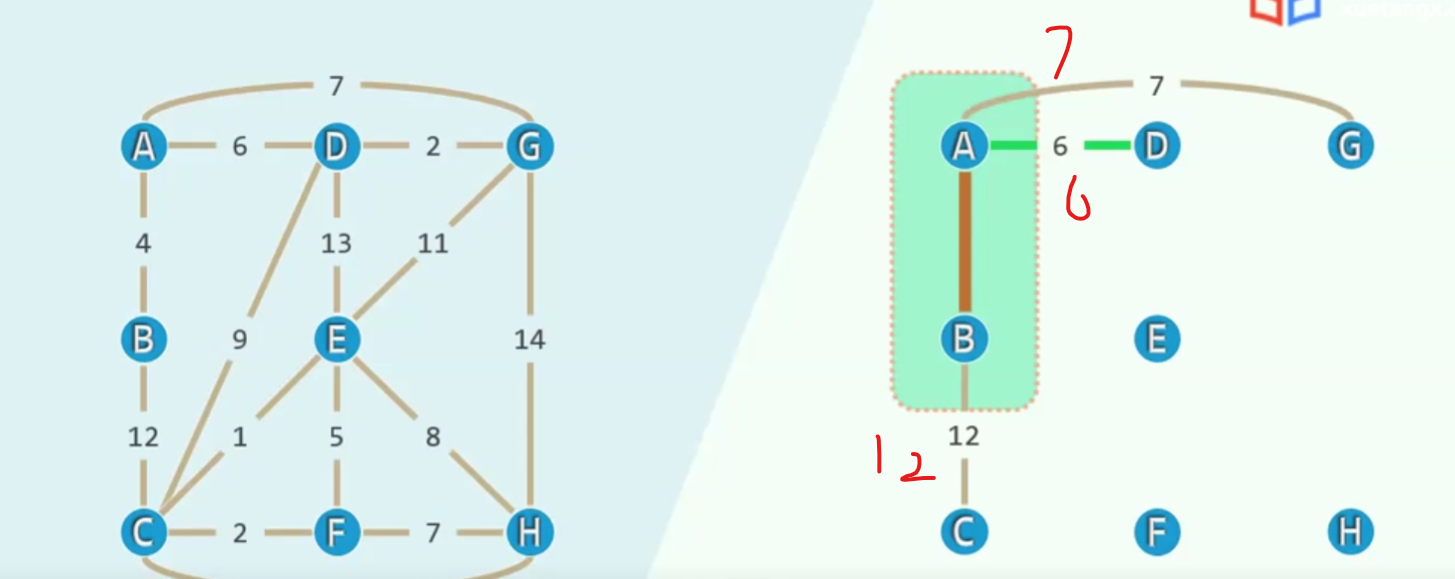
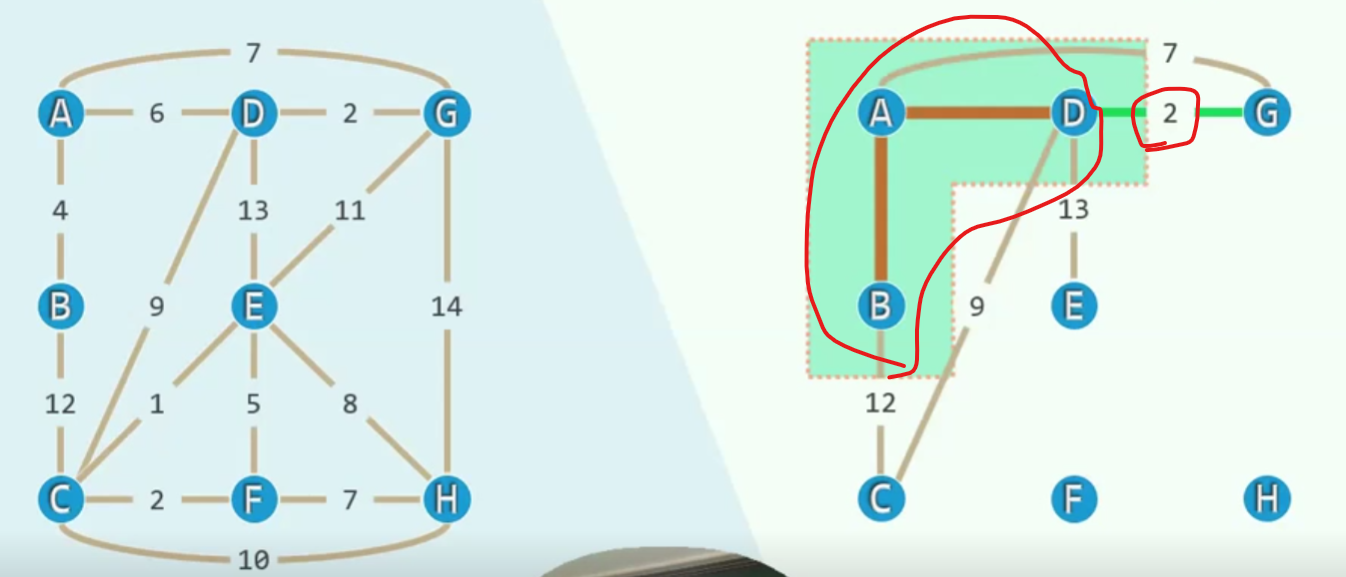
Priority = Distance

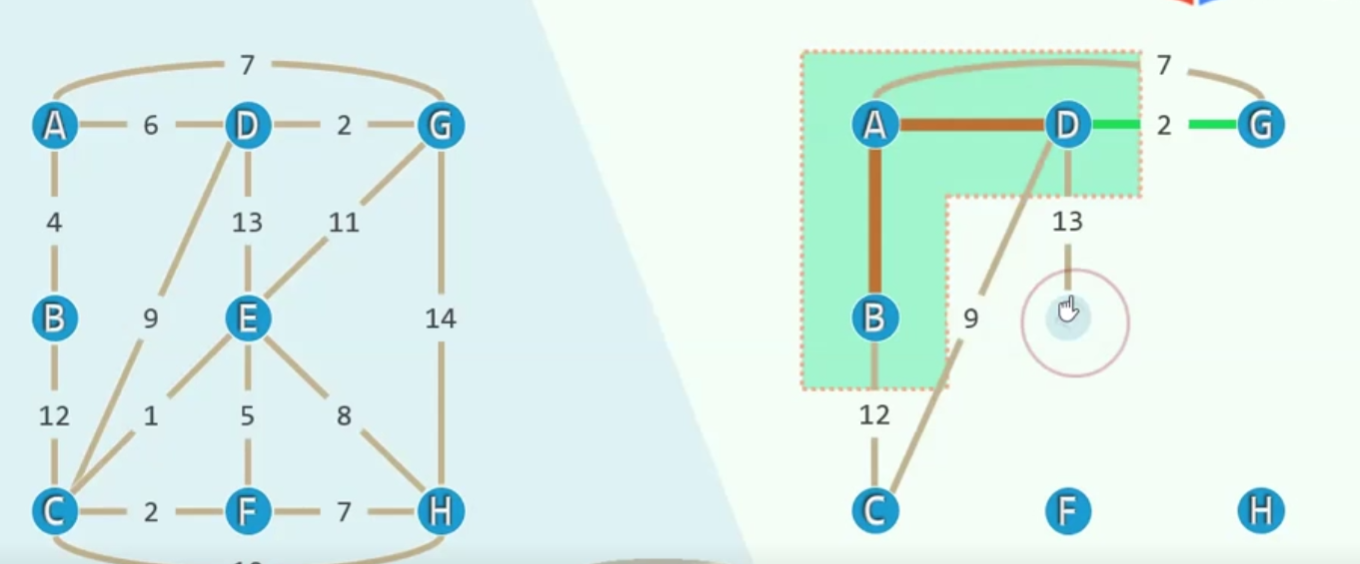
image-20220304132844777

对于E来说（鼠标位置）与其说那条边是13，不如说当前他的优先级是13（优先级在这里越小越好）对于G，它之前的优先级是7（之前还没有加入D）现在优先级变成了2

所以说，这个优先级是会变动的，欣然的更新

Implementation

更新器-prim

与kstra的差别仅仅一行半

重载括号（含这个传参列表的括号）

image-20220304133530596

代码–PFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
template <typename Tv, typename Te> template <typename PU> //优先级搜索（全图）
0002 void Graph<Tv, Te>::pfs ( Rank s, PU prioUpdater ) { //s < n
0003    reset(); Rank v = s; //初始化
0004    do //逐一检查所有顶点
0005       if ( UNDISCOVERED == status ( v ) ) //一旦遇到尚未发现的顶点
0006          PFS ( v, prioUpdater ); //即从该顶点出发启动一次PFS
0007    while ( s != ( v = ( ( v+1 ) % n ) ) ); //按序号检查，故不漏不重
0008 }
0009 
0010 template <typename Tv, typename Te> template <typename PU> //顶点类型、边类型、优先级更新器
0011 void Graph<Tv, Te>::PFS ( Rank s, PU prioUpdater ) { //优先级搜索（单个连通域）
0012    priority ( s ) = 0; status ( s ) = VISITED; parent ( s ) = -1; //初始化，起点s加至PFS树中
0013    while ( 1 ) { //将下一顶点和边加至PFS树中
0014       for ( Rank w = firstNbr ( s ); -1 < w; w = nextNbr ( s, w ) ) //枚举s的所有邻居w
0015          prioUpdater ( this, s, w ); //更新顶点w的优先级及其父顶点
0016       for ( int shortest = INT_MAX, w = 0; w < n; w++ )
0017          if ( UNDISCOVERED == status ( w ) ) //从尚未加入遍历树的顶点中
0018             if ( shortest > priority ( w ) ) //选出下一个
0019                { shortest = priority ( w ); s = w; } //优先级最高的顶点s
0020       if ( VISITED == status ( s ) ) break; //直至所有顶点均已加入
0021       status ( s ) = VISITED; type ( parent ( s ), s ) = TREE; //将s及与其父的联边加入遍历树
0022    }
0023 } //通过定义具体的优先级更新策略prioUpdater，即可实现不同的算法功能