以下笔记为jjyaoao本人制作，欢迎借鉴学习和提出相关建议，转载需要标明出处www.jjyaoao.space

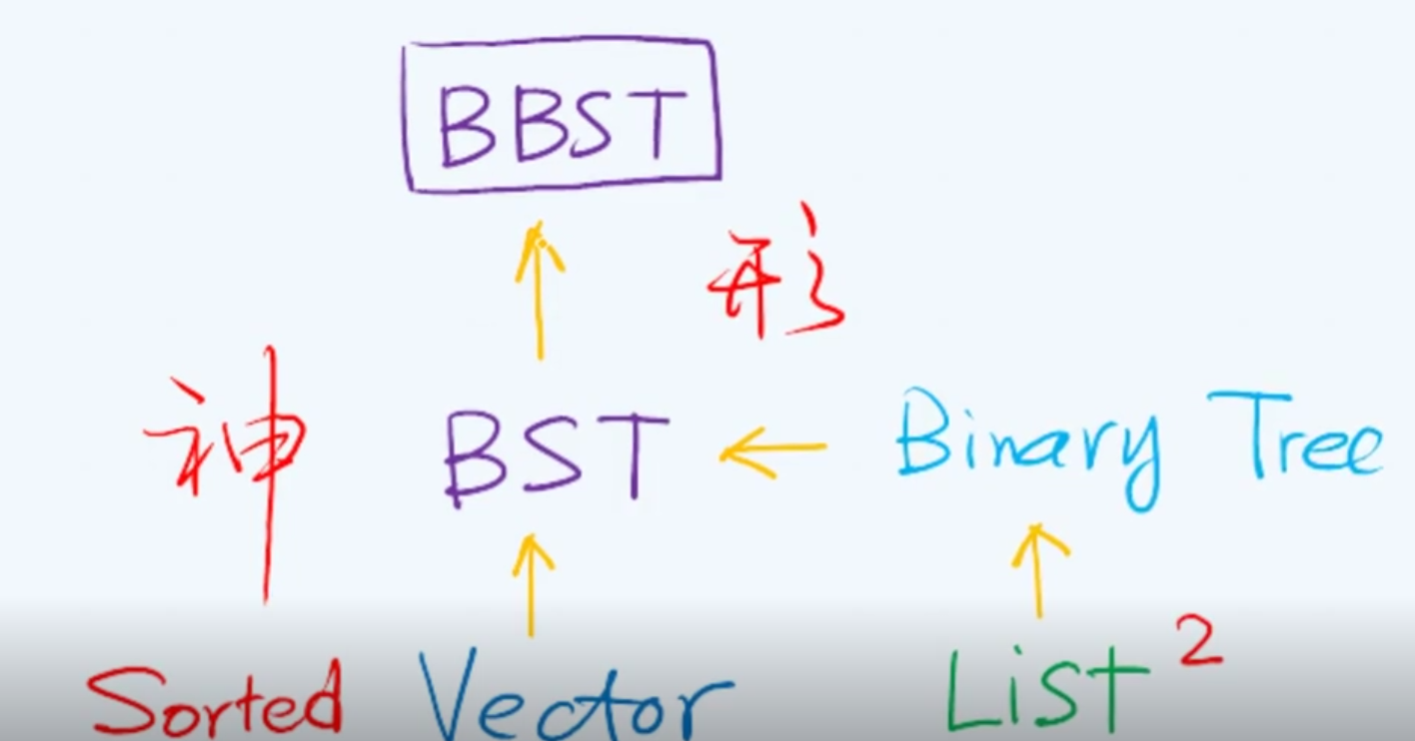
二叉搜索树

寻关键码访问

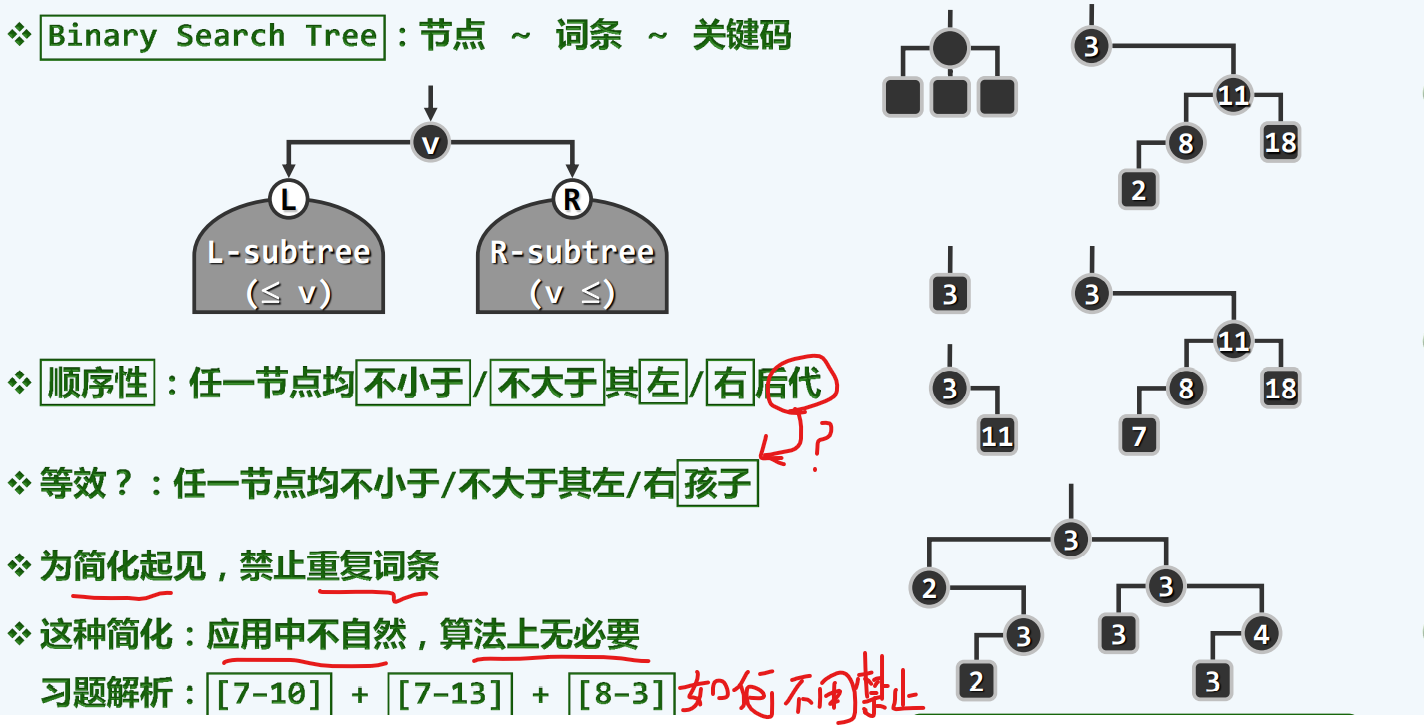
有序性

为了简单而言节点 = 词条 = 关键码

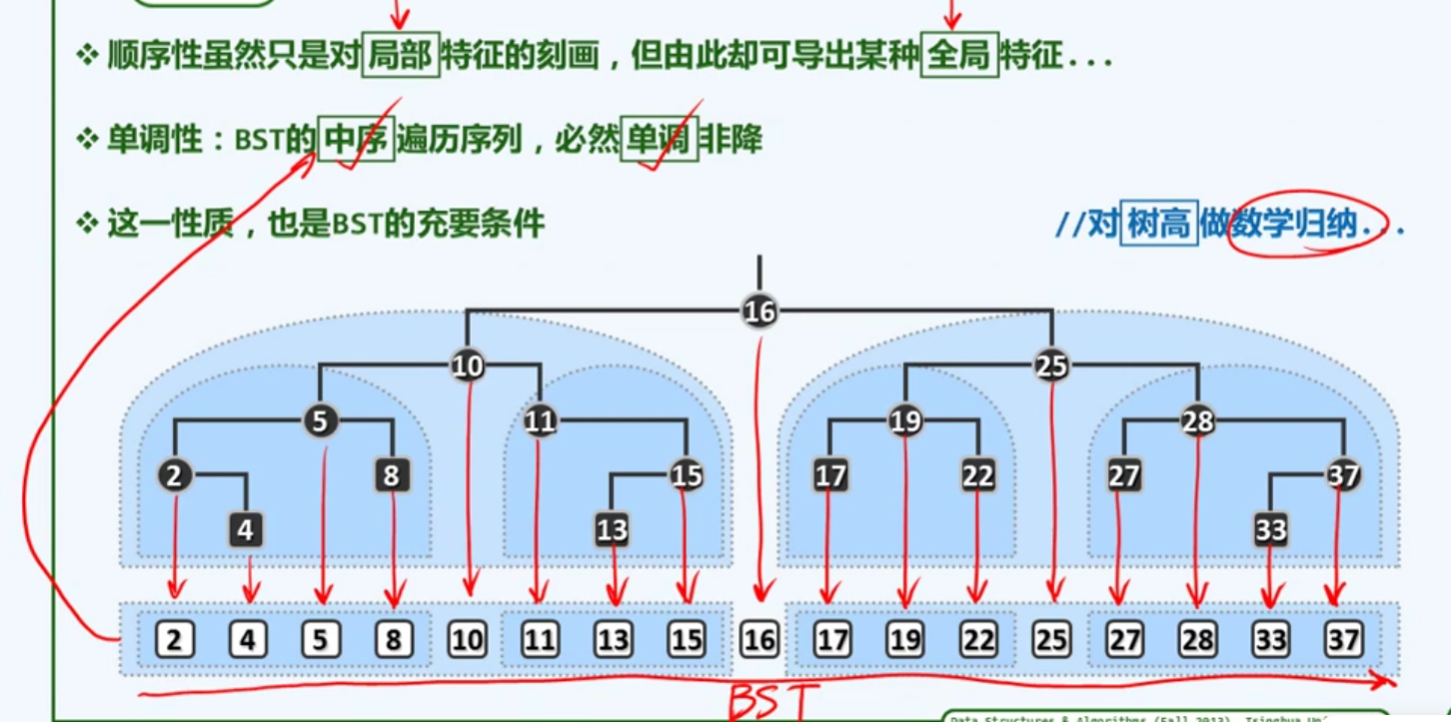
单调性

在微观上处处满足顺序性，宏观上每一个的垂直投影，满足单调性

ADT

查找

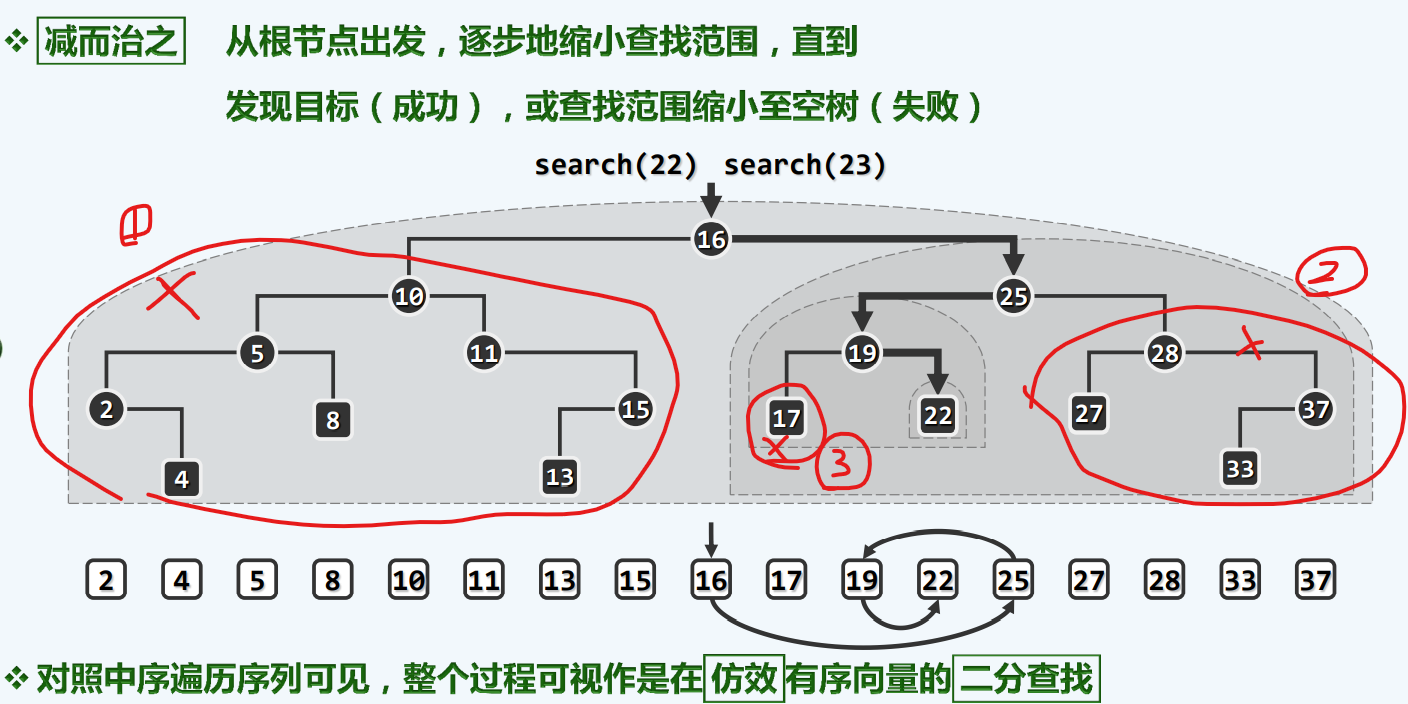
可以看到，和二分查找过程相仿

template <typename T> BinNodePosi<T> & BST<T>::search ( const T & e ) { //在BST中查找关键码e
0010    if ( !_root || e == _root->data ) { _hot = NULL; return _root; } //空树，或恰在树根命中
0011    for ( _hot = _root; ; ) { //否则，自顶而下
0012       BinNodePosi<T> & v = ( e < _hot->data ) ? _hot->lc : _hot->rc; //确定方向，深入一层
0013       if ( !v || e == v->data ) return v; _hot = v; //一旦命中或抵达叶子，随即返回
0014    } //返回目标节点位置的引用，以便后续插入、删除操作
0015 } //无论命中或失败，_hot均指向v之父亲（v是根时，hot为NULL）

*两种表现形式*，下面一种更易理解

每运行一次，下降一层

hot会记下此前访问过的非空节点，总体而言，hot最终将会指向谁呢？

我们引入一个假想的哨兵（上图右边的e），它的位置在我们树的叶节点的下一位，我们可以看到，如果我们引入之后，这个BST仍然是合法的，更重要的是，它让我们的hot语义变得完整起来，也就是，无论如何，hot总是能指向命中节点的父亲。

插入

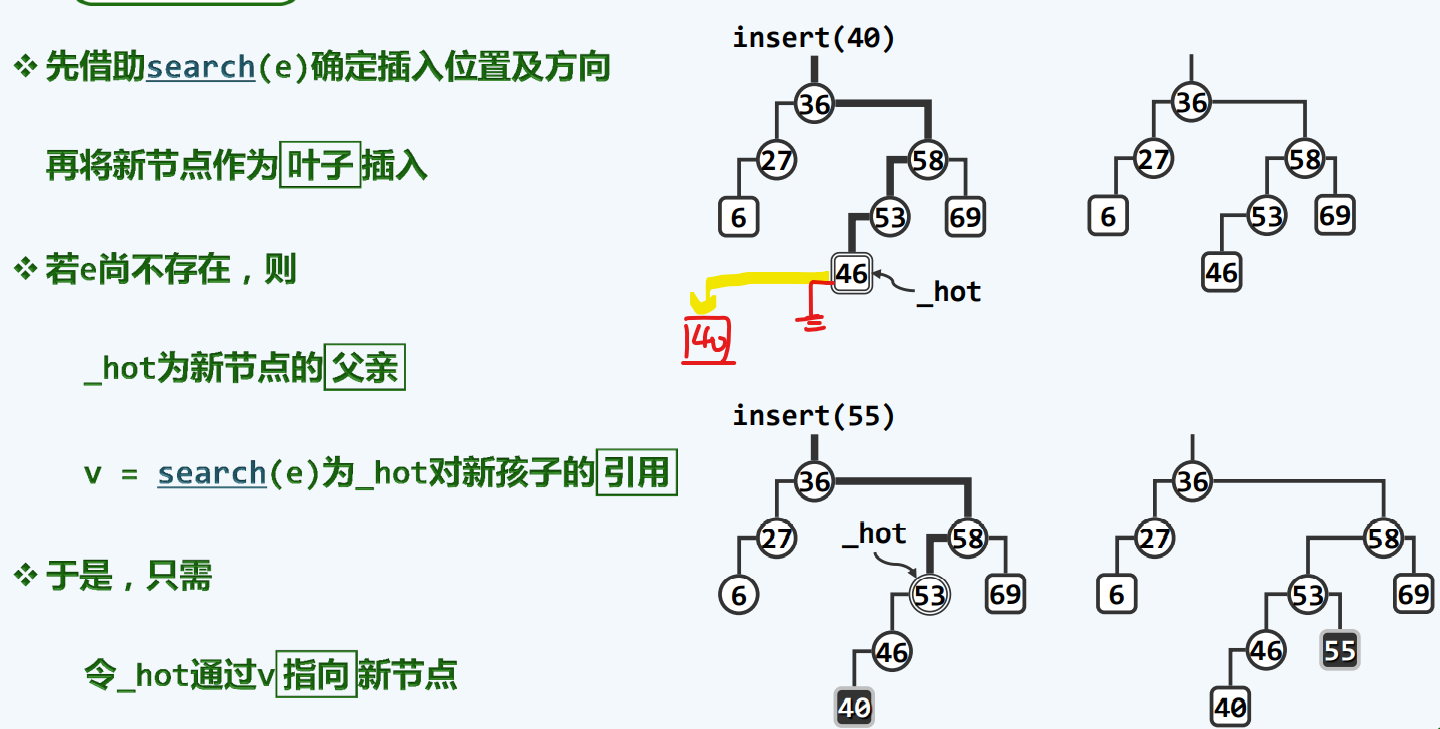
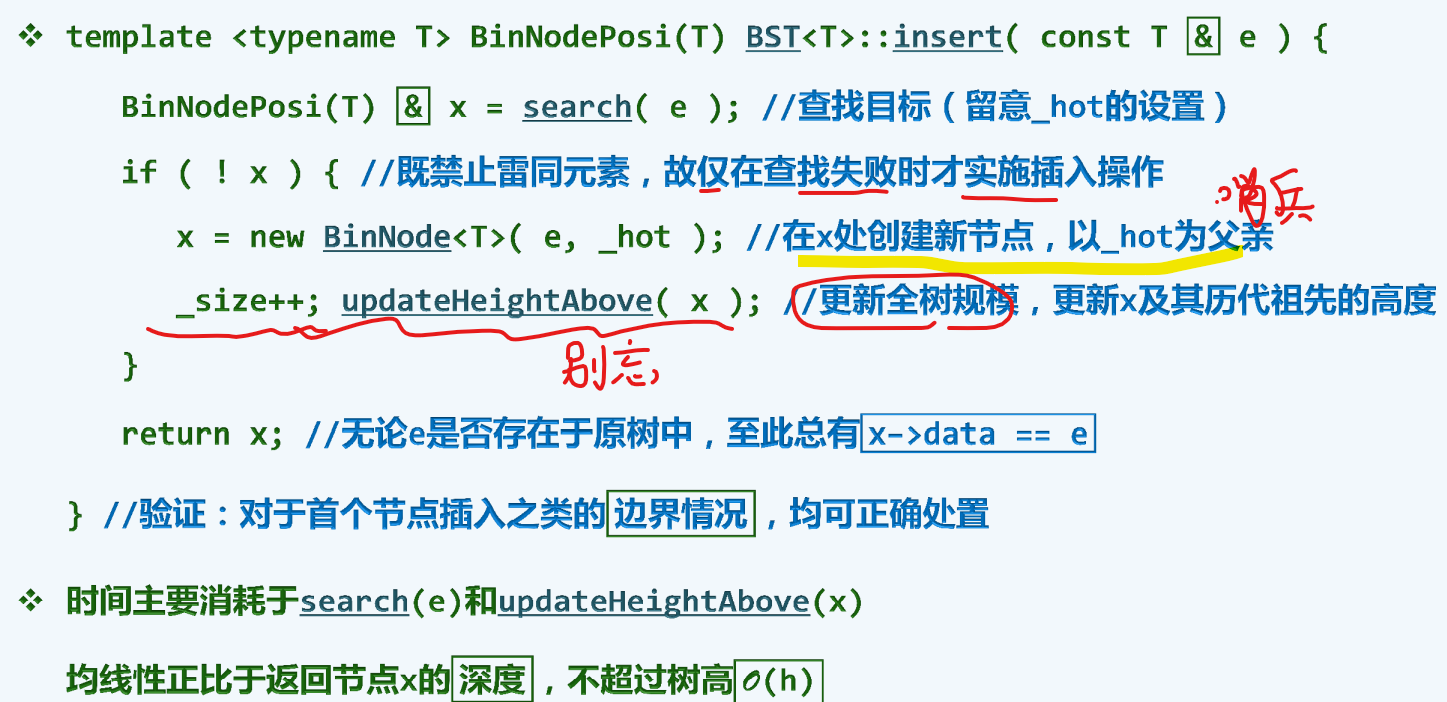
删除

if x 不存在那么退出删除和插入正好对称，接下来的问题是removeAt可能需要处理哪几种情况，各种情况又当如何应对呢

单分支删除

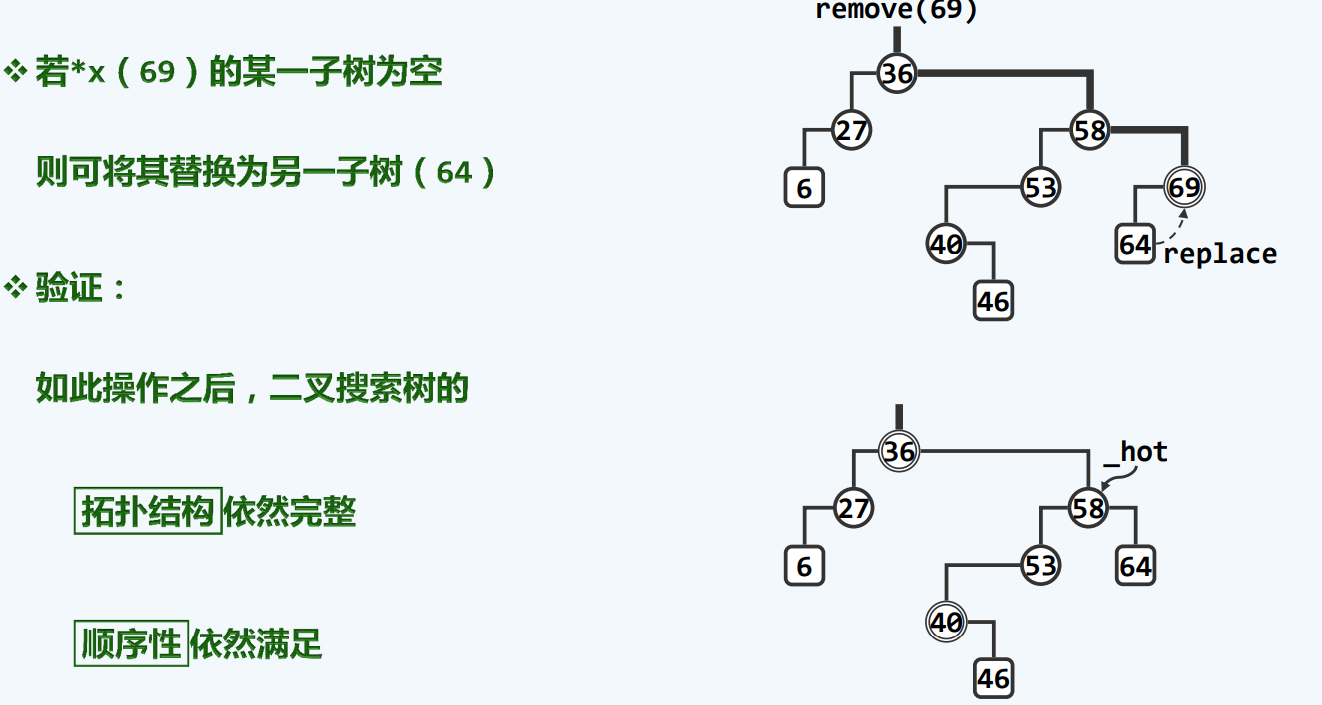
实现

双分支删除

化繁为简！

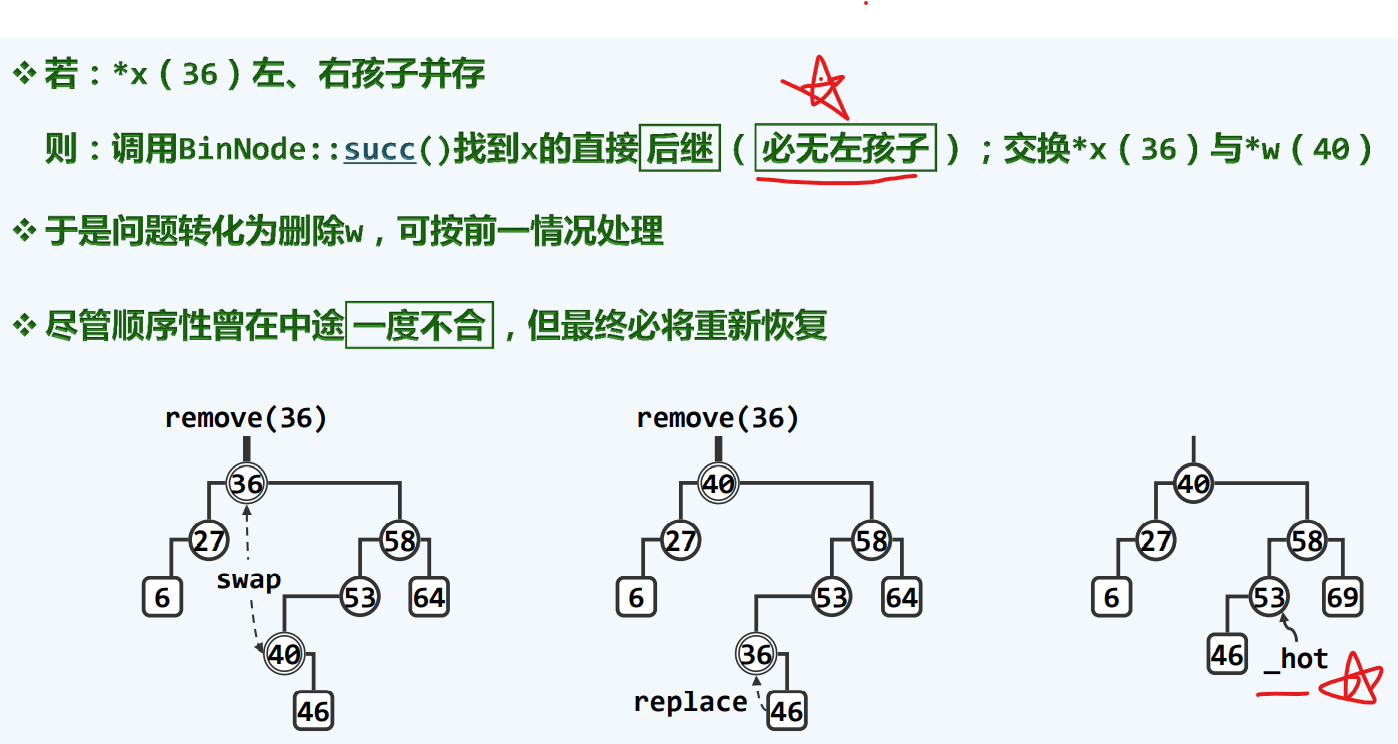
必无左孩子（因为直接后继一定是右孩子的最左边的左子代

需要说明的是，hot需要在删除完节点后更新为刚刚被实际删除节点的父亲节点，并且向上遍历，因为有可能祖先的高度会发生变化（因为后代的删除）

实现

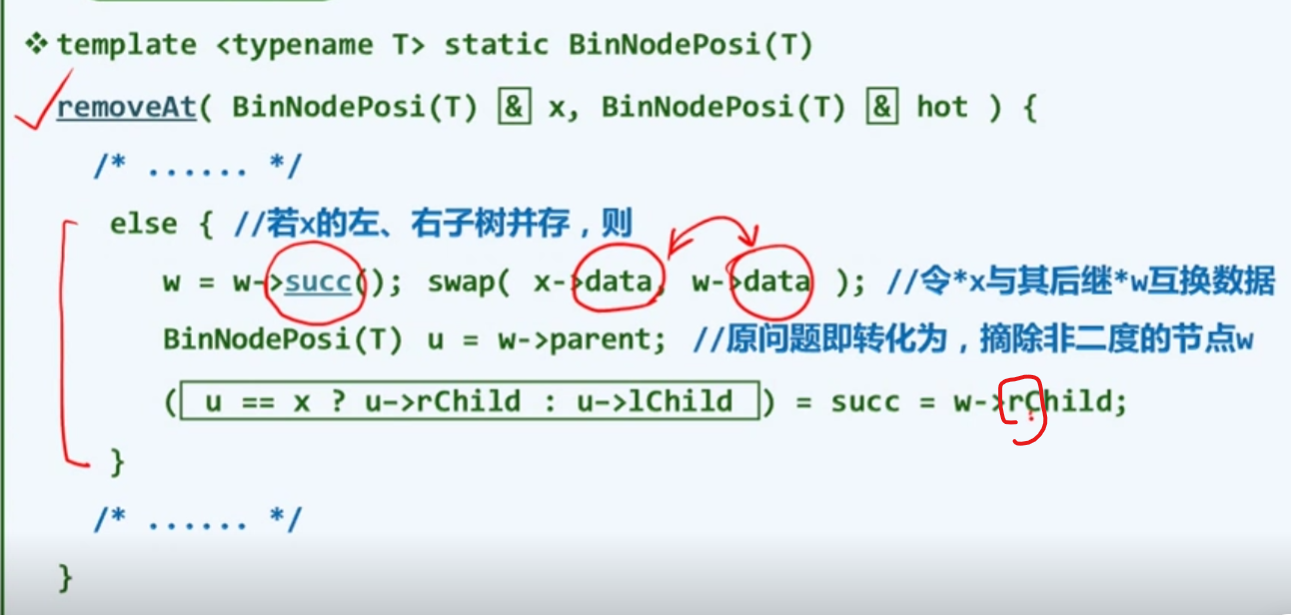
首先找到待删除节点的直接后继，令他和待删除节点交换，等效的将待删除的节点转移到新的位置，并且至多只有一个分支，当然，这个节点一定只有右孩子（或者没有孩子

我们现在只需要在他和祖父之间正确的完成一次双向连接

w为待删除数据，x为它的直接后继

后面那一句三元即为桥梁，将w在这个BST树里剔除掉

SUCC()

template <typename T> BinNodePosi<T> BinNode<T>::succ() { //定位节点v的直接后继
0002    BinNodePosi<T> s = this; //记录后继的临时变量
0003    if ( rc ) { //若有右孩子，则直接后继必在右子树中，具体地就是
0004       s = rc; //右子树中
0005       while ( HasLChild ( *s ) ) s = s->lc; //最靠左（最小）的节点
0006    } else { //否则，直接后继应是“将当前节点包含于其左子树中的最低祖先”，具体地就是
0007       while ( IsRChild ( *s ) ) s = s->parent; //逆向地沿右向分支，不断朝左上方移动
0008       s = s->parent; //最后再朝右上方移动一步，即抵达直接后继（如果存在）
0009    }
0010    return s;
0011 }

removeAt ()

template <typename T>
0007 static BinNodePosi<T> removeAt ( BinNodePosi<T> & x, BinNodePosi<T> & hot ) {
0008    BinNodePosi<T> w = x; //实际被摘除的节点，初值同x
0009    BinNodePosi<T> succ = NULL; //实际被删除节点的接替者
0010    if ( !HasLChild ( *x ) ) //若*x的左子树为空，则可
0011       succ = x = x->rc; //直接将*x替换为其右子树
0012    else if ( !HasRChild ( *x ) ) //若右子树为空，则可
0013       succ = x = x->lc; //对称地处理——注意：此时succ != NULL
0014    else { //若左右子树均存在，则选择x的直接后继作为实际被摘除节点，为此需要
0015       w = w->succ(); //（在右子树中）找到*x的直接后继*w
0016       swap ( x->data, w->data ); //交换*x和*w的数据元素
0017       BinNodePosi<T> u = w->parent;
0018       ( ( u == x ) ? u->rc : u->lc ) = succ = w->rc; //隔离节点*w
0019    }
0020    hot = w->parent; //记录实际被删除节点的父亲
0021    if ( succ ) succ->parent = hot; //并将被删除节点的接替者与hot相联
0022    release ( w->data ); release ( w ); return succ; //释放被摘除节点，返回接替者
0023 } //release()负责释放复杂结构，与算法无直接关系，具体实现详见代码包

复杂度

我们观察，BST的删除操作，所需要的时间主要来源于更新祖先高度，和找到直接后继，经过推理验证，不难得出，两者都不会超过O(h)的复杂度，因此，删除算法和插入一样，都是O(h)的复杂度，

那么，这个结论，是好还是不够好呢？

我们将进行进一步探讨（后续

平衡与等价

极端退化

BST = List + Vector

平均高度

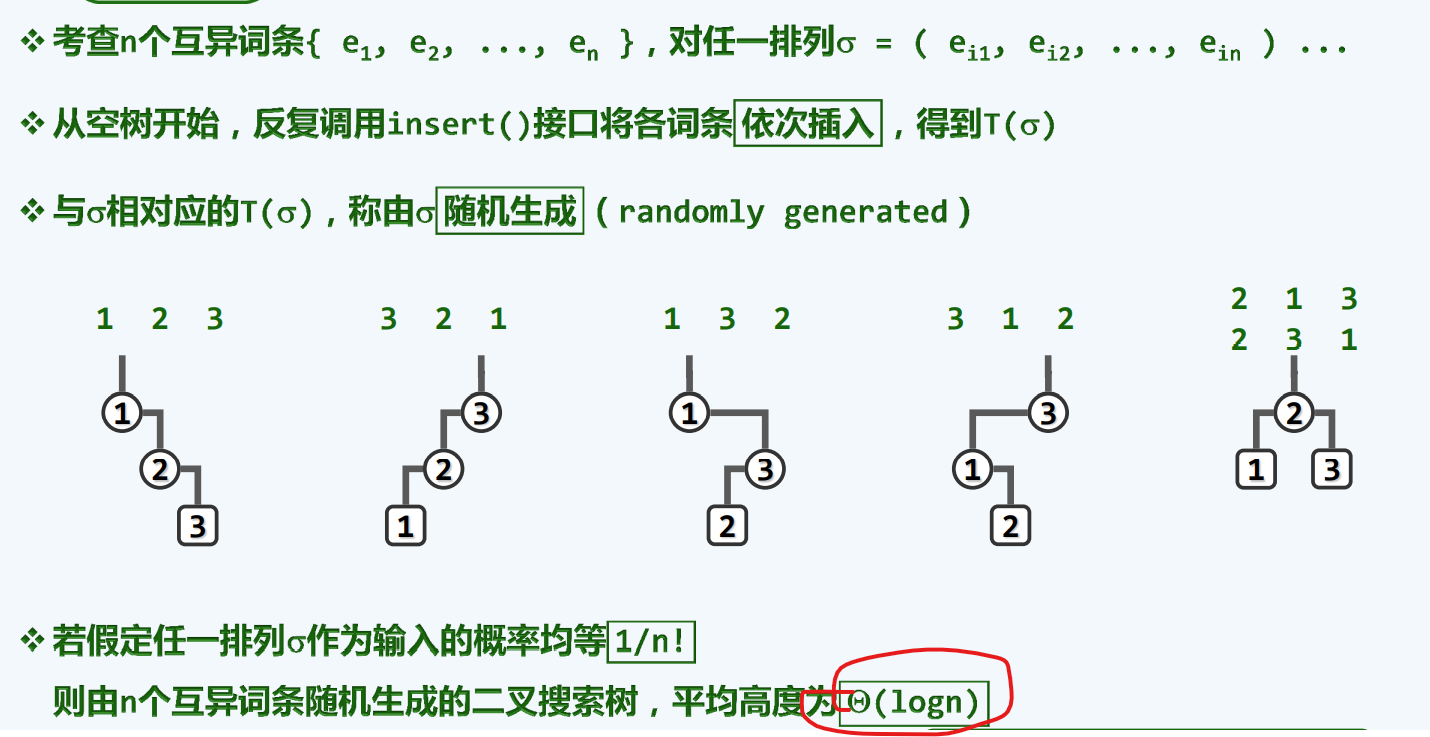
n！和卡特兰数，谁的统计更为准确呢？我们认为，是Catalan数，因为n！统计会有重复，因为在前一统计口径所得到的估算值，在高度更小的时候，会出现更多的重复（比如2 1 3 ，2 3 1）这也使得，重复在高度低的位置充作统计对象，这也是它为什么会统计的平均高度更小的原因

从这一观点来看，logn过于乐观了，根号n也许更加可信

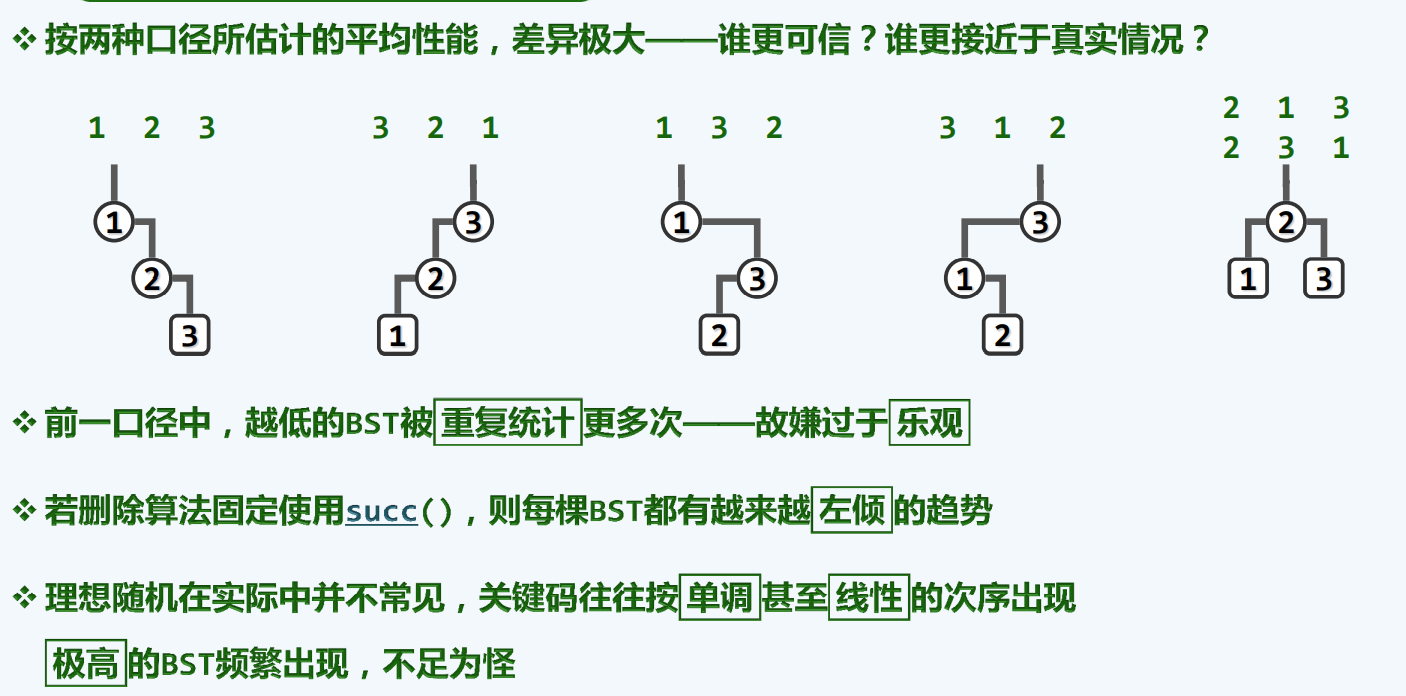
为了控制树高，我们也许应该做点什么，同时，我们也可以发现，我们需要采取一系列的技巧

理想+适度

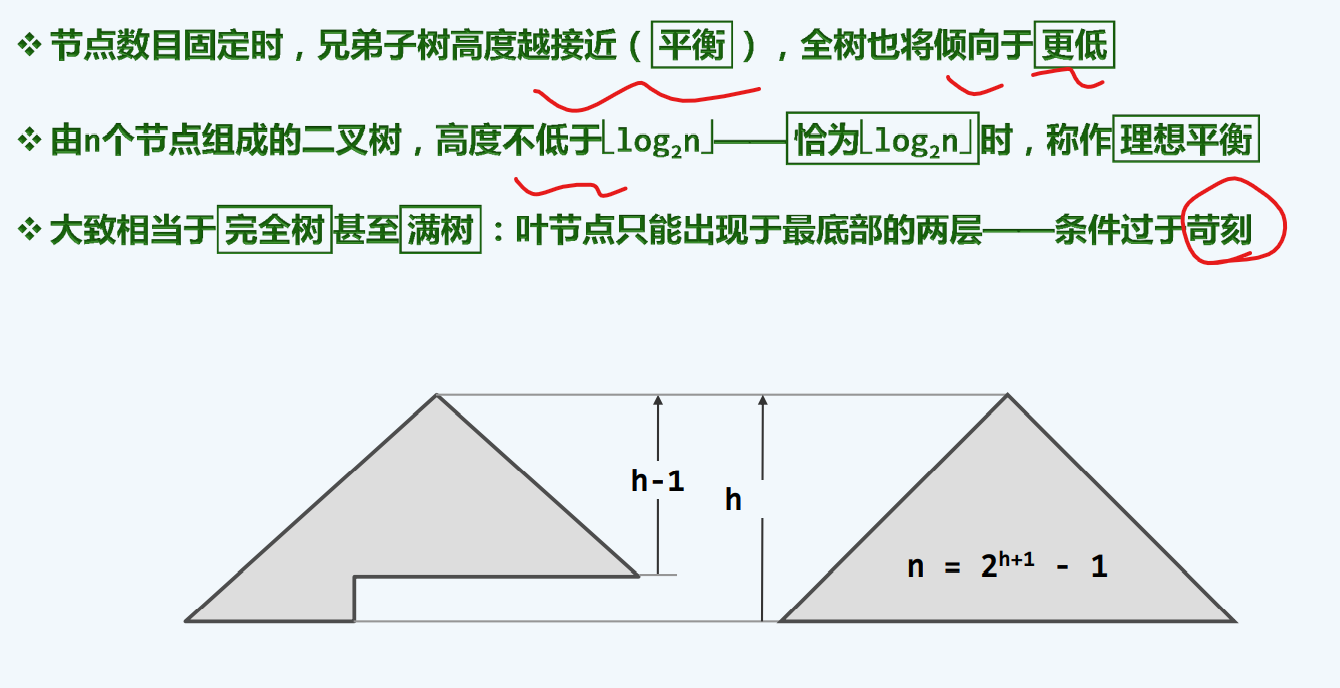
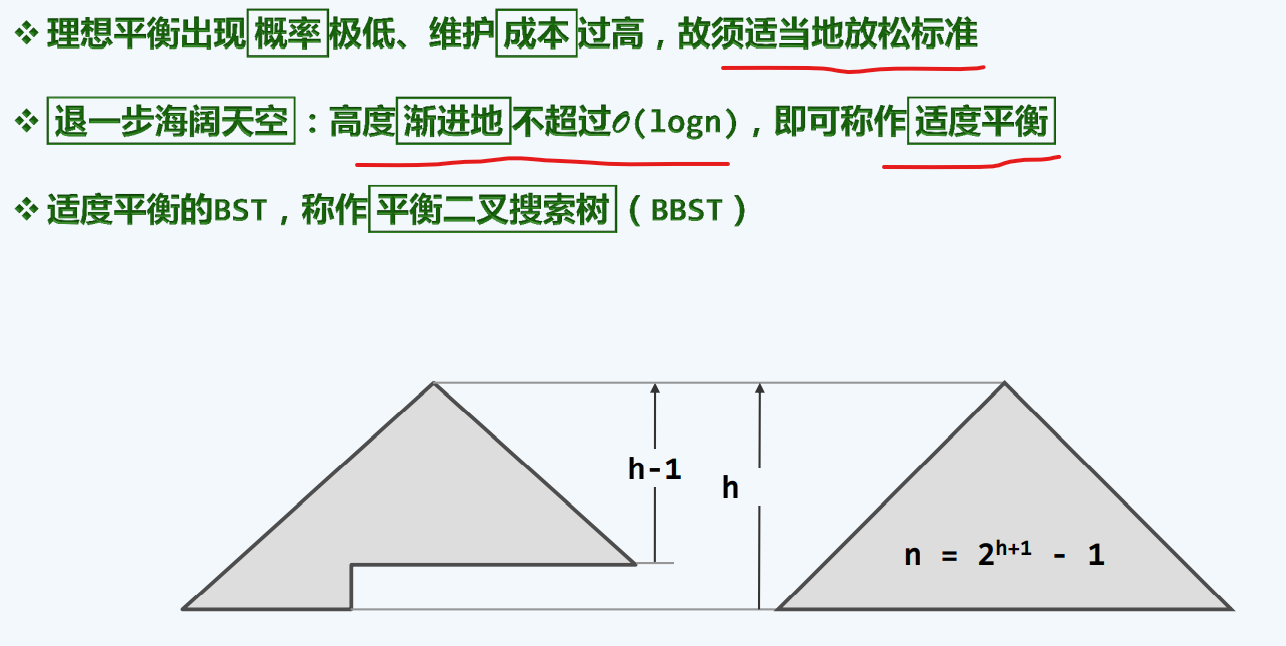
而这种适度平衡的树，我们就把他叫做 BBST

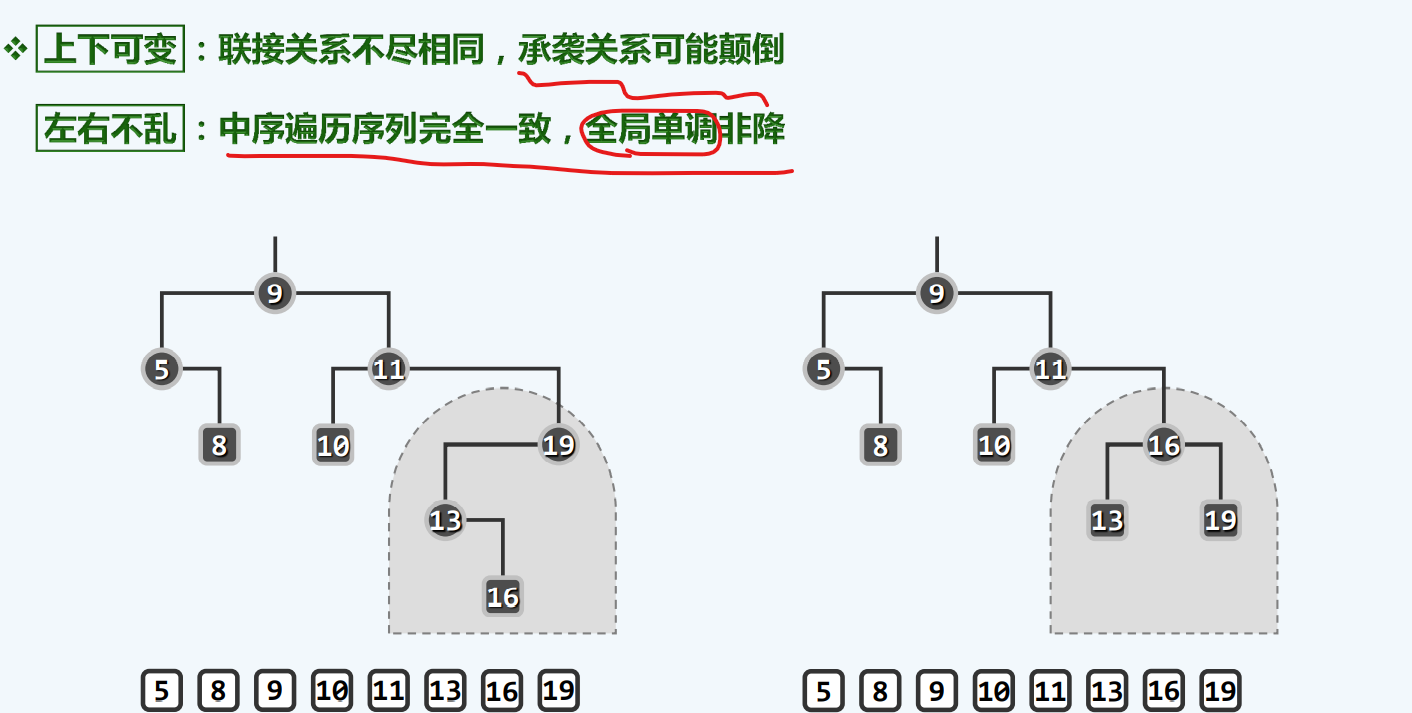
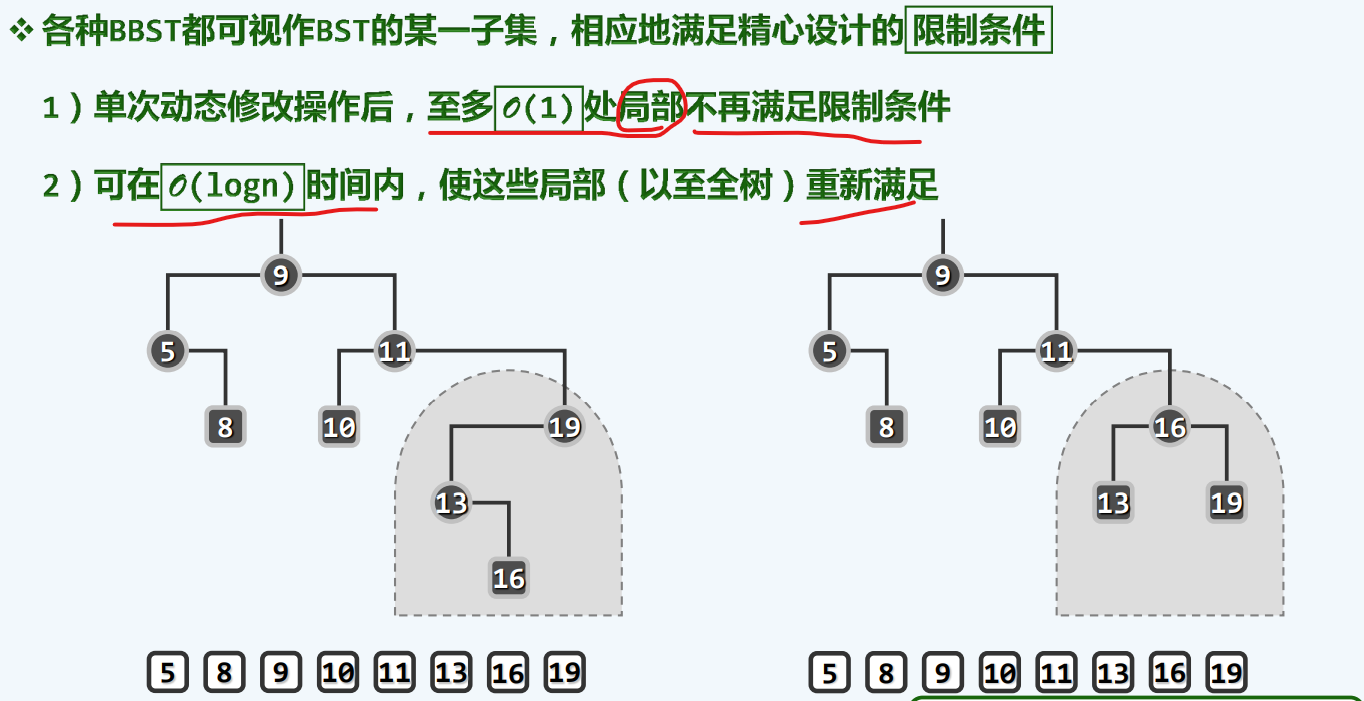
歧义=等价

全局上任然是BST

在微观上可以改变

AVL

了解就好，已经过时

平衡因子

balfac()

一种适度的平衡标准

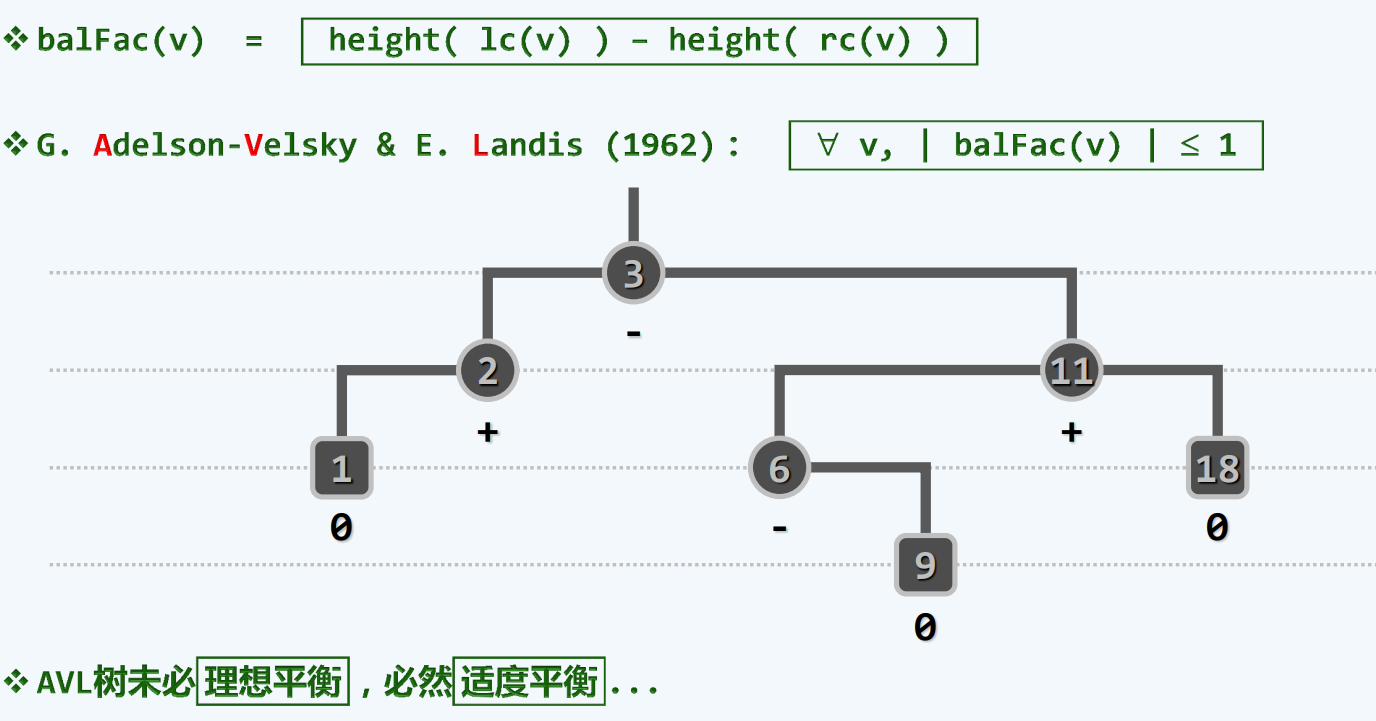
适度平衡

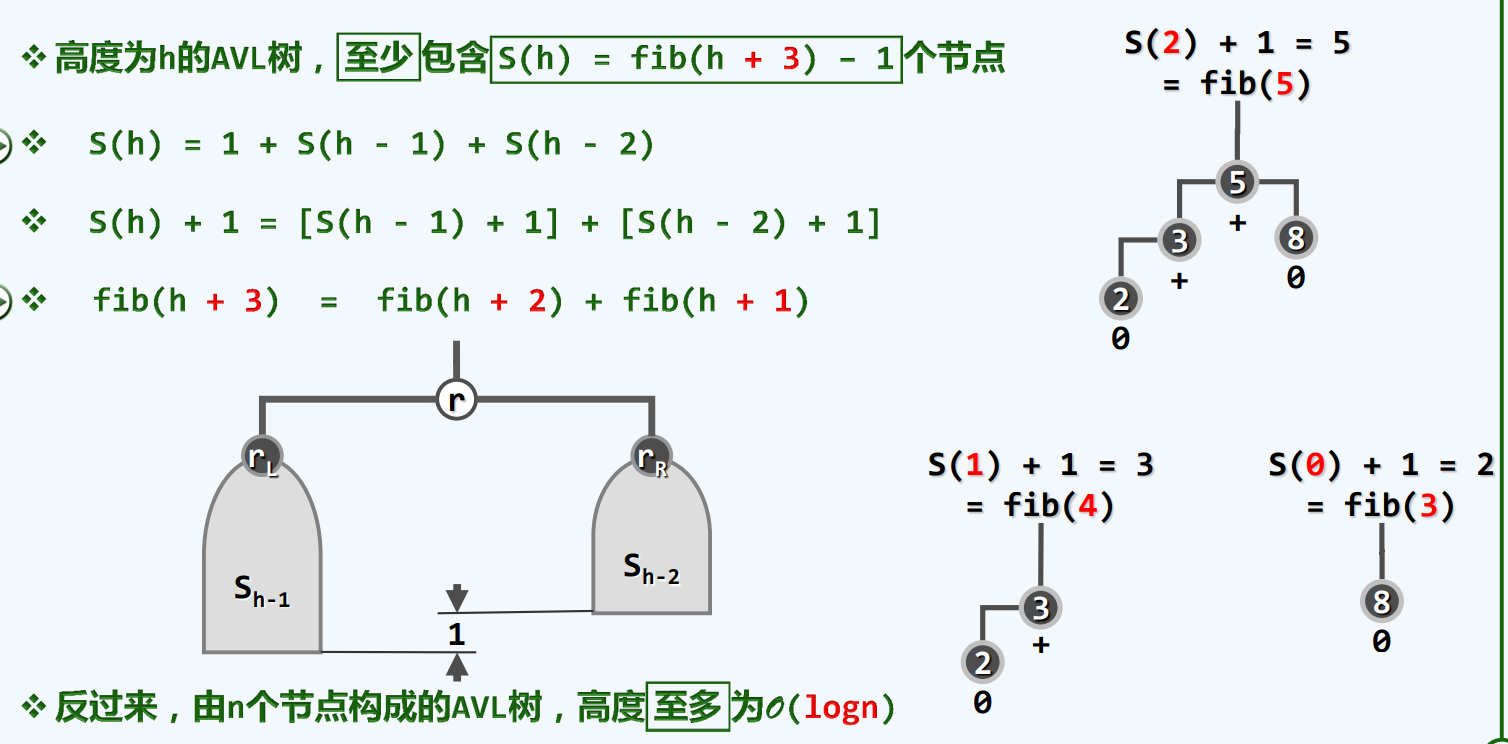
ADT

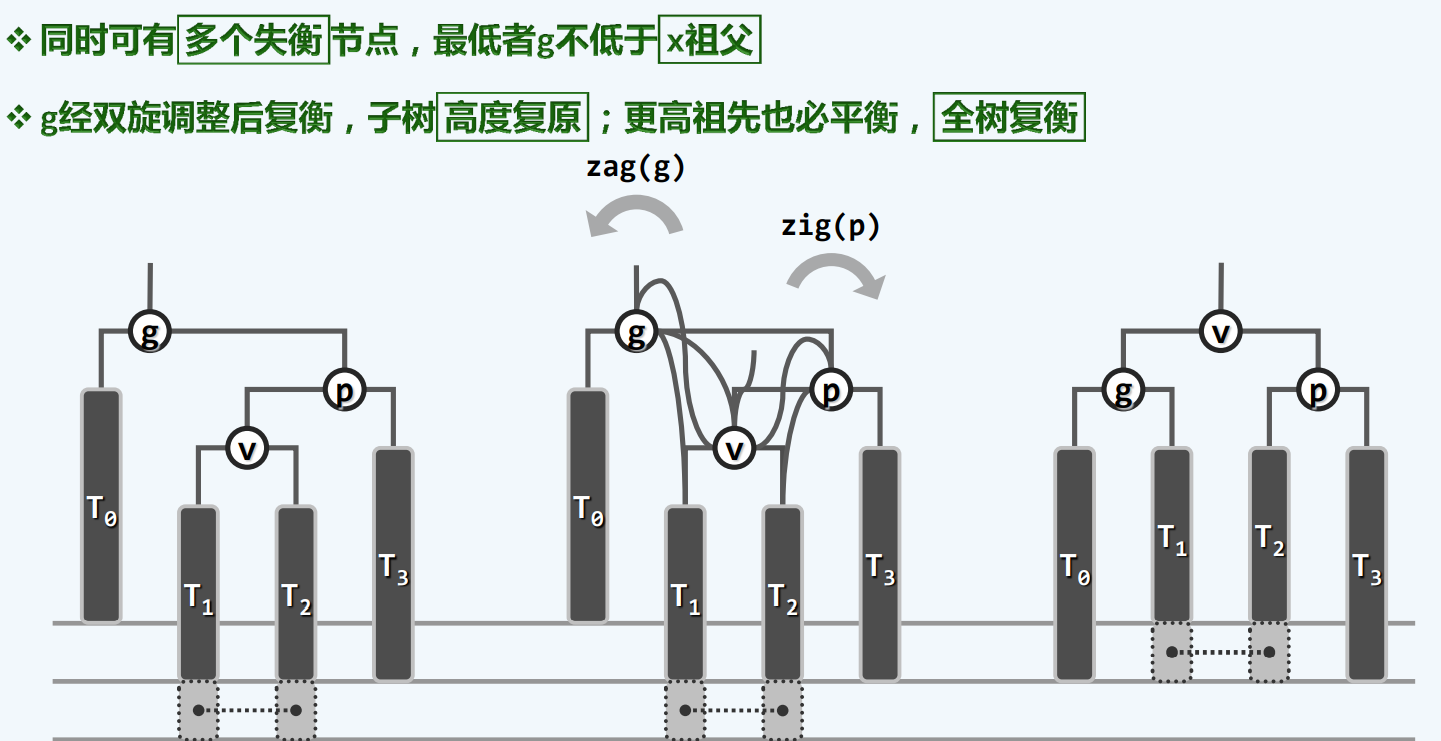
失衡与重平衡

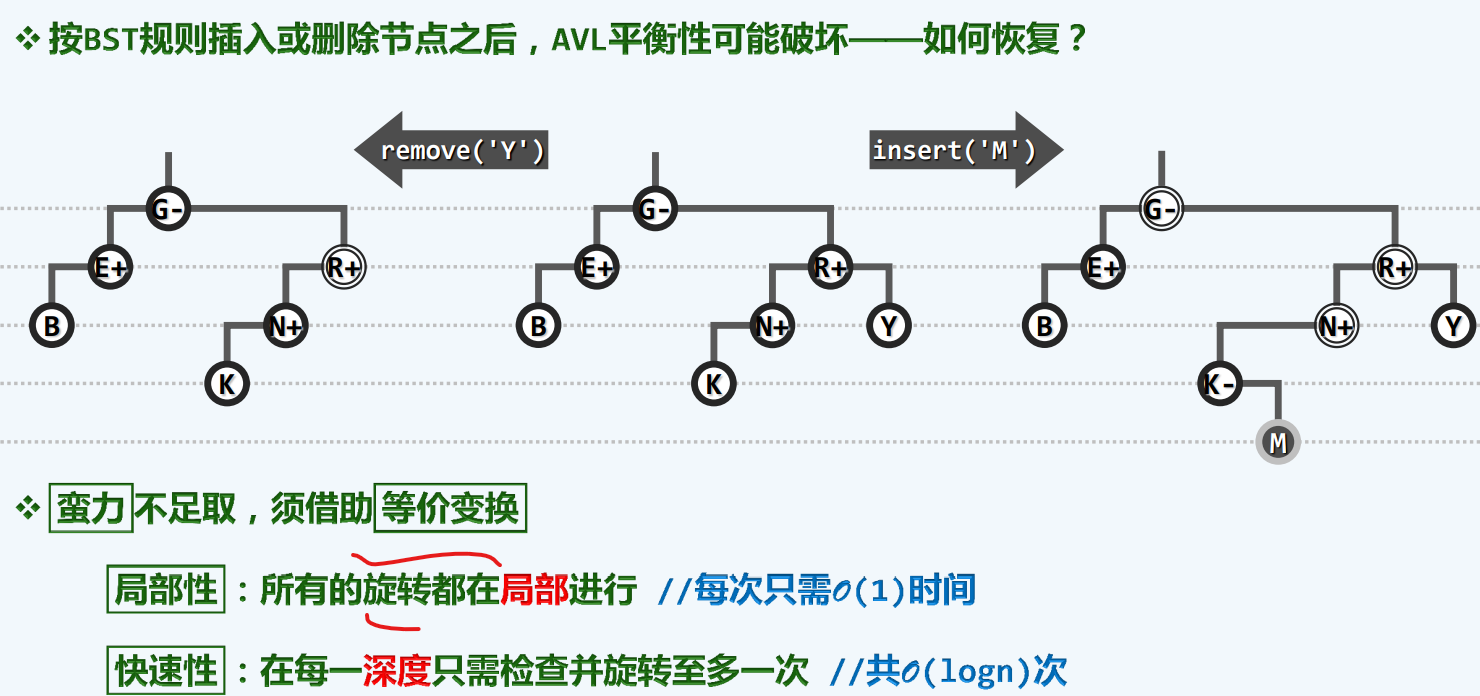
插入

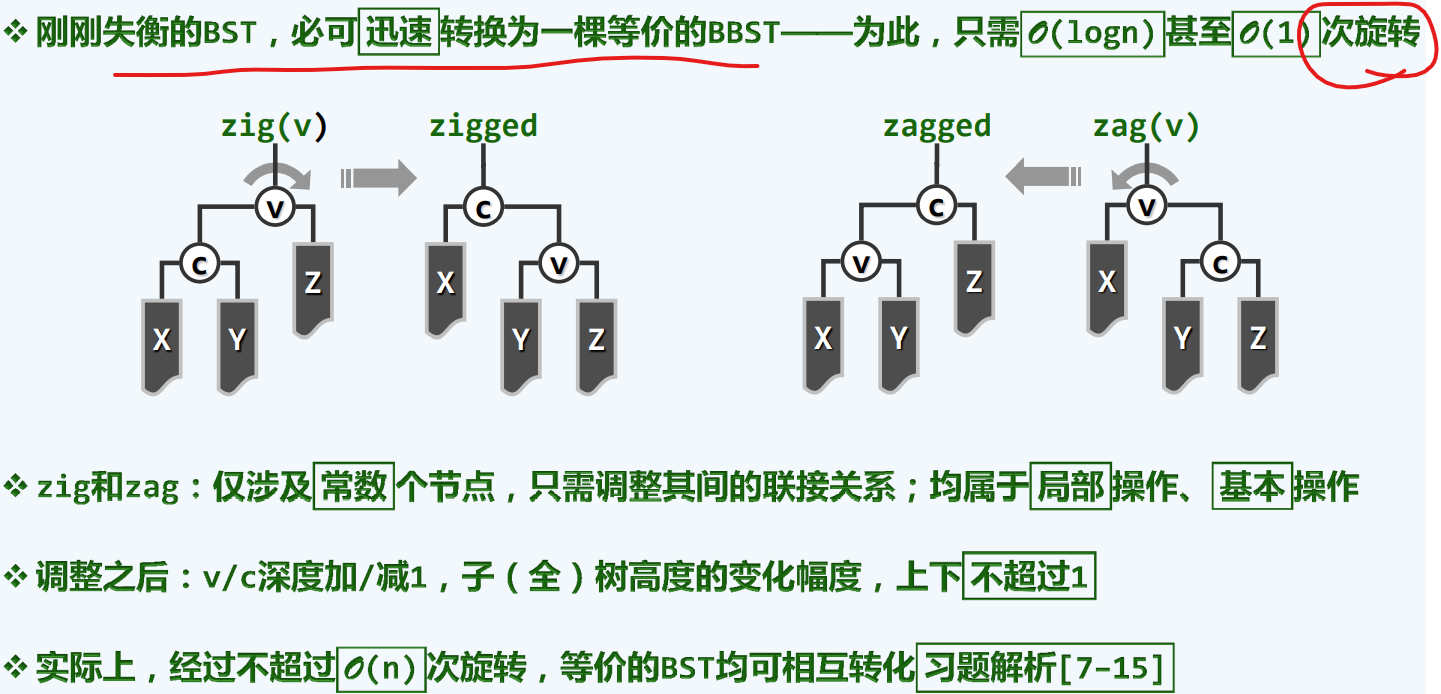
插入：单旋转

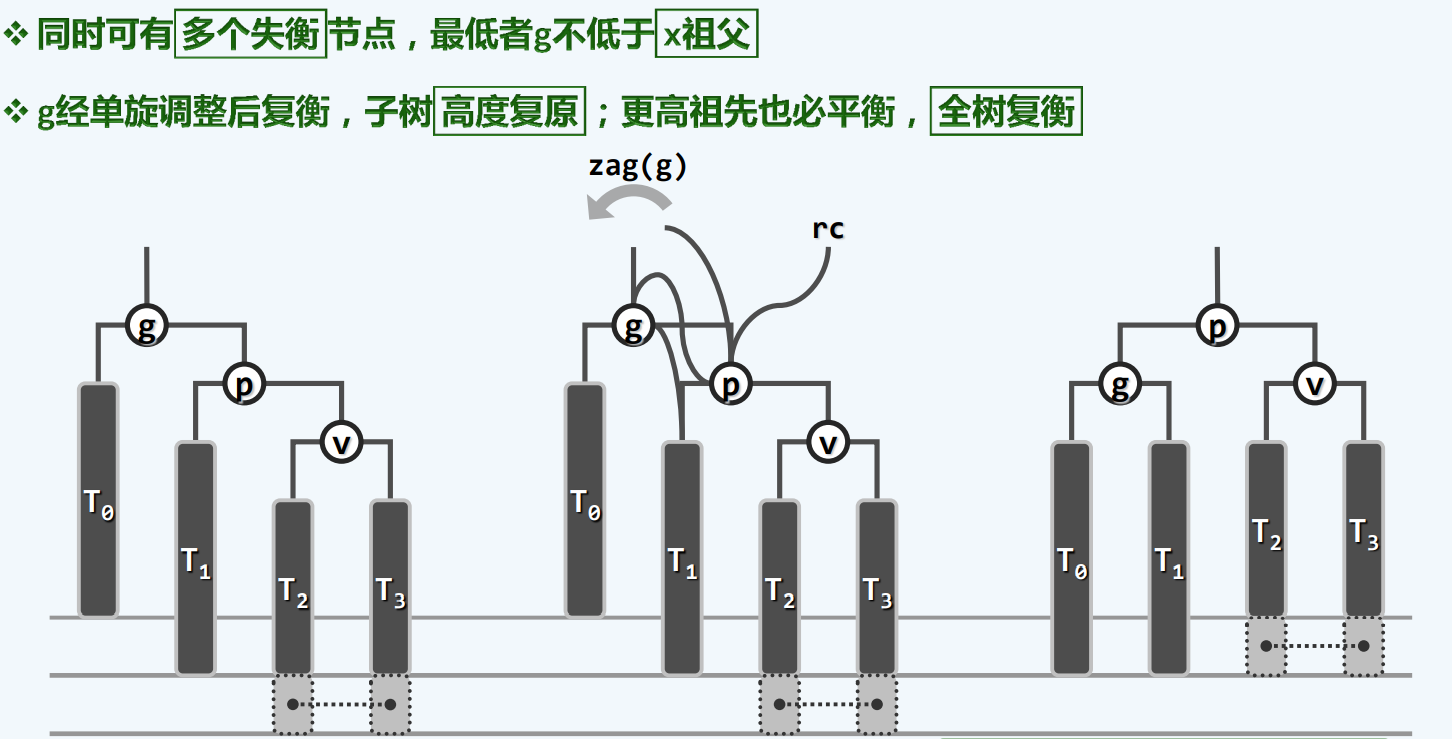
插入：双旋

插入：实现

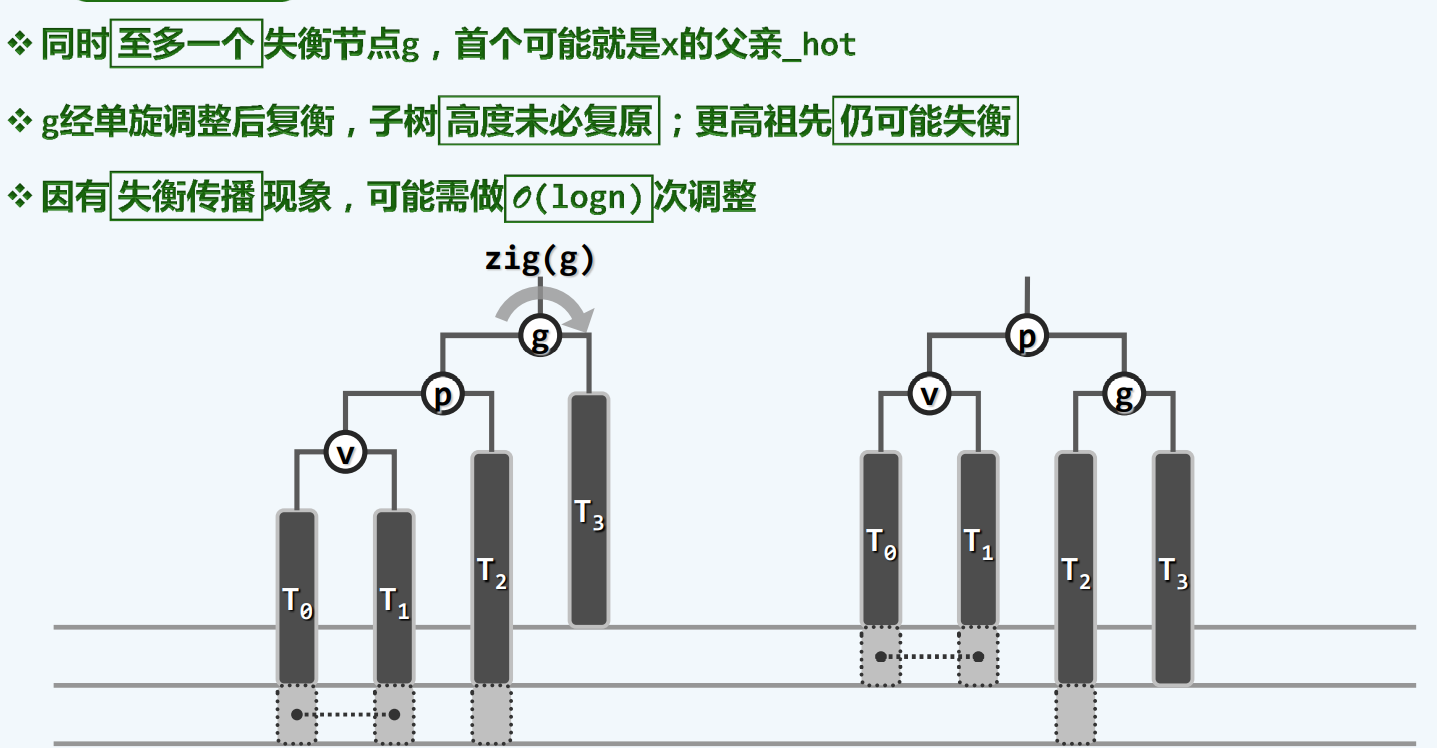
删除

单旋转

双旋转

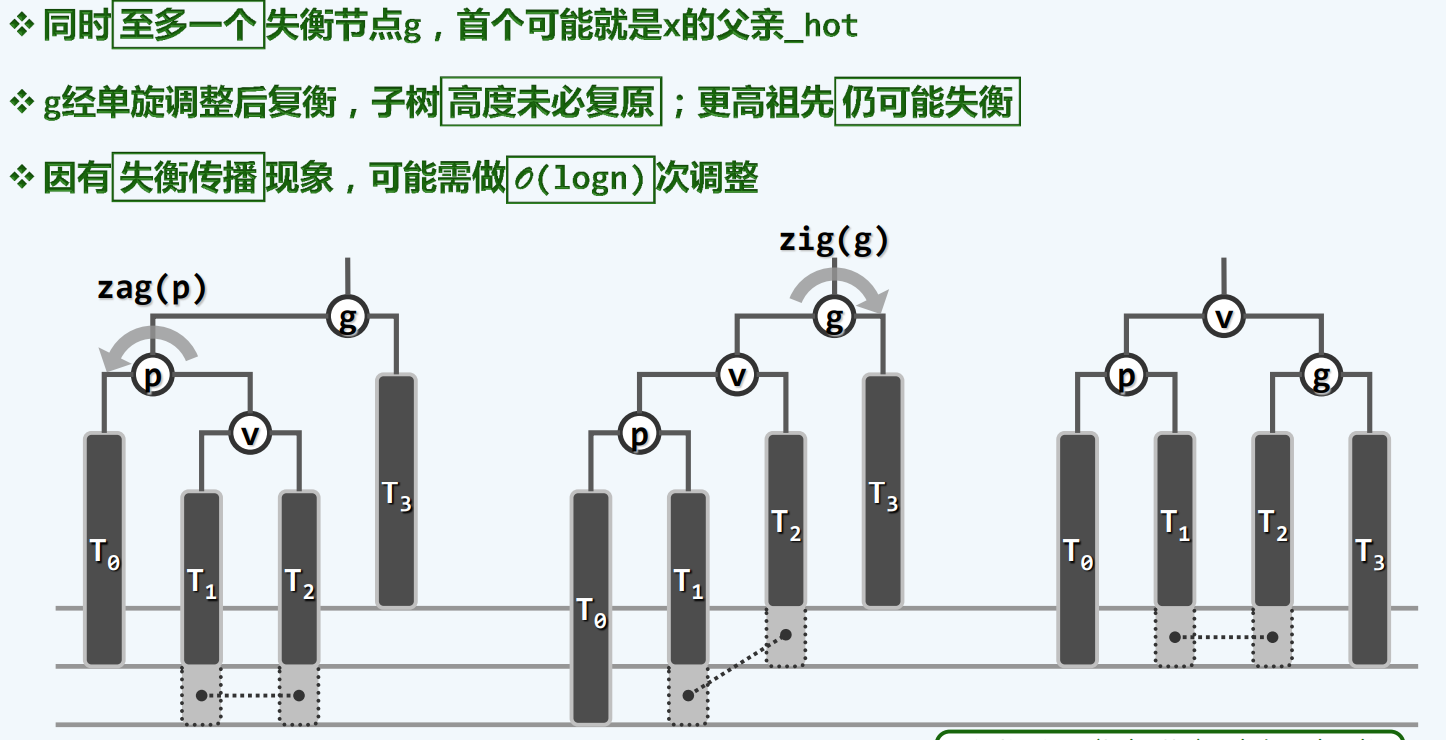
实现

3+4重构

以上删除插入，使用旋转，无非是帮助理解算法如何实现

而真正实施，大可不必这样，因为我们是追求的效率，而不是所谓的技巧

对于魔方工人而言，可以选择随便组装，然后再转到标准的魔方样子，更可以直接拆散，然后进行组装

算法

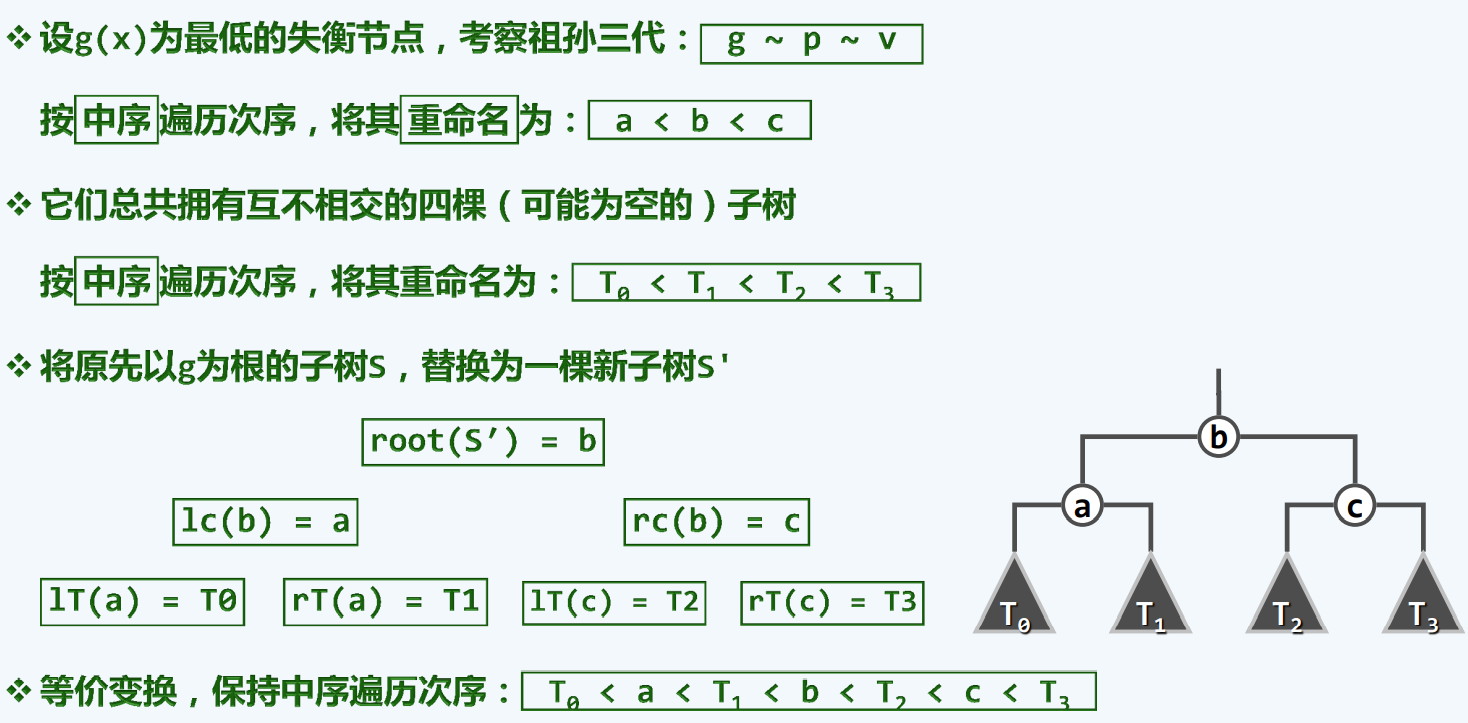
注意重新命名

实现

connect34()

template <typename T> BinNodePosi<T> BST<T>::connect34 (
0007    BinNodePosi<T> a, BinNodePosi<T> b, BinNodePosi<T> c,
0008    BinNodePosi<T> T0, BinNodePosi<T> T1, BinNodePosi<T> T2, BinNodePosi<T> T3
0009 ) {
0010    a->lc = T0; if ( T0 ) T0->parent = a;
0011    a->rc = T1; if ( T1 ) T1->parent = a; updateHeight ( a );
0012    c->lc = T2; if ( T2 ) T2->parent = c;
0013    c->rc = T3; if ( T3 ) T3->parent = c; updateHeight ( c );
0014    b->lc = a; a->parent = b;
0015    b->rc = c; c->parent = b; updateHeight ( b );
0016    return b; //该子树新的根节点
0017 }

统一调整

rotateAt()

我们通过判断p和v到底是左孩子还是右孩子，就可以准确的区分选用zig-zig，zig-zag……..

而在每一种情况下，v,p,g究竟该如何命名为a,b,c，以及属下的四棵子树该如何命名，都是固定的，甚至可以绘制成一张表，这张表也就是rotateAt所作的事情

/******************************************************************************************
0002  * BST节点旋转变换统一算法（3节点 + 4子树），返回调整之后局部子树根节点的位置
0003  * 注意：尽管子树根会正确指向上层节点（如果存在），但反向的联接须由上层函数完成
0004  ******************************************************************************************/
0005 template <typename T> BinNodePosi<T> BST<T>::rotateAt ( BinNodePosi<T> v ) { //v为非空孙辈节点
0006    BinNodePosi<T> p = v->parent; BinNodePosi<T> g = p->parent; //视v、p和g相对位置分四种情况
0007    if ( IsLChild ( *p ) ) /* zig */
0008       if ( IsLChild ( *v ) ) { /* zig-zig */
0009          p->parent = g->parent; //向上联接
0010          return connect34 ( v, p, g, v->lc, v->rc, p->rc, g->rc );
0011       } else { /* zig-zag */
0012          v->parent = g->parent; //向上联接
0013          return connect34 ( p, v, g, p->lc, v->lc, v->rc, g->rc );
0014       }
0015    else  /* zag */
0016       if ( IsRChild ( *v ) ) { /* zag-zag */
0017          p->parent = g->parent; //向上联接
0018          return connect34 ( g, p, v, g->lc, p->lc, v->lc, v->rc );
0019       } else { /* zag-zig */
0020          v->parent = g->parent; //向上联接
0021          return connect34 ( g, v, p, g->lc, v->lc, v->rc, p->rc );
0022       }
0023 }