无题
 https://oi-wiki.org/math/bit/
https://oi-wiki.org/math/bit/ https://oi-wiki.org/math/quick-pow/
https://oi-wiki.org/math/quick-pow/ https://oi-wiki.org/math/number-theory/basic/
https://oi-wiki.org/math/number-theory/basic/ https://oi-wiki.org/math/number-theory/prime/
https://oi-wiki.org/math/number-theory/prime/ https://oi-wiki.org/math/number-theory/gcd/
https://oi-wiki.org/math/number-theory/gcd/ https://oi-wiki.org/math/number-theory/sqrt-decomposition/
https://oi-wiki.org/math/number-theory/sqrt-decomposition/ https://oi-wiki.org/math/number-theory/euler/
https://oi-wiki.org/math/number-theory/euler/ https://oi-wiki.org/math/number-theory/sieve/
https://oi-wiki.org/math/number-theory/sieve/ https://oi-wiki.org/math/number-theory/bezouts/
https://oi-wiki.org/math/number-theory/bezouts/ https://oi-wiki.org/math/number-theory/fermat/
https://oi-wiki.org/math/number-theory/fermat/ https://oi-wiki.org/math/number-theory/inverse/
https://oi-wiki.org/math/number-theory/inverse/ https://oi-wiki.org/math/number-theory/linear-equation/
https://oi-wiki.org/math/number-theory/linear-equation/ https://oi-wiki.org/math/number-theory/crt/
https://oi-wiki.org/math/number-theory/crt/ https://oi-wiki.org/math/number-theory/lucas/
https://oi-wiki.org/math/number-theory/lucas/ https://oi-wiki.org/math/gauss/
https://oi-wiki.org/math/gauss/ https://oi-wiki.org/math/combinatorics/inclusion-exclusion-principle/
https://oi-wiki.org/math/combinatorics/inclusion-exclusion-principle/ https://oi-wiki.org/math/game-theory/impartial-game/
https://oi-wiki.org/math/game-theory/impartial-game/ https://oi-wiki.org/math/integral/
https://oi-wiki.org/math/integral/
 https://www.luogu.com.cn/problem/P1226
https://www.luogu.com.cn/problem/P1226 https://www.luogu.com.cn/problem/P3383
https://www.luogu.com.cn/problem/P3383 https://www.luogu.com.cn/problem/P3811
https://www.luogu.com.cn/problem/P3811 https://www.luogu.com.cn/problem/P1939
https://www.luogu.com.cn/problem/P1939 https://www.luogu.com.cn/problem/P3390
https://www.luogu.com.cn/problem/P3390 https://www.luogu.com.cn/problem/P4549
https://www.luogu.com.cn/problem/P4549 https://www.luogu.com.cn/problem/P5431
https://www.luogu.com.cn/problem/P5431 https://www.luogu.com.cn/problem/P2613
https://www.luogu.com.cn/problem/P2613 https://www.luogu.com.cn/problem/P5656
https://www.luogu.com.cn/problem/P5656 https://www.luogu.com.cn/problem/P1495
https://www.luogu.com.cn/problem/P1495 https://www.luogu.com.cn/problem/P4525
https://www.luogu.com.cn/problem/P4525
位运算
位运算就是基于整数的二进制表示进行的运算。由于计算机内部就是以二进制来存储数据,位运算是相当快的。
基本的位运算共 6 种,分别为按位与、按位或、按位异或、按位取反、左移和右移。
为了方便叙述,下文中省略“按位”。
与、或、异或¶
这三者都是两数间的运算,因此在这里一起讲解。
它们都是将两个整数作为二进制数,对二进制表示中的每一位逐一运算。

取反¶
取反是对一个数 进行的位运算,即单目运算。
取反暂无默认的数学符号表示,其对应的运算符为 ~。它的作用是把 的二进制补码中的 和 全部取反( 变为 , 变为 )。有符号整数的符号位在 ~ 运算中同样会取反。
补码:在二进制表示下,正数和 的补码为其本身,负数的补码是将其对应正数按位取反后加一。
举例(有符号整数):
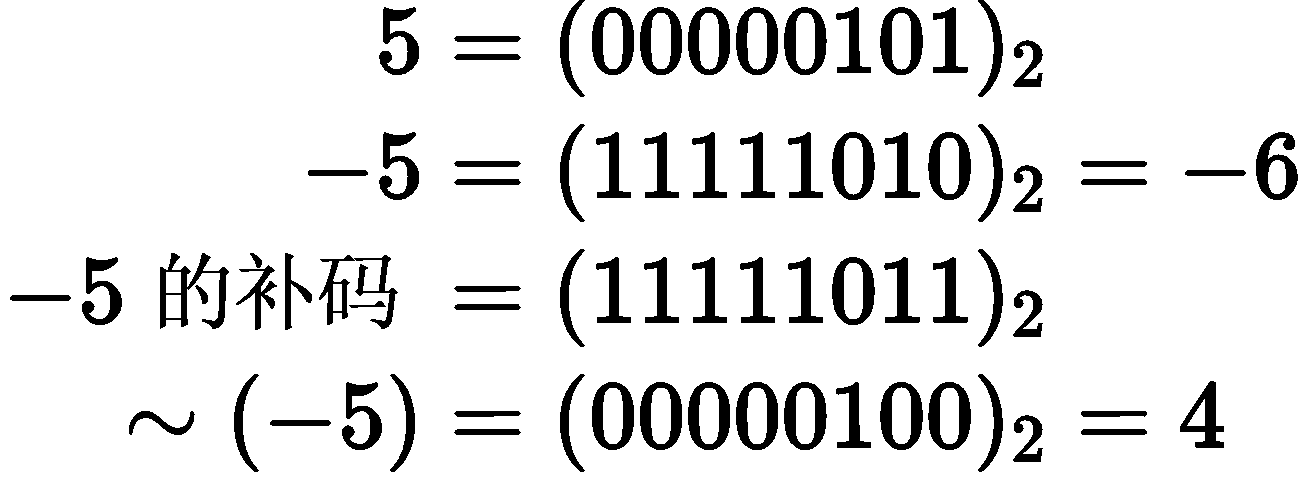
左移和右移¶

复合赋值位运算符¶
和 += , -= 等运算符类似,位运算也有复合赋值运算符: &= , |= , ^= , <<= , >>= 。(取反是单目运算,所以没有。)
关于优先级¶
位运算的优先级低于算术运算符(除了取反),而按位与、按位或及异或低于比较运算符(详见 运算页面 ),所以使用时需多加注意,在必要时添加括号。
位运算的应用¶
位运算一般有三种作用:
- 高效地进行某些运算,代替其它低效的方式。
- 表示集合。(常用于 状压 DP 。)
- 题目本来就要求进行位运算。
需要注意的是,用位运算代替其它运算方式(即第一种应用)在很多时候并不能带来太大的优化,反而会使代码变得复杂,使用时需要斟酌。(但像“乘 2 的非负整数次幂”和“除以 2 的非负整数次幂”就最好使用位运算,因为此时使用位运算可以优化复杂度。)
有关 2 的幂的应用¶
由于位运算针对的是变量的二进制位,因此可以推广出许多与 2 的整数次幂有关的应用。
将一个数乘(除) 2 的非负整数次幂:
1 | // C++ Version |
1 | # Python Version |
Warning
我们平常写的除法是向 0 取整,而这里的右移是向下取整(注意这里的区别),即当数大于等于 0 时两种方法等价,当数小于 0 时会有区别,如: -1 / 2 的值为0 ,而 -1 >> 1 的值为**-1** 。
取绝对值¶
在某些机器上,效率比 n > 0 ? n : -n 高。
1 | // C++ Version |
1 | # Python Version |
取两个数的最大/最小值¶
在某些机器上,效率比 a > b ? a : b 高。
1 | // C++ Version |
1 | # Python Version |
判断两非零数符号是否相同¶
1 | // C++ Version |
1 | # Python Version |
交换两个数¶
该方法具有局限性
这种方式只能用来交换两个整数,使用范围有限。
对于一般情况下的交换操作,推荐直接调用 algorithm 库中的 std::swap 函数。
1 | void swap(int &a, int &b) { a ^= b ^= a ^= b; } |
快速幂


迭代实现
实现方法是非递归式的。它在循环的过程中将二进制位为 1 时对应的幂累乘到答案中。尽管两者的理论复杂度是相同的,但第二种在实践过程中的速度是比第一种更快的,因为递归会花费一定的开销。
a的b次方
b要更新,a要更新,结果要更新
1 | // C++ Version |
1 | # Python Version |
应用
模意义下取幂¶
问题描述
计算x^n mod m
这是一个非常常见的应用,例如它可以用于计算模意义下的乘法逆元。
既然我们知道取模的运算不会干涉乘法运算,因此我们只需要在计算的过程中取模即可。
1 | // C++ Version |
1 | # Python Version |
相关题目
1、N 的 N 次幂的个位数
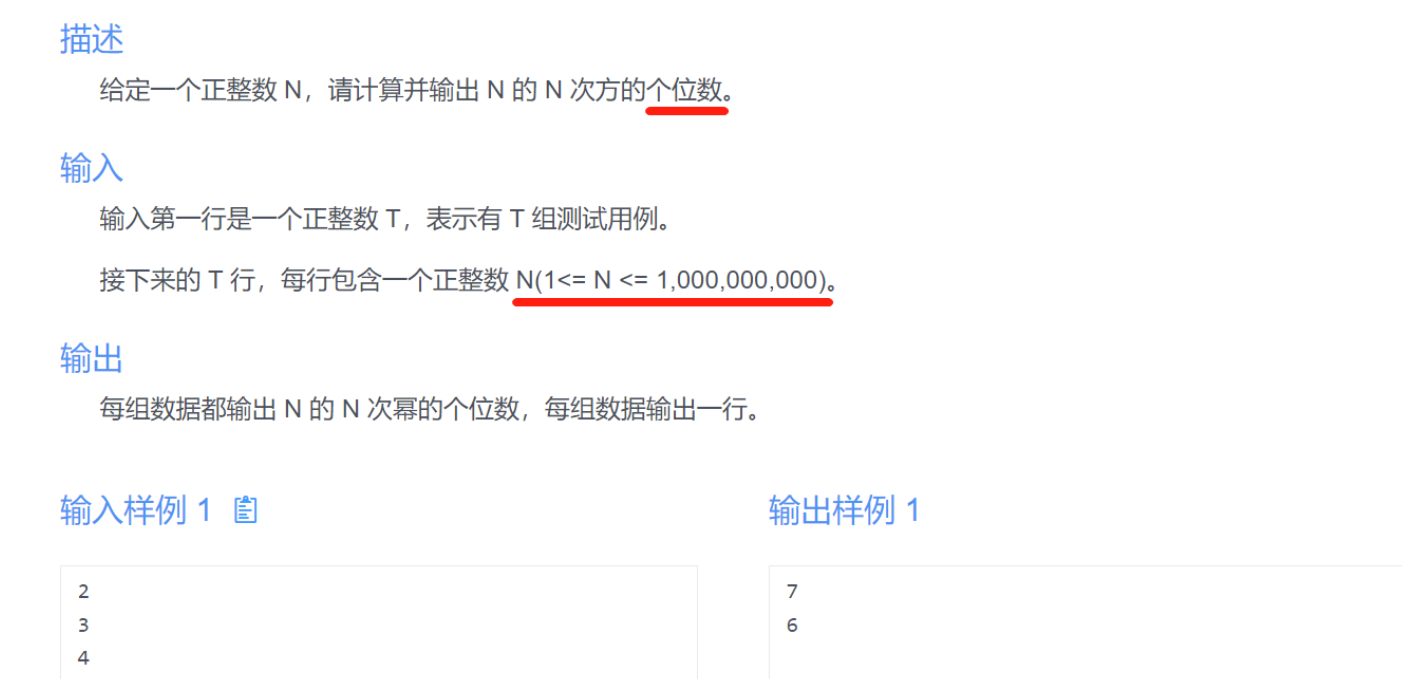
参考思路
看到只求个位数,其实就是暗示所有结果都mod10,那么就可能用到我们的乘法的取模运算法则;看到N的范围109,那么显然暴力幂的方式肯定不太行,而要用快速幂,并且还需要借助mod10这个先决条件先把数据范围给降下来。那么思路就有了:快速幂+取模乘法性质一条龙解题。
自写代码。
1 |
|
2、求A^B的最后三位整数

参考思路
类似于第一题,看到只求最后三位数,其实就是暗示所有结果都mod1000,那么就可能用到我们的乘法的取模运算法则;看到A,B的范围104,很可能暴力幂的方式还是不太行,继续用快速幂。
思路就又有了:还是快速幂+取模乘法性质一条龙解题。
1 |
|
素数
素数判定¶
我们自然地会想到,如何用计算机来判断一个数是不是素数呢?
暴力做法¶
自然可以枚举从小到大的每个数看是否能整除
1 | // C++ Version 版本一 |
1 | # Python Version |

1 | // C++ Version |
1 | # Python Version |
素性测试¶
素性测试(Primality test)是一类在 不对给定数字进行素数分解(prime factorization)的情况下,测试其是否为素数的算法。
素性测试有两种:
- 确定性测试:绝对确定一个数是否为素数。常见示例包括 Lucas-Lehmer 测试和椭圆曲线素性证明。
- 概率性测试:通常比确定性测试快很多,但有可能(尽管概率很小)错误地将 合数 识别为质数(尽管反之则不会)。因此,通过概率素性测试的数字被称为 可能素数,直到它们的素数可以被确定性地证明。而通过测试但实际上是合数的数字则被称为 伪素数。有许多特定类型的伪素数,最常见的是费马伪素数,它们是满足费马小定理的合数。概率性测试的常见示例包括 Miller–Rabin 测试。
Miller-Rabin 素性测试¶
Miller-Rabin 素性测试(Miller–Rabin primality test)是进阶的素数判定方法。它是由 Miller 和 Rabin 二人根据费马小定理的逆定理(费马测试)优化得到的。因为和许多类似算法一样,它是使用伪素数的概率性测试,我们必须使用慢得多的确定性算法来保证素性。然而,实际上没有已知的数字通过了高级概率性测试(例如 Rabin-Miller)但实际上却是复合的。因此我们可以放心使用。

1 | // C++ Version |
1 | # Python Version |
反素数¶
如果某个正整数 n 满足如下条件,则称为是 反素数: 任何小于 n 的正数的约数个数都小于 n 的约数个数
注:注意区分 emirp,它是用来表示从后向前写读是素数的数。
简介¶
其实顾名思义,素数就是因子只有两个的数,那么反素数,就是因子最多的数(并且因子个数相同的时候值最小),所以反素数是相对于一个集合来说的。
我所理解的反素数定义就是,在一个集合中,因素最多并且值最小的数,就是反素数。
分解质因数
因为看不懂,所以我们先去补分解质因数吧!,具体参照的这篇
今天带给大家的题目是:180的约数有多少个?
首先,请允许我普及一下约数的概念。
约数:如果一个自然数A能被自然数B整除,那么称B是A的约数。
知道了约数的概念后,题目就可以重新表述为:180可以被多少个自然数整除?
我现在开始数:有1,2,3,4,5,6,9,10,12,……
停停停!!!
妈呀,好像很多的样子嘛,得一直数到180吗?那也太麻烦了吧。
怎么办,怎么办???
化繁为简!
化繁为简是一种非常重要的数学方法,比如在这儿,我们可以把题目改为:
18的约数有多少个?
这样,题目是不是就变得简单多了。
然后通过对这个简单题目的研究,去挖掘其中的一般性结论,最后再推广到数180。
这样不就完美了,哈哈~
好的,说干就干,18的约数有:
1,2,3,6,9,18.
共6个约数,这会有什么结论呢?
老实说,我也看不出!
不过,对于数学老师来说,聊到约数一般都会联系“分解质因数”。
那啥叫“分解质因数”呢?
我再普及一下:把合数表示为质因数乘积的形式叫做“分解质因数”。
那啥又叫“质数”呢?
只能被1和本身这两个不同的自然数整数的自然数叫质数,例如:2,3,5,7,11,……
现在,我们将18进行分解,具体如下:
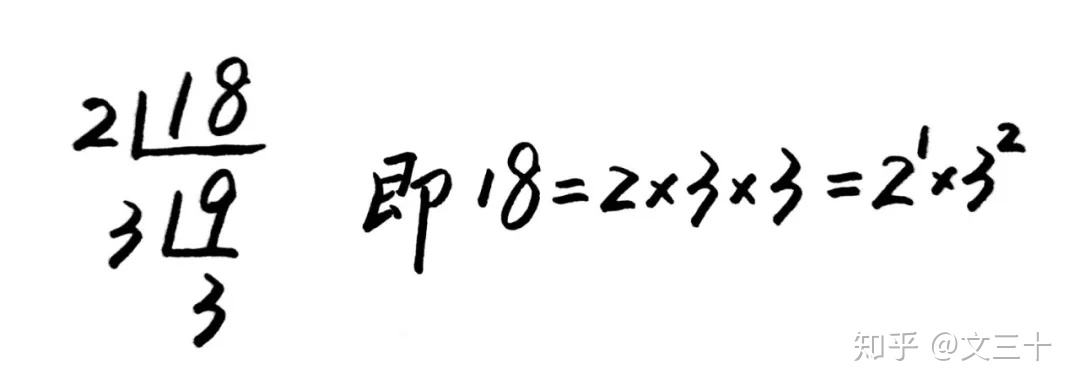
能从上述式子中找到约数的个数6吗?
我相信你肯定会问我:是质因数2 × 3 = 6,对吗?
哈哈,刚好凑巧罢了,事实上并不对。
那会是什么呢???
细心的你肯定是注意到了,
我在质因数2和3的右上角分别标上了它们各自的次数1和2。
这会儿你肯定要笑话我了,
质因数2 × 3 = 6不去相信,次数1和2又怎么能变成6呢?
事实上的结论是:(1 + 1)×(2 + 1)= 6个。
即某一自然数的约数个数是它各质因数的次数分别加1相乘的积!!!
那么,根据上述结论,
我们将180进行分解,具体如下:
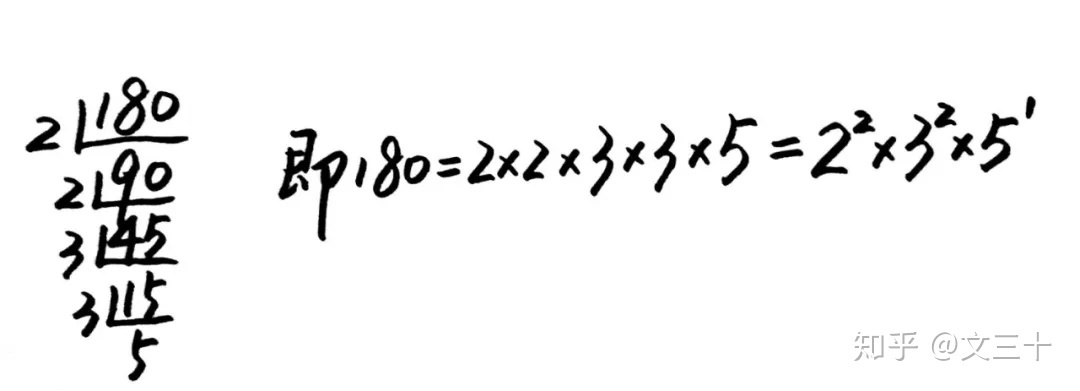
则180的约数有:(2 + 1)×(2 + 1)×(1 + 1)= 18个。
到这里,你也许还会想,不是真的吧。
那么,我将180的约数逐一枚举出来,请大家自行检验:
1,2,3,4,5,6,9,10,12,15,18,20,30,36,45,60,90,180.
共18个。
求解反素数
那么,如何来求解反素数呢?


DFS
既然这道题要用到DFS,那么我们去练一道DFS板子题再来吧QW,先继续往下学习


