以下笔记为jjyaoao本人制作,欢迎借鉴学习和提出相关建议,转载需要标明出处www.jjyaoao.space
伸展树(Splay Tree)
虽然对于标准平衡树而言,AVL已经在条件上略有放松,但是这种平衡任然显得过于苛刻,就像一个小心谨慎走路的人,那么我们能否走的更潇洒一点呢?
也就是说,我们可否秉持一种更为宽泛的准则,并且从长远来看仍然不失一定的稳定性呢?
逐层伸展
局部性

自适应调整
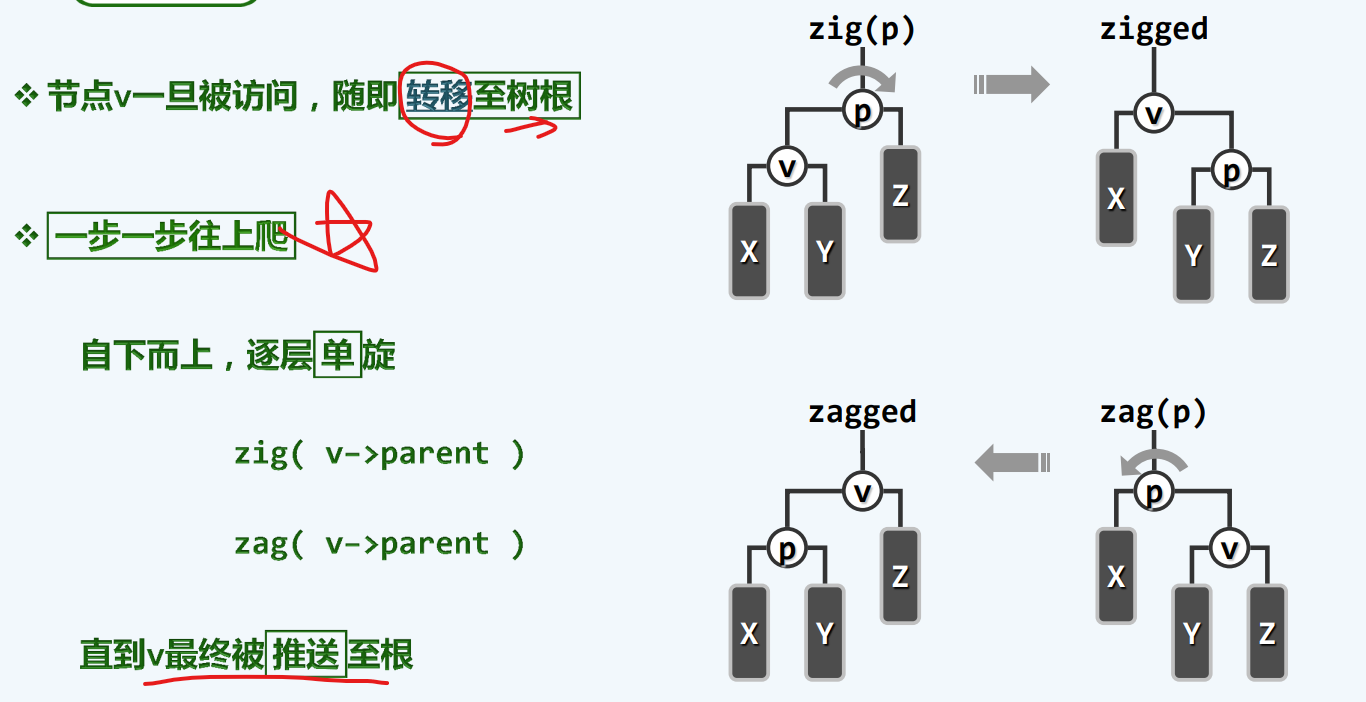
使刚被访问的节点往上走
逐层伸展
实例
我们通过观察这个实例,发现这个过程是一个左右摇摆,逐渐伸展的过程
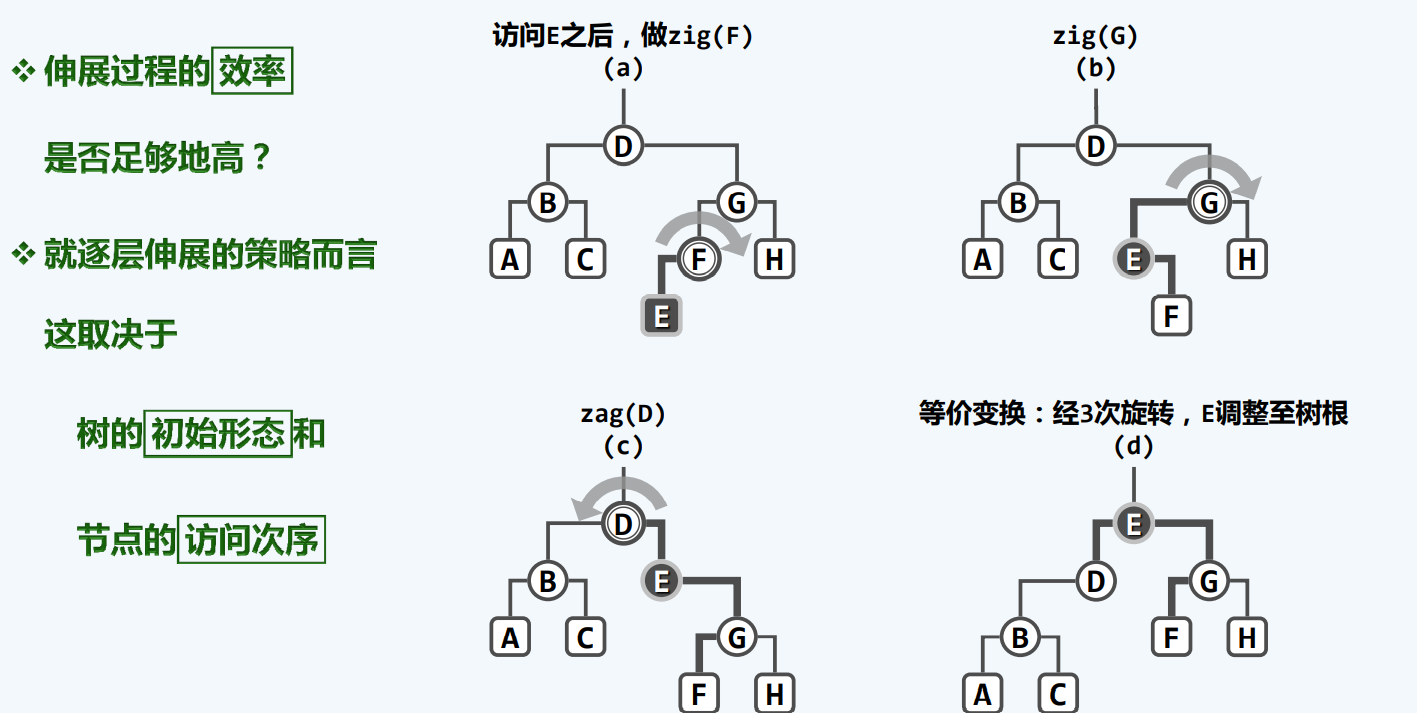
所以我们也称这个过程叫伸展,Splay
然而就效率而言,这并不是最佳的选择,原因在于,他有最坏情况
最坏情况
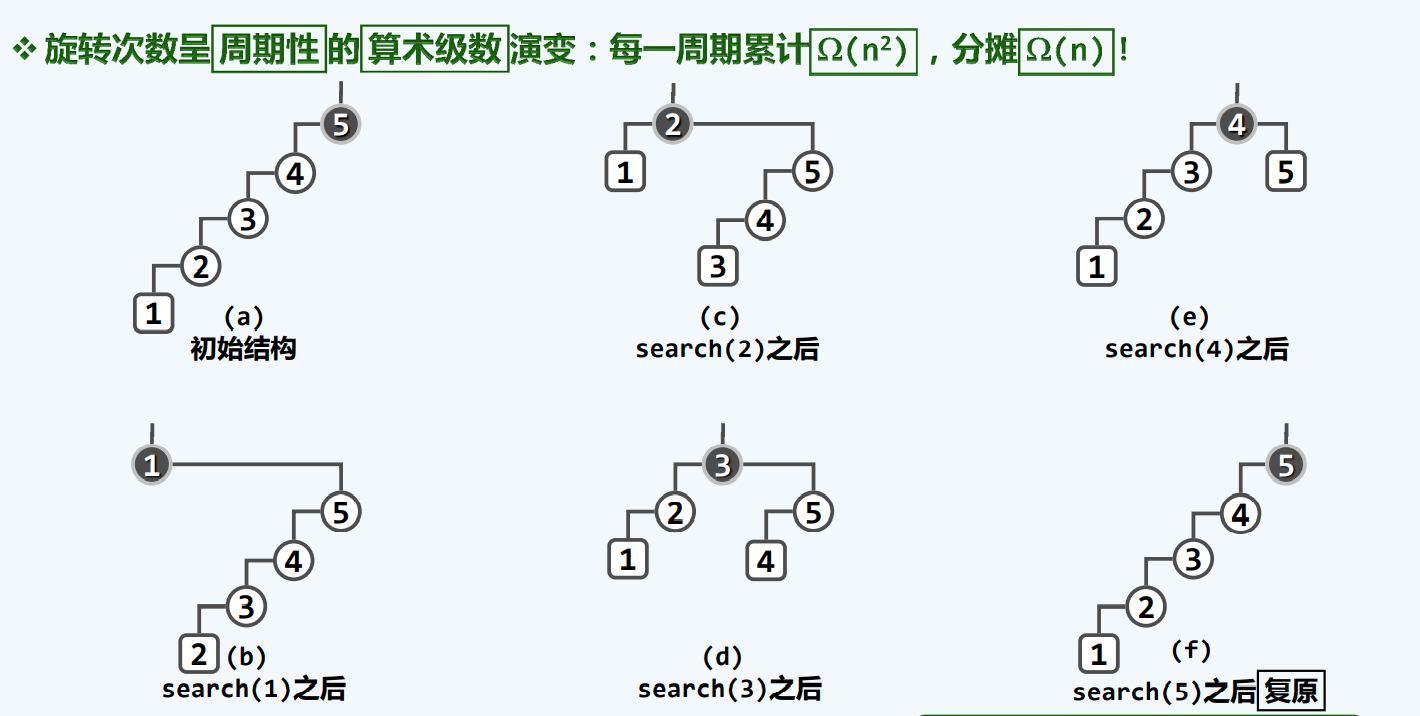
这也并不是令我们满意的,甚至离logn都相距甚远
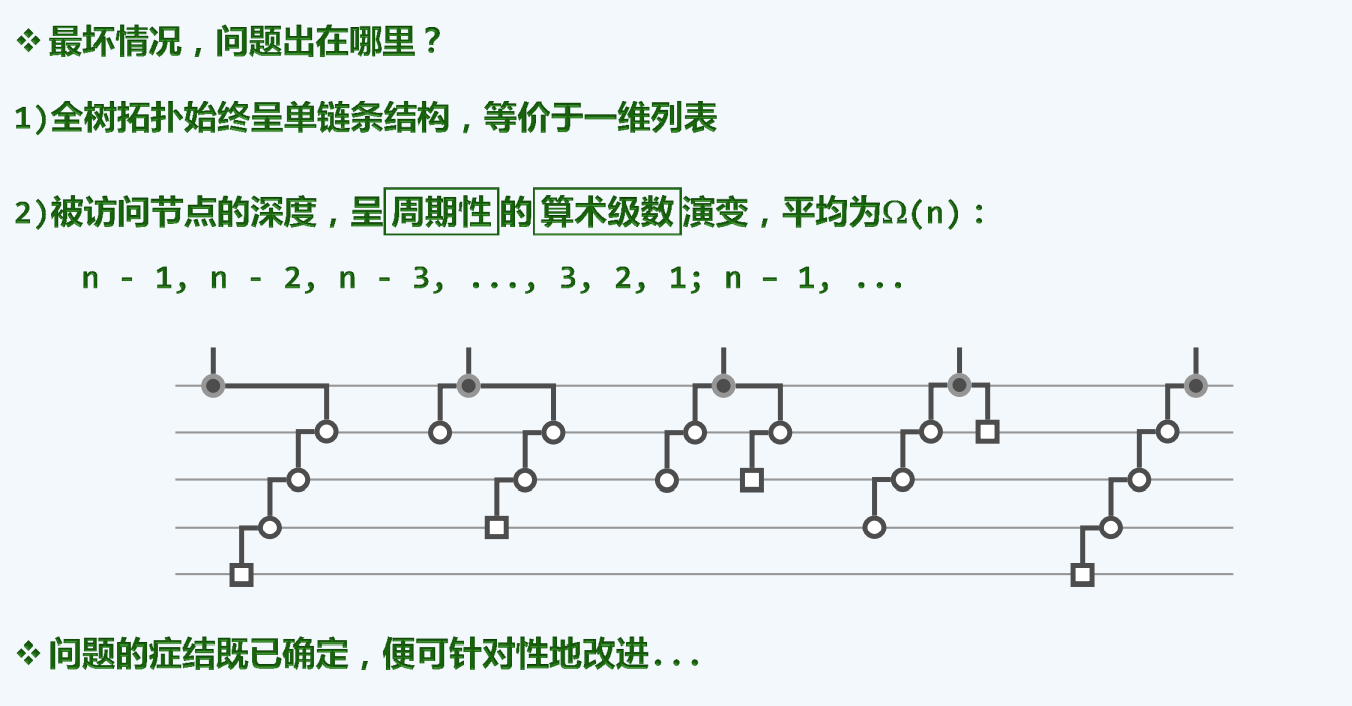
不过好消息是,造成这一结果并不是伸展本身,而是我们伸展的方式,就好比画龙点睛,作为一条龙,目前的伸展策略已经相当完备,它所缺少的只是体现其灵魂的一只眼睛,没错,不是一双眼睛,仅仅是一只
双层伸展
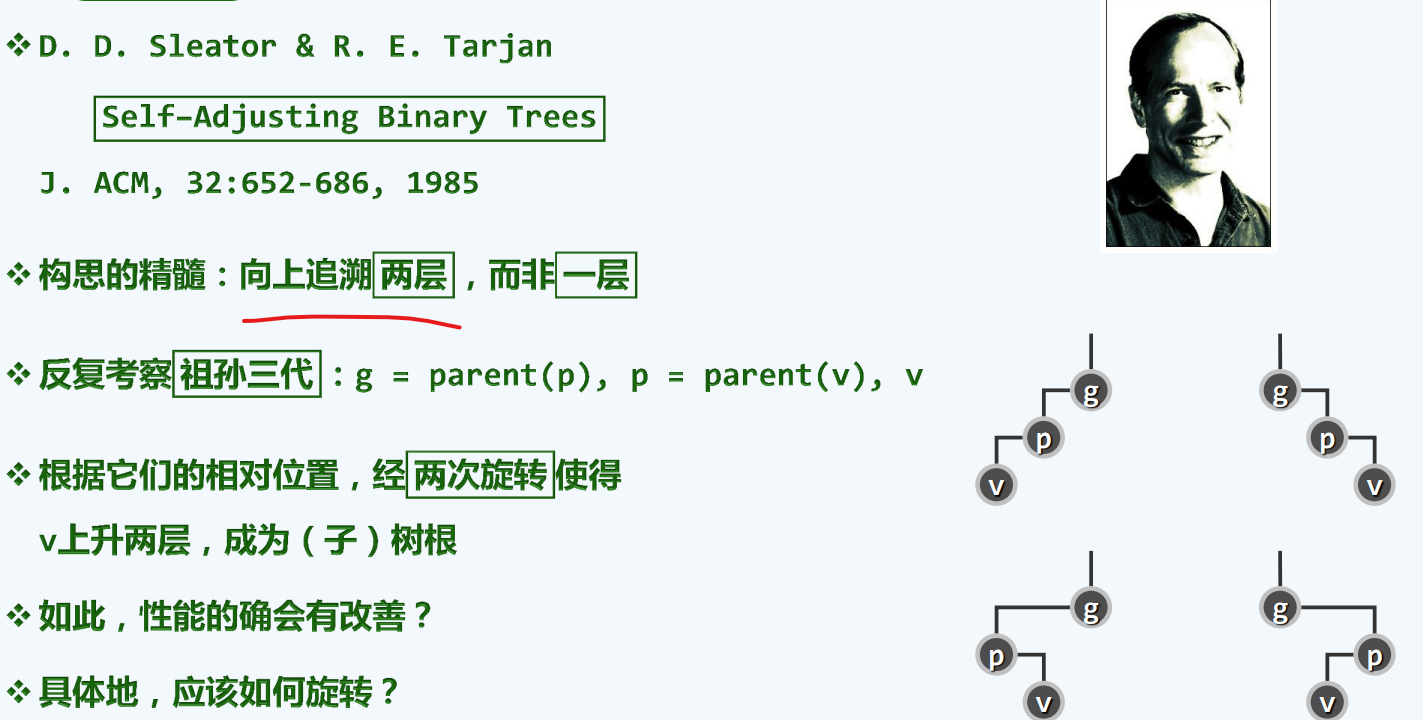
子孙异侧
如果能发现这两个策略,那其实是非常好的,因为这就是那条龙的一只眼睛,真正有差别的在于另一只眼睛….
子孙同侧
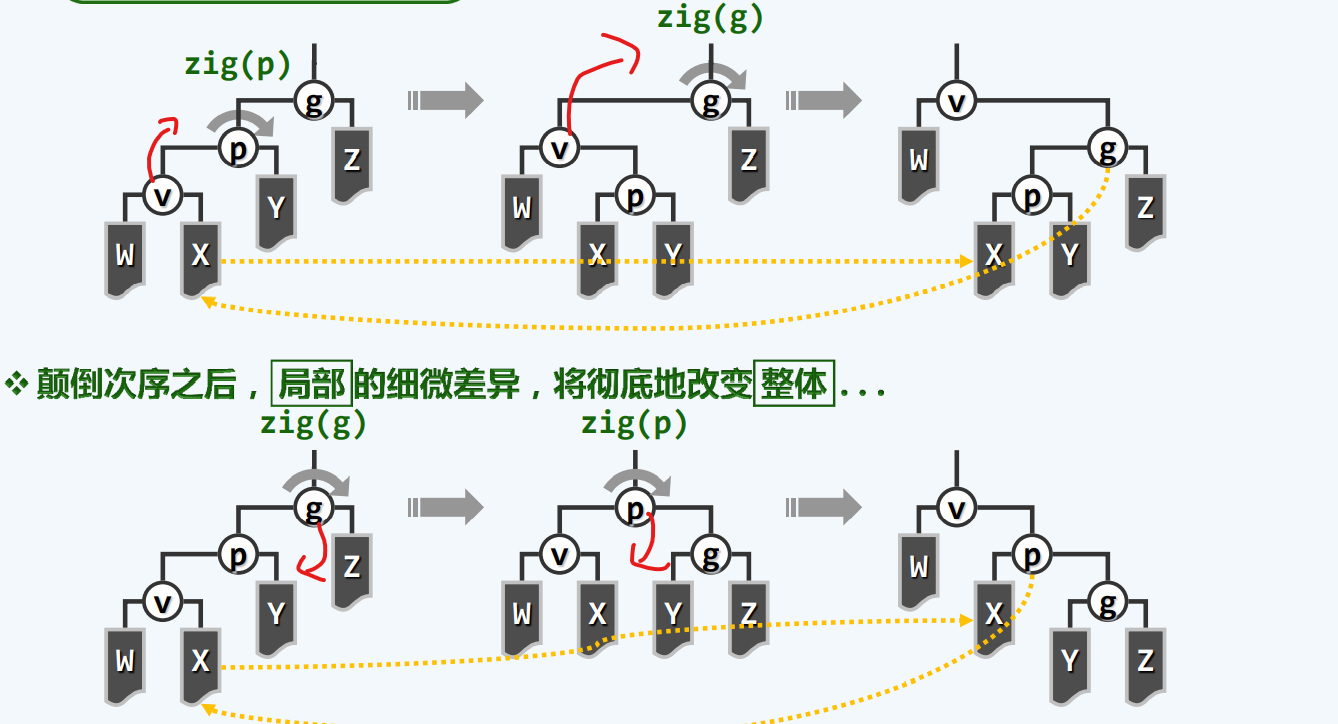
的确不易察觉,更重要的是,这种局部的微妙差异将导致全局的不同,这种不同将是根本性的,颠覆性的。
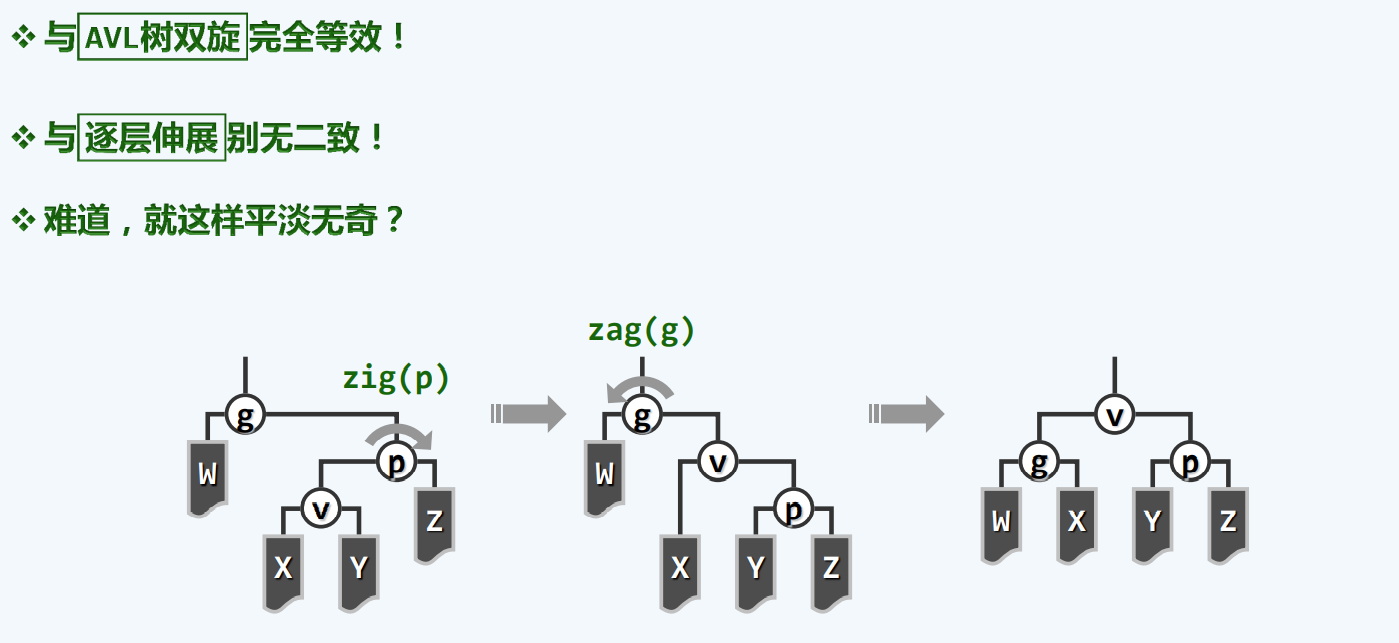
点睛之笔
第一次调整以后,它拥有了新的祖父和父亲(5,4)
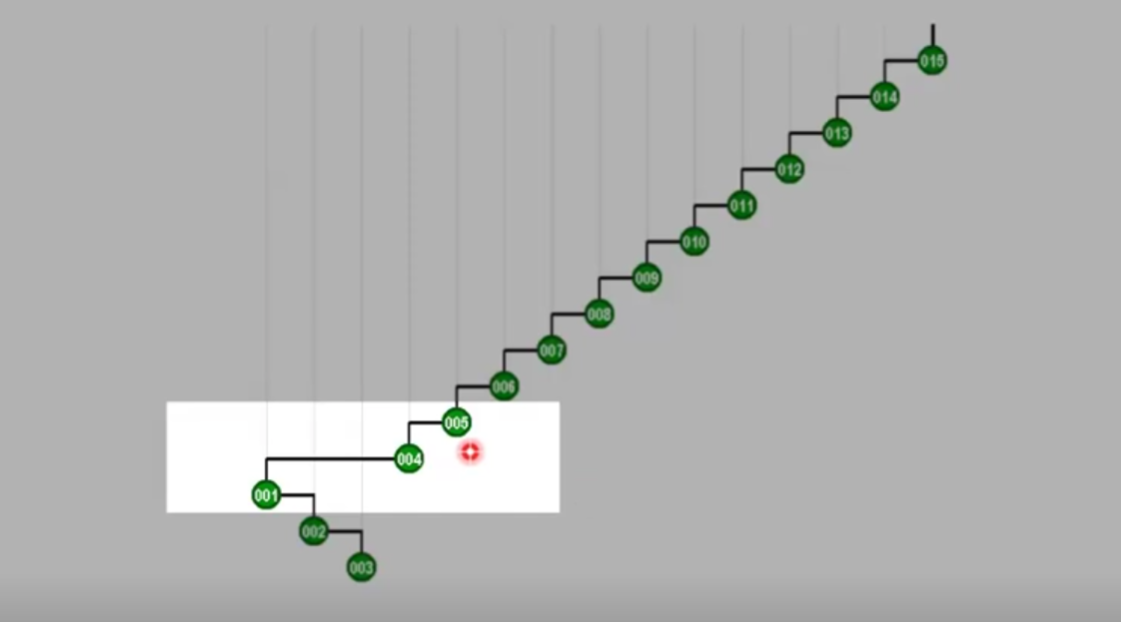
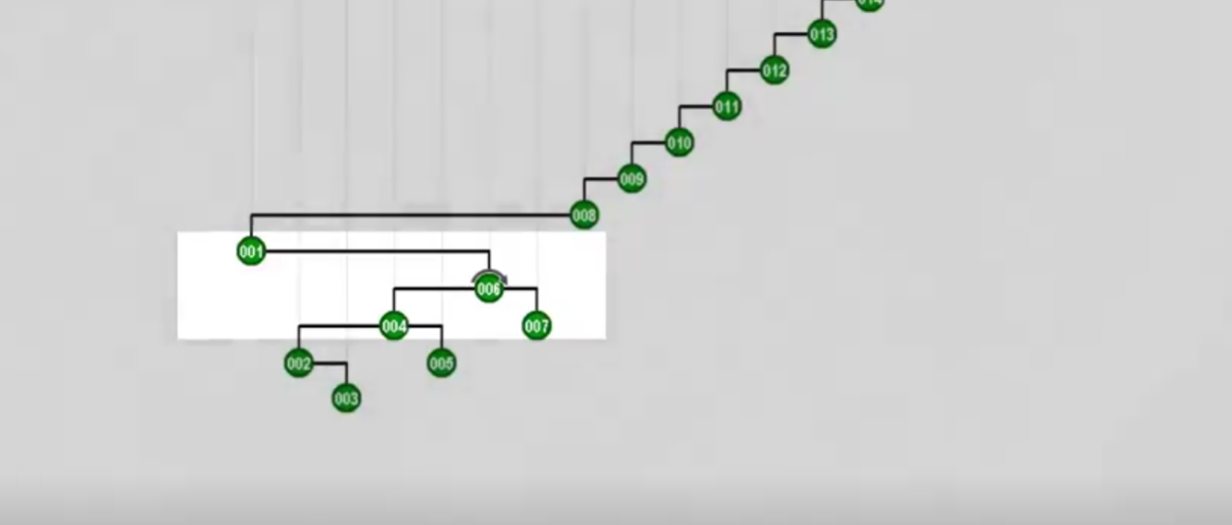
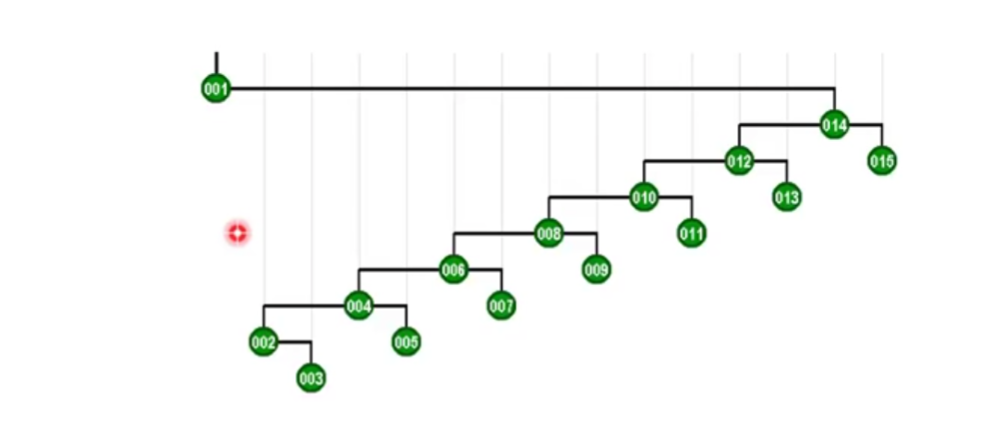
每调整一次,树的高度都将缩减一半
性能分析
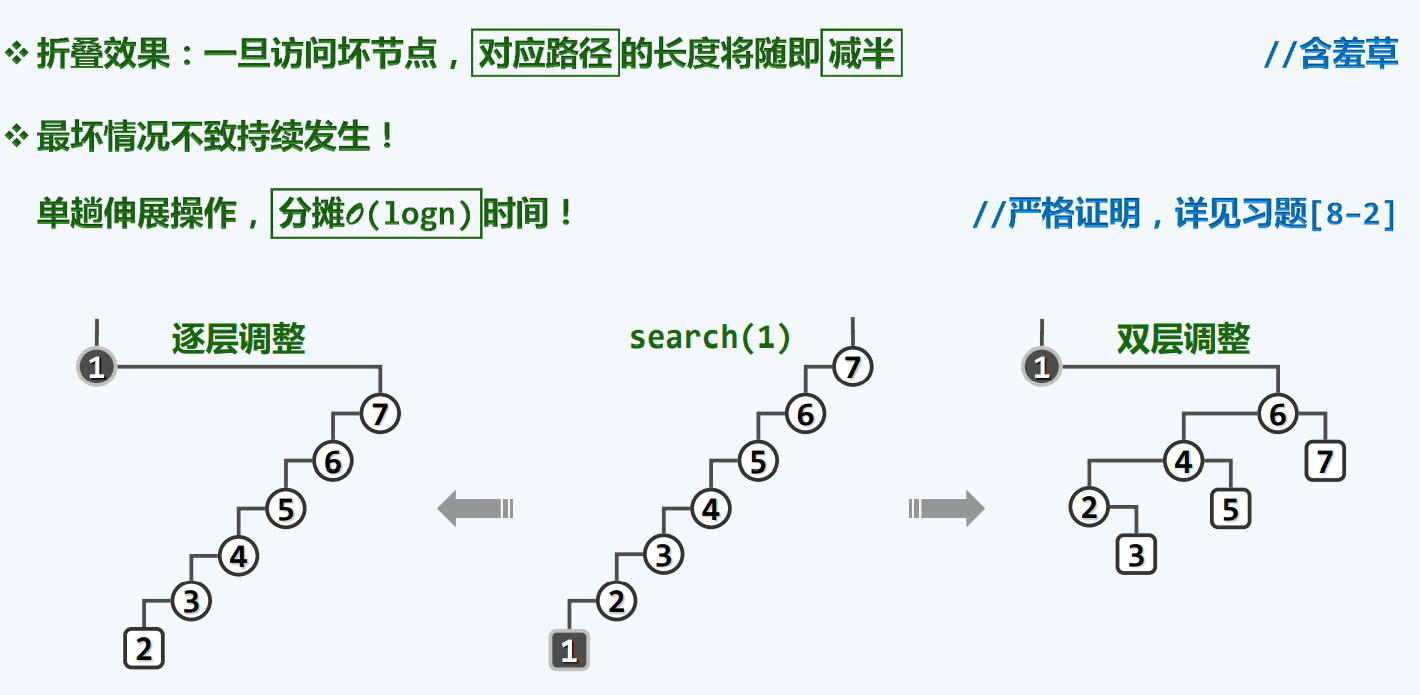
因此,我们不仅能处理之前那种最坏情况,还能面队其他的最坏情况,这是再好不过的消息了
最后一步
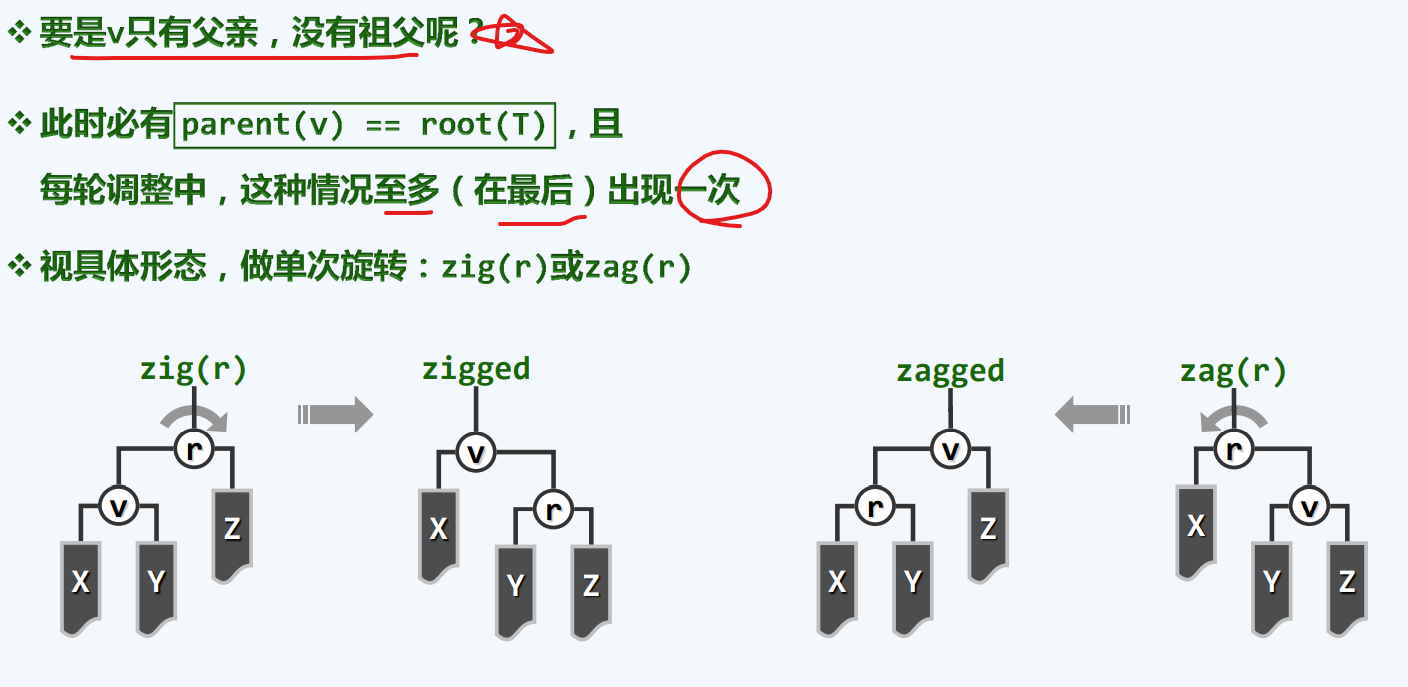
我们说这个情况并不严重,我们只需要在最后做一次左旋或者右旋就好,那么,这种策略又当如何具体实现呢?
ADT

在这里,除了重写插入和删除,search()也需要重写,即便是查找操作,也会引起全树的拓扑结构变换,我们马上就可以知道,这种变换是举足轻重的。
这个search的实质功能无非是完成伸展,我们这也提供了一个splay的保护接口用以实现这个功能
伸展算法

zIg-zIg示范
右旋-右旋
第一句将p的右孩子当作g的左孩子
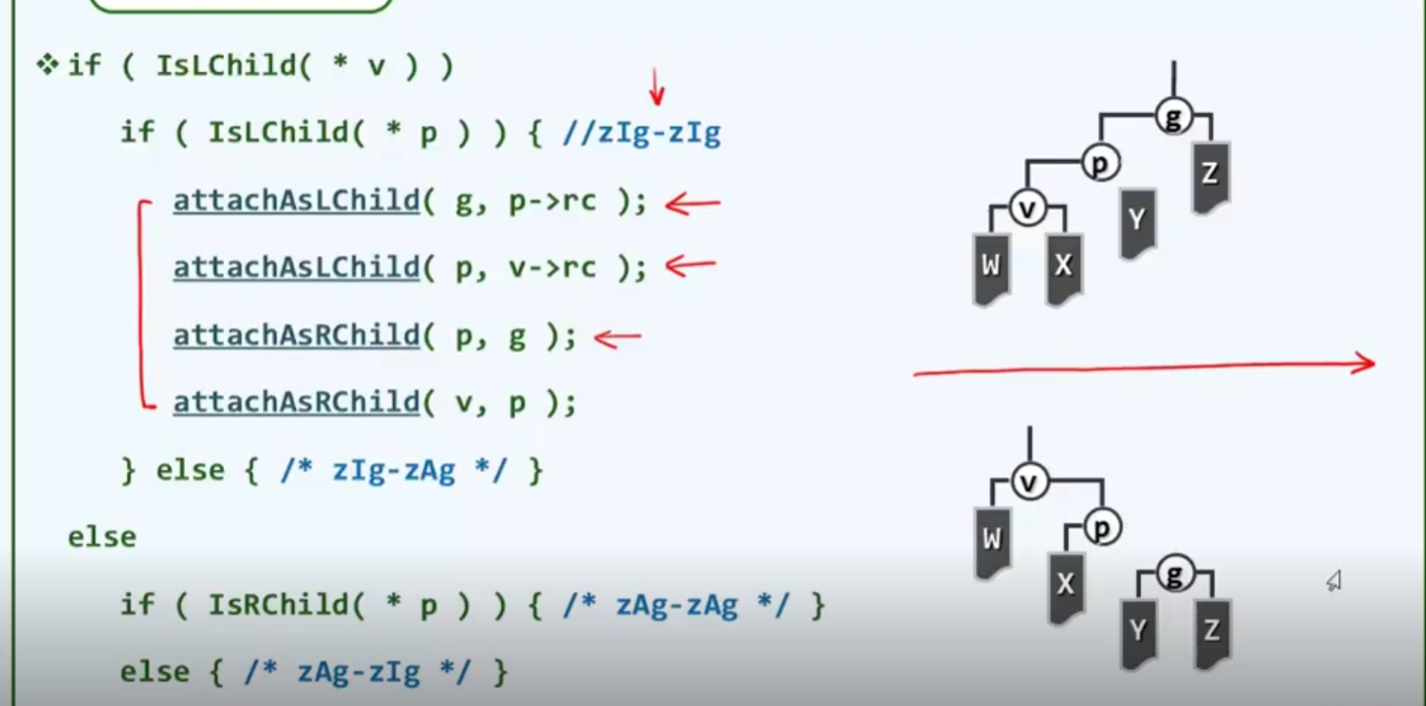
实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| template <typename NodePosi> inline
0002 void attachAsLC ( NodePosi lc, NodePosi p ) { p->lc = lc; if ( lc ) lc->parent = p; }
0003
0004 template <typename NodePosi> inline
0005 void attachAsRC ( NodePosi p, NodePosi rc ) { p->rc = rc; if ( rc ) rc->parent = p; }
0006
0007 template <typename T>
0008 BinNodePosi<T> Splay<T>::splay ( BinNodePosi<T> v ) {
0009 if ( !v ) return NULL; BinNodePosi<T> p; BinNodePosi<T> g;
0010 while ( ( p = v->parent ) && ( g = p->parent ) ) {
0011 BinNodePosi<T> gg = g->parent;
0012 if ( IsLChild ( *v ) )
0013 if ( IsLChild ( *p ) ) {
0014 attachAsLC ( p->rc, g ); attachAsLC ( v->rc, p );
0015 attachAsRC ( p, g ); attachAsRC ( v, p );
0016 } else {
0017 attachAsLC ( v->rc, p ); attachAsRC ( g, v->lc );
0018 attachAsLC ( g, v ); attachAsRC ( v, p );
0019 }
0020 else if ( IsRChild ( *p ) ) {
0021 attachAsRC ( g, p->lc ); attachAsRC ( p, v->lc );
0022 attachAsLC ( g, p ); attachAsLC ( p, v );
0023 } else {
0024 attachAsRC ( p, v->lc ); attachAsLC ( v->rc, g );
0025 attachAsRC ( v, g ); attachAsLC ( p, v );
0026 }
0027 if ( !gg ) v->parent = NULL;
0028 else
0029 ( g == gg->lc ) ? attachAsLC ( v, gg ) : attachAsRC ( gg, v );
0030 updateHeight ( g ); updateHeight ( p ); updateHeight ( v );
0031 }
0032 if ( p = v->parent ) {
0033 if ( IsLChild ( *v ) ) { attachAsLC ( v->rc, p ); attachAsRC ( v, p ); }
0034 else { attachAsRC ( p, v->lc ); attachAsLC ( p, v ); }
0035 updateHeight ( p ); updateHeight ( v );
0036 }
0037 v->parent = NULL; return v;
0038 }
|
查找算法

插入算法

实现
1
2
3
4
5
6
7
8
9
10
11
12
| template <typename T> BinNodePosi<T> Splay<T>::insert ( const T& e ) {
0002 if ( !_root ) { _size = 1; return _root = new BinNode<T> ( e ); }
0003 BinNodePosi<T> t = search( e ); if ( e == t->data ) return t;
0004 if ( t->data < e ) {
0005 t->parent = _root = new BinNode<T> ( e, NULL, t, t->rc );
0006 if ( t->rc ) { t->rc->parent = _root; t->rc = NULL; }
0007 } else {
0008 t->parent = _root = new BinNode<T> ( e, NULL, t->lc, t );
0009 if ( t->lc ) { t->lc->parent = _root; t->lc = NULL; }
0010 }
0011 _size++; updateHeightAbove ( t ); return _root;
0012 }
|
删除算法
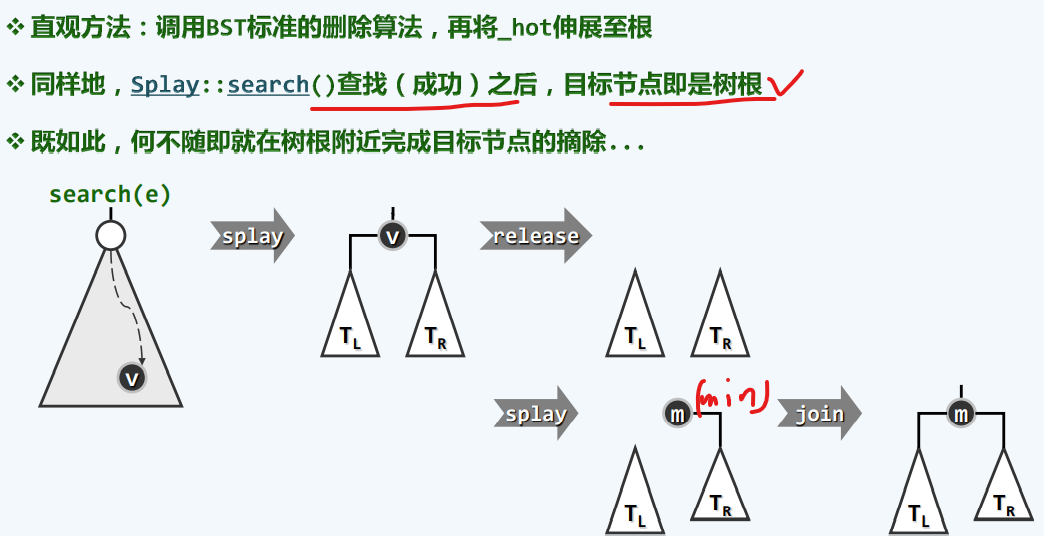
找右子树最小来代替当树根,如果忘记了去看中序遍历迭代板
1
2
3
4
5
6
7
8
9
10
11
| template <typename T> bool Splay<T>::remove ( const T& e ) {
0002 if ( !_root || ( e != search ( e )->data ) ) return false;
0003 BinNodePosi<T> L = _root->lc, R = _root->rc; release(_root);
0004 if ( !R ) {
0005 if ( L ) L->parent = NULL; _root = L;
0006 } else {
0007 _root = R; R->parent = NULL; search( e );
0008 if (L) L->parent = _root; _root->lc = L;
0009 }
0010 if ( --_size ) updateHeight ( _root ); return true;
0011 }
|
评价
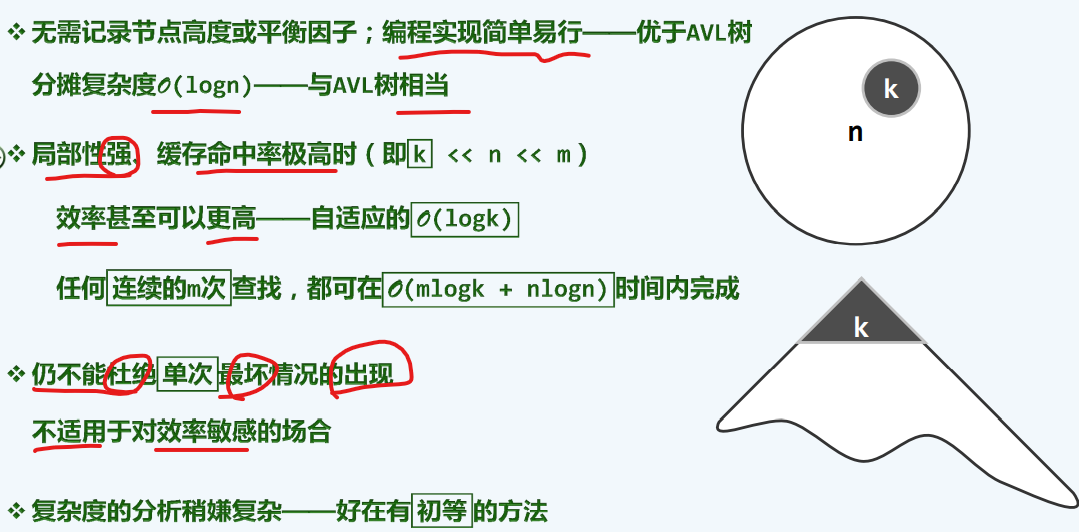
我们仍然无法避免,必须要走n次才能找到点的最坏情况
效率敏感:手术室里辅助的机器
B(-)树
概述
我花了O(325+10000*4)s的时间看完了本节视频,没想到看如此大的视频竟然在渐进意义下O(1)时间完成了(bushi

越来越大的数据

越来越小的内存
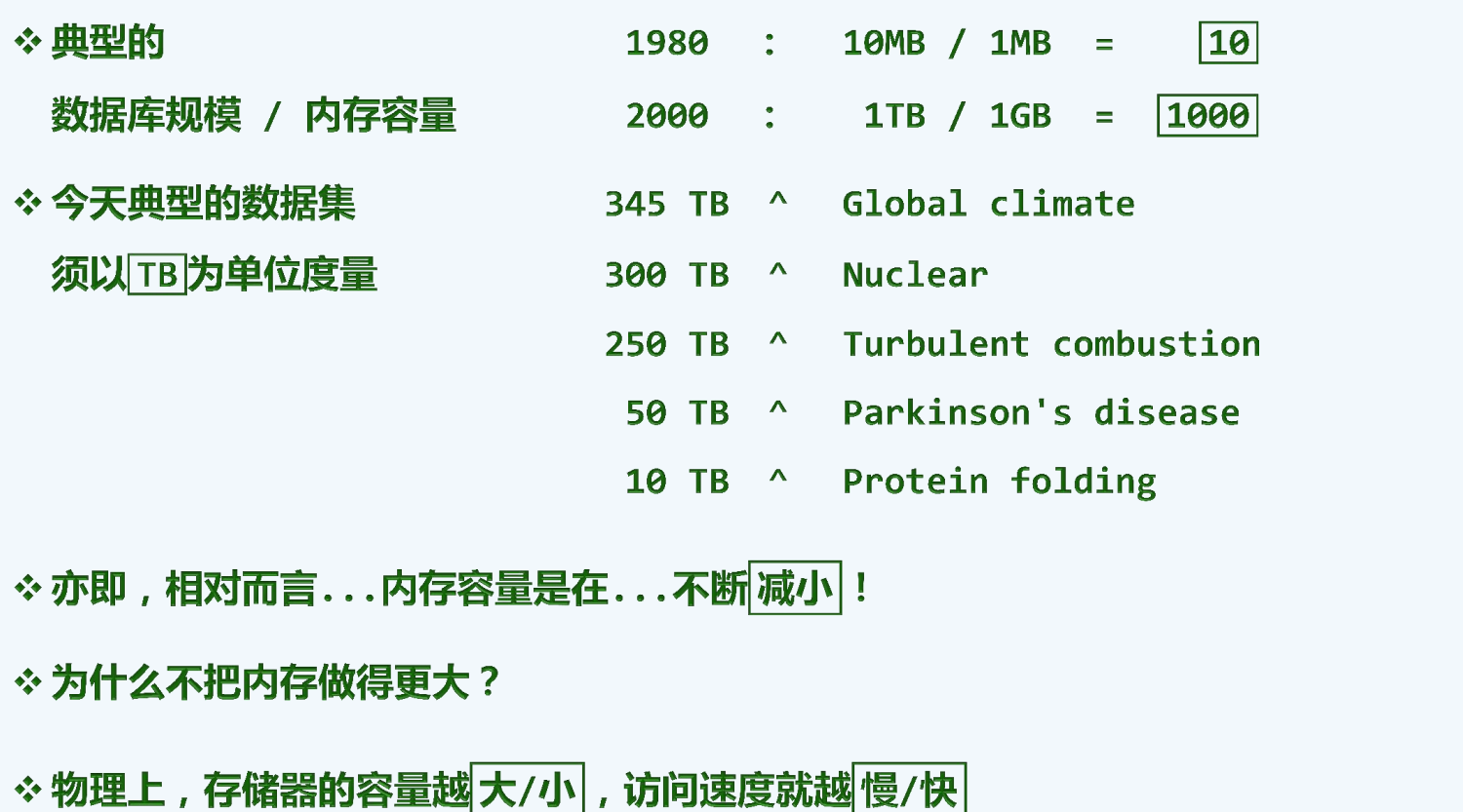
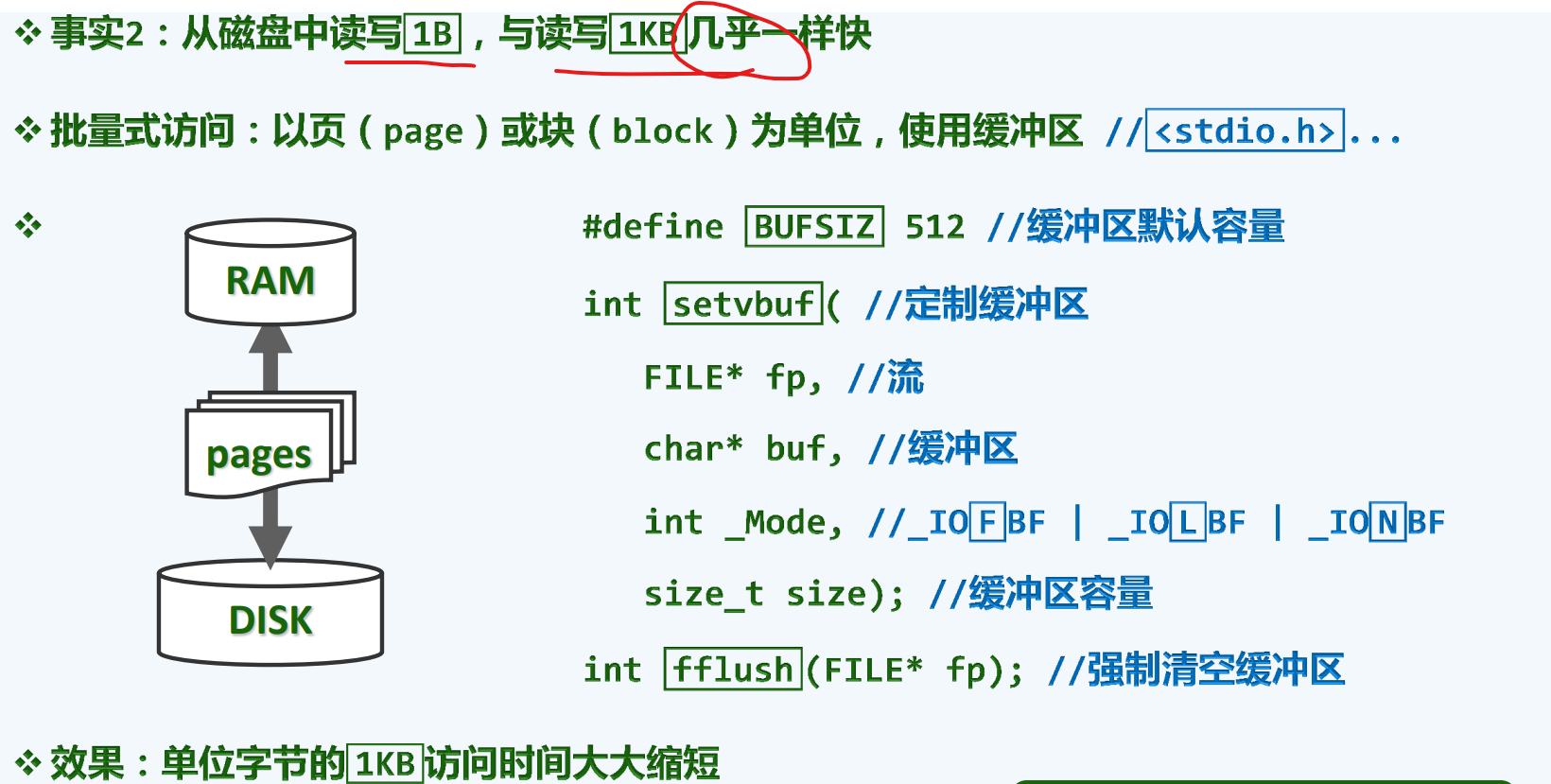
高速缓存

多路平衡
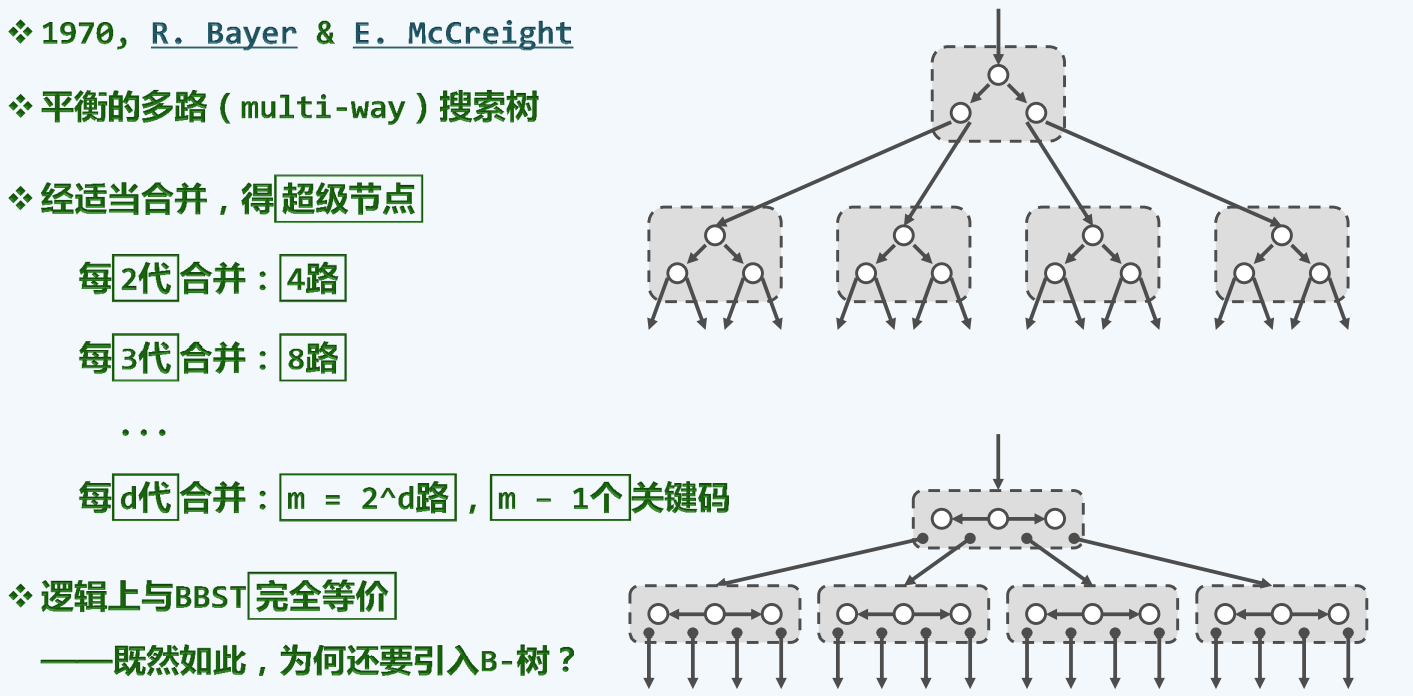
我们忽略掉方框,看右上面那个,毫无疑问就是一颗二叉搜索树,现在我们两层两层的来考察每一个节点,也就是它和左右孩子,如果将每一层的父子三个节点合并成一个超级节点,整棵树就可以等价变换成下面那样
我们的确可以把他称为超级节点,因为它其中并不含有一个关键码,而是多个,就这个例子而言,每个超级节点都含有三个关键码,并且对应有四个分支,推而广之,我们可以合并三代,使得含有七个关键码和八个分支,一般的,如果每D代都进行一次合并,那么每次超级节点都具有m = 2^d分支,和m-1个关键码
与我们此前的二路搜索树并没有本质的区别,那么为什么我们还要引入二路搜索树呢?这是我们需要回答的问题
还是I/O

树的高度,即为io次数,(每下降一层,一次io)
我们可能会想,这样的改进,不也是常数意义的提升吗,可如果常数的单位巨大,那我们就不得不斤斤计较了。

深度统一
于其他树不同,B树的高度是相对于外部节点,而不是叶节点的
外部节点:数值为0,叶节点其实不存在的孩子….
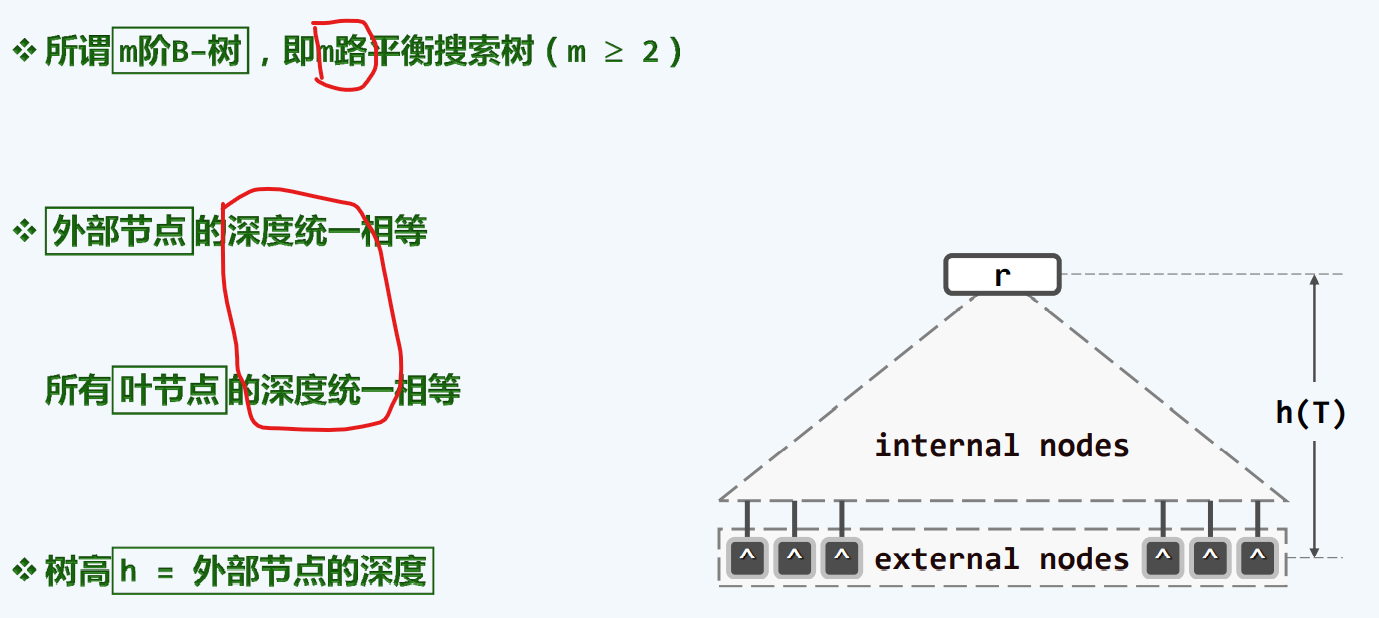
阶次含义
这里定义,以n来代表所含关键码数,也就是对应了n+1个分支
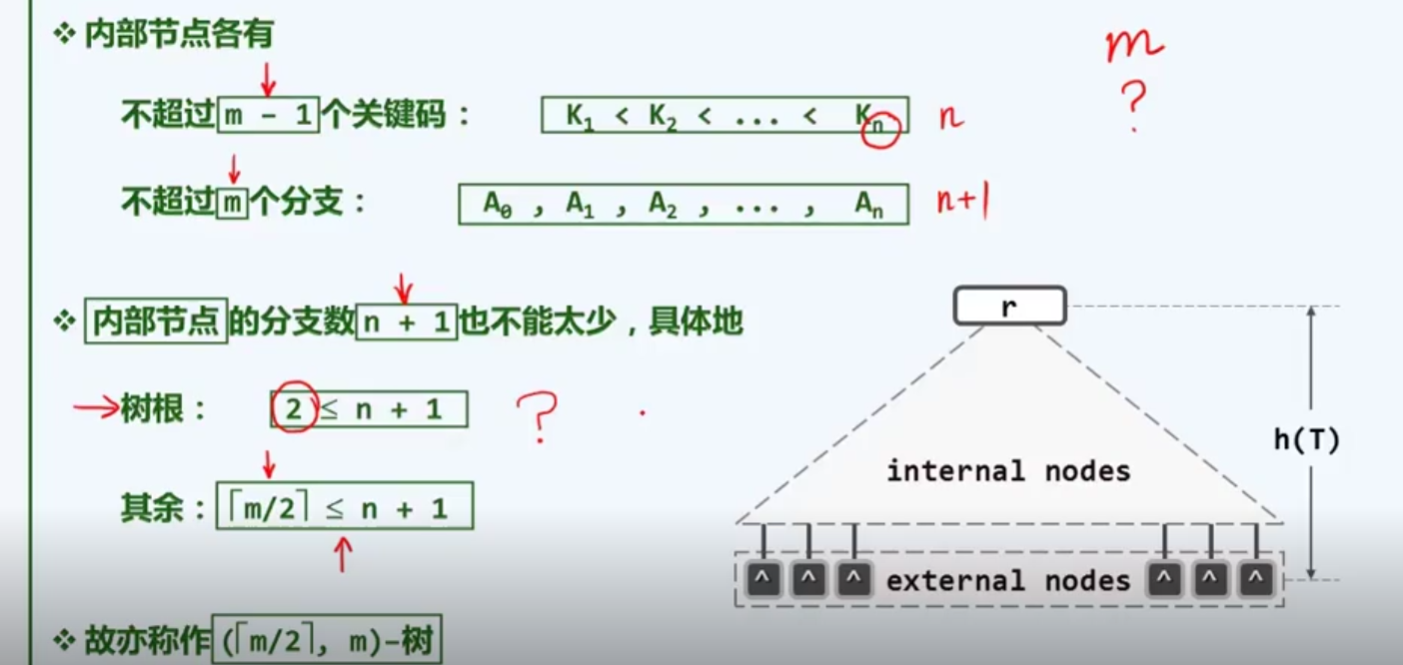

紧凑表示
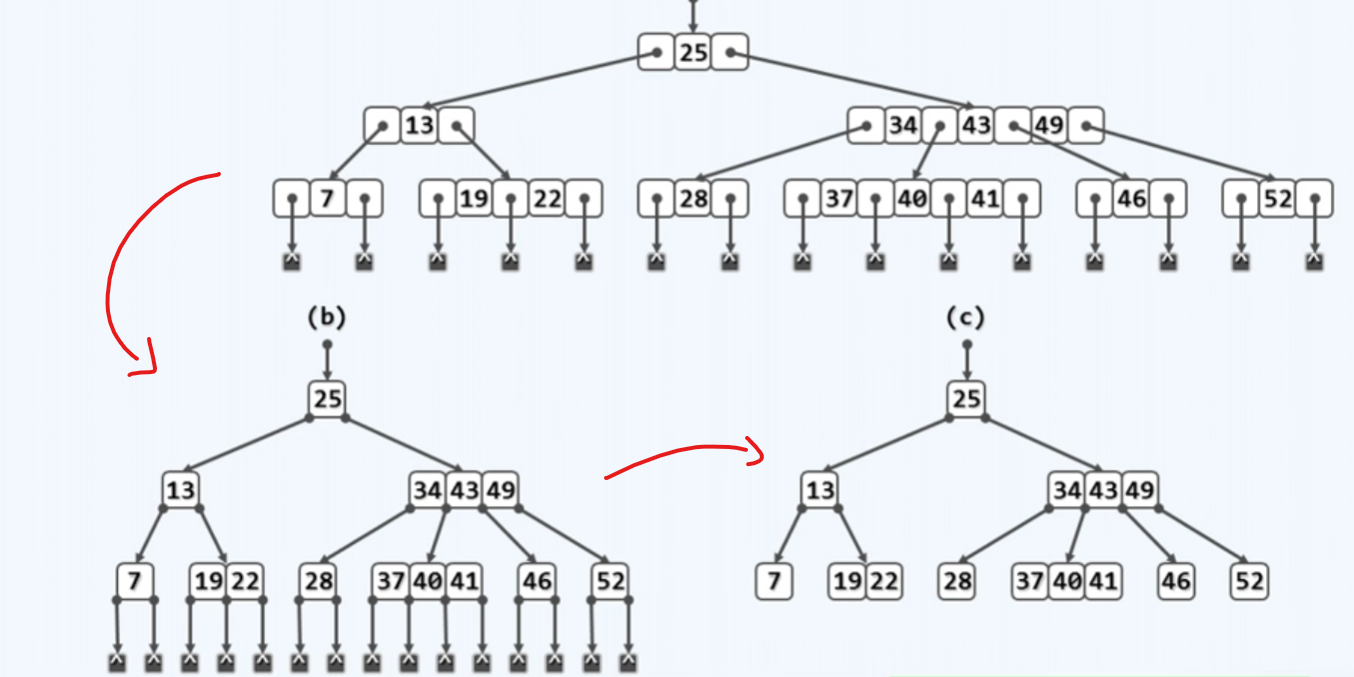
讲授过程中将采用c的方式,节约版面,但是实际上,B树的确存在这么多外部节点,和这么多个引用,不要被误导了!
意义

M阶
定义:

描述一颗 B树时,需要指定它的阶数,什么是 阶数 ?
阶数 表示 此树的节点 最多 有多少个孩子结点(子树),一般用字母 M 表示阶数。
M 阶的B树 :以【子树】讨论
- 上限:每个节点 最多 有 M 个子树 ;
- 下限:
- 根节点至少2个子树,
- 非根节点至少有 ⌈M /2⌉ 个子树 。(M /2 向上取整,如 5/2等于3)
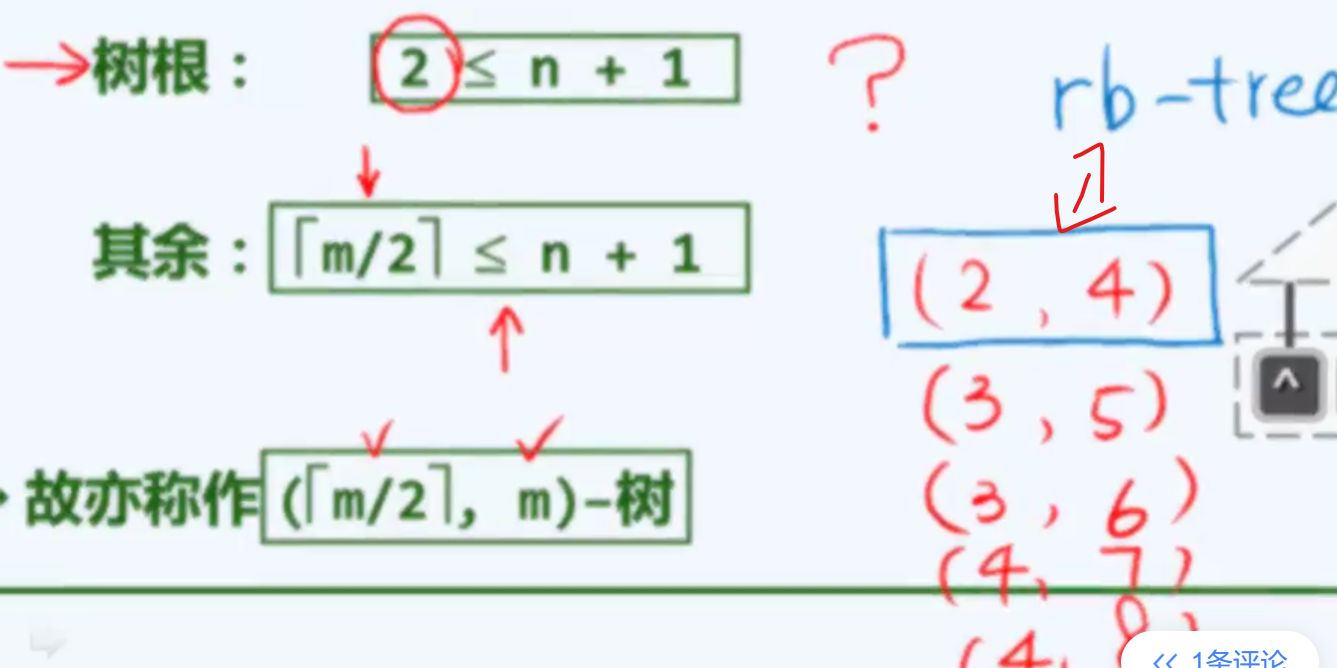
所以也称 M 阶的 B树 为 ( ⌈M /2⌉ , M ) 树 ,即超级节点(除根节点)的子树数的上下限 。
另外,关键字(码)的个数 = 节点子树数 - 1 。
示例:
1
2
3
4
| M = 4 阶的B树,子树个数是(2, 4), 最多含有 3个关键字 和 4个子树
M = 5 阶 , (3, 5), 最多含有 4个关键字 和 5个子树
M = 6 阶 , (3, 6), 最多含有 5个关键字 和 6个子树
123
|
总结,M阶 可理解为 M树,即内含(M-1)个关键字 和 M 个子树。
ADT
BTNode

实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| #include "vector/vector.h"
0002 template <typename T> struct BTNode;
0003 template <typename T> using BTNodePosi = BTNode<T>*;
0004
0005 template <typename T> struct BTNode {
0006
0007 BTNodePosi<T> parent;
0008 Vector<T> key;
0009 Vector<BTNodePosi<T>> child;
0010
0011 BTNode() { parent = NULL; child.insert ( NULL ); }
0012 BTNode ( T e, BTNodePosi<T> lc = NULL, BTNodePosi<T> rc = NULL ) {
0013 parent = NULL; key.insert ( e );
0014 child.insert ( lc ); if ( lc ) lc->parent = this;
0015 child.insert ( rc ); if ( rc ) rc->parent = this;
0016 }
0017 };
|
BTree

实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| #include "BTNode.h"
0002
0003 template <typename T> class BTree {
0004 protected:
0005 int _size;
0006 int _m;
0007 BTNodePosi<T> _root;
0008 BTNodePosi<T> _hot;
0009 void solveOverflow ( BTNodePosi<T> );
0010 void solveUnderflow ( BTNodePosi<T> );
0011 public:
0012 BTree ( int m = 3 ) : _m ( m ), _size ( 0 )
0013 { _root = new BTNode<T>(); }
0014 ~BTree() { if ( _root ) release ( _root ); }
0015 int const order() { return _m; }
0016 int const size() { return _size; }
0017 BTNodePosi<T> & root() { return _root; }
0018 bool empty() const { return !_root; }
0019 BTNodePosi<T> search ( const T& e );
0020 bool insert ( const T& e );
0021 bool remove ( const T& e );
0022 };
|
查找
诀窍:
算法过程
一系列顺序查找,一系列IO操作,相间隔组成的搜寻
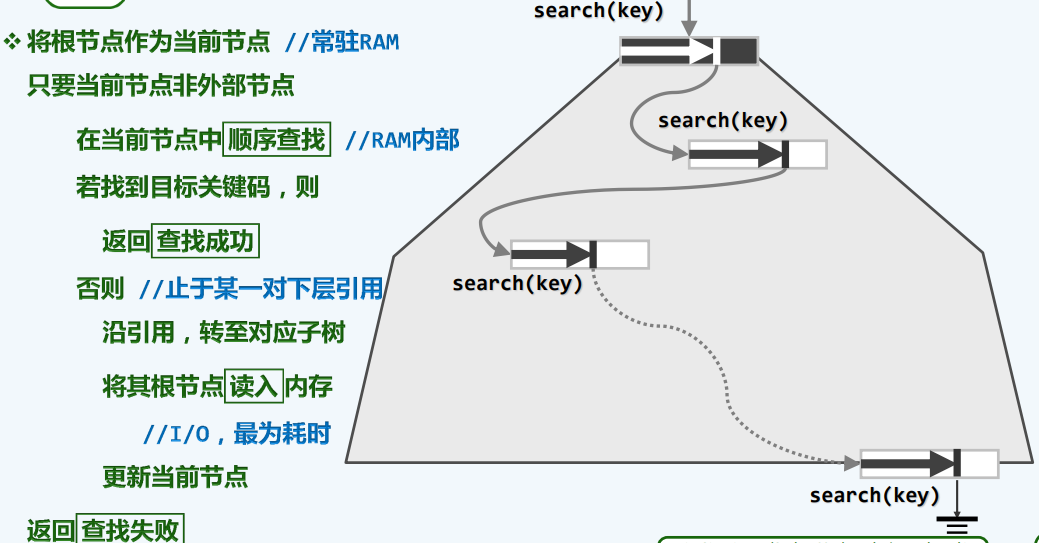
实例
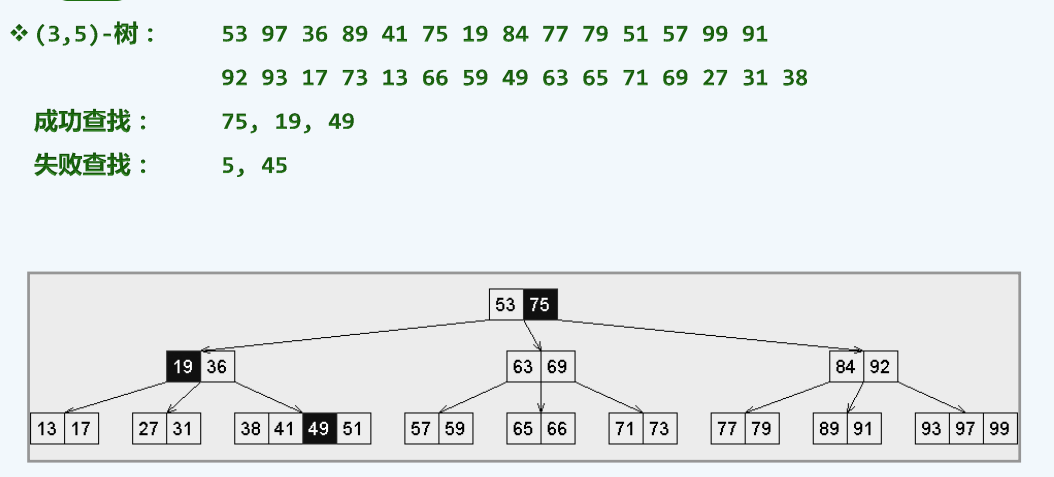
算法实现
O处失败,代表着没有比O+1更大,也就是直接走它的Rchild里继续搜索
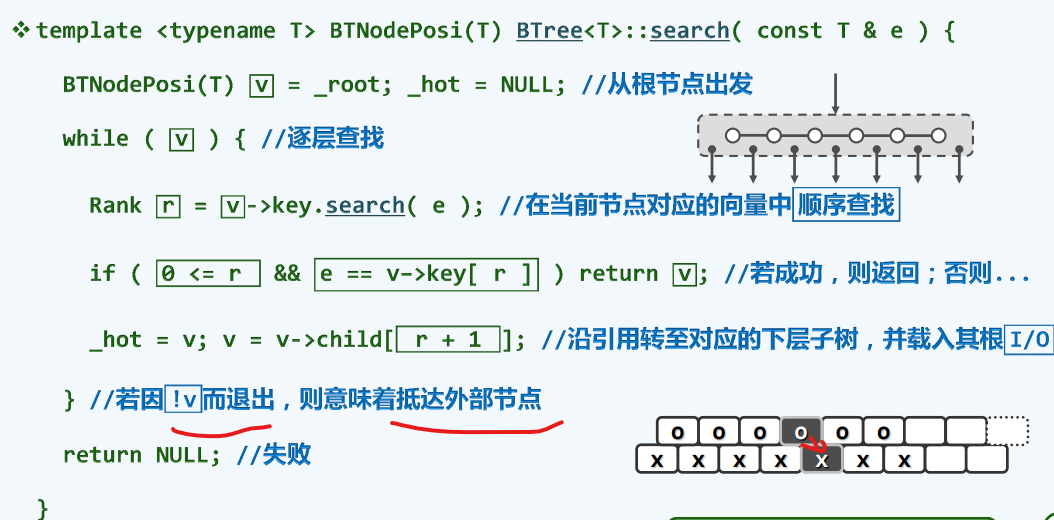
主次成本
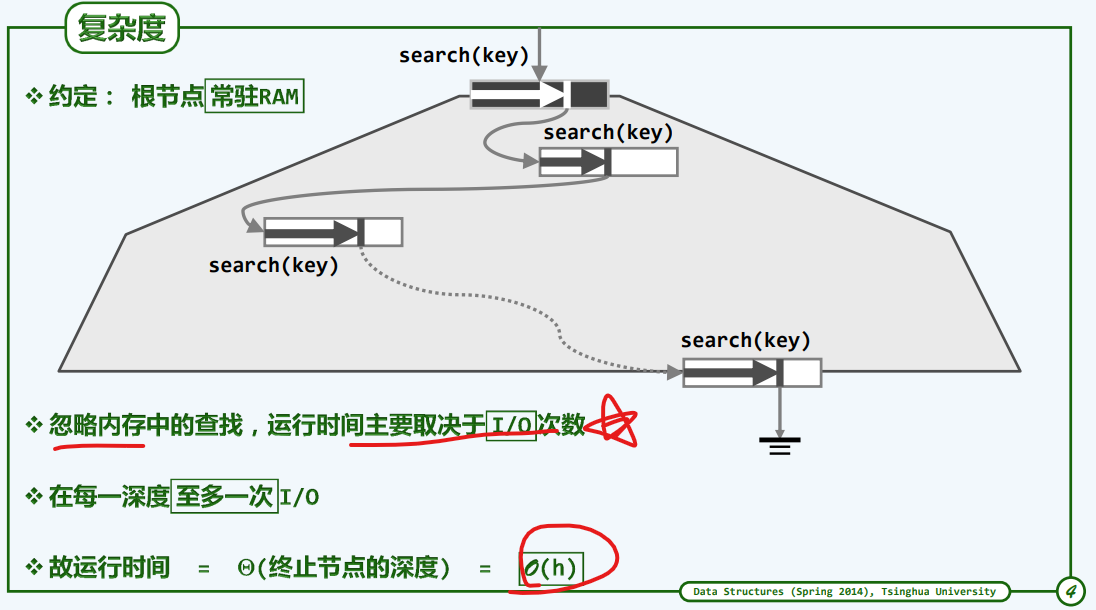
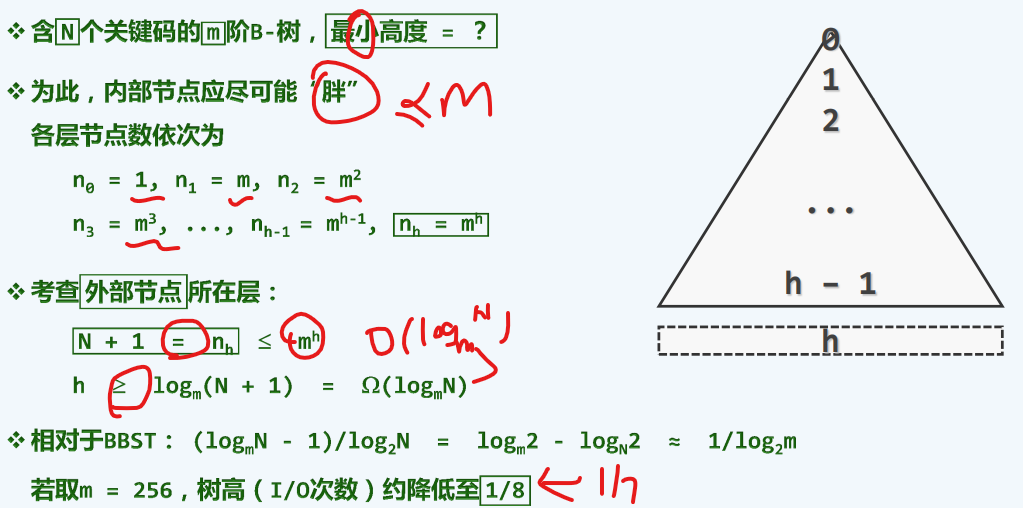
最大高度


要想树最高,则边最少,每个分支取做下限([m/2]),关键点就取1个作为一个超级节点
此时树高降低1/7
最小高度
M详情看前面M阶
插入
中位数
因为这里左闭右开,所以如此定义

分裂

为何如此游刃有余,则得益于B树定义的精妙

插上去之后,下面的两部分,也不会低于m/2的上整
再分裂
该节点上溢之后,它上去了会有继续上溢的风险,可能会持续的发生,不过好消息是,满足单调性,充其量是遍历各层,抵达根节点,但根节点处理有所不同。
分裂到根
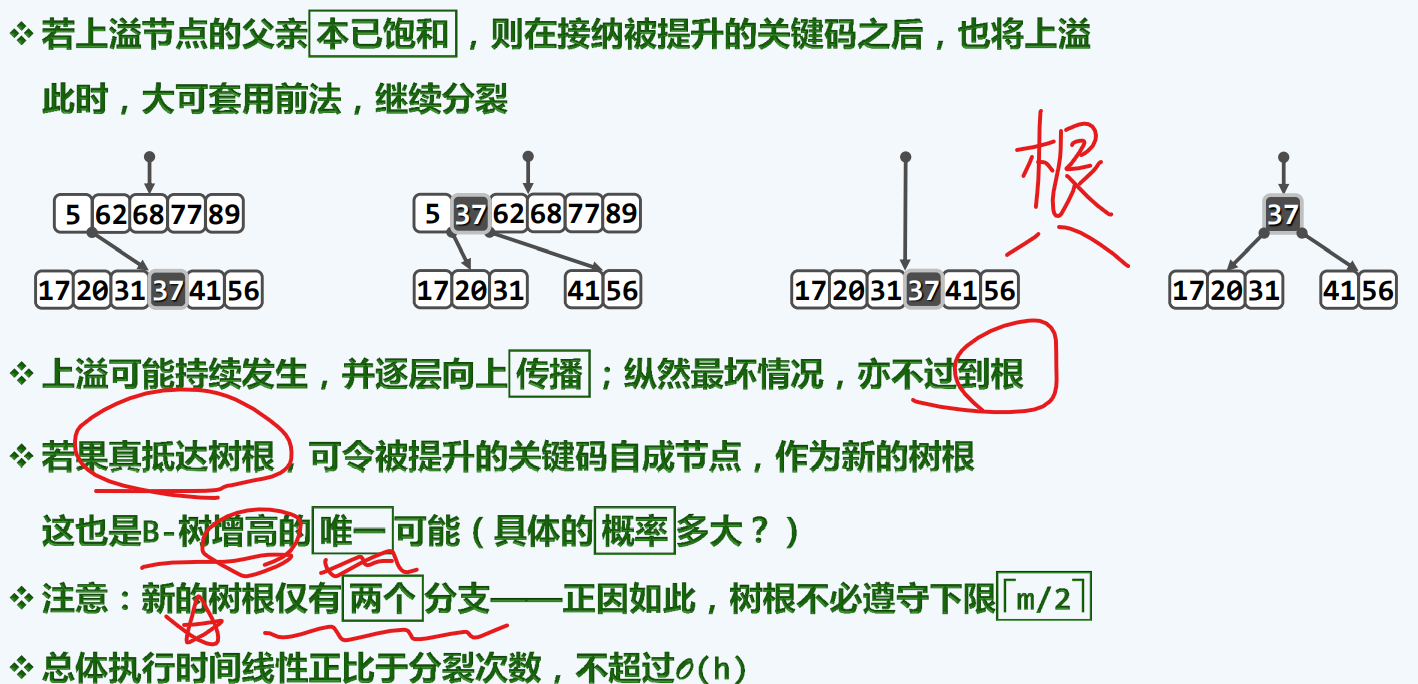
所以说!!阶次含义中加入的那条修正案,是断乎不可省略的!!!!
累计不过h次,所以整个时间不会高于它的高度,这也是我们所期望的。
实例
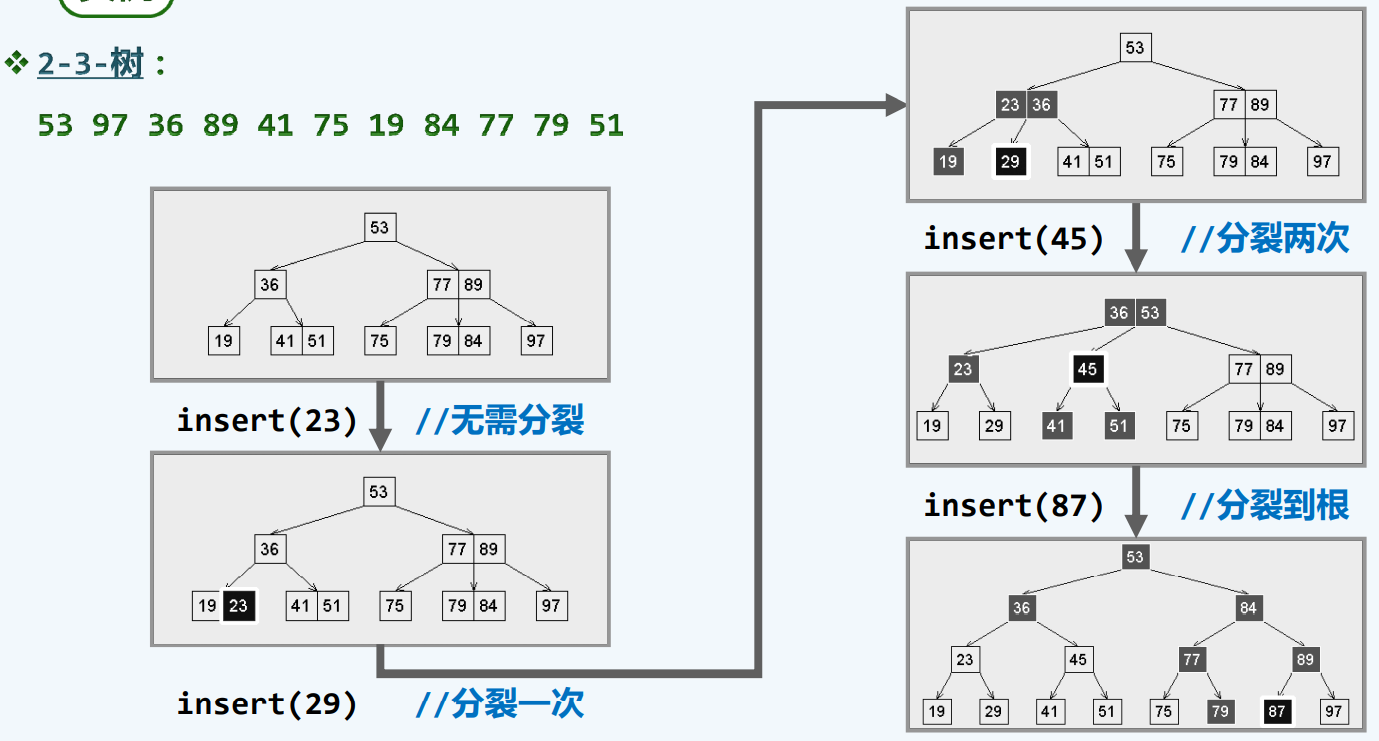
实战代码
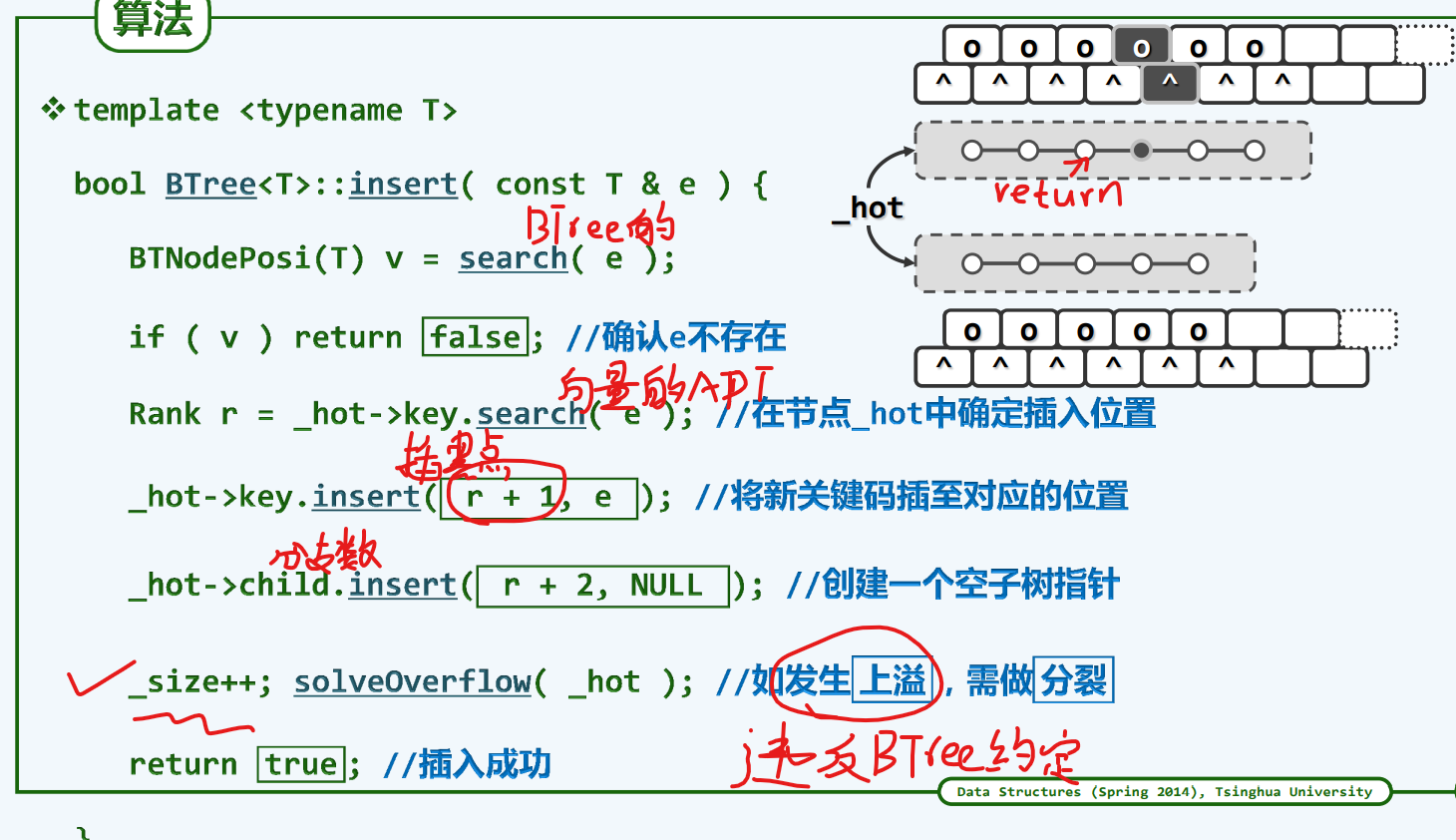
Insert()
1
2
3
4
5
6
7
8
9
| template <typename T> bool BTree<T>::insert ( const T& e ) {
0002 BTNodePosi<T> v = search ( e ); if ( v ) return false;
0003 Rank r = _hot->key.search ( e );
0004 _hot->key.insert ( r + 1, e );
0005 _hot->child.insert ( r + 2, NULL );
0006 _size++;
0007 solveOverflow ( _hot );
0008 return true;
0009 }
|
上溢修复
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| template <typename T>
0002 void BTree<T>::solveOverflow ( BTNodePosi<T> v ) {
0003 if ( _m > v->key.size() ) return;
0004 Rank s = _m / 2;
0005 BTNodePosi<T> u = new BTNode<T>();
0006 for ( Rank j = 0; j < _m - s - 1; j++ ) {
0007 u->child.insert ( j, v->child.remove ( s + 1 ) );
0008 u->key.insert ( j, v->key.remove ( s + 1 ) );
0009 }
0010 u->child[_m - s - 1] = v->child.remove ( s + 1 );
0011 if ( u->child[0] )
0012 for ( Rank j = 0; j < _m - s; j++ )
0013 u->child[j]->parent = u;
0014 BTNodePosi<T> p = v->parent;
0015 if ( !p ) { _root = p = new BTNode<T>(); p->child[0] = v; v->parent = p; }
0016 Rank r = 1 + p->key.search ( v->key[0] );
0017 p->key.insert ( r, v->key.remove ( s ) );
0018 p->child.insert ( r + 1, u ); u->parent = p;
0019 solveOverflow ( p );
0020 }
|
删除
结合刚刚插入所采用的分裂策略,我们可能很容易想到删除使用合并,是的,这的确是可以采用的预案之一,但优先级最高的并不是它

旋转

合并

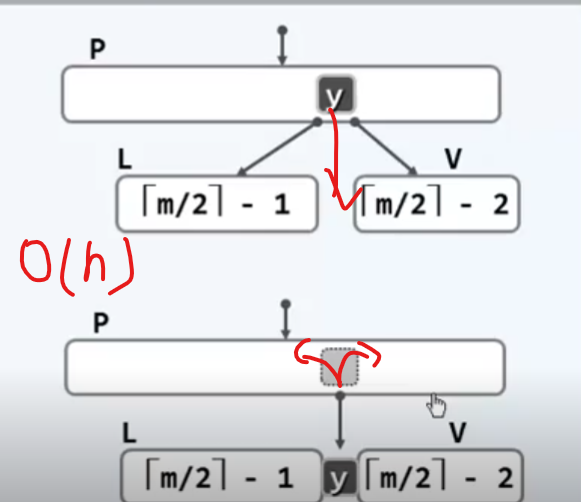
这也是我们预期的好结果!
实例
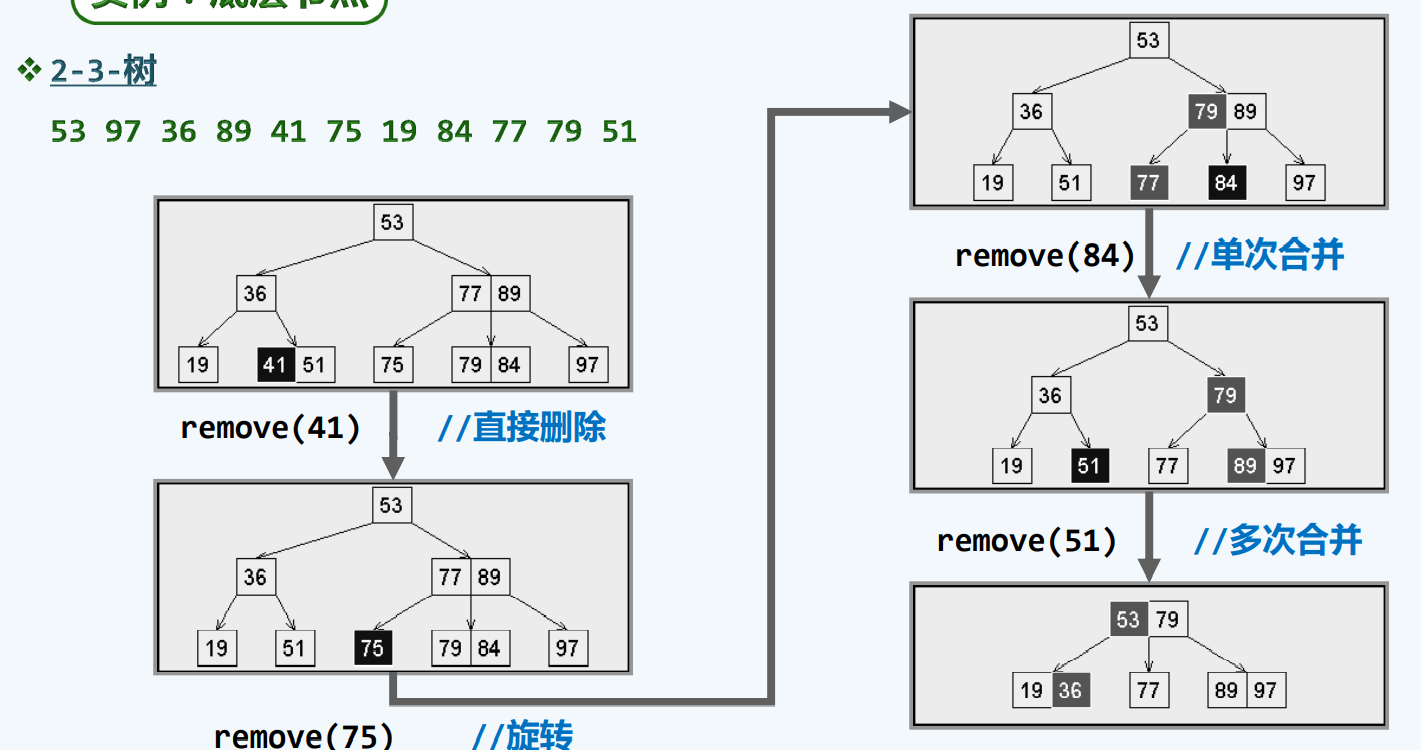
实战代码
remove
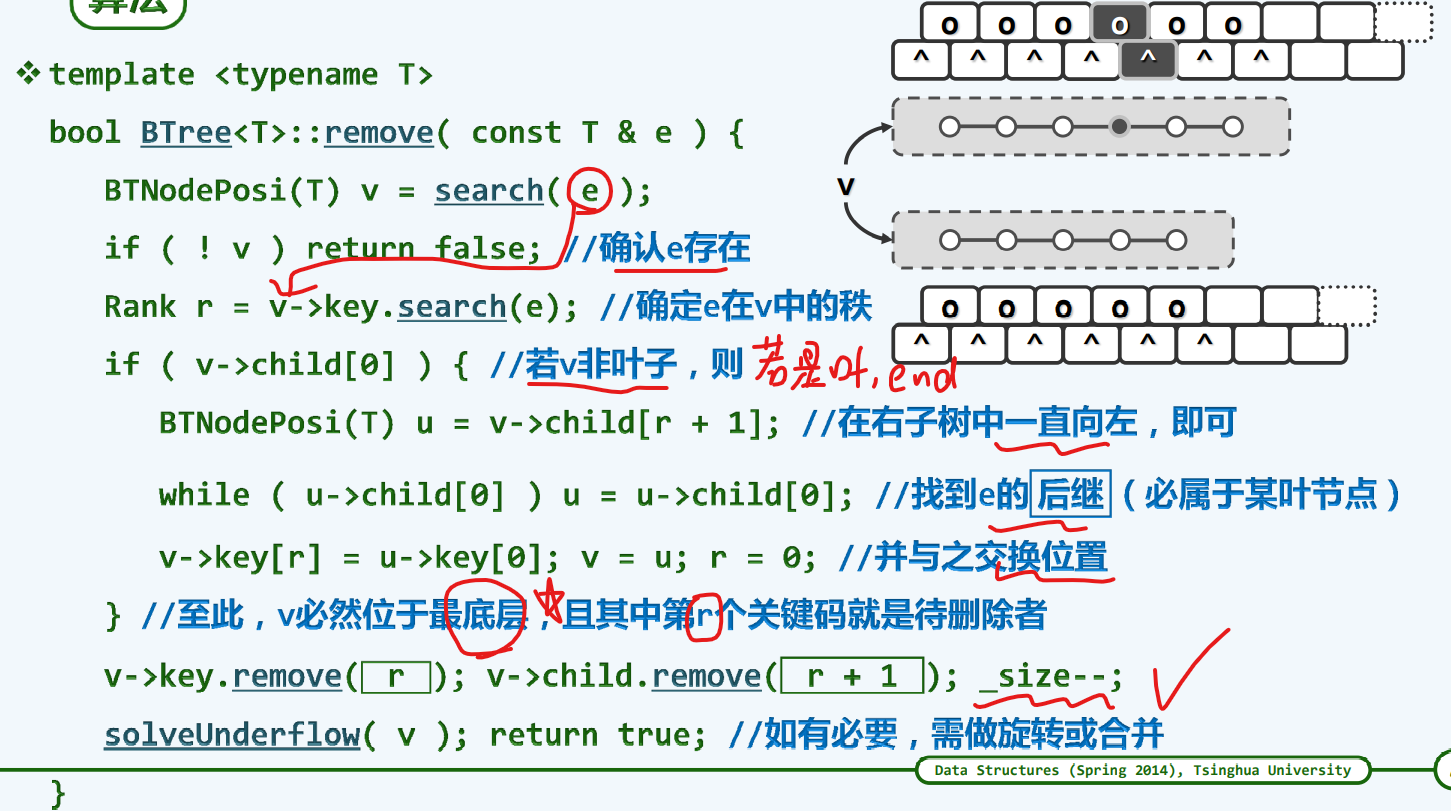
1
2
3
4
5
6
7
8
9
10
11
12
| template <typename T> bool BTree<T>::remove ( const T& e ) {
0002 BTNodePosi<T> v = search ( e ); if ( !v ) return false;
0003 Rank r = v->key.search ( e );
0004 if ( v->child[0] ) {
0005 BTNodePosi<T> u = v->child[r+1];
0006 while ( u->child[0] ) u = u->child[0];
0007 v->key[r] = u->key[0]; v = u; r = 0;
0008 }
0009 v->key.remove ( r ); v->child.remove ( r + 1 ); _size--;
0010 solveUnderflow ( v );
0011 return true;
0012 }
|
下溢修复

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
| template <typename T>
0002 void BTree<T>::solveUnderflow ( BTNodePosi<T> v ) {
0003 if ( ( _m + 1 ) / 2 <= v->child.size() ) return;
0004 BTNodePosi<T> p = v->parent;
0005 if ( !p ) {
0006 if ( !v->key.size() && v->child[0] ) {
0007
0008 _root = v->child[0]; _root->parent = NULL;
0009 v->child[0] = NULL; release ( v );
0010 }
0011 return;
0012 }
0013 Rank r = 0; while ( p->child[r] != v ) r++;
0014
0015
0016
0017 if ( 0 < r ) {
0018 BTNodePosi<T> ls = p->child[r - 1];
0019 if ( ( _m + 1 ) / 2 < ls->child.size() ) {
0020 v->key.insert ( 0, p->key[r - 1] );
0021 p->key[r - 1] = ls->key.remove ( ls->key.size() - 1 );
0022 v->child.insert ( 0, ls->child.remove ( ls->child.size() - 1 ) );
0023
0024 if ( v->child[0] ) v->child[0]->parent = v;
0025 return;
0026 }
0027 }
0028
0029 if ( p->child.size() - 1 > r ) {
0030 BTNodePosi<T> rs = p->child[r + 1];
0031 if ( ( _m + 1 ) / 2 < rs->child.size() ) {
0032 v->key.insert ( v->key.size(), p->key[r] );
0033 p->key[r] = rs->key.remove ( 0 );
0034 v->child.insert ( v->child.size(), rs->child.remove ( 0 ) );
0035
0036 if ( v->child[v->child.size() - 1] )
0037 v->child[v->child.size() - 1]->parent = v;
0038 return;
0039 }
0040 }
0041
0042 if ( 0 < r ) {
0043 BTNodePosi<T> ls = p->child[r - 1];
0044 ls->key.insert ( ls->key.size(), p->key.remove ( r - 1 ) ); p->child.remove ( r );
0045
0046 ls->child.insert ( ls->child.size(), v->child.remove ( 0 ) );
0047 if ( ls->child[ls->child.size() - 1] )
0048 ls->child[ls->child.size() - 1]->parent = ls;
0049 while ( !v->key.empty() ) {
0050 ls->key.insert ( ls->key.size(), v->key.remove ( 0 ) );
0051 ls->child.insert ( ls->child.size(), v->child.remove ( 0 ) );
0052 if ( ls->child[ls->child.size() - 1] ) ls->child[ls->child.size() - 1]->parent = ls;
0053 }
0054 release ( v );
0055 } else {
0056 BTNodePosi<T> rs = p->child[r + 1];
0057 rs->key.insert ( 0, p->key.remove ( r ) ); p->child.remove ( r );
0058
0059 rs->child.insert ( 0, v->child.remove ( v->child.size() - 1 ) );
0060 if ( rs->child[0] ) rs->child[0]->parent = rs;
0061 while ( !v->key.empty() ) {
0062 rs->key.insert ( 0, v->key.remove ( v->key.size() - 1 ) );
0063 rs->child.insert ( 0, v->child.remove ( v->child.size() - 1 ) );
0064 if ( rs->child[0] ) rs->child[0]->parent = rs;
0065 }
0066 release ( v );
0067 }
0068 solveUnderflow ( p );
0069 return;
0070 }
|
复杂度分析
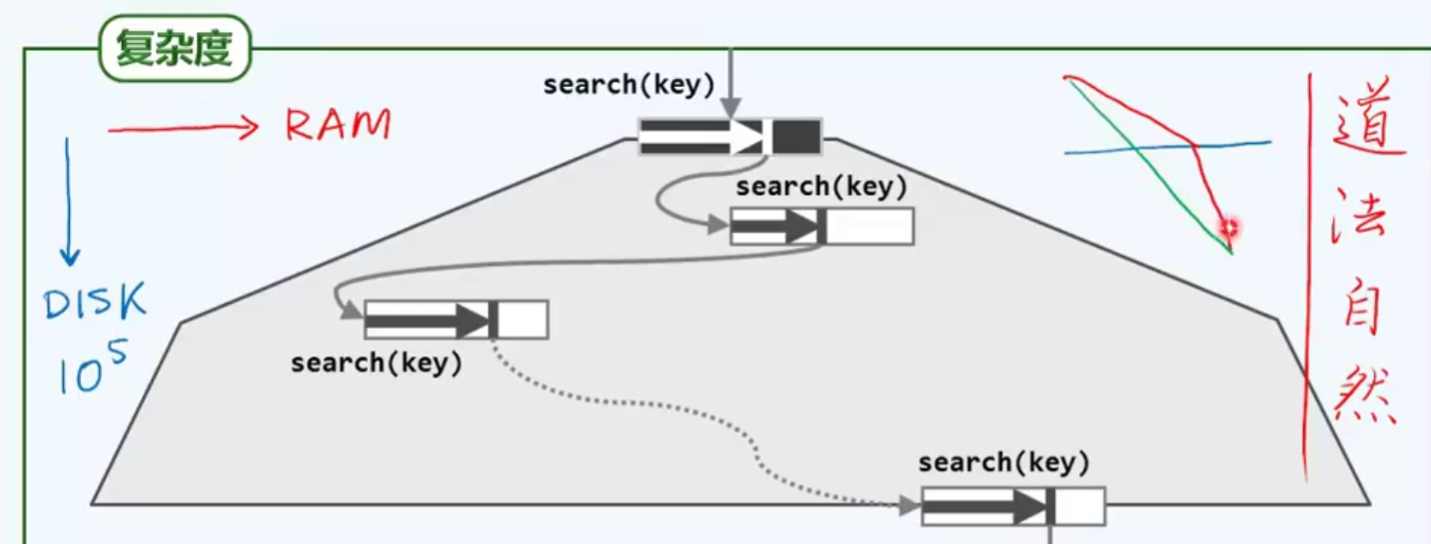
通过自然界的光透射原理,来得到,B树为了满足实际需要,而适当调整自己的形态,变得又宽又矮也就再自然不过的了!
红黑树
概述
为何需要引入?

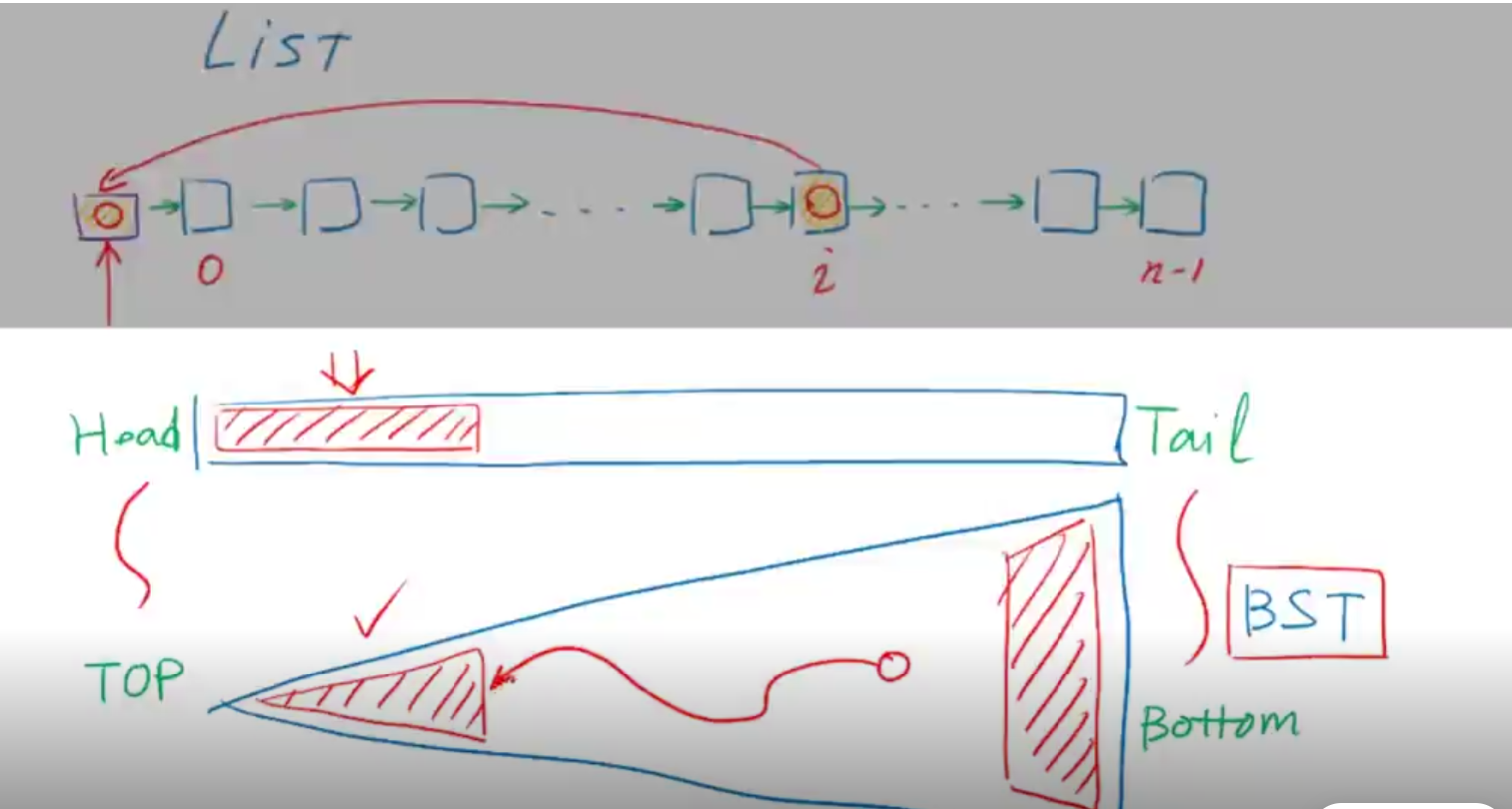
回顾我们之前学习过的结构,每一个状态都是动态变化,往往只存在于朝生暮死的瞬间,我们或许会对它的历史档案感兴趣,如果一个数据结构能支持这种需求,那我们可以把他称为持久性结构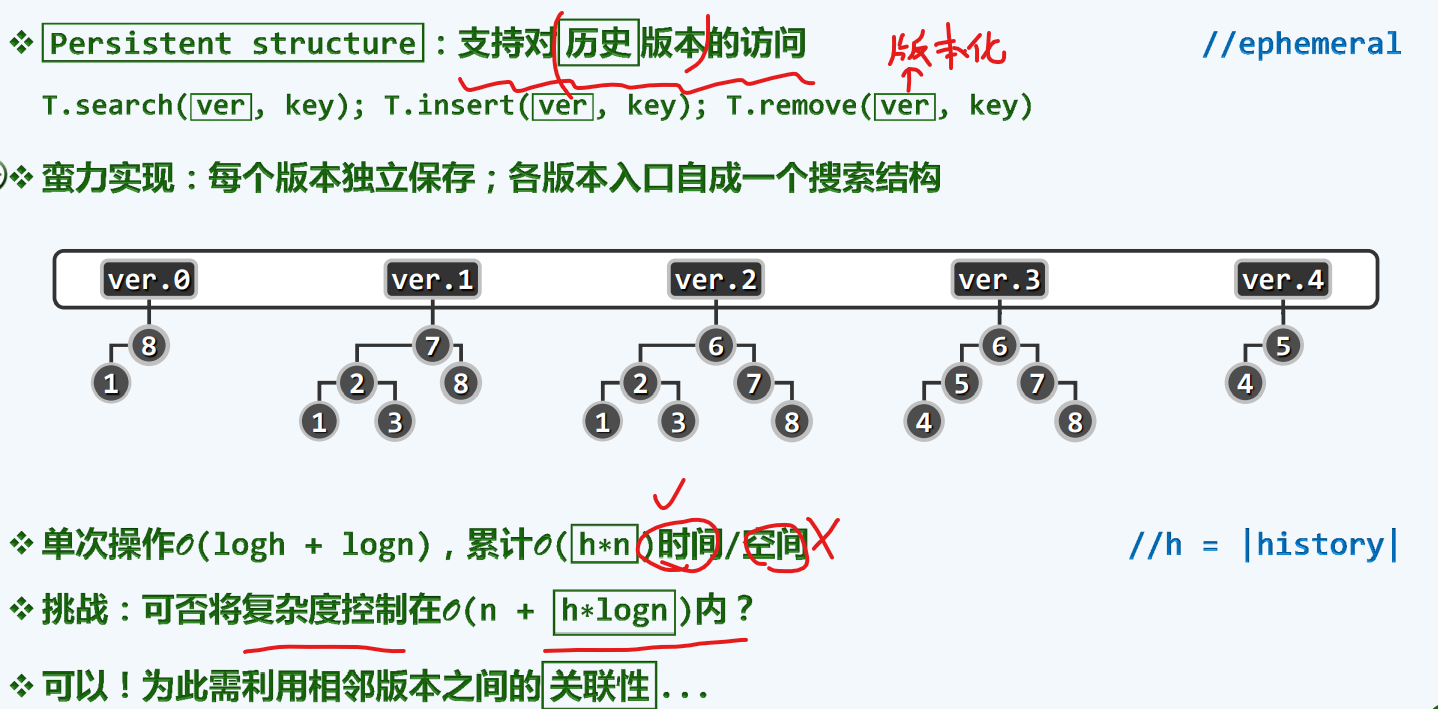
蛮力实现也可以做到,存每一个版本号与一个位置,并且组装成search接口
可是空间消耗是断乎不可接受的。
为此,新的挑战出现了
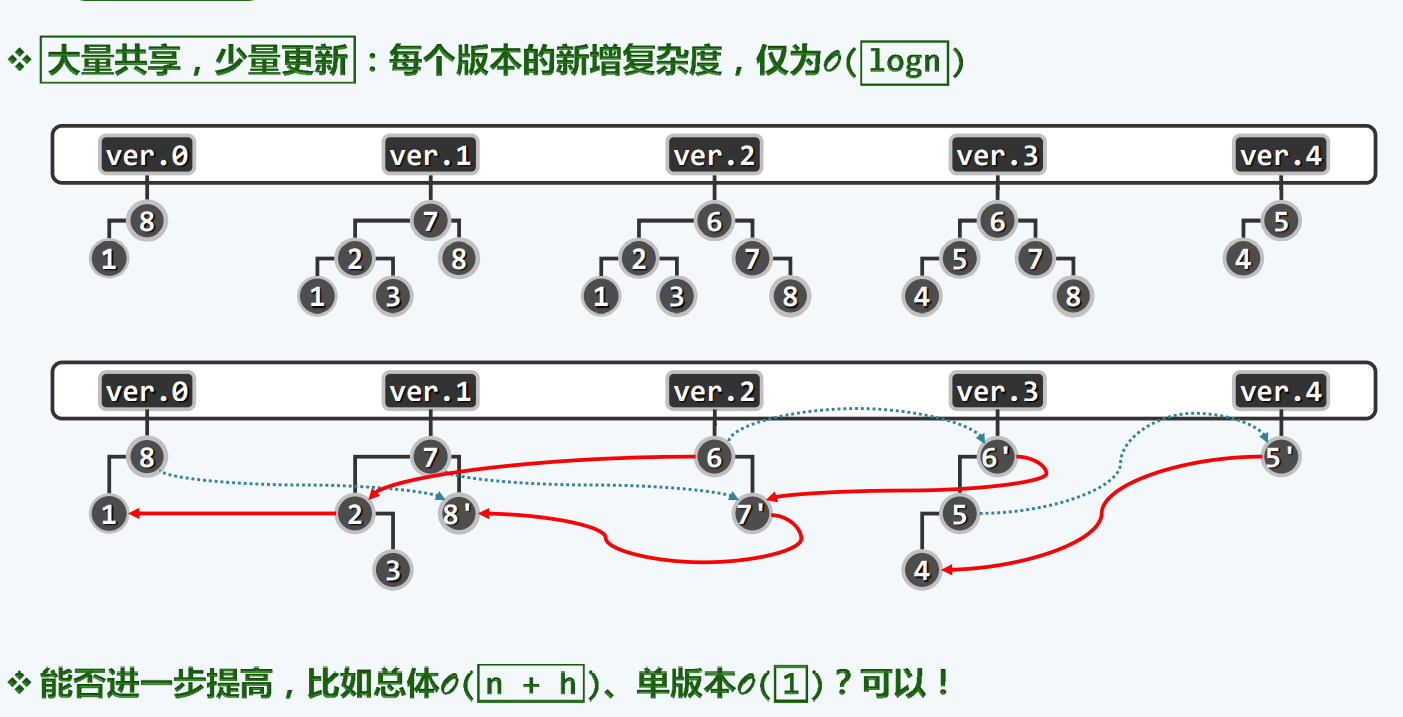
为了做到这一点,(大量共享少量更新),我们需要一种数据结构

定义
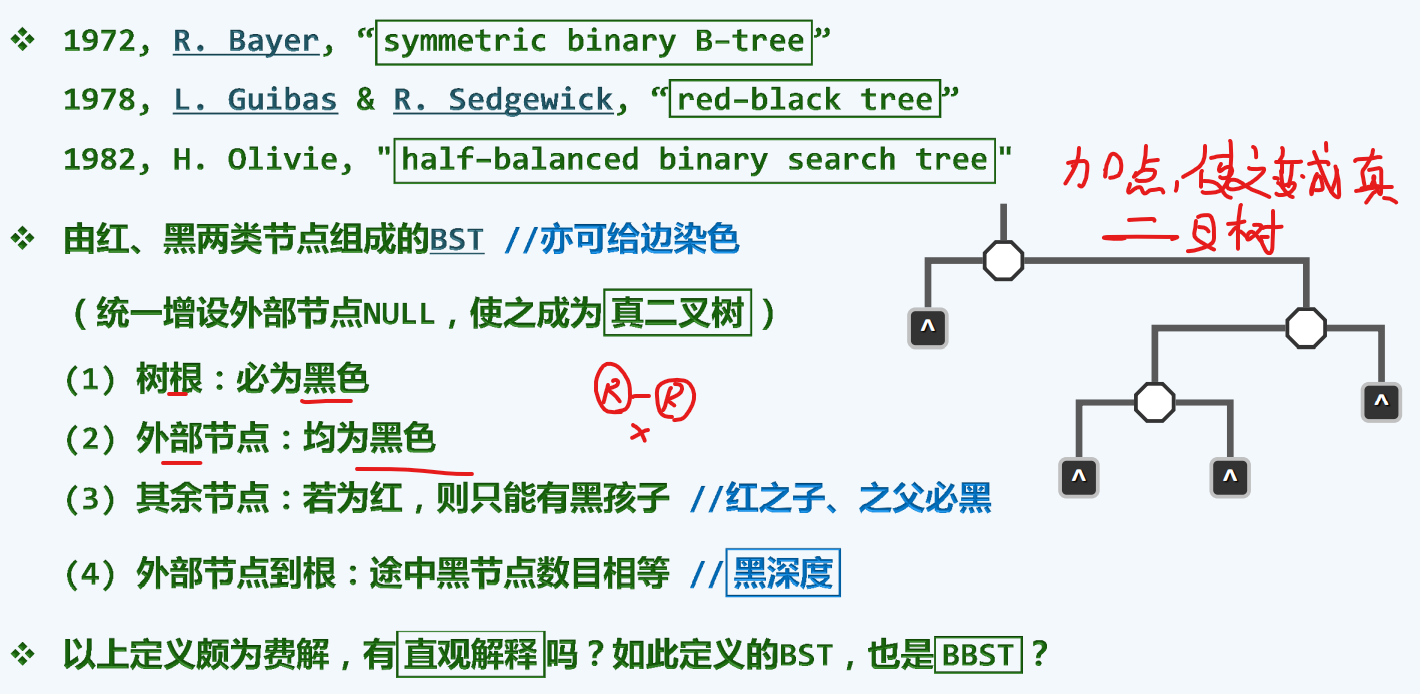
实例验证
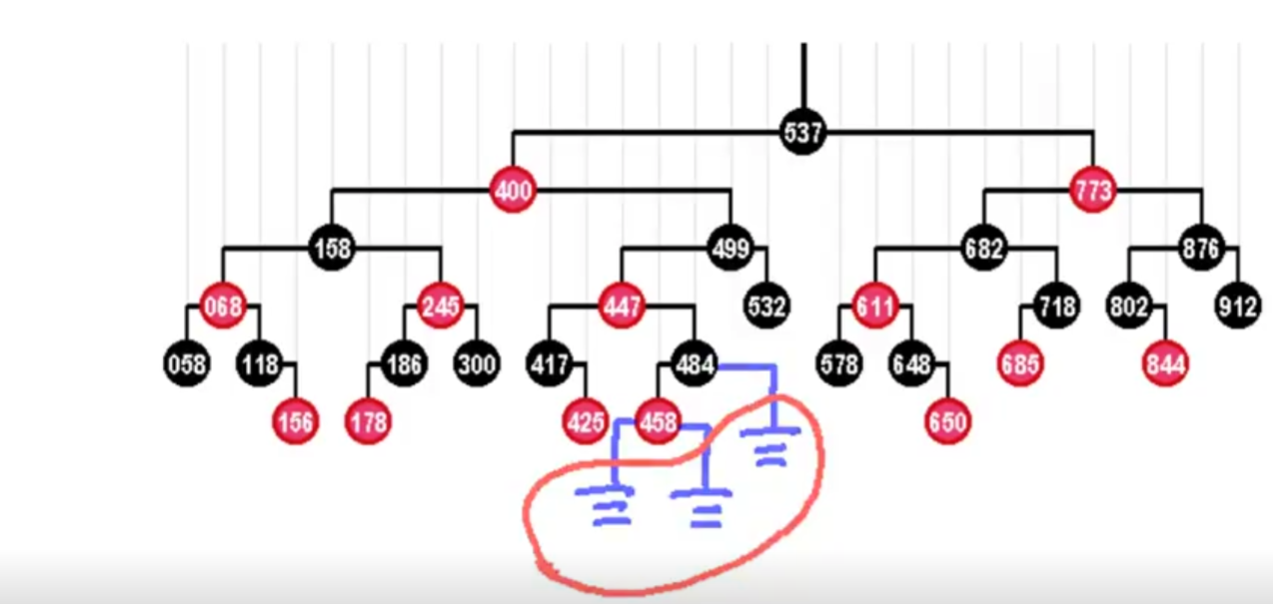
第二条乍一看不满足,其实事实上我们已经对有需要的节点都增加了外部节点
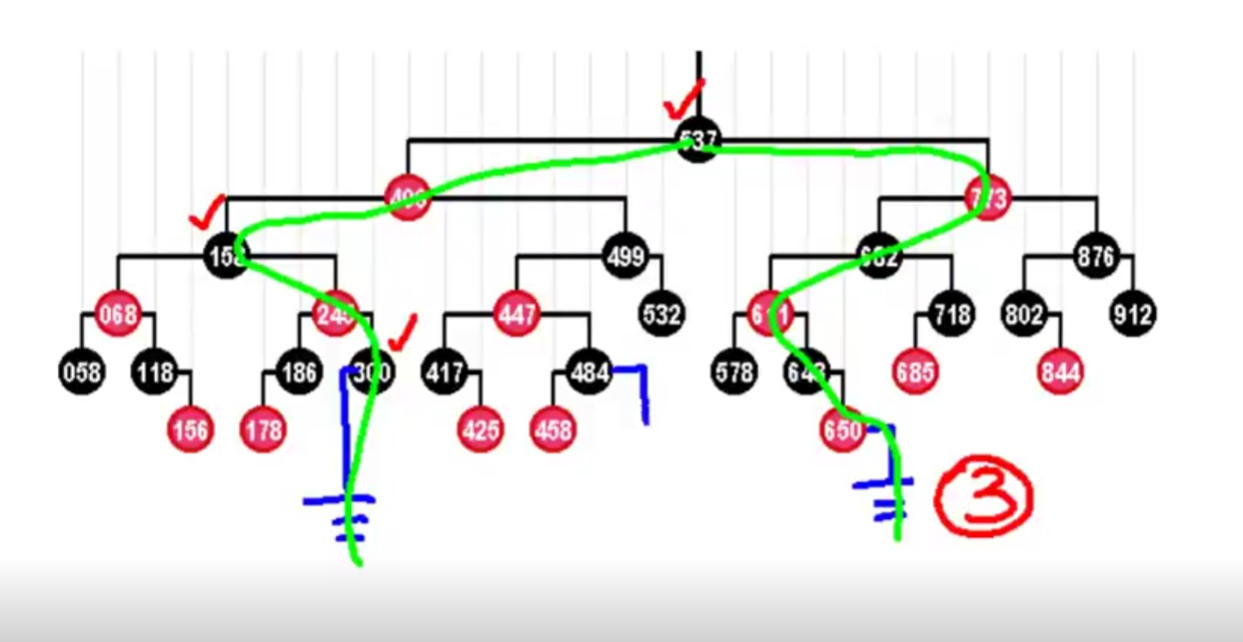
提升变换
变换之前
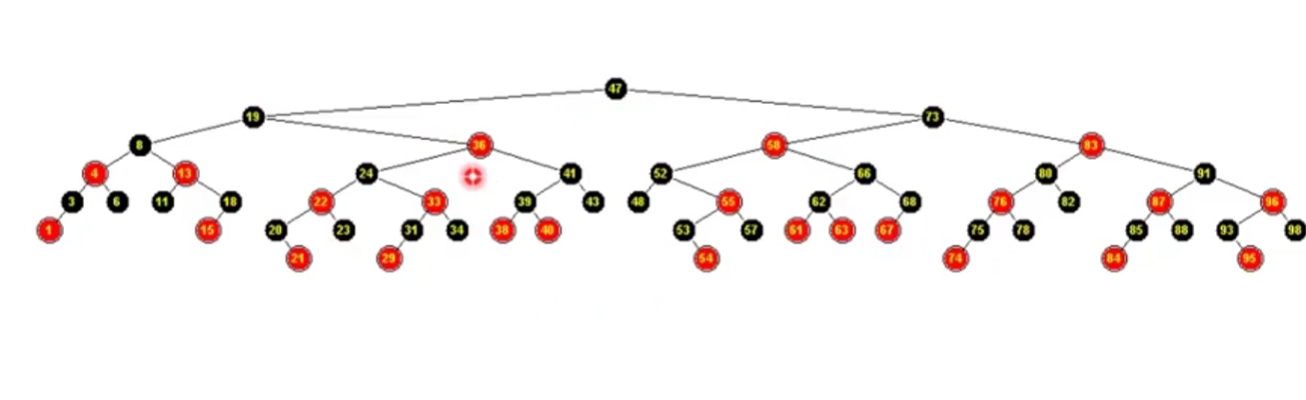
变换之后

Red-Black = B-
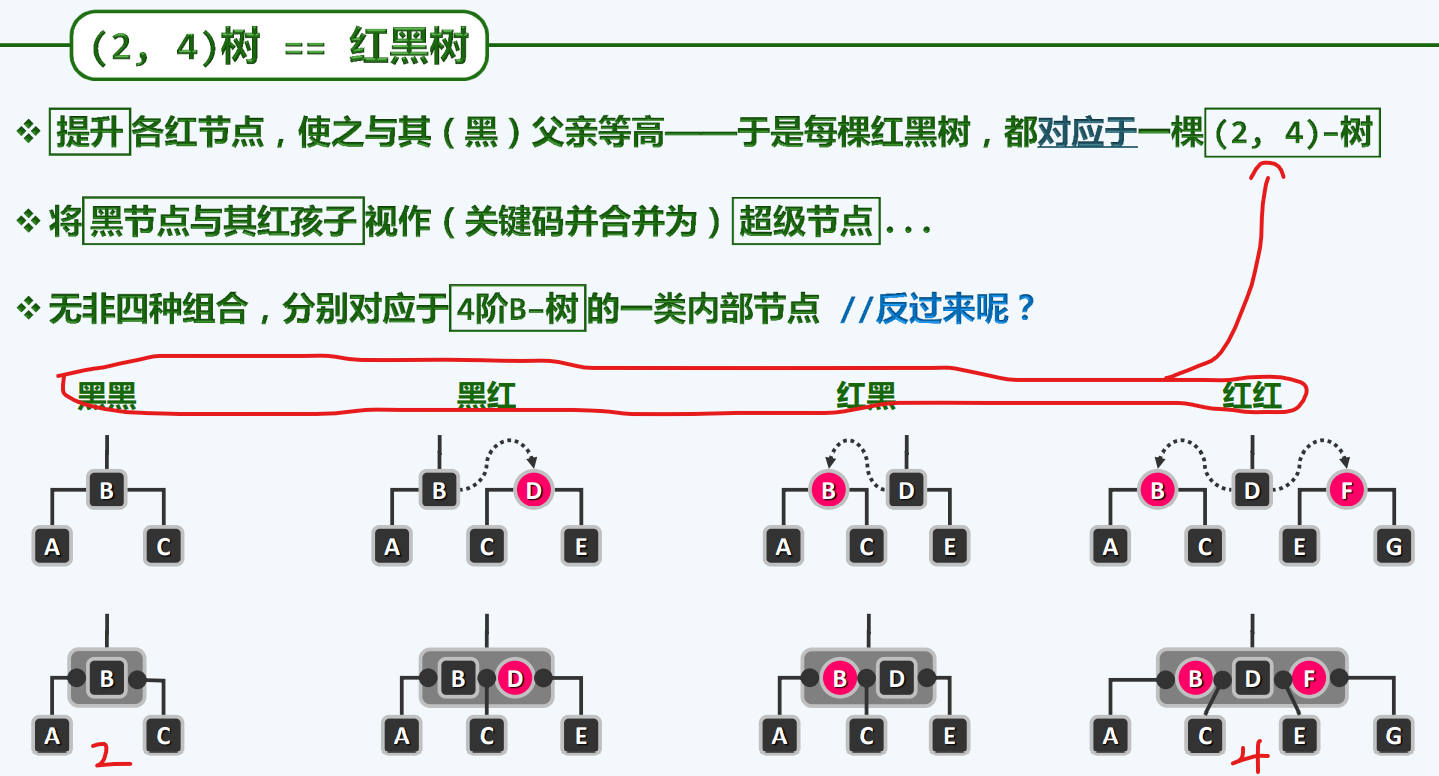
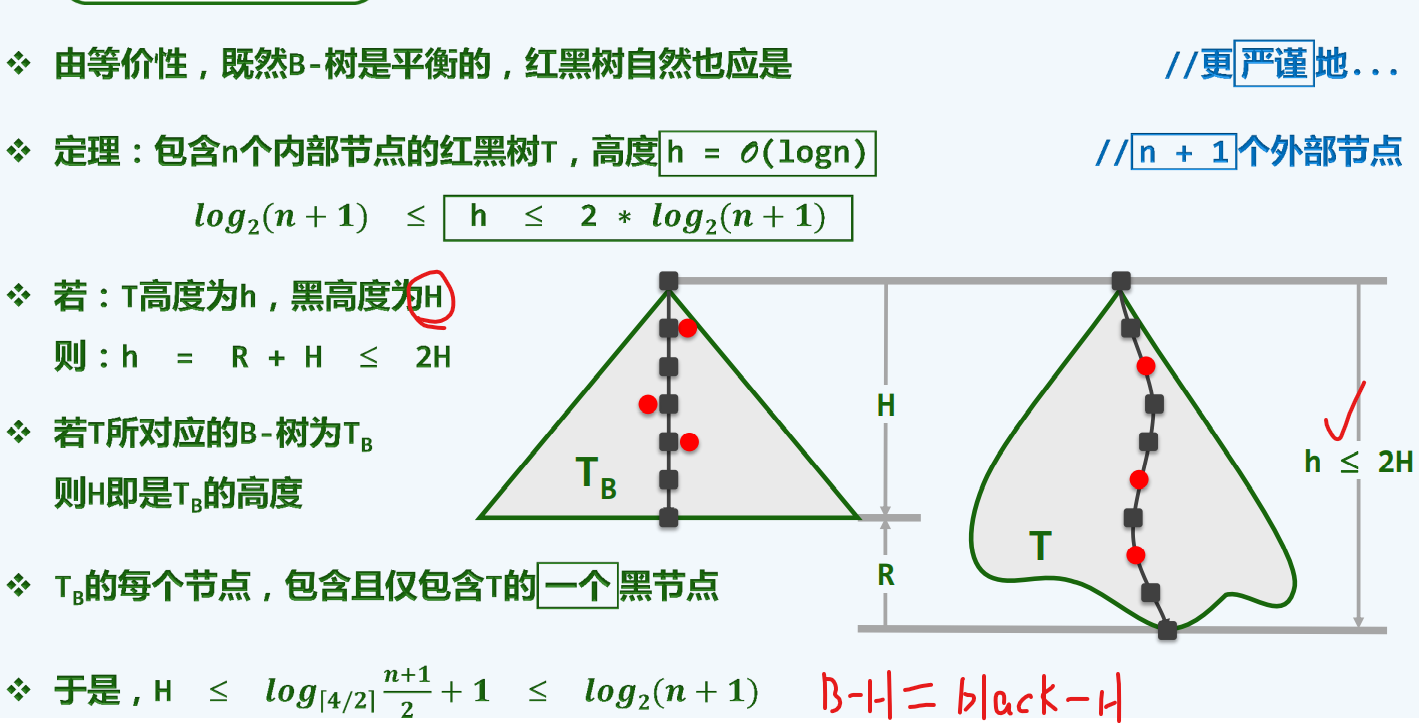
插入

以曲为直
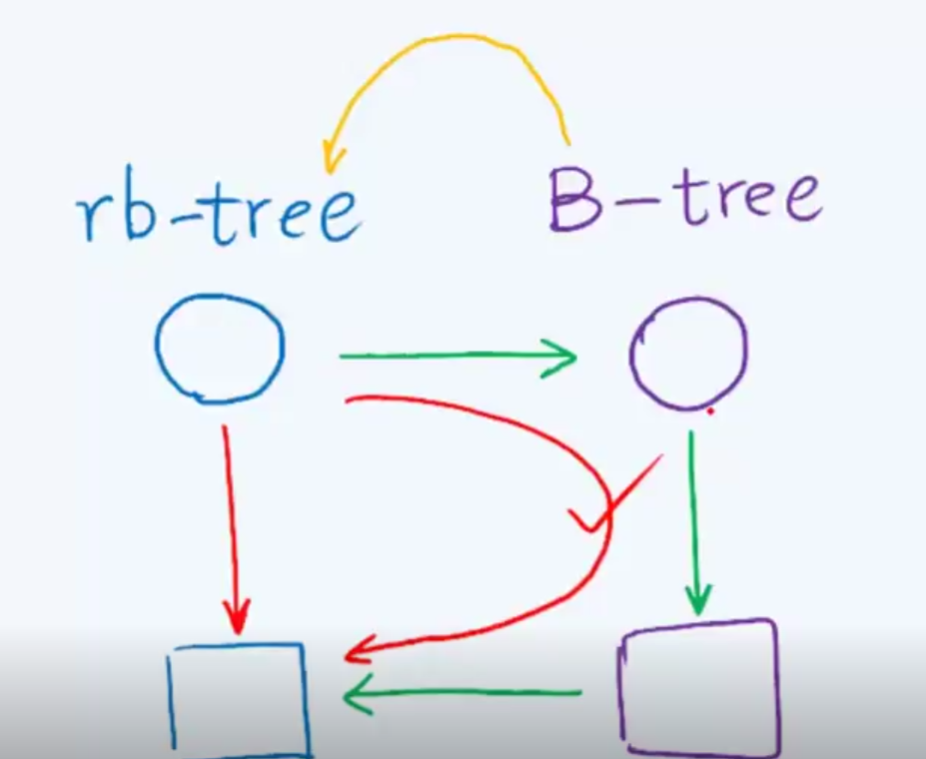
我们做每一颗红黑树的时候,心里都要有对应的一颗B树,通过B树得到最终结果,再返还为红黑树,这样表面上看有点迂回,其实效率反而是最高的。
双红缺陷
我们不妨约定,圆形为红色结点,方型为黑色结点,八边形为待定颜色结点,每一个指向红色结点的边都用虚线表示,每一个指向黑色都实线表示,这样对我们理解有更多的好处。
因为红色结点都要向上提升
染红结点是因为,为了不改变黑色结点的数量
虚线是因为,这类虚线对黑高度是没有影响的

insert()
实现

1
2
3
4
5
| template <typename T> BinNodePosi<T> RedBlack<T>::insert ( const T& e ) {
0002 BinNodePosi<T> & x = search ( e ); if ( x ) return x;
0003 x = new BinNode<T> ( e, _hot, NULL, NULL, 0 ); _size++;
0004 BinNodePosi<T> xOld = x; solveDoubleRed ( x ); return xOld;
0005 }
|
RR-1
若叔父是黑结点,则从b树的角度无需改变拓扑结构,只需要将超级结点中间的红色与祖父的黑色交换即可
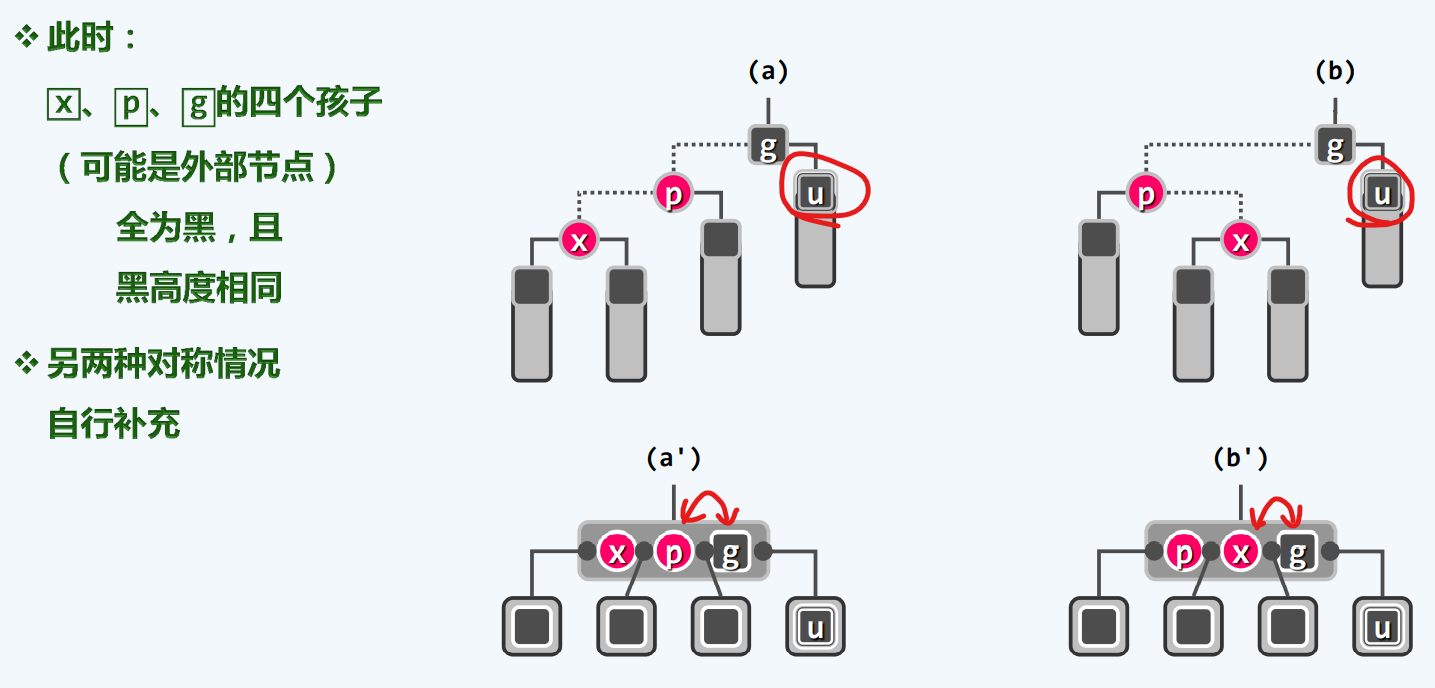

实现

RR-2
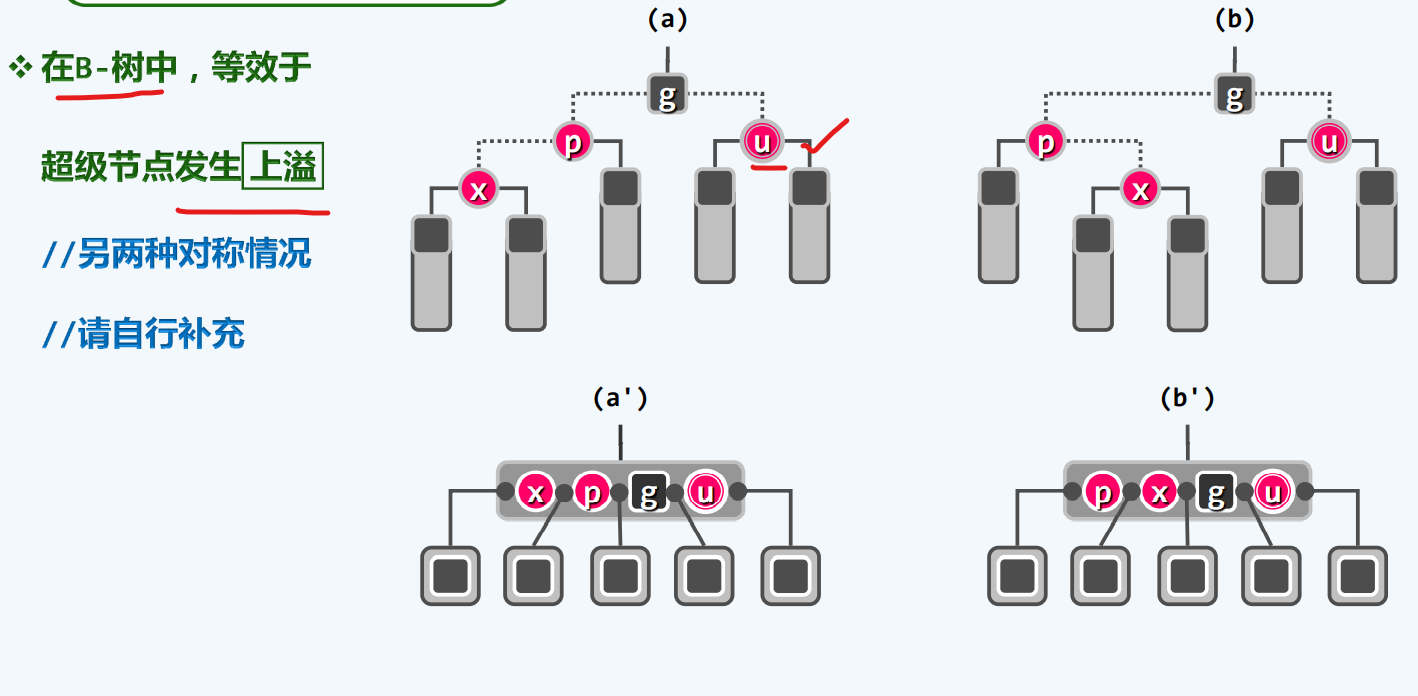
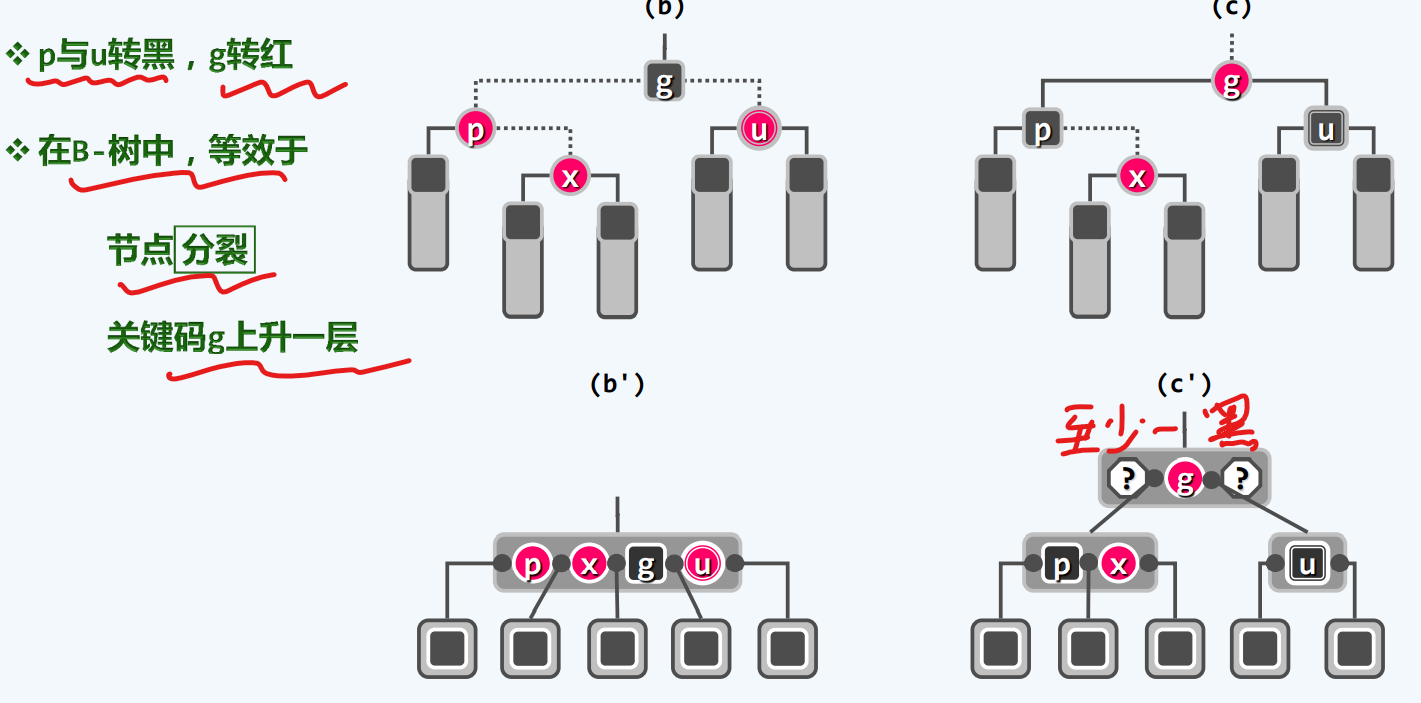
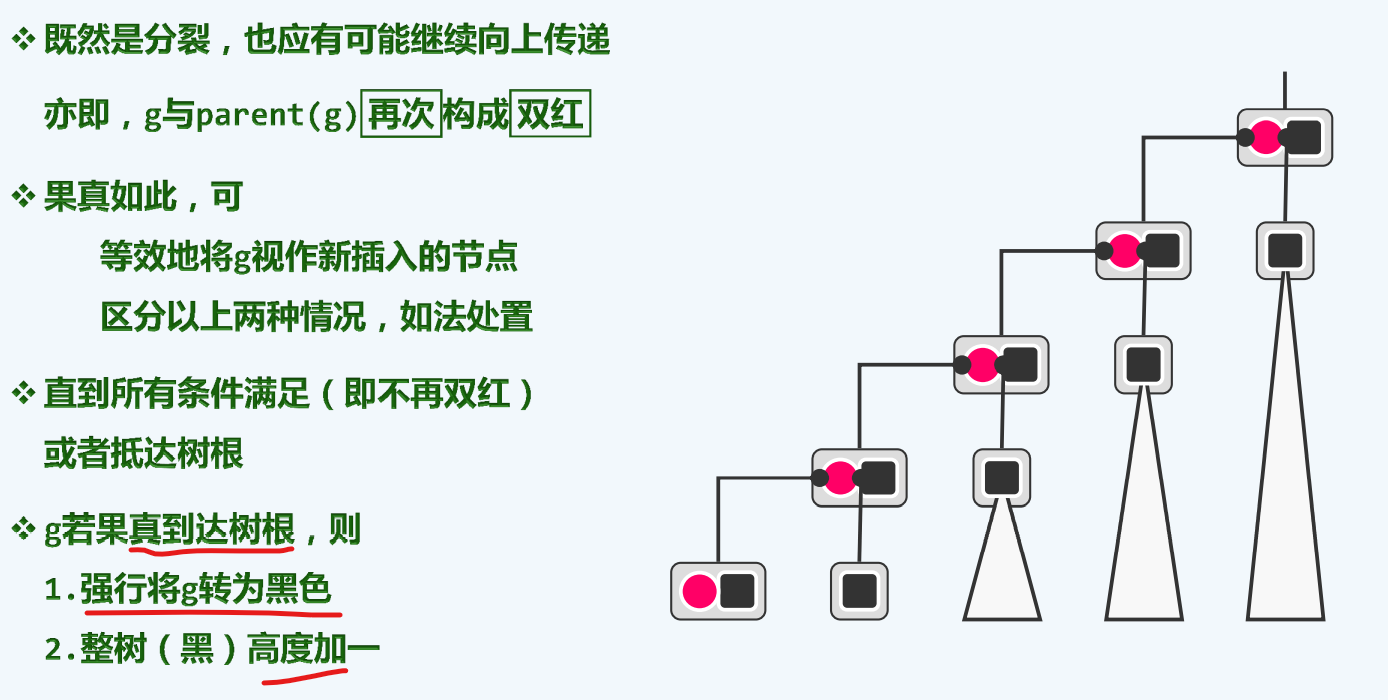
实现

实战代码
解决双红缺陷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
0006 template <typename T> void RedBlack<T>::solveDoubleRed ( BinNodePosi<T> x ) {
0007 if ( IsRoot ( *x ) )
0008 { _root->color = RB_BLACK; _root->height++; return; }
0009 BinNodePosi<T> p = x->parent; if ( IsBlack ( p ) ) return;
0010 BinNodePosi<T> g = p->parent;
0011 BinNodePosi<T> u = uncle ( x );
0012 if ( IsBlack ( u ) ) {
0013 if ( IsLChild ( *x ) == IsLChild ( *p ) )
0014 p->color = RB_BLACK;
0015 else
0016 x->color = RB_BLACK;
0017 g->color = RB_RED;
0018
0019
0020 BinNodePosi<T> gg = g->parent;
0021 BinNodePosi<T> r = FromParentTo ( *g ) = rotateAt ( x );
0022 r->parent = gg;
0023 } else {
0024 p->color = RB_BLACK; p->height++;
0025 u->color = RB_BLACK; u->height++;
0026 if ( !IsRoot ( *g ) ) g->color = RB_RED;
0027 solveDoubleRed ( g );
0028 }
0029 }
|
isBlack()
1
2
3
4
5
6
| #define IsBlack(p) ( ! (p) || ( RB_BLACK == (p)->color ) )
0002 #define IsRed(p) ( ! IsBlack(p) )
0003 #define BlackHeightUpdated(x) ( \
0004 ( stature( (x).lc ) == stature( (x).rc ) ) && \
0005 ( (x).height == ( IsRed(& x) ? stature( (x).lc ) : stature( (x).lc ) + 1 ) ) \
0006 )
|
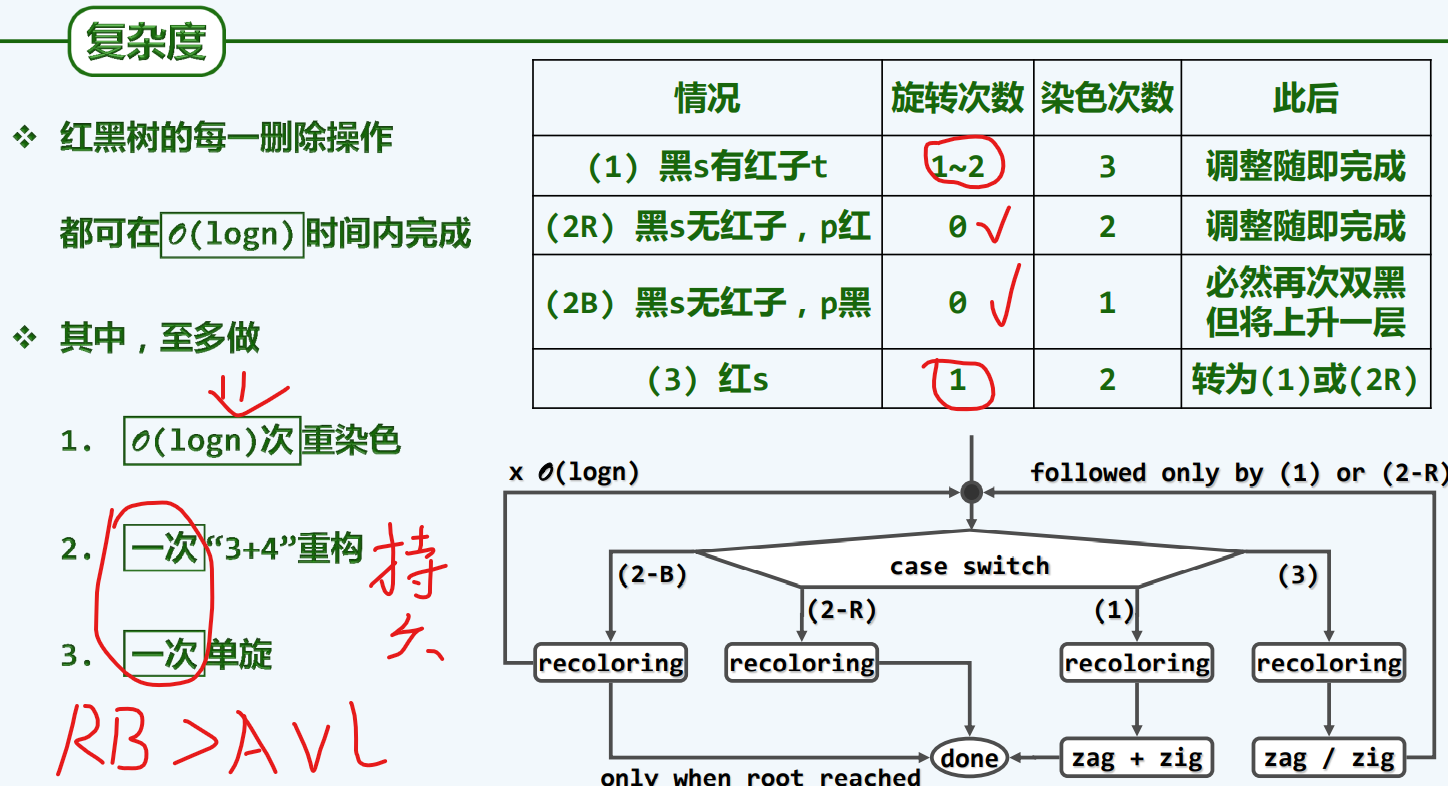
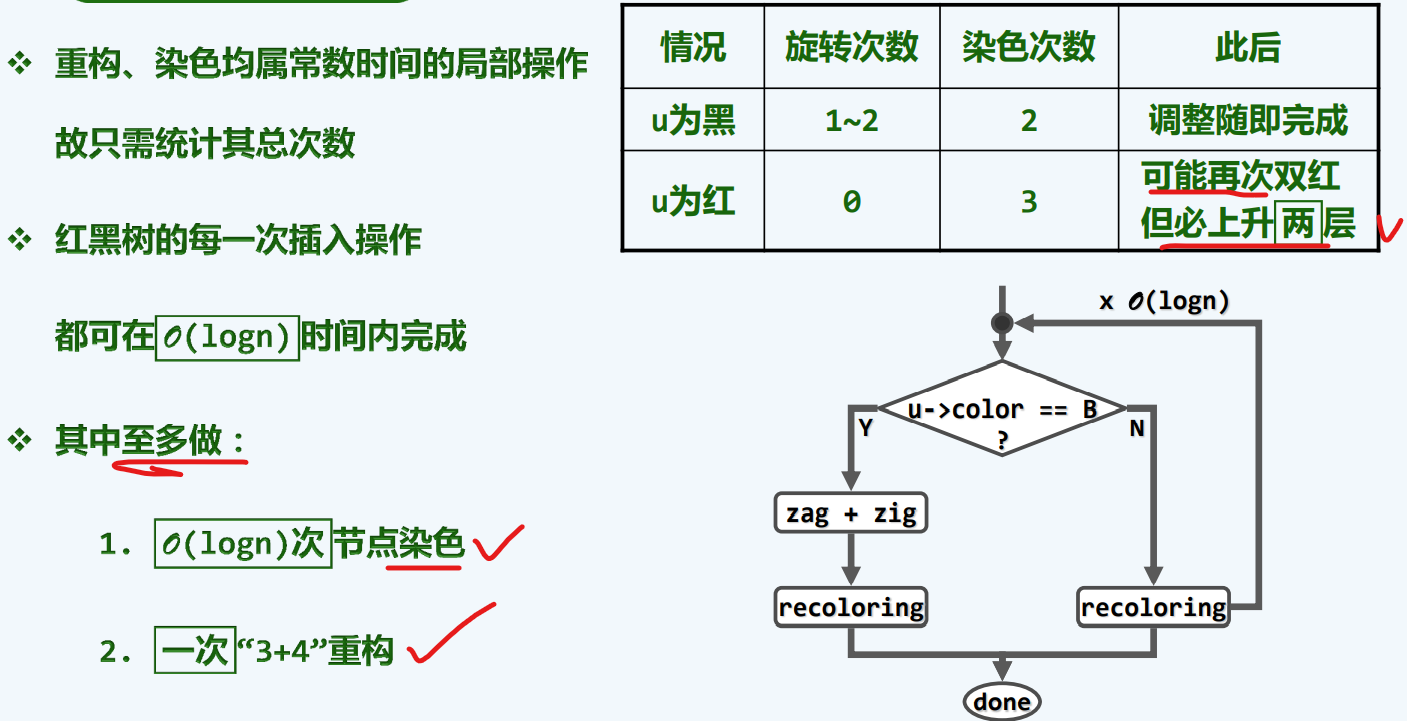
复杂度分析

删除
算法框架
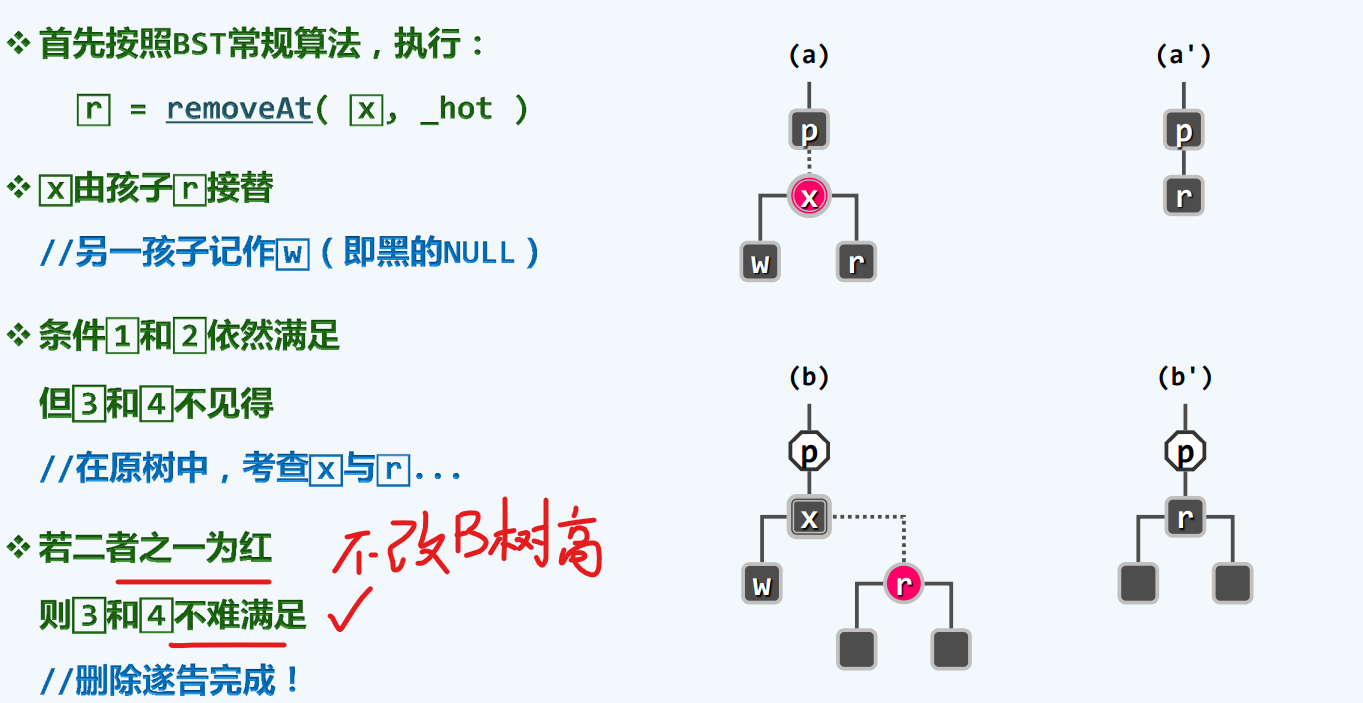
双黑缺陷
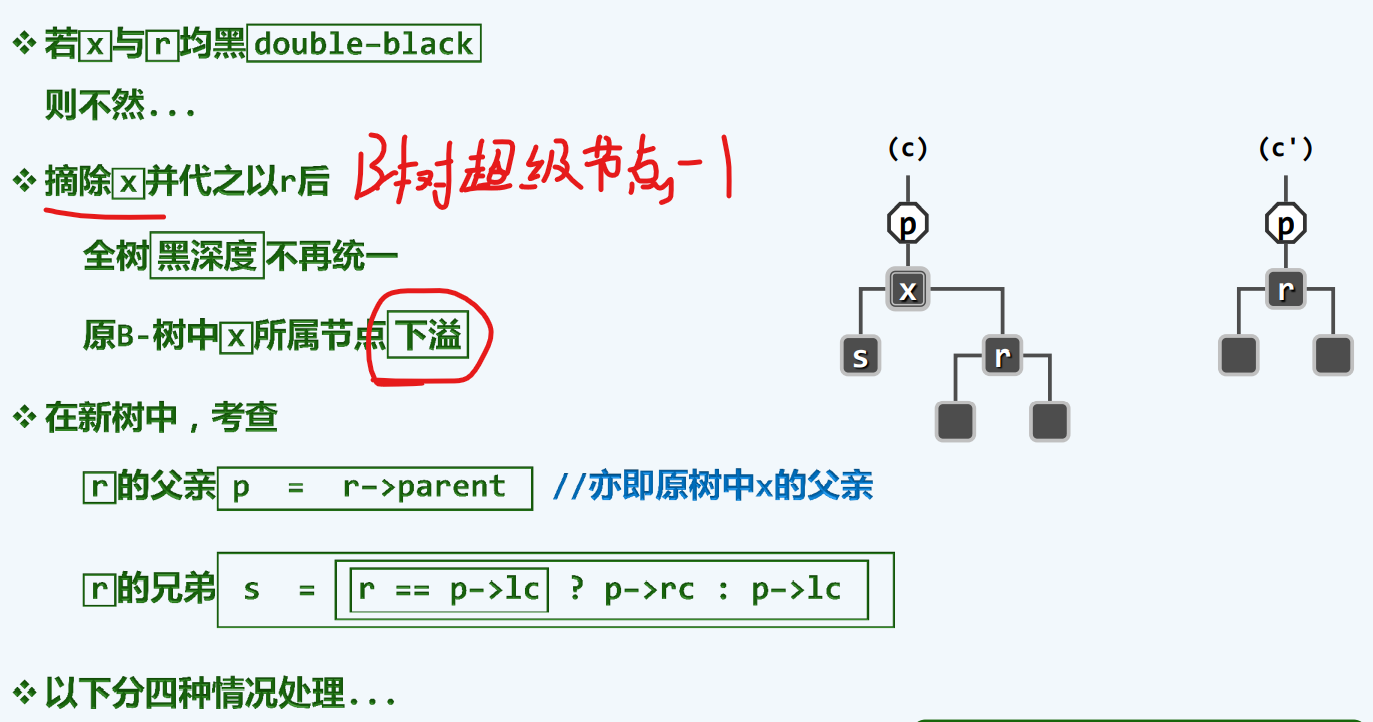
考察父亲—兄弟
BB-1
如果将双黑称作BB,那么第一种情况称为BB-1,这种情况特点是r或者x的兄弟s是黑的,同时至少有一个红色的孩子,记作t
注意,x为删除的结点哈
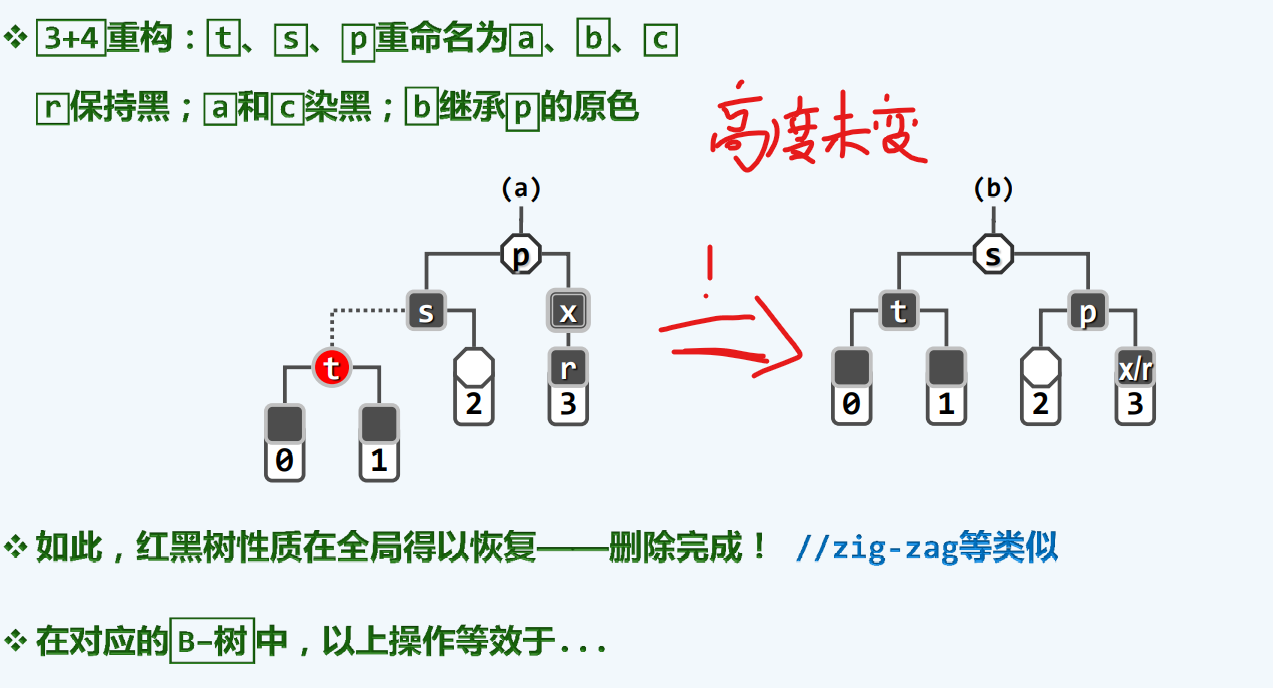
反观回味
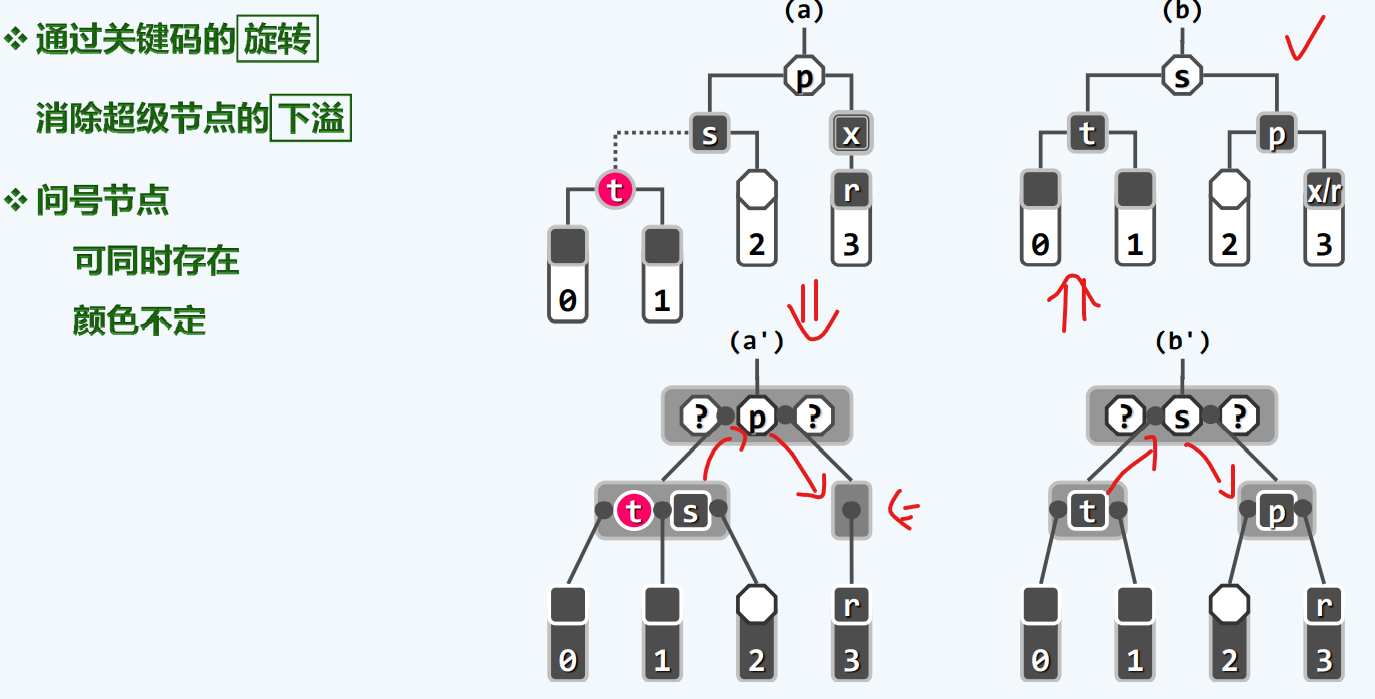
我们说,这种情况还是相对算简单的,这种简单在于,我们至少还有旋转调整的余地,也就是说,兄弟节点还足够富有,或者说,兄弟节点至少有一个虚边
如果兄弟的两个孩子都是黑,此时我们又应该如何应对呢?
BB-2R
(BB-2)R
对应于兄弟的两个孩子都是黑的,此时,父节点开始扑朔迷离,影响全局,我们首先讨论父节点为红的情况
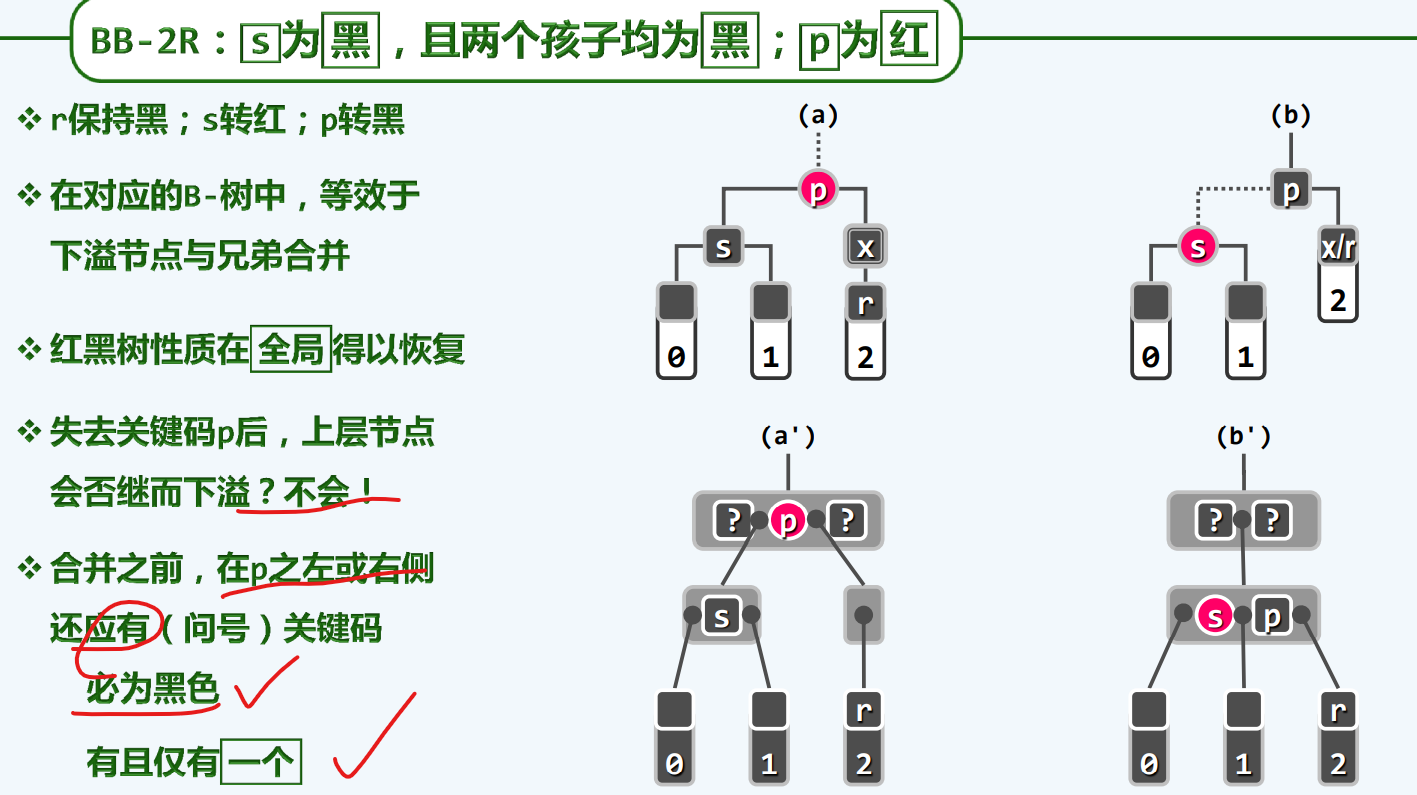
选择的策略就是,父节点借出+与子节点合并
BB-2B
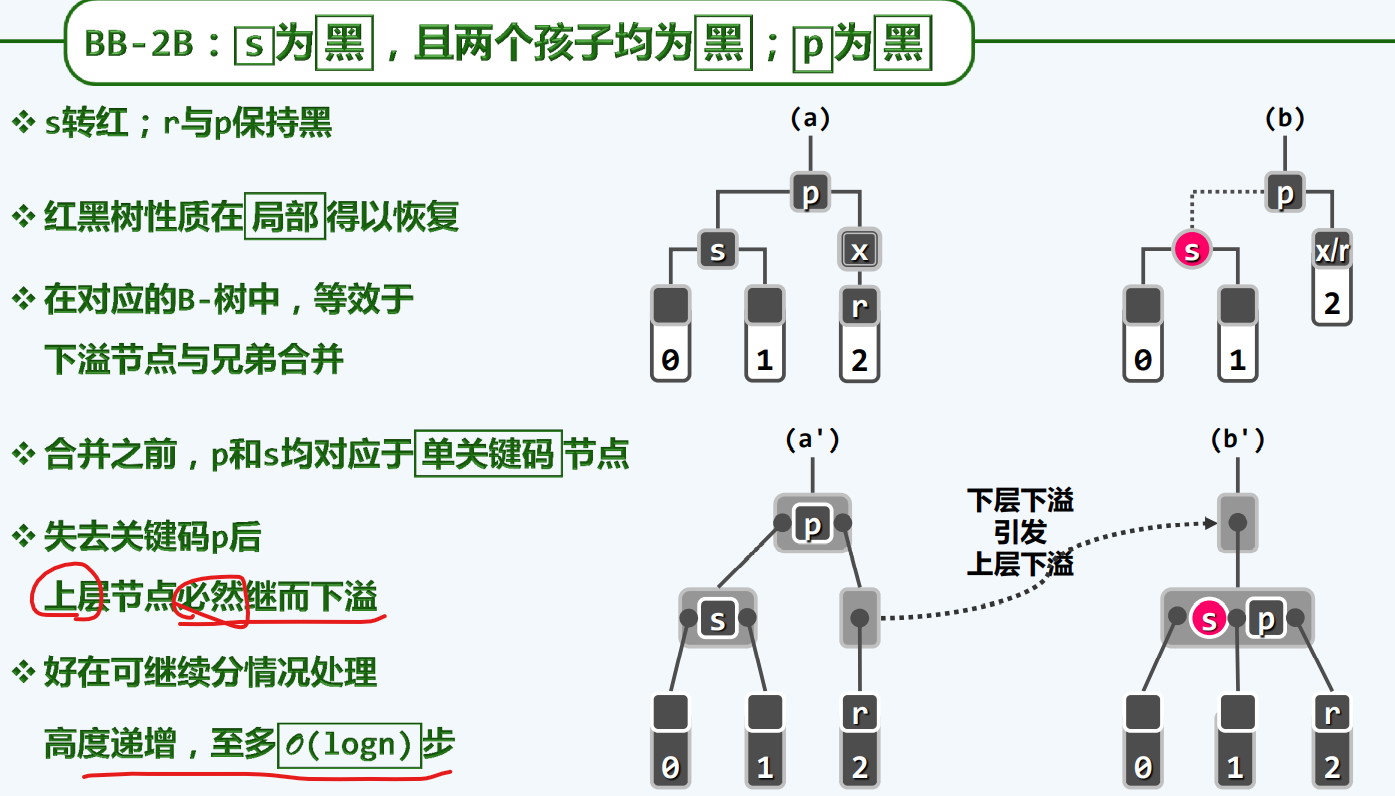
S转为红色,p下来借出,使得性质在局部一直得以恢复
换言之,我们最多执行logN次染色调整,这时,我们可能会关心,红黑树的拓扑结构难道需要logN次变动吗???
为此,我们说,是不必的,看从a—->b的过程,其实红黑树的拓扑结构并没有发生任何的变化。
也就是说,整个拓扑结构的调整不超过常数依然有可能落实。
BB-3
S的三个(父亲,儿子,都是黑)他为红
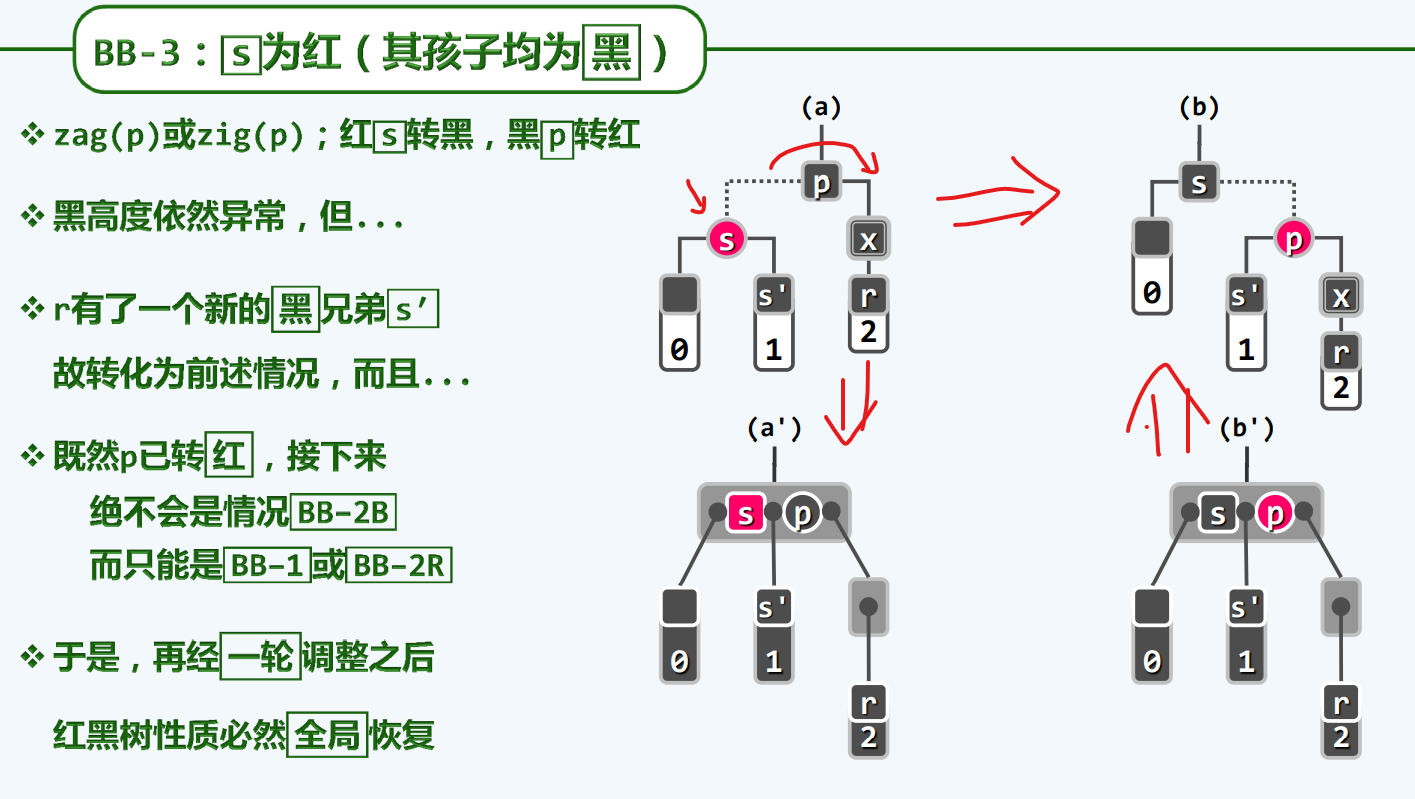
虽然黑高度问题仍然未能解决,但是我们说这样做并非没有意义。
因此r在无形中,增添了一个黑兄弟,以至于,他在下一时刻,必定脱离当前情况
更好的消息是,只会转入BB-1,BB-2R,绝不会是情况BB-2B,BB-2B的要点是父节点P必须是黑的,然而父节点p已经悄然变成了黑色,而我们应该能想到,从复杂度的角度来看,BB-1,BB-2R无疑是更简单的,因为他们不会像BB-2B一样不断向上蔓延,因此我们可以断定,再经过一轮调整,整个红黑树必定修复
实现汇总
remove()
1
2
3
4
5
6
7
8
9
10
11
12
13
| template <typename T> bool RedBlack<T>::remove ( const T& e ) {
0002 BinNodePosi<T> & x = search ( e ); if ( !x ) return false;
0003 BinNodePosi<T> r = removeAt ( x, _hot ); if ( ! ( --_size ) ) return true;
0004
0005 if ( ! _hot )
0006 { _root->color = RB_BLACK; updateHeight ( _root ); return true; }
0007
0008 if ( BlackHeightUpdated ( *_hot ) ) return true;
0009 if ( IsRed ( r ) )
0010 { r->color = RB_BLACK; r->height++; return true; }
0011
0012 solveDoubleBlack ( r ); return true;
0013 }
|
双黑缺陷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
0009 template <typename T> void RedBlack<T>::solveDoubleBlack ( BinNodePosi<T> r ) {
0010 BinNodePosi<T> p = r ? r->parent : _hot; if ( !p ) return;
0011 BinNodePosi<T> s = ( r == p->lc ) ? p->rc : p->lc;
0012 if ( IsBlack ( s ) ) {
0013 BinNodePosi<T> t = NULL;
0014 if ( IsRed ( s->rc ) ) t = s->rc;
0015 if ( IsRed ( s->lc ) ) t = s->lc;
0016 if ( t ) {
0017 RBColor oldColor = p->color;
0018
0019 BinNodePosi<T> b = FromParentTo ( *p ) = rotateAt ( t );
0020 if ( HasLChild ( *b ) ) { b->lc->color = RB_BLACK; updateHeight ( b->lc ); }
0021 if ( HasRChild ( *b ) ) { b->rc->color = RB_BLACK; updateHeight ( b->rc ); }
0022 b->color = oldColor; updateHeight ( b );
0023 } else {
0024 s->color = RB_RED; s->height--;
0025 if ( IsRed ( p ) ) {
0026 p->color = RB_BLACK;
0027 } else {
0028 p->height--;
0029 solveDoubleBlack ( p );
0030 }
0031 }
0032 } else {
0033 s->color = RB_BLACK; p->color = RB_RED;
0034 BinNodePosi<T> t = IsLChild ( *s ) ? s->lc : s->rc;
0035 _hot = p; FromParentTo ( *p ) = rotateAt ( t );
0036 solveDoubleBlack ( r );
0037 }
0038 }
|
复杂度