词典
以下笔记为jjyaoao本人制作,欢迎借鉴学习和提出相关建议,转载需要标明出处www.jjyaoao.space
词典
散列
引例

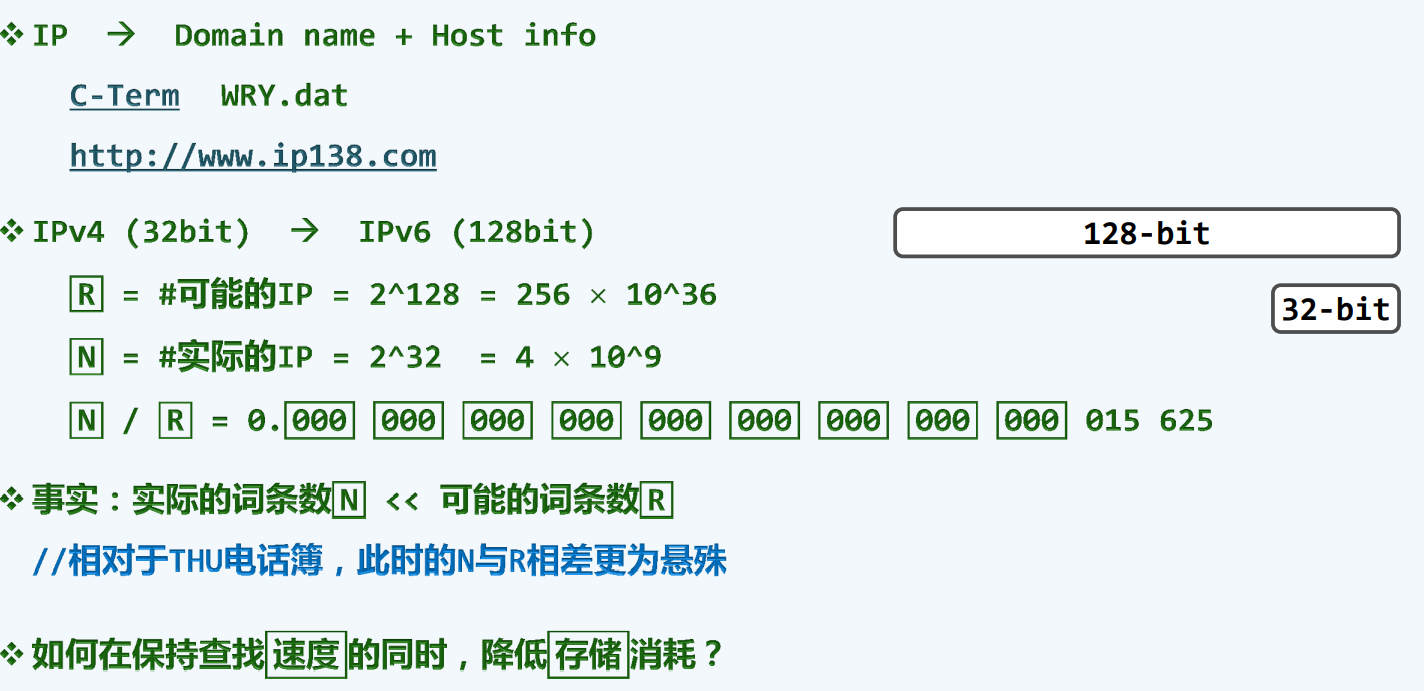
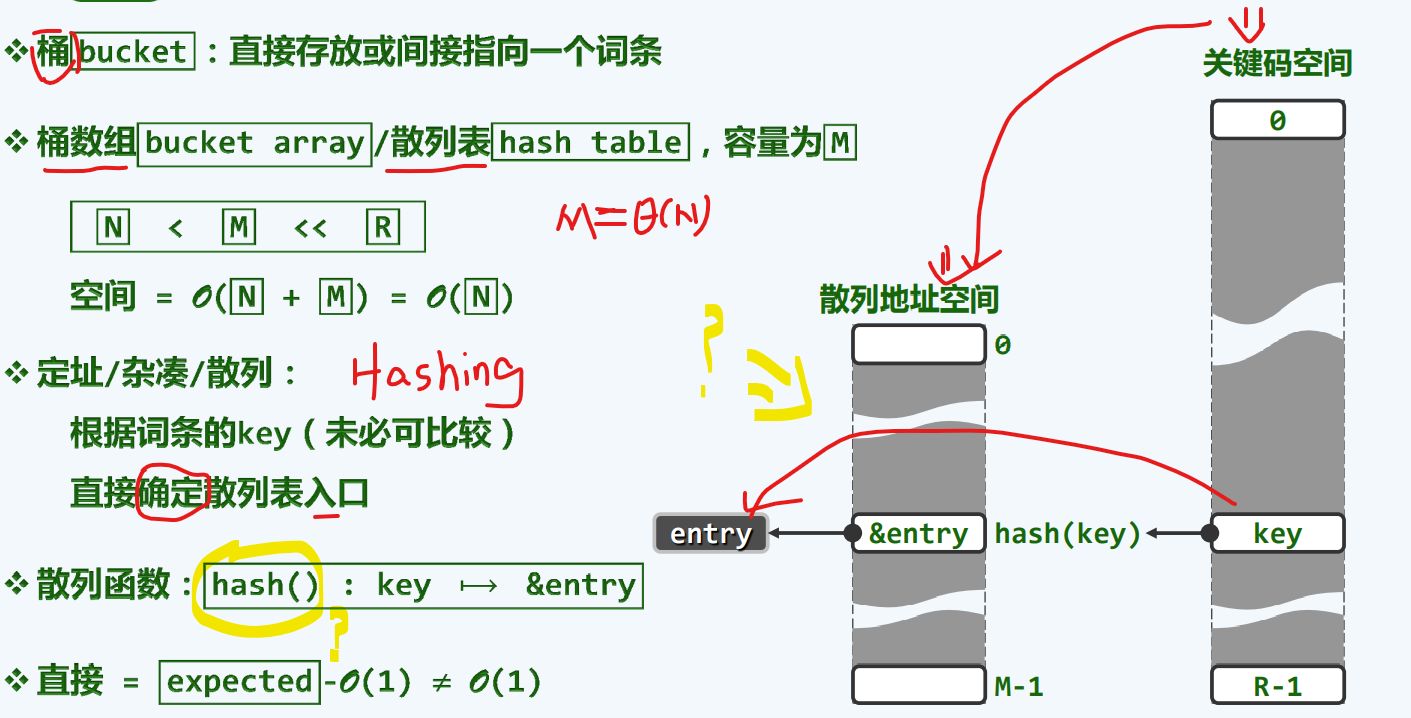
原理
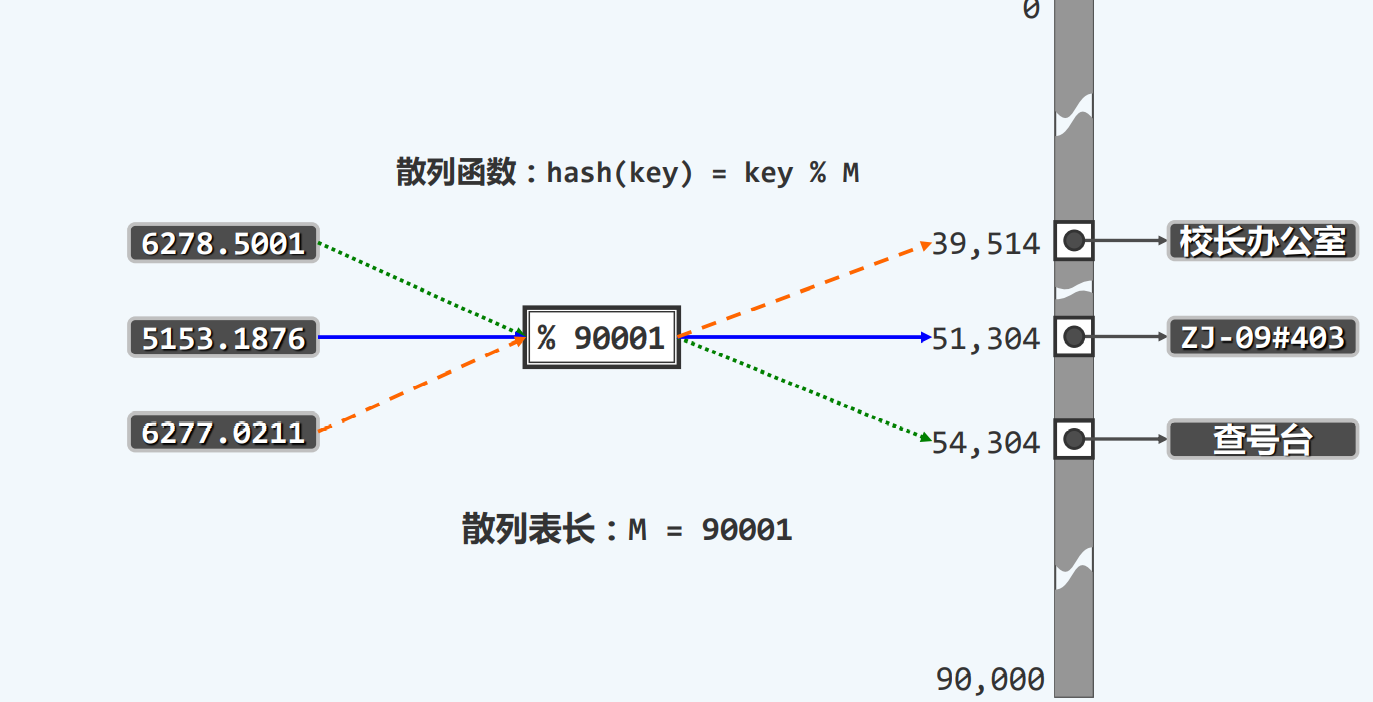
实例
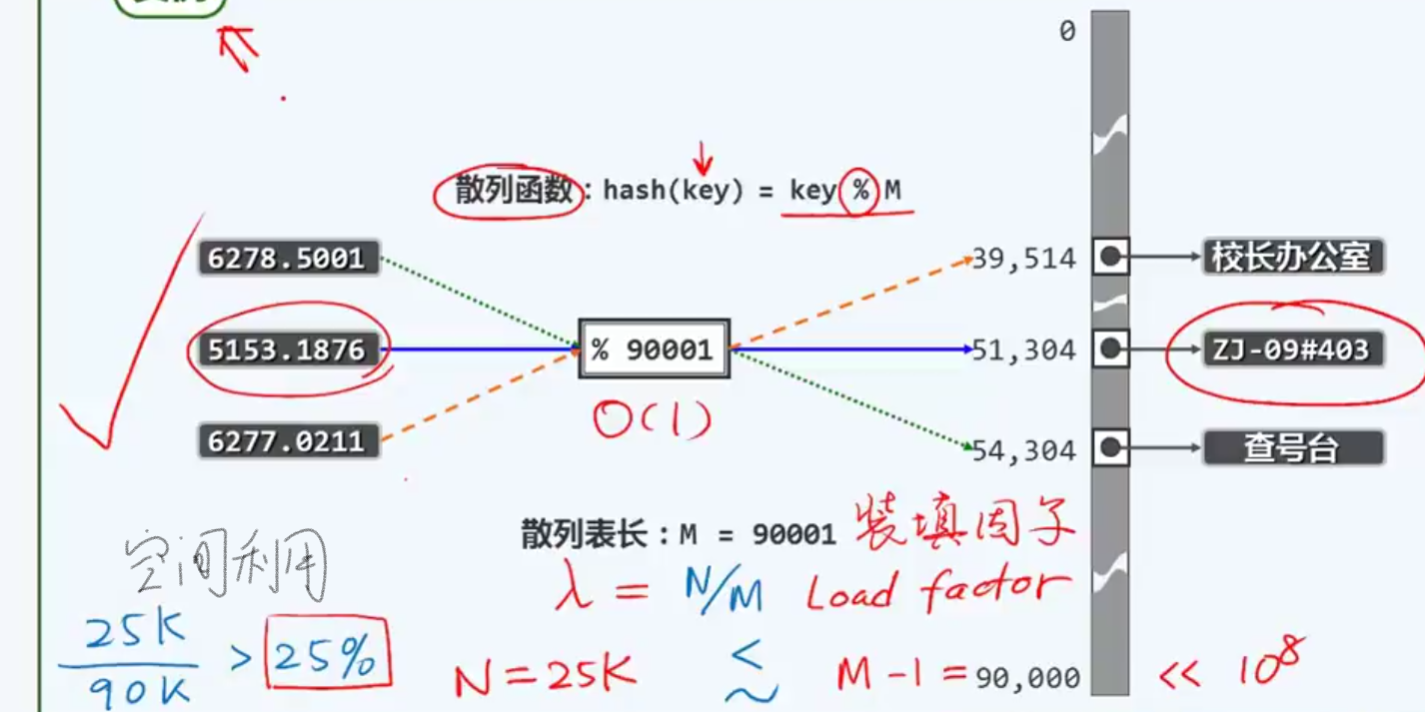
冲突

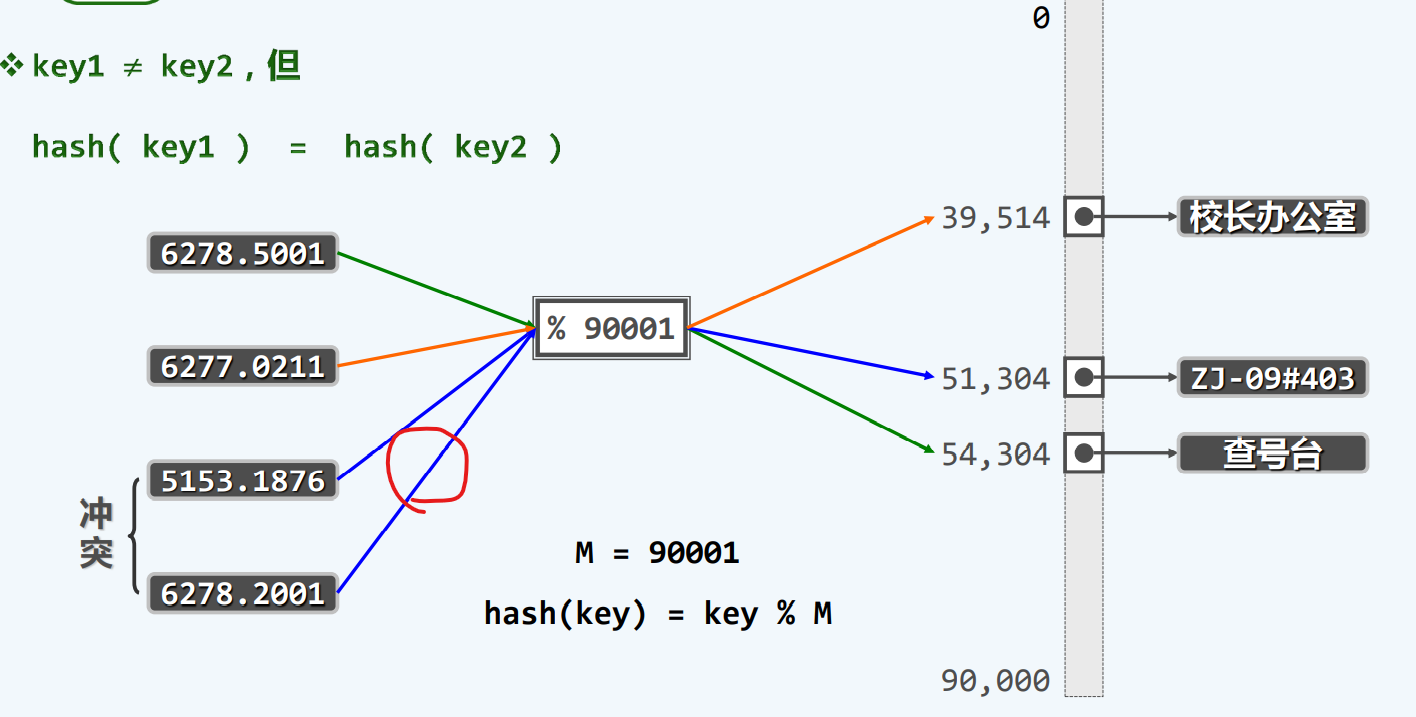
散列函数
冲突难免


何谓优劣
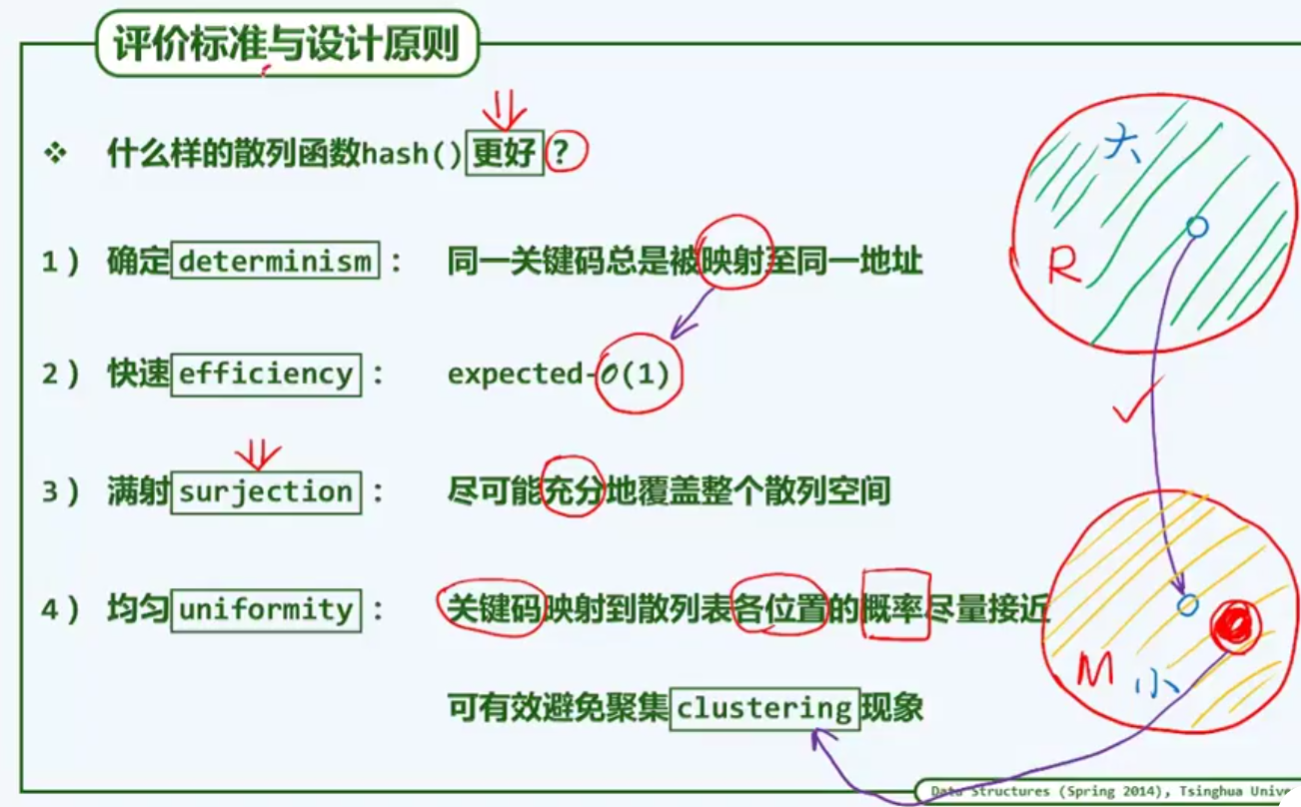
几种散列函数
除余法

1 |
|

平方取中

折叠/异或

(伪)随机数法

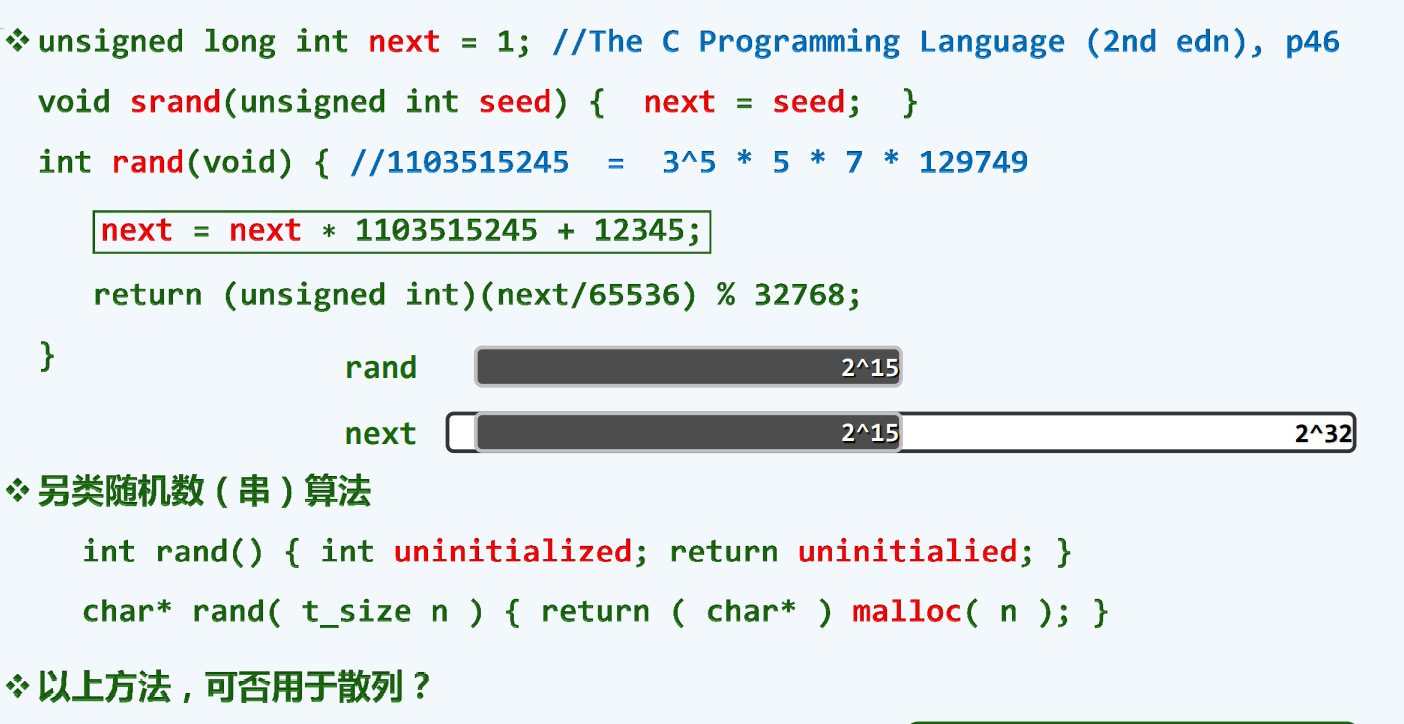
多项式法


排解冲突
多槽位

类似于一山不容二虎,将每个虎用铁丝网封锁在不同的山
每个桶不同的槽位就用来存储多出来的重复的散列表

只要槽位控制在常数,整体的速度不会太降低,不过缺陷是显而易见的。
每个桶需要分多少个槽位是无法预估的,如果分的过细,浪费空间,分的太少,可能装不下,反过来,无论分的多细,仍有可能面对大规模的冲突,那么我们如何破解呢?
独立链
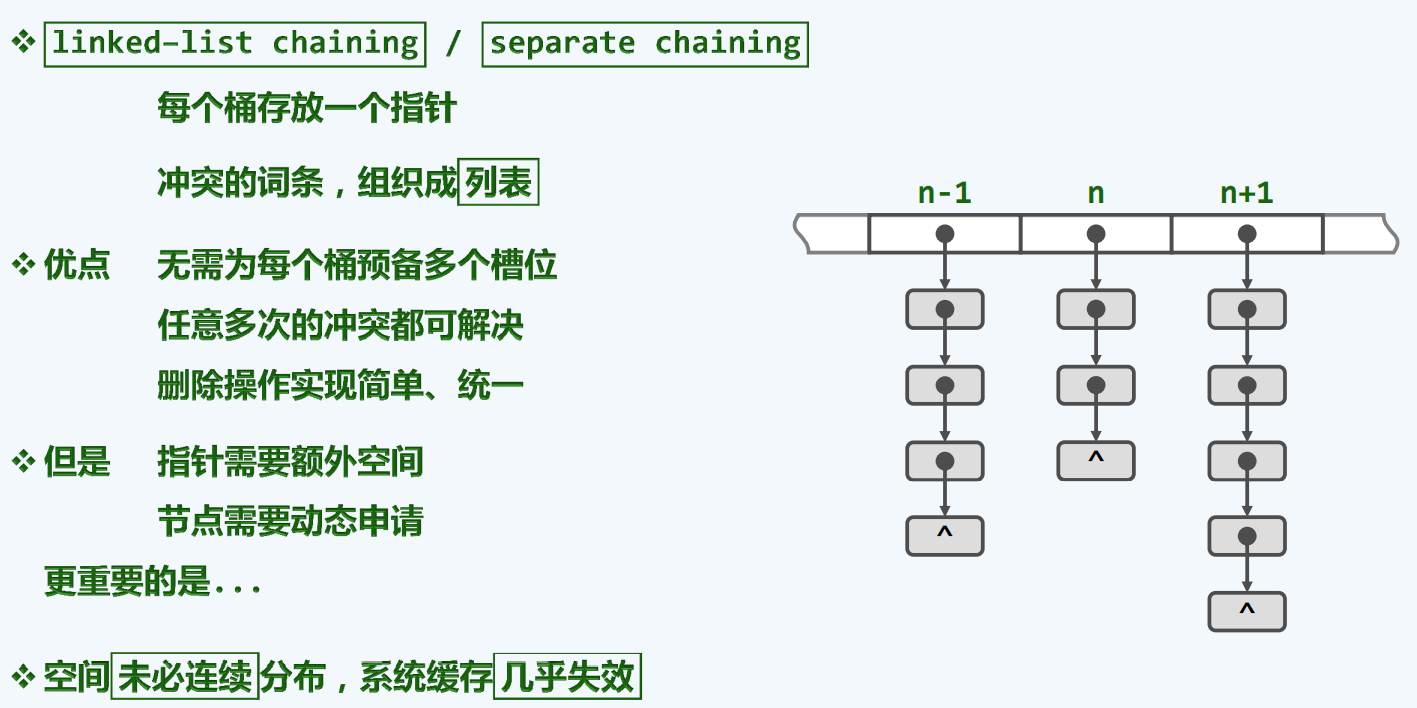
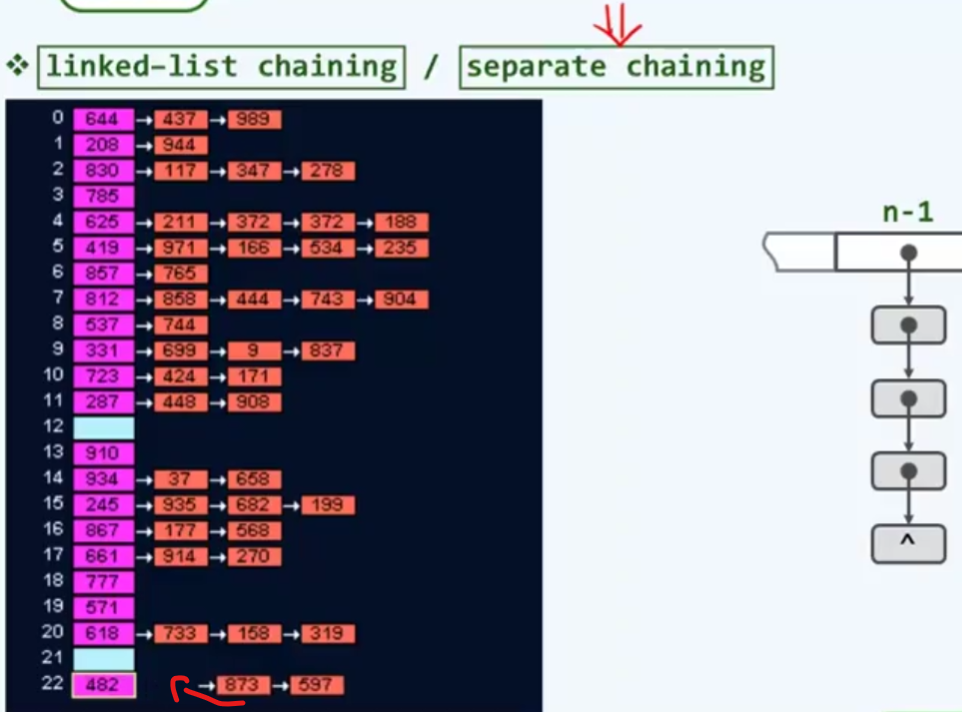
虽然这种方式良好的解决了空间上的问题,但是引入了时间上巨大迟钝
系统的缓存几乎失效
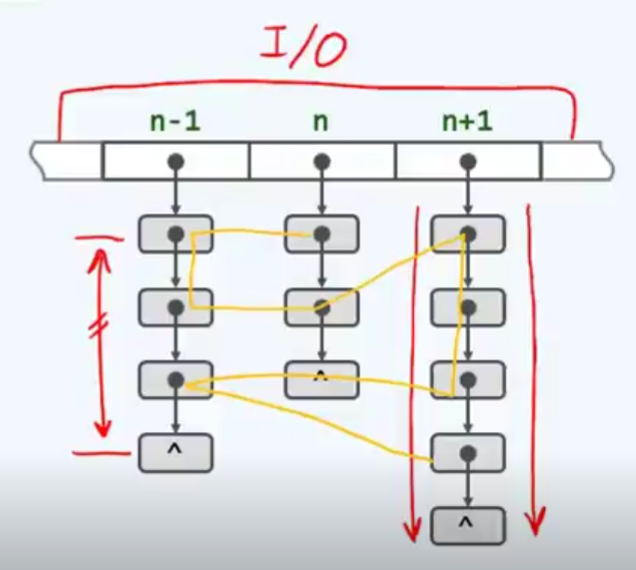
那么为了有效的激活缓存功能,我们又应该如何改进呢?
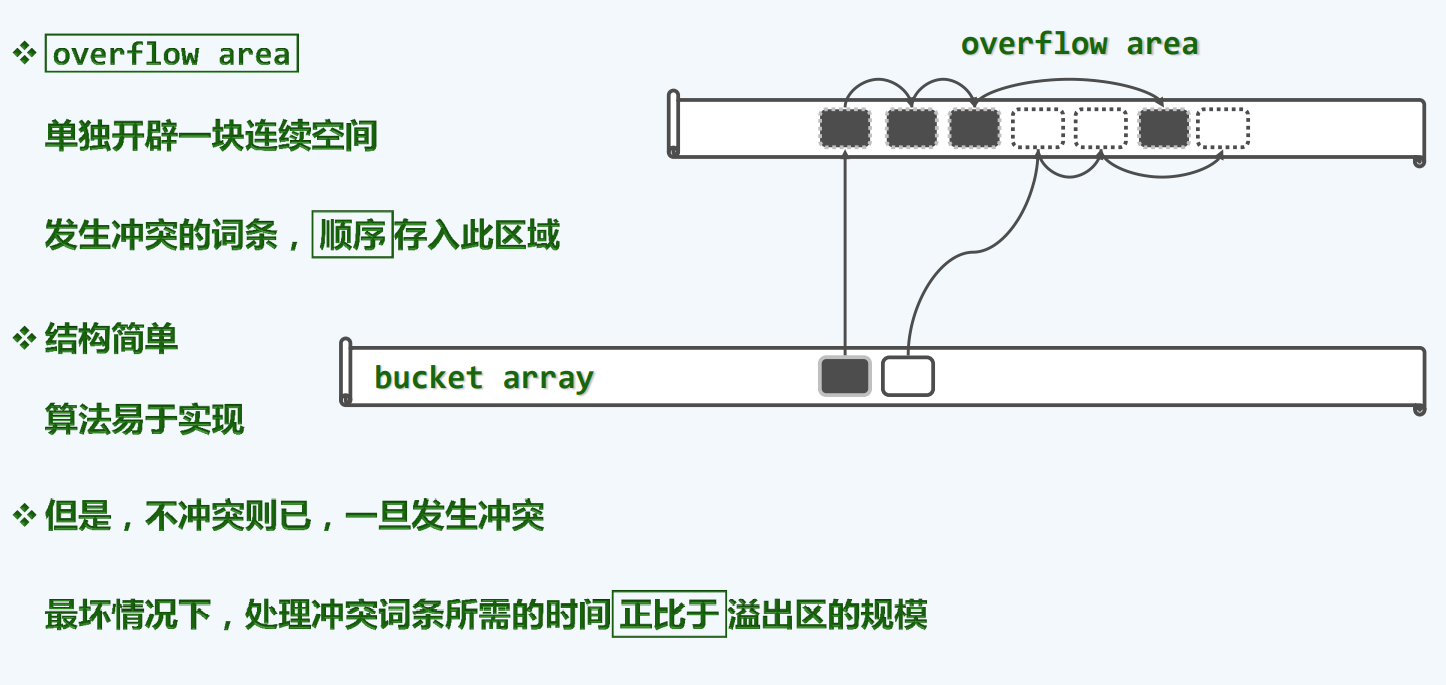
公共溢出区
为了保证空间上彼此毗邻,我们可能应该放弃这种策略,并且反其道而行之,采用开放定址
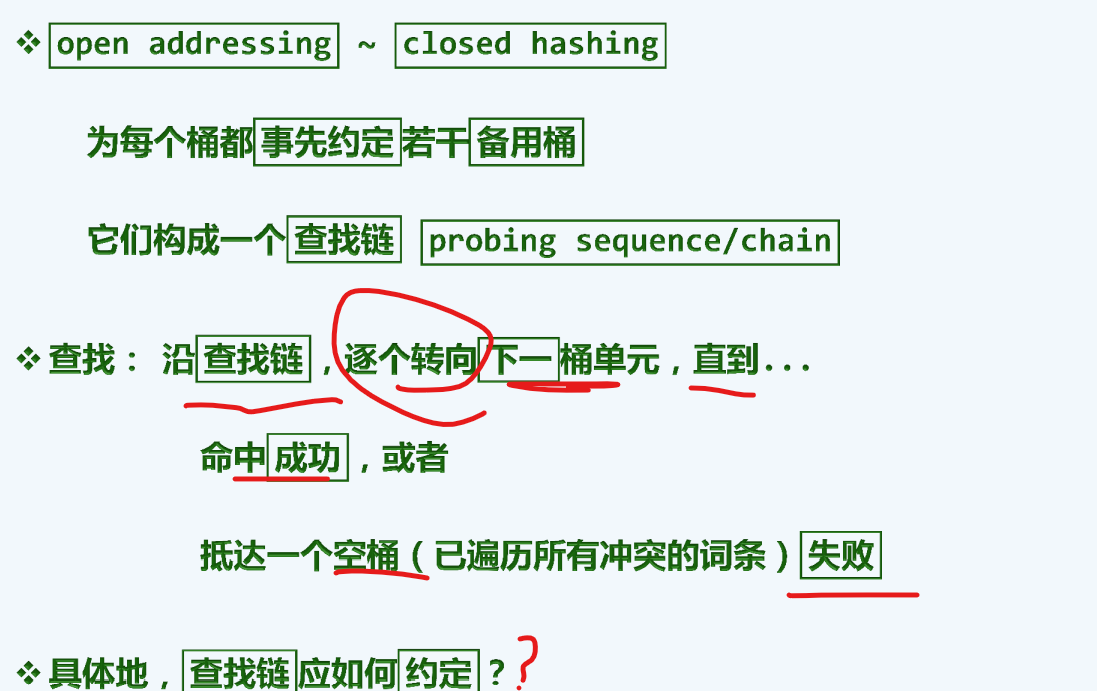
查找链约定
线性试探
紧邻的试探,使得越后面进来的,需要的时间(冲突)越来越多
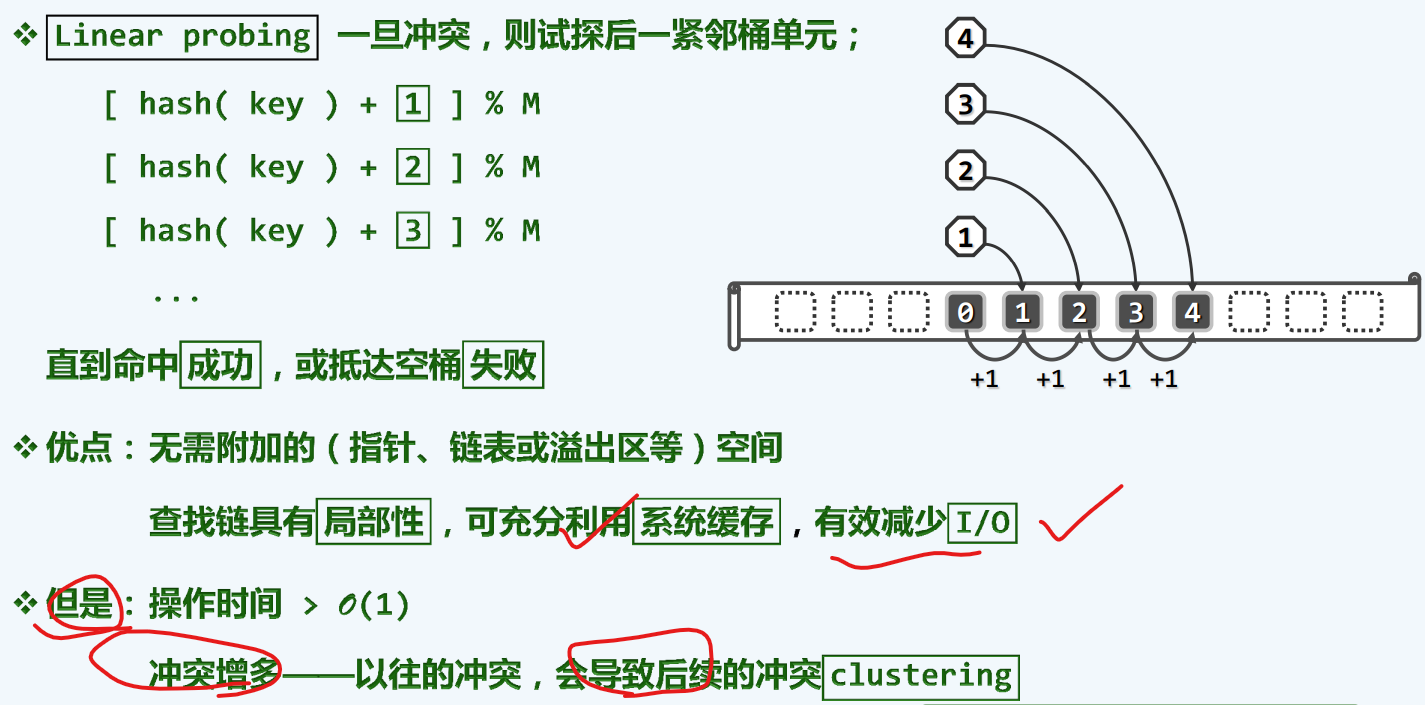
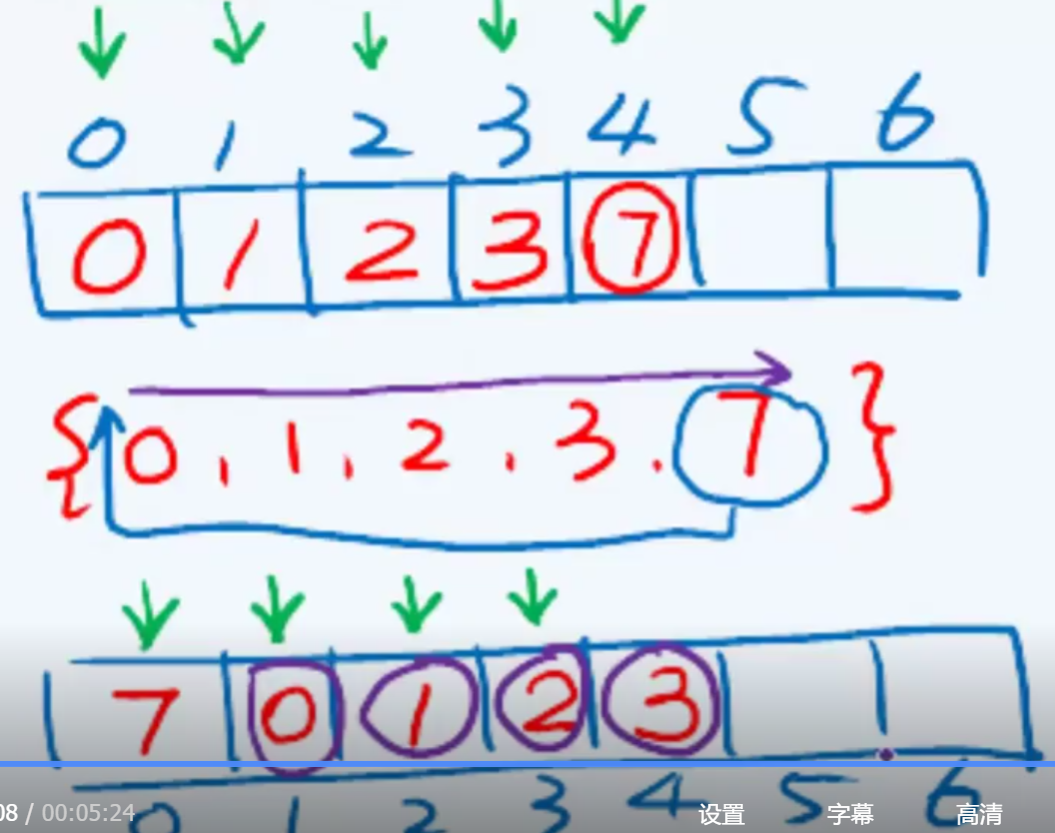
前后对比,可以发现,后一种插入所发生的的多次冲突(紫色圈起来的)的确是可以避免的。[如果对应桶的位置有人占了,则以此向后遍历,直到找到一个空桶]
【对7而言,对应的桶就应该是0】
懒惰删除

实战代码

1 | /****************************************************************************************** |
1 | /****************************************************************************************** |
平方试探
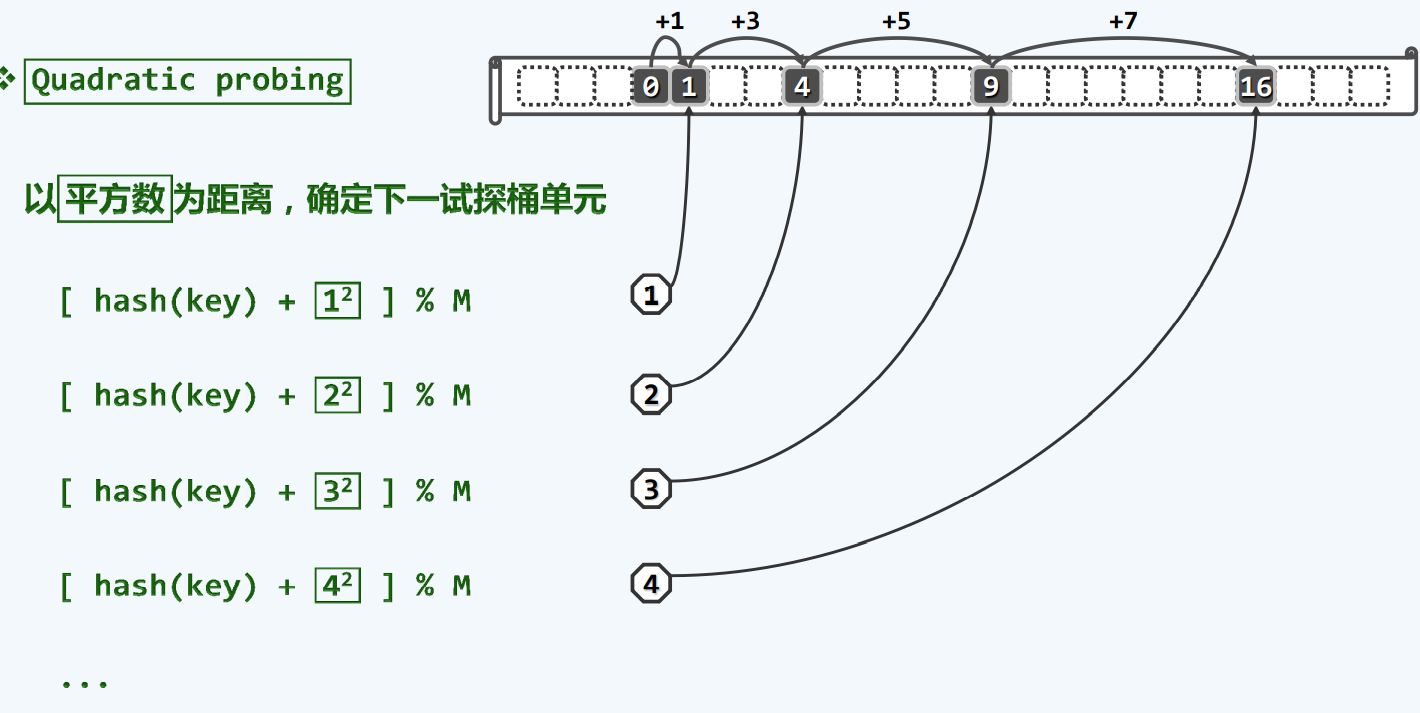
一利一弊
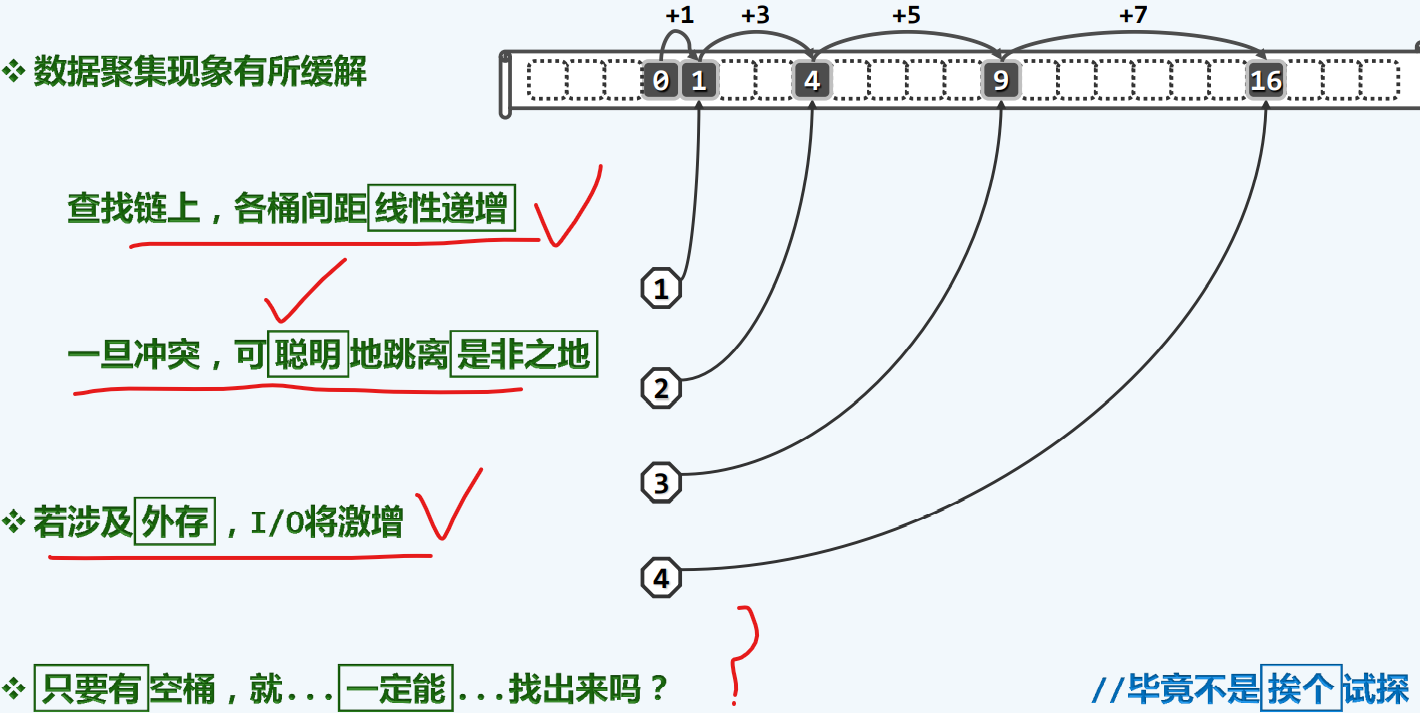
至多半载
我们装填的东西必须少于这个查找桶的一半
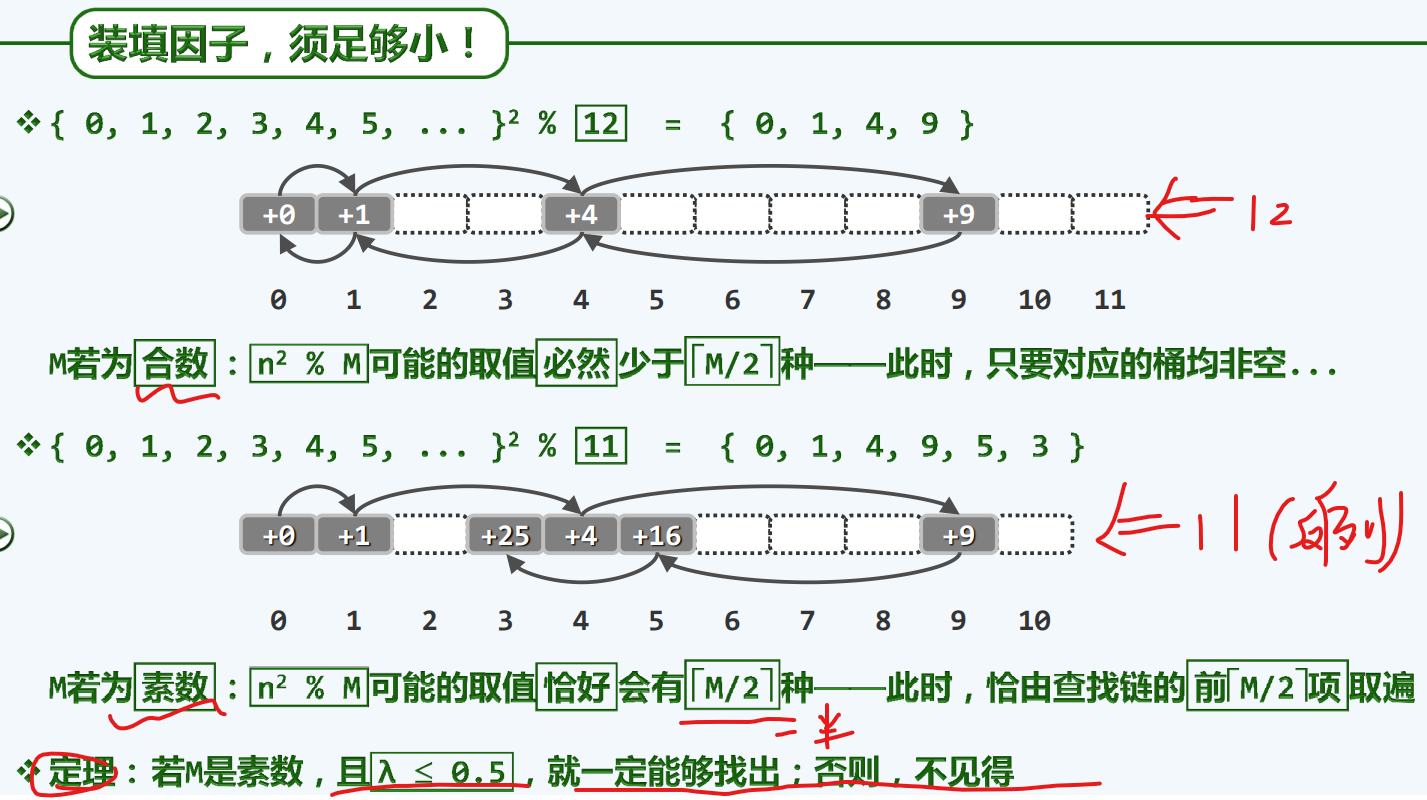

双向平方试探
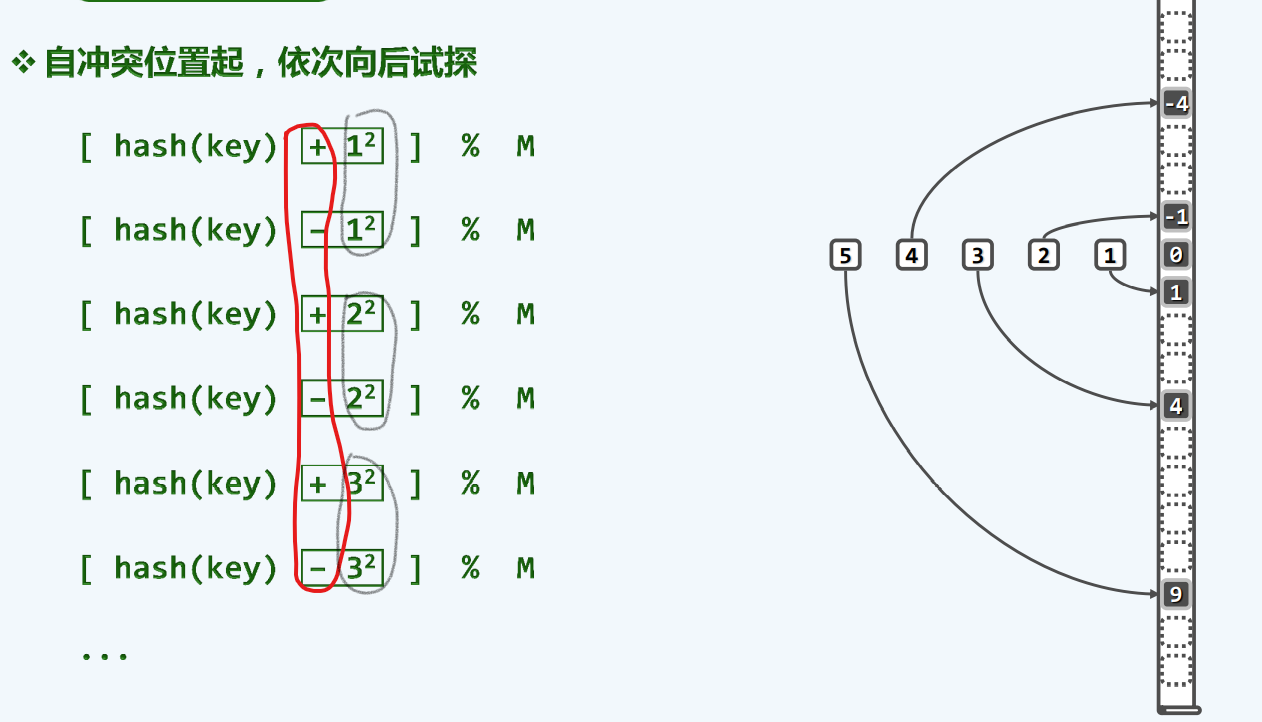
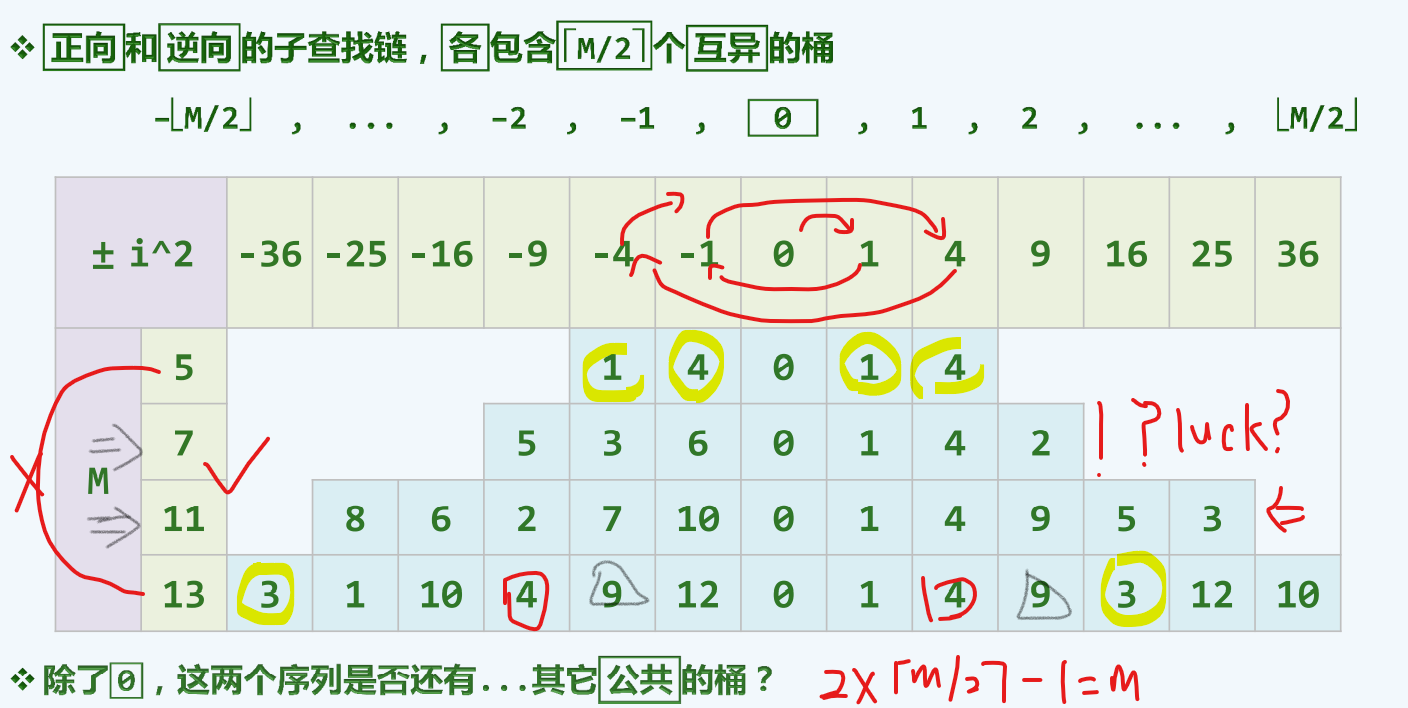
4k+3
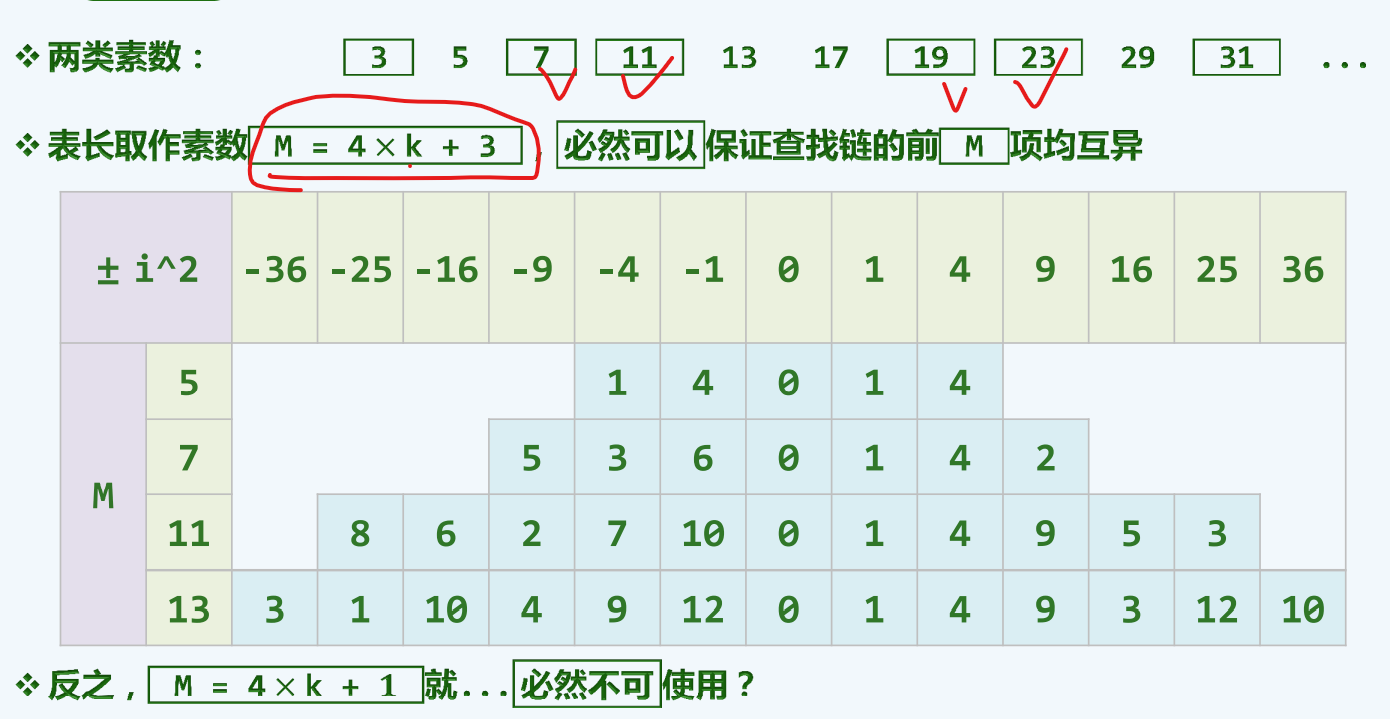
双平方定理

反证法
假设取表长为M, 里面a,b是发生冲突的,那么冲突是什么呢?
在mod M 的情况下 ,a^2 -b^2取余后相等,我们把a方b方之和看做为n
所以n可以整除m平方(根据费马双平方定理推论,不仅能被m,还能被m方),证明a方b方大于m方,然而就a,b的取值范围而言,这一关系是断乎不可能成立的。
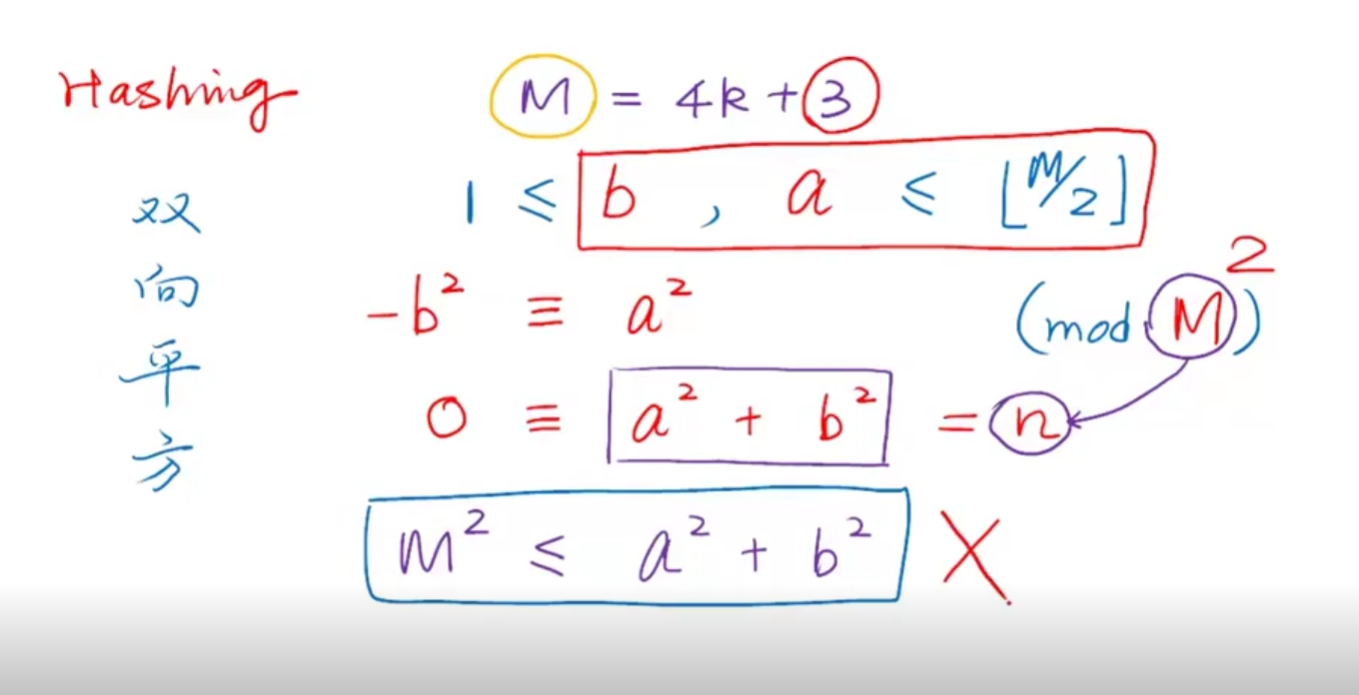
桶排序/计数排序
待排序序列的长度–n 待排序序列的取值范围–M
M越小,算法优势越明显
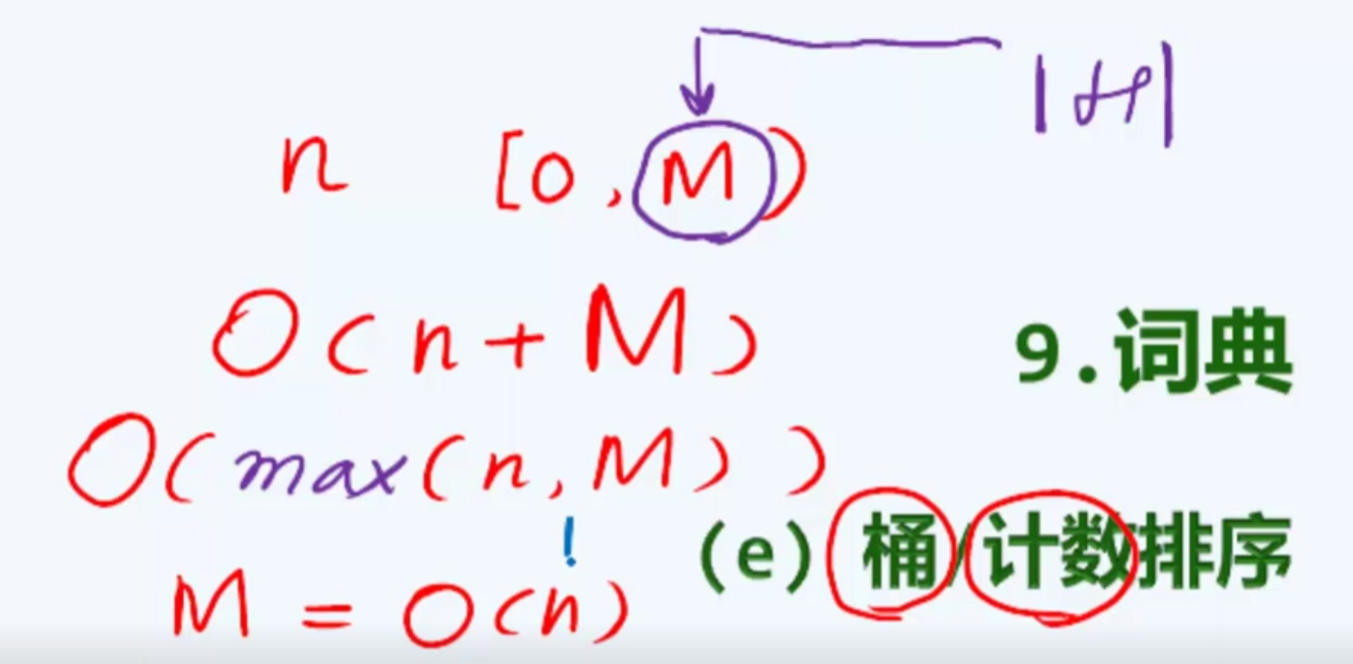

而若果真如此,这个算法有望在线性时间完成排序

实例
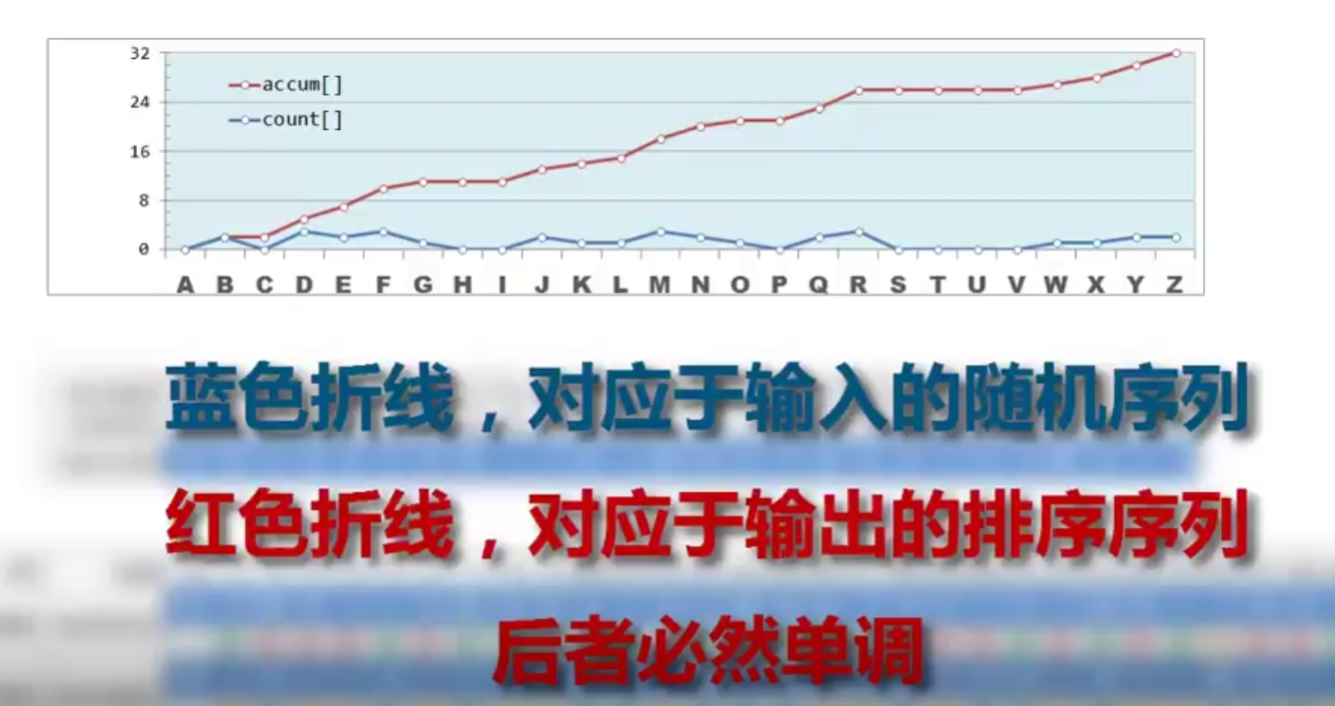
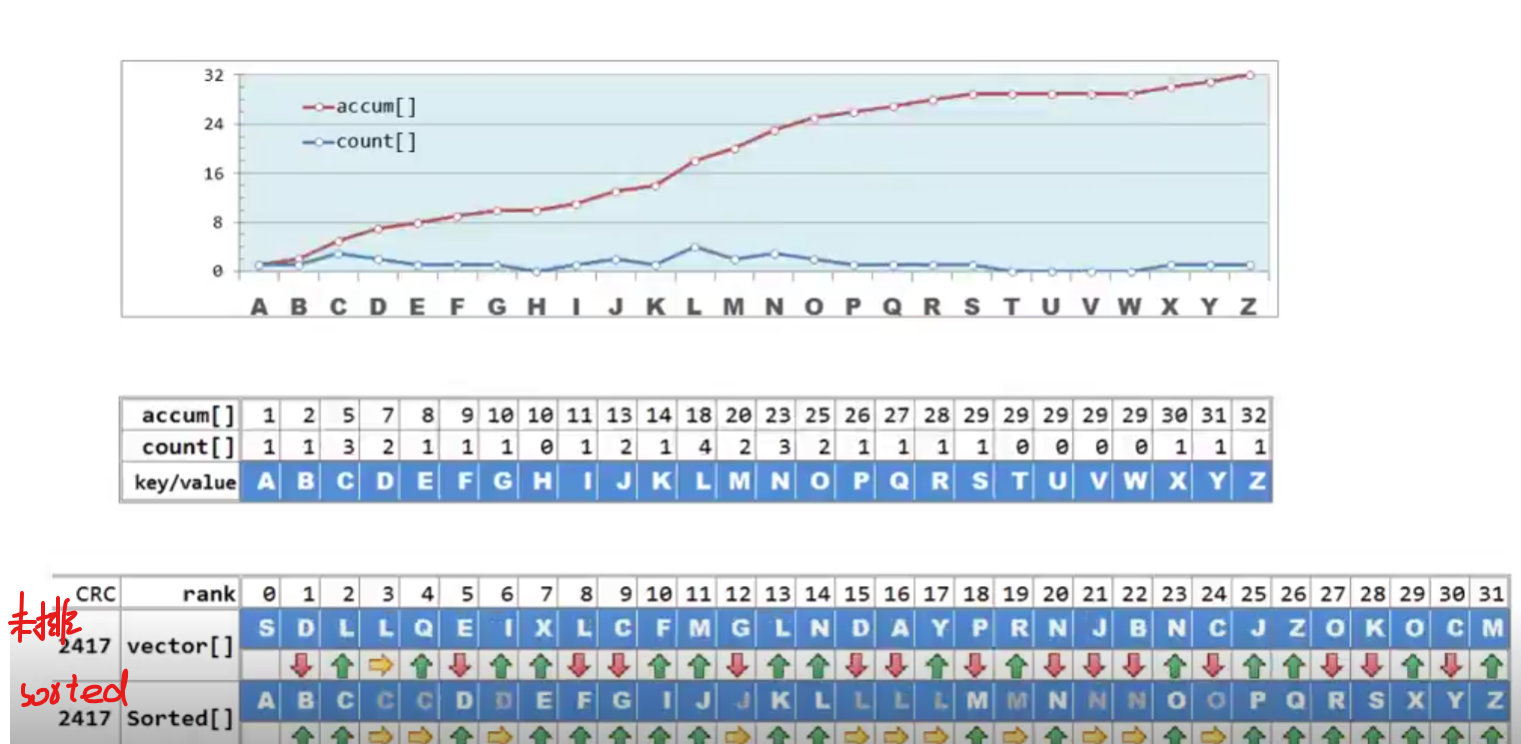
我们只需要遍历一次数据集,在此当中,每遇到一个数据,就对他的计数器做累加,形象的说,这样的作用就像把它对应的元素都扔到桶单元中,因此这一步骤也称为 分配 (distribution)
count:每个字符所出现的次数
accum:暗示着是累计值,更精确的说,红色取现任何一个点,都对应在这个点以及之前所有蓝色的点对应的积分
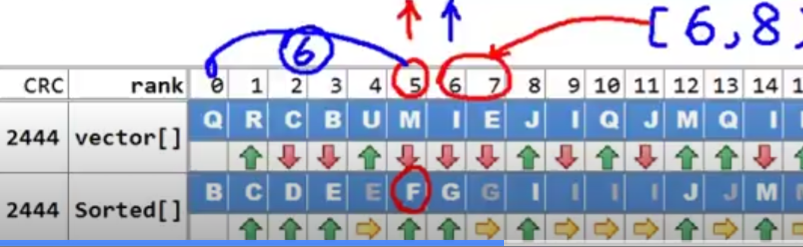
没错,这个反应的就是它在有序序列中的位置,也就是,出现的区间

以这个为例,对应这比G小的总共有6个,因此作为这些字母的最大者F应该编号为5的位置,G的位置也同理得到
具体的算法
从头到尾线性扫描一遍即可

前一项的累计值,加上这一项的count值
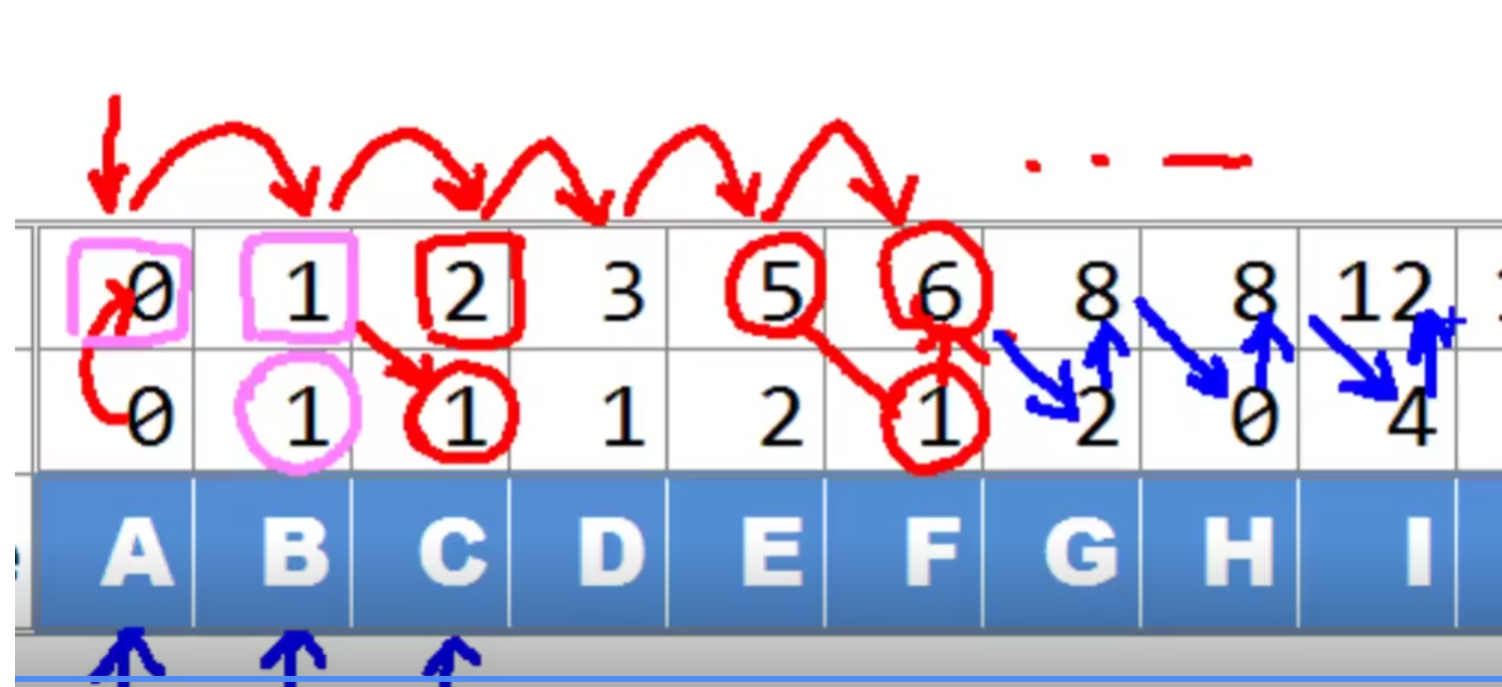
累计,更新,累计,更新……








