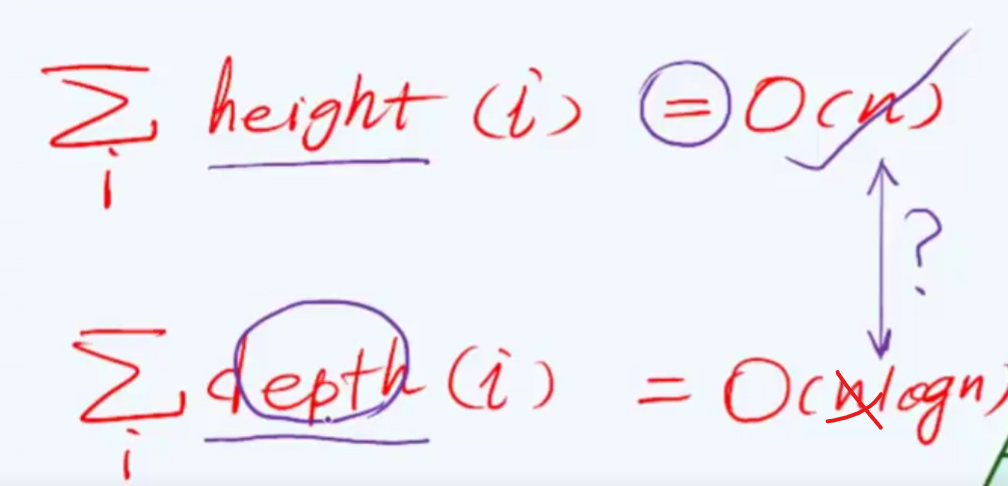以下笔记为jjyaoao本人制作，欢迎借鉴学习和提出相关建议，转载需要标明出处www.jjyaoao.space

优先级队列

需求和动机

应用需求

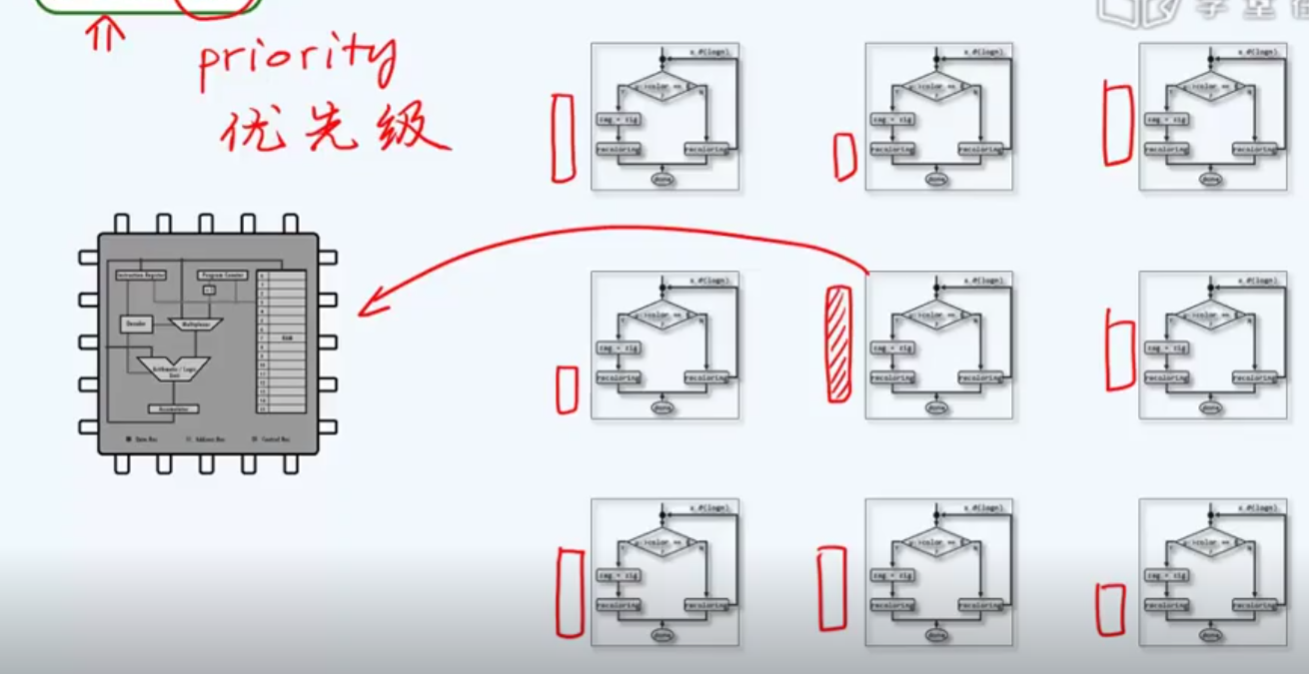
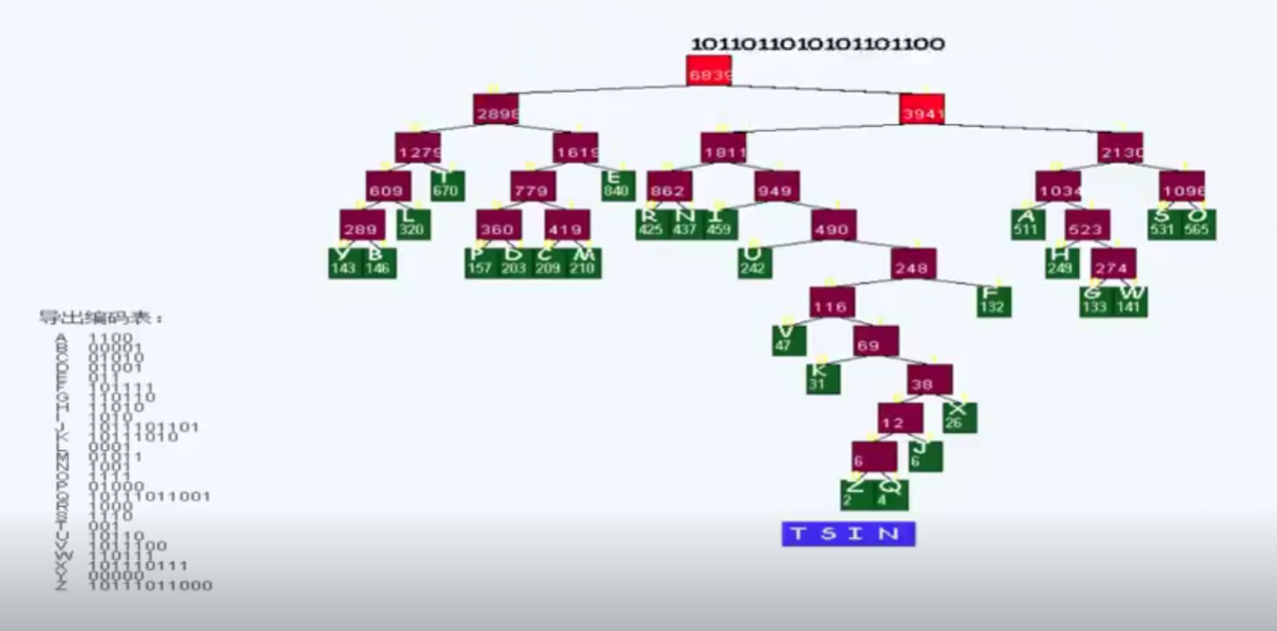
问题模式

服务端–客户

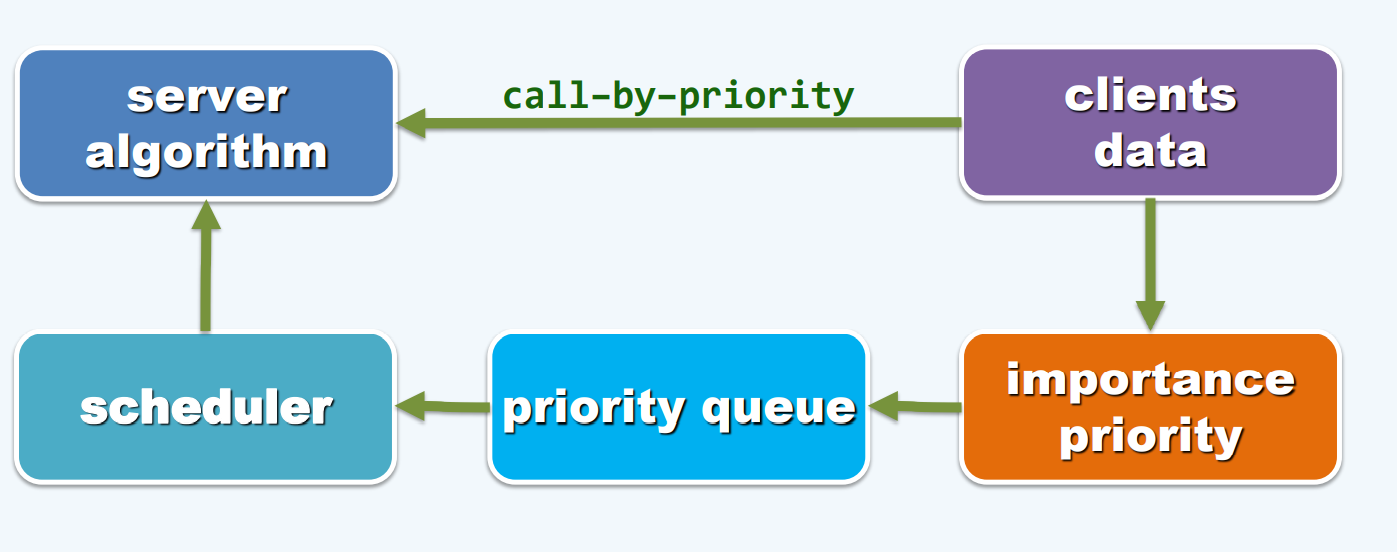
ADT

基本实现

Vector

Sorted Vector

List

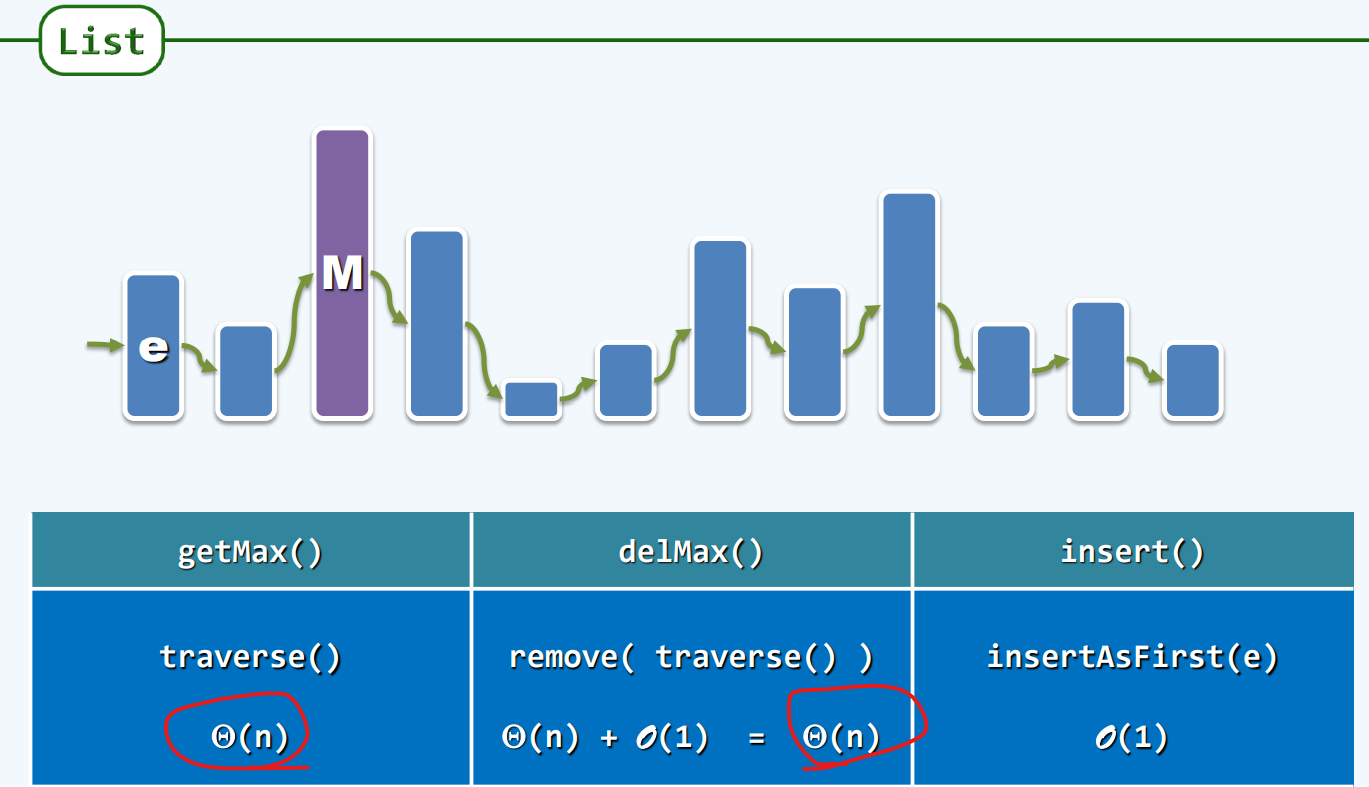
Sorted List

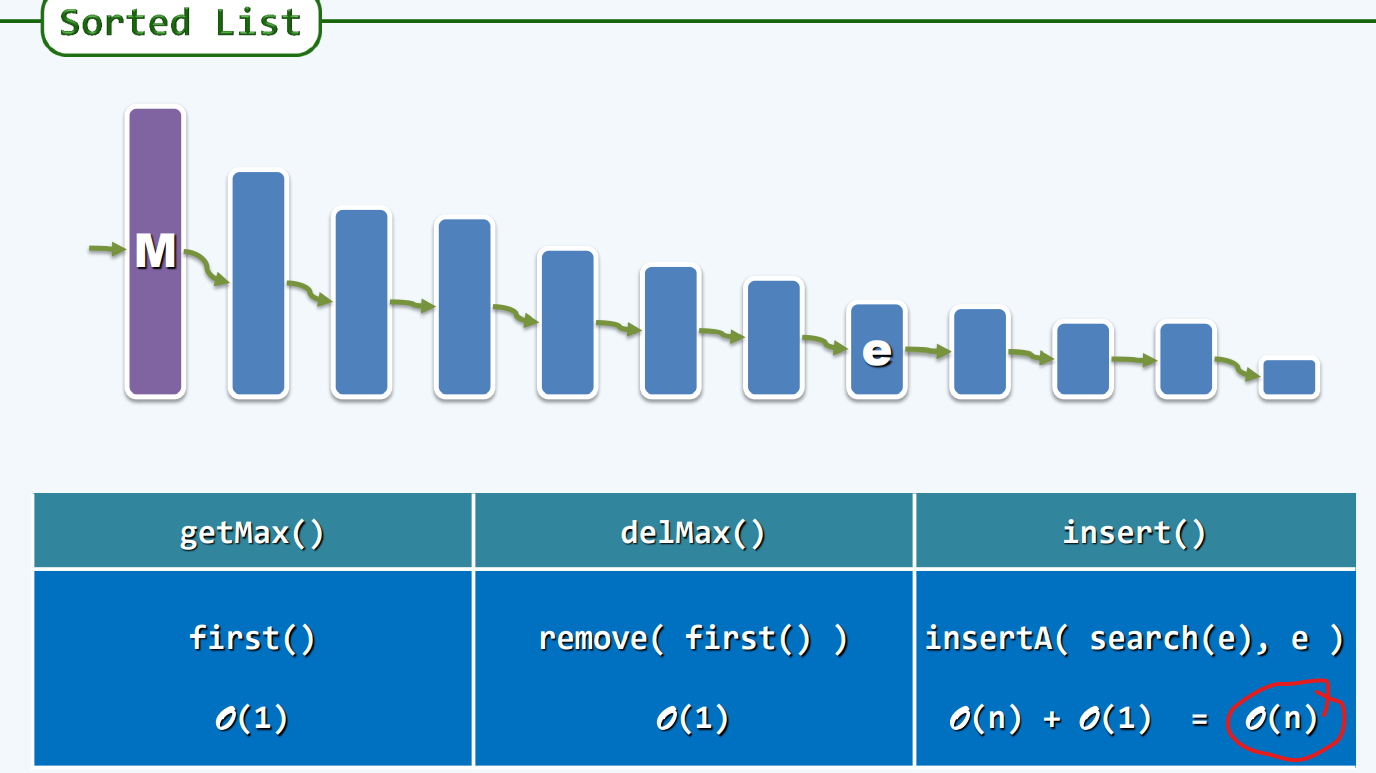
BBST

实现尝试

/******************************************************************************************
0002  * Test of PQ_ComplHeap & PQ_LeftHeap
0003  ******************************************************************************************/
0004 #include "PQ_test.h"
0005 #include <windows.h>
0006 
0007 /******************************************************************************************
0008  * 针对基于列表、向量以及左式堆实现的优先级队列，做过程统一的测试
0009  ******************************************************************************************/
0010 template <typename PQ, typename T> //堆类型、词条类型
0011 void  testHeap ( int n ) {
0012    T* A = new T[2*n/3]; //创建容量为2*n/3的数组，并
0013    for ( int i = 0; i < 2 * n / 3; i++ ) A[i] = dice ( ( T ) 3 * n ); //在其中随机生成2*n/3个词条
0014    PQ heap ( A + n / 6, n / 3 ); //批量建堆（PQ_ComplHeap实现了Robert Floyd算法）
0015    delete [] A;
0016    while ( heap.size() < n ) { //随机测试
0017       if ( dice ( 100 ) < 70 ) { //70%概率插入新词条
0018          T e = dice ( ( T ) 3 * n );
0019          heap.insert ( e );
0020       } else { //30%概率摘除最大词条
0021          if ( !heap.empty() ) {
0022             T e = heap.delMax();
0023          }
0024       }
0025    }
0026    while ( !heap.empty() ) { //清空
0027       T e = heap.delMax();
0028    }
0029 }
0030 
0031 /******************************************************************************************
0032  * 优先级队列测试
0033  ******************************************************************************************/
0034 int main ( int argc, char* argv[] ) {
0035    if ( 2 > argc ) { printf ( "Usage: %s <size of test>\a\a\n", argv[0] ); return 1; }
0036    srand ( ( unsigned int ) time ( NULL ) );
0037    //srand( 1234567 );
0038 #if defined(DSA_PQ_LEFTHEAP)
0039    testHeap<PQ_LeftHeap<int>, int> ( atoi ( argv[1] ) ); //词条类型可以在这里任意选择
0040 #elif defined(DSA_PQ_COMPLHEAP)
0041    testHeap<PQ_ComplHeap<int>, int> ( atoi ( argv[1] ) ); //词条类型可以在这里任意选择
0042 #elif defined(DSA_PQ_LIST)
0043    testHeap<PQ_List<int>, int> ( atoi ( argv[1] ) ); //词条类型可以在这里任意选择
0044 #else
0045    printf ( "PQ type not defined yet\n" );
0046 #endif
0047    return 0;
0048 }

完全二叉堆

完全二叉树

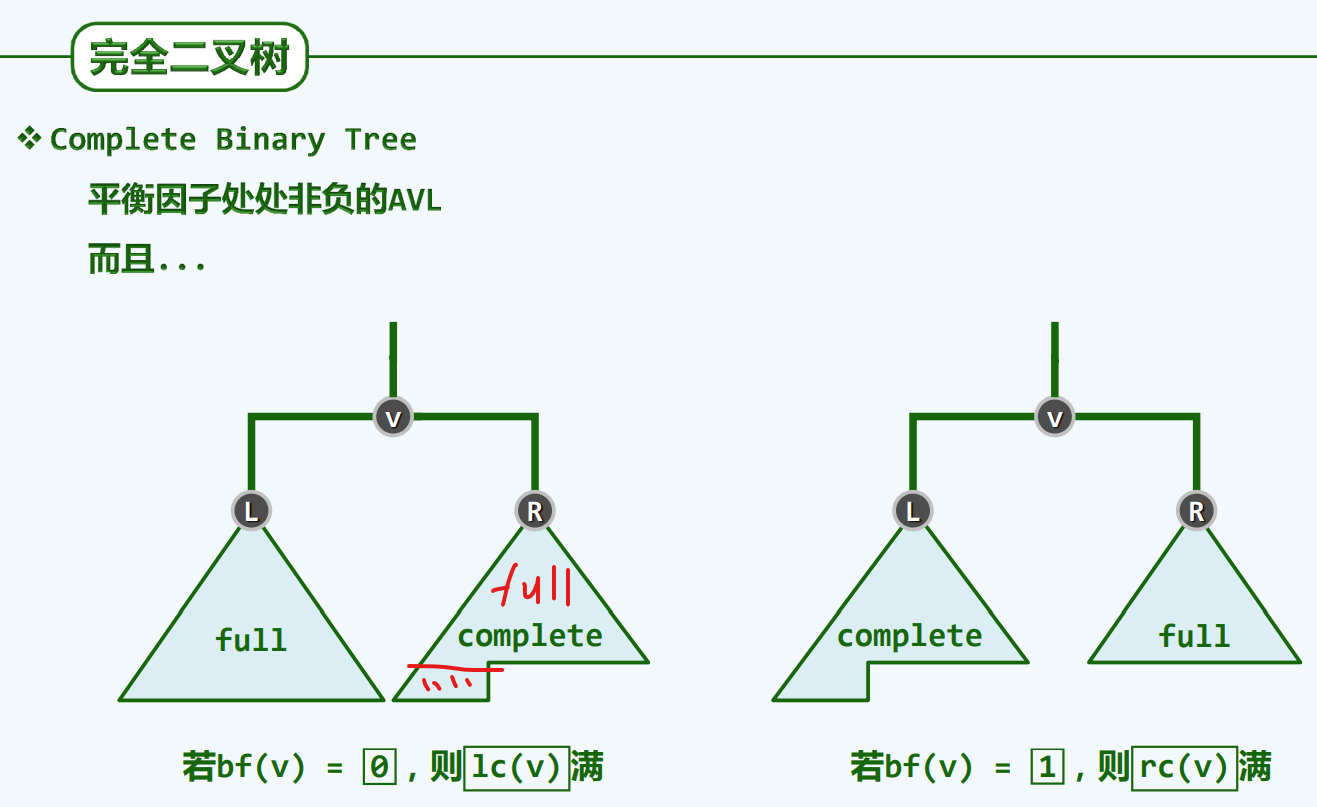
结构性

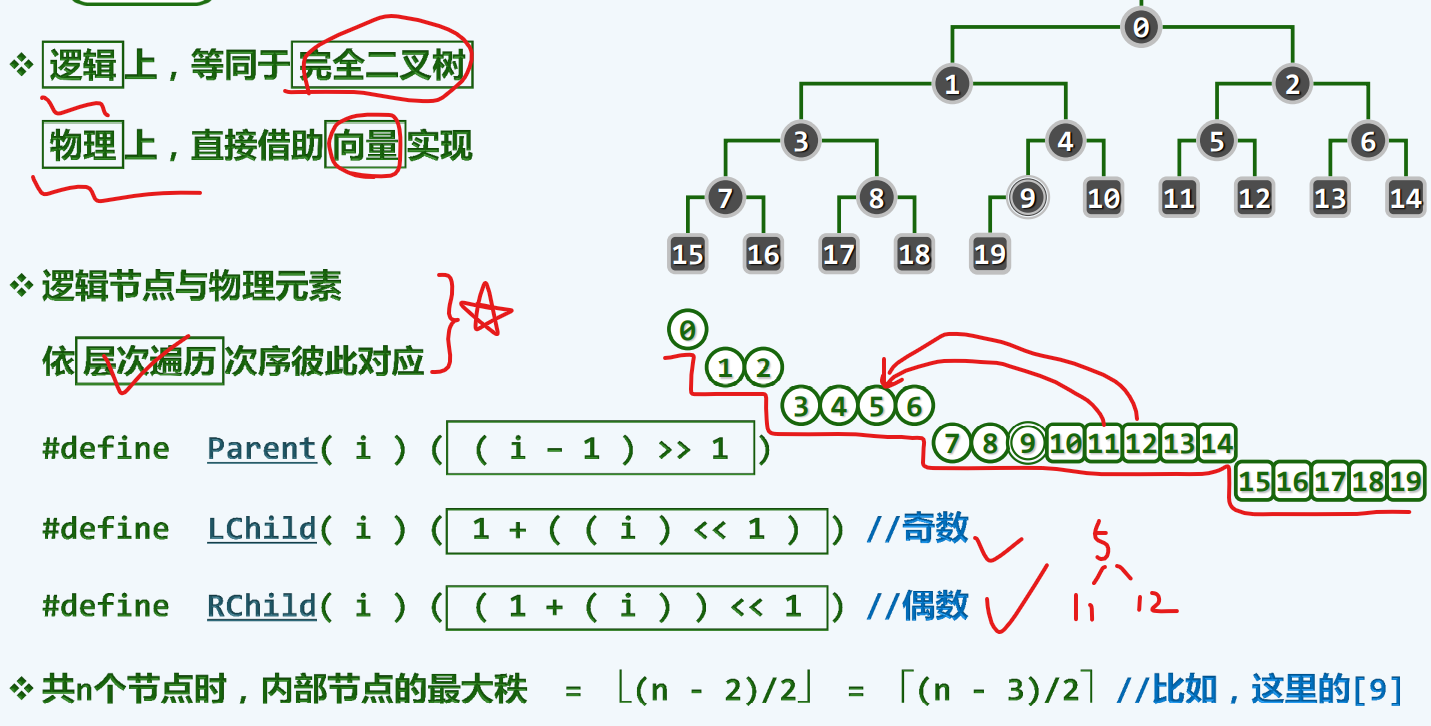
形具神备

堆序性*

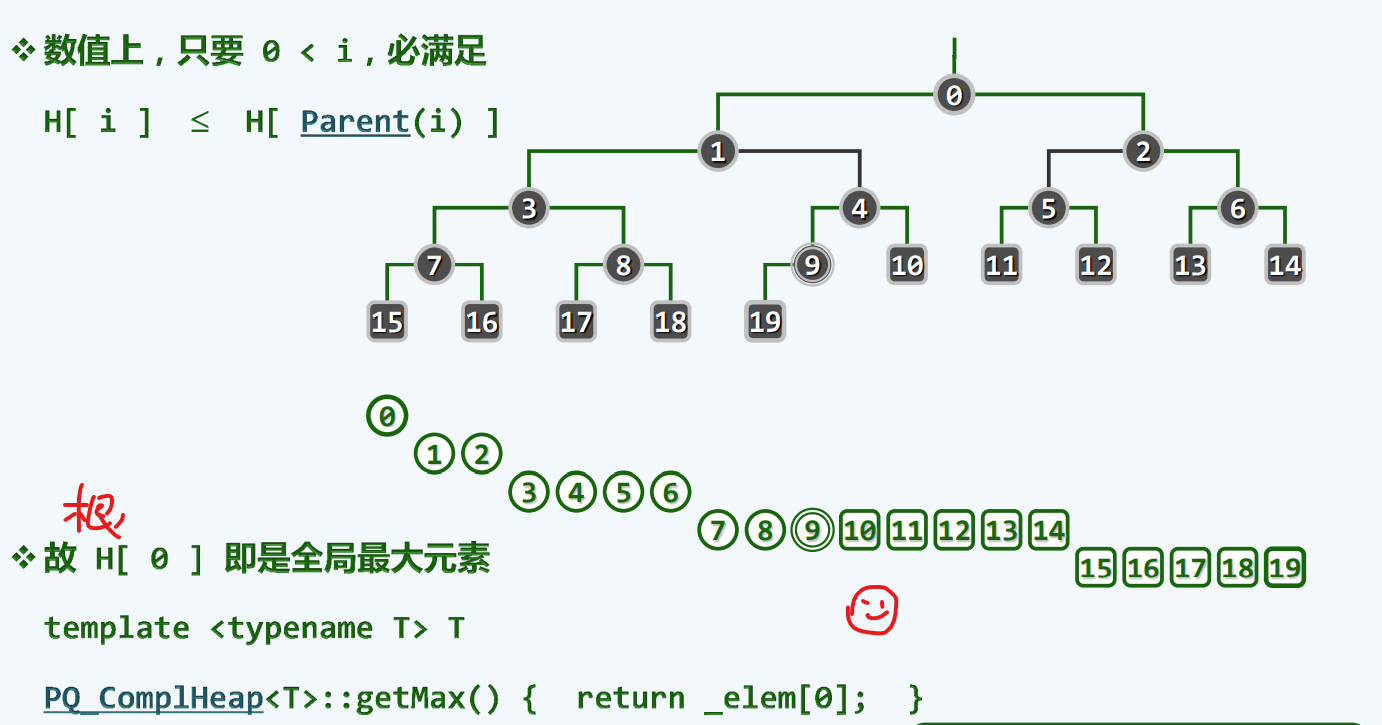
根节点为全局最大的元素

ADT

#include "Vector/Vector.h" //借助多重继承机制，基于向量
0002 #include "PQ/PQ.h" //按照优先级队列ADT实现的
0003 template <typename T> struct PQ_ComplHeap : public PQ<T>, public Vector<T> { //完全二叉堆
0004    PQ_ComplHeap() { } //默认构造
0005    PQ_ComplHeap ( T* A, Rank n ) { copyFrom ( A, 0, n ); heapify ( _elem, n ); } //批量构造
0006    void insert ( T ); //按照比较器确定的优先级次序，插入词条
0007    T getMax(); //读取优先级最高的词条
0008    T delMax(); //删除优先级最高的词条
0009 }; //PQ_ComplHeap
0010 template <typename T> void heapify ( T* A, Rank n ); //Floyd建堆算法
0011 template <typename T> Rank percolateDown ( T* A, Rank n, Rank i ); //下滤
0012 template <typename T> Rank percolateUp ( T* A, Rank i ); //上滤
0013 

上滤-插入

算法描述

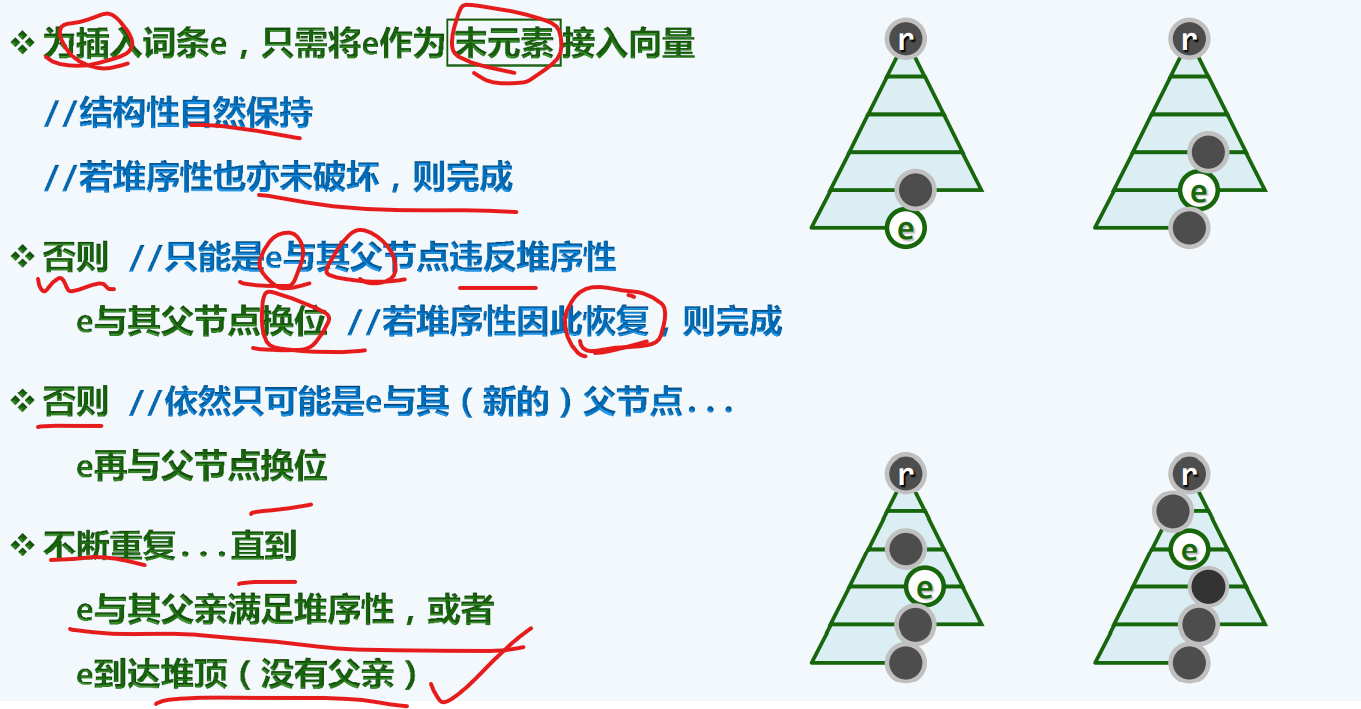
实例

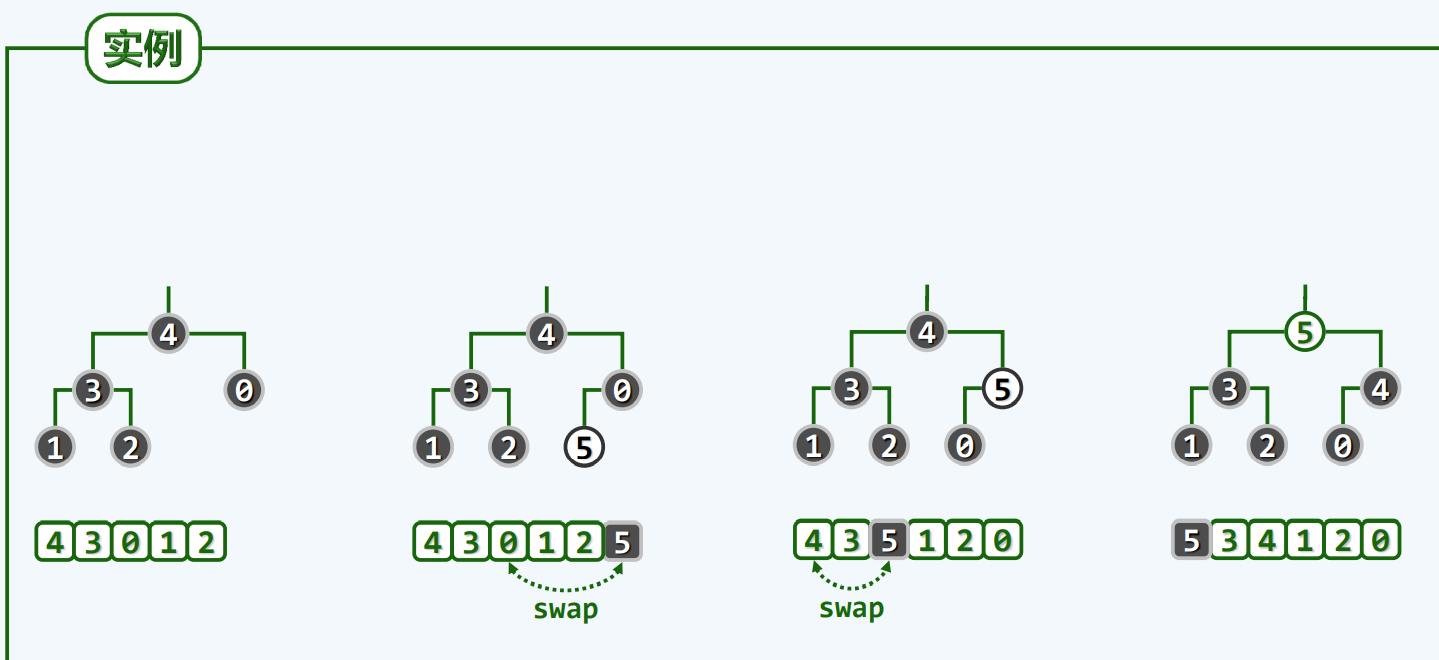
实现

insert()

将待插入的e，接入向量之中（末尾元素,对应的秩为n-1）

template <typename T> void PQ_ComplHeap<T>::insert ( T e ) { //将词条插入完全二叉堆中
0002    Vector<T>::insert ( e ); //首先将新词条接至向量末尾
0003    percolateUp ( _elem, _size - 1 ); //再对该词条实施上滤调整
0004 }

上滤调整

迭代式的调整过程是用while循环完成的

//对向量中的第i个词条实施上滤操作，i < _size
0002 template <typename T> Rank percolateUp ( T* A, Rank i ) {
0003    while ( 0 < i ) { //在抵达堆顶之前，反复地
0004       Rank j = Parent ( i ); //考查[i]之父亲[j]
0005       if ( lt ( A[i], A[j] ) ) break; //一旦父子顺序，上滤旋即完成；否则
0006       swap ( A[i], A[j] ); i = j; //父子换位，并继续考查上一层
0007    } //while
0008    return i; //返回上滤最终抵达的位置
0009 }

效率

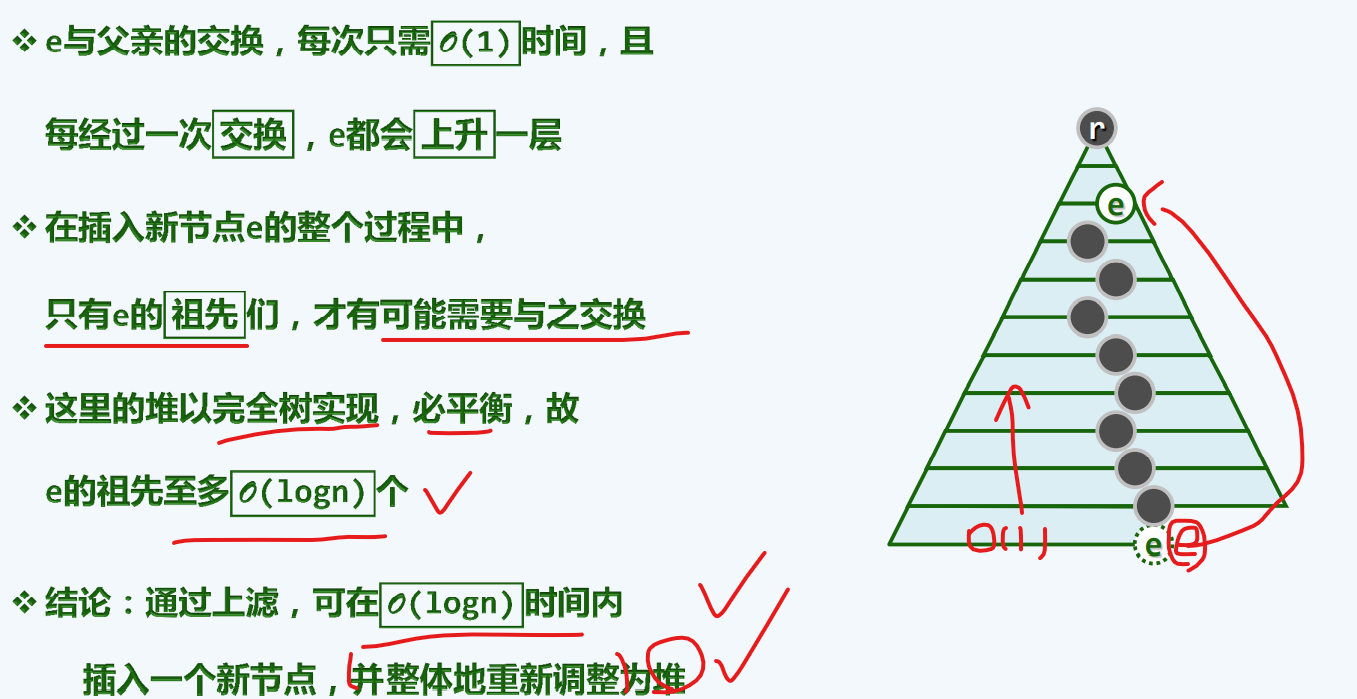
下滤-删除

算法描述

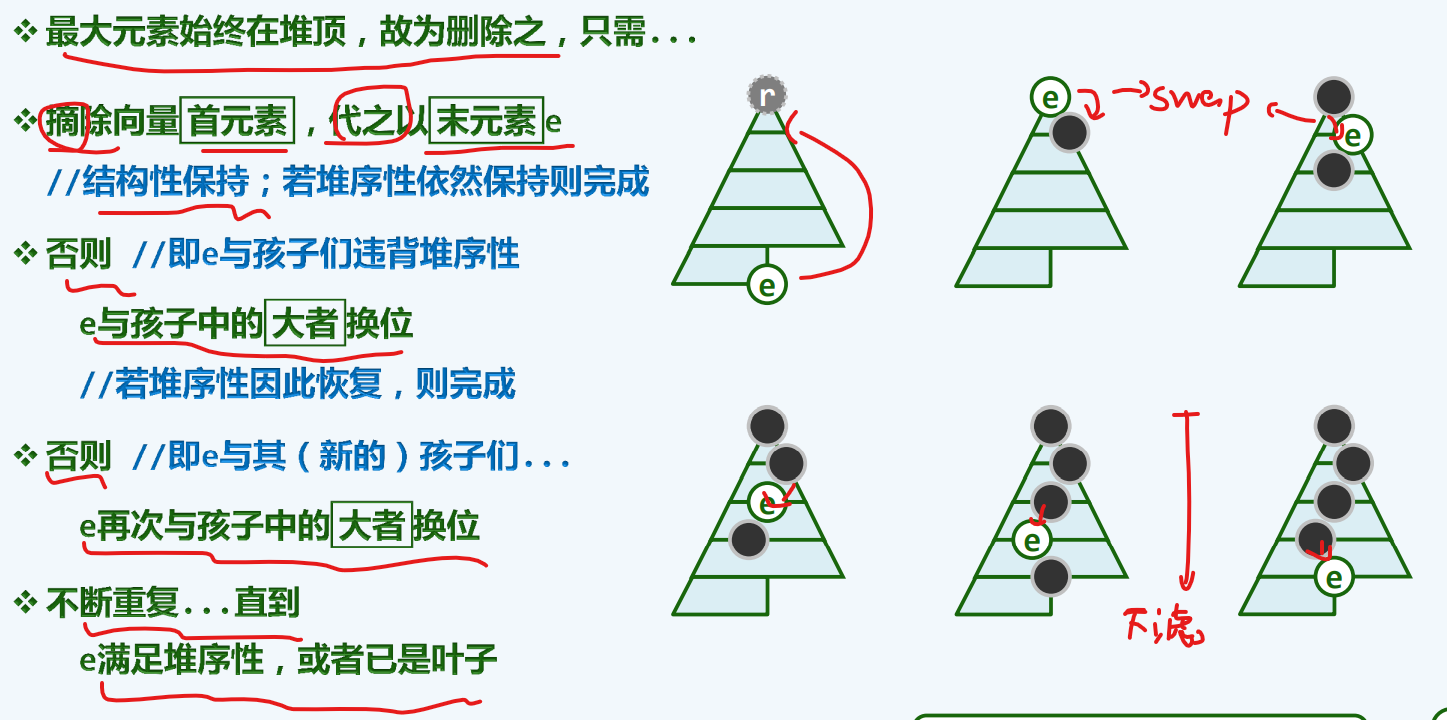
实例

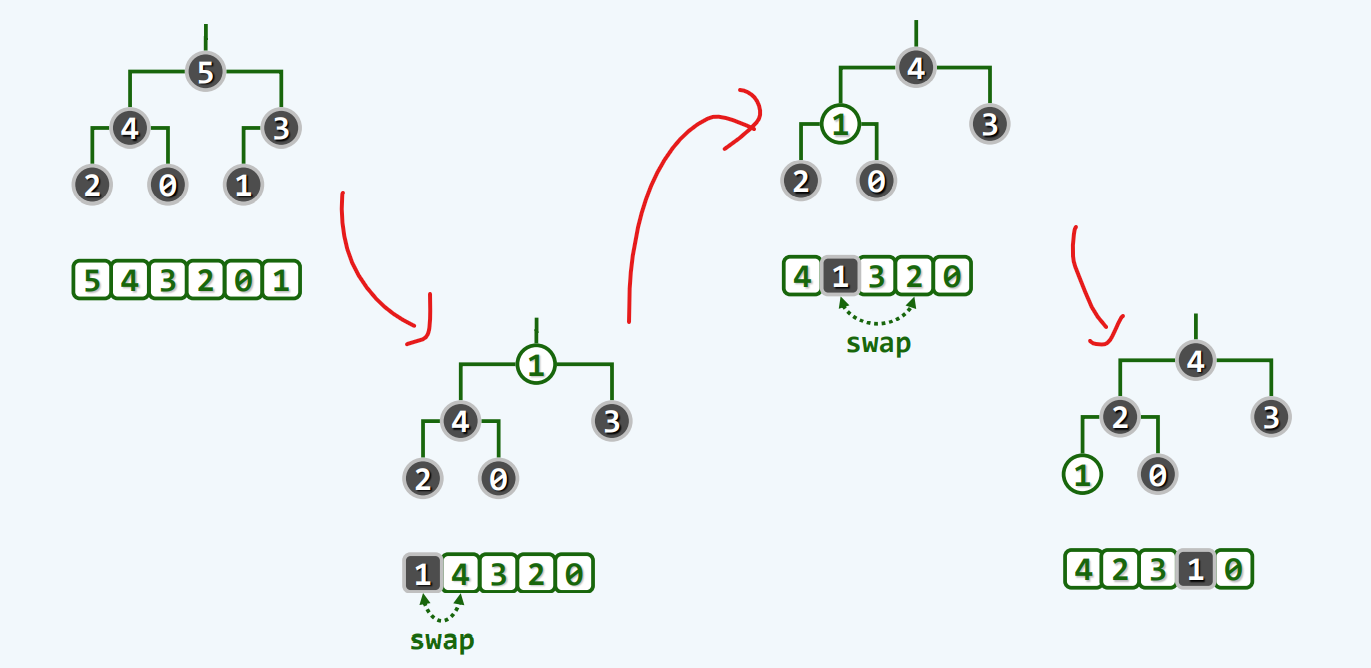
实现

ProertParent()

#define  Parent(i)         ( ( ( i ) - 1 ) >> 1 ) //PQ[i]的父节点（floor((i-1)/2)，i无论正负）
0002 #define  LChild(i)         ( 1 + ( ( i ) << 1 ) ) //PQ[i]的左孩子
0003 #define  RChild(i)         ( ( 1 + ( i ) ) << 1 ) //PQ[i]的右孩子
0004 #define  InHeap(n, i)      ( ( ( -1 ) < ( i ) ) && ( ( i ) < ( n ) ) ) //判断PQ[i]是否合法
0005 #define  LChildValid(n, i) InHeap( n, LChild( i ) ) //判断PQ[i]是否有一个（左）孩子
0006 #define  RChildValid(n, i) InHeap( n, RChild( i ) ) //判断PQ[i]是否有两个孩子
0007 #define  Bigger(PQ, i, j)  ( lt( PQ[i], PQ[j] ) ? j : i ) //取大者（等时前者优先）
0008 #define  ProperParent(PQ, n, i) /*父子（至多）三者中的大者*/ \
0009             ( RChildValid(n, i) ? Bigger( PQ, Bigger( PQ, i, LChild(i) ), RChild(i) ) : \
0010             ( LChildValid(n, i) ? Bigger( PQ, i, LChild(i) ) : i \
0011             ) \
0012             ) //相等时父节点优先，如此可避免不必要的交换

delMax()

template <typename T> T PQ_ComplHeap<T>::delMax() { //删除非空完全二叉堆中优先级最高的词条
0002    T maxElem = _elem[0]; _elem[0] = _elem[ --_size ]; //摘除堆顶（首词条），代之以末词条
0003    percolateDown ( _elem, _size, 0 ); //对新堆顶实施下滤
0004    return maxElem; //返回此前备份的最大词条
0005 }

percolateDown()

//对向量前n个词条中的第i个实施下滤，i < n
0002 template <typename T> Rank percolateDown ( T* A, Rank n, Rank i ) {
0003    Rank j; //i及其（至多两个）孩子中，堪为父者
0004    while ( i != ( j = ProperParent ( A, n, i ) ) ) //只要i非j，则
0005       { swap ( A[i], A[j] ); i = j; } //二者换位，并继续考查下降后的i
0006    return i; //返回下滤抵达的位置（亦i亦j）
0007 }

效率

批量造堆

自上而下的上滤

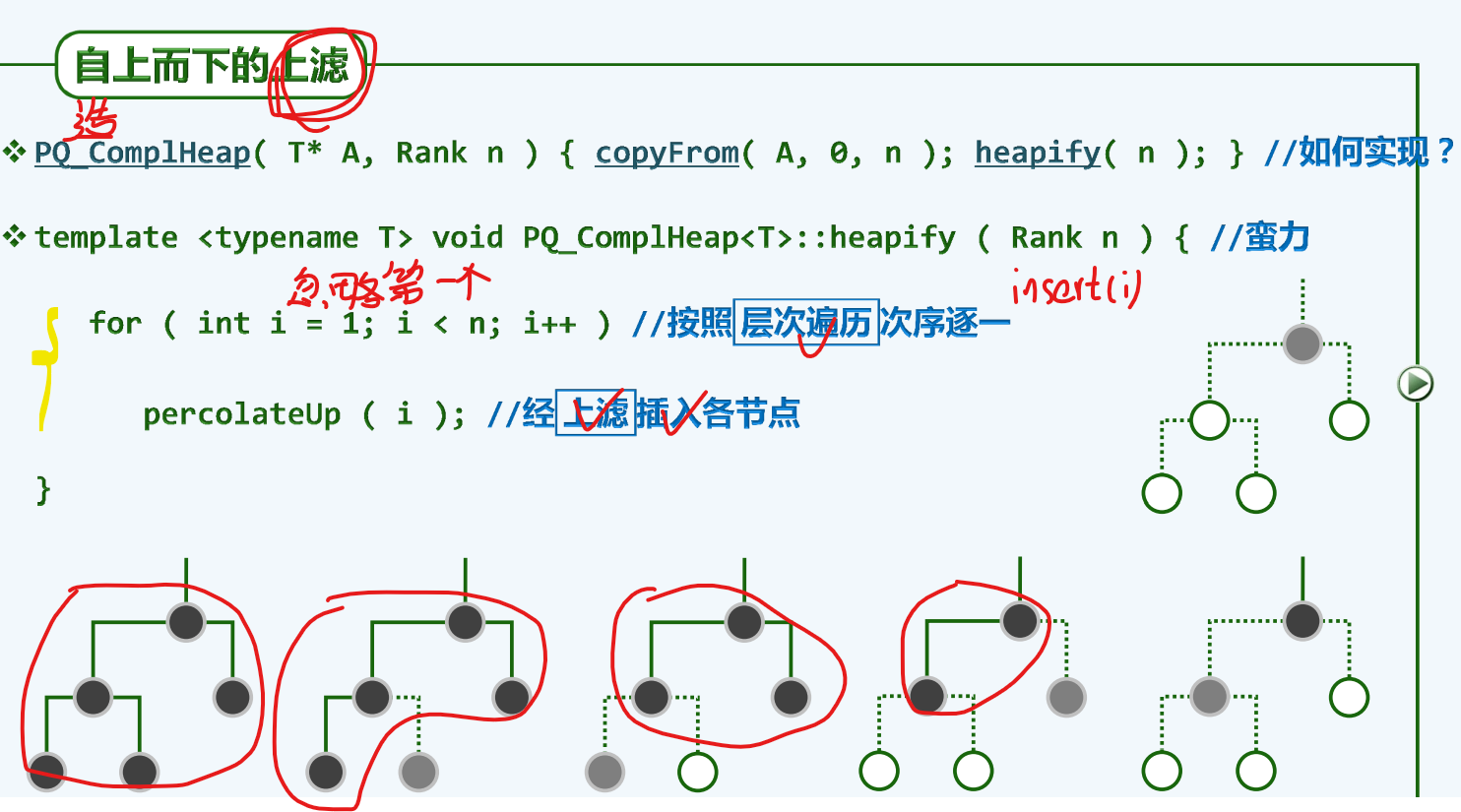
效率

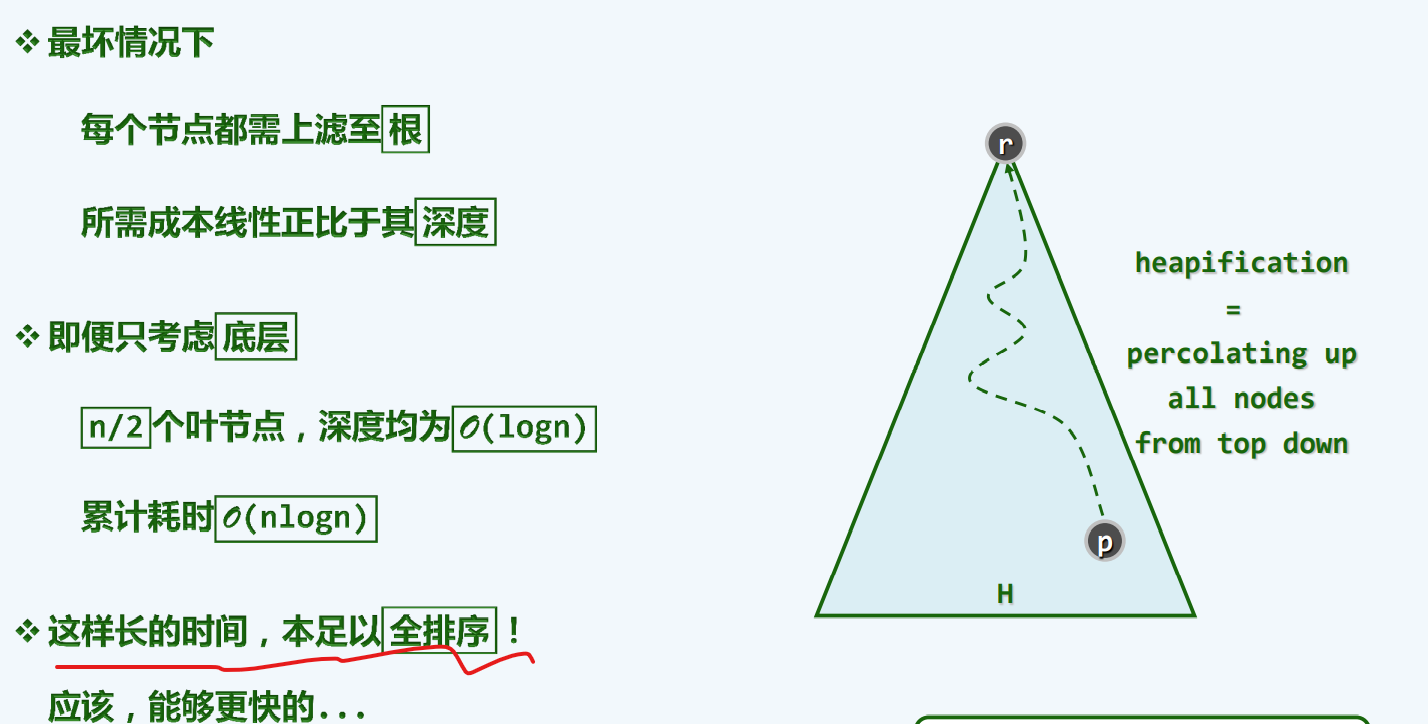
自下而上的下滤

算法

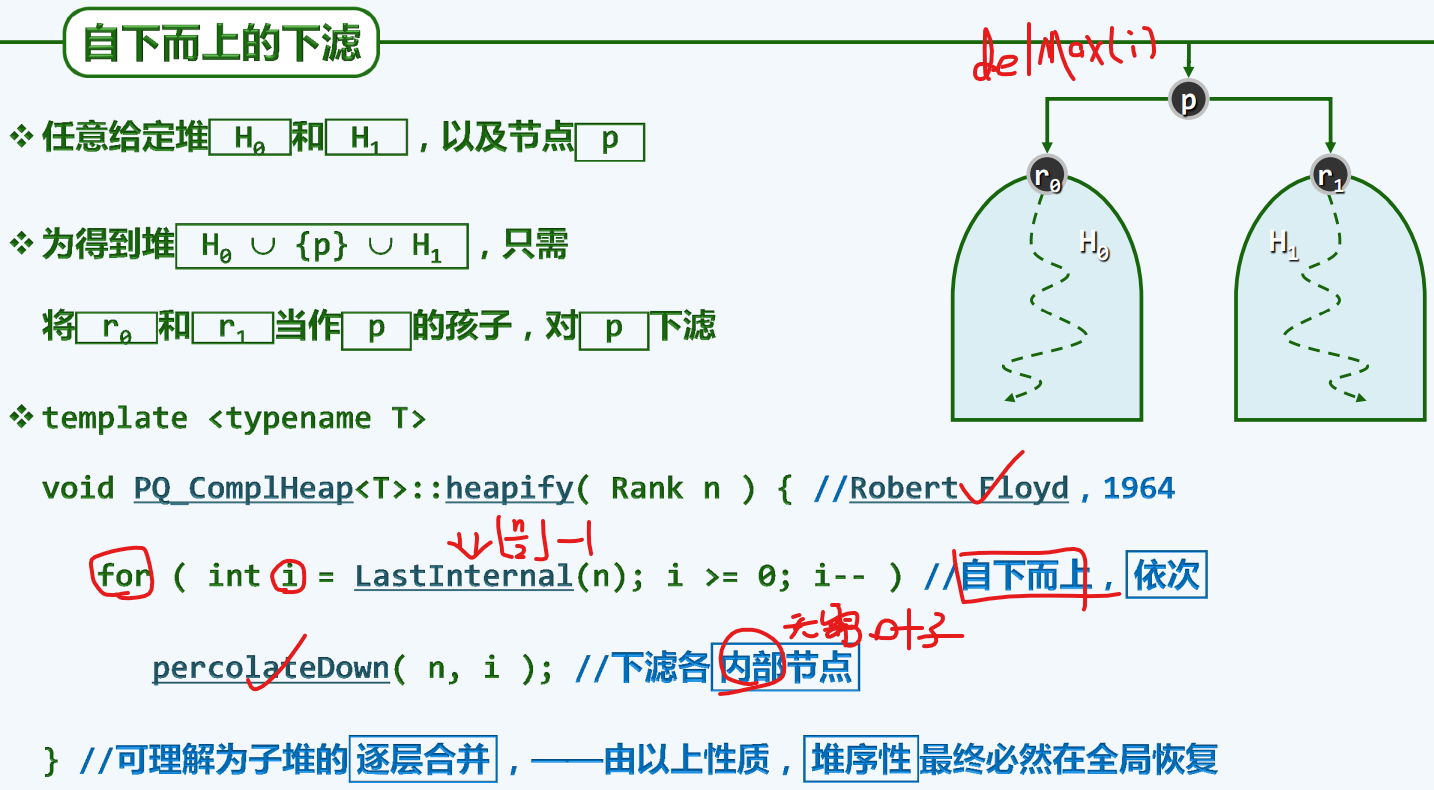
实现

template <typename T> void heapify ( T* A, const Rank n ) { //Floyd建堆算法，O(n)时间
0002    for ( Rank i = n/2 - 1; 0 <= i; i-- ) //自底而上，依次
0003       percolateDown ( A, n, i ); //下滤各内部节点
0004 }

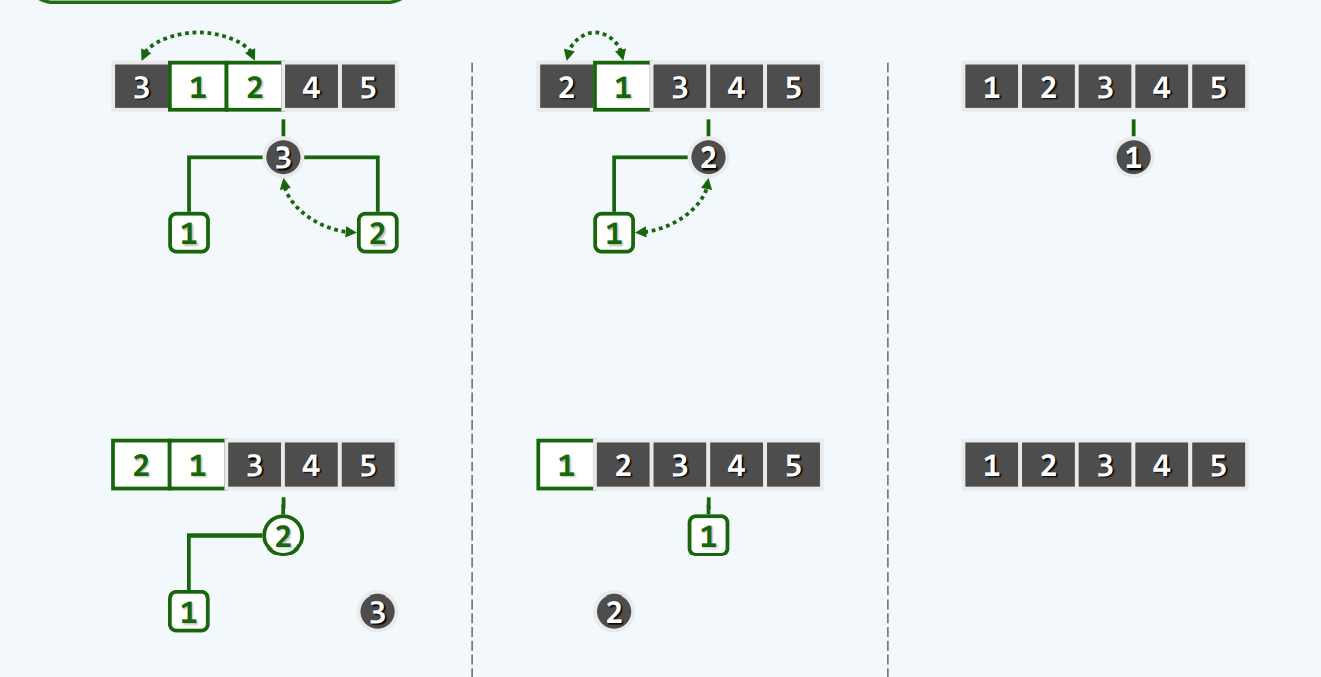
实例

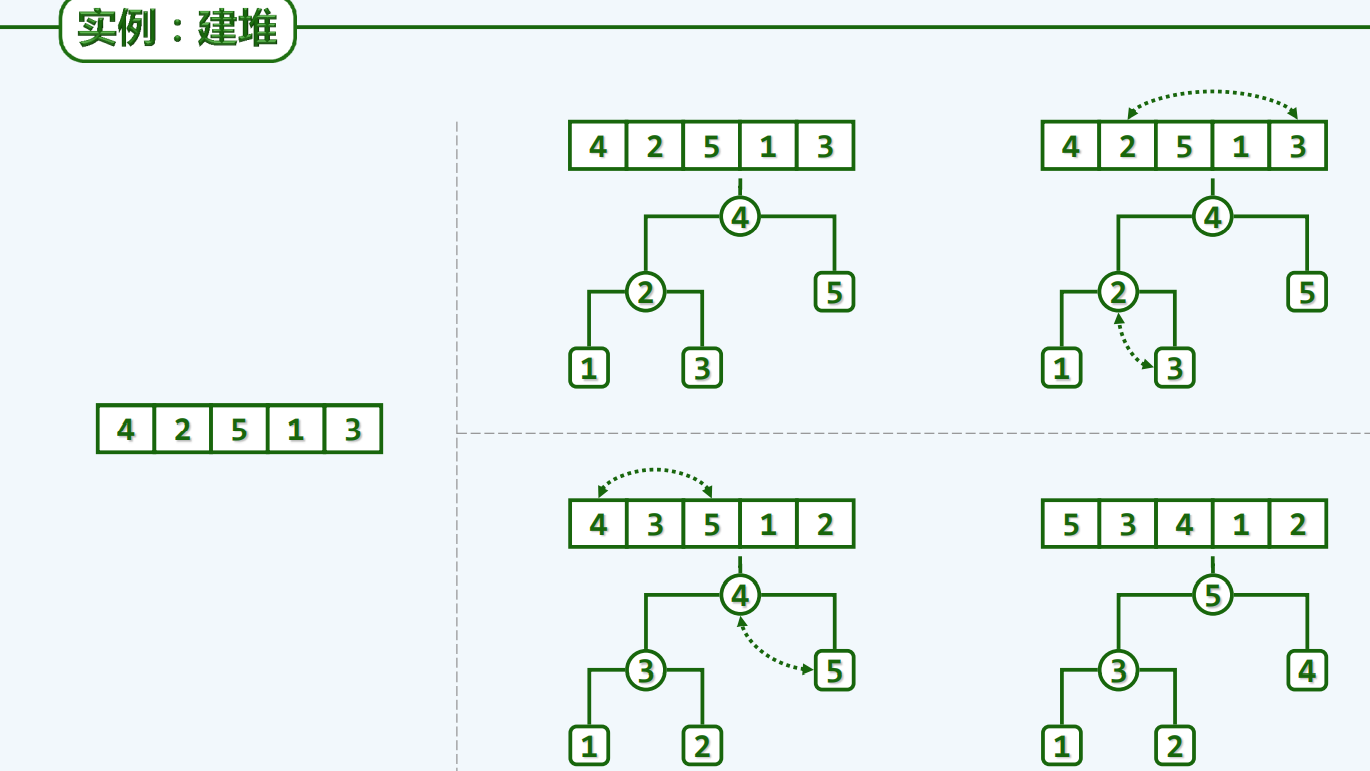
这里数值为3纯属巧合

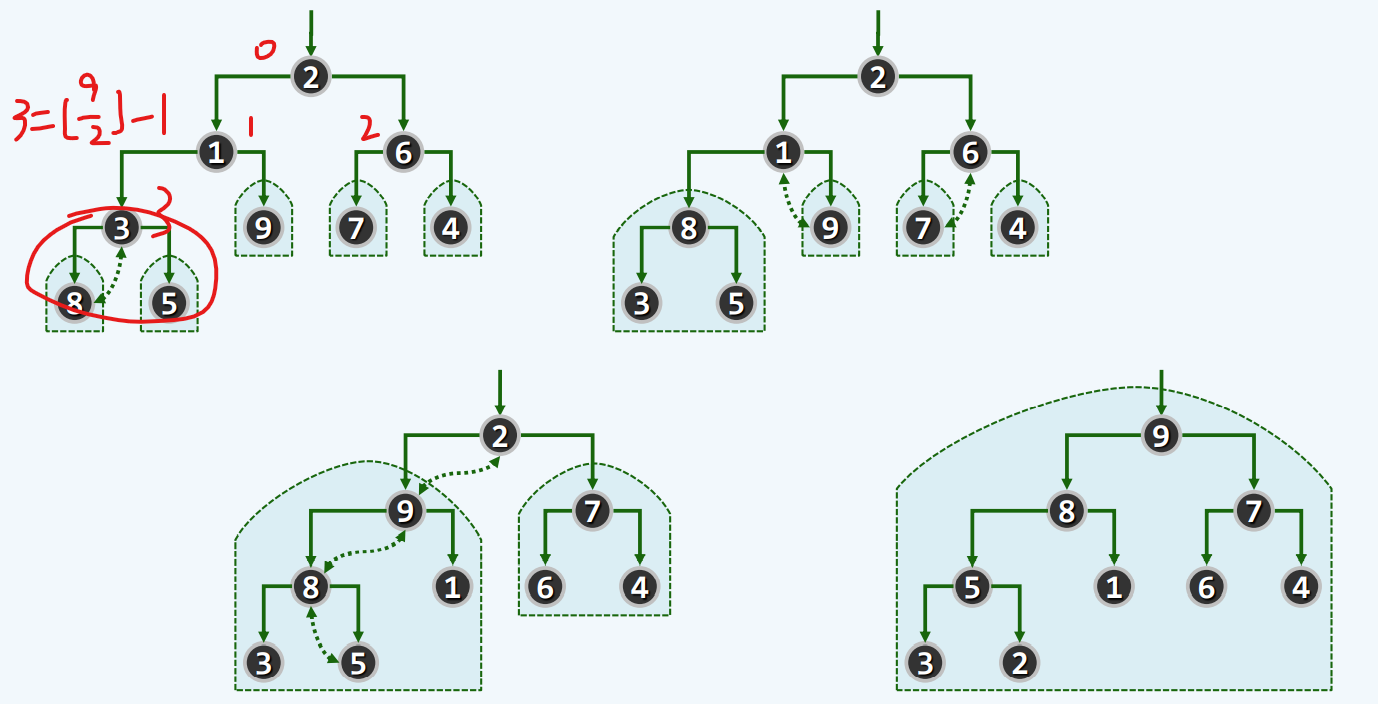
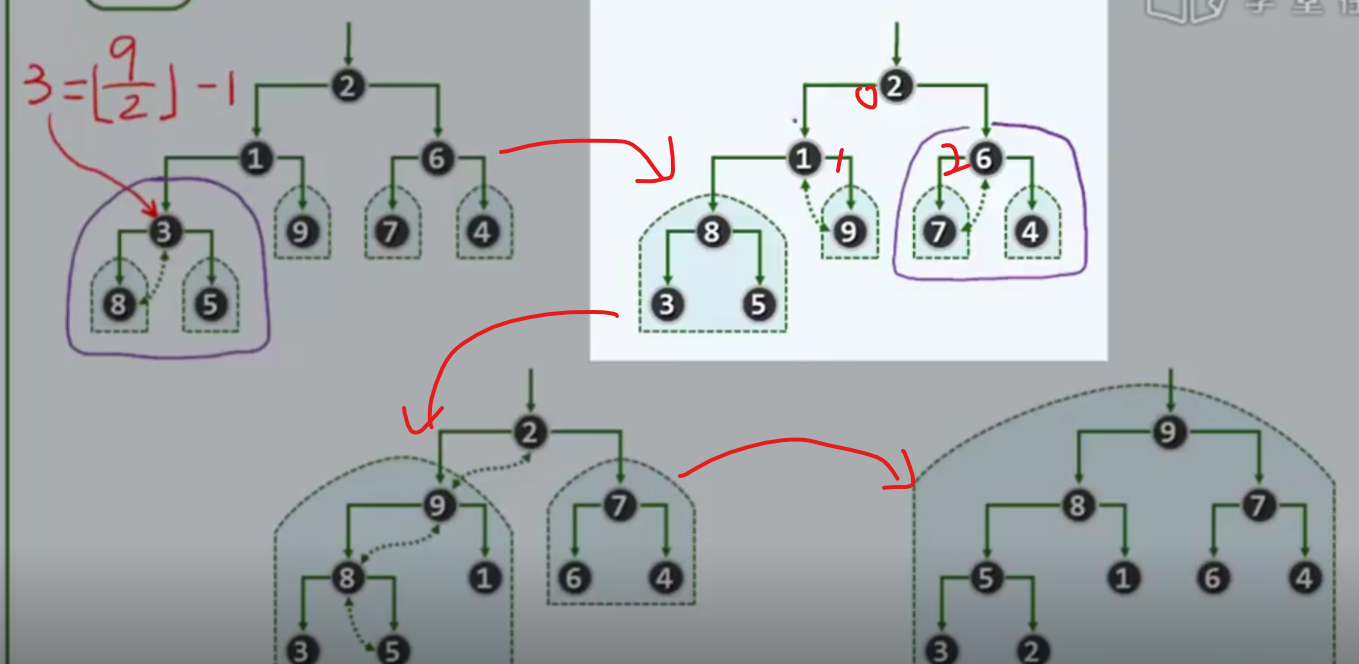
效率

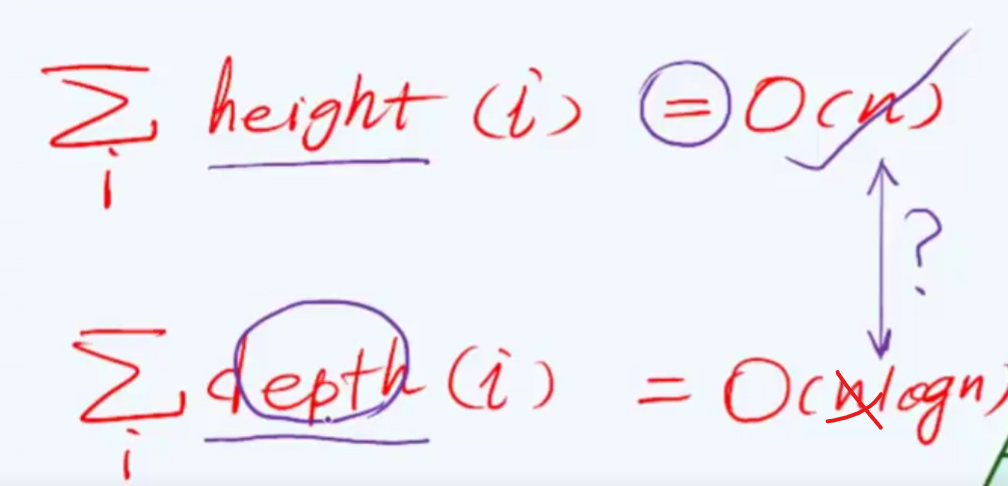
与自上而下相比，自下而上采用的是高度作为指标，得到的时间复杂度为O（h）为何以高度为指标会低这么多时间？，这是因为，高度低的人群为大多数（树的底层），这就像税收，大部分人都属于中低层阶级，因此他们所需要缴纳的税收少，总体阶层全部加起来税收也不过n，这是再合适不过的了，如果自上而下缴纳税收，这反而是迎合的收入高的阶级，使得收入低的人交更多的税，这样必然会受到惩罚。

堆排序

算法

就地

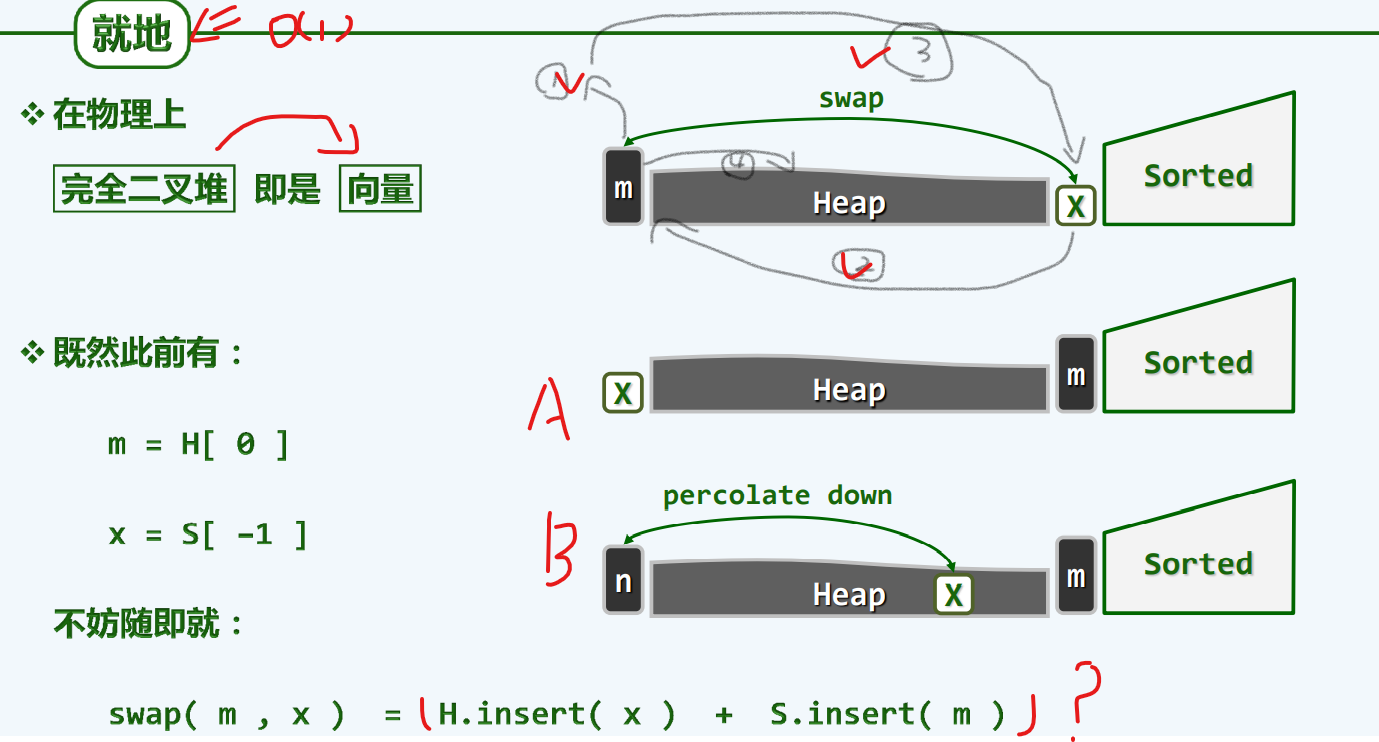
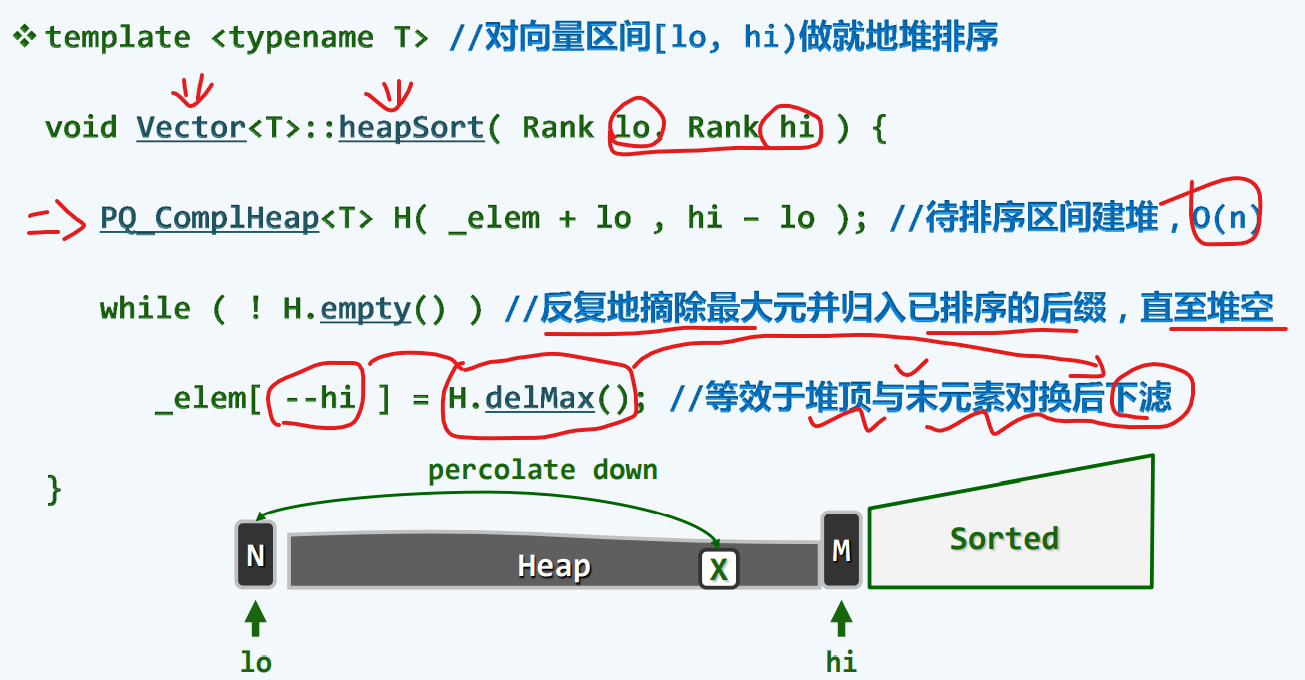
实现

按照我们的惯例，lo对应的是首元素，hi对应的是尾部的哨兵

实例

预处理

选取+调整

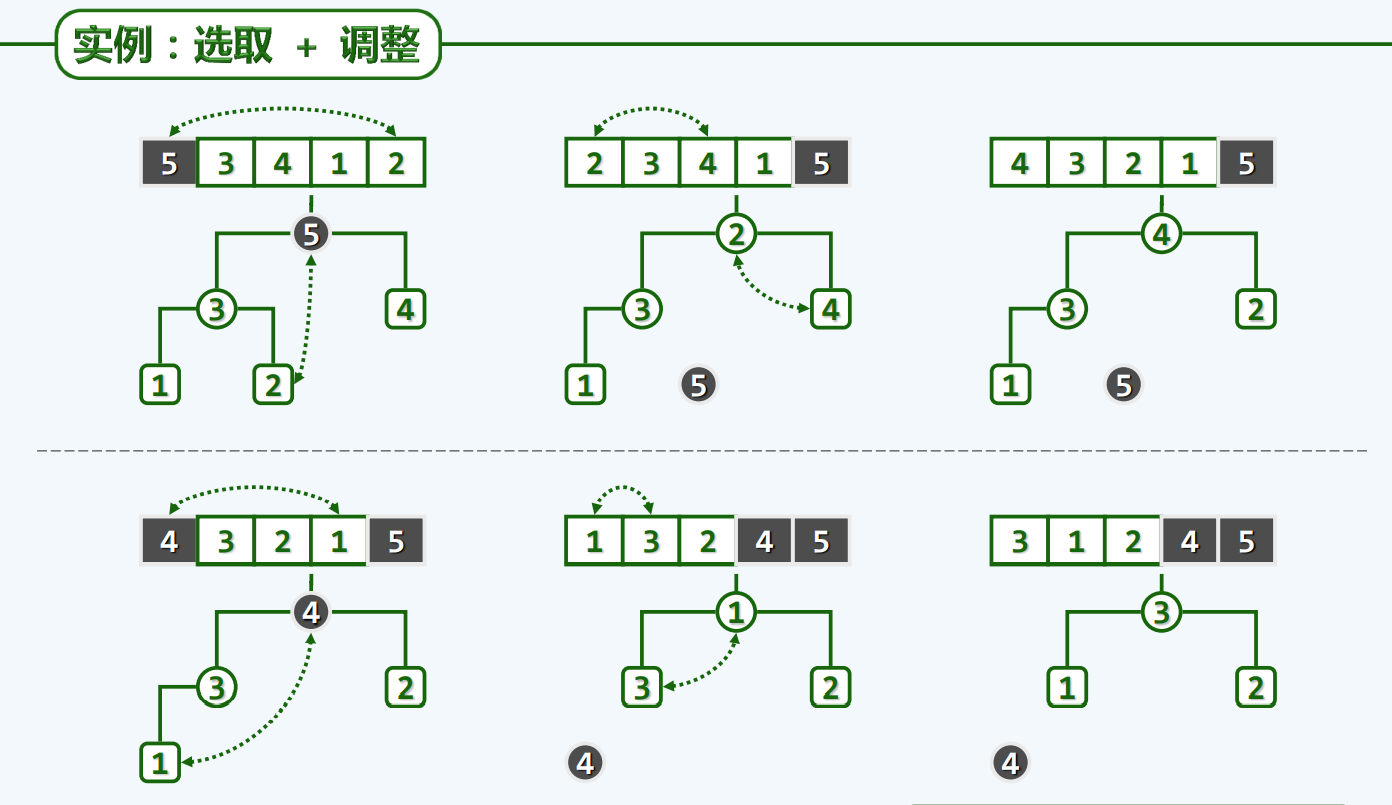
左式堆

第一印象

堆之合并

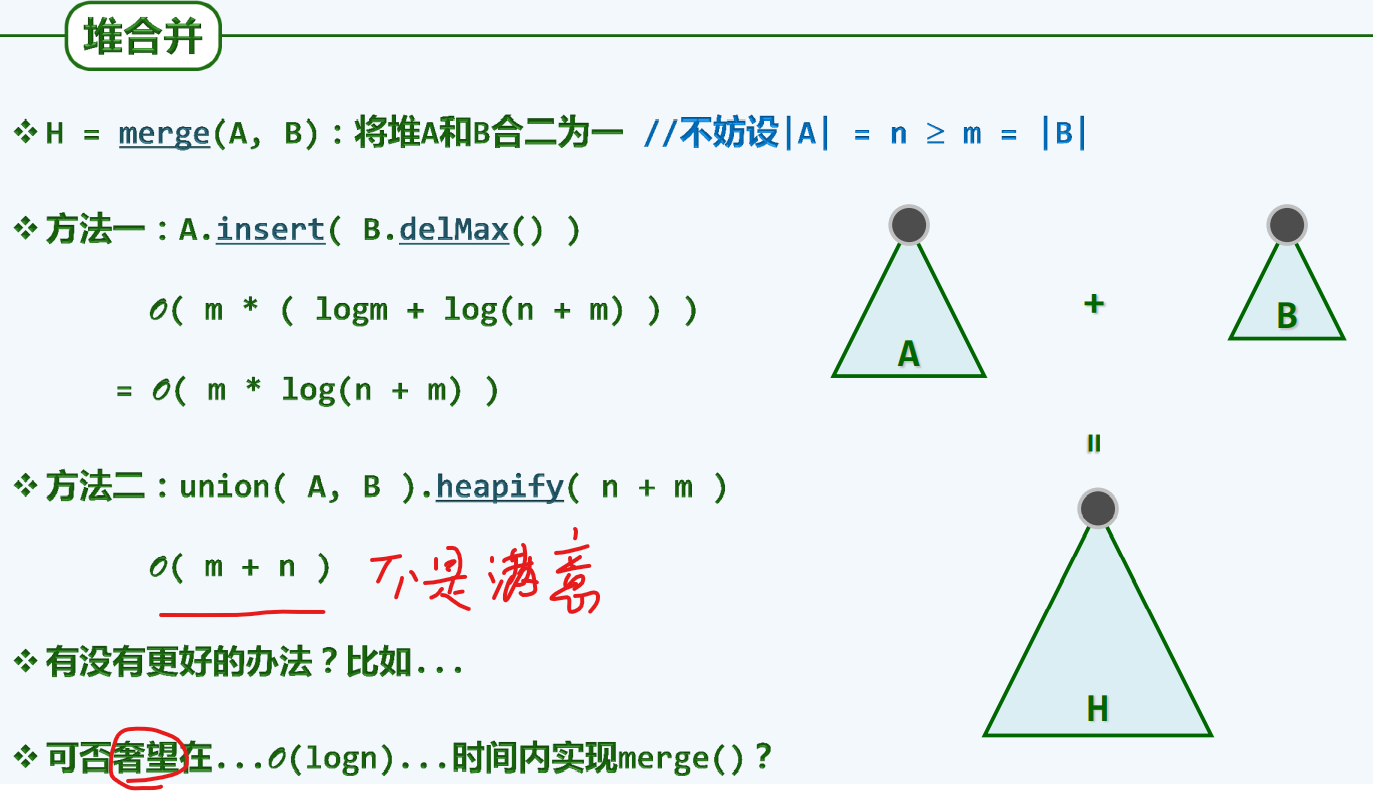
为何我们不满意于O(m+n)的时间复杂度？

​ 事实上弗洛伊德的算法是基于完全无序给出的，我们这已经分好了两堆，而且分别知道了内部偏序关系，从这一角度出发，我们完全有理由相信存在更加高效的算法，事实上，左式堆就是答案。

奇中求正

虽然，这种偏向一个方向的左式堆能将时间复杂度降到O（logn），但是，我们仔细观察，这还是一颗严格意义的完全二叉树吗？事实上，我们说，对于堆而言，结构性并不是必要遵守的条件，堆序性才是。在适当的时候，我们完全可以做一些必要的舍弃。

NPL

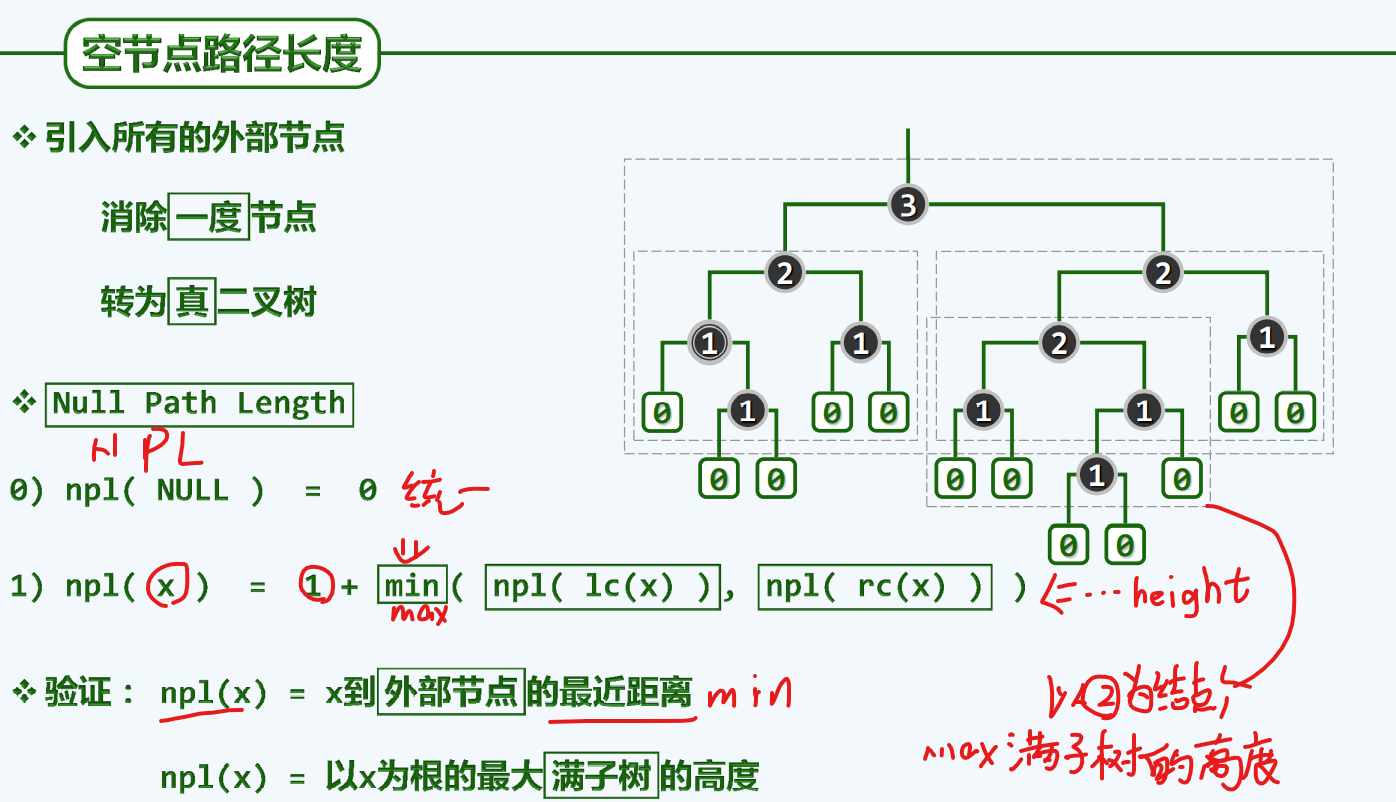
至此，我们建立了一个重要的指标(NPL)，以这个指标为基准，我们可以来度量根节点的倾斜性

左倾性

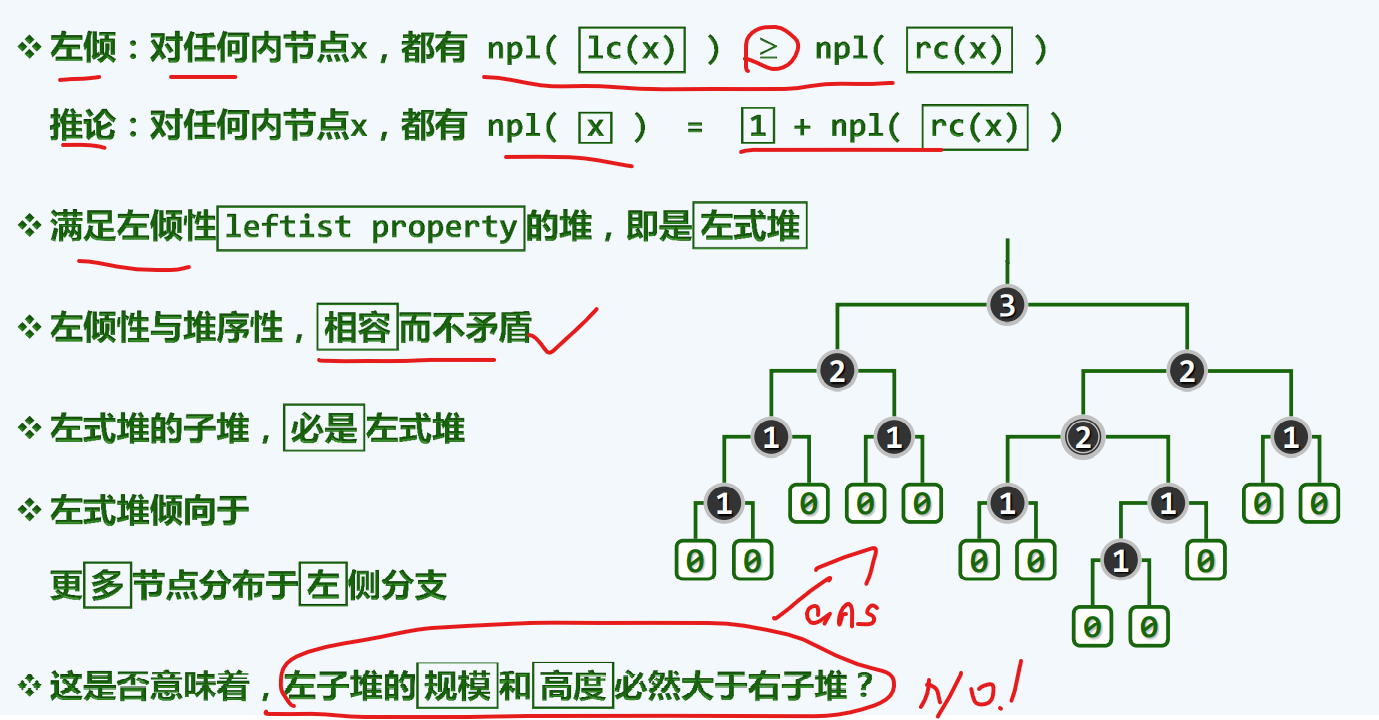
我们说，更重要的是看他的右侧链

左展右敛

如果根节点的NPL为d，那么至少含有2^d个结点

反过来，如果将左式堆的规模固定为n，那么右侧链的长度不过logn

这难道不正是我们最初的设计目标吗

合并算法

LeftHeap

#include "PQ/PQ.h" //引入优先级队列ADT
0002 #include "BinTree/BinTree.h" //引入二叉树节点模板类
0003 
0004 template <typename T>
0005 class PQ_LeftHeap : public PQ<T>, public BinTree<T> { //基于二叉树，以左式堆形式实现的PQ
0006 public:
0007    PQ_LeftHeap() { } //默认构造
0008    PQ_LeftHeap ( T* E, int n ) //批量构造：可改进为Floyd建堆算法
0009    {  for ( int i = 0; i < n; i++ ) insert ( E[i] );  }
0010    PQ_LeftHeap( PQ_LeftHeap & A, PQ_LeftHeap & B ) { //合并构造
0011       _root = merge(A._root, B._root); _size = A._size + B._size;
0012       A._root = B._root = NULL; A._size = B._size = 0;
0013    }
0014    void insert ( T ); //按照比较器确定的优先级次序插入元素
0015    T getMax(); //取出优先级最高的元素
0016    T delMax(); //删除优先级最高的元素
0017 }; //PQ_LeftHeap

算法讲述

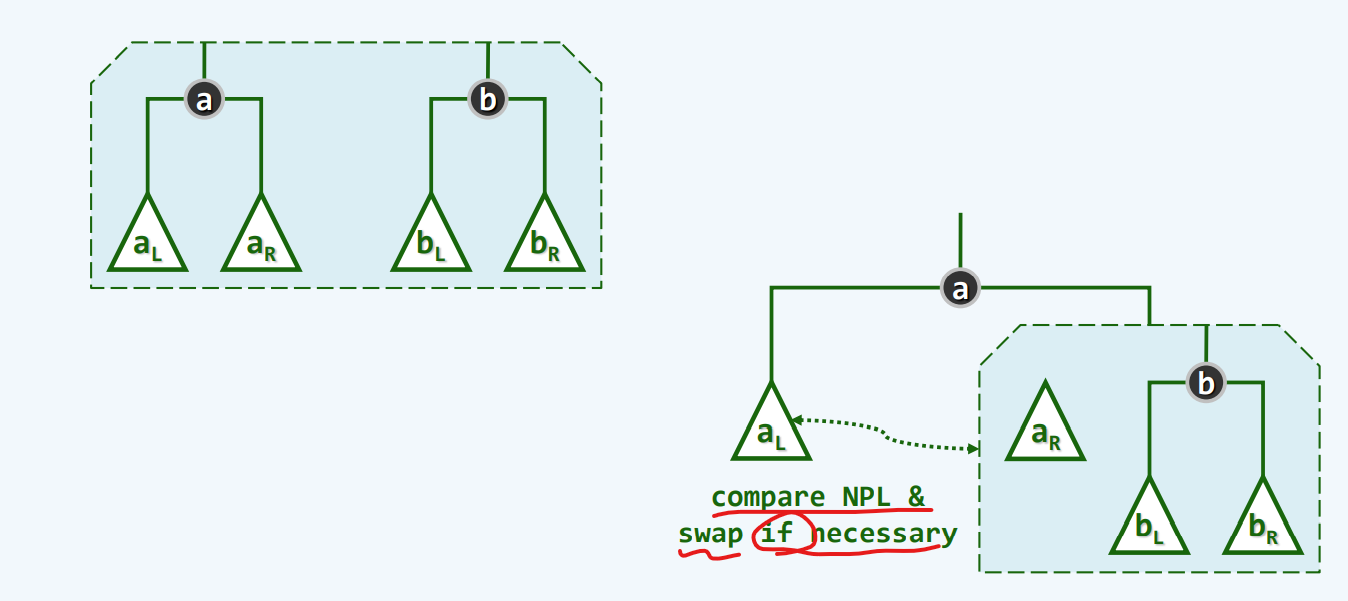
实现

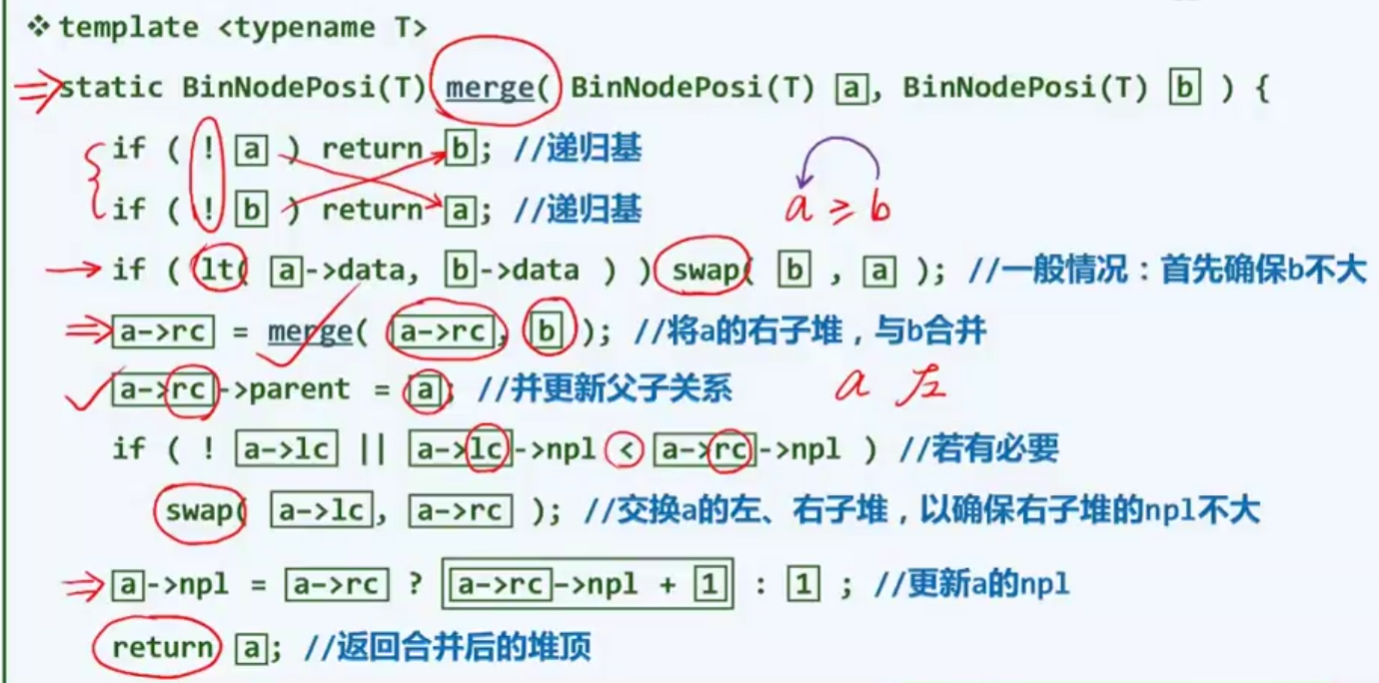
代码

template <typename T> //根据相对优先级确定适宜的方式，合并以a和b为根节点的两个左式堆
0002 static BinNodePosi<T> merge ( BinNodePosi<T> a, BinNodePosi<T> b ) {
0003    if ( ! a ) return b; //退化情况
0004    if ( ! b ) return a; //退化情况
0005    if ( lt ( a->data, b->data ) ) swap ( a, b ); //一般情况：首先确保b不大
0006    ( a->rc = merge ( a->rc, b ) )->parent = a; //将a的右子堆，与b合并
0007    if ( !a->lc || a->lc->npl < a->rc->npl ) //若有必要
0008       swap ( a->lc, a->rc ); //交换a的左、右子堆，以确保右子堆的npl不大
0009    a->npl = a->rc ? a->rc->npl + 1 : 1; //更新a的npl
0010    return a; //返回合并后的堆顶
0011 } //本算法只实现结构上的合并，堆的规模须由上层调用者负责更新

实例

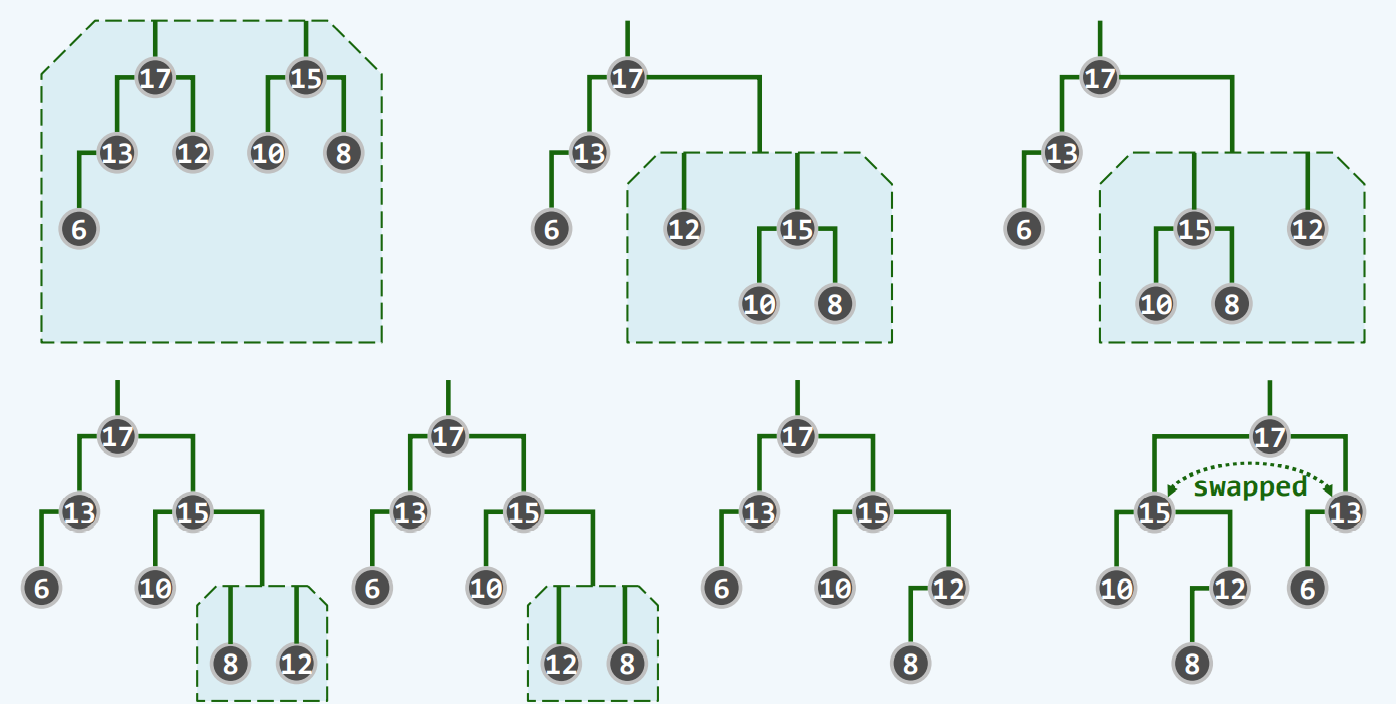
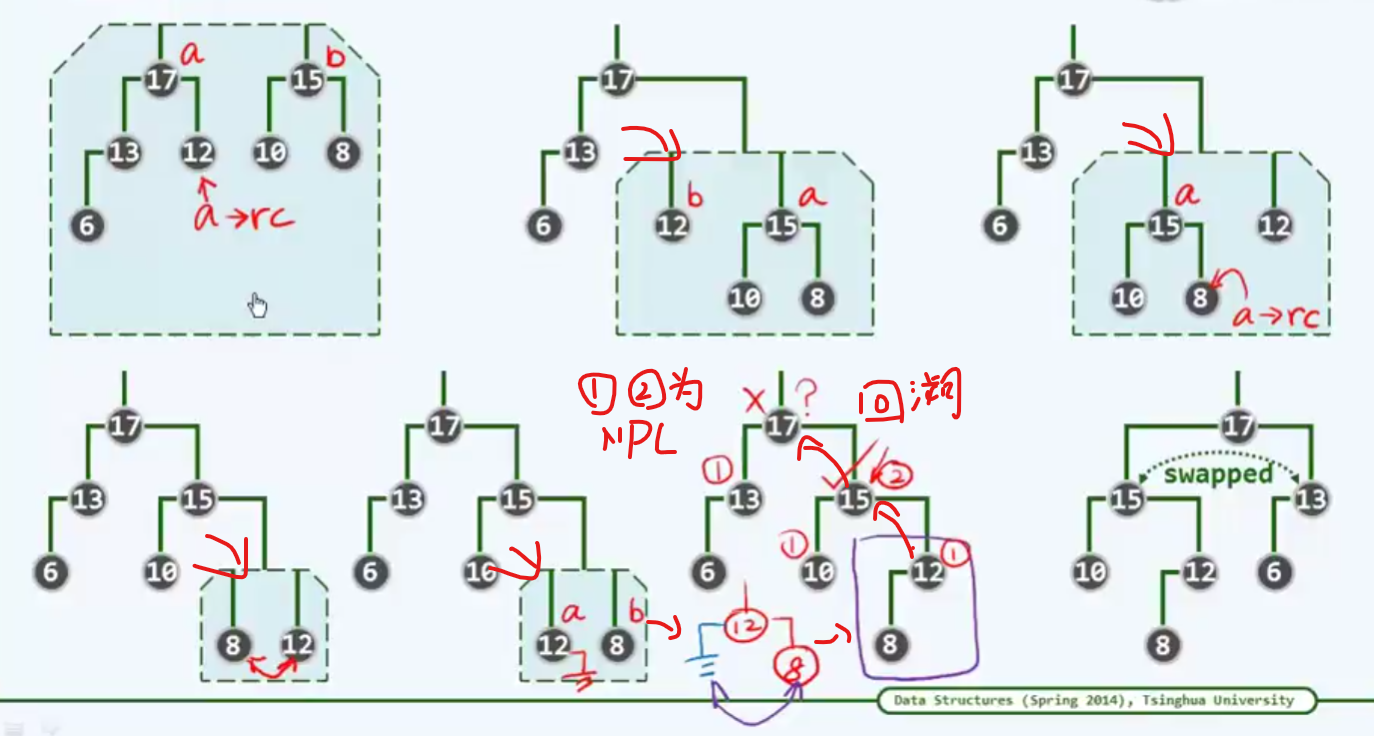
整个过程围绕右侧链展开，我们说过，他的右侧链，不会超过O(logN)我们说，这个结果再好不过了

插入+删除

插入即是合并

删除亦是合并