串
以下笔记为jjyaoao本人制作,欢迎借鉴学习和提出相关建议,转载需要标明出处www.jjyaoao.space
串
ADT
定义和特点

术语
统一约定:
联系:在i+k长度的前缀中,长度为k的后缀
任何串,也是他自身的子串,前缀,后缀,长度严格小于原串的子串,前缀,后缀,也成为了真子串,真前缀,真后缀

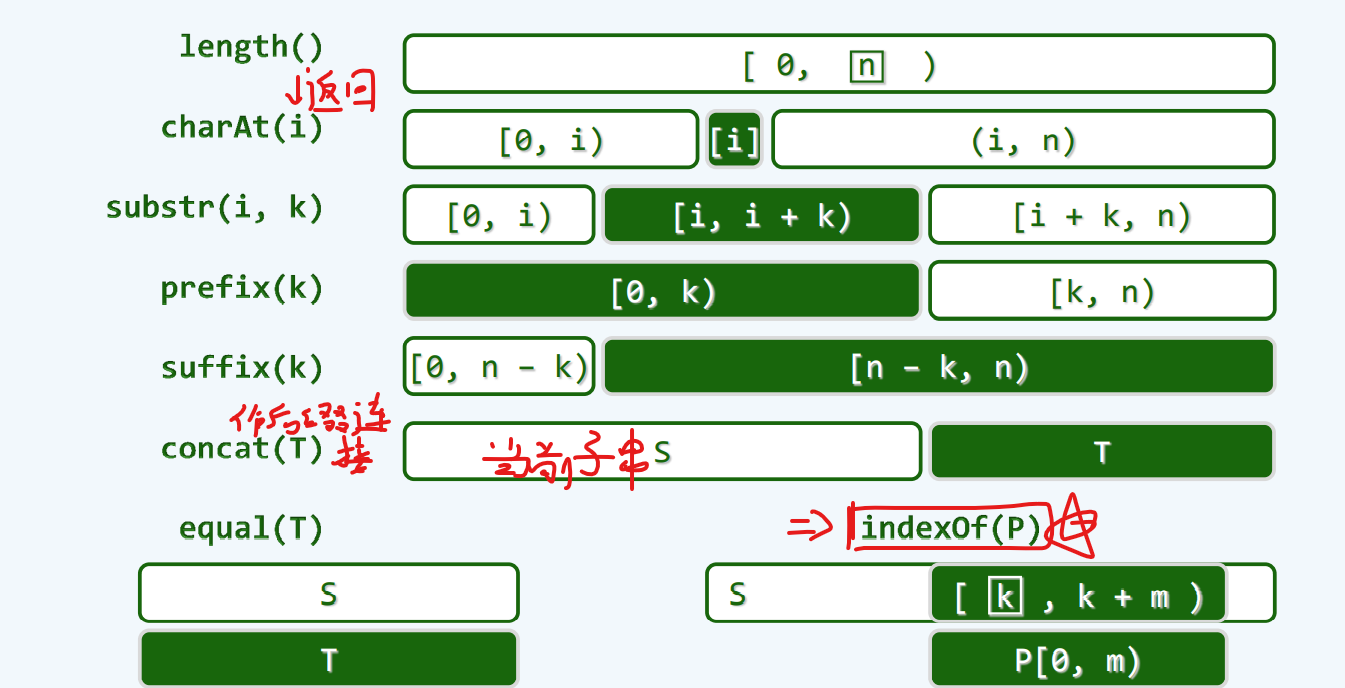
接口定义

模式匹配
问题与需求
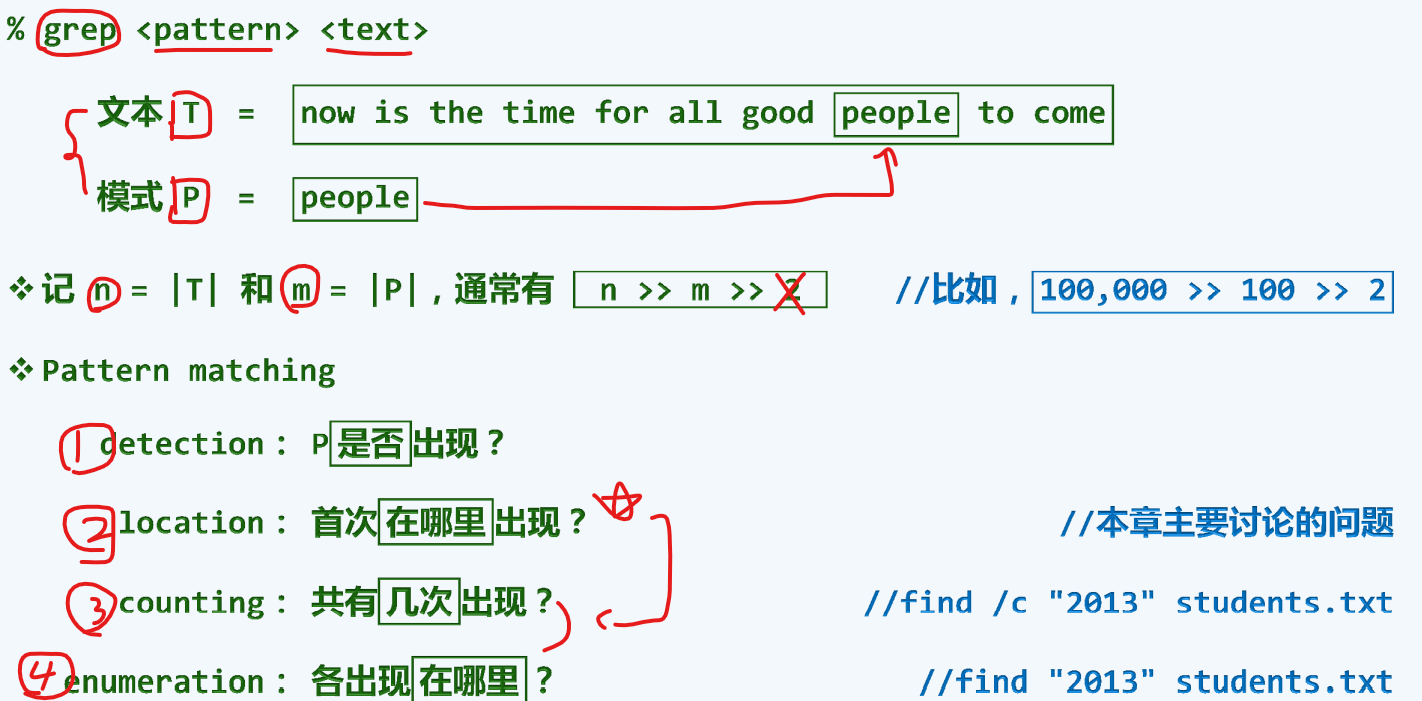
算法评测

蛮力匹配
构思
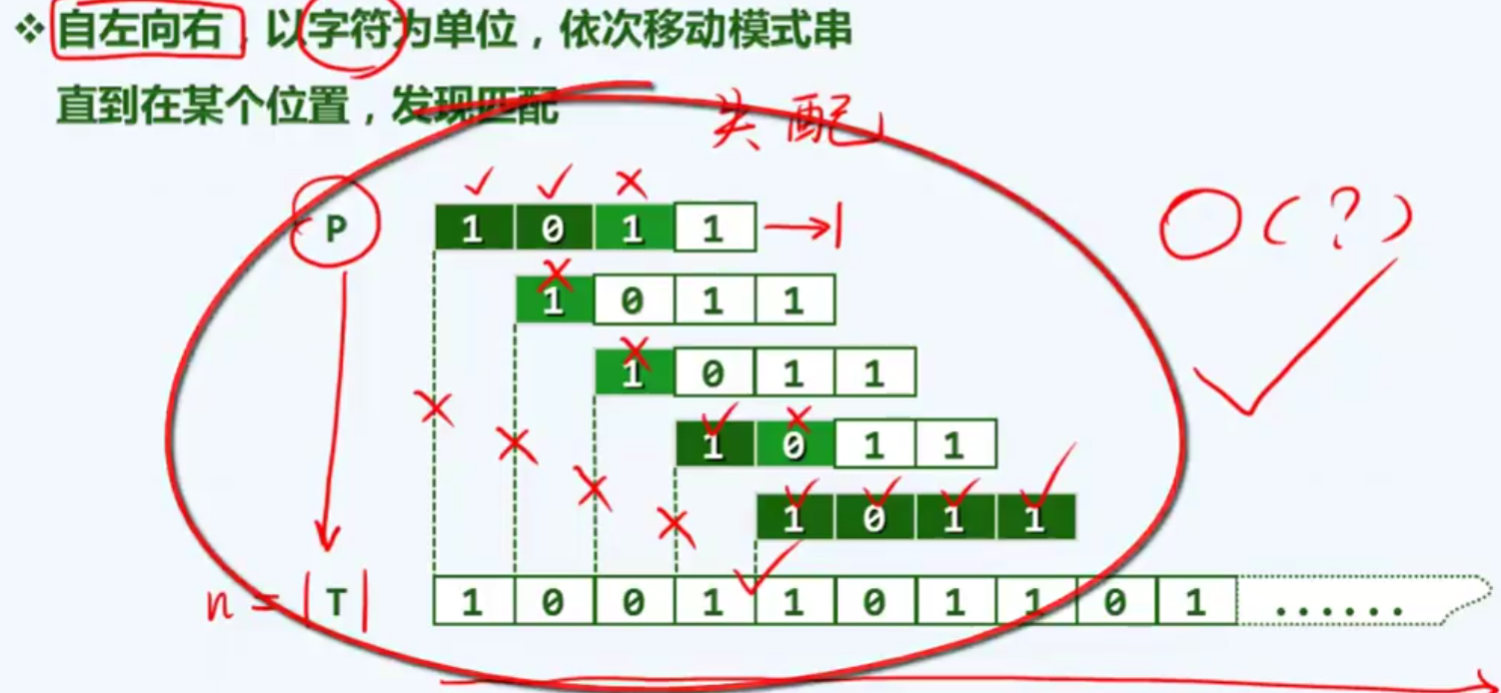
版本一


版本二

复杂度分析

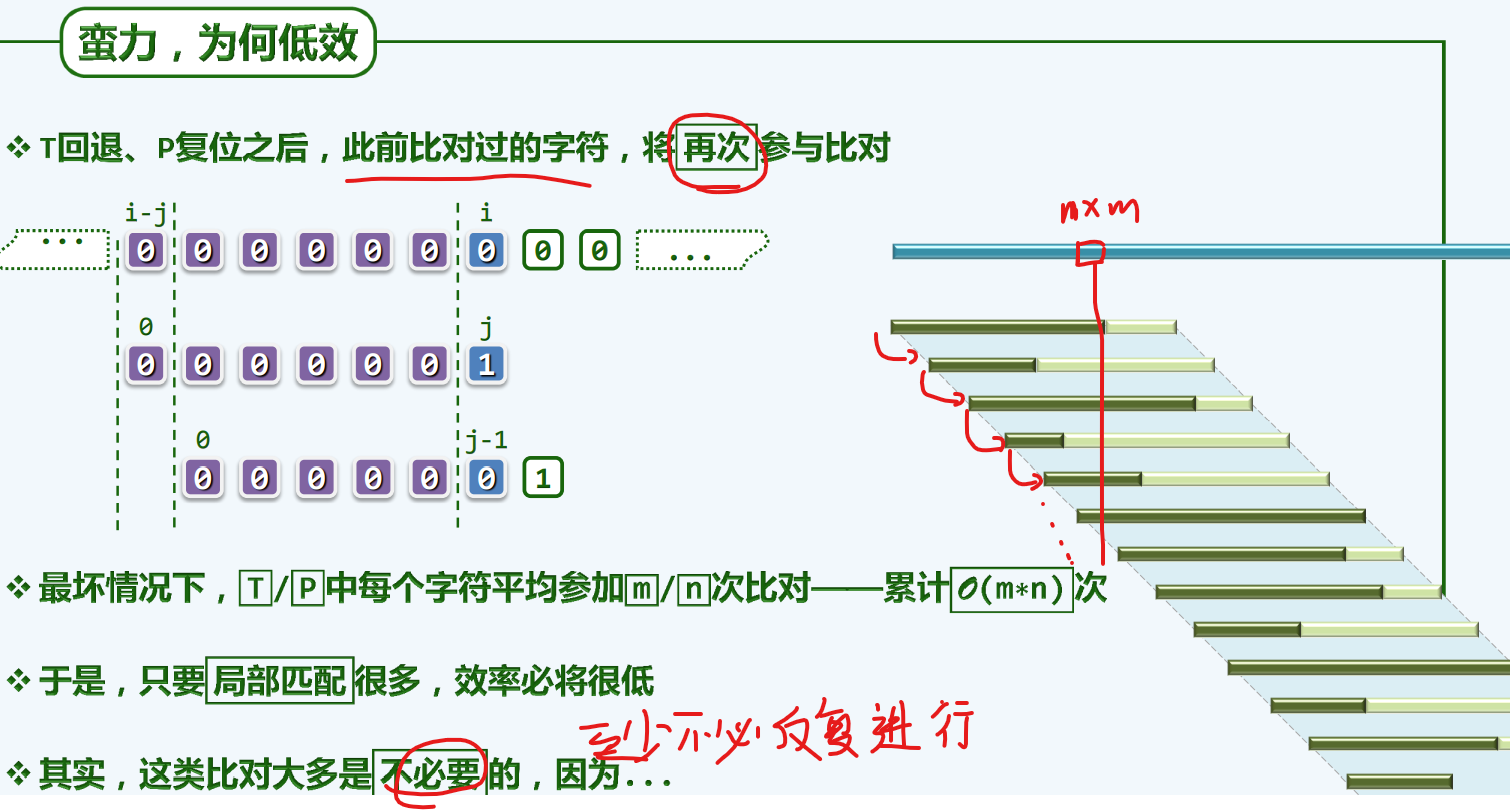
但是就期望而言,对于日常使用,往往可以每一个位置都达到o(1),总共累计不过线性O(n)复杂度
我们不满足于次,想要把期望抹掉,好消息是这类算法的确存在,比如下面的知名的KMP
KMP算法:记忆法
阐述
蛮力为何低效
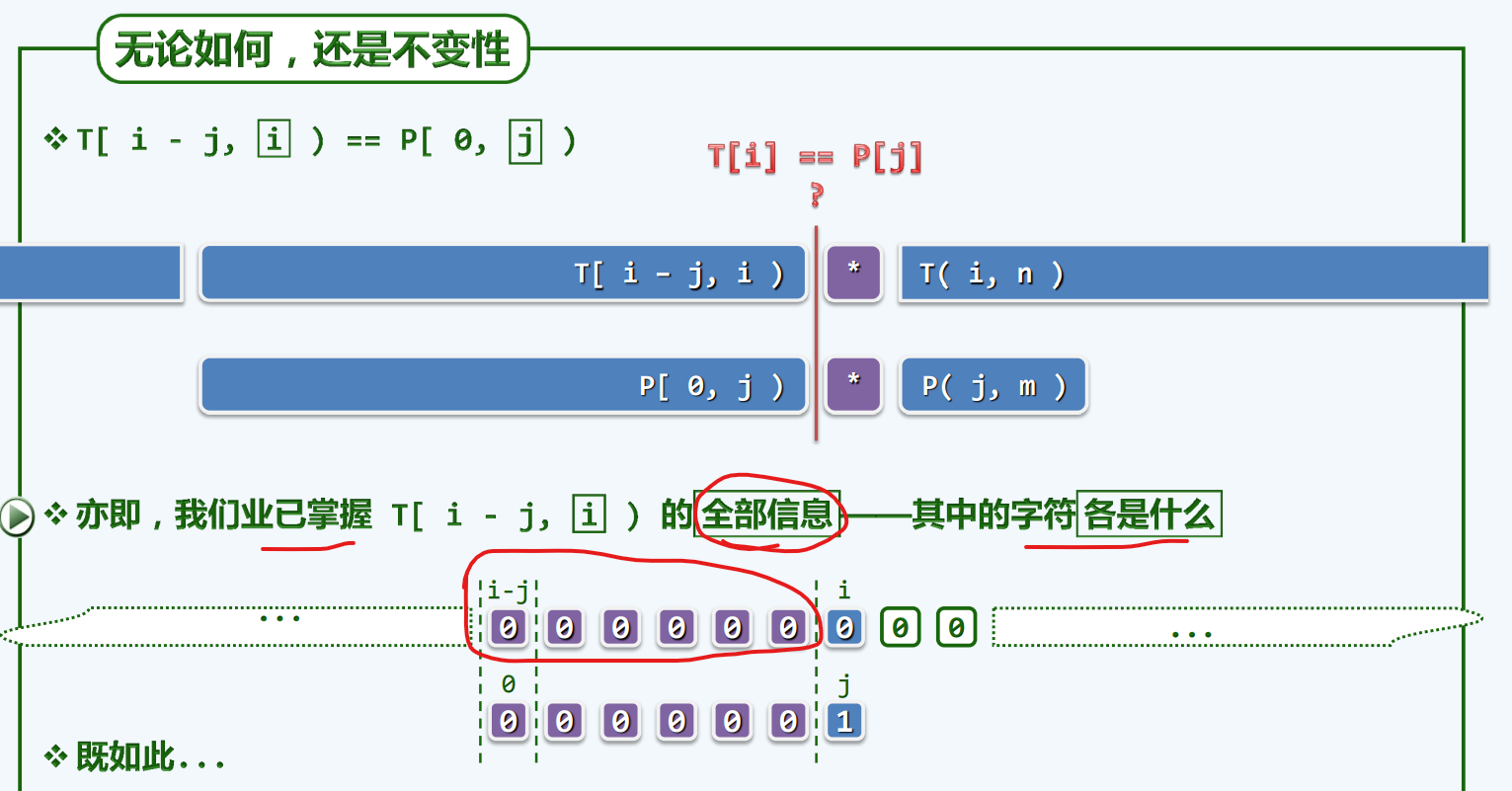
不变性
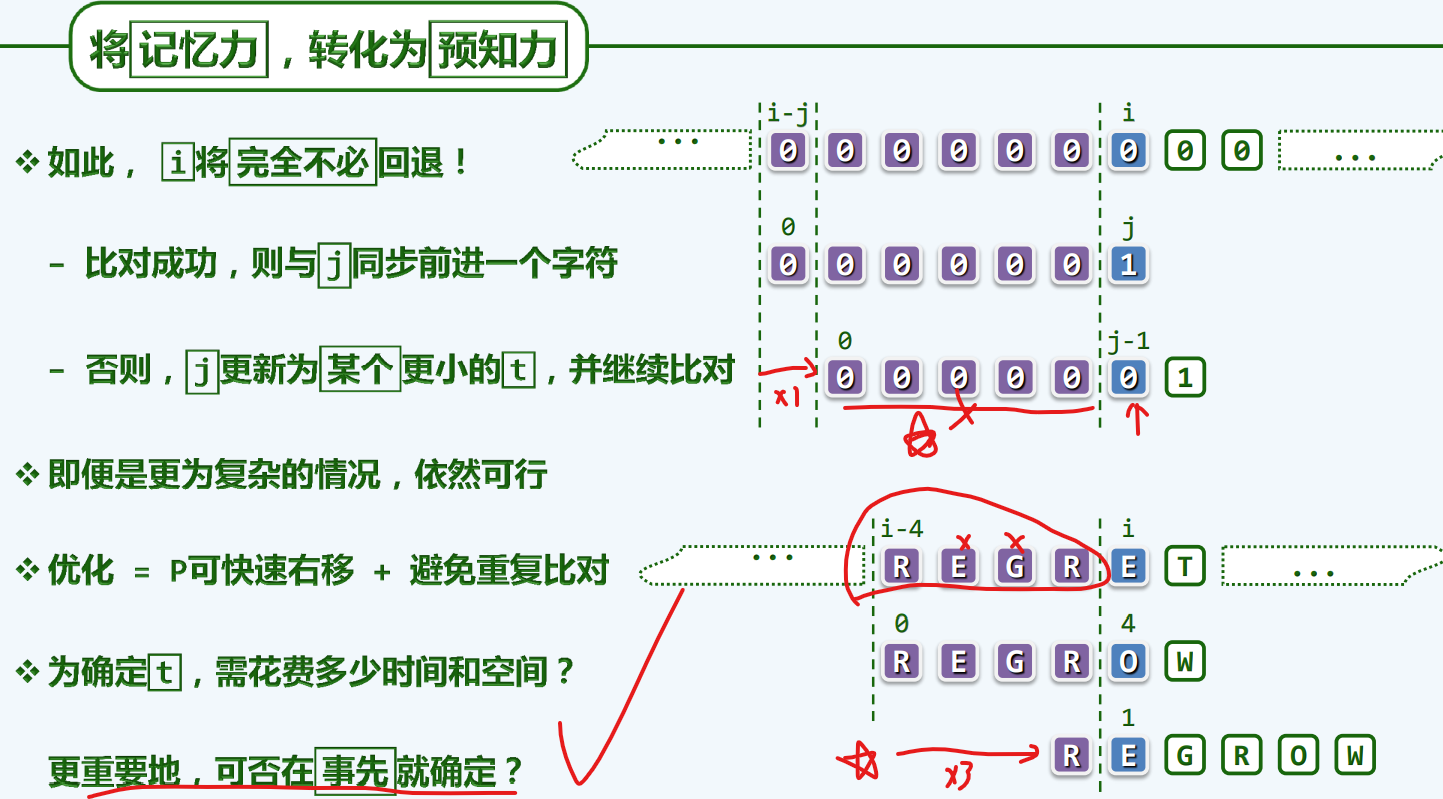
记忆力

预知力
查询表
制表备查

主算法

实例
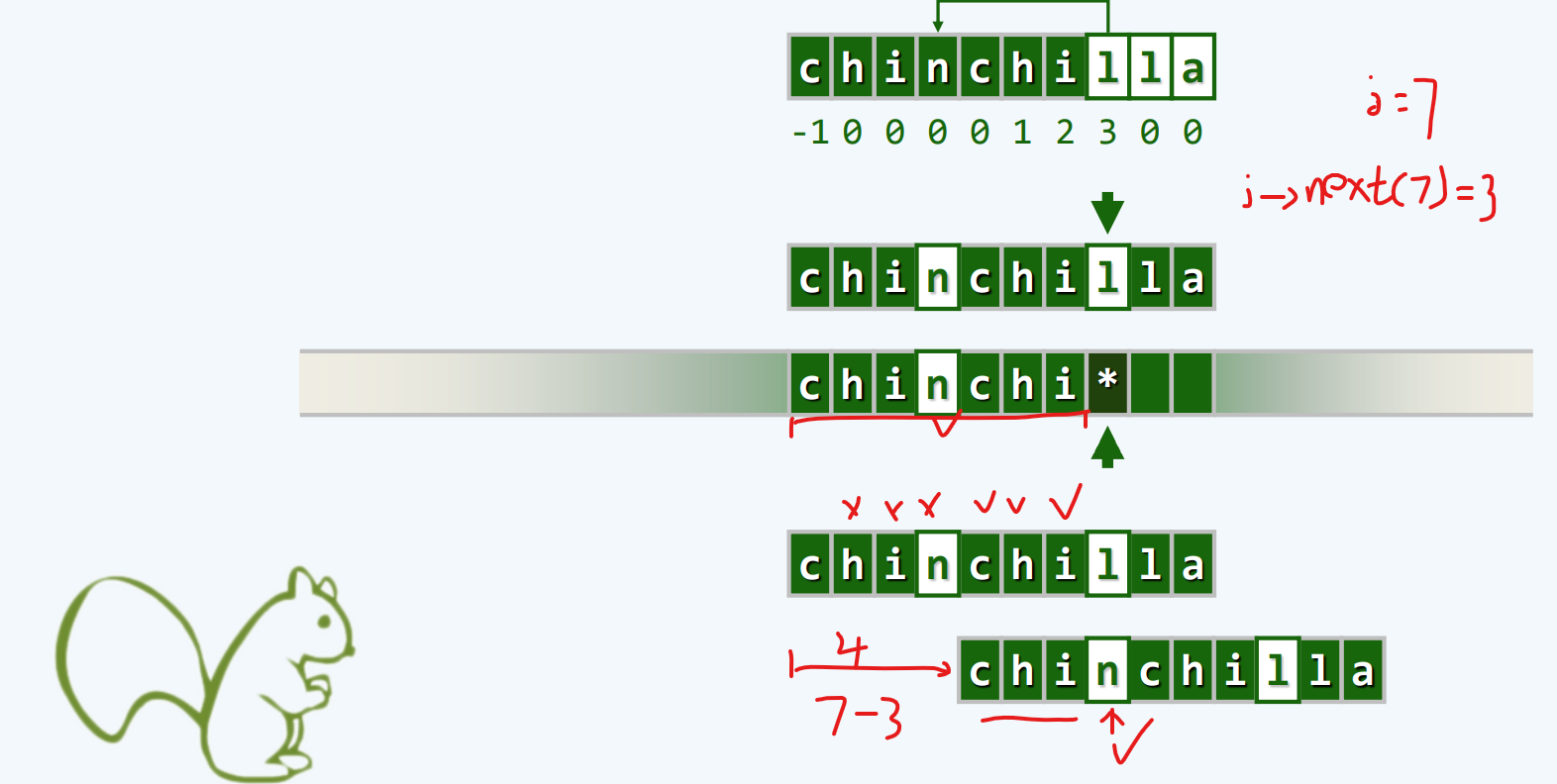
理解Next[]表
快速移动
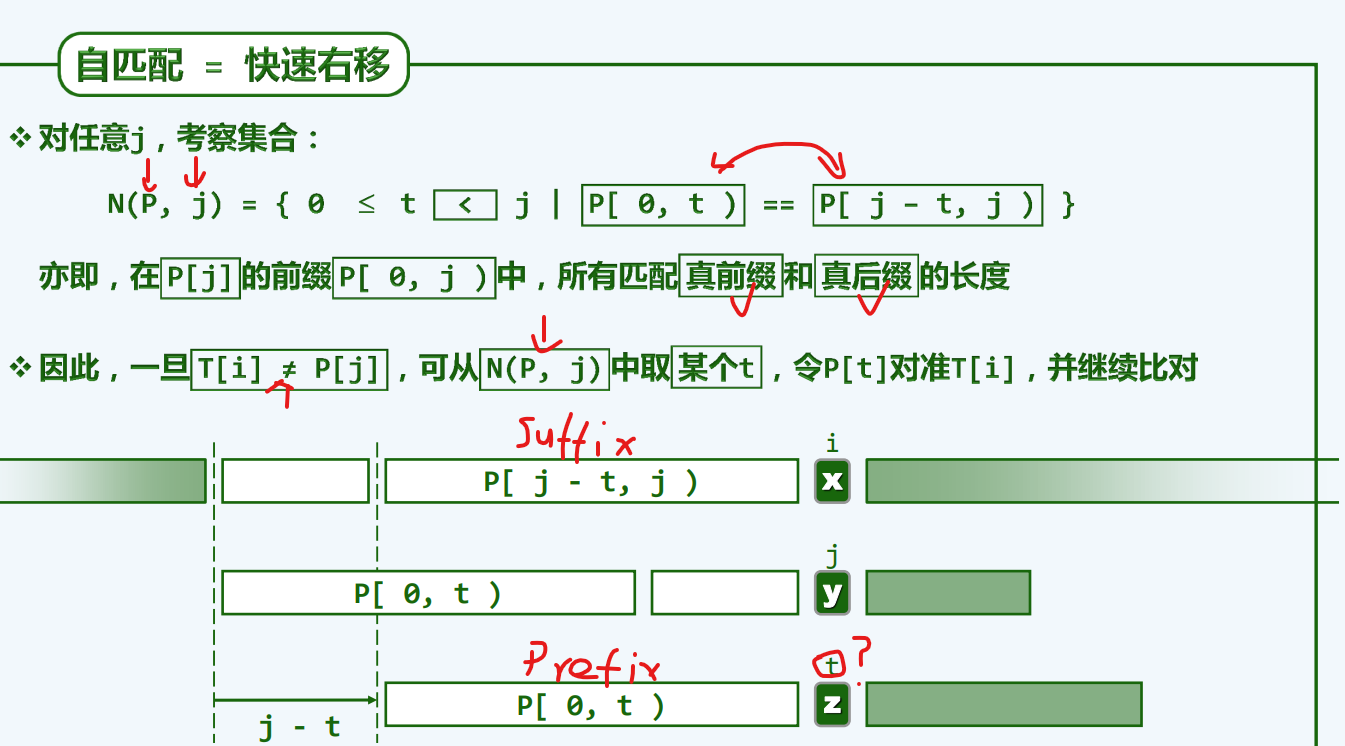
避免回溯

t越小,对应的位移越大,反之,对应的位移越小,而位移量更小,就意味着更安全,这也暗示了另一个不变性,也就是由KMP舍弃的哪些位置,的确是不值得对齐的
通配哨兵



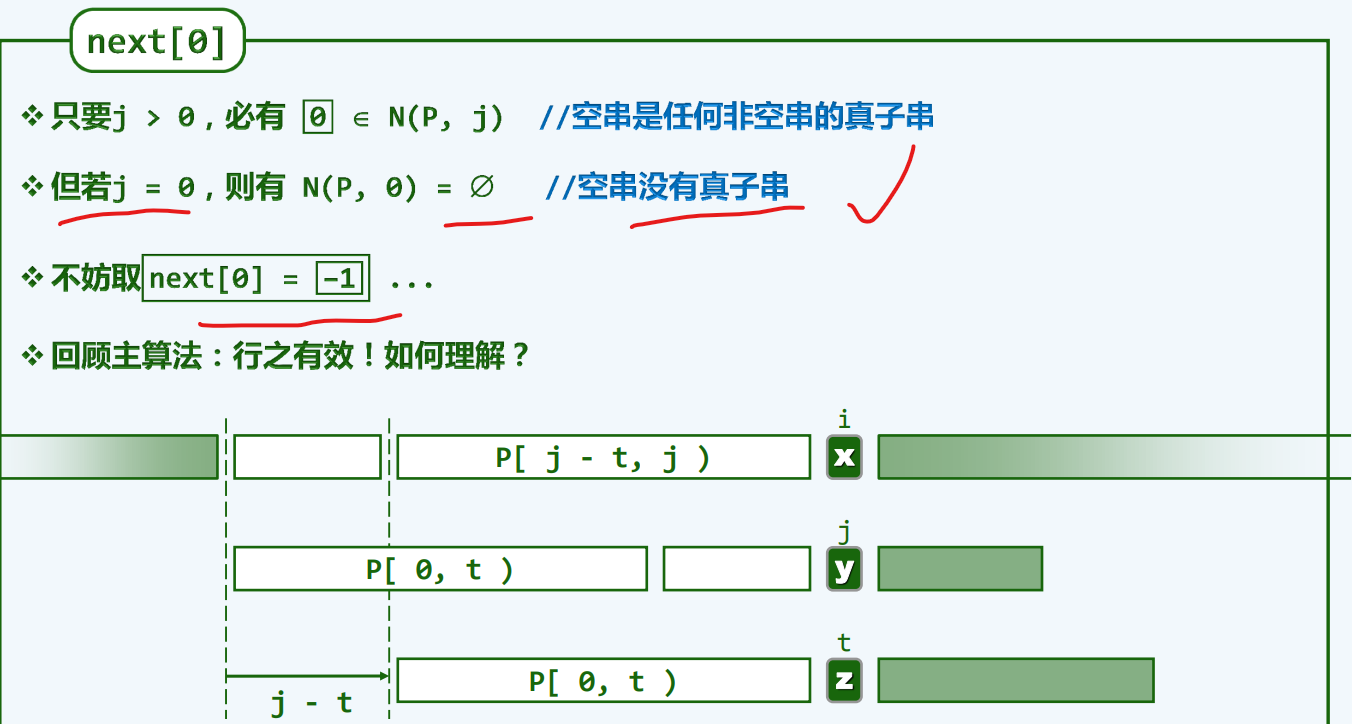
当j<0时,通过通配的哨兵结点,使得T[i] == T[j] 必然成功,从而使模板表位置回到第一位
构造Next[]表
递推

算法

显而易见,该过程也就是next自己与自己逐一比对的过程,(哨兵使得算法鲁棒性良好)我们可以通过修改KMP的框架简要得出模板表的代码
实现

1 | int* buildNext ( char* P ) { //构造模式串P的next表 |
实例
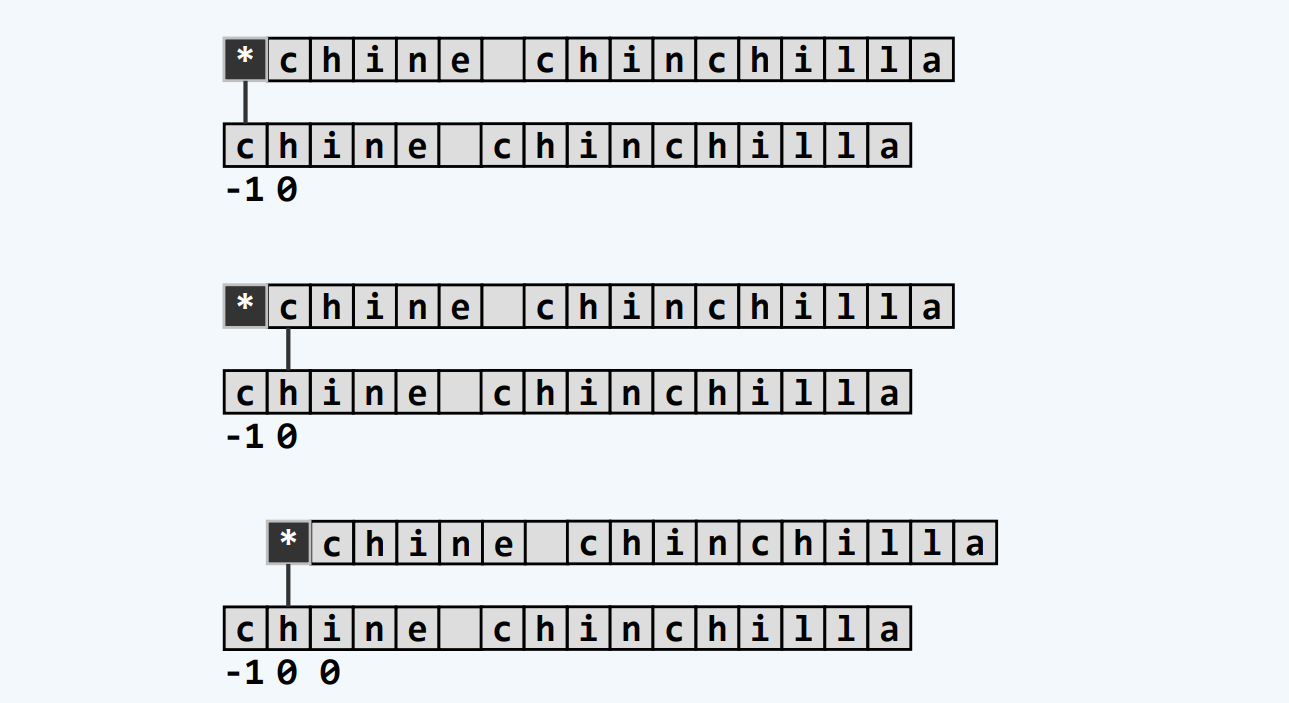
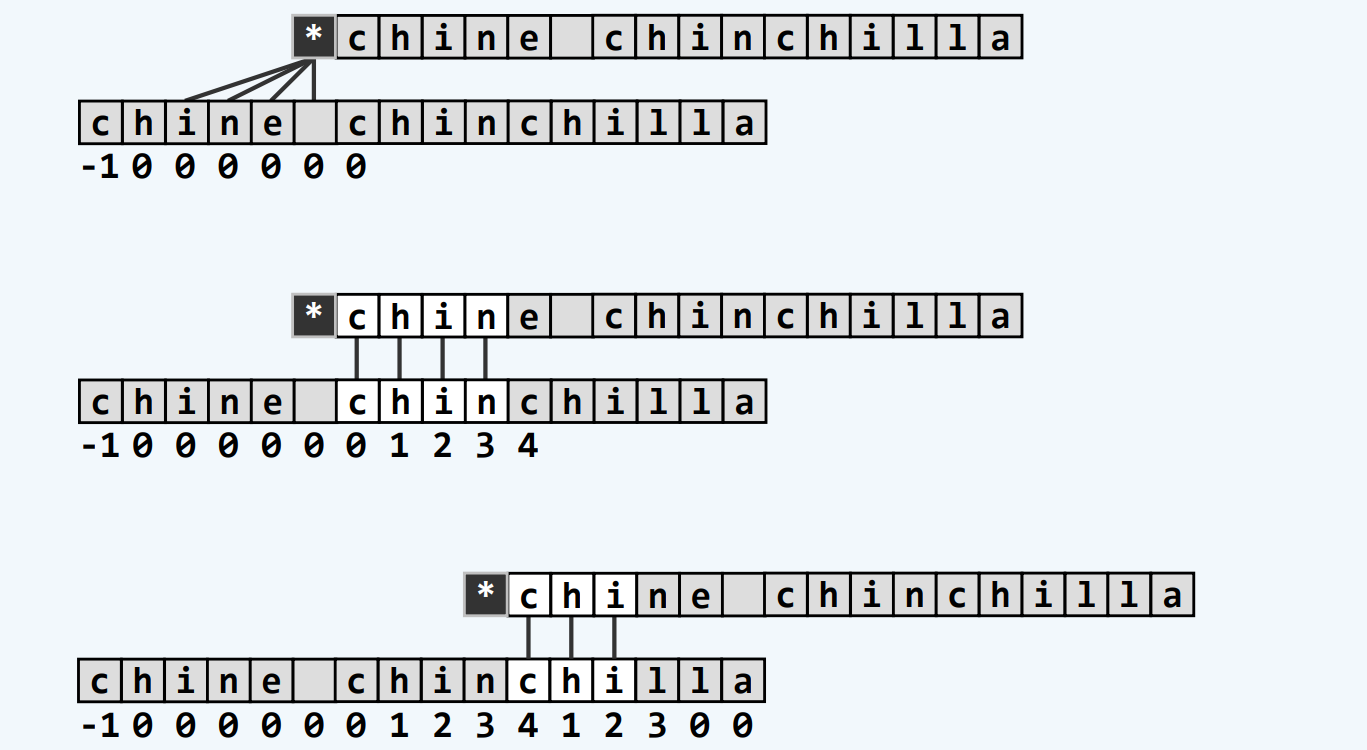
分摊分析
失之粗糙
通过过程分析


精准估计
根据代码主体分析
若对k为何这样取,看习题解析(下次一定

再改进
美中不足
这种反例的情况,如果说第一次的比对还是有意义的话,那么后面的比对都是多余的。
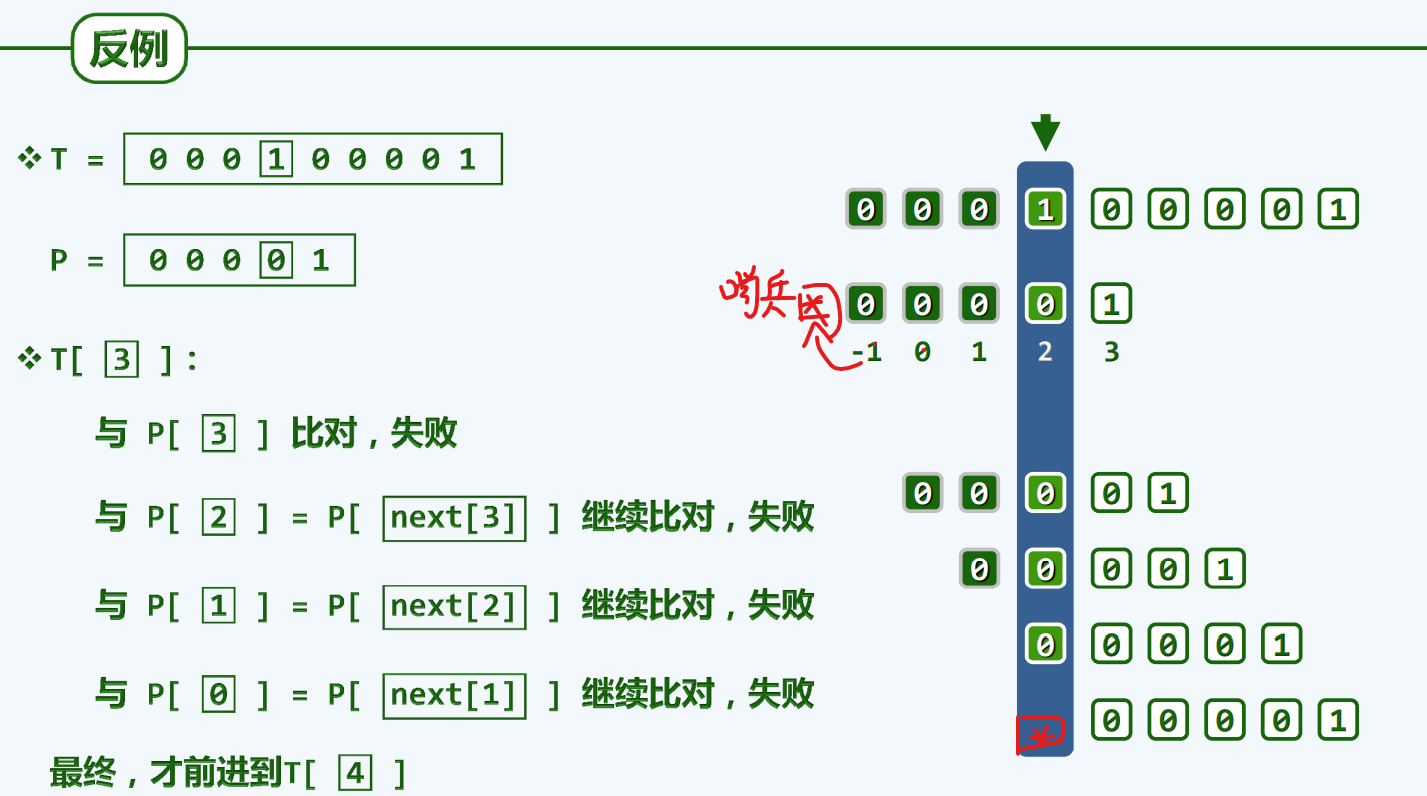
以卵击石
为何一错再错???Next[]表。Next[]表为整个算法的灵魂所在
把1比作石头,0比作鸡蛋
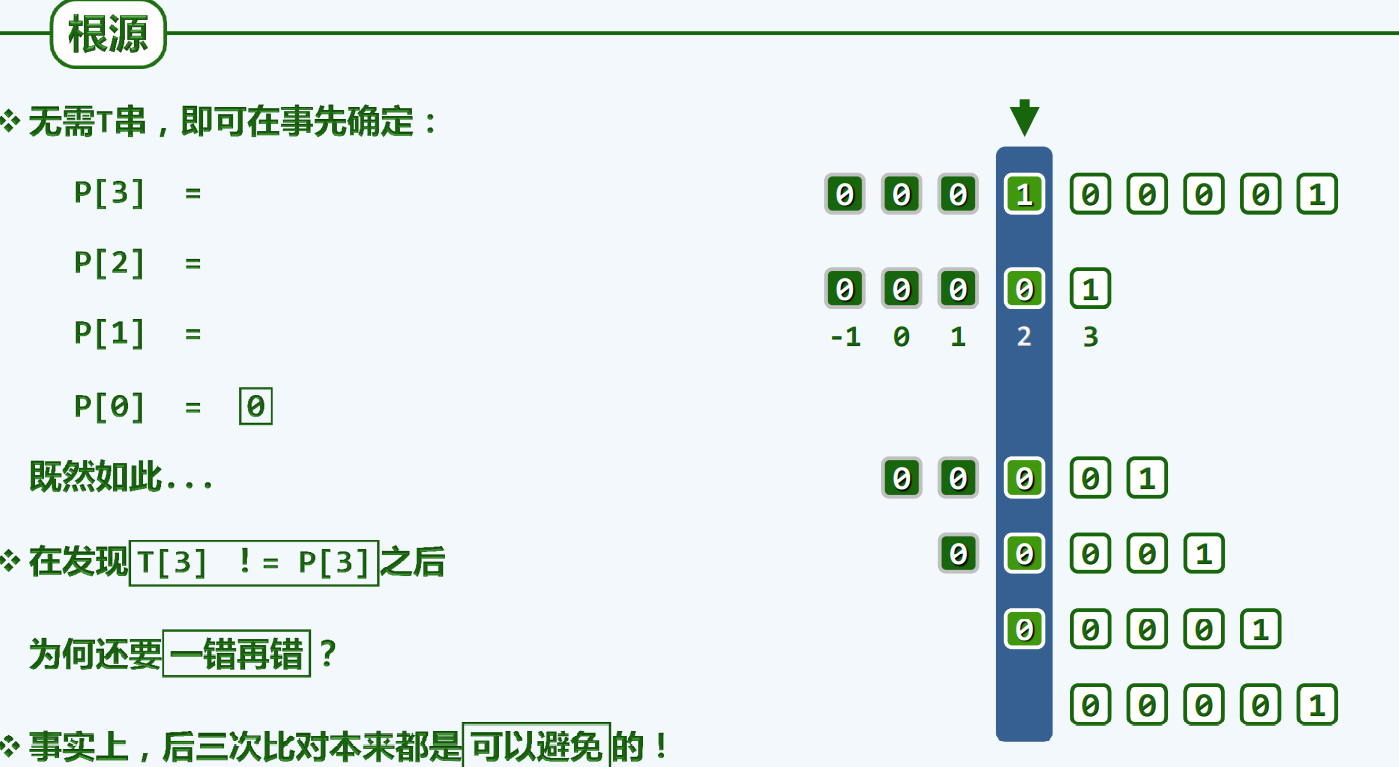
前车之鉴
我们在if里增加一句判断语句,新的字符必须与此前那个字符不一样,新的字符不一定会比石头更硬,但他至少不应该仍然是一枚鸡蛋

实例
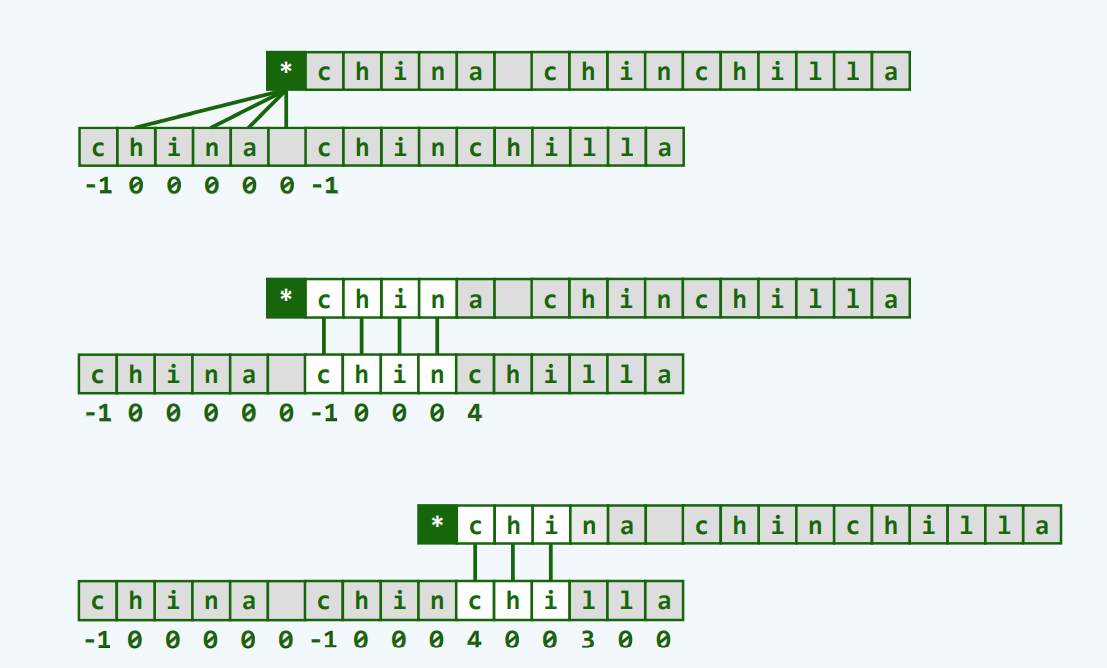
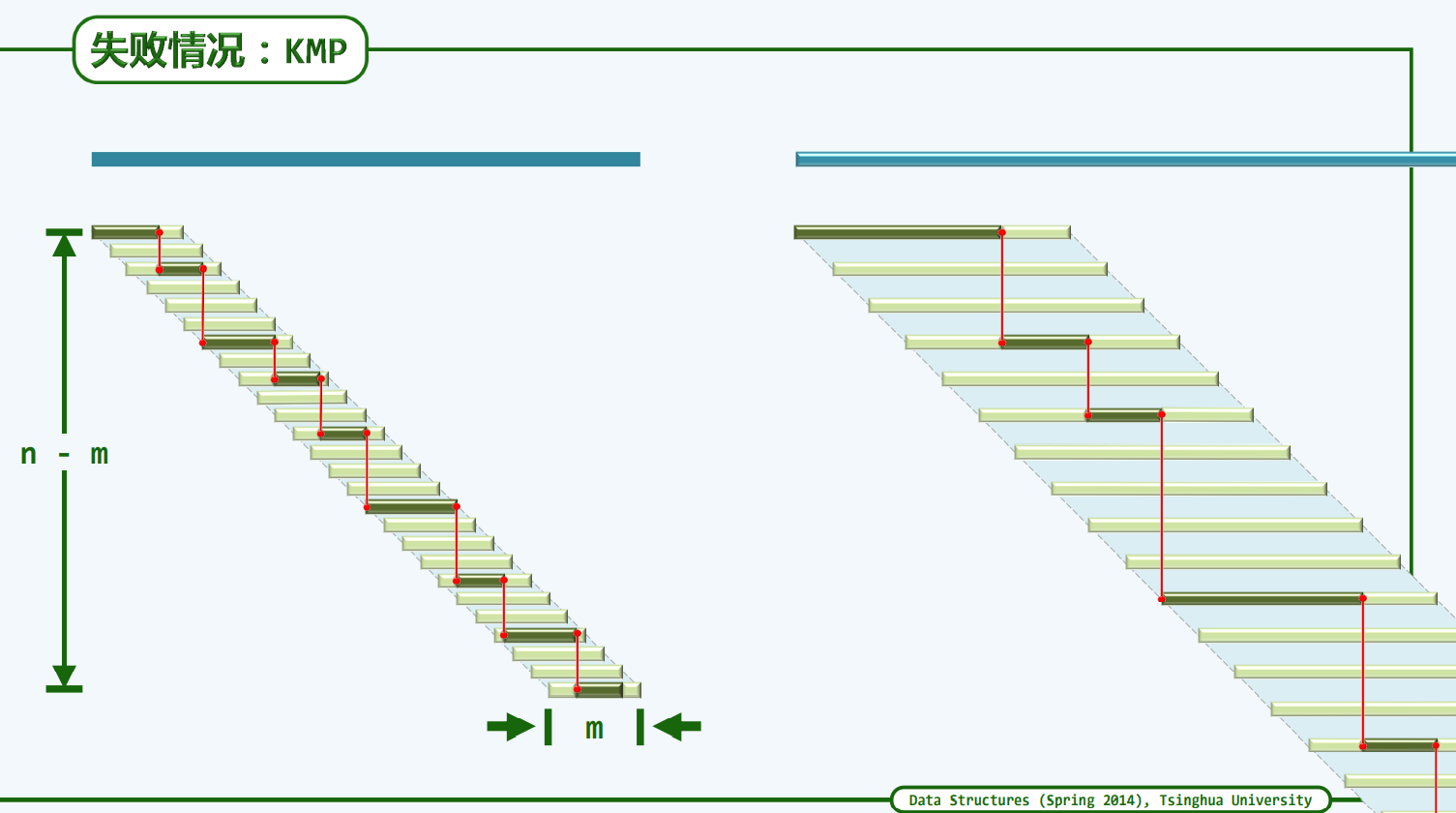
可视对比
每一个区间的计算成本,都可以用深色区域来度量
蛮力算法
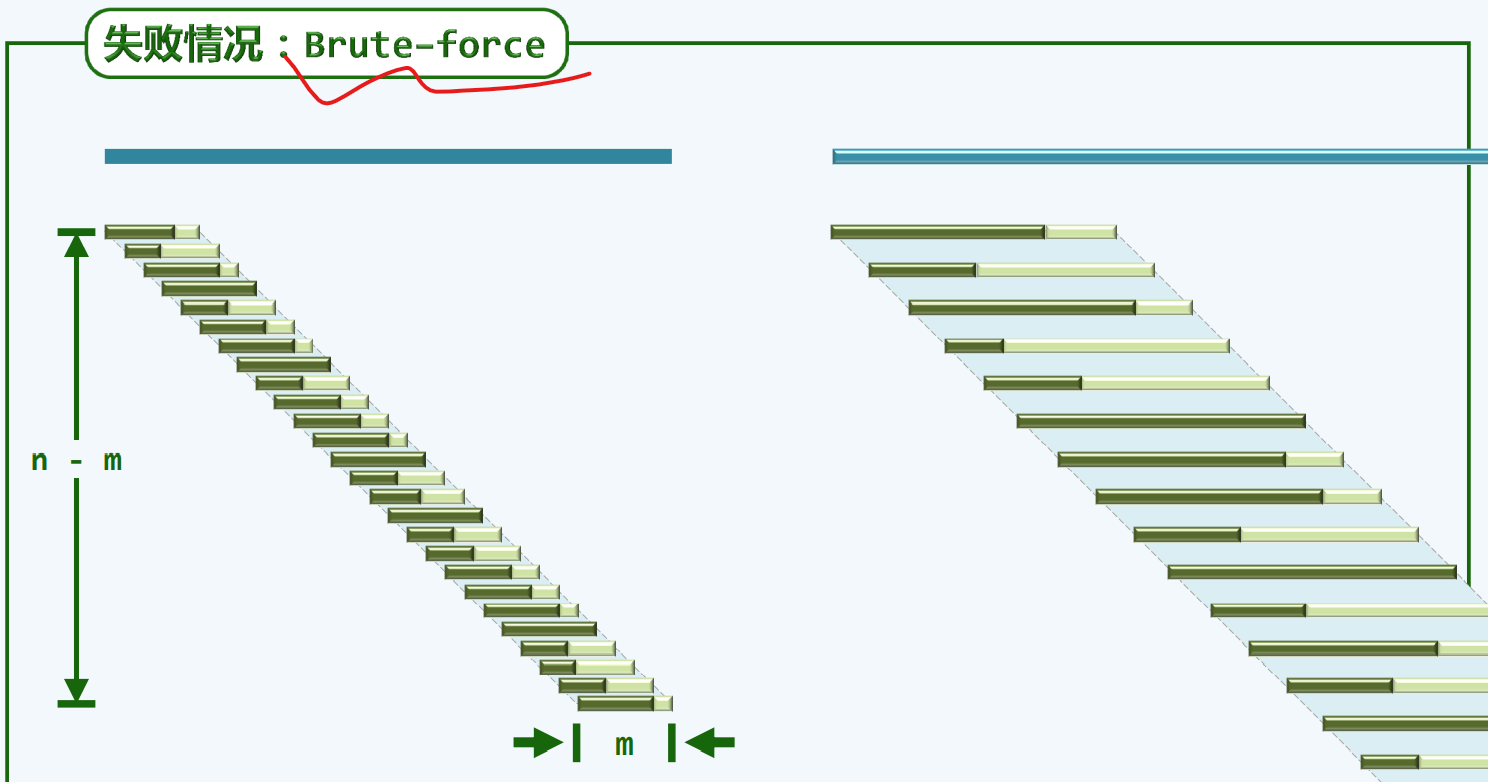
KMP
BM_BC:以终为始
善待教训
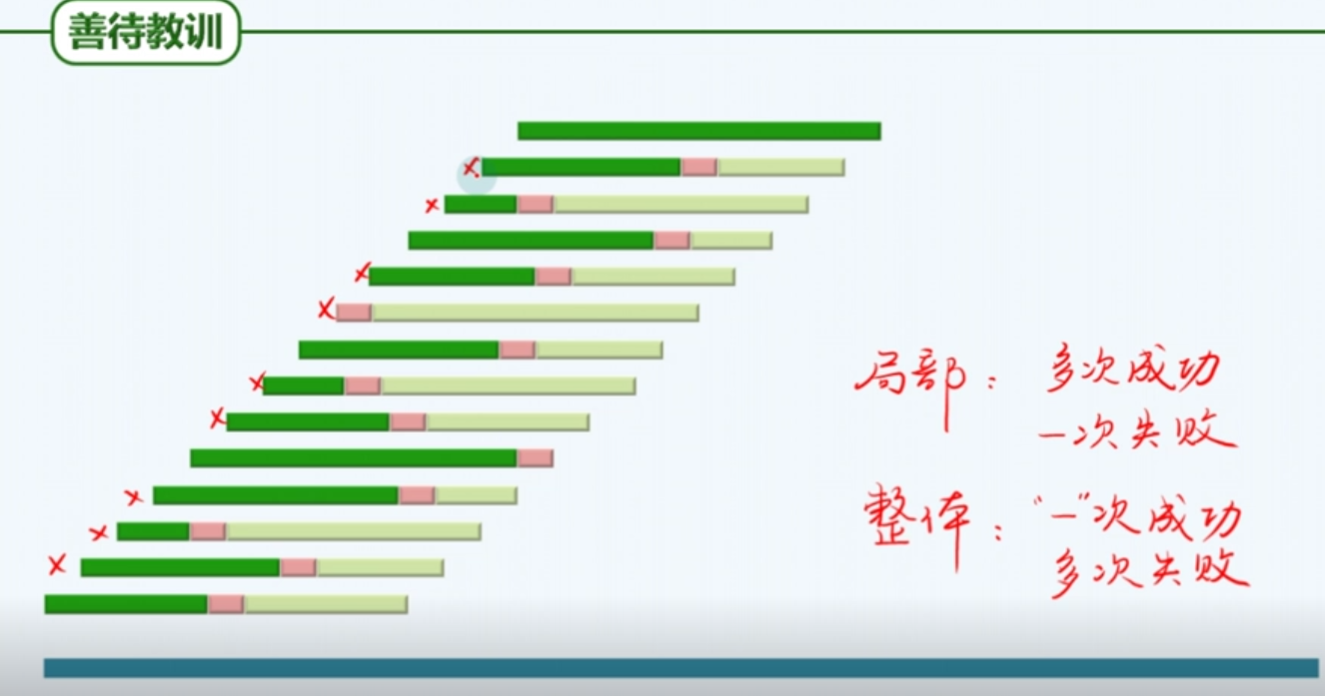
前轻后重
我们在后面获得教训,利用价值往往更大(排除更多的位置)
我们获得失败的概率也远远大于成功的概率

以终为始
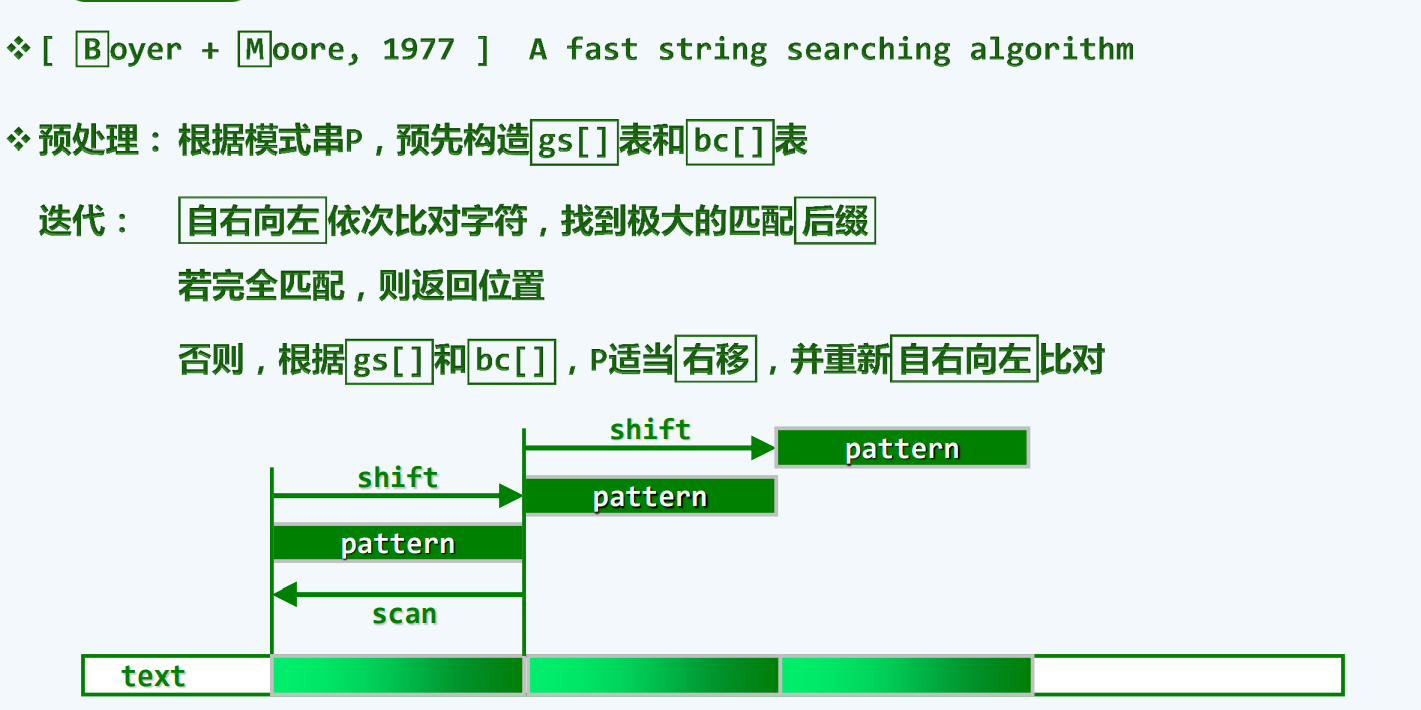
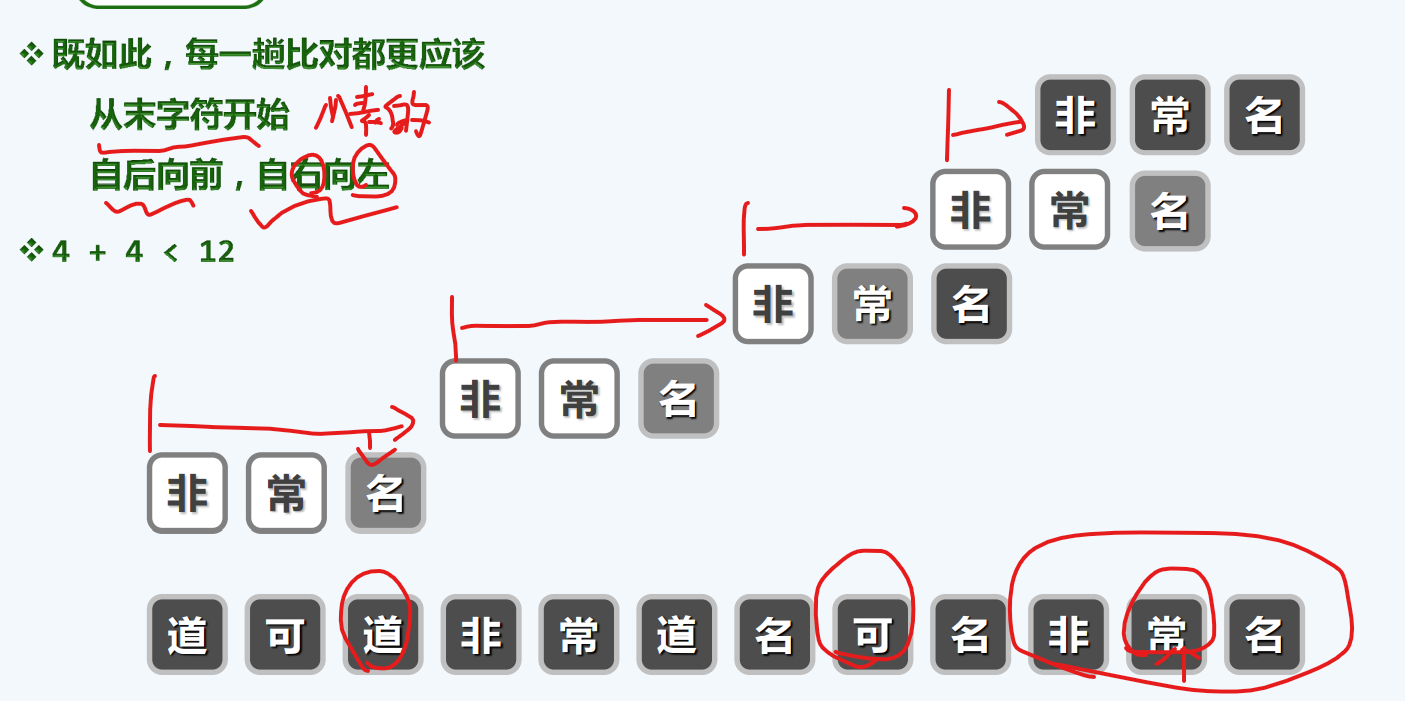
坏字符
这一策略,将我们之前称为的教训,转名为 坏字符
当出现坏字符,使我们在这次匹配能获得成功带来失望,所以说是坏字符
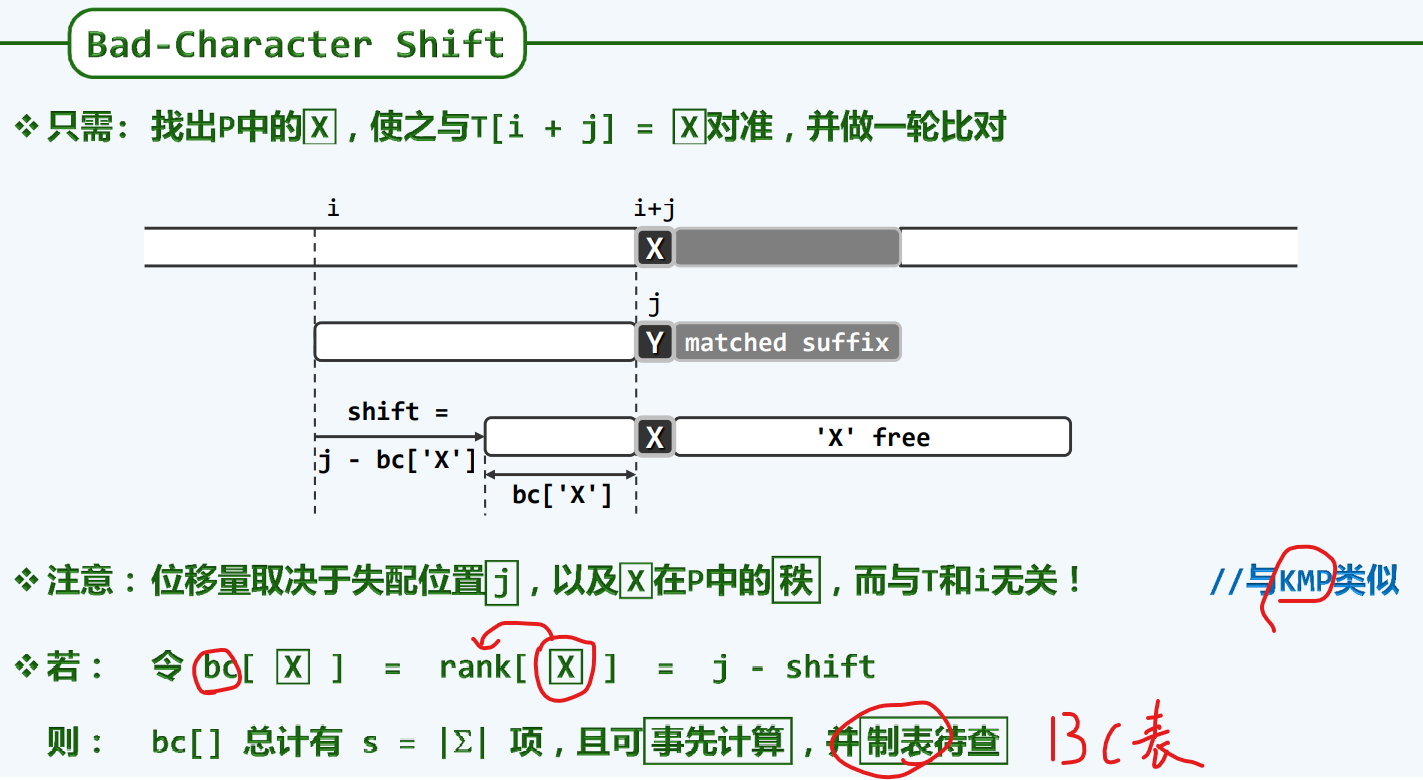
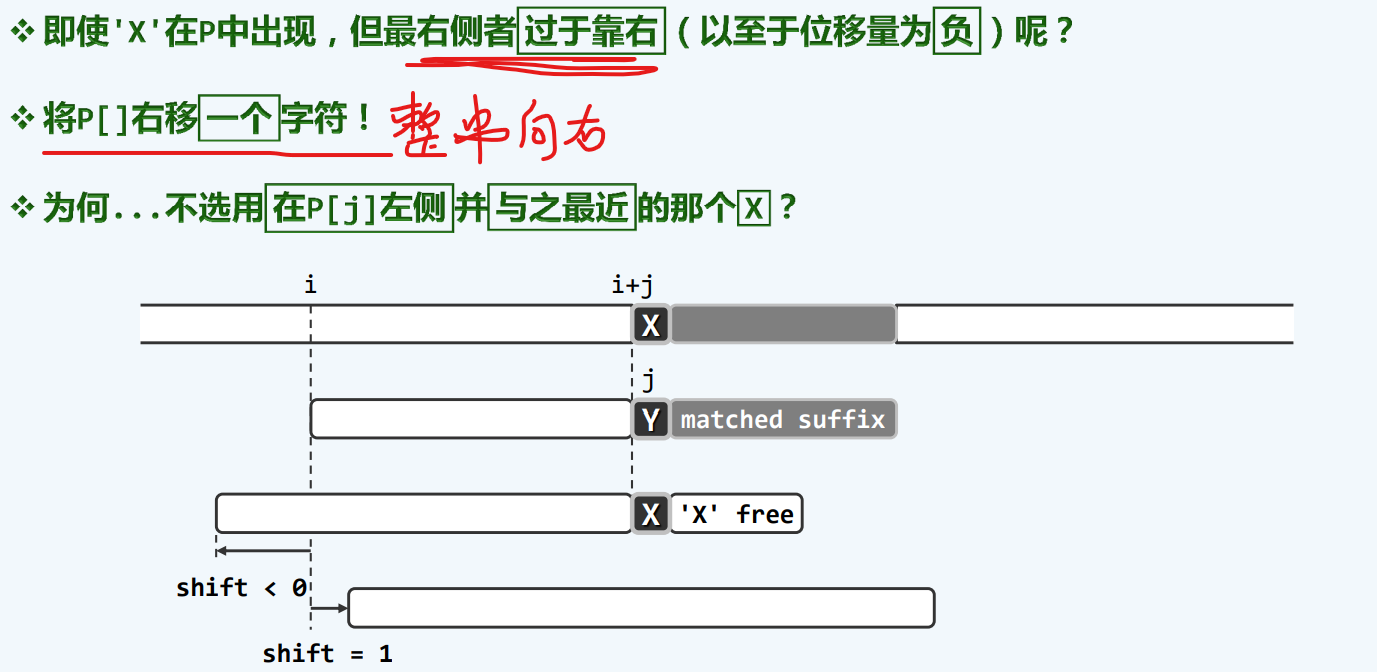
特殊情况

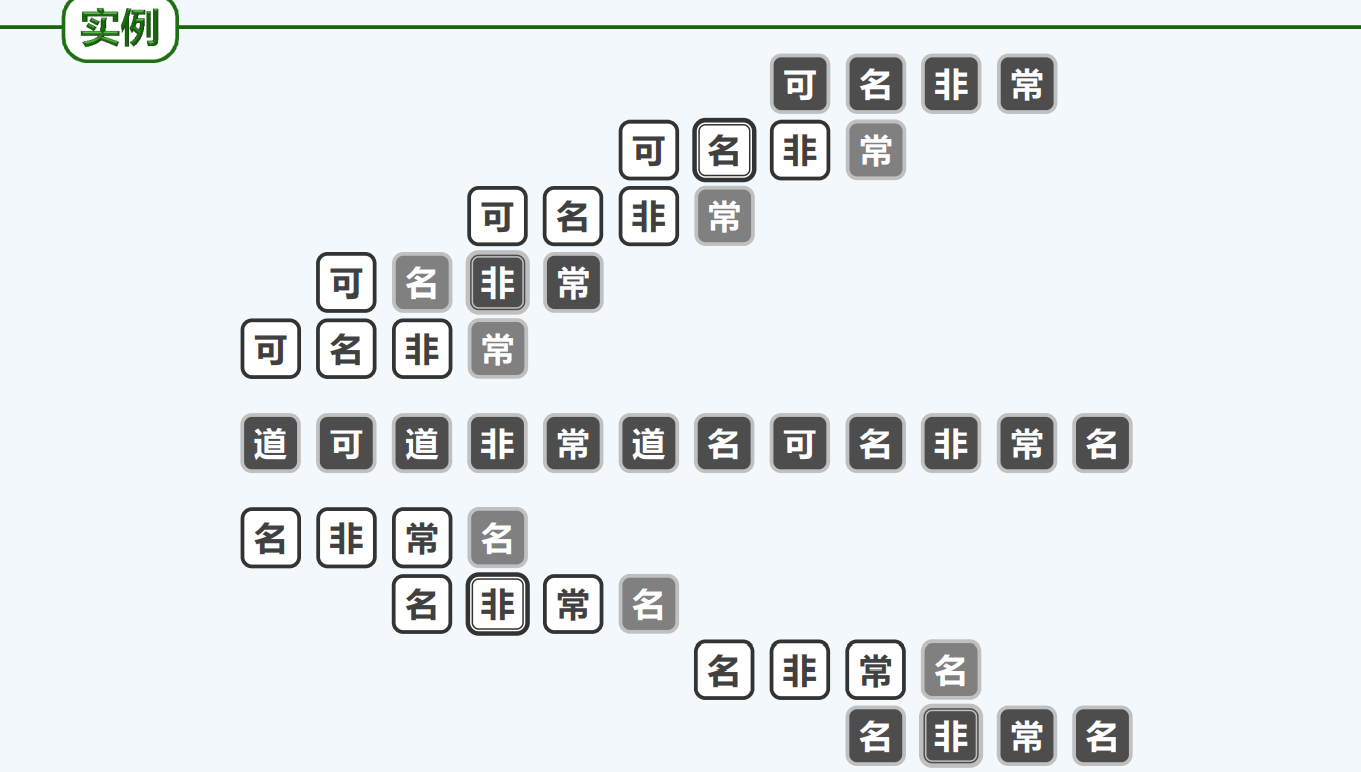
实例
构造BC[]

性能分析
最好情况
适配概率越大越好
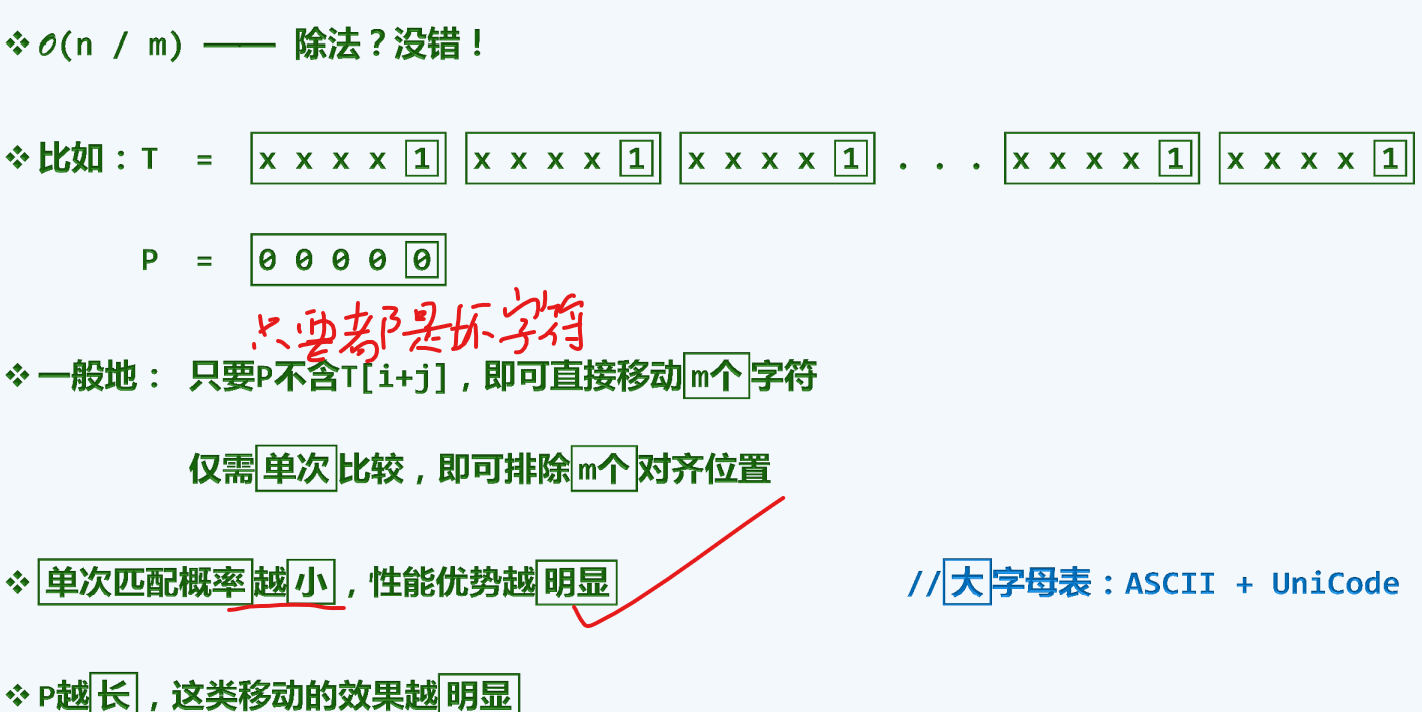

最坏情况

BM_GS:好后缀
兼顾经验

好后缀
制表
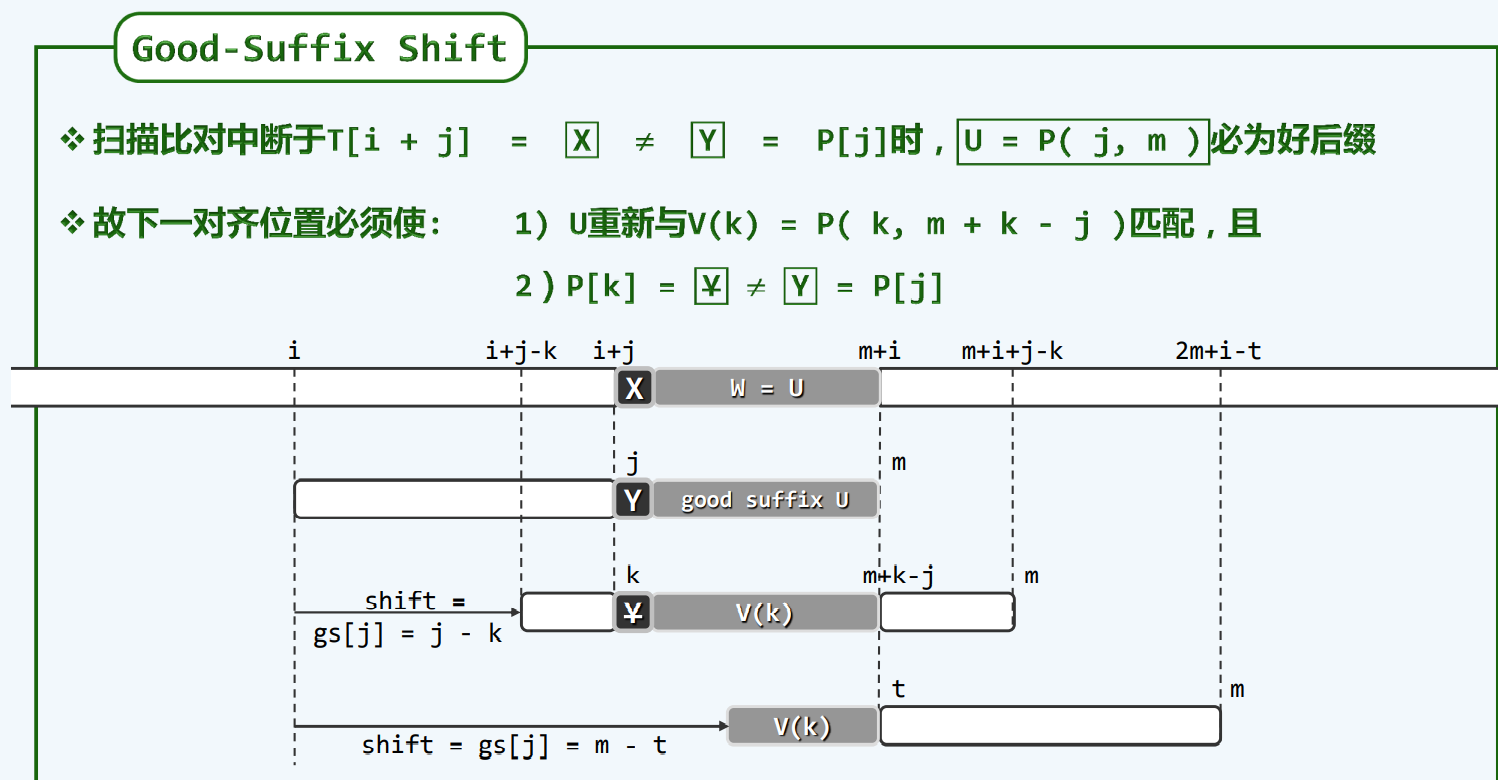


实例体验
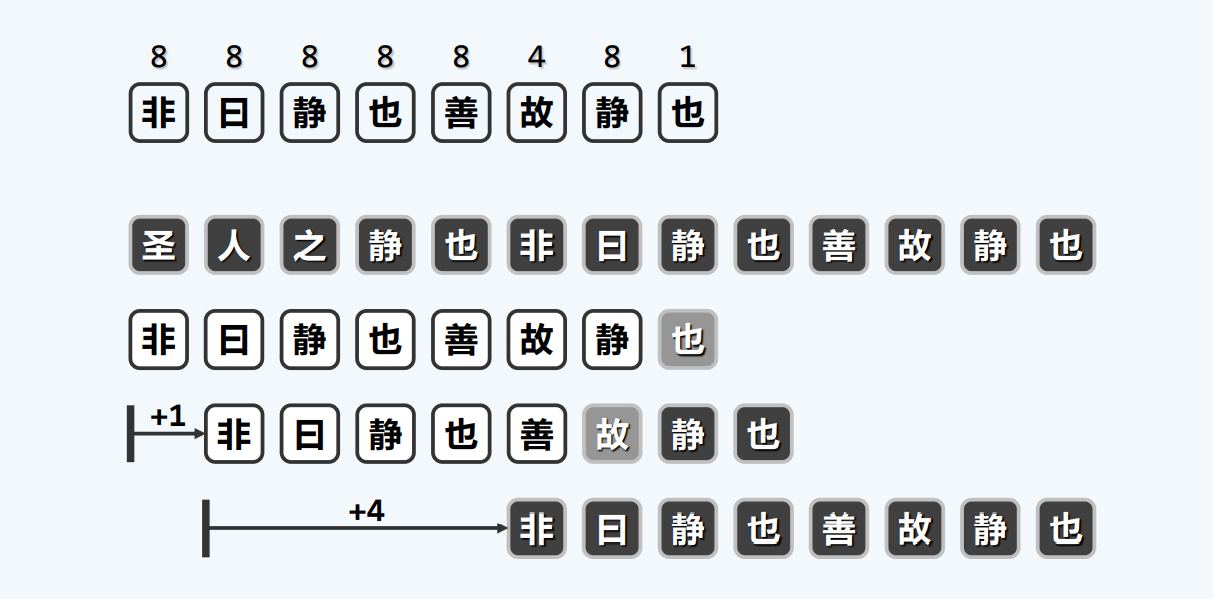
构造GS表
构造MS[]

构造SS[]
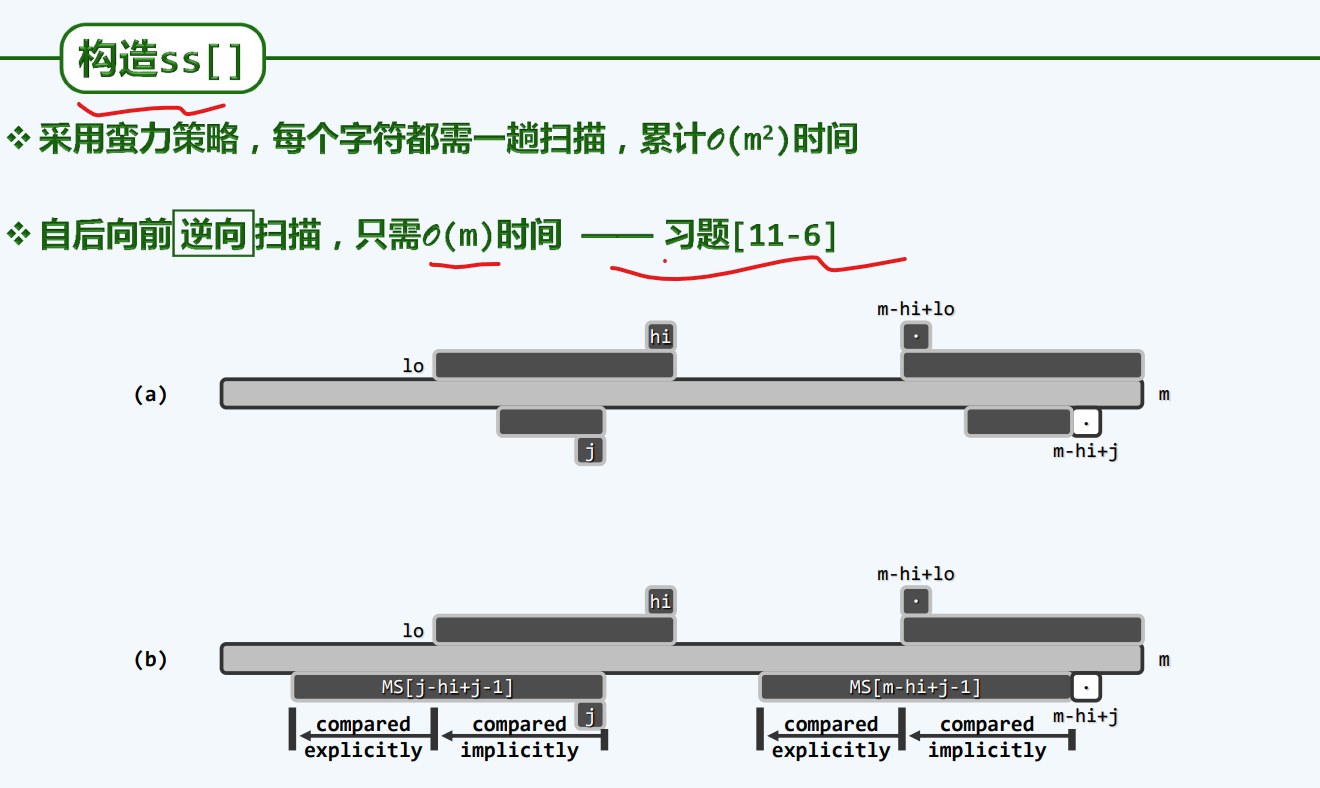
构造GS[]
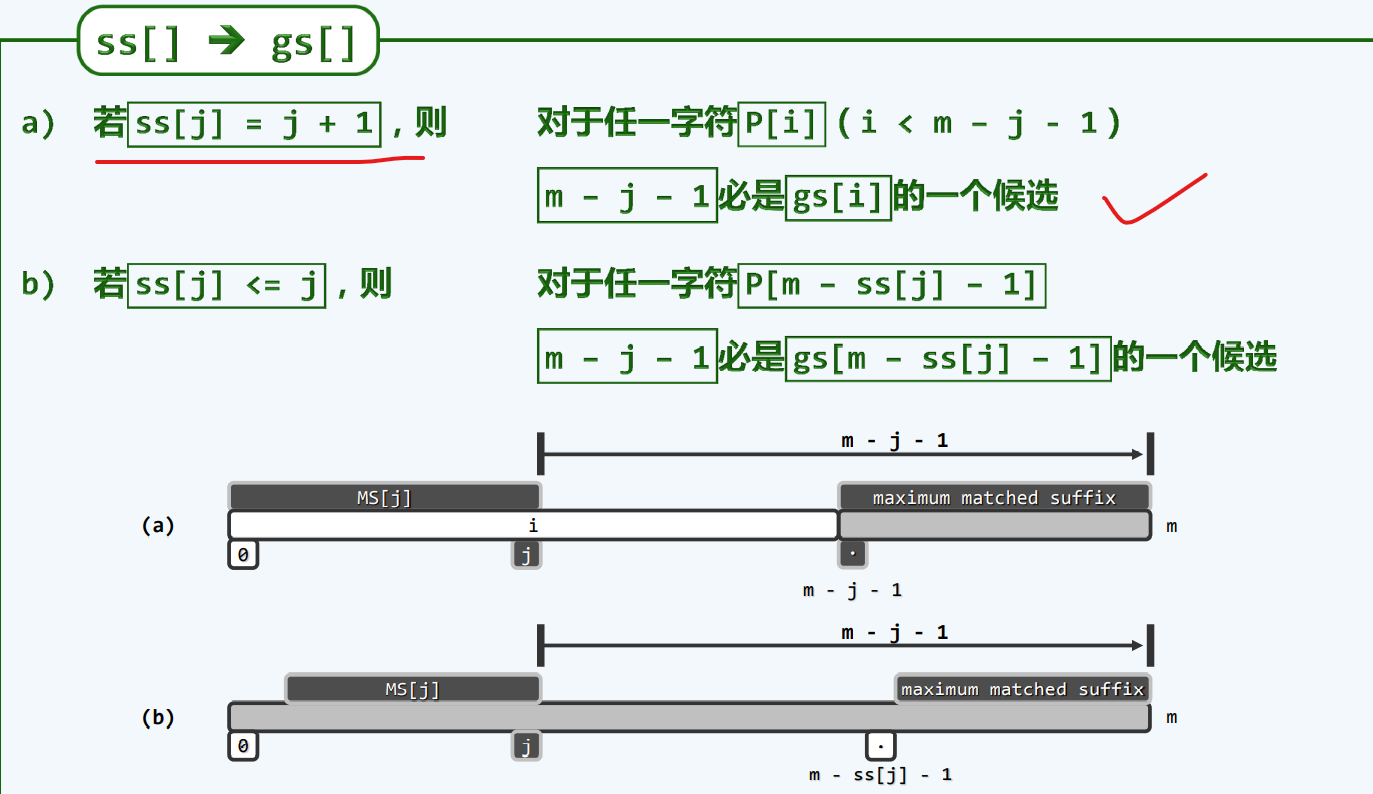
性能分析

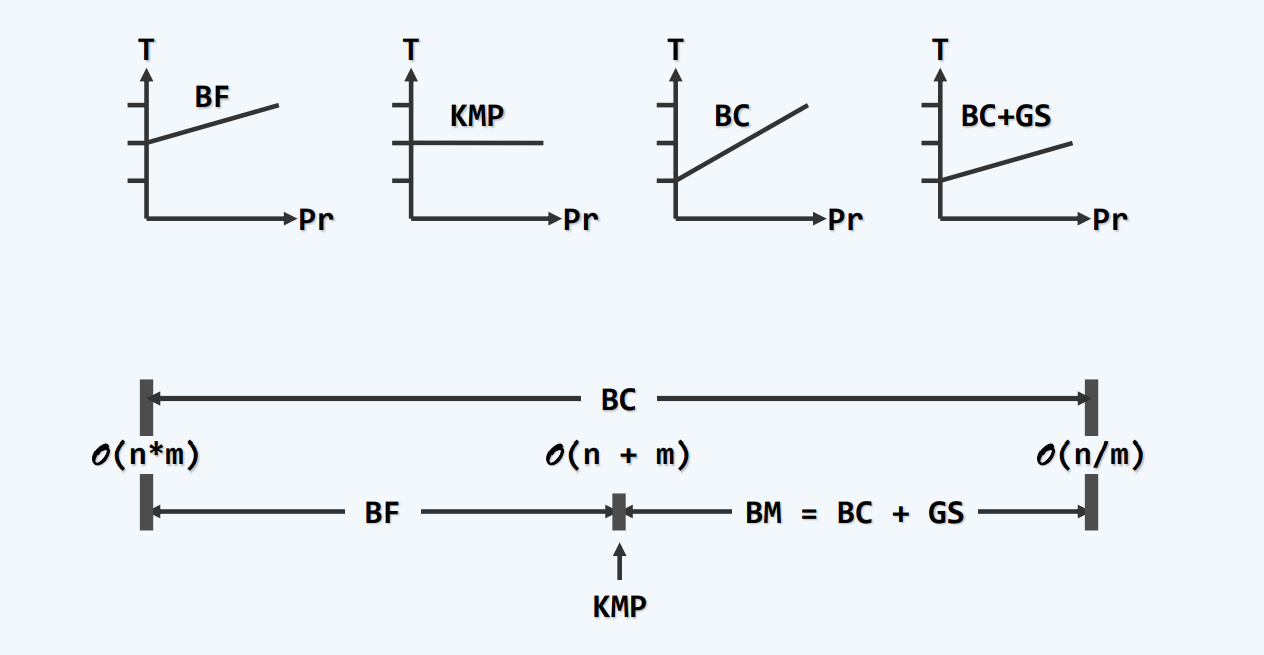
各算法总览
KMP:适用于规模小的情况 适合容易匹配到的情况
BC:适用于大字符集 适合容易匹配不到的情况
BC+GS:无敌
Karp-Rabin:串即是数
化串为数
凡物皆数


串亦是数

数位溢出

散列压缩

应对冲突
只要有散列,就会有冲突
因此,一旦检测到散列码一样,我们也不会贸然的选取,这里采用的是,散列码一样之后,在进行逐位比对

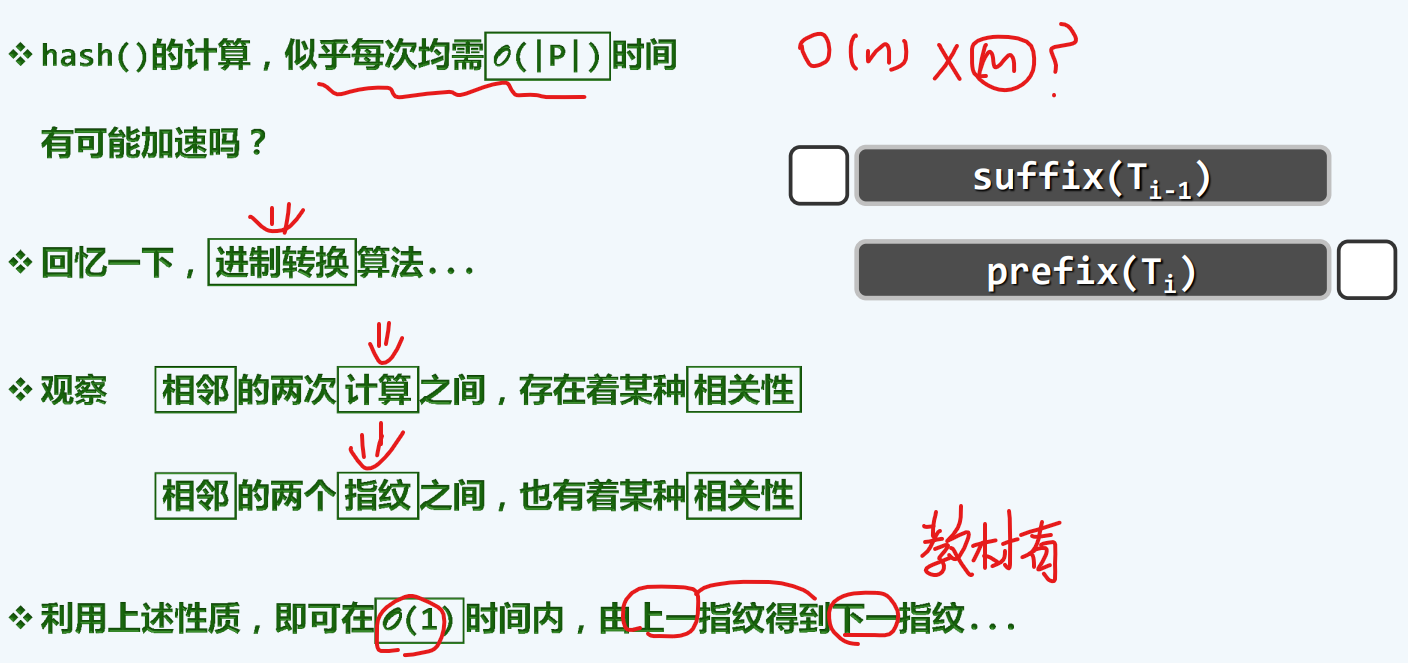
指纹更新