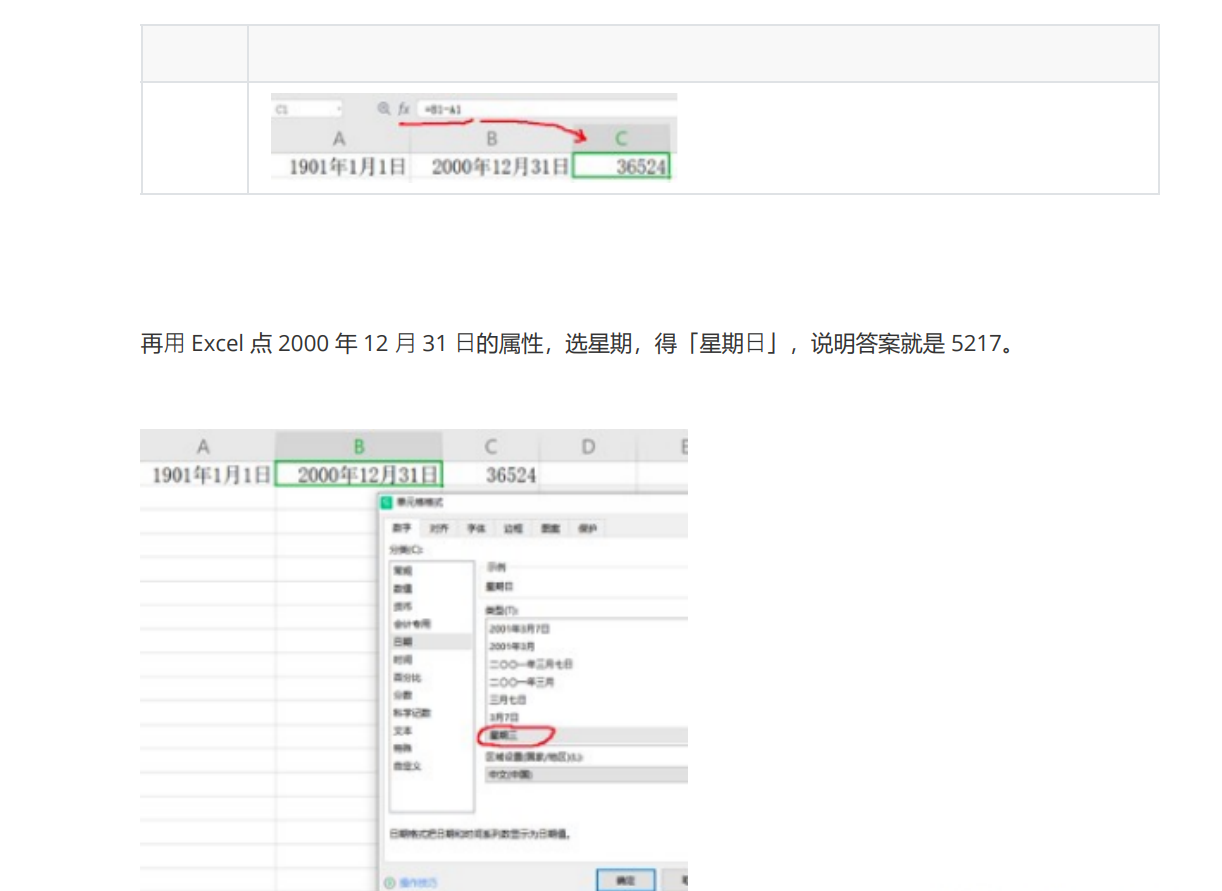
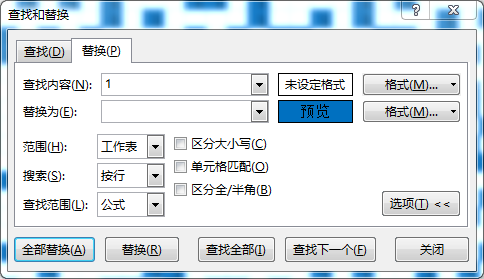
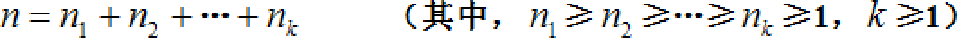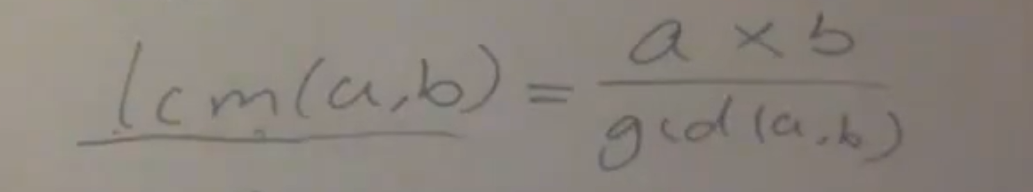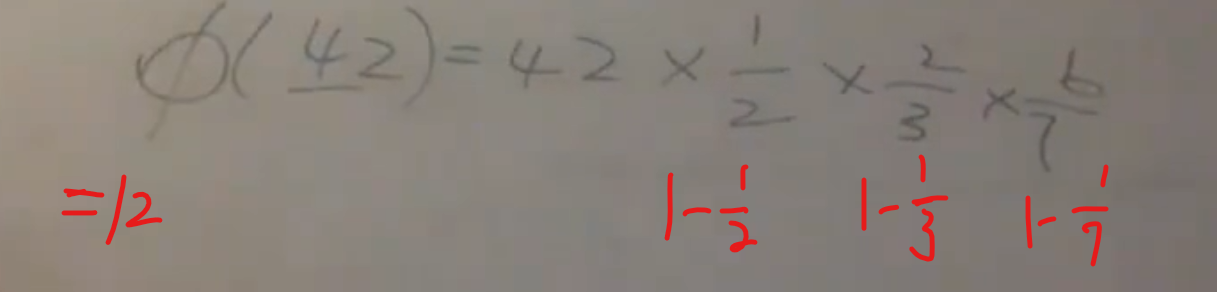本笔记用作个人学习和查漏补缺使用,欢迎借鉴学习,提出建议,转载需标注出处www.jjyaoao.space
环境配置(周六记得来补上 主题,行闪光,复制粘贴
学习excel一些操作,复习一下java
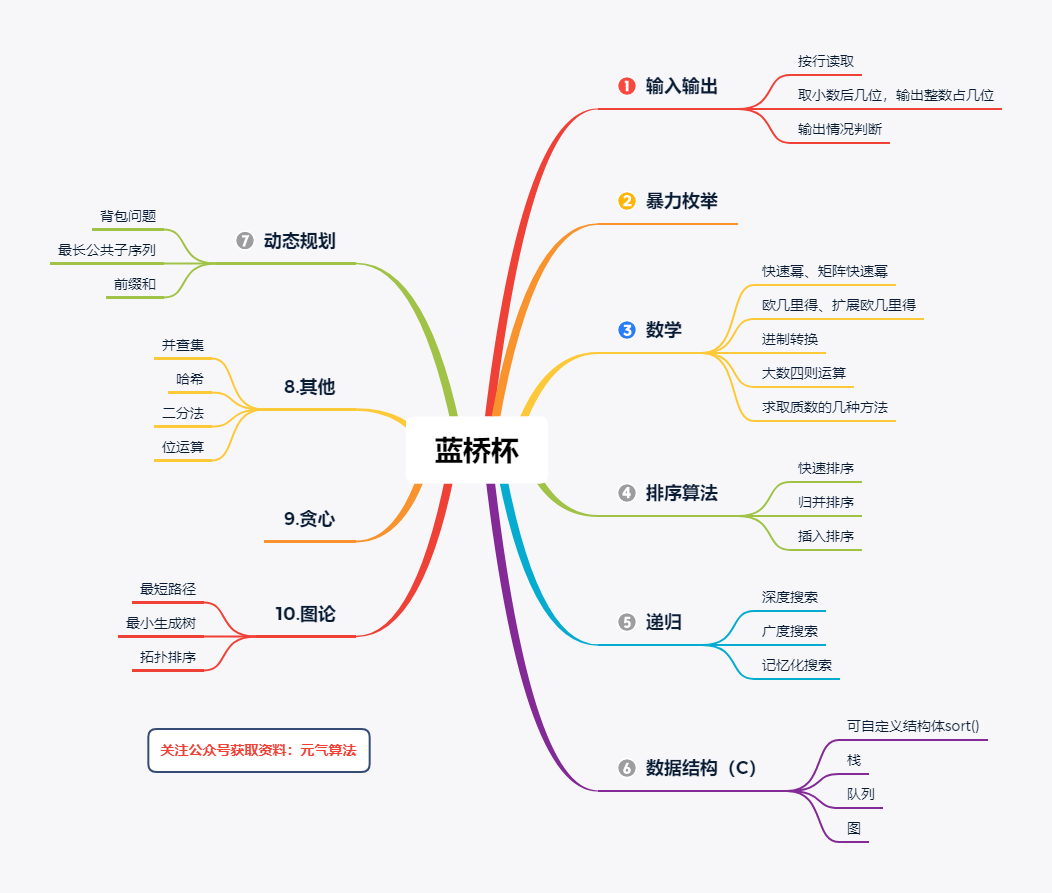
比赛规则 题型
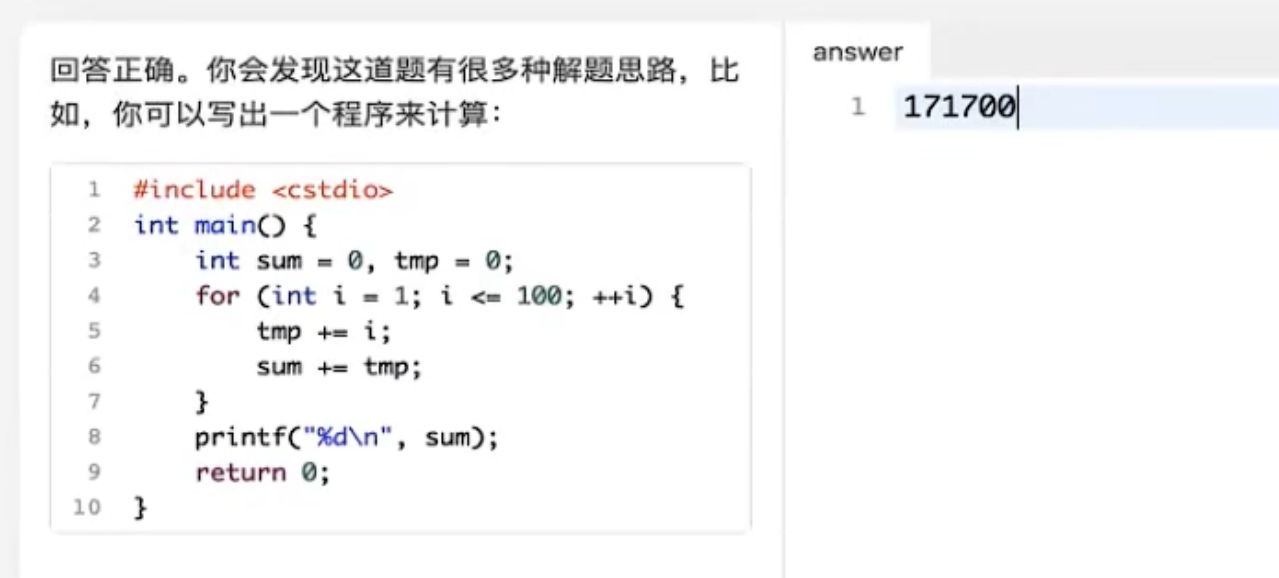
结果填空题
例子
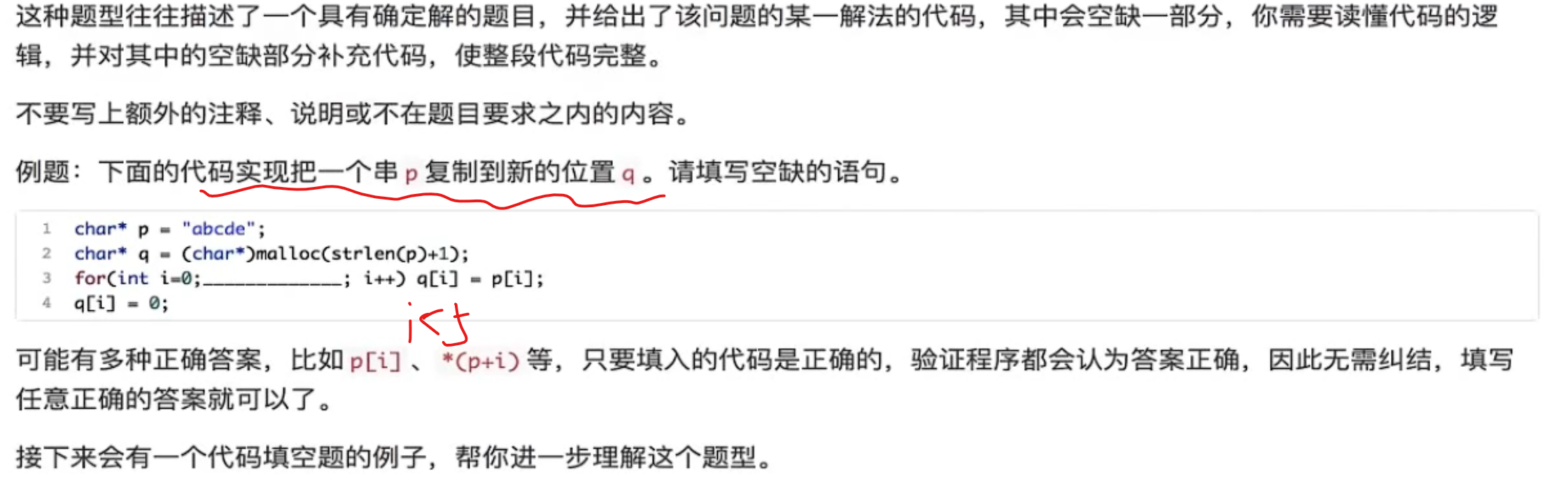
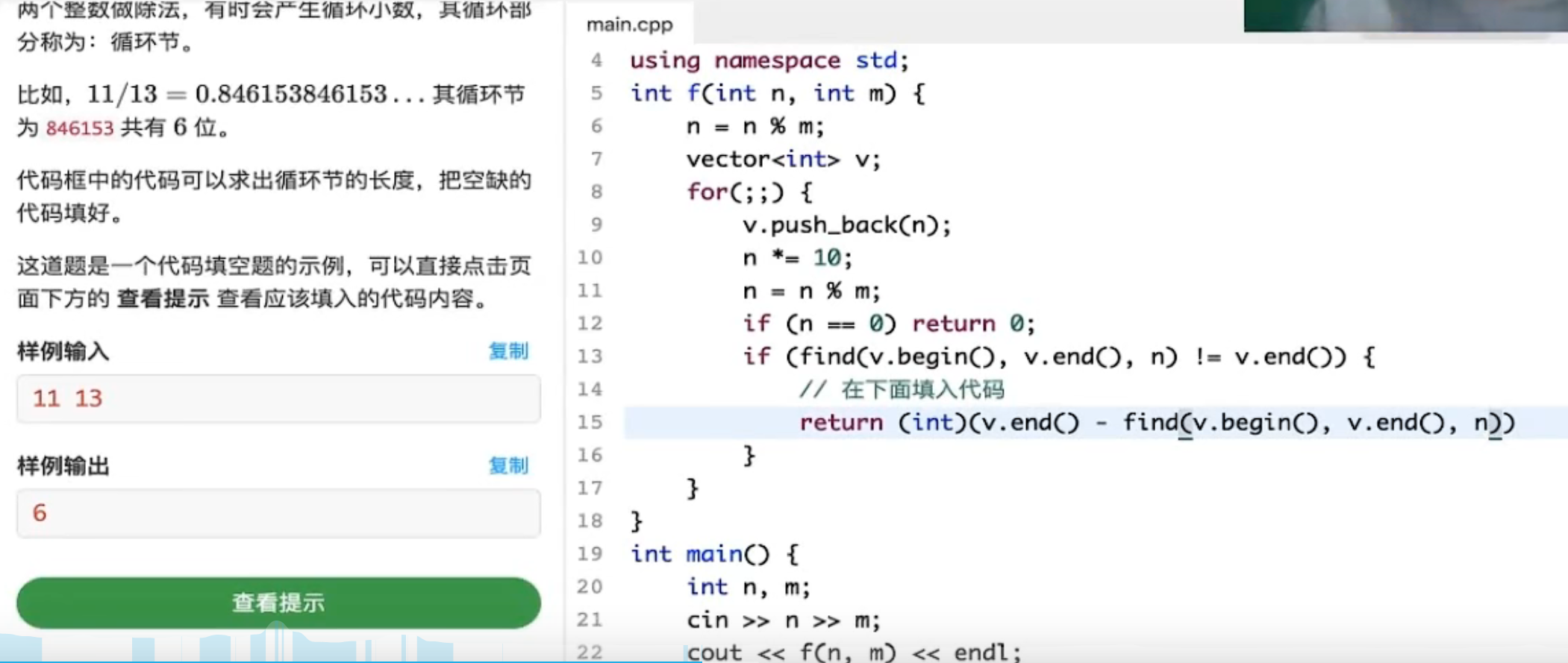
程序填空题
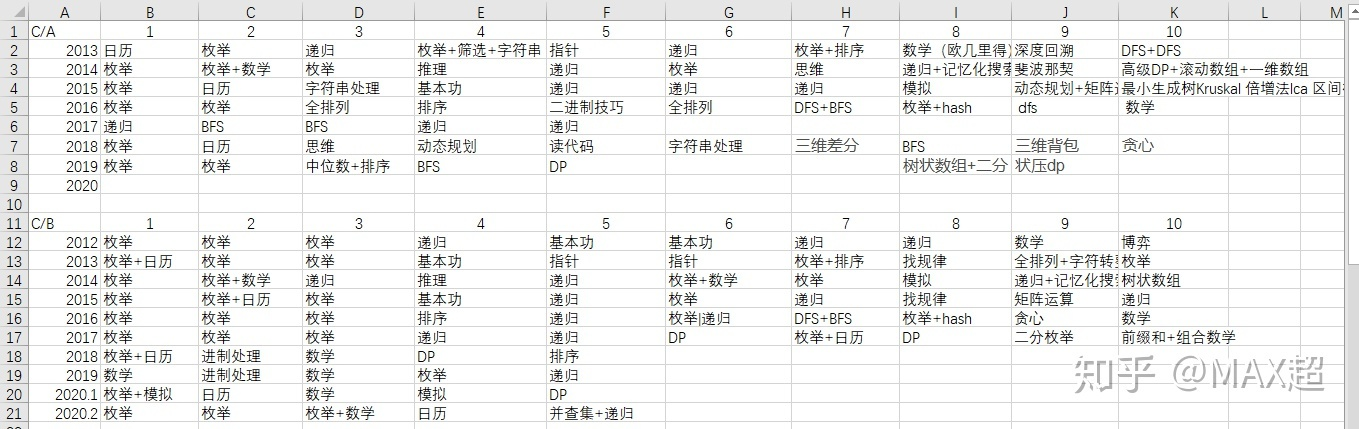
赛题分析
重点复习5 6 7
注意事项 #include <bits/stdc++ .h> 万能头
数组都开到全局变量!!!!,防止栈溢出
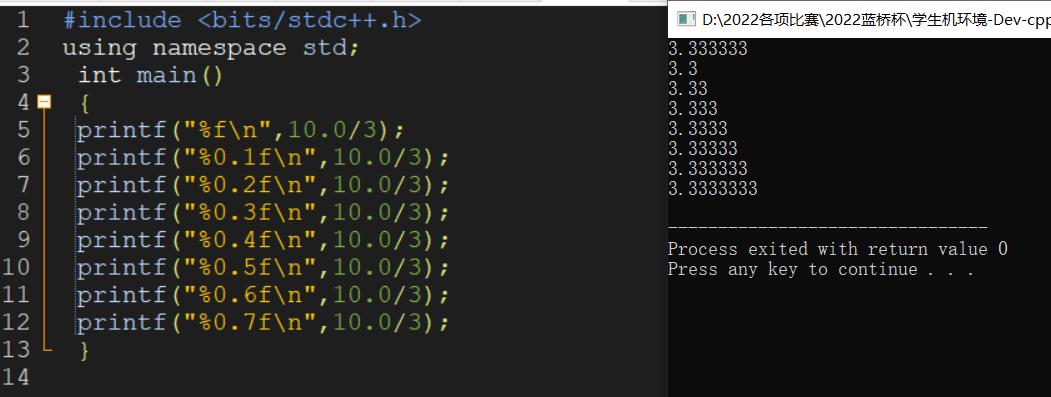
保留小数点后n位 如果是int 类的数值,那么我们应该乘以1.0或者1.00之类的,然后强转为精度类型,再输出,应该0.2、.2差不多,都可以用
四舍五入round() 1 2 3 4 5 6 7 8 9 10 11 12 #include <stdio.h> #include <math.h> int main () char str[80 ]; sprintf (str, "Pi 的值 = %.1lf" , round (2888.45 *10 )/10 ); printf ("%s" , str); return (0 ); }
复杂度
时间复杂度 基本控制在10的八次方量级,最好10的七次方
空间复杂度 一般3*10^7 int(总的数组量
一般不容易超,别玩脱
预处理数据 memset初始化 memset只能赋值0 和 -1 不能赋值为1! !!!!
这里dest需要清0,全局变量可以自动清理,局部变量最好清零,不然可能会出现各种各样的问题,memset 可以清零
void *memset(void *s, int ch, size_t n);
函数解释:将s中当前位置后面的n个字节 (typedef unsigned int size_t )用 ch 替换并返回 s 。
memset:作用是在一段内存块中填充某个给定的值,它是对较大的结构体 或数组 进行清零操作的一种最快方法
但是一般数组,或者变量,只要我们开到全局 ,就不会有这个问题!
scanf读入 数据量上了10^5 次读入,就需要采用scanf 了,小读入量可以cin
在C语言中,输入变量的语法是:scanf(“格式控制”,”变量地址 “)
可以看出,第二个的格式为变量地址。
在C语言中,变量在定义之后,就会在计算机内存中非配一块空间给这个变量,该空间在内存中的地址称为变量的地址。
为了得到变量的地址,需要在变量前加一个&(称为取地址运算符),也就是“&变量名”的写法。
%lf/%f %f和%lf分别 是float 类型和double 类型用于格式化输入输出时对应的格式符号。
在用于输出时:
在用于输入时:
所以在输入输出时,一定要区分好 double和float,而使用对应的格式符号。
sprintf赋值 下面的实例演示了 sprintf() 函数的用法。
实例
1 2 3 4 5 6 7 8 9 10 11 12 #include <stdio.h> #include <math.h> int main () char str[80 ]; sprintf (str, "Pi 的值 = %f" , M_PI); puts (str); return (0 ); }
让我们编译并运行上面的程序,这将产生以下结果:
printf输出 printf(“%04d-%02d-%02d”,y,m,d); //2017-01-09
printf(“%4d-%2d-%2d”,y,m,d); //2017- 1- 9 //不写0默认空格代替0的位置
%8d是将数字按宽度为8,采用右对齐方式输出,如果数据位数不到8位,则左边补空格。
%-8d 将数字按宽度为8,采用左对齐方式输出,如果数据位数不到8位,则右边补空格。
%08d:默认情况下,数据数据宽度不够8位是用空格填补的,但是因为8d前面有0,表示,数据宽度不足时用0填补。
%.8d和%08d一样。
gets()读入 char a[40000];gets(a); 必须是char型数组 ,即char a[40000];这个40000代表的就是buffer
1 2 3 4 5 6 7 8 9 10 11 12 13 14 #include <iostream> #include <cstring> #include <stdio.h> using namespace std;int main () char a[40000 ]; gets (a); int len=strlen (a); return 0 ; }
EOF读入 scanf也是一个函数,也是有返回值的,读入成功时,他会返回你读入了几个,读到文件尾 他会返回EOF,手动截断读入就ctrl + z
scanf的返回值由后面的参数决定
scanf(“%d%d”, &a, &b);
如果a和b都被成功读入,那么scanf的返回值就是2
如果只有a被成功读入,返回值为1
如果a和b都未被成功读入,返回值为0
如果遇到错误或遇到end of file,返回值为EOF。
且返回值为int型.
验证:
1 2 3 4 sign=scanf("%d %d",&a,&b); printf("%d %d\n",a,b); printf("%d\n",sign); 123
但是输入“a X”的时候 输出的sign为0
什么时候输出EOF? 在stdio.h中 宏定义为-1
按照说明,scanf函数只有在第一个参数为NULL(空指针)的情况下,才可能返回EOF,否则,返回成功格式化并赋值的参数个数(>=0)。
End Of File,在电脑的术语缩写通常为 EOF,在作业系统决定资料源无更多的资料可读取。
**//**while(scanf(“%d”,&n)!=EOF)也可以表示为while(~scanf(“%d”,&n));
2.~的含义 是按位取反,如果scanf函数没有输入值或输入错误就是返回-1,-1按位取反结果是0。scanf(“%d”, &n))就是当没有输入的时候退出循环,等价于while(scanf(“%d”,&n)!=EOF)。
例子
1 2 3 4 5 6 7 8 #include <bits/stdc++.h> using namespace std;char s[10005 ];int main () while (scanf ("%s" , s) != EOF); printf ("%d\n" , strlen (s)); return 0 ; }
文件读入 1 2 freopen ("fx.in" , "r" , stdin);freopen ("fx.out" , "w" , stdout);
->/.?? 简单来讲,迭代器(iterator)和 C++ 的 指针 非常类似 ,它可以是需要的任意类型,通过迭代器可以指向容器中的某个元素,如果需要,还可以对该元素进行读/写操作。
定义了一个成员变量,我们用点号取出属性,如果是一个迭代器之类的,我们用->得到他内部的东西
字符串和日期 简单实例 实例一 1 2 3 4 5 6 7 #include <bits/stdc++.h> int main () printf (" A\n" ); printf ("BBB\n" ); return 0 ; }
实例二
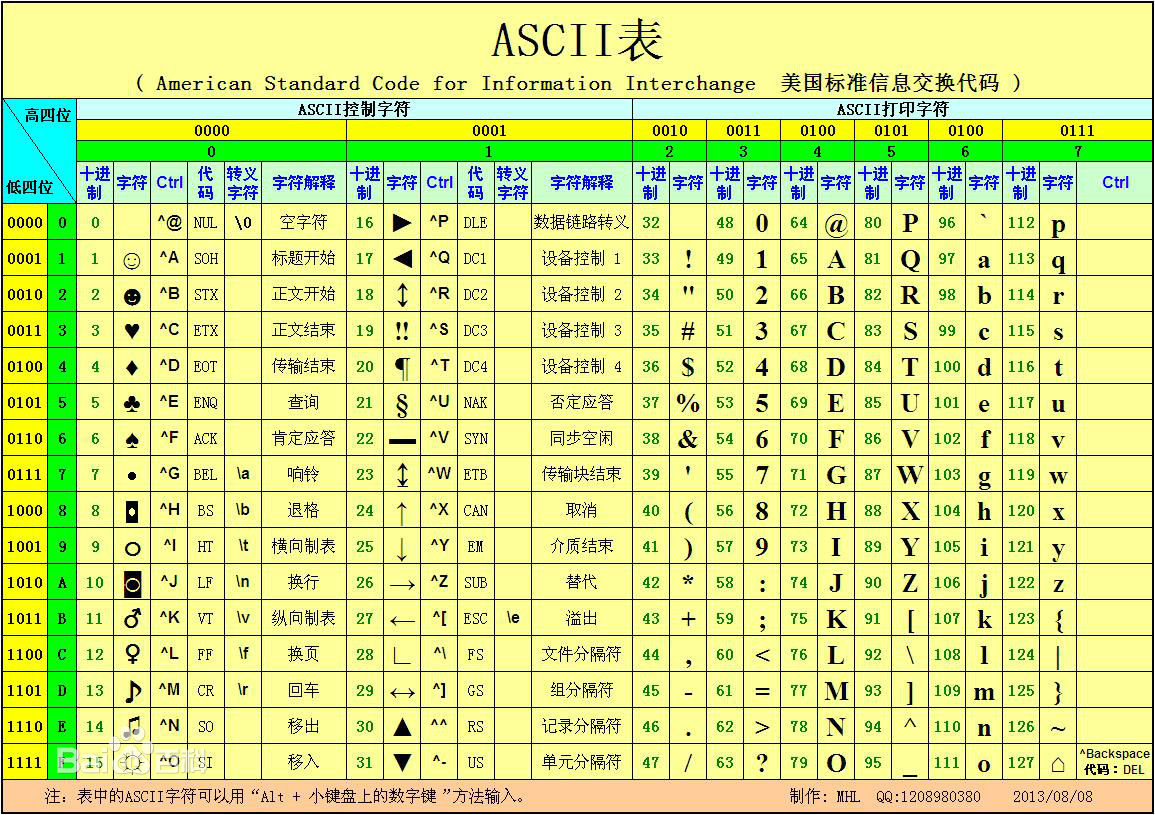
ASCII表 A:65 a:97
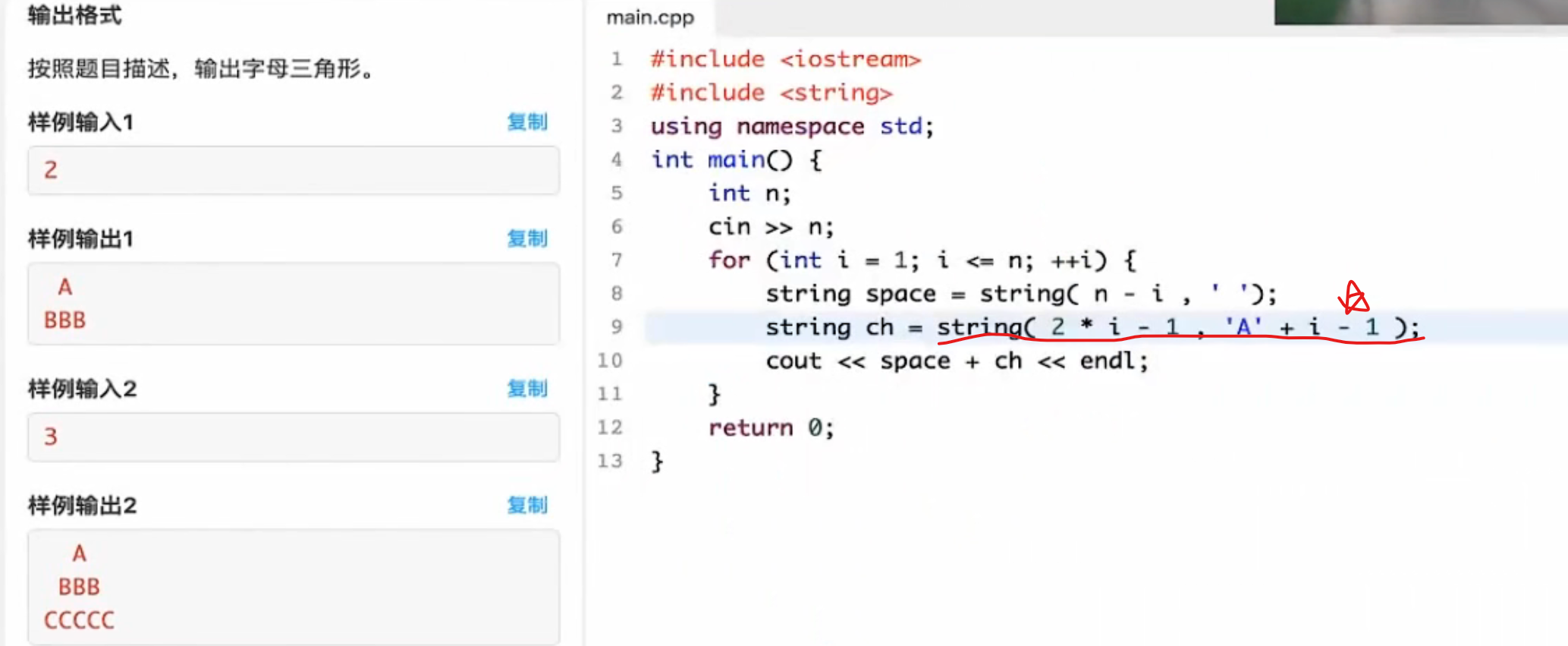
复杂实例 实例一
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 #include <bits/stdc++.h> using namespace std;int main () char c; cin >> c; if (c >= 'A' && c <= 'Z' ) { for (int i = 1 ; i <= c - 'A' + 1 ; i++) { for (int j = 1 ; j <= c - 'A' + 1 - i; j++) { cout << " " ; } for (int j = 1 ; j<=i; j++) { cout << (char )('A' + j - 1 ); } for (int j = i - 1 ; j >= 1 ; j--) { cout << (char )('A' + j - 1 ); } cout << endl; } }else { for (int i = 1 ; i <= c - '1' + 1 ; i++) { for (int j = 1 ; j <= c - '1' + 1 - i; j++) { cout << " " ; } for (int j = 1 ; j<=i; j++) { cout << (char )('1' + j - 1 ); } for (int j = i - 1 ; j >= 1 ; j--) { cout << (char )('1' + j - 1 ); } cout << endl; } } }
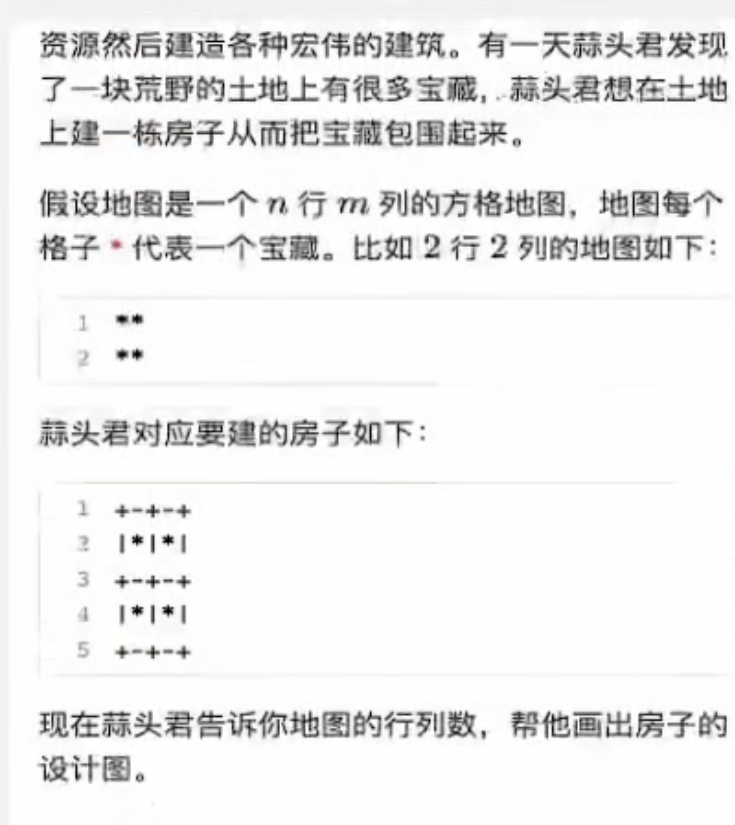
实例二
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 #include <bits/stdc++.h> using namespace std;int main () int n,m; cin >> n >> m; for (int i = 1 ; i <= n; i++){ for (int j = 1 ; j <= m; j++){ cout << "+-" ; } cout << "+" <<endl; for (int j = 1 ; j <= m; j++){ cout << "|*" ; } cout << "|" <<endl; } for (int j =1 ; j<=m; j++){ cout << "+-" ; } cout << "+" <<endl; return 0 ; }
实例三 字符串
如果不是以\0结尾的话,那就真的只能称为字符数组。
并且如果使用%s输出这样的数组的话,那么就会一直一直输出,不会停下来
它把\0当做结尾 ,没有找到的话就会一直往后找
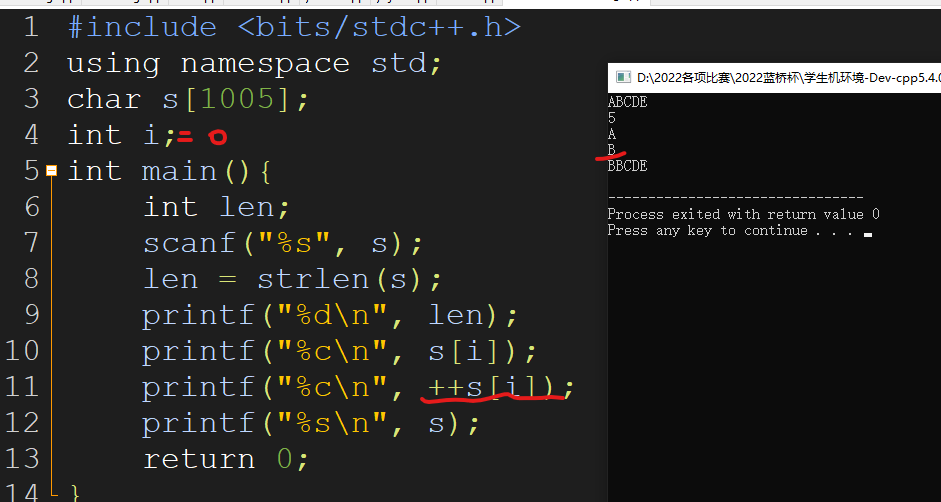
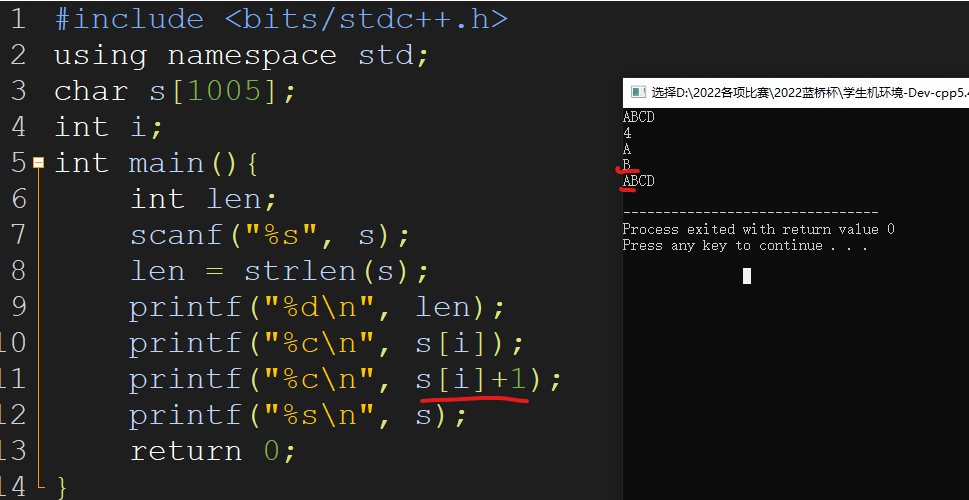
char类型+1 **++ –**会改变的是他底层的ASCII码值吧!不存在类型转换,仍然是char类型
而如果+1的话…
我们观察char的第一位,他没有改变,但是却可以输出第一位的ASCII码的下一位,C++真的太牛马了,莫名其妙问题一大堆
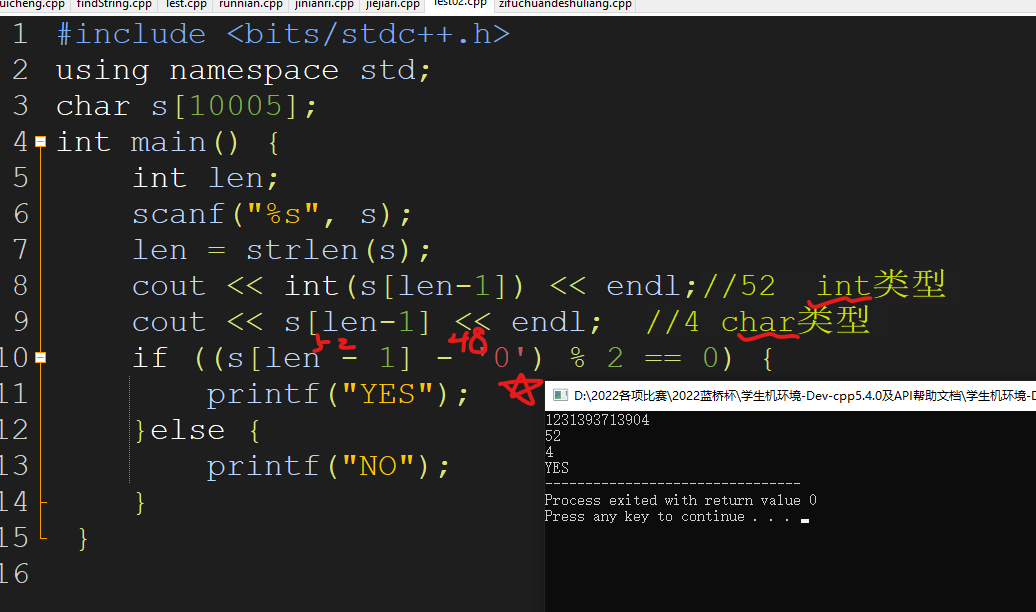
char与数字转换 太求细节了,比针还细,我觉得啊,有些时候,真的人要聪明一点,收货才大
用char的数字来作计算,一定要减’0’ 或者减48嘛
C++String的坑 String直接赋值是不改变长度的
你只要用String赋值了之后,那怕你把中间的字符改为\0,或者说在length之后的一些位置赋值,直接复制,而不是用+的方式,都是不改变长度的,会出一定的问题
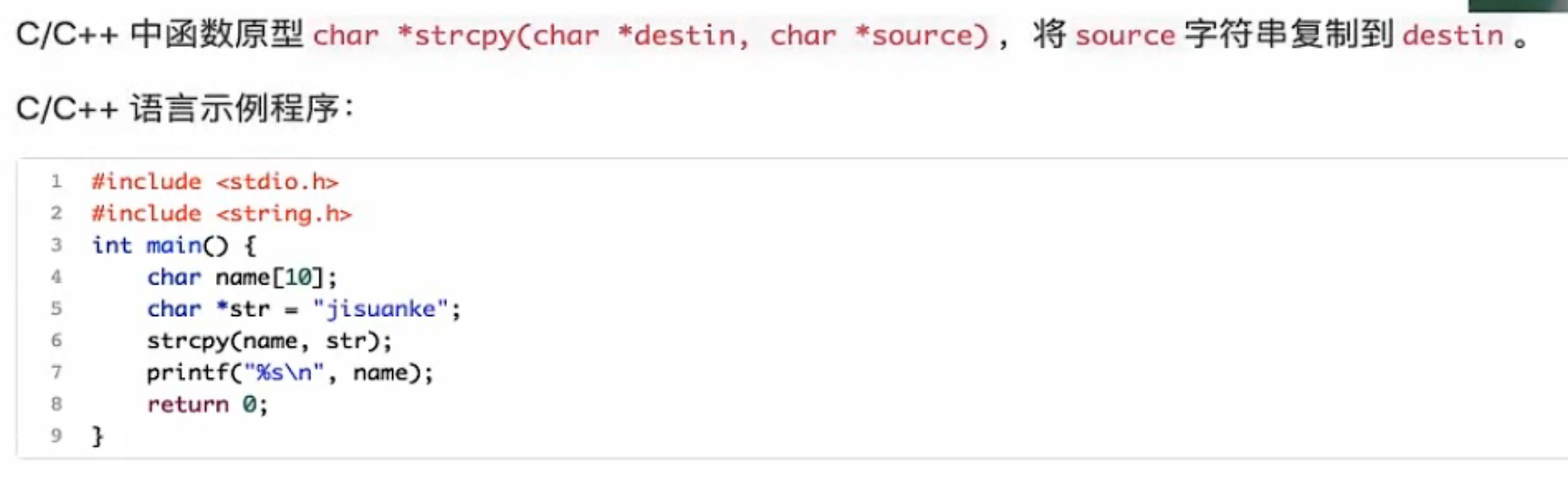
复制 C++的String也可以直接等号赋值
拼接 C++也是可以直接加号,拼接
1 extern char *strcat(char *dest, const char *src);
我们可以看到,函数的原型是传入了两个char类型的指针,中文定义如下:
**char * strcat (目标字符串,*源字符串* );**//将源字符串的副本附加到目标字符串上,目标字符串中的终止空字符由源字符串的第一个字符覆盖,并将这两个字符串连接形成的新字符串,末尾包含一个空字符。
参数定义
拼接小例题
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 #include <bits/stdc++.h> using namespace std; char res[5000000 ]; int main () int n; scanf ("%d" ,&n); int len = 0 ; for (int i = 1 ; i <= n; ++i){ strcat (res + len + 1 , res); res[len] = 'A' + i - 1 ; len = strlen (res); } printf ("%s\n" ,res); return 0 ; }
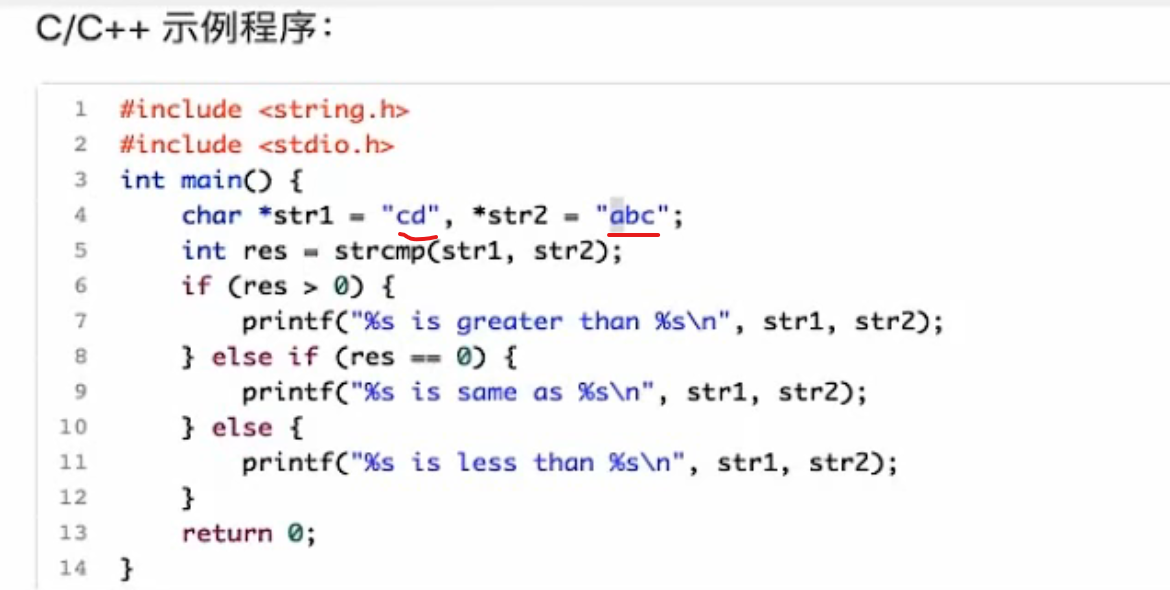
比较大小 c比a大,所以比到这里就结束了,str1大,我们一般只关注正负即可
建议平时用的时候用char[],给它一个足够长的长度,char*经常会出现各种各样的问题,比如说忘记开空间了。
c++可以直接用> <直接进行比较,比如这里我们就可以把res > 0 改成str1>str2 这个意思,不过可能这里不行=-=因为他是指针的嘛,具体我也不清楚,是不是应该解引用哦
更新 :对于string而言,可以直接><比较,但是char数组(每一位存放一个指针嘛)我们采用strcmp()
获取字符串长度 描述 C 库函数 size_t strlen(const char *str) 计算字符串 str 的长度,直到空结束字符,但不包括空结束字符。
声明 下面是 strlen() 函数的声明。
1 size_t strlen(const char *str)
时间复杂度内部O(n)
返回值 该函数返回字符串的长度。
实例 下面的实例演示了 strlen() 函数的用法。
使用方法最好像这个一样,先把这个strlen(str)变量的值存下来为len,在用len去写for循环(如果要写循环的话)不然每次循环,就执行一次strlen,时间复杂度可能会达到n^2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 #include <stdio.h> #include <string.h> int main () char str[50 ]; int len; strcpy (str, "This is runoob.com" ); len = strlen (str); printf ("|%s| 的长度是 |%d|\n" , str, len); return (0 ); }
让我们编译并运行上面的程序,这将产生以下结果:
1 |This is runoob.com| 的长度是 |18 |
查找字符串 char数组的\0问题 字符数组保存时有可能最后一位有‘\0’,需要注意。参考:
并且有:
1 2 3 4 5 6 sizeof 5 ;strlen (a) == 4 ;char a[5 ] = "abcde" ; char a[5 ] = {'a' ,'b' ,'c' ,'d' ,'d' };
1 2 3 4 5 char * a = “abcde”;sizeof 4 ; strlen (a) == 5 ;
strlen:从数组指针开始,直到找到’\0’结束,这中间的字符个数;
如果char* 类型变量不是用常量直接初始化的,那么在赋值结束时一定要手动添加一个’\0‘(分配空间时,也需要多分配一个char空间),这样用strlen才可以正确得返回长度,后面的使用也不会有问题,例如:没有加’\0‘时,这个变量作为参数传入函数就出了问题invalid_argument。
最后一位的’\0‘不参与计算==》》 a[strlen(a)-1] == e;
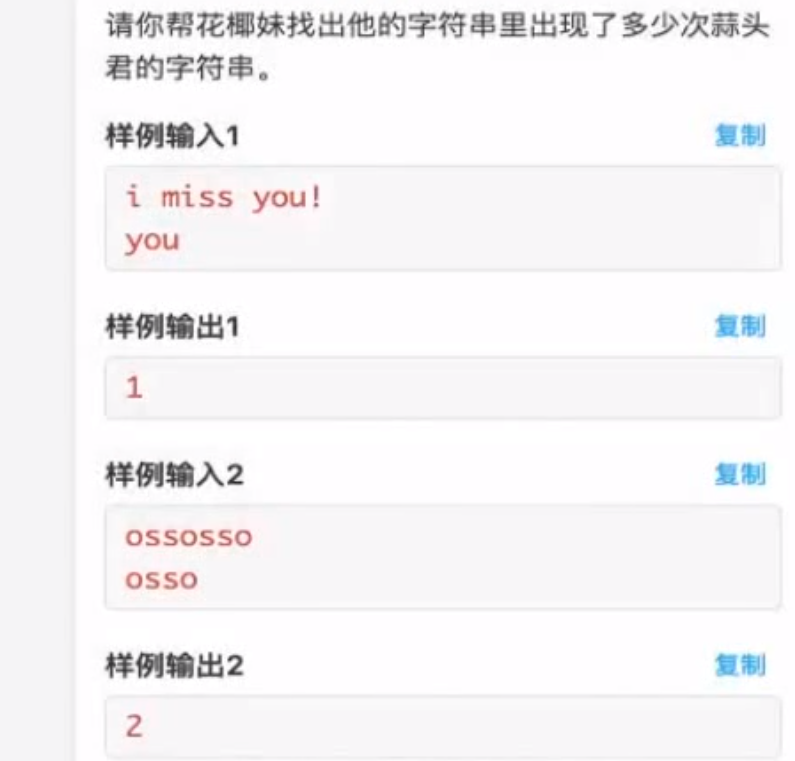
例题
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 #include <bits/stdc++.h> using namespace std;char s1[1005 ], s2[1005 ]; int main () gets (s1); gets (s2); int len1 = strlen (s1) - 1 ,len2 = strlen (s2) -1 ; int ans = 0 ; for (int i = 0 ; i + len2 - 1 < len1; i++){ bool matched = true ; for (int j = 0 ; j < len2; j++){ if (s1[i+j] != s2[j]){ matched = false ; break ; } } if (matched) { ans++; } } printf ("%d" ,len1); cout << ans << endl; return 0 ; }
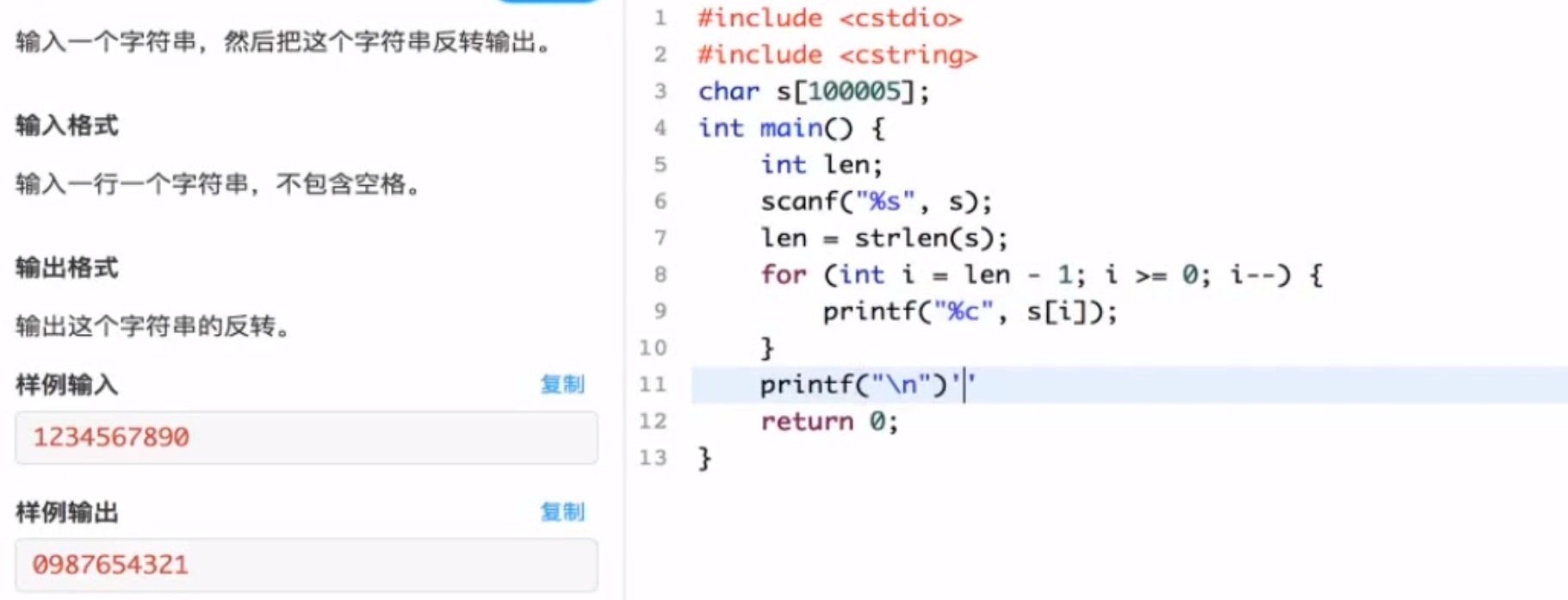
字符串反转 直接输出就好了,我做的话肯定会想先存,什么前一个和后一个交换啥的,不过这个确实最简单(思路
字符串难度终极 历届试题 打印十字图 问题描述
输入格式
输出格式
样例输入1
样例输出2
提示
思路 这道题吧,我觉得启发有如下:
第一,做图形问题,先把整体初始化为全部点图 ,或者全部*图,然后再操作,思路会清晰很多,我最开始想的是,一点一点凑出来,*号和点号相交来做,这样无疑复杂了
第二,找规律,放手去干就好,一般难度大,肯定做不了,留到最后,能做多少做多少,实在不行整个样例(其实我最开始想的启发可能不是这个,但我也想不起了=-=
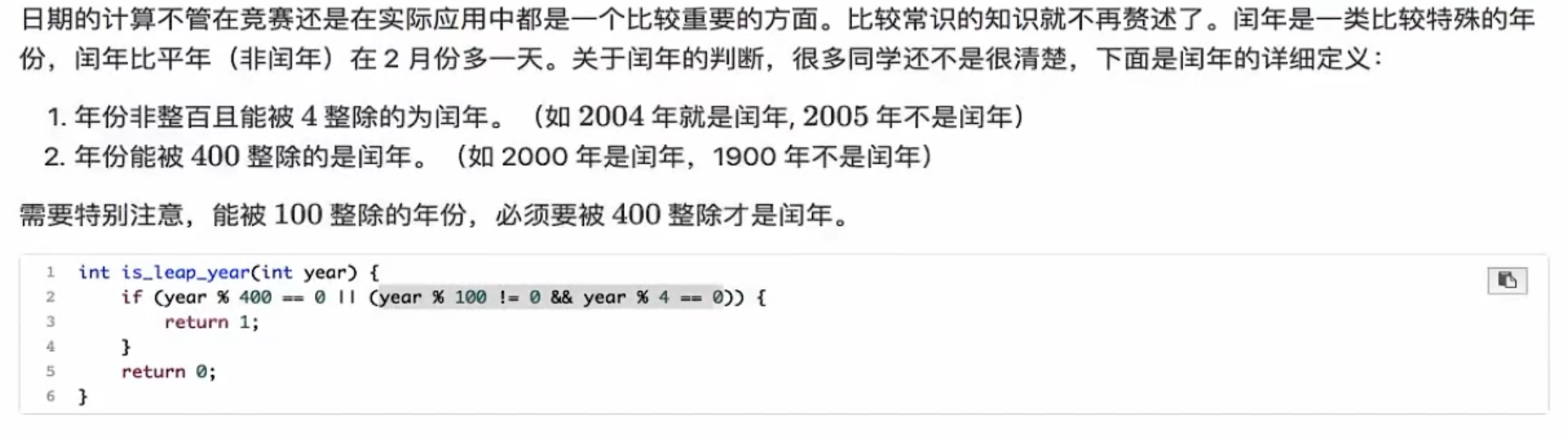
日期 润年
1 2 3 4 5 6 7 8 #include <bits/stdc++.h> using namespace std;int is_leap_year (int year) if (year % 400 == 0 ||(year % 100 != 0 && year % 4 == 0 )){ return 1 ; } return 0 ; }
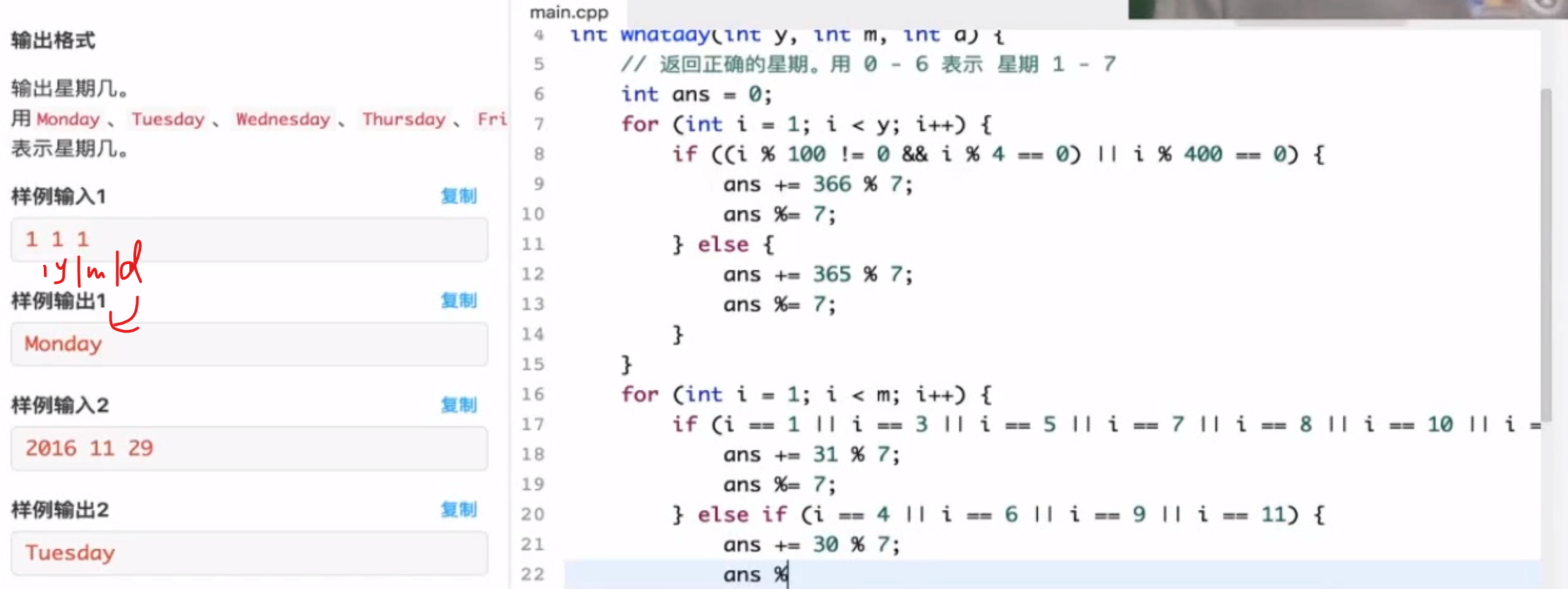
日期公式
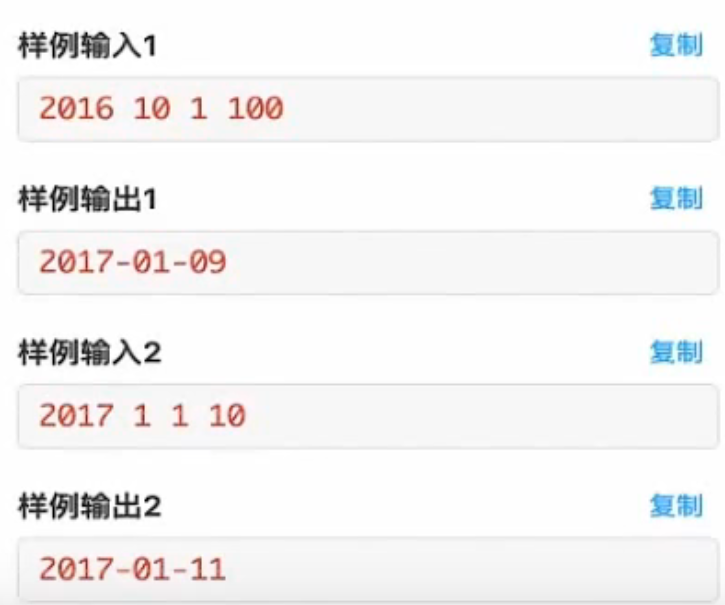
生日
纪念日
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 #include <bits/stdc++.h> using namespace std;char mon[13 ]= {0 ,31 ,28 ,31 ,30 ,31 ,30 ,31 ,31 ,30 ,31 ,30 ,31 }; int main () int y, m, d, k; scanf ("%d%d%d%d" ,&y,&m,&d,&k); for (int i = 0 ; i < k ; i++){ if (y % 400 == 0 || (y % 100 != 0 && y % 4 == 0 )) mon[2 ] = 29 ; d++; if (d > mon[m]){ d = 1 ; m++; } if (m > 12 ){ m = 1 ; y++; } } printf ("%04d-%02d-%02d" ,y,m,d); return 0 ; }
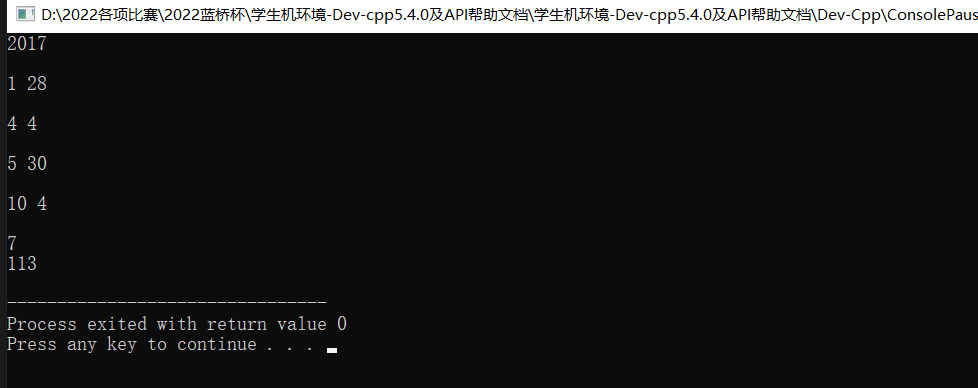
节假日 日历有阳历(公历)和阴历(农历)之分。每年都有法定节假日,这些分成三类——双休、阳历节假日、阴历节假日。春节:阴历每年1月1日,放假3天 //可能会出现跳月输入 格式
1 28
4 4
5 30
10 4
7
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 #include <bits/stdc++.h> using namespace std;int mm[10 ] = {1 , 5 , 10 , 10 , 10 , 12 };int dd[10 ] = {1 , 1 , 1 , 2 , 3 , 25 };int day[13 ] = {0 ,31 ,28 ,31 ,30 ,31 ,30 ,31 ,31 ,30 ,31 ,30 ,31 }; int y; int m=1 ,d=1 ; int sf; int ans; int w; int main () scanf ("%d" , &y); for (int i = 6 ; i < 10 ; i++){ scanf ("%d%d" , &mm[i],&dd[i]); } scanf ("%d" , &w); if (y % 400 == 0 || (y % 100 != 0 && y % 4 == 0 )) day[2 ] = 29 ; else day[2 ] = 28 ; while (m < 13 ){ if (m == mm[6 ] && d == dd[6 ]){ ans++; sf=2 ; }else if (sf){ sf--; ans++; }else if (w == 6 || w == 7 ){ ans++; }else { for (int i = 1 ; i < 10 ; i++){ if (m == mm[i] && d == dd[i]){ ans++; break ; } } } d++; if (d > day[m]){ d = 1 ; m++; } w++; if (w == 8 ){ w = 1 ; } } cout << ans << endl; return 0 ; }
傲世之帅!!!!
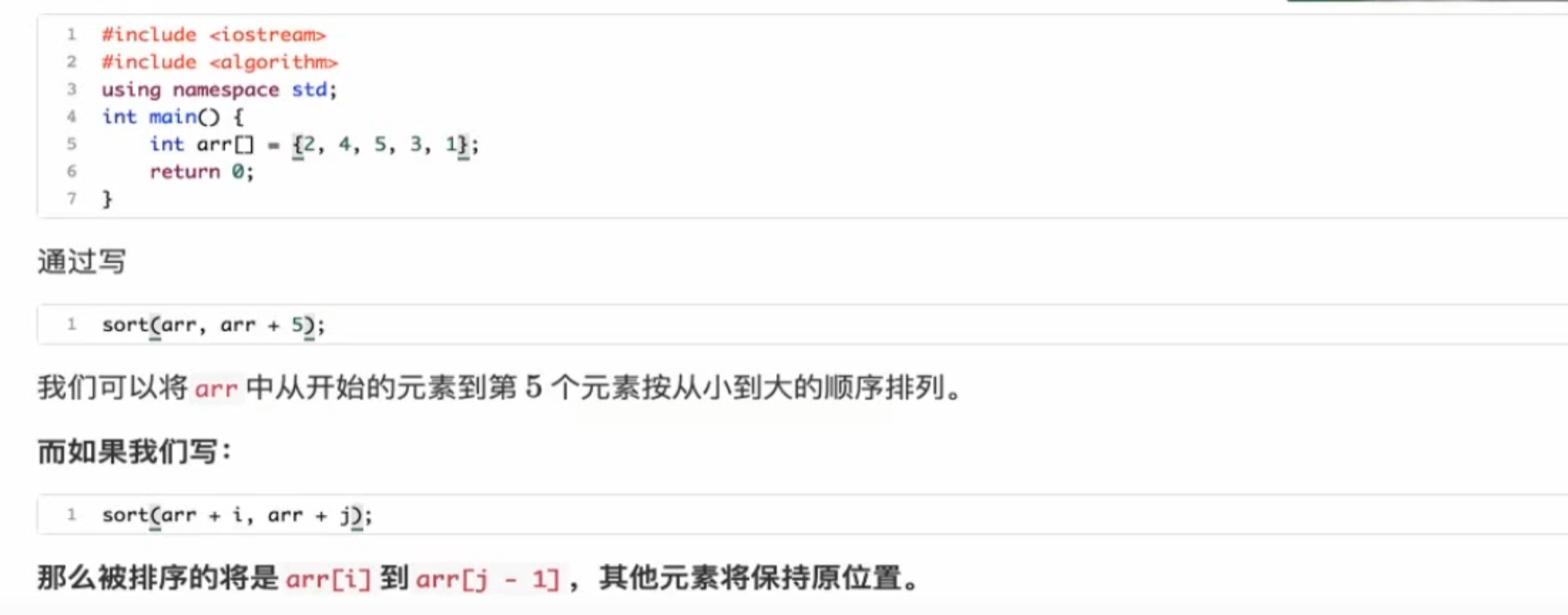
Sort排序 左闭右开 ,所以sort的第二个参数需要再想要的数值基础上+1
升序:sort(begin,end,less()) //从小到大排,less可以省略
降序:sort(begin,end,greater()) //从大到小
greater里面的 我们可以放以这样的形式来写 sort(arr, arr + 10, greater());
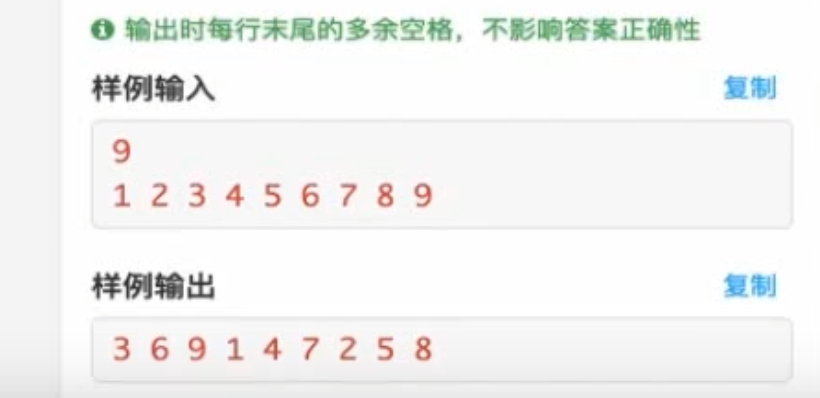
输出数据空格提醒 输出数据的时候,如果知道有多少位数据,我们判断最后一位打一个空格,如果不知道有多少位,我们可以判断开头空格 (使得开头第一位不需要空格),对于其他位置而言,也就是先打一个空格,再打一个数,确保最后一位不会多出一个空格
1 2 3 4 5 if (i != N - 1 ){ printf ("%d " , num[i]); }else { printf ("%d \n" , num[i]); }
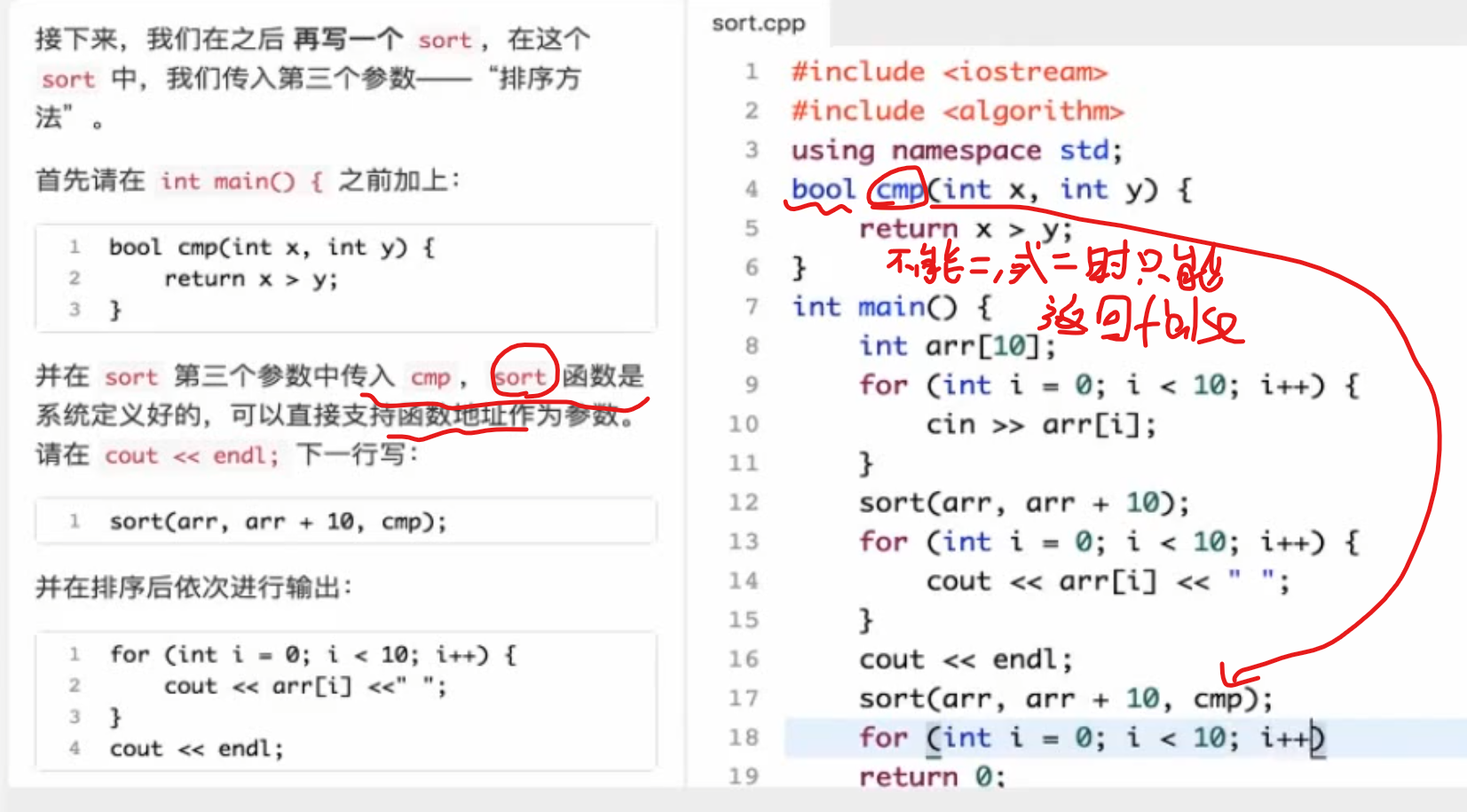
自己定义排序 我们通过什么方式来排序
从大到小排
用余数排
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 #include <bits/stdc++.h> using namespace std; int num[105 ];bool cmp (int x, int y) if (x % 3 != y % 3 ){ return x % 3 < y % 3 ; } else { return x < y; } } int main () int N; scanf ("%d" , &N); for (int i = 0 ; i < N; i++){ scanf ("%d" , &num[i]); } sort (num, num+N, cmp); for (int i = 0 ; i < N ;i++){ if (i != N - 1 ){ printf ("%d " , num[i]); }else { printf ("%d \n" , num[i]); } } return 0 ; }
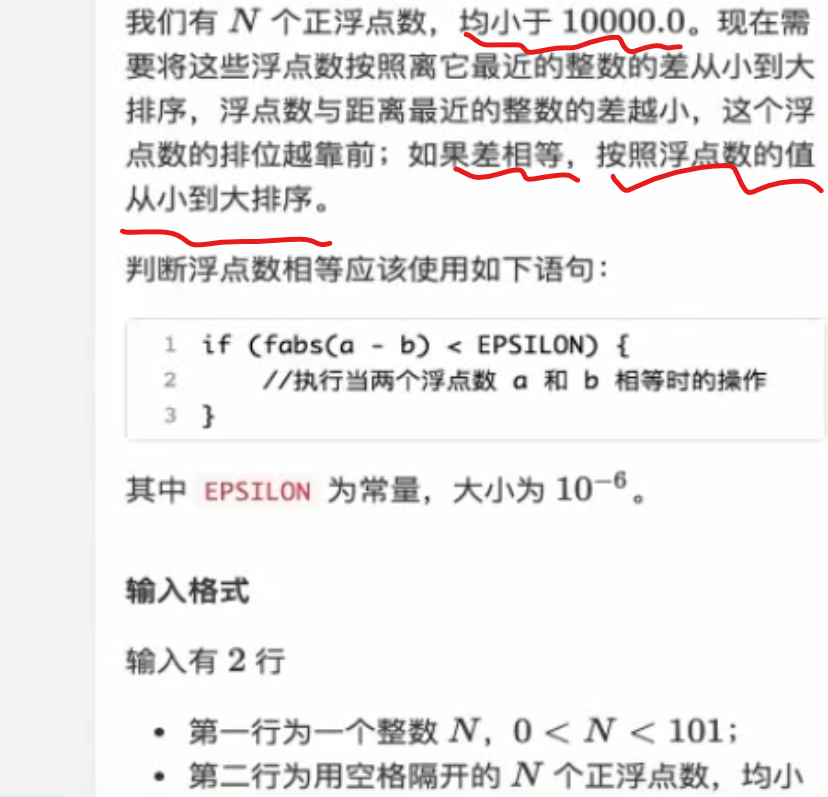
浮点数离整数距离排序
1 2 3 4 输入 9 1.001 2.1 3.2 4.0001 5.000001 6.9 7.2 8.001 9.0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 #include <bits/stdc++.h> using namespace std; const double EPSILON = 1e-6 ;double num[105 ];bool cmp (double a, double b) double da = fabs (a - round (a)); double db = fabs (b - round (b)); if (fabs (da - db) < EPSILON) { return a < b; } return da < db; } int main () int N; scanf ("%d" , &N); for (int i = 0 ; i < N; i++){ scanf ("%lf" , &num[i]); } sort (num, num + N, cmp); for (int i = 0 ; i < N; i++){ if (i != N - 1 ){ printf ("%lf " , num[i]); }else { printf ("%lf\n" , num[i]); } } return 0 ; }
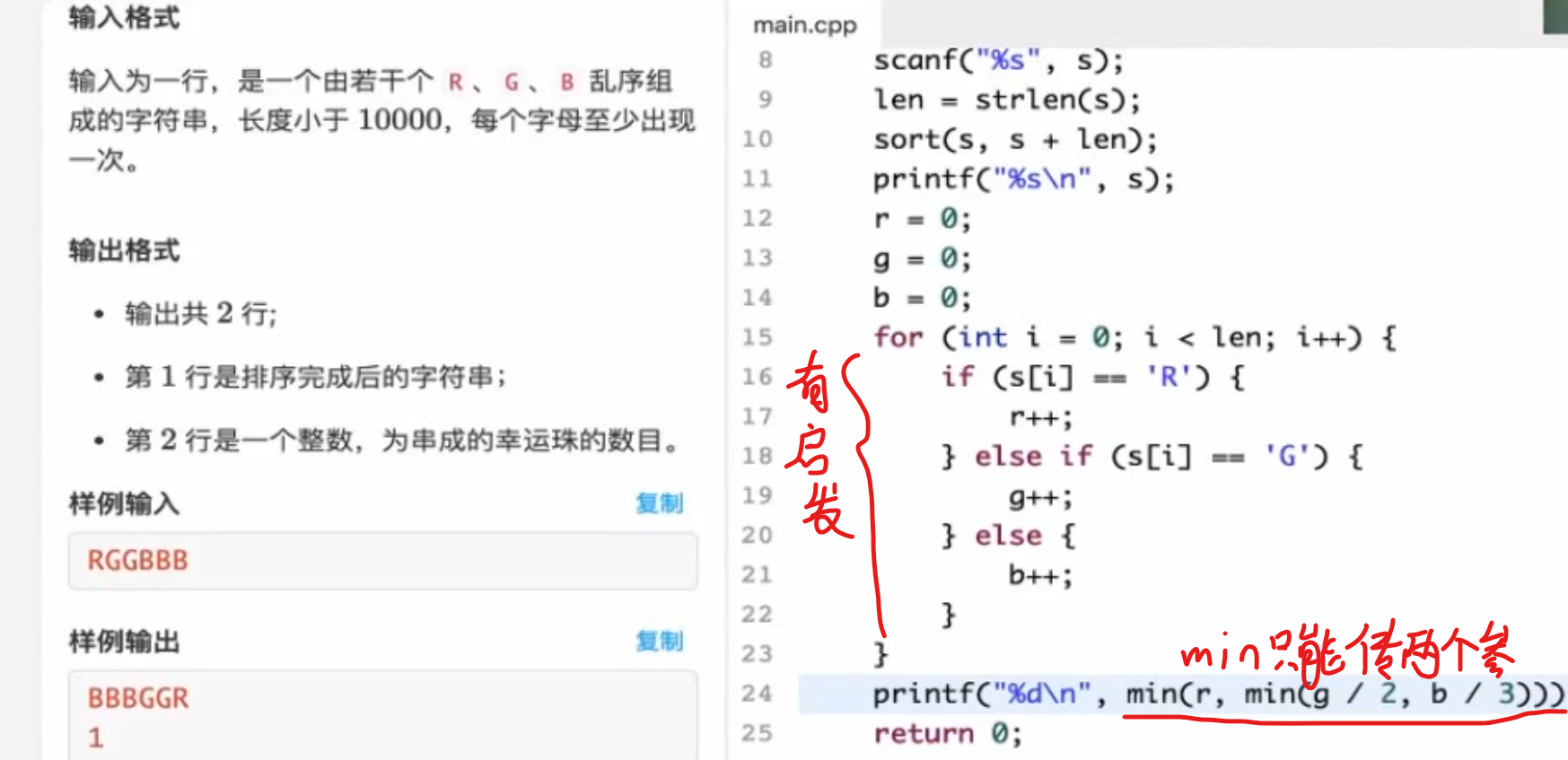
串珠子
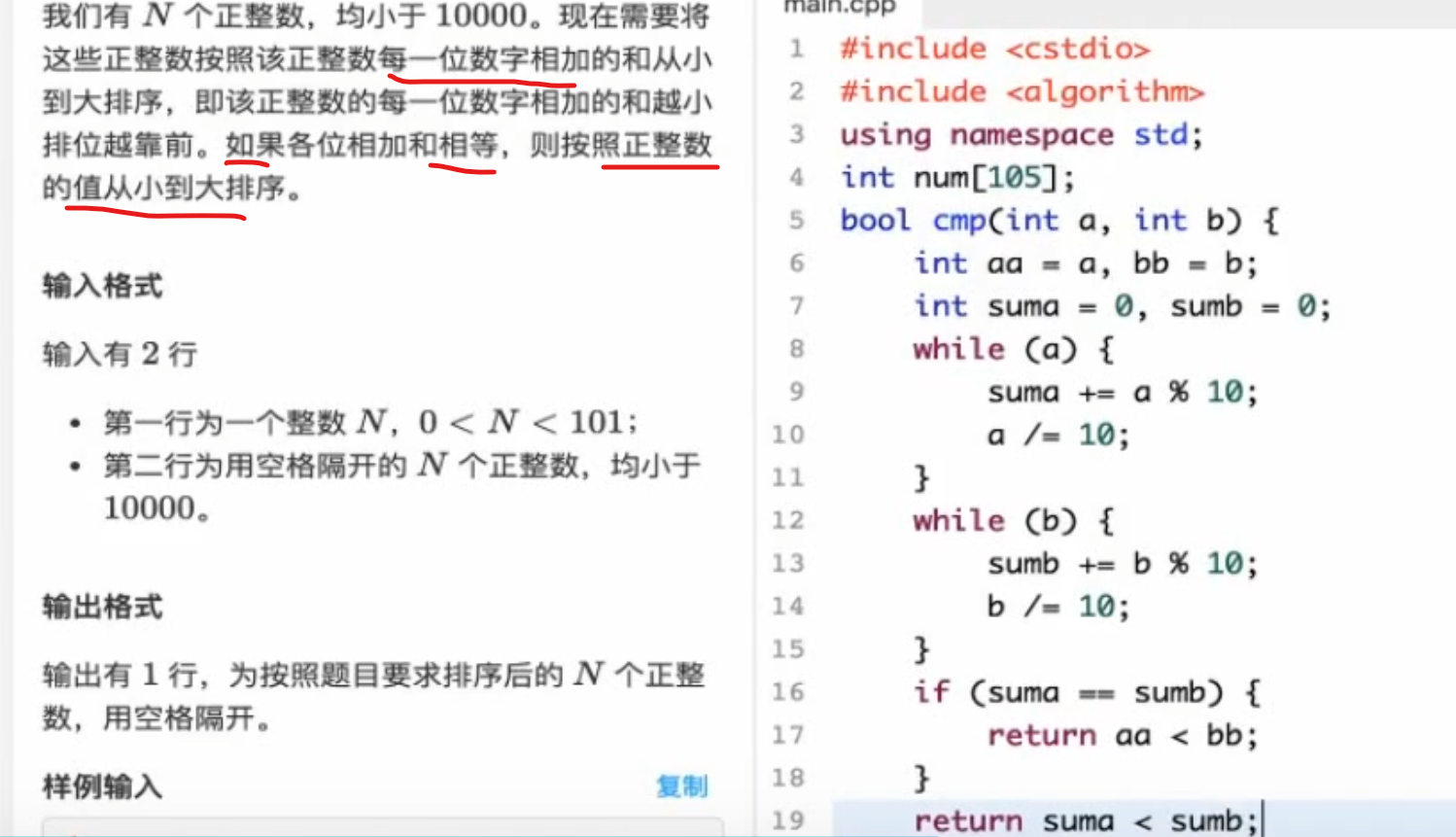
按数字每一位之和排序
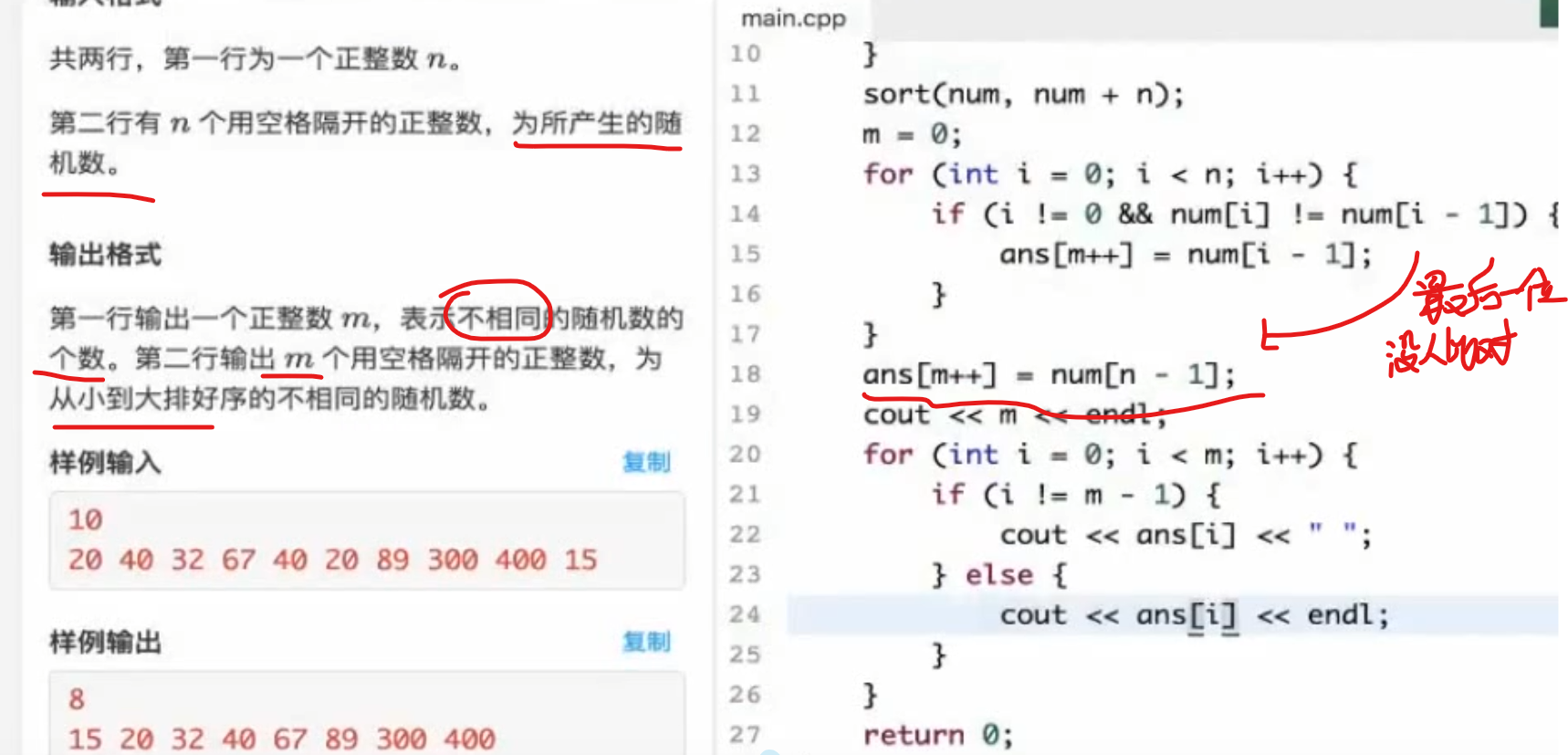
去重排序
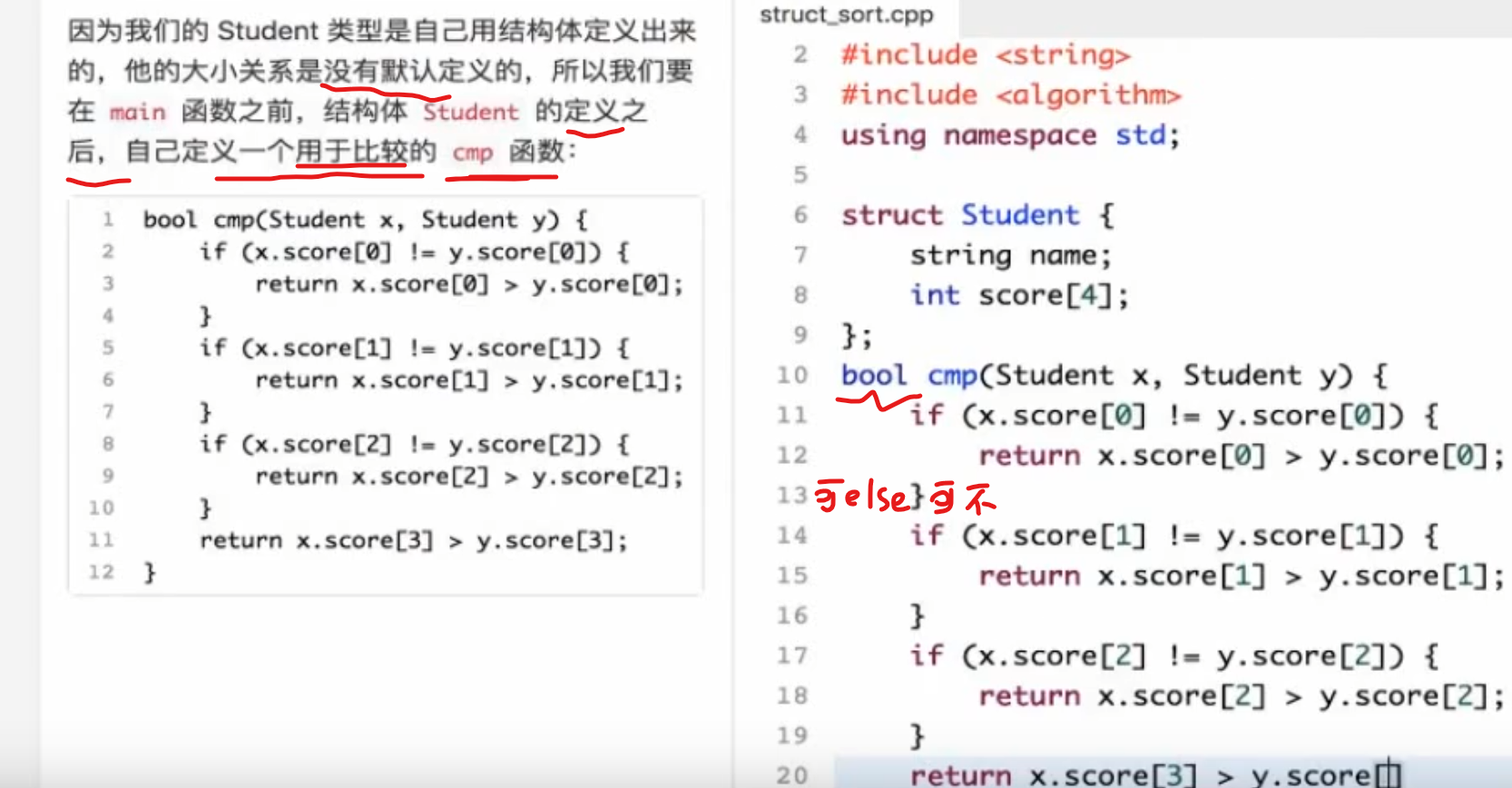
结构体排序
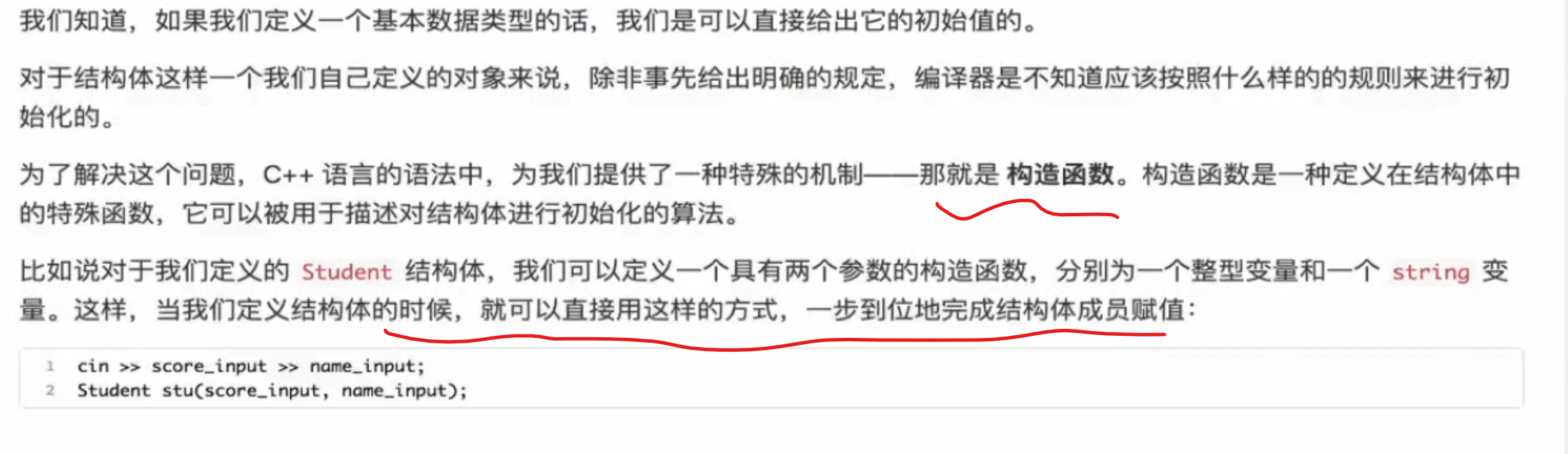
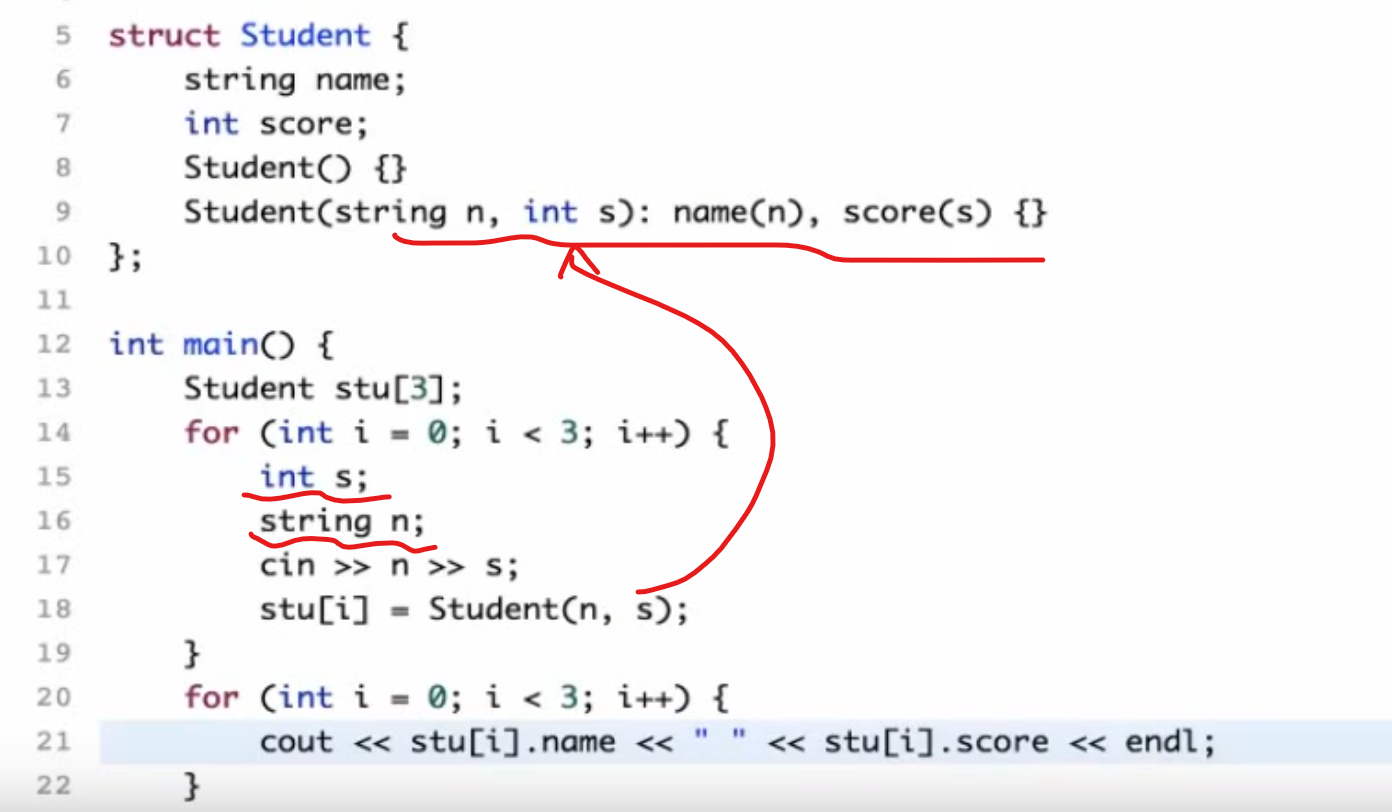
定义构造函数
构造器性质
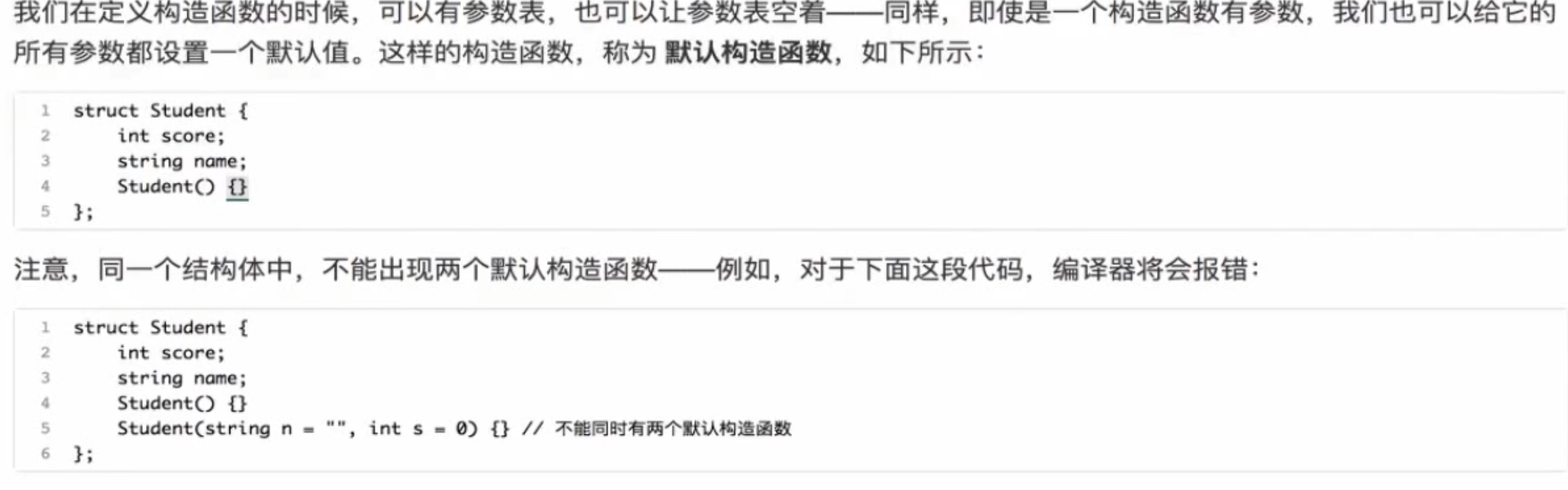
默认构造函数 这种方法通常冗杂,我们在竞赛不常用,而用初始化列表!
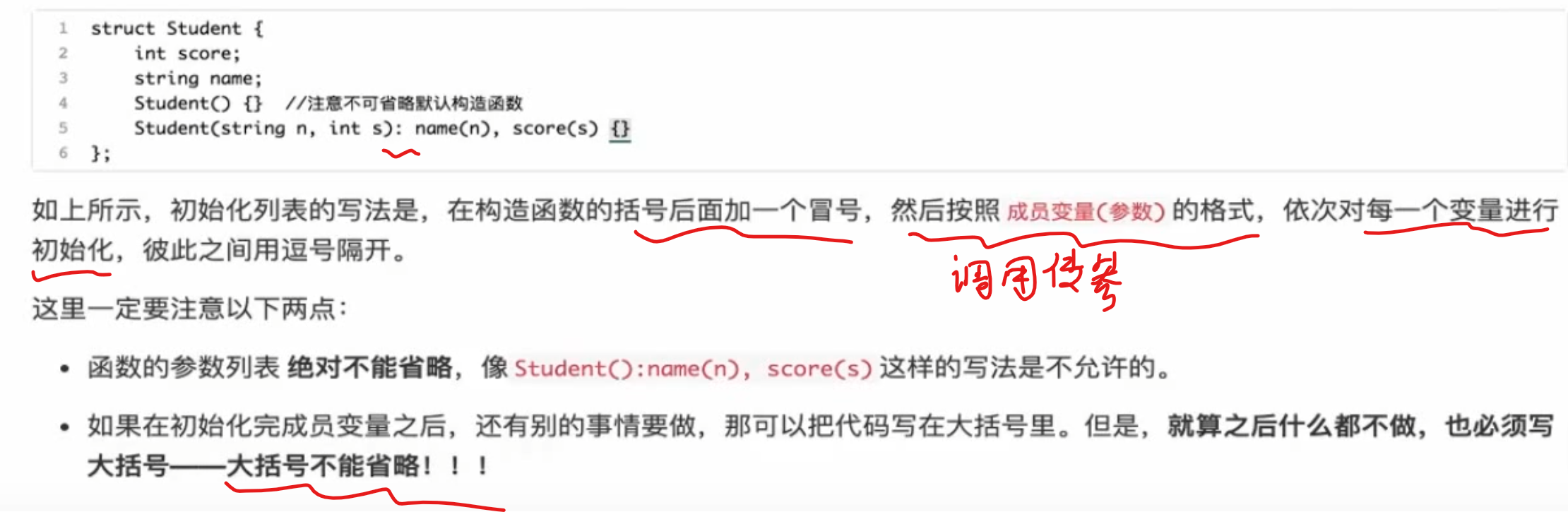
初始化列表
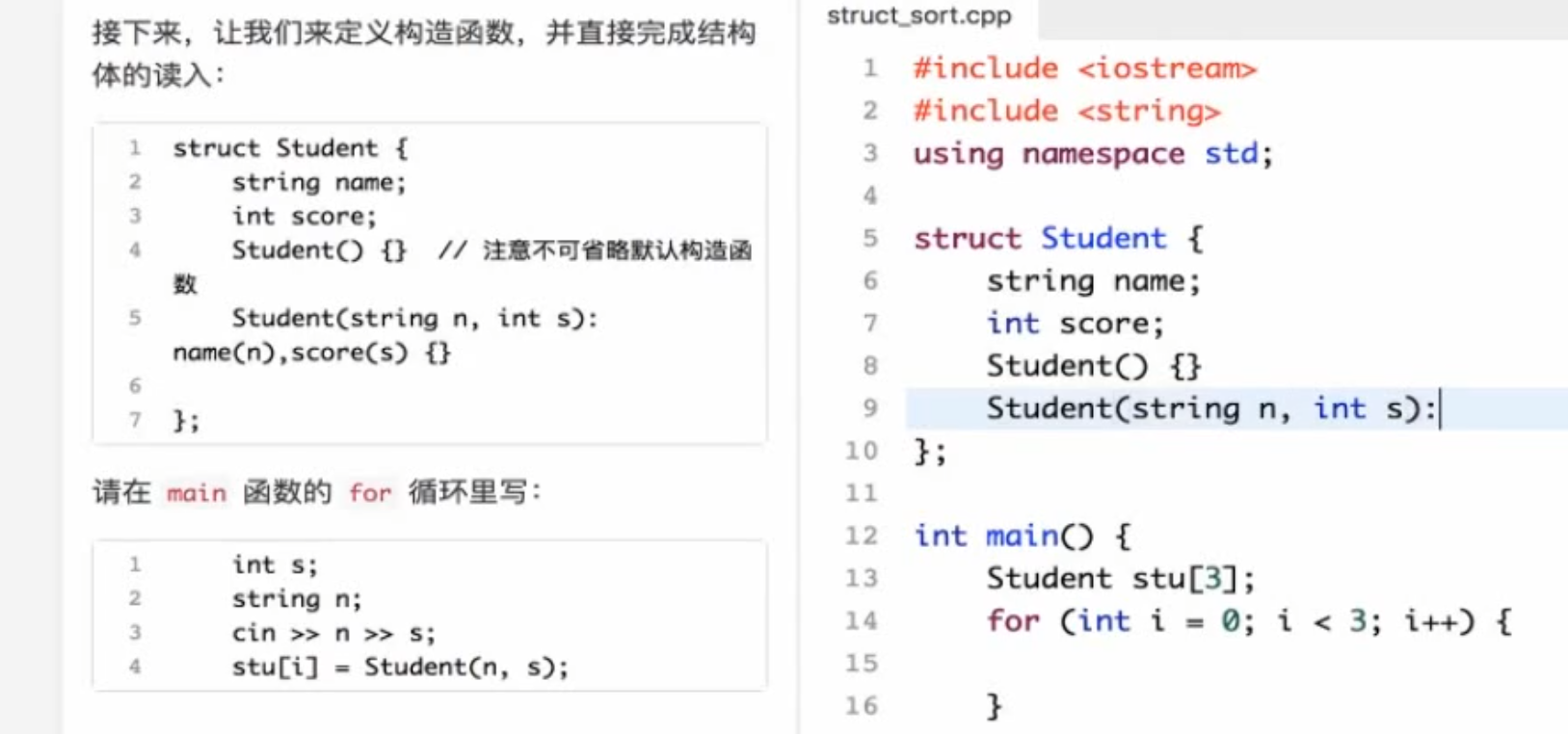
初始化实例
练习结构体排序 成绩排成绩
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 输入 5 97 68 51 85 73 输出 1 4 5 2 3
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 #include <bits/stdc++.h> using namespace std;struct Student { int score; int id; }; bool cmp (Student a,Student b) return a.score > b.score; } Student stu[105 ]; int N;int main () scanf ("%d" , &N); for (int i = 0 ; i < N ; i++){ scanf ("%d" , &stu[i].score); stu[i].id = i+1 ; } sort (stu, stu + N, cmp); for (int i = 0 ; i < N ; i++){ if (i != N - 1 ) printf ("%d " , stu[i].id); else { printf ("%d\n" , stu[i].id); } } return 0 ; }
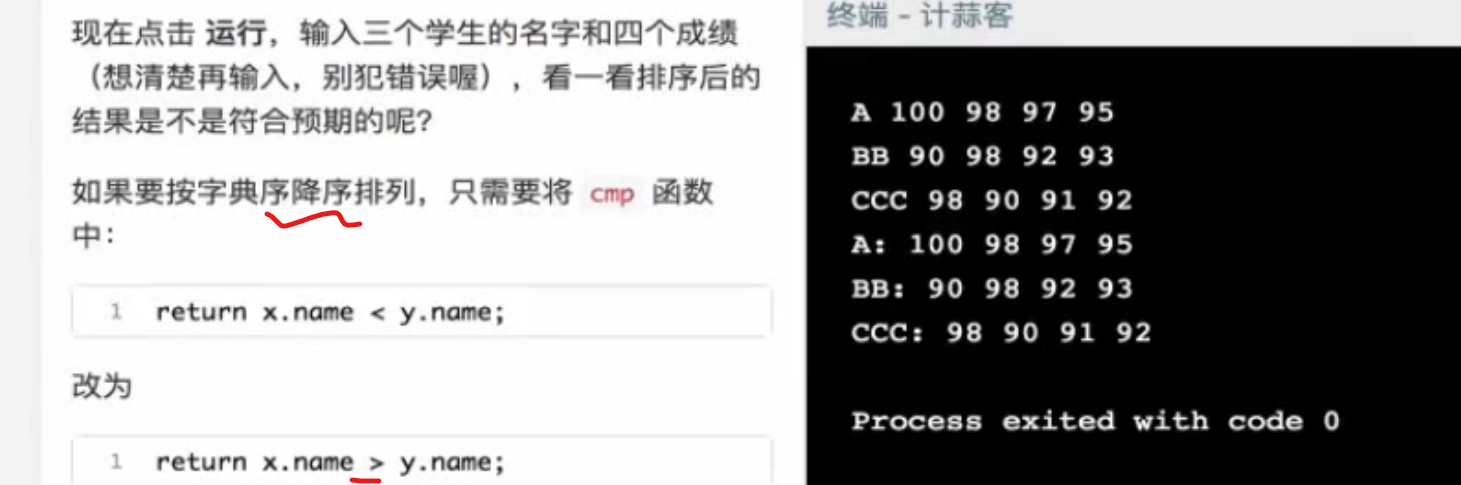
姓名排成绩
顺序成绩排成绩
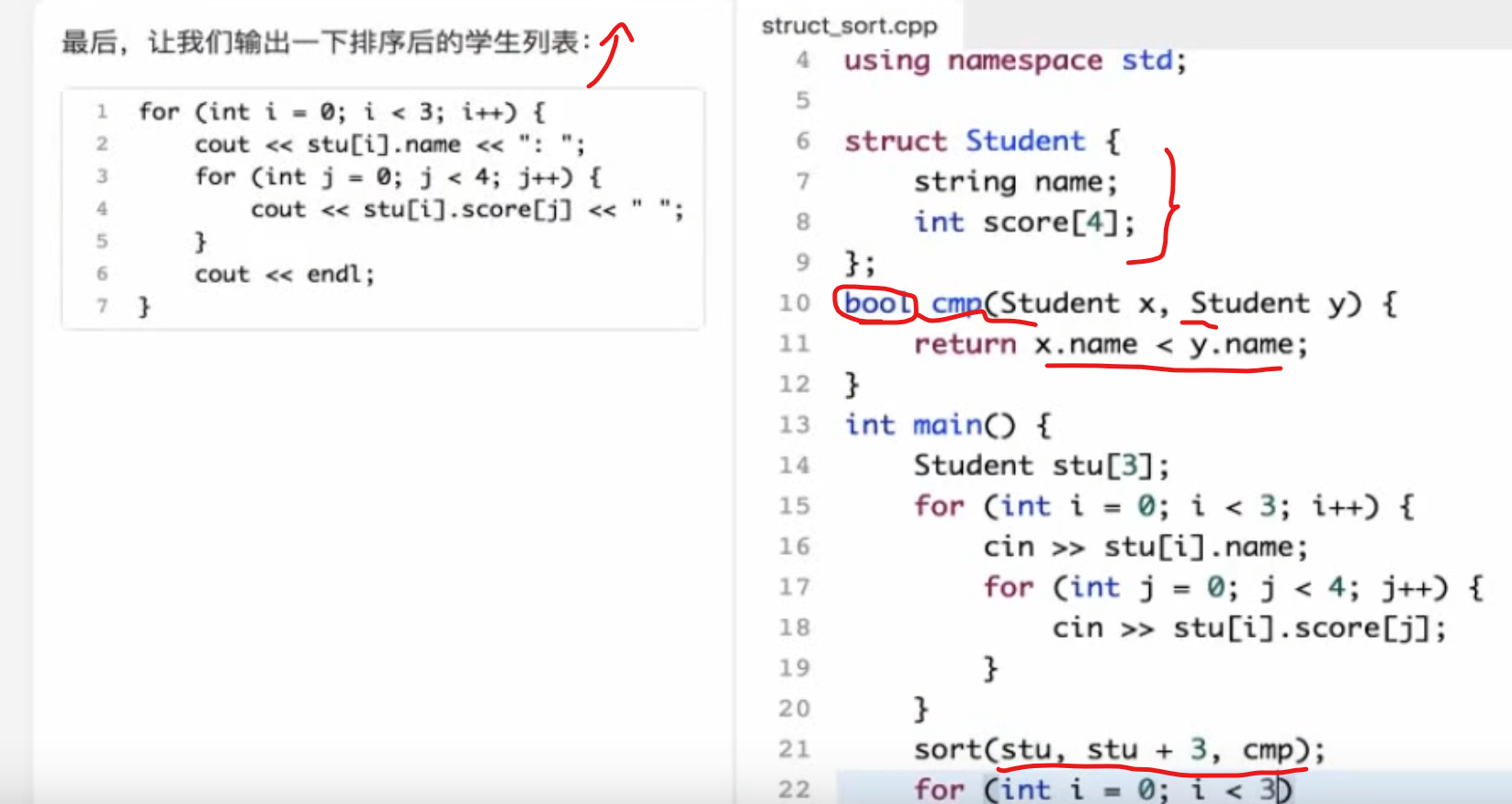
总分前三名 如果放在四个数组里,那么四个数组不能动态跟着动,但是放在结构体里就可以做到
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 样例 4 jing 98 90 87 74 ming 96 92 85 97 jun 95 78 56 91 hong 95 100 85 78 输出 ming hong jing
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 #include <bits/stdc++.h> using namespace std;struct Student { char name[15 ]; int score[4 ]; }; bool cmp (Student x, Student y) int sumx = x.score[0 ] + x.score[1 ] + x.score[2 ] + x.score[3 ]; int sumy = y.score[0 ] + y.score[1 ] + y.score[2 ] + y.score[3 ]; return sumx > sumy; } Student stu[50 ]; int main () int N; scanf ("%d" , &N); for (int i = 0 ; i<N;i++){ scanf ("%s" , stu[i].name); for (int j = 0 ; j < 4 ; j++){ scanf ("%d" , &stu[i].score[j]); } } sort (stu, stu + N, cmp); for (int i = 0 ; i < 3 ; i++){ printf ("%s\n" , stu[i].name); } }
摘气球
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 输入 10 10 1 2 3 4 5 6 7 8 9 10 3 1 4 6 7 8 9 9 4 12 输出 1 0 1 2 0 1 1 1 2 0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 #include <bits/stdc++.h> using namespace std; struct Children { int a; int id; }; bool cmp (Children a, Children b) return a.a < b.a; } Children child[100005 ]; int h[100005 ];int ans[100005 ];int main () int n, m, p; scanf ("%d%d" , &n, &m); for (int i = 0 ; i < n; i++){ scanf ("%d" , &child[i].a); child[i].id = i; } for (int i = 0 ; i < m; i++){ scanf ("%d" , &h[i]); } sort (child, child + n, cmp); sort (h, h+m); p = 0 ; for (int i = 0 ; i < n; i++){ while (p < m && h[p] <= child[i].a){ ans[child[i].id]++; p++; } } for (int i = 0 ; i < n; i++){ printf ("%d\n" , ans[i]); } return 0 ; }
数学 斐波那契数列取模
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 #include <bits/stdc++.h> using namespace std;int f[100005 ];const int mod = 1e9 + 7 ;int main () int n; cin >> n; f[1 ] = 1 ; f[2 ] = 1 ; for (int i = 3 ; i <= n; i++){ f[i] = f[i - 1 ] % mod + f[i - 2 ] % mod; } cout << f[n] << endl; return 0 ; }
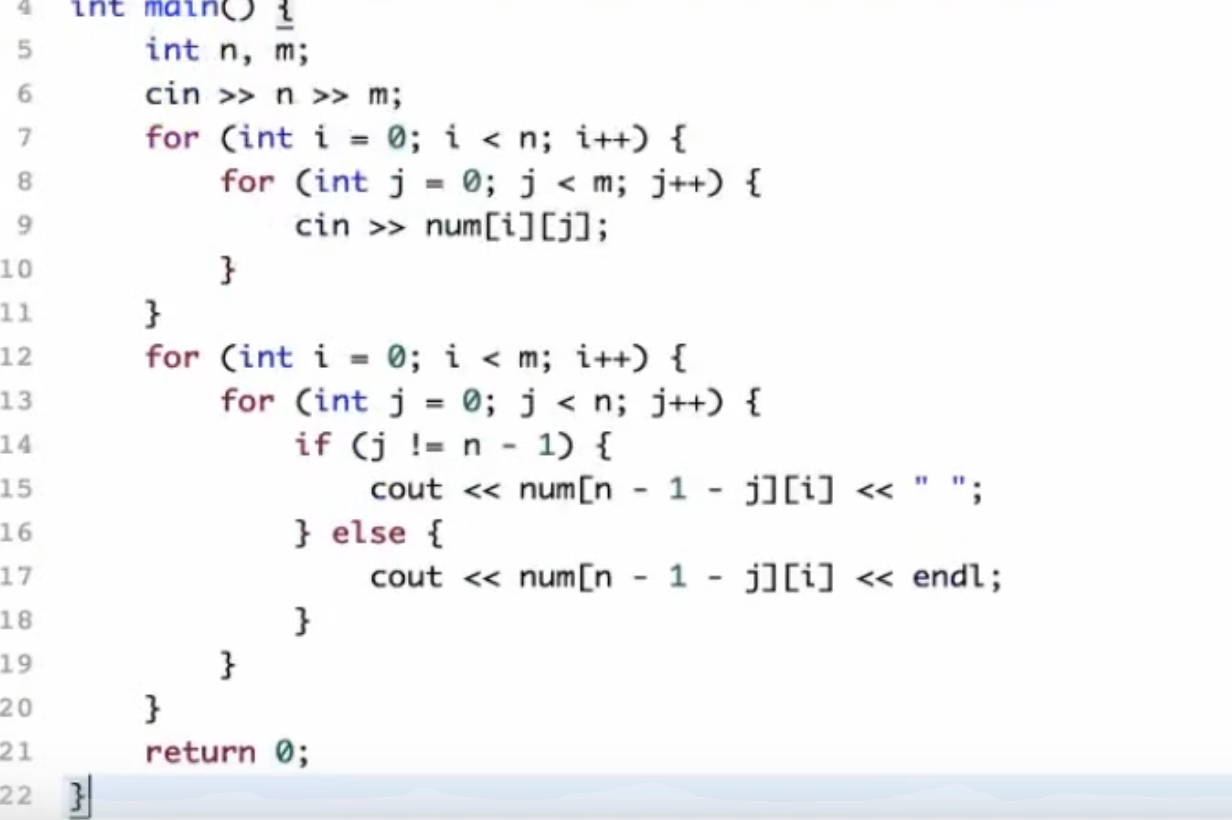
旋转矩阵
两个思路 1.按照我想的,确实可以先开辟一个数组,读入,然后再开一个输出,存转置以后的
2.不过还有一个思路,既然只叫直接输出,那我们可以直接打印出来,不用单独开空间了
最大子矩阵 1 2 3 4 5 6 7 8 9 问题描述 给定一个n*m的矩阵A,求A中的一个非空子矩阵,使这个子矩阵中的元素和最大。 其中,A的子矩阵指在A中行和列均连续的一块。 输入格式 输入的第一行包含两个整数n, m,分别表示矩阵A的行数和列数。 接下来n行,每行m个整数,表示矩阵A。 输出格式 输出一行,包含一个整数,表示A中最大的子矩阵中的元素和
暴力穷举 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 #include <bits/stdc++.h> using namespace std;int dp[105 ][105 ]; int main () int n , m , ans = 0 , max = -999999 ; scanf ("%d%d" , &n, &m); for (int i=1 ;i<=n;i++) for (int j=1 ;j<=m;j++) scanf ("%d" ,&dp[i][j]); for (int x1 = 1 ;x1 <= n; x1++) for (int y1=1 ;y1<= m;y1++) for (int x2=x1;x2<=n;x2++) for (int y2=y1;y2<=m;y2++) { ans = 0 ; for (int ii = x1; ii <= x2; ii++){ for (int jj=y1;jj <= y2; jj++){ ans += dp[ii][jj]; } } if (max < ans) max = ans; } cout << max; }
一维前缀和优化 方法 就是在计算矩阵大小的步骤上进行优化,原本是两层forfor循环,去将矩阵上的每个点都加起来,而一维前缀和优化就是将矩阵拆分为一条一条,这每一条都经前缀和优化过,这样计算的时候,就可简化计算矩阵的每一行,时间复杂度就会降低。
核心代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 int n,ans,max=-999999 ; cin>>n; for (int i=1 ;i<=n;i++) for (int j=1 ;j<=n;j++) {cin>>martix[i][j];pr[i][j]=pr[i][j-1 ]+martix[i][j];} for (int x1=1 ;x1<=n;x1++) for (int y1=1 ;y1<=n;y1++) for (int x2=x1;x2<=n;x2++) for (int y2=y1;y2<=n;y2++) { ans=0 ; for (int k=y1;k<=y2;k++) ans+=pr[k][x2]-pr[k][x1-1 ]; if (max<ans) max=ans; } cout<<max;
二维前缀和优化 都有了一维前缀和,为什么不用二维得呢。
延续一维前缀和的思路,二维前缀和就是将整个矩阵的计算过程都约化成表达式
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 int n,max=-9999999 ;scanf ("%d" ,&n);for (int i=1 ;i<=n;i++)for (int j=1 ;j<=n;j++){ scanf ("%d" ,&martix[i][j]); pr[i][j]=pr[i-1 ][j]+pr[i][j-1 ]-pr[i-1 ][j-1 ]+martix[i][j]; } for (int x1=1 ;x1<=n;x1++) for (int y1=1 ;y1<=n;y1++) for (int x2=x1;x2<=n;x2++) for (int y2=y1;y2<=n;y2++) { int ans=pr[x2][y2]-pr[x1-1 ][y2]-pr[x2][y1-1 ]+pr[x1-1 ][y1-1 ]; if (ans>max) max=ans; } printf ("%d" ,max);
动态规划 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 int i,j,n,ans,max=-9999999 ;scanf ("%d" ,&n);for (i=1 ;j<=n;i++) for (j=1 ;j<=n;j++) { scanf ("%d" ,&a[i][j]); a[i][j]+=a[i][j-1 ]; } for (i=0 ;i<=n-1 ;++i) for (j=i+1 ;j<=n;j++) { ans=0 ; for (int k=1 ;k<=n;k++) { ans+=a[k][j]-a[k][i]; if (ans > max) max = ans; if (ans < 0 ) ans = 0 ; } } cout << max << endl;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 4 4 0 -2 -7 0 9 2 -6 2 -4 1 -4 1 -1 8 0 -2 输出 15 样例输入 3 3 -1 -4 3 3 4 -1 -5 -2 8 样例输出 10
进制转换
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 #include <bits/stdc++.h> using namespace std;char ans[105 ];int main () int N,R; cin >> N >> R; if (N < 0 ){ cout << "-" ; N = -N; } int m = 0 ; int now; while (N){ now = N % R; if (now <= 9 ){ ans[m++] = '0' + now; } else { ans[m++] = 'A' + now - 10 ; } N /= R; } for (int i = m-1 ; i >= 0 ; i-- ){ cout << ans[i]; } cout <<endl; return 0 ; }
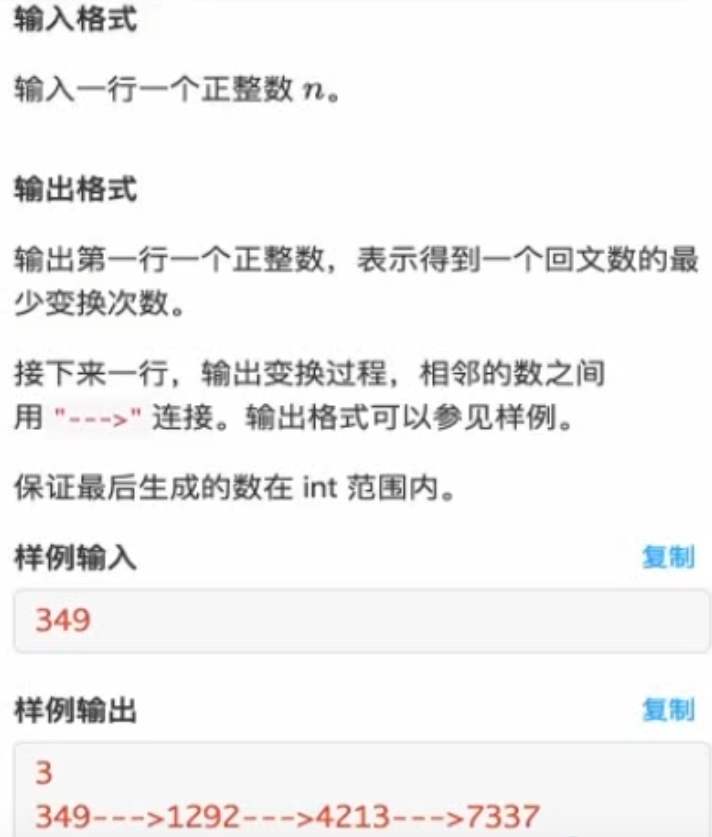
回文数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 #include <bits/stdc++.h> using namespace std; int num[1005 ];int digit[1005 ];bool judge (int x) int cnt = 0 ; while (x){ digit[cnt++] = x % 10 ; x = x / 10 ; } for (int i = 0 ; i < cnt / 2 ; i++){ if (digit[i] != digit[cnt - 1 -i]) return false ; else return true ; } } int rev (int x) int cnt = 0 ; while (x){ cnt = cnt * 10 + x % 10 ; x = x / 10 ; } return cnt; } int main () int n , m; cin >> n; m = 0 ; num[m++] = n; while (!judge (n)){ n += rev (n); num[m++] = n; } if (n == 0 ){ cout << 0 << endl; } cout << m-1 << endl; for (int i = 0 ; i < 1005 ; i++){ if (i != m-1 ) cout << num[i] << "--->" ; else { cout << num[i] << endl; break ; } } }
机器人转向
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 输入 10 back -9 left 3 left 8 back 15 right 10 right -7 right -3 left 11 right 17 left 3 输出 9 -7
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 #include <bits/stdc++.h> using namespace std;int dx[4 ] = {0 , -1 , 0 , 1 };int dy[4 ] = {1 , 0 , -1 , 0 };char op[15 ];int main () int n, d, x, nowx = 0 , nowy = 0 ; cin >> n; d = 3 ; for (int i = 0 ; i < n; i++){ cin >> op >> x; if (op[0 ] == 'b' ){ d = (d+2 ) % 4 ; }else if (op[0 ] == 'l' ){ d = (d+1 ) % 4 ; }else if (op[0 ] == 'r' ){ d = (d+3 ) % 4 ; } nowx += dx[d] * x; nowy += dy[d] * x; } cout << nowx << " " << nowy << endl; return 0 ; }
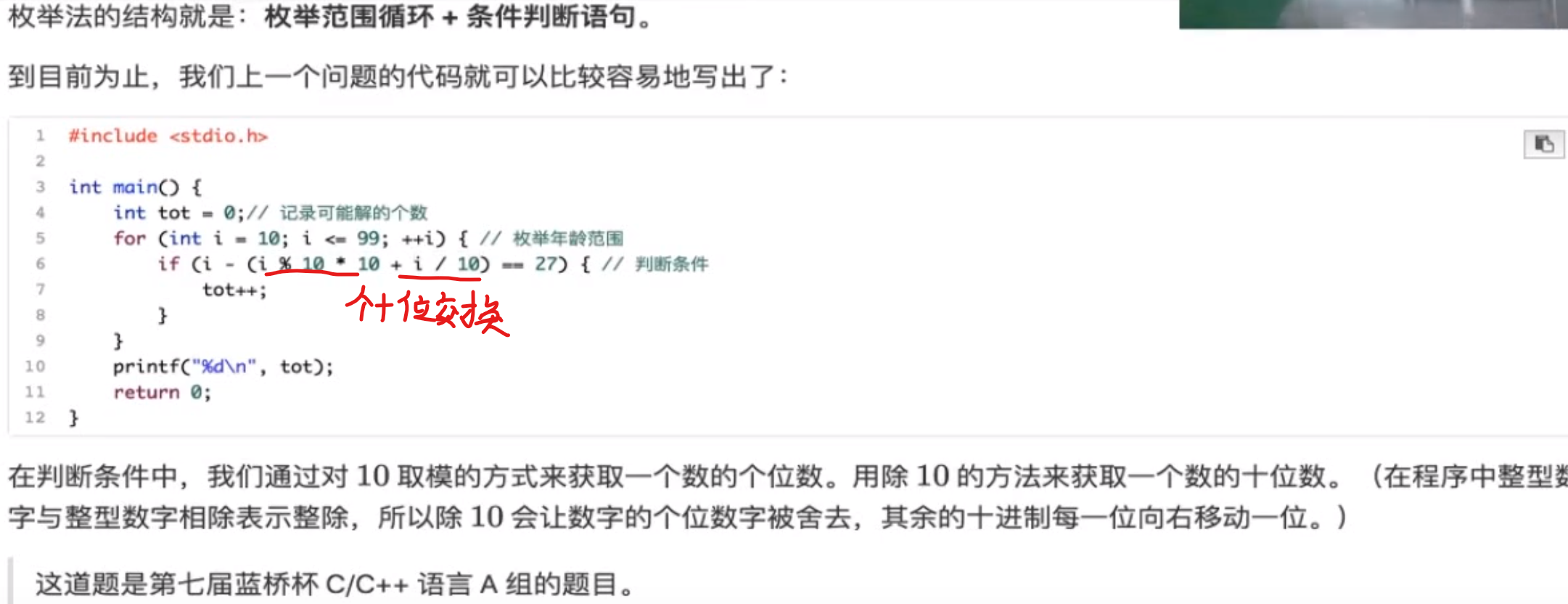
枚举 父子年龄猜测
经久不衰质数 质数是只有1和他本身两个因数的存在,我们可以得出,找到一个数是否为质数,我们把它拆成两个数的乘积,那么其中一定会有一个数<=根号j,所以他真的是个质数,而不是合数的话,一定能在根号j以内找到
为了写根号j for条件里我们可以写
1 2 3 4 i <= sqrt (j); i++) 也可以写 i * i <= j; i++ 也是一样的 这样我们判断一个质数,复杂度会从 O (n) 降到 O (根号n)
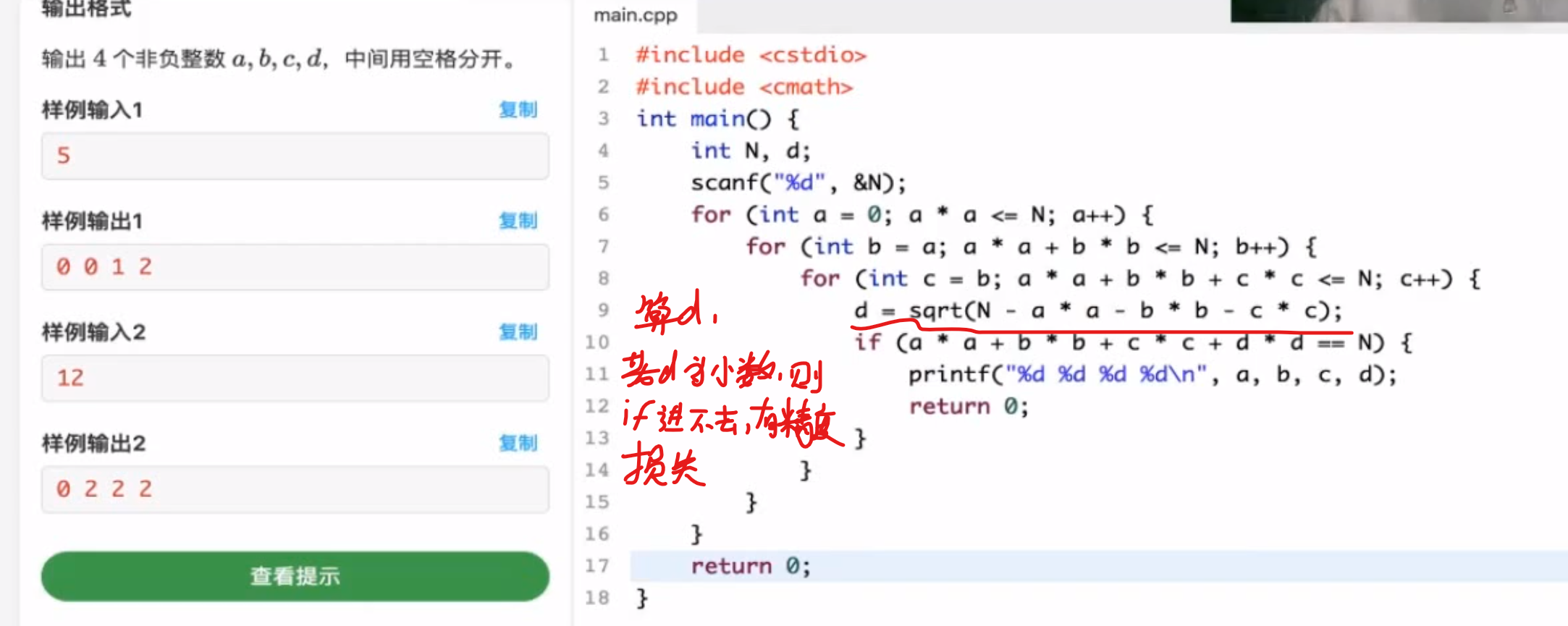
四平方和
STL
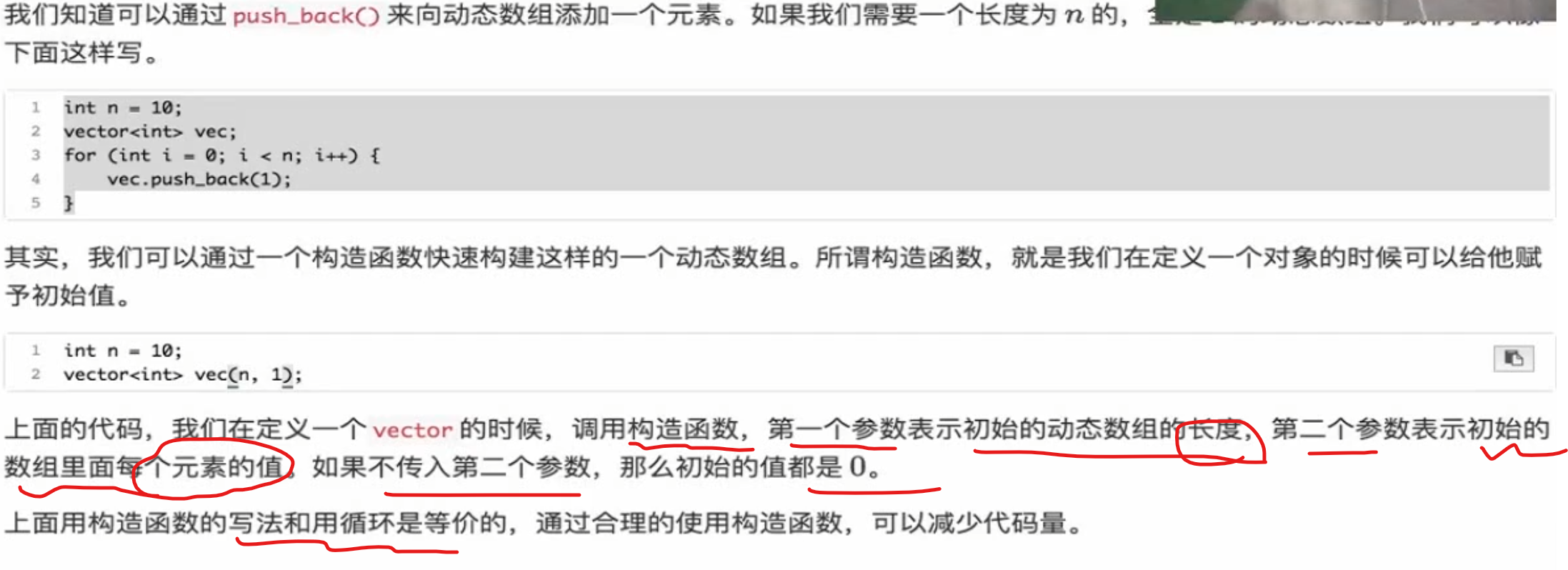
Vector 构造
推入
访问
修改
删除 对于删除而言,只是说在数组里清空了那个元素,但是空间中仍然存在被清空的尾部元素,只有重新push覆盖掉之前的,不然仍然可以调用之前的那个位置索引
清空 只是说size变成0,里面的数据没了,但是不会把内存释放
有一个办法就是,新构造出一个vector,把它和之前的vector交换一下
储存自定义数据
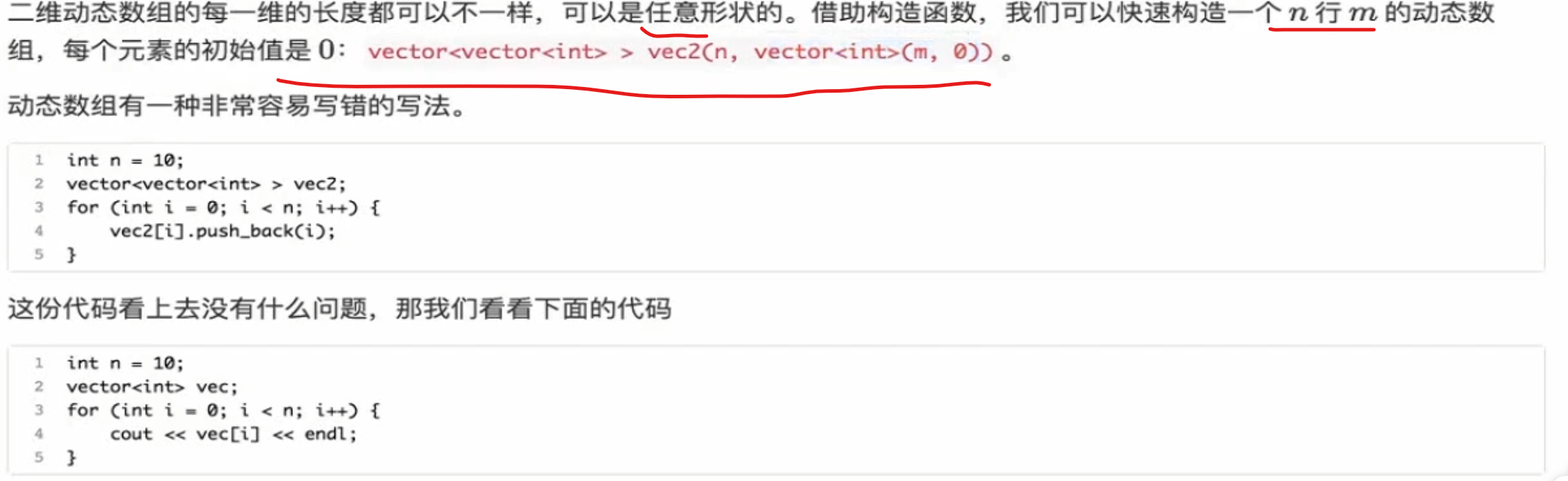
二维动态数组 下面的for嵌套,主要意思是先对每一个vec2的每一个维度的长度,做遍历,再遍历n的维度(可能不对)
我们要了一个能装vector的vector ,里面可以装下n个vector,每一个vector都是由m个0组成
打印乘法表
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 #include <bits/stdc++.h> using namespace std;vector<vector<int > > v2d; int main () int n = 10 ; for (int i = 0 ; i < 5 ; i++){ v2d.push_back (vector<int >()); } for (int i = 0 ; i < v2d.size (); i++){ for (int j = 0 ; j <= i; j++){ v2d[i].push_back ((i + 1 ) * (j + 1 )); } } for (int i = 0 ; i < v2d.size (); i++){ for (int j = 0 ; j < v2d[i].size (); j++){ cout << i + 1 << " * " << j + 1 << " = " << v2d[i][j] << "\t" ; } cout << endl; } return 0 ; }
存动态数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 输入 3 12 1 3 2 2 2 3 2 4 3 1 3 6 1 5 1 2 1 6 3 2 3 7 1 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 #include <bits/stdc++.h> using namespace std;vector<int > mat[10005 ]; int main () int n, m; int digit=0 ; int hang = 0 ; cin >> n >> m; for (int i = 1 ; i <= m; i++){ cin >> hang >> digit; mat[hang].push_back (digit); } for (int i = 1 ; i <= n; i++){ for (int j = 0 ; j < mat[i].size (); j++) if (j < mat[i].size ()-1 ) cout << mat[i][j] << " " ; else cout << mat[i][j]; } cout << endl; return 0 ; }
Set
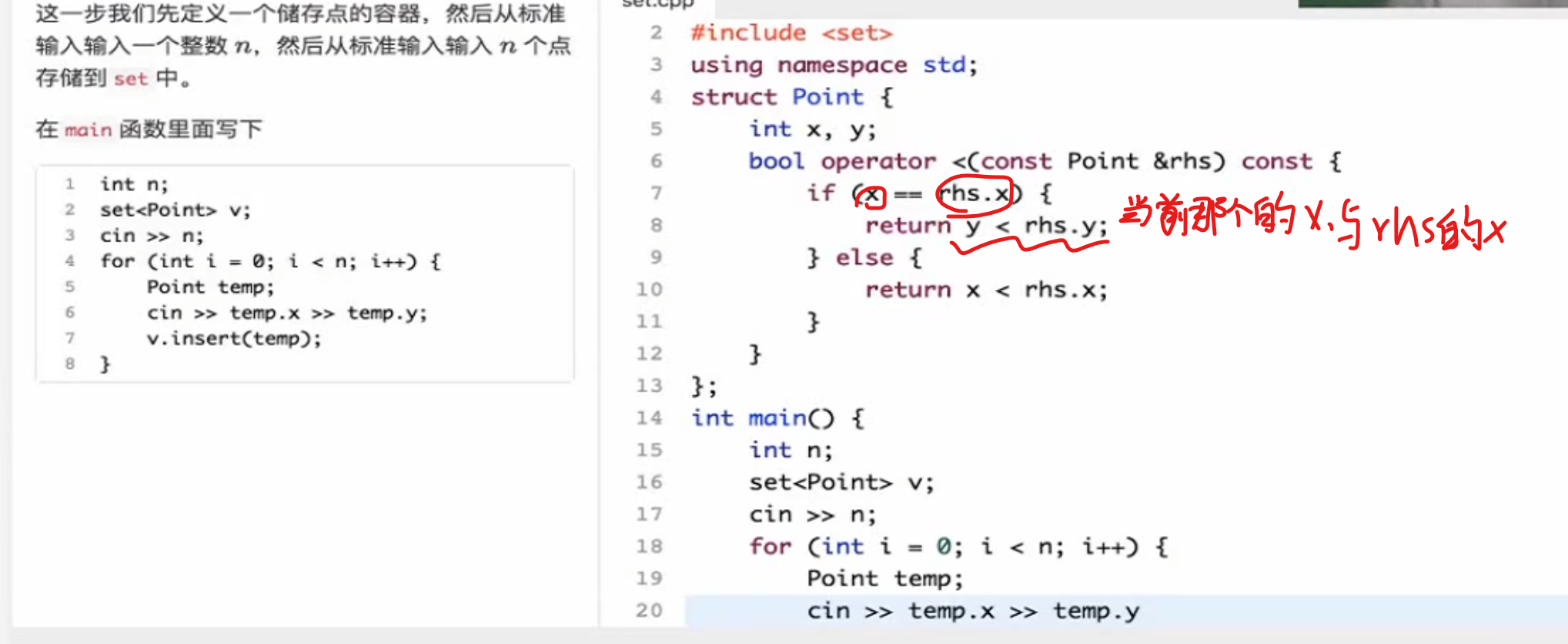
结构体用Set必须重载小于号 !即便不适用小于号的功能,随便写一个重载就好了
1 2 3 bool operator <(const people &rhs) const {return h < rhs.h;}
构造
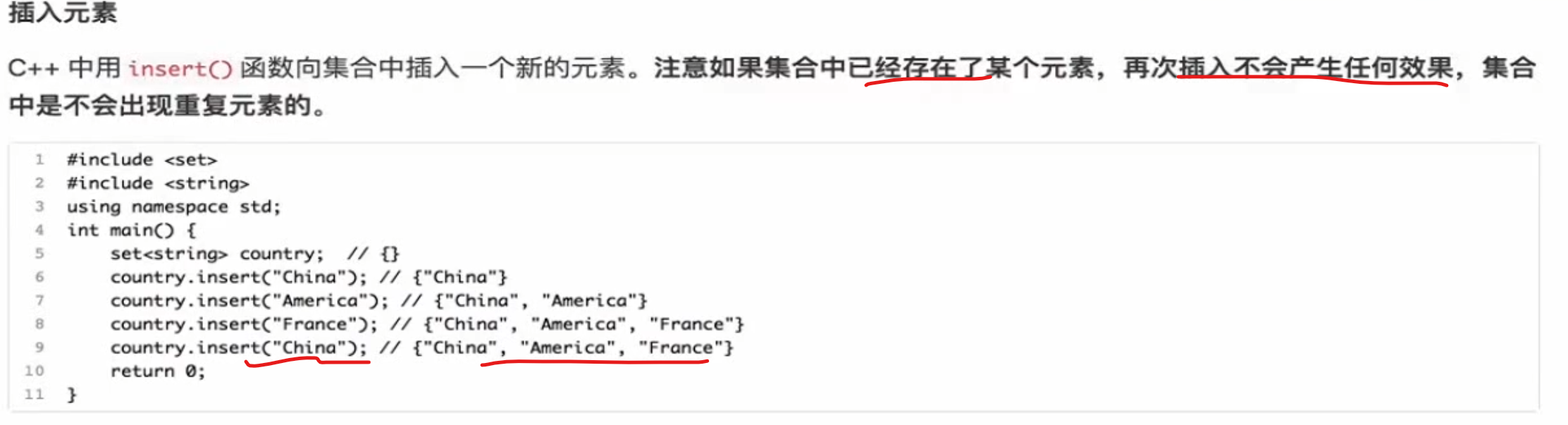
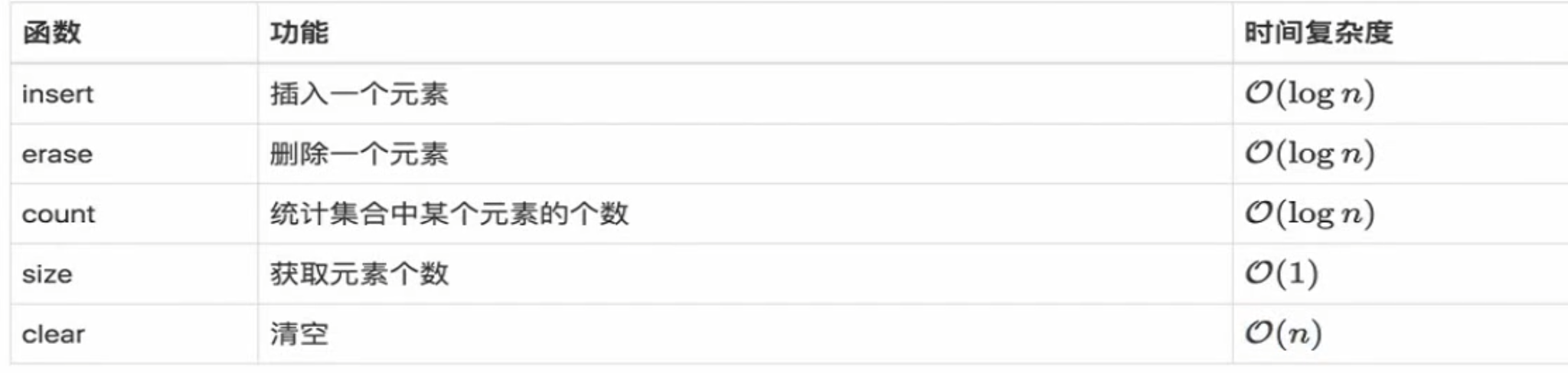
插入 集合是不出现重复 元素的
删除
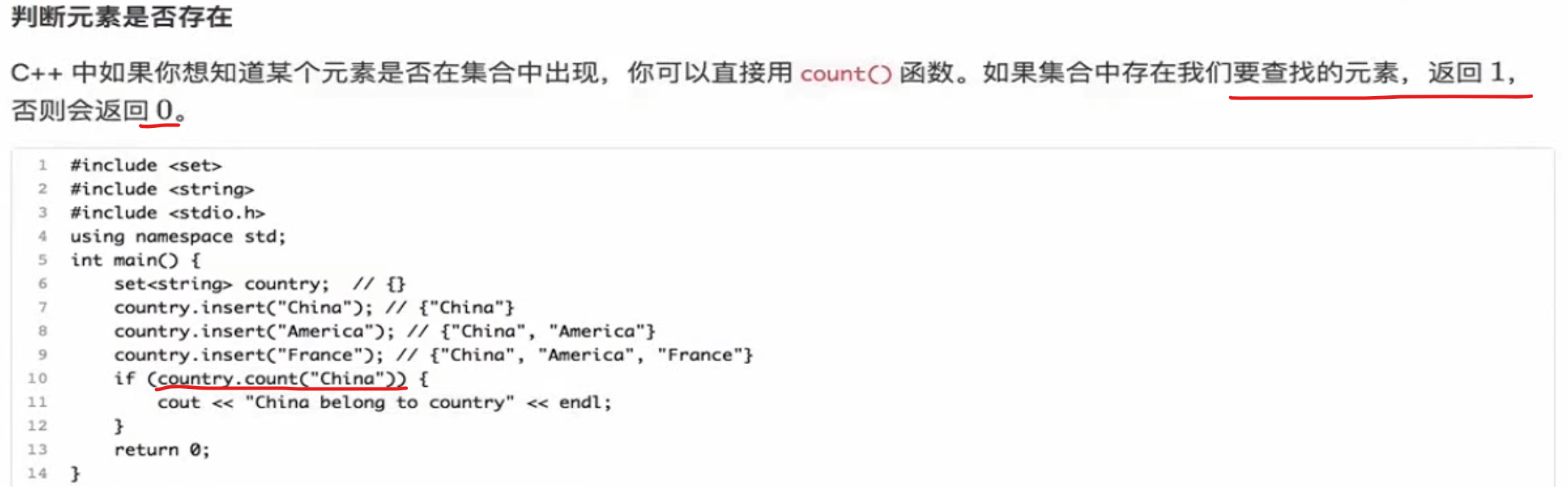
判断元素存在
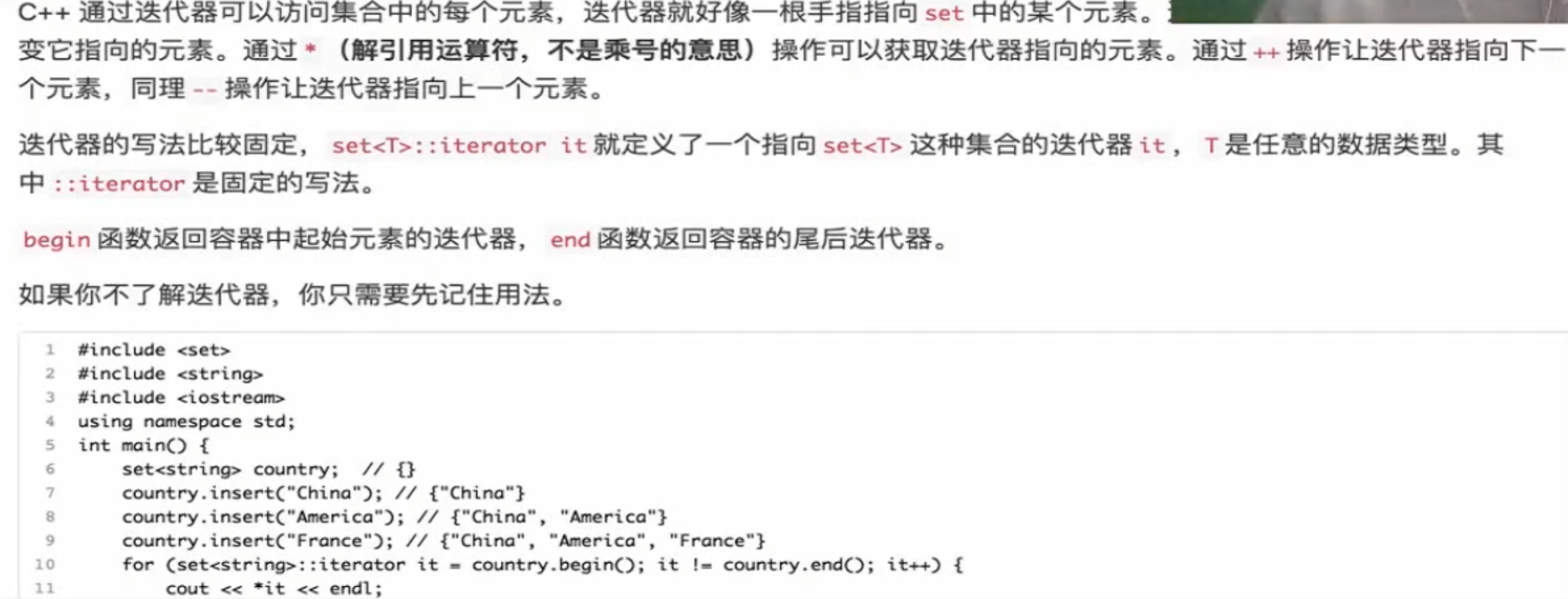
迭代器 end是空位,要取到带元素的需是end–后即可
要用set需要重载小于号=-=,会自动排序
总结
set使用实例 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 #include <bits/stdc++.h> using namespace std;int main () set<string> country; country.insert ("China" ); country.insert ("American" ); country.insert ("France" ); set<string>::iterator it; for (it = country.begin (); it != country.end (); it++){ cout << *it << " " ; } cout << endl; country.erase ("American" ); country.erase ("England" ); if (country.count ("China" )){ cout << "China ing." << endl; } country.clear (); return 0 ; }
重载小于号
合并集
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 #include <bits/stdc++.h> using namespace std;set<int > s; int k;int main () int n, m; int cnt = 0 ; scanf ("%d%d" , &n, &m); for (int i = 0 ; i < n + m ; i++){ scanf ("%d" , &k); s.insert (k); } for (set<int > :: iterator it = s.begin (); it != s.end (); it++){ if (cnt != s.size () - 1 ){ printf ("%d " , *it); cnt ++; }else { printf ("%d\n" , *it); } } return 0 ; }
Map 关键字集合不能有两个相同的,值可以
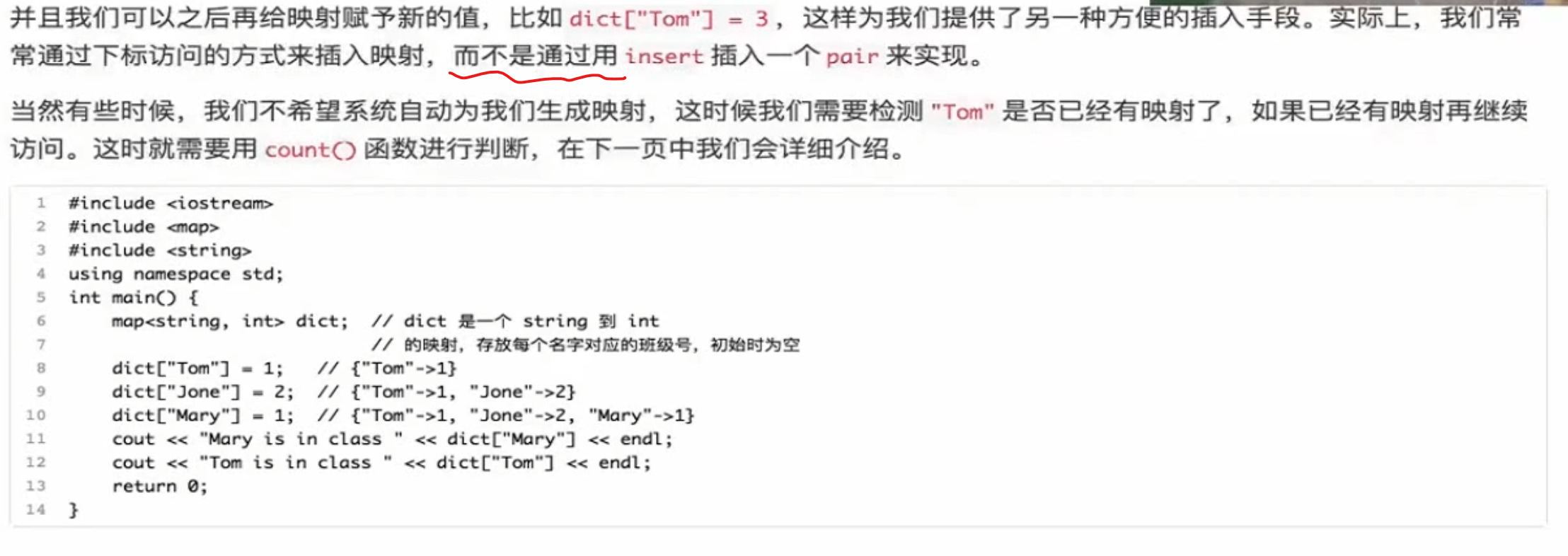
构造映射 如果原先没有这个映射,它会自动帮你创造,类似于一个动态数组哦
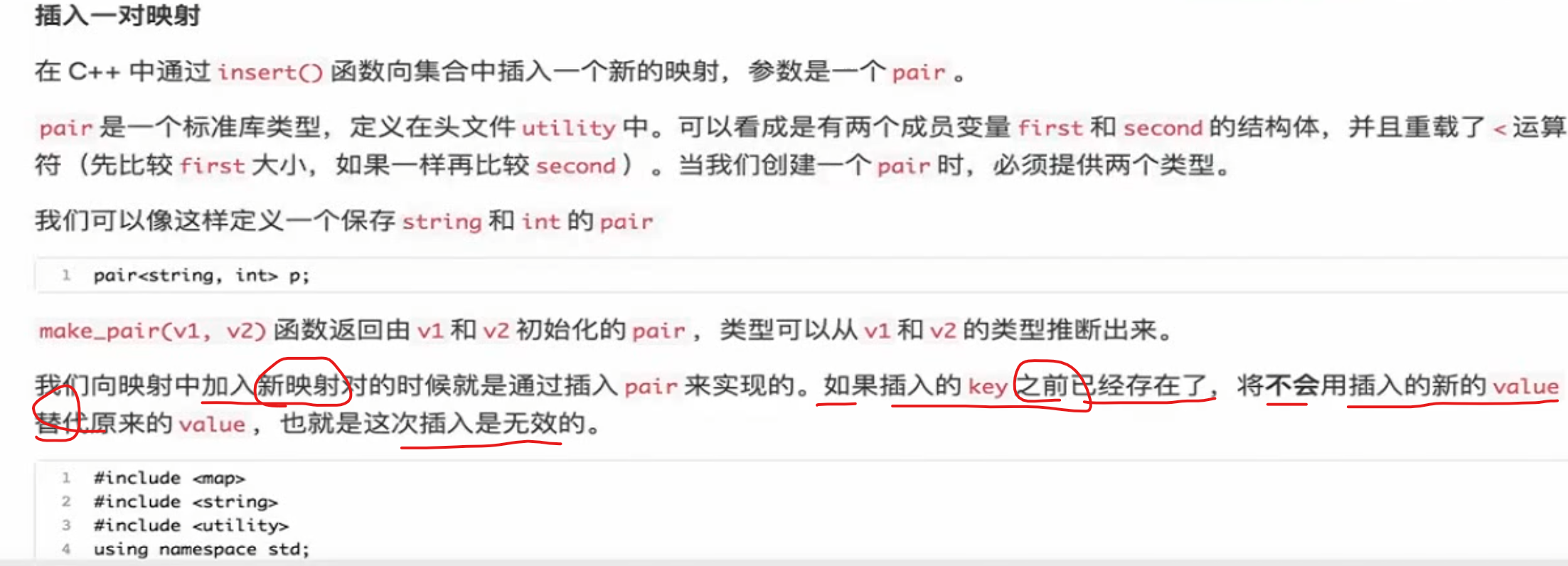
插入一对映射
数组赋值最大的好处就是在于可以篡改 key中的value ;
1 2 3 4 5 6 7 8 9 10 11 12 #include <bits/stdc++.h> using namespace std;int main () map<string, int > dict; dict["Tom" ] = 1 ; dict["Jone" ] = 2 ; dict["Mary" ] = 1 ; cout << dict["Mary" ] << endl; dict["Mary" ] = 2 ; cout << dict["Mary" ] << endl; }
引入pair函数 Pairs
pair可以将两个值视为一个单元。容器类别map 和multimap 就是使用pairs来管理其健值/实值(key/value)的成对元素。
两个pairs互相比较时, 第一个元素正具有较高的优先级.
make_pair():
无需写出型别, 就可以生成一个pair对象
当有必要对一个接受pair参数的函数传递两个值时, make_pair()尤其显得方便, //不需要写泛型,直接在括号里填入数值即可
void foo{
判断存在
总结
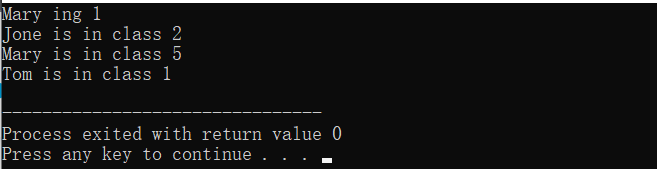
map使用实例 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 #include <bits/stdc++.h> using namespace std;int main () map<string, int > dict; dict["Tom" ] = 1 ; dict["Jone" ] = 2 ; dict["Mary" ] = 1 ; if (dict.count ("Mary" )){ cout << "Mary ing " << dict["Mary" ]; dict["Mary" ] = 5 ; } cout << endl; for (map<string, int > :: iterator it = dict.begin (); it != dict.end () ; it++){ cout << it -> first << " is in class " << it -> second << endl; } dict.clear (); return 0 ; }
二维map map + set
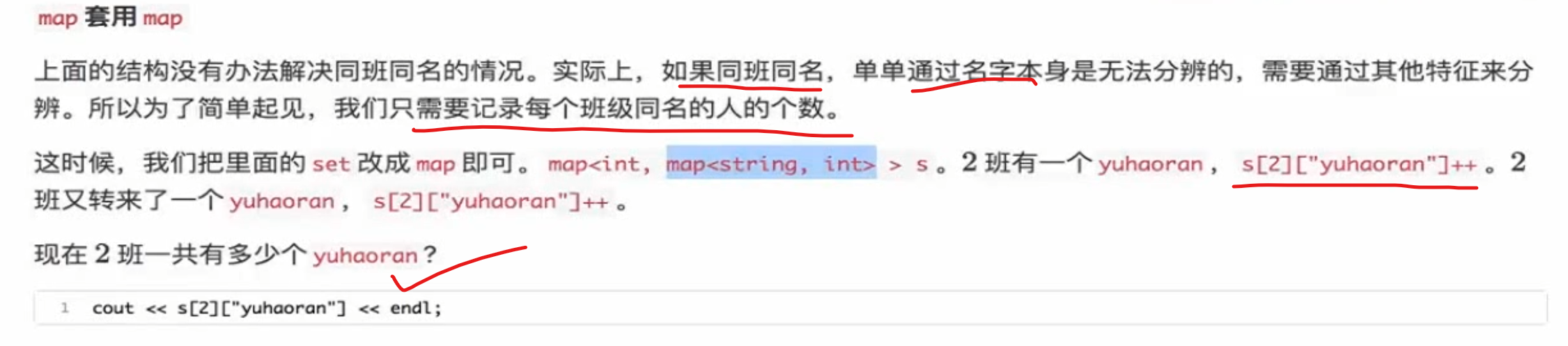
map + map
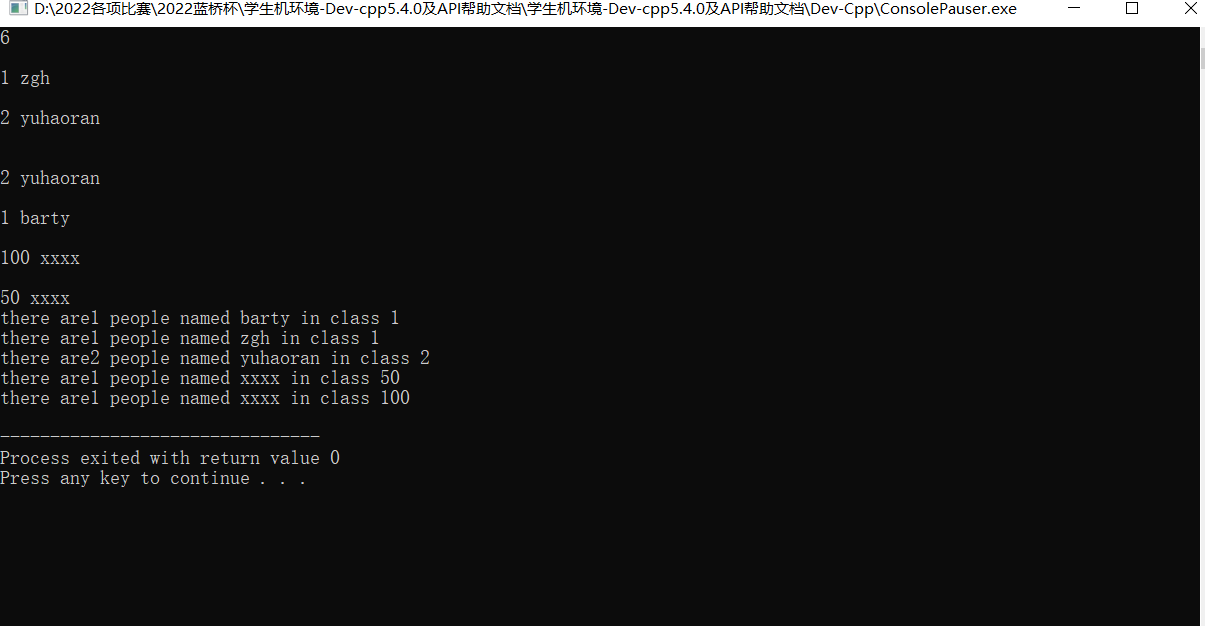
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 #include <bits/stdc++.h> using namespace std;int main () map<int , map<string, int > > info; int n ; cin >> n; for (int i = 0 ; i < n; i++){ int class_id; string name; cin >> class_id >> name; info[class_id][name]++; } for (map<int , map<string, int > > ::iterator it1 = info.begin (); it1 != info.end (); it1++){ for (map<string, int > :: iterator it2 = it1-> second.begin (); it2 != it1 -> second.end (); it2++){ cout << "there are " << it2 -> second << " people named " << it2 -> first <<" in class " << it1 -> first << endl; } } return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 输入 6 1 zgh 2 yuhaoran 2 yuhaoran 1 barty 100 xxxx 50 xxxx 输出
map寻重复最多
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 #include <bits/stdc++.h> using namespace std;map<int , int > mp; int main () int n, x; scanf ("%d" , &n); for (int i = 0 ; i < n; i++){ scanf ("%d" , &x); mp[x]++; } int ans1 = -1000 ; int ans2 = 0 ; for (map<int , int >::iterator it = mp.begin (); it != mp.end (); it++){ if (it -> second >= ans2){ ans2 = it -> second; ans1 = it -> first; } } printf ("%d %d\n" , ans1, ans2); }
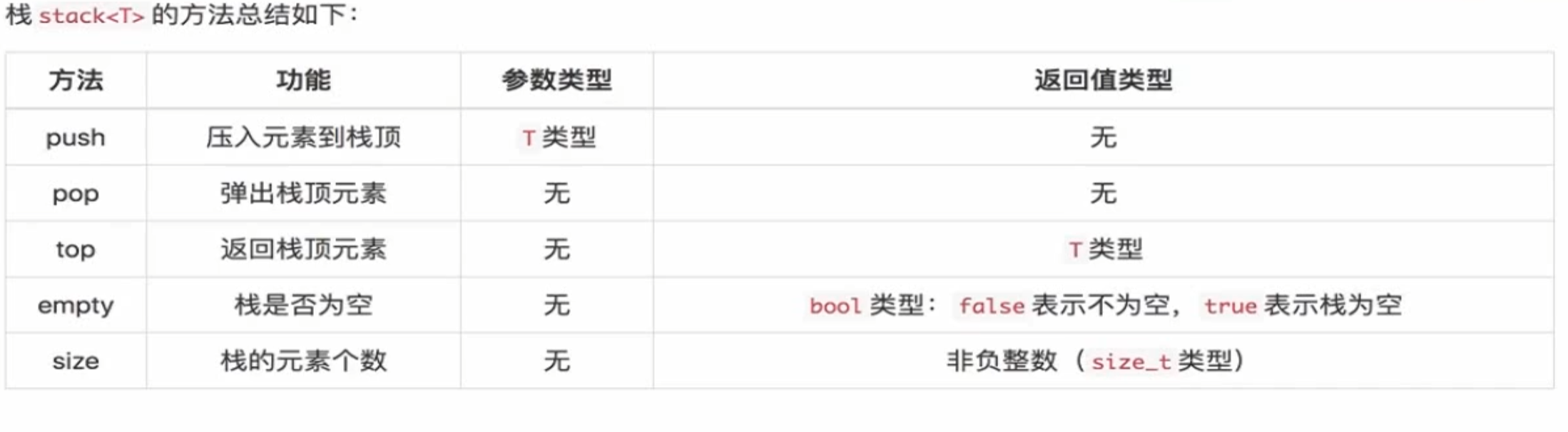
栈
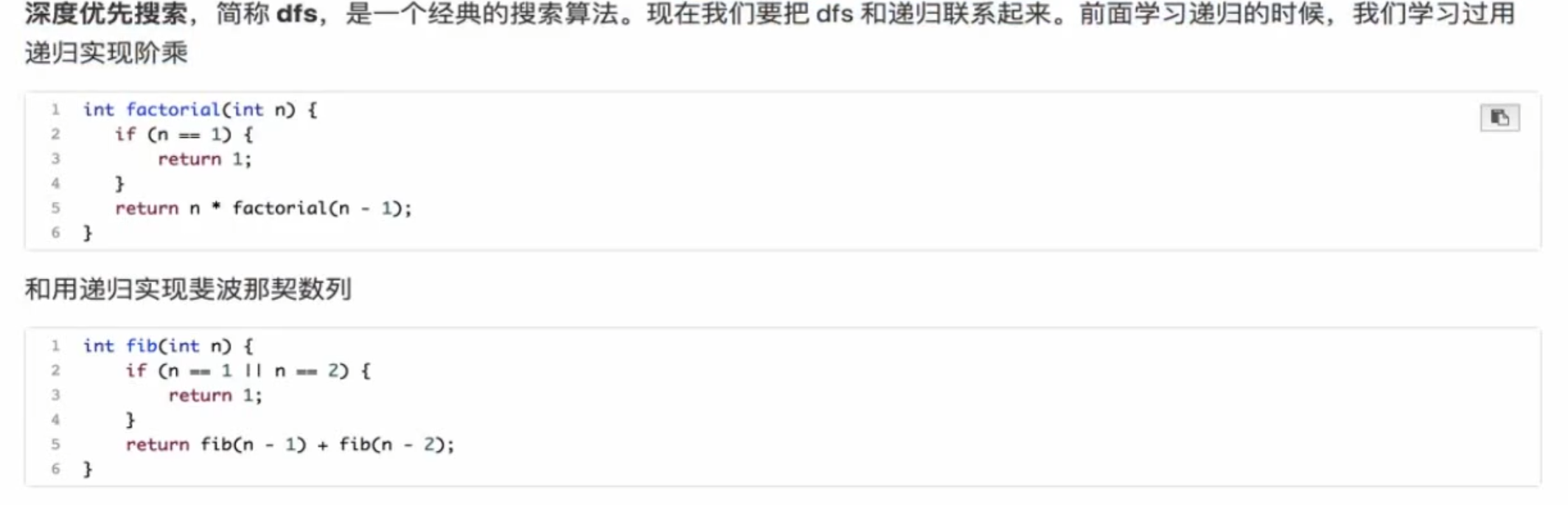
递归 递归函数实例
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 #include <bits/stdc++.h> using namespace std;long long f (int x) if (x <= 0 ){ return 0 ; } if ( x == 1 ){ return 1 ; } if ( x > 1 && x % 2 == 0 ){ return 3 * f (x / 2 ) -1 ; } if ( x > 1 && x % 2 == 1 ){ return 3 * f ((x + 1 ) / 2 ) -1 ; } } int main () int x; scanf ("%d" , &x); cout << f (x); return 0 ; } 输入 3 输出 5 另一组: 10 输出 41
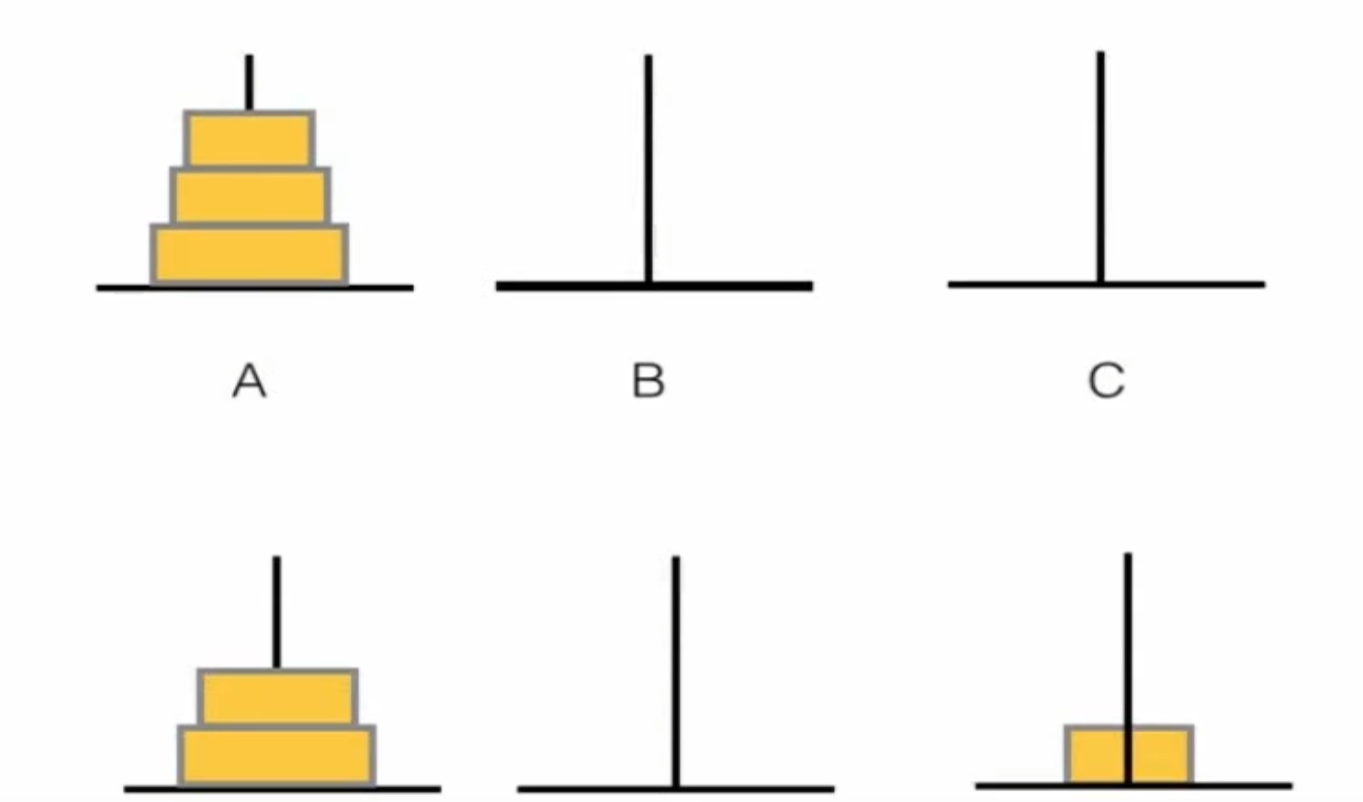
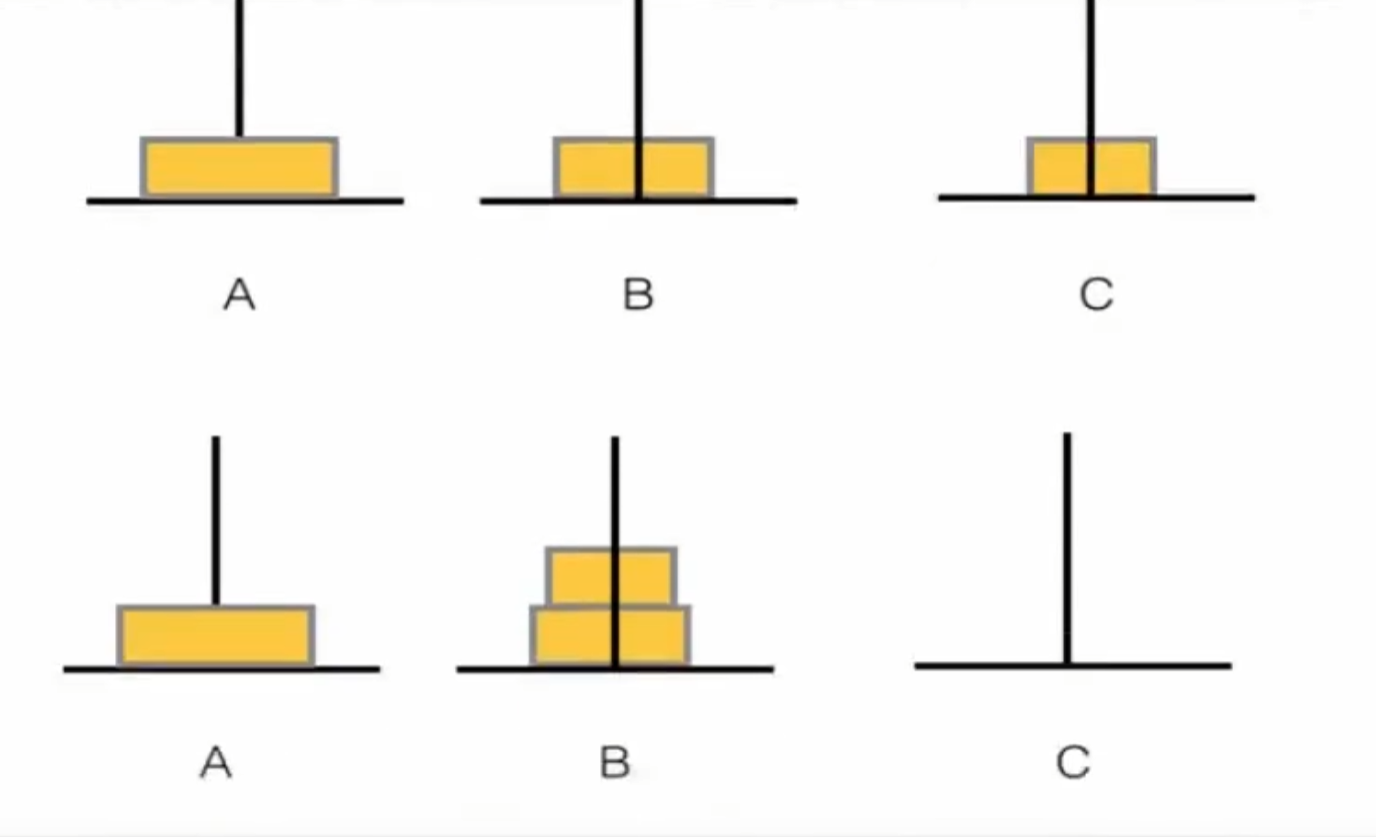
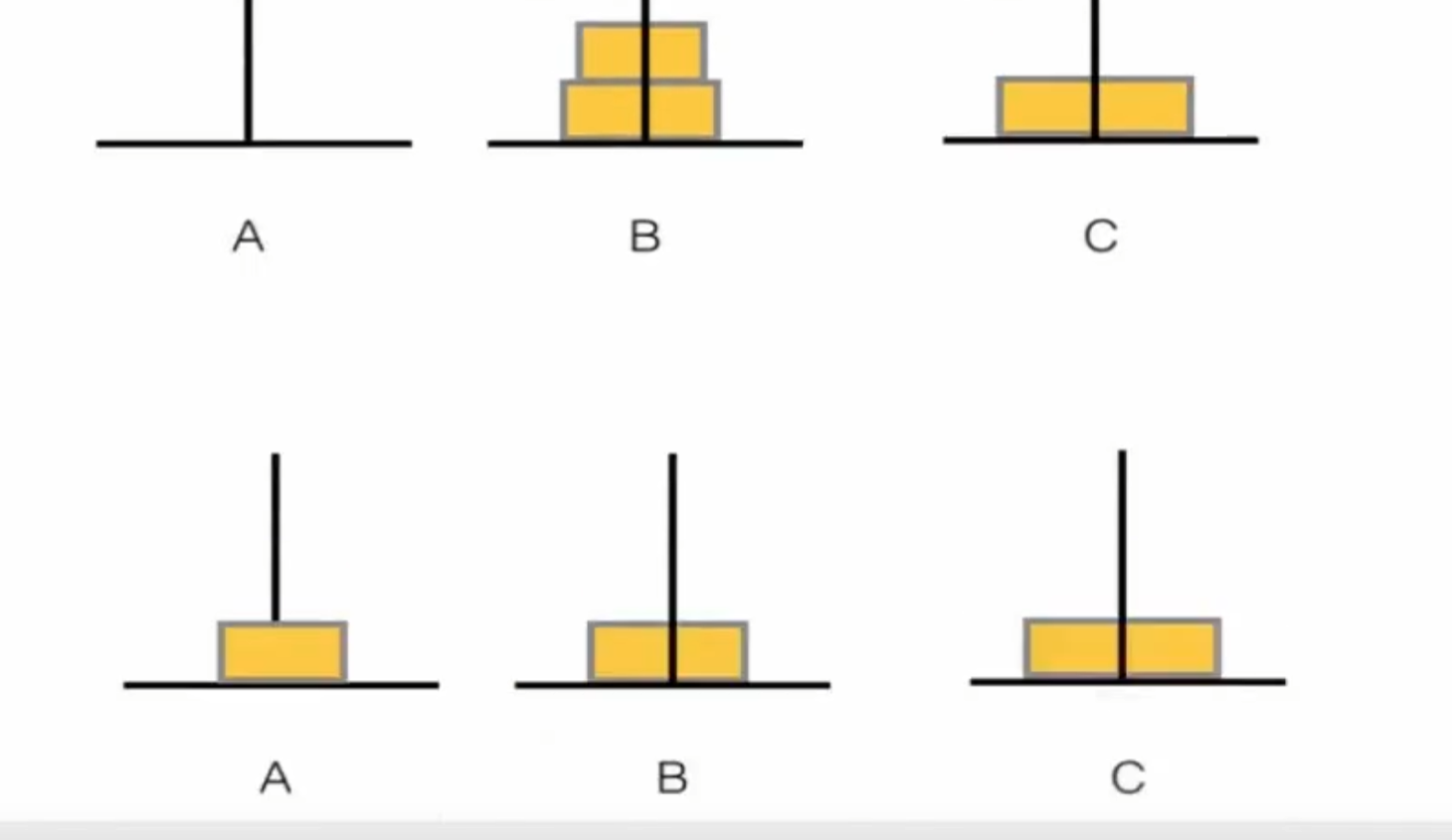
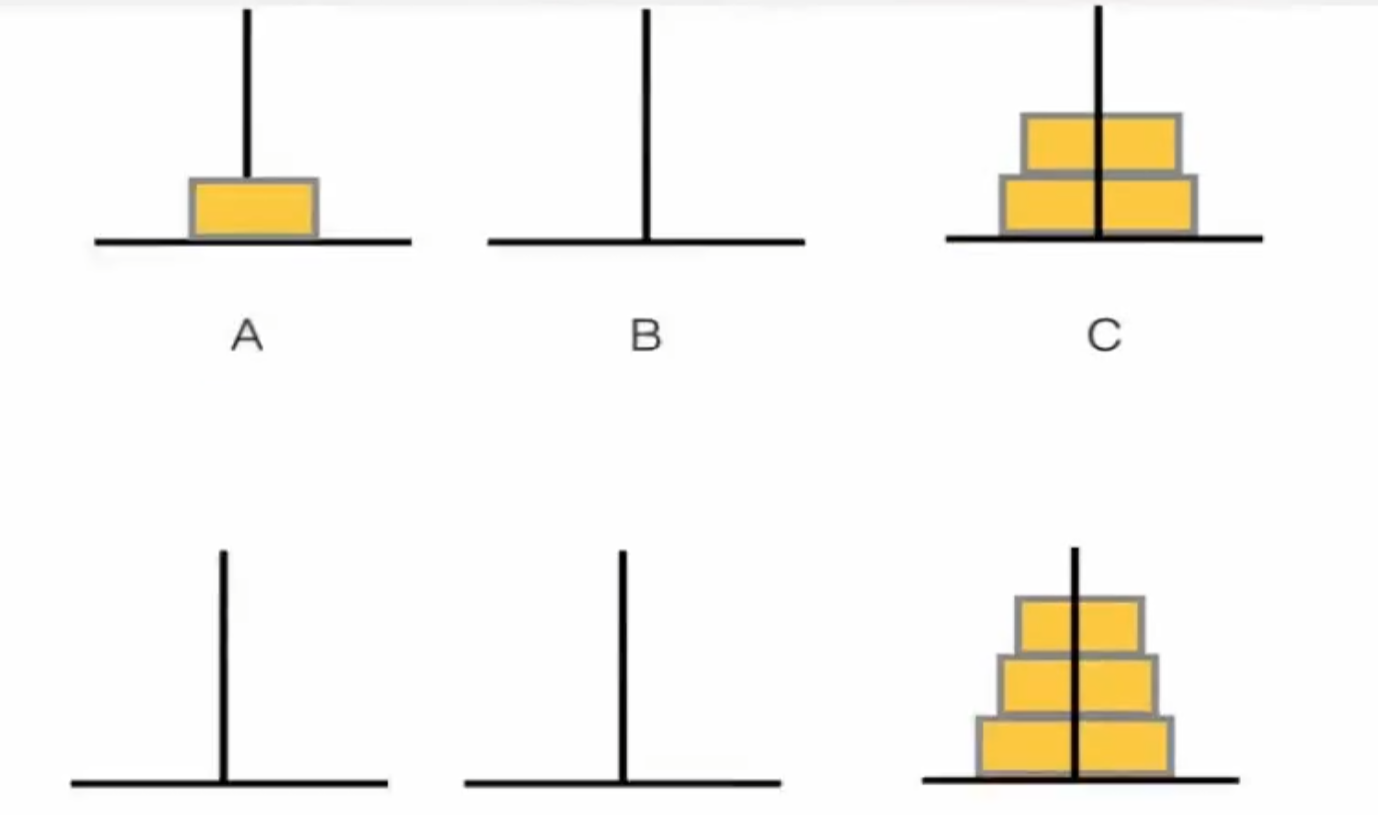
汉诺塔问题
最优解
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 #include <bits/stdc++.h> using namespace std;stack<int > S[3 ]; void move (int x, int y) int temp = S[x].top (); S[x].pop (); S[y].push (temp); cout << x << "-->" << y << endl; } void hanoi (int A, int B, int C, int n) if (n == 1 ){ move (A, C); return ; } hanoi (A, C, B, n - 1 ); move (A, C); hanoi (B, A, C, n - 1 ); } int main () int n; cin >> n; for (int i = n; i >= 1 ; i--){ S[0 ].push (i); } hanoi (0 , 1 , 2 , n); while (!S[2 ].empty ()){ cout << S[2 ].top () << " " ; S[2 ].pop (); } return 0 ; }
汉诺塔升级
递推
f[1]:只有一个盘子的时候,一步就可以搞定
f[n]:移动n个盘子的步数,就是先移动n-1个盘子(次)的步数,再加一个,再加移动n-1个盘子的步数
f[n]:结果,2的n-1次方,可以手写循环,也可以位运算 1ll 代表把1当做long long的数据类型来看待(因为步数我们害怕超步数,fn用long long类型
g[n] : 先把n-1个盘子移到除开目标柱子的另外柱子,再+n,把第n个盘子移走,再加n-1(移动n-1个盘子
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 #include <bits/stdc++.h> using namespace std;long long f[65 ], g[65 ];int main () int n; scanf ("%d" , &n); f[1 ] = 1 ; for (int i = 2 ; i<= n; i++){ f[i] = 2 * f[i-1 ] + 1 ; } g[1 ] = 1 ; for (int i = 2 ; i <= n; i++){ g[i] = 2 * g[i - 1 ] + i; } printf ("%lld %lld\n" , f[n], g[n]); return 0 ; }
快速幂
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 #include <bits/stdc++.h> using namespace std;long long f (long long x, long long y, long long p) if (y == 0 ){ return 1 % p; }else if (y % 2 == 0 ){ long long temp = f (x, y/2 ,p); return temp * temp % p; }else { long long temp = f (x, y/2 , p); return temp * temp % p * x % p; } } int main () int t; long long x, y, p; scanf ("%d" , &t); while (t--){ scanf ("%lld%lld%lld" , &x, &y, &p); printf ("%lld\n" , f (x,y,p)); } return 0 ; }
迭代 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 #include <bits/stdc++.h> using namespace std;long long binpow (long long a, long long b, long long m) a %= m; long long res = 1 ; while (b != 0 ){ if (b & 1 )res = res * a % m; a = a * a % m; b >>= 1 ; } return res; } int main () int t; long long x, y, p; scanf ("%d" , &t); while (t--){ scanf ("%lld%lld%lld" , &x, &y, &p); printf ("%lld\n" , binpow (x,y,p)); } return 0 ; }
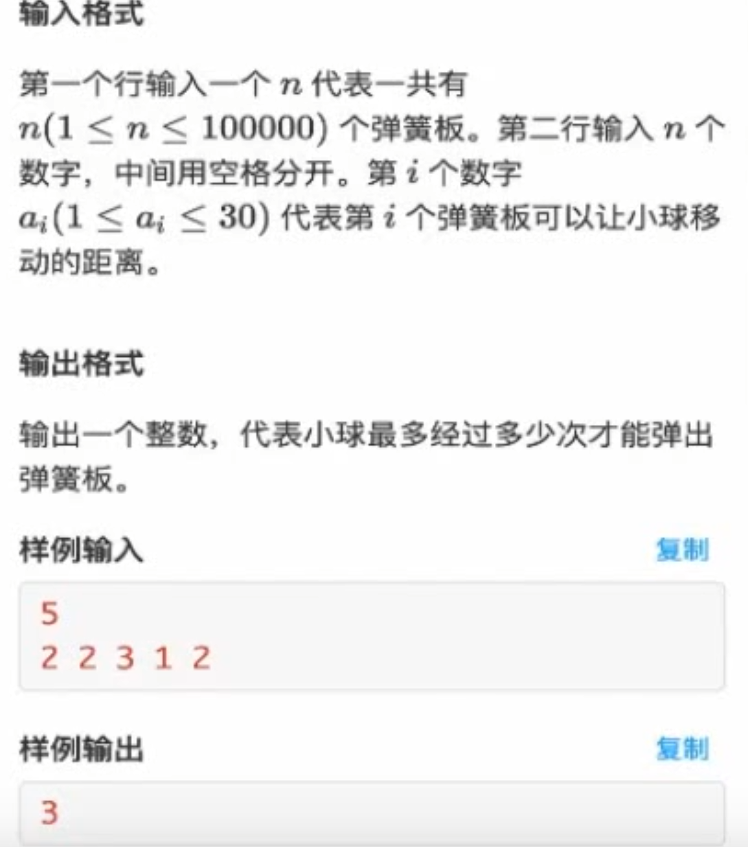
弹簧板 题目 现在n个弹簧板,小球从第i个弹簧板落下,可以向前弹a[i-1]个距离或者b[i-1]个距离,现在从第一个弹簧板落下,计算弹多少次,弹出弹簧板。( 1 ≤ n ≤ 200 ) , ( 0 < a [ i ] , b [ i ] ≤ 30 ) (1 \leq n \leq 200),(0 < a[i],b[i]\leq 30 )(1≤n ≤200),(0<a [i ],b [i ]≤30)
分析 c(x)意味着从下标为x到下标变化到>n-1需要几次定是x+a[x]或者x+b[x],那么 只需找 ** 下个板到弹出所需最小次数 ,再 加上次到这一个板弹的那 一次**即可。这就是一个递推式,c(x)=min(c(x+a[x]),c(x+b[x]))+1
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 #include <iostream> #include <algorithm> using namespace std;int a[300 ];int b[300 ];int n;int c (int x) if (x>=n) return 0 ; else return min (c (x+a[x]),c (x+b[x]))+1 ; } int main () cin>>n; for (int i=0 ;i<n;++i){ cin>>a[i]; } for (int i=0 ;i<n;++i){ cin>>b[i]; } cout<<c (0 ); }
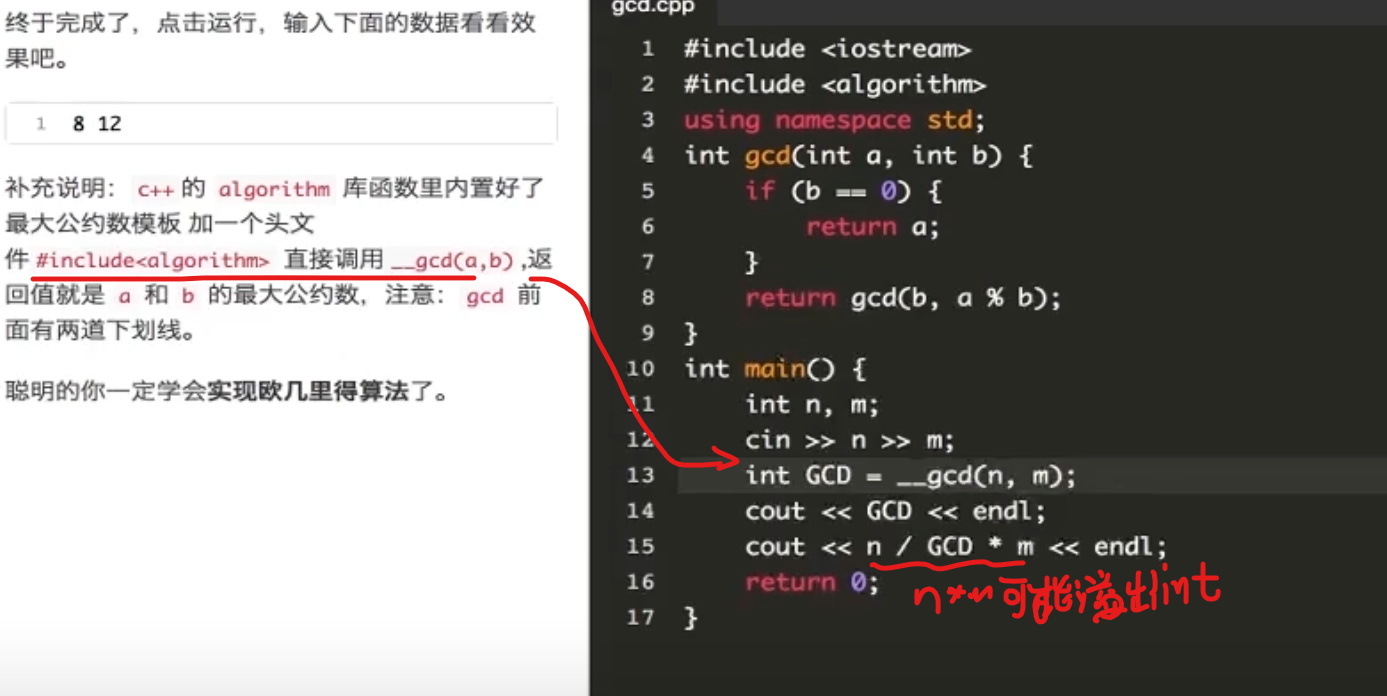
最大公约数/最小公倍数 1 2 3 4 5 int gcd (int a, int b) if (b == 0 ) return a; return gcd (b, a % b); }
最小公倍数即
例如,这是66和30的最小公因数
我们只需要把30 / 6 = 5, 66 / 6 =11 在11 * 6 * 5即为它的最小公倍数
DFS 引入
迷宫问题
默认顺序右下左上
例题实战 家谱
1 2 3 4 5 6 7 8 9 10 输入 4 1 2 1 3 2 4 输出 3 1 0 0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 #include <bits/stdc++.h> using namespace std;vector<int > son[100005 ]; bool f[100005 ];int ans[100005 ];int dfs (int u) int ret = 0 ; for (int i = 0 ; i < son[u].size (); i++){ ret += dfs (son[u][i]); } ans[u] = ret; return ret + 1 ; } int main () int n, x, y, u; scanf ("%d" , &n); for (int i = 0 ; i < n - 1 ; i++){ scanf ("%d%d" , &x, &y); son[x].push_back (y); f[y] = true ; } for (int i = 1 ; i < n; i++){ if (!f[i]){ u = i; break ; } } dfs (u); for (int i = 1 ; i <= n; i++){ printf ("%d\n" , ans[i]); } return 0 ; }
象棋
1 2 3 4 5 6 7 8 9 10 11 12 13 14 输入 10 9 10 1 输出 ......... ......... ......... .#.#..... #.#.#.... ####.#... #####.#.. ##.###... #.###.#.. ######...
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 #include <bits/stdc++.h> using namespace std;char s[105 ][105 ];int n, m;int dir[8 ][2 ] = {{-2 , -1 }, {-2 , 1 }, {2 , -1 }, {2 , 1 }, {1 , 2 }, {1 , -2 }, {-1 , -2 }, {-1 , 2 }};void dfs (int x, int y, int step) if (step > 3 ) return ; if (x < 0 || x >= n || y < 0 || y >= m ){ return ; } s[x][y] = '#' ; for (int i = 0 ; i < 8 ; i++){ dfs (x + dir[i][0 ], y + dir[i][1 ], step + 1 ); } } int main () int x, y; scanf ("%d%d%d%d" , &n, &m, &x, &y); for (int i = 0 ; i < n; i++){ for (int j = 0 ; j < m; j++){ s[i][j] = '.' ; } } dfs (x - 1 , y - 1 , 0 ); for (int i = 0 ; i < n; i++){ printf ("%s\n" , s[i]); } return 0 ; }
王子救公主
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 #include <bits/stdc++.h> using namespace std;int n, m;char mp[105 ][105 ][2 ];bool vis[105 ][105 ][2 ];void dfs (int x,int y, int d) if (x < 0 || x > n || y < 0 || y > m || vis[x][y][d] || mp[x][y][d] == '#' ){ return ; } vis[x][y][d] = true ; dfs (x - (2 -d), y, d); dfs (x + (2 -d), y, d); dfs (x , y - (2 -d), d); dfs (x , y + (2 -d), d); } int main () int x, y; bool ans; scanf ("%d%d" , &n, &m); for (int i = 0 ; i < n; i++){ scanf ("%s" , mp[i]); } for (int i = 0 ; i < n; i++){ for (int j = 0 ; j < m; j++){ if (mp[i][j][0 ] == 'w' ){ x = i; y = j; } } } dfs (x, y, 0 ); for (int i = 0 ; i < n; i++){ for (int j = 0 ; j < m; j++){ if (mp[i][j][1 ] == 'g' ){ x = i; y = j; } } } dfs (x, y, 1 ); for (int i = 0 ; i < n; i++){ for (int j = 0 ; j < m; j++){ if (vis[i][j][0 ] == vis[i][j][1 ] == true ){ ans = true ; } } } if (ans){ cout << "yes" << endl; }else { cout << "no" << endl; } return 0 ; }
开公司 ps :感觉上就是匈牙利算法啊
1 2 3 4 5 6 7 8 9 10 输入 6 10 11 12 11 9 11 11 9 10 13 11 12 12 10 11 10 13 9 9 14 9 10 10 11 10 10 9 11 12 11 10 7 10 10 10 8 输出 54
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 #include <bits/stdc++.h> using namespace std;int task[15 ][15 ];bool used[15 ];int ans;int n;void dfs (int x, int t) if (x == n){ if (t < ans){ ans = t; } return ; } for (int i = 0 ; i < n; i++){ if (!used[i]){ used[i] = true ; dfs (x + 1 , task[x][i] + t); used[i] = false ; } } } int main () scanf ("%d" , &n); for (int i = 0 ; i < n; i++){ for (int j = 0 ; j < n; j++){ scanf ("%d" , &task[i][j]); } } ans = 20000 ; dfs (0 , 0 ); printf ("%d\n" , ans); return 0 ; }
抽象DFS 引例:求和
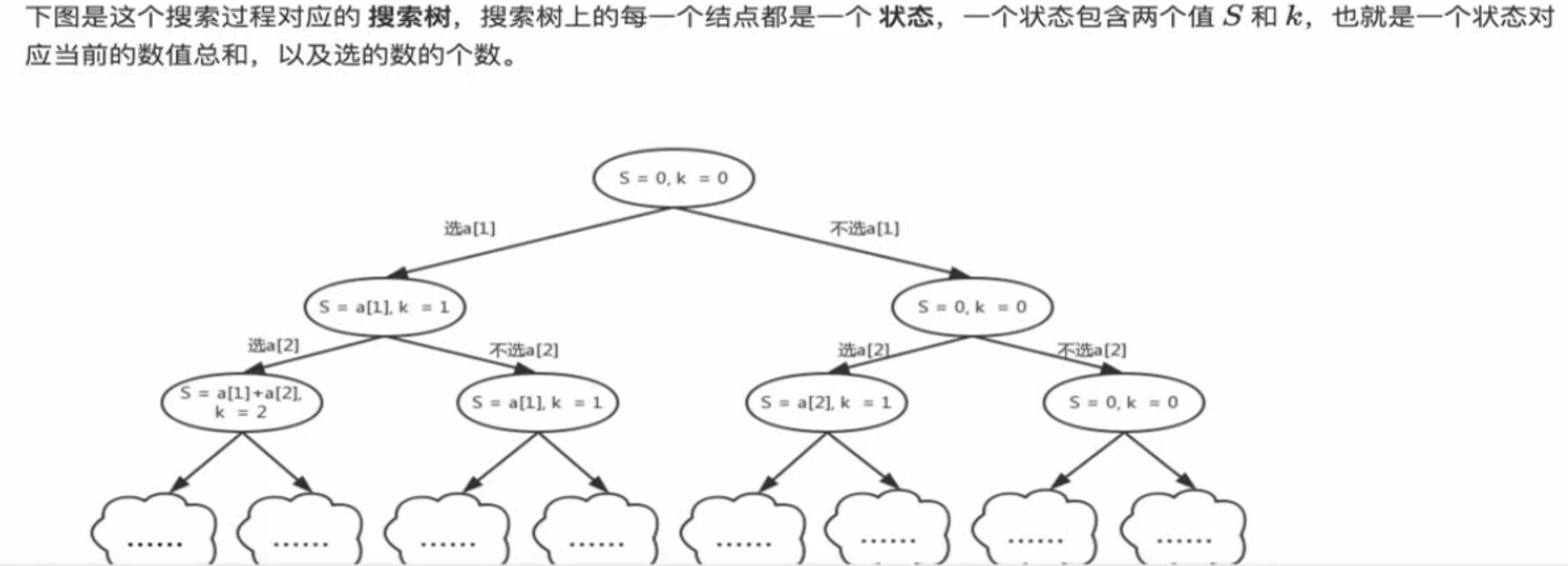
搜索树和状态
1 2 3 4 5 输入// n 个数 选 k个数 求和sum的问题 5 3 9 1 2 3 4 5 输出 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 #include <bits/stdc++.h> using namespace std;int n, k, sum, ans;int a[40 ];void dfs (int i , int cnt, int s) if (i == n){ if (cnt == k && s == sum){ ans++; } return ; } dfs (i + 1 , cnt, s); dfs (i + 1 , cnt+1 , s+a[i]); } int main () cin >> n >> k >> sum; for (int i = 0 ; i < n; i++){ cin >> a[i]; } ans = 0 ; dfs (0 , 0 , 0 ); cout << ans << endl; return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 #include <bits/stdc++.h> using namespace std;int n, k, sum, ans;int a[40 ];int i;bool xuan[40 ];void dfs (int s , int cnt) if (cnt == k){ if (s == sum){ ans++; } return ; } for (int i = 0 ; i < n; i++){ if (!xuan[i]){ xuan[i] = true ; dfs (s + a[i], cnt++); xuan[i] = false ; } } } int main () cin >> n >> k >> sum; for (int i = 0 ; i < n; i++){ cin >> a[i]; } ans = 0 ; dfs (0 , 0 ); cout << ans << endl; return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 #include <bits/stdc++.h> using namespace std;int n, k, sum, ans;int a[40 ];int i;bool xuan[40 ]; void dfs (int s , int cnt, int xx) if (cnt == k){ if (s == sum){ ans++; } return ; } for (int i = 0 ; i < n; i++){ if (!xuan[i]){ xuan[i] = true ; dfs (s + a[i], cnt + 1 , i + 1 ); xuan[i] = false ; } } } int main () cin >> n >> k >> sum; for (int i = 0 ; i < n; i++){ cin >> a[i]; } ans = 0 ; dfs (0 , 0 , 0 ); cout << ans << endl; return 0 ; }
等边三角形
1 2 3 4 5 6 7 8 9 10 输入 5 1 2 3 4 5 输出 yes 输入 4 1 1 1 1 输出 no
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 #include <bits/stdc++.h> using namespace std;int p[15 ];int n, sum = 0 ;bool vis[15 ];bool f; void dfs (int cnt, int s, int st) if (f){ return ; } if (cnt == 3 ){ f = true ; return ; } if (s == sum / 3 ){ dfs (cnt + 1 , 0 , 0 ); return ; } for (int i = st; i < n; i++){ if (!vis[i]){ vis[i] = true ; dfs (cnt, s + p[i], i+1 ); vis[i] = false ; } } } int main () scanf ("%d" , &n); for (int i = 0 ; i < n; i++){ scanf ("%d" , &p[i]); sum += p[i]; } if (sum % 3 != 0 ){ printf ("no\n" ); }else { dfs (0 , 0 , 0 ); if (f) printf ("yes\n" ); else printf ("no\n" ); } return 0 ; }
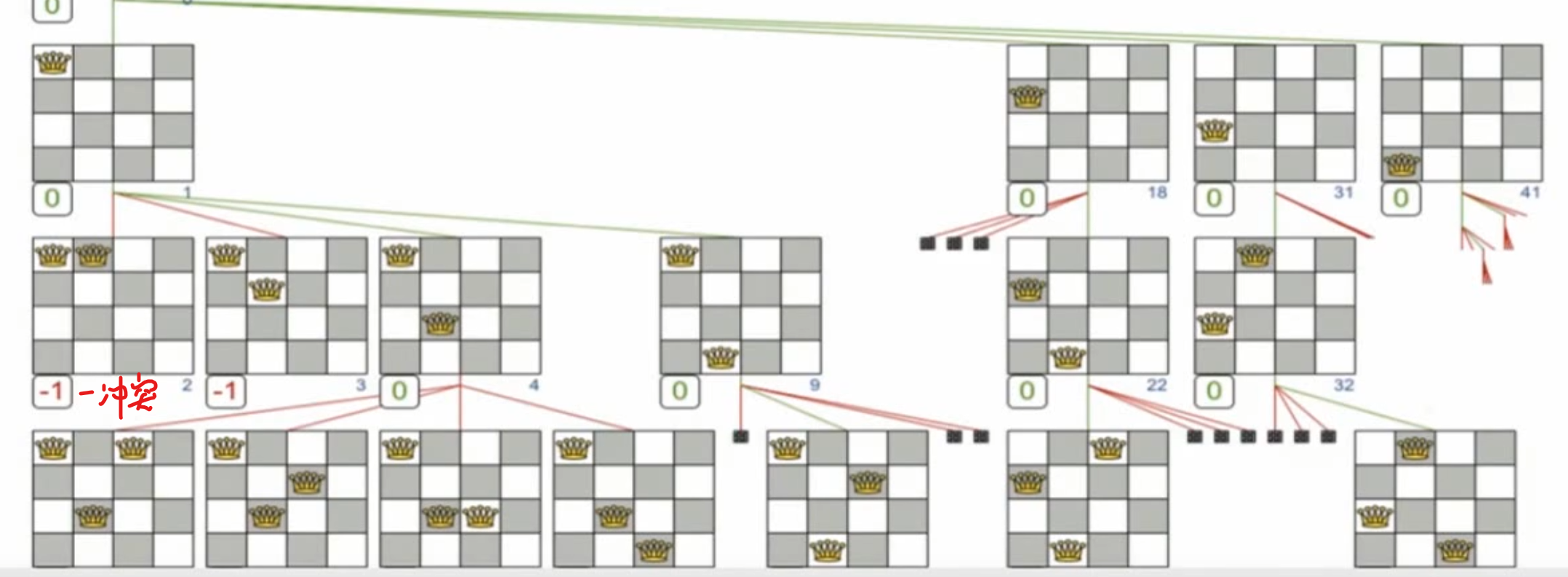
N皇后 行已经只放一个了,已经保证
列的话去标记一下之前是否放过
处理列
八皇后
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 #include <bits/stdc++.h> using namespace std;int ans = 0 ;bool col[10 ], x1[20 ], x2[20 ]; bool check (int r, int i) return !col[i] && !x1[r + i] && !x2[r - i + 8 ]; } void dfs (int r) if (r == 8 ){ ans++; return ; } for (int i =0 ; i < 8 ; i++){ if (check (r,i)){ col[i] = x1[r + i] = x2[r - i + 8 ] = true ; dfs (r + 1 ); col[i] = x1[r + i] = x2[r - i + 8 ] = false ; } } return ; } int main () dfs (0 ); cout << ans << endl; return 0 ; }
方程的解数
1 2 3 4 5 6 7 8 输入 3 100 1 2 -1 2 1 2 输出 104
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 #include <bits/stdc++.h> using namespace std; int k[5 ], p[5 ]; int n, M, ans; long long poww (int x, int y) long long ret = 1 ; for (int i = 0 ; i < y; i++){ ret *= x; } return ret; } void dfs (int x, long long s) if (x == n){ if (s == 0 ){ ans++; } return ; } for (int i = 1 ; i <= M; i++){ dfs (x + 1 , s + k[x] * poww (i,p[x])); } } int main () scanf ("%d" , &n); scanf ("%d" , &M=); for (int i = 0 ; i < n; i++){ scanf ("%d%d" , &k[i], &p[i]); } dfs (0 , 0 ); printf ("%d\n" , ans); return 0 ; }
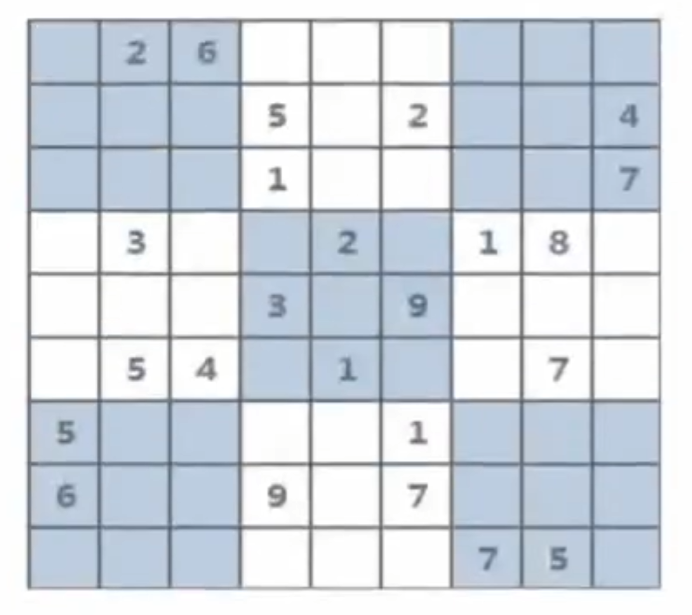
数独
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 输入数据 *23****** ***5*2**4 ***1****7 *3**2*18* ***3*9*** *54*1**7* 5****1*** 6**9*7*** ******75* 我的输出 0 2 3 4 7 6 5 1 8 1 6 7 5 8 2 0 3 4 4 8 5 1 0 3 2 6 7 7 3 0 6 2 4 1 8 5 8 1 6 3 5 9 4 0 2 2 5 4 0 1 8 3 7 6 5 7 2 8 3 1 6 4 0 6 0 1 9 4 7 8 2 3 3 4 8 2 6 0 7 5 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 #include <bits/stdc++.h> using namespace std;char s[10 ][10 ];bool f;bool vx[10 ][10 ], vy[10 ][10 ], vv[10 ][10 ];void dfs (int x, int y) if (f){ return ; } if ( x == 9 ){ f = true ; for (int i = 0 ; i < 9 ; i++){ for (int j = 0 ; j < 9 ; j++){ if (j != 8 ){ printf ("%c " , s[i][j]); } else { printf ("%c\n" , s[i][j]); } } } return ; } if ( y == 9 ){ dfs (x+1 , 0 ); return ; } if (s[x][y] != '*' ) { dfs (x, y + 1 ); return ; } for (int i = 0 ; i < 9 ; i++ ){ if (!vx[x][i] && !vy[y][i] && !vv[(x / 3 ) * 3 + y / 3 ][i]){ s[x][y] = '0' + i; vx[x][i] = true ; vy[y][i] = true ; vv[(x / 3 ) * 3 + y / 3 ][i] = true ; dfs (x, y + 1 ); vx[x][i] = false ; vy[y][i] = false ; vv[(x / 3 ) * 3 + y / 3 ][i] = false ; } } } int main () for (int i = 0 ; i < 9 ; i++){ for (int j = 0 ; j < 9 ; j++){ scanf (" %c" , &s[i][j]); } } for (int i = 0 ; i < 9 ; i++){ for (int j = 0 ; j < 9 ; j++){ if (s[i][j] != '*' ){ vx[i][s[i][j] - '0' ] = true ; vy[j][s[i][j] - '0' ] = true ; vv[(i / 3 ) * 3 + j / 3 ][s[i][j] - '0' ] = true ; } } } dfs (0 , 0 ); return 0 ; }
2n皇后
1 2 3 4 5 6 7 8 输入 4 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 输出 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 #include <bits/stdc++.h> using namespace std;int mp[10 ][10 ];int vy[10 ], vd1[20 ], vd2[20 ];int n, ans;void dfs (int x, int p) if (x == n && p == 2 ){ ans++; return ; } if (x == n){ dfs (0 , p+1 ); return ; } for (int i = 0 ; i < n; i++){ if (mp[x][i] && vy[i] != 3 && vy[i] != p && vd1[x + i] != 3 && vd1[x + i] != p\ && vd2[x - i + n] != 3 && vd2[x - i + n] != p){ mp[x][i] == 0 ; vy[i] += p; vd1[x + i] += p; vd2[x - i + n] += p; dfs (x + 1 , p); vy[i] -= p; vd1[x + i] -= p; vd2[x - i + n] -= p; mp[x][i] == 1 ; } } } int main () scanf ("%d" , &n); for (int i = 0 ; i < n; i++){ for (int j = 0 ; j < n; j++){ scanf ("%d" , &mp[i][j]); } } dfs (0 , 1 ); printf ("%d" , ans); return 0 ; }
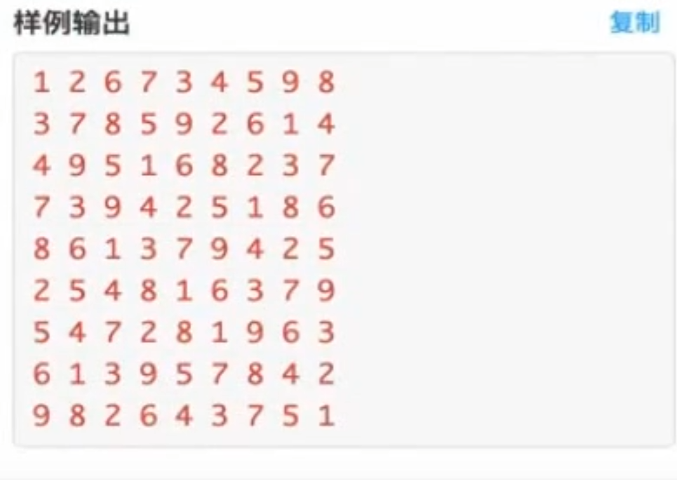
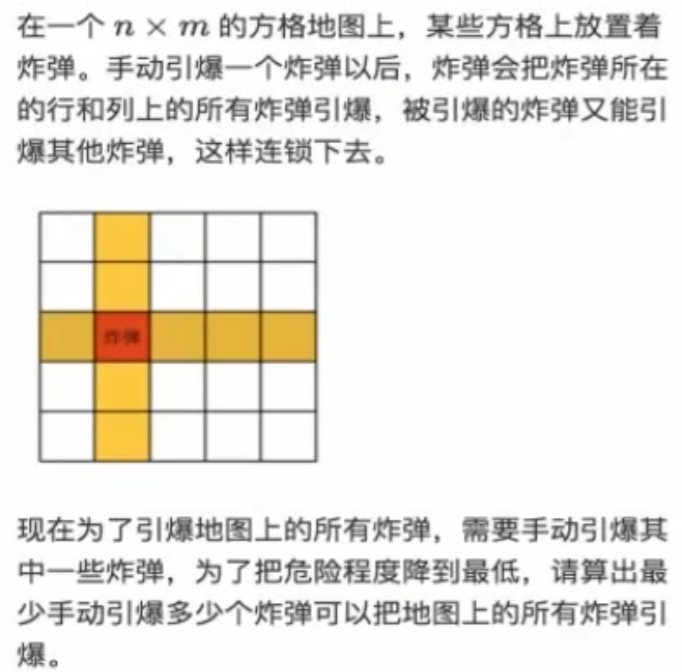
引爆炸弹
1 2 3 4 5 6 7 8 9 输入 5 5 00010 00010 01001 10001 01000 输出 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 #include <bits/stdc++.h> using namespace std;int n, m, ans, bomb;char mp[1005 ][1005 ];int vis[1005 ][1005 ];bool flag;void dfs (int x, int y) if (bomb == 0 ){ return ; } if (y > m){ dfs (x+1 , 0 ); return ; } if (mp[x][y] == '0' ){ dfs (x, y + 1 ); return ; } for (int i = 0 ; i < m; i++){ if (mp[x][i] == '1' ){ mp[x][i] == '0' ; bomb--; for (int j = 0 ; j < m; j++){ if (mp[x][j] == '1' ) dfs (x, j); } for (int k = 0 ; k < n; k++){ if (mp[k][y] == '1' ) dfs (k, y); } } } for (int j = 0 ; j < m; j++){ for (int k = 0 ; k < n; k++){ if (mp[x][j] == '0' ) if (mp[k][y] == '0' ) flag = true ; if (flag){ ans++; flag = false ; } } } } int main () scanf ("%d%d" , &n, &m); for (int i = 0 ; i < n; i++){ scanf ("%s" , &mp[i]); for (int j = 0 ; j < m; j++){ if (mp[i][j] == '1' ){ bomb++; } } } dfs (0 , 0 ); printf ("%d" , ans); return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 #include <bits/stdc++.h> using namespace std;int n, m, ans;char mp[1005 ][1005 ];int vx[1005 ], vy[1005 ];void dfs (int x, int y) mp[x][y] = '0' ; if (!vx[x]){ vx[x] = true ; for (int i = 0 ; i < m; i++){ if (mp[x][i] == '1' ) dfs (x, i); } } if (!vy[y]){ vy[y] = true ; for (int i = 0 ; i < n; i++){ if (mp[i][y] == '1' ) dfs (i, y); } } } int main () scanf ("%d%d" , &n, &m); for (int i = 0 ; i < n; i++){ scanf ("%s" , &mp[i]); } for (int i = 0 ; i < n; i++){ for (int j = 0 ; j < m; j++){ if (mp[i][j] == '1' ){ ans++; dfs (i, j); } } } printf ("%d" , ans); }
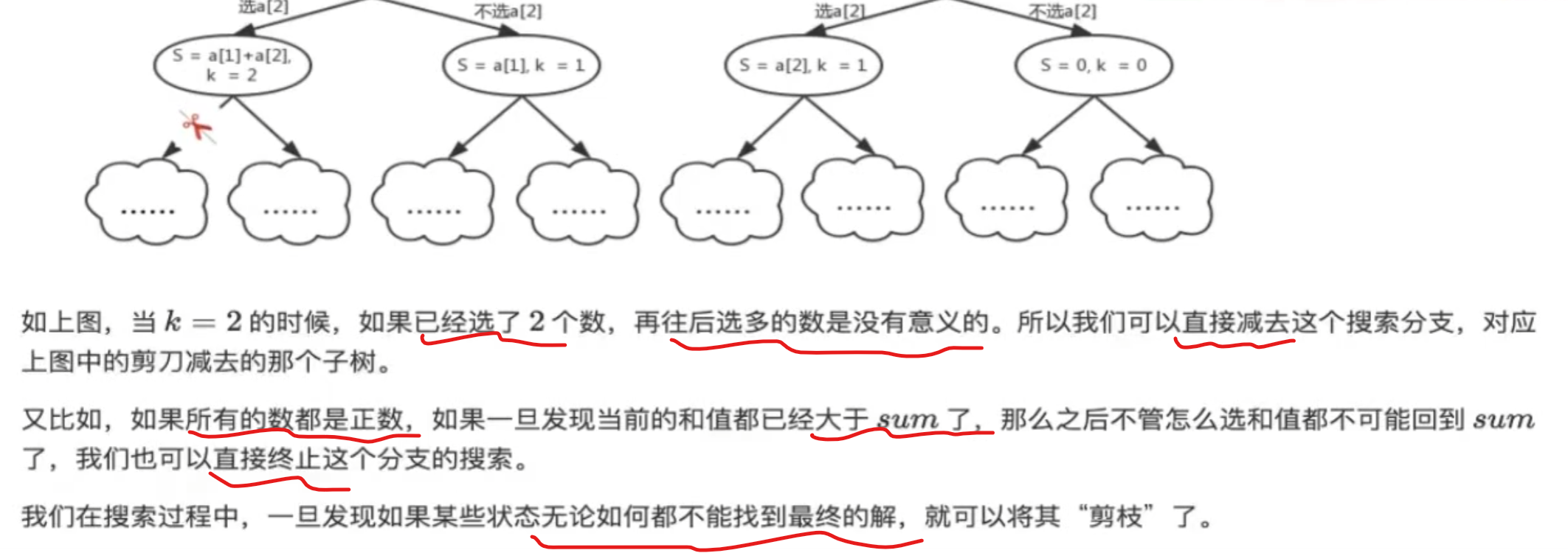
剪枝
可行性剪枝 减掉不可能的
最优解剪枝 减掉可能但不优的
引例:再度迷宫
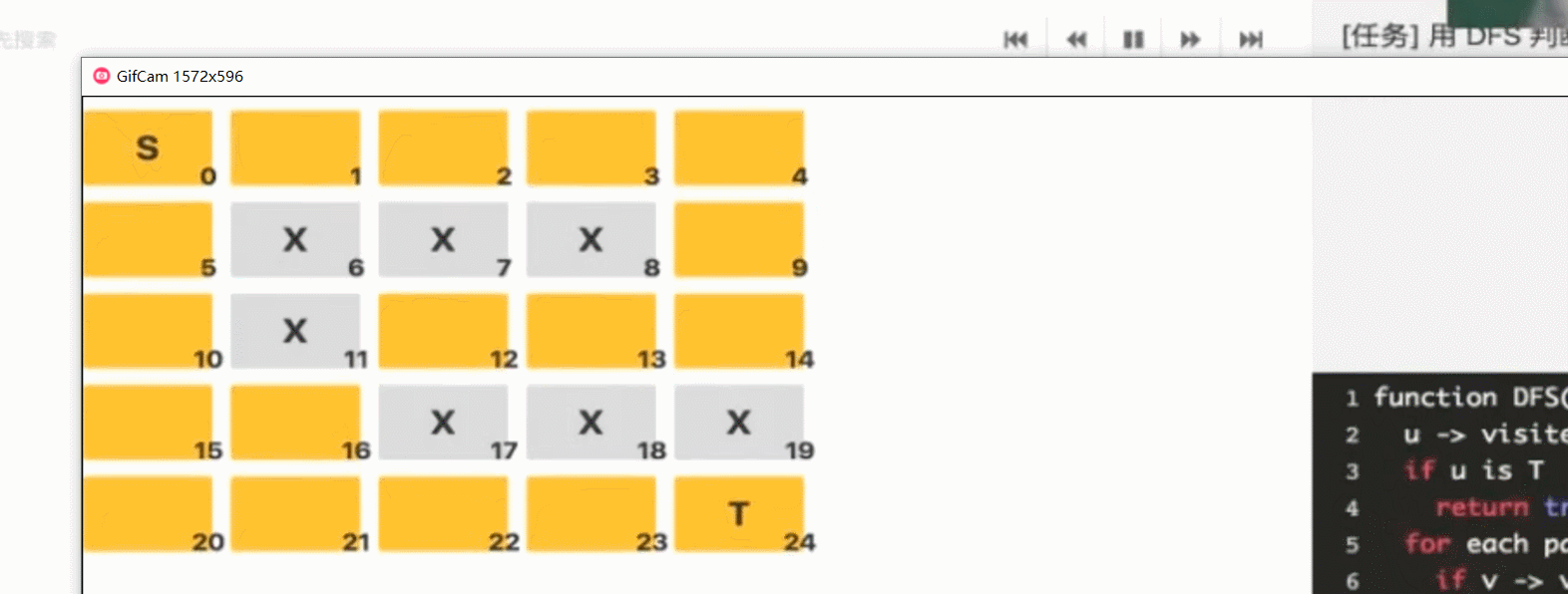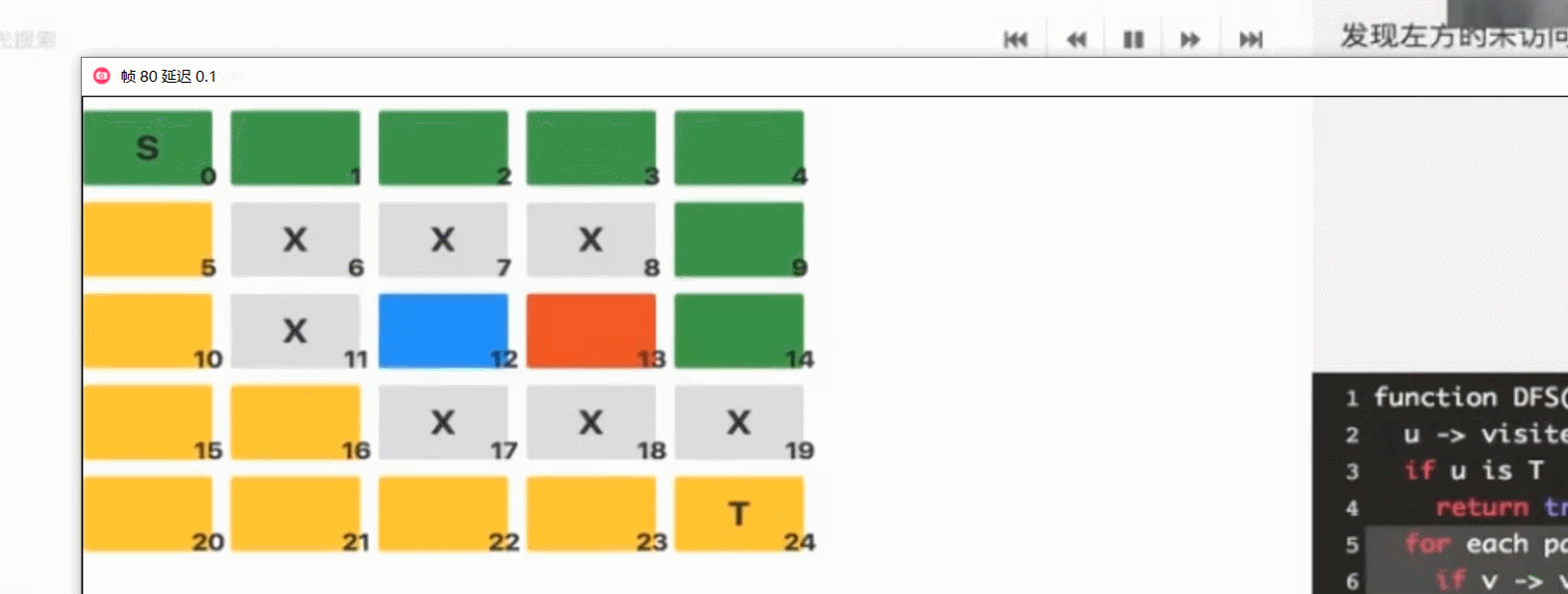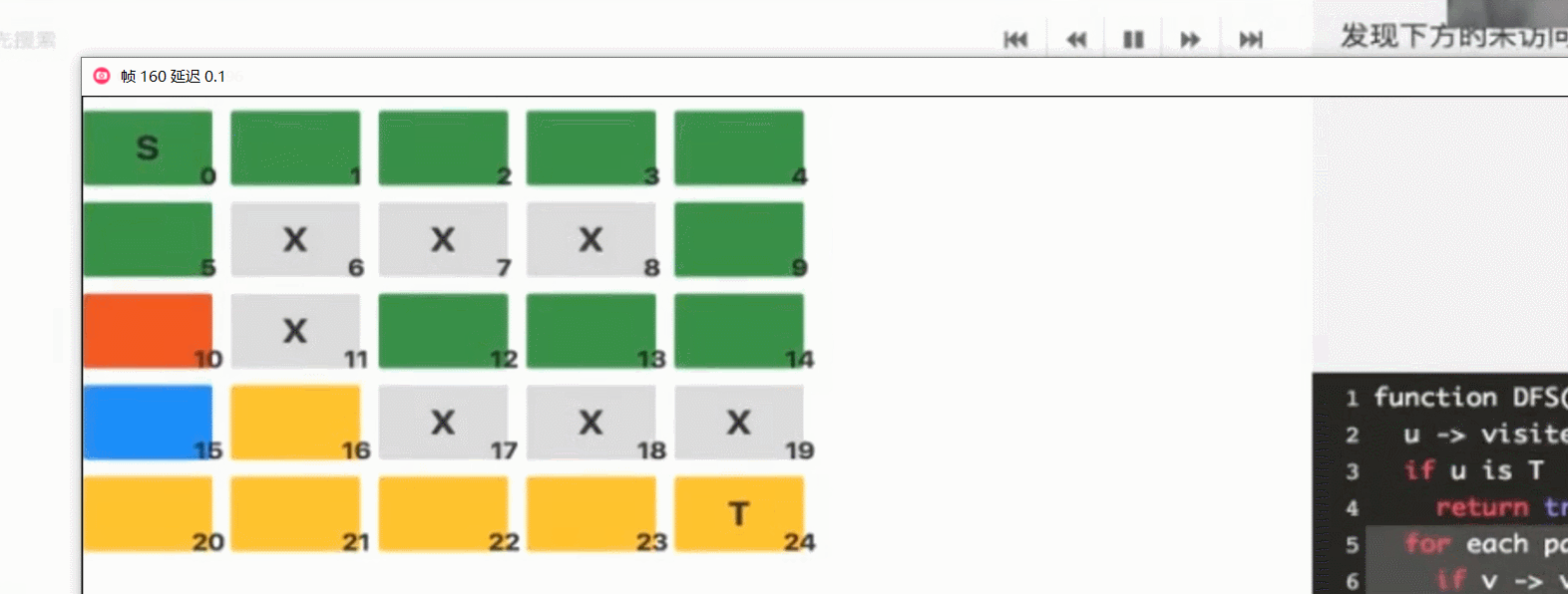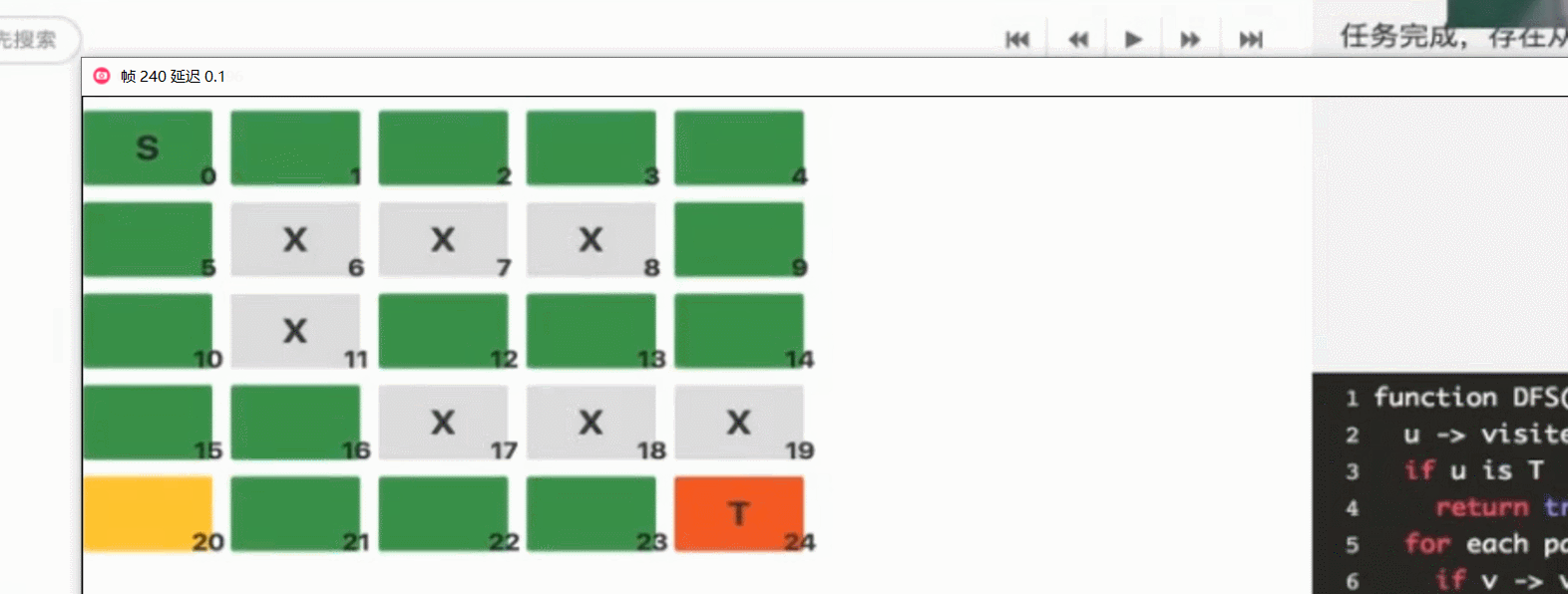
1 2 3 4 5 6 7 输入 3 4 S**. .... ***T 输出 5
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 #include <bits/stdc++.h> using namespace std;int n, m;string maze[110 ]; bool vis[110 ][110 ];int dir[4 ][2 ] = {{-1 , 0 }, {0 , -1 }, {1 , 0 }, {0 , 1 }};int ans = 10000 ;bool in (int x, int y) return 0 <= x && x < n && 0 <= y && y < m; } void dfs (int x, int y, int step) if (step >= ans){ return ; } if (maze[x][y] == 'T' ){ ans = step; return ; } vis[x][y] = 1 ; for (int i = 0 ; i < 4 ; i++){ int tx = x + dir[i][0 ]; int ty = y + dir[i][1 ]; if (in (tx, ty) && maze[tx][ty] != '*' && !vis[tx][ty]){ dfs (tx, ty, step+1 ); } } vis[x][y] = 0 ; } int main () cin >> n >> m; for (int i = 0 ; i < n; i++){ cin >> maze[i]; } int x,y; for (int i = 0 ; i < n; i++){ for (int j = 0 ; j < m; j++){ if (maze[i][j] == 'S' ){ x = i; y = j; } } } dfs (x, y, 0 ); cout << ans << endl; return 0 ; }
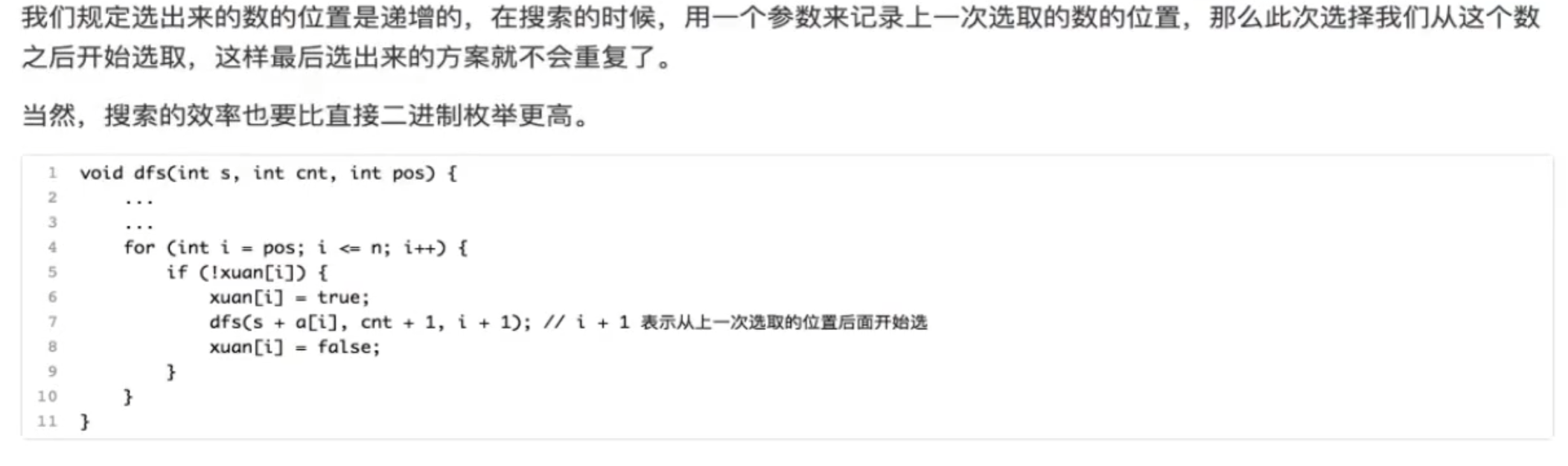
重复性剪枝 减掉的是重复的
关键 :增加一个参数用来记录当前位置,每一次dfs就从下一个位置开始选,就不会重复
奇偶性剪枝 黑白棋盘
1 2 3 4 5 6 7 8 输入 4 4 5 S.X. ..X. ..XD .... 输出 NO
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 #include <bits/stdc++.h> using namespace std;const int N = 10 ;int n, m, T;char mat[N][N];bool vis[N][N];int dx[4 ] = {0 , 0 , -1 , 1 };int dy[4 ] = {1 , -1 , 0 , 0 };bool ok;void dfs (int x, int y, int t) if (ok) return ; if (t == T){ if (mat[x][y] == 'D' ) ok == true ; return ; } vis[x][y] = true ; for (int i = 0 ; i < 4 ; i++){ int tx = x + dx[i]; int ty = y + dy[i]; if (tx < 0 || tx >= n || ty < 0 || ty >= m || mat[tx][ty] == 'X' || vis[tx][ty]) continue ; dfs (ty, ty, t+1 ); } vis[x][y] = false ; } int main () cin >> n >> m >> T; for (int i = 0 ; i < n; ++i){ cin >> mat[i]; } int sx, sy, ex, ey; for (int i = 0 ; i < n; i++){ for (int j = 0 ; j < m; j++){ if (mat[i][j] == 'S' ){ sx = i; sy = j; } if (mat[i][j] == 'D' ){ ex = i; ey = j; } } } if ((sx + sy + ex + ey + T) % 2 != 0 ){ cout << "NO" << endl; }else { ok = false ; dfs (sx, sy, 0 ); if (ok){ cout << "YES" << endl; }else { cout << "NO" << endl; } } return 0 ; }
剪枝例题 引爆炸弹
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 #include <bits/stdc++.h> using namespace std;int n, m, ans;char mp[1005 ][1005 ];int vx[1005 ], vy[1005 ];void dfs (int x, int y) mp[x][y] = '0' ; if (!vx[x]){ vx[x] = true ; for (int i = 0 ; i < m; i++){ if (mp[x][i] == '1' ) dfs (x, i); } } if (!vy[y]){ vy[y] = true ; for (int i = 0 ; i < n; i++){ if (mp[i][y] == '1' ) dfs (i, y); } } } int main () scanf ("%d%d" , &n, &m); for (int i = 0 ; i < n; i++){ scanf ("%s" , &mp[i]); } for (int i = 0 ; i < n; i++){ for (int j = 0 ; j < m; j++){ if (mp[i][j] == '1' ){ ans++; dfs (i, j); } } } printf ("%d" , ans); }
全排列
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 输入 2 输出 2 12 21 输入 3 输出 6 123 132 213 231 312 321
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 #include <bits/stdc++.h> using namespace std;int n;int num;int vis[20 ];void dfs (int x, int cnt) if (cnt == n){ printf ("%d\n" , x); return ; } for (int i = 1 ; i <= n; i++){ if (!vis[i]){ vis[i] = true ; dfs (x * 10 + i, cnt + 1 ); vis[i] = false ; } } } int main () scanf ("%d" , &n); num = 1 ; for (int i = 1 ; i <= n; i++){ num *= i; } printf ("%d\n" , num); dfs (0 , 0 ); return 0 ; }
全排列(洛谷) 太太太感动了,自己做起了!!!!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 #include <bits/stdc++.h> using namespace std;int n;int vis[20 ];int poiEnd, poi; int npoi[10 ];int cnnt;void dfs (int data, int cnt) if (cnt == n){ poi = data; while (poi){ poiEnd = poi % 10 ; poi /= 10 ; npoi[cnnt++] = poiEnd; } for (int i = n-1 ; i >= 0 ; i--) if (i != 0 ) printf (" %d" , npoi[i]); else printf (" %d\n" , npoi[i]); cnnt = 0 ; poiEnd = data % 10 ; return ; } for (int i = 1 ; i <= n; i++){ if (!vis[i]){ vis[i] = true ; dfs (data*10 + i, cnt + 1 ); vis[i] = false ; } } } int main () cin >> n; dfs (0 , 0 ); return 0 ; }
因数最多的数 最重要的一个公式:1 * 31 ,所以按照公式,它的因数个数为4(1,2,3,6)。再一个例子,2^2^ * 3^3^那么就是(2+1) * (3+1)这么多个因数任何合数 都可以被分解为质数之积的形式,所以我们可以只选用质数 进行求解。
1 2 3 4 5 6 7 8 9 输入 3 10 100 1000 输出 6 60 840
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 #include <bits/stdc++.h> using namespace std;int n;int ansY;int ansNum;int prime[15 ] = {2 , 3 , 5 , 7 , 11 , 13 , 17 , 19 , 23 , 29 , 31 , 37 , 41 , 43 , 47 };void dfs (int u, int m, int x, int cnt) if (u == 15 ){ return ; } if (cnt > ansY){ ansY = cnt; ansNum = x; }else if ((cnt == ansY) && (ansNum > x)){ ansNum = x; } for (int i = 1 ; i <= m; i++){ x *= prime[u]; if (x > n) return ; dfs (u + 1 , i, x, cnt * (i+1 )); } } int main () int T; scanf ("%d" , &T); for (int i = 0 ; i < T; i++){ scanf ("%d" , &n); dfs (0 , 60 , 1 , 1 ); cout << ansNum << endl; } return 0 ; }
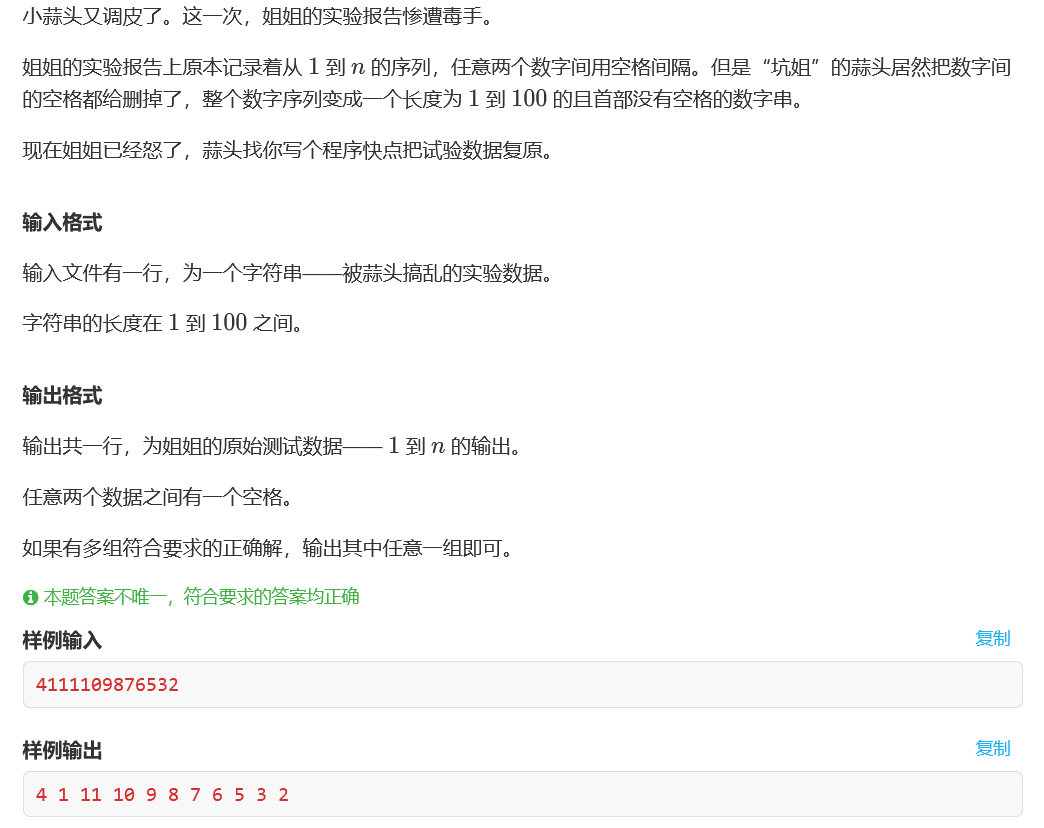
置换的玩笑 题目
1 2 3 4 输入 4111109876532 输出 4 1 11 10 9 8 7 6 5 3 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 #include <bits/stdc++.h> using namespace std;int n;string s; bool vis[100 ];bool ok;int ans[100 ];void dfs (int u, int cnt) if (ok) return ; if (u == s.size ()){ for (int i = 0 ; i < cnt; i++){ cout << ans[i] << " " ; } cout << endl; ok = true ; return ; } int x = s[u] - '0' ; if (x <= n && !vis[x]){ ans[cnt] = x; vis[x] = true ; dfs (u+1 , cnt+1 ); vis[x] = false ; } if (u + 1 >= s.size ()) return ; x = x * 10 + s[u + 1 ] - '0' ; if (x <= n && !vis[x]){ ans[cnt] = x; vis[x] = true ; dfs (u + 2 , cnt + 1 ); vis[x] = false ; } } int main () cin >> s; n = s.size () <= 9 ? s.size () : (s.size () - 9 ) / 2 + 9 ; dfs (0 , 0 ); return 0 ; }
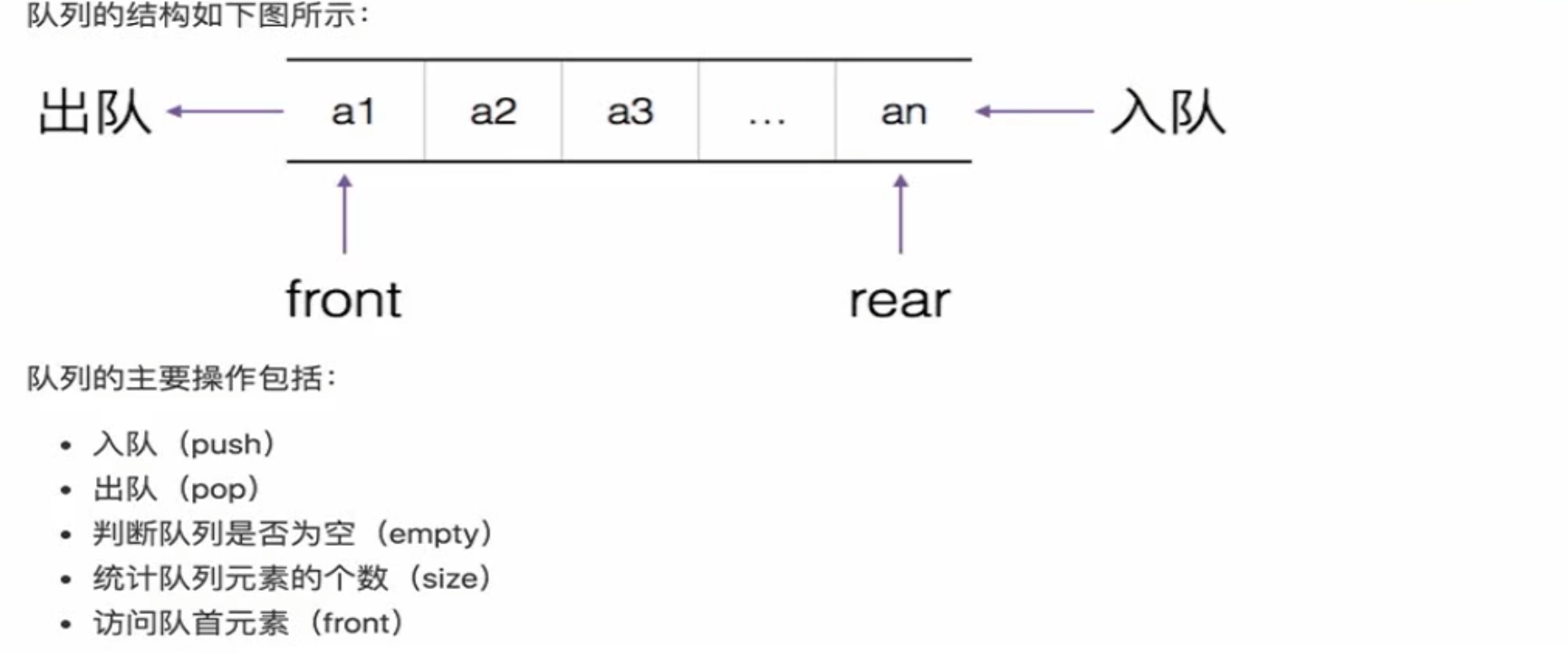
BFS 队列
结构
构造
入队
获取队首
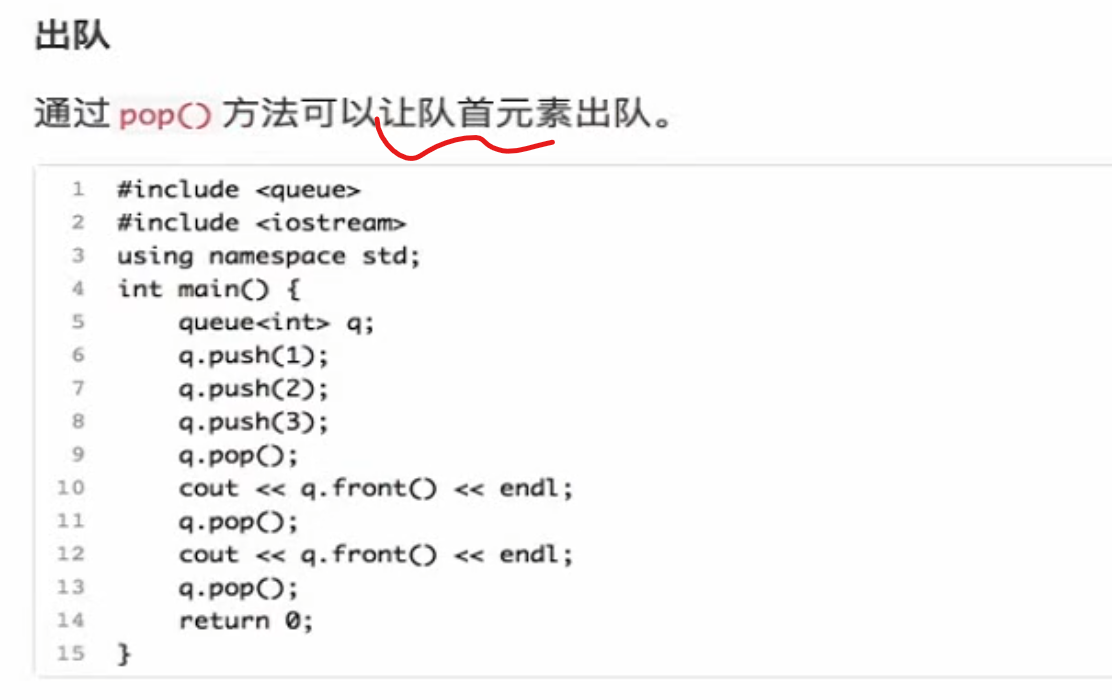
出队
判断空
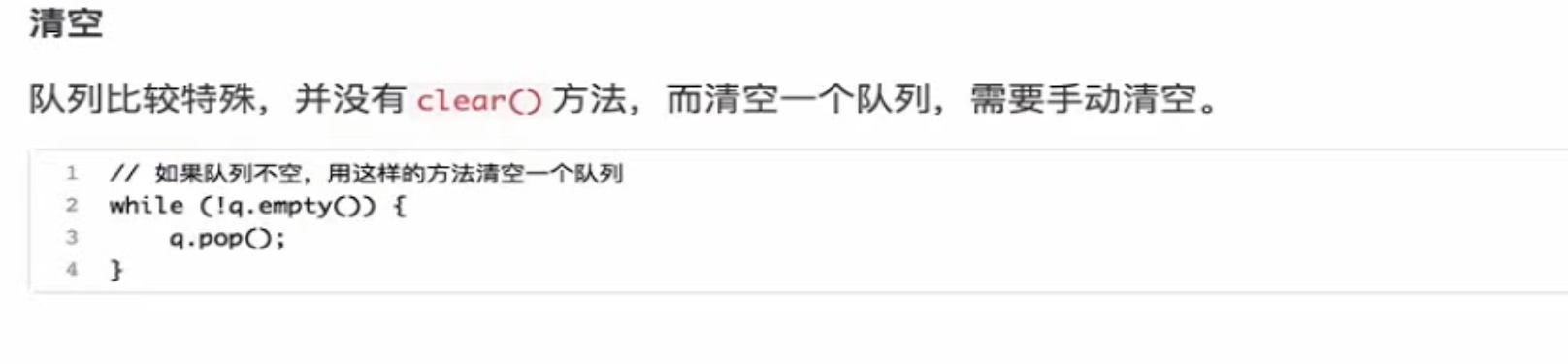
清空
报数游戏
当然我们不能每次都心算,下面程序,输入7 5 返回 6
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 #include <bits/stdc++.h> using namespace std;int main () int n, m; cin >> n >> m; queue<int > q; for (int i = 1 ; i <= n; i++){ q.push (i); } int cur = 1 ; while (q.size () > 1 ){ int x = q.front (); q.pop (); if (cur == m){ cur = 1 ; }else { q.push (x); cur++; } } cout << q.front () << endl; return 0 ; }
引入
代码框架
搜索演示 BFS可能有多种搜索点,取决于先放那个儿子
例题 一维坐标的移动
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 #include <bits/stdc++.h> using namespace std;queue<pair<int , int > >q; bool vis[5005 ];int main () int n, A, B, now, step; scanf ("%d%d%d" , &n, &A, &B); q.push (make_pair (A, 0 )); vis[A] = true ; while (!q.empty ()){ now = q.front ().first; step = q.front ().second; q.pop (); if (now == B){ printf ("%d\n" , step); break ; } if (now + 1 <= n && !vis[now + 1 ]){ q.push (make_pair (now + 1 , step + 1 )); vis[now + 1 ] = true ; } if (now - 1 >= 0 && !vis[now - 1 ]){ q.push (make_pair (now - 1 , step + 1 )); vis[now - 1 ] = true ; } if (now * 2 <= n && !vis[now * 2 ]){ q.push (make_pair (now * 2 , step + 1 )); vis[now * 2 ] = true ; } } return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 #include <bits/stdc++.h> using namespace std;queue<pair<int , int > > q; bool vis[5005 ];int main () int n, A, B, now, step; scanf ("%d%d%d" , &n, &A, &B); q.push (make_pair (A, 0 )); vis[A] = true ; while (!q.empty ()){ if (now == B) break ; now = q.front ().first; step = q.front ().second; q.pop (); if (now + 1 <= n && !vis[now+1 ]){ q.push (make_pair (now+1 , step + 1 )); vis[now+1 ] = true ; } if (now - 1 >= 0 && !vis[now+1 ]){ q.push (make_pair (now-1 , step + 1 )); vis[now-1 ] = true ; } if (now * 2 <= n && !vis[now*2 ]){ q.push (make_pair (now*2 , step + 1 )); vis[now*2 ] = true ; } } printf ("%d\n" , step); return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 #include <bits/stdc++.h> using namespace std;queue<pair<int , int > > q; bool vis[5005 ];int main () int n, A, B, now, step; scanf ("%d%d%d" , &n, &A, &B); q.push (make_pair (A, 0 )); vis[A] = true ; while (!q.empty ()){ if (A == B) break ; A = q.front ().first; step = q.front ().second; q.pop (); if (A + 1 <= n && !vis[A+1 ]){ q.push (make_pair (A+1 , step + 1 )); vis[A+1 ] = true ; } if (A - 1 >= 0 && !vis[A+1 ]){ q.push (make_pair (A-1 , step + 1 )); vis[A-1 ] = true ; } if (A * 2 <= n && !vis[A*2 ]){ q.push (make_pair (A*2 , step + 1 )); vis[A*2 ] = true ; } } printf ("%d\n" , step); return 0 ; }
密码锁
动态规划 引例
爬楼梯
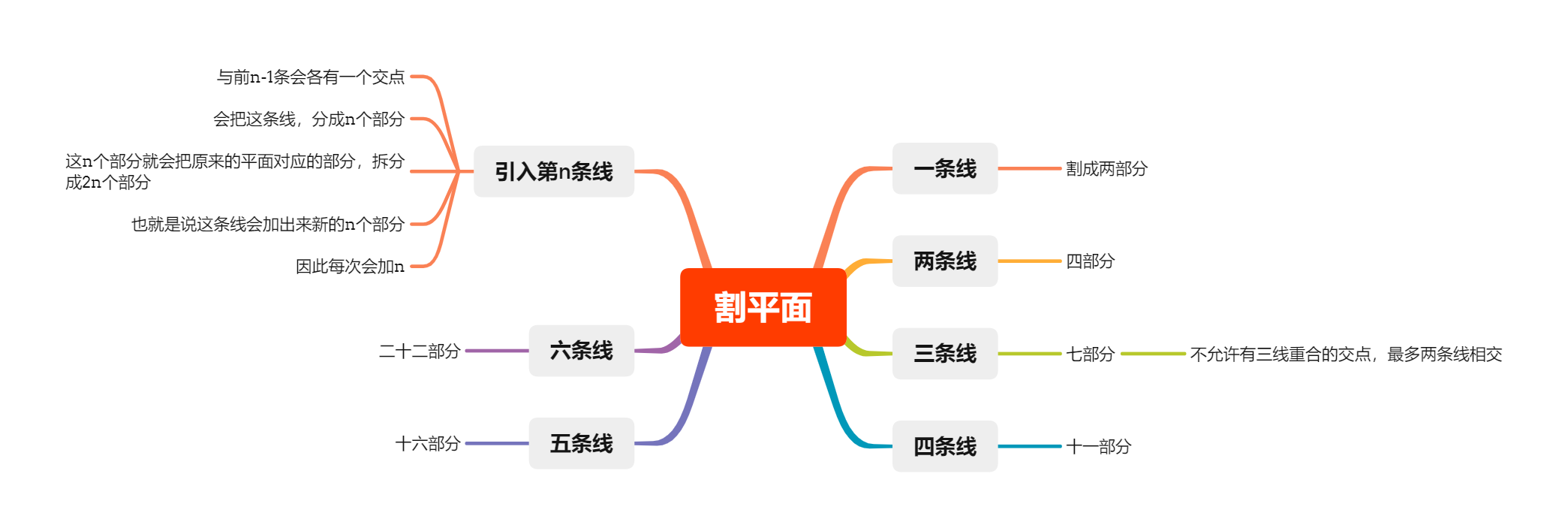
割平面
递推
递归引例 兔子数列
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 #include <bits/stdc++.h> using namespace std; const int N = 1e3 ;typedef long long ll;ll f[N]; int main () int n; cin >> n; f[0 ] = f[1 ] = 1 ; for (int i = 2 ; i <= n; ++i){ f[i] = f[i-1 ] + f[i-2 ]; } cout << f[n] << endl; ll a = 1 , b = 1 , c = 1 ; for (int i = 2 ; i <= n; ++i){ c = a + b; a = b; b = c; } cout << c << endl; return 0 ; }
装错信封
梳理
之前的均是错排,这第n个加进去之后,可以和任意n-1个信封进行交换,最终结果都是对的
之前有一个信封仍在原位,n-2个已经发生错排,此时可以直接使第n个加入的与那个仍处于原位的信封互换位置,原位的同样有n-1个可能性,并且此时错排的可能性是F(n-2),意思是此时的分析是建立在已经有F(n-2)个元素发生错拍的基础上,才能考虑这n-1的可能性
我们也可以继续考虑两个信封在原位,三个信封在原位,可是已经没有必要了,动态规划只考虑每一步,只要能够递推了就不用考虑了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 #include <bits/stdc++.h> using namespace std; const int N = 1e3 ;typedef long long ll;ll f[N]; int main () int n; cin >> n; f[1 ] = 0 ; f[2 ] = 1 ; for (int i = 3 ; i <= n; ++i){ f[i] = (f[i-1 ] + f[i-2 ]) * (i - 1 ); } cout << f[n] << endl; ll a = 0 , b = 1 , c = 1 ; for (int i = 3 ; i <= n; ++i){ c = (a + b) * (i - 1 ); a = b; b = c; } if (n != 1 ){ cout << c << endl; } else { cout << 0 << endl; } return 0 ; }
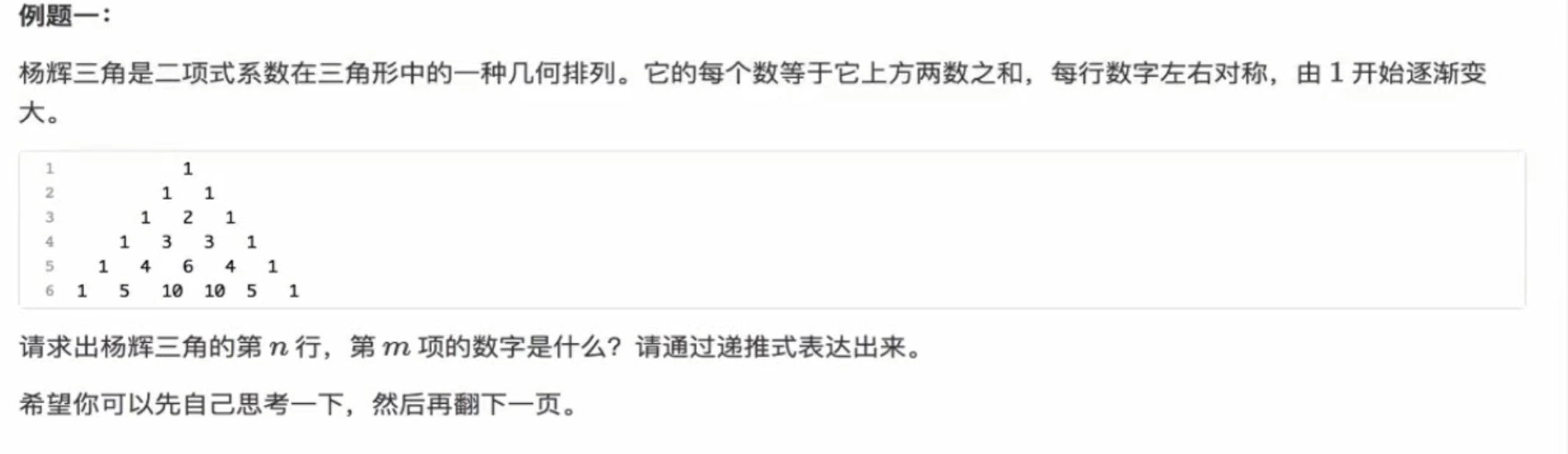
二维递推 引例 杨辉三角
马踏过河卒
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 #include <bits/stdc++.h> using namespace std; int dir[8 ][2 ] = {{1 , 2 }, {1 , -2 }, {2 , 1 }, {2 , -1 }, {-1 , -2 }, {-2 , -1 }, {-2 , 1 }, {-1 , 2 }};bool d[30 ][30 ];long long dp[30 ][30 ];int main () int n, m, cx, cy; cin >> n >> m >> cx >> cy; d[cx][cy] = true ; for (int i = 0 ; i < 8 ; i++){ int tx = cx + dir[i][0 ]; int ty = cy + dir[i][1 ]; if (tx >= 0 && tx <= n && ty >= 0 && ty <= m){ d[tx][ty] = true ; } } dp[0 ][0 ] = 1 ; for (int i = 0 ; i <= n; i++){ for (int j = 0 ; j <= m; j++){ if (d[i][j] == false ){ if (i){ dp[i][j] += dp[i - 1 ][j]; } if (j){ dp[i][j] += dp[i][j - 1 ]; } } } } cout << dp[n][m] << endl; return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 #include <bits/stdc++.h> using namespace std;int mov[8 ][2 ] = {{1 , 2 }, {1 , -2 }, {2 , 1 }, {2 , -1 }, {-1 , 2 }, {-1 , -2 }, {-2 , 1 }, {-2 , -1 }};bool vis[30 ][30 ];int dp[30 ][30 ];int tx, ty;int main () int n, m, cx, cy; cin >> n >> m >> cx >> cy; vis[cx][cy] = true ; for (int i = 0 ; i < 8 ; i++){ tx = cx + mov[i][0 ]; ty = cy + mov[i][1 ]; if (tx >=0 && tx <= n && ty >=0 && ty <= m) vis[tx][ty] = true ; } dp[0 ][0 ] = 0 ; for (int i = 0 ; i <= n; i++){ for (int j = 0 ; j <= m; j++){ if (!vis[i][j]) if (i){ dp[i][j] = dp[i-1 ][j] + 1 ; } if (j){ dp[i][j] = dp[i][j-1 ] + 1 ; } } } cout << dp[n][m] << endl; return 0 ; }
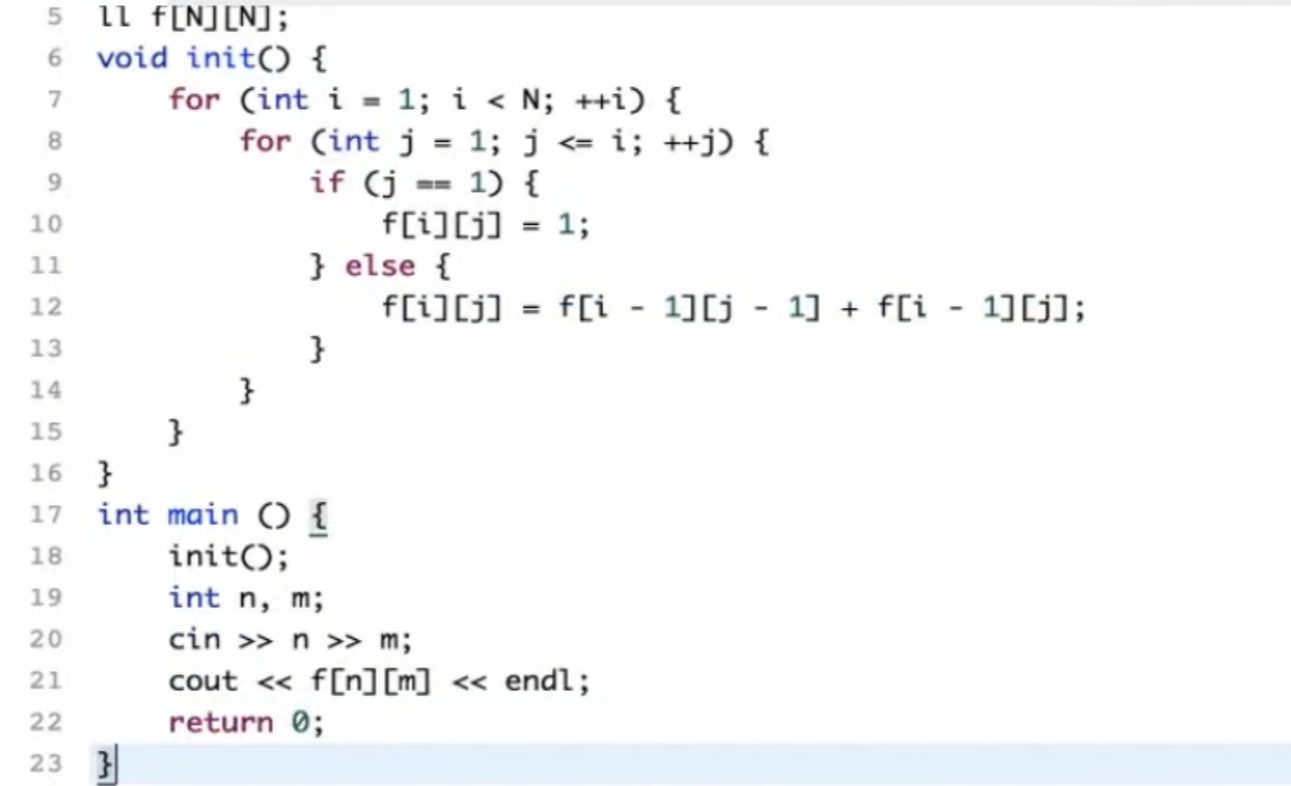
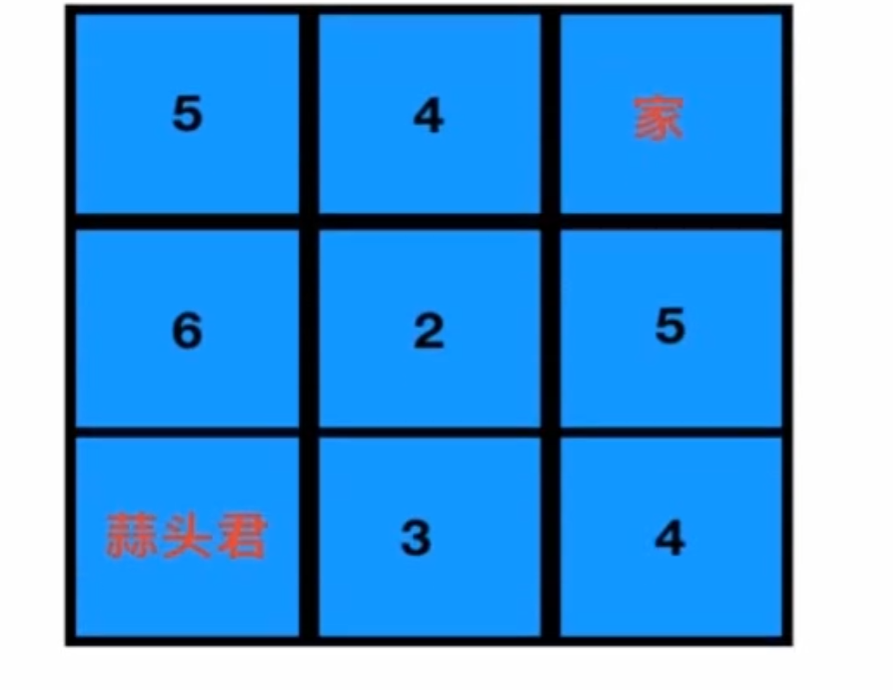
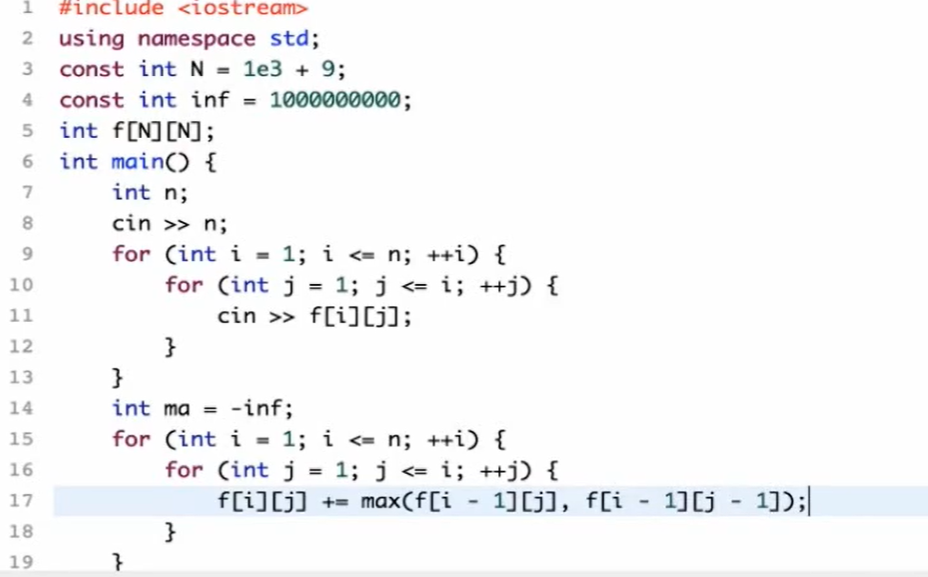
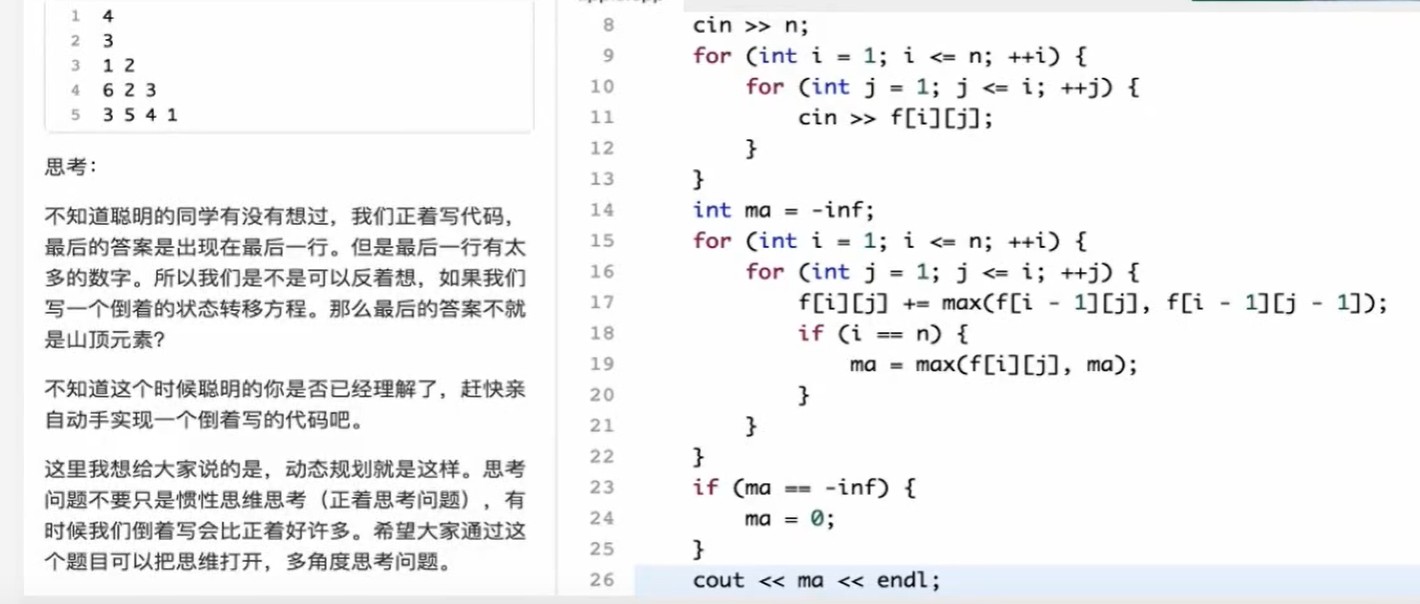
回家是最好的礼物 下面DP入门再做
我们的推法只能选择从左往右,从下往上,因为我们只有知道了这次的结果,才能预判下一次的结果,最佳结果 3 2 4
动态规划入门 确定一个方便我们解决问题的状态 + 我们能做出状态之间的转移 + 边界处理
基本概念
回家问题 和上面二维递推题目描述一样的,我们这次正式开做!
1 2 3 4 5 6 7 输入 3 0 3 4 6 2 5 5 4 3 输出 12
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 #include <bits/stdc++.h> using namespace std; int main () int a[110 ][110 ]; int dp[110 ][110 ]; int n; cin >> n; for (int i = 1 ; i <= n; i++){ for (int j = 1 ; j <= n; j++){ cin >> a[i][j]; } } dp[1 ][1 ] = 0 ; for (int i = 1 ; i <= n; i++){ for (int j = 1 ; j <= n; j++){ if (i == 1 && j == 1 ){ continue ; } else if (i == 1 ){ dp[i][j] = dp[i][j-1 ] + a[i][j]; } else if (j == 1 ){ dp[i][j] = dp[i-1 ][j] + a[i][j]; } else { dp[i][j] = min (dp[i-1 ][j], dp[i][j-1 ]) + a[i][j]; } } } cout << dp[n][n] << endl; return 0 ; }
捡水果
多维动态简要
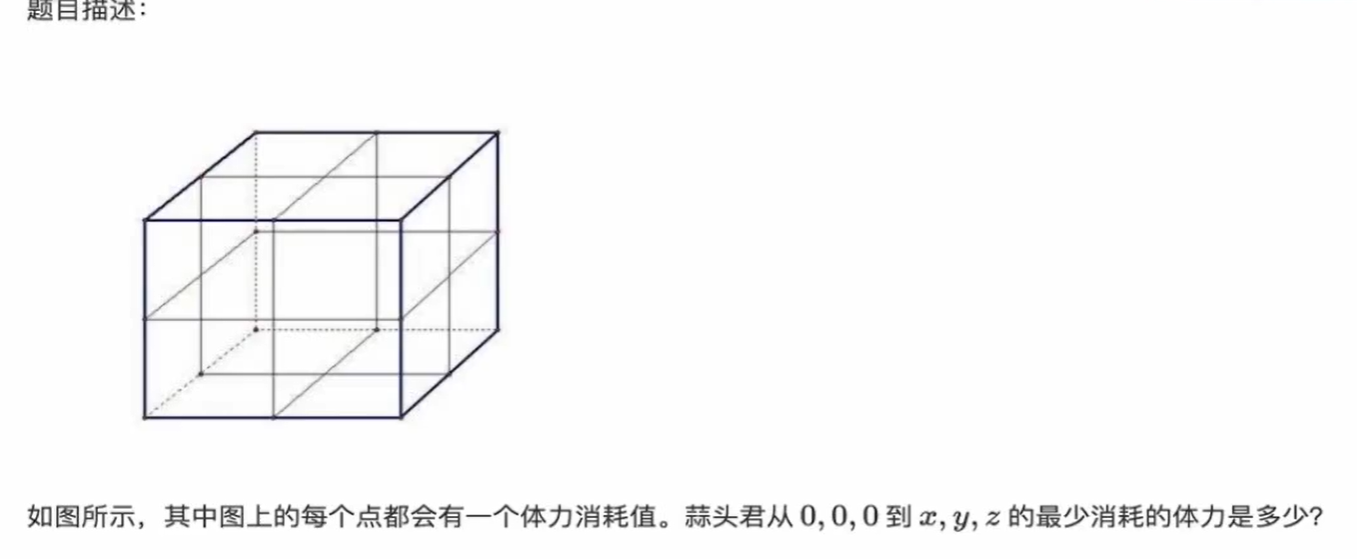
回家plus
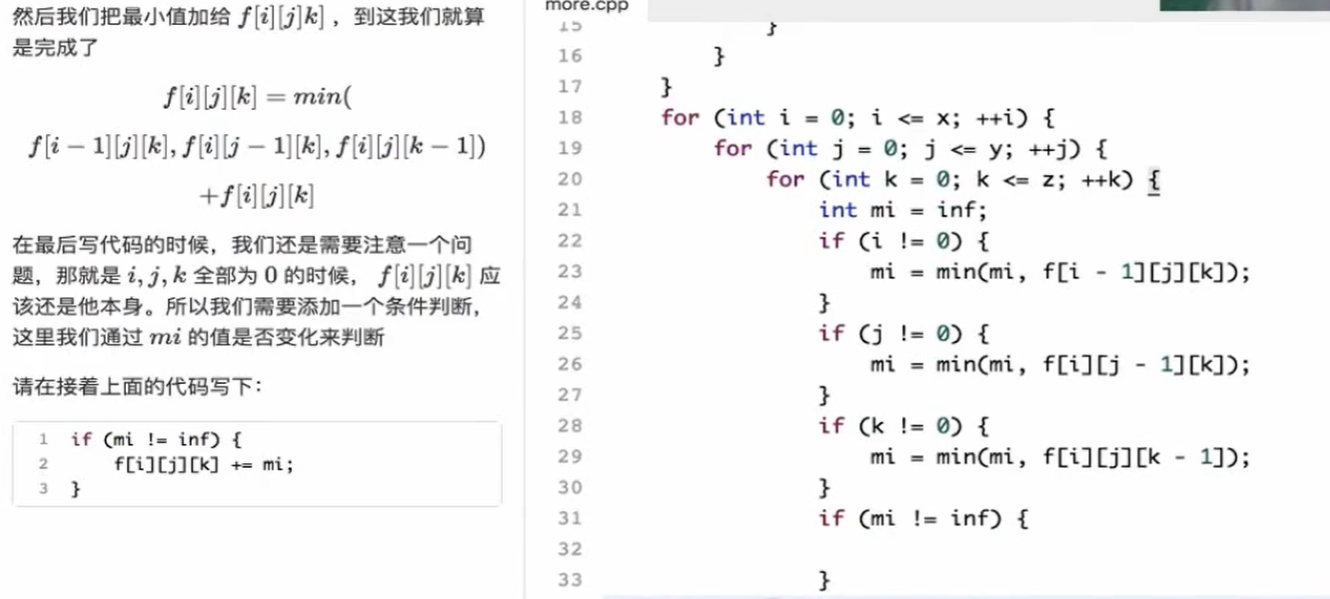
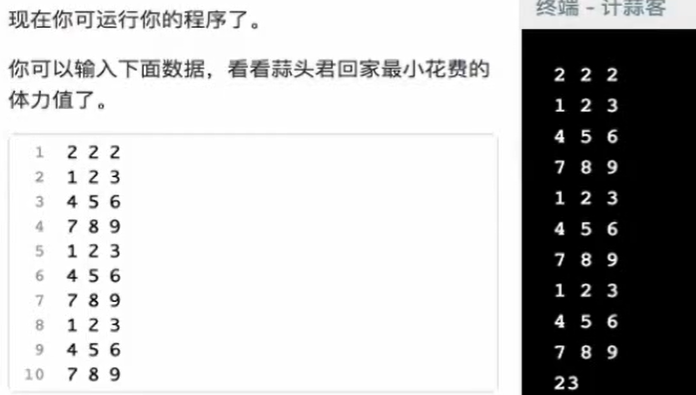
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 #include <bits/stdc++.h> using namespace std;const int N =1e2 + 9 ;const int inf = 0x3f3f3f3f ;int f[N][N][N];int main () int x, y, z; cin >> x >> y >> z; for (int i = 0 ; i <= x; i++){ for (int j = 0 ; j <= y; j++){ for (int k = 0 ; k <= z; k++){ cin >> f[i][j][k]; } } } for (int i = 0 ; i <= x; i++){ for (int j = 0 ; j <= y; j++){ for (int k = 0 ; k <= z; k++){ int mi = inf; if (i != 0 ){ mi = min (mi, f[i-1 ][j][k]); } if (j != 0 ){ mi = min (mi, f[i][j-1 ][k]); } if (k != 0 ){ mi = min (mi, f[i][j][k-1 ]); } if (mi != inf){ f[i][j][k] = mi; } } } } cout << f[x][y][z] << endl; return 0 ; }
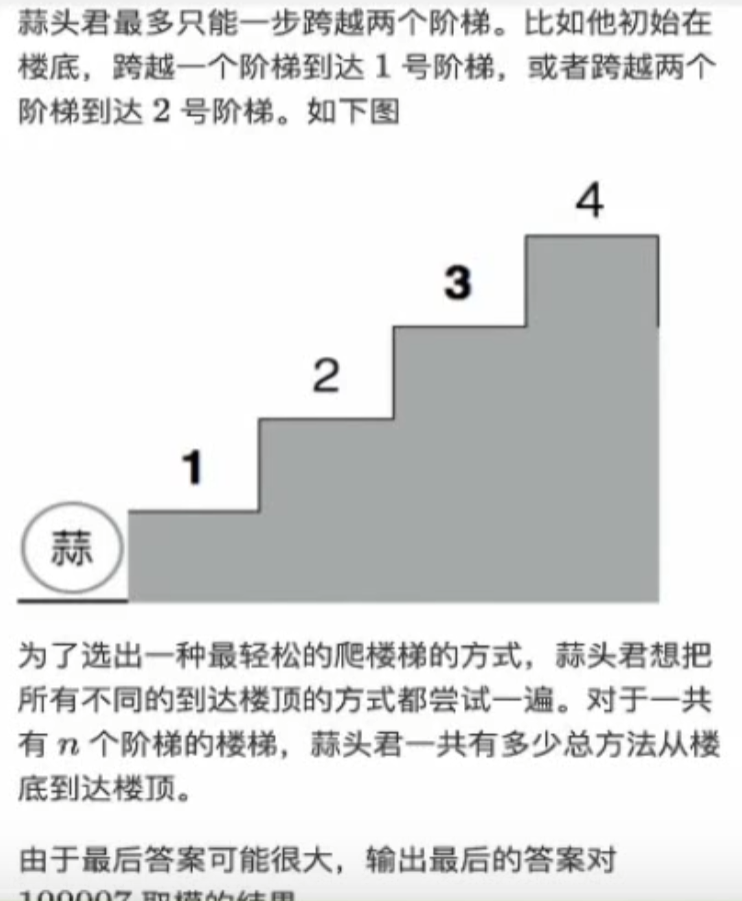
奇数爬梯子
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 #include <bits/stdc++.h> using namespace std;const int mod = 100007 ;int dp[1010 ];int main () int n; cin >> n; dp[0 ] = 1 ; for (int i = 1 ; i <= n; i++){ for (int j = i-1 ; j >= 0 ; j -= 2 ){ dp[i] += dp[j]; dp[i] %= mod; } } cout << dp[n] << endl; return 0 ; }
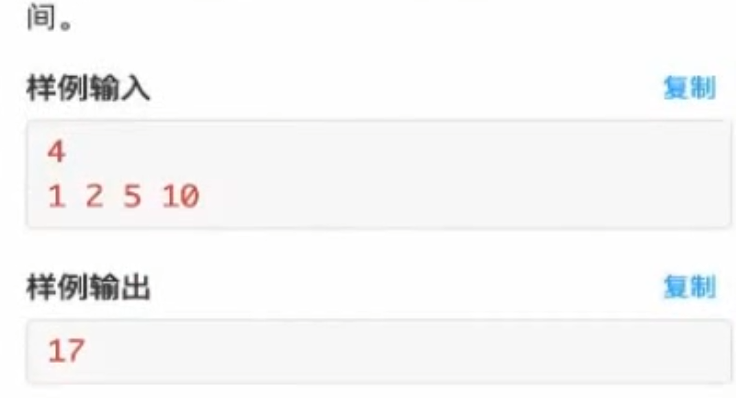
弹簧板加强
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 #include <bits/stdc++.h> using namespace std;const int maxn = 100010 ;int a[maxn], dp[maxn];int main () int n; cin >> n; for (int i = 1 ; i <= n; ++i){ cin >> a[i]; } int ans = 0 ; for (int i = 0 ; i <= n; i++){ if (i-a[i] >=0 ){ dp[i] = dp[i - a[i]] + 1 ; ans = max (ans, dp[i]); } } cout << ans << endl; return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 #include <bits/stdc++.h> const int maxn = 100010 ;int a[maxn], dp[maxn];int main () int n; cin >> n; memset (dp, 0 , sizeof for (int i = 1 ; i <= n; ++i){ cin >> a[i]; } int ans = 0 ; for (int i = n; i >= 1 ; i--){ dp[i] = dp[i + a[i]] + 1 ; ans = max (ans, dp[i]); } cout << ans << endl; }
传娃娃
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 #include <bits/stdc++.h> using namespace std;int f[35 ][35 ];int main () int n, m; cin >> n >> m; f[0 ][1 ] = 1 ; for (int i = 1 ; i <= m; i++){ for (int j = 1 ; j <= n; j++){ if (j == n){ f[i][j] = f[i-1 ][1 ] + f[i-1 ][n-1 ]; }else if (j == 1 ){ f[i][j] = f[i-1 ][2 ] + f[i-1 ][n]; }else { f[i][j] = f[i-1 ][j-1 ] + f[i-1 ][j+1 ]; } } } cout << f[m][1 ] << endl; }
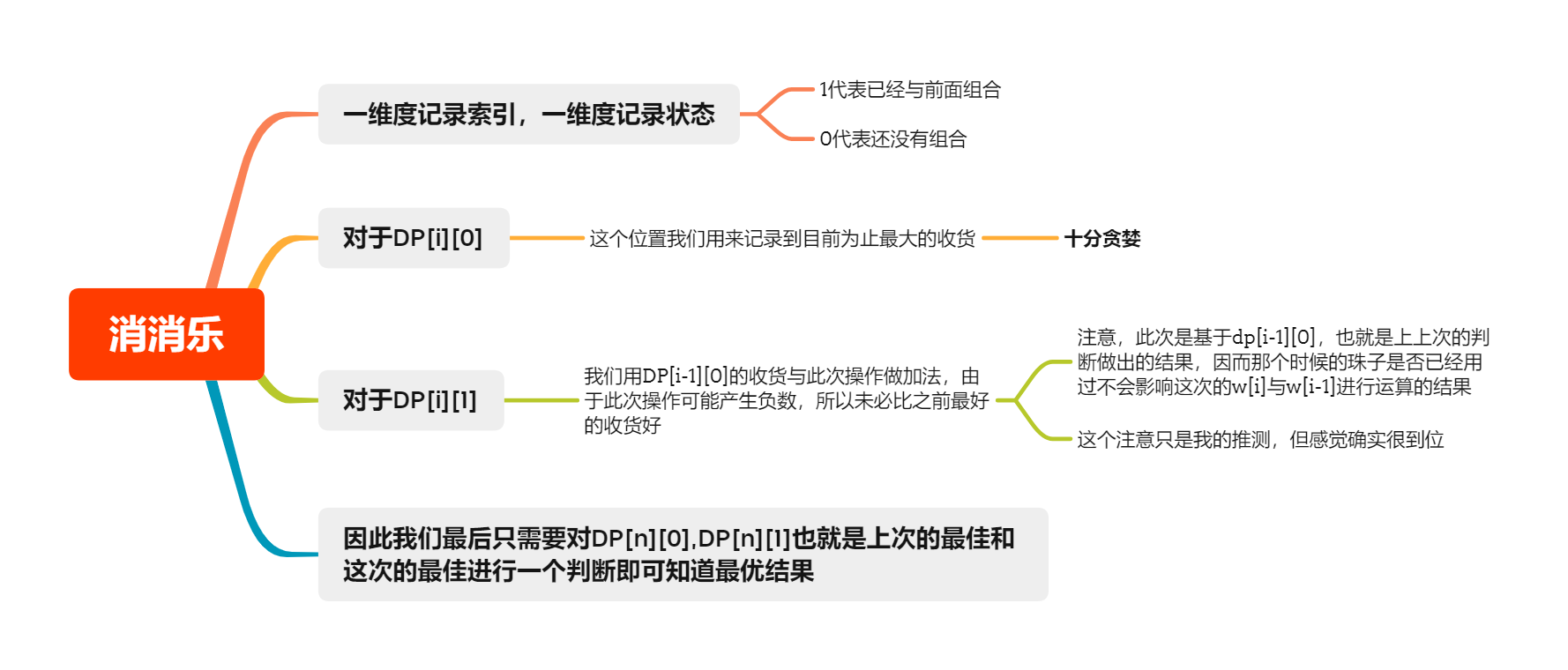
消消乐
1 2 3 4 5 输入 8 -9 -5 -4 -2 4 -5 -4 2 输出 73
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 #include <bits/stdc++.h> using namespace std;const int maxn = 10010 ;int dp[maxn][2 ];int w[maxn];int main () int n; cin >> n; for (int i = 1 ; i <= n; i++){ cin >> w[i]; } dp[1 ][0 ] = 0 ; for (int i = 2 ; i <= n; ++i){ dp[i][0 ] = max (dp[i-1 ][0 ], dp[i-1 ][1 ]); dp[i][1 ] = dp[i-1 ][0 ] + w[i]*w[i-1 ]; } cout << max (dp[n][0 ],dp[n][1 ]) << endl; return 0 ; }
抓住动态规划的核心思想!只考虑当前的这一步可能造成的影响 ,别去想太多
数组分组 考虑我们最后一组分的是那一组,前面我们不考虑,假定前面已经分完了,这一堆是新的一组,他的情况
1 2 3 4 5 输入 7 52 26 1 36 72 48 43 输出 1596
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 #include <bits/stdc++.h> using namespace std;const int maxn = 1010 ;const int mod = 1000 ;int a[maxn];int dp[maxn];int pre[maxn][maxn];int main () int n; cin >> n; for (int i = 1 ; i <= n; ++i){ cin >> a[i]; } for (int i = 1 ; i <= n; ++i){ pre[i][i] = a[i]; for (int j = i + 1 ; j <= n; ++j){ pre[i][j] = pre[i][j-1 ] * a[j] % mod; } } dp[0 ] = 0 ; dp[1 ] = a[1 ]; for (int i = 2 ; i <= n; ++i){ for (int j = 0 ; j < i; ++j){ dp[i] = max (dp[i], dp[j] + pre[j+1 ][i]); } } cout << dp[n] << endl; return 0 ; }
墙壁涂色 注意是环形
想象一下,第n个加入,只有两种可能,n的两边(n-1)(1)相同/不相同,不相同即为F(n-1)个可行解,相同即为F(n-2)在加上n自己有两种可能的颜色选择(由于两端颜色相同,将其中一个看做是透明的不参与就好,因为它的颜色情况已然固定,且一定不会与他除了n的另一端产生矛盾)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 #include <bits/stdc++.h> using namespace std;int main () int n; long long a[51 ]; a[1 ] = 3 ; a[2 ] = 6 ; a[3 ] = 6 ; for (int i = 4 ; i <= 50 ; i++){ a[i] = a[i-1 ] + a[i-2 ] * 2 ; } cin >> n; cout << a[n] << endl; return 0 ; }
过河
由于一次允许两个人过河,我们就拆分成,一次带一个人过河,和一次带两个人过河的最短时间问题,末状态为现在该过河的都已经过去了,正式开始:一次带一个人,注意经过了sort排序,所以0号最快,他由于已经过去了,他得回来,花费dp[0]时间,然后他带着a[i]还有dp[i-1](之前处理累计最小时间)成为这次带一个人过河所需要的真正时间;对于一次带两个人,那dp[0]得回来送手电筒,然后i和i-1两个人过去,此时需要带的时间是dp[i-2](这个时候i和i-1都未过河),并且由于dp[0]没有回到河对岸,dp[1]应该回来带带他,所以2*dp[1]也就是dp[1]过来,带着dp[0]再过去,恢复状态.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 #include <bits/stdc++.h> using namespace std;int a[1010 ];int dp[1010 ];int main () int n; cin >> n; for (int i = 0 ; i < n; i++){ cin >> a[i]; } sort (a,a+n); dp[0 ] = a[0 ]; dp[1 ] = a[1 ]; for (int i = 2 ; i < n; i++){ dp[i] = min (dp[i-1 ] + dp[0 ] + a[i], dp[i-2 ] + dp[0 ] + a[i] + 2 *dp[1 ]); } cout << dp[n-1 ] << endl; return 0 ; }
常见动态规划模型 最大子段和
暴力+前缀和优化
动态规划
1 2 3 4 5 输入 6 -2 11 -4 13 -5 -2 输出 20
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 #include <bits/stdc++.h> using namespace std;const int inf = 0x3f3f3f3f ;int num[101 ];int main () int N; cin >> N; for (int i = 0 ; i < N; i++){ cin >> num[i]; } int ans = -inf; for (int i = 0 ; i < N; i++){ ans = max (ans, num[i]); } if (ans <= 0 ){ cout << ans << endl; }else { int sum = 0 ; for (int i = 0 ; i < N; i++){ if (sum + num[i] <= 0 ){ sum = 0 ; }else { sum += num[i]; } ans = max (ans, sum); } } cout << ans << endl; return 0 ; }
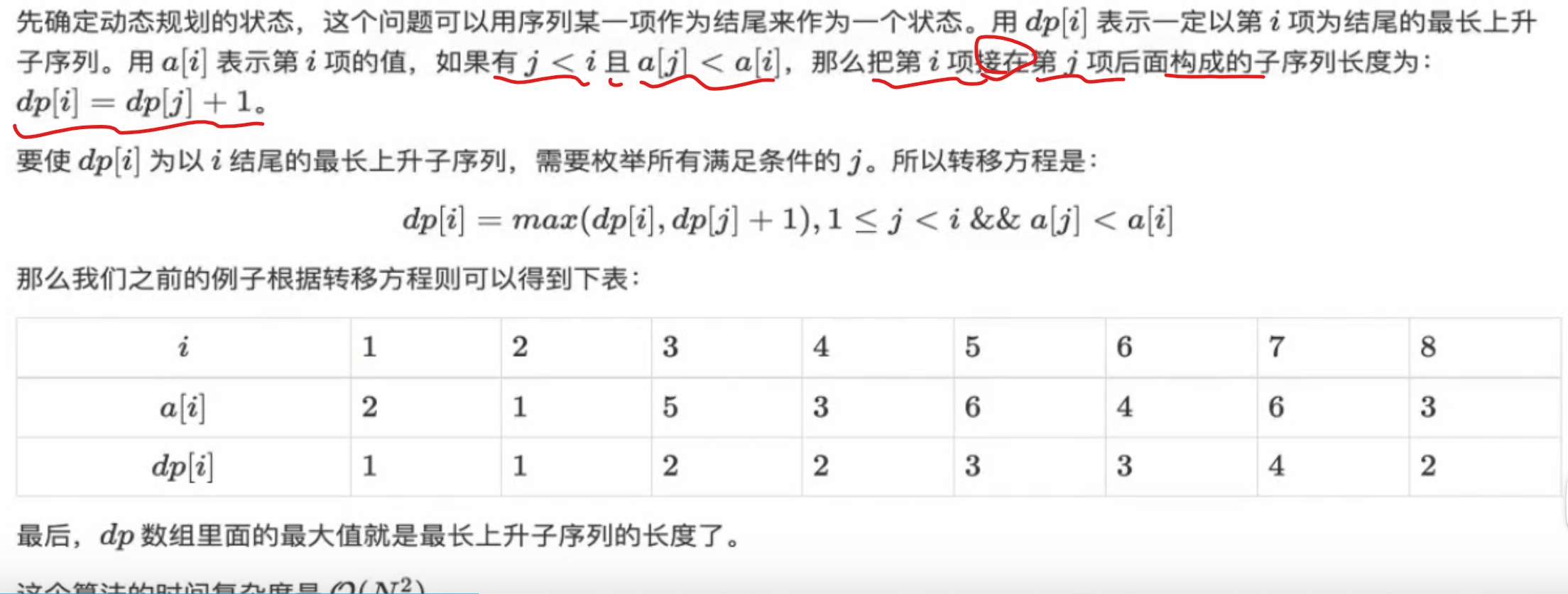
最长上升子序列 可以是取任意 ,但是不改变顺序
1 2 3 4 5 6 输入 6 3 2 6 1 4 5 输出//2 4 5 3
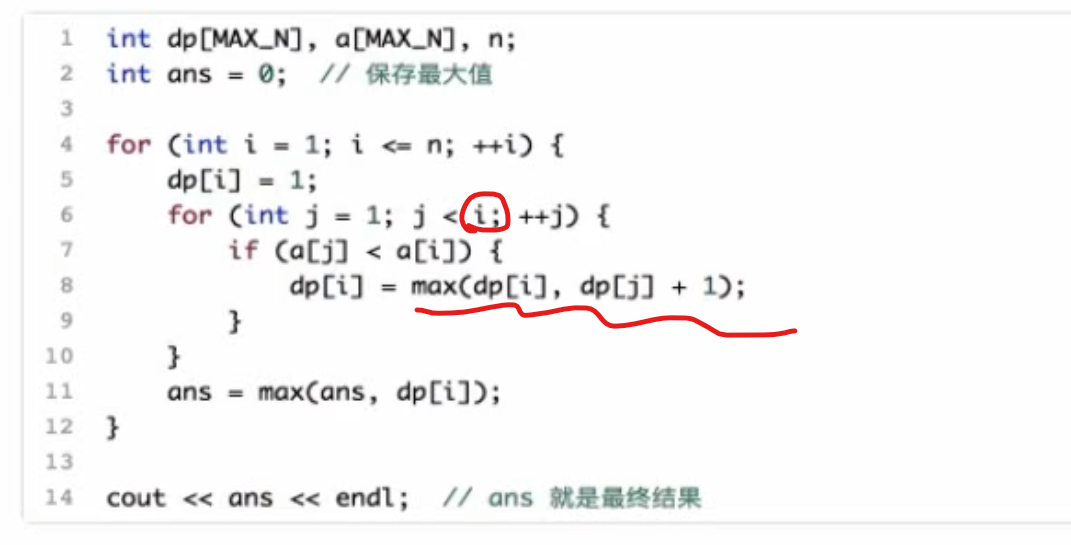
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 #include <bits/stdc++.h> using namespace std;int dp[101 ], a[101 ], n;int LIS () int ans = 0 ; for (int i = 1 ; i <= n; i++){ dp[i] = 1 ; for (int j = 1 ; j < i ; j++){ if (a[j] < a[i]){ dp[i] = max (dp[i], dp[j] + 1 ); } ans = max (ans, dp[i]); } } return ans; } int main () cin >> n; for (int i = 1 ; i <= n; i++){ cin >> a[i]; } cout << LIS () << endl; return 0 ; }
最长公共子序列 上一个应用是考虑以每一个为结尾,这个是考虑,到目前为止 ,有可能不以它为结尾
先要搞明白:最长公共子串和最长公共子序列的区别。
最长公共子串 (Longest Common Substirng):连续
最长公共子序列 (Longest Common Subsequence,LCS):不必连续
1 2 3 4 5 输入 abcdefgh acjlfabhh 输出//acfh 4
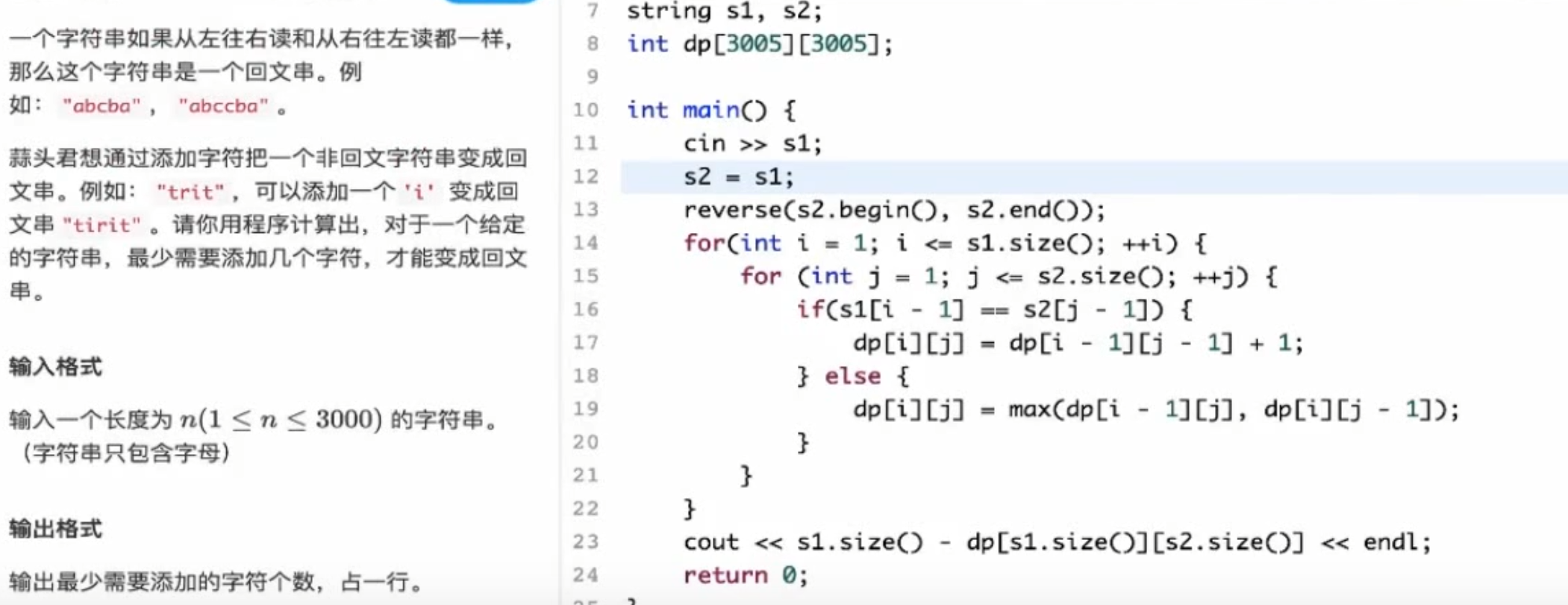
回文串 把这个字符串,倒过来,然后做一次公共子序列,这样我们就知道了这里面有多少个是已经回文了的,那么我们拿s1.size() 减掉这个数,就是最后的结果,并且,我们很容易可以想到,删除和添加字符,本质是一模一样,因为你添加了一个字符,就让本应该删除的字符对称 了!
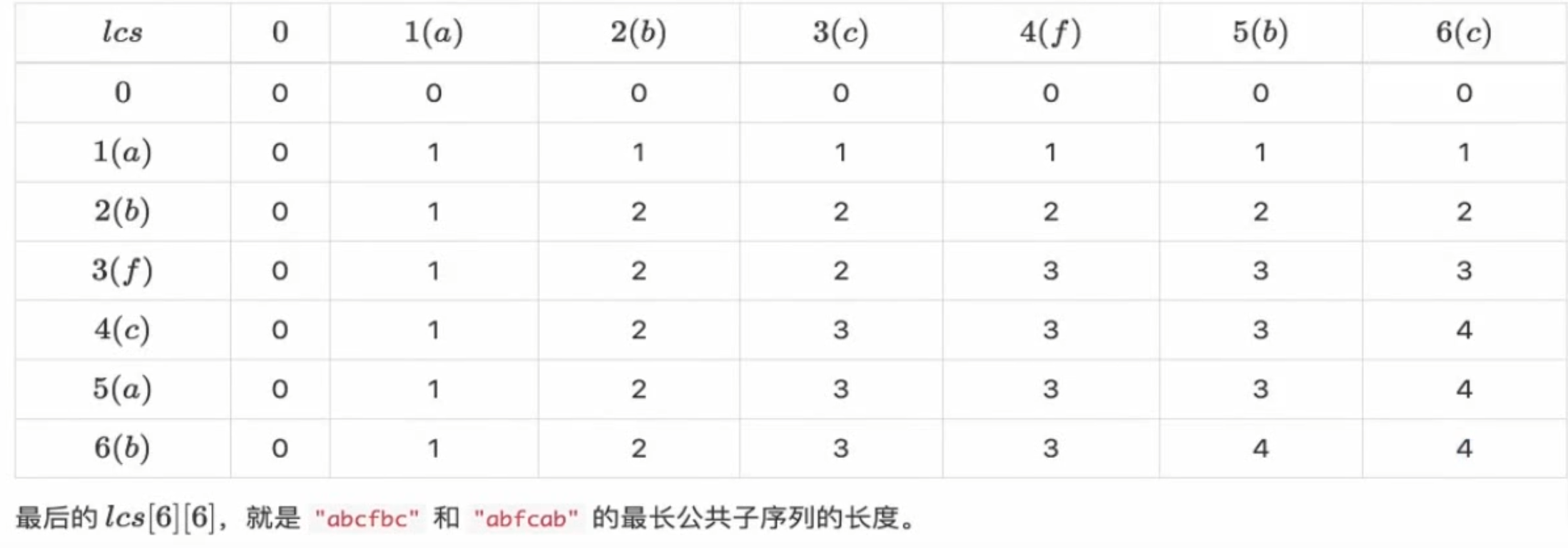
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 #include <bits/stdc++.h> using namespace std; string s1, s2; int dp[1005 ][1005 ]; int main () cin >> s1; s2 = s1; reverse (s2.begin (), s2.end ()); for (int i = 1 ; i <= s1.size (); i++){ for (int j = 1 ; j <= s2.size (); j++){ if (s1[i - 1 ] == s2[j - 1 ]){ dp[i][j] = dp[i-1 ][j-1 ] + 1 ; }else { dp[i][j] = max (dp[i-1 ][j], dp[i][j-1 ]); } } } cout << s1.size () - dp[s1.size ()][s1.size ()] << endl; return 0 ; }
1 2 3 4 案例解释 最长公共子序列,即为两个串,公共的序列(不限制是否连续)最长有多少 例如trit 和 tirt 他们的最长公共子序列,可以是trt 也可以是 tit ,长度为3
最大子矩阵和 二维题目,之前也有暴力解法做过,应该是枚举的哪一章,这也是最大子段的扩展
将最大字段和问题引申,给定一个矩阵,求一子矩阵的和,使该子矩阵中元素和是所有子矩阵元素和最大的一个。
对于这个问题,可以将“矩阵的和”通过叠放 转化为最大子段和问题中的数组,然后将这个数组再通过最大子段和问题找出sum。
1 2 3 4 5 6 7 输入 3 3 1 -2 3 -4 5 -6 7 -8 9 输出 9
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 #include <bits/stdc++.h> using namespace std;long long num[401 ][401 ];long long presum[401 ][401 ];int main () int N, M; long long sum=0 , ans; cin >> N >> M; ans = -0x3f3f3f3f ; for (int i = 1 ; i <= N; i++){ for (int j = 1 ; j <= M; j++){ cin >> num[i][j]; ans = max (ans, num[i][j]); } } if (ans <= 0 ){ cout << ans << endl; }else { for (int i = 1 ; i <= N; i++){ for (int j = 1 ; j <= M; j++){ presum[i][j] = presum[i-1 ][j] + num[i][j]; } } } for (int i = 1 ; i <= N; i++){ for (int j = i; j <= N; j++){ sum = 0 ; for (int k = 1 ; k <= M; k++){ if (sum + presum[j][k] - presum[i-1 ][k] < 0 ){ sum = 0 ; }else { sum += presum[j][k] - presum[i-1 ][k]; if (sum > ans) ans = sum; } } } } cout << ans <<endl; return 0 ; }
最大环状矩阵 拆环一般考虑复制几份,像这个就是往右往下往右下各复制成四份然后来做
我们这里采用的手段是取余,把空间控制在n,m的范围内,分别用两个能遍历到n,m的参数来整
控制一下所选的列数不超过n,行数不超过m,然后在这四个的区间里遨游遍历,这样就可以达到一个环状的效果
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 #include <bits/stdc++.h> using namespace std;long long num[100 ][100 ];long long presum[100 ][100 ];int main () int n, m; int ans = -0x3f3f3f3f ; cin >> n >> m; for (int i = 1 ; i <= n; i++){ for (int j = 0 ; j < m; j++){ cin >> num[i][j]; if (ans < num[i][j]) ans = num[i][j]; } } if (ans <= 0 ){ cout << ans << endl; } else { for (int i = 1 ; i <= n; i++){ for (int j = 0 ; j < m; j++){ presum[i][j] = presum[i-1 ][j] + num[i][j]; } } } int t = 0 ;int nowSum = 0 ; for (int i = 1 ; i <= n; i++){ for (int j = 1 ; j <= n; j++){ nowSum = 0 ; for (int k = 0 ; k < m; k++){ for (int l = 0 ; l < m; l++){ if (i <= j){ t = presum[j][(k+l) % m] - presum[i-1 ][(k+l) % m]; }else { t = presum[n][(k+l) % m] - (presum[i-1 ][(k+l) % m] - presum[j][(k+l) % m]); } if (nowSum + t < 0 ){ nowSum = 0 ; }else { nowSum += t; } if (ans < nowSum){ ans = nowSum; } } } } } cout << ans << endl; return 0 ; }
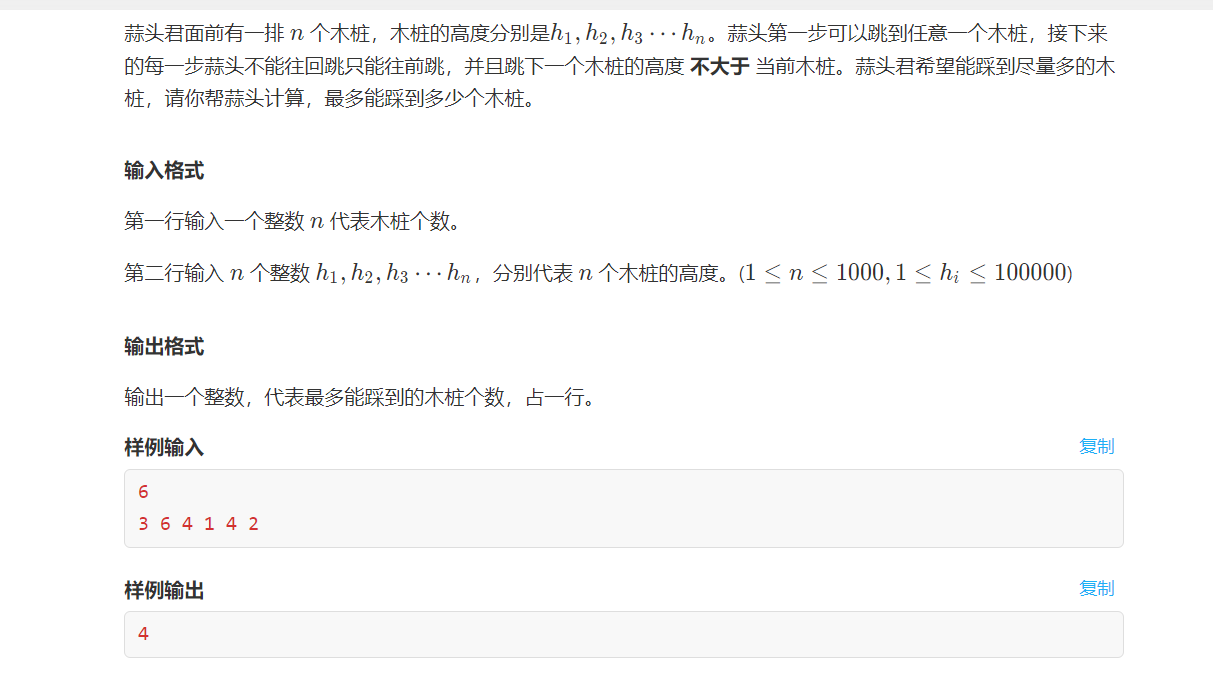
跳木桩(下降序列)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 #include <bits/stdc++.h> using namespace std;int a[1005 ];int dp[1005 ];int ans; int main () int n; cin >> n; for (int i = 0 ; i < n; i++){ cin >> a[i]; } for (int i = 0 ; i < n; i++){ dp[i] = 1 ; for (int j = 0 ; j < i; j++){ if (a[j] >= a[i]){ dp[i] = max (dp[i], dp[j] + 1 ); } ans = max (dp[i], ans); } } cout << ans << endl; return 0 ; }
背包问题 01背包(ZeroOnePack): 有N件物品和一个容量为V的背包。(每种物品均只有一件)第i件物品的费用是c[i],价值是w[i]。求解将哪些物品装入背包可使价值总和最大。
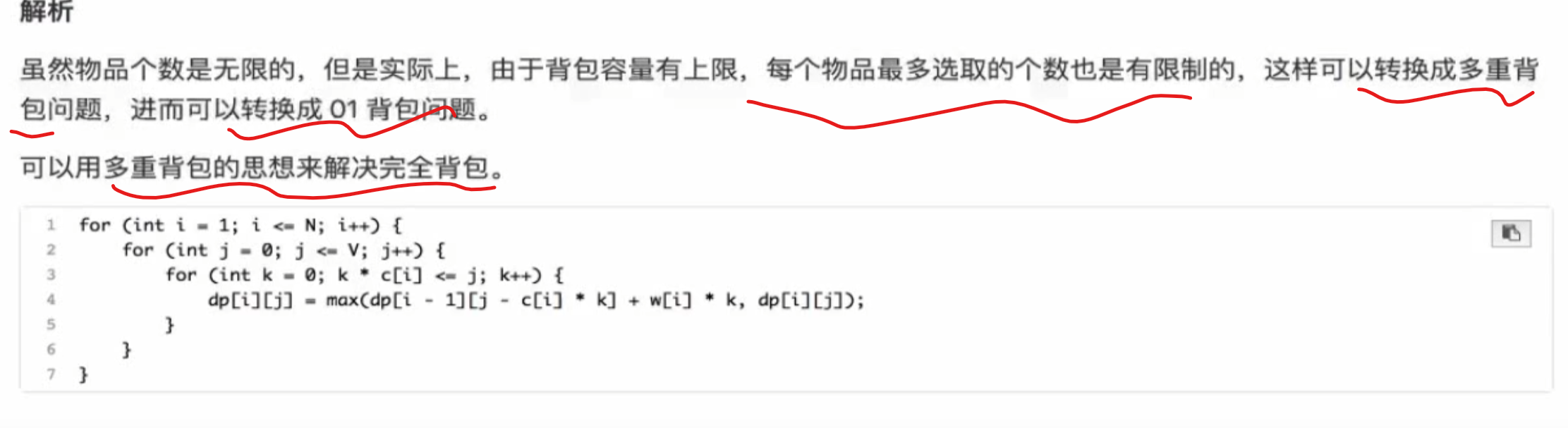
完全背包(CompletePack): 有N种物品和一个容量为V的背包,每种物品都有无限件可用。第i种物品的费用是c[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
多重背包(MultiplePack): 有N种物品和一个容量为V的背包。第i种物品最多有n[i]件可用,每件费用是c[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
比较三个题目,会发现不同点在于每种背包的数量,01背包是每种只有一件 ,完全背包是每种无限件 ,而多重背包是每种有限件 。
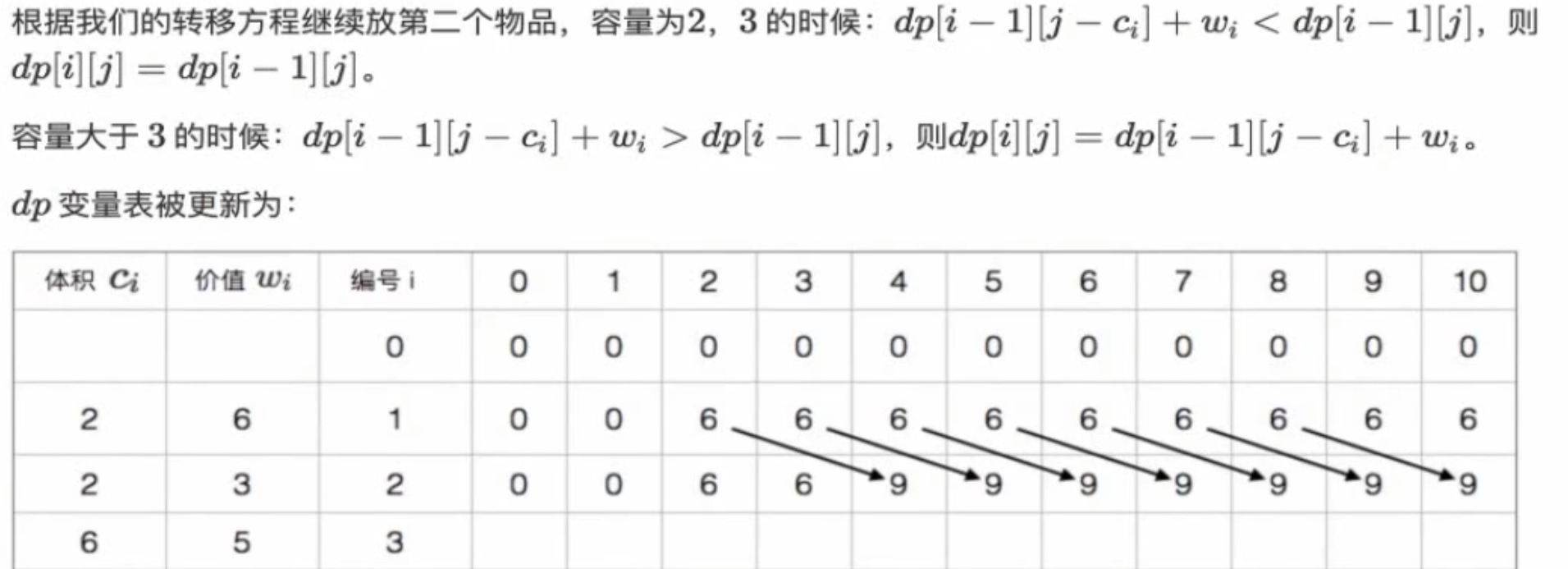
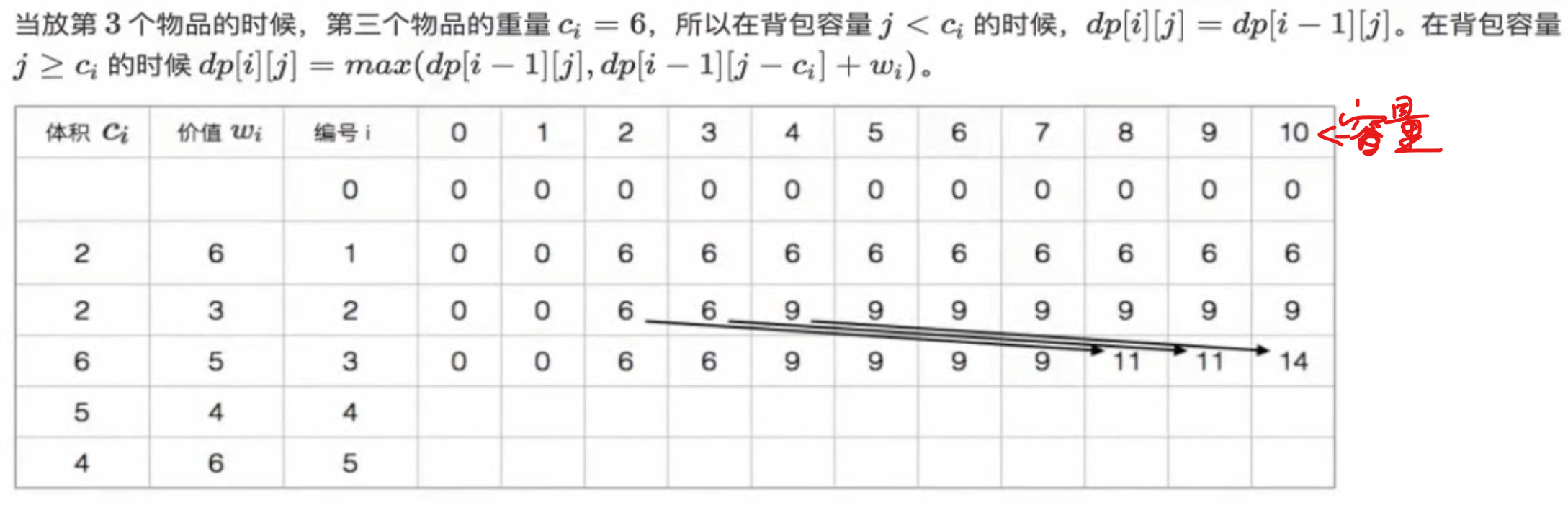
01背包
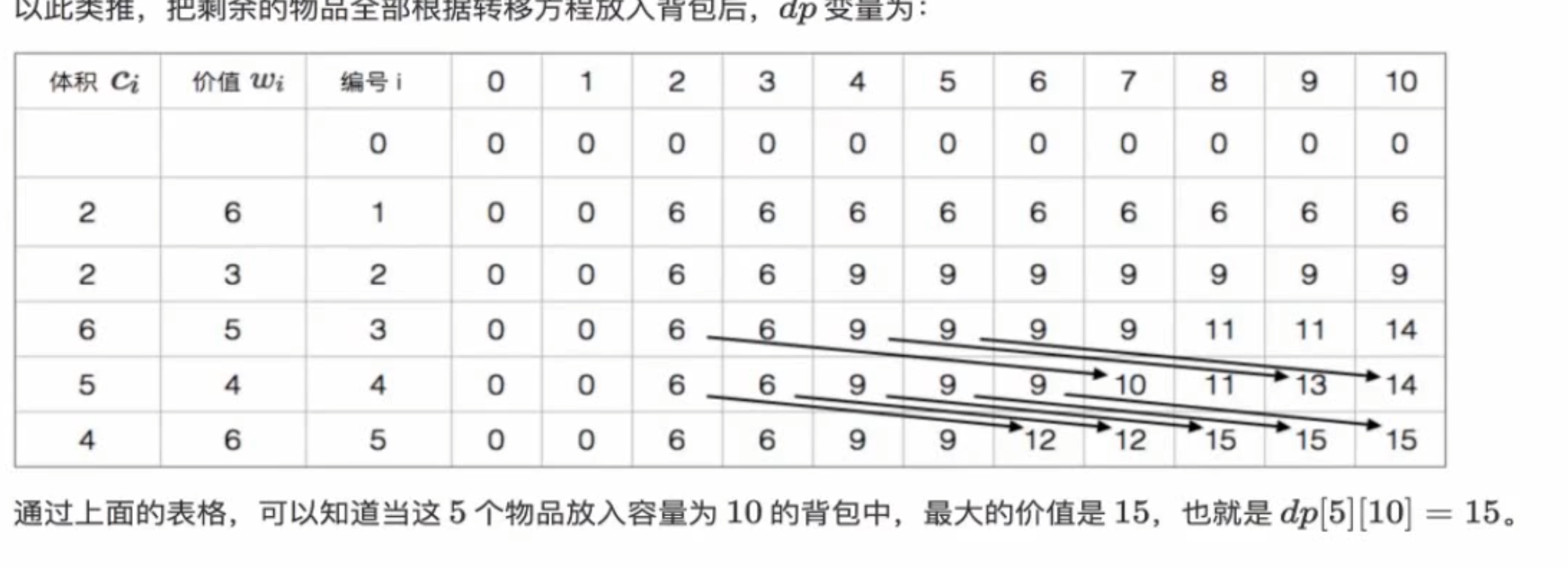
演示
观察最后一个图里面,有一个箭头指向10,他就是说明当体积为7的时候,这个时候的最大价值为10,第一个和第四个
实现01背包
1 2 3 4 5 6 7 8 9 输入 5 10 2 1 3 5 2 5 3 4 4 3 输出 9
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 #include <bits/stdc++.h> using namespace std; int dp[21 ][1010 ];int w[21 ], c[21 ];int main () int N, V; cin >> N >> V; for (int i = 1 ; i <= N; i++){ cin >> w[i] >> c[i]; } for (int i = 1 ; i <= N; i++){ for (int j = 0 ; j <= V; j++){ if (j >= c[i]){ dp[i][j] = max (dp[i-1 ][j-c[i]] + w[i], dp[i-1 ][j]); }else { dp[i][j] = dp[i-1 ][j]; } } } cout << dp[N][V] << endl; return 0 ; }
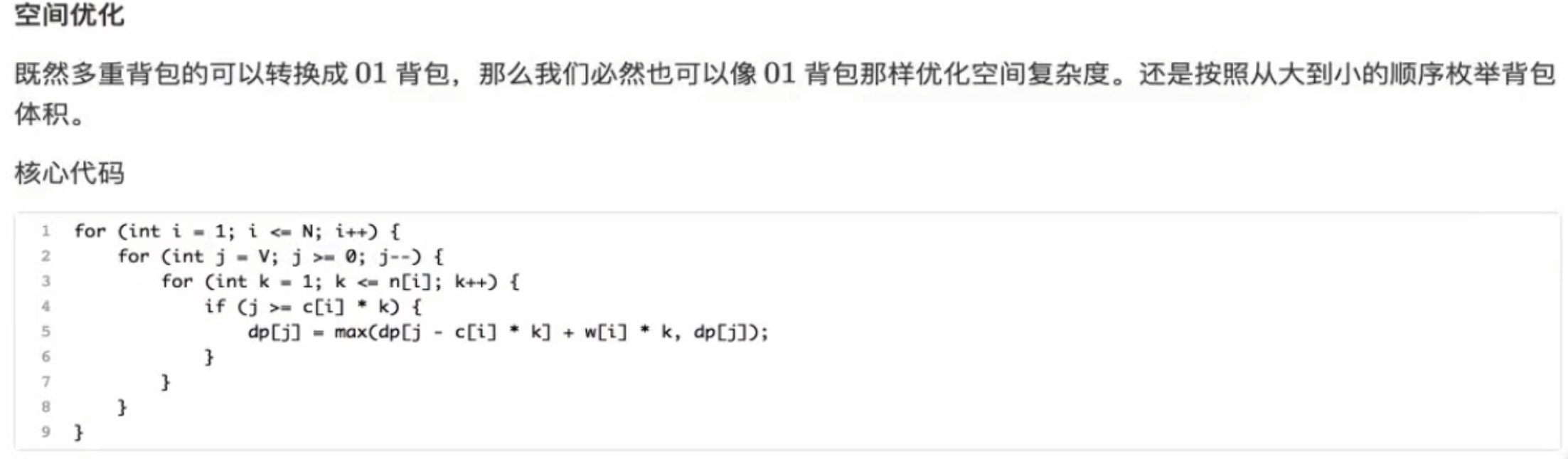
空间优化 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 #include <bits/stdc++.h> using namespace std;int dp[1010 ];int w[21 ], c[21 ];int main () int N, V; cin >> N >> V; for (int i = 1 ; i <= N; i++){ cin >> w[i] >> c[i]; } for (int i = 1 ; i <= N; i++){ for (int j = V; j >= c[i]; j--){ dp[j] = max (dp[j - c[i]] + w[i], dp[j]); } } cout << dp[V] << endl; return 0 ; }
多重背包 与完全背包的区别是:每种物品的数量是有限的
特殊的完全背包
朴素想法
实现
1 2 3 4 5 6 7 8 9 输入 5 10 2 1 2 3 5 3 2 5 1 3 4 2 4 3 8 输出 14?16?(原本是14,跑出来是16
1 2 3 4 5 6 7 8 for (int i = 0 ; i < N; i++){ for (int j = v; j >= c[i]; j--){ for (int k = 0 ; k <= n[i]; k++){ if (v >= k * c[i]) dp[j] = max (dp[j], dp[j- (c[i] * k)] + k * w[i]); } } }
二进制优化 用二进制表示,则能凑出来每一个正整数
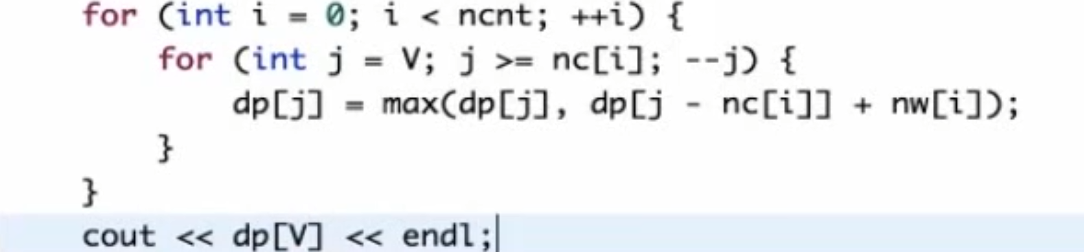
完全背包 每种物品的数量是无限的
利用多重背包
时间优化
空间优化
1 2 3 4 5 6 7 8 9 输入 5 10 2 1 3 5 2 5 3 4 4 3 输出 20
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 #include <bits/stdc++.h> using namespace std; int dp[1010 ];int w[21 ], c[21 ];int main () int n, v; cin >> n >> v; for (int i = 1 ; i <= n; i++){ cin >> w[i] >> c[i]; } for (int i = 1 ; i <= n; i++){ for (int j = c[i]; j <= v; j++){ dp[j] = max (dp[j - c[i]] + w[i], dp[j]); } } cout << dp[v] << endl; return 0 ; }
例题练习 购物袋1 蒜头君去超市购物,他有一只容量为 V 的购物袋,同时他买了 n 件物品,已知每件物品的体积 vi 。蒜头君想知道,挑选哪些物品放入购物袋中,可以使袋子剩余的空间最小。输入格式 输出格式 样例输入 样例输出
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 #include <bits/stdc++.h> using namespace std; int vi[10005 ]; int dp[10005 ]; int main () int v, n; int ans; cin >> v >> n; for (int i = 0 ; i < n; i++){ cin >> vi[i]; for (int j = v ; j >= vi[i] ; j--){ dp[j] = max (dp[j - vi[i]] + vi[i], dp[j]); } } cout << v - dp[v] << endl; return 0 ; }
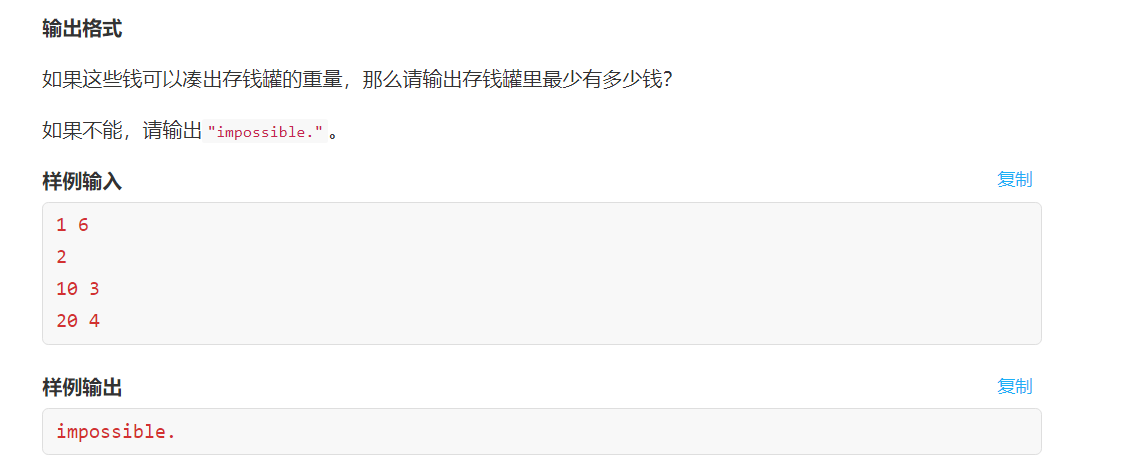
存钱罐
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 #include <bits/stdc++.h> using namespace std; int wi[10005 ], pi[10005 ]; int dp[10005 ]; int main () int e, f; int wEn; int n; cin >> e >> f >> n; wEn = f - e; memset (dp, 0x3f , sizeof dp[0 ] = 0 ; for (int i = 0 ; i < n; i++){ cin >> pi[i] >> wi[i]; for (int j = wi[i]; j <= wEn; j++){ dp[j] = min (dp[j], dp[j - wi[i]] + pi[i]); } } if (dp[wEn] != 0x3f3f3f3f ) cout << dp[wEn] << endl; else cout << "impossible." << endl; return 0 ; }
等和的分割子集
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 #include <bits/stdc++.h> using namespace std; long long dp[4000 ]; int main () int n; cin >> n; int sum = n * (n + 1 ) / 2 ; dp[0 ] = 1 ; for (int i = 1 ; i <= n; i++){ for (int j = sum; j >= i; j--){ dp[j] += dp[j-i]; } } if (sum % 2 == 1 ) cout << 0 ; else cout << dp[sum / 2 ] / 2 << endl; return 0 ; }
饭卡
思路: 要使卡上余额最少,在卡上余额最小且大于等于5时,买一份最贵的菜即可,求满足上述卡上余额,类似01背包,可以先拿出5元买最贵的菜,剩下m-5的钱,买n-1种菜,即01背包问题,求最大花费
1 2 3 4 5 6 7 8 9 10 11 12 Sample Input 1 50 5 10 1 2 3 2 1 1 2 3 2 1 50 0 Sample Output -45 32
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 #include <bits/stdc++.h> using namespace std;int a[1100 ],dp[1100 ];int main () int n,m,i,j; while (scanf ("%d" ,&n),n) { memset (dp,0 ,sizeof for (i=0 ;i<n;i++) scanf ("%d" ,&a[i]); scanf ("%d" ,&m); if (m<5 ) { printf ("%d\n" ,m); continue ; } sort (a,a+n); m=m-5 ; for (i=0 ;i<n-1 ;i++) { for (j=m;j>=a[i];j--) dp[j]=max (dp[j],dp[j-a[i]]+a[i]); } cout << 1 <<endl; printf ("%d\n" , m+5 -dp[m]-a[n-1 ]); } return 0 ; }
整数划分 整数划分问题是算法中的一个经典命题之一。把一个正整数n表示成一系列正整数之和:
正整数n的这种表示称为正整数n的划分。正整数n的不同划分个数称为正整数n的划分数,记作 p(n) 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 #include <bits/stdc++.h> using namespace std;int n[15 ];int dp[10005 ];int mod = 1e9 + 9 ;int main () int m; cin >> m; dp[0 ] = 1 ; for (int i = 0 ; i < m; i++){ cin >> n[i]; for (int j = 1 ; j <= n[i]; j++){ for (int k = j; k <= n[i]; k++){ (dp[k] += dp[k - j]) %= mod; } } cout << dp[n[i]] << endl; } return 0 ; }
offer 至少一份即转化为一份也没有
1 2 3 4 5 6 7 输入 10 3 4 0.1 4 0.2 5 0.3 输出 44.0%
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 #include <bits/stdc++.h> using namespace std;const int N = 1e4 + 9 ;double dp[N];int main () int n, m; cin >> n >> m; int x; double y; while (m--){ cin >> x >> y; for (int j = n; j >= x; j--){ dp[j] = max (dp[j], 1.0 - (1 - dp[j-x]) * (1 - y)); } } printf ("%.1lf%%\n" , dp[n] * 100 ); printf ("%.1lf" , dp[n] * 100 ); cout << "%" << endl; return 0 ; }
并查集
白嫖自(20条消息) 2021年SWPUACM暑假集训day2并查集算法_MangataTS的博客-CSDN博客
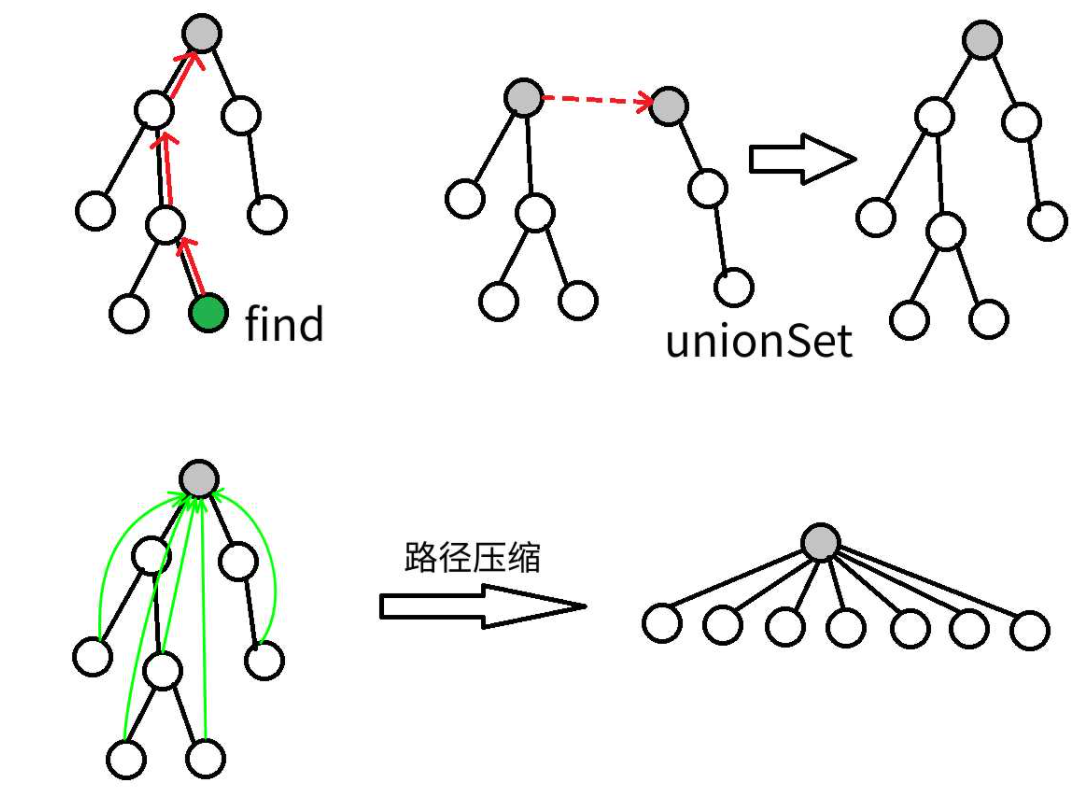
并查集是一种树形的数据结构 ,顾名思义,它用于处理一些不交集的 合并 及 查询 问题。 它支持两种操作:
1.查找(find):确定某个元素处于哪个子集
2.合并(merge):将两个子集合并成一个集合
并查集能方便并有效的处理元素和元素之间的分类关系
初始化 1 2 3 void init (int n) for (int i = 1 ;i <= n; ++i) fa[i] = i; }
先让每一个元素的父亲元素等于自己
查找 引用一个小故事:几个家族进行宴会,但是家族普遍长寿,所以人数众多。由于长时间的分离以及年龄的增长,这些人逐渐忘掉了自己的亲人,只记得自己的爸爸是谁了,而最长者(称为「祖先」)的父亲已经去世,他只知道自己是祖先。为了确定自己是哪个家族,他们想出了一个办法,只要问 自己的爸爸 是不是祖先,一层一层的向上 问,直到问到祖先。如果要判断两人是否在同一家族,只要看两人的祖先是不是同一人就可以了。
这就是并查集的思想,我们只用记录当前元素的父元素是谁,每当需要判断是否一类时,通过寻找该元素的祖先元素即可区分
实现代码:
非递归式 //推荐非递归,免得栈溢出
1 2 3 4 int find (int x) while (x != fa[x]) x = fa[x]; return x; }
递归式 1 2 3 4 int find (int x) if (x == fa[x]) return x; return find (fa[x]); }
路径压缩 路径压缩的目的是为了提高查找效率 ,大家不难想到当这个并查集树退化成了一条链的时候,每次查询都需要遍历整个链,这样十分的费时间,所以我们可以通过路径压缩的方式对这个树形结构进行优化,也就是将每一个节点的父节点直接变成根节点也就是祖先节点。
非递归实现: 1 2 3 4 5 6 7 8 9 10 int find (int x) int t = x; while (t != fa[t]) t = fa[t]; while (x != fa[x]) { int temp = fa[x]; fa[x] = t; x = temp; } return fa[x]; }
递归实现: 1 2 3 4 int find (int x) if (x != fa[x]) fa[x] = find (fa[x]); return fa[x]; }
1 2 3 int find (int x) return x == fa[x] ? x : (fa[x] = find (fa[x])); }
合并 接着上面的故事,如果说有两个家族突然交好,他们的关系想合在一起,这个时候就需要进行合并操作,让一边的祖先变成另一个祖先的父节点即可
代码实现:
1 2 3 4 5 void merge (int a,int b) a = find (a); b = find (b); if (a != b) fa[b] = a; }
前缀和优化
白嫖多个博客内容进行自己的梳理
前缀和以及差分看这一篇就够了 - xbhog - 博客园 (cnblogs.com)
前缀和与差分 - 知乎 (zhihu.com)
(20条消息) 前缀和与差分 图文并茂 超详细整理(全网最通俗易懂)_林深时不见鹿的博客-CSDN博客_前缀和与差分
1、前缀和-差分概念 首先需要知道前缀和的概念:即数组该位置之前的元素之和 ,可以把它理解为数学上的数列的前n项和,而差分 可以看成前缀和的逆运算 。合理的使用前缀和与差分,可以将某些复杂的问题简单化。
还有一个重要的点,在进行前缀和的运算时,下标从1开始,设数组a[0]=0 ;
比如a[5] = {0,1,2,3,4};
求a[1]的前缀和:a[1];
求a[2]的前缀和:a[1]+a[2];
……
为什么下标要从1 开始:为了方便后面的计算,避免下标转换,设为零,不影响结果(因为我们通常用a[i] += a[i-1])
2、前缀和算法有什么好处? 先来了解这样一个问题:
输入一个长度为n的整数序列。接下来再输入m个询问,每个询问输入一对l, r。对于每个询问,输出原序列中从第l个数到第r个数的和。
我们很容易想出暴力解法,遍历区间求和。
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 int n,m;scanf ("%d%d" ,&n,&m);for (int i=1 ;i<=n;i++) scanf ("%d" ,&a[i]);while (m--){ int l,r; int sum=0 ; scanf ("%d%d" ,&l,&r); for (int i=l;i<=r;i++) { sum+=a[i]; } printf ("%d\n" ,sum); } 1234567891011121314
这样的时间复杂度为O(n*m),如果n和m的数据量稍微大一点就有可能超时,而我们如果使用前缀和的方法来做的话就能够将时间复杂度降到O(n+m),大大提高了运算效率。
具体做法:
首先做一个预处理,定义一个sum[]数组,sum[i]代表a数组中前i个数的和。
求前缀和运算:
1 2 3 4 5 6 7 const int N=1e5 +10 ;int sum[N],a[N]; for (int i=1 ;i<=n;i++){ sum[i]=sum[i-1 ]+a[i]; } 123456
然后查询操作:
1 2 3 scanf ("%d%d" ,&l,&r); printf ("%d\n" , sum[r]-sum[l-1 ]); 12
对于每次查询,只需执行sum[r]-sum[l-1] ,时间复杂度为O(1)
原理
sum[r] =a[1]+a[2]+a[3]+a[l-1]+a[l]+a[l+1]......a[r];sum[l-1]=a[1]+a[2]+a[3]+a[l-1];sum[r]-sum[l-1]=a[l]+a[l+1]+......+a[r];
图解 只需要执行 sum[r]-sum[l-1]。输出原序列中从第l个数到第r个数的和的时间复杂度变成了O(1)。
我们把它叫做一维前缀和 。
总结:
例题 练习一道题目 输入格式 输出格式 数据范围 输入样例: 输出样例: 代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 #include <iostream> using namespace std;const int N = 100010 ;int n, m;int a[N], s[N];int main () scanf ("%d%d" , &n, &m); for (int i = 1 ; i <= n; i ++ ) scanf ("%d" , &a[i]); for (int i = 1 ; i <= n; i ++ ) s[i] = s[i - 1 ] + a[i]; while (m -- ) { int l, r; scanf ("%d%d" , &l, &r); printf ("%d\n" , s[r] - s[l - 1 ]); } return 0 ; }
3、二维前缀和 如果数组变成了二维数组怎么办呢?
先给出问题:
输入一个n行m列的整数矩阵,再输入q个询问,每个询问包含四个整数x1, y1, x2, y2,表示一个子矩阵的左上角坐标和右下角坐标。对于每个询问输出子矩阵中所有数的和。
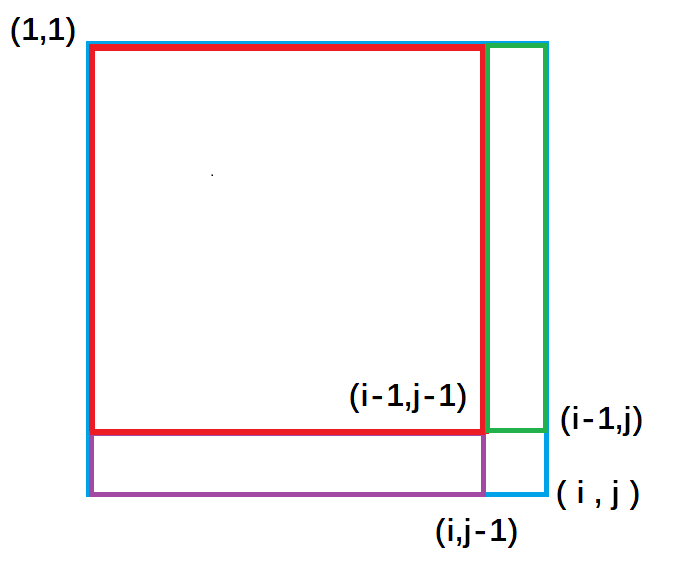
同一维前缀和一样,我们先来定义一个二维数组s[][], s[i][j]表示二维数组中,左上角(1,1)到右下角( i,j )所包围的矩阵元素的和。接下来推导二维前缀和的公式。
先看一张图:
紫色面积 是指(1,1)左上角到(i,j-1)右下角的矩形面积, 绿色面积 是指(1,1)左上角到(i-1, j )右下角的矩形面积。每一个颜色的矩形面积都代表了它所包围元素的和。 从图中我们很容易看出 ,整个外围蓝色矩形面积s[i][j] = 绿色面积s[i-1][j] + 紫色面积s[i][j-1] - 重复加的红色的面积s[i-1][j-1]+小方块的面积a[i][j];
因此得出二维前缀和预处理公式
1 s[i] [j] = s[i-1][j] + s[i][j-1 ] + a[i] [j] - s[i-1][ j-1]
接下来回归问题 去求以(x1,y1)为左上角和以(x2,y2)为右下角的矩阵的元素的和。
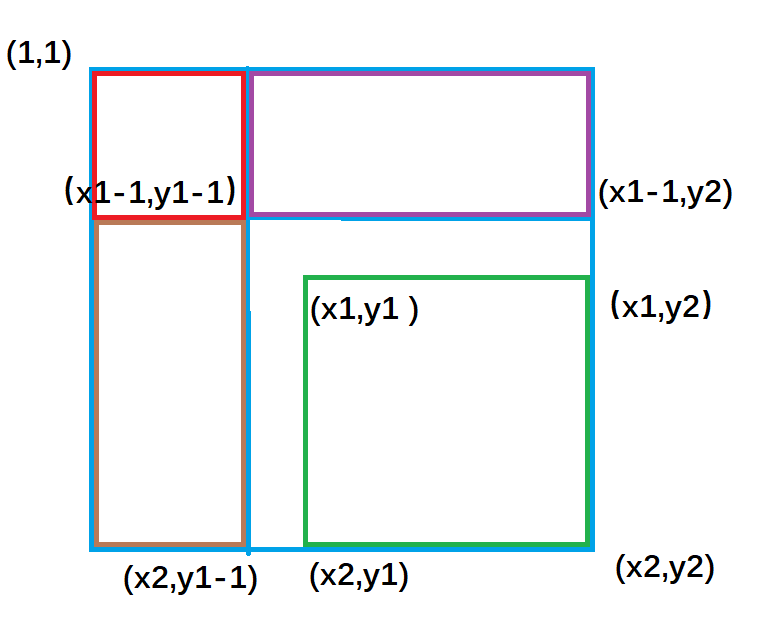
如图:
紫色面积 是指 ( 1,1 )左上角到(x1-1,y2)右下角的矩形面积 ,黄色面积 是指(1,1)左上角到(x2,y1-1)右下角的矩形面积;
不难推出:
绿色矩形的面积 = 整个外围面积s[x2, y2] - 黄色面积s[x2, y1 - 1] - 紫色面积s[x1 - 1, y2] + 重复减去的红色面积 s[x1 - 1, y1 - 1]
因此二维前缀和的结论为:
以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:s[x2, y2] - s[x1 - 1, y2] - s[x2, y1 - 1] + s[x1 - 1, y1 - 1]
总结:
例题 练习一道完整题目:
对于每个询问输出子矩阵中所有数的和。
输入格式
接下来n行,每行包含m个整数,表示整数矩阵。
接下来q行,每行包含四个整数x1, y1, x2, y2,表示一组询问。
输出格式
数据范围 输入样例: 输出样例:
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 #include <iostream> #include <cstdio> using namespace std;const int N=1010 ;int a[N][N],s[N][N];int main () int n,m,q; scanf ("%d%d%d" ,&n,&m,&q); for (int i=1 ;i<=n;i++) for (int j=1 ;j<=m;j++) scanf ("%d" ,&a[i][j]); for (int i=1 ;i<=n;i++) for (int j=1 ;j<=m;j++) s[i][j]=s[i-1 ][j]+s[i][j-1 ]+a[i][j]-s[i-1 ][j-1 ]; while (q--) { int x1,y1,x2,y2; scanf ("%d%d%d%d" ,&x1,&y1,&x2,&y2); printf ("%d\n" ,s[x2][y2]-s[x2][y1-1 ]-s[x1-1 ][y2]+s[x1-1 ][y1-1 ]); } return 0 ; }
4、差分
5、一维差分 类似于数学中的求导和积分,差分可以看成前缀和的逆运算。
差分数组:
首先给定一个原数组a:a[1], a[2], a[3],,,,,, a[n];
然后我们构造一个数组b : b[1] ,b[2] , b[3],,,,,, b[i];
使得 a[i] = b[1] + b[2 ]+ b[3] +,,,,,, + b[i]
也就是说,a数组是b数组的前缀和数组,反过来我们把b数组叫做a数组的差分数组 。换句话说,每一个a[i]都是b数组中从头开始的一段区间和。
考虑如何构造差分b数组?
最为直接的方法
如下:
b[1] = a[1] - a[0];
b[2] = a[2] - a[1];
b[3] =a [3] - a[2];
b[n] = a[n] - a[n-1];
图示:
我们只要有b数组,通过前缀和运算,就可以在O(n) 的时间内得到a数组 。
知道了差分数组有什么用呢? 别着急,慢慢往下看。
话说有这么一个问题:
给定区间[l ,r ],让我们把a数组中的[ l, r]区间中的每一个数都加上c,即 a[l] + c , a[l+1] + c , a[l+2] + c ,,,,,, a[r] + c;
暴力做法是for循环l到r区间,时间复杂度O(n),如果我们需要对原数组执行m次这样的操作,时间复杂度就会变成O(n*m)。有没有更高效的做法吗? 考虑差分做法 ,(差分数组派上用场了)。
始终要记得,a数组是b数组的前缀和数组 ,比如对b数组的b[i]的修改,会影响到a数组中从a[i]及往后的每一个数。
首先让差分b数组中的 b[l] + c ,通过前缀和运算,a数组变成 a[l] + c ,a[l+1] + c,,,,,, a[n] + c;
然后我们打个补丁,b[r+1] - c, 通过前缀和运算,a数组变成 a[r+1] - c,a[r+2] - c,,,,,,,a[n] - c;
为啥还要打个补丁?
我们画个图理解一下这个公式的由来: b[l] + c,效果使得a数组中 a[l]及以后的数都加上了c(红色部分),但我们只要求l到r区间加上c, 因此还需要执行 b[r+1] - c,让a数组中a[r+1]及往后的区间再减去c(绿色部分),这样对于a[r] 以后区间的数相当于没有发生改变。
因此我们得出一维差分结论 :给a数组中的[ l, r]区间中的每一个数都加上c,只需对差分数组b做 b[l] + = c, b[r+1] - = c。时间复杂度为O(1), 大大提高了效率。
总结:
例题 题目练习: AcWing 797. 差分
输入一个长度为n的整数序列。输入格式 输出格式 数据范围 输入样例: 输出样例: AC代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 #include <iostream> using namespace std;const int N=1e5 +10 ;int a[N],b[N]; int main () int n,m; scanf ("%d%d" ,&n,&m); for (int i=1 ;i<=n;i++) { scanf ("%d" ,&a[i]); b[i]=a[i]-a[i-1 ]; } int l,r,c; while (m--) { scanf ("%d%d%d" ,&l,&r,&c); b[l]+=c; b[r+1 ]-=c; } for (int i=1 ;i<=n;i++) { b[i]+=b[i-1 ]; printf ("%d " ,b[i]); } return 0 ; } 12345678910111213141516171819202122232425262728
6、二维差分 如果扩展到二维,我们需要让二维数组被选中的子矩阵中的每个元素的值加上c,是否也可以达到O(1)的时间复杂度。答案是可以的,考虑二维差分 。
a[][]数组是b[][]数组的前缀和数组,那么b[][]是a[][]的差分数组
原数组: a[i][j]
我们去构造差分数组: b[i][j]
使得a数组中a[i][j]是b数组左上角(1,1)到右下角(i,j)所包围矩形元素的和。
如何构造b数组呢?
其实关于差分数组,我们并不用考虑其构造方法,因为我们使用差分操作在对原数组进行修改的过程中,实际上就可以构造出差分数组。
同一维差分,我们构造二维差分数组目的是为了 让原二维数组a中所选中子矩阵中的每一个元素加上c的操作,可以由O(n*n)的时间复杂度优化成O(1)
已知原数组a中被选中的子矩阵为 以(x1,y1)为左上角,以(x2,y2)为右下角所围成的矩形区域;
始终要记得,a数组是b数组的前缀和数组 ,比如对b数组的b[i][j]的修改,会影响到a数组中从a[i][j]及往后的每一个数。
假定我们已经构造好了b数组,类比一维差分,我们执行以下操作c
b[x1][y1] + = c;
b[x1,][y2+1] - = c;
b[x2+1][y1] - = c;
b[x2+1][y2+1] + = c;
每次对b数组执行以上操作,等价于:
1 2 3 4 for (int i=x1;i<=x2;i++) for (int j=y1;j<=y2;j++) a[i][j]+=c; 123
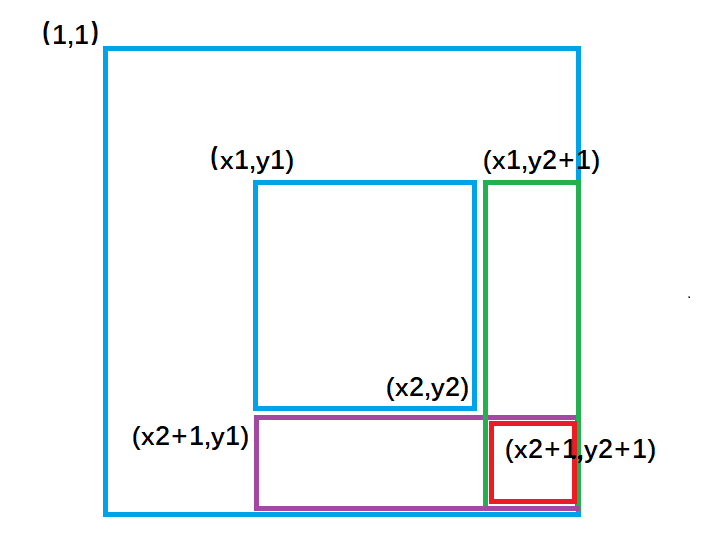
我们画个图去理解一下这个过程:
b[x1][ y1 ] +=c ; 对应图1 ,让整个a数组中蓝色矩形面积 的元素都加上了c。b[x1,][y2+1]-=c ; 对应图2 ,让整个a数组中绿色矩形面积 的元素再减去c,使其内元素不发生改变。b[x2+1][y1]- =c ; 对应图3 ,让整个a数组中紫色矩形面积 的元素再减去c,使其内元素不发生改变。b[x2+1][y2+1]+=c; 对应图4,让整个a数组中红色矩形面积 的元素再加上c,红色内的相当于被减了两次 ,再加上一次c,才能使其恢复。我们将上述操作封装成一个插入函数:
1 2 3 4 5 6 7 8 void insert (int x1,int y1,int x2,int y2,int c) b[x1][y1]+=c; b[x2+1 ][y1]-=c; b[x1][y2+1 ]-=c; b[x2+1 ][y2+1 ]+=c; } 1234567
我们可以先假想a数组为空,那么b数组一开始也为空,但是实际上a数组并不为空,因此我们每次让以(i,j)为左上角到以(i,j)为右下角面积内元素(其实就是一个小方格的面积)去插入 c=a[i][j],等价于原数组a中(i,j) 到(i,j)范围内 加上了 a[i][j] ,因此执行n*m次插入操作,就成功构建了差分b数组.
这叫做曲线救国。
代码如下:
1 2 3 4 5 6 7 8 for (int i=1 ;i<=n;i++) { for (int j=1 ;j<=m;j++) { insert (i,j,i,j,a[i][j]); } } 1234567
当然关于二维差分操作也有直接的构造方法,公式如下:
1 b[i][j]=a[i][j]−a[i−1][j]−a[i][j−1]+a[i−1][j−1]
二维差分数组的构造同一维差分思维相同,因次在这里就不再展开叙述了。
总结:
例题 题目练习: AcWing 798. 差分矩阵 输入格式 输出格式 数据范围 输入样例: 输出样例: AC代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 include<iostream> #include <cstdio> using namespace std;const int N=1e3 +10 ;int a[N][N],b[N][N];void insert (int x1,int y1,int x2,int y2,int c) b[x1][y1]+=c; b[x2+1 ][y1]-=c; b[x1][y2+1 ]-=c; b[x2+1 ][y2+1 ]+=c; } int main () int n,m,q; cin>>n>>m>>q; for (int i=1 ;i<=n;i++) for (int j=1 ;j<=m;j++) cin>>a[i][j]; for (int i=1 ;i<=n;i++) { for (int j=1 ;j<=m;j++) { insert (i,j,i,j,a[i][j]); } } while (q--) { int x1,y1,x2,y2,c; cin>>x1>>y1>>x2>>y2>>c; insert (x1,y1,x2,y2,c); } for (int i=1 ;i<=n;i++) { for (int j=1 ;j<=m;j++) { b[i][j]+=b[i-1 ][j]+b[i][j-1 ]-b[i-1 ][j-1 ]; } } for (int i=1 ;i<=n;i++) { for (int j=1 ;j<=m;j++) { printf ("%d " ,b[i][j]); } printf ("\n" ); } return 0 ; }
二分法 1024 = 10^3^ = 2^10^ logn的底数一般取的是2 10^6^也就是一百万的数据量我们可以把它优化到20,相当的夸张了。
因此我们有必要好好地学习二分法
一定只会去搜索其中的一部分 ,而不会两部分都去搜索
1 2 3 4 5 6 7 8 9 10 template <typename T>static Rank binSearch (T* A, T const & e, Rank lo, Rank hi) while (lo < hi) { Rank mi = (lo + hi) >> 1 ; (e < A[mi]) ? hi = mi : lo = mi + 1 ; } return --lo; }
引例:计算根号三 往往我们不会说判断区间为空才结束,而是判断区间足够小,也就是足够精确,就结束了
一般情况开到需要精度的两倍 ,那么这个精度就是精确的,例如需要你算到10^-5^的精确答案那么你算到10^-10^次方使得算法结束(答案里小数点后10个数时结束),这样一定没问题
方程近似解 不过必须都是有序的区间 ,我们才能进行查找
这道题是单调递增的
所以说二分法虽然很快,但是是有局限的。
给你y,要求计算x
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 #include <bits/stdc++.h> using namespace std;const double eps = 1e-3 ;double f (double x) return pow (x, 4 ) + 5 * pow (x, 3 ) + 6 * pow (x, 2 ) + 7 * x + 4 ; } double cal (double y) if (f (0 ) > y || f (100 ) < y){ return -1 ; } double lo = 0 , hi = 100 ; while (hi - lo > eps){ double mid = (lo + hi) / 2 ; if (f (mid) > y){ hi = mid; }else { lo = mid; } } return hi; } int main () double y; cin >> y; printf ("%.3f\n" , cal (y)); return 0 ; }
二分快速幂
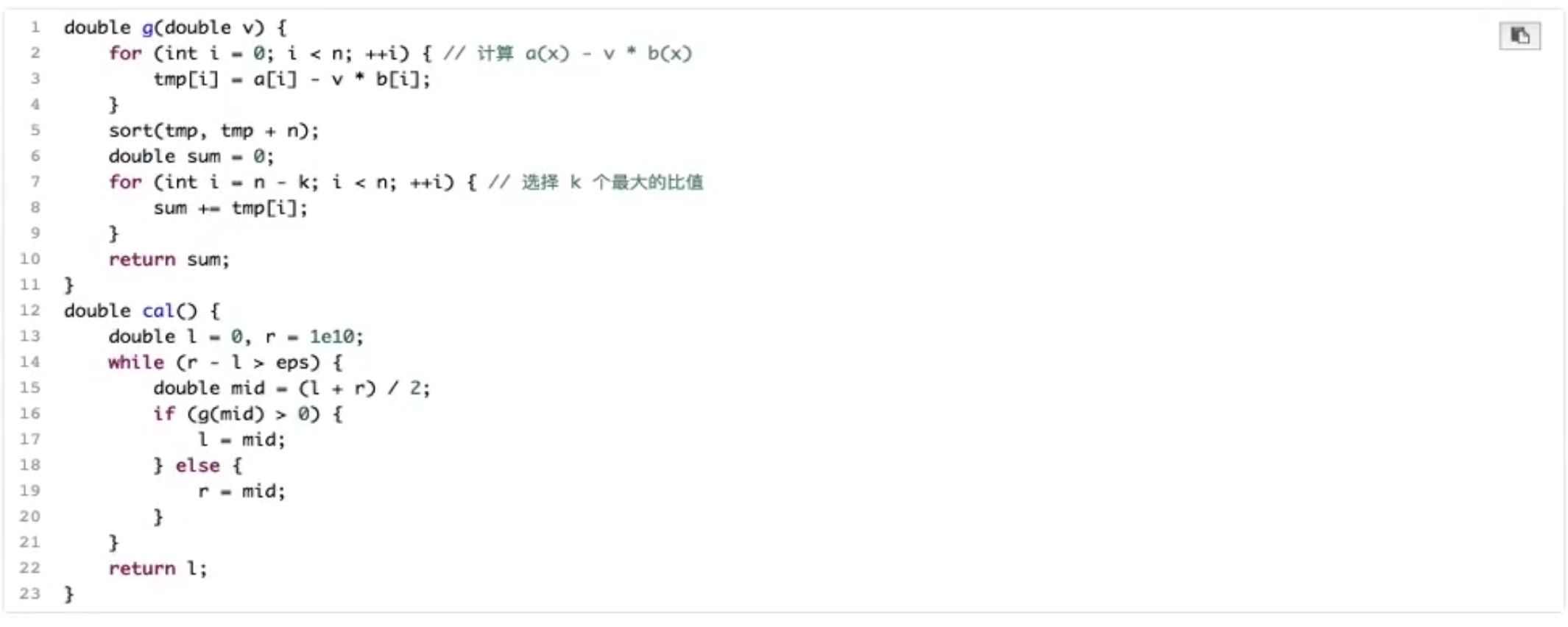
二分答案
ma:所有数中最小的,我们分组确保不可能小于单个数分组的最小的数
sum:所有的数一组时,最大值一定不会超过所有元素之和
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 #include <bits/stdc++.h> using namespace std;const int N = 1e3 + 9 ;const int inf = 0x3f3f3f3f ;int n, k, a[N]; bool check (int x) int now = 0 , cnt = 0 ; for (int i = 0 ; i < n; i++){ if (now + a[i] > x){ ++cnt; now = a[i]; }else { now += a[i]; } } return cnt <= k; } int cal (int l, int r) int mid; while (l < r){ mid = (l + r) >> 1 ; if (check (mid)){ r = mid; }else { l = mid + 1 ; } } } int now = 0 , cnt = 0 ; int main () int ma = -inf, sum = 0 ; cin >> n >> k; for (int i = 0 ; i < n; i++){ cin >> a[i]; ma = max (ma, a[i]); sum += a[i]; } cout << cal (ma, sum) << endl; return 0 ; }
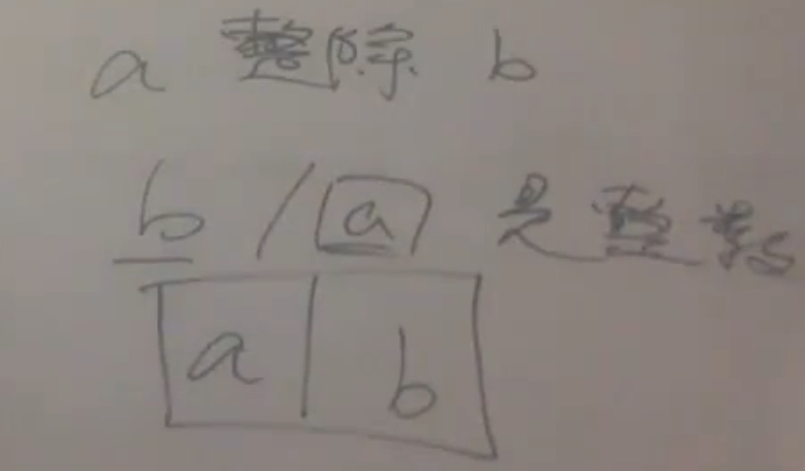
基础数论 除与除以
这是一个有关汉语状语的问题,需要区分的两者我们看作“A除B”和“A除以B”。
那么在“A除B”中,实际上想要表达的是“用A除B”,即用A来“分开”B。这里B作被除数,A作除数。下面是一个例子:
2除6:用2来分6,用算式标明计算过程就是:6÷2=3
而“A除以B”是一个状语后置的结构,更换状语位置可看做“A以B除”,其表意为“将A以B除”或“把A用B分开”。这里A作被除数,而B作除数。即式A÷B,同样一例:
2除以6:2以6除,算式为:2÷6=⅓
最大公约数/最小公倍数 gcd/lcm
最小公倍数即为,a,b两数均除以gcd后得到的数,在将得到的两个数乘以gcd,即为最小公倍数
我靠,居然有api可以调
质数 1既不是质数,也不是合数
质数筛选 暴力
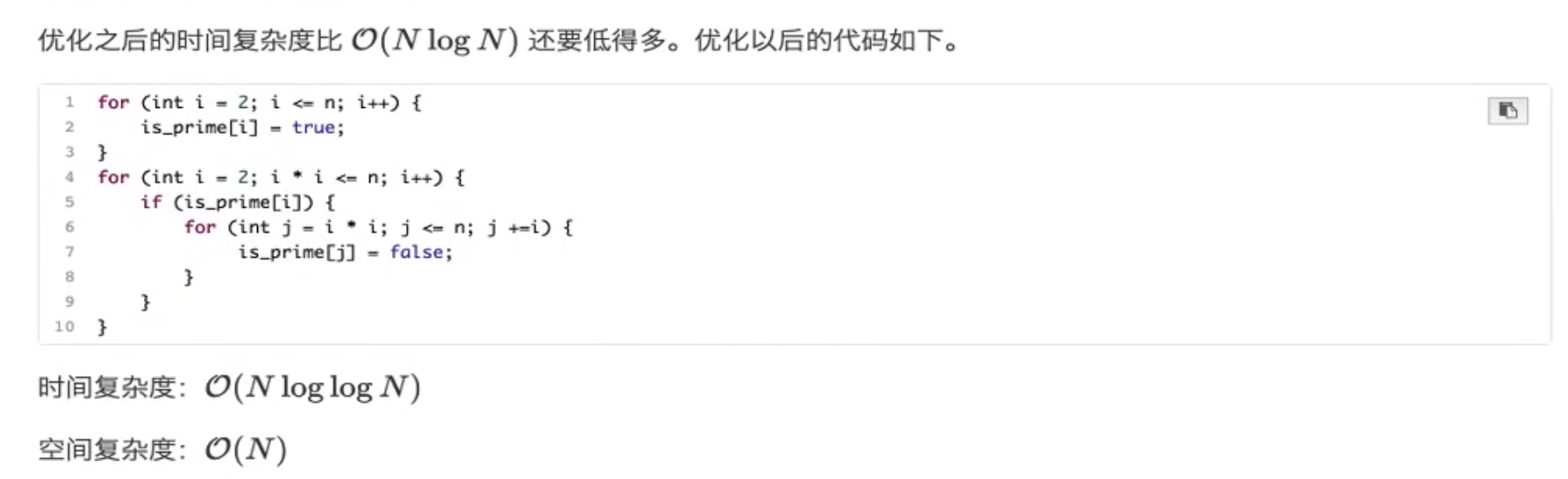
预处理筛 把完全不可能质数的筛出去了,不用做循环判断,筛的是当前该数的2倍,3倍…..直到不大于n的所有倍(没有1倍)
注意j循环是j+=i;
可是我们进一步想,是否能优化一下这个过程……
例如 6 = 2 * 3 6 = 3 * 2这样6会被筛选两遍,所以我们每一次从i * 2开始,确保不会重复筛
我们再想,如果一个数轮到他了也一直没有被筛掉,说明他之前的数没有任何一个的任何倍数等于他,也就是他一定是一个质数,所以这个过程我们就可以把质数筛出来了
唯一的区别就是if判断一下,加上j = 2 * i 变成了j = i * i 也就是从第一个和他不相同的数一个一个枚举,变成了i * i 确保之前没筛过
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 #include <bits/stdc++.h> using namespace std;bool is_prime[100 ];int main () for (int i = 2 ; i < 100 ; i++) is_prime[i] = true ; for (int i = 2 ; i*i < 100 ; i++){ if (is_prime[i]){ for (int j = i*i; j < 100 ; j += i){ is_prime[j] = false ; } } } for (int i = 2 ; i < 100 ; i++){ if (is_prime[i]){ cout << i << endl; } } return 0 ; }
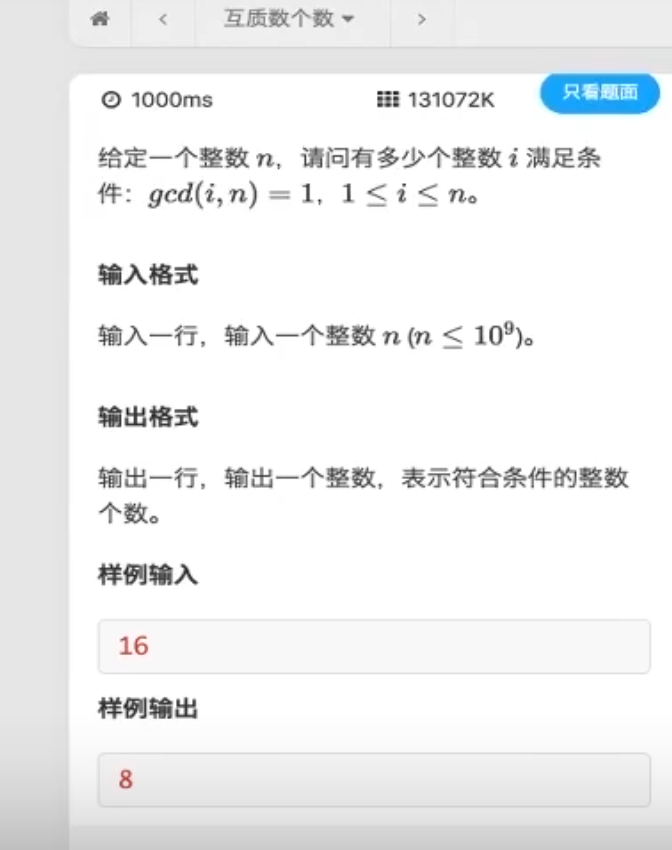
欧拉函数 当前数,与小于等于当前数的互斥数的个数 就是欧拉函数
写法就是一个圈加上一条竖线
暴力的思想 我们可以先枚举每一个数,对每一个数和12做一次辗转相除法,如果最后得出的最大公约数是一,那么他就是一个欧拉数
公式
通过这样的规律,我们就能找到任意一个正整数的欧拉函数 的结果
单个数的欧拉函数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 #include <bits/stdc++.h> using namespace std;int main () int n ; cin >> n; int res = n; for (int i = 2 ; i*i <= n; i++){ if (n % i == 0 ){ res = res / i * (i-1 ); while (n % i == 0 ){ n /= i; } } } if (n > 1 ){ res = res / n * (n - 1 ); } cout << res << endl; return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 #include <bits/stdc++.h> using namespace std;int main () int n; cin >> n; int res = n; for (int i = 2 ; i <= n; i++){ if (res % i == 0 ){ res = res / i * (i-1 ); while (n % i == 0 ){ n /= i; } } } if (n > 1 ){ res = res / n * (n-1 ); } cout << res << endl; return 0 ; }
区间预处理筛 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 18 phi(1)=1 phi(2)=1 phi(3)=2 phi(4)=2 phi(5)=4 phi(6)=2 phi(7)=6 phi(8)=4 phi(9)=6 phi(10)=4 phi(11)=10 phi(12)=4 phi(13)=12 phi(14)=6 phi(15)=8 phi(16)=8 phi(17)=16 phi(18)=6
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 #include <bits/stdc++.h> using namespace std;int phi[10001 ];int main () int n ; cin >> n; for (int i = 1 ; i <= n; i++){ phi[i] = i; } for (int i = 2 ; i <= n; i++){ if (phi[i] == i){ for (int j = i; j <= n; j+=i){ phi[j] = phi[j] / i * (i - 1 ); } } } for (int i = 1 ; i <= n; i++){ cout << "phi(" << i << ")=" << phi[i] << endl; } return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 18//自己写的程序 1 1 2 2 4 2 6 4 6 4 10 4 12 6 8 8 16 6
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 #include <bits/stdc++.h> using namespace std;int phi[10001 ];int main () int n; cin >> n; for (int i = 1 ; i <= n; i++){ phi[i] = i; } for (int i = 2 ; i <= n; i++){ if (phi[i] == i){ for (int j = i; j <=n; j+=i){ phi[j] = phi[j] / i * (i - 1 ); } } } for (int i = 1 ; i <= n; i++){ cout << phi[i] << endl; } return 0 ; }
矩阵 矩阵的定义 在计算机里,我们通常用二维数组 来当做矩阵
矩阵加减乘
乘法实战 1 2 3 4 5 6 7 8 9 10 11 输入 2 3 1 0 2 -1 3 1 3 2 3 1 2 1 1 0 输出 5 1 4 2
单位矩阵
矩阵二分快速幂
1 2 3 4 5 6 7 输入 2 2 100 1 2 3 4 输出 7 10 15 22
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 #include <bits/stdc++.h> using namespace std;struct matrix { int a[100 ][100 ]; int n; }; matrix matrix_mul (matrix A, matrix B, int mod) { matrix ret; ret.n = A.n; for (int i = 0 ; i < ret.n; i++){ for (int j = 0 ; j < ret.n; j++){ ret.a[i][j] = 0 ; } } for (int i = 0 ; i < ret.n; i++){ for (int j = 0 ; j < ret.n; j++){ for (int k = 0 ; k < A.n; k++){ ret.a[i][j] = (ret.a[i][j] + A.a[i][k]*B.a[k][j]%mod)%mod; } } } return ret; } matrix unit (int n) { matrix ret; ret.n = n; for (int i = 0 ; i < n; i++){ for (int j = 0 ; j < n; j++){ if (i == j){ ret.a[i][j] = 1 ; }else { ret.a[i][j] = 0 ; } } } return ret; } matrix matrix_pow (matrix A, int p, int mod) { matrix ret = unit (A.n); while (p){ if (p & 1 ){ ret = matrix_mul (ret, A, mod); } A = matrix_mul (A, A, mod); p /= 2 ; } return ret; } int main () int p, mod; matrix A; cin >> A.n >> p >> mod; for (int i = 0 ; i < A.n; i++){ for (int j = 0 ; j < A.n; j++){ cin >> A.a[i][j]; } } matrix C = matrix_pow (A, p, mod); for (int i = 0 ; i < C.n; i++){ for (int j = 0 ; j < C.n; j++){ if (j != C.n-1 ){ cout << C.a[i][j] << " " ; }else { cout << C.a[i][j] << endl; } } } return 0 ; }
比赛小技巧 1.巧用编辑器 门牌制作
1 2 3 4 5 6 7 8 #include <bits/stdc++.h> using namespace std;int main () int k=0 ; for (int i=1 ;i<=2020 ;i++) cout<<i; }
然后,将输出结果粘贴到编辑器中(⽐赛时可以选择:Word、Codeblocks 都⾏)中,选搜索功能,搜 索字符 「2」,
共搜索出结果 624 次,这就是答案。
卡片 题目描述
⼩蓝有很多数字卡⽚,每张卡⽚上都是数字 0 到 9。⼩蓝准备⽤这些卡⽚来拼⼀些数,他想从 1 开始拼 出正整数,每拼⼀个,就保存起来,卡⽚就不能⽤来拼其它数了。⼩蓝想知道⾃⼰能从 1 拼到多少。例 如,当⼩蓝有 30 张卡⽚,其中 0 到 9 各 3 张,则⼩蓝可以拼出 1 到 10,但是拼 11 时卡⽚ 1 已经只有 ⼀张了,不够拼出 11。现在⼩蓝⼿⾥有 0 到 9 的卡⽚各 2021 张,共 20210 张,请问⼩蓝可以从 1 拼 到多少?提示:建议使⽤计算机编程解决问题。
解题思路
和上⾯的例⼦差不多的做法。 先估计可能拼出 3000 多个数。
编个⼩程序打印出 13500,然后全部贴到 Word ⾥⾯,看 1 ⽤了多少次,2 ⽤了多少次。 最后发现,13181,⽤了 2021 个 1。所以答案是 3181
2.眼看手数 走迷宫
解题思路
这道题是典型的 DFS,编码⾄少 10 分钟。不过因为是个填空题,⽽且迷宫很简单,只有 100 个字符, 可以直接数
,从左往右数,从上往下数,约 2 分钟就能数完。数出来的结果⻅下⾯,加粗字符上的⼈能⾛出来。
七段码
分 7 种情况: 亮⼀个灯:有 7 种情况,1、2、3、4、5、6、7;
亮两个灯:有 12、13、24、25、……. 等等;
亮三个灯:有 123、124、125、134、136、234、257……. 等等;
亮四个灯,这时不要直接数四个灯,情况与灭三个灯是等价的:灭 123、灭 124. 等等;
亮五个灯,与灭两个灯等价:灭 12、灭 13、灭 14、 等等;
亮六个灯,与灭⼀个灯等价,有 7 种情况;
亮七个灯,有 1 种情况。 对以上所有情况求和。
3.巧用Excel 分数
注意,这个时候,如果没有看出来,分子分母一定互素,那我们要写一个辗转相除法判断最大公约数;然后同时约它,当然,如果能看出来,规律就是(n + (n-1) ) / n——>(2n - 1) / n ,这种样子的情况一定是互素
1 2 3 4 5 6 7 8 9 10 11 12 13 #include <bits/stdc++.h> using namespace std;int gcd (int a, int b) if (b == 0 ) return a; gcd (b, a%b); } int main () int fm = 524288 ;int fz = 1048575 ;int a = gcd (fz, fm); cout << a; }
星期一 题⽬描述 整个 20世纪( 1901年 1⽉ 1⽇⾄ 2000年12 ⽉31 ⽇之间),⼀共有多少个星期⼀?
(不要告诉 我你不知道今天是星期⼏)
解题思路 ⾸先,⽤ Excel,⼀个格⼦输⼊⽇期 1901 年 1 ⽉ 1 ⽇,另⼀个格⼦输⼊ 2000 年 12 ⽉ 31 ⽇,然后两 个格⼦相减
得 36524 天,除以 7 得 5217.7 周。
天梯赛复盘 L1-2 拉格朗日中值定理 (5 分) 拉格朗日中值定理又称拉氏定理,是微分学中的基本定理之一,它反映了可导函数在闭区间上的整体的平均变化率与区间内某点的局部变化率的关系。拉格朗日中值定理是罗尔中值定理的推广,同时也是柯西中值定理的特殊情形,是泰勒公式的弱形式。
拉格朗日中值定理表述如下:
如果函数f (x )满足:
(1) 在闭区间[a ,b ]上连续;
(2) 在开区间(a ,b )内可导;
那么在开区间(a ,b )内至少有一点ε (a <ε <b )使等式f (b )−f (a )=f ′(ε )(b −a )成立。
精彩的大学生活体现在高等数学中,拉格朗日中值定理也是快乐的源泉之一。
小周在学这个定理的时候意识到虽然这个定理很漂亮,但是这个点ε其实并不好找,于是向高数成绩特别好的你求助。
为了方便你研究这个问题,小周贴心地令 f (x )=x 2 ,然后只告诉你a与b的值(a,b即为区间的左、右端点),你只需将点ε求出后输出即可。
输入格式:
输入在一行中给出两个整数,分别为a和b。其中,a表示区间的左端点,b表示区间的右端点。
题目保证整数a,b均在int类型可表示范围内。
输出格式:
在一行中输出点ε的值。结果保留1位小数。
输入样例:
输出样例:
样例解释:
将a =1,b =3代入方程f (b )−f (a )=f ′(ε )(b −a ),有32−12=2∗ε ∗(3−1)⇒8=4∗ε ⇒ε =2.0,即ε =2.0
1 2 3 4 5 6 7 8 9 10 11 #include <bits/stdc++.h> using namespace std;int main () int a, b; double ans; cin >> a >> b; ans = 1.0 *(b*b - a*a) / (2 * (b - a)); printf ("%.1lf" , ans); return 0 ; }
L1-6 xrf的镜子碎了? (15 分) xrf有一面镜子,可以把任何接触镜面的东西变成原来的两倍,同时呢,那增加的那部分是反的。 xrf很喜欢他的镜子,但是因为一股神秘力量(可能来自pltdhll),xrf的镜子碎了!xrf很伤心。
lyx知道后想要把自己的镜子送给xrf,(lyx的镜子有一个独属于lyx的名字,叫做“lyx的镜子”)。而lyx的镜子虽然可以把接触镜面的东西变成原来的两倍,但增加的那部分是相同的。
lyx为了展示他的镜子,不知道从哪拿来了一串珍珠项链。我们把项链用AB来表示,不同的字母表示不同颜色的珍珠。如果把A端接触镜面的话,镜子会把这条项链变成ABAB;如果再用B端接触的话,则会变成ABABABAB,即不论用哪端接触增加的部分都是相同的。
xrf收到镜子后迫不及待的想要试一下,于是想拿出随身带的珍珠项链,可是不知道珍珠项链哪去了,只好重新找了一条珍珠项链测试了。
xrf始终只用项链的一端接触镜子,经过多次与镜子接触最终得到了一条新的项链,xrf觉得这面镜子很有意思,但是忘了最初的项链长什么样了,只记得最初始的项链是不可能与lyx的镜子接触过。现在xrf把这个新的项链给你,请你帮他找出原来项链的形状。
注:
xrf给你的项链可能没有接触过lyx的镜子(可能是因为xrf很幽默\斜眼笑)。
若项链为ABAB,则我们认为该项链可能与lyx的镜子接触过。
若项链为AB,则我们认为该项链不可能与lyx的镜子接触过。
输入格式:
一个由大写英文字母(A~`Z`)组成的字符串(长度不超过100000),表示xrf给你的项链。
输出格式:
一个字符串,表示项链的形状。
输入样例1:
输出样例1:
输入样例2:
输出样例2:
只得了6分的两个思路
从最开始遍历和从最后面遍历,进而判断是否出现相同子串判断
从第二个索引开始不断朝后遍历,进而确认相同子串
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 #include <bits/stdc++.h> using namespace std;char s[100005 ];char ans1[100005 ], ans2[100005 ];bool flag;int main () scanf ("%s" , s); int len = strlen (s); int k = 1 ; ans1[0 ] = s[0 ]; for (int i = 1 ; i < len; i++){ ans1[i] = s[i]; if (ans1[0 ] == s[i]){ ans2[0 ] = s[i]; for (int j = 1 ; j < i; j++){ ans2[j] = s[j]; if (ans2[j] != ans1[j]){ flag = true ; break ; } k++; } if (flag == false ){ for (int j = 0 ; j < k; j++) printf ("%c" , ans2[j]); break ; } flag = false ; k = 1 ; } } return 0 ; }
14分代码(少了最后的if判断)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 #include <bits/stdc++.h> using namespace std;string s; bool flag;int main () string s1, s2; cin >> s; if (s.length () % 2 != 0 ){ cout << s << endl; return 0 ; } for (int i = 1 ; i < s.length (); i++){ if (s.length () % i != 0 ) continue ; s1 = s.substr (0 , i); for (int j = i; j < s.length (); j+=i){ s2 = s.substr (j, i); if (s1 != s2){ flag = true ; break ; } if (s1 == s2) flag = false ; } if (flag == false ){ cout << s2 << endl; break ; } } if (flag){ cout << s << endl; } return 0 ; }
AC代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 #include <bits/stdc++.h> using namespace std;string s; int main () cin>>s; if (s.length ()%2 !=0 ){ cout<<s; return 0 ; }else { string x; int flag; for (int i=1 ;i<=s.length ();i++){ flag = 1 ; if (s.length ()%i != 0 ) continue ; x = s.substr (0 ,i); for (int j=0 ; j<s.length (); j+=i) if (s.substr (j,i) != x){ flag = 0 ; break ; } if (flag == 1 ){ cout<<x<<endl; break ; } } if (flag == 0 ) cout<<s<<endl; } return 0 ; }
自己的AC代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 #include <bits/stdc++.h> using namespace std;string s; bool flag;int main () string s1, s2; cin >> s; if (s.length () % 2 != 0 ){ cout << s << endl; return 0 ; } for (int i = 1 ; i < s.length (); i++){ if (s.length () % i != 0 ) continue ; s1 = s.substr (0 , i); for (int j = i; j < s.length (); j+=i){ s2 = s.substr (j, i); if (s1 != s2){ flag = true ; break ; } if (s1 == s2) flag = false ; } if (flag == false ){ cout << s2 << endl; break ; } } if (flag){ cout << s << endl; } return 0 ; }
L1-8 天梯赛团队总分 (20 分) “天梯赛”的竞赛题目一共有 15 道,分为 3 个梯级:
基础级设 8 道题,其中 5 分、10 分、15 分、20 分的题各 2 道,满分为 100 分;题目编号相应为L1-X,X取1,2,3,4,5,6,7,8,分别表示基础级的8道题,如L1-1表示基础级的第1题。
进阶级设 4 道题,每道题 25 分,满分为 100 分;题目编号相应为L2-X,X取1,2,3,4,分别表示进阶级的4道题,如L2-2表示进阶级的第2题。
登顶级设 3 道题,每道题 30 分,满分为 90 分。题目编号相应为L3-X,X取1,2,3,分别表示登顶级的3道题,如L3-2表示登顶级的第2题。
注:若对以上表述仍有不理解或者不清楚的,则请参考本套考题的题号与分值。
在我们校赛中,积分规则和正式天梯赛积分规则有些许不同,校赛的积分规则简化后如下:
参赛者须独立按照严格的输入输出要求提交每一题的解题程序。程序须经过若干测试用例的测试,每个测试用例分配一定分数。每题的得分为通过的测试用例得分之和;整场比赛得分为各题得分之和。程序可反复提交,取最高分,提交错误不扣分。
参赛者的个人总分由每题得分和先锋奖励组成。只有当该队员的基础题总分超过 60 分时,其进阶部分的题目分数(包括奖励)才被判为对其个人有效;当其进 阶题总分超过 25 分时,其登顶部分的题目分数(包括奖励)才被判为对其个人有效。
当一支参赛团队的基础题总分超过 300 分时,该队进阶部分的题目分数才被判为对团队有效;只有当其进阶题总分超过 125 分时,该队登顶部分的题目分数才被判为对团队有效。
校赛中每个参赛团队由5名参赛者组成。
注:基础题是默认有效的。对个人/团队无效得分的部分视为0分。
团队的基础题总分为所有队员在基础题的得分总和;
团队的进阶题总分为所有队员在进阶题的得分总和;
团队的登顶题总分为所有队员在登顶题的得分总和。
当队员在进阶题或登顶题的得分对个人来说是无效时,但是这部分仍然计入团队进阶题和登顶题得分,只有当团队基础题得分/进阶题得分达到了进阶条件,团队的进阶题得分/登顶题得分才能被判定为对团队有效。
在竞赛的过程中你和你的队友都如此 沉迷,以至于 你们都忘记看实时榜单,比赛结束后你们只能通过提交记录计算你们团队每个人的得分以及团队总得分。具有团队精神的你想要亲自编写程序来解决这个问题。
天梯赛是善良的,同一道题你可以多次提交,该题最终得分为多次提交的最高分(参考样例1)。
若有些题没有提交记录,即该题记做0分。
同样因为一股神秘力量(可能来自参赛团队本身 只有自己团队的提交记录),本题不考虑先锋奖励 。
输入格式:
输入第一行给出一个非负整数N(0<=N<200),表示提交记录的数量。
接下来N行,每行给出一条提交记录的详细情况,其格式为:队员编号 题目编号 分数。你们队员的编号依次为1,2,3,4,5。
题目保证所有的提交记录只有你们团队的记录,不会出现其他队伍的记录;同时,同一道题可能有多次提交。
输出格式:
一共输出6行。
第1行输出团队总得分。
接下来5行输出团队5个人每个人的成绩,按总分由高到低的顺序。若总分相同,则优先输出编号较小者。
输入样例1:
1 2 3 4 5 6 5 1 L1-1 5 1 L1-1 3 1 L1-1 4 1 L1-1 2 1 L1-1 1
输出样例1:
输入样例2:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 22 1 L1-8 20 1 L1-7 20 1 L1-6 15 1 L1-5 15 2 L1-8 20 2 L1-7 20 2 L1-6 15 2 L1-5 15 3 L1-8 20 3 L1-6 15 3 L1-5 15 4 L1-8 20 4 L1-7 20 4 L1-6 15 4 L1-5 15 4 L1-4 10 4 L1-3 10 1 L1-4 10 1 L1-3 10 1 L1-2 5 5 L2-1 25 5 L2-2 25
输出样例2:
1 2 3 4 5 6 355 1 95 4 90 2 70 3 50 5 0
样例解释2:
5号队员虽然进阶题得到50分,但是他基础题得分为0,所以,对于5号队员个人来说,他的最后总得分为0;对于整个团队来说,团队的基础题部分得分为305,达到了进阶条件;5号选手在进阶部分的得分可以计入团队的进阶部分得分,所以团队最后的总得分为355。接下来请继续你的快乐作答!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 #include <bits/stdc++.h> using namespace std;const int N = 205 ;int n;int l1[6 ][10 ];int l2[6 ][5 ];int l3[6 ][4 ];int suml1[6 ],suml2[6 ],suml3[6 ];int sum1,sum2,sum3;struct node { int id; int level,ji; int score; }a[N]; struct node2 { int id; int sum; }ans[6 ]; bool cmp1 (node a, node b) return a.id<b.id; if (a.id == b.id) { return a.level < b.level; } if (a.level==b.level) { return a.ji<b.ji; } if (a.ji == b.ji) return a.score > b.score; } bool cmp2 (node2 a, node2 b) if (a.sum == b.sum) return a.id<b.id; return a.sum>b.sum; } int main () cin>>n; string s; for (int i=1 ; i<=n; i++) { cin>>a[i].id>>s>>a[i].score; a[i].level = s[1 ] -'0' ; a[i].ji = s[3 ] - '0' ; } sort (a+1 , a+n+1 , cmp1); for (int i=1 ; i<=n; i++) { if (a[i].level == 1 ) { l1[a[i].id][a[i].ji] = max (l1[a[i].id][a[i].ji], a[i].score); } if (a[i].level == 2 ) { l2[a[i].id][a[i].ji] = max (l2[a[i].id][a[i].ji], a[i].score); } if (a[i].level == 3 ) { l3[a[i].id][a[i].ji] = max (l3[a[i].id][a[i].ji], a[i].score); } } for (int i=1 ; i<=5 ; i++) { for (int j=1 ; j<=8 ; j++) { sum1 += l1[i][j]; suml1[i] += l1[i][j]; } } for (int i=1 ; i<=5 ; i++) { for (int j=1 ; j<=4 ; j++) { if (sum1 >=300 ) sum2 += l2[i][j]; if (suml1[i]>=60 ) suml2[i] += l2[i][j]; } } for (int i=1 ; i<=5 ; i++) { for (int j=1 ; j<=3 ; j++) { if (sum1 >=300 && sum2 >=125 ) sum3 += l3[i][j]; if (suml1[i]>=60 && suml2[i] >=25 ) suml3[i] += l3[i][j]; } } cout<<sum1+sum2+sum3<<endl; for (int i=1 ; i<=5 ;i++) { ans[i].id = i; ans[i].sum = suml1[i]+suml2[i]+suml3[i]; } sort (ans+1 , ans+6 , cmp2); for (int i=1 ; i<=5 ; i++) cout<<ans[i].id<<" " <<ans[i].sum<<endl; return 0 ; }
L2-1 Bang Bang Klee Ba! (25 分) 可莉今天抓到了花纹奇怪的蜥蜴,很多很多条!
可莉很想知道她到底抓到了多少种不同的蜥蜴,每一种蜥蜴各抓了多少只。所以,求求你啦!帮帮可莉吧!
可莉一共抓到了n只蜥蜴,分别编号1~n,但她不知道每只蜥蜴的具体种类。派蒙作为你的好向导,告诉你了m条信息,每条信息可以知道其中哪两只蜥蜴属于同一种类,但十分聪明的派蒙算不出来蜥蜴的种类数和每种蜥蜴的具体数量,所以就交给非常聪明的你了!
输入格式:
第一行有n,m两个正整数,n为可莉今天抓到的蜥蜴总数,m为信息的数量。(1≤n ,m ≤105 )
接下来m行,每行两个正整数a,b,表示第a只蜥蜴与第b只蜥蜴属于同一类别。
输出格式:
第一行输出一个正整数sum,表示抓到的蜥蜴种数。
第二行有sum个正整数,以降序 输出每种蜥蜴的数量,两数间使用一个空格隔开,行末没有多余的空格。
输入样例:
输出样例:
样例解释:
6只蜥蜴当中,第1,2,3,4,5只蜥蜴属于同一类别,所以共计2类。
按照蜥蜴数量降序排列后,第一类蜥蜴共5只,第二类蜥蜴共1只。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 #include <bits/stdc++.h> using namespace std;int root[100005 ], sum[100005 ];int n, m;int find (int x) if (x!=root[x]) root[x] = find (root[x]); return root[x]; } int main () scanf ("%d %d" , &n, &m); for (int i=1 ;i<=n;i++) { root[i] = i; sum[i] = 1 ; } for (int i=0 ;i<m;i++) { int a, b; scanf ("%d %d" , &a, &b); if (find (a)!=find (b)) { sum[find (a)] += sum[find (b)]; root[find (b)] = find (a); } } vector<int > ve; for (int i=1 ;i<=n;i++) { if (root[i]==i) ve.push_back (sum[i]); } cout << ve.size () << '\n' ; sort (ve.begin (),ve.end ()); for (int i=ve.size ()-1 ;i>0 ;i--) cout<<ve[i]<<' ' ; cout<<ve[0 ]; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 #include <bits/stdc++.h> using namespace std;int fa[10005 ];int kind[10005 ];int kinds;bool flag[10005 ];void init (int n) for (int i = 1 ; i <= n; i++) fa[i] = i; } int find (int x) int t = x; while (t != fa[t]) t = fa[t]; while (x != fa[x]){ int temp = fa[x]; fa[x] = t; x = temp; } return x; } void merge (int a,int b) a = find (a); b = find (b); if (a != b) fa[b] = a; } int main () int n, m; int sum = 0 ; int j=0 ; cin >> n >> m; int x, y; init (n); for (int i = 1 ; i <= n; kind[i++] = 1 ); for (int i = 1 ; i <= m; i++){ cin >> x >> y; if (x > y) swap (x, y); merge (x, y); } for (int i = 1 ; i <= n; i++){ if (fa[i] != i){ flag[fa[i]] = true ; kind[fa[i]]++; } } for (int i = 1 ; i <= n; i++){ if (flag[i]) kinds++; if (kind[i] != 1 ){ sum += kind[i]; } } if (sum < n){ kinds += (n - sum); } cout << kinds << endl; sort (kind, kind+n, greater<int >()); for (int i = 0 ; i < kinds; i++){ if (i != kinds-1 ) cout << kind[i] << " " ; else cout << kind[i]; } return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 #include <bits/stdc++.h> using namespace std;int fa[100005 ];int sum[100005 ];void init (int n) for (int i = 1 ; i <= n; i++){ fa[i] = i; sum[i] = 1 ; } } int find (int x) if (x!=fa[x]) fa[x] = find (fa[x]); return fa[x]; } void merge (int a,int b) a = find (a); b = find (b); if (a != b){ fa[b] = a; sum[a] += sum[b]; } } int main () int n, m; int j=0 ; cin >> n >> m; int x, y; init (n); for (int i = 1 ; i <= m; i++){ cin >> x >> y; merge (x, y); } vector<int > ve; for (int i = 1 ; i <=n; i++){ if (fa[i] == i) ve.push_back (sum[i]); } cout << ve.size () << endl; sort (ve.begin (), ve.end (), greater<int >()); for (int i = 0 ; i < ve.size (); i++){ if (i != ve.size ()-1 ) cout << ve[i] << " " ; else cout << ve[i]; } return 0 ; }
L2-2 走马 (25 分) Alice和Bob在下象棋,现在他们玩腻了,想找点别的事做。他们突然想知道,如果将一个马随机的放在一张大小为n * n的棋盘的某一位置,走到棋盘的四个角落(1,1),(1,n),(n,1),(n,n)的格子分别最少需要多少步。
请写个程序你帮帮他们计算吧。
PS:象棋中马的走法如下:马走“日”,假设当前马的坐标为(x,y),在不走出棋盘的情况下,可以走到(x-1,y-2) , (x+1,y-2) , (x-2,y-1) , (x+2,y-1) , (x-1,y+2) , (x+1,y+2) , (x-2,y+1) , (x+2 , y+1)这八个格子中。
输入格式:
第一行为一个整数n,表示棋盘大小为n * n。(4 ≤ n ≤ 1000)
第二行为两个整数x, y,表示马当前的坐标。
输出格式:
输出共4行
第一行为到达(1,1)所需步数,第二行为到达(1,n)所需步数,第三行为到达(n,1)所需步数,第四行为到达(n,n)所需步数。
输入样例:
在这里给出一组输入。例如:
输出样例:
在这里给出相应的输出。例如:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 #include <bits/stdc++.h> using namespace std;#define x first #define y second typedef pair<int ,int > PII;int n; const int N = 1e6 +5 ;int dx[8 ] = {-1 ,1 ,-2 ,2 ,-1 ,1 ,-2 ,2 };int dy[8 ] = {-2 ,-2 ,-1 ,-1 ,2 ,2 ,1 ,1 };int ans[1005 ][1005 ],vis[1005 ][1005 ] = {false };int main () cin>>n; int x,y; cin>>x>>y; queue<PII> q; q.push ({x,y}); vis[x][y] = true ; while (!q.empty ()) { PII now = q.front (); q.pop (); int nx,ny; for (int i=0 ; i<8 ; i++) { nx = now.x + dx[i]; ny = now.y + dy[i]; if (nx>=1 && nx<=n && ny>=1 && ny<=n && !vis[nx][ny]) { vis[nx][ny] = true ; ans[nx][ny] = ans[now.x][now.y] + 1 ; q.push ({nx,ny}); } } } cout<<ans[1 ][1 ]<<endl<<ans[1 ][n]<<endl<<ans[n][1 ]<<endl<<ans[n][n]; return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 #include <bits/stdc++.h> using namespace std;int ans[4 ];int dx[8 ] = {-1 , +1 , -2 , +2 , -1 , +1 , -2 , +2 };int dy[8 ] = {-2 , -2 , -1 , -1 , +2 , +2 , +1 , +1 };int vis[1005 ][1005 ];int dp[1005 ][1005 ];pair<int , int > pii; int main () int n; cin >> n; queue<pair<int , int > > que; int x, y; cin >> x >> y; vis[x][y] = true ; que.push (make_pair (x, y)); while (!que.empty ()){ pii = que.front (); que.pop (); int nowx, nowy; for (int i = 0 ; i < 8 ; i++){ nowx = pii.first + dx[i]; nowy = pii.second + dy[i]; if (nowx > 0 && nowx <= n && nowy > 0 && nowy <= n && (vis[nowx][nowy] == false )){ que.push (make_pair (nowx, nowy)); vis[nowx][nowy] = true ; dp[nowx][nowy] = dp[nowx - dx[i]][nowy - dy[i]] + 1 ; } } } cout << dp[1 ][1 ] << endl; cout << dp[1 ][n] << endl; cout << dp[n][1 ] << endl; cout << dp[n][n] << endl; return 0 ; }
L2-4 接金币 (25 分) Chocola在玩游戏,现在他来到了第一个奖励关卡。这个关卡有着n枚金币,第i枚金币初始(第0秒时)所在的位置为(Xi, Yi),价值为Vi,它们会匀速向下掉落,每秒移动1格。
在本关中,玩家可以选择地面上任意位置作为起点,且只能在高度为 0 的地面上移动,对于每一秒,你可以选择向左或者向右移动1格,也可以选择站在原地。当金币掉落至地面时如果恰好与玩家的位置重合(即横坐标X相等),玩家将会获得等同于该金币价值的积分,否则金币会立即消失。
请你告诉Chocola,他最多能获得多少分数?
输入格式:
第一行为一个整数n ,表示地图上共有n 枚金币。(1≤n ≤1000)
接下来n 行,每行有3个整数 X**i ,Yi ,Vi 分为表示在初始时刻,第i枚金币的横纵坐标与其价值。(1≤X**i ,Yi ≤1000 , 1≤Vi ≤1000)
输出格式:
仅一行,输出最多可以获得的积分数。
输入样例:
1 2 3 4 3 10 1 10 11 2 10 1 2 10
输出样例:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 #include <bits/stdc++.h> using namespace std;int a[1005 ][1005 ], maxx;int main () int n; cin >> n; for (int i=0 ;i<n;i++) { int x, y, v; cin >> x >> y >> v; a[y][x] = v; } for (int i=1 ;i<=1000 ;i++) { for (int j=1 ;j<=1000 ;j++) { int x; x = max (a[i-1 ][j],a[i-1 ][j+1 ]); x = max (x,a[i-1 ][j-1 ]); a[i][j]+=x; maxx = max (a[i][j],maxx); } } cout<<maxx; }
真题模拟 2019-01迷宫 本题总分:15 分
【问题描述】
下图给出了一个迷宫的平面图,其中标记为 1 的为障碍,标记为 0 的为可 以通行的地方。
010000
迷宫的入口为左上角,出口为右下角,在迷宫中,只能从一个位置走到这 个它的上、下、左、右四个方向之一。
对于上面的迷宫,从入口开始,可以按DRRURRDDDR 的顺序通过迷宫,一共 10 步。其中 D、U、L、R 分别表示向下、向上、向左、向右走。
对于下面这个更复杂的迷宫(30 行 50 列),请找出一种通过迷宫的方式, 其使用的步数最少,在步数最少的前提下,请找出字典序最小的一个作为答案。 请注意在字典序中D<L<R<U。(如果你把以下文字复制到文本文件中,请务必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 maze.txt,内容与下面的文本相同)
01010101001011001001010110010110100100001000101010
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一 个字符串,包含四种字母 D、U、L、R,在提交答案时只填写这个字符串,填写多余的内容将无法得分。
答案:DDDDRRURRRRRRDRRRRDDDLDDRDDDDDDDDDDDDRDDRRRURRUURRDDDDRDRRRRRRDRRURRDDDRRRRUURUUUUUUULULLUUUURRRRUULLLUUUULLUUULUURRURRURURRRDDRRRRRDDRRDDLLLDDRRDDRDDLDDDLLDDLLLDLDDDLDDRRRRRRRRRDDDDDDRR
思路:看到与最少步数有关,自然要想到bfs,每搜索一次还要记录路径,题目还说要字典序最小,那么我们在搜索路径的时候不妨就按照字典序的顺序来安排搜索方向的先后顺序。
Excel求解 效果图:(迷宫的设计还是蛮耿直的,陷阱不多)
Excel在蓝桥中的普及已经不是第一次了,这里要求会使用替换功能即可。
好了话不多说,第一步需要将01迷宫复制粘贴进txt里,然后将“0”“1”分别替换为“(Tab)0”“(Tab)1”。
(Tab)注:在txt里敲入Tab,即可显示一段空白,复制下来就好。
如图所示:
替换完后是这个样子的:
然后将txt中的内容粘到Excel中,就成了下图:
将表格中1的底色替换为其他颜色,同理也可以将0替换成空格,目的都是为了便于识别。
好了,现在障碍设成了深蓝色,我们也可以将列宽适当得调小些,使单元格看起来更像正方形。
最后一步,把表格截图后用画图打开,就可以用笔来模拟走迷宫了~(如效果图所示)
BFS求解 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 #include <bits/stdc++.h> using namespace std;int n = 30 , m = 50 ;char mp[30 ][50 ]; int vis[30 ][50 ];char ch[4 ] = {'D' , 'L' , 'R' , 'U' };int dir[4 ][2 ] = {{1 , 0 }, {0 , -1 }, {0 , 1 }, {-1 , 0 }};struct point { int x, y; string road; point (int a, int b){ x = a; y = b; } }; void bfs () queue<point> q; point p (0 , 0 ) ; p.road = "" ; q.push (p); vis[0 ][0 ] = 1 ; while (!q.empty ()){ point t = q.front (); q.pop (); if (t.x == n-1 && t.y == m-1 ){ cout << t.road<< endl; break ; } for (int i = 0 ; i < 4 ; i++){ int dx = t.x + dir[i][0 ]; int dy = t.y + dir[i][1 ]; if (dx >= 0 && dx < n && dy >= 0 && dy < m){ if (mp[dx][dy] == '0' && !vis[dx][dy]){ point tt (dx, dy) ; tt.road = t.road + ch[i]; q.push (tt); vis[dx][dy] = 1 ; } } } } } int main () for (int i = 0 ; i < n; i++) scanf ("%s" , mp[i]); bfs (); return 0 ; }
DFS求解 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 #include <bits/stdc++.h> using namespace std;int n, m;char dp[1005 ][1005 ];int dir[4 ][2 ] = {{1 , 0 }, {0 , -1 }, {0 , 1 }, {-1 , 0 }};string fro[4 ] = {"D" , "L" , "R" , "U" }; int vis[1005 ][1005 ];int mi = 0x3f3f3f3f ;string anss; void dfs (int x, int y, string ans) if (vis[n-1 ][m-1 ] == 1 && ans.length () < mi){ anss = ans; return ; } if (x < 0 || x>=n || y < 0 || y >= m || dp[x][y] == '1' || vis[x][y] == 1 ){ return ; } for (int i = 0 ; i < 4 ; i++){ if (!vis[x][y]){ vis[x][y] = 1 ; ans+=fro[i]; dfs (x + dir[i][0 ], y + dir[i][1 ], ans); vis[x][y] = 0 ; } } return ; } int main () cin >> n >> m; for (int i = 0 ; i < n; i++) scanf ("%s" , dp[i]); dfs (0 , 0 , "" ); cout << anss; return 0 ; }
2020-02Plus: 扩散 最开始做成国赛,让我怀疑人生,我觉得这难度,这TM圈钱杯?????
本题总分:5 分
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 #include <bits/stdc++.h> using namespace std;bool vis[10000 ][10000 ];int cnt;int x[4 ] = {1 , 0 , -1 , 0 };int y[4 ] = {0 , 1 , 0 , -1 };int ans = 0 ;void dfs (int nx,int ny,int cnt) if (cnt == 2020 ) return ; if (vis[nx - 1 ][ny] == 1 && vis[nx + 1 ][ny] == 1 && vis[nx][ny - 1 ] == 1 && vis[nx][ny + 1 ] == 1 ) return ; for (int i = 0 ; i < 4 ; i++){ if (vis[nx+x[i]][ny+y[i]] == 0 ){ ans++; vis[nx+x[i]][ny+y[i]] = true ; dfs (nx+x[i], ny+y[i], cnt+1 ); }else { dfs (nx+x[i], ny+y[i], cnt+1 ); } } return ; } int main () int k = 3030 ; vis[0 +k][0 +k] = true ; vis[2020 +k][11 +k] = true ; vis[11 +k][14 +k] = true ; vis[2000 +k][2000 +k] = true ; dfs (0 +k, 0 +k, 0 ); dfs (2020 +k, 11 +k, 0 ); dfs (11 +k, 14 +k, 0 ); dfs (2000 +k, 2000 +k, 0 ); cout << ans; return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 #include <iostream> #include <cstring> using namespace std;int vis[6080 ][6080 ] = { 0 };int ans = 1 ;int m[5 ][2 ] = { {-1 ,0 }, {0 ,-1 },{0 ,1 }, {1 ,0 } }; void dfs (int x, int y, int index) if (index == 2020 ) { return ; } if (vis[x - 1 ][y] == 1 && vis[x + 1 ][y] == 1 && vis[x][y - 1 ] == 1 && vis[x][y + 1 ] == 1 ) return ; for (int i = 0 ; i < 4 ; i++) { int dx = x + m[i][0 ]; int dy = y + m[i][1 ]; if (vis[dx][dy]==0 ) { ans++; vis[dx][dy] = 1 ; dfs (dx, dy, index + 1 ); } else if (vis[dx][dy] == 1 ) { dfs (dx, dy, index + 1 ); } } return ; } int main () vis[2020 ][2020 ] = 1 ; dfs (2020 , 2020 , 0 ); vis[4040 ][2031 ] = 1 ; dfs (4040 , 2031 , 0 ); vis[2031 ][2034 ] = 1 ; dfs (2031 , 2034 , 0 ); vis[4020 ][4020 ] = 1 ; dfs (4020 , 4020 , 0 ); cout << ans; }
2020-01 门牌制作 【问题描述】
小蓝要为一条街的住户制作门牌号。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
答案:624
用Word即可解决 ctrl + f
2020-02 既约分 数 【问题描述】
如果一个分数的分子和分母的最大公约数 是1,这个分数称为既约分数。例如,3/4 , 5/2 , 1/8 , 7/1都是既约分数。请问,有多少个既约分数,分子和分母都是1 到2020 之间的整数(包括1和2020)?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
答案:2481215
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 #include <bits/stdc++.h> using namespace std;int gcd (int a, int b) if (b == 0 ) return a; return gcd (b, a%b); } int main () int ans = 0 ; for (int i = 1 ; i <= 2020 ; i++){ for (int j = 1 ; j <= 2020 ; j++){ if (gcd (i, j) == 1 ){ ans++; } } } cout << ans; return 0 ; }
2020-03 蛇形填数 【问题描述】
如下图所示,小明用从1 开始的正整数“蛇形”填充无限大的矩阵。
容易看出矩阵第二行第二列中的数是5。请你计算矩阵中第20 行第20 列的数是多少?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一
答案:761
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 #include <bits/stdc++.h> using namespace std;int main () int cnt=1 ; for (int i = 1 ; i <= 50 ; i++){ for (int j = cnt; j <= cnt+i; j++){ if (j == cnt+i){ cout << endl; } printf ("%d " , j); } cnt += i; } return 0 ; }
思路:打表出奇迹,暴力出省一,推算,我们观察那张图里的13,他所在的位置,他两边的距离相等的,因此推断20行20列,就是前面有19行19列
后面也有19行19列,加上哪行那列,就是我们需要锁定的对角线为39行-39列,再仔细观察,11+15)/2为13,4 + 6)/2 为5,所以说,我们只需要找1行39列和39行1列加起来除以二即可,over
最终找到的是742和780
2020-04 跑步锻炼 【问题描述】
小蓝每天都锻炼身体。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一
答案:8879
思路一:最开始使用excel,算出来8878=-=,处理边界条件的时候本来把九月末最后一个周一提出来了,但是加进去忘记了,所以说打表需谨慎,一错全无了,我通过excel,两个时间相减,得到了总共的天数(注意边界条件需要+1)其次用日历表,数20年内,有多少个一号正好是周一,好像是34个,最后将剔除边界的时间/7得到总共多少整周,再得到有多少个周一,再得到有多少个一日,从而一日和周一相加,减去34即为加两km的天数,再把总天数-加2km的天数,最后和加2km的天数*2的结果做和,即为最终结果
思路二:
天,月,年,到边界要特别注意,我这里就是天的边界没处理好,每个月少算一天,提前到下个月,于是少了两百多天,哭死
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 #include <bits/stdc++.h> using namespace std;int mon[13 ] = {0 , 31 , 28 , 31 , 30 , 31 , 30 , 31 , 31 , 30 , 31 , 30 , 31 };int main () int y = 2000 , m = 1 , d = 1 ; int day = 6 ; int ty, tm, td; int tday; int ans = 0 ; while (1 ){ if ((y % 400 == 0 ) || (y % 100 != 0 && y % 4 == 0 )) mon[2 ] = 29 ; else mon[2 ] = 28 ; if (day == 1 || d == 1 ) ans += 2 ; else ans++; if ((y == 2020 ) && (m == 10 ) && (d == 1 )) break ; d++; day++; if (d == mon[m]+1 ){ m++; d = 1 ; } if (m == 13 ){ y++; m = 1 ; } if (day == 8 ){ day = 1 ; } } cout << ans << endl; cout << day << endl; cout << y << m << d; return 0 ; }
2020-05 七段码
tot = 7 + 10 + 16 + 20 + 19 + 7 + 1 = 80
2021-01
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 #include <bits/stdc++.h> using namespace std; int main () int cnt[10 ] = {0 }; int count = 2021 ; int a; for (int i = 1 ; ; i++){ int n = i; while (n){ cnt[n%10 ]++; n /= 10 ; } if (cnt[1 ] > count){ a = i - 1 ; break ; } } cout << a << endl; return 0 ; }
程序设计题 2020-06 成绩统计 【问题描述】
小蓝给学生们组织了一场考试,卷面总分为 100 分,每个学生的得分都是
【输入格式】
输入的第一行包含一个整数 n,表示考试人数。
【输出格式】
输出两行,每行一个百分数,分别表示及格率和优秀率。百分号前的部分
【样例输入】
1 2 3 4 5 6 7 8 9 7 80 92 56 74 88 100 0 12345678
【样例输出】
【评测用例规模与约定】
对于50% 的评测用例, 1 ≤ n ≤ 100。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 #include <bits/stdc++.h> using namespace std;int main () int n; cin >> n; int cnt; int youxiu = 0 ; int jige = 0 ; double ans; for (int i = 0 ; i < n ; i++){ cin >> cnt; if (cnt >= 85 ){ youxiu++; jige++; }else if (cnt >= 60 ){ jige++; } } printf ("%.lf%%\n" , (1.0 *jige / n)*100 ); printf ("%.lf%%\n" , (1.0 *youxiu / n)*100 ); return 0 ; }
2020-07 回文日期 题目描述
2020 年春节期间,有一个特殊的日期引起了大家的注意:2020 年2 月2日。因为如果将这个日期按“yyyymmdd” 的格式写成一个8 位数是20200202,恰好是一个回文数。我们称这样的日期是回文日期。
输入格式
输入包含多组测试数据,第一行为正整数T。(T≤1000)
输出格式
对于每组测试数据输出两行,每行1 个八位数。
输入样例 复制
输出样例 复制
1 2 3 4 20211202 21211212 20300302 21211212
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 #include <bits/stdc++.h> using namespace std;bool cmp (string a, string b) return a < b; } int main () int n; string date; int i, j, y; char buff[9 ]; vector <string> str; for (i = 1 ; i <= 31 ; i++) for (j = 1 ; j <= 12 ; j++){ if (i > 29 && j == 2 ) continue ; else if (i == 31 && (j == 4 || j == 6 || j == 9 || j == 11 )) continue ; y = (i % 10 ) * 1000 + (i / 10 )*100 + (j % 10 ) * 10 + j / 10 ; if (i == 29 && j == 2 && !(y % 400 == 0 || (y % 100 != 0 && y % 4 == 0 ))) continue ; sprintf (buff, "%04d%02d%02d" , y, j, i); str.push_back (buff); } sort (str.begin (), str.end (), cmp); cin >> n; for (int s = 0 ; s < n; s++){ cin >> date; for (int i = 0 ; i < str.size (); i++){ if (date < str[i]){ cout << str[i] << "\n" ; for (j = i; j < str.size (); j++){ if (str[j][0 ] == str[j][2 ] && str[j][1 ] == str[j][3 ]){ cout << str[j] << "\n" ; break ; } } break ; } } } return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 #include <bits/stdc++.h> using namespace std;int aa[10 ];int a;int flag1, flag2;int main () int n; cin >> n; for (int i = 0 ; i < n; i++){ cin >> a; while (1 ){ int cnt = a; for (int j = 1 ; j <= 8 ; j++){ aa[j] = cnt % 10 ; cnt /= 10 ; } a++; if (aa[1 ] == aa[8 ] && aa[2 ] == aa[7 ] && aa[3 ] == aa[6 ] && aa[4 ] == aa[5 ] && flag1 == 0 ){ cout << a << endl; flag1 = 1 ; } if (aa[1 ] == aa[3 ] == aa[6 ] == aa[8 ] && aa[2 ] == aa[4 ] == aa[5 ] == aa[7 ] && aa[1 ] != aa[2 ] && flag2 == 0 ){ cout << a << endl; flag2 = 1 ; } if (flag1 && flag2){ break ; } } } return 0 ; }
2020-08 子串分值和 资源限制
时间限制:1.0s 内存限制:256.0MB问题描述 字符串 S ,我们定义 S 的分值 f(S) 为S 中出现的不同的字符个数。例如 f(“aba”)=2,f(“abc”)=3, f(“aaa”)=1。
现在给定一个字符串 S[0…n-1](长度为n ),请你计算对于所有S 的非空子串S[i…j] ,(0<=i<=j<=n-1)的和是多少。
输入格式
输出格式
样例输入
样例输出
样例说明
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 a 1 ab 2 aba 2 abab 2 ababc 3 b 1 ba 2 bab 2 babc 3 a 1 ab 2 abc 3 b 1 bc 2 c 1 123456789101112131415
评测用例规模与约定 (n为正整数)
AC50% 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 #include <bits/stdc++.h> using namespace std; int main () int ret = 0 ; string s; set<char > st; cin >> s; int n = s.size (); for (int i = 0 ; i < n; i++) for (int j = i; j < n; j++){ for (int k = i; k <= j; k++){ st.insert (s[k]); } ret += st.size (); st.clear (); } cout << ret << endl; return 0 ; }
AC60% 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 #include <bits/stdc++.h> using namespace std; int main () int ret = 0 ; string s; set<char > st; cin >> s; int n = s.size (); for (int i = 0 ; i < n; i++){ for (int j = i; j < n; j++){ st.insert (s[j]); ret += st.size (); } st.clear (); } cout << ret << endl; return 0 ; }
AC100% 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 #include <bits/stdc++.h> using namespace std; int main () long long int ans = 0 ; char s[100005 ]; int vis[26 ] = {0 }; scanf ("%s" , s); int len = strlen (s); for (int i = 0 ; i < len; i++){ vis[s[i] - 'a' ] = 1 ; } int num = 0 ; for (int i = 0 ; i < 26 ; i++){ if (vis[i] == 1 ) num++; } for (int i = 0 ; i < len; i++){ set<char > e; for (int j = i; j < len; j++){ e.insert (s[j]); int size = e.size (); ans += size; if (size == num){ ans += (len - 1 - j) * size; break ; } } } printf ("%lld" , ans); return 0 ; }
2020-09 平面切分 【问题描述】 【输入格式】 【输出格式】 【样例输入】 【样例输出】
在同一个平面内,如果添加的每一条直线互不相交,则每添加一条直线,就会增加一个平面;当添加一条直线时,这条直线与当前平面内已有直线每产生一个不同位置的交点时,这条直线对平面总数量的贡献会额外增多一个, 记为Si,值Si的值为经过该直线的点+1, 1为直线自身贡献的平面 , 结果为每一条直线的贡献加上最开始的一个平面,既:S1到Sk的和(k为所有不重合直线的数量)再加上1。
一个简单的例子,新来的一条线切割了三条之前的线,那么将那三条线本来已有的4个区域,分割成了8个区域,也就是,增加了4个区域,也就是,他进入会加1,然后割了三条,一共加了四个区域
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 #include <bits/stdc++.h> using namespace std;long double s[1010 ][2 ];long long ans;bool st[1010 ];pair<long double , long double > p; int main () int n; cin >> n; for (int i = 0 ; i < n; i++){ cin >> s[i][0 ] >> s[i][1 ]; set<pair<long double , long double > > points; for (int j = 0 ; j < i; j++){ if (st[j]) continue ; if (s[i][0 ] == s[j][0 ]){ if (s[i][1 ] == s[j][1 ]){ st[i] = true ; break ; }else continue ; } p.first = (s[j][1 ] - s[i][1 ]) / (s[i][0 ] - s[j][0 ]); p.second = s[i][0 ] * p.first + s[i][1 ]; points.insert (p); } if (!st[i]) ans += points.size () + 1 ; } cout << ans+1 << endl; return 0 ; }
AC50% 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 #include <bits/stdc++.h> using namespace std;long double x[1005 ][2 ];long double b[1005 ][2 ];long double tx, ty;bool flag[1005 ];int ans = 1 ;pair<long double , long double > p; int main () int n; cin >> n; for (int i = 0 ; i < n; i++){ cin >> x[i][0 ] >> x[i][1 ]; set<pair<long double , long double > > points; for (int j = 0 ; j < i; j++){ if (x[i][0 ] == x[j][0 ]) { flag[i] = true ; continue ; } tx = (x[i][0 ] - x[j][0 ]) / (x[j][1 ] - x[i][1 ]); ty = x[i][0 ] * tx + x[i][1 ]; points.insert (make_pair (tx, ty)); } ans += points.size () + 1 ; } cout << ans << endl; return 0 ; }
AC60% 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 #include <bits/stdc++.h> using namespace std;long double x[1005 ][2 ];long double b[1005 ][2 ];long double tx, ty;bool flag[1005 ];int ans = 1 ;pair<long double , long double > p; int main () int n; cin >> n; for (int i = 0 ; i < n; i++){ cin >> x[i][0 ] >> x[i][1 ]; set<pair<long double , long double > > points; for (int j = 0 ; j < i; j++){ if (x[i][0 ] == x[j][0 ] || x[i][1 ] == x[j][1 ]){ flag[i] = true ; continue ; } tx = (x[i][0 ] - x[j][0 ]) / (x[j][1 ] - x[i][1 ]); ty = x[i][0 ] * tx + x[i][1 ]; points.insert (make_pair (tx, ty)); } if (!flag[i])ans += points.size () + 1 ; } cout << ans << endl; return 0 ; }
AC75% 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 #include <bits/stdc++.h> using namespace std;long double x[1005 ][2 ];long double b[1005 ][2 ];long double tx, ty;bool flag[1005 ];int ans = 1 ;pair<long double , long double > p; int main () int n; cin >> n; for (int i = 0 ; i < n; i++){ cin >> x[i][0 ] >> x[i][1 ]; set<pair<long double , long double > > points; for (int j = 0 ; j < i; j++){ if (x[i][0 ] == x[j][0 ]) { flag[i] = true ; continue ; } tx = (x[i][0 ] - x[j][0 ]) / (x[j][1 ] - x[i][1 ]); ty = x[i][0 ] * tx + x[i][1 ]; points.insert (make_pair (tx, ty)); } if (!flag[i])ans += points.size () + 1 ; } cout << ans << endl; return 0 ; }
AC90% 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 #include <bits/stdc++.h> using namespace std;long double x[1005 ][2 ];long double b[1005 ][2 ];long double tx, ty;bool flag[1005 ];int ans = 1 ;pair<long double , long double > p; int main () int n; cin >> n; for (int i = 0 ; i < n; i++){ cin >> x[i][0 ] >> x[i][1 ]; set<pair<long double , long double > > points; for (int j = 0 ; j < i; j++){ if (x[i][0 ] == x[j][0 ]){ if (x[i][1 ] == x[j][1 ]){ flag[i] = true ; continue ; }else continue ; } tx = (x[i][0 ] - x[j][0 ]) / (x[j][1 ] - x[i][1 ]); ty = x[i][0 ] * tx + x[i][1 ]; points.insert (make_pair (tx, ty)); } if (!flag[i])ans += points.size () + 1 ; } cout << ans << endl; return 0 ; }
AC100% 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 #include <bits/stdc++.h> using namespace std;long double x[1005 ][2 ];long double b[1005 ][2 ];long double tx, ty;bool flag[1005 ];int ans = 1 ;pair<long double , long double > p; int main () int n; cin >> n; for (int i = 0 ; i < n; i++){ cin >> x[i][0 ] >> x[i][1 ]; set<pair<long double , long double > > points; for (int j = 0 ; j < i; j++){ if (x[i][0 ] == x[j][0 ]){ if (x[i][1 ] == x[j][1 ]){ flag[i] = true ; continue ; }else continue ; } tx = (x[i][1 ] - x[j][1 ]) / (x[j][0 ] - x[i][0 ]); ty = x[i][0 ] * tx + x[i][1 ]; points.insert (make_pair (tx, ty)); } if (!flag[i])ans += points.size () + 1 ; } cout << ans << endl; return 0 ; }