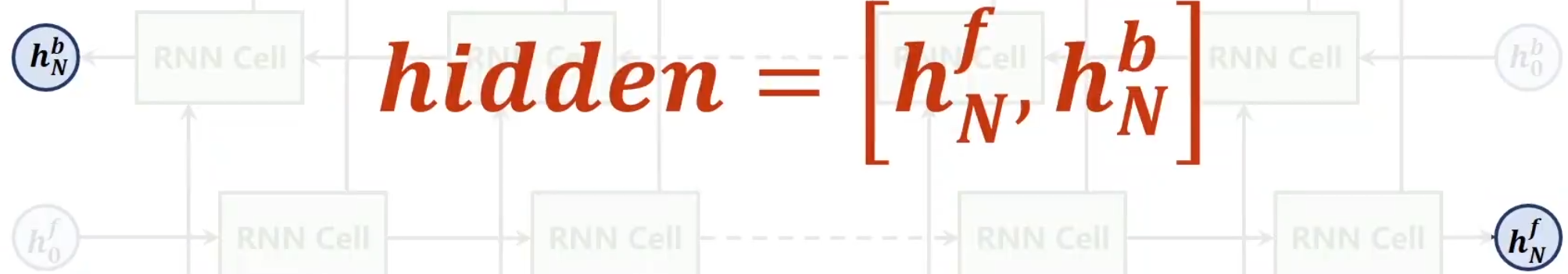环境配置 打开Anaconda Prompt (Anaconda3)
创建环境
1 2 3 4 5 * * * * conda create -n pytorch python=3.6
输入conda activate pytorch进入pytorch操作界面
pip install xxx(==***)下载相关包，==后是版本号，可忽略
pip uninstall xxx 删除相关包
conda info --envs查看已经创建好的房间
conda activate pytorch激活python房间
腾讯云配置pytorch
Pytorch入门——手把手带你配置云服务器环境 - 知乎 (zhihu.com)
1 2 3 4 5 6 7 8 9 10 jupyter nbconvert --to markdown *.ipynb jupyter nbconvert --to script file_name.ipynb 1.%load语句，在notebook新建一个ipynb记事本输入%load file_name.py就会把整个py文件的代码加载到一个cell里面来，之后自己整理了。 2.如果只是单纯要调用py文件的函数的话可以像一般掉包一样from xx import xx但是脚本语言嘛，平时写的py文件可能只是处理一些临时事务，就没有封装好，可能都没有main函数，是从头到尾顺序执行，这个时候就要用到%run语句了，相当于直接执行py文件。
一点点学习路线 朴素贝叶斯，逻辑回归最大熵 ，提升树看gdbt和adboost？xgboost，必须要手推公式
有不会的去看刘建平老师的博客
机器学习实战入门看两个任务
学习实践
本实践全部来自于课程《PyTorch深度学习实践》完结合集_哔哩哔哩_bilibili
线性模型 $$
解释数据集和模型，这里我们先完成不加b的情况
取MSE为损失函数
开始构建模型，手撸冲冲冲
1 2 import numpy as npimport matplotlib.pyplot as plt
1 2 x_data = [1. , 2. , 3. ] y_data = [2. , 4. , 6. ]
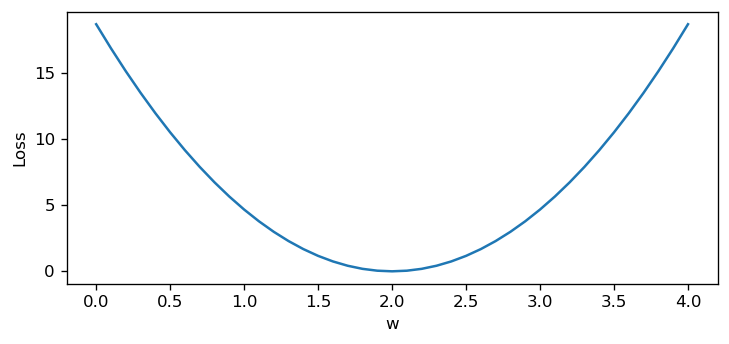
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 def forward (x_data ): return x_data * w def loss (y_pred, y_data ): return (y_pred - y_data) ** 2 w_list = [] mse_list = [] for w in np.arange(0. , 4.1 , 0.1 ): loss_ = 0 for x_val, y_val in zip (x_data, y_data): y_pred = forward(x_val) loss_ += loss(y_pred, y_val) loss_ /= len (x_data) w_list.append(w) mse_list.append(loss_) plt.figure(figsize=(7 ,3 ), dpi=120 ) plt.plot(w_list, mse_list) plt.ylabel('Loss' ) plt.xlabel('w' ) plt.show()
梯度下降法
引言
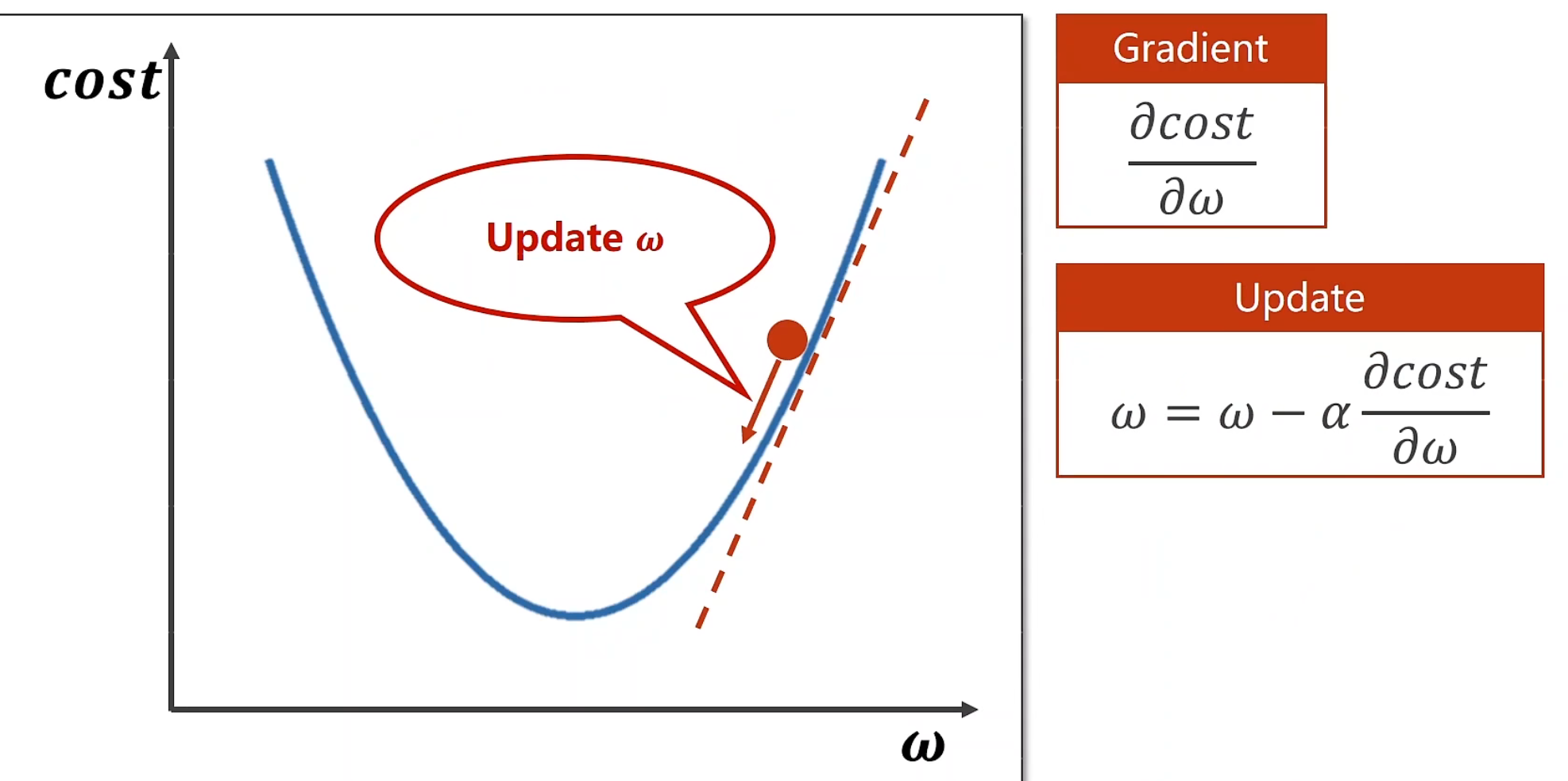
让我们从导数开始讲起，一个点在该处对某一个方向的导数，是梯度，我们也可以看做是方向，但是这个方向，比如这里，此时他的导数是正的，但是很显然，我们应该往与他导数相反的方向前进，才能得到我们想要的结果，也就是min(cost)，因此我们的迭代函数为下图中的update，其中α为学习率
当α比较大时，可能会发生跨度太大，从而一步就错过了最低点，然后就不断的交叉交叉，始终无法逼近最小点
当α太小时，可能会陷入局部最优走不出来，这也是很不好的，不过我们还是应该适当取得小一点，因为后续有方法可以尽可能客服局部最优的问题
通过我们这种一小步一小步逼近的方法，其实就反应了DSA中的贪心思想
这个是梯度的更新公式：我们推导出以后直接定义graident函数就好
以下是实现代码：
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 x_data = [1.0 , 2.0 , 3.0 ] y_data = [2.0 , 4.0 , 6.0 ] w = 1.0 def forward (x ): return x * w def cost (xs, ys ): cost = 0 for x, y in zip (xs, ys): y_pred = forward(x) cost += (y_pred - y) ** 2 return cost / len (xs) def gradient (xs, ys ): grad = 0 for x, y in zip (xs, ys): grad += 2 * x * (x * w - y) return grad / len (xs) print ('Predict (before training)' , 4 , forward(4 ))for epoch in range (100 ): cost_val = cost(x_data, y_data) grad_val = gradient(x_data, y_data) w -= 0.01 * grad_val print ('Epoch:' , epoch, 'w=' , w, 'loss=' , cost_val) print ('Predict (after training)' , 4 , forward(4 ))
版本二（自己实现）：
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 x_data = [1.0 , 2.0 , 3.0 ] y_data = [2.0 , 4.0 , 6.0 ] w = 1.0 def forward (x ): return x*w def cost (x, y ): return ((forward(x)-y) ** 2 ) def gradient (x, y ): return 2 *x*(x*w-y) epoch_list = [i for i in range (101 )] cost_list = [] for epoch in range (101 ): cost_ = 0 for x_digit, y_digit in zip (x_data, y_data): cost_ =+ cost(x_digit, y_digit) w -= 0.01 *gradient(x_digit, y_digit) cost_ /= len (x_data) cost_list.append(cost_) print ('cost: ' , cost_, 'w: ' , w) plt.figure(figsize=(7 ,3 ), dpi=120 ) plt.plot(epoch_list, cost_list) plt.ylabel('cost' ) plt.xlabel('epoch' ) plt.show()
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 cost: 2.4386476799999994 w: 1.260688 cost: 1.3329214952735635 w: 1.453417766656 cost: 0.7285512077588492 w: 1.5959051959019805 cost: 0.3982131462423004 w: 1.701247862192685 cost: 0.21765623082005736 w: 1.7791289594933983 cost: 0.11896702874286423 w: 1.836707389300983 cost: 0.06502526426457467 w: 1.8792758133988885 cost: 0.03554165416551504 w: 1.910747160155559 cost: 0.019426436710527316 w: 1.9340143044689266 cost: 0.010618145163155871 w: 1.9512159834655312 cost: 0.005803689497248529 w: 1.9639333911678687 cost: 0.0031721935670412514 w: 1.9733355232910992 cost: 0.0017338646444728853 w: 1.9802866323953892 cost: 0.0009476996096921988 w: 1.9854256707695 cost: 0.0005179957692047892 w: 1.9892250235079405 cost: 0.00028312728439470265 w: 1.9920339305797026 cost: 0.0001547523434250841 w: 1.994110589284741 cost: 8.458488148449721e-05 w: 1.9956458879852805 cost: 4.6232593428939405e-05 w: 1.9967809527381737 cost: 2.526991416967284e-05 w: 1.9976201197307648 ... cost: 8.693904559623234e-26 w: 1.9999999999998603 cost: 4.7496000335181754e-26 w: 1.9999999999998967 cost: 2.6091574440184965e-26 w: 1.9999999999999236 cost: 1.4153216454205246e-26 w: 1.9999999999999436
如果曲线不是这么的平滑，或者局部震荡很大，我们通常可以采用指数加权均值，举个例子，设我们现在每一步的loss为$c\begin{array}{c}0\\end{array},c\begin{array}{c}1\\end{array},c\begin{array}{c}2\\end{array}….$
设指数加权均值后loss为$c\begin{array}{c} ‘\ 0\\end{array},c\begin{array}{c}’\ 1\\end{array},c\begin{array}{c} ‘\ 2\\end{array}….$
则现在可以得到该转换公式$\left{ \begin{array}{l} c\begin{array}{c} ‘\ 0\\end{array}=c\begin{array}{c} \ 0\\end{array}\ c\begin{array}{c} ‘\ i\\end{array}=\beta c\begin{array}{c} \ i\\end{array}+\left( 1-\beta \right) c\begin{array}{c} ‘\ i-1\\end{array}\ i\ne 0\\end{array} \right. $
如果曲线发散了，也就是loss呈现增大趋势了，例如这样：
那么就说明这次训练是失败的，失败原因有很多，其中最常见的一个原因就是学习率 取得太大 了。
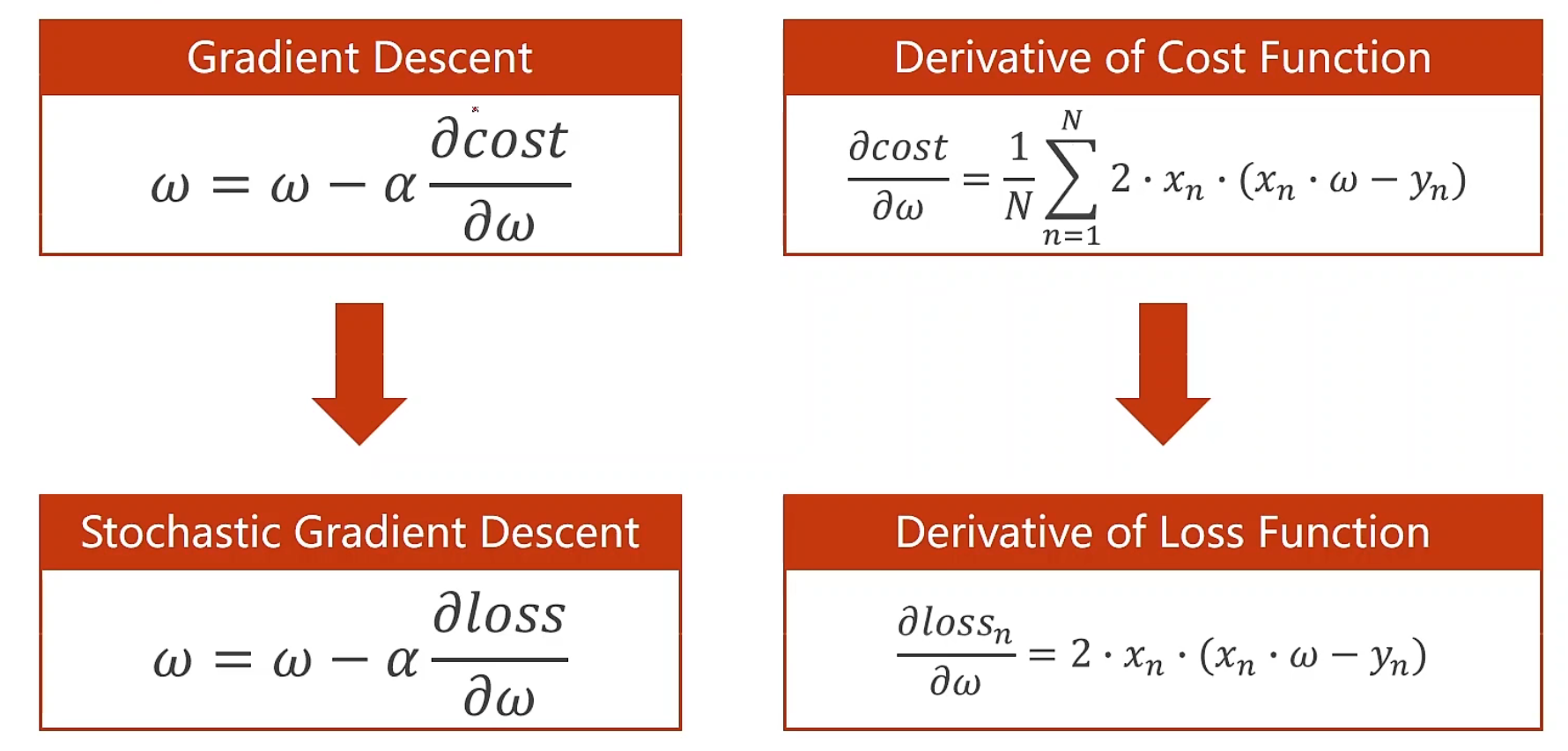
随机梯度下降 定义：提供n个数据，我们从里面随机的选一个数据，拿单个样本的权重求导，然后对权重进行更新
换句话说，梯度下降我们是利用了整个函数损失的均值，也就是每一个数据集都参与了计算损失，随机梯度下降就是指从这数据集里的n个数据中随机的取出一个
这样做的好处是，即使下降过程中陷入鞍点，我们使用随机梯度，将有可能跨过这个鞍点，向我们的最低值前进
但是 ：选点具有随机性，也就是可能会发生与最小点相距很远，或者处于走不出的局部最优的情况
因此，让我们分析一下梯度下降法和随机梯度下降法
梯度下降法的精度高，但是数据处理需要一定时间，因此时间复杂度相对高
随机梯度下降，精度低，只需处理单个数据，时间复杂度比较低
以下是实现的代码：
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 x_data = [1.0 , 2.0 , 3.0 ] y_data = [2.0 , 4.0 , 6.0 ] w = 1.0 def forward (x ): return x * w def loss (x, y ): y_pred = forward(x) return (y_pred - y) ** 2 def gradient (x, y ): return 2 * x * (x * w - y) print ('Predict (before training)' , 4 , forward(4 ))for epoch in range (100 ): for x, y in zip (x_data, y_data): grad = gradient(x, y) w = w - 0.01 * grad print ("\tgrad: " , x, y, grad) l = loss(x, y) print ("progress:" , epoch, "w=" , w, "loss=" , l) print ('Predict (after training)' , 4 , forward(4 ))
所以，对于深度学习而言，我们会在精度和时间复杂度中取一个折中
批量随机梯度下降 和计算机组成原理与操作系统一样，经典套娃，我们这里将原有数据集分成若干相同数量的组，每次用这一组样本的mean去更新梯度，我们可以将原有的数据集称为batch,那么这个数据集就叫做Mini-Batch但是我们很多时候都使用这个Mini-Batch，因此在很多接口里就把mini去掉，统称为batch
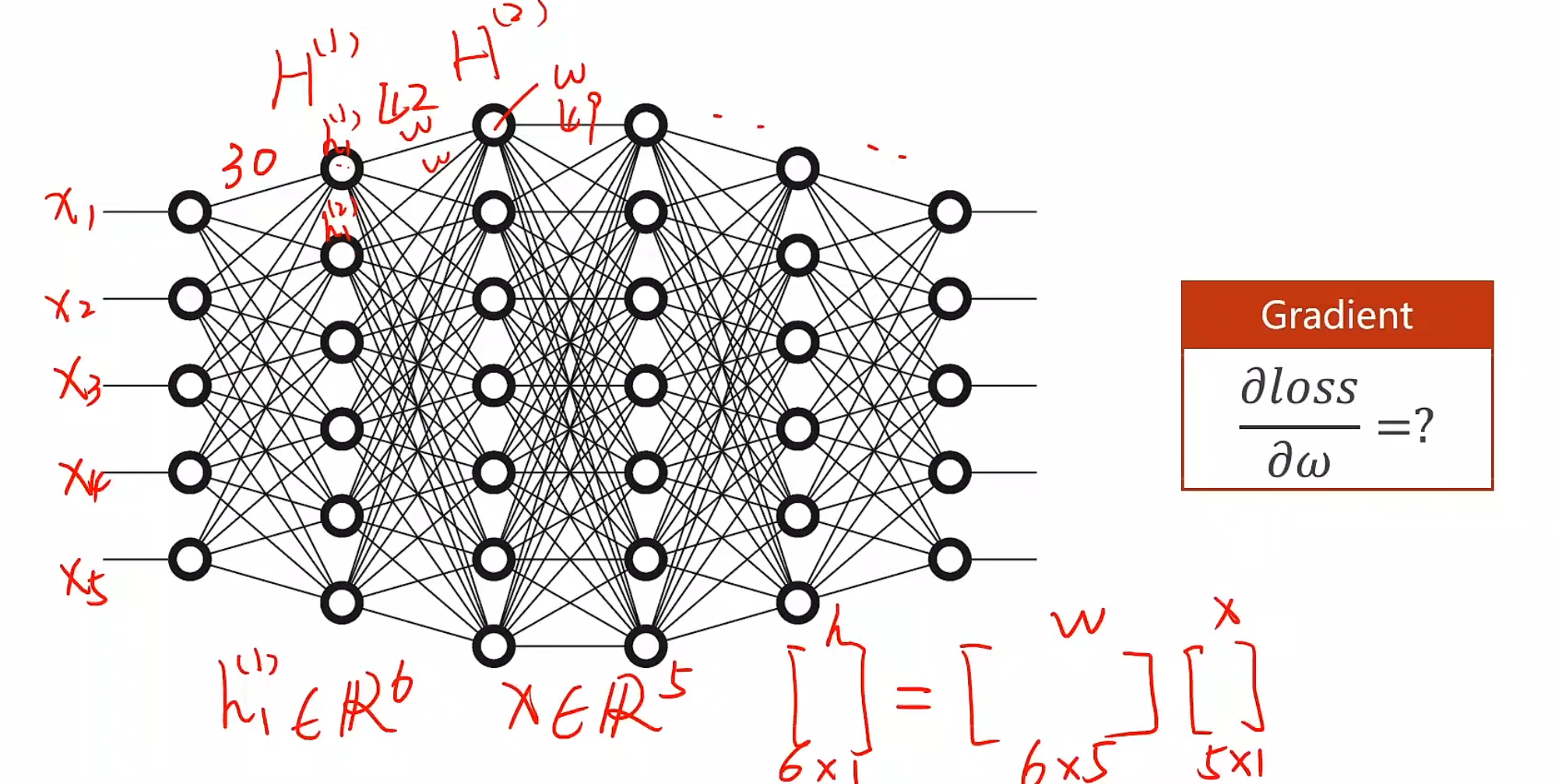
反向传播 对于简单的模型，我们可以手动计算导数，然后更新权重，但是对于复杂的模型…
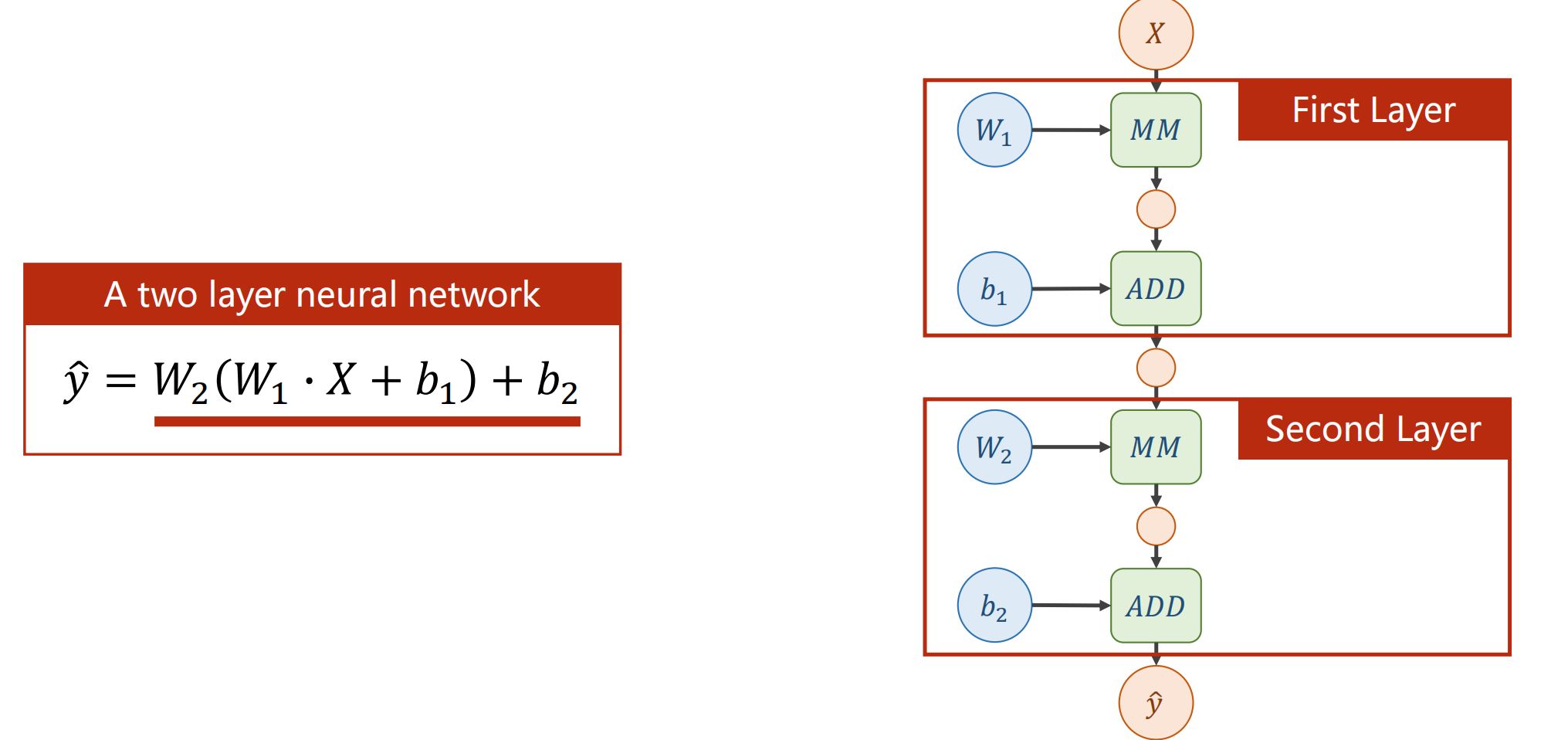
例如，我们总共有5个输入x，他们共在同一维度，我们隐藏层的第一层有六个h，需要从5个x正向传播到6个h，很容易想到我们需要增加权重矩阵，这里顺理成章的增加6×5，共三十个w，以此类推，隐藏第二层需要42个w，第三层需要49个w….因此我们不可能全部都手动生成，故引入反向传播机制
一个layer代表一层，其中，X为input，MM为Matrix multiplication，ADD为Vector addition，W1为Weight，b1为Bias
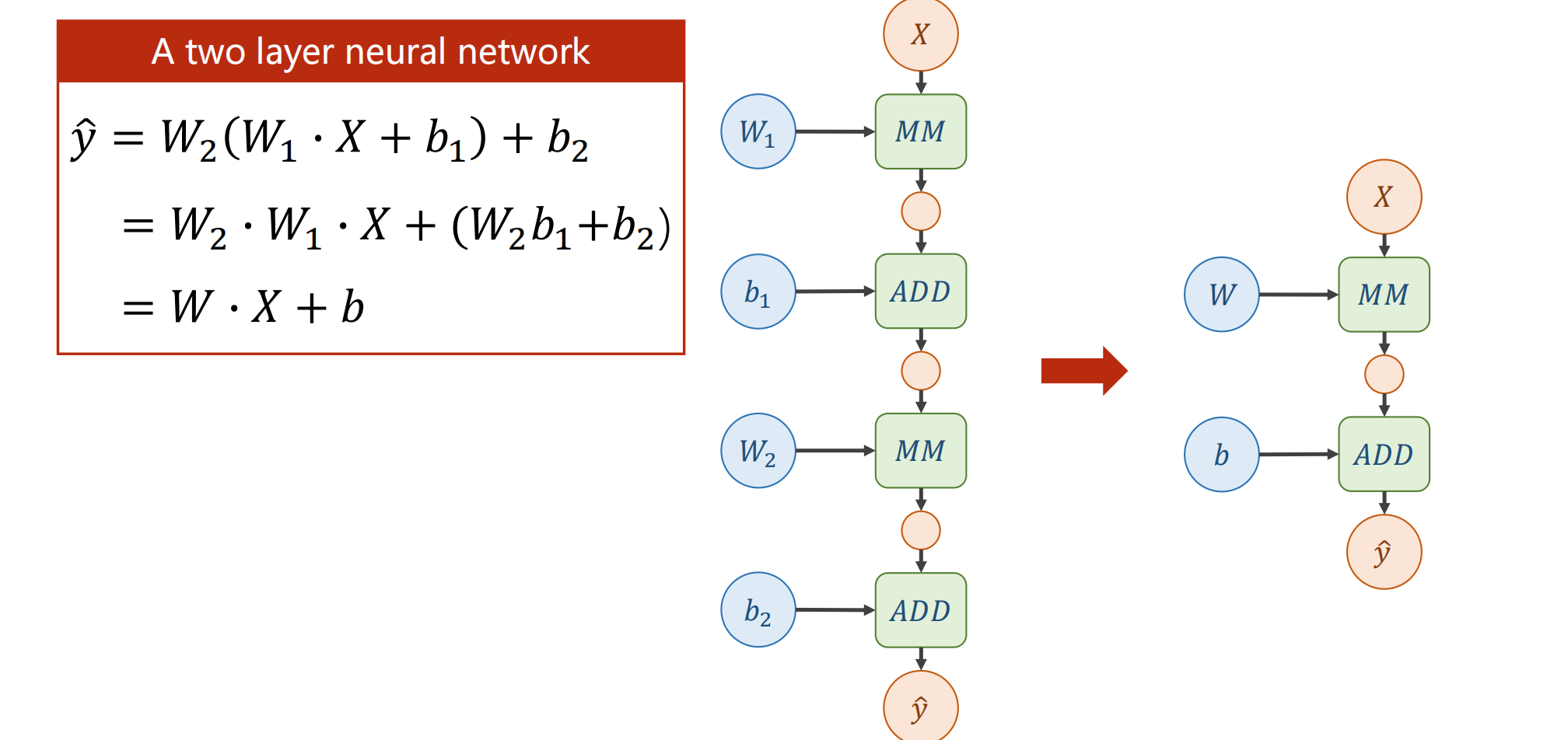
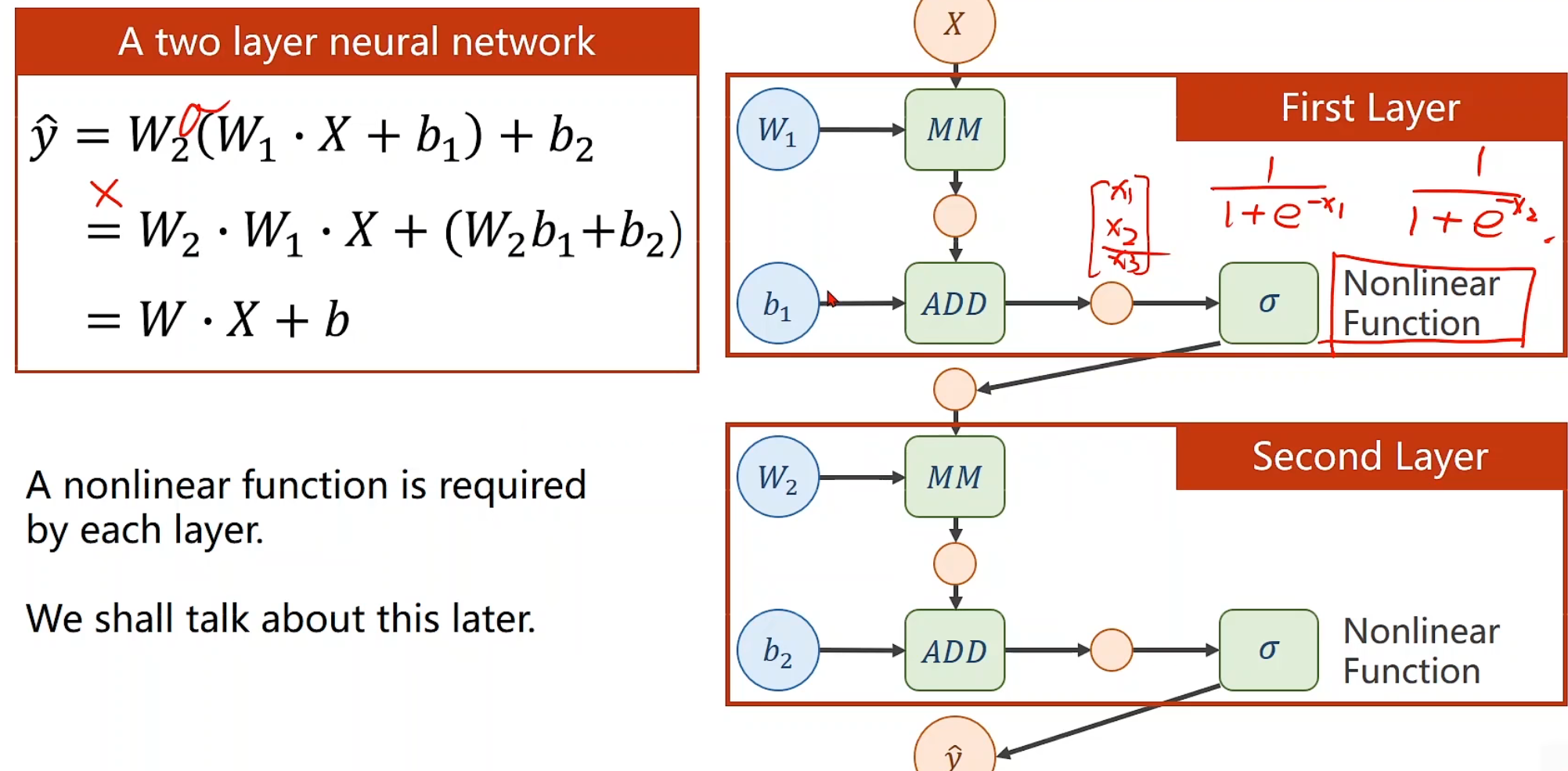
可是这样也会有麻烦，不难看出增加了层数和减少层数，对最终表达式的形式是没有区别的，为了解决这一问题(提高模型的复杂程度)，我们对每一层的输出增加非线性的变化函数，比如sigmoid
简单来说，就是我们对输出的每一个值，都做一个变换，使得式子无法变换成同一个形式，将权值可以进行很好得累加。
链式求导法则
简单来说，链式求导就是循环往复，在复合函数里面进行不断求导，最终得到最外层因变量对最内层自变量的偏导。
在我们反向传播的运用中，首先需要通过每一个单元节点来观察。
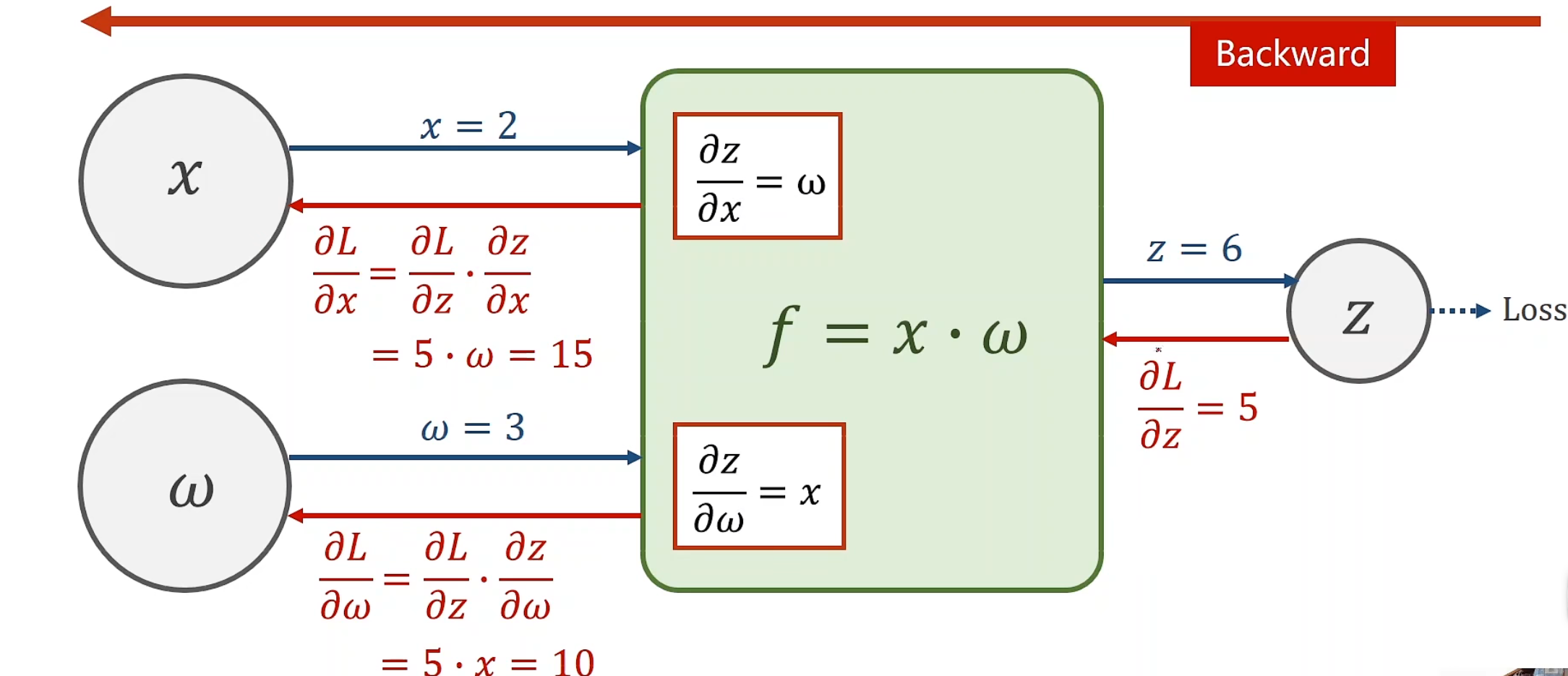
这里假设此时传入f的w为3，x为2，f=x*w，每一个f层都能计算局部的梯度，所以顺理成章传出的z即为6，这个过程我们称为前向传播forward, 后，到传到终止时，此时计算出L对最末隐藏层的导数，以此从后往前，因为每一个参数现在全都已经知晓，故可以轻松不断求导，使得分子分母相消，最终得到目标偏导
当然，就实际而言，pytorch总是把局部偏导存到变量里面，而非函数里面，这取决于我们的设定方式。
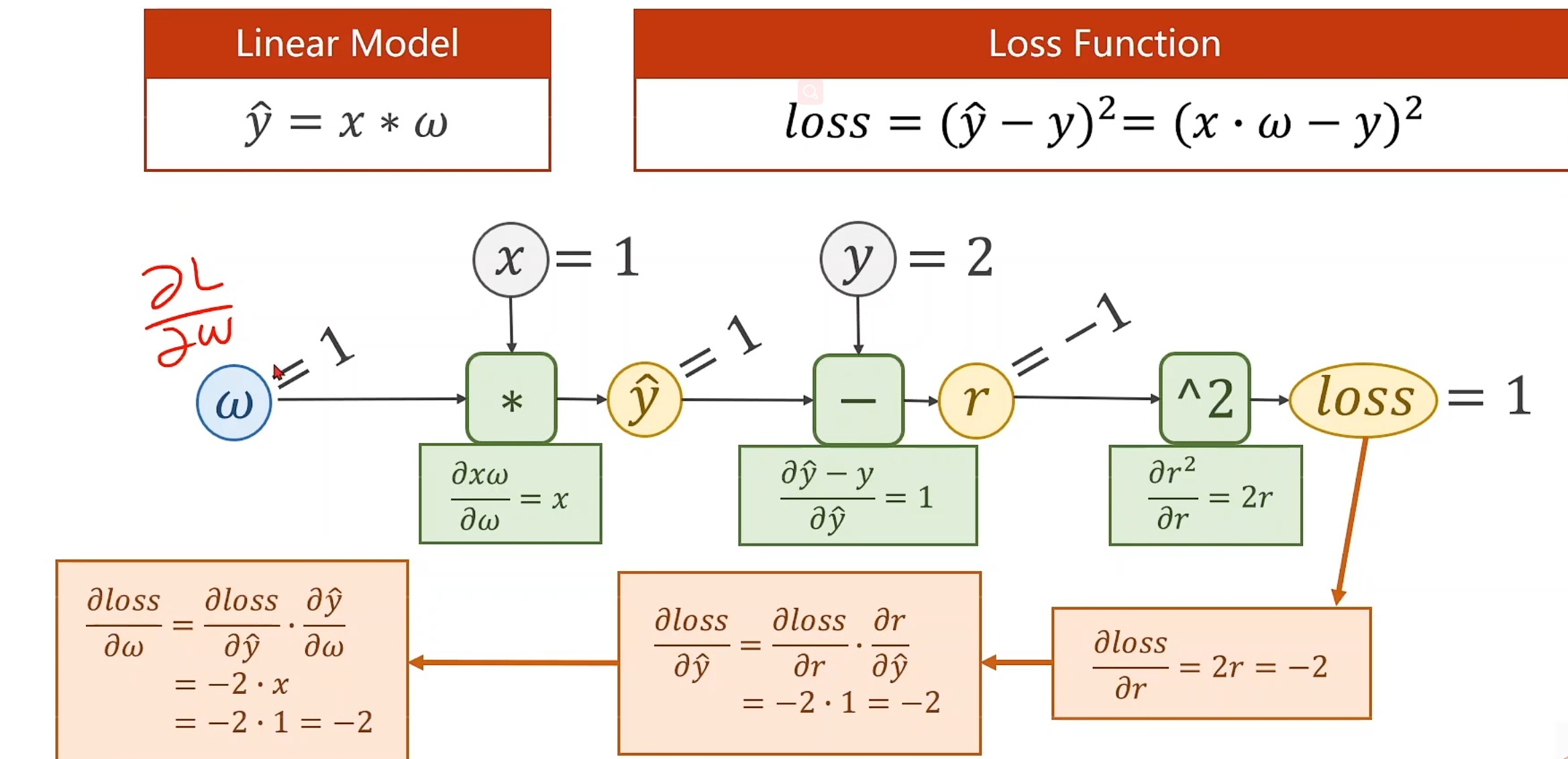
接下来我们来看一下完整的计算图
注意，loss就是r^2^，并且反向传播第一步是从^2的function开始的，而不是loss，loss是顺带打印出来的。
^2的偏导结果是2r，r为-1，因此传回-2，到 -的function，对y_hat求偏导，结果就是1 乘以^2传回来的-2，对*的function，只有对w的偏导，结果为x，因为x=1，所以答案就是1 * 1 * -2，为-2
我们拿到损失值(loss)以后，通常也要把它打印出来，看看我们最终的w是否是真正收敛后计算出来的w，简言之过程就是这样。
引入Tensor Tensor名为张量，是pytorch的重要成员，该类包含两个属性，分别是数据（data）和梯度（gradient）
一旦我们定义了一个Tensor，我们就可以去建立一个链式的求导计算图
现在，我们在利用反向传播机制来重新优化我们最开始的线性模型
将w设置为一个Tensor变量，注意一定要加方括号 ，因为Tensor默认是一个类似于多维数组 的概念
前向——>损失
本质是一个构建计算图的过程，不断迭代。
backward()及其他实用fuc pytorch帮助我们很方便实现梯度求解的过程，也就是直接能将链式求导的最终结果返回给最开始调用它的Tensor（这里即w）中的Grad里面
同时一个小贴士，backward()之后，计算图就会被释放了，之前正向的那些权重就不会留下了，所以下一次进行loss计算的时候它会创建一个新的计算图，很明显这样其实有的时候是不好的，但我们在进行计算的时候，可能计算图会是不一样的，我们每次释放之后重构，这是一个非常灵活的方式，这也是pytorch的核心竞争力
另外一个注意点，w.grad，grad也是一个Tensor，所以我们不能把grad直接做乘除运算，不然这样本质也是在建立一个计算图，因此我们要取w.grad.data,data虽然也是tensor，但此时不会建立计算图了。
第三个，item()是取得标量（默认int），将tensor变成数值，这也是为了防止产生计算图，或者直接给我们得到相应数据
易错提示（已经错过了=-=）
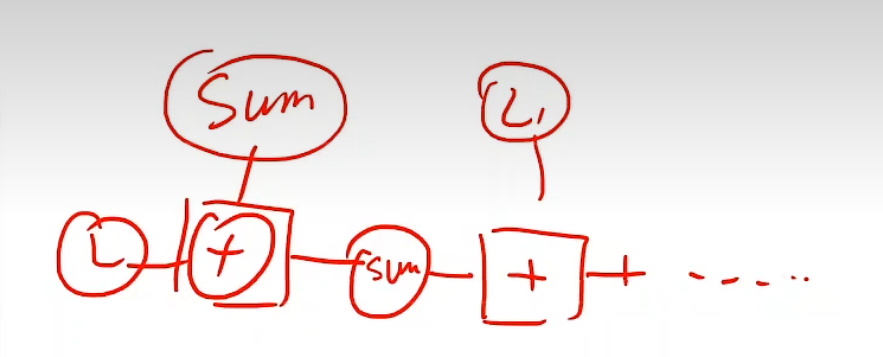
sum+=l，l是一个loss函数，但是操纵的是一个张量（w是张量，x*w就是，从而一系列都是=-=）
所以他就会通过+=，不断迭代生成图
在内存里，随着你迭代的次数，越增越大越增越大，就把内存吃饱了hhh
所以我们每次需要把值取出来哦
另外另外，每一次做完之后我们都需要对w.grad.data进行更新，这里我们使用w.grad.data.zero()，为何要更新呢？，我们仔细观察
对于标记①的循环而言，我们每一次都是用所有我们有的数据，从而对w进行推进，让他朝着loss更低的方向前进，此时我们首先使用loss求得单个损失，然后将其backward传给w.grad，backward可以保证计算完后将图清空不占用内存，接着用此时得到的这个w.grad.data*学习率来更新w.data，使得每组xy都可以起到修正w的作用，修正完毕后我们一定要设置w.gard.data为0，因为backward()是会累加grad的 ！！！，他不会自动帮我们清空，一定要注意,这个技巧可以为我们所用！
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 import torchx_data = [1 , 2 , 3 ] y_data = [2 , 4 , 6 ] w = torch.tensor([1. ]) w.requires_grad = True def Forward (x ): return x*w def Loss (x, y ): return (Forward(x)-y) ** 2 for epoch in range (100 ): for x, y in zip (x_data, y_data): l = Loss(x, y) l.backward() w.data -= 0.01 *w.grad.data.item() print ('grad: {} {} {}' .format (x, y, w.data.item())) w.grad.data.zero_() print ('process: ' , epoch, ' ' , l.item()) w
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 grad: 1 2 1.0199999809265137 grad: 2 4 1.0983999967575073 grad: 3 6 1.260688066482544 process: 0 7.315943717956543 grad: 1 2 1.2754743099212646 grad: 2 4 1.333436369895935 grad: 3 6 1.4534177780151367 process: 1 3.9987640380859375 grad: 1 2 1.464349389076233 grad: 2 4 1.5072014331817627 grad: 3 6 1.5959051847457886 process: 2 2.1856532096862793 grad: 1 2 1.6039870977401733 grad: 2 4 1.635668158531189 grad: 3 6 1.7012479305267334 process: 3 1.1946394443511963 grad: 1 2 1.7072229385375977 grad: 2 4 1.7306450605392456 grad: 3 6 1.779128909111023 process: 4 0.6529689431190491 grad: 1 2 1.7835463285446167 grad: 2 4 1.8008626699447632 grad: 3 6 1.836707353591919 process: 5 0.35690122842788696 grad: 1 2 1.8399732112884521 ... grad: 1 2 1.9999996423721313 grad: 2 4 1.9999996423721313 grad: 3 6 1.9999996423721313 process: 99 9.094947017729282e-13 tensor([2.0000 ], requires_grad=True )
线性回归 在之前的学习中，我们其实都是利用python或者仅用Tensor来构建模型，没有用太多pytorch的实质功能，接下来我们仍然通过前面介绍的简单的数据集x=[1, 2, 3], y=[2, 4, 6]，基于pytorch框架，构建出可拓展的、有良好弹性的pytorch框架
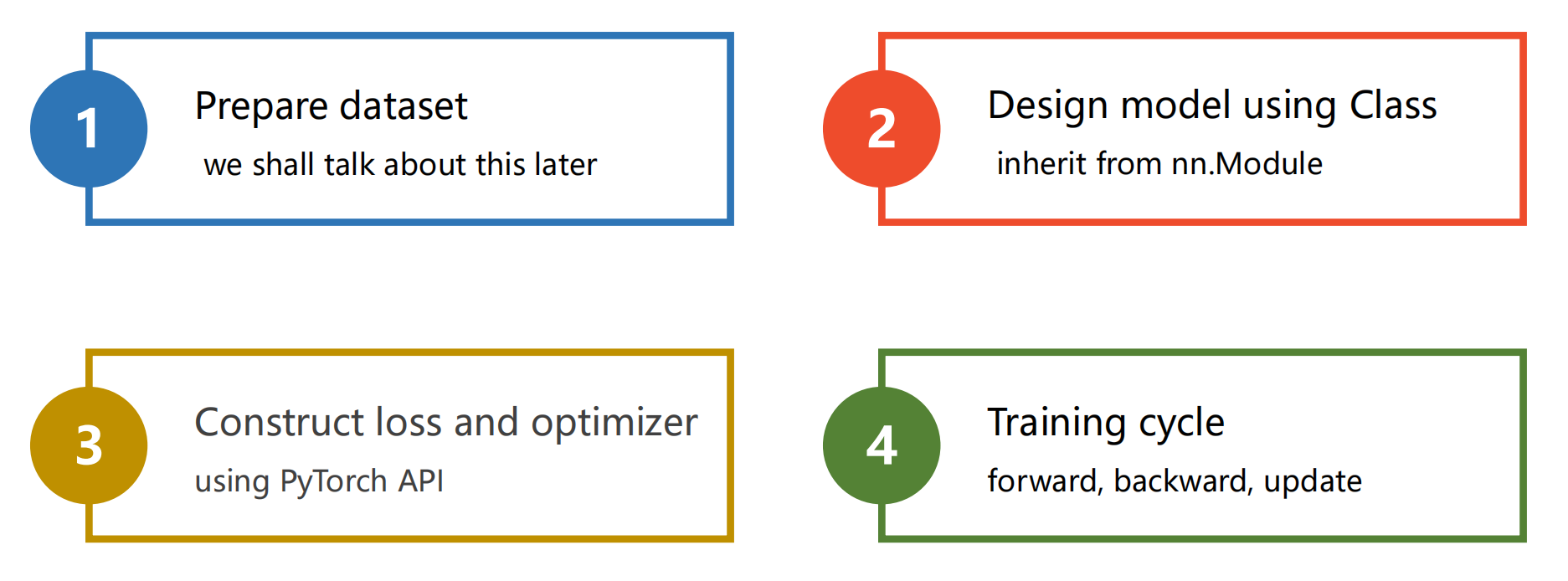
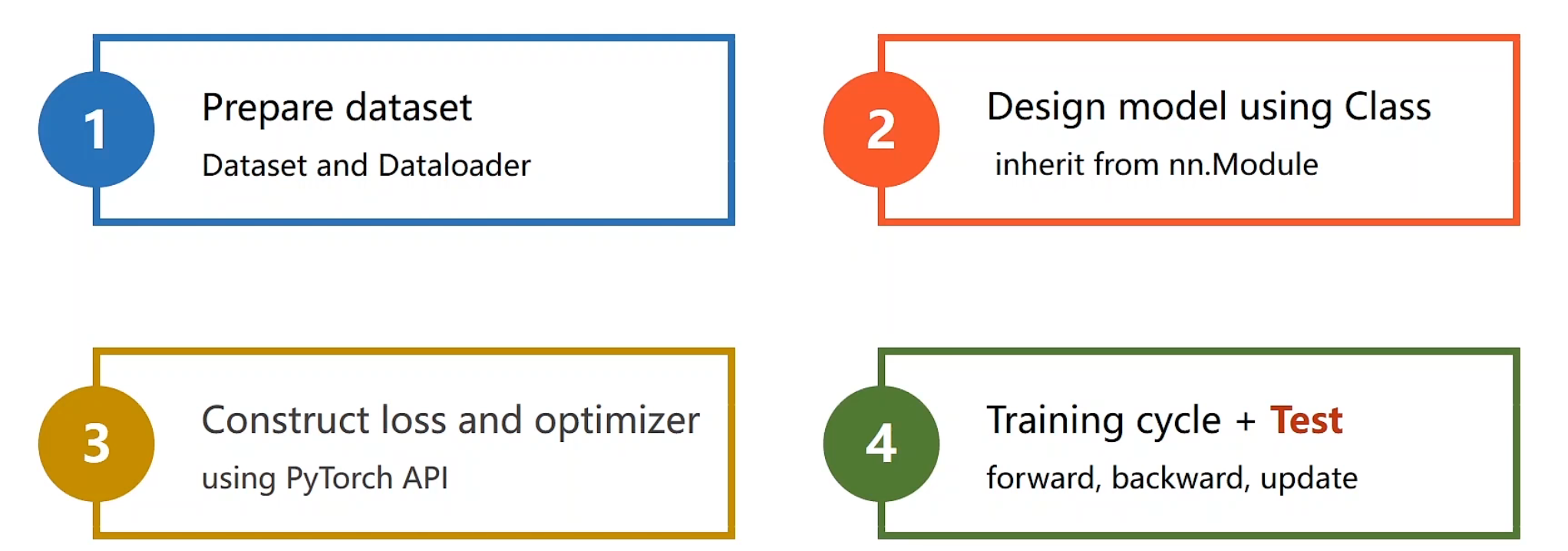
pytorch模型框架 主要分为以下四步:
构造数据集，作为构建模型而言，需要统一的输入输出，方便模型有规律的运转
nn.Module重写模型，构建出属于自己的模型（主要用于求得y_hat）
使用pytorch自带的损失函数和迭代器
设定训练周期：前馈、反馈、更新、前馈、反馈、更新….
前馈算损失，反馈算梯度，更新,利用梯度下降算法给各点更新权重
构建数据集 由于我们的数据很少，因此可以采用小批量建集法
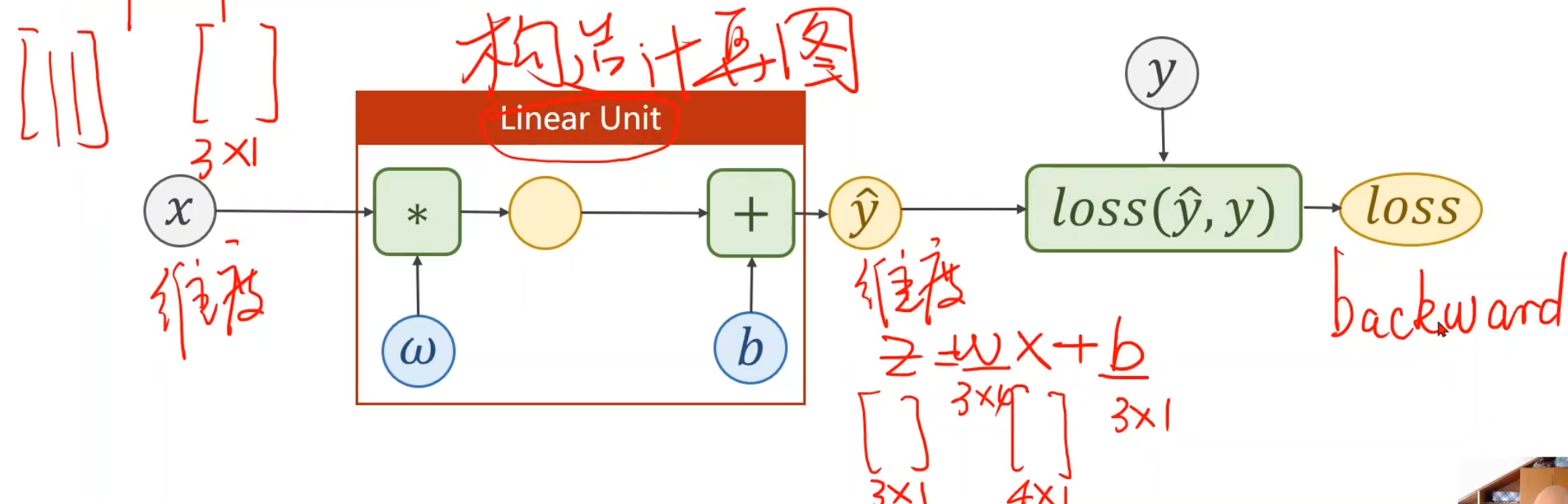
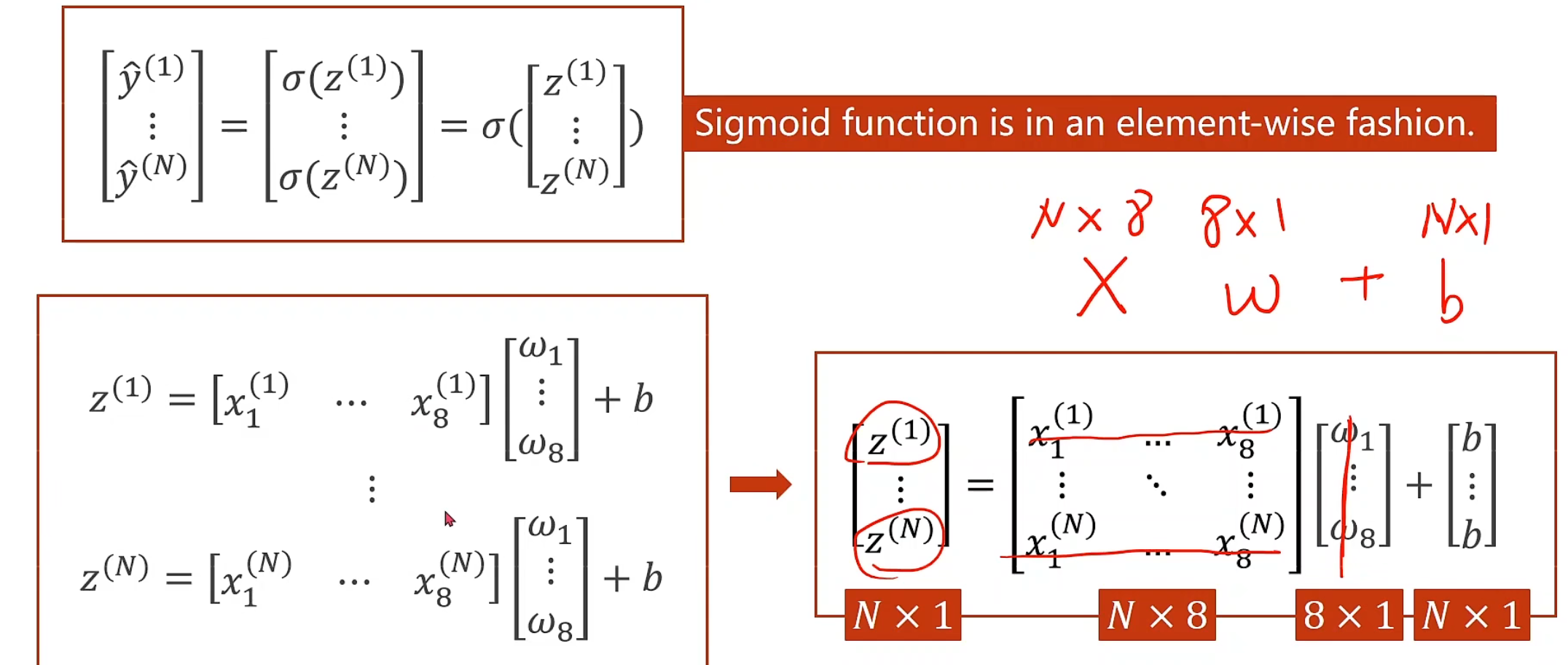
上半部分是利用numpy构建数据集，由于numpy具有广播机制，例：如果一个3 * 3的矩阵和3 * 1的矩阵不能直接做加法，那么他会把1 * 3按照规律扩容成3 * 3 如图上绿色部分所示
下半部分是利用pytorch，我们只需要让他们一一对应，即y_hat和x都是3*1的矩阵，然后权重w，b会自动进行广播，变成3 * 1的矩阵进行数乘
接下来我们将别的变量都构成这种形式，loss和y都应该构建成3 * 1的矩阵
在我们这个例子里，构建数据准备如以下形式
曾经我们需要人工求导数，现在我们就不再考虑人工求了，backward()YYDS，现在我们重点的目标变成构造计算图，也就是我们的第二部，构建模型，一旦构建好将来就可以自动的求出了
构建只有两个要求，我们需要知道输入的维度(x)和输出的维度(y_hat)，不过要注意，backward()只能使用标量，所以最后我们的loss矩阵求出需要对他进行求和、求均值之类的处理
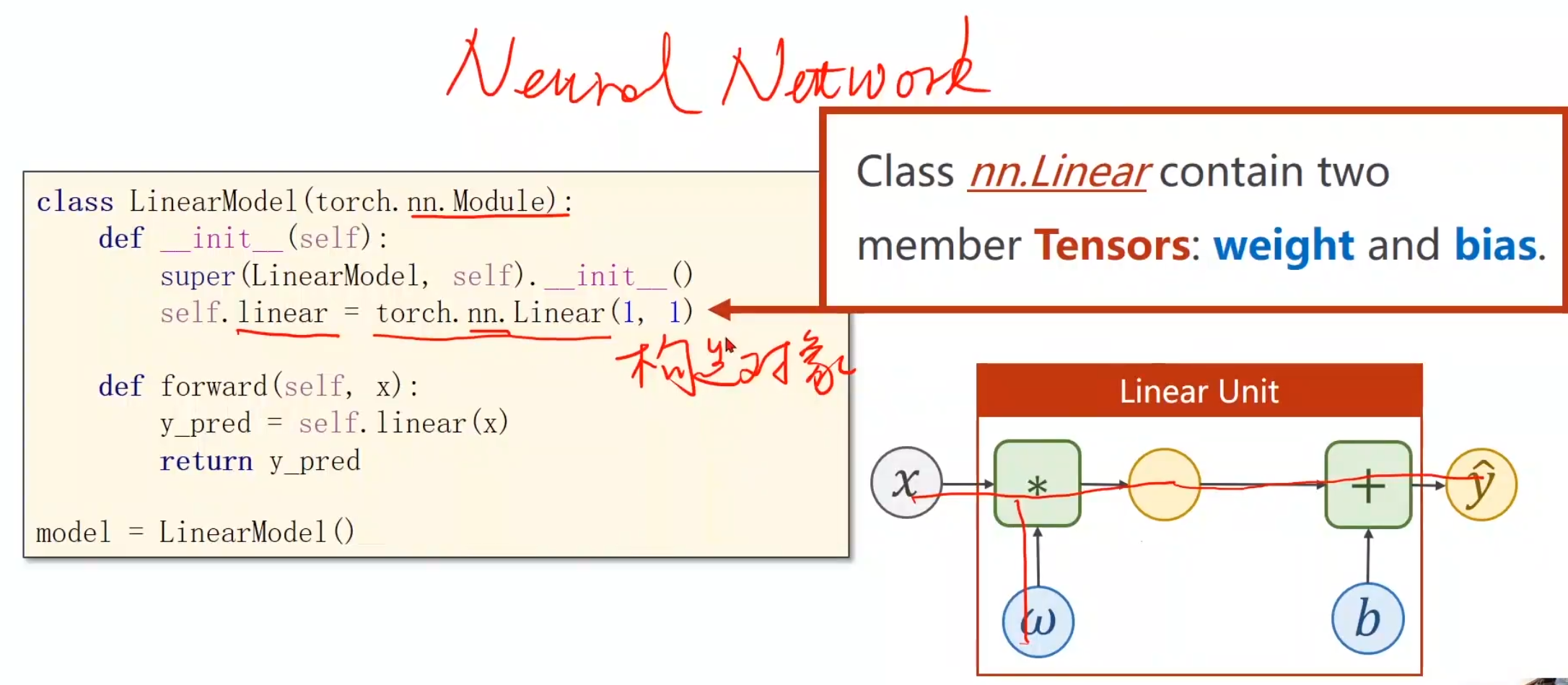
定义模型 首先定义一个类–需要继承Module
实现_init_ ()和forward(),构造函数init是初始化对象所要调用的函数，forward是进行前向时所执行的计算
不难发现并没有backward()，这是因为用Module构造出来的对象会自动根据计算图帮助我们实现backward()的构成
万一pytorch的backward()无法实现你的高端计算，你可以自定义一个pytorch.function类实现反向传播，构建自己的计算块
linear()参数解释 这是linear()的参数详细解释
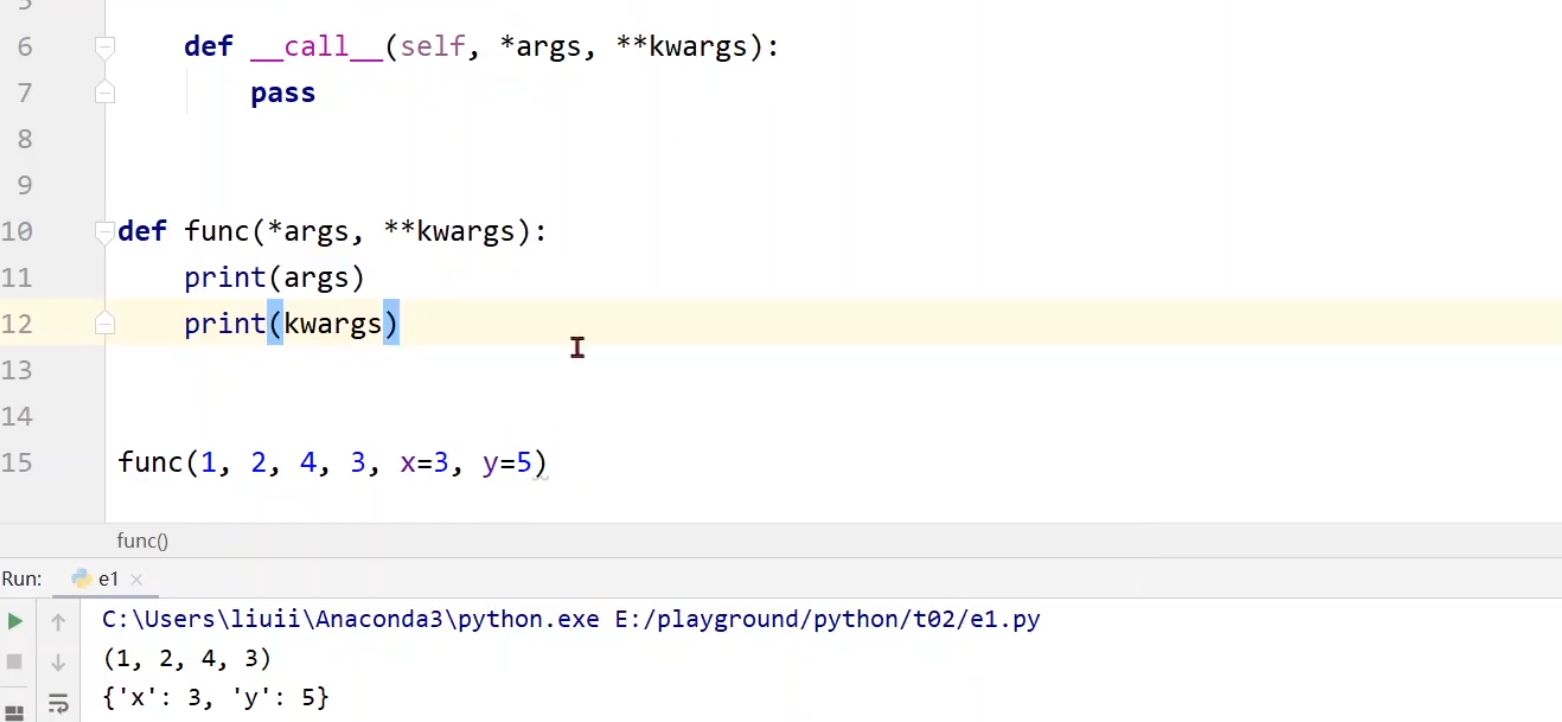
call()方法与自定传参
可以看见我们写成*args的形式，则会将传入参数存为元组，写成**kwargs可会将传入的参数存在词典
call()中会去调用forward()，所以我们在我们的方法中必须去实现forward()，重写覆盖掉父类函数
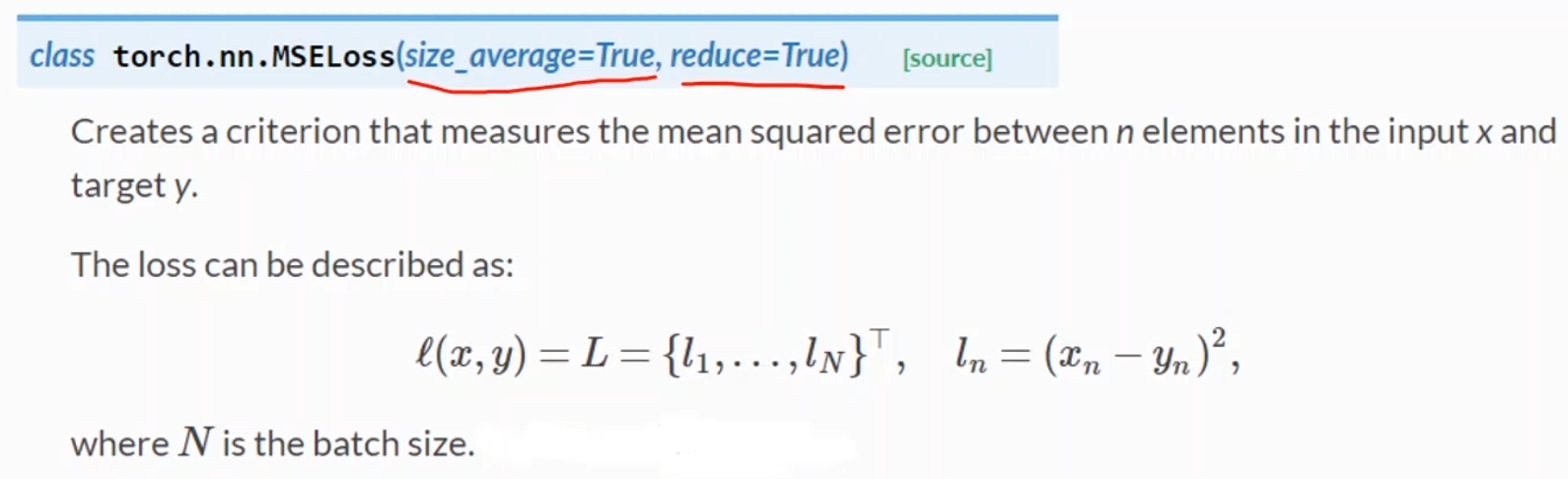
构建迭代器和损失函数 损失函数
一般来说只考虑size_average是否需要设置，一般来说都可以，影响不大，就是需不需要求均值。False就是叠加loss
需要的参数就是y_hat和y
优化器
model.parameters()类似于你无论使用多么复杂的模型，它都能把你的各种模型的参数找到，lr就是学习率，目前是固定的，在pytorch里面甚至可以对模型的不同板块做不同的学习率处理
训练过程
在model的forward中算y_hat
利用criterion算loss
利用optimizer使得训练的权重都清零（特指上一次训练的权重，注意1、2步都并未对optimizer进行操作，而下一步的backward()则叠加梯度）
进行反向传播backward()
利用step()进行更新，会根据所有参数包含的梯度以及学习率进行更新
这个训练就等价于之前
1 2 3 4 5 for x, y in zip (x_data, y_data): grad = gradient(x, y) w = w - 0.01 * grad print ("\tgrad: " , x, y, grad) l = loss(x, y)
的过程
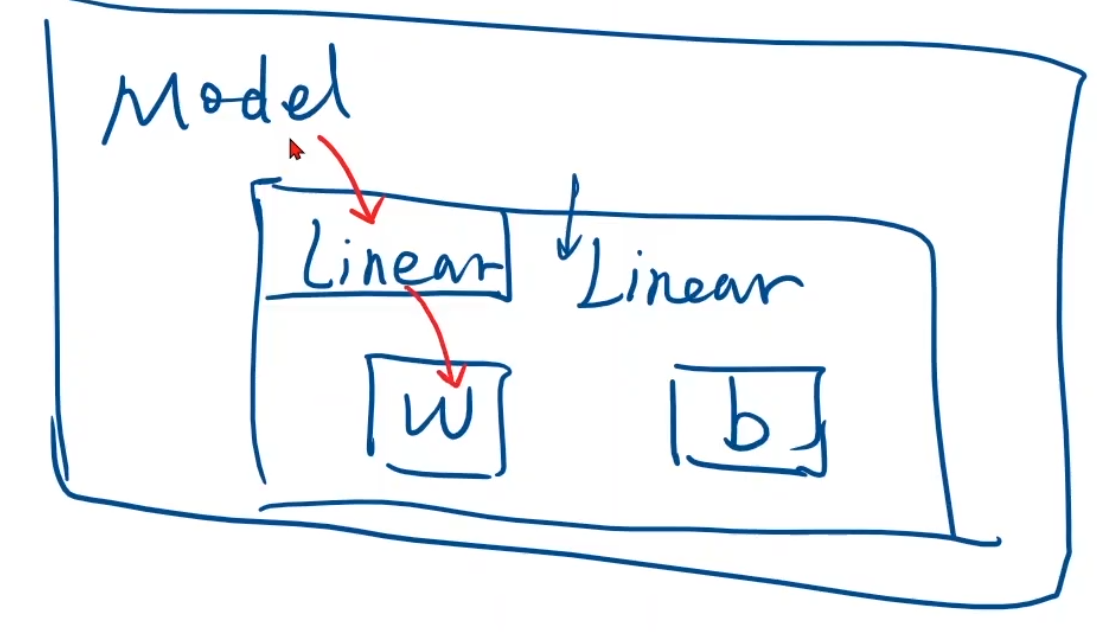
打印结果 最后打印训练后的参数
拿出来的值
model内的linear，linear内的weight
x_test使用二维矩阵，意思是1*1的矩阵，
代码实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 import torchx_data = torch.Tensor([[1. ], [2. ], [3. ]]) y_data = torch.Tensor([[2. ], [4. ], [6. ]]) class linearModel (torch.nn.Module ): def __init__ (self ): super (linearModel, self).__init__() self.linear = torch.nn.Linear(1 , 1 ) def forward (self, x ): y_pred = self.linear(x) return y_pred model = linearModel() criterion = torch.nn.MSELoss(size_average=False ) optimizer = torch.optim.Adam(model.parameters(), lr=0.04 ) for epoch in range (1000 ): y_pred = model.forward(x_data) loss = criterion(y_data, y_pred) print (epoch, loss.item()) optimizer.zero_grad() loss.backward() optimizer.step() print ('w= ' , model.linear.weight.item())print ('b= ' , model.linear.bias.item())x_test = torch.Tensor([[4 ]]) y_test = model(x_test) print ('y_test= ' , y_test)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 0 10.964780807495117 1 9.638935089111328 2 8.408780097961426 3 7.27571439743042 4 6.240664005279541 5 5.304004669189453 6 4.465476989746094 7 3.7241055965423584 8 3.0781075954437256 9 2.524812698364258 10 2.0606095790863037 11 1.6808964014053345 12 1.3800746202468872 13 1.1515748500823975 14 0.987949788570404 15 0.8810074925422668 16 0.8220123052597046 17 0.8019364476203918 18 0.8117435574531555 19 0.8427058458328247 20 0.886695384979248 21 0.9364582300186157 22 0.9858223795890808 23 1.0298420190811157 24 1.064853549003601 ... 999 4.547473508864641e-13 w= 1.9999995231628418 b= 9.625380243960535e-07 y_test= tensor([[8.0000 ]], grad_fn=<AddmmBackward0>)
Logistic回归
一个有意思的模型，虽然叫做回归，却用来做分类任务
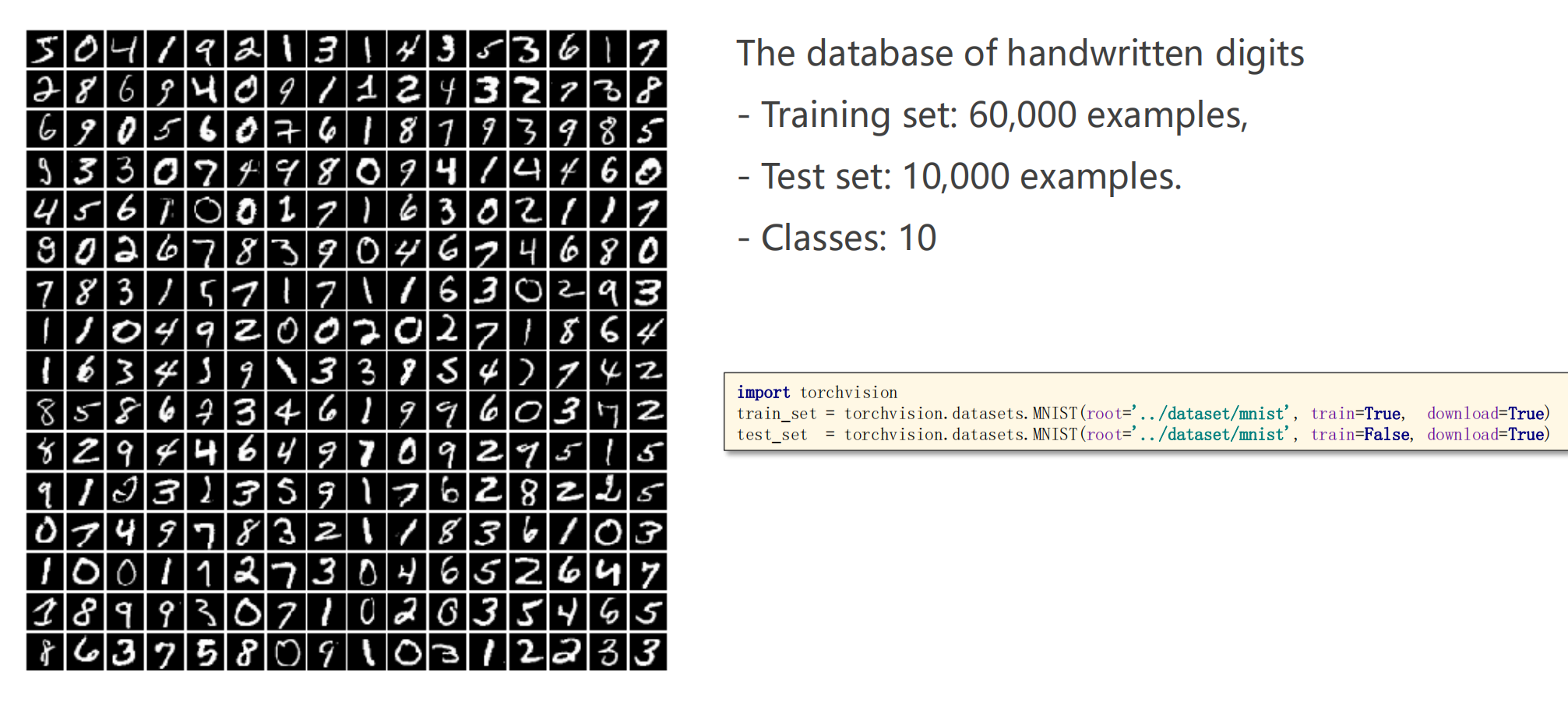
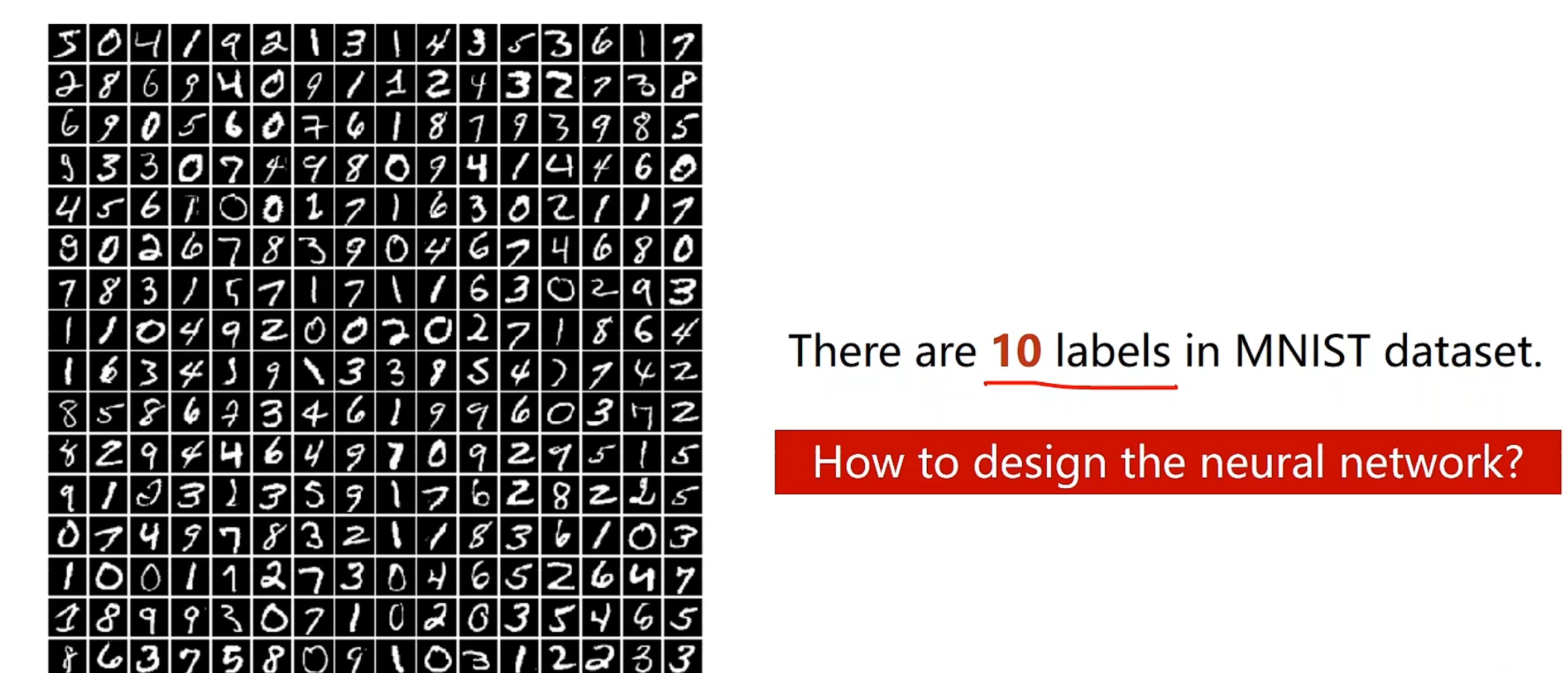
数据集介绍 深度学习的hello world！ MNIST数据集,总共有十个类，0-9数字
我们考虑做这个分类任务，并不能考虑一维实数空间数值大小的含义啥的，就好像7和9长得反而像一点，但中间却隔了一个8，相反，我们应该对当前输入的图片，他长得像啥，对十个类别分别学习出十个概率，然后选择这十个概率中最大概率的一类作为他应该归入的一类。
CIFAR数据集为32*32的小图片，10个分类，十种动物
使用的参数和MNIST近似，模仿着做法即可下载
logistic函数 回归任务y的2,4,6就表示它将来能拿到的分数，而分类任务就是True和False，仅仅看得是他能否通过考试，看起来二分类任务是计算两个值，实际上是计算一个值，因为二者和为1，但如果两种可能都是近似0.5，那么就是说学习器没有十足的把握判断，我们可以加一句判断条件，就是说在0.4~0.6区间内，给出具体概率，提示用户，我们不确定，因为报错总比出错好。
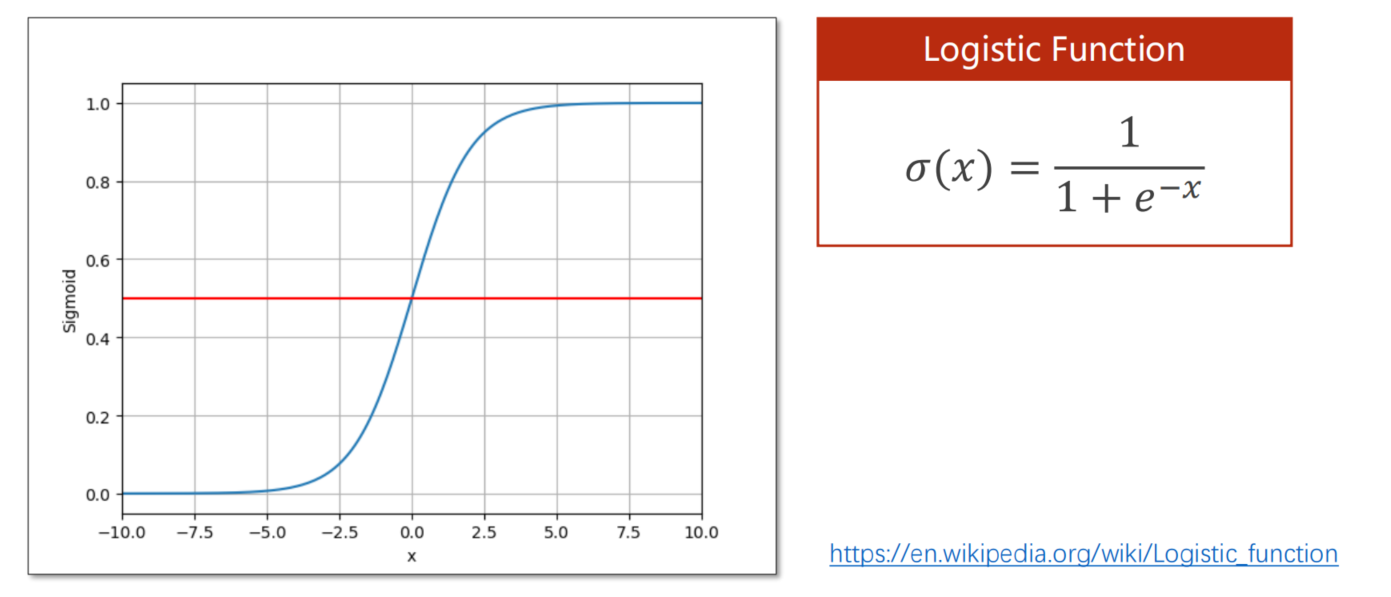
对于线性模型来说，输出属于实数范围内，但我们现在要得分类的输出是一个概率，所以我们这个输出应该属于0~1这个区间内，所以我们需要把输出值从实数空间映射到[0, 1]
我们不难看出，他越往0靠或者越往1靠的时候，他的变化是不大的，但是0.5左右波动很大，这样的称为饱和函数，这非常满足我们做分类任务的需求。logistic的导数长成这样
非常的符合正态分布，这也解释了为什么logistic是由于正态分布的存在而产生的的一种函数。
注意这里并不是说有logistic函数就能进行概率转换，而是说我们想要计算概率，必须保证 我们的输出值在0~1之间
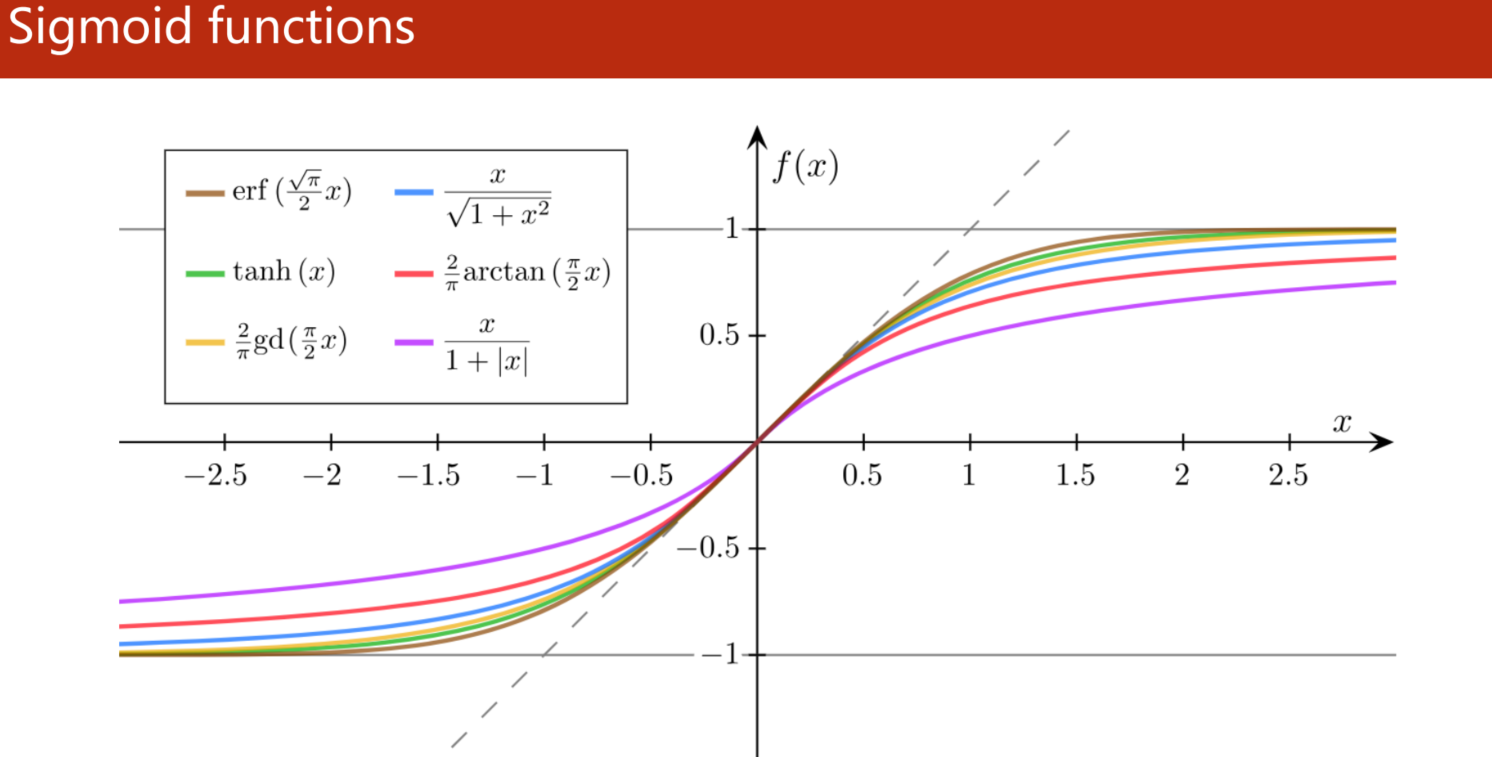
饱和函数 所有的饱和函数都满足：
函数值有极限
都是单调的增 函数
都是饱和函数
只要满足这三个条件都叫做sigmoid函数，其中，logistic最出名，所以有的框架中我们直接把它称作sigmoid函数
当然，logistic的函数收敛是在0~ 1，有的时候我们可能更希望它在-1~1或者其他区间,这个时候就要用tanh或者其他啥函数
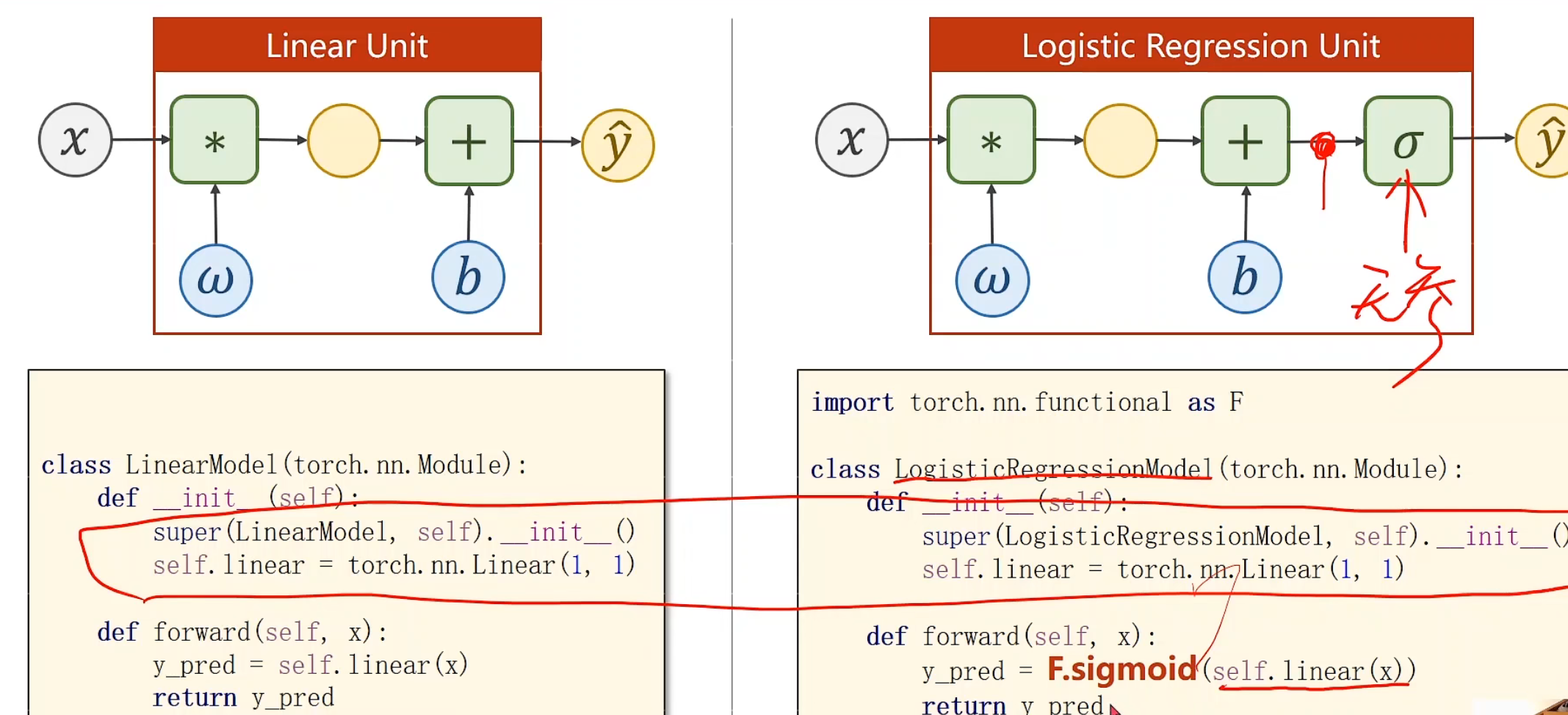
与线性模型对比 方程式
凡是有这个歪着的6，我们就把他看做是logistic回归的符号
损失函数
我们以前的loss是用来计算欧式距离的，而现在我们的输出不再是一个数值的，我们输出是一个分布，分布不是数轴上的距离，这里我们引入交叉熵（Cross-entropy）的概念
假设我们现在有两个分布，一个PD一个PT
我们可以用这个式子表示两个分布之间的差异，并希望这个求和的结果越大越好（ln0.x的结果是为负的），但为了和MSE，MAE等等统一标准，所以我们在最前面加一个负号，使得结果越小是越好的
现在，我们来进一步分析一下交叉熵是如何做到，辨别分类准确情况的。首先需要明确一点，y的取值只有0和1，因为这是二分类问题，其次，当y为1时，原式变为了-ylog^y_hat^，想要这个式子最小，那么y_hat就得越大越好，所以说越趋近于1，预测值就越准确，同时，1就是该的分类物品所占有的对应数字，0也是同样的道理，这样就使得预测的东西越与标准答案接近，loss越低，从而达到我们想要的目的。这个函数，被我们称为BCE
这就是一个具体实例，对于有多个样本的BCE，直接求均值就好
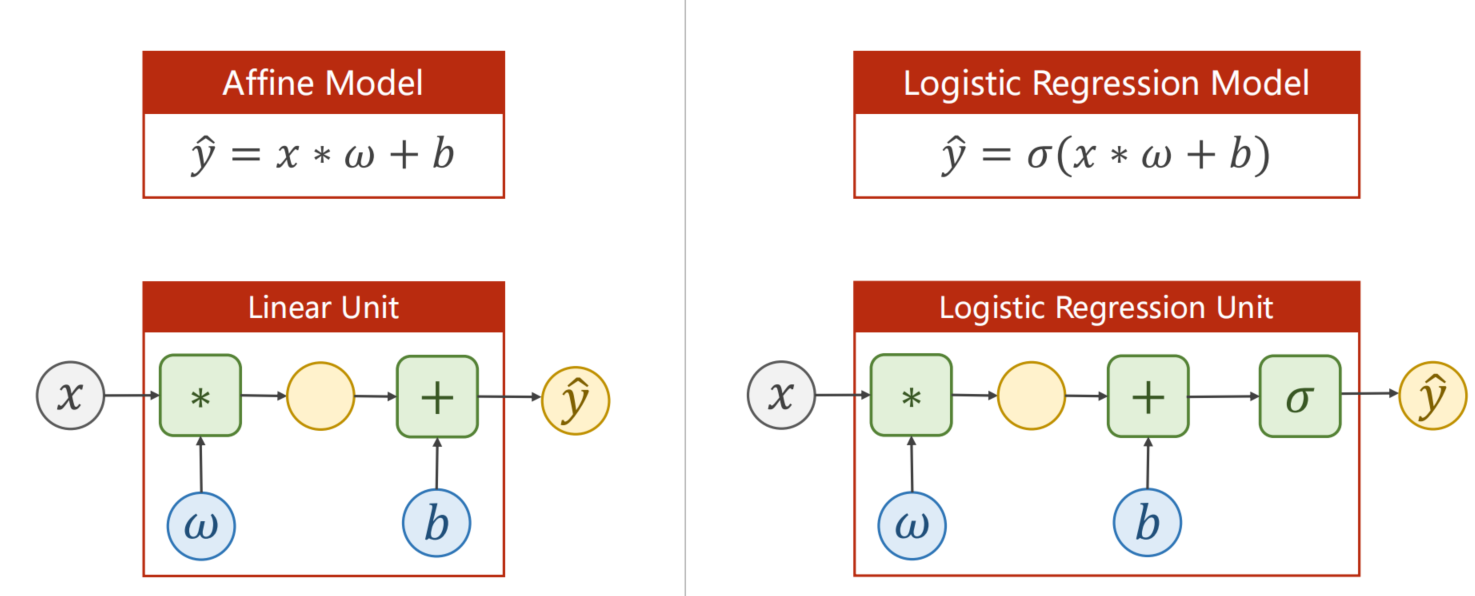
代码对比
其实就多了一个sigmoid嵌套就行，σ本身不需要参数，不需要在构造函数里初始化。
是否求均值，影响学习率的设置。因为你的函数损失变小了，你将来求出来的导数也会乘以这个常数
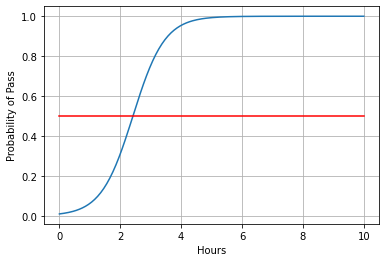
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 import torchimport torch.nn.functional as Fimport numpy as npimport matplotlib.pyplot as pltx_data = torch.Tensor([[1. ], [2. ], [3. ]]) y_data = torch.Tensor([[0 ], [0 ], [1 ]]) class LogisticRegressionModel (torch.nn.Module ): def __init__ (self ): super (LogisticRegressionModel, self).__init__() self.linear = torch.nn.Linear(1 , 1 ) def forward (self, x ): return F.sigmoid(self.linear(x)) model = LogisticRegressionModel() criterion = torch.nn.BCELoss(size_average=False ) optimizer = torch.optim.Adam(model.parameters(), lr=0.01 ) for epoch in range (1000 ): y_pred = model.forward(x_data) loss = criterion(y_pred, y_data) print ('epoch' , epoch, 'loss=' , loss.item()) optimizer.zero_grad() loss.backward() optimizer.step() x = np.linspace(0 , 10 , 200 ) x_t = torch.Tensor(x).view((200 , 1 )) y_t = model(x_t) y = y_t.data.numpy() plt.plot(x, y) plt.plot([0 , 10 ], [0.5 , 0.5 ], c='r' ) plt.xlabel('Hours' ) plt.ylabel('Probability of Pass' ) plt.grid() plt.show()
1 2 3 4 5 6 7 8 9 10 11 12 epoch 0 loss= 3.4830539226531982 epoch 1 loss= 3.4443485736846924 epoch 2 loss= 3.405913829803467 epoch 3 loss= 3.367762804031372 epoch 4 loss= 3.329906702041626 epoch 5 loss= 3.292354106903076 epoch 6 loss= 3.255119800567627 ... epoch 996 loss= 0.7208291292190552 epoch 997 loss= 0.7202318906784058 epoch 998 loss= 0.7196354866027832 epoch 999 loss= 0.7190396189689636
不难看出，达到0.5可能的点位是2.5，我们可以深度思考一下他的原因，其实最主要是因为，我们x=1,2，的概率都是设置的y=0；x=3的概率设置的是y=1，所以自然在x=2.5的位置就达到了50%左右的可能性
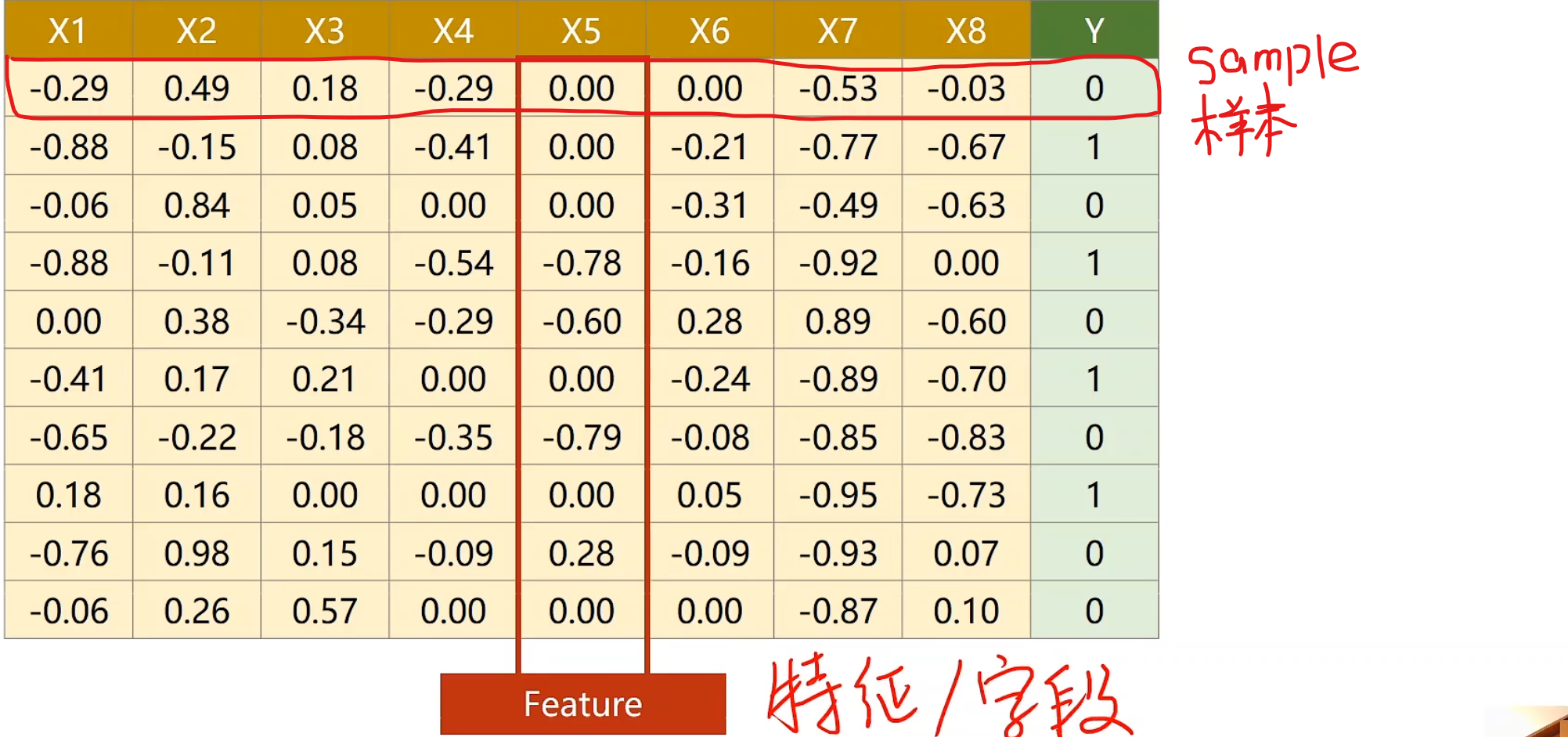
多维输入 数据集解释
x1，x2，x3…..y我们可以把它看做不同的特征，每一组特征（feature）称为一个样本（sample）
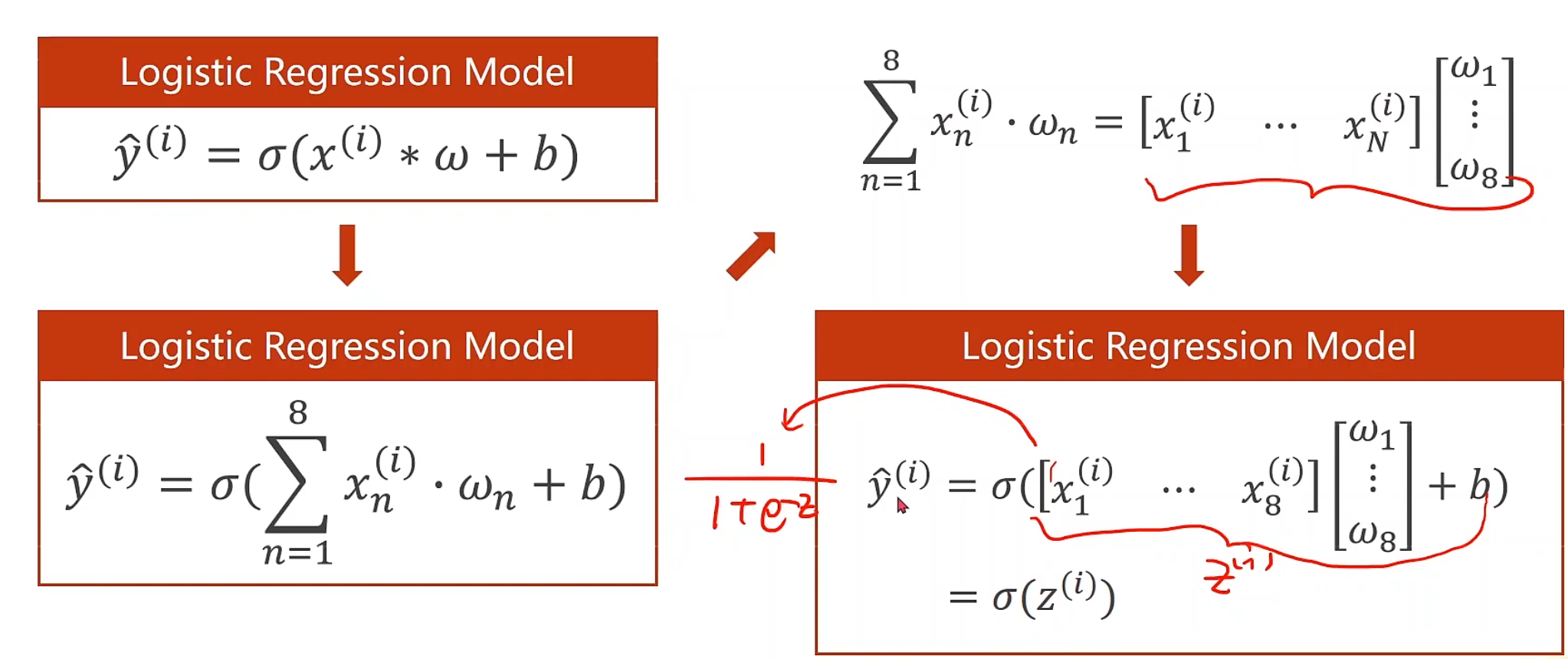
清晰的推导
我们可以把logistic回归的方程转换为可以升维的形式，这里使用输入八维来举例
注意观察图中式子的变换，很有启发意义，线代的知识又捡回来了！！！
为什么我们一定要转化为矩阵运算呢？矩阵转换为向量化的计算后，我们可以利用并行计算的能力（GPU、CPU）来提高整个运算的速度，如果用for循环来写一定是相当慢的
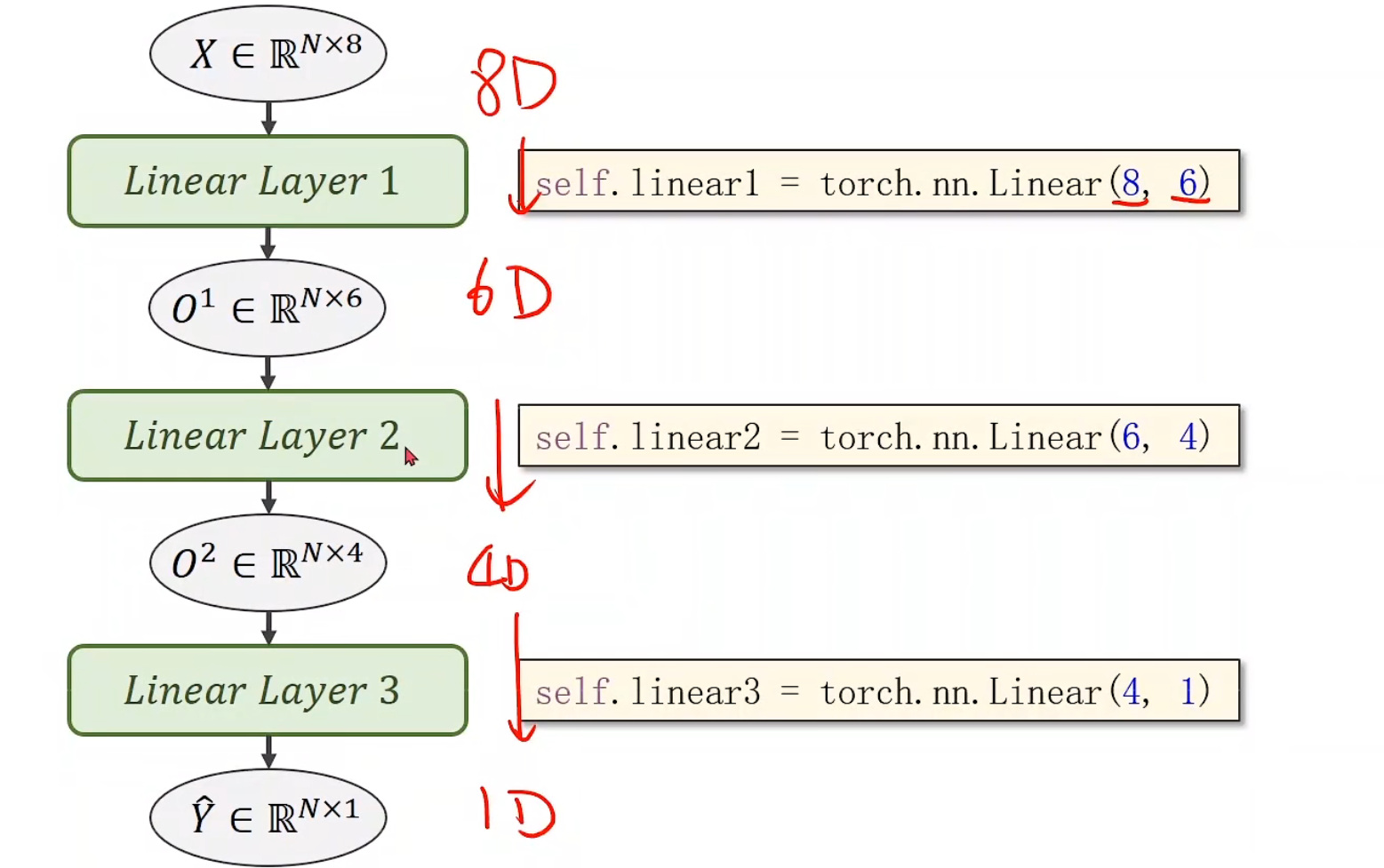
对代码的修改而言，我们需要做的仅仅只有把代码里面线性的(1, 1)改成(8, 1)就可以了
另外就是，x输入，我们只需要改成8 * 1的Tensor， y继续1 * 1即可
降维处理
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 import numpy as npimport torchxy = np.loadtxt('diabetes.csv.gz' , delimiter=',' , dtype=np.float32) x_data = torch.from_numpy(xy[:,:-1 ]) y_data = torch.from_numpy(xy[:, [-1 ]]) class model (torch.nn.Module ): def __init__ (self ): super (model, self).__init__() self.linear1 = torch.nn.Linear(8 , 6 ) self.linear2 = torch.nn.Linear(6 , 4 ) self.linear3 = torch.nn.Linear(4 , 1 ) self.sigmoid = torch.nn.Sigmoid() def forward (self, x ): x = self.sigmoid(self.linear1(x)) x = self.sigmoid(self.linear2(x)) x = self.sigmoid(self.linear3(x)) return x model = model() criterion = torch.nn.BCELoss(size_average=False ) optimizer = torch.optim.Adam(model.parameters(), lr = 0.1 ) for epoch in range (10000 ): y_pred = model(x_data) loss = criterion(y_pred, y_data) print (epoch, loss.item()) optimizer.zero_grad() loss.backward() optimizer.step()
1 2 3 4 5 6 7 8 9 10 0 499.0527038574219 1 489.77032470703125 2 493.4767761230469 3 493.3719787597656 4 490.6575927734375 ... 9996 258.5865478515625 9997 258.5833435058594 9998 258.5801696777344 9999 258.5771789550781
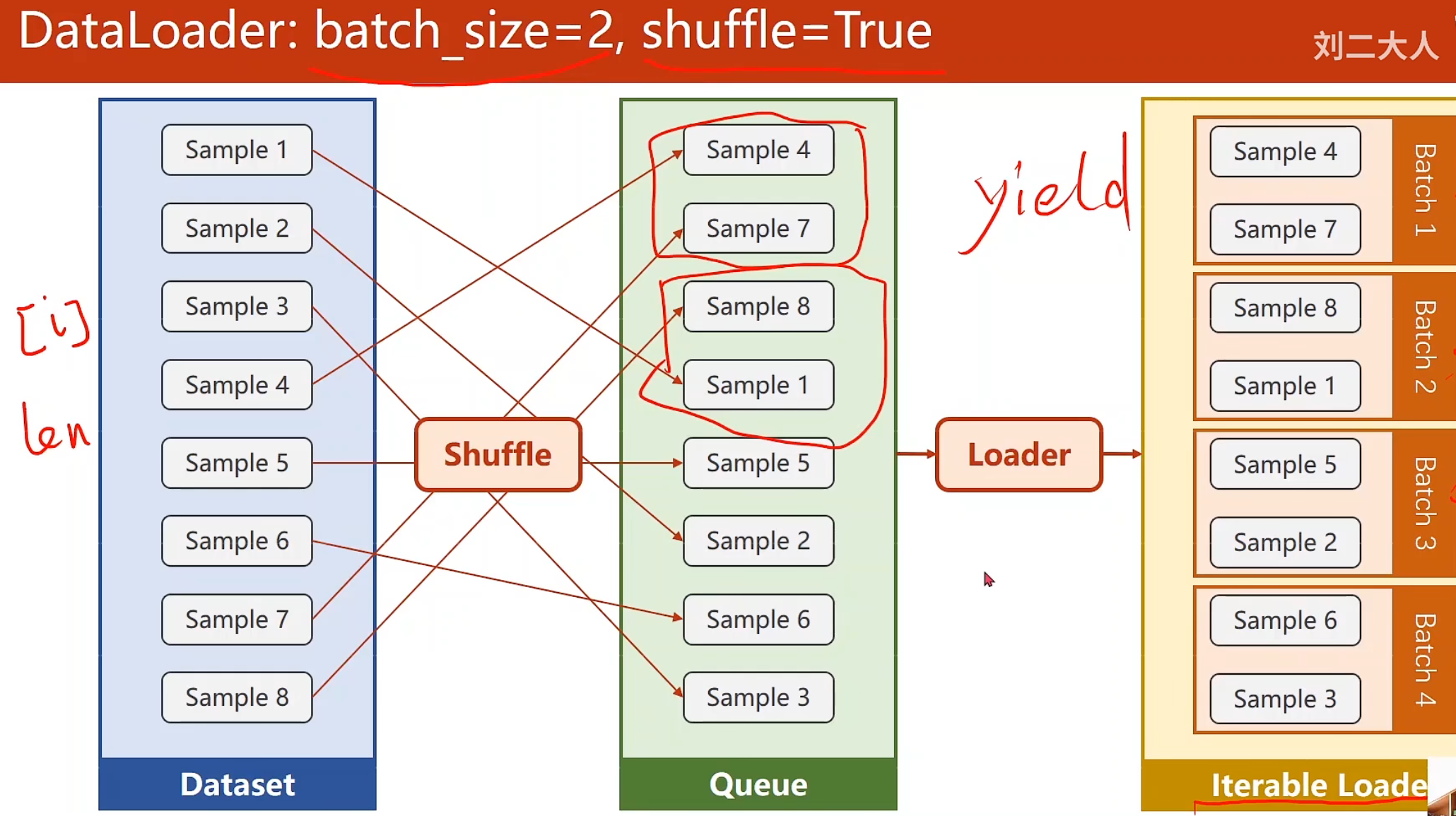
加载数据集 概念说明 我们使用数据集，即把已有的整个batch构成mini-batch，分别有Epoch, Batch-Size, Iterations.
Epoch：当所有的样本，都进行了正向传播和反向传播一次 ，那么这个过程就叫做Epoch
Batch-Size：每次训练时所用的样本数量，也就是每进行一次 前馈和反馈所用的
Iteration： 在一个Epoch内，样本迭代的次数，也就是Batch-Size的总数
Batch = Mini-Batch- * Iteration
shuffle为True，意味着打乱顺序，Loader按照每个mini-batch的尺寸为2，装载数据集
代码实现 首先有以下几个注意点
Dataset是一个抽象类，他在实现的时候需要继承（例如DiabetesDataset(Dataset）)这感觉就和构建模型继承torch.nn.Module一样，我们这样做了以后，从而构造自定义的数据集
Dataloader是用来加载数据的，我们实例化一个对象来帮我们做就是，他的参数中，dataset为数据集，batch_size为minibatch尺寸，shuffle就是洗牌，num_workers表示到底要几个并行的进程去读取你的数据
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 import torchfrom torch.utils.data import Datasetfrom torch.utils.data import DataLoaderclass DiabetesDataset (Dataset ): def __init__ (self ): pass def __getitem__ (self, index ): pass def __len__ (self ): pass dataset = DiabetesDataset() train_loader = DataLoader(dataset=dataset, batch_size=32 , shuffle=True , num_workers=2 )
这里还要提醒一些构造数据集的注意点
我们可以把所有数据都先加载到内存里面，然后每次使用getitem()的时候，把对应的数据[i]传出去就好了，这种适用于数据集本身的容量不大。
如果处理，图像，语言等非结构的数据，我们要考虑能不能把它加载到内存当中，通常这会涉及到列表和标签，如果标签比较少，类似于也是一个回归问题，我们也可以把它都读进来，如果标签也是一个特别复杂的张量，那么我们就把标签也放到一个列表里面，然后在getitem()里面读取列表的第i个文件，分别把标签和数据本身的第i个文件返回，保证内存的高效使用。
就是说用文件的文件名作为文件内容的索引，读到内存中，等到用的时候，在用文件名去读文件内容。
1 2 3 4 5 6 7 8 9 10 11 12 class DiabetesDataset (Dataset ): def __init__ (self, filepath ): xy = np.loadtxt(filepath, delimiter=',' , dtype=np.float32) self.len = xy.shape[0 ] self.x_data = torch.from_numpy(xy[:, :-1 ]) self.y_data = torch.from_numpy(xy[:, [-1 ]]) def __getitem__ (self, index ): return self.x_data[index], self.y_data[index] def __len__ (self ): return self.len dataset = DiabetesDataset('diabetes.csv.gz' ) train_loader = DataLoader(dataset=dataset, batch_size=32 , shuffle=True , num_workers=2 )
1 2 3 4 5 6 7 8 9 10 11 12 13 for epoch in range (100 ):for i, data in enumerate (train_loader, 0 ):inputs, labels = data y_pred = model(inputs) loss = criterion(y_pred, labels) print (epoch, i, loss.item())optimizer.zero_grad() loss.backward() optimizer.step()
多分类 我们在多维输入里介绍了这个hello world，现在我们就来考虑如何实现它
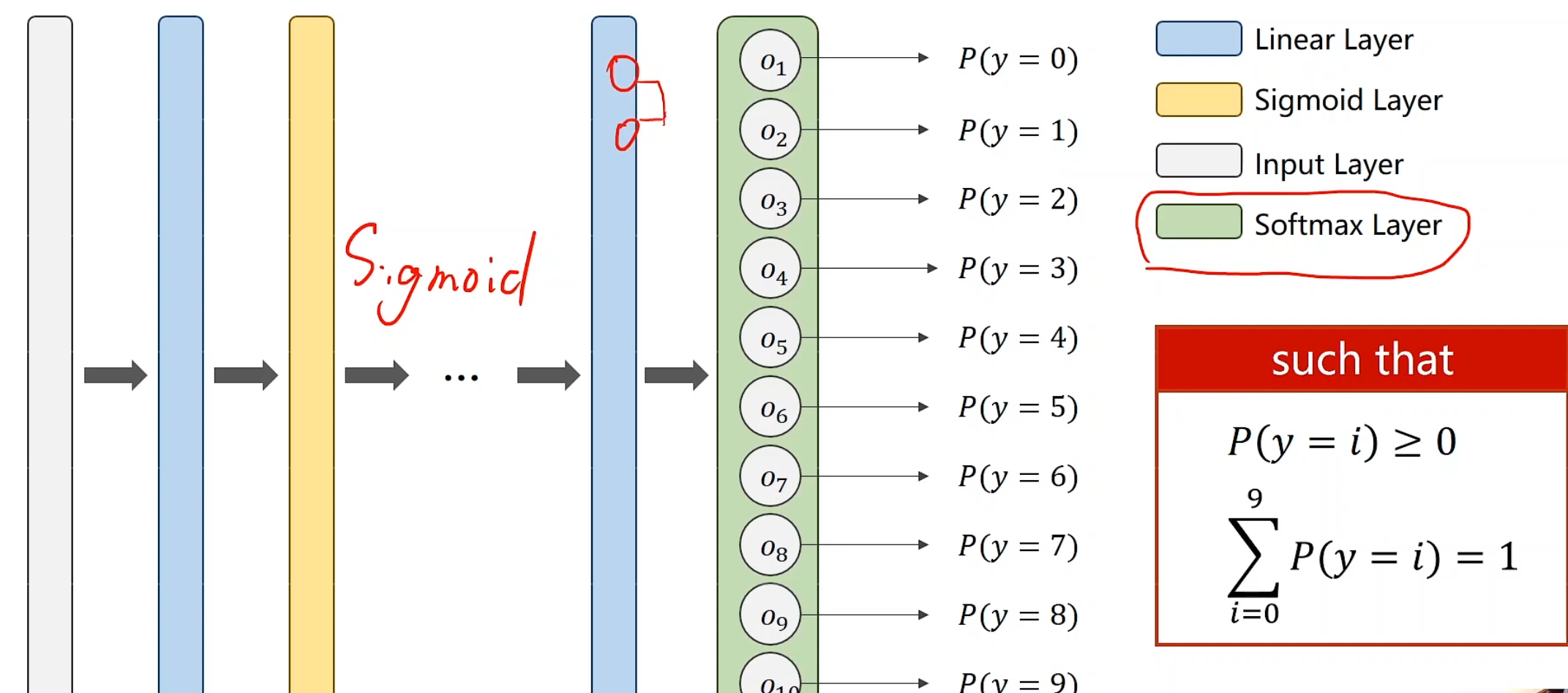
对于这个神经网络，我们引入Softmax层。它能使得输出的每个概率满足累加起来为1，并且均＞0的条件
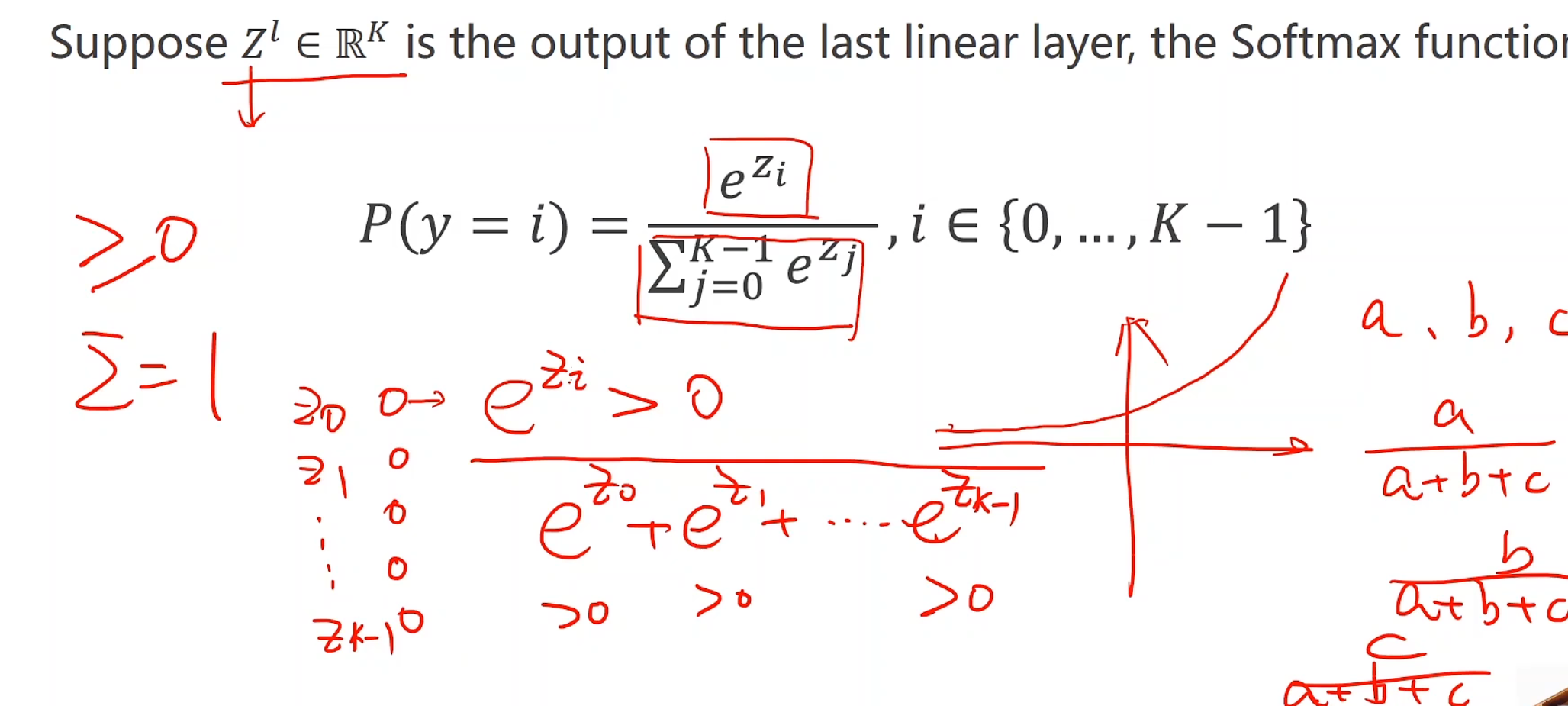
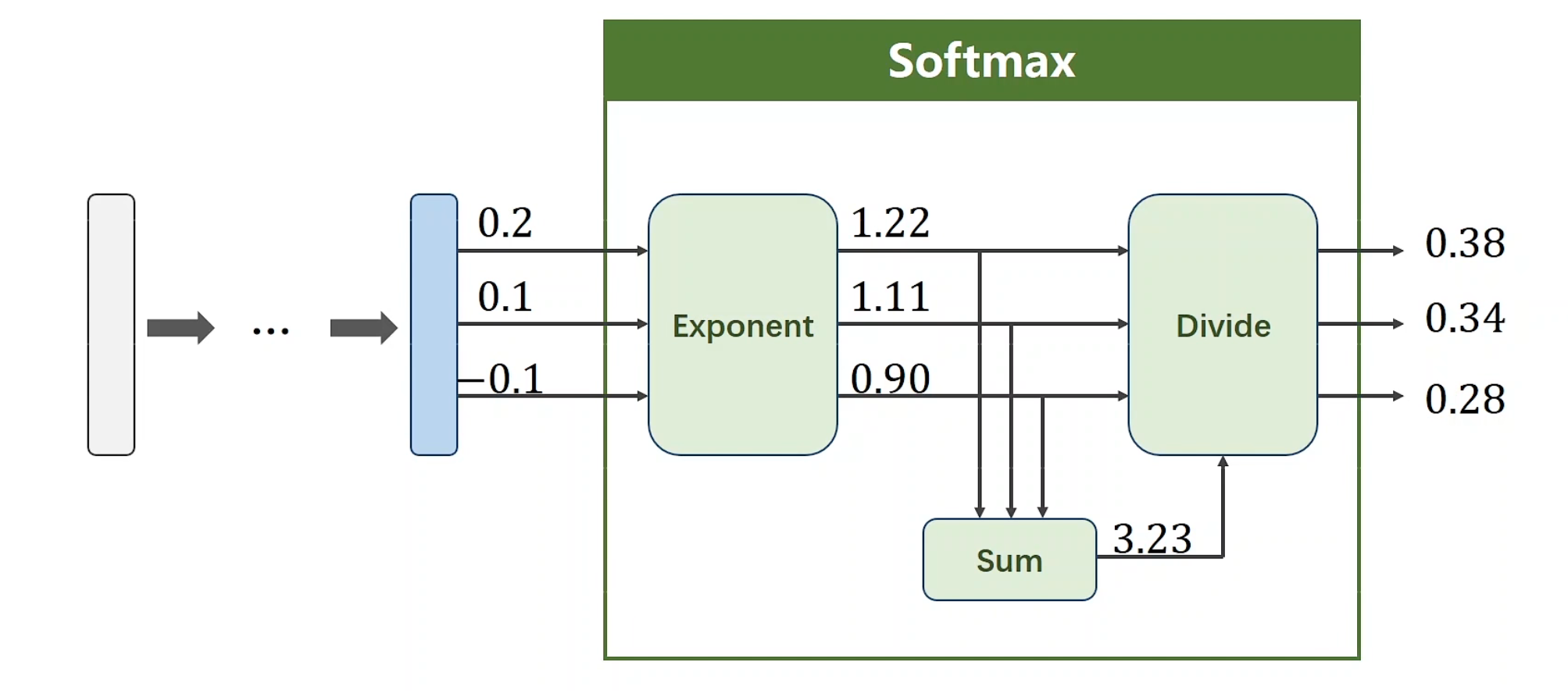
softmax函数
引入e为底，这样可以使得，不管线性层最后是正是负，终能达到如上所需要求，具体的算法描述已经在老师的白板中显示的很清楚了，将a，b，c看做三个分类就行，也就是Z0,Z1,Z2。
那么为何用e为底数呢？最简单的理解就是这个函数会相应扩大最大概率值的比重，有利于分类
现在，我们得出了当前输入，属于三个分类可能的分别的概率
再考虑我们的交叉熵
意味着最后只有一个可以输出。
我们要算损失，应该怎么来实现呢？
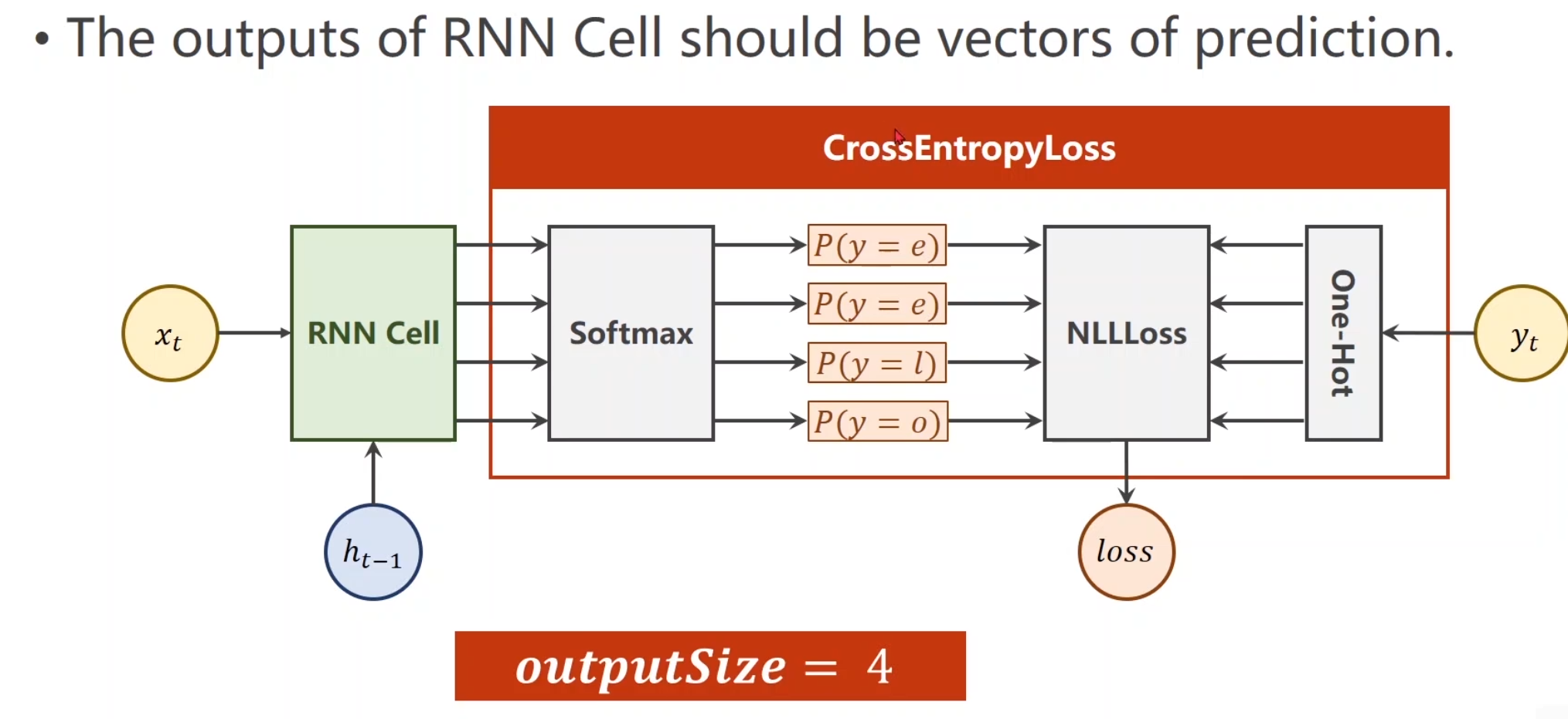
这就要引入经久不衰的one-hot了！
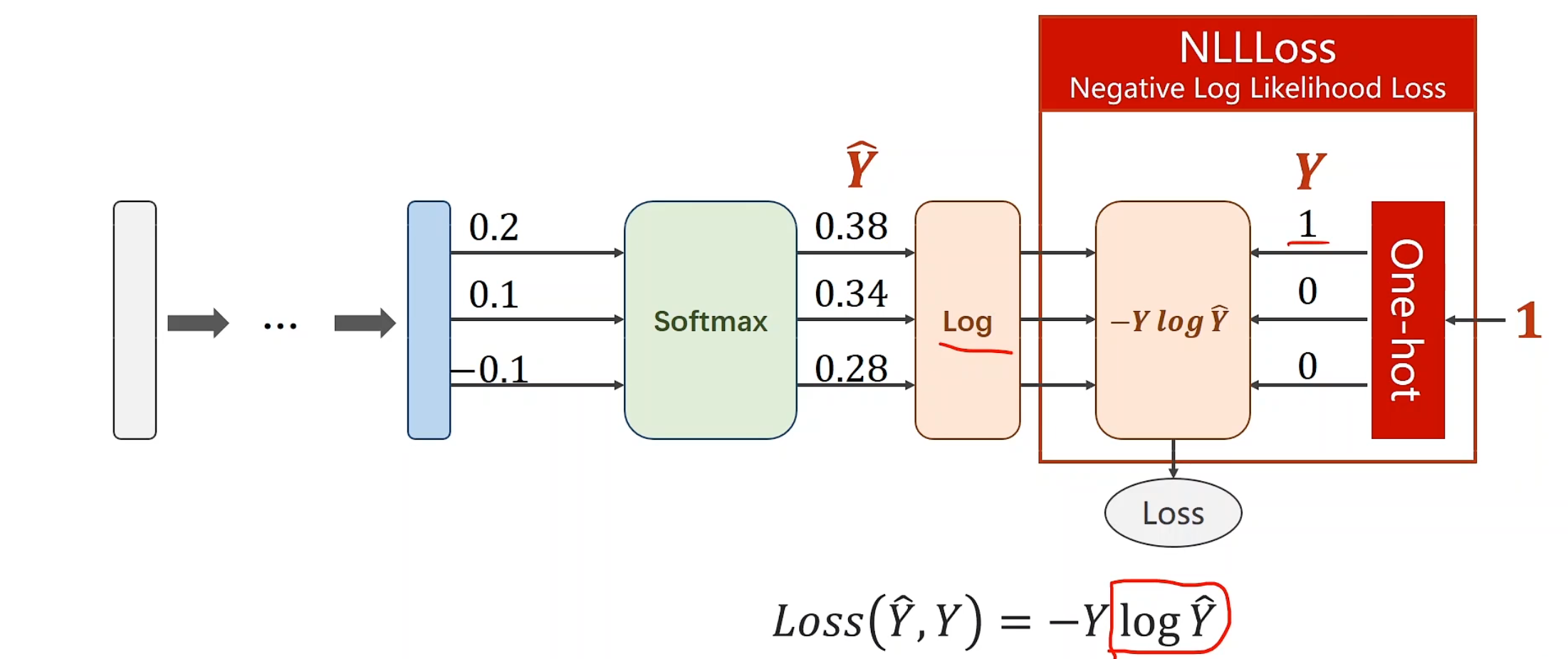
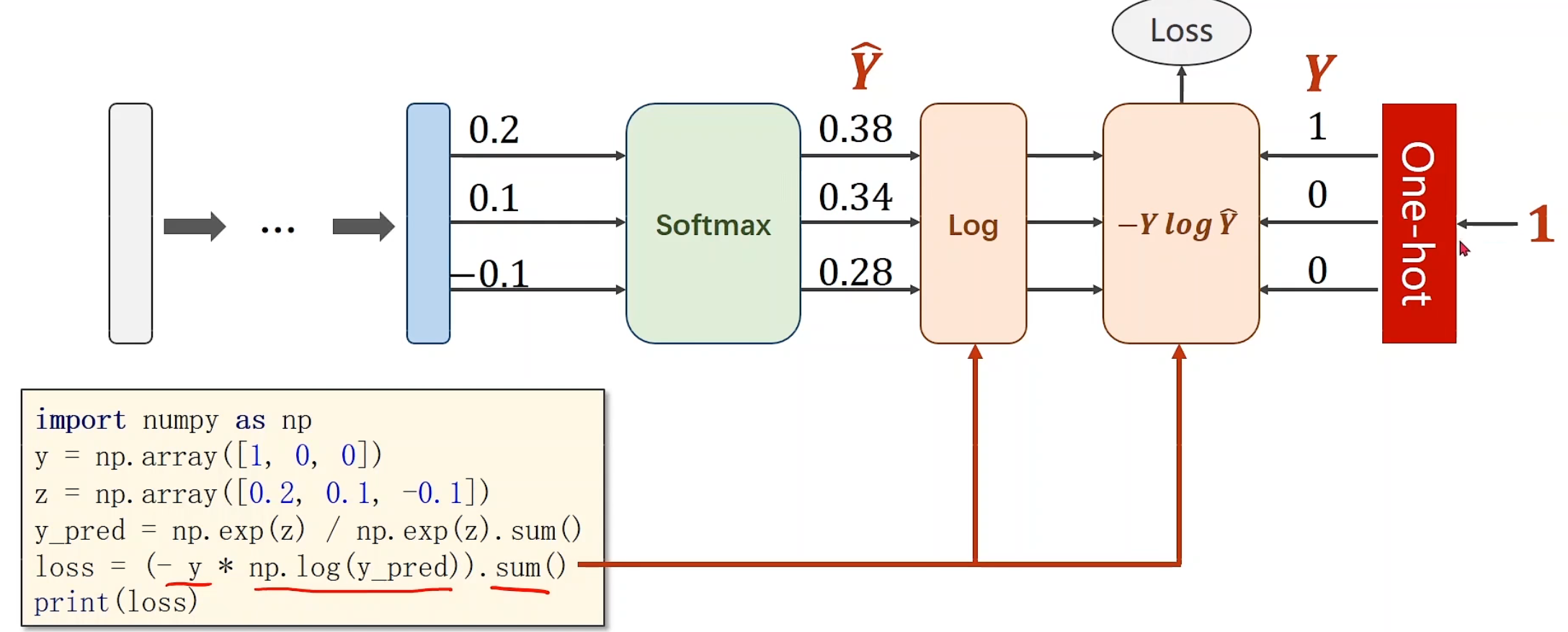
NLLLoss
NLLLoss，y输入的就是标签号，0,1,2,3，但他要求你的y_hat需要在计算完后先自行log再放入，他不会帮你计算交叉熵公式中的log
过程看着其实挺繁琐，but，pytorchYYDS
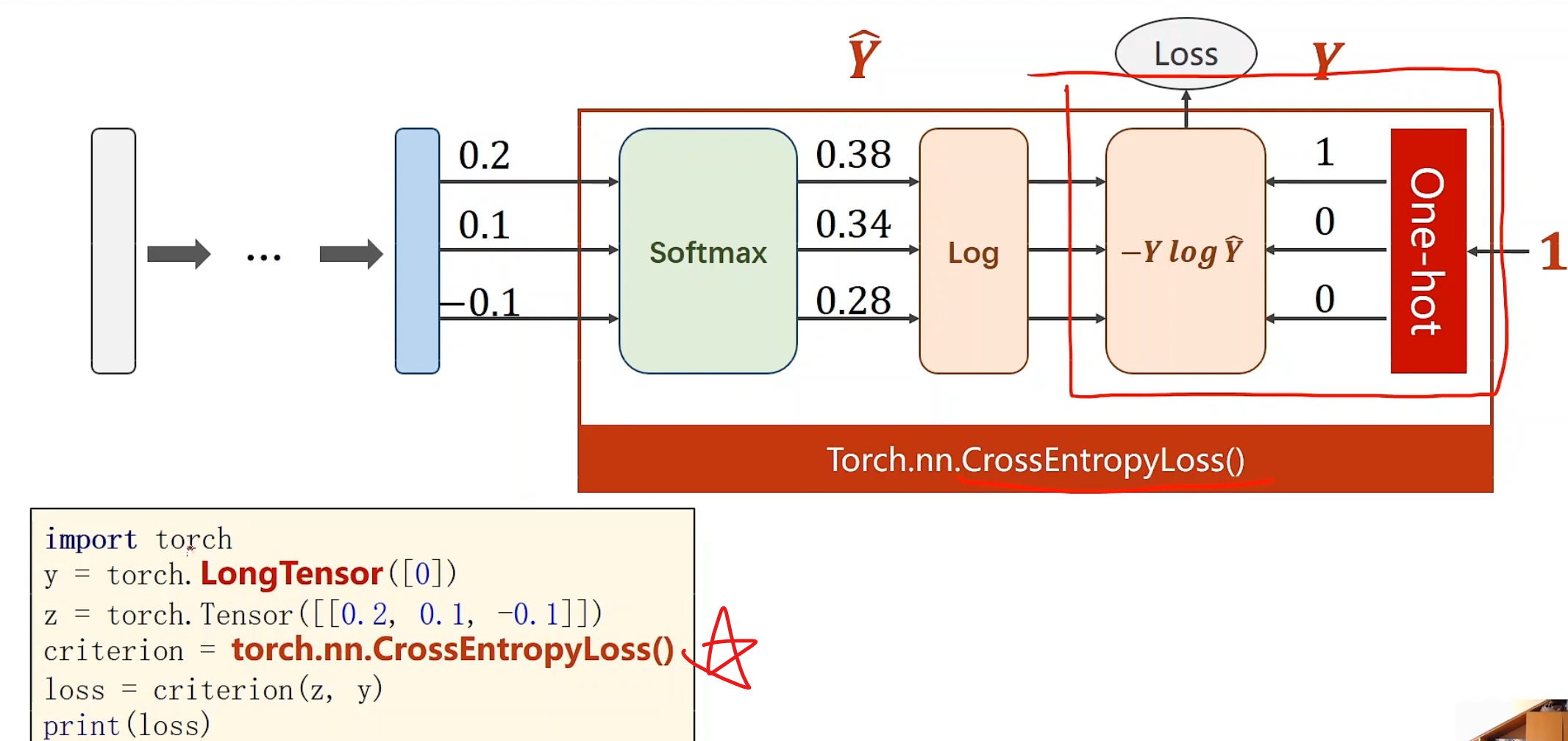
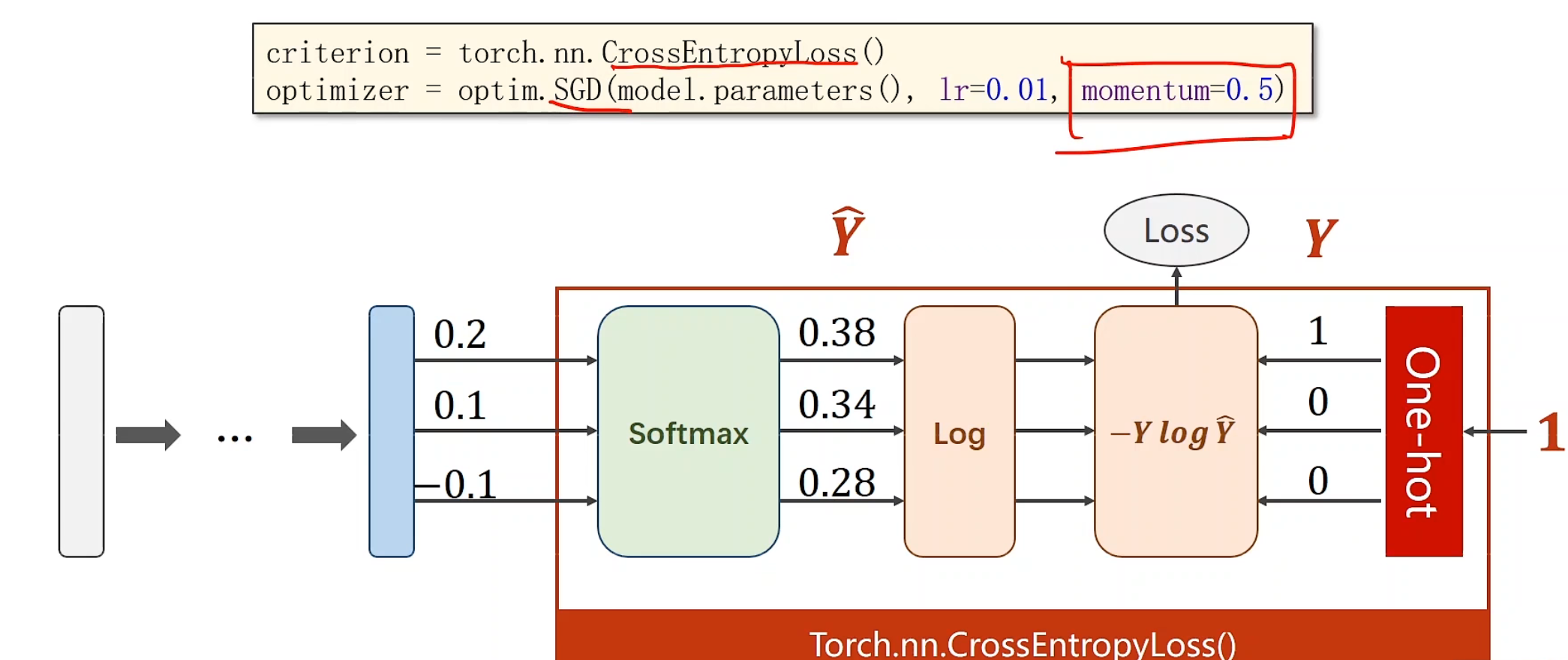
CrossEntropyLoss()帮你把一切封装好，甚至都不需要激活层softmax，一键生成损失！
好用如他也要注意：分类标准y需要是长整型张量 ，这里是指，标准分类仅有0，然后看z和[[0, 0, 0]]的交叉熵
在举一个实例，加深理解：
Y为标准分类类别，2,0,1。 对于Y_pred1内，我们横向看，总共有3组训练好的预测结果，是没有经过softmax的，很轻松看出这三组的概率，分别第二个元素，第零个元素，第一个元素最大，和标准分类结果吻合，所以右边loss1也明显很小，Y_pred2同样方式，看出是0，2,2，极度不搭边，所以loss偏大
最后，两者都需要搞清楚适用场景，两者都有合适的领域。
MNIST Solution
对于单个数字的图片，我们先来感受一下
这次，我们要加入测试集，用一部分数据来看看我们的训练效果到底怎么样
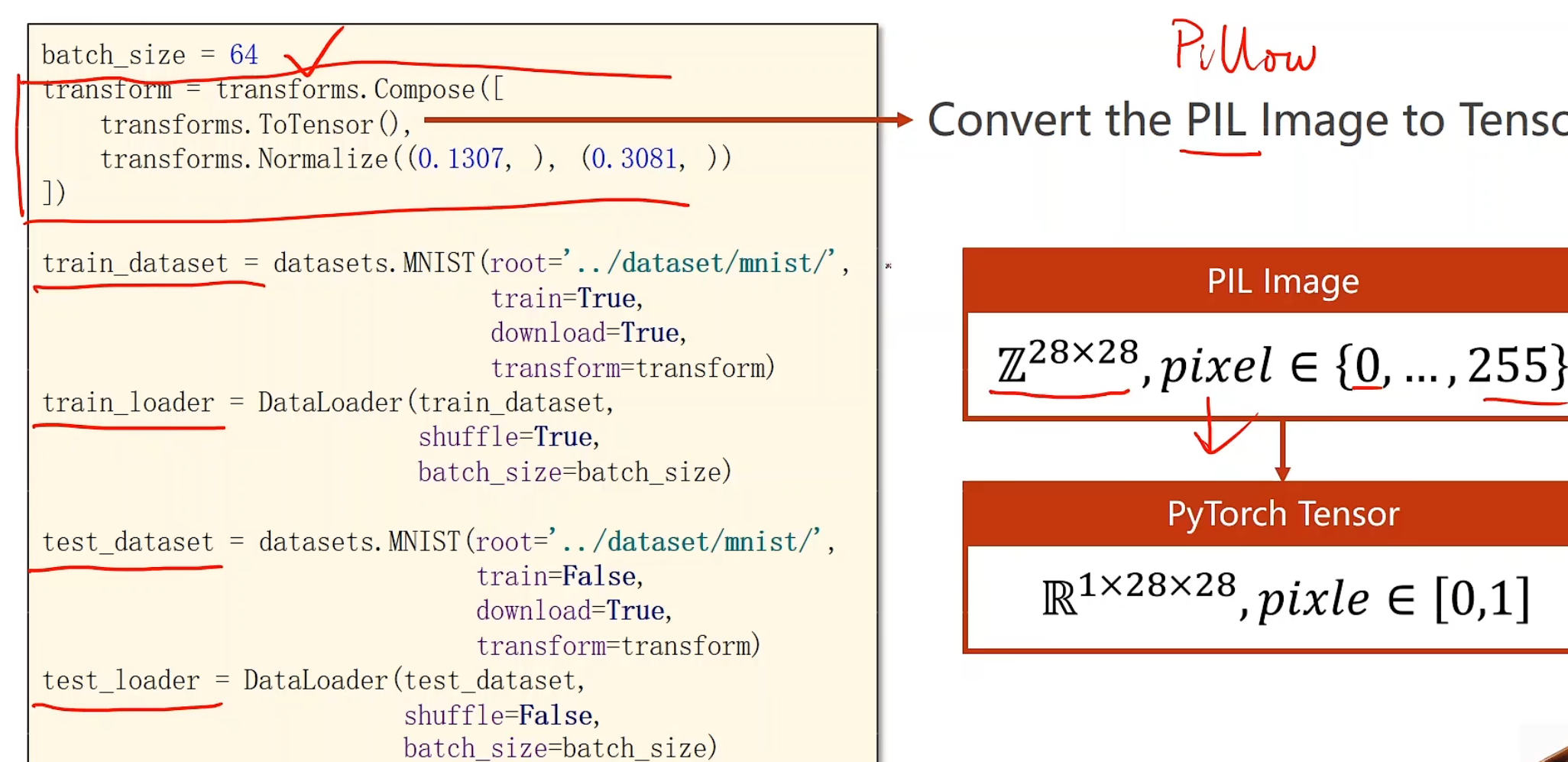
这是实现了的代码，对于第一个部分transforms的ToTensor()，我们可以先来理解一下他为什么要这样做
首先引入通道的概念
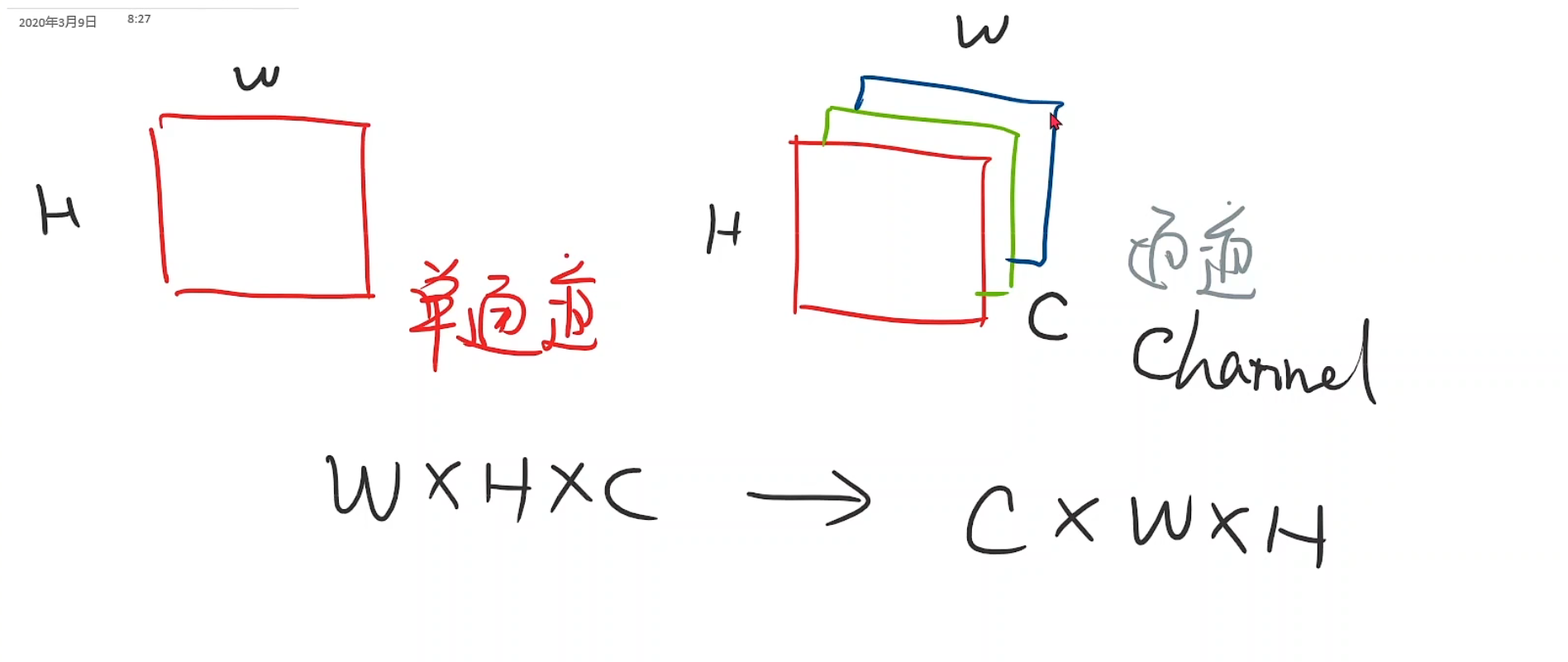
在我们的视觉中，看上去每一个灰度图像，他实际叫做单通道，有单通道就有多通道，其中高为H，宽为W，通道层数为Channel
图像张量，一般都是w * h * c，在pytorch需要转化为c * w * h,这是为了在pytorch里进行更高效的卷积运算
所以在这里，我们要把28*28的像素值先扩张成1 * 28 * 28的单通道图像，并把【0-255】的值压缩成【0-1】的浮点数，这个过程就可以通过ToTensor()来实现
后我们使用Normalize来进行标准化操作，这两个值是提前算出的方差和标准差。
MNIST调用的transform()可以放到getitem()里面来实现，也可以就在这里使用。
这里使用线性模型配套激活函数不断调整权重，为何要降低这么多次维度，而不直接降到10，这主要是因为这样的话丢掉的信息太多，训练出来的效果并不好，另外要注意的一个小点，是最后的output层，我们要对他进行交叉熵函数，所以不需要激活。
momentum，给数据一个惯性集，让他在鞍点走出来，让他加速，助推！
代码实现 1 2 3 4 5 6 import torchfrom torchvision import transformsfrom torchvision import datasetsfrom torch.utils.data import DataLoader import torch.nn.functional as Fimport torch.optim as optim
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 batch_size = 64 transform = transforms.Compose([ transforms.ToTensor(), transforms.Normalize((0.1307 , ), (0.3081 , )) ]) train_dataset = datasets.MNIST(root='../dataset/mnist/' , train=True , download=True , transform=transform) train_loader = DataLoader(train_dataset, shuffle=True , batch_size=batch_size) test_dataset = datasets.MNIST(root='../dataset/mnist/' , train=False , download=True , transform=transform) test_loader = DataLoader(train_dataset, shuffle=False , batch_size=batch_size)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Net (torch.nn.Module ): def __init__ (self ): super (Net, self).__init__() self.l1 = torch.nn.Linear(784 , 512 ) self.l2 = torch.nn.Linear(512 , 256 ) self.l3 = torch.nn.Linear(256 , 128 ) self.l4 = torch.nn.Linear(128 , 64 ) self.l5 = torch.nn.Linear(64 , 10 ) def forward (self, x ): x = x.reshape(-1 , 784 ) x = F.relu(self.l1(x)) x = F.relu(self.l2(x)) x = F.relu(self.l3(x)) x = F.relu(self.l4(x)) x = F.relu(self.l5(x)) return x model = Net()
1 2 criterion = torch.nn.CrossEntropyLoss() optimizer = torch.optim.SGD(model.parameters(), lr=0.01 , momentum = 0.5 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 def train (epoch ): running_loss = 0. for batch_idx, data in enumerate (train_loader, 0 ): inputs, target = data optimizer.zero_grad() output = model(inputs) loss = criterion(output, target) loss.backward() optimizer.step() running_loss += loss.item() if batch_idx % 300 == 299 : print ('[%d, %5d] loss: %.3f' % (epoch+1 , batch_idx+1 , running_loss/300 )) running_loss = 0.
1 2 3 4 5 6 7 8 9 10 11 def test (): correct = 0 total = 0 with torch.no_grad(): for data in test_loader: images, labels = data outputs = model(images) _, predicted = torch.max (outputs.data, axis = 1 ) total += labels.size(0 ) correct += (predicted == labels).sum ().item() print ('Accuracy on test set: %d %%' % (100 * correct/total))
1 2 3 4 if __name__ == '__main__' : for epoch in range (10 ): train(epoch) test()
1 2 3 4 5 6 7 8 9 10 11 12 13 [1 , 300 ] loss: 0.473 [1 , 600 ] loss: 0.476 [1 , 900 ] loss: 0.465 Accuracy on test set : 80 % [2 , 300 ] loss: 0.461 [2 , 600 ] loss: 0.468 [2 , 900 ] loss: 0.469 .... Accuracy on test set : 80 % [10 , 300 ] loss: 0.436 [10 , 600 ] loss: 0.444 [10 , 900 ] loss: 0.451 Accuracy on test set : 80 %
其实我也不是很明白为啥80%，可能我的cpu太菜了
CNN初阶 每一个输入节点都要参与到下一层任何一个输出结点的计算上，我们把这样的一层叫做全连接层
构建卷积层 先放上整体过程，后续介绍细节。
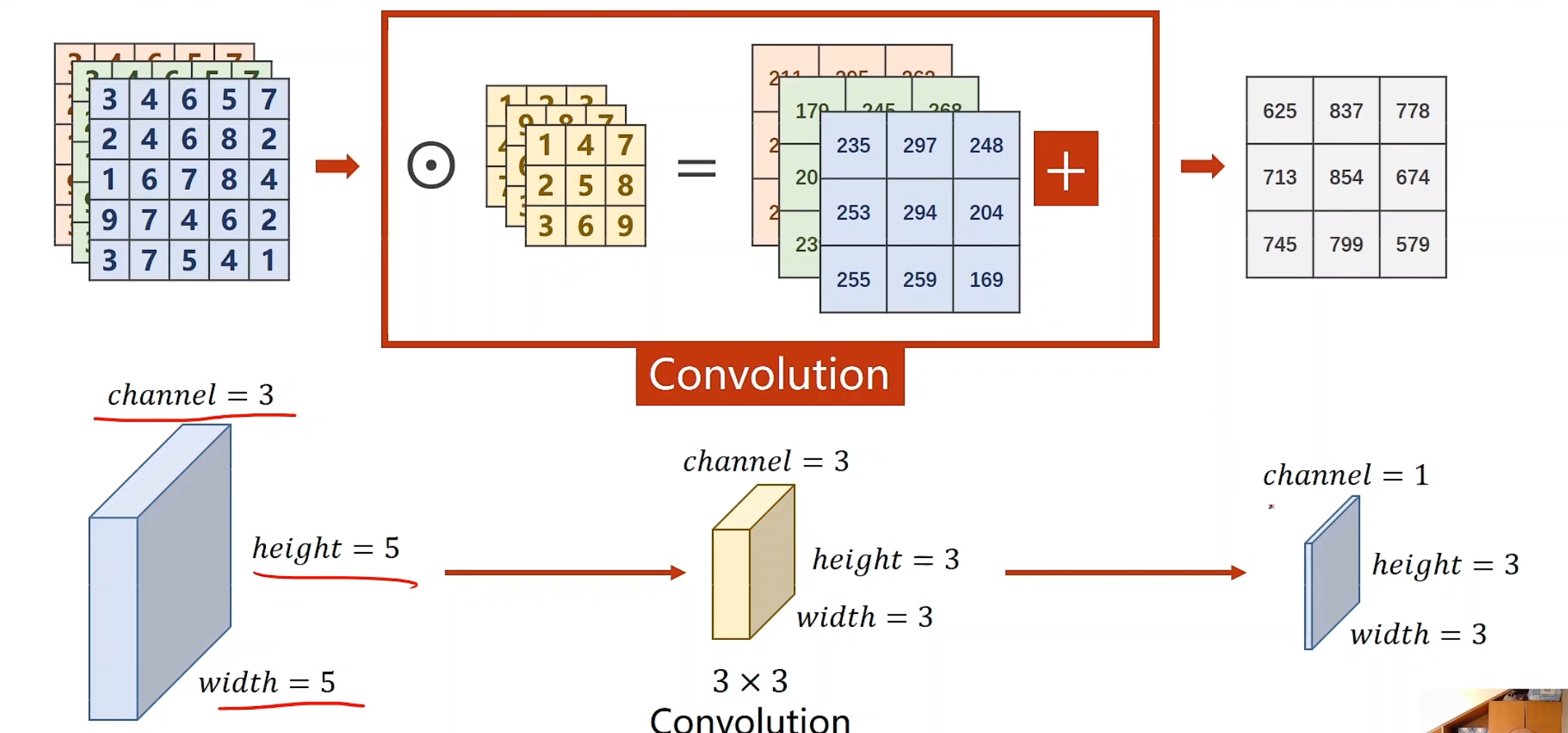
Convolution
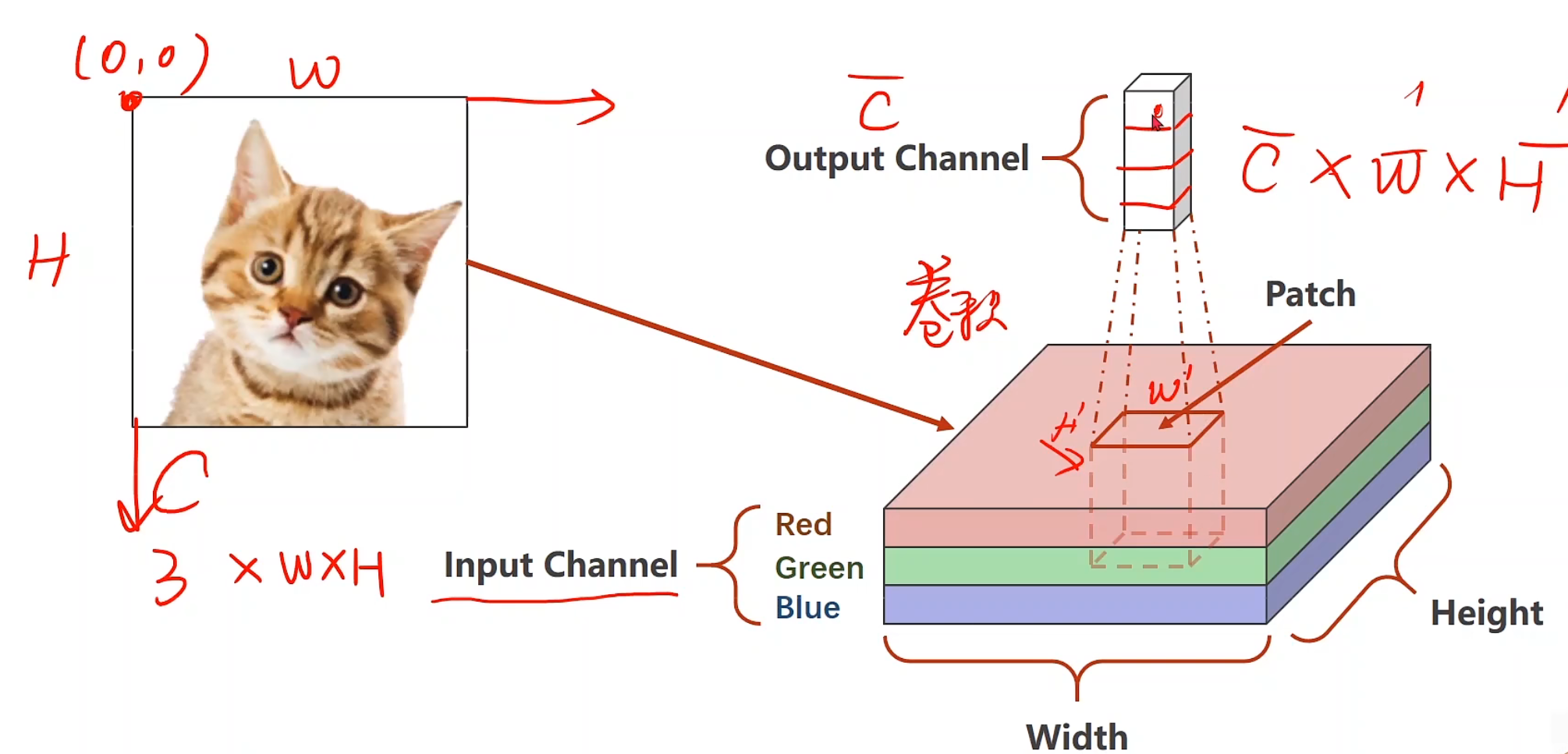
我们在计算机中，所使用到的都是RGB颜色的通道图像，我们要表示一个像素，把它分成若干个格子，每一个格子有一个颜色值，用它们来表示这个图像，我们把这样的图像叫做栅格图像。
通常彩色图片是三通道
我们将猫猫的图像信息输入，很显然，输入信息是3 * w * h的
假设下一层output cannel为 3 * 1 * 1，然后我们就取一个patch中的数据，对他们进行压缩，使得ouput的每一个1，都包含对应patch-size的原图像的信息，最终不断运用这些信息进行调整，得到我们想要的结果
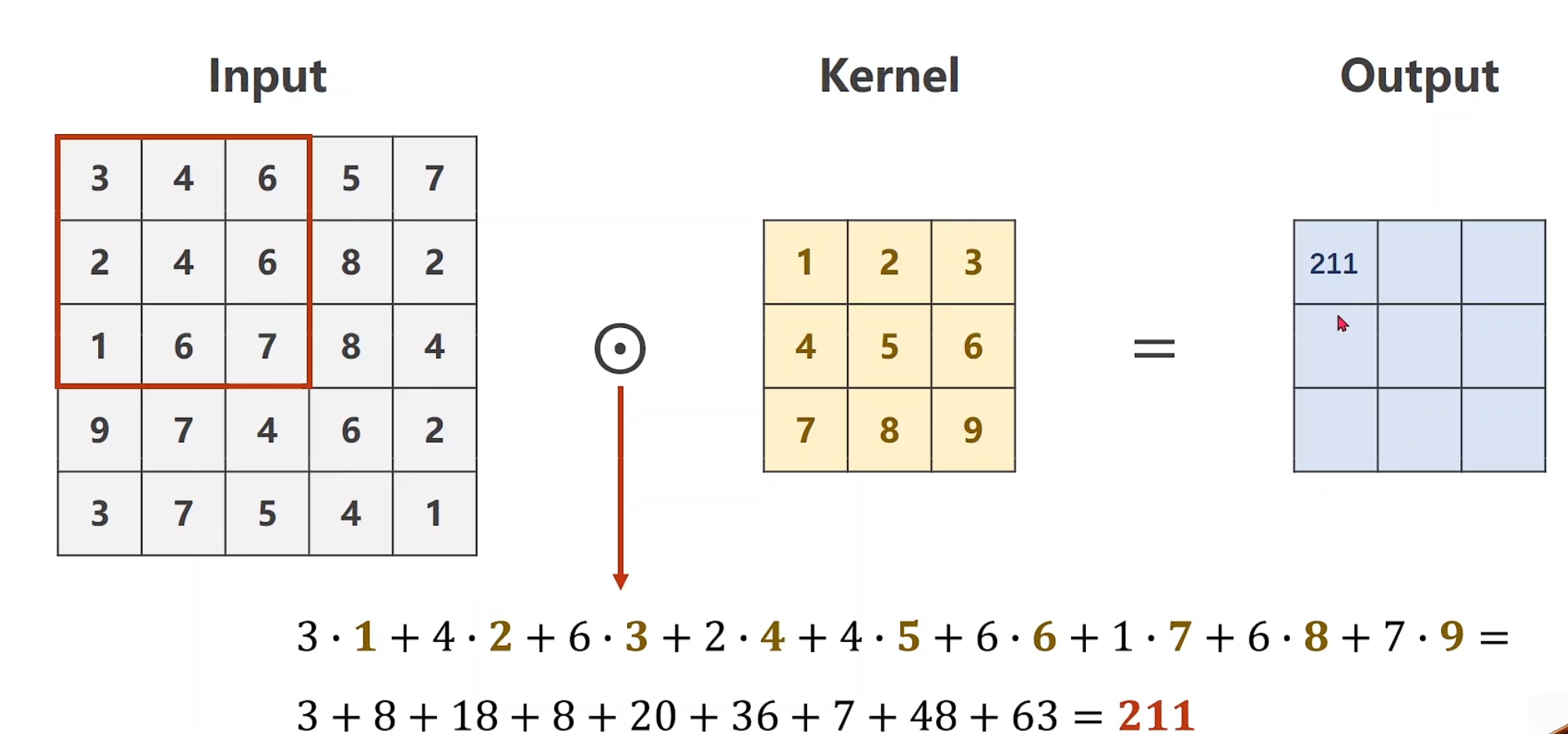
卷积运算，通过选择对应的batch-size和对应的kernel-size，后对其做数乘处理，并将累加结果放入output的第一个位置
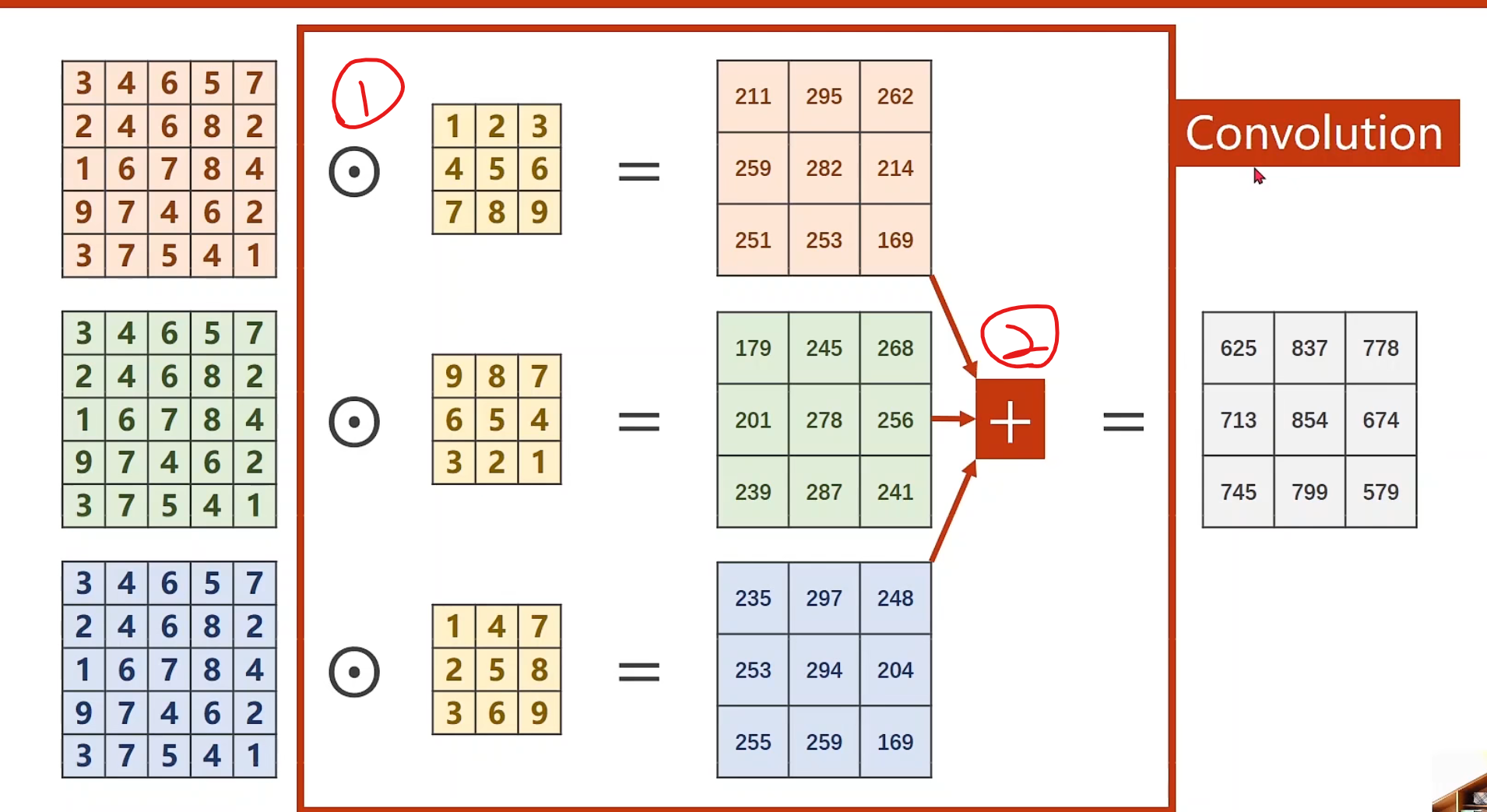
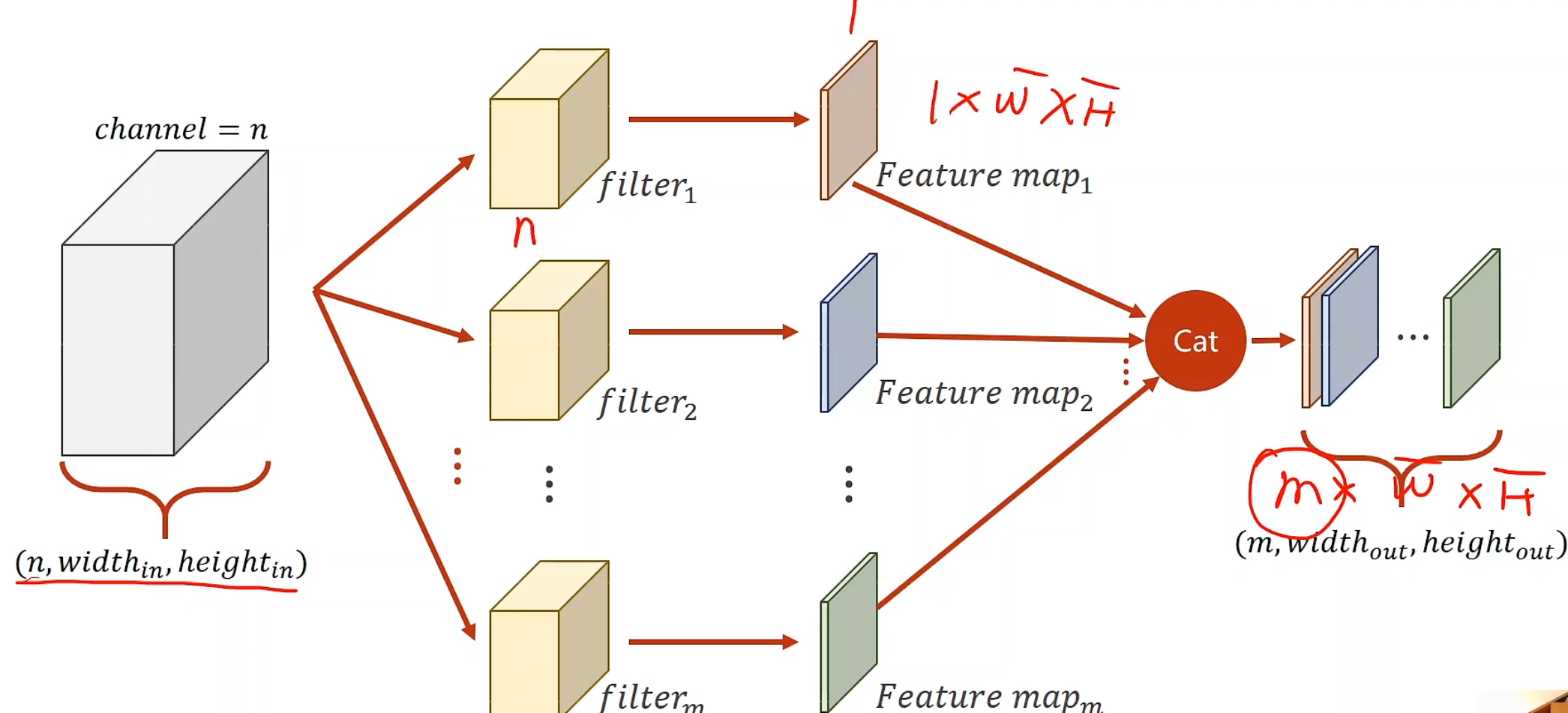
若有多个维度，可以构建多个卷积核，对同样的样本做卷积数乘运算，运算以后的output对应位置叠加，即可得到最后的一层output
若我们要得到m个输出通道，那我们就准备m个卷积核，把这m个output进行cat，后就可以变成一个m * w * h的张量
对于每个卷积核大小的确定，我们可以发现：
每一个卷积核的通道数量要求和输入通道（n）一样
卷积核的总数有多少个，和输出通道的数量（m）一样
整个卷积过程的尺寸，我们可以用四维张量来表示
代码实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 import torchin_channels, out_channels= 5 , 10 width, height = 100 , 100 kernel_size = 3 batch_size = 1 input = torch.randn(batch_size, in_channels, width, height) conv_layer = torch.nn.Conv2d(in_channels, out_channels, kernel_size=kernel_size) output = conv_layer(input ) print (input .shape)print (output.shape)print (conv_layer.weight.shape)
1 2 3 torch.Size([1 , 5 , 100 , 100 ]) torch.Size([1 , 10 , 98 , 98 ]) torch.Size([10 , 5 , 3 , 3 ])
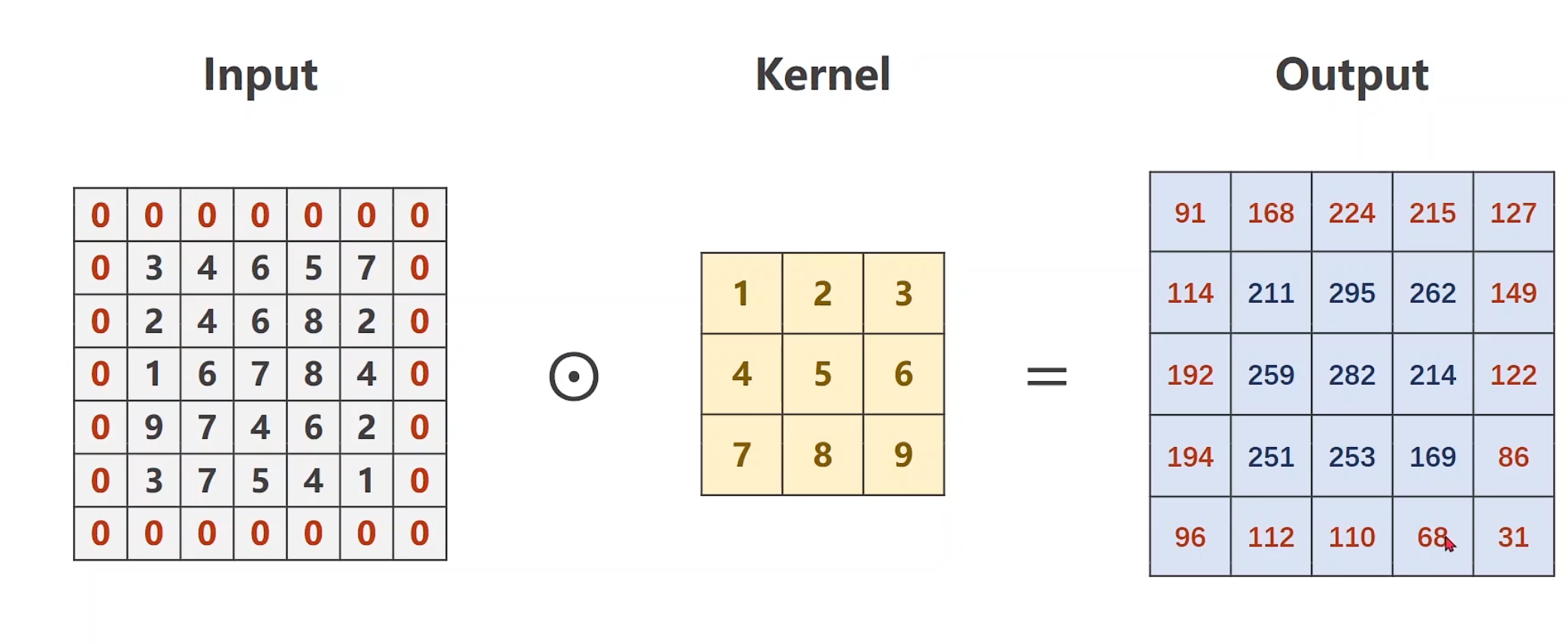
padding 卷积层初始化时的常见参数之一， padding的目的是填充补齐，比如说input和卷积层大小已经确定，例如就是5 * 5和3 * 3，那么最后得到的output肯定就是3 * 3（这里步长默认都是1）。如果我们不想让他是3 * 3，或者说，最后维度和input一样, 应该怎么办呢？默认来说，就是给input周围补0，使得卷积后的结果能是5 * 5。
在这个过程中我们也发现了一些公式，目前目标仍然是使得output和input维度相同，做padding，看kernel是多少。这个时候我们通常用kernel_size / 2（整除哈）得到多少，那么就需要在外面padding多少层，例如下图是3*3的话，就需要填充3 / 2 = 1层
1 2 3 4 5 6 7 8 9 10 11 12 import torchinput = [3 ,4 ,6 ,5 ,7 , 2 ,4 ,6 ,8 ,2 , 1 ,6 ,7 ,8 ,4 , 9 ,7 ,4 ,6 ,2 , 3 ,7 ,5 ,4 ,1 ] input = torch.Tensor(input ).view(1 , 1 , 5 , 5 ) conv_layer = torch.nn.Conv2d(1 , 1 , kernel_size=3 , padding=1 , bias=False ) kernel = torch.Tensor([1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ,9 ]).view(1 , 1 , 3 , 3 ) conv_layer.weight.data = kernel.data output = conv_layer(input ) print (output)
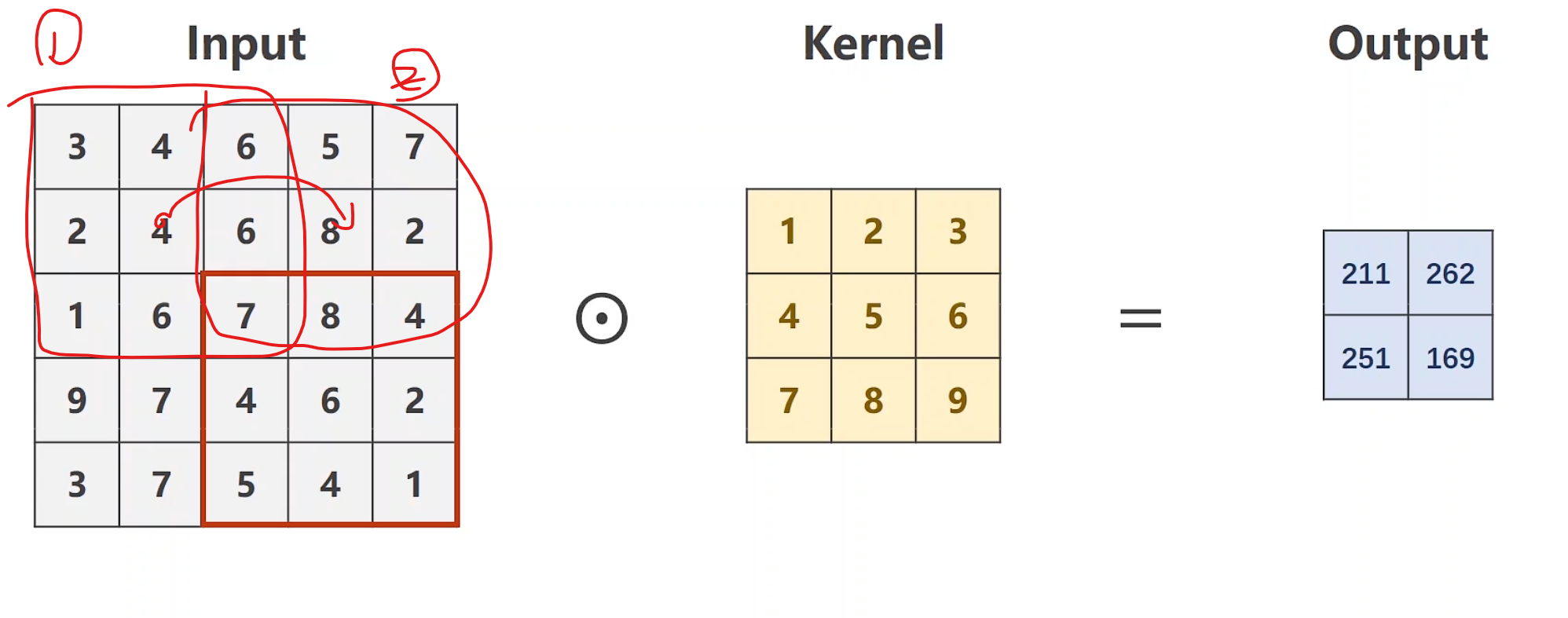
stride 步长。
1 2 3 4 5 6 7 8 9 10 11 12 import torchinput = [3 ,4 ,6 ,5 ,7 , 2 ,4 ,6 ,8 ,2 , 1 ,6 ,7 ,8 ,4 , 9 ,7 ,4 ,6 ,2 , 3 ,7 ,5 ,4 ,1 ] input = torch.Tensor(input ).view(1 , 1 , 5 , 5 )conv_layer = torch.nn.Conv2d(1 , 1 , kernel_size=3 , stride=2 , bias=False ) kernel = torch.Tensor([1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ,9 ]).view(1 , 1 , 3 , 3 ) conv_layer.weight.data = kernel.data output = conv_layer(input ) print (output)
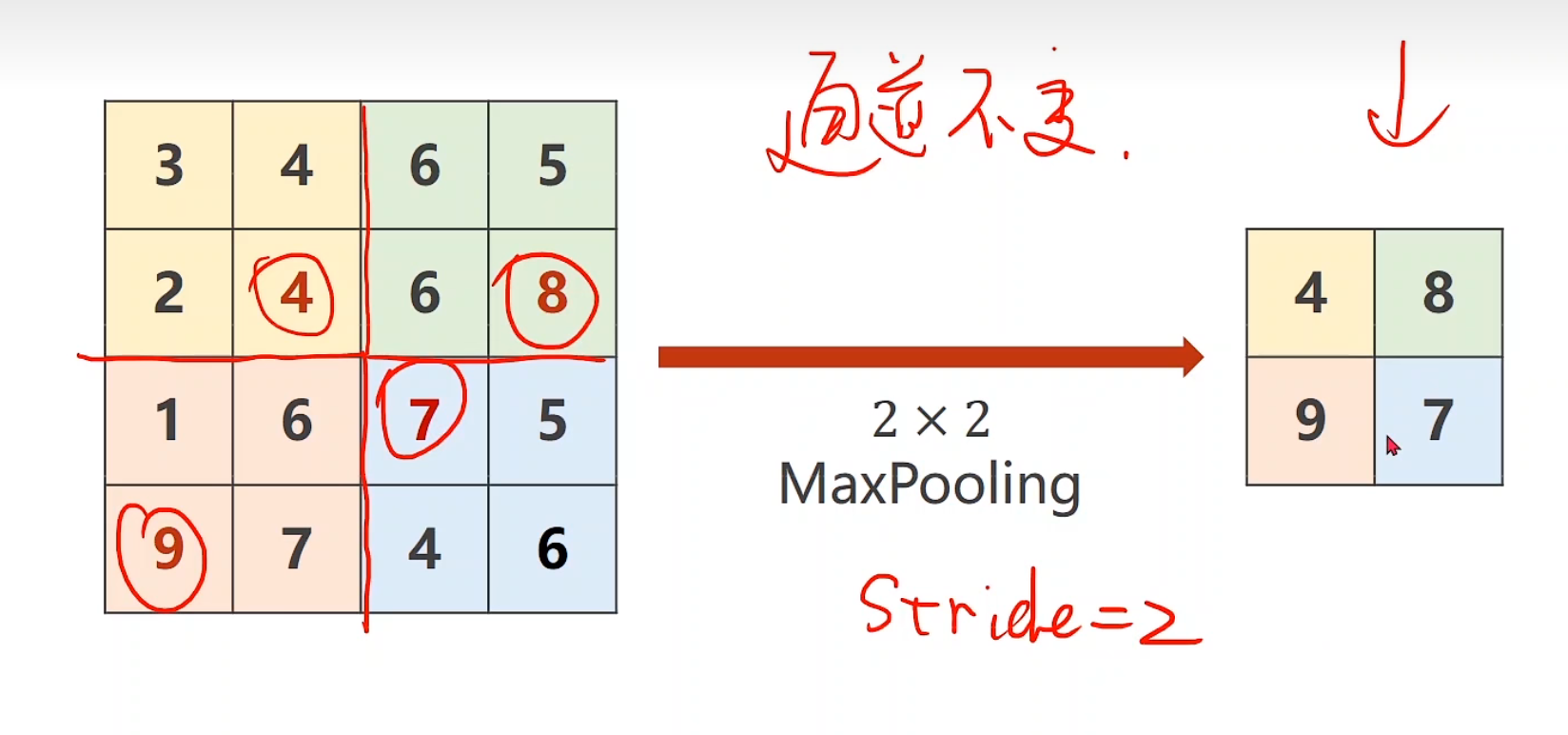
Max Pooling Layer 通道数量不变，池化层2 * 2默认是stride为2
1 2 3 4 5 6 7 8 9 10 import torchinput = [3 ,4 ,6 ,5 , 2 ,4 ,6 ,8 , 1 ,6 ,7 ,8 , 9 ,7 ,4 ,6 , ] input = torch.Tensor(input ).view(1 , 1 , 4 , 4 )maxpooling_layer = torch.nn.MaxPool2d(kernel_size=2 ) output = maxpooling_layer(input ) print (output)
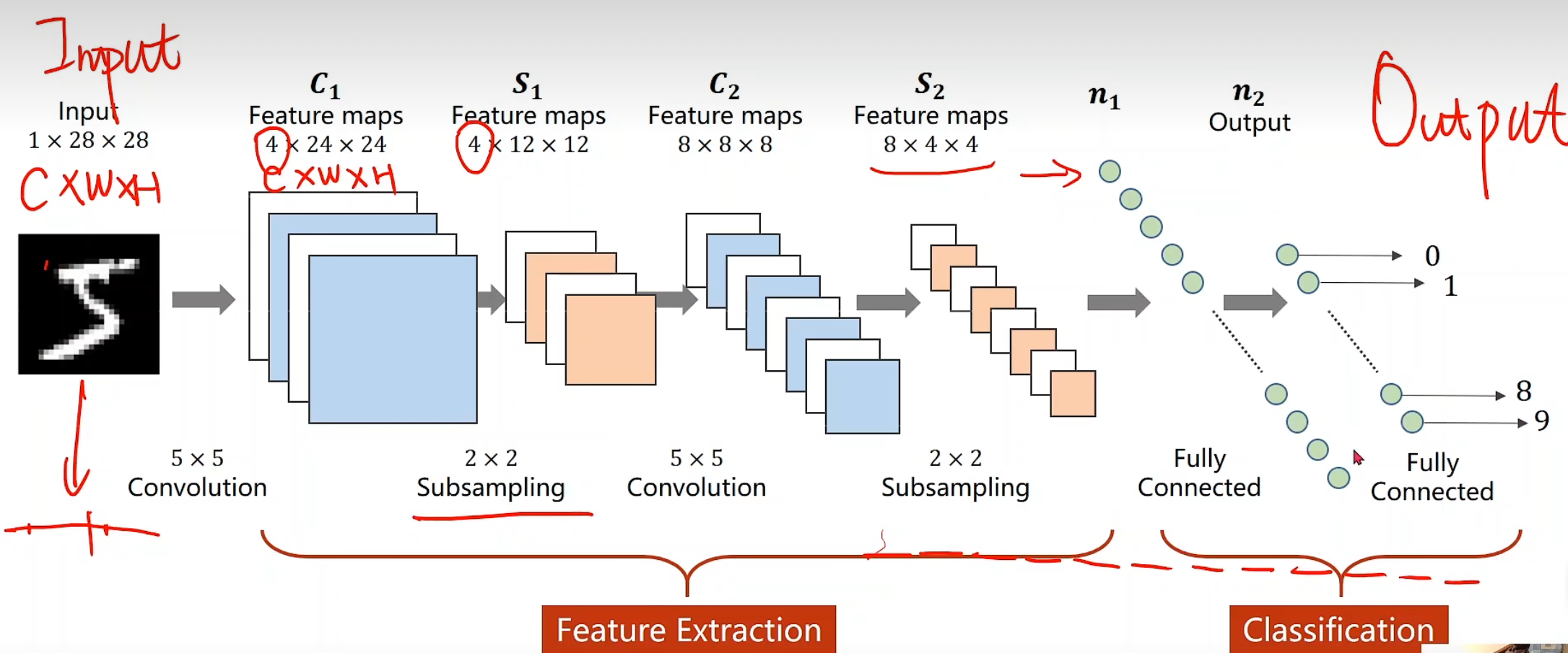
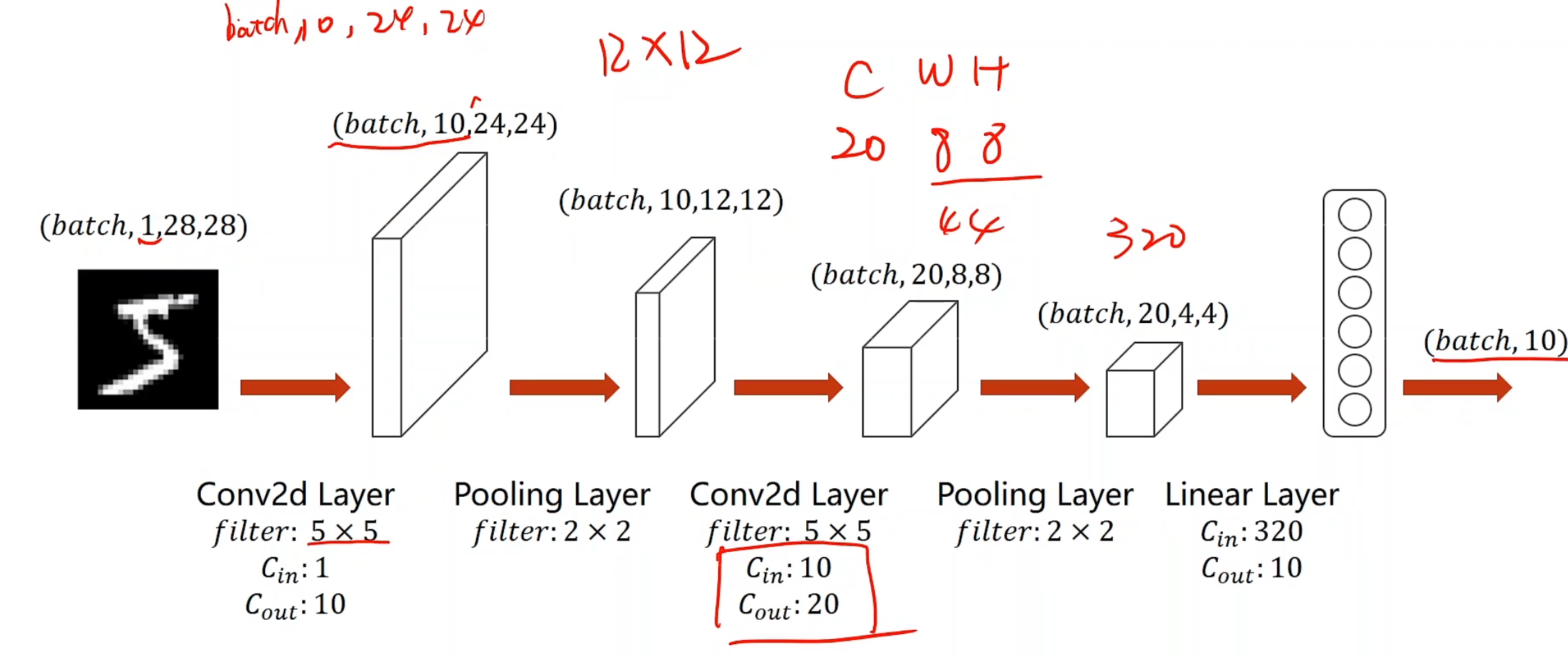
实例一代码总结 现在我们再来看这个图，是不是格外清楚啦？
我们要保证一层一层输出，池化，他的维度一定是要能对上的，但其实，卷积层和池化层，它并不在意你的输入大小，因为设置好以后，无论多大的图像，它都能处理，但是，我们最后的分类器，就是通过我们这层层筛选出信息最后给予它的，所以也要好好分析怎么构建。
实际上我们也有偷懒的办法，不去算维度，直接print其实也不错hhhhh
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Net (torch.nn.Module ): def __init__ (self ): super (Net, self).__init__() self.conv1 = torch.nn.Conv2d(1 , 10 , kernel_size=5 ) self.conv2 = torch.nn.Conv2d(10 , 20 , kernel_size=5 ) self.pooling = torch.nn.MaxPool2d(2 ) self.fc = torch.nn.Linear(320 , 10 ) def forward (self, x ): batch_size = x.size(0 ) x = F.relu(self.pooling(self.conv1(x))) x = F.relu(self.pooling(self.conv2(x))) x = x.view(batch_size, -1 ) x = self.fc(x) return x model = Net()
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 import torch class Net (torch.nn.Module ): def __init__ (self ): super (Net, self).__init__() self.conv1 = torch.nn.Conv2d(1 , 12 , kernel_size=3 ) self.conv2 = torch.nn.Conv2d(12 , 30 , kernel_size=4 ) self.conv3 = torch.nn.Conv2d(30 , 24 , kernel_size=2 ) self.pooling = torch.nn.MaxPool2d(2 ) self.linear = torch.nn.Linear(96 , 10 ) def forward (self, x ): batch_size = x.size(0 ) x = self.pooling(F.relu(self.conv1(x))) x = self.pooling(F.relu(self.conv2(x))) x = self.pooling(F.relu(self.conv3(x))) x = x.view(batch_size, -1 ) return self.linear(x) model = Net()
完整代码
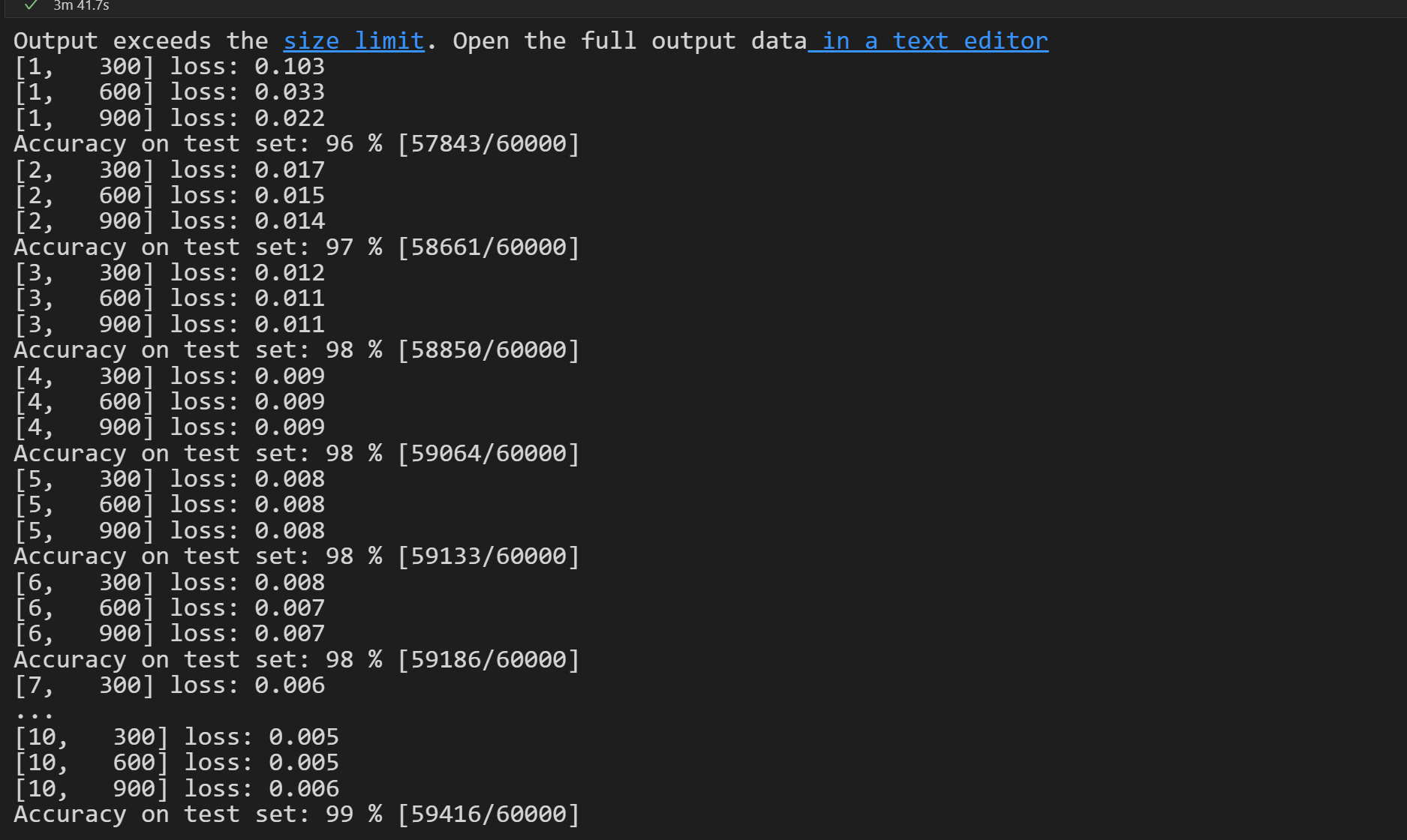
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 import torchfrom torchvision import transformsfrom torchvision import datasetsfrom torch.utils.data import DataLoader import torch.nn.functional as Fimport torch.optim as optimbatch_size = 64 transform = transforms.Compose([ transforms.ToTensor(), transforms.Normalize((0.1307 , ), (0.3081 , )) ]) train_dataset = datasets.MNIST(root='../dataset/mnist/' , train=True , download=True , transform=transform) train_loader = DataLoader(train_dataset, shuffle=True , batch_size=batch_size) test_dataset = datasets.MNIST(root='../dataset/mnist/' , train=False , download=True , transform=transform) test_loader = DataLoader(train_dataset, shuffle=False , batch_size=batch_size) class Net (torch.nn.Module ): def __init__ (self ): super (Net, self).__init__() self.conv1 = torch.nn.Conv2d(1 , 10 , kernel_size=5 ) self.conv2 = torch.nn.Conv2d(10 , 20 , kernel_size=5 ) self.pooling = torch.nn.MaxPool2d(2 ) self.fc = torch.nn.Linear(320 , 10 ) def forward (self, x ): batch_size = x.size(0 ) x = F.relu(self.pooling(self.conv1(x))) x = F.relu(self.pooling(self.conv2(x))) x = x.view(batch_size, -1 ) x = self.fc(x) return x model = Net() device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu" ) model.to(device) criterion = torch.nn.CrossEntropyLoss() optimizer = torch.optim.SGD(model.parameters(), lr=0.01 , momentum = 0.5 ) def train (epoch ): running_loss = 0.0 for batch_idx, data in enumerate (train_loader, 0 ): inputs, target = data inputs, target = inputs.to(device), target.to(device) optimizer.zero_grad() outputs = model(inputs) loss = criterion(outputs, target) loss.backward() optimizer.step() running_loss += loss.item() if batch_idx % 300 == 299 : print ('[%d, %5d] loss: %.3f' % (epoch + 1 , batch_idx + 1 , running_loss / 2000 )) running_loss = 0.0 def test (): correct = 0 total = 0 with torch.no_grad(): for data in test_loader: inputs, target = data inputs, target = inputs.to(device), target.to(device) outputs = model(inputs) _, predicted = torch.max (outputs.data, dim=1 ) total += target.size(0 ) correct += (predicted == target).sum ().item() print ('Accuracy on test set: %d %% [%d/%d]' % (100 * correct / total, correct, total)) if __name__ == '__main__' : for epoch in range (10 ): train(epoch) test()
显卡运算 1 2 3 device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu" ) model.to(device)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 def train (epoch ): running_loss = 0. for batch_idx, data in enumerate (train_loader, 0 ): inputs, target = data optimizer.zero_grad() output = model(inputs) loss = criterion(output, target) loss.backward() optimizer.step() running_loss += loss.item() if batch_idx % 300 == 299 : print ('[%d, %5d] loss: %.3f' % (epoch+1 , batch_idx+1 , running_loss/300 )) running_loss = 0.
高级CNN 我们在之前介绍的网络架构中，他们都是串行的结构，也就是每一层与每一层之间，依次构建输入输出关系，但神经网络往往会有更为复杂的结构，比如说可能会有分支，或者将此次的输出取出，用于别的作用。
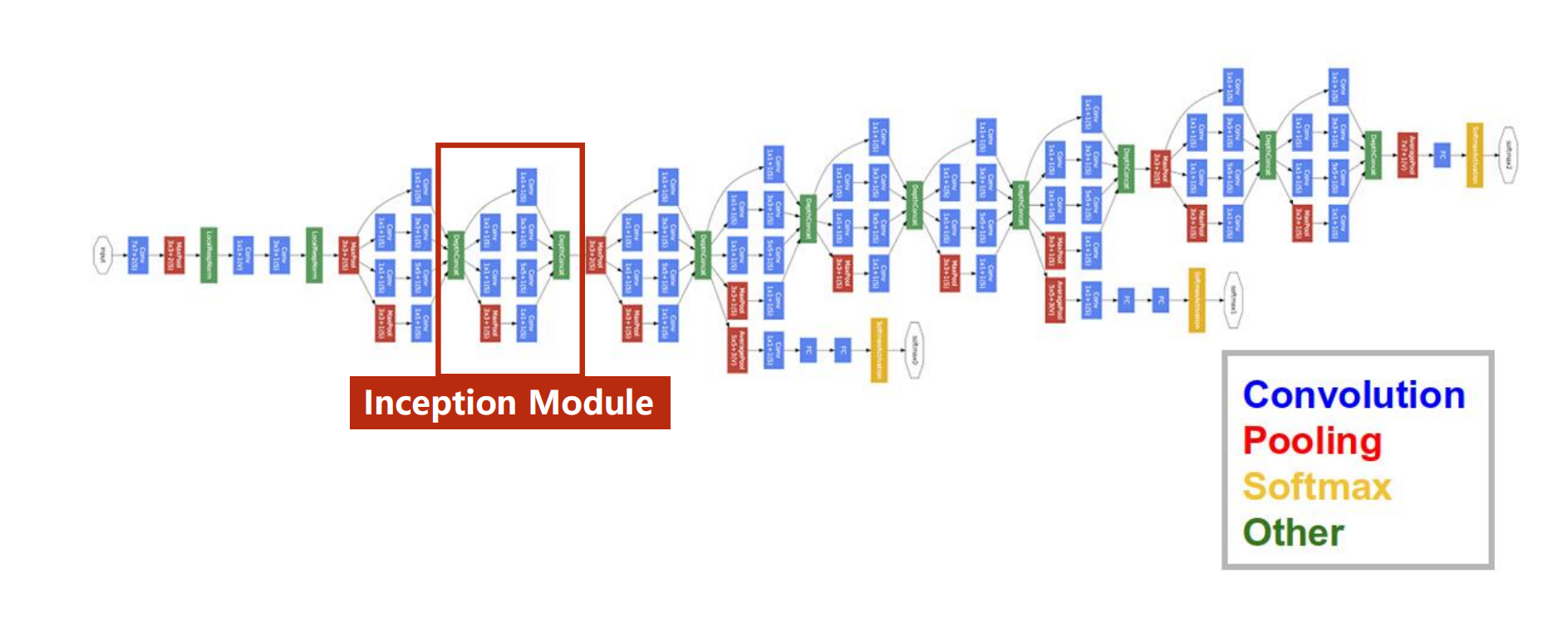
GoogleNet
看到这种代码也许会手足无措，很明显如果我们要一一去定义的话，就太麻烦了，代码十分冗余，为此，我们先介绍一下减少代码冗余——-函数，类
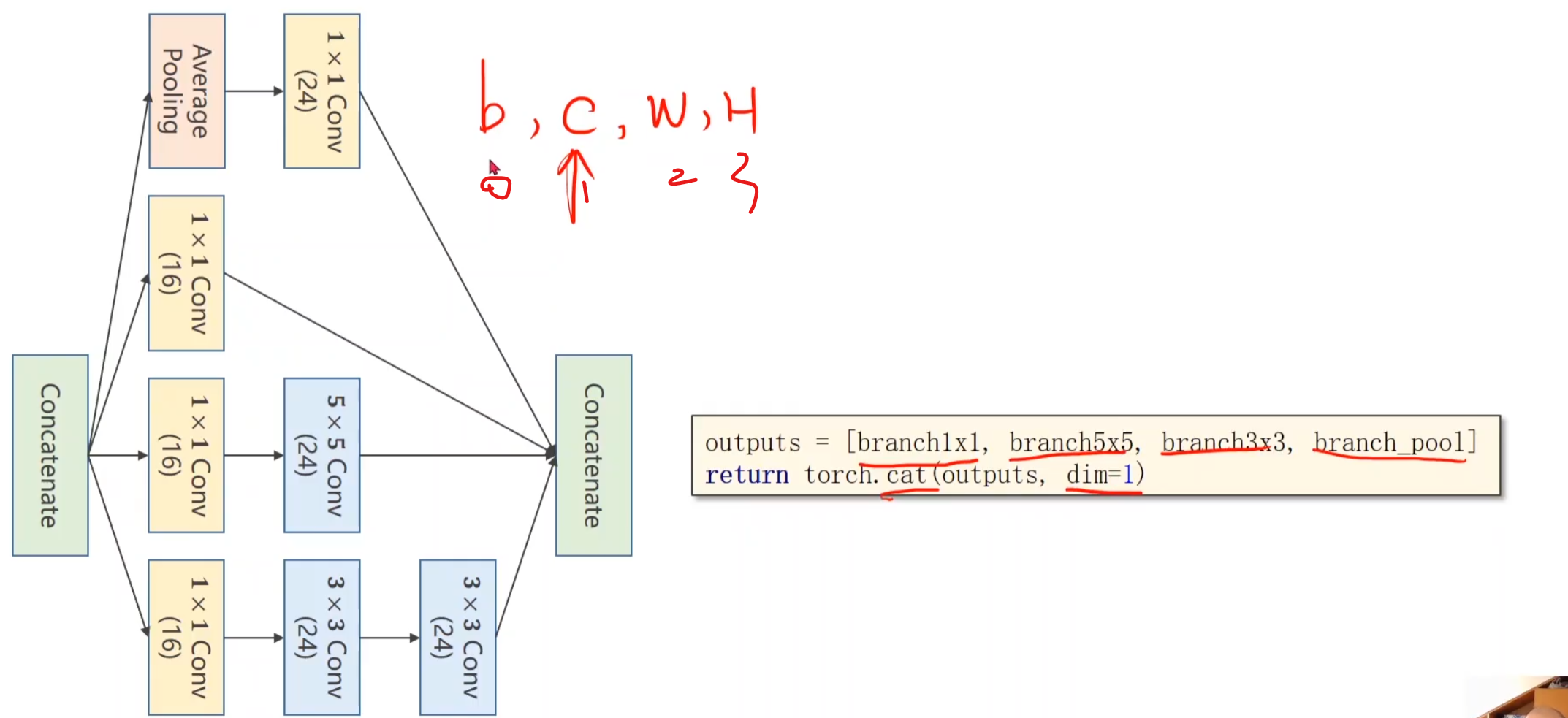
图中的Inception Module是如何实现的，就是我们要考虑的问题，观察一下其实发现存在大量重复的区域块。
在我们构建网络的过程中，选择哪一个卷积核尺寸比较好用，其实是比较难的，这也是googlenet的出发点，我们不知道那个尺寸比较好用，那我们就在一个块中把几个卷积都用一下，然后把结果摞到一起，将来如果3 * 3好用，自然而然，这个块的权重就比较大，比较重要了。
我们在构建的时候必须保证每一个小节点的宽度高度一致（b，c，w，h）唯一不同的就只能是cannel，保证高宽一致，做做padding就可以了
一维卷积运算过程
这是一维卷积的计算过程，也是信息融合 ，类比于高中的科目，有多种科目，可能两个人均存在优势科目和弱势科目，导致分数有来有回，最简单的一个办法就是求总分来评判一个人的实力。
1 * 1卷积最重要的作用也在于此，就是改变通道的数量
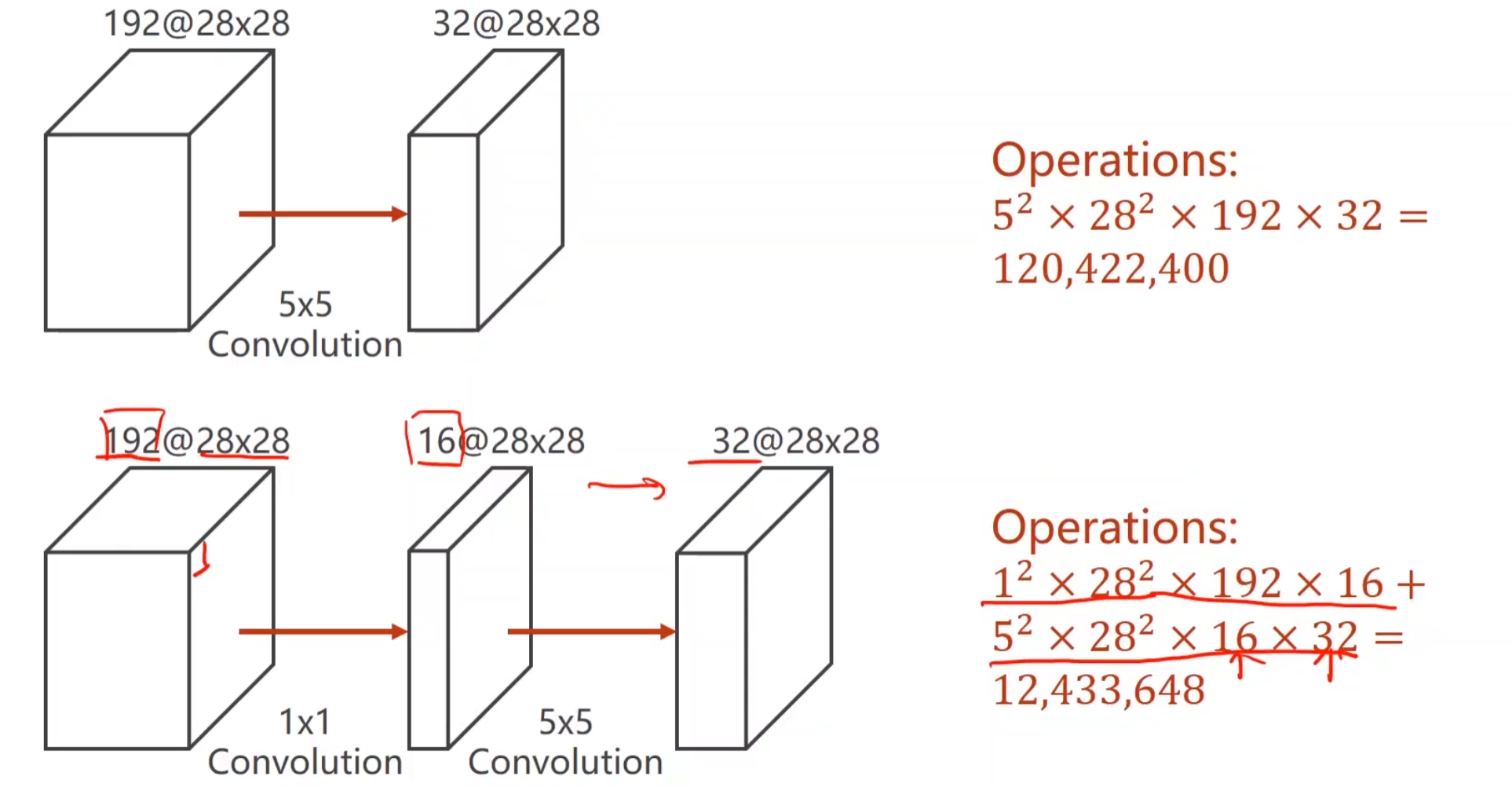
从输入经过卷积层到输出的网络，计算次数是如何算出来的呢? 首先5 * 5，是一次卷积运算后得到的计算次数，其次因为我们要保证输入输出的w h一致，所以做了padding，也就是在一层中，我们要做28 * 28次卷积运算，然后我们总共有192个通道，所以说要 * 192，这样，我们能得到 28 * 28的单通道输出，由于输出需要32层，所以我们要做32次同样的运算，可以用相同的卷积层（可能），也可以用不同的卷积层，总之结果而言，就是要重复32次相同的操作，输出32层对应层，这算是人为设定的超参数。
注意观察加入了1 * 1卷积层后的网络，以退为进 的思想，很显然它使得运算次数大大降低，只有十分之一的运算次数。
我们将每个分支的输出结果的cannel都叠加在一起，这个过程就称为Concatenate
注意我们要沿着第一个维度拼接起来，所以维度为1，（b，c，w，h）
代码实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 class InceptionA (nn.Module ): def __init__ (self, in_channels ): super (InceptionA, self).__init__() self.branch1x1 = nn.Conv2d(in_channels, 16 , kernel_size=1 ) self.branch5x5_1 = nn.Conv2d(in_channels,16 , kernel_size=1 ) self.branch5x5_2 = nn.Conv2d(16 , 24 , kernel_size=5 , padding=2 ) self.branch3x3_1 = nn.Conv2d(in_channels, 16 , kernel_size=1 ) self.branch3x3_2 = nn.Conv2d(16 , 24 , kernel_size=3 , padding=1 ) self.branch3x3_3 = nn.Conv2d(24 , 24 , kernel_size=3 , padding=1 ) self.branch_pool = nn.Conv2d(in_channels, 24 , kernel_size=1 ) def forward (self, x ): branch1x1 = self.branch1x1(x) branch5x5 = self.branch5x5_1(x) branch5x5 = self.branch5x5_2(branch5x5) branch3x3 = self.branch3x3_1(x) branch3x3 = self.branch3x3_2(branch3x3) branch3x3 = self.branch3x3_3(branch3x3) branch_pool = F.avg_pool2d(x, kernel_size=3 , stride=1 , padding=1 ) branch_pool = self.branch_pool(branch_pool) outputs = [branch1x1, branch5x5, branch3x3, branch_pool] return torch.cat(outputs, dim=1 ) class Net (nn.Module ): def __init__ (self ): super (Net, self).__init__() self.conv1 = nn.Conv2d(1 , 10 , kernel_size=5 ) self.conv2 = nn.Conv2d(88 , 20 , kernel_size=5 ) self.incep1 = InceptionA(in_channels=10 ) self.incep2 = InceptionA(in_channels=20 ) self.mp = nn.MaxPool2d(2 ) self.fc = nn.Linear(1408 , 10 ) def forward (self, x ): in_size = x.size(0 ) x = F.relu(self.mp(self.conv1(x))) x = self.incep1(x) x = F.relu(self.mp(self.conv2(x))) x = self.incep2(x) x = x.view(in_size, -1 ) x = self.fc(x) return x
ResNet
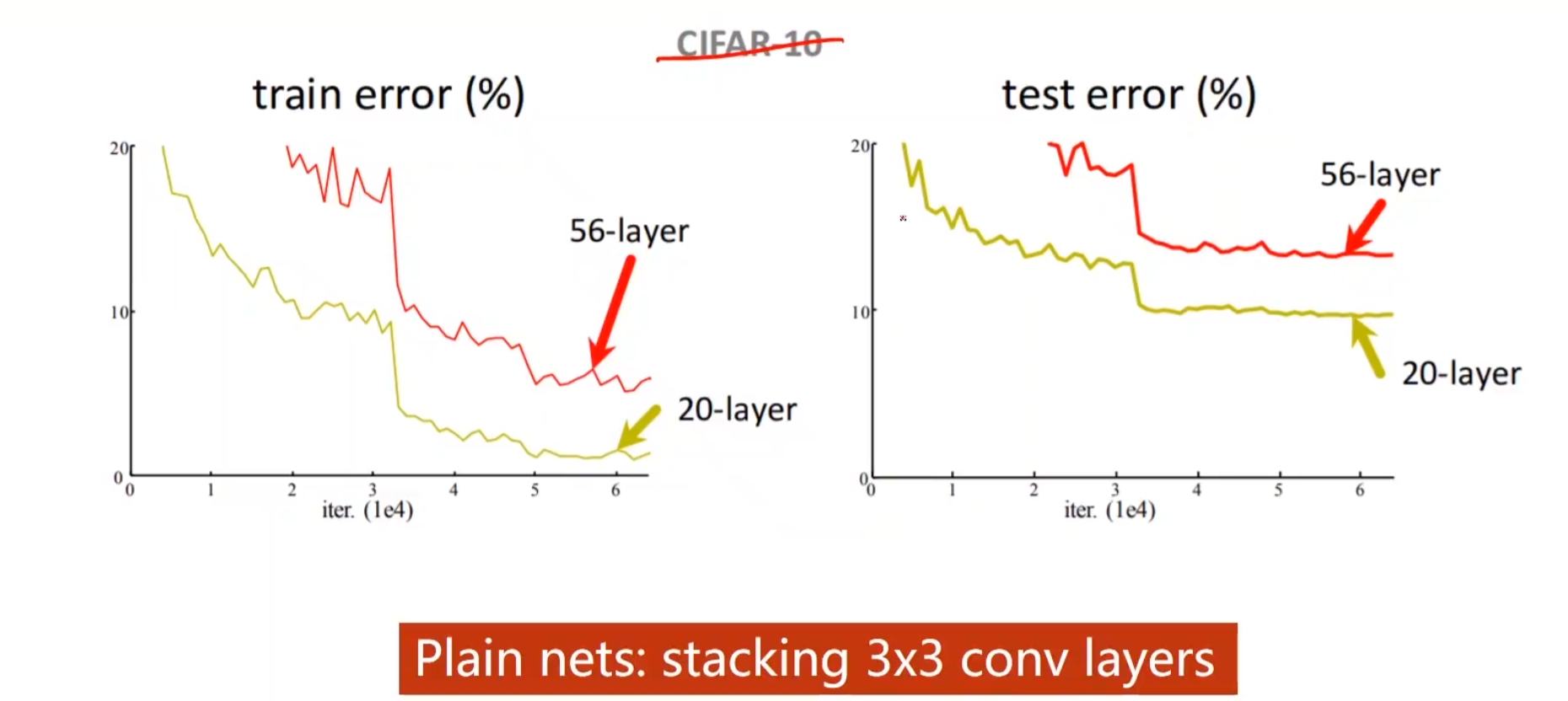
引言：如果把3 * 3的卷积一直堆叠下去，它的性能会不会变好呢？ 在CIFAR 10这数据集中，的确不会变好。
引起这个现象的一个可能，叫做梯度消失，因为我们做的是反向传播，所以需要用链式法则，把一连串的梯度乘起来，假如我们每一处的梯度都是小于1的，把一连串的梯度乘起来，这个值就会越来越小越来越小最终趋于0了，当它趋于0的时候
权重将会得不到什么更新，所以说在最开始，离输入比较近的那些块没办法得到充分的训练（反向传播，越乘回去越小）
所以以前为了解决梯度消失，提出了一些方法
用MNIST举例，这采用的是逐层训练，比如最后都是10个分类器，我们就每训练一层，就对它加一把锁，每次就训练一层，但是对于深度学习，这是非常困难的，因为层数太多了。
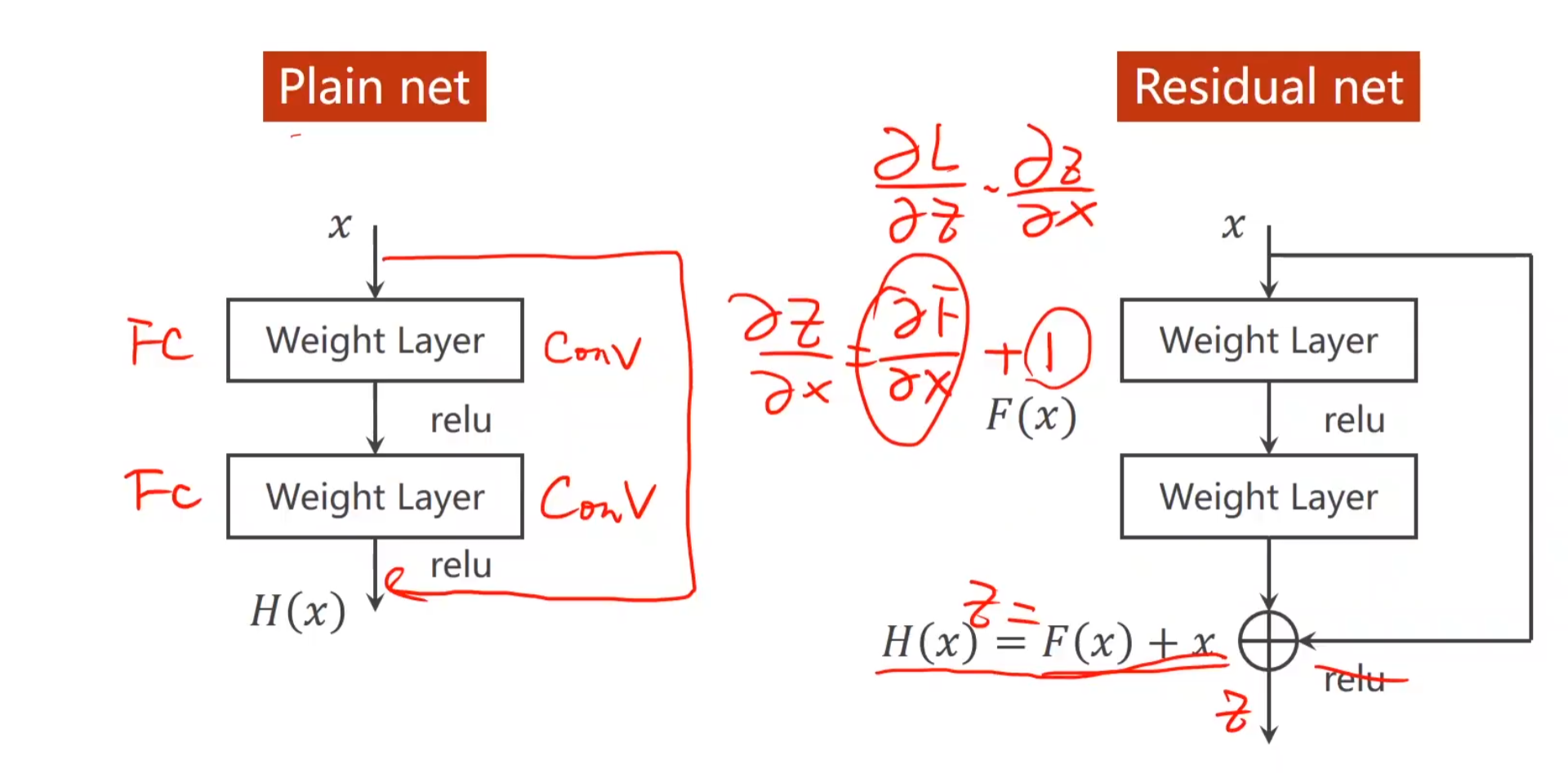
这就是Residual net，为什么说它能解决梯度消失的问题呢？
这里我们就用反向传播的一步来举例，假如说这一步的结果就是Z，反向传播后偏导为是σz / σx，因此每一步运算，都会在最初那个小于1的很小的值基础上加1，这样就保证了，即使数值真的很小，但他不会趋近于0，而是趋近于1，这样也能很好的训练到最开始的那些权重。
其中x直接连接到relu层那一步也有时被称为跳连接。对每一步的输入都做这样的操作，就能实现resNet
MNIST again 整体过程的描述：
代码实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class ResiualBlock (nn.Module ): def __init__ (self, channels ): super (ResiualBlock, self).__init__() self.channel = channels self.conv1 = nn.Conv2d(channels, channels, kernel_size=3 , padding=1 ) self.conv2 = nn.Conv2d(channels, channels, kernel_size=3 , padding=1 ) def forward (self, x ): y = F.relu(self.conv1(x)) y = self.conv2(y) return F.relu(x+y) class Net (nn.Module ): def __init__ (self ): super (Net, self).__init__() self.conv1 = nn.Conv2d(1 , 16 , kernel_size=5 ) self.pooling = nn.MaxPool2d(2 ) self.conv2 = nn.Conv2d(16 , 32 , kernel_size=5 ) self.linear = nn.Linear(512 , 10 ) self.RBlock1 = ResiualBlock(16 ) self.RBlock2 = ResiualBlock(32 ) def forward (self, x ): in_size = x.size(0 ) x = self.pooling(F.relu(self.conv1(x))) x = self.RBlock1(x) x = self.pooling(F.relu(self.conv2(x))) x = self.RBlock2(x) x = x.view(in_size, -1 ) return self.linear(x)
基本RNN 什么叫做RNN?
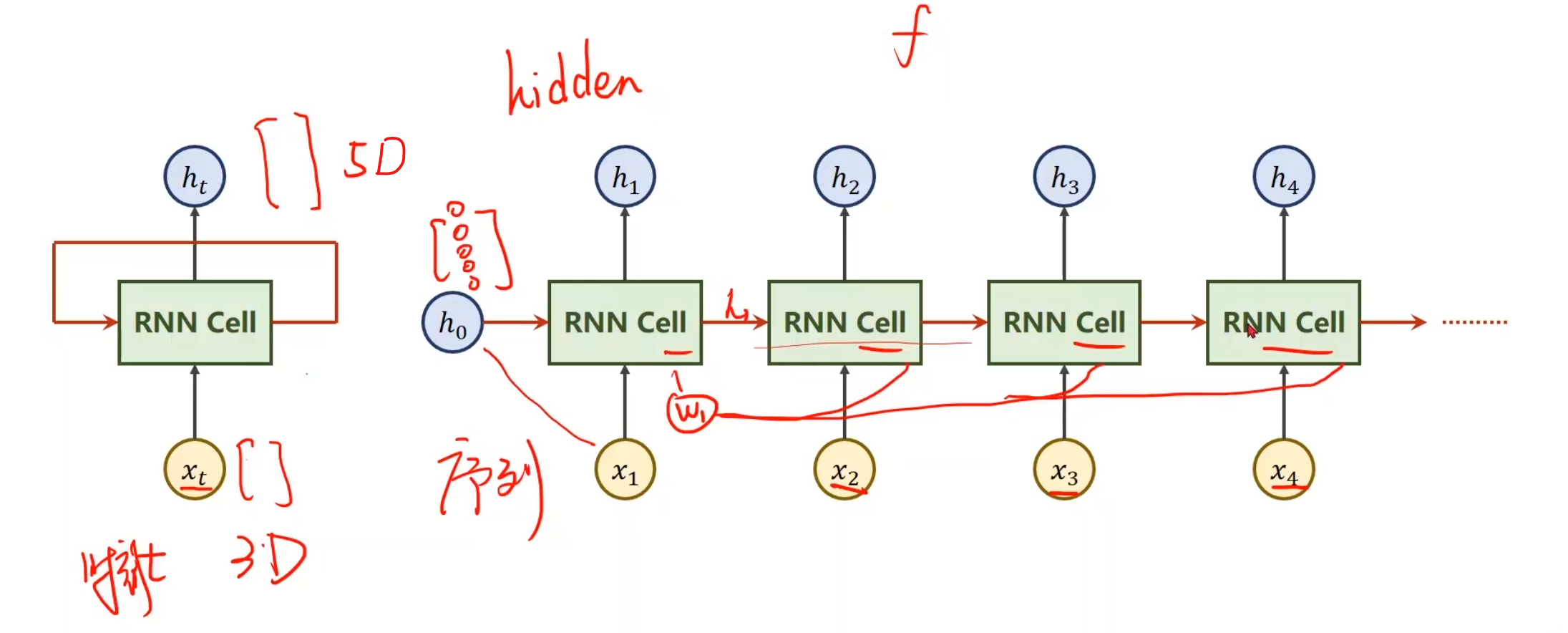
假设我们现在有一个序列，这里面x1，x2，x3，x4是我们的输入序列，比如说预测下一天天气，那么这个x就是这一天的某几个特征啥的，将x送到RNN里面，做一个线性变换（RNN其实就是线性变换），最后得到一个输出，叫做hidden，并且顺手可以把当前的h送到下一层的RNN中，对于第一项，如果h0没有值，那就设置成和之后的输出h同样维度的全0矩阵就行。对于每一个RNN线性层，我们可以设置为同样的权重，这样节省权重对内存的损耗使得同一个RNN层循环使用。
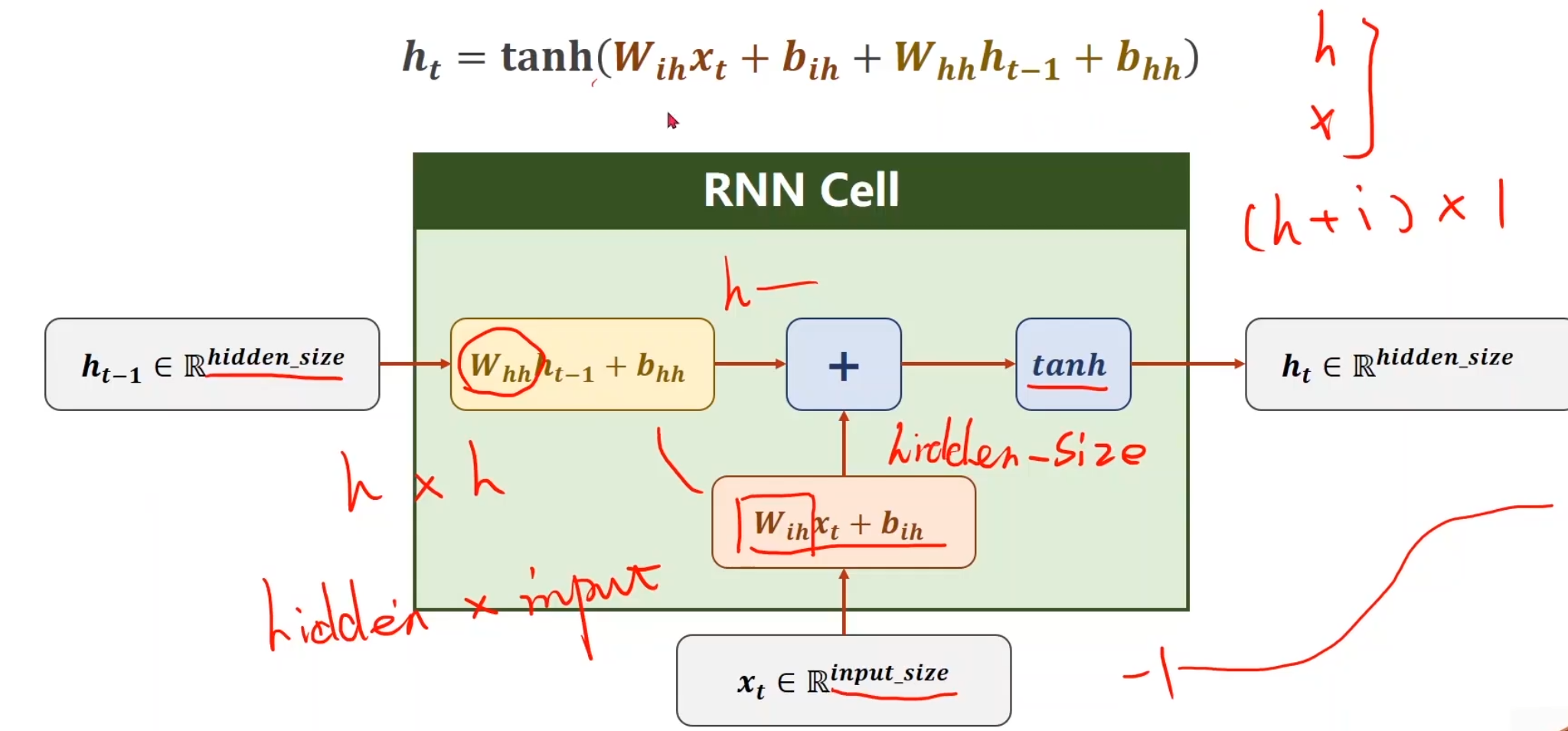
对于一层的RNN我们通常这样构建，（Wih其实写成Whi会更加容易理解）我们采用tanh作为激活函数是因为我们通常更加偏向于想让值保证在[-1, 1]之间。总之最后我们会通过一种构建矩阵的形式，使得它生成对应的h
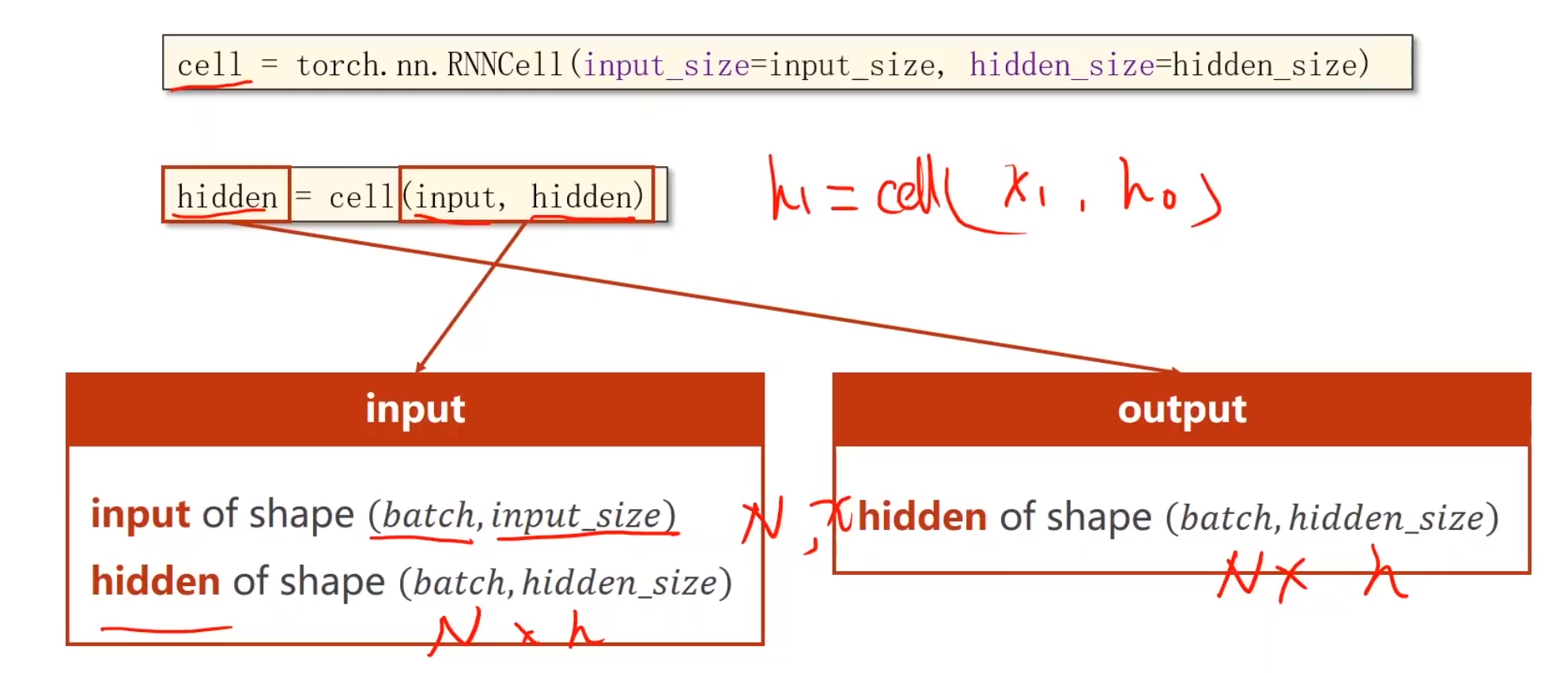
pytorch里有函数可以帮助你构建
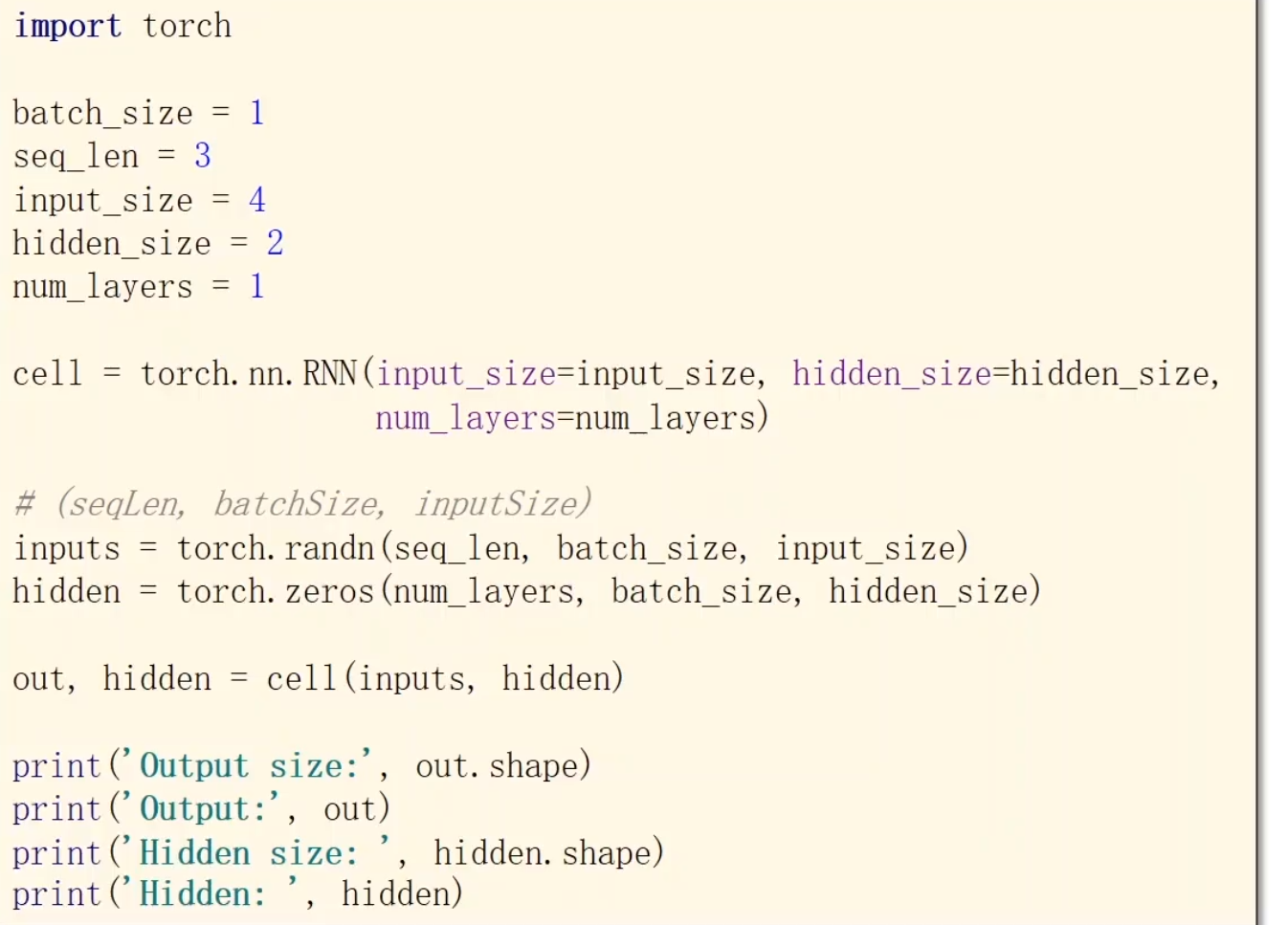
现在我们来举一个例
batchSize是一次取出多少个句子seqLen为句子的长度，也就是有三个词汇嘛，inputsize为每个词汇的特征个数，hiddensize为隐层的变换函数
要自己构建RNNCell层，就需要考虑这些，特别是维度
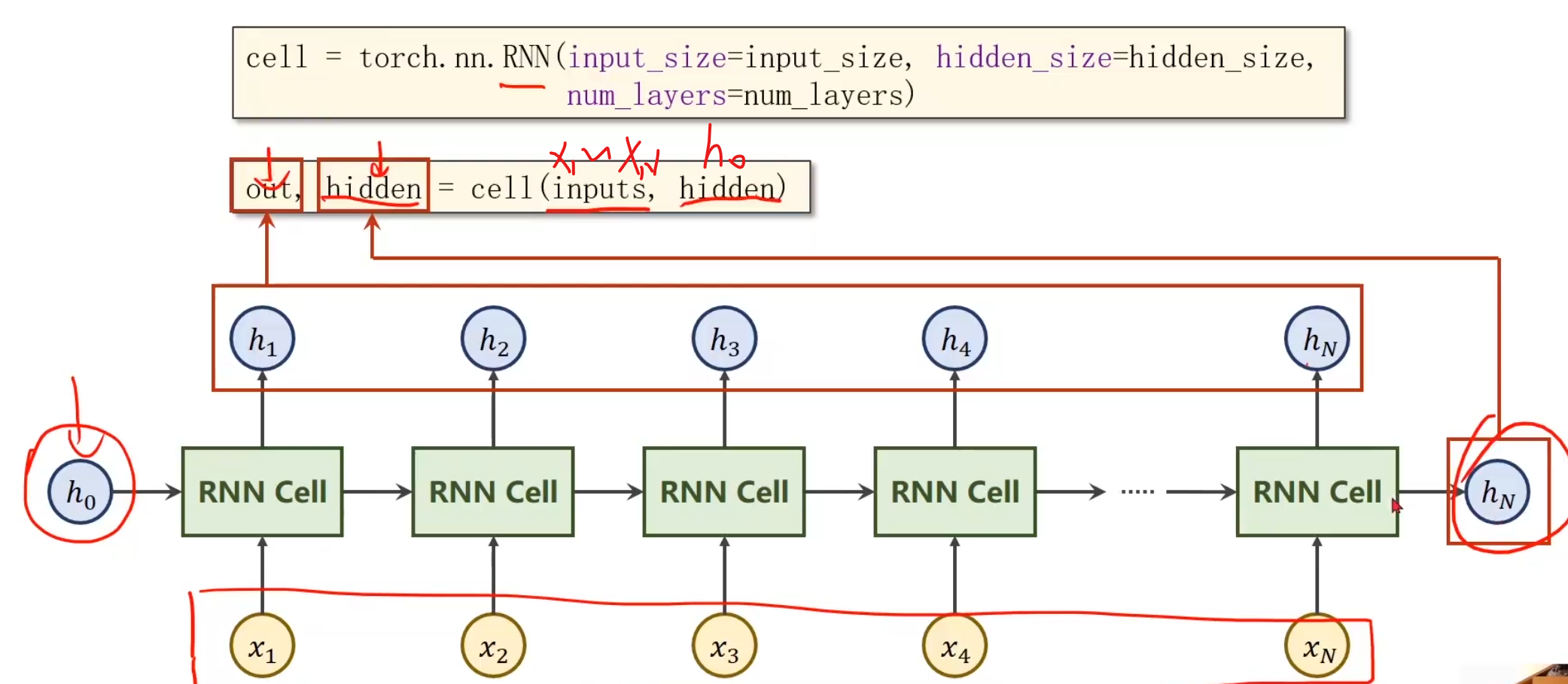
要构建RNN，先搞清楚每一个传入参数对应着什么。
需要使用RNN，仍然需要上述RNNCell的变量，同时还加了一个numLayers
那么什么是numLayers?
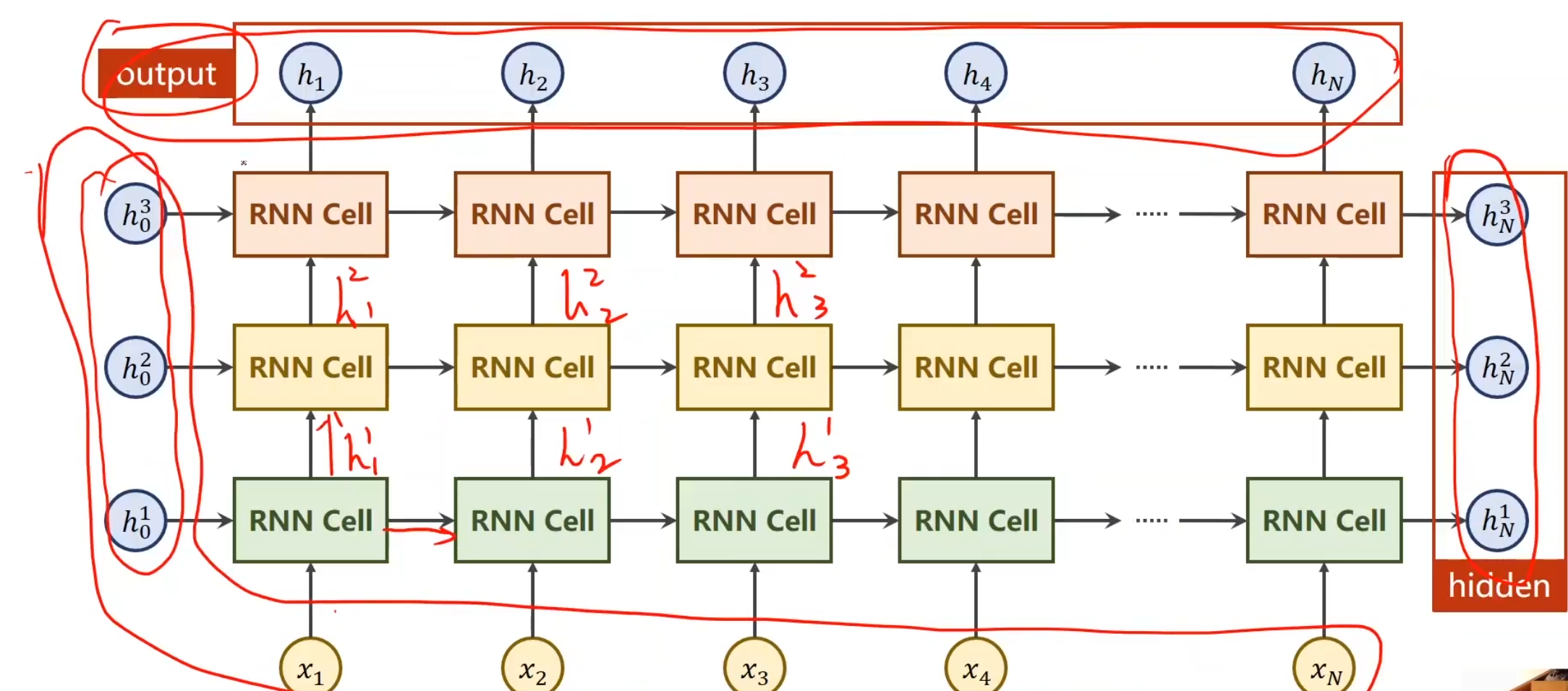
numLayers就是RNN的层数，例如这里有红，黄，绿三种线性变换层，就是有3层numLayers，本质上就是三种线性变换，然后不断循环就完事，只不过第一层的输出作为第二层的输入继续传，并且第一层的输出也作为第一层的后续迭代输入就绪传，看图就可知，左下为输入，右上为输出，整体式比较清晰的。
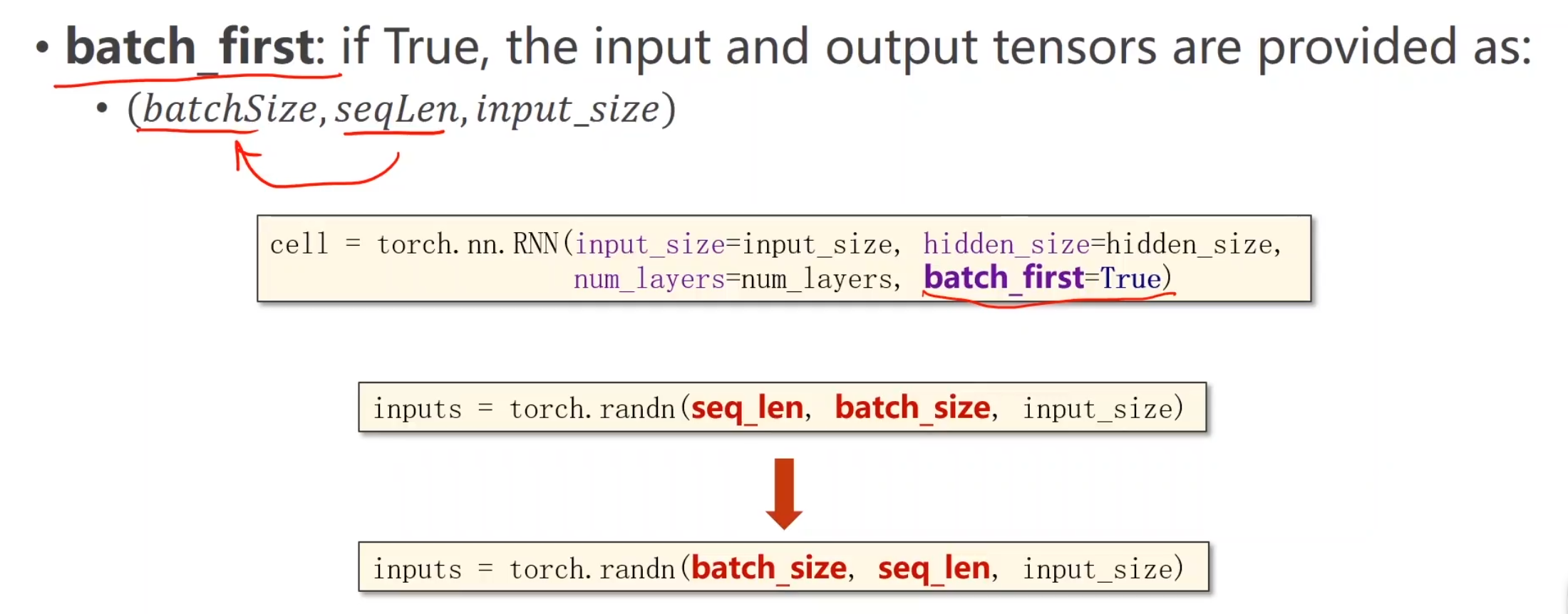
除此之外，RNN还有一些其他的参数，例如batch_first，它的作用就是交换输入数据集的两个维度，把batch_size放最前面方便与其他函数进行交互，例如将输出的out再接一层线性层，因为如果out维度batchsize在中间，线性变换肯定就是错的嘛
RNN小任务
首先我们会遇到一个问题，hello和ohlol并不是一个向量，我们往里面输入肯定会导致无法计算，所以我们要把字符向量化，用向量来表示它。
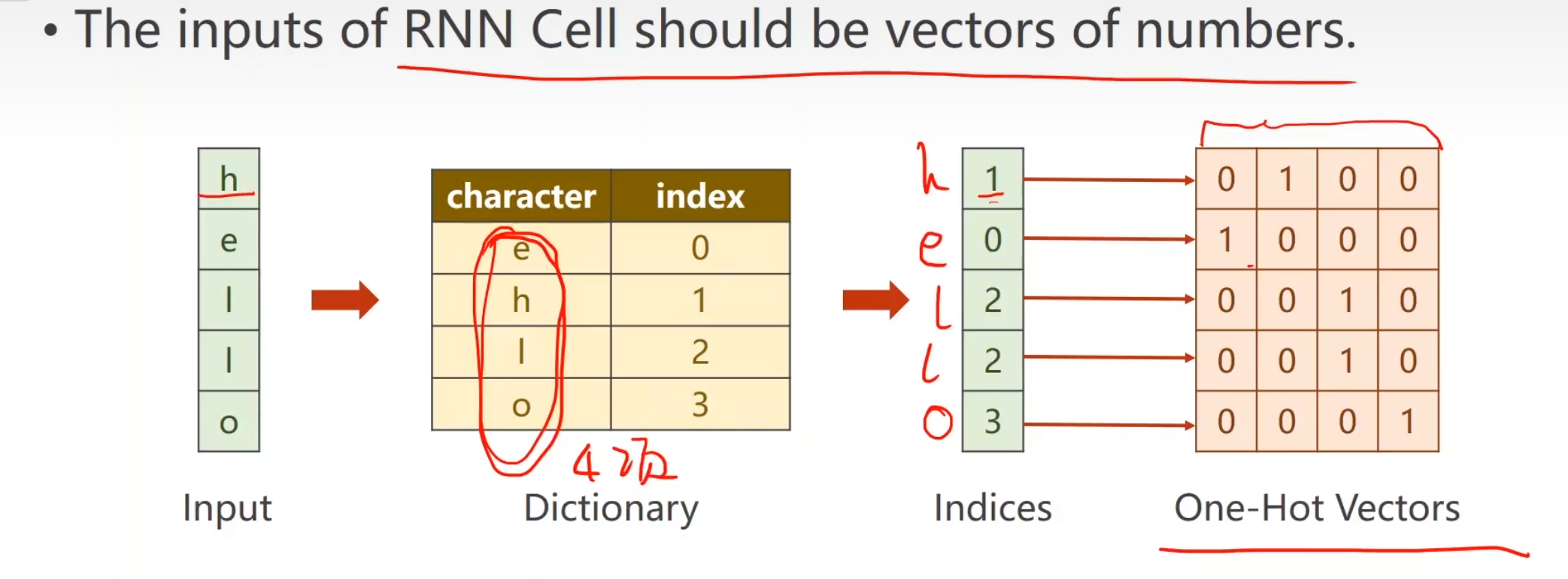
第一步 ，给每一个词，分配一个索引。
使用one-hot分配索引，可以消除索引之间隐形存在的大小关系，并且保证每个索引独一无二且方便矩阵运算。
一共有四个特殊的字符，所以input_size为4，seqlen为5
此时，所有输入就变成一个一个的独热向量了。所以这个问题转变为一个多分类问题
最后得出的结果，进行交叉熵损失即可得到loss
代码实现 RNNCell实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 import torchinput_size = 4 hidden_size = 4 batch_size = 1 idx2char = ['e' , 'h' , 'l' , 'o' ] x_data = [1 , 0 , 2 , 2 , 3 ] y_data = [3 , 1 , 2 , 3 , 2 ] one_hot_lookup = [[1 , 0 , 0 , 0 ], [0 , 1 , 0 , 0 ], [0 , 0 , 1 , 0 ], [0 , 0 , 0 , 1 ]] x_one_hot = [one_hot_lookup[x] for x in x_data] inputs = torch.Tensor(x_one_hot).view(-1 , batch_size, input_size) labels = torch.LongTensor(y_data).view(-1 , 1 ) inputs
tensor([[[0., 1., 0., 0.]],
[[1., 0., 0., 0.]],
[[0., 0., 1., 0.]],
[[0., 0., 1., 0.]],
[[0., 0., 0., 1.]]])
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Model (torch.nn.Module ): def __init__ (self, input_size, hidden_size, batch_size ): super (Model, self).__init__() self.batch_size = batch_size self.hidden_size = hidden_size self.input_size = input_size self.rnncell = torch.nn.RNNCell(input_size=self.input_size, hidden_size=self.hidden_size) def forward (self, input , hidden ): hidden = self.rnncell(input , hidden) return hidden def init_hidden (self ): return torch.zeros(self.batch_size, self.hidden_size) net = Model(input_size, hidden_size, batch_size)
1 2 criterion = torch.nn.CrossEntropyLoss() optimizer = torch.optim.Adam(net.parameters(), lr=0.1 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 for epoch in range (15 ): loss = 0 optimizer.zero_grad() hidden = net.init_hidden() print ('Predicted string: ' , end='' ) for input , label in zip (inputs, labels): hidden = net(input , hidden) loss += criterion(hidden, label) _, idx = hidden.max (dim=1 ) print (idx2char[idx.item()], end='' ) loss.backward() optimizer.step() print (', Epoch [%d/15] loss=%.4f' % (epoch + 1 , loss.item()))
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Predicted string: ooool, Epoch [1 /15 ] loss=6.5547 Predicted string: ooool, Epoch [2 /15 ] loss=5.5869 Predicted string: olool, Epoch [3 /15 ] loss=4.9142 Predicted string: ollll, Epoch [4 /15 ] loss=4.4360 Predicted string: oholl, Epoch [5 /15 ] loss=4.0270 Predicted string: ohool, Epoch [6 /15 ] loss=3.7041 Predicted string: ohlol, Epoch [7 /15 ] loss=3.4379 Predicted string: ohlol, Epoch [8 /15 ] loss=3.1885 Predicted string: ohlol, Epoch [9 /15 ] loss=2.9624 Predicted string: ohlol, Epoch [10 /15 ] loss=2.7789 Predicted string: ohlol, Epoch [11 /15 ] loss=2.6578 Predicted string: ohlol, Epoch [12 /15 ] loss=2.5847 Predicted string: ohlol, Epoch [13 /15 ] loss=2.5270 Predicted string: ohlol, Epoch [14 /15 ] loss=2.4630 Predicted string: ohlol, Epoch [15 /15 ] loss=2.3770
改进模型 RNN实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 import torchinput_size = 4 hidden_size = 4 num_layers = 1 batch_size = 1 seq_len = 5 class Model (torch.nn.Module ): def __init__ (self, input_size, hidden_size, batch_size, num_layers=1 ): super (Model, self).__init__() self.num_layers = num_layers self.batch_size = batch_size self.input_size = input_size self.hidden_size = hidden_size self.rnn = torch.nn.RNN(input_size=self.input_size, hidden_size=self.hidden_size, num_layers=self.num_layers ) def forward (self, input ): hidden = torch.zeros(self.num_layers, self.batch_size, self.hidden_size) out, _= self.rnn(input , hidden) return out.view(-1 , self.hidden_size) net = Model(input_size, hidden_size, batch_size, num_layers)
1 2 criterion = torch.nn.CrossEntropyLoss() optimizer = torch.optim.Adam(net.parameters(), lr=0.05 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 labels = torch.LongTensor(y_data) for epoch in range (15 ): optimizer.zero_grad() outs = net(inputs) loss = criterion(outs, labels) _, idx = outs.max (dim=1 ) loss.backward() optimizer.step() idx = idx.data.numpy() print ('predicted:' , '' .join([idx2char[x] for x in idx]), end='' ) print (', Epoch [%d/15] loss=%.3f' % (epoch + 1 , loss.item()))
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 predicted: ohohh, Epoch [1 /15 ] loss=1.366 predicted: ohooh, Epoch [2 /15 ] loss=1.208 predicted: ohooh, Epoch [3 /15 ] loss=1.081 predicted: ohool, Epoch [4 /15 ] loss=0.990 predicted: ohool, Epoch [5 /15 ] loss=0.924 predicted: ohlol, Epoch [6 /15 ] loss=0.872 predicted: ohlol, Epoch [7 /15 ] loss=0.829 predicted: ohlol, Epoch [8 /15 ] loss=0.788 predicted: ohlol, Epoch [9 /15 ] loss=0.750 predicted: ohlol, Epoch [10 /15 ] loss=0.714 predicted: ohlol, Epoch [11 /15 ] loss=0.680 predicted: ohlol, Epoch [12 /15 ] loss=0.649 predicted: ohlol, Epoch [13 /15 ] loss=0.621 predicted: ohlol, Epoch [14 /15 ] loss=0.596 predicted: ohlol, Epoch [15 /15 ] loss=0.572
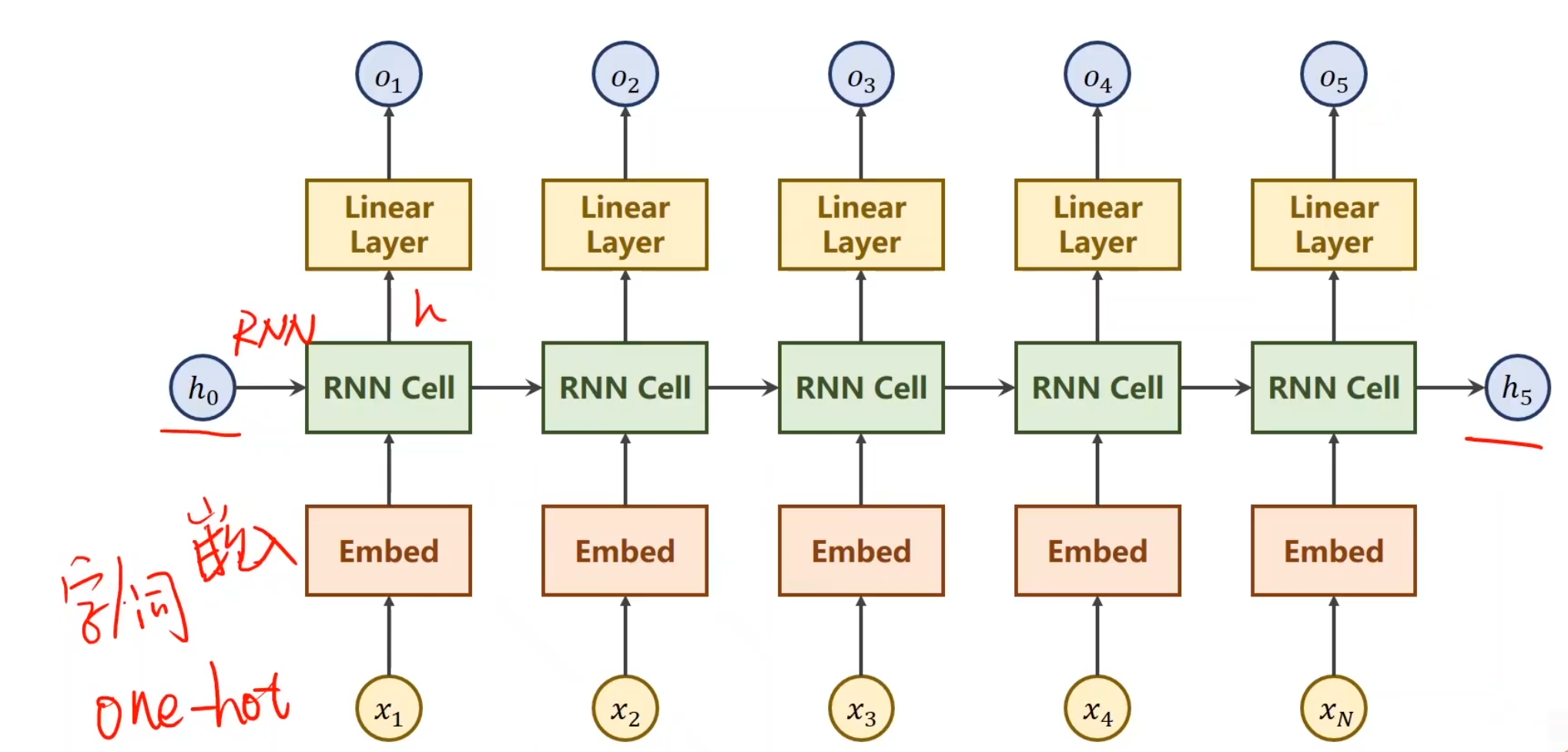
Embedding
Using embedding and linear layer
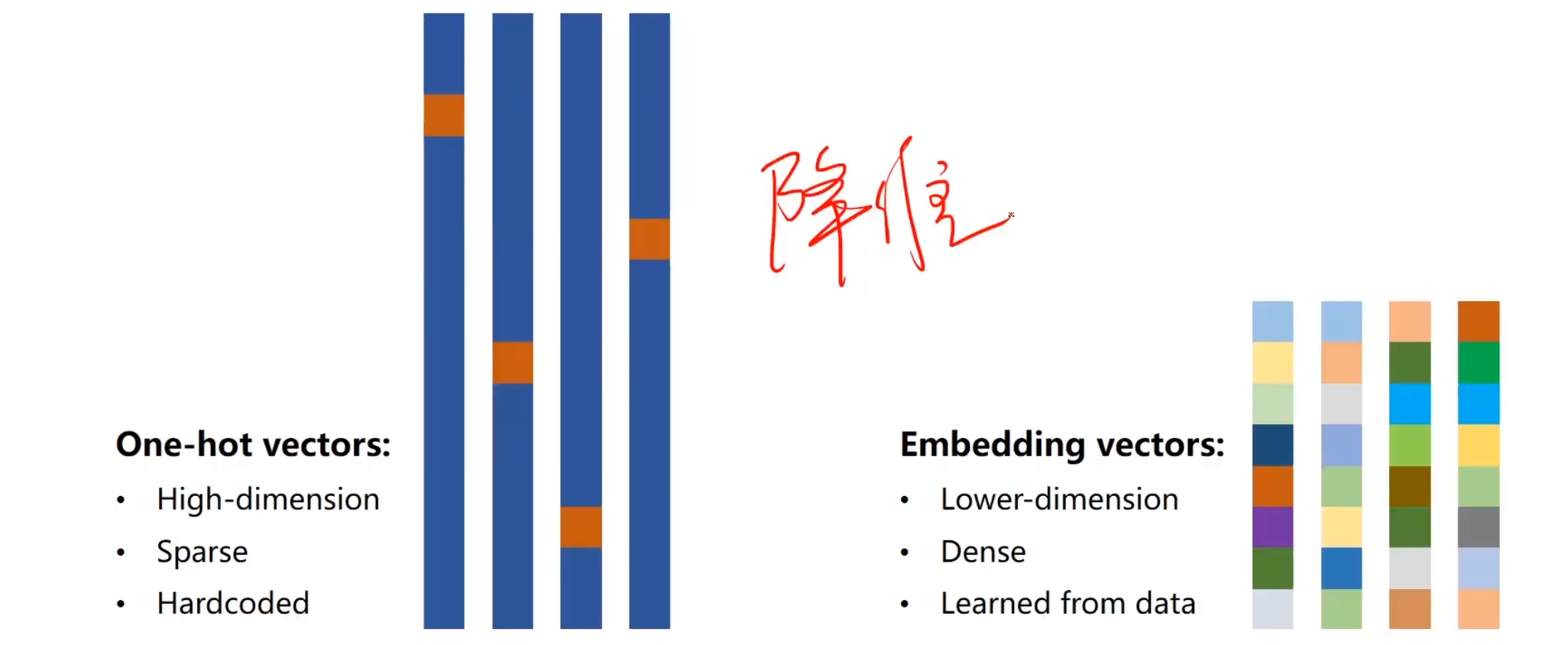
独热向量虽然能解决问题，也是有缺点的
因此我们想要构建一个低维，稠密，可学习的变换
这就引出了大名鼎鼎的Embedding
注意：这里数据准备这样写会报错，要改为input=torch.LongTensor(x_data).view(batch_size,seq_len)
最后实现 代替独热再次实现小任务
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 import torchnum_class = 4 input_size = 4 hidden_size = 8 embedding_size = 10 num_layers = 2 batch_size = 1 seq_len = 5 class Model (torch.nn.Module ): def __init__ (self ): super (Model, self).__init__() self.emb = torch.nn.Embedding(input_size, embedding_size) self.rnn = torch.nn.RNN(input_size=embedding_size, hidden_size=hidden_size, num_layers=num_layers, batch_first=True ) self.fc = torch.nn.Linear(hidden_size, num_class) def forward (self, x ): hidden = torch.zeros(num_layers, x.size(0 ), hidden_size) x = self.emb(x) x, _ = self.rnn(x, hidden) x = self.fc(x) return x.view(-1 , num_class)
1 2 3 4 5 6 7 8 9 10 11 idx2char = ['e' , 'h' , 'l' , 'o' ] x_data = [[1 , 0 , 2 , 2 , 3 ]] y_data = [3 , 1 , 2 , 3 , 2 ] inputs = torch.LongTensor(x_data) labels = torch.LongTensor(y_data) net = Model() criterion = torch.nn.CrossEntropyLoss() optimizer = torch.optim.Adam(net.parameters(), lr=0.05 )
1 2 3 4 5 6 7 8 9 10 11 for epoch in range (15 ): optimizer.zero_grad() outputs = net(inputs) loss = criterion(outputs, labels) loss.backward() optimizer.step() _, idx = outputs.max (dim=1 ) idx = idx.data.numpy() print ('predicted:' , '' .join([idx2char[x] for x in idx]), end='' ) print (', Epoch [%d/15] loss = %.3f' % (epoch, loss.item()))
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 predicted: eeell, Epoch [0 /15 ] loss = 1.400 predicted: ollll, Epoch [1 /15 ] loss = 1.104 predicted: ohlll, Epoch [2 /15 ] loss = 0.891 predicted: ohlll, Epoch [3 /15 ] loss = 0.682 predicted: ohlol, Epoch [4 /15 ] loss = 0.503 predicted: ohlol, Epoch [5 /15 ] loss = 0.362 predicted: ohlol, Epoch [6 /15 ] loss = 0.250 predicted: ohlol, Epoch [7 /15 ] loss = 0.168 predicted: ohlol, Epoch [8 /15 ] loss = 0.117 predicted: ohlol, Epoch [9 /15 ] loss = 0.083 predicted: ohlol, Epoch [10 /15 ] loss = 0.060 predicted: ohlol, Epoch [11 /15 ] loss = 0.044 predicted: ohlol, Epoch [12 /15 ] loss = 0.033 predicted: ohlol, Epoch [13 /15 ] loss = 0.025 predicted: ohlol, Epoch [14 /15 ] loss = 0.019
可以看到，达到了前所未有的效果！
高级RNN 例子 我们从一个简单的任务，引入语言模型
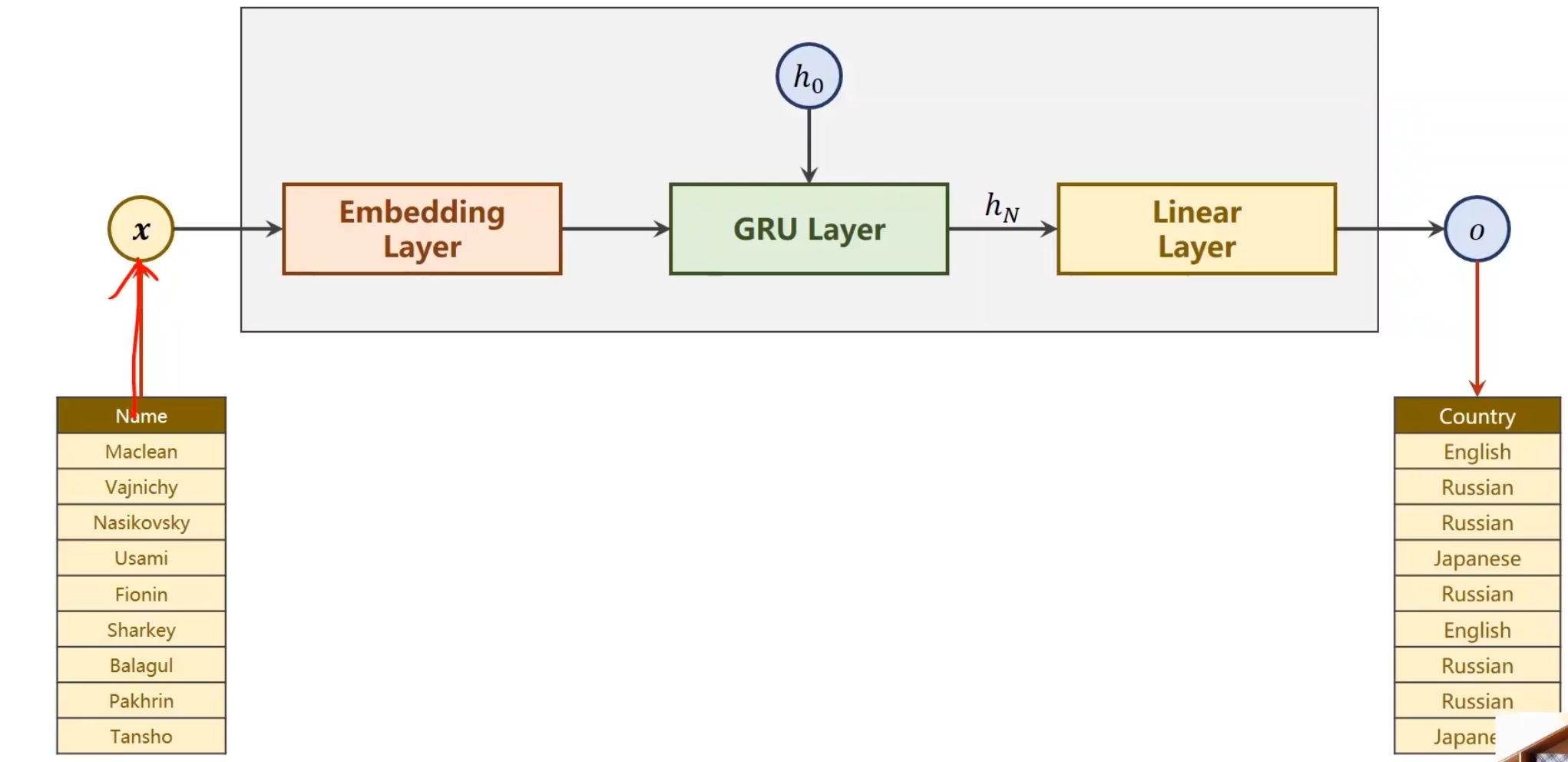
这个任务提供18种类别的国家，然后通过名字，判断这个人是来自于哪个国家的，
也就是说，它的输出只有一个
上一讲里，我们的RNNCell，就是需要o1，o2，o3，o4，o5等多个输出。但是现在我们只需要一个，因此，其实模型不需要这么麻烦。
我们只需将最后一个输出取出，并将它做线性变换，使之映射到18个种类即可。
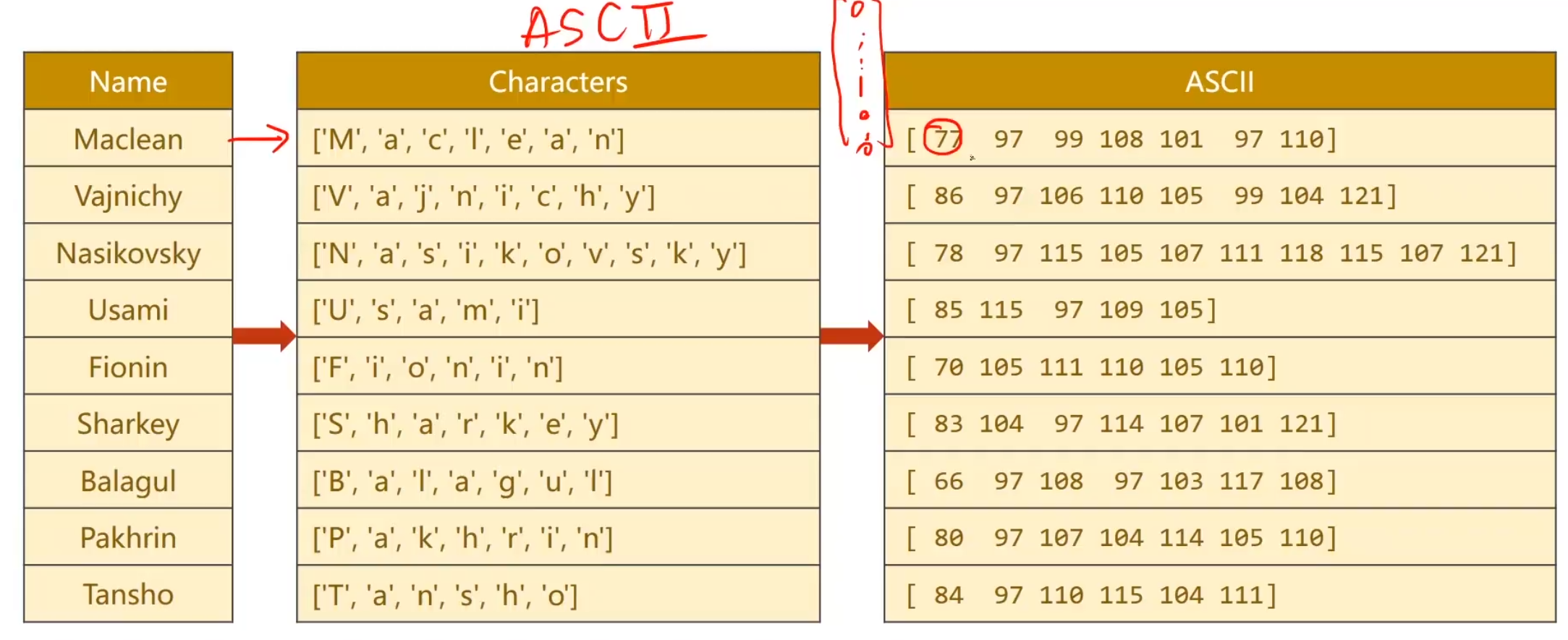
不过请注意，例如Name，随便找一个，比如Maclean，他是一个句子，seqlen是为7，’M’,’a’,’c’,’l’,’e’,’a’,’n’分别是x1，x2，x3，x4…的词汇哈，其实我们词汇就52个字母吧差不多（大小写）。
准备数据 首先我们需要把每一个名字构成一个序列，把数据拆分成一个又一个的词汇，为了要构建词典，我们选用ASCII表来进行每一个字母，但值得注意的是，这里的ASCII表的数字，其实就代表了独热编码的，第几行几列，它的值为1，剩下的就交给Embedding层就好了。
另外一个问题，这些序列是长短不一的，因此我们做一个padding，因为将来我们把它构成一个批量（当然，我们就训练单个就不必，这是为了保证训练集的整齐），进行运算，seqlen和batchsize，input得一样。因为张量需要保证所有的维度数据得填满，是一个完整的矩阵
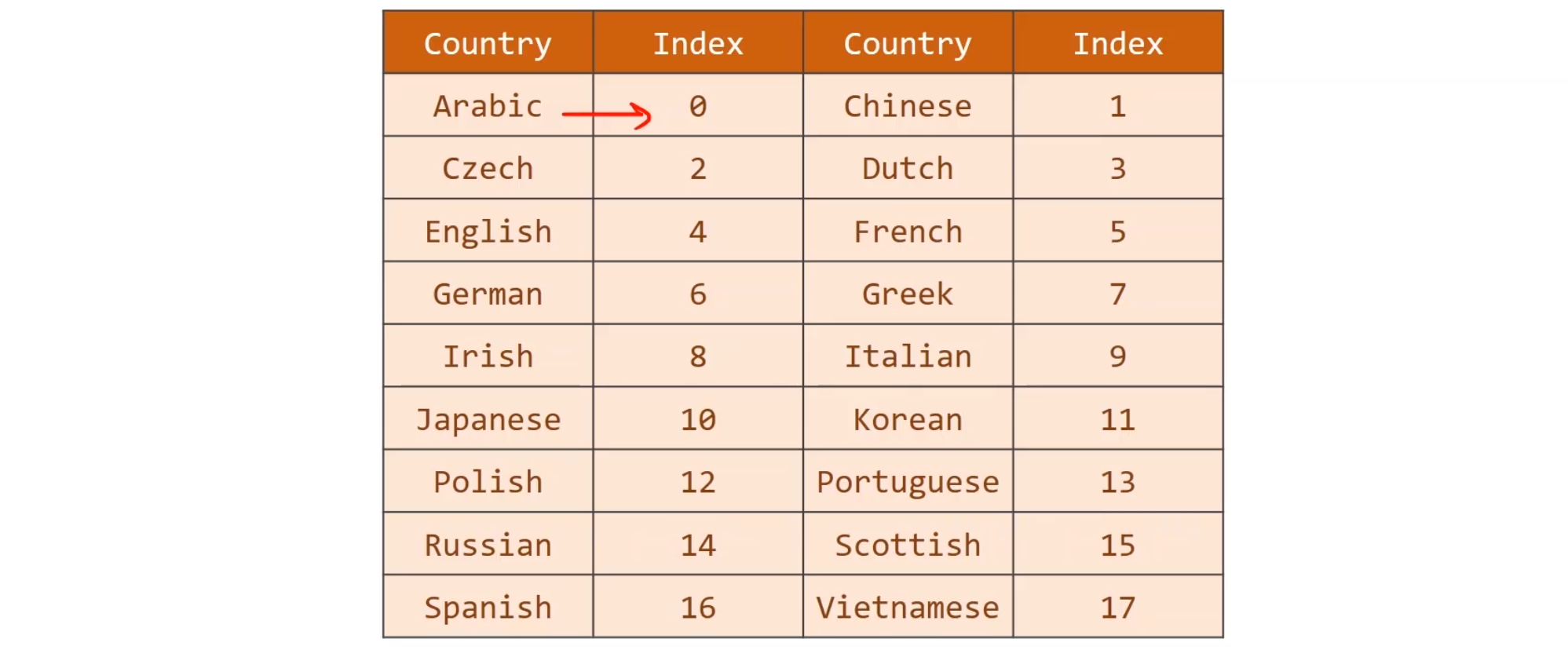
对于国家数据集，我们将每个数据集填上一个索引，就保证能进行查找了。
双向循环网络
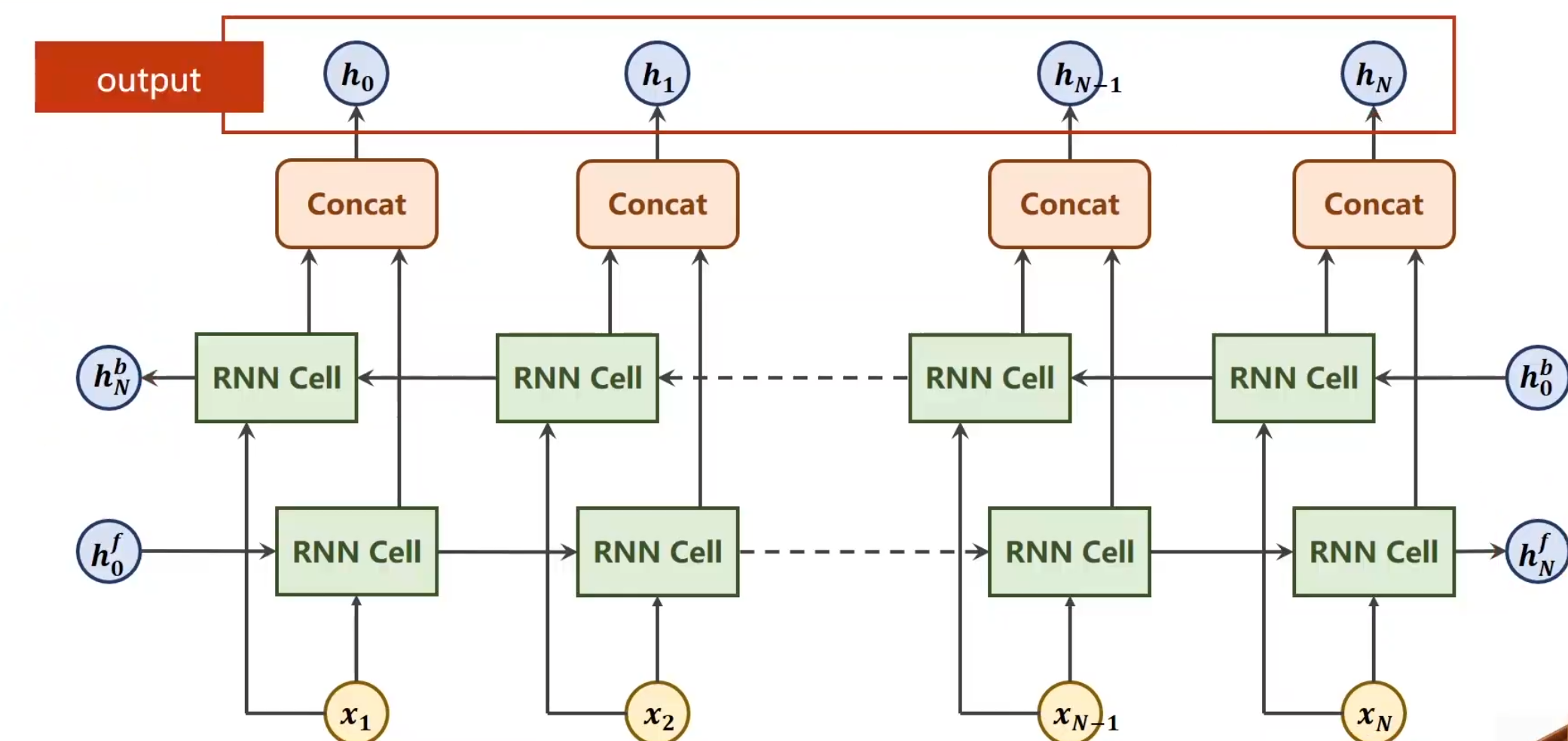
双向首先，一定要和神经网络的forward，backward区分开，二者并不相同，他真的就是单纯的反向再走一次，第一个是从x1+h^f^0经过RNN Cell的线性变换后得到权重，在与X2进行结合，最终不断传播到Xn，得到最后的隐藏层h^f^N,而另外一个就是从Xn+h^b^0开始同样进行相同的RNN Cell线性变换得到权重，逐渐运算，最终得到h^b^n然后将同一个词汇Xn的两向计算结果concat，得到最终应该输出的隐藏层
hidden只有这两个。所以GRU最终输出的隐层会有两个
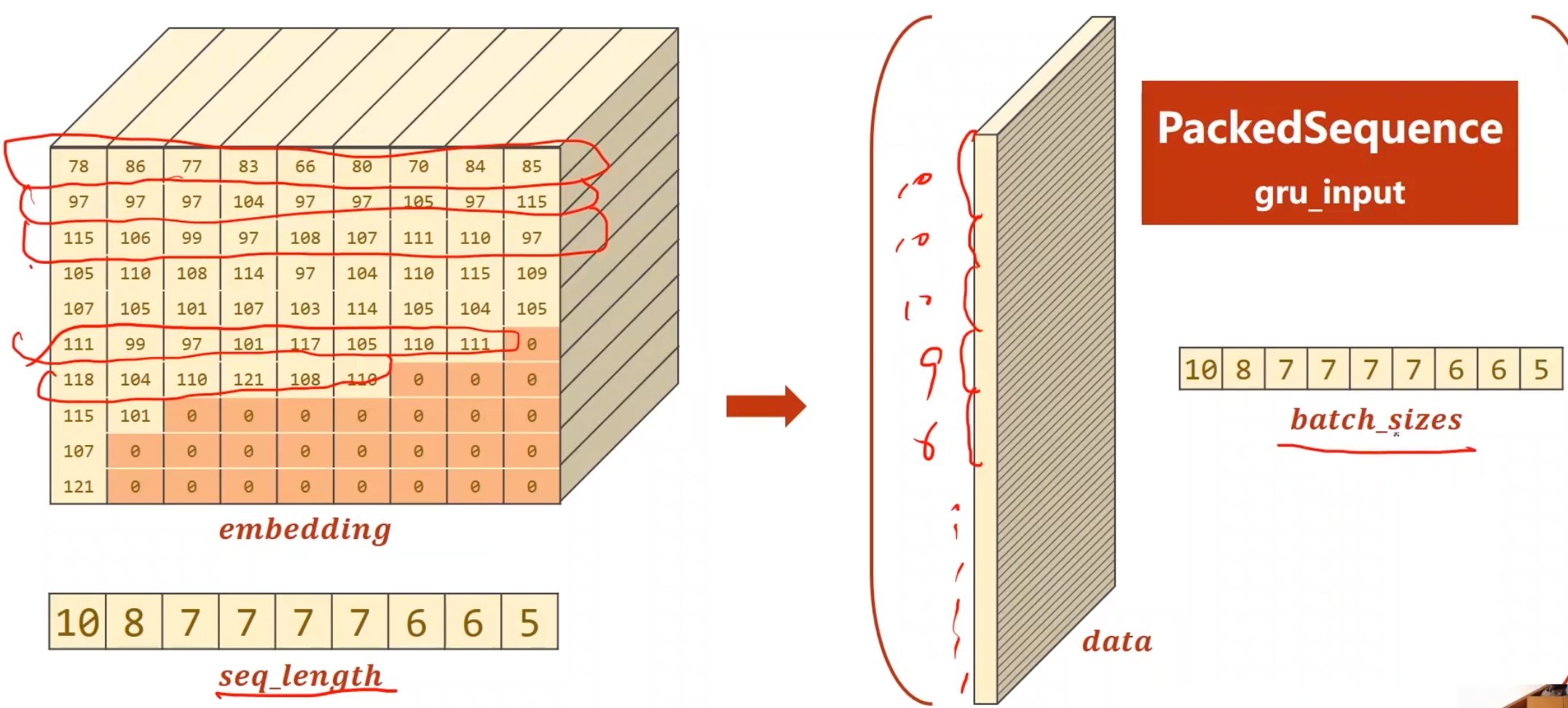
对于GRU，有一个提升效率的工具，叫做pack_padded_sequence,他能将数据进行打包，就是使得padding填充的无用数据不进行计算，每次只使用实际有效的数据，但他有个怪癖，他必须只能要降序的数据，也就是说我们在打包之前，应该对Embedding后的数据集进行降序排序，并且把每一个seqlen做成一个列表传给他，具体打包过程见下图。
注意，每一纵行的数据也是从大到小排序的, 别被误导了
代码实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 import torchfrom torch.utils.data import DataLoaderfrom torch.utils.data import Datasetimport matplotlib.pyplot as pltimport numpy as npimport gzipimport csvclass NameDataset (Dataset ): def __init__ (self, is_train_set=True ): super (NameDataset, self).__init__() filename = 'names_train.csv.gz' if is_train_set else 'names_test.csv.gz' with gzip.open (filename, 'rt' ) as f: reader = csv.reader(f) rows = list (reader) self.names = [row[0 ] for row in rows] self.len = len (self.names) self.countries = [row[1 ] for row in rows] self.country_list = list (sorted (set (self.countries))) self.country_dict = self.getCountryDict() self.country_num = len (self.country_list) def __getitem__ (self, index ): return self.names[index], self.country_dict[self.countries[index]] def __len__ (self ): return self.len def getCountryDict (self ): country_dict = dict () for idx, country_name in enumerate (self.country_list, 0 ): country_dict[country_name] = idx return country_dict def idx2country (self, index ): return self.country_list[index] def getCountriesNum (self ): return self.country_num
1 2 3 4 5 6 7 8 9 10 11 12 13 14 HIDDEN_SIZE = 100 BATCH_SIZE = 256 N_LAYER = 2 N_EPOCHS = 100 N_CHARS = 128 USE_GPU = False trainset = NameDataset(is_train_set=True ) trainloader = DataLoader(trainset, batch_size=BATCH_SIZE, shuffle=True ) testset = NameDataset(is_train_set=False ) testloader = DataLoader(testset, batch_size=BATCH_SIZE, shuffle=False ) N_COUNTRY = trainset.getCountriesNum()
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 def name2list (name ): arr = [ord (c) for c in name] return arr, len (arr) def make_tensors (names, countries ): sequences_and_lengths = [name2list(name) for name in names] name_sequences = [s1[0 ] for s1 in sequences_and_lengths] seq_lengths = torch.LongTensor([s1[1 ] for s1 in sequences_and_lengths]) countries = countries.long() seq_tensor = torch.zeros(len (name_sequences), seq_lengths.max ()).long() for idx, (seq, seq_len) in enumerate (zip (name_sequences, seq_lengths), 0 ): seq_tensor[idx, :seq_len] = torch.LongTensor(seq) seq_lengths, perm_idx = seq_lengths.sort(dim=0 , descending=True ) seq_tensor = seq_tensor[perm_idx] countries = countries[perm_idx] return create_tensor(seq_tensor), \ create_tensor(seq_lengths), \ create_tensor(countries)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 from torch.nn.utils.rnn import pack_padded_sequencedef create_tensor (tensor ): if USE_GPU: device = torch.device("cuda:0" ) tensor = tensor.to(device) return tensor class RNNClassifier (torch.nn.Module ): def __init__ (self, input_size, hidden_size, output_size, n_layers=1 , bidirectional=True ): super (RNNClassifier, self).__init__() self.hidden_size = hidden_size self.n_layers = n_layers self.n_directions = 2 if bidirectional else 1 self.embedding = torch.nn.Embedding(input_size, hidden_size) self.gru = torch.nn.GRU(hidden_size, hidden_size, n_layers, bidirectional=bidirectional) self.fc = torch.nn.Linear(hidden_size*self.n_directions, output_size) def _init_hidden (self, batch_size ): hidden = torch.zeros(self.n_layers*self.n_directions, batch_size, self.hidden_size) return create_tensor(hidden) def forward (self, input , seq_lengths ): print (input ) input = input .t() batch_size = input .size(1 ) hidden = self._init_hidden(batch_size) embedding = self.embedding(input ) gru_input = pack_padded_sequence(embedding, seq_lengths) output, hidden = self.gru(gru_input, hidden) if self.n_directions == 2 : hidden_cat = torch.cat([hidden[-1 ], hidden[-2 ]], dim=1 ) else : hidden_cat = hidden[-1 ] fc_output = self.fc(hidden_cat) return fc_output
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 def trainModel (): total_loss = 0 for i, (names, countries) in enumerate (trainloader, 1 ): inputs, seq_lengths, target = make_tensors(names, countries) output = classifier(inputs, seq_lengths) loss = criterion(output, target) optimizer.zero_grad() loss.backward() optimizer.step() total_loss += loss.item() if i % 10 == 0 : print (f'[{time_since(start)} ] Epoch {epoch} ' , end='' ) print (f'[{i * len (inputs)} /{len (trainset)} ] ' , end='' ) print (f'loss={total_loss / (i * len (inputs))} ' ) return total_loss
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 def testModel (): correct = 0 total = len (testset) print ('evaluting trained model ...' ) with torch.no_grad(): for i, (names, countries) in enumerate (testloader, 1 ): inputs, seq_lengths, target = make_tensors(names, countries) output = classifier(inputs, seq_lengths) pred = output.max (dim=1 , keepdim=True )[1 ] correct += pred.eq(target.view_as(pred)).sum ().item() percent = '%.2f' % (100 * correct / total) print (f'Test set: Accuracy {correct} /{total} {percent} %' ) return correct / total
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 import timeimport mathdef time_since (since ): s = time.time() - since m = math.floor(s / 60 ) s -= m * 60 return '%dm %ds' % (m, s) if __name__ == '__main__' : classifier = RNNClassifier(N_CHARS, HIDDEN_SIZE, N_COUNTRY, N_LAYER) if USE_GPU: device = torch.device("cuda:0" ) classifier.to(device) criterion = torch.nn.CrossEntropyLoss() optimizer = torch.optim.Adam(classifier.parameters(), lr=0.001 ) start = time.time() print ("Training for %d epochs..." % N_EPOCHS) acc_list = [] for epoch in range (1 , N_EPOCHS + 1 ): trainModel() acc = testModel() acc_list.append(acc) import matplotlib.pyplot as plt import numpy as np epoch = np.arange(1 , len (acc_list) + 1 , 1 ) acc_list = np.array(acc_list) plt.plot(epoch, acc_list) plt.xlabel('Epoch' ) plt.ylabel('Accuracy' ) plt.grid() plt.show()
Training for 100 epochs...
AttributeError: 'NoneType' object has no attribute 't' # 最后这里报了个错，百思不得其解，但前面的意思已经差不多理解了。
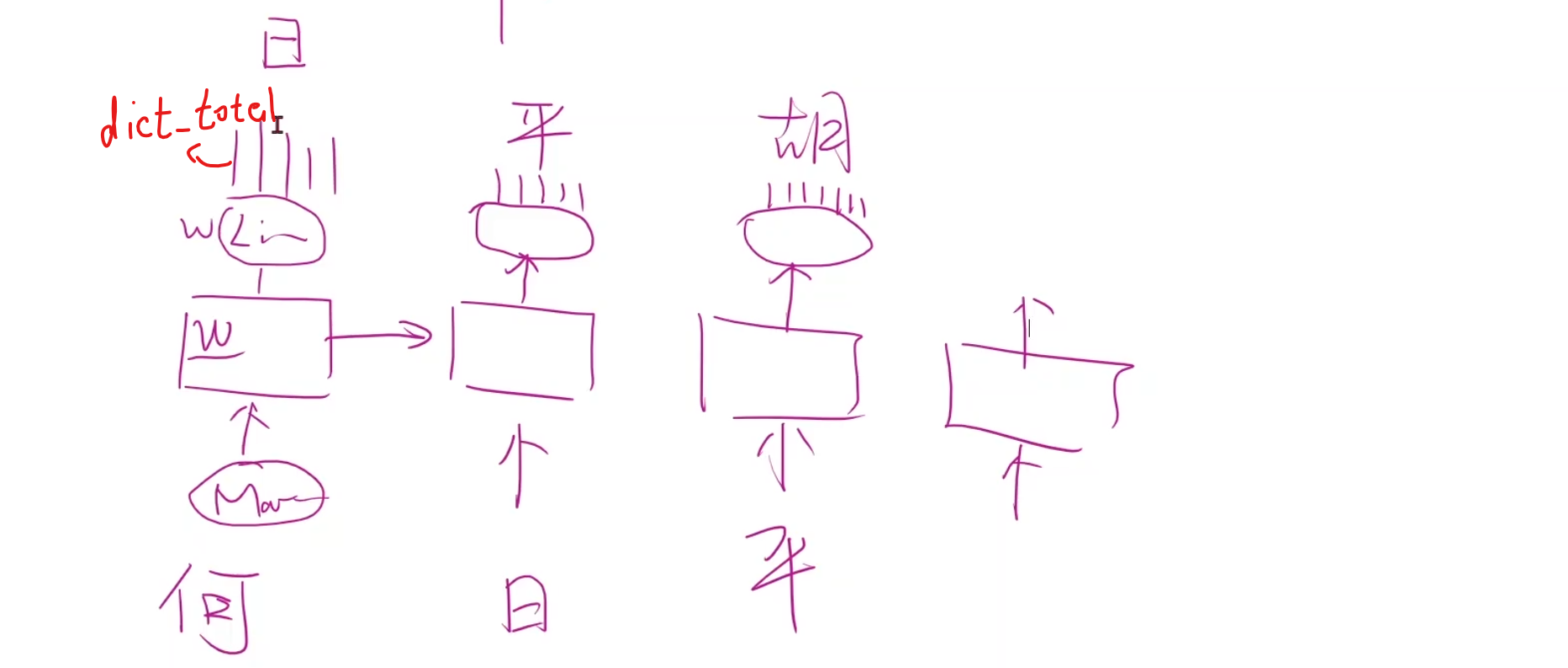
做古诗（了解）
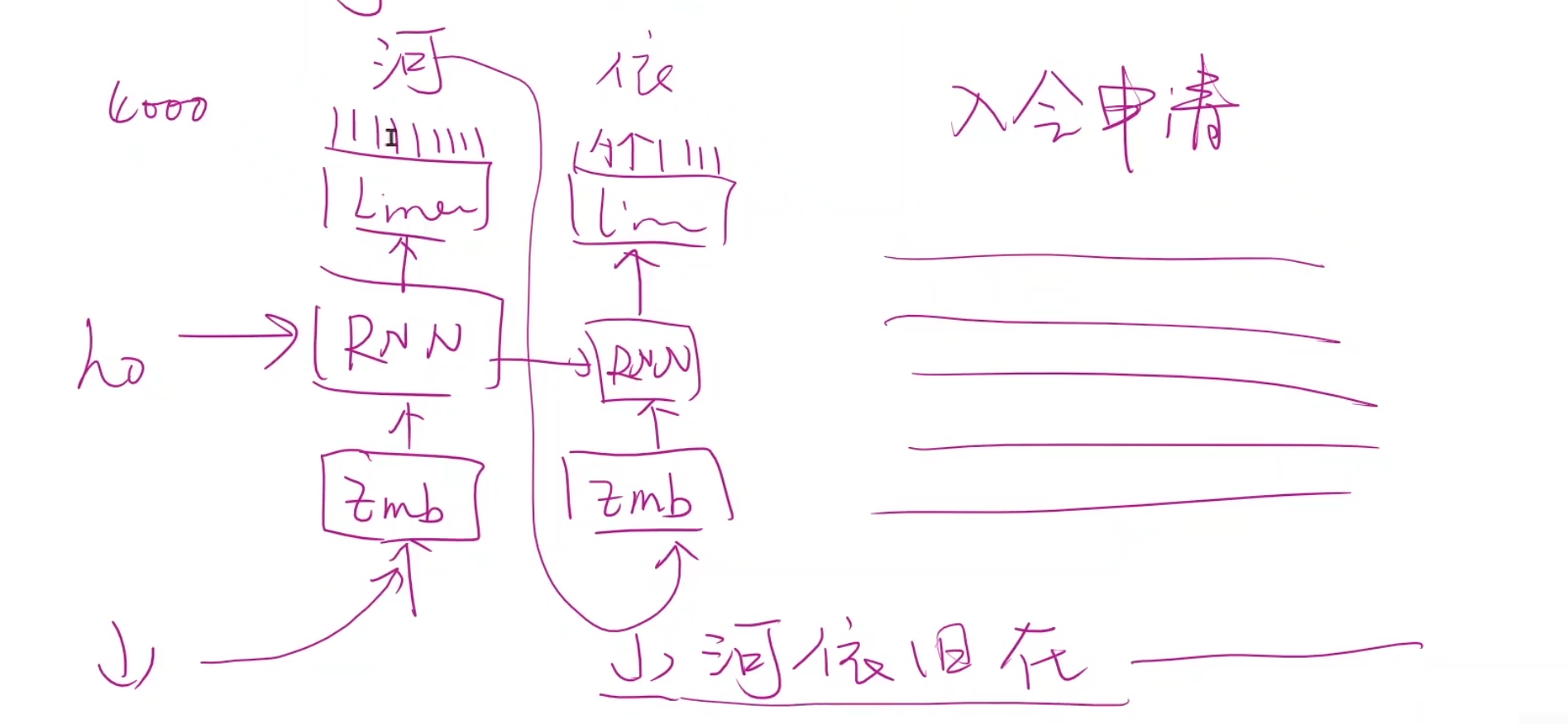
给出入会申请的标题，生成一大堆文字
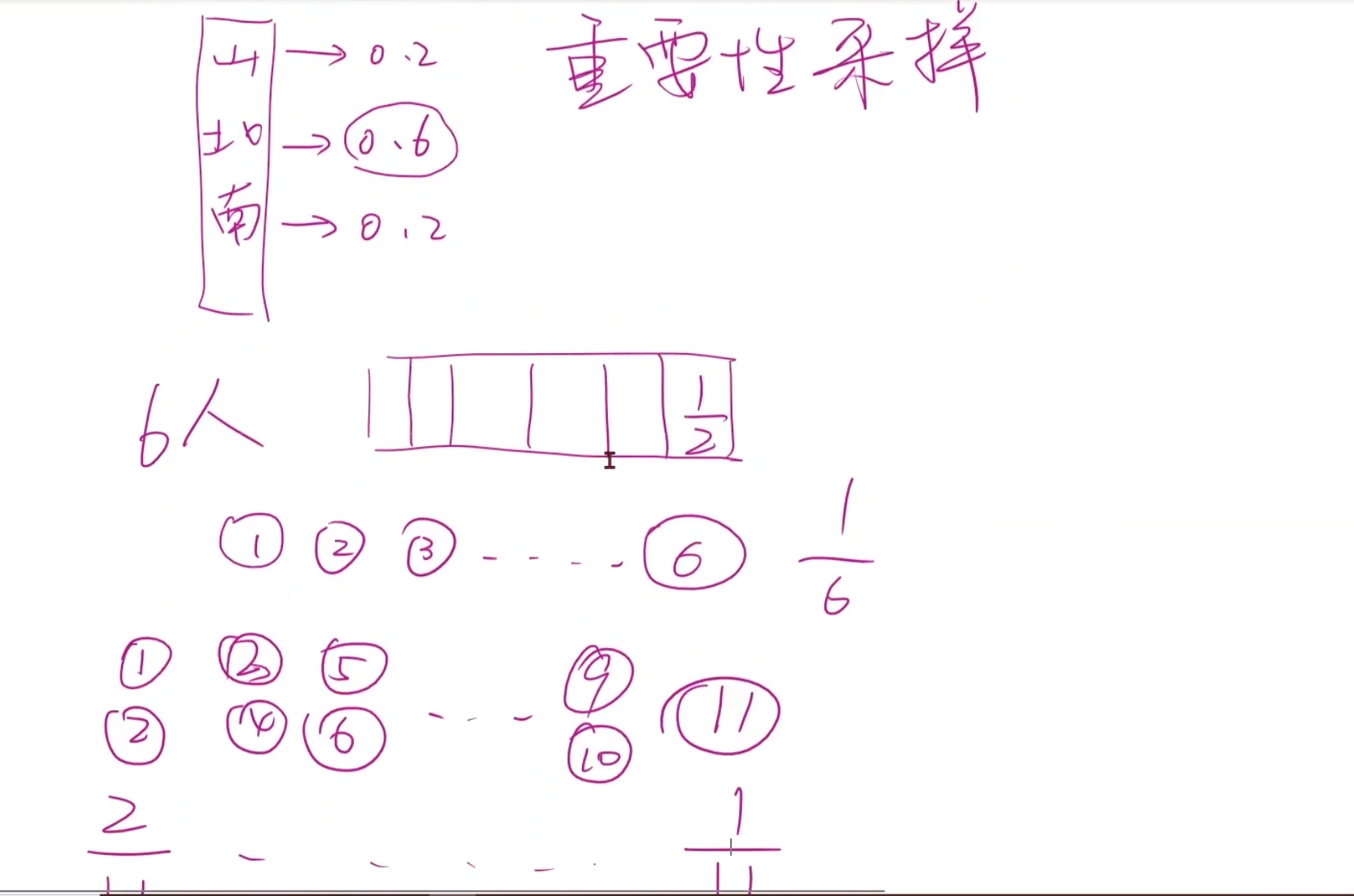
但我们又不希望每次生成都一样，引入一种机制
重要性采样 为此我们可以引入重要性采样，也就是不以谁的概率大就输出谁，而是说，谁的概率大，那么就有更大的机会抽中它，类似于一共六个人抽签，有五个人都只有一个球代表它自己，有一个人同时有两个球代表他，将七个球一起放到池子中，那么有两个球的同学会更容易被抽到，但的确是未必被抽到的。
尾言 RNN主要用于解决各种各样序列问题，CNN主要用于解决平面，空间的，带有二维以及以上的序列图像，这个时候我们就考虑用CNN。
由于神经网络这几年发展的很快，还会有各种各样的变体，比如RNN引入Attention，神经网络+传统概率模型近似的新模型，input为Graph，在Graph上进行信息融合。
不管是什么样的神经网络，最终的套路是什么呢？它肯定是一个数值型的输入变成我们想要的输出
也就是：我们需要把原始的数据形式，转变为能够进行网络运算的数据，不管是CNN，RNN，GNN还是什么，都是再找的非线性空间变换，只要把空间变换做好，将来得到我们想要的输出就可以了。所以我们制定网络结构，先要满足前几个条件，然后我们可以加入各种各样改进的办法，提高模型的性能。
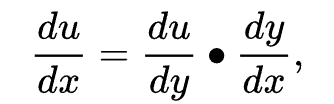
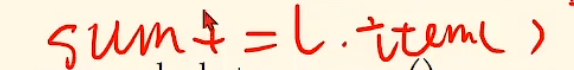
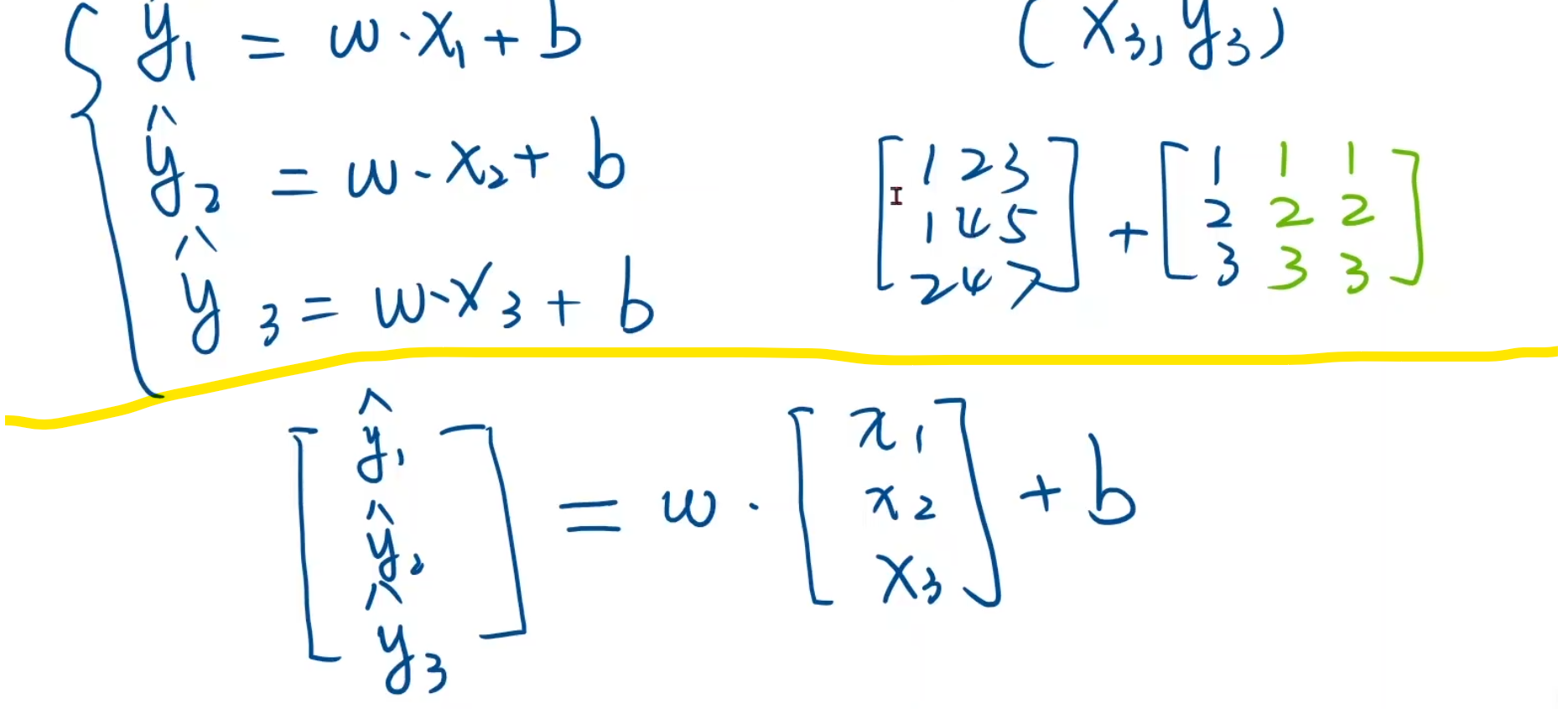
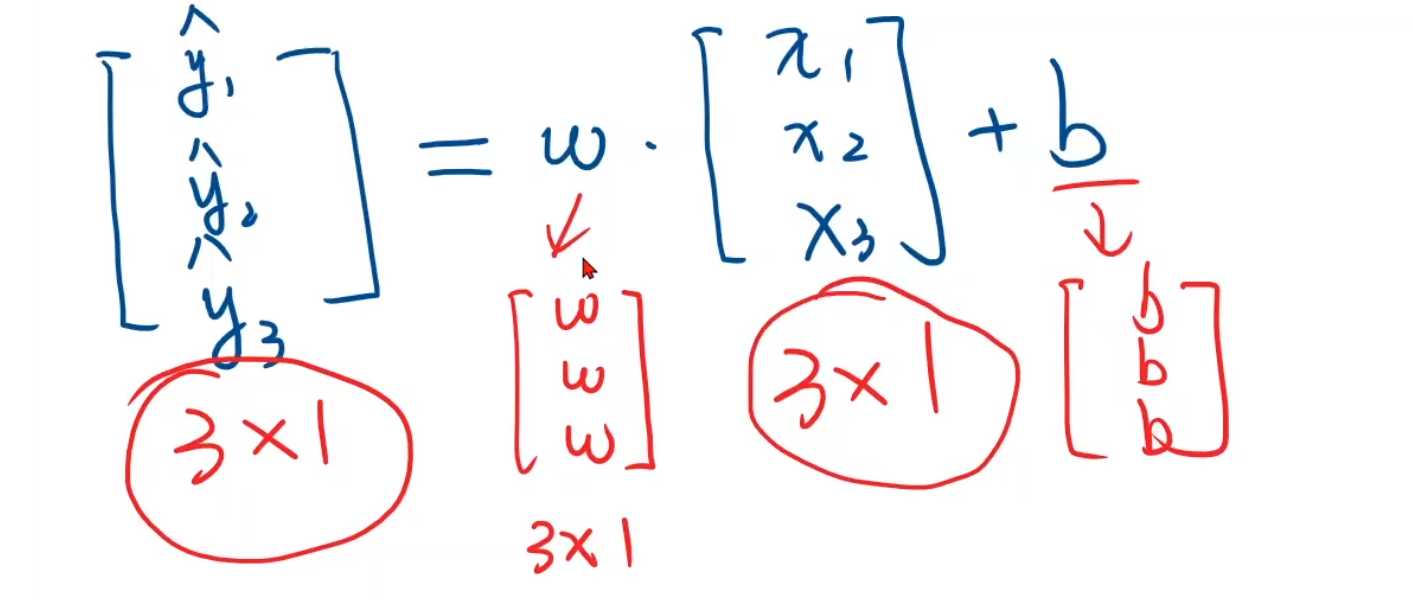
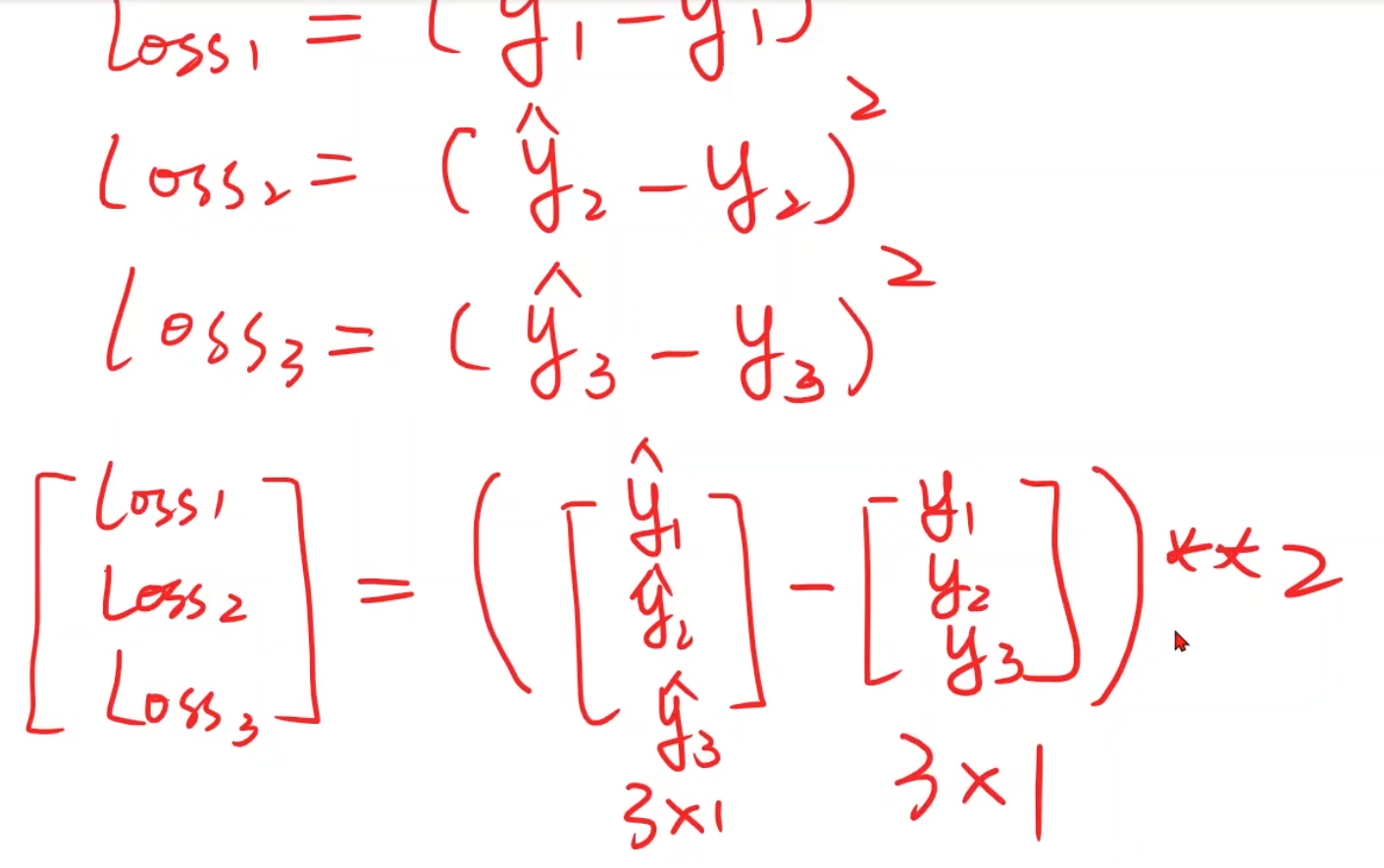
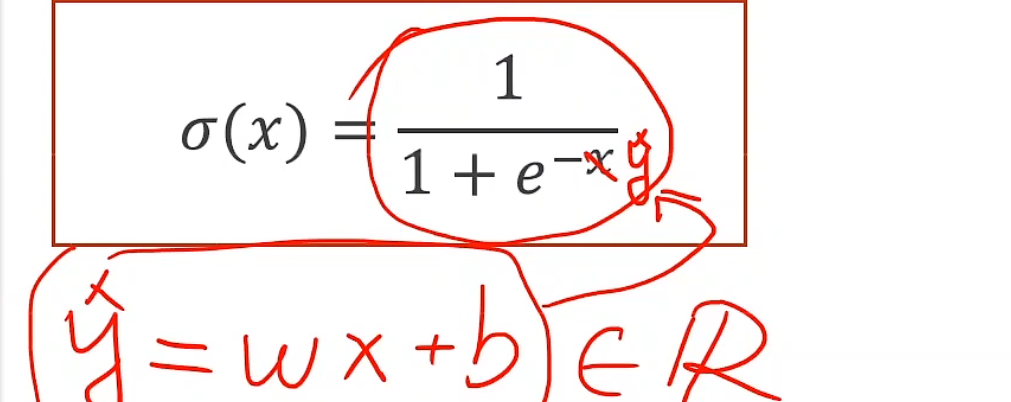
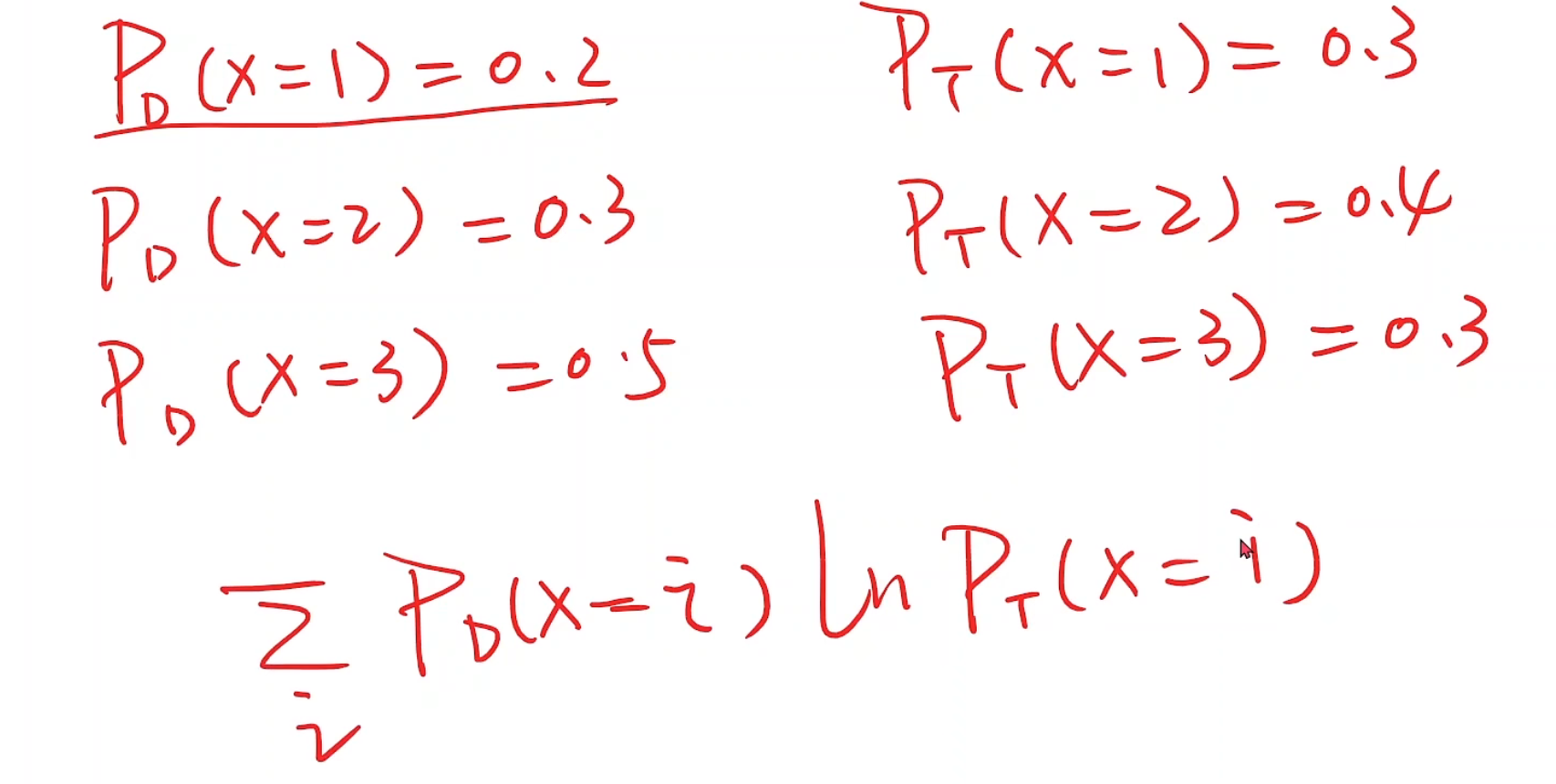
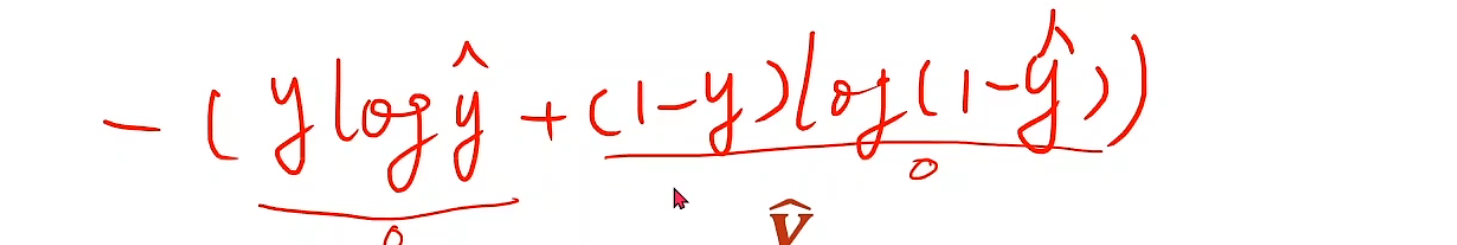
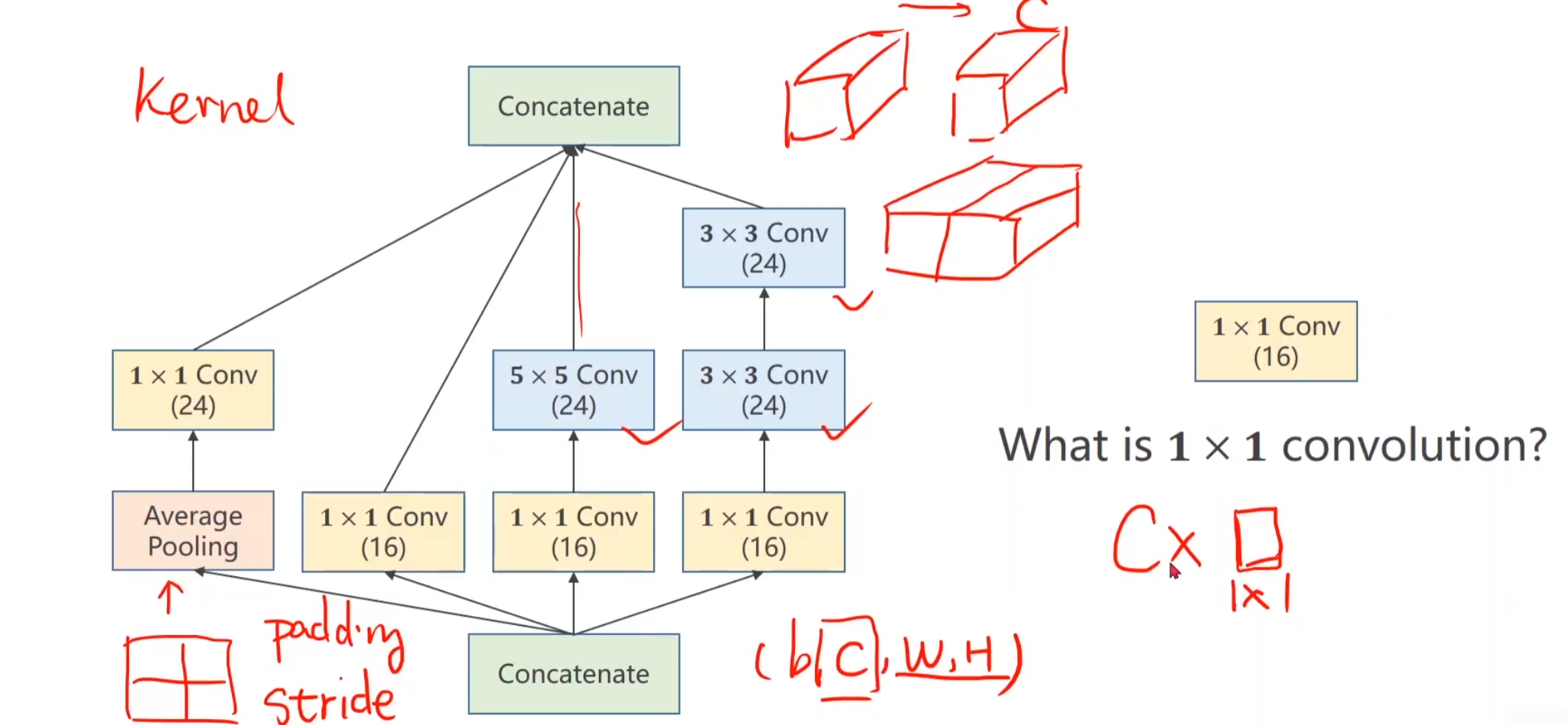这里就给出多种方案，只要保证最后传出去的一样就行，AveragePooling，如果设置他stride和padding，其实他就是一个一维的卷积核，只不过权重是平均值而已。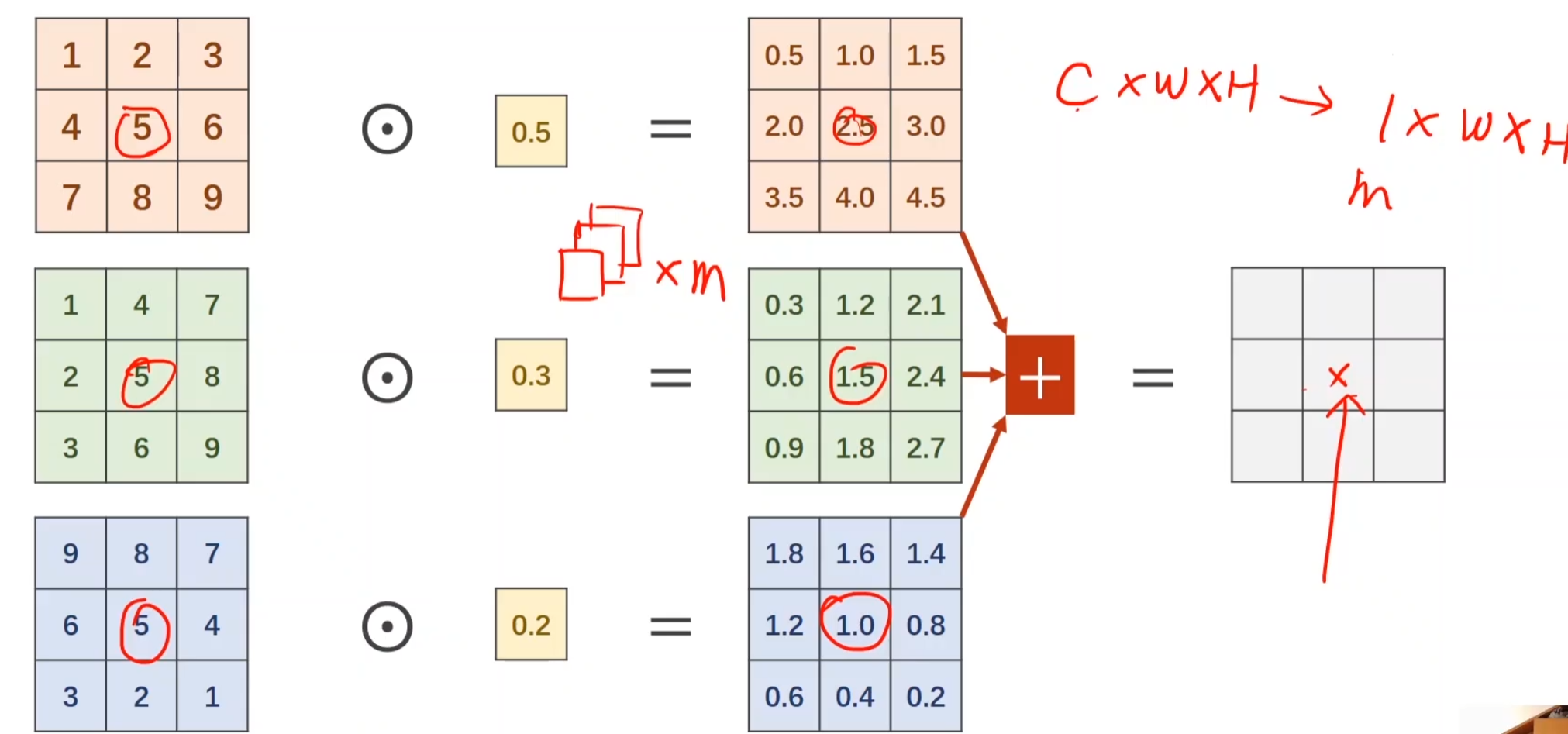
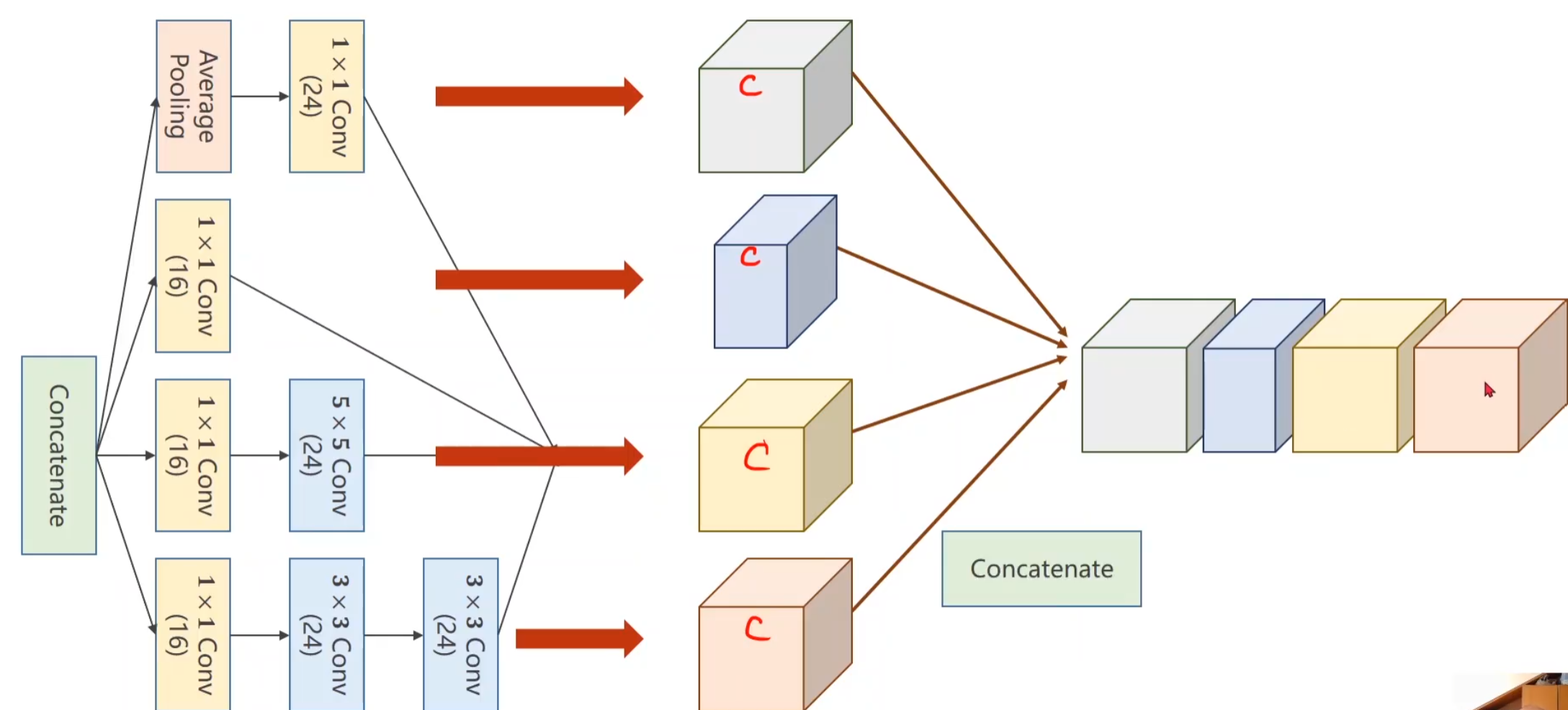
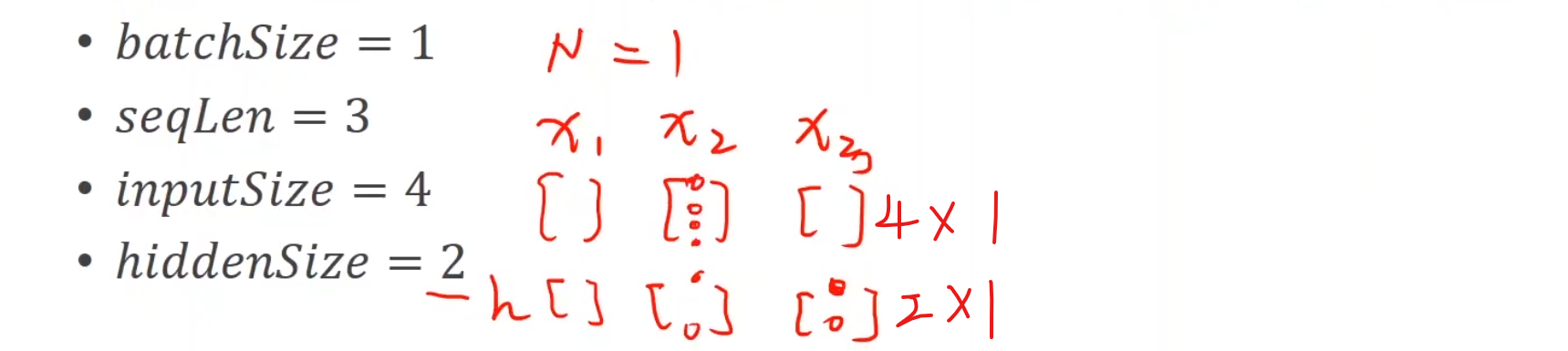
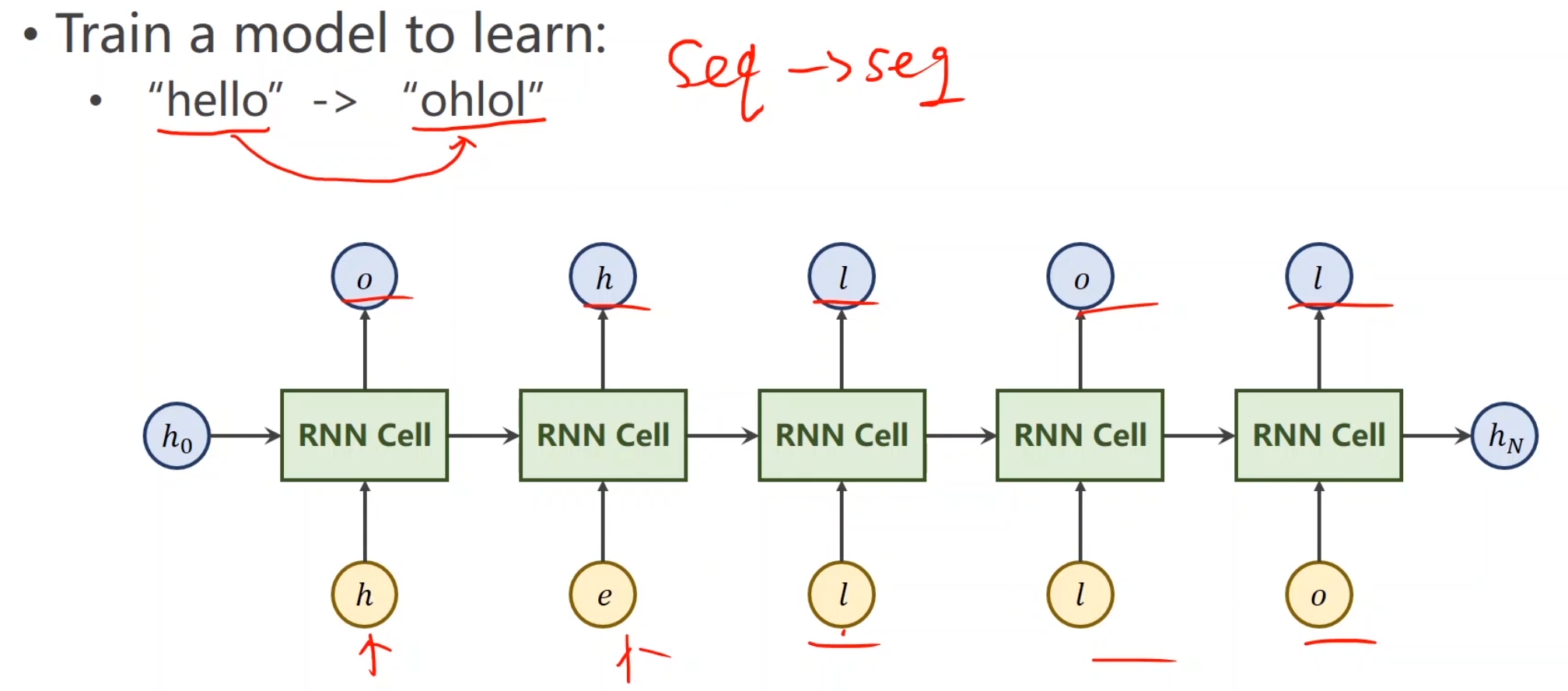
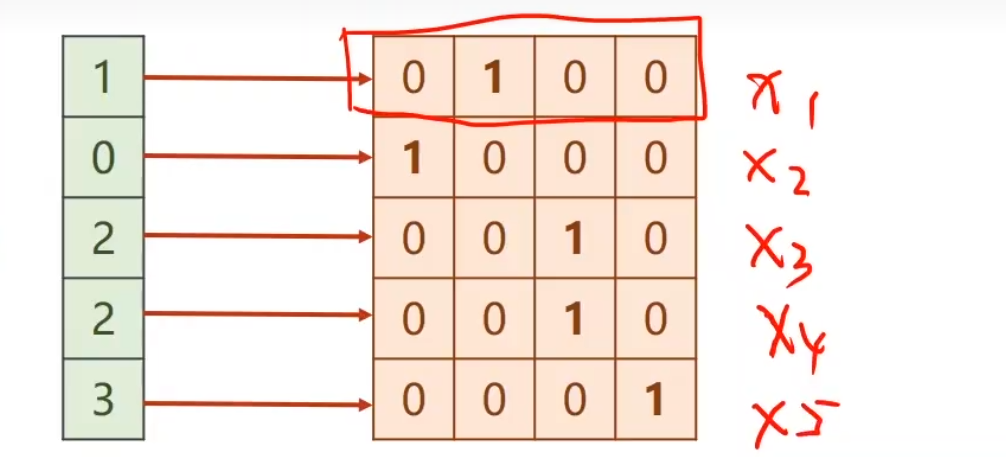
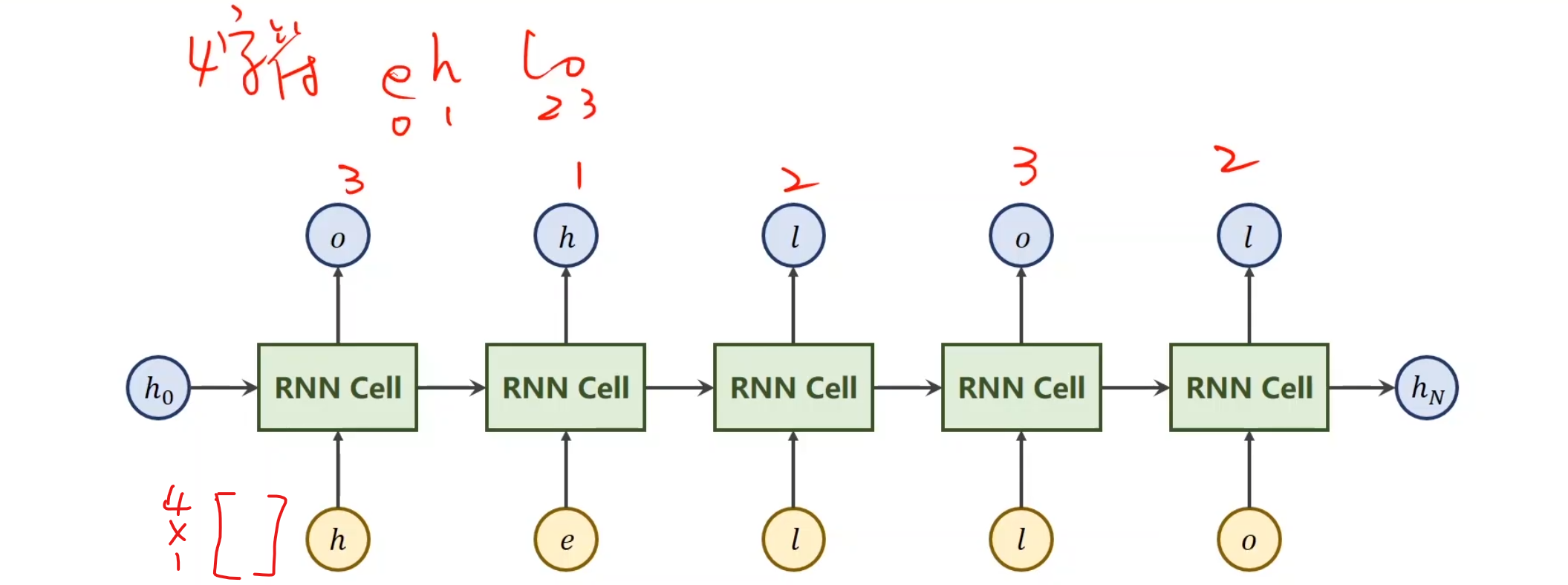这就是我们将来的输入和输出所需要的结构。
微信
支付宝
