这里将自己觉得实用的东西进行记录，以便快速学习和速成，主要内容参考一下博客

Python(Genetic Algorithm)之Geatpy - 知乎 (zhihu.com)

框架介绍

Geatpy2整体上看由工具箱内核函数（内核层）和面向对象进化算法框架（框架层）两部分组成。其中面向对象进化算法框架主要有四个大类：Problem问题类、Algorithm算法模板类、Population种群类和PsyPopulation多染色体种群类。UML图如下所示：

Problem类定义了与问题相关的一些信息，如问题名称name、优化目标的维数M、决策变量的个数Dim、决策变量的范围ranges、决策变量的边界borders等。maxormins是一个记录着各个目标函数是最小化抑或是最大化的Numpy array行向量，其中元素为1表示对应的目标是最小化目标；为-1表示对应的是最大化目标。

Population 类是一个表示种群的类。一个种群包含很多个个体，而每个个体都有一条染色体(若要用多染色体，则使用多个种群、并把每个种群对应个体关联起来即可)。除了染色体外，每个个体都有一个译码矩阵Field(或俗称区域描述器) 来标识染色体应该如何解码得到表现型，同时也有其对应的目标函数值以及适应度。种群类就是一个把所有个体的这些数据统一存储起来的一个类。比如里面的Chrom 是一个存储种群所有个体染色体的矩阵，它的每一行对应一个个体的染色体；ObjV 是一个目标函数值矩阵，每一行对应一个个体的所有目标函数值，每一列对应一个目标。

PsyPopulation类是继承了Population的支持多染色体混合编码的种群类。一个种群包含很多个个体，而每个个体都有多条染色体。用Chroms列表存储所有的染色体矩阵(Chrom)；Encodings列表存储各染色体对应的编码方式(Encoding)；Fields列表存储各染色体对应的译码矩阵(Field)。

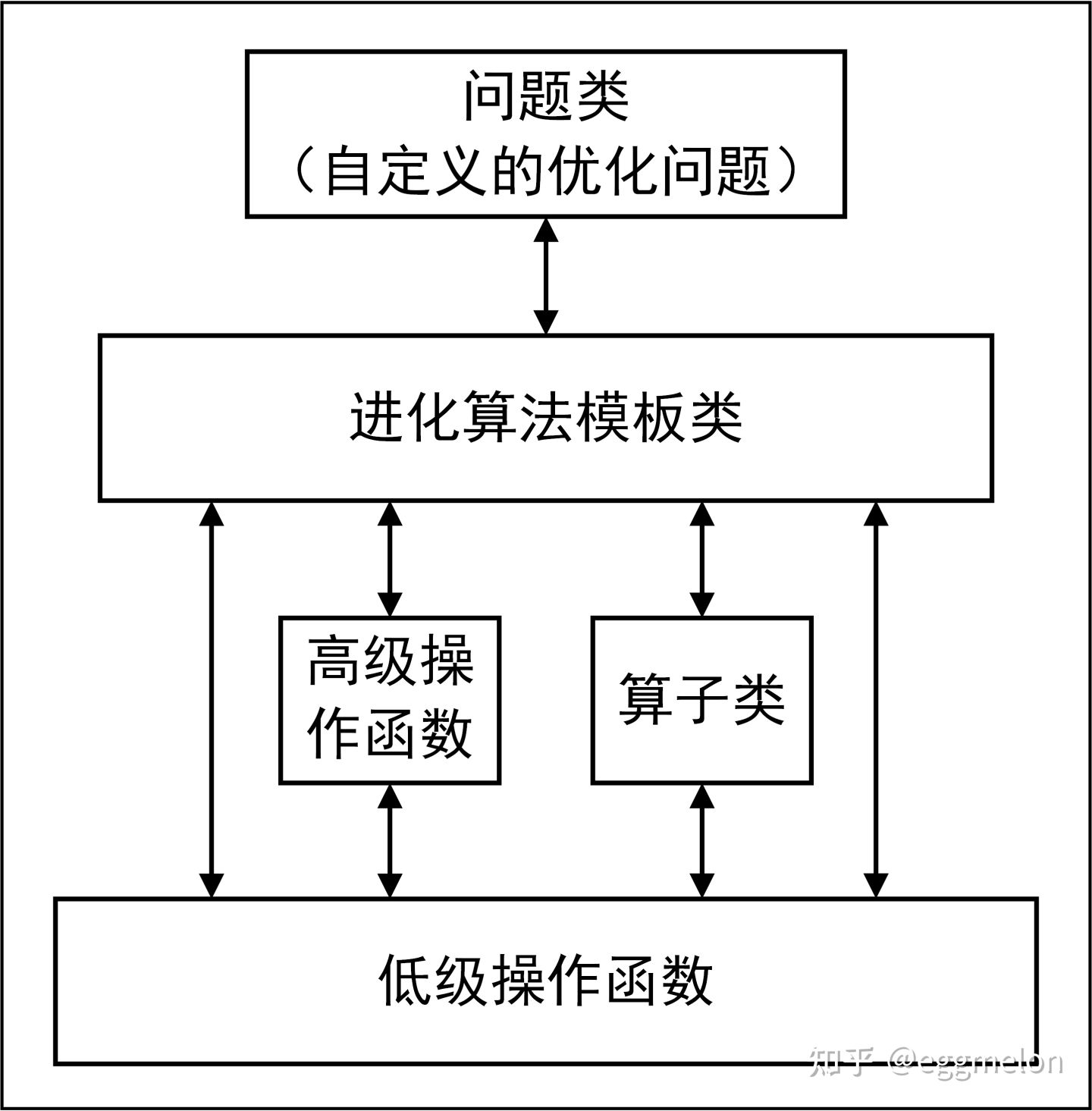
Algorithm 类是进化算法的核心类。它既存储着跟进化算法相关的一些参数，同时也在其继承类中实现具体的进化算法。比如Geatpy 中的moea_NSGA3_templet.py 是实现了多目标优化NSGA-III 算法的进化算法模板类，它是继承了Algorithm 类的具体算法的模板类。关于Algorithm 类中各属性的含义可以查看Algorithm.py 源码。这些算法模板通过调用Geatpy 工具箱提供的进化算法库函数实现对种群的进化操作，同时记录进化过程中的相关信息，其基本层次结构如下图：

其中“算子类”是2.2.2版本之后增加的新特性，通过实例化算子类来调用低级操作函数，可以利用面向对象编程的优势使得对传入低级操作函数的一些参数的修改变得更加方便。目前内置的“算子类”有“重组算子类”和“变异算子类”。用户可以绕开对底层的低级操作函数的修改而直接通过新增“算子类”来实现新的算子例如自适应的重组、变异算子等。

下面以一个多目标优化问题为例：对于求解一个优化问题，无论是单目标优化、还是多目标优化、抑或是组合优化、约束优化等，需要做两件工作：（1）自定义问题类；（2）编写执行代码。一般来说自定义问题类和执行代码可以专门分别写在独立的文件中，下面的代码中为了方便直接把两者写在同一个地方（原网站写在了同一个文件，本处改为两个独立文件）。

自定义问题类是把与问题模型有关的内容在此处进行定义和设置，比如变量范围、待优化的目标、约束条件的处理等；执行代码是调用算法模板进行进化优化。

一、单目标优化案例：

1.1 问题：Myproblem.py

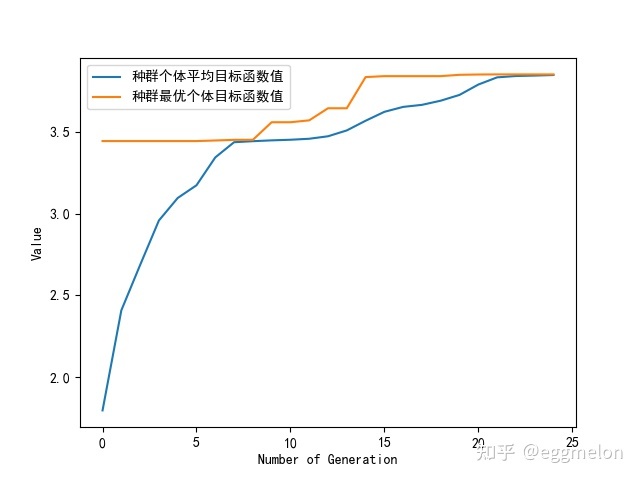
该案例展示了一个简单的连续型决策变量最大化目标的单目标优化问题。

max f = x * np.sin(10 * np.pi * x) + 2.0

s.t. -1 <= x <= 2

# -*- coding: utf-8 -*-
import numpy as np
import geatpy as ea

"""
该案例展示了一个简单的连续型决策变量最大化目标的单目标优化问题。
max f = x * np.sin(10 * np.pi * x) + 2.0
s.t.
-1 <= x <= 2
"""


class MyProblem(ea.Problem):  # 继承Problem父类
    def __init__(self):
        name = 'MyProblem'  # 初始化name（函数名称，可以随意设置）
        M = 1  # 初始化M（目标维数）
        maxormins = [-1]  # 初始化maxormins（目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标）
        Dim = 1  # 初始化Dim（决策变量维数）
        varTypes = [0] * Dim  # 初始化varTypes（决策变量的类型，元素为0表示对应的变量是连续的；1表示是离散的）
        lb = [-1]  # 决策变量下界
        ub = [2]  # 决策变量上界
        lbin = [1] * Dim  # 决策变量下边界（0表示不包含该变量的下边界，1表示包含）
        ubin = [1] * Dim  # 决策变量上边界（0表示不包含该变量的上边界，1表示包含）
        # 调用父类构造方法完成实例化
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)

    def aimFunc(self, pop):  # 目标函数
        x = pop.Phen  # 得到决策变量矩阵
        pop.ObjV = x * np.sin(10 * np.pi * x) + 2.0  # 计算目标函数值，赋值给pop种群对象的ObjV属性

main.py

# -*- coding: utf-8 -*-
import geatpy as ea  # import geatpy
from MyProblem import MyProblem  # 导入自定义问题接口

if __name__ == '__main__':
    """===============================实例化问题对象==========================="""
    problem = MyProblem()  # 生成问题对象
    """=================================种群设置=============================="""
    Encoding = 'BG'  # 编码方式
    NIND = 40  # 种群规模
    Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders)  # 创建区域描述器
    population = ea.Population(Encoding, Field, NIND)  # 实例化种群对象（此时种群还没被初始化，仅仅是完成种群对象的实例化）
    """===============================算法参数设置============================="""
    myAlgorithm = ea.soea_SEGA_templet(problem, population)  # 实例化一个算法模板对象
    myAlgorithm.MAXGEN = 25  # 最大进化代数
    myAlgorithm.logTras = 1  # 设置每隔多少代记录日志，若设置成0则表示不记录日志
    myAlgorithm.verbose = True  # 设置是否打印输出日志信息
    myAlgorithm.drawing = 1  # 设置绘图方式（0：不绘图；1：绘制结果图；2：绘制目标空间过程动画；3：绘制决策空间过程动画）
    """==========================调用算法模板进行种群进化========================"""
    [BestIndi, population] = myAlgorithm.run()  # 执行算法模板，得到最优个体以及最后一代种群
    BestIndi.save()  # 把最优个体的信息保存到文件中
    """=================================输出结果=============================="""
    print('评价次数：%s' % myAlgorithm.evalsNum)
    print('时间已过 %s 秒' % myAlgorithm.passTime)
    if BestIndi.sizes != 0:
        print('最优的目标函数值为：%s' % BestIndi.ObjV[0][0])
        print('最优的控制变量值为：')
        for i in range(BestIndi.Phen.shape[1]):
            print(BestIndi.Phen[0, i])
    else:
        print('没找到可行解。')

评价次数：1000

时间已过 0.07295060157775879 秒

最优的目标函数值为：3.850230733449206

最优的控制变量值为：

1.8507644886623735

1.2 问题：Myproblem.py

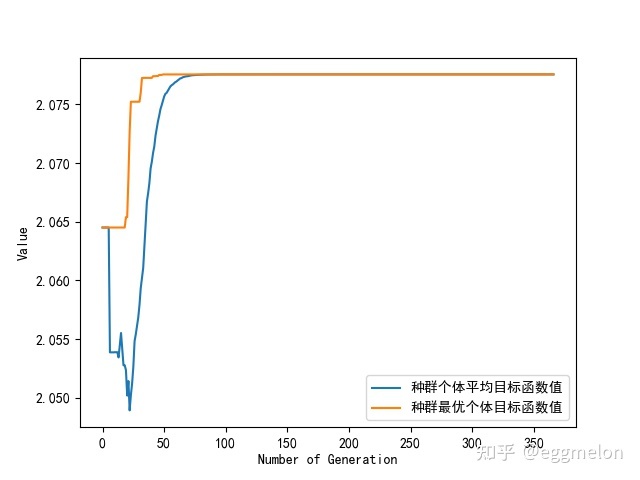
该案例展示了一个带等式约束的连续型决策变量最大化目标的单目标优化问题。
该函数存在多个欺骗性很强的局部最优点。
max f = 4x1 + 2x2 + x3
s.t.
2x1 + x2 - 1 <= 0
x1 + 2x3 - 2 <= 0
x1 + x2 + x3 - 1 == 0
0 <= x1,x2 <= 1
0 < x3 < 2

# -*- coding: utf-8 -*-
"""MyProblem.py"""
import numpy as np
import geatpy as ea

"""
    该案例展示了一个带等式约束的连续型决策变量最大化目标的单目标优化问题。
    该函数存在多个欺骗性很强的局部最优点。
    max f = 4*x1 + 2*x2 + x3
    s.t.
    2*x1 + x2 - 1 <= 0
    x1 + 2*x3 - 2 <= 0
    x1 + x2 + x3 - 1 == 0
    0 <= x1,x2 <= 1
    0 < x3 < 2
"""


class MyProblem(ea.Problem):  # 继承Problem父类
    def __init__(self):
        name = 'MyProblem'  # 初始化name（函数名称，可以随意设置）
        M = 1  # 初始化M（目标维数）
        maxormins = [-1]  # 初始化maxormins（目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标）
        Dim = 3  # 初始化Dim（决策变量维数）
        varTypes = [0] * Dim  # 初始化varTypes（决策变量的类型，元素为0表示对应的变量是连续的；1表示是离散的）
        lb = [0, 0, 0]  # 决策变量下界
        ub = [1, 1, 2]  # 决策变量上界
        lbin = [1, 1, 0]  # 决策变量下边界（0表示不包含该变量的下边界，1表示包含）
        ubin = [1, 1, 0]  # 决策变量上边界（0表示不包含该变量的上边界，1表示包含）
        # 调用父类构造方法完成实例化
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)

    def aimFunc(self, pop):  # 目标函数
        Vars = pop.Phen  # 得到决策变量矩阵
        x1 = Vars[:, [0]]
        x2 = Vars[:, [1]]
        x3 = Vars[:, [2]]
        pop.ObjV = 4 * x1 + 2 * x2 + x3  # 计算目标函数值，赋值给pop种群对象的ObjV属性
        # 采用可行性法则处理约束
        pop.CV = np.hstack([2 * x1 + x2 - 1,
                            x1 + 2 * x3 - 2,
                            np.abs(x1 + x2 + x3 - 1)])

    def calReferObjV(self):  # 设定目标数参考值（本问题目标函数参考值设定为理论最优值）
        referenceObjV = np.array([[2.5]])
        return referenceObjV

main.py

# -*- coding: utf-8 -*-
import geatpy as ea  # import geatpy
from MyProblem import MyProblem  # 导入自定义问题接口

if __name__ == '__main__':
    """================================实例化问题对象==========================="""
    problem = MyProblem()  # 生成问题对象
    """==================================种群设置=============================="""
    Encoding = 'RI'  # 编码方式
    NIND = 100  # 种群规模
    Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders)  # 创建区域描述器
    population = ea.Population(Encoding, Field, NIND)  # 实例化种群对象（此时种群还没被初始化，仅仅是完成种群对象的实例化）
    """================================算法参数设置============================="""
    myAlgorithm = ea.soea_DE_rand_1_bin_templet(problem, population)  # 实例化一个算法模板对象
    myAlgorithm.MAXGEN = 500  # 最大进化代数
    myAlgorithm.mutOper.F = 0.5  # 差分进化中的参数F
    myAlgorithm.recOper.XOVR = 0.7  # 重组概率
    myAlgorithm.logTras = 1  # 设置每隔多少代记录日志，若设置成0则表示不记录日志
    myAlgorithm.verbose = True  # 设置是否打印输出日志信息
    myAlgorithm.drawing = 1  # 设置绘图方式（0：不绘图；1：绘制结果图；2：绘制目标空间过程动画；3：绘制决策空间过程动画）
    """===========================调用算法模板进行种群进化========================"""
    [BestIndi, population] = myAlgorithm.run()  # 执行算法模板，得到最优个体以及最后一代种群
    BestIndi.save()  # 把最优个体的信息保存到文件中
    """==================================输出结果=============================="""
    print('评价次数：%s' % myAlgorithm.evalsNum)
    print('时间已过 %s 秒' % myAlgorithm.passTime)
    if BestIndi.sizes != 0:
        print('最优的目标函数值为：%s' % BestIndi.ObjV[0][0])
        print('最优的控制变量值为：')
        for i in range(BestIndi.Phen.shape[1]):
            print(BestIndi.Phen[0, i])
    else:
        print('没找到可行解。')

评价次数：50000

时间已过 0.43572211265563965 秒

最优的目标函数值为：2.077554093241303

最优的控制变量值为：

0.07755414367376987

0.8448916622199935

0.07755419410623668

1.3 问题：Myproblem.py

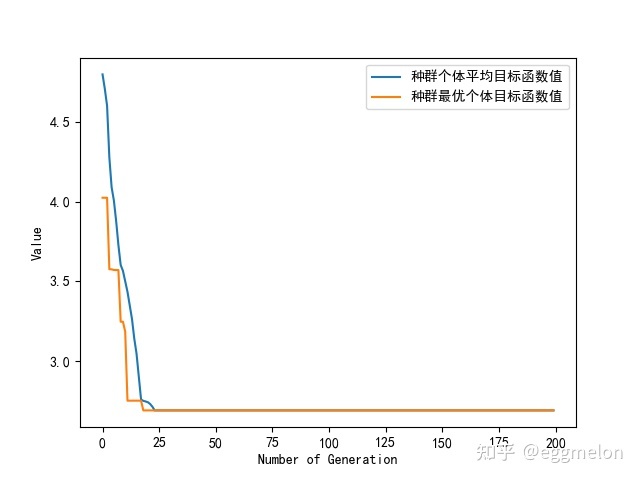
一个带约束的单目标旅行商问题：有十座城市：A, B, C, D, E, F, G, H, I, J，坐标如下： X Y [[0.4, 0.4439], [0.2439,0.1463], [0.1707,0.2293], [0.2293,0.761], [0.5171,0.9414], [0.8732,0.6536], [0.6878,0.5219], [0.8488,0.3609], [0.6683,0.2536], [0.6195,0.2634]] 某旅行者从A城市出发，想逛遍所有城市，并且每座城市去且只去一次，最后要返回出发地，而且需要从G地拿重要文件到D地，另外要从F地把公司的车开到E地，那么他应该如何设计行程方案，才能用最短的路程来满足他的旅行需求？分析：在这个案例中，旅行者从A地出发，把其他城市走遍一次后回到A地，因此我们只需要考虑中间途径的9个城市的访问顺序即可。这9个城市需要排列组合选出满足约束条件的最优的排列顺序作为最终的路线方案。

# -*- coding: utf-8 -*-
import numpy as np
import geatpy as ea

"""
"""


class MyProblem(ea.Problem):  # 继承Problem父类
    def __init__(self):
        name = 'MyProblem'  # 初始化name（函数名称，可以随意设置）
        M = 1  # 初始化M（目标维数）
        maxormins = [1]  # 初始化maxormins（目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标）
        Dim = 9  # 初始化Dim（决策变量维数）
        varTypes = [1] * Dim  # 初始化varTypes（决策变量的类型，元素为0表示对应的变量是连续的；1表示是离散的）
        lb = [1] * Dim  # 决策变量下界
        ub = [9] * Dim  # 决策变量上界
        lbin = [1] * Dim  # 决策变量下边界（0表示不包含该变量的下边界，1表示包含）
        ubin = [1] * Dim  # 决策变量上边界（0表示不包含该变量的上边界，1表示包含）
        # 调用父类构造方法完成实例化
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)
        # 新增一个属性存储旅行地坐标
        self.places = np.array([[0.4, 0.4439],
                                [0.2439, 0.1463],
                                [0.1707, 0.2293],
                                [0.2293, 0.761],
                                [0.5171, 0.9414],
                                [0.8732, 0.6536],
                                [0.6878, 0.5219],
                                [0.8488, 0.3609],
                                [0.6683, 0.2536],
                                [0.6195, 0.2634]])

    def aimFunc(self, pop):  # 目标函数
        x = pop.Phen  # 得到决策变量矩阵

        # 添加从0地出发且最后回到出发地
        # zeros参数即是维度，这里生成（x.shape[0](50), 1）的0矩阵
        # hstack进行参数之间的横向拼接
        X = np.hstack([np.zeros((x.shape[0], 1)), x, np.zeros((x.shape[0], 1))]).astype(int)

        ObjV = []  # 存储所有种群个体对应的总路程
        for i in range(X.shape[0]):
            journey = self.places[X[i]][:]  # 按既定顺序到达的地点坐标
            
            # diff算离散差
            # journey为11 * 2的矩阵，diff是横向计算，所以得先转置，后就很容易理解了
            # a=np.array([1, 6, 7, 8, 12])
            # diff_x1 = np.diff(a)
            # print("diff_x1",diff_x1)
            # # diff_x1 [5 1 1 4]
            # # [6->1,7->6,8->7,12->8]
            distance = np.sum(np.sqrt(np.sum(np.diff(journey.T) ** 2, 0)))  # 计算总路程
            # 每算出一个，追加一个距离为答案
            ObjV.append(distance)
        pop.ObjV = np.array([ObjV]).T  # 把求得的目标函数值赋值给种群pop的ObjV
        # 找到违反约束条件的个体在种群中的索引，保存在向量exIdx中（如：若0、2、4号个体违反约束条件，则编程找出他们来）
        # np.where 将满足括号内参数条件的元素取出
        # 按照理解，例如exIdx2，可能是指要求先到f（5），再到e（4），所以的话顺序应该F存放数值的小于E的，也就是(5)< (4)为正确
        # 我们这里是构造约束条件，所以筛选出去的应该是(4) < (5)的，注意看外面还有一个np.where
        exIdx1 = np.where(np.where(x == 3)[1] - np.where(x == 6)[1] < 0)[0]
        exIdx2 = np.where(np.where(x == 4)[1] - np.where(x == 5)[1] < 0)[0]
        # exIdx就是所有需要筛选出去的，如果还有啥条件我们继续加！
        exIdx = np.unique(np.hstack([exIdx1, exIdx2]))
        
        # 生成pop.sizes * 1的矩阵列表
        pop.CV = np.zeros((pop.sizes, 1))
        # CV只要大于0就死，所以把这一次迭代的约束传给pop
        pop.CV[exIdx] = 1  # 把求得的违反约束程度矩阵赋值给种群pop的CV

main.py

# -*- coding: utf-8 -*-
import numpy as np
import geatpy as ea  # import geatpy
import matplotlib.pyplot as plt
from MyProblem import MyProblem  # 导入自定义问题接口

if __name__ == '__main__':
    """================================实例化问题对象============================"""
    problem = MyProblem()  # 生成问题对象
    """==================================种群设置=============================="""
    Encoding = 'P'  # 编码方式，采用排列编码
    NIND = 50  # 种群规模
    Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders)  # 创建区域描述器
    population = ea.Population(Encoding, Field, NIND)  # 实例化种群对象（此时种群还没被初始化，仅仅是完成种群对象的实例化）
    """================================算法参数设置============================="""
    myAlgorithm = ea.soea_SEGA_templet(problem, population)  # 实例化一个算法模板对象
    myAlgorithm.MAXGEN = 200  # 最大进化代数
    myAlgorithm.mutOper.Pm = 0.5  # 变异概率
    myAlgorithm.logTras = 1  # 设置每隔多少代记录日志，若设置成0则表示不记录日志
    myAlgorithm.verbose = True  # 设置是否打印输出日志信息
    myAlgorithm.drawing = 1  # 设置绘图方式（0：不绘图；1：绘制结果图；2：绘制目标空间过程动画；3：绘制决策空间过程动画）
    """===========================调用算法模板进行种群进化========================"""
    [BestIndi, population] = myAlgorithm.run()  # 执行算法模板，得到最优个体以及最后一代种群
    BestIndi.save()  # 把最优个体的信息保存到文件中
    """==================================输出结果=============================="""
    print('评价次数：%s' % myAlgorithm.evalsNum)
    print('时间已过 %s 秒' % myAlgorithm.passTime)
    if BestIndi.sizes != 0:
        print('最短路程为：%s' % BestIndi.ObjV[0][0])
        print('最佳路线为：')
        best_journey = np.hstack([0, BestIndi.Phen[0, :], 0])
        for i in range(len(best_journey)):
            print(int(best_journey[i]), end=' ')
        print()
        # 绘图
        plt.figure()
        plt.plot(problem.places[best_journey.astype(int), 0], problem.places[best_journey.astype(int), 1], c='black')
        plt.plot(problem.places[best_journey.astype(int), 0], problem.places[best_journey.astype(int), 1], 'o',
                 c='black')
        for i in range(len(best_journey)):
            plt.text(problem.places[int(best_journey[i]), 0], problem.places[int(best_journey[i]), 1],
                     chr(int(best_journey[i]) + 65), fontsize=20)
        plt.grid(True)
        plt.xlabel('x坐标')
        plt.ylabel('y坐标')
        plt.savefig('roadmap.svg', dpi=600, bbox_inches='tight')
    else:
        print('没找到可行解。')

最短路程为：2.690670637009413

最佳路线为：

0 2 1 9 8 7 6 5 4 3 0

1.4问题：Myproblem.py

该案例展示了一个利用单目标进化算法实现句子匹配的应用实例。

# -*- coding: utf-8 -*-
import numpy as np
import geatpy as ea

"""
该案例展示了一个利用单目标进化算法实现句子匹配的应用实例。
"""


class MyProblem(ea.Problem):  # 继承Problem父类
    def __init__(self):
        name = 'MyProblem'  # 初始化name（函数名称，可以随意设置）
        # 定义需要匹配的句子
        strs = 'Tom is a little boy, isn\'t he? Yes he is, he is a good and smart child and he is always ready to help others, all in all we all like him very much.'
        self.words = []
        for c in strs:
            self.words.append(ord(c))  # 把字符串转成ASCII码
        M = 1  # 初始化M（目标维数）
        maxormins = [1]  # 初始化maxormins（目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标）
        Dim = len(self.words)  # 初始化Dim（决策变量维数）
        varTypes = [1] * Dim  # 初始化varTypes（决策变量的类型，元素为0表示对应的变量是连续的；1表示是离散的）
        lb = [32] * Dim  # 决策变量下界
        ub = [122] * Dim  # 决策变量上界
        lbin = [1] * Dim  # 决策变量下边界（0表示不包含该变量的下边界，1表示包含）
        ubin = [1] * Dim  # 决策变量上边界（0表示不包含该变量的上边界，1表示包含）
        # 调用父类构造方法完成实例化
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)

    def aimFunc(self, pop):  # 目标函数
        Vars = pop.Phen  # 得到决策变量矩阵
        diff = np.sum((Vars - self.words) ** 2, 1)
        pop.ObjV = np.array([diff]).T  # 把求得的目标函数值赋值给种群pop的ObjV

Tom is a little boy, isn’t he? Yes he is, he is a good and smart child and he is always ready to help others, all in all we all like him very much.

1.5问题：Myproblem.py

该案例展示了一个需要混合编码种群来进化的最大化目标的单目标优化问题。模型：

max f = sin(2x1) - cos(x2) + 2x3^2 -3x4 + (x5-3)^2 + 7x6

s.t. -1.5 <= x1,x2 <= 2.5， 1 <= x3,x4,x5,x6 <= 7，且x3,x4,x5,x6为互不相等的整数。

分析：该问题可以单纯用实整数编码’RI’来实现，但由于有一个”x3,x4,x5,x6互不相等“的约束，因此把x3,x4,x5,x6用排列编码’P’，x1和x2采用实整数编码’RI’来求解会更好。 MyProblem是问题类，本质上是不需要管具体使用什么编码的，因此混合编码的设置在执行脚本main.py中进行而不是在此处。

# -*- coding: utf-8 -*-
import numpy as np
import geatpy as ea

"""
"""


class MyProblem(ea.Problem):  # 继承Problem父类
    def __init__(self):
        name = 'MyProblem'  # 初始化name（函数名称，可以随意设置）
        M = 1  # 初始化M（目标维数）
        maxormins = [-1]  # 初始化maxormins（目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标）
        Dim = 6  # 初始化Dim（决策变量维数）
        varTypes = [0, 0, 1, 1, 1, 1]  # 初始化varTypes（决策变量的类型，元素为0表示对应的变量是连续的；1表示是离散的）
        lb = [-1.5, -1.5, 1, 1, 1, 1]  # 决策变量下界
        ub = [2.5, 2.5, 7, 7, 7, 7]  # 决策变量上界
        lbin = [1] * Dim  # 决策变量下边界（0表示不包含该变量的下边界，1表示包含）
        ubin = [1] * Dim  # 决策变量上边界（0表示不包含该变量的上边界，1表示包含）
        # 调用父类构造方法完成实例化
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)

    def aimFunc(self, pop):  # 目标函数
        X = pop.Phen  # 得到决策变量矩阵
        x1 = X[:, [0]]
        x2 = X[:, [1]]
        x3 = X[:, [2]]
        x4 = X[:, [3]]
        x5 = X[:, [4]]
        x6 = X[:, [5]]
        pop.ObjV = np.sin(2 * x1) - np.cos(x2) + 2 * x3 ** 2 - 3 * x4 + (
                x5 - 3) ** 2 + 7 * x6  # 计算目标函数值，赋值给pop种群对象的ObjV属性

main.py

# -*- coding: utf-8 -*-
import geatpy as ea  # import geatpy
from MyProblem import MyProblem  # 导入自定义问题接口

if __name__ == '__main__':
    """================================实例化问题对象==========================="""
    problem = MyProblem()  # 生成问题对象
    """==================================种群设置=============================="""
    NIND = 40  # 种群规模
    # 创建区域描述器，这里需要创建两个，前2个变量用RI编码，剩余变量用排列编码
    Encodings = ['RI', 'P']
    Field1 = ea.crtfld(Encodings[0], problem.varTypes[:2], problem.ranges[:, :2], problem.borders[:, :2])
    Field2 = ea.crtfld(Encodings[1], problem.varTypes[2:], problem.ranges[:, 2:], problem.borders[:, 2:])
    Fields = [Field1, Field2]
    population = ea.PsyPopulation(Encodings, Fields, NIND)  # 实例化种群对象（此时种群还没被初始化，仅仅是完成种群对象的实例化）
    """================================算法参数设置============================="""
    myAlgorithm = ea.soea_psy_EGA_templet(problem, population)  # 实例化一个算法模板对象
    myAlgorithm.MAXGEN = 25  # 最大进化代数
    myAlgorithm.logTras = 1  # 设置每隔多少代记录日志，若设置成0则表示不记录日志
    myAlgorithm.verbose = True  # 设置是否打印输出日志信息
    myAlgorithm.drawing = 1  # 设置绘图方式（0：不绘图；1：绘制结果图；2：绘制目标空间过程动画；3：绘制决策空间过程动画）
    """===========================调用算法模板进行种群进化========================"""
    [BestIndi, population] = myAlgorithm.run()  # 执行算法模板，得到最优个体以及最后一代种群
    BestIndi.save()  # 把最优个体的信息保存到文件中
    """==================================输出结果=============================="""
    print('评价次数：%s' % myAlgorithm.evalsNum)
    print('时间已过 %s 秒' % myAlgorithm.passTime)
    if BestIndi.sizes != 0:
        print('最优的目标函数值为：%s' % (BestIndi.ObjV[0][0]))
        print('最优的控制变量值为：')
        for i in range(BestIndi.Phen.shape[1]):
            print(BestIndi.Phen[0, i])
    else:
        print('没找到可行解。')

1.6问题：Myproblem.py

该案例展示了如何利用进化算法+多进程/多线程来优化SVM中的两个参数：C和Gamma。在执行本案例前，需要确保正确安装sklearn，以保证SVM部分的代码能够正常执行。本函数需要用到一个外部数据集，存放在同目录下的iris.data中，并且把iris.data按3:2划分为训练集数据iris_train.data和测试集数据iris_test.data。有关该数据集的详细描述详见http://archive.ics.uci.edu/ml/datasets/Iris 在执行脚本main.py中设置PoolType字符串来控制采用的是多进程还是多线程。注意：使用多进程时，程序必须以“if name == ‘main‘:”作为入口，这个是multiprocessing的多进程模块的硬性要求。

# -*- coding: utf-8 -*-
import numpy as np
import geatpy as ea
from sklearn import svm
from sklearn import preprocessing
from sklearn.model_selection import cross_val_score
import multiprocessing as mp
from multiprocessing import Pool as ProcessPool
from multiprocessing.dummy import Pool as ThreadPool

"""
"""


class MyProblem(ea.Problem):  # 继承Problem父类
    def __init__(self, PoolType):  # PoolType是取值为'Process'或'Thread'的字符串
        name = 'MyProblem'  # 初始化name（函数名称，可以随意设置）
        M = 1  # 初始化M（目标维数）
        maxormins = [-1]  # 初始化maxormins（目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标）
        Dim = 2  # 初始化Dim（决策变量维数）
        varTypes = [0, 0]  # 初始化varTypes（决策变量的类型，元素为0表示对应的变量是连续的；1表示是离散的）
        lb = [2 ** (-8)] * Dim  # 决策变量下界
        ub = [2 ** 8] * Dim  # 决策变量上界
        lbin = [1] * Dim  # 决策变量下边界（0表示不包含该变量的下边界，1表示包含）
        ubin = [1] * Dim  # 决策变量上边界（0表示不包含该变量的上边界，1表示包含）
        # 调用父类构造方法完成实例化
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)
        # 目标函数计算中用到的一些数据
        fp = open('iris_train.data')
        datas = []
        data_targets = []
        for line in fp.readlines():
            line_data = line.strip('\n').split(',')
            data = []
            for i in line_data[0:4]:
                data.append(float(i))
            datas.append(data)
            data_targets.append(line_data[4])
        fp.close()
        self.data = preprocessing.scale(np.array(datas))  # 训练集的特征数据（归一化）
        self.dataTarget = np.array(data_targets)
        # 设置用多线程还是多进程
        self.PoolType = PoolType
        if self.PoolType == 'Thread':
            self.pool = ThreadPool(2)  # 设置池的大小
        elif self.PoolType == 'Process':
            num_cores = int(mp.cpu_count())  # 获得计算机的核心数
            self.pool = ProcessPool(num_cores)  # 设置池的大小

    def aimFunc(self, pop):  # 目标函数，采用多线程加速计算
        Vars = pop.Phen  # 得到决策变量矩阵
        args = list(
            zip(list(range(pop.sizes)), [Vars] * pop.sizes, [self.data] * pop.sizes, [self.dataTarget] * pop.sizes))
        if self.PoolType == 'Thread':
            pop.ObjV = np.array(list(self.pool.map(subAimFunc, args)))
        elif self.PoolType == 'Process':
            result = self.pool.map_async(subAimFunc, args)
            result.wait()
            pop.ObjV = np.array(result.get())

    def test(self, C, G):  # 代入优化后的C、Gamma对测试集进行检验
        # 读取测试集数据
        fp = open('iris_test.data')
        datas = []
        data_targets = []
        for line in fp.readlines():
            line_data = line.strip('\n').split(',')
            data = []
            for i in line_data[0:4]:
                data.append(float(i))
            datas.append(data)
            data_targets.append(line_data[4])
        fp.close()
        data_test = preprocessing.scale(np.array(datas))  # 测试集的特征数据（归一化）
        dataTarget_test = np.array(data_targets)  # 测试集的标签数据
        svc = svm.SVC(C=C, kernel='rbf', gamma=G).fit(self.data, self.dataTarget)  # 创建分类器对象并用训练集的数据拟合分类器模型
        dataTarget_predict = svc.predict(data_test)  # 采用训练好的分类器对象对测试集数据进行预测
        print("测试集数据分类正确率 = %s%%" % (
                len(np.where(dataTarget_predict == dataTarget_test)[0]) / len(dataTarget_test) * 100))


def subAimFunc(args):
    i = args[0]
    Vars = args[1]
    data = args[2]
    dataTarget = args[3]
    C = Vars[i, 0]
    G = Vars[i, 1]
    svc = svm.SVC(C=C, kernel='rbf', gamma=G).fit(data, dataTarget)  # 创建分类器对象并用训练集的数据拟合分类器模型
    scores = cross_val_score(svc, data, dataTarget, cv=30)  # 计算交叉验证的得分
    ObjV_i = [scores.mean()]  # 把交叉验证的平均得分作为目标函数值
    return ObjV_i

main.py

# -*- coding: utf-8 -*-
import geatpy as ea  # import geatpy
from MyProblem import MyProblem  # 导入自定义问题接口

if __name__ == '__main__':
    """===============================实例化问题对象==========================="""
    PoolType = 'Thread'  # 设置采用多线程，若修改为: PoolType = 'Process'，则表示用多进程
    problem = MyProblem(PoolType)  # 生成问题对象
    """=================================种群设置=============================="""
    Encoding = 'RI'  # 编码方式
    NIND = 50  # 种群规模
    Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders)  # 创建区域描述器
    population = ea.Population(Encoding, Field, NIND)  # 实例化种群对象（此时种群还没被初始化，仅仅是完成种群对象的实例化）
    """===============================算法参数设置============================="""
    myAlgorithm = ea.soea_DE_rand_1_bin_templet(problem, population)  # 实例化一个算法模板对象
    myAlgorithm.MAXGEN = 30  # 最大进化代数
    myAlgorithm.trappedValue = 1e-6  # “进化停滞”判断阈值
    myAlgorithm.maxTrappedCount = 10  # 进化停滞计数器最大上限值，如果连续maxTrappedCount代被判定进化陷入停滞，则终止进化
    myAlgorithm.logTras = 1  # 设置每隔多少代记录日志，若设置成0则表示不记录日志
    myAlgorithm.verbose = True  # 设置是否打印输出日志信息
    myAlgorithm.drawing = 1  # 设置绘图方式（0：不绘图；1：绘制结果图；2：绘制目标空间过程动画；3：绘制决策空间过程动画）
    """==========================调用算法模板进行种群进化========================"""
    [BestIndi, population] = myAlgorithm.run()  # 执行算法模板，得到最优个体以及最后一代种群
    BestIndi.save()  # 把最优个体的信息保存到文件中
    """=================================输出结果=============================="""
    print('评价次数：%s' % myAlgorithm.evalsNum)
    print('时间已过 %s 秒' % myAlgorithm.passTime)
    if BestIndi.sizes != 0:
        print('最优的目标函数值为：%s' % (BestIndi.ObjV[0][0]))
        print('最优的控制变量值为：')
        for i in range(BestIndi.Phen.shape[1]):
            print(BestIndi.Phen[0, i])
        """=================================检验结果==============================="""
        problem.test(C=BestIndi.Phen[0, 0], G=BestIndi.Phen[0, 1])
    else:
        print('没找到可行解。')

1.7问题：Myproblem.py

该案例展示了如何利用SCOOP库进行分布式加速计算Geatpy进化算法程序，
本案例和soea_demo6类似，同样是用进化算法来优化SVM的参数C和Gamma，
不同的是，本案例选用更庞大的数据集，使得每次训练SVM模型时耗时更高，从而更适合采用分布式加速计算。
该数据集存放在同目录下的Data_User_Modeling_Dataset_Hamdi Tolga KAHRAMAN.xls中，
有关该数据集的详细描述详见http://archive.ics.uci.edu/ml/datasets/User+Knowledge+Modeling。
在执行本案例前，需要确保正确安装sklearn以及SCOOP，以保证SVM和SCOOP部分的代码能够正常执行。
SCOOP安装方法：控制台执行命令pip install scoop
分布式加速计算注意事项：
1.当aimFunc()函数十分耗时，比如无法矩阵化计算、或者是计算单个个体的目标函数值就需要很长时间时，
适合采用分布式计算，否则贸然采用分布式计算反而会大大降低性能。
2.分布式执行方法：python -m scoop -n 10 main.py 其中10表示把计算任务分发给10个workers。
非分布式执行方法：python main.py

# -*- coding: utf-8 -*-
import numpy as np
import xlrd
import geatpy as ea
from sklearn import svm
from sklearn import preprocessing
from sklearn.model_selection import cross_val_score
from scoop import futures

"""
该案例展示了如何利用SCOOP库进行分布式加速计算Geatpy进化算法程序，
本案例和soea_demo6类似，同样是用进化算法来优化SVM的参数C和Gamma，
不同的是，本案例选用更庞大的数据集，使得每次训练SVM模型时耗时更高，从而更适合采用分布式加速计算。
该数据集存放在同目录下的Data_User_Modeling_Dataset_Hamdi Tolga KAHRAMAN.xls中，
有关该数据集的详细描述详见http://archive.ics.uci.edu/ml/datasets/User+Knowledge+Modeling。
在执行本案例前，需要确保正确安装sklearn以及SCOOP，以保证SVM和SCOOP部分的代码能够正常执行。
SCOOP安装方法：控制台执行命令pip install scoop
分布式加速计算注意事项：
1.当aimFunc()函数十分耗时，比如无法矩阵化计算、或者是计算单个个体的目标函数值就需要很长时间时，
  适合采用分布式计算，否则贸然采用分布式计算反而会大大降低性能。
2.分布式执行方法：python -m scoop -n 10 main.py 其中10表示把计算任务分发给10个workers。
  非分布式执行方法：python main.py
"""


class MyProblem(ea.Problem):  # 继承Problem父类
    def __init__(self):
        name = 'MyProblem'  # 初始化name（函数名称，可以随意设置）
        M = 1  # 初始化M（目标维数）
        maxormins = [-1]  # 初始化maxormins（目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标）
        Dim = 2  # 初始化Dim（决策变量维数）
        varTypes = [0, 0]  # 初始化varTypes（决策变量的类型，元素为0表示对应的变量是连续的；1表示是离散的）
        lb = [2 ** (-8), 2 ** (-8)]  # 决策变量下界
        ub = [2 ** 8, 1]  # 决策变量上界
        lbin = [1] * Dim  # 决策变量下边界（0表示不包含该变量的下边界，1表示包含）
        ubin = [1] * Dim  # 决策变量上边界（0表示不包含该变量的上边界，1表示包含）
        # 调用父类构造方法完成实例化
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)
        # 目标函数计算中用到的一些数据
        workbook = xlrd.open_workbook(
            "Data_User_Modeling_Dataset_Hamdi Tolga KAHRAMAN.xls")  # 打开文件，获取excel文件的workbook（工作簿）对象
        worksheet = workbook.sheet_by_name("Training_Data")  # 通过sheet名获得sheet对象
        self.data = np.vstack([worksheet.col_values(0)[1:],
                               worksheet.col_values(1)[1:],
                               worksheet.col_values(2)[1:],
                               worksheet.col_values(3)[1:],
                               worksheet.col_values(4)[1:]]).T  # 获取特征数据
        self.data = preprocessing.scale(self.data)  # 归一化特征数据
        self.dataTarget = worksheet.col_values(5)[1:]  # 获取标签数据

    def aimFunc(self, pop):  # 目标函数
        Vars = pop.Phen  # 得到决策变量矩阵
        args = list(
            zip(list(range(pop.sizes)), [Vars] * pop.sizes, [self.data] * pop.sizes, [self.dataTarget] * pop.sizes))
        pop.ObjV = np.array(list(futures.map(subAimFunc, args)))  # 调用SCOOP的map函数进行分布式计算，并构造种群所有个体的目标函数值矩阵ObjV

    def test(self, C, G):  # 代入优化后的C、Gamma对测试集进行检验
        # 读取测试集数据
        workbook = xlrd.open_workbook(
            "Data_User_Modeling_Dataset_Hamdi Tolga KAHRAMAN.xls")  # 打开文件，获取excel文件的workbook（工作簿）对象
        worksheet = workbook.sheet_by_name("Test_Data")  # 通过sheet名获得sheet对象
        data_test = np.vstack([worksheet.col_values(0)[1:],
                               worksheet.col_values(1)[1:],
                               worksheet.col_values(2)[1:],
                               worksheet.col_values(3)[1:],
                               worksheet.col_values(4)[1:]]).T  # 获取特征数据
        data_test = preprocessing.scale(data_test)  # 归一化特征数据
        dataTarget_test = worksheet.col_values(5)[1:]  # 获取标签数据
        svc = svm.SVC(C=C, kernel='rbf', gamma=G).fit(self.data, self.dataTarget)  # 创建分类器对象并用训练集的数据拟合分类器模型
        dataTarget_predict = svc.predict(data_test)  # 采用训练好的分类器对象对测试集数据进行预测
        print("测试集数据分类正确率 = %s%%" % (
                len(np.where(dataTarget_predict == dataTarget_test)[0]) / len(dataTarget_test) * 100))


def subAimFunc(args):  # 单独计算单个个体的目标函数值
    i = args[0]
    Vars = args[1]
    data = args[2]
    dataTarget = args[3]
    C = Vars[i, 0]
    G = Vars[i, 1]
    svc = svm.SVC(C=C, kernel='rbf', gamma=G).fit(data, dataTarget)  # 创建分类器对象并用训练集的数据拟合分类器模型
    scores = cross_val_score(svc, data, dataTarget, cv=20)  # 计算交叉验证的得分
    ObjV_i = [scores.mean()]  # 把交叉验证的平均得分作为目标函数值
    return ObjV_i

main.py

# -*- coding: utf-8 -*-
import geatpy as ea  # import geatpy
from MyProblem import MyProblem  # 导入自定义问题接口

if __name__ == '__main__':
    """===============================实例化问题对象==========================="""
    problem = MyProblem()  # 生成问题对象
    """=================================种群设置=============================="""
    Encoding = 'RI'  # 编码方式
    NIND = 20  # 种群规模
    Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders)  # 创建区域描述器
    population = ea.Population(Encoding, Field, NIND)  # 实例化种群对象（此时种群还没被初始化，仅仅是完成种群对象的实例化）
    """===============================算法参数设置============================="""
    myAlgorithm = ea.soea_DE_rand_1_bin_templet(problem, population)  # 实例化一个算法模板对象
    myAlgorithm.MAXGEN = 30  # 最大进化代数
    myAlgorithm.trappedValue = 1e-6  # “进化停滞”判断阈值
    myAlgorithm.maxTrappedCount = 10  # 进化停滞计数器最大上限值，如果连续maxTrappedCount代被判定进化陷入停滞，则终止进化
    myAlgorithm.logTras = 1  # 设置每隔多少代记录日志，若设置成0则表示不记录日志
    myAlgorithm.verbose = True  # 设置是否打印输出日志信息
    myAlgorithm.drawing = 1  # 设置绘图方式（0：不绘图；1：绘制结果图；2：绘制目标空间过程动画；3：绘制决策空间过程动画）
    """==========================调用算法模板进行种群进化========================"""
    [BestIndi, population] = myAlgorithm.run()  # 执行算法模板，得到最优个体以及最后一代种群
    BestIndi.save()  # 把最优个体的信息保存到文件中
    """=================================输出结果=============================="""
    print('评价次数：%s' % myAlgorithm.evalsNum)
    print('时间已过 %s 秒' % myAlgorithm.passTime)
    if BestIndi.sizes != 0:
        print('最优的目标函数值为：%s' % (BestIndi.ObjV[0][0]))
        print('最优的控制变量值为：')
        for i in range(BestIndi.Phen.shape[1]):
            print(BestIndi.Phen[0, i])
        """=================================检验结果==============================="""
        problem.test(C=BestIndi.Phen[0, 0], G=BestIndi.Phen[0, 1])
    else:
        print('没找到可行解。')

EA-KMeans

该案例展示了如何利用进化算法进行仿k-means聚类（可称之为EA-KMeans算法）。
本案例采用与k-means类似的聚类方法，采用展开的聚类中心点坐标作为染色体的编码，基本流程大致如下：
\1) 初始化种群染色体。
\2) 迭代进化（循环第3步至第6步），直到满足终止条件。
\3) 重组变异，然后根据得到的新染色体计算出对应的聚类中心点。
\4) 计算各数据点到聚类中心点的欧式距离。
\5) 把与各中心点关联的数据点的坐标平均值作为新的中心点，并以此更新种群的染色体。
\6) 把各中心点到与其关联的数据点之间的距离之和作为待优化的目标函数值。
注意：导入的数据是以列为特征的，即每一列代表一个特征（如第一列代表x，第二列代表y……）。

# -*- coding: utf-8 -*-
import numpy as np
import geatpy as ea
import matplotlib.pyplot as plt
from scipy.spatial.distance import cdist

class MyProblem(ea.Problem):  # 继承Problem父类
    def __init__(self):
        # 目标函数计算中用到的一些数据
        self.datas = np.loadtxt('data.csv', delimiter=',')  # 读取数据
        self.k = 4  # 分类数目
        # 问题类设置
        name = 'MyProblem'  # 初始化name（函数名称，可以随意设置）
        M = 1  # 初始化M（目标维数）
        maxormins = [1]  # 初始化maxormins（目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标）
        Dim = self.datas.shape[1] * self.k  # 初始化Dim
        varTypes = [0] * Dim  # 初始化varTypes（决策变量的类型，元素为0表示对应的变量是连续的；1表示是离散的）
        lb = list(np.min(self.datas, 0)) * self.k  # 决策变量下界
        ub = list(np.max(self.datas, 0)) * self.k  # 决策变量上界
        lbin = [1] * Dim  # 决策变量下边界（0表示不包含该变量的下边界，1表示包含）
        ubin = [1] * Dim  # 决策变量上边界（0表示不包含该变量的上边界，1表示包含）
        # 调用父类构造方法完成实例化
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)

    def aimFunc(self, pop):  # 目标函数
        centers = pop.Phen.reshape(int(pop.sizes * self.k), int(pop.Phen.shape[1] / self.k))  # 得到聚类中心
        dis = cdist(centers, self.datas, 'euclidean')  # 计算距离
        dis_split = dis.reshape(pop.sizes, self.k, self.datas.shape[0])  # 分割距离矩阵，把各个聚类中心到各个点之间的距离的数据分开
        labels = np.argmin(dis_split, 1)[0]  # 得到聚类标签值
        uni_labels = np.unique(labels)
        for i in range(len(uni_labels)):
            centers[uni_labels[i], :] = np.mean(self.datas[np.where(labels == uni_labels[i])[0], :], 0)
        # 直接修改染色体为已知的更优值，加快收敛
        pop.Chrom = centers.reshape(pop.sizes, self.k * centers.shape[1])
        pop.Phen = pop.decoding()  # 染色体解码（要同步修改Phen，否则后面会导致数据不一致）
        dis = cdist(centers, self.datas, 'euclidean')
        dis_split = dis.reshape(pop.sizes, self.k, self.datas.shape[0])
        pop.ObjV = np.sum(np.min(dis_split, 1), 1, keepdims=True)  # 计算个体的目标函数值

    def draw(self, centers):  # 绘制聚类效果图
        dis = cdist(centers, self.datas, 'euclidean')
        dis_split = dis.reshape(1, self.k, self.datas.shape[0])
        labels = np.argmin(dis_split, 1)[0]
        colors = ['r', 'g', 'b', 'y']
        fig = plt.figure()
        ax = fig.add_subplot(111, projection='3d')
        for i in range(self.k):
            idx = np.where(labels == i)[0]  # 找到同一类的点的下标
            datas = self.datas[idx, :]
            ax.scatter(datas[:, 0], datas[:, 1], datas[:, 2], c=colors[i])

main.py

# -*- coding: utf-8 -*-
import geatpy as ea  # import geatpy
from MyProblem import MyProblem  # 导入自定义问题接口

if __name__ == '__main__':
    """===============================实例化问题对象==========================="""
    problem = MyProblem()  # 生成问题对象
    """=================================种群设置=============================="""
    Encoding = 'RI'  # 编码方式
    NIND = 2  # 种群规模
    Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders)  # 创建区域描述器
    population = ea.Population(Encoding, Field, NIND)  # 实例化种群对象
    """===============================算法参数设置============================="""
    myAlgorithm = ea.soea_DE_rand_1_L_templet(problem, population)
    myAlgorithm.MAXGEN = 20  # 最大进化代数
    myAlgorithm.trappedValue = 1e-4  # “进化停滞”判断阈值
    myAlgorithm.maxTrappedCount = 10  # 进化停滞计数器最大上限值，如果连续maxTrappedCount代被判定进化陷入停滞，则终止进化
    myAlgorithm.logTras = 1  # 设置每隔多少代记录日志，若设置成0则表示不记录日志
    myAlgorithm.verbose = True  # 设置是否打印输出日志信息
    myAlgorithm.drawing = 1  # 设置绘图方式（0：不绘图；1：绘制结果图；2：绘制目标空间过程动画；3：绘制决策空间过程动画）
    """==========================调用算法模板进行种群进化========================"""
    [BestIndi, population] = myAlgorithm.run()  # 执行算法模板，得到最优个体以及最后一代种群
    BestIndi.save()  # 把最优个体的信息保存到文件中
    """=================================输出结果=============================="""
    print('评价次数：%s' % myAlgorithm.evalsNum)
    print('时间已过 %s 秒' % myAlgorithm.passTime)
    if BestIndi.sizes != 0:
        print('最优的目标函数值为：%s' % (BestIndi.ObjV[0][0]))
        print('最优的聚类中心为：')
        Phen = BestIndi.Phen[0, :]
        centers = Phen.reshape(problem.k, int(len(Phen) / problem.k))  # 得到最优的聚类中心
        print(centers)
        """=================================检验结果==============================="""
        problem.draw(centers)
    else:
        print('没找到可行解。')

1.9问题：Myproblem.py

该案例是soea_demo1的拓展，展示了如何利用多种群来进行单目标优化。
在执行脚本main.py中，通过调用带”multi”字样的进化算法模板来进行多种群进化优化。
max f = x * np.sin(10 * np.pi * x) + 2.0
s.t.
-1 <= x <= 2

# -*- coding: utf-8 -*-
import numpy as np
import geatpy as ea

class MyProblem(ea.Problem):  # 继承Problem父类
    def __init__(self):
        name = 'MyProblem'  # 初始化name（函数名称，可以随意设置）
        M = 1  # 初始化M（目标维数）
        maxormins = [-1]  # 初始化maxormins（目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标）
        Dim = 1  # 初始化Dim（决策变量维数）
        varTypes = [0] * Dim  # 初始化varTypes（决策变量的类型，元素为0表示对应的变量是连续的；1表示是离散的）
        lb = [-1]  # 决策变量下界
        ub = [2]  # 决策变量上界
        lbin = [1] * Dim  # 决策变量下边界（0表示不包含该变量的下边界，1表示包含）
        ubin = [1] * Dim  # 决策变量上边界（0表示不包含该变量的上边界，1表示包含）
        # 调用父类构造方法完成实例化
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)

    def aimFunc(self, pop):  # 目标函数
        x = pop.Phen  # 得到决策变量矩阵
        pop.ObjV = x * np.sin(10 * np.pi * x) + 2.0  # 计算目标函数值，赋值给pop种群对象的ObjV属性

main.py

# -*- coding: utf-8 -*-
import geatpy as ea  # import geatpy
from MyProblem import MyProblem  # 导入自定义问题接口

if __name__ == '__main__':
    """===============================实例化问题对象==========================="""
    problem = MyProblem()  # 生成问题对象
    """=================================种群设置=============================="""
    Encoding = 'RI'  # 编码方式
    NINDs = [5, 10, 15, 20]  # 种群规模
    population = []  # 创建种群列表
    for i in range(len(NINDs)):
        Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders)  # 创建区域描述器
        population.append(ea.Population(Encoding, Field, NINDs[i]))  # 实例化种群对象（此时种群还没被初始化，仅仅是完成种群对象的实例化）
    """===============================算法参数设置============================="""
    myAlgorithm = ea.soea_multi_SEGA_templet(problem, population)  # 实例化一个算法模板对象
    myAlgorithm.MAXGEN = 50  # 最大进化代数
    myAlgorithm.trappedValue = 1e-6  # “进化停滞”判断阈值
    myAlgorithm.maxTrappedCount = 5  # 进化停滞计数器最大上限值，如果连续maxTrappedCount代被判定进化陷入停滞，则终止进化
    myAlgorithm.logTras = 1  # 设置每隔多少代记录日志，若设置成0则表示不记录日志
    myAlgorithm.verbose = True  # 设置是否打印输出日志信息
    myAlgorithm.drawing = 1  # 设置绘图方式（0：不绘图；1：绘制结果图；2：绘制目标空间过程动画；3：绘制决策空间过程动画）
    """==========================调用算法模板进行种群进化========================"""
    [BestIndi, population] = myAlgorithm.run()  # 执行算法模板，得到最优个体以及最后一代种群
    BestIndi.save()  # 把最优个体的信息保存到文件中
    """=================================输出结果=============================="""
    print('评价次数：%s' % myAlgorithm.evalsNum)
    print('时间已过 %s 秒' % myAlgorithm.passTime)
    if BestIndi.sizes != 0:
        print('最优的目标函数值为：%s' % (BestIndi.ObjV[0][0]))
        print('最优的控制变量值为：')
        for i in range(BestIndi.Phen.shape[1]):
            print(BestIndi.Phen[0, i])
    else:
        print('没找到可行解。')

1.10问题：Myproblem.py

该案例展示了一个带等式约束的连续型决策变量最大化目标的单目标优化问题，
该函数存在多个欺骗性很强的局部最优点，
与soea_demo2不同之处是采用先验知识帮助进化优化。
max f = 4x1 + 2x2 + x3
s.t.
2x1 + x2 - 1 <= 0
x1 + 2x3 - 2 <= 0
x1 + x2 + x3 - 1 == 0
0 <= x1,x2 <= 1
0 < x3 < 2

# -*- coding: utf-8 -*-
"""MyProblem.py"""
import numpy as np
import geatpy as ea


class MyProblem(ea.Problem):  # 继承Problem父类
    def __init__(self):
        name = 'MyProblem'  # 初始化name（函数名称，可以随意设置）
        M = 1  # 初始化M（目标维数）
        maxormins = [-1]  # 初始化maxormins（目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标）
        Dim = 3  # 初始化Dim（决策变量维数）
        varTypes = [0] * Dim  # 初始化varTypes（决策变量的类型，元素为0表示对应的变量是连续的；1表示是离散的）
        lb = [0, 0, 0]  # 决策变量下界
        ub = [1, 1, 2]  # 决策变量上界
        lbin = [1, 1, 0]  # 决策变量下边界（0表示不包含该变量的下边界，1表示包含）
        ubin = [1, 1, 0]  # 决策变量上边界（0表示不包含该变量的上边界，1表示包含）
        # 调用父类构造方法完成实例化
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)

    def aimFunc(self, pop):  # 目标函数
        Vars = pop.Phen  # 得到决策变量矩阵
        x1 = Vars[:, [0]]
        x2 = Vars[:, [1]]
        x3 = Vars[:, [2]]
        pop.ObjV = 4 * x1 + 2 * x2 + x3  # 计算目标函数值，赋值给pop种群对象的ObjV属性
        # 采用可行性法则处理约束
        pop.CV = np.hstack([2 * x1 + x2 - 1,
                            x1 + 2 * x3 - 2,
                            np.abs(x1 + x2 + x3 - 1)])

    def calReferObjV(self):  # 设定目标数参考值（本问题目标函数参考值设定为理论最优值）
        referenceObjV = np.array([[2.5]])
        return referenceObjV

main.py

# -*- coding: utf-8 -*-
import numpy as np
import geatpy as ea  # import geatpy
from MyProblem import MyProblem  # 导入自定义问题接口

if __name__ == '__main__':
    """================================实例化问题对象==========================="""
    problem = MyProblem()  # 生成问题对象
    """==================================种群设置=============================="""
    Encoding = 'RI'  # 编码方式
    NIND = 20  # 种群规模
    Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders)  # 创建区域描述器
    population = ea.Population(Encoding, Field, NIND)  # 实例化种群对象（此时种群还没被初始化，仅仅是完成种群对象的实例化）
    """================================算法参数设置============================="""
    myAlgorithm = ea.soea_DE_currentToBest_1_bin_templet(problem, population)  # 实例化一个算法模板对象
    myAlgorithm.MAXGEN = 400  # 最大进化代数
    myAlgorithm.mutOper.F = 0.7  # 差分进化中的参数F
    myAlgorithm.recOper.XOVR = 0.7  # 重组概率
    myAlgorithm.logTras = 1  # 设置每隔多少代记录日志，若设置成0则表示不记录日志
    myAlgorithm.verbose = True  # 设置是否打印输出日志信息
    myAlgorithm.drawing = 1  # 设置绘图方式（0：不绘图；1：绘制结果图；2：绘制目标空间过程动画；3：绘制决策空间过程动画）
    """===========================根据先验知识创建先知种群========================"""
    prophetChrom = np.array([[0.4, 0.2, 0.4]])  # 假设已知[0.4, 0.2, 0.4]为一条比较优秀的染色体
    prophetPop = ea.Population(Encoding, Field, 1, prophetChrom)  # 实例化种群对象（设置个体数为1）
    myAlgorithm.call_aimFunc(prophetPop)  # 计算先知种群的目标函数值及约束（假如有约束）
    """===========================调用算法模板进行种群进化========================"""
    [BestIndi, population] = myAlgorithm.run(prophetPop)  # 执行算法模板，得到最优个体以及最后一代种群
    BestIndi.save()  # 把最优个体的信息保存到文件中
    """=================================输出结果==============================="""
    print('评价次数：%s' % (myAlgorithm.evalsNum))
    print('时间已过 %s 秒' % (myAlgorithm.passTime))
    if BestIndi.sizes != 0:
        print('最优的目标函数值为：%s' % (BestIndi.ObjV[0][0]))
        print('最优的控制变量值为：')
        for i in range(BestIndi.Phen.shape[1]):
            print(BestIndi.Phen[0, i])
    else:
        print('没找到可行解。')

1.11问题：Myproblem.py

该案例展示2个决策变量的单目标优化，决策变量的值将取自于一个设定好的变量集合。
max f = (-1+x1+((6-x2)*x2-2)*x2)**2+(-1+x1+((x2+2)*x2-10)*x2)**2
s.t.
x∈{1.1, 1, 0, 3, 5.5, 7.2, 9}

# -*- coding: utf-8 -*-
import numpy as np
import geatpy as ea

"""
该案例展示2个决策变量的单目标优化，决策变量的值将取自于一个设定好的变量集合。
max f = (-1+x1+((6-x2)*x2-2)*x2)**2+(-1+x1+((x2+2)*x2-10)*x2)**2
s.t.
x∈{1.1, 1, 0, 3, 5.5, 7.2, 9}
"""


class MyProblem(ea.Problem):  # 继承Problem父类
    def __init__(self):
        name = 'MyProblem'  # 初始化name（函数名称，可以随意设置）
        M = 1  # 初始化M（目标维数）
        maxormins = [1]  # 初始化maxormins（目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标）
        self.var_set = np.array([1.1, 1, 0, 3, 5.5, 7.2, 9])  # 设定一个集合，要求决策变量的值取自于该集合
        Dim = 2  # 初始化Dim（决策变量维数）
        varTypes = [1] * Dim  # 初始化varTypes（决策变量的类型，元素为0表示对应的变量是连续的；1表示是离散的）
        lb = [0, 0]  # 决策变量下界
        ub = [6, 6]  # 决策变量上界
        lbin = [1] * Dim  # 决策变量下边界（0表示不包含该变量的下边界，1表示包含）
        ubin = [1] * Dim  # 决策变量上边界（0表示不包含该变量的上边界，1表示包含）
        # 调用父类构造方法完成实例化
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)
        

    def aimFunc(self, pop):  # 目标函数
        Vars = pop.Phen.astype(np.int32)  # 强制类型转换确保元素是整数
        x1 = self.var_set[Vars[:, [0]]]  # 得到所有的x1组成的列向量
        x2 = self.var_set[Vars[:, [1]]]  # 得到所有的x2组成的列向量
        pop.ObjV = (-1 + x1 + ((6 - x2) * x2 - 2) * x2)**2 + (-1 + x1 + ((x2 + 2)*x2 - 10)*x2)**2  # 计算目标函数值，赋值给pop种群对象的ObjV属性

main.py

# -*- coding: utf-8 -*-
import geatpy as ea  # import geatpy
from MyProblem import MyProblem  # 导入自定义问题接口

if __name__ == '__main__':
    """===============================实例化问题对象==========================="""
    problem = MyProblem()  # 生成问题对象
    """=================================种群设置=============================="""
    Encoding = 'RI'  # 编码方式
    NIND = 20  # 种群规模
    Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders)  # 创建区域描述器
    population = ea.Population(Encoding, Field, NIND)  # 实例化种群对象（此时种群还没被初始化，仅仅是完成种群对象的实例化）
    """================================算法参数设置============================="""
    myAlgorithm = ea.soea_DE_rand_1_bin_templet(problem, population)  # 实例化一个算法模板对象
    myAlgorithm.MAXGEN = 25  # 最大进化代数
    myAlgorithm.mutOper.F = 0.5  # 差分进化中的参数F
    myAlgorithm.recOper.XOVR = 0.2  # 重组概率
    myAlgorithm.trappedValue = 1e-6  # “进化停滞”判断阈值
    myAlgorithm.maxTrappedCount = 10  # 进化停滞计数器最大上限值，如果连续maxTrappedCount代被判定进化陷入停滞，则终止进化
    myAlgorithm.logTras = 1  # 设置每隔多少代记录日志，若设置成0则表示不记录日志
    myAlgorithm.verbose = True  # 设置是否打印输出日志信息
    myAlgorithm.drawing = 1  # 设置绘图方式（0：不绘图；1：绘制结果图；2：绘制目标空间过程动画；3：绘制决策空间过程动画）
    """===========================调用算法模板进行种群进化======================="""
    [BestIndi, population] = myAlgorithm.run()  # 执行算法模板，得到最优个体以及最后一代种群
    BestIndi.save()  # 把最优个体的信息保存到文件中
    """==================================输出结果=============================="""
    print('用时：%f 秒' % myAlgorithm.passTime)
    print('评价次数：%d 次' % myAlgorithm.evalsNum)
    if BestIndi.sizes != 0:
        print('最优的目标函数值为：%s' % BestIndi.ObjV[0][0])
        print('最优的控制变量值为：')
        for i in range(BestIndi.Phen.shape[1]):
            print(problem.var_set[BestIndi.Phen[0, i].astype(int)])
    else:
        print('没找到可行解。')