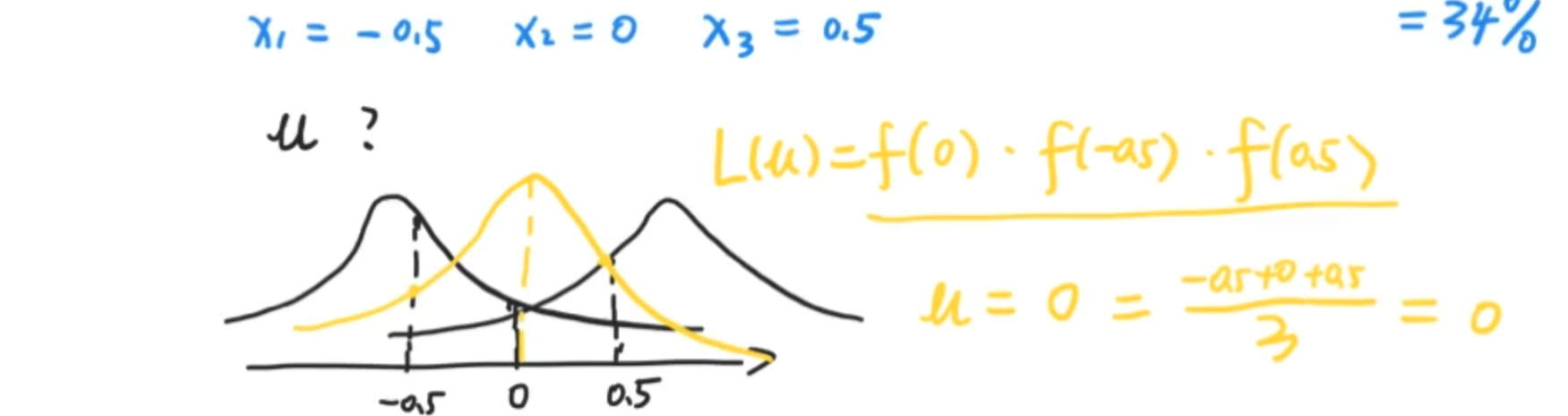概率论与数理分析
中央极限定理
中心、分散度、形状
它的中心思想是:无论你的样本总体有多抽象(就算不服从正态分布),但是只要样本数量足够大(n>=30)那么他们的样本均值一定服从正态分布

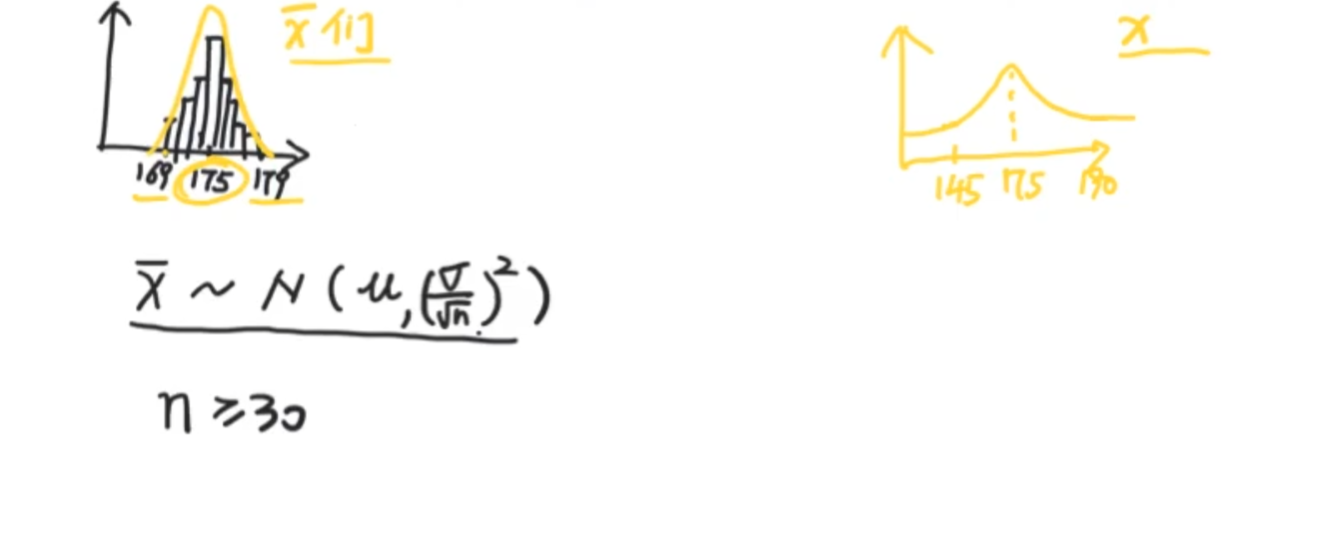

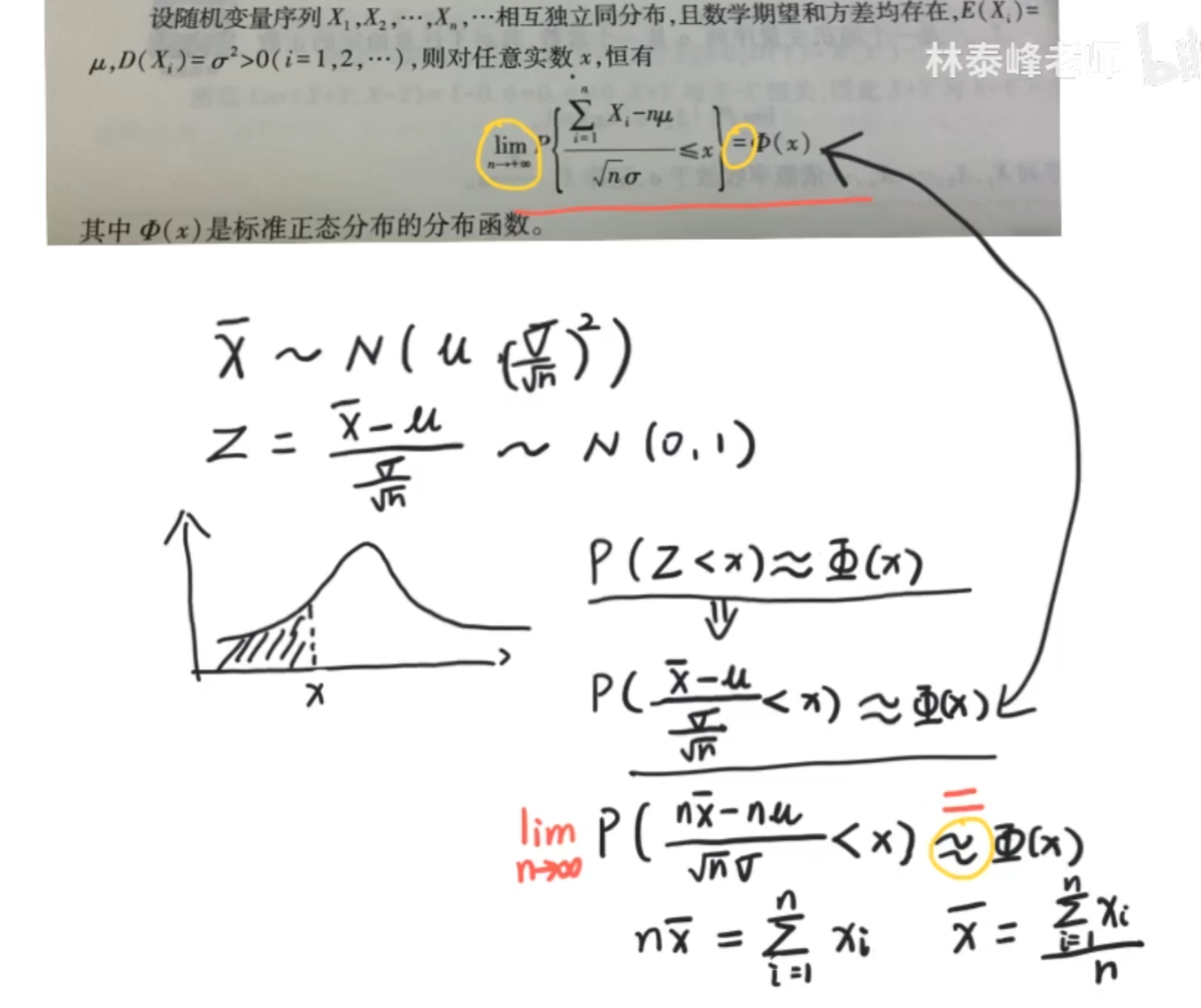
x^-服从正态分布N(u,…) 其中u为全部样本均值,…为方差,σ为总体标准差(SD也是Standard deviation),n为x ^-的个数
Z的公式为标准正态分布公式(归一化到0~1之间)
x^-为采样部分样本的均值。
关于lim,就是说,如果n>30,那么我们可以说该式子约等于φ(x),但,如果n足够大,趋近于极限,那肯定就直接等于了呗
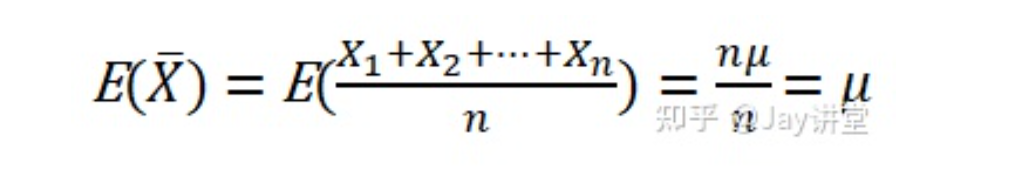
正太分布
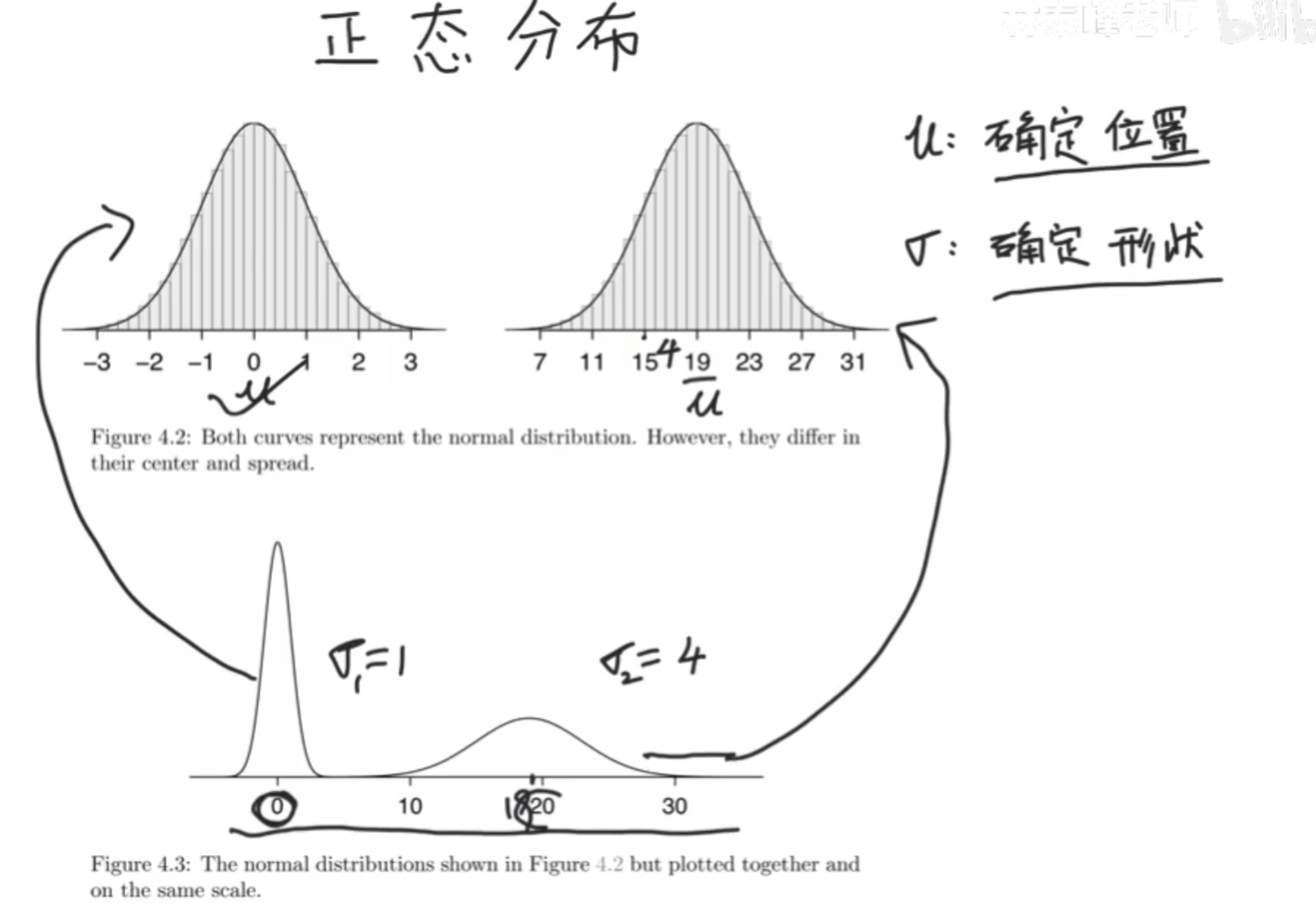
SAT与ACT同为美国高考,是两种形式,现在两位同学想要申请同一所学校,比较谁更优秀
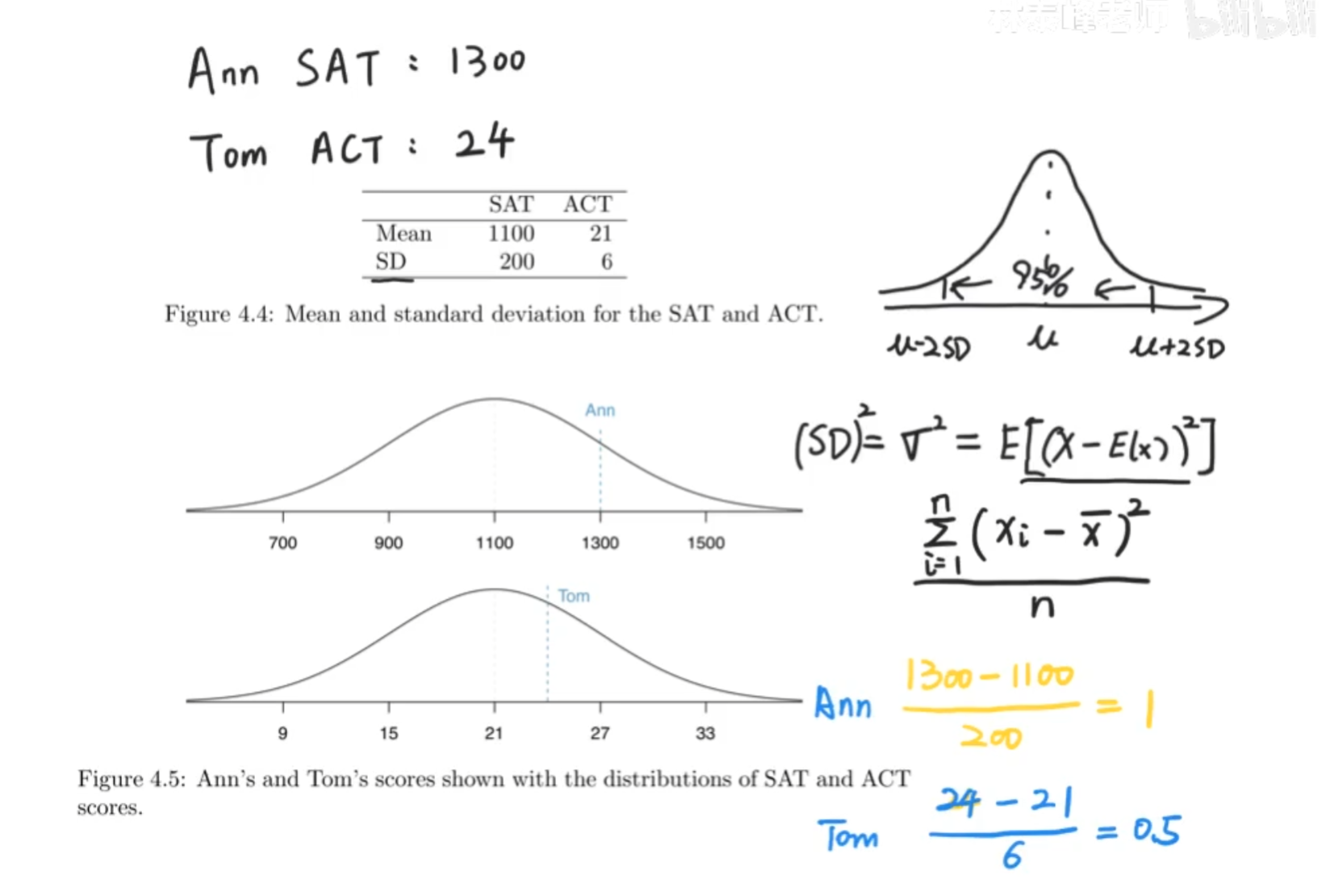
我们用标准差来计算,σ离中心越远,在同样大于平均值的情况,就说明谁更出众。
Z-score,含义就是数据距离均值的距离有几个标准差!!!!
因为x服从正态分布,所以z服从正态分布,并且z的公式就是标准正态分布的公式,即z的均值为0,z的标准差为1
一般的正态分布X N(μ,σ^2)
其概率密度函数为:f(x) = e^[-(x - μ)^2/(2σ^2)] / [√(2π)σ]
引入标准正态变量Z:z = (x - μ) / σ
可以算出 z的平均值为0、标准差为1:
z的平均值 = E(Z) = E(X- μ)/σ = (E(X)-μ)/σ = (μ-μ)/σ = 0
z的标准差 = E[(Z-E(Z))^2] = E[(X-μ)^2/σ^2]=σ^2/σ^2 = 1
因此标准正态变量的平均值是为0、标准差为1,记作:Z N(0,1)
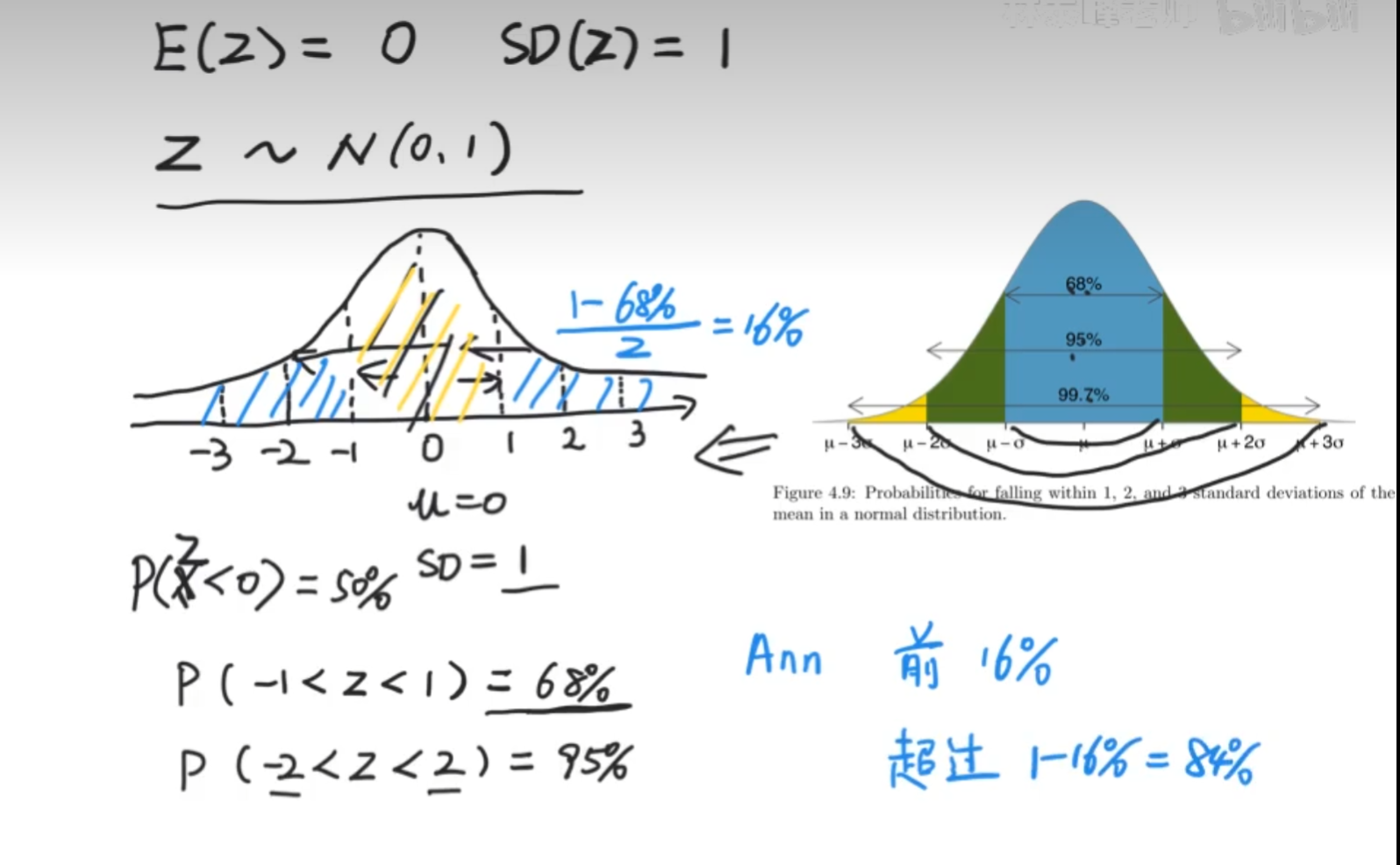
二项分布
二项分布:二项概率的集合
伯努利事件:独立的,可重复的,而且只有两个结果的事件
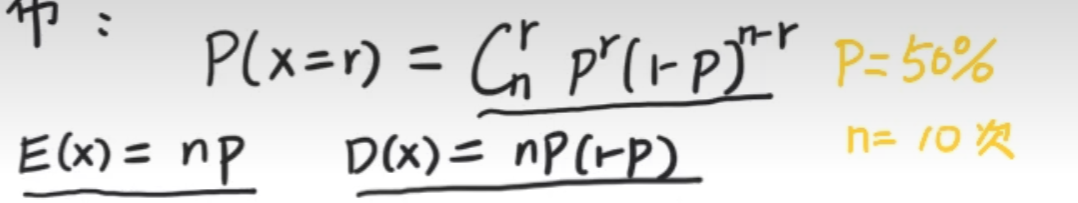
E(x)=np D(x)=np(1-p) 均值和方差
投十次,期望进五次
E(x)和D(x)证明:
证明:X可以分解成n个相互独立的,都服从以p为参数的(0-1)分布的随机变量之和:
X=X1+X2+…+Xn,Xi~b(1,p),i=1,2,…,n.
P{Xi=0}= 1 - p,P(Xi=1)=p.
EXi=0 * (1-p)+1 * p=p,
E(Xi^2^)=0^2^* (1-p)+1^2^ * p=p,
DXi=E(Xi^2^)-(EXi)^2^=p-p^2^=p(1-p).
EX=EX1+EX2+…+EXn=np,
DX=DX1+DX2+…+DXn=np(1-p).
D(X)=E{[X-E(X)]²}
=E{X² - 2XE(X)+[E(X)]²}
=E(X²)- 2E(X)E(X)+[E(X)]²
=E(X²)- [E(X)]²

因为我们是把这几个s看成不同的字母(s1,s2……)但是实际上在同一个位子上s1=s2=……是一样的,所以要除去重复的字母

二项分布从下图可以看出有一点点像正态分布,并且实际上,也确实可以做到近似
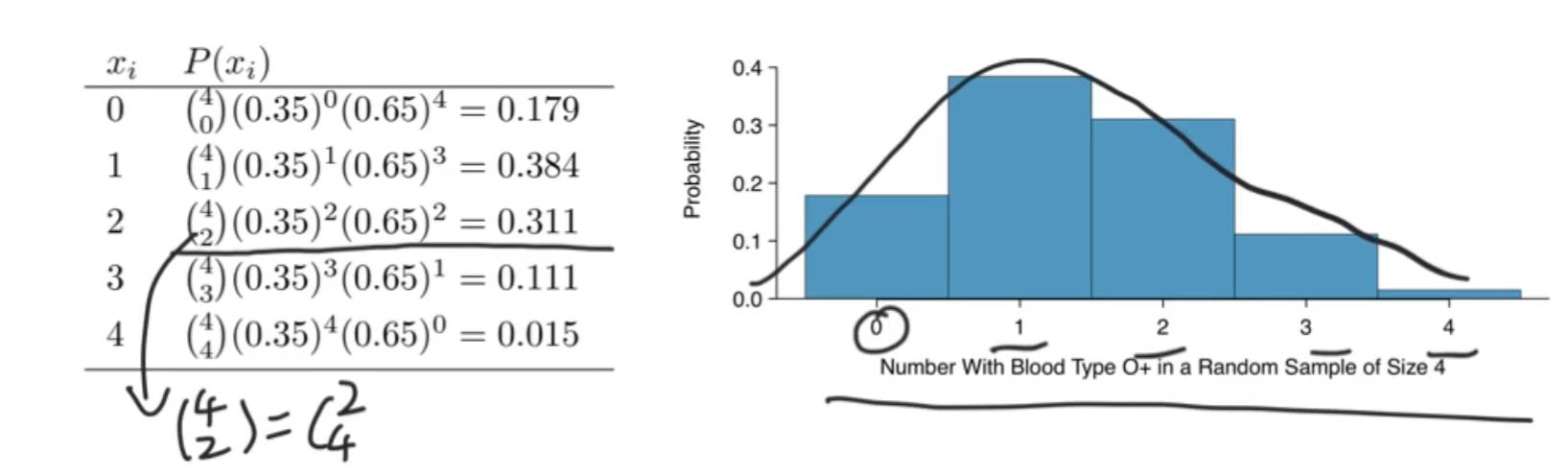
二项分布近似正态分布
为何有这样关系的原因是因为他们都服从0-1分布或者说是正态分布。
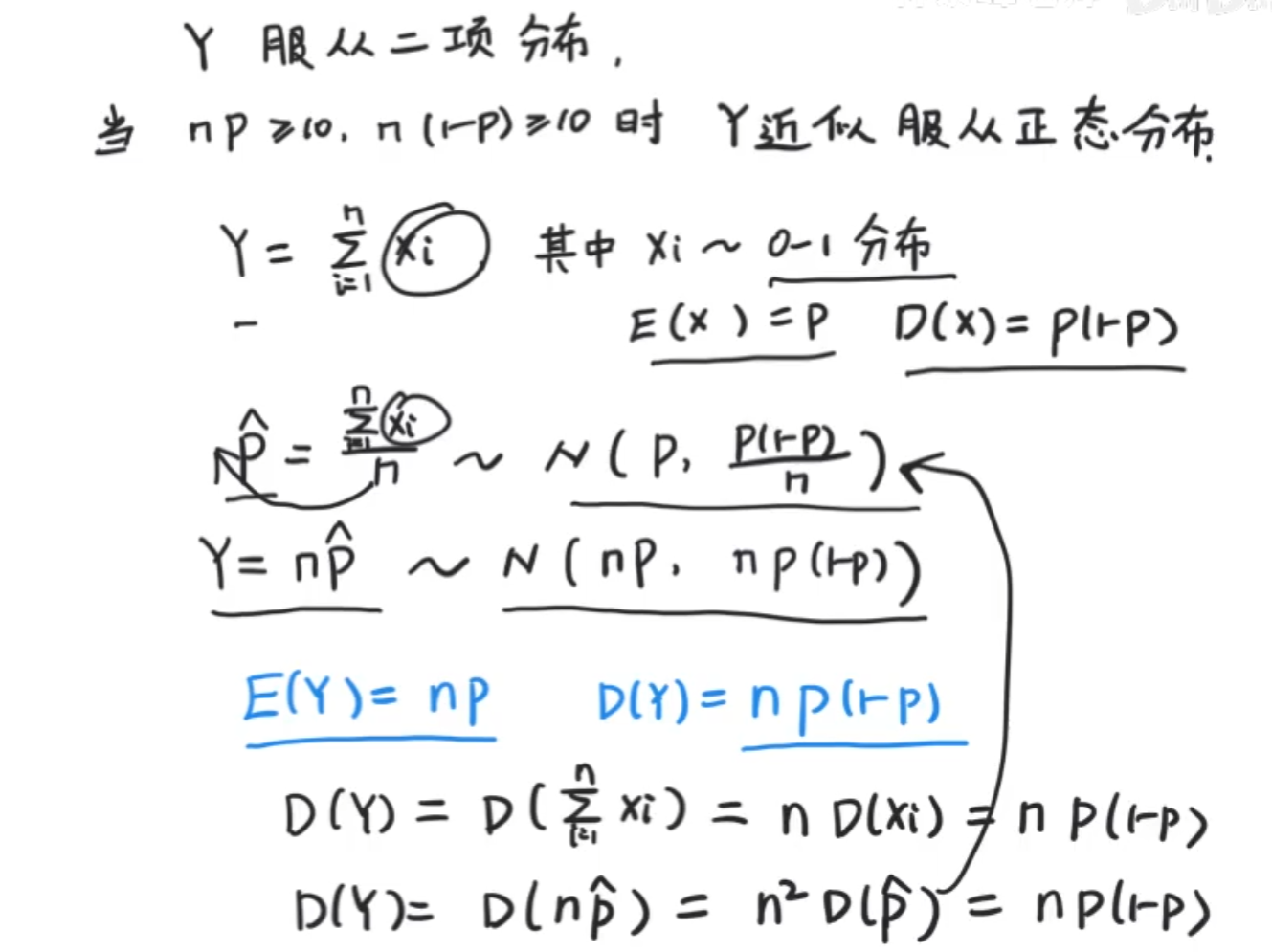
正态分布近似二项分布
n比较大时
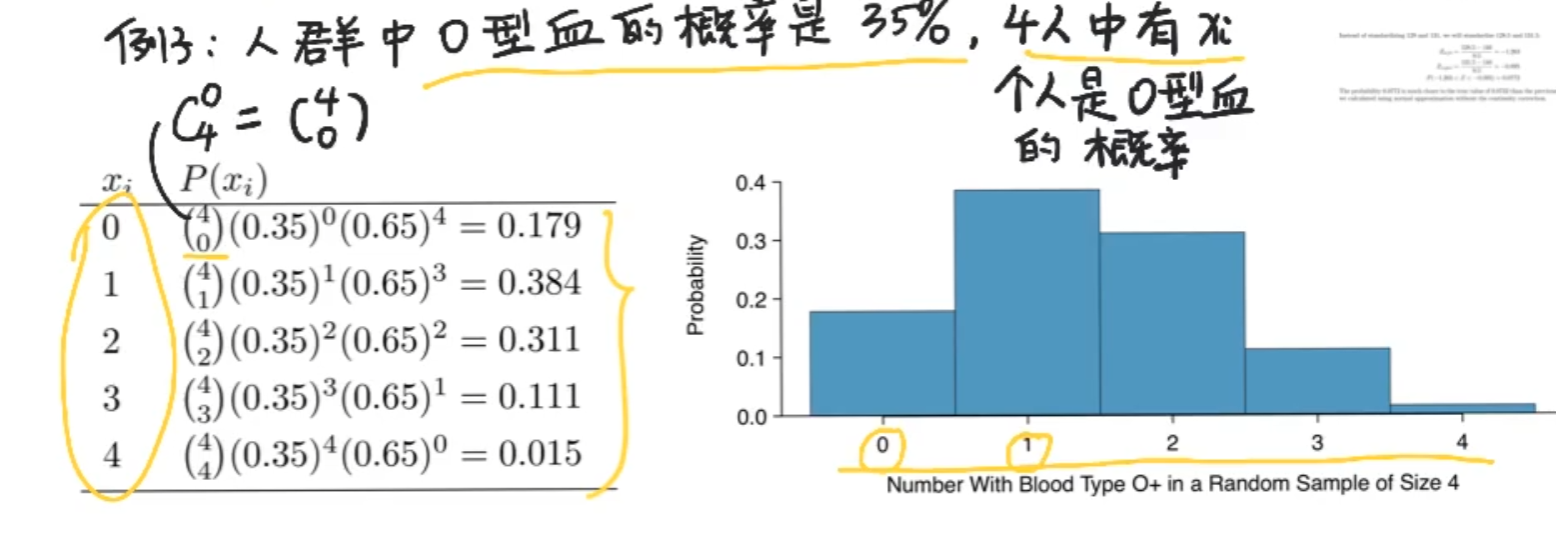
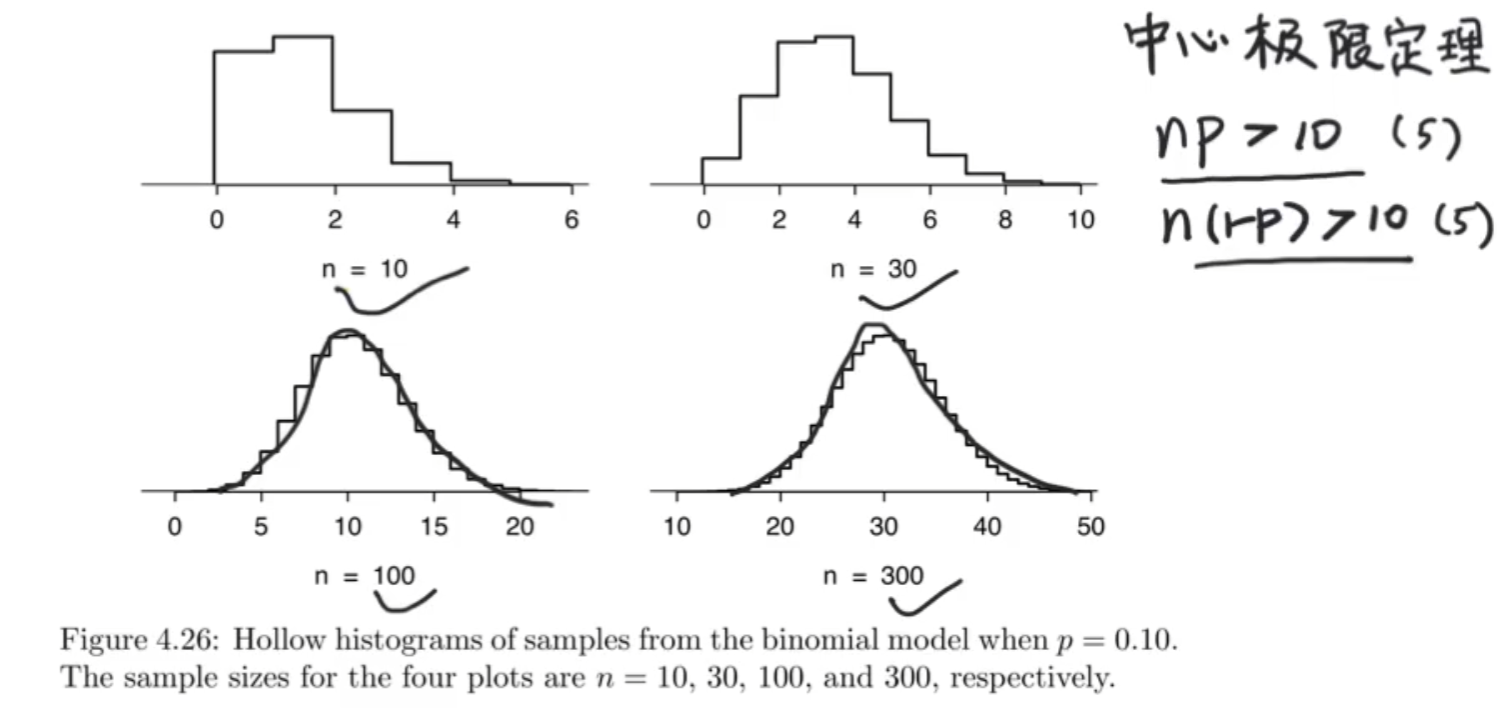
那么n需要多大呢?保守起见np>10并且n(1-p)>10,若不满足,且n很大,p很小,用泊松分布来近似二项分布

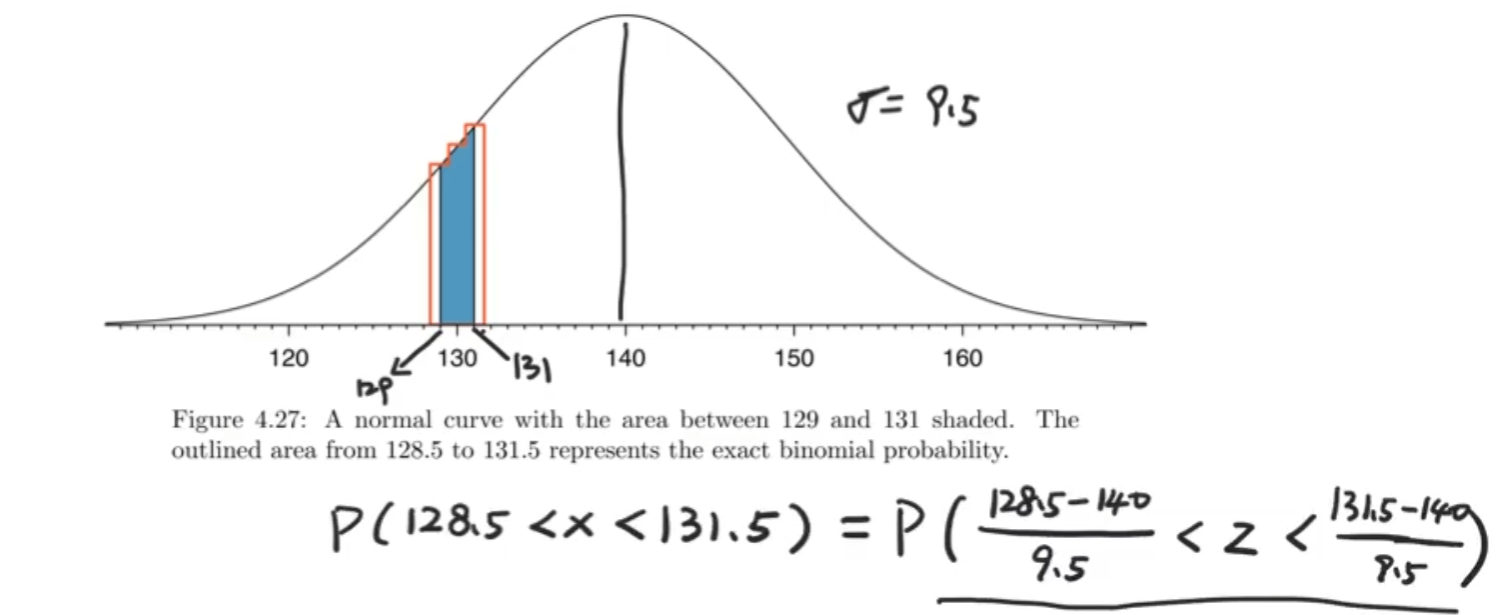
多少个标准差,如果我们用的是一个值,就比如说解出来的130.5,那么可能就会产生相当大的误差,通常是用一段范围来进行修正,这个就采用的取前后1.5的来求得一片区间替代单点。

泊松分布和指数分布
我们可以看到他们的数学期望是呈倒数关系,那么他们两种分布是否有某种关系呢?
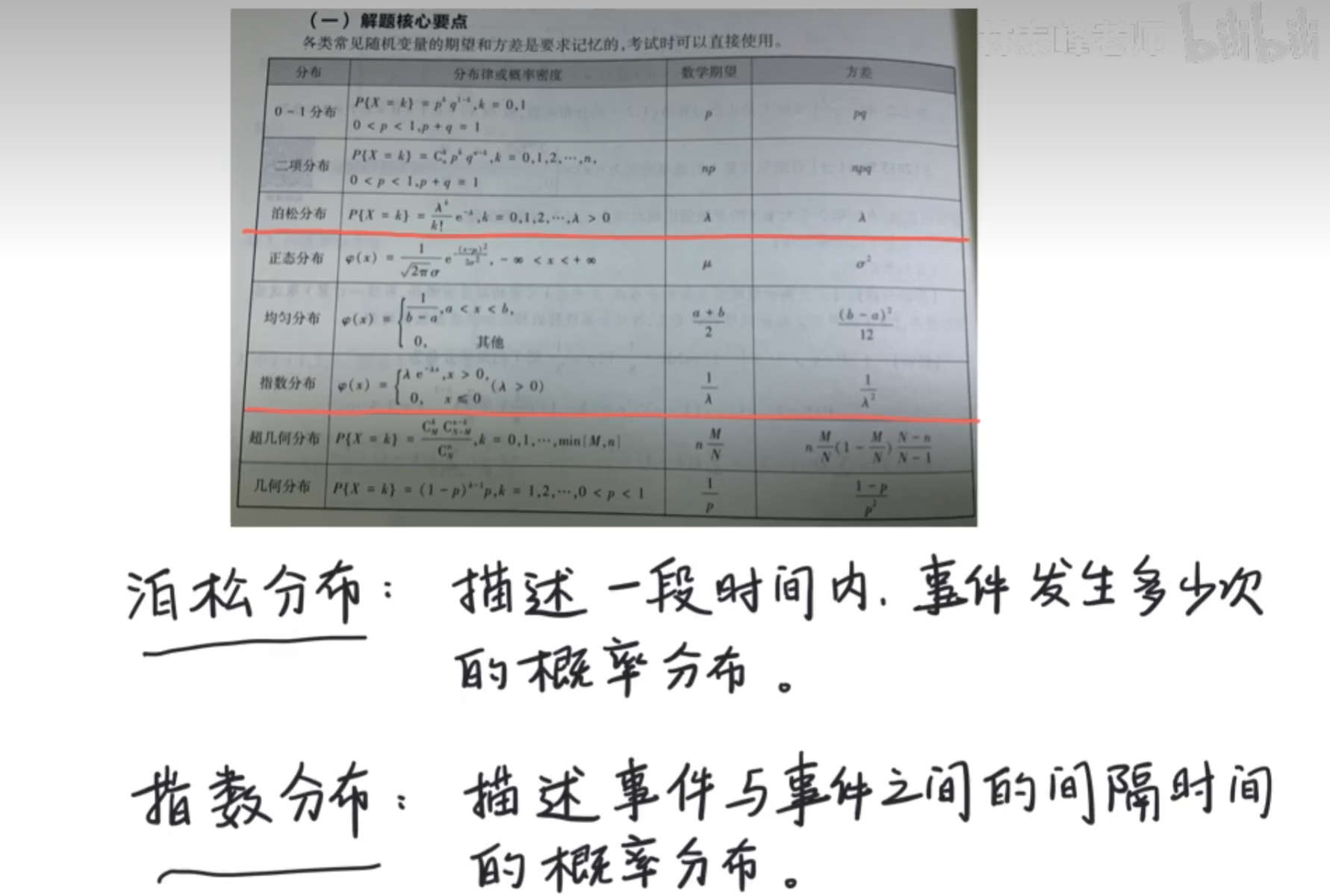

看到这里可能还以为两种分布的期望和概率是一样的,其实不是这样的,这种情况只是巧合

因此可以得到结论,在单位时间里,λ的取值才有可能相同, 但是呢,概率通常都是一样的~
泊松分布近似二项分布
n很大,p很小的情况,用泊松分布代替二项分布的计算

t分布和t检验
t分布是对z分布(标准正态分布)的一个修正
换句话说,也是基于中央极限定理的
df是自由度的意思,如下例,也就是我们都锁定了x1,x2,和x^-,那么x3就没有自由了,他的值就确定了,所以df等于n-1
注意:σ是总体标准差,s是样本标准差,如是总体,标准差公式根号内除以n,如是样本,标准差公式根号内除以(n-1)
因为我们大部分时候找到我们假设中的全部总体是不现实的,比如调查全体中国男性,因此通常都只能采取抽样的方式,也就是用样本标准差进行计算。普遍发现,除以n-1会使得效果更加接近于真实标准差。

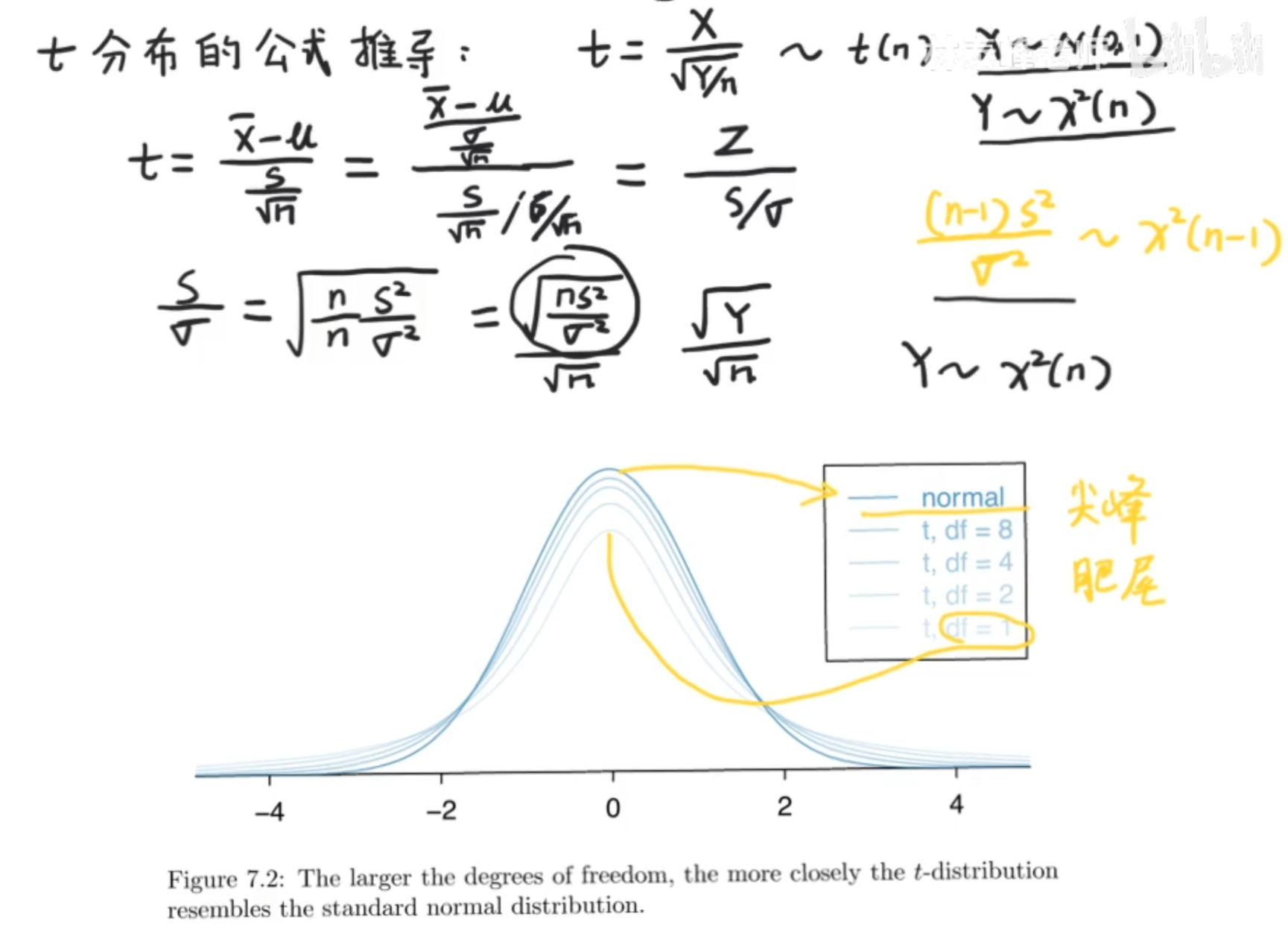
t分布主要适合于两个不同种类的比较,超过两个就不用这个,用F分布
问题,女性吸烟对婴儿体重是否产生影响

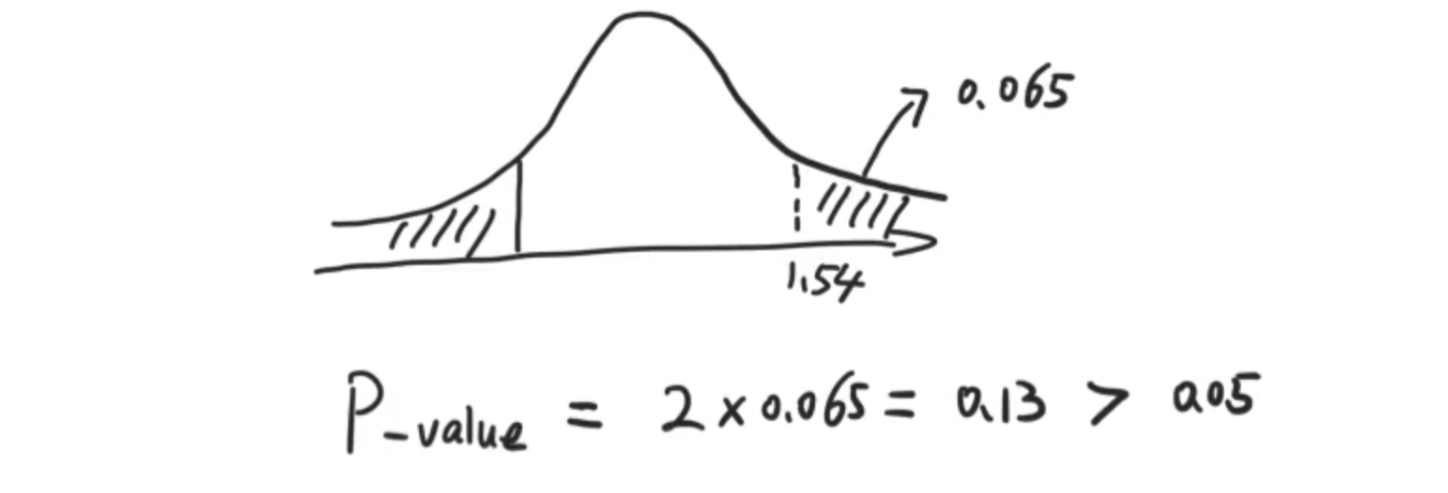
自由度取保守一点,为49(n-1),通过下面的正态分布图,找到1.54那个t检验的点,因为判断条件为=和≠,所以为双侧检验,最终得到的概率是0.13>0.05(设置的显著水平),所以拒绝原假设,不能得到是否吸烟和孩子体重的关系
卡方分布
用于定类问题,使用观察数据和期望数据的差异,差异越大,模型越不合适(变量越独立),这个用于类别型变量(有无新搜索),之前的T检验用于数值型变量(婴儿的体重)

用人数总数比例,再乘每个算法的测试人数,得到no new search的期望应该是3539

在这个情况下得到的x²的值太小了,也就是说并不能观测到是否他们一不一样好,拒绝原假设。说明他们并不一样好,不是成比例分布的。并且卡方检验也不能告诉我们那个算法好
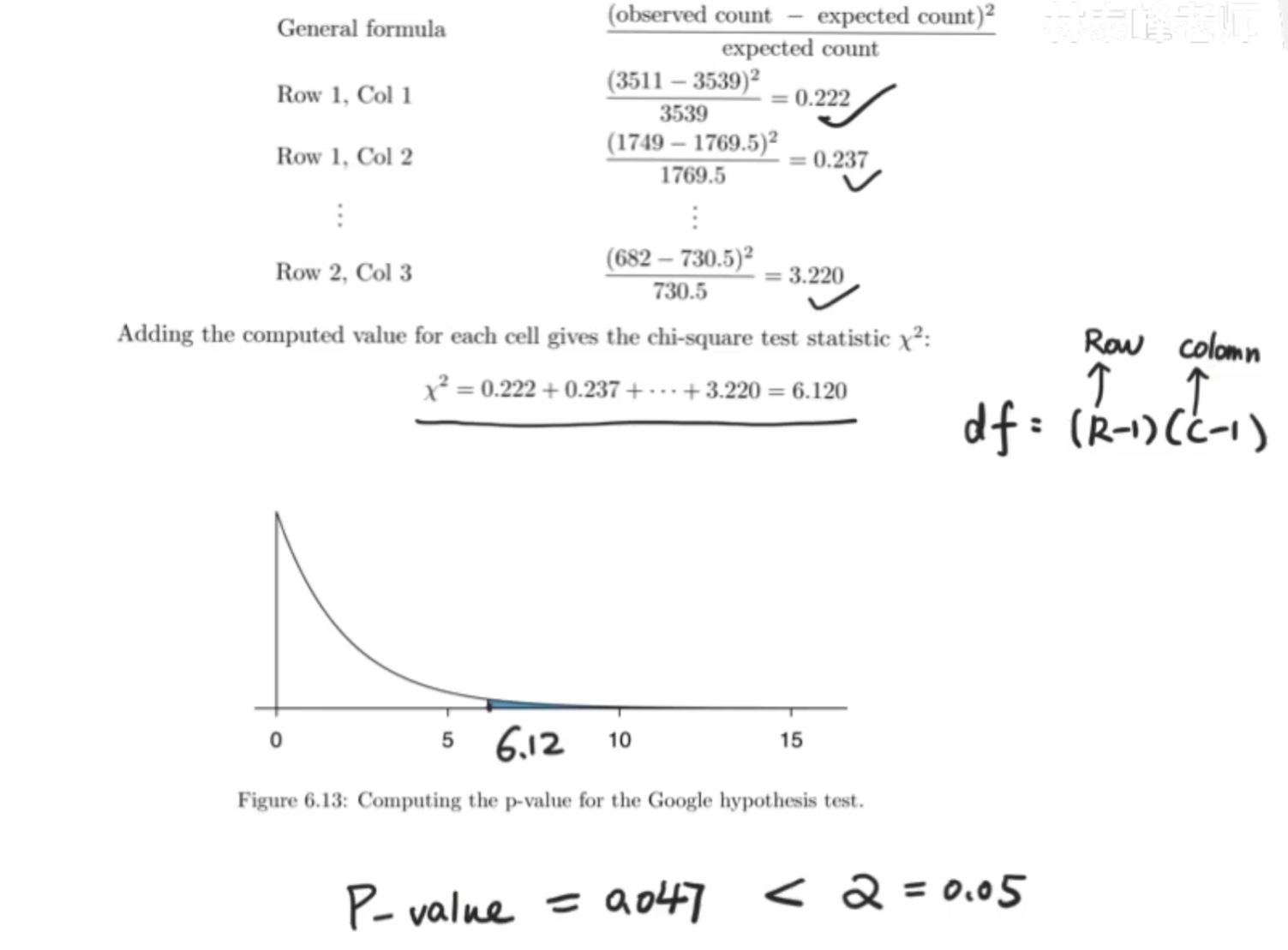
卡方分布证明

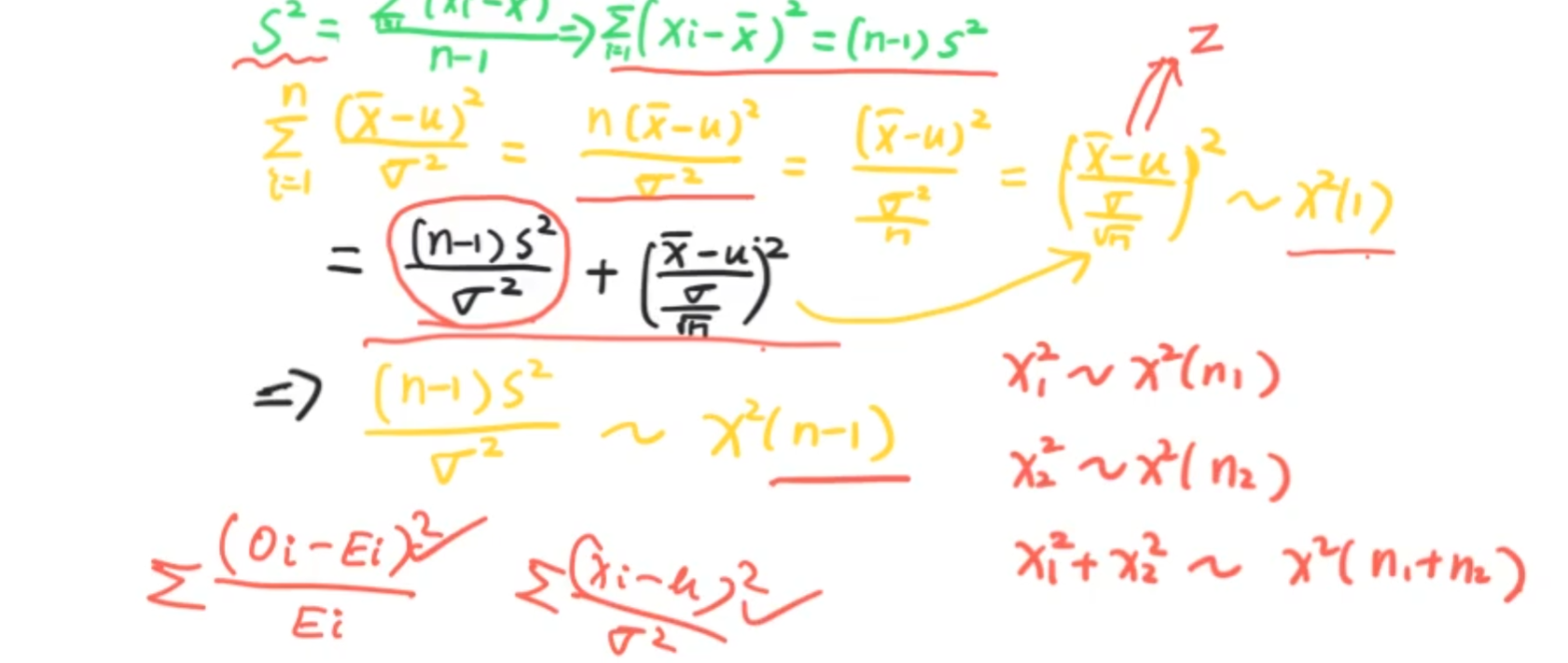
F分布和方差分析
方差分析(Anova:analysis of variance)并不是对方差进行分析,而是用方差的思想去分析多总体均值的比较
这里的重点是多,,如果是两个总体,就用t检验和t分布
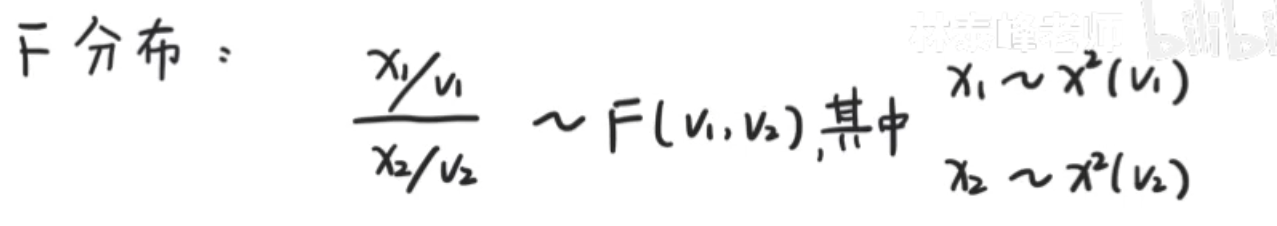
快速回顾T检验

组间平均差异:同样要除以自由度利用样本方差的思想
组间平均差异:对组内平均差异的标准化。
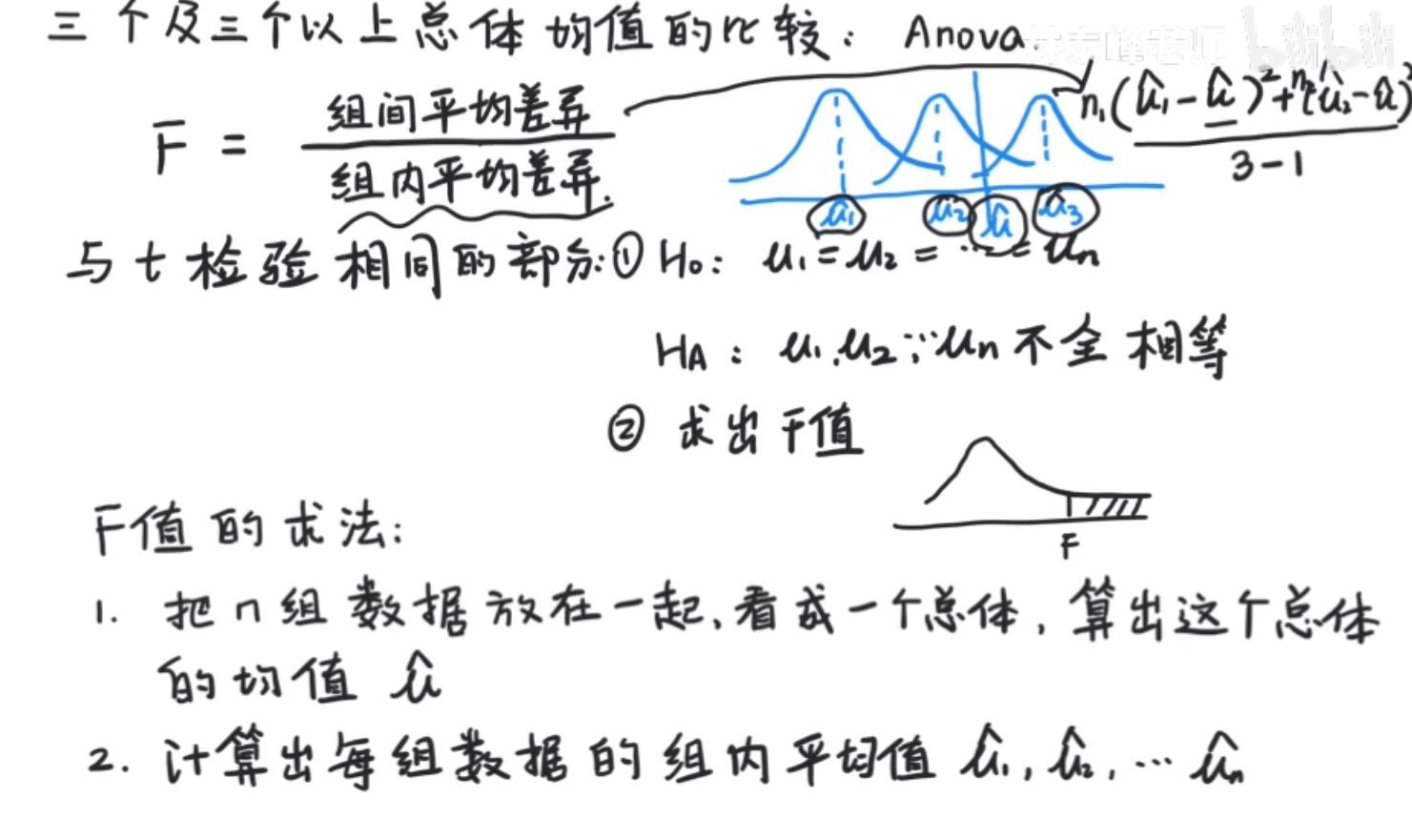
m - n是ssw的自由度,n就是选了多少个组计算组内分布,m就是这些组一共的数据,反正最多每个组有一个是不自由的,加起来也就是m-n的自由度
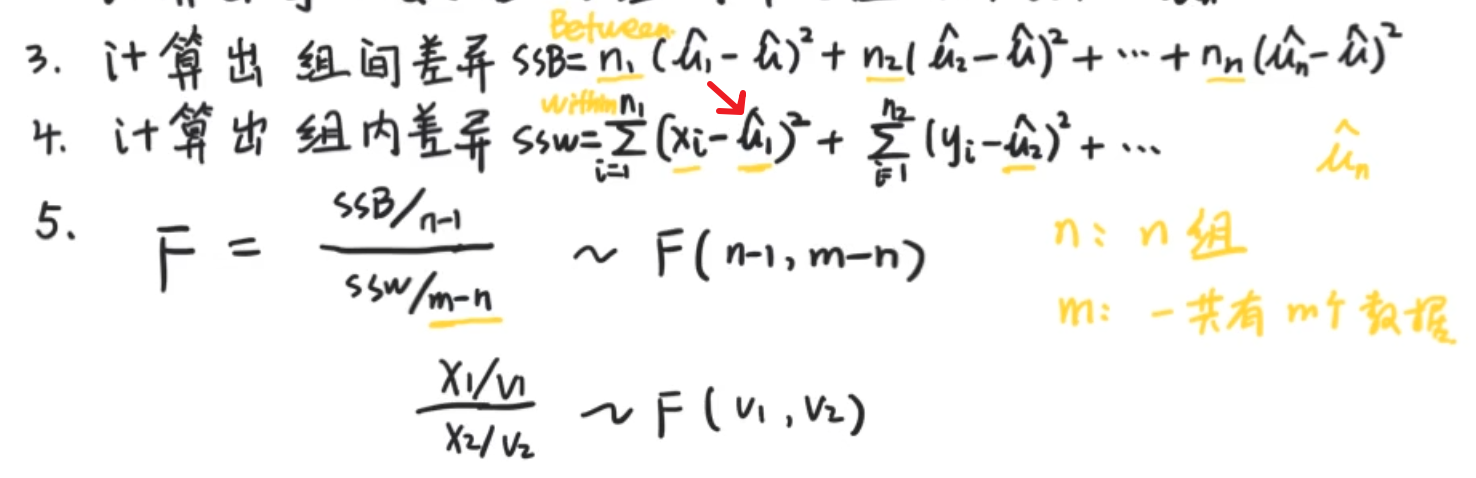
例题
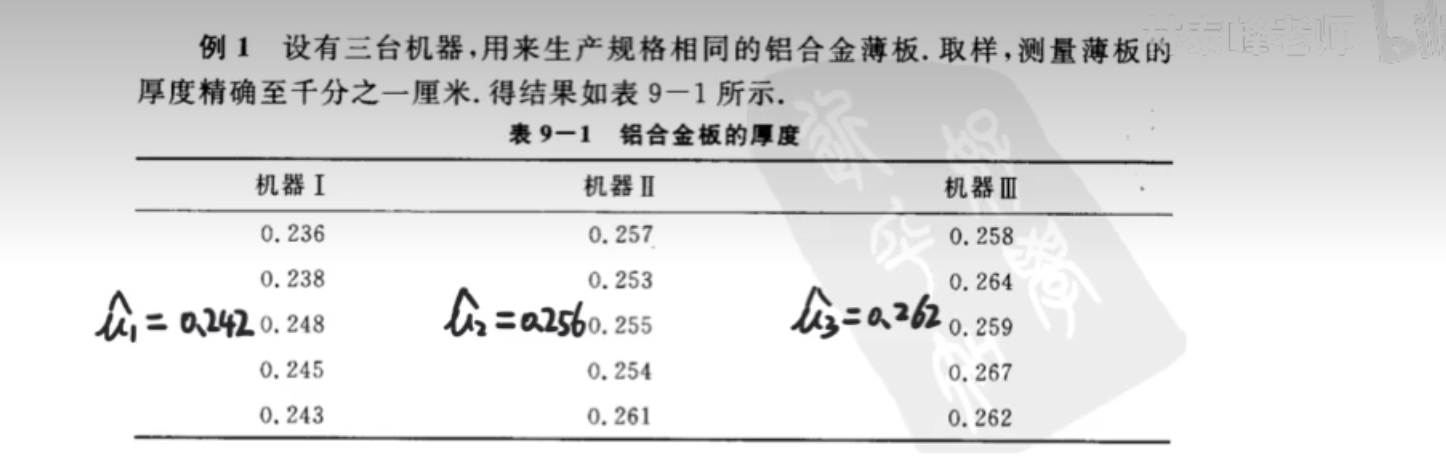

样本比率服从正态分布
其实我们观察$\bar{x}$和$\hat{p}$的值,其实他们是相等的。也就是说,样本比率其实就可以看做是样本均值,只不过是伯努利分布下的样本均值,他是置信区间和假设检验的基础

置信区间
已知样本个数和样本均值,求总体均值。听上去很让人一头雾水,但我们得试着分析他
背后的理论是正态分布和中心极限定理
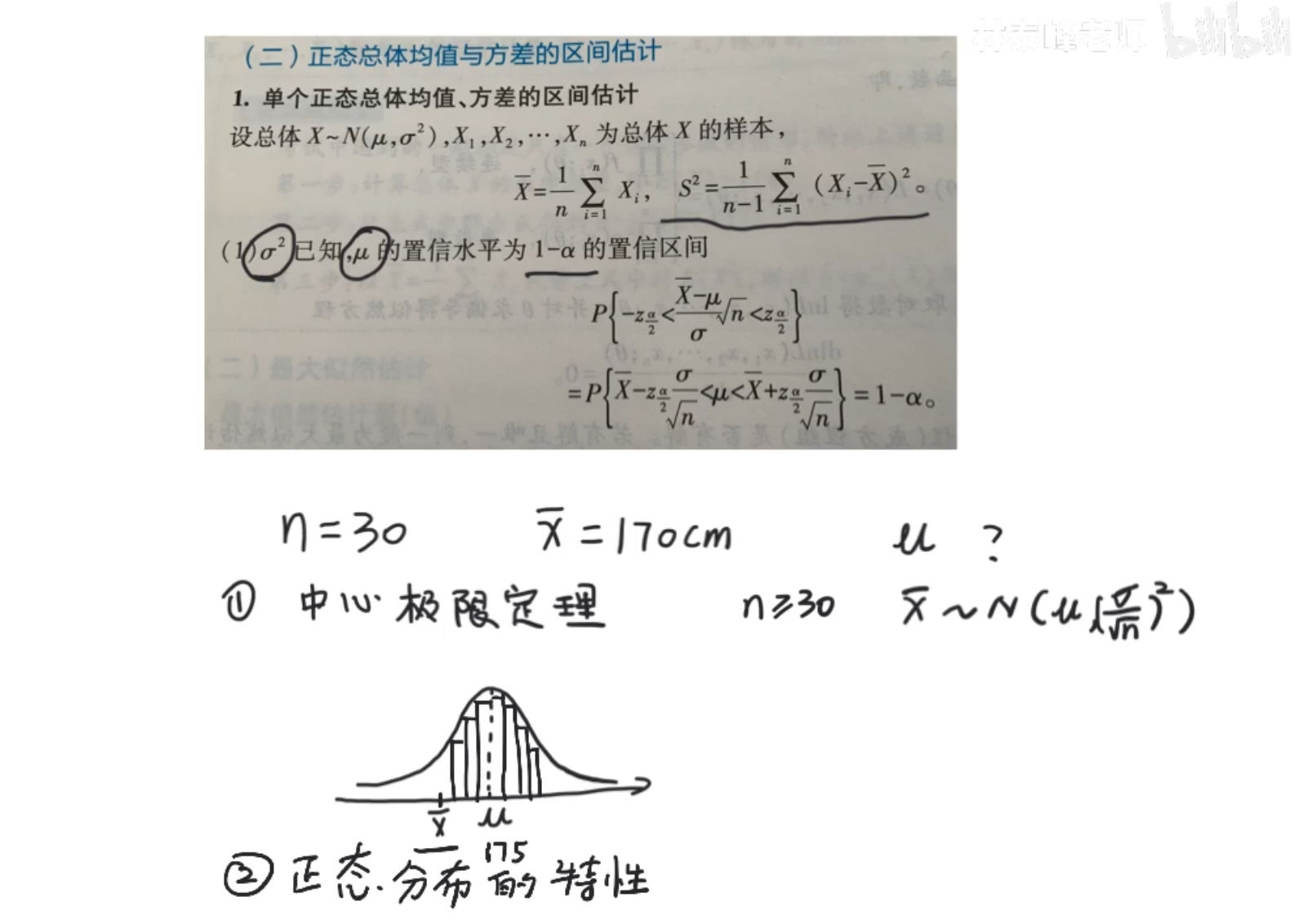
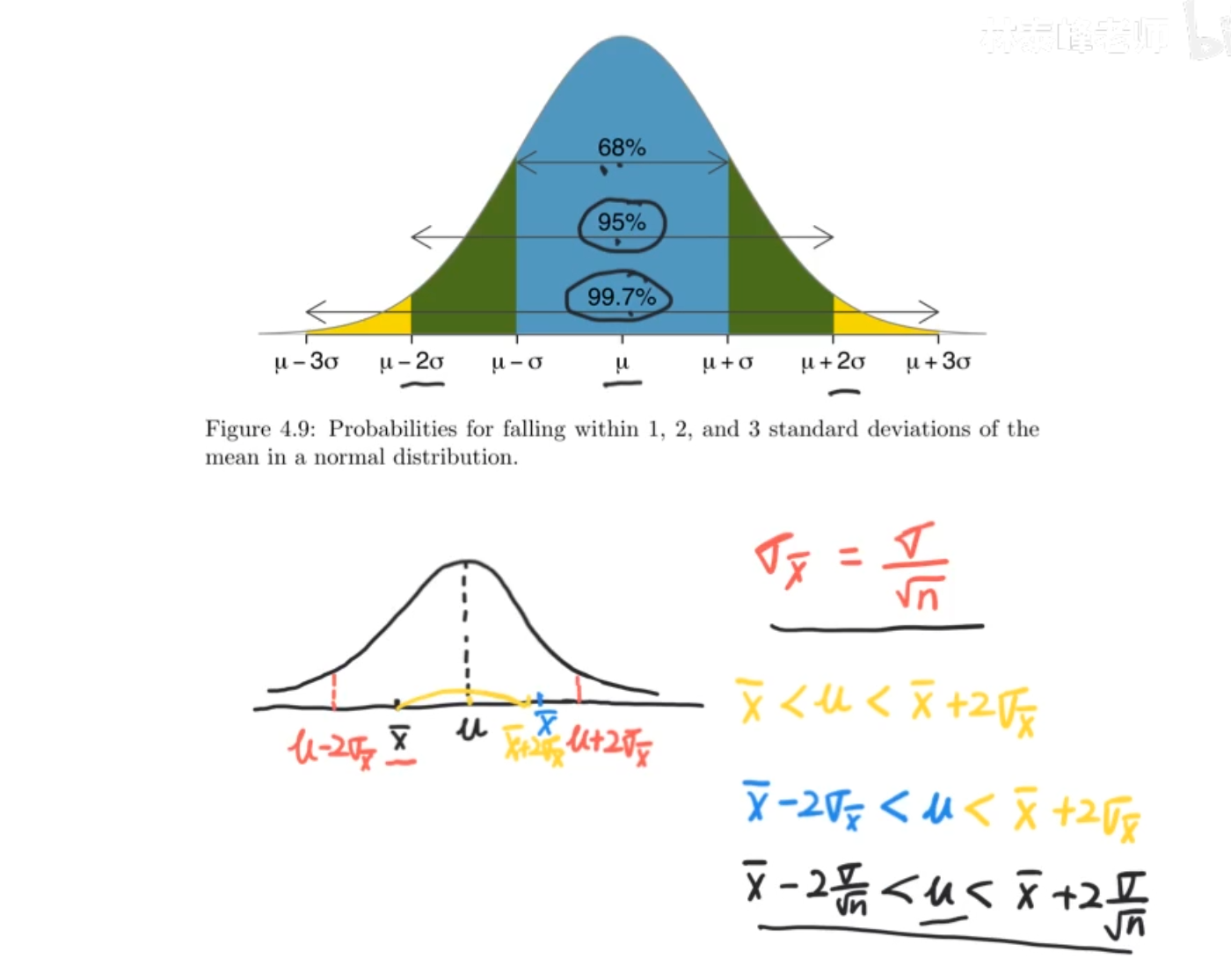

这里是用正态分布来举例的,也就是我们如果有了一个样本均值x^-(n> 30),那么我们有95%的信心,这个总体均值的位置就在样本均值正负两个标准差之间。
假设检验
假设检验专治各种夸大其词,用科学的手段合理怀疑原假设,证明它是错的

因为待机时间为36小时,所以小于36小时的数据都可以当做证明物,那么我们求出来(这里σ没给你,就随便大概取了一个)算出来的值远远小于显著水平,我们来想一下我们现在做的事,我们要证明待机时间为48小时(46作为正太分布的均值)声明下面,我们观察到的平均时间36小时发生的概率太小了,此时48是理想情况,36是真实情况,但是最终得到的概率是p-value为0.0062<<0.05的显著水平,说明实际观测与理想不符,拒绝原假设,选择另外一个区间
α可以理解为事件发生的概率有多小算反常的一个值:通常叫做显著性水平或者第一类错误概率

协方差和相关系数
有的时候从生活出发,理解往往更佳简单,统计学是源于生活的规律
协方差是衡量两个因素之间关系的工具,相关系数是协方差的归一化
协方差除以标准差,也就是把协方差中变量变化幅度对协方差的影响剔除掉,这样协方差也就标准化了,它反应的就是两个变量每单位变化时的情况。

如果光看答案才头疼

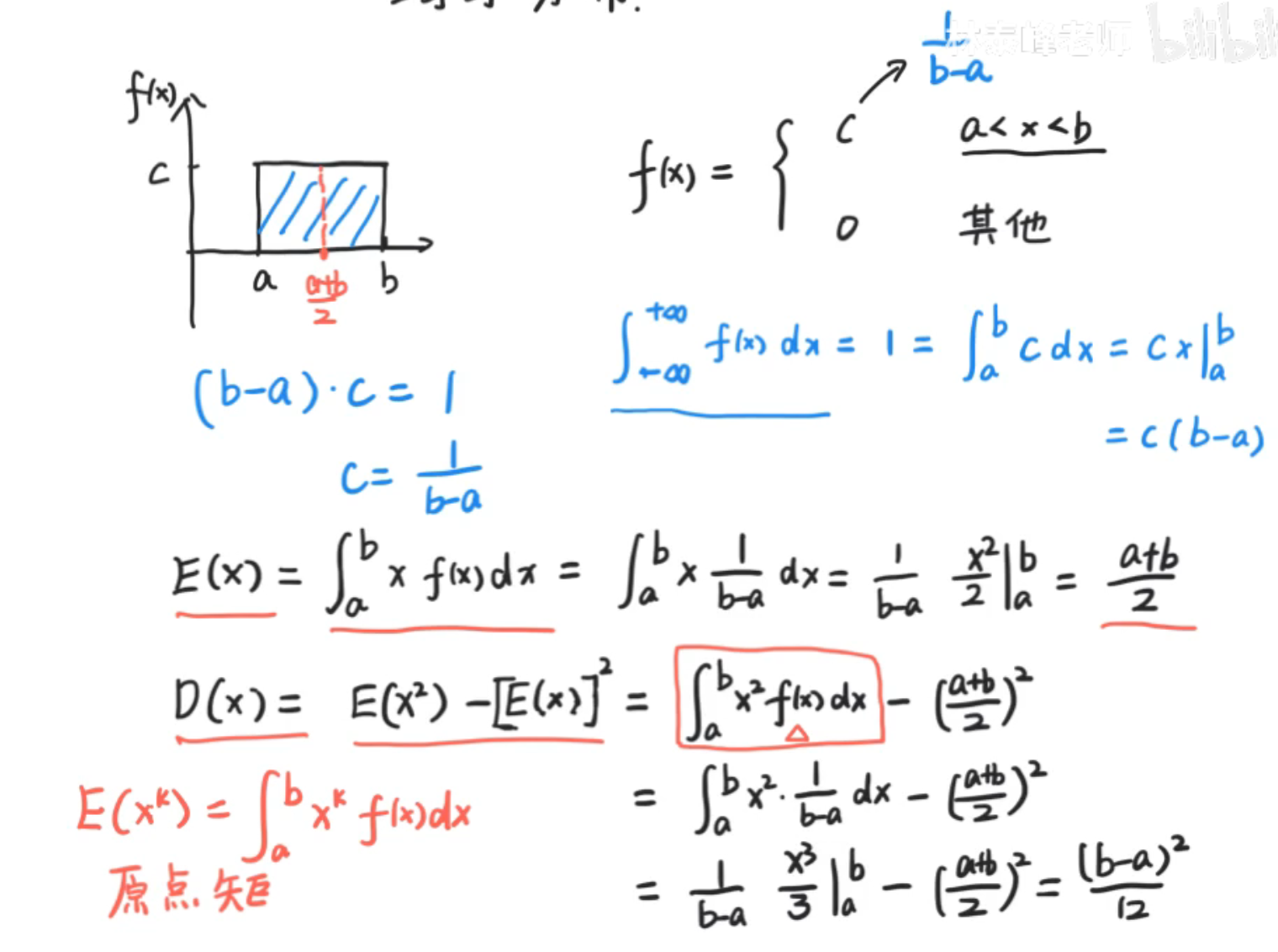
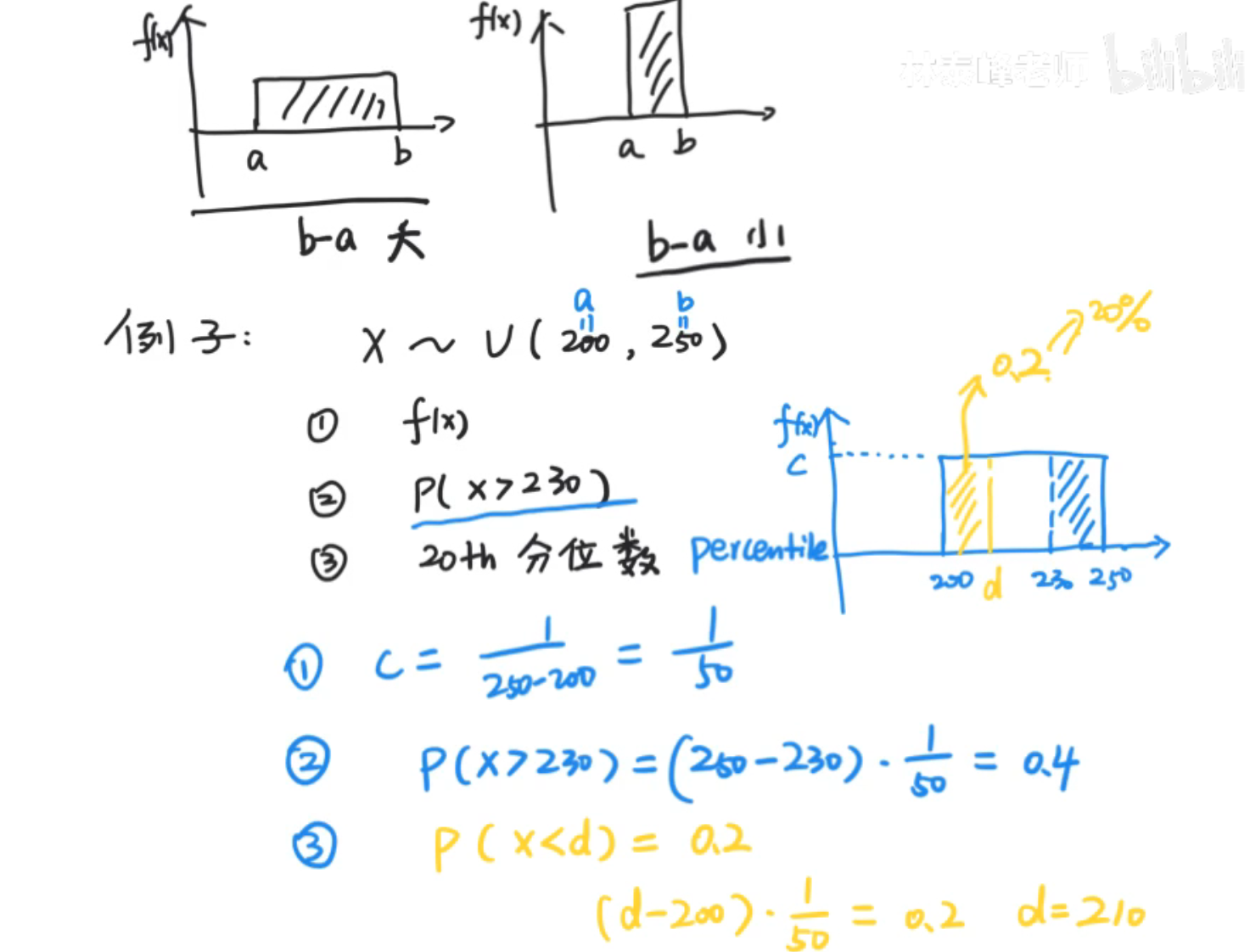
均匀分布
原点矩:将x^k^看作是一个整体,则极限a到bx^k^f(x)dx为x^k^的原点矩,显然,一阶原点矩矩即为期望
负二项分布
负二项分布是几何分布和二项分布的集合


几何分布
几何分布,可以理解为等比分布,几何级数,也可以理解为等比数列的前n项和。
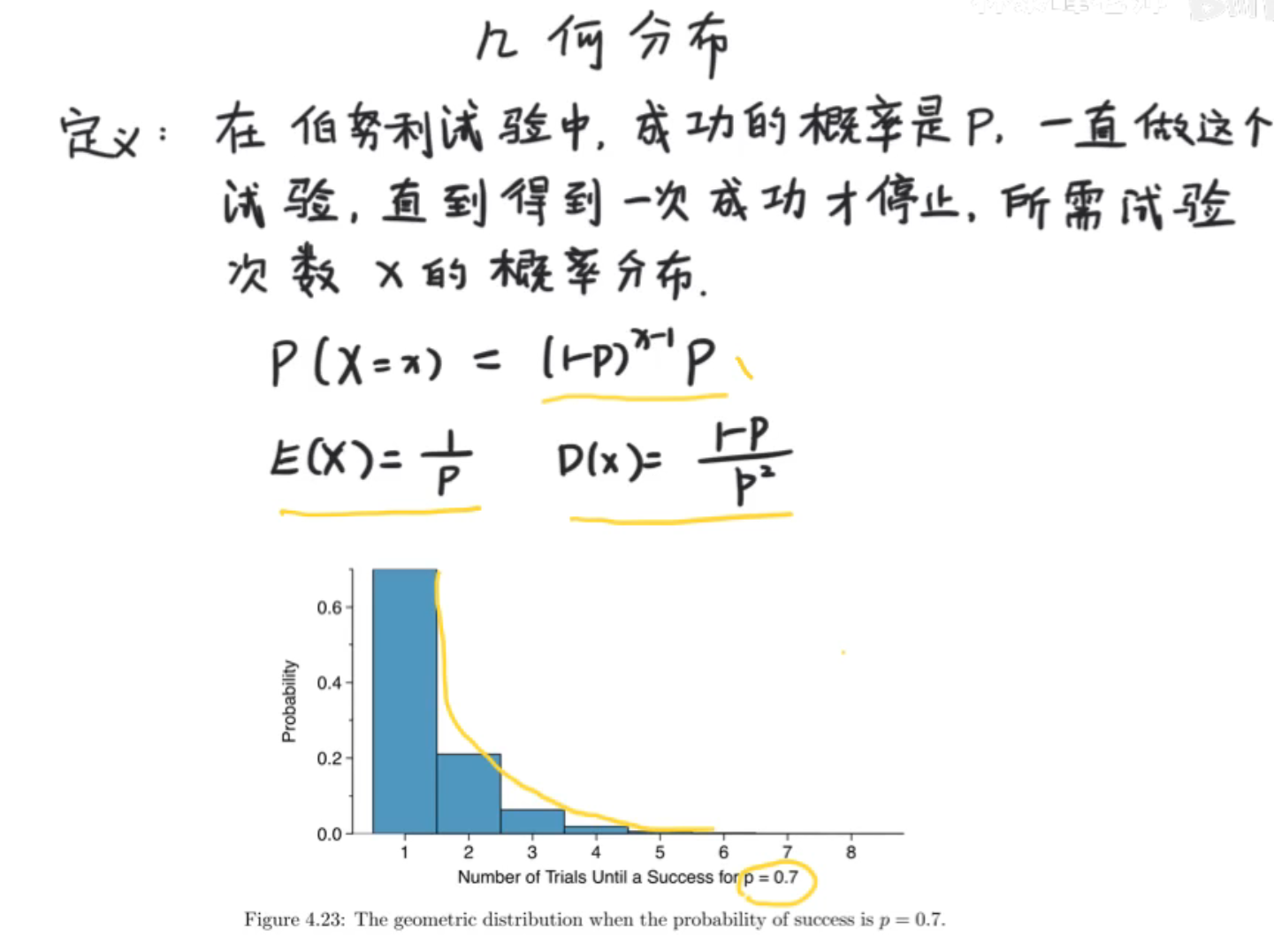
他的期望是1/p,我们观察,其实这个是符合我们的直觉的,通过率为30%,说明可能考试比较难,就大约3次才能通过,这也是我们为什么把E(x)翻译成期望,而不是平均值的原因。

为何我们将其称之为几何分布?我们从图像已经感觉到是指数级别的递减,指数级在数学上又称为几何级,从代数上看呢,有跟几何级数有关。以下是证明几何分布的期望是1/p.用了错位相减法。

超几何分布
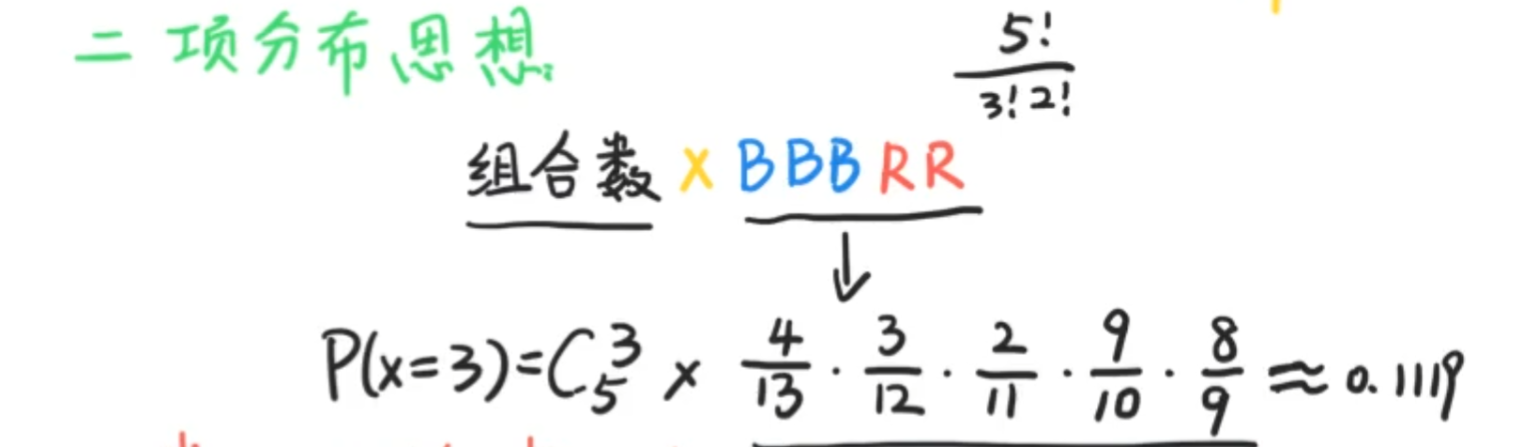
他和二项分布的关系相当紧密,我们先来看一个二项分布的例子

将其改为不放回,则为超几何分布。
以下为用定义的思想。

还可以使用乘法法则。(二项分布的思想)
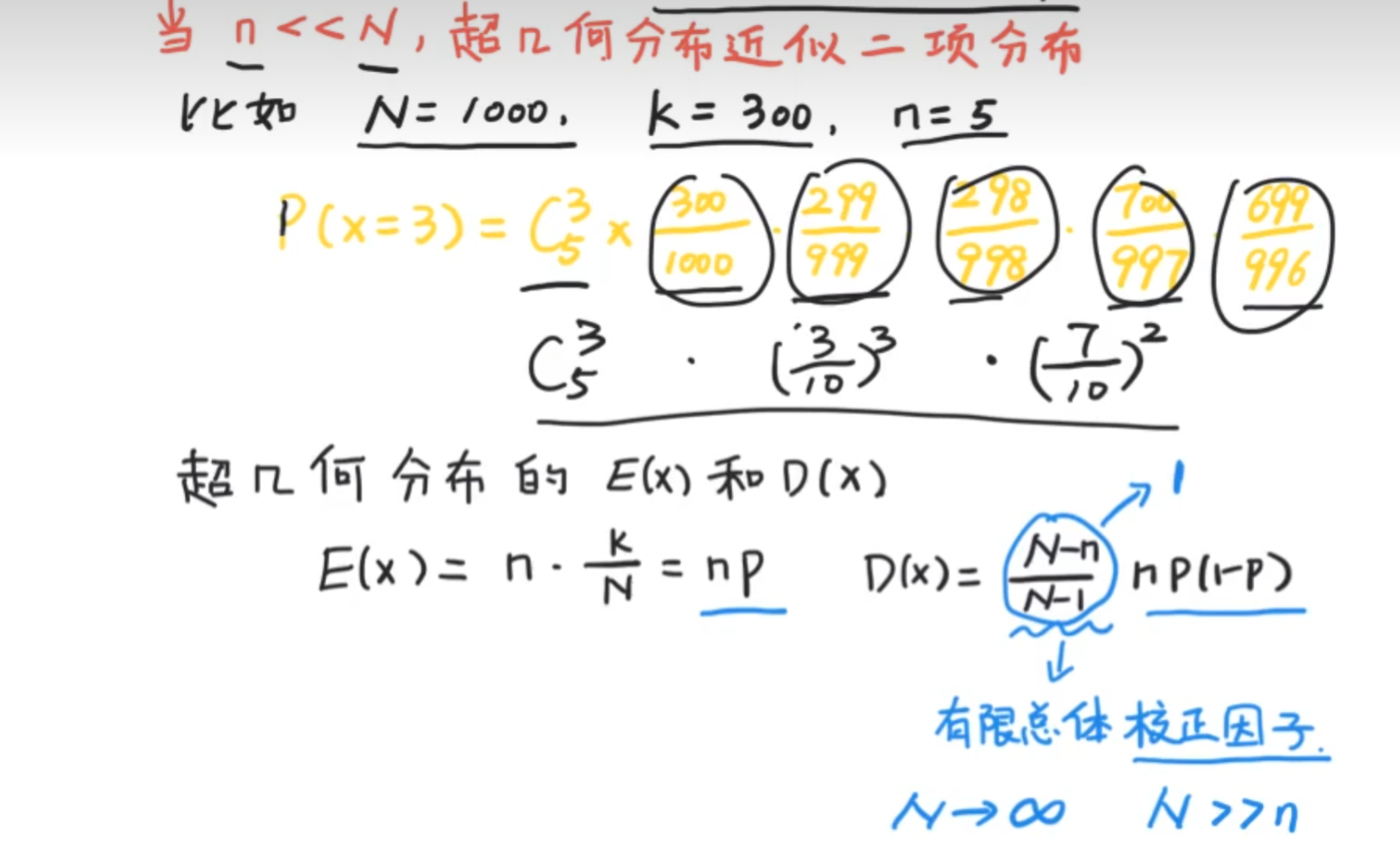
当样本基数远远大于抽取数量,可以使得超几何分布近似为二项分布(放不放回都一样)
伯努利分布(0-1分布)
其实这个是二项分布的前置,是最基础的分布。

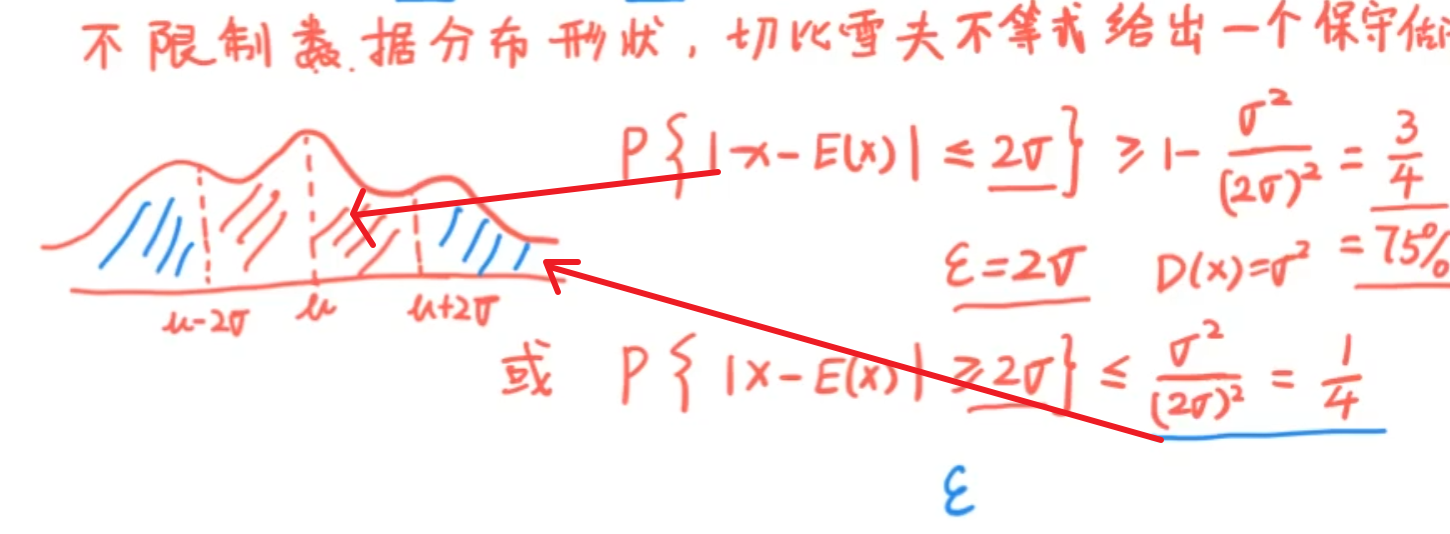
切比雪夫不等式

最大似然估计
未知参数取何值时,样本的观测值出现的概率最大
现在我们的任务是:公务员考试的考试次数与通过人数之间的关系(共100人),这里举个例子,考了三次通过的人数是多少?是不是p(x=3)= (1-p)² * p ,假设p等于0.3(代表考试难,也就是说,E(x)= 3,大概三次可以通过,p = 0.8代表考试比较容易,大概就是一次也能通过

离散性中,似然函数和概率等价,连续性问题则不与概率等价了

数学的魅力,crazy,为何可以ln?取到的最大值其实是不变的。也就是求导之后的鞍点。我们可以观察,这种估计在大数定律和公式法估计之间,我们认为最大似然估计是一个合理估计,因为他用到了能用到的所有信息。
这里运算的是有100个独立事件同时发生时的最大概率。因为最大似然估计要做的是让概率最大化,因为存在即合理,并且存在一定合理,那我们要取最大的可能性。既然已经发生了这样的情况,并且已经有100个真实的数据,那么只需要得出最大可能的P,那就是真实的P
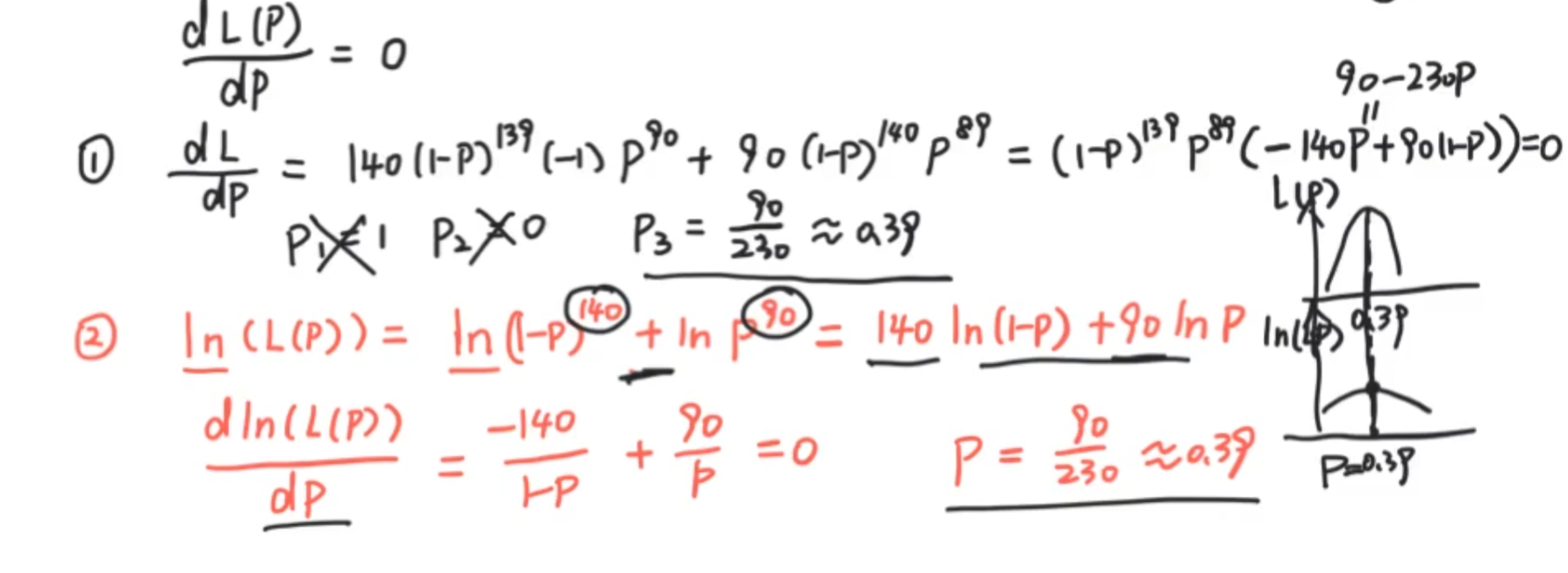
似然和概率的区别
对于离散型随机变量而言呢,似然函数就是n个样本观测值同时发生的概率
对于连续性变量,似然函数则是概率密度的乘积,而不是概率的乘积。
- 进一步说,似然函数是模型的度量值的乘积,似然函数的值大呢,说明样本数据支持假设的模型以及参数
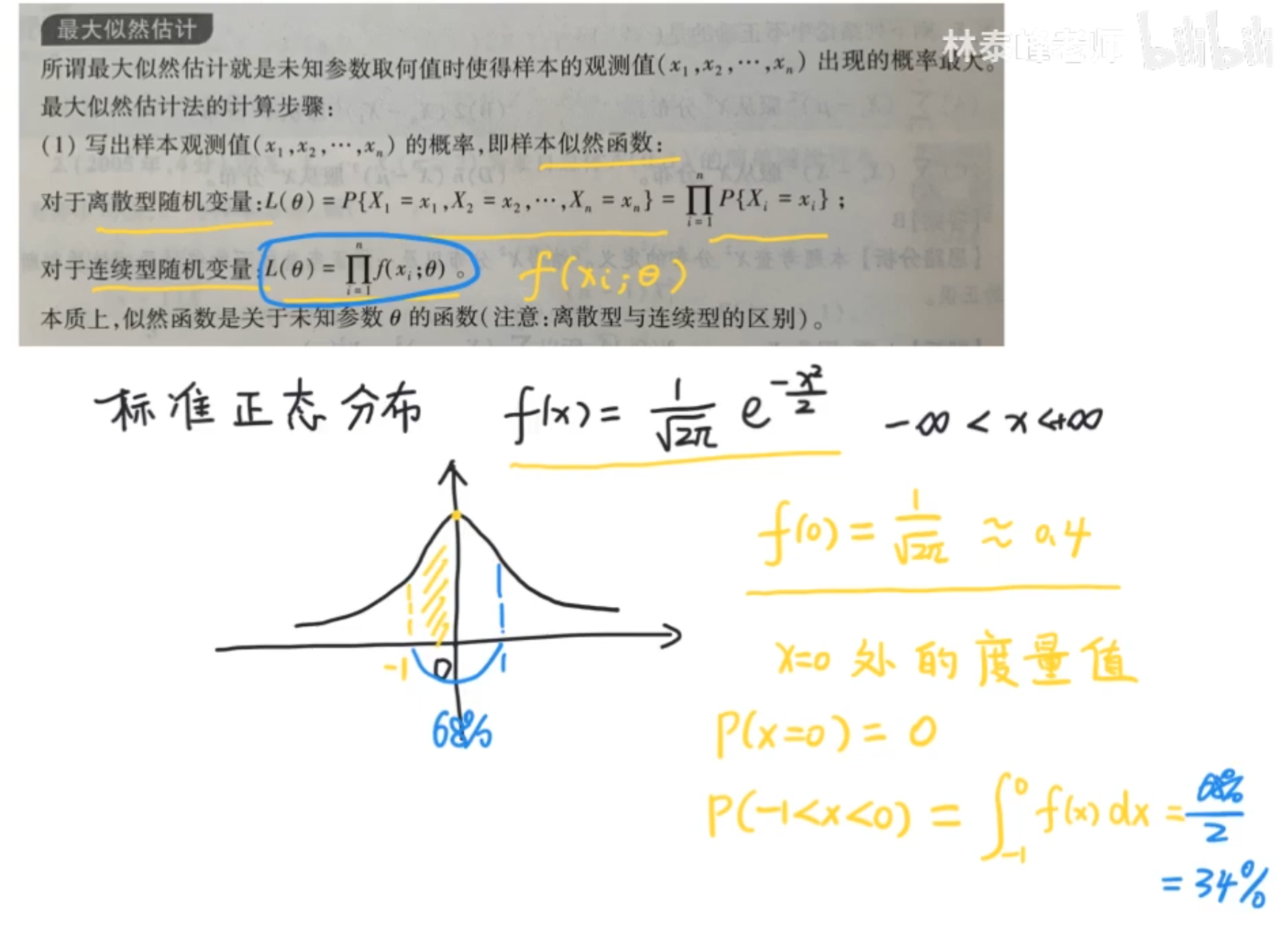
我们观察其实可以发现,似然函数大,黄色的分布时,似然函数一定是最大的,所以说这个其实不是指样本发生的概率大,而是样本的数据支持我们给定的一个假设模型以及它的参数,也就是说,我们黄色的模型得到了样本数据的最大支持