总结

对立，独立和互不相容怎么区分？

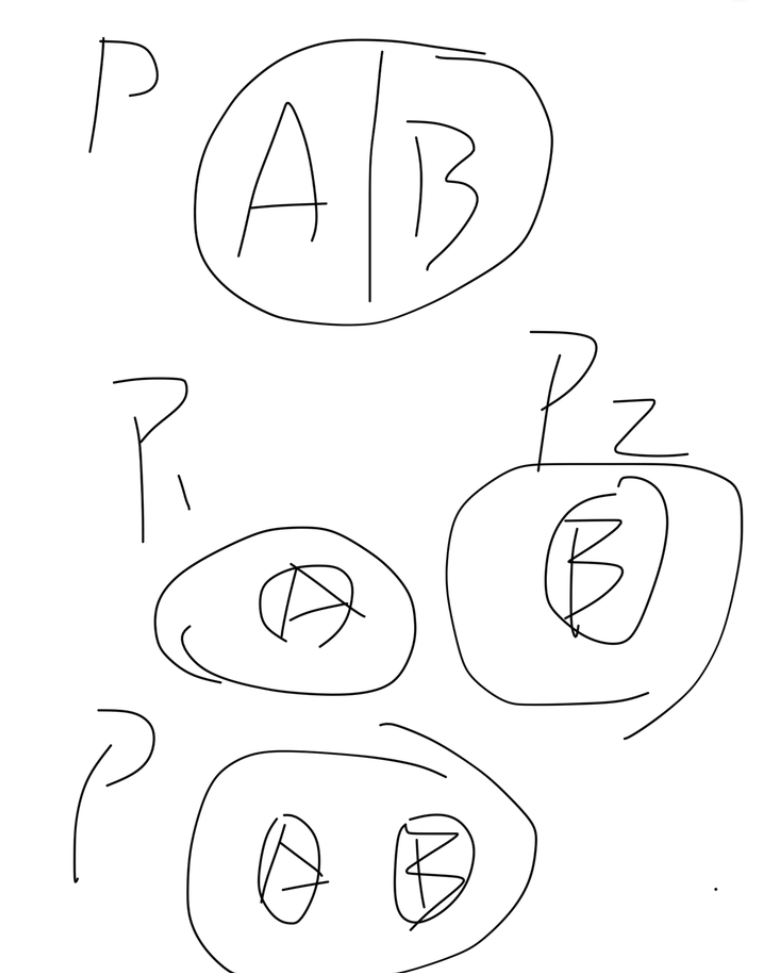
image-20230526213304294

image-20230526212020699

减法公式：元素属于A，但不属于B（默认AB相交为一般情况，因此A-B通常为A-AB

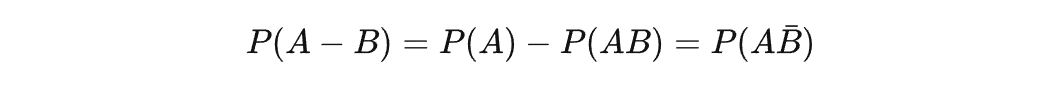
image-20230526220042820

期望方差

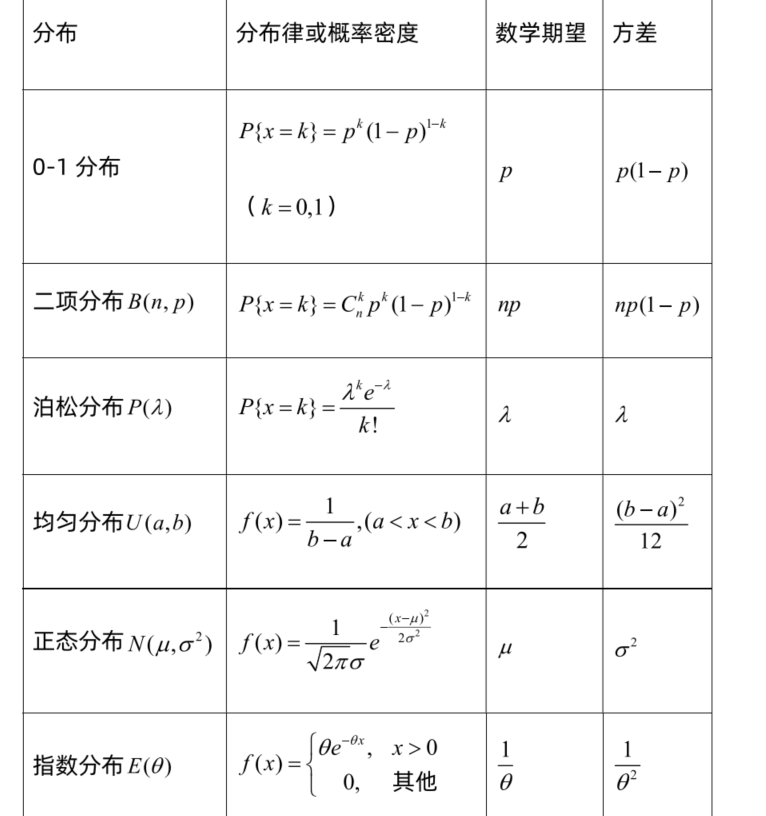
image-20230527143559807

image-20230527142310620

期望

image-20230527142817831

方差

image-20230527142800541

协方差

image-20230527145932624

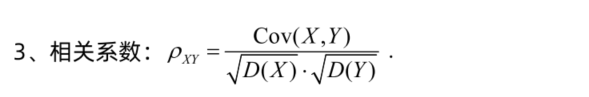
image-20230527145952786

不相关和独立

image-20230527150814874

image-20230527150823492

三大分布

image-20230527173922012

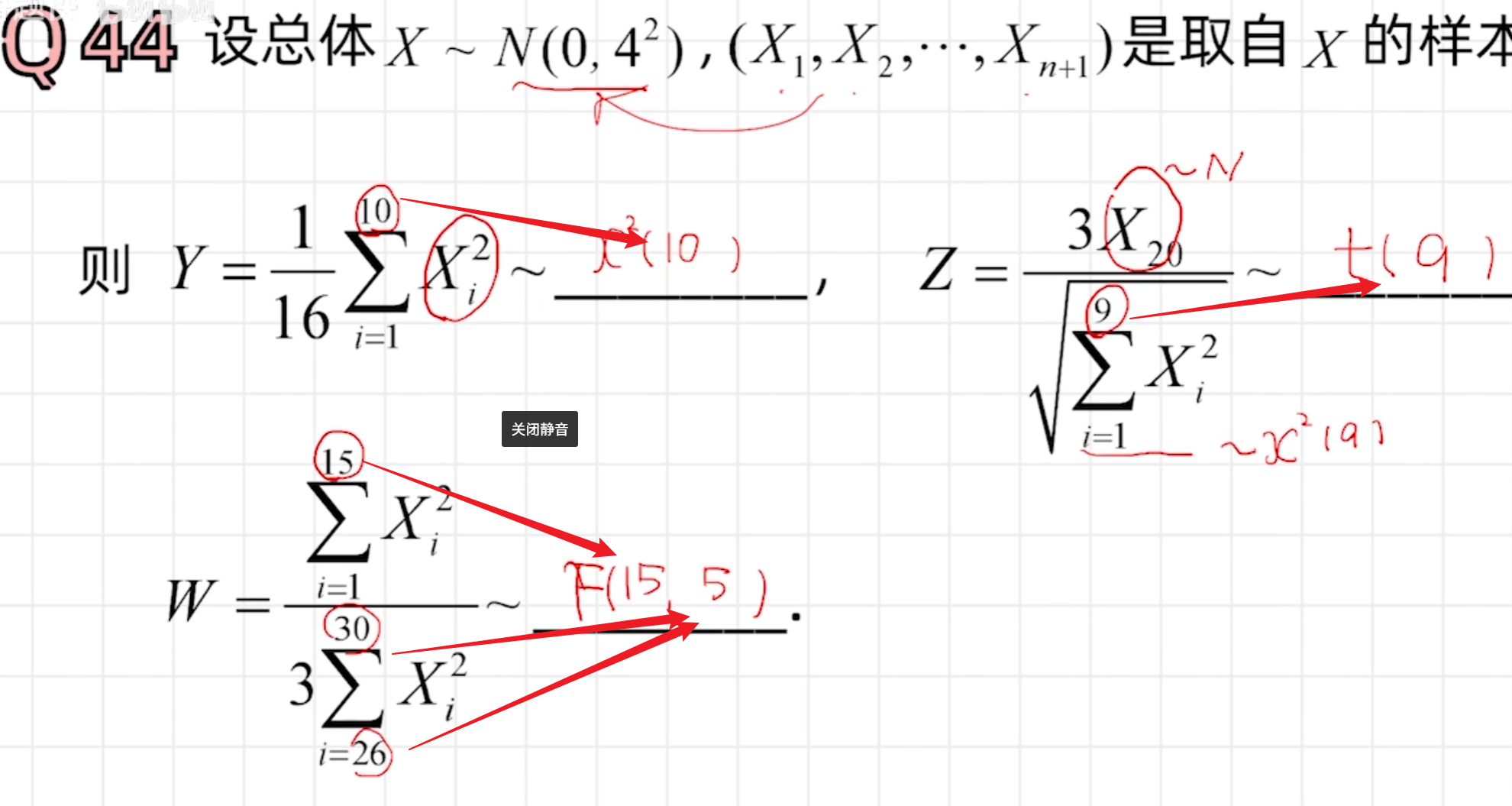
image-20230527174439058

矩估计

1、求总体均值（得关于未知参数的方程）

2、令总体矩等于样本矩

3、解得矩估计量

离散

image-20230527175026085

image-20230527175037855

连续

image-20230527175508627

似然函数

1、构造似然函数L(θ)

2、取对数lnL(θ)

3、令dlnL(θ)/dθ求极值

image-20230527180230364

image-20230527180223459

假设检验

image-20230527181202824

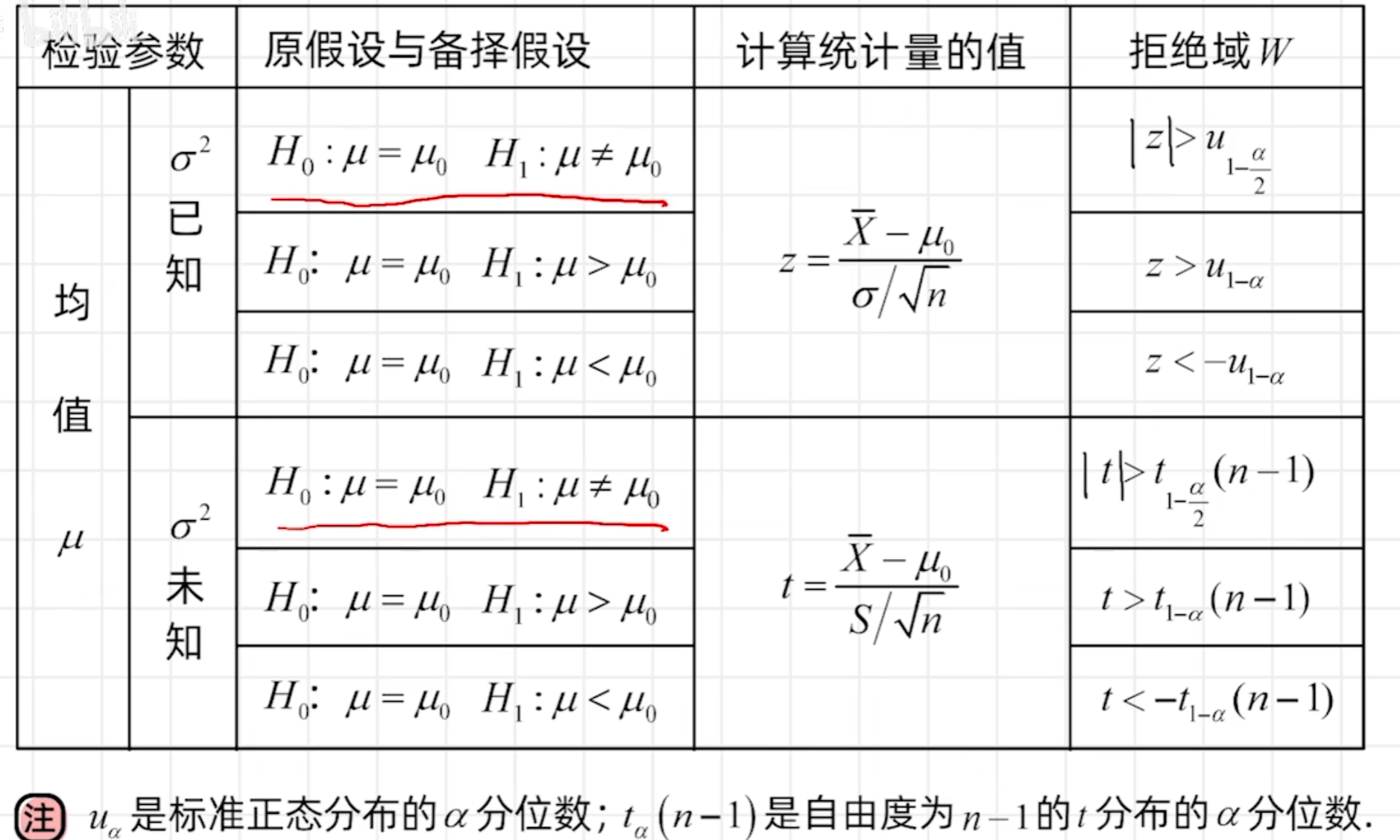
image-20230527181538983

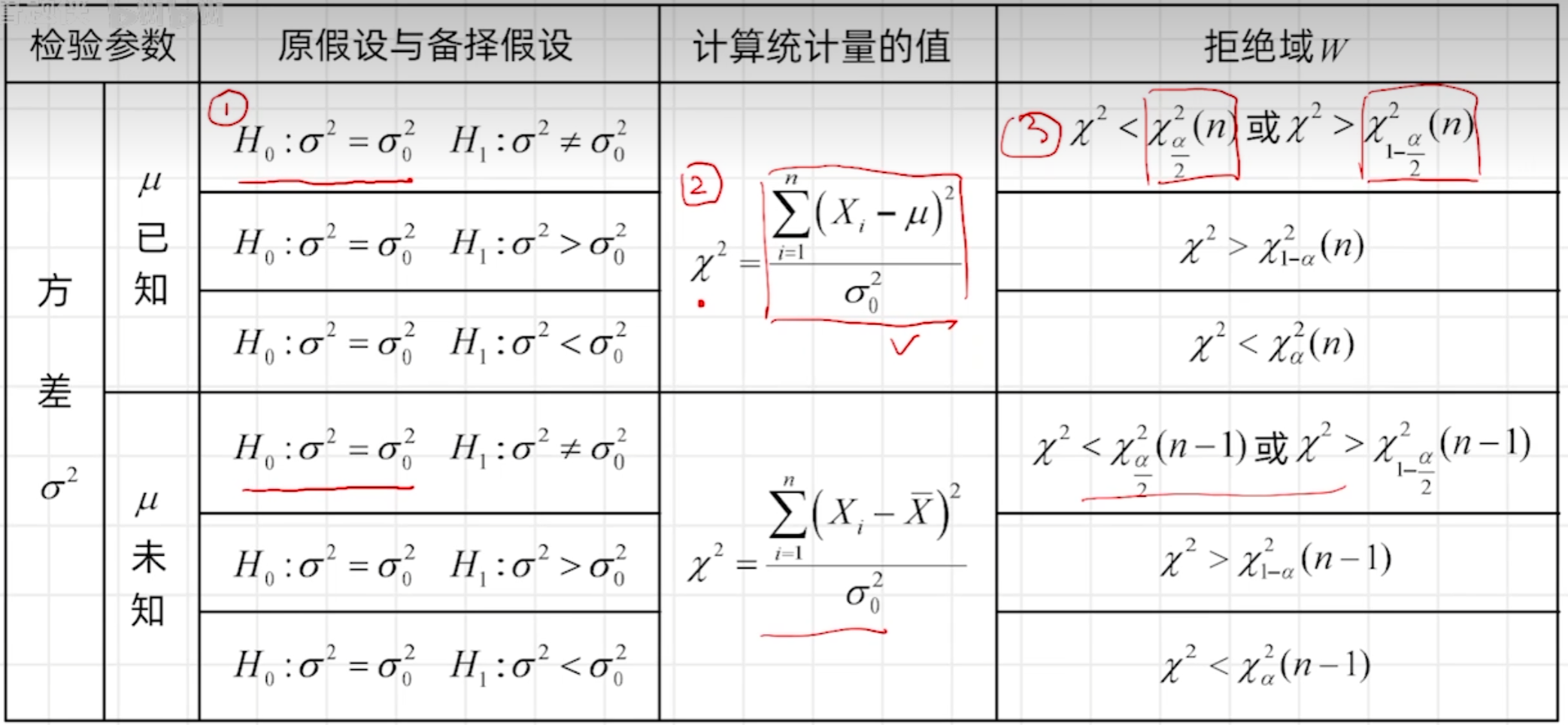
image-20230527181623192

image-20230527181830660

image-20230527181935723

事件的概率

事件与运算

image-20230329104156017

image-20230329104439580

image-20230329105536500

image-20230329105917485

image-20230329110146949

需要画图的题

image-20230327210450044

image-20230327210509658

6666666，悟了，关键死抓x与大于小于符号，画箭头

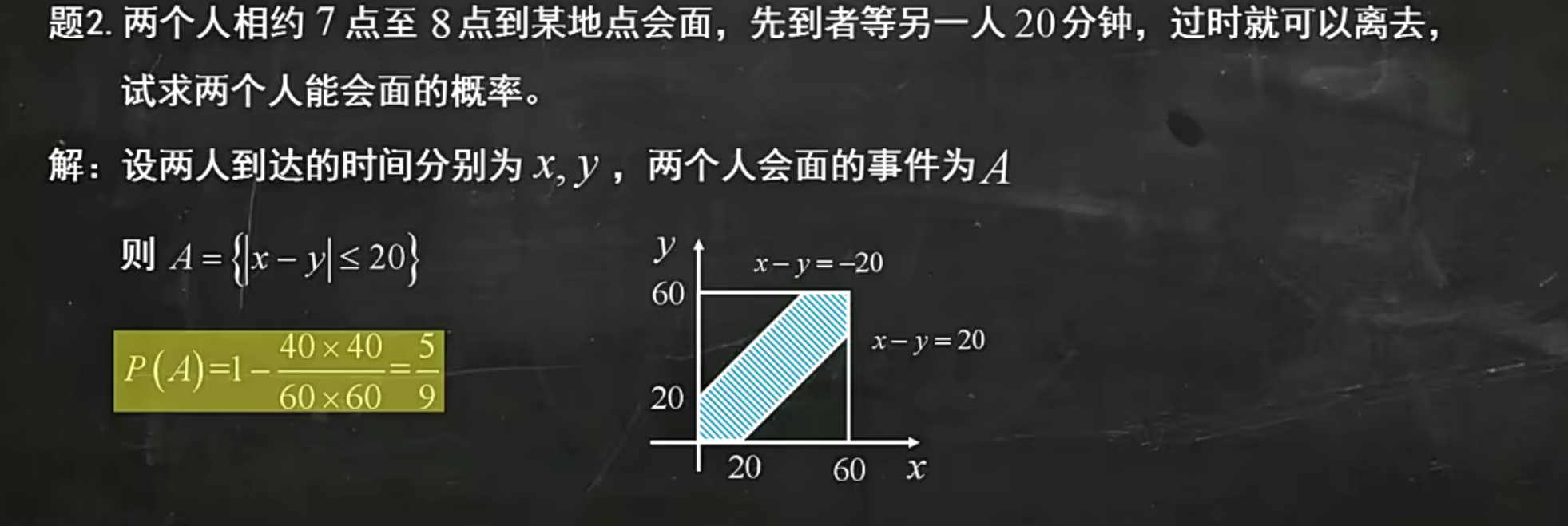
image-20230329110421362

条件概率

image-20230329132005143

image-20230327210935685

套路: 设已知时间为A，求的事件为B

image-20230327211117607

那么，P(B|A)自然是我们需要求得概率，且由题意可知，P(AB)为已知小明60分以上，且小明80分以上的概率，则可以直接转换为小明80分以上的概率，为0.8

即最后答案为：

image-20230327211245138

再换一道更难的题

image-20230327211445413

我们现在无法直接求出P(AB)：今年没发洪水，明年发洪水，那我们分析一下已有条件

image-20230327211423132

无外乎四种情况，分析可知，P(AB)为5%

image-20230327211640039

全概率公式

A是最浅显的事件，B是为了使A发生而需要完成的事件

image-20230329133124345

贝叶斯公式

不同个体均可能出现同一件事，这就是和条件概率题型的区别，条件概率只会出现一个个体。

解题就是求，(A出现 * A发生)/各个个体发生

image-20230327212543280

image-20230327212906374

一维随机变量

只需要抓住，f是F的导数，F是f的积分

f是密度函数，F是分布函数

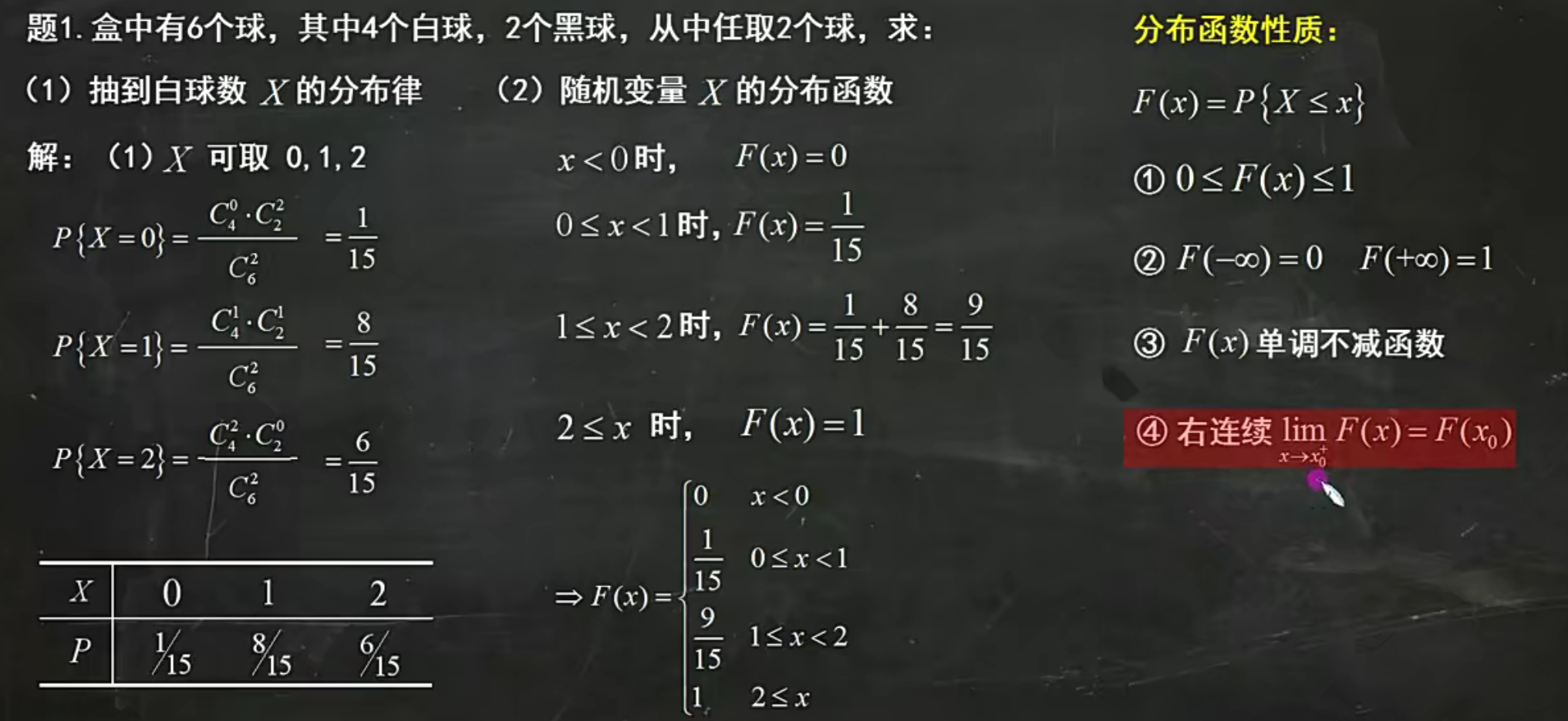
image-20230329135848005

image-20230329140034062

F与f，已知一个求另一个

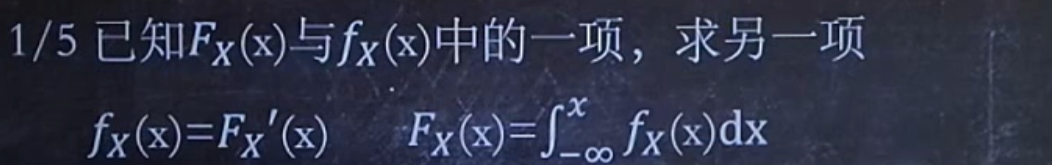
image-20230327213455867

要记住一个关键点是，FX(x)一定是恒大于0的，且从左往右不断累计。

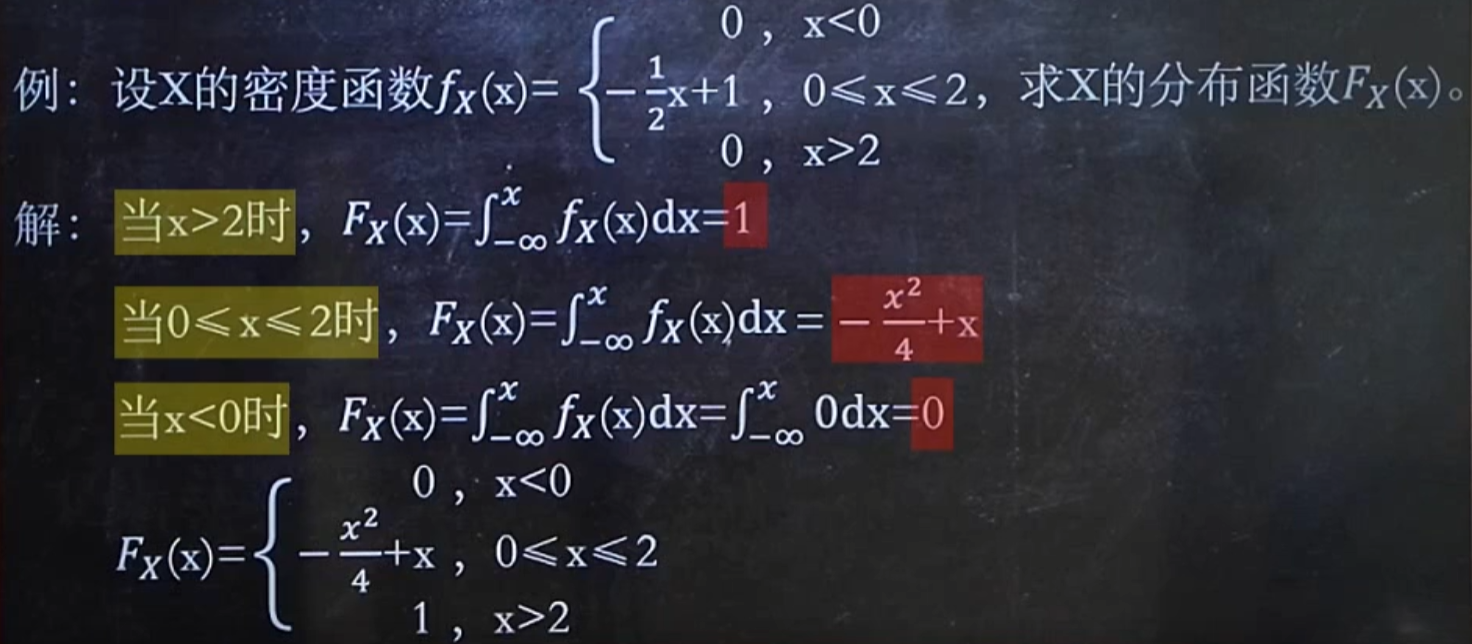
image-20230327214435021

F与f已知一个，求P

下图中的公式，a<X<b，也可以是a<=X<=b，a<=X<b…

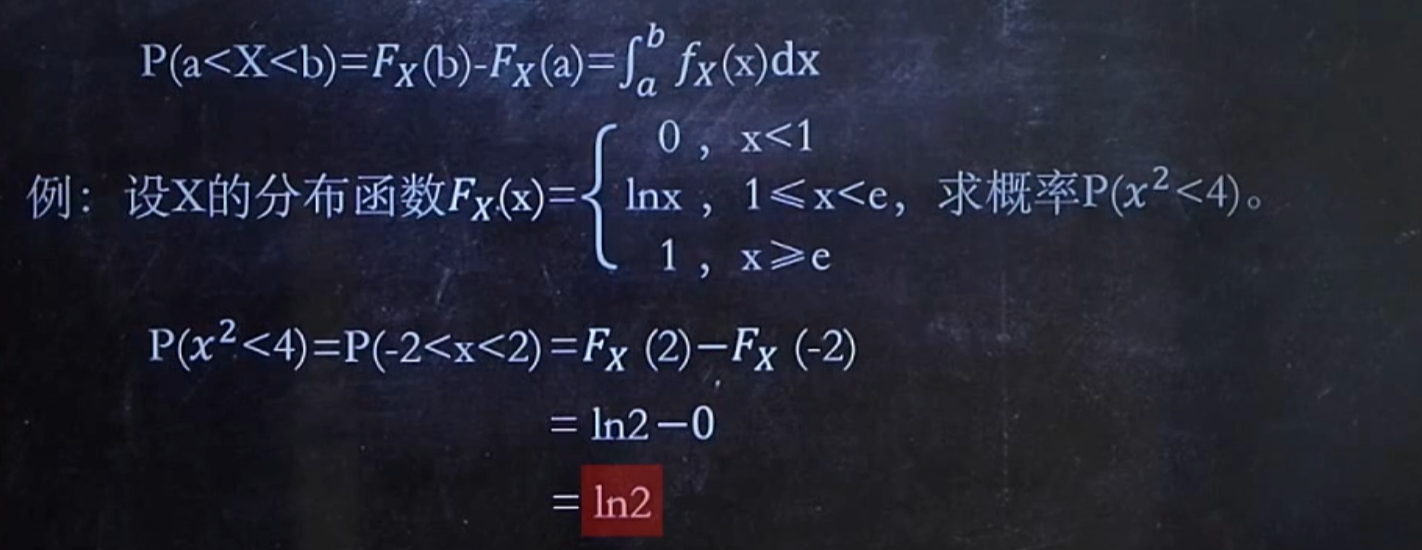
image-20230327214551940

F与f含未知数

抓住F 正无穷为1，负无穷为0，分界点和f累计为1

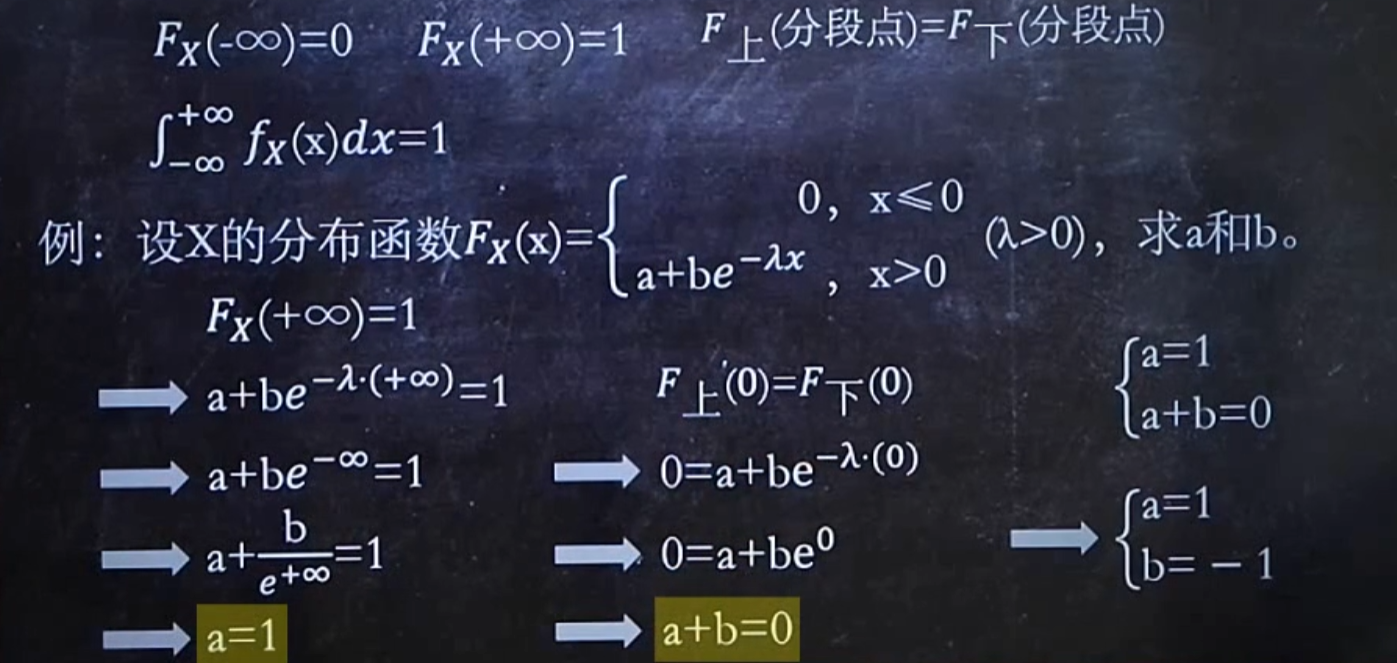
image-20230327215711507

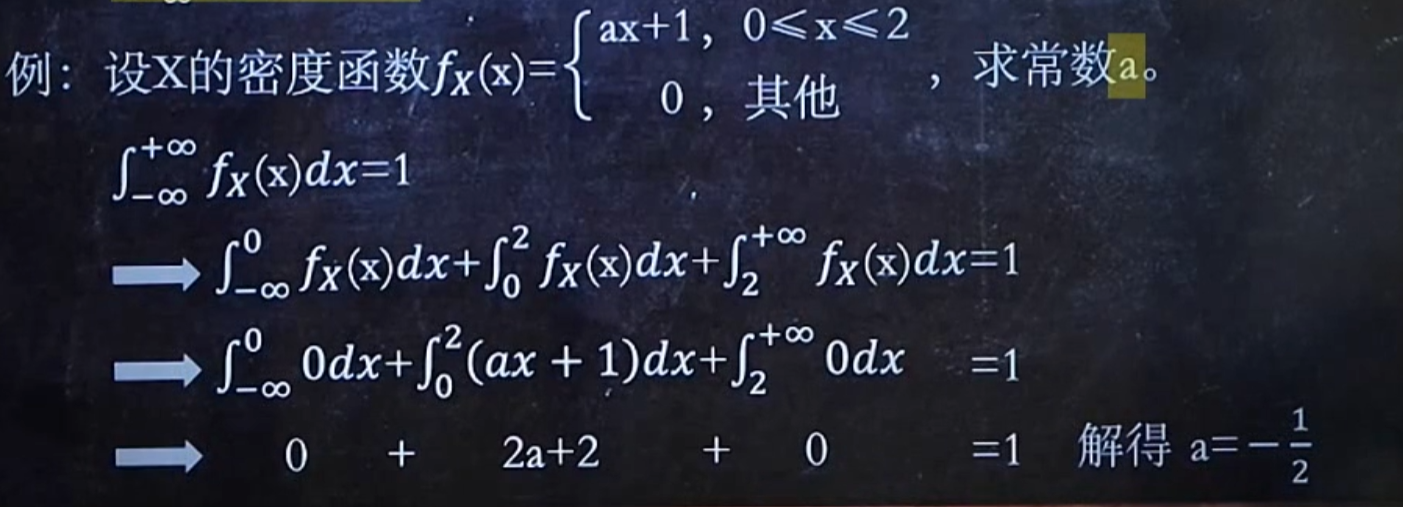
image-20230327215725117

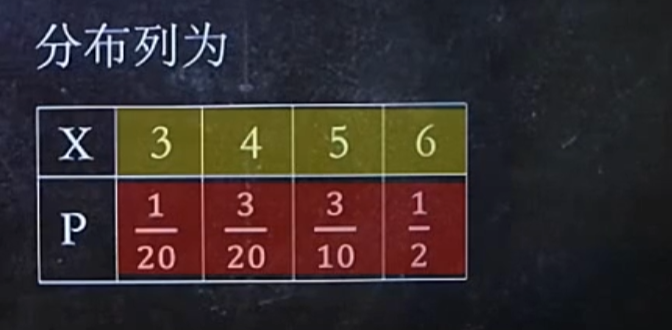
求分布律

转化问题，思考的角度很重要

image-20230327220155659

image-20230327220436832

image-20230327220446153

一维随机变量的函数

三步

1：写成X=xxxY

2：用Y替换式子中的X

3：有符号，则该项换成1-F(xxxY)

image-20230329140350692

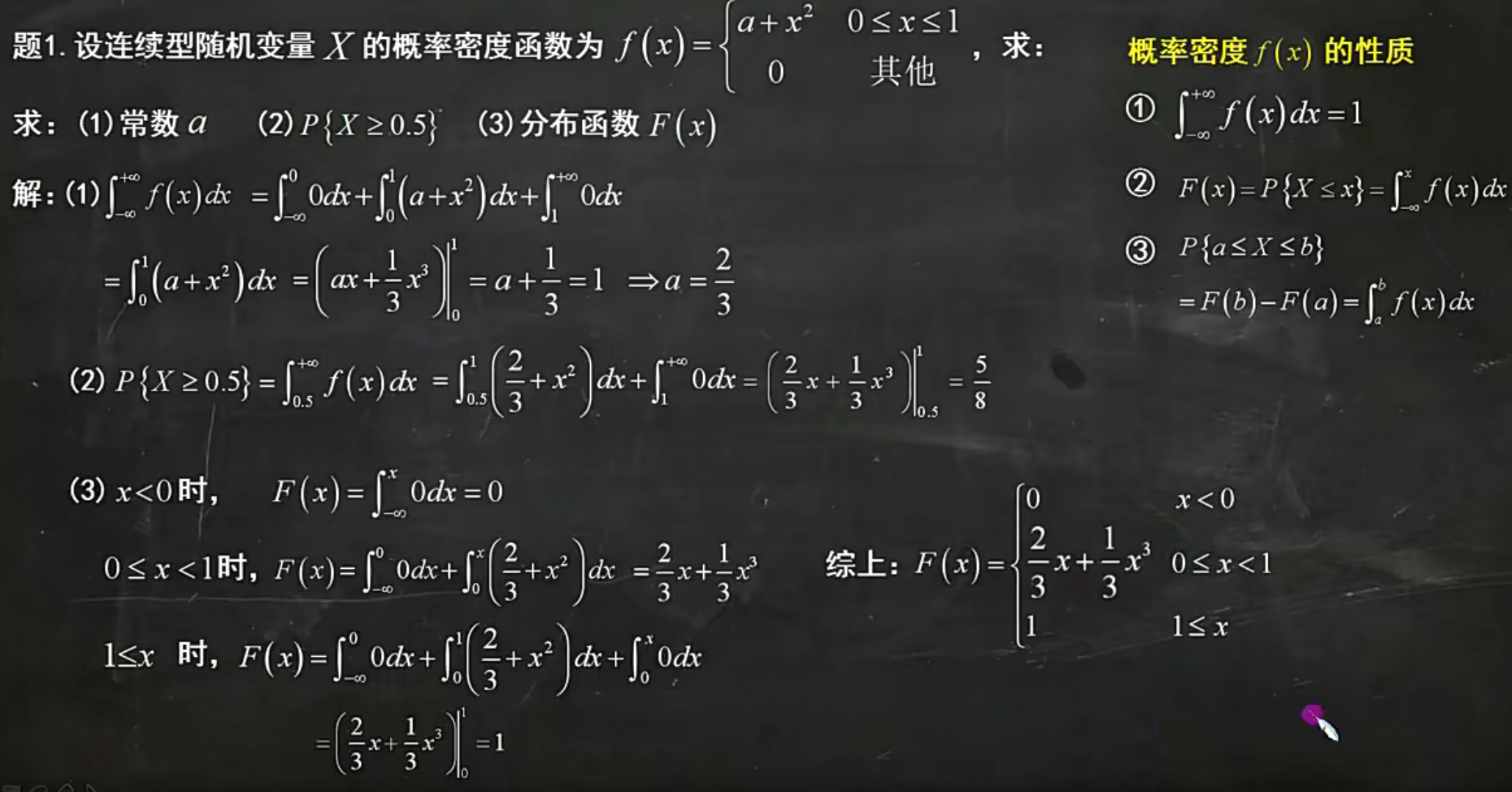
image-20230329140841753

已知Fx，求Fy

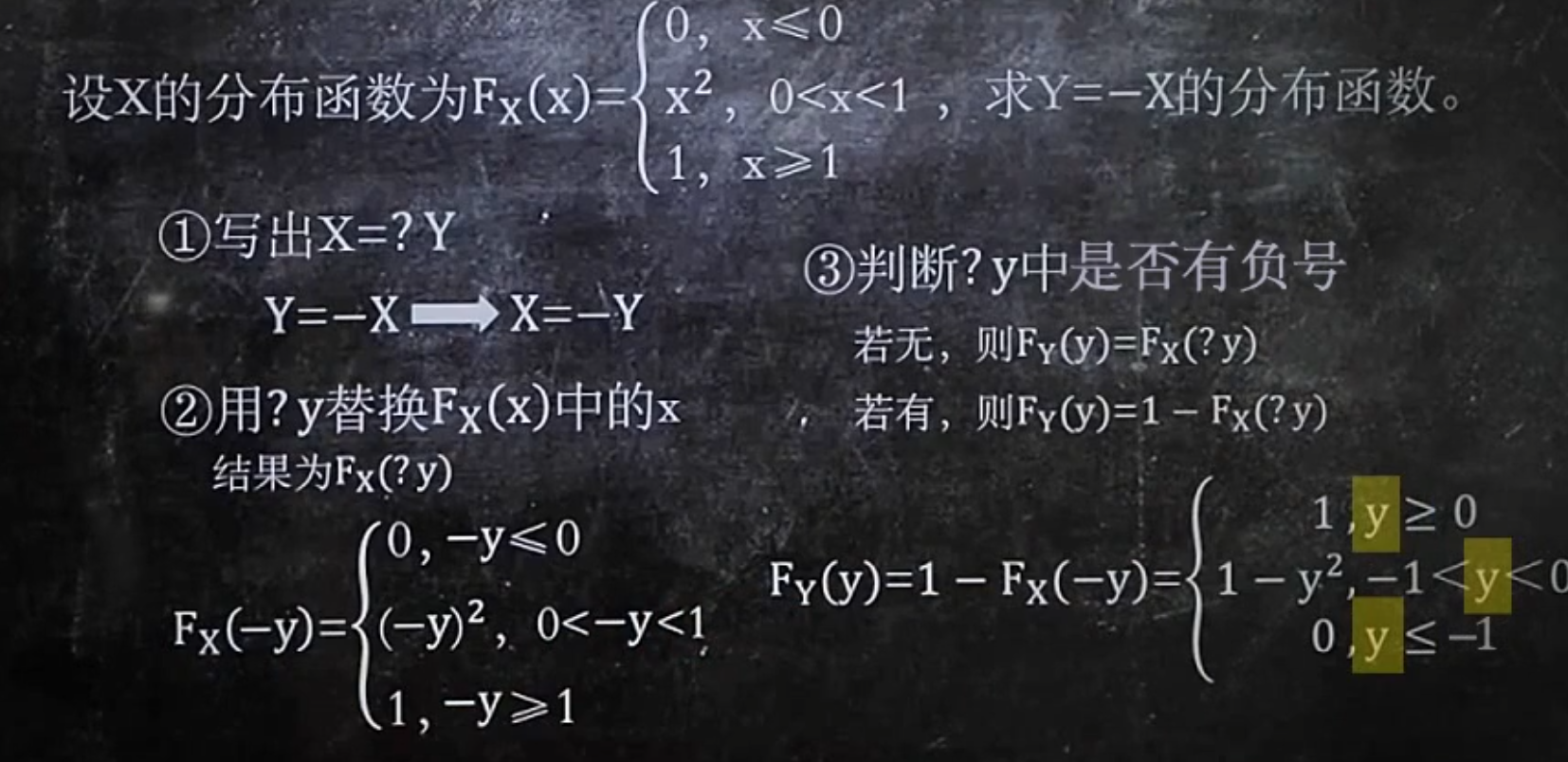
image-20230327220844354

已知fx，求fy

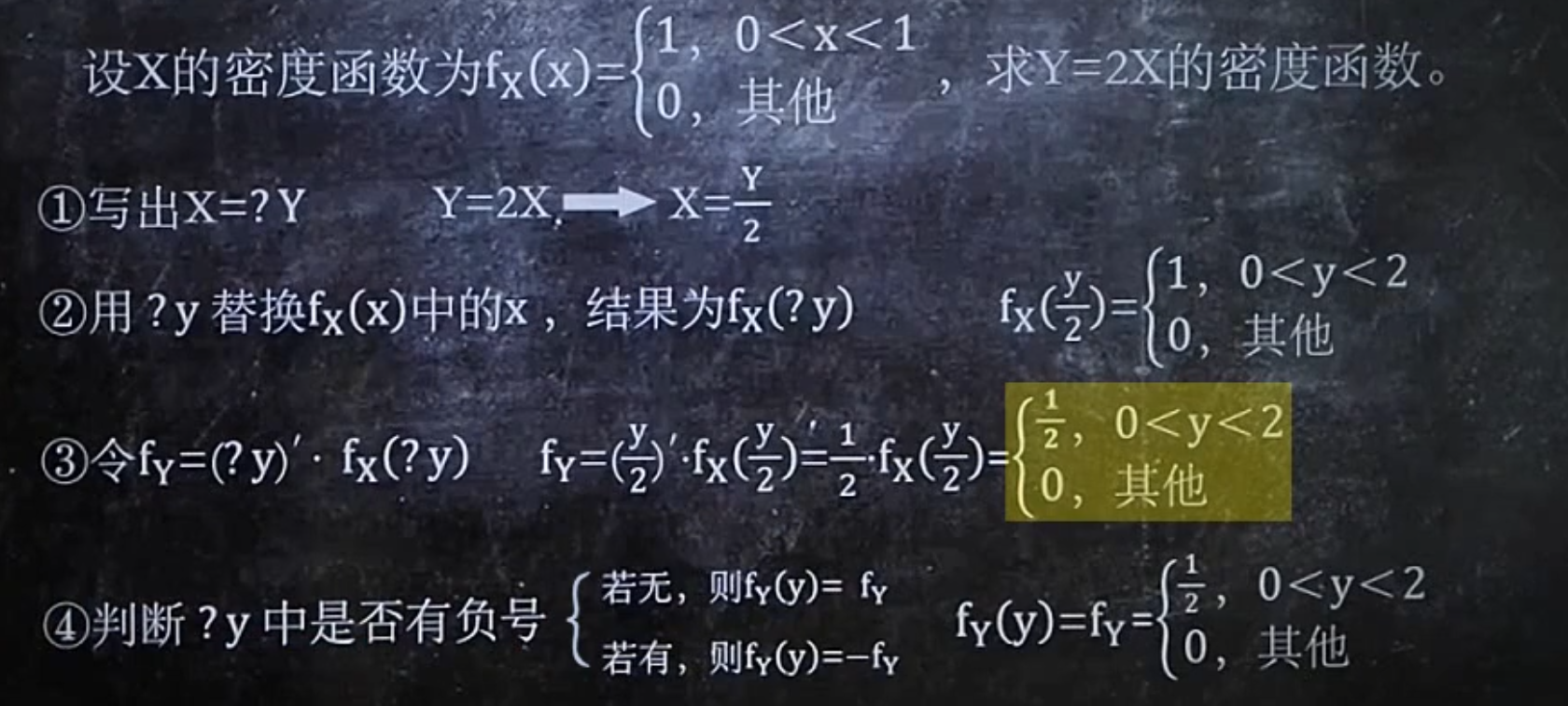
image-20230327221355112

连续性随机变量

为何最后f(y) = f[h(y)]*h^`^(y),我认为是因为f(x)->f(y)的过程其实就是先求积分转为F(x)，再替换为F(h(y))，最后求导可得，此时求导的时候也要求一次h(y)仅此而已。

image-20230329142225784

一般题型都这样做，大同小异

image-20230329143540370

五种分布

服从均匀分布，求概率

image-20230328212337054

image-20230328215320663

服从泊松分布，求概率

image-20230328212553117

image-20230328214943837

符合二项分布求概率

image-20230328212941656

image-20230328215357613

指数分布

指数分布的无记忆性

image-20230328220512982

二维离散随机变量

P{X=-1,Y=2} yu P{X <= Y}

image-20230328223437649

XY边缘分布律

image-20230328223522520

XY是否独立

一般在题目中要求验证，都是不独立的，不然你需要验证所有的组合，太麻烦了

image-20230328223733064

求Max分布律

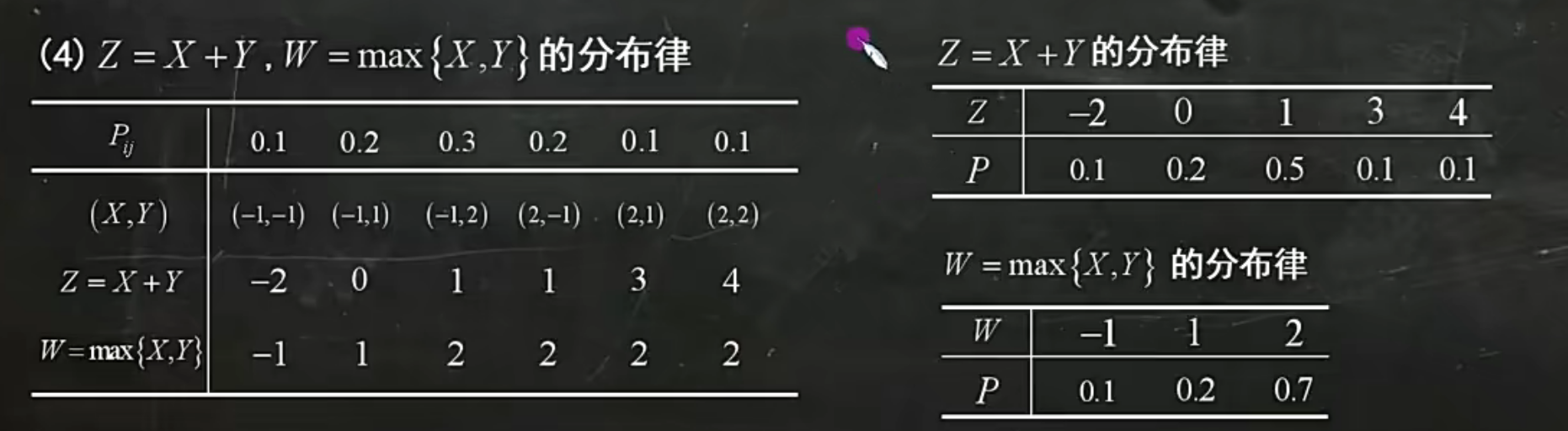
image-20230328223841935

二维随机变量

image-20230328223957930

二维连续随机变量

求联合概率密度

image-20230328224836299

求边缘概率密度

求谁的边缘概率密度，就把另外一个砍掉不出现

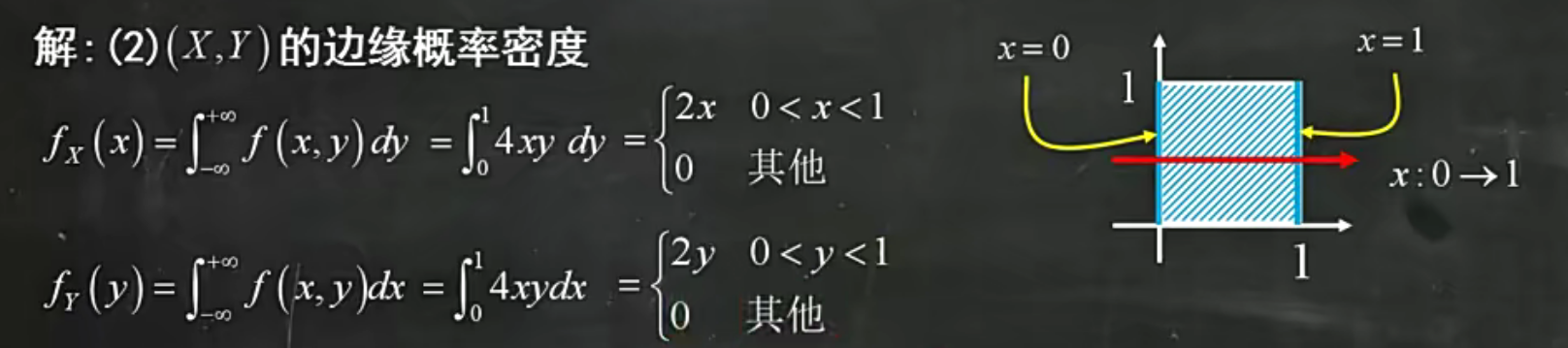
image-20230328225027748

条件密度概率

image-20230328225254467

独立性

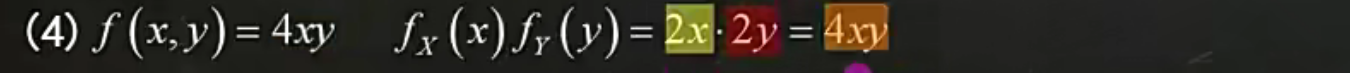
image-20230328225655531

更复杂的一道题

分区域

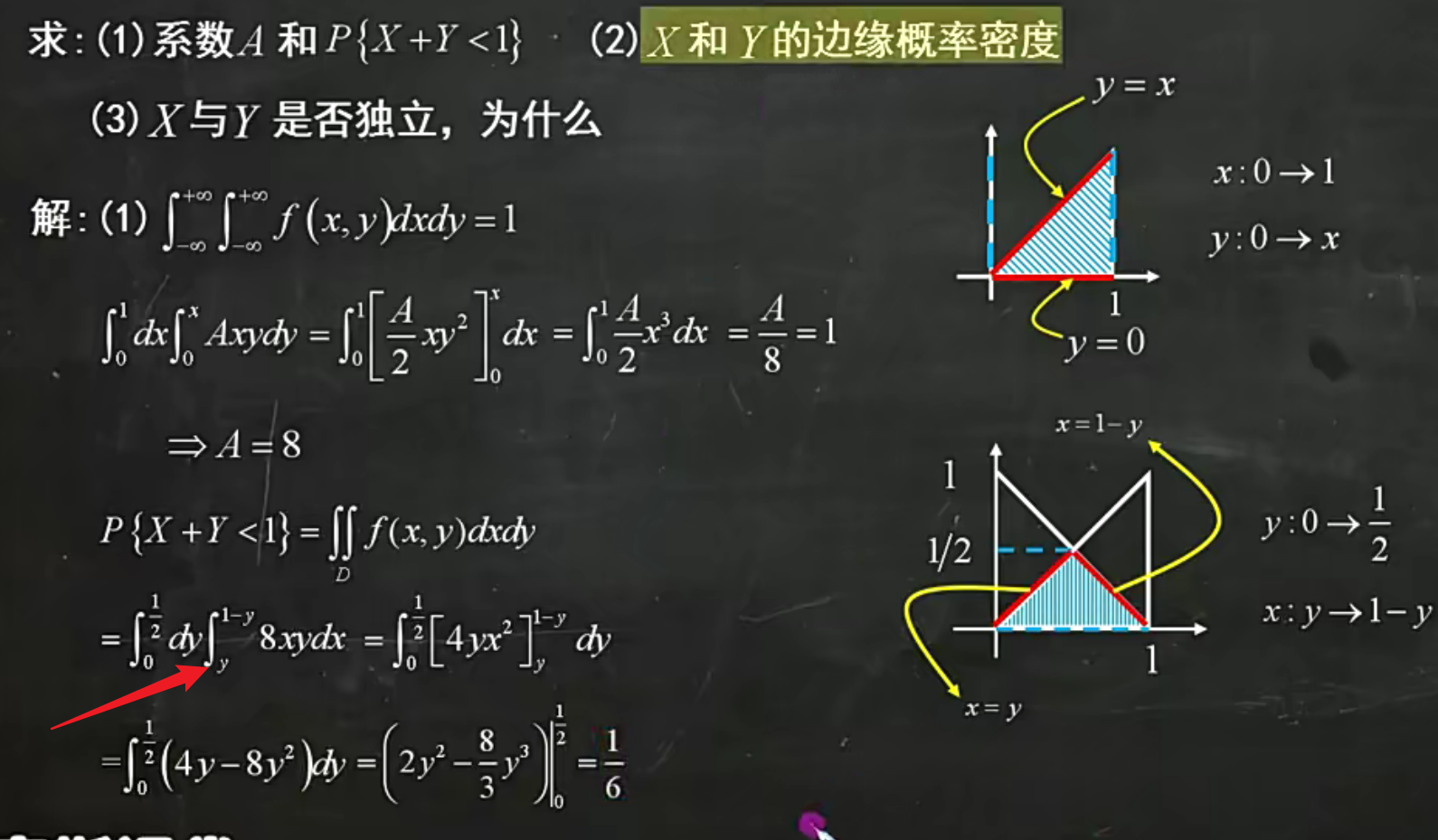
image-20230328230926724

划线求界

image-20230328231307253

求分布

Z=X+Y

image-20230329103331726

image-20230329103317456

Z=XY

image-20230329103627077

Z=max{X, Y}

image-20230329103840245

image-20230329103918707

noise0.15 2.75003 Eval：2.76743 15000：2.72753

noise0.2 2.70960 Eval：2.71937 15000：2.69329

image-20230328220121928