jjyaoao's Home

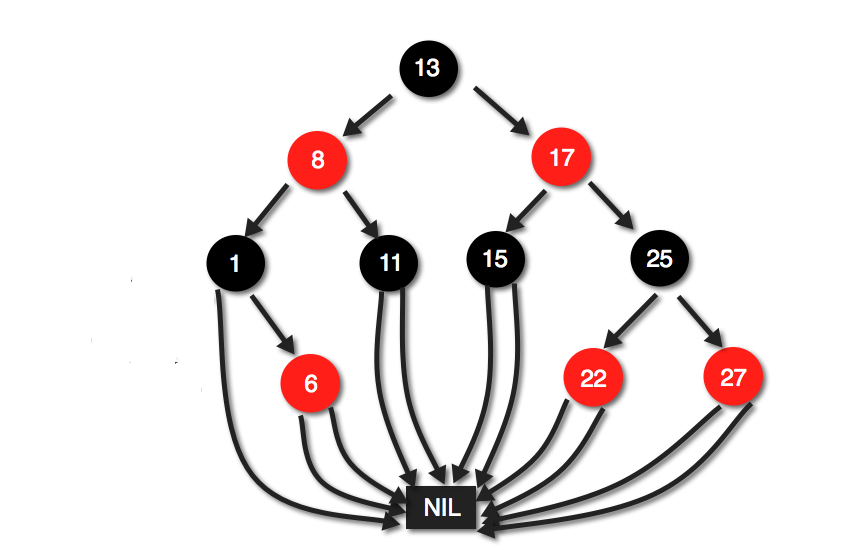
以下笔记为jjyaoao本人制作，欢迎借鉴学习和提出相关建议，转载需要标明出处www.jjyaoao.space 伸展树(Splay Tree)​ 虽然对于标准平衡树而言，AVL已经在条件上略有放松，但是这种平衡任然显得过于苛刻，就像一个小心谨慎走路的人，那么我们能否走的更潇洒一点呢？ ​ 也就是说，我们可否秉持一种更为宽泛的准则，并且从长远来看仍然不失一定的稳定性呢？ 逐层伸展局部性 自适应调整使刚被访问的节点往上走 逐层伸展 实例我们通过观察这个实例，发现这个过程是一个左右摇摆，逐渐伸展的过程 ​ 所以我们也称这个过程叫伸展，Splay ​ 然而就效率而言，这并不是最佳的选择，原因在于，他有最坏情况 最坏情况 ​ ​ 这也并不是令我们满意的，甚至离logn都相距甚远 ​ 不过好消息是，造成这一结果并不是伸展本身，而是我们伸展的方式，就好比画龙点睛，作为一条龙，目前的伸展策略已经相当完备，它所缺少的只是体现其灵魂的一只眼睛，没错，不是一双眼睛，仅仅是一只 双层伸展 子孙异侧 ...

https://oi-wiki.org/math/bit/https://oi-wiki.org/math/quick-pow/https://oi-wiki.org/math/number-theory/basic/https://oi-wiki.org/math/number-theory/prime/https://oi-wiki.org/math/number-theory/gcd/https://oi-wiki.org/math/number-theory/sqrt-decomposition/https://oi-wiki.org/math/number-theory/euler/https://oi-wiki.org/math/number-theory/sieve/https://oi-wiki.org/math/number-theory/bezouts/https://oi-wiki.org/math/number-theory/fermat/https://oi-wiki.org/math/number-theory/inverse/https://oi-wiki ...

以下笔记为jjyaoao本人制作，欢迎借鉴学习和提出相关建议，转载需要标明出处www.jjyaoao.space 二叉搜索树 寻关键码访问 有序性为了简单而言 节点 = 词条 = 关键码 单调性在微观上处处满足顺序性，宏观上每一个的垂直投影，满足单调性 ADT 查找 可以看到，和二分查找过程相仿 1234567template <typename T> BinNodePosi<T> & BST<T>::search ( const T & e ) { //在BST中查找关键码e0010 if ( !_root || e == _root->data ) { _hot = NULL; return _root; } //空树，或恰在树根命中0011 for ( _hot = _root; ; ) { //否则，自顶而下0012 BinNodePosi<T> & v = ( e < _hot->data ) ? _hot-&g ...

以下笔记为jjyaoao本人制作，欢迎借鉴学习和提出相关建议，转载需要标明出处www.jjyaoao.space 图概述邻接+关联此课程不讨论自环 无向+有向 路径+环路欧拉环路，所有的边可以拉通走一遍（恰好一次） 哈密尔顿环路，每一个顶点可以拉通走一次（恰好一次） 环：一条只有第一个和最后一个顶点重复的非空路径 邻接矩阵接口 邻接矩阵和关联矩阵在这堂课中，使用邻接矩阵来描述（尽管有些时候关联矩阵同样可以大显身手） 实例邻接矩阵在无向图，有向图，带权图中的表现形式 顶点和边顶点五角星部分后续遍历时详细介绍 入度，出度，也就是当前顶点和多少个别的顶点相互关联 边边需要有data记录自己携带的信息，对于带权网络，还需要记录权重，并且边也有含义，为了创建一条边，我们也需对相应的各项进行初始化设置即可 实现图(邻接矩阵)顶点集：由一组顶点所构成的向量 边集：由一组边所构成的向量，进而由这一组向量所构成的向量 每个顶点，最多可能与n条边相关，所以每个向量的长度也是n 总共可能就n个向量（每一个向量是E[0] [ ]) —-这n个向量构成一个边集 0是第0个顶点，后面是与他关联 ...

以下笔记为jjyaoao本人制作，欢迎借鉴学习和提出相关建议，转载需要标明出处www.jjyaoao.space 树应用 有根树 有序树凡是兄弟之间有明确次序的树，我们把它叫做有序树 任何一颗树中所含的边数 = 顶点数目-1 = 其中所有定点度数之和 这个结论之所以重要，是因为我们可以得到边数和顶点个数是同阶的 也就是说，如果一棵树的总体规模，如果可以度量为顶点数+边数，那么它从渐进的意义来讲，是与顶点个数同阶的，也就是我们后面评判一棵树的规模，可以以顶点的数目n作为参照 路径+环路这里我们用边的数目来代表它的路径长度 连通+无环 深度+层次 何时取等号？ 当节点v是深度最大的叶节点或祖先节点时，取等号 树的表示ADT接口 父节点 孩子节点 父亲+孩子整合了父亲 和 孩子的优点 长子+兄弟反观父亲+孩子出现的问题 根源在于每一个节点的出度是不尽相同的 解决方案：每一个节点均设两个引用 这种方式是 对树本质的深刻理解 二叉树有根有序树 真二叉树如果某一棵树原先度数是0，那么我们为他引入两个节点，如果原先度数是1，那么我们为他引入一个节点。 一方面从渐进的意义 ...

以下笔记为jjyaoao本人制作，欢迎借鉴学习和提出相关建议，转载需要标明出处www.jjyaoao.space 4.栈ADT接口 操作实例 实现 实际应用 进制转换手动实现 难点 思路 算法实现 convert1234567void convert ( Stack<char>& S, __int64 n, int base ) { //整数n的1<base<=16进制打印（迭代版）0002 char digit[] = "0123456789ABCDEF"; //数位符号，如有必要可相应扩充0003 while ( n > 0 ) { //由低到高，逐一计算出新进制下的各数位0004 S.push ( digit[ n % base ] ); //余数（当前位）入栈0005 n /= base; //n更新为其对base的除商0006 }0007 } //新进制下由高到低的各数位，自顶而下保存于栈S中 括号匹配问题描述判断括号是匹配还是失配 ...

以下笔记为jjyaoao本人制作，欢迎借鉴学习和提出相关建议，转载需要标明出处www.jjyaoao.space 3.列表从向量到列表没有前驱/后继的唯一节点称为首/末 从静态到动态 从秩到位置寻秩访问到循位置访问 列表所需模板类ListNode接口 1234567891011121314using Rank = int; //秩0002 template <typename T> struct ListNode;0003 template <typename T> using ListNodePosi = ListNode<T>*; //列表节点位置0004 template <typename T> struct ListNode { //列表节点模板类（以双向链表形式实现）0005 // 成员0006 T data; ListNodePosi<T> pred; ListNodePosi<T> succ; //数值、前驱、后继0007 // 构造函数0008 ListNode() ...

以下笔记为jjyaoao本人制作，欢迎借鉴学习和提出相关建议，转载需要标明出处www.jjyaoao.space 2.向量接口与实现 抽象数据类型：即自定义的class 数据结构：解决某类问题的可靠模板 ADT即为说明书，也就是接口 Vector Vector的底层实现 构造器与析构器 使用一次构造器，销毁一次 [] _elem，以便重新调用新的内存空间，_size还需要初始化哈，虽然好像int本身初始化就是0安。 copyFrom函数实现 可扩充容量静态 动态 算法与策略 无序向量插入 12345678910111213#include <iostream>#include "vector.h"template <typename T>Rank Vector<T>::insert(Rank r, T const& e) { expand(); for (int i = _size; i > r; i--) { _elem[i] = _elem[i - 1]; } _e ...

以下系列内容，是基于清华大学邓俊辉教授所授课程数据结构的笔记，本人结合PPT与自身感悟制成，算是学习后的填坑，仅当作学习笔记使用，欢迎借鉴学习和提出相关建议，转载需标明出处www.jjyaoao.space 1.序章 时间复杂度 最坏情况：以大O记号形式表示的时间复杂度，给出了一个算法的最坏情况，即–对于规模为n的任意输入，算法的运行时间都不会超过O(f(n)) 最好情况 ：大 Ω记号–>如果存在正的常数c和函数g(n)，对任意n>>2，有T(n) > c * g(n)，即认为：在n足够 大后，g(n)给出了T(n)的一个下界，记为： ​ T(n) =Ω (g(n)) 大 Θ记号–>存在正的常数c1和c2，以及函数h(n)，对任意n>>2，有 c1*h(n) < T(n) < c2 * h(n)，即认为：在n足够大后，h(n)给出了T(n)的一个确界，记为： ​ ...

本笔记用作个人学习和查漏补缺使用，欢迎借鉴学习，提出建议，转载需标注出处www.jjyaoao.space